TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Ex 1(c)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 1 Circle Ex 1(c) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Exercise 1(c)

I.

Question 1.
Find the equation of the tangent at P of the circle S = 0 where P and S are given by
(i) P = (7, -5), S ≡ x² + y² – 6x + 4y – 12
Solution:
P = (7, -5), S ≡ x² + y² – 6x + 4y – 12
Comparing the equation x² + y² – 6x + 4y – 12 =0 with the general equation we have
2g = -6, 2f = 4 and c = -12
g = -3, f = 2, c = -12
∴Equation of tangent at P(x₁, y₁) to the circle S = 0 is given by xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(7) + y(-5) – 3(x + 7) + 2(y – 5) – 12 = 0
⇒ 4x – 3y – 43 = 0

(ii) P = (-1, 1), S ≡ x² + y² – 6x + 4y – 12
Solution:
P = (-1, 1), S ≡ x² + y² – 6x + 4y – 12
Comparing the equation x² + y² – 6x + 4y – 12 = 0 with the general equation S = 0, we get
2g = -6, 2f = 4 and c = -12
g = -3, f = 2, c = -12
∴ Equation of tangent at P(x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(-1) + y(1) – 3(x – 1) + 2(y + 1) – 12 = 0
⇒ -4x + 3y – 7 = 0
⇒ 4x – 3y + 7 = 0

(iii) P = (-6, -9), S ≡ x² + y² + 4x + 6y – 39
Solution:
Given P = (-6, -9) = (x₁, y₁) and S ≡ x² + y² + 4x + 6y – 39 = 0
Also 2g = 4, 2f = 6 and c = -39
g = 2, f = 3, c = -39
∴ Equation of tangent at P(x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(-6) + y(-9) + 2(x – 6) + 3(y – 9) – 39 = 0
⇒ -4x – 6y – 78 = 0
⇒ 2x + 3y + 39 = 0

(iv) P = (3, 4), S ≡ x² + y² – 4x – 6y + 11
Solution:
Given P = (3, 4) = (x₁, y₁) and S ≡ x² + y² – 4x – 6y + 11 = 0
2g = -4, 2f = -6 and c = 11
g = -2, f = -3, c = 11
∴ Equation of tangent at P(x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ 3x + 4y – 2(x + 3) – 3(y + 4) + 11 = 0
⇒ x + y – 7 = 0

Question 2.
Find the equation of normal at P of the circle S = 0 where P and S are given by
(i) P = (3, -4), S ≡ x² + y² + x + y – 24
Solution:
P = (3, -4) = (x₁, y₁) and S ≡ x² + y² + x + y – 24 = 0
we have g = \(\frac{1}{2}\), f = \(\frac{1}{2}\), c = -24
∴ Equation of normal at (x₁, y₁) is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
⇒ (x – 3) (-4 + \(\frac{1}{2}\)) – (y + 4) (3 + \(\frac{1}{2}\)) = 0
⇒ (x – 3) + (-7) – (y + 4) (7) = 0
⇒ -7x – 7y – 7 = 0
⇒ x + y + 1 = 0

(ii) P = (3, 5), S ≡ x² + y² – 10x – 2y + 6
Solution:
P = (3, 5) = (x₁, y₁) and S ≡ x² + y² – 10x – 2y + 6 = 0
2g = -10, 2f = -2, c = 6
g = -5, f = -1
∴ Equation of normal at (x₁, y₁) to S = 0 is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
⇒ (x – 3) (5 – 1) – (y – 5) (3 – 5) = 0
⇒ 4(x – 3) + 2(y – 5) = 0
⇒ 4x + 2y – 22 = 0
⇒ 2x + y – 11 = 0

(iii) P = (1, 3), S ≡ 3(x² + y²) – 19x – 29y + 76
Solution:
P = (1, 3) = (x₁, y₁) and S ≡ \(x^2+y^2-\frac{19}{3} x-\frac{29}{3} y+\frac{76}{3}=0\)
\(2 g=-\frac{19}{3}, 2 f=-\frac{29}{3}, c=\frac{76}{3}\)
\(g=-\frac{19}{6}, f=-\frac{29}{3}\)
∴ Equation of normal at (x₁, y₁) to S = 0 is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
⇒ (x – 1) (3 – \(\frac{29}{6}\)) – (y – 3) (1 – \(\frac{19}{6}\)) = 0
⇒ (x – 1) (\(\frac{-11}{6}\)) – (y – 3) (\(\frac{-13}{6}\)) = 0
⇒ -11(x – 1) + 13(y – 3) = 0
⇒ -11x + 13y – 28 = 0
⇒ 11x – 13y + 28 = 0

(iv) P = (1, 2), S ≡ x² + y² – 22x – 4y + 25
Solution:
P = (1, 2) = (x₁, y₁) and S ≡ x² + y² – 22x – 4y + 25 = 0
2g = -22, 2f = -4 and c = 25
g = -11, f = -2
∴ Equation of normal at (x₁, y₁) to S = 0 is (x – x₁) (y₁ + f) – (y – y₁) (x₁ + g) = 0
⇒ (x – 1) (2 – 2) – (y – 2) (1 – 11) = 0
⇒ -(y – 2) (-10) = 0
⇒ y – 2 = 0
⇒ y = 2

II.

Question 1.
Find the length of the chord intercepted by the circle x² + y² – x + 3y – 22 = 0 on the line y = x – 3. (May. ’11)
Solution:
Given equation of circle is x² + y² – x + 3y – 22 = 0
comparing with general equation S = 0, we get
2g = -1, 2f = 3 and c = -22
g = \(-\frac{1}{2}\), f = \(\frac{3}{2}\)

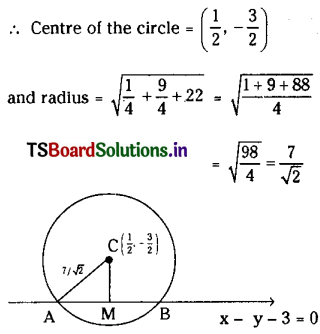
Given line is y = x – 3 and L = x – y – 3 = 0.
AB is the chord intercepted by the line L = 0 on the circle.
CM = Perpendicular distance from C\(\left(\frac{1}{2},-\frac{3}{2}\right)\) to x – y – 3 = 0.

∴ AM = √24
and the length of the chord AB = 2 AM
= 2√24
= 4√6 units

Question 2.
Find the length of the chord intercepted by the circle x² + y² – 8x – 2y – 8 = 0 on the line x + y + 1 = 0.
Solution:
The Centre of the given circle is C(4, 1)
and radius = \(\sqrt{16+1+8}\) = 5

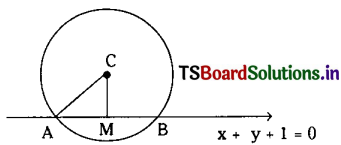
AB is the chord intercepted by the line x + y + 1 = 0 on the circle.
CM = Perpendicular distance from C(4, 1) to x + y + 1 = 0.
∴ CM = \(\left|\frac{4+1+1}{\sqrt{1^2+1^2}}\right|=\frac{6}{\sqrt{2}}\) = 3√2
In the ∆ACM, we have AM² = AC² – CM²
= 25 – 18
= 7
∴ AM = √7
∴ Length of the chord AB = 2 AM = 2√7 units.

Question 3.
Find the length of the chord formed by x² + y² = a² on the line x cos α + y sin α = p.
Solution:
Centre of the circle x² + y² = a² is C(0, 0) and radius = ‘a’

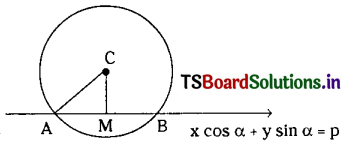
CM = Perpendicular distance from the centre C(0, 0) to the line x cos α + y sin α = p.
∴ CM = \(\left|\frac{0(\cos \alpha)+0(\sin \alpha)-p}{\sqrt{\cos ^2 \alpha+\sin ^2 \alpha}}\right|\) = p
In the ∆ACM, we have AM² = AC² – CM² = a² – p²
∴ AM = \(\sqrt{a^2-p^2}\)
and length of the chord AB = 2.AM = 2\(\sqrt{a^2-p^2}\)

Question 4.
Find the equation of the circle with centre (2, 3) and touch the line 3x – 4y + 1 = 0.
Solution:

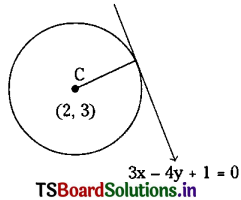
If a given line touches the circle, then the perpendicular distance from the centre to the line is equal to the radius of the circle.
∴ Radius = perpendicular distance from C(2, 3) to the line 3x – 4y + 1 = 0.
∴ Radius = \(\left|\frac{3(2)-4(3)+1}{\sqrt{9+16}}\right|=\left|\frac{-5}{5}\right|\) = 1
∴ The equation of a circle with radius ‘1’ and centre (2, 3) is given by (x – 2)² + (y – 3)² = 12
∴ x² + y² – 4x – 6y + 12 = 0

Question 5.
Find the equation of the circle with centre (-3, 4) and touching y-axis.
Solution:

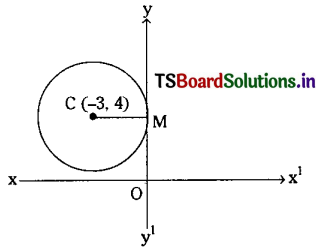
Equation of y-axis is x = 0 and given that the centre C = (-3, 4)
CM = perpendicular distance from C to y = axis
i.e., x = 0,
= |-3|
= 3
∴ The equation of a circle with centre (-3, 4) and radius ‘3’ is given by (x + 3)² + (y – 4)² = 9
x² + y² + 6x – 8y + 16 = 0

Question 6.
Find the equations of tangents to the circle x² + y² – 8x – 2y + 12 = 0 at the points whose ordinates are 1.
Solution:
Let P(x₁, y₁) be a point on the circle x² + y² – 8x – 2y + 12 = 0
given that ordinates of points is ‘1’ i.e., y₁ = 1
∴ \(x_1^2\) + 1 – 8x₁ – 2 + 12 – 0
\(x_1^2\) – 8x₁ + 11 = 0 which is a quadratic equation.

∴ Points on the circle are P = (4 + √5, 1) and Q = (4 – √5, 1)
Equation of tangent at P(4 + √5, 1) is by the formula xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(4 + √5) + y – 4(x + 4 + √5) – 1(y + 1) + 12 = 0
⇒ 4x + √5x + y – 4x – 16 – 4√5 – y – 1 + 12 = 0
⇒ √5x – 4√5 – 5 = 0
⇒ x – 4 – √5 = 0
⇒ x = 4 + √5
Similarly the equation of tangent at Q(4 – √5, 1) is
x(4 – √5) + y – 4(x + 4 – √5) – 1(y + 1) + 12 = 0
⇒ 4x – √5x + y – 4x – 16 + 4√5 – y – 1 + 12 = 0
⇒ -√5x + 4√5 – 5 = 0
⇒ x – 4 + √5 = 0
⇒ x = 4 – √5
∴ The equation of tangents of the given circle at the points when ordinates are ‘1’ are given by x = 4 + √5, x = 4 – √5

Question 7.
Find the equations of the tangents of the circle x² + y² – 10 = 0 at the points whose abscissae are 1.
Solution:
Let P(x1, y1) be a point on the circle x² + y² – 10 = 0
given that abscissae are ‘1’
i.e., x₁ = 1
1 + \(y_1^2\) – 10 = 0
y₁ = ±3
Hence the points on the circle are P(1, 3), Q(1, -3).
Equation of tangent at the point P(1, 3) on the circle x² + y² – 10 = 0 is xx₁ + yy₁ – 10 = 0
x + 3y – 10 = 0
Similarly equation of tangent at the point Q(1, -3) on the circle x² + y² – 10 = 0 is xx₁ + yy₁ – 10 = 0
x – 3y – 10 = 0

III.

Question 1.
If x² + y² = c² and \(\frac{x}{a}+\frac{y}{b}=1\) intersect at A and B then find \(\overline{\mathbf{A B}}\). Hence deduce the condition that the line touches the circle.
Solution:
Given x² + y² = c² ……..(1)
and \(\frac{x}{a}+\frac{y}{b}=1\)
⇒ bx + ay – ab = 0 ……….(2)
Centre of the circle C = (0, 0) and the radius of the circle CA = ‘c’.

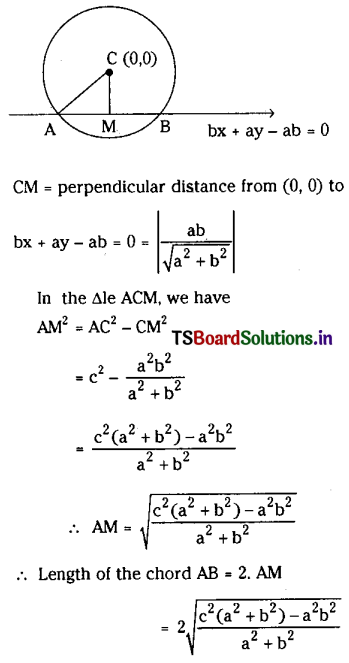
If the line touches the circle that is if the line becomes a tangent to the circle, then the perpendicular distance from (0, 0) to the given line is equal to the radius of the circle.

Question 2.
The line y = mx + c and the circle x² + y² = a² intersect at A and B and if AB = 2λ then show that c² = (1 + m²) (a² – λ²).
Solution:

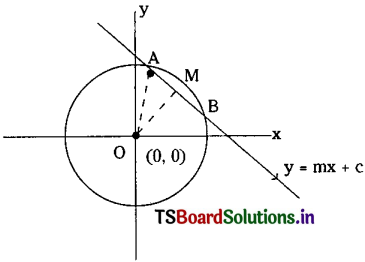
Centre of the circle C = (0, 0).
The line y = mx + c intersects the circle at A and B.
OM = Perpendicular distance from (0, 0) to mx – y + c = 0

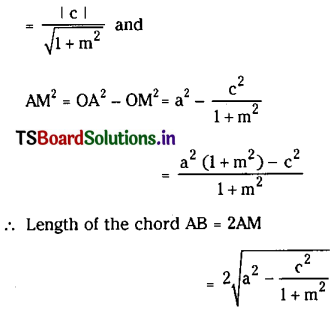
Question 3.
Find the equation of the circle with centre (-2, 3) cutting a chord of length 2 units on 3x + 4y + 4 = 0. (Mar. ’11)
Solution:

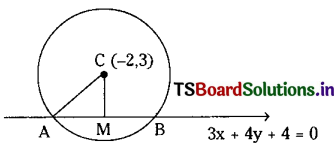
Given the length of the chord AB = 2 units
∴ AM = 1 unit
CM = Perpendicular distance from the centre (-2, 3) to the line 3x + 4y + 4 = 0.
= \(\left|\frac{3(-2)+4(3)+4}{\sqrt{3^2+4^2}}\right|=\left|\frac{-6+12+4}{5}\right|=\frac{10}{5}=2\)
In the ΔACM, we have
AC² = AM² + CM²
= 1 + 4
= 5
∴ The equation of a circle with centre (-2, 3) and radius √5 units is (x + 2)² + (y – 3)² = 5
⇒ x² + 4x + 4 + y² – 6y + 9 = 5
⇒ x² + y² + 4x – 6y + 8 = 0

Question 4.
Find the equation of the tangent and normal at (3, 2) of the circle x² + y² – x – 3y – 4 = 0.
Solution:
Let S = x² + y² – x – 3y – 4 = 0 be the given circle, comparing with the general equation.
2g = -1, 2f = 3 and c = -4
∴ Equation of tangent at (x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
⇒ x(3) + y(2) – \(\frac{1}{2}\)(x + 3) – \(\frac{3}{2}\)(y + 2) – 4 = 0
⇒ 3x + 2y – \(\frac{1}{2}\)(x + 3) – \(\frac{3}{2}\)(y + 2) – 4 = 0
⇒ 6x + 4y – x – 3 – 3y – 6 – 8 = 0
⇒ 5x + y – 17 = 0
Equation of normal at (x₁, y₁) to S = 0 is (x – x₁) (y₁ + f) – (y – y₁)(x₁ + g) = 0
⇒ (x – 3) (2 – \(\frac{3}{2}\)) – (y – 2) (3 – \(\frac{1}{2}\)) = 0
⇒ (x – 3) (\(\frac{1}{2}\)) – (y – 2) (\(\frac{5}{2}\)) = 0
⇒ x – 3 – 5y + 10 = 0
⇒ x – 5y + 7 = 0

Question 5.
Find the equation of the tangent and normal at (1, 1) of the circle 2x² + 2y² – 2x – 5y + 3 = 0.
Solution:
Given equation of circle is x² + y² – x – \(\frac{5}{2}\)y + \(\frac{3}{2}\) = 0
2g = -1, 2f = \(-\frac{5}{2}\) and c = \(\frac{3}{2}\)
The point (1, 1) = (x₁, y₁)
The equation of the tangent at (x₁, y₁) to S = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0

Question 6.
Prove that the tangent at (3, -2) of the circle x² + y² = 13 touches the circle x² + y² + 2x – 10y – 26 = 0 and find its point of contact
Solution:
The equation of tangent at (3, -2) to the circle x² + y² = 13 is x(3) + y(-2) – 13 = 0
3x – 2y – 13 = 0 ………..(1) [∵ By the formula, xx₁ + yy₁ – a2 = 0]
To show that (1) touches the circle x² + y² + 2x – 10y – 26 = 0.
We have to show that the perpendicular distance from the centre of the circle (-1, 5) to the line 3x- 2y – 13 = 0 is equal to the radius of the circle which is \(\sqrt{1+25+26}=\sqrt{52}\).
∴ The perpendicular distance from (-1, 5) to the line 3x – 2y – 13 = 0 is \(\left|\frac{3(-1)-2(5)-13}{\sqrt{9+4}}\right|\)
= \(\left|\frac{-26}{\sqrt{13}}\right|\)
= 2√13
= √52
Hence the tangent 3x – 2y – 13 = 0 touches the circle x² + y² + 2x – 10y – 26 = 0
Let P(h, k) be the point of contact between the tangent and the circle.

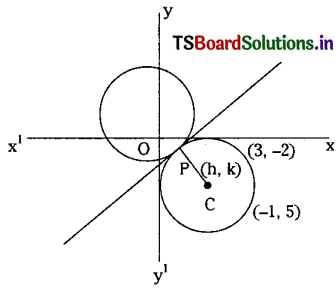
Then P(h, k) will be the foot of the perpendicular drawn from C(-1, 5) to 3x – 2y – 13 = 0.
So by the formula

∴ The point of contact of the line (1) to the circle x² + y² + 2x – 10y – 26 = 0 is (5, 1).

Question 7.
Show that the tangent at (-1, 2) of the circle x² + y² – 4x – 8y + 7 = 0 touches the circle x² + y² + 4x + 6y = 0 and also finds its point of contact. (New Model Paper and June ’10)
Solution:
Let S = x² + y² – 4x – 8y + 7 = 0 and S’ = x² + y² + 4x + 6y = 0,
comparing S = 0 with x² + y² + 2gx + 2fy + c = 0
we have 2g = -4, 2f = -8, c = 7
g = -2, f = -4, c = 7
Equation of tangent at (-1, 2) to the circle S = 0 is xx1 + yy1 + g(x + x1) + f(y + y1) + c = 0
⇒ x(-1) + y(2) + (-2)(x – 1) – 4(y + 2) + 7 = 0
⇒ -x + 2y – 2x + 2 – 4y – 8 + 7 = 0
⇒ -3x – 2y + 1 = 0
⇒ 3x + 2y – 1 = 0 ……….(1)
Centre of the circle S’ = x² + y² + 4x + 6y = 0 is (-2, -3)
If (1) touches S’ = 0, then the perpendicular distance from (-2, -3) to the line 3x + 2y -1 = 0 is equal to the radius of the circle.
Radius = \(\sqrt{4+9}=\sqrt{13}\)
Perpendicular distance from (-2, -3) to 3x + 2y – 1 = 0 is equal to \(\left|\frac{3(-2)+2(-3)-1}{\sqrt{9+4}}\right|=\left|\frac{-6-6-1}{\sqrt{13}}\right|=\sqrt{13}\)
Hence tangent at (-1, 2) to the circle S = 0 touches the circle S’ = 0.
Let P(h, k) be the point of contact of (1) and S’ = 0.
Then P(h, k) will be the foot of the perpendicular drawn from the centre (-2, -3) to the line 3x + 2y – 1 = 0.
By the formula

∴ The point of contact = (1, -1)

Question 8.
Find the equations of tangents to the circle x² + y² – 4x + 6y – 12 = 0 which are parallel to x + y – 8 = 0.
Solution:
Let S = x² + y² – 4x + 6y – 12 = 0 and comparing with x² + y² + 2gx + 2fy + c = 0 we get
g = -2, f = 3, c = -12
Centre of the circle = (2, -3)
and radius = \(\sqrt{4+9+12}\) = 5
The equation of any line parallel to x + y – 8 = 0 is of the form x + y + k = 0.
So the perpendicular distance from (2, -3) to x + y + k = 0 is equal to the radius.
∴ \(\left|\frac{2-3+k}{\sqrt{2}}\right|\) = 5
⇒ \(\left|\frac{k-1}{\sqrt{2}}\right|\) = 5
⇒ k – 1 = ±5√2
⇒ k = 1 ± 5√2
The equations of tangents to the circle S = 0 which are parallel to the line x + y – 8 = 0 are x + y + (1 ± 5√2) = 0.

Question 9.
Find the equations of the circle x² + y² + 2x – 2y – 3 = 0 which are perpendicular to 3x – y + 4 = 0.
Solution:
Centre of the circle x² + y² + 2x – 2y – 3 = 0 is (-1, 1) and radius = \(\sqrt{1+1+3}=\sqrt{5}\)
Equation of any line perpendicular to 3x – y + 4 = 0 is x + 3y + k = 0
If this is a tangent to the above circle then the perpendicular distance from (-1, 1) to the line x + 3y + k = 0 is equal to radius √5.
∴ \(\left|\frac{-1+3+\mathbf{k}}{\sqrt{1+9}}\right|\) = √5
⇒ \(\left|\frac{k+2}{\sqrt{10}}\right|\) = √5
⇒ k + 2 = ±5√2
⇒ k = -2 ± 5√2
∴ Equations of required tangents is x + 3y – 2 ± 5√2 = 0.

Question 10.
Find the equation of the tangents to the circle x² + y² – 4x – 6y + 3 = 0 which makes an angle of 45° with the X-axis.
Solution:
Centre of the circle x² + y² – 4x – 6y + 3 = 0 is (2, 3)
and radius = \(\sqrt{4+9-3}=\sqrt{10}\)
Since the tangents make an angle of 45° with X-axis we have
m = tan 45° = 1.
∴ The equation of tangent will be y = x + c
x – y + c = 0 ……….(1)
The perpendicular distance from (2, 3) to x – y + c = 0is equal to the radius of circle
∴ \(\left|\frac{2-3+c}{\sqrt{1+1}}\right|\) = √10
⇒ \(\left|\frac{c-1}{\sqrt{2}}\right|\) = √10
⇒ c – 1 = ±2√5
⇒ c = 1 ± 2√5
∴ Equations of required tangents are x – y + (1 ± 2√5) = 0

Question 11.
Find the equation of the circle passing through (-1, 0) and touching the line x + y – 7 = 0 at (3, 4).
Solution:

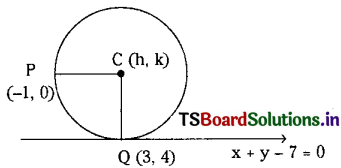
Let the circle passes through P(-1, 0) and touching the line x + y – 7 = 0 …….(1)
at Q(3, 4), suppose centre of the circle be C = (h, k)
Then PC = PQ
⇒ PC² = PQ²
⇒ (h + 1)² + k² = (h – 3)² + (k – 4)²
⇒ h² + 2h + 1 + k² = h² – 6h + 9 + k² – 8k + 16
⇒ 8h + 8k – 24 = 0
⇒ h + k – 3 = 0 ……..(2)
Slope of the line x + y – 7 = 0 is -1
and slope of CQ is = \(\frac{\mathrm{k}-4}{\mathrm{~h}-3}\)
Since CQ is perpendicular to the line x + y – 7 = 0
we have a product of slopes = -1
∴ (\(\frac{\mathrm{k}-4}{\mathrm{~h}-3}\)) (-1) = (-1)
⇒ k – 4 = h – 3
⇒ h – k + 1 = 0 ……….(3)
Solving (2) and (3)
2h – 2 = 0
⇒ h = 1
and -k + 2 = 0
⇒ k = 2
∴ Centre of the circle C(h, k) = C(1, 2)
and radius PC = \(\sqrt{(1+1)^2+(2-0)^2}\) = √8
Hence equation of a circle with centre (1, 2) and radius √8 is given by (x – 1)² + (y – 2)² = 8
⇒ x² – 2x + 1 + y² – 4y + 4 = 8
⇒ x² + y² – 2x – 4y – 3 = 0

Question 12.
Find the equation of the circle passing through (1, -1) touching the lines 4x + 3y + 5 = 0 and 3x – 4y – 10 = 0.
Solution:
Given lines are
4x + 3y + 5 = 0 ……..(1)
3x – 4y – 10 = 0 ………(2)
Since the circle touches the given lines which are perpendicular, centre of the circle lies on the bisectors of angles between the given lines.
The bisectors of angles between the given lines are
\(\frac{4 x+3 y+5}{\sqrt{16+9}} \pm \frac{3 x-4 y-10}{\sqrt{16+9}}=0\)
⇒ (4x + 3y + 5) ± (3x – 4y – 10) = 0
⇒ 4x + 3y + 5 + 3x – 4y – 10 = 0
⇒ 7x – y – 5 = 0 ……….(3)
or
4x + 3y + 5 – 3x + 4y + 10 = 0
⇒ x + 7y + 15 = 0 ………(4)
From (3) we have y = 7x – 5
and from (4), x = -(7y + 15)
If the centre lies on y = 7x – 5 then the centre will be of the form (k, 7k – 5).
∴ The perpendicular distance from (k, 7k – 5) to the line (1) is equal to the radius of the circle.
∴ \(\left|\frac{4 k+3(7 k-5)+5}{\sqrt{16+9}}\right|=\sqrt{(k-1)^2+(7 k-5+1)^2}\)
⇒ \(\frac{|4 k+21 \mathrm{k}-10|}{5}=\sqrt{(\mathrm{k}-1)^2+(7 \mathrm{k}-4)^2}\)
⇒ \(\frac{|25 k-10|}{5}=\sqrt{k^2-2 k+1+49 k^2-56 k+16}\)
⇒ |5k – 2| = \(\sqrt{50 k^2-58 k+17}\)
⇒ (5k – 2)² = 50k² – 58k + 17
⇒ 25k² – 20k + 4 = 50k² – 58k + 17
⇒ 25k² – 38k + 13 = 0
⇒ 25k² – 25k – 13k + 13 = 0
⇒ 25k(k – 1) – 13(k – 1) = 0
⇒ k = 1 or k = \(\frac{13}{25}\)
when k = 1, centre of the circle is [1, 7(1) – 5] = (1, 2)
and radius of the centre = \(\sqrt{(1-1)^2+(2+1)^2}\) = 3
∴ Equation of required circle is (x – 1)² + (y – 2)² = 3²
⇒ x² + y² – 2x – 4y – 4 = 0

Question 13.
Show that x + y + 1 = 0 touches the circle x² + y² – 3x + 7y + 14 = 0 and find its point of contact. (May ’09)
Solution:
The equation of the given circle is x² + y² – 3x + 7y + 14 = 0 ………(1)
If the line x + y + 1 = 0 ……..(2) touches the circle (1)
then the perpendicular distance from the centre of the circle C\(\left(\frac{3}{2},-\frac{7}{2}\right)\) to the line x + y + 1 = 0 is equal to the radius of the circle.
Radius of the given circle = \(\sqrt{\frac{9}{4}+\frac{49}{4}-14}=\sqrt{\frac{2}{4}}=\frac{1}{\sqrt{2}}\)
Perpendicular distance from C\(\left(\frac{3}{2},-\frac{7}{2}\right)\) to the line x + y + 1 = 0 is \(\left|\frac{\frac{3}{2}-\frac{7}{2}+1}{\sqrt{1^2+1^2}}\right|=\left|-\frac{1}{\sqrt{2}}\right|=\frac{1}{\sqrt{2}}\)
Hence circle (1) touches line (2).
Let P(h, k) be the point of contact between the circle (1) and line (2).
Then P(h, k) will be the foot of the perpendicular drawn from C\(\left(\frac{3}{2},-\frac{7}{2}\right)\) to the line x + y + 1 = 0.
∴ By the formula

∴ The point of contact of the given line with the circle (1) is (2, -3).