TS Inter 2nd Year

Students must practice this TS Intermediate Maths 2B Solutions Chapter 6 Integration Ex 6(f) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Exercise 6(f)

I. Evaluate the following integrals.

Question 1.
∫e^x (1 + x²) dx
Solution:
∫e^x (1 + x²) dx = ∫(e^x + e^x x²) dx
= ∫e^x dx + ∫e^x x² dx
= e^x + x² e^x – ∫2x e^x dx
= e^x + x² e^x – [2x e^x – ∫2e^x dx]
= e^x + x² e^x – 2x e^x + 2e^x + c
= e^x [1 + x² – 2x + 2] + c
= e^x (x² – 2x + 3) + c
[Integration by parts ∫uv dx = u∫v dx – ∫(\(\frac{\mathrm{d}}{\mathrm{dx}}\)(u) ∫v dx) is used]

Question 2.
∫x² e^-3x dx
Solution:
Use integration by parts successively using u = x² and v = e^-3x then

Question 3.
∫x³ e^ax dx
Solution:

II.

Question 1.
Show that ∫xⁿ e^-x dx = -xⁿ e^-x + n ∫x^n-1 e^-x dx
Solution:
∫xⁿ e^-x dx using integration by parts
= xⁿ (e^-x) – ∫n x^n-1 (-e^-x) dx
= -xⁿ e^-x + n∫x^n-1 e^-x dx

Question 2.
If I_n = ∫cosⁿx dx, then show that I_n = \(\frac{1}{n} \cos ^{n-1} x \sin x+\frac{n-1}{n} I_{n-2}\)
Solution:

III.

Question 1.
Obtain the reduction formula for I_n = ∫cotⁿx dx, n being a positive integer, n ≥ 2 and deduce the value of ∫cot⁴x dx. (May ’11)
Solution:

Question 2.
Obtain the reduction formula for I_n = ∫cosecⁿx dx, n being a positive integer, n ≥ 2 and deduce the value of ∫cosec⁵x dx.
Solution:

Question 3.
If I_m,n = ∫sin^mx cosⁿx dx, then show that \(I_{m, n}=-\frac{\sin ^{m-1} x \cos ^{n+1} x}{m+n}+\frac{m-1}{m+n} I_{m-2, n}\) for a positive Integer n and an integer m ≥ 2.
Solution:

Question 4.
Evaluate ∫sin⁵x cos⁴x dx
Solution:
Denote I_5,4 = ∫sin⁵x cos⁴x dx using the above reduction formula

Question 5.
If I_n = ∫(log x)ⁿ dx then show that I_n = x(log x)ⁿ – n I_n-1 and hence find ∫(log x)⁴ dx.
Solution:

Put n = 4, 3, 2, 1 we get
I₄ = x(log x)⁴ – 4I₃
= x(log x)⁴ – 4[x(log x)³ – 3I₂]
= x(log x)⁴ – 4x(log x)³ + 12[x(log x)² – 2I₁]
= x(log x)⁴ – 4x(log x)³ + 12x(log x)² – 24I₁]
= x(log x)⁴ – 4x(log x)³ + 12x(log x)² – 24 ∫log x dx
= x(log x)⁴ – 4x(log x)³ + 12x(log x)² – 24[x log x – x] + c
= x(log x)⁴ – 4x(log x)³ + 12x(log x)² – 24x log x – 24x + c

Students must practice this TS Intermediate Maths 2B Solutions Chapter 6 Integration Ex 6(e) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Exercise 6(e)

I. Evaluate the following integrals.

Question 1.
\(\int \frac{x-1}{(x-2)(x-3)} d x\)
Solution:
\(\int \frac{x-1}{(x-2)(x-3)} d x\)

= x + 2 log|x – 3| – x – log|x – 2| + c
= 2 log|x – 3| – log|x – 2| + c
Alter: Let \(\frac{x-1}{(x-2)(x-3)}=\frac{A}{x-2}+\frac{B}{x-3}\) (Partial fractions method)
∴ x – 1 = A(x – 3) + B(x – 2)
Comparing coefficients of x and constant terms on both sides
A + B = 1 ………(1) and
-3A – 2B = -1
⇒ 3A + 2B = 1 ………(2)
From (1), 2A + 2B = 2
Solving A = -1 and B = 2

= -log|x – 2| + 2 log|x – 3| + c
= 2 log|x – 3| – log|x – 2| + c

Question 2.
\(\int \frac{x^2}{(x+1)(x+2)^2} d x\)
Solution:
Let \(\frac{x^2}{(x+1)(x+2)^2}=\frac{A}{x+1}+\frac{A}{x+2}+\frac{C}{(x+2)^2}\)
∴ x² = A(x + 2)² + B(x + 1)(x + 2) + C(x + 1)
Put x = -1, then A = 1
Comparing the coefficient of x²,
A + B = 1 ⇒ B = 0
Put x = -2, and we get
4 = C(-1)
⇒ C = -4

Question 3.
\(\int \frac{x+3}{(x-1)\left(x^2+1\right)} d x\)
Solution:
Let \(\frac{x+3}{(x-1)\left(x^2+1\right)}=\frac{A}{x-1}+\frac{B x+C}{x^2+1}\)
∴ x + 3 = A(x² + 1) + (Bx + C)(x – 1)
Put x = 1, then 4 = 2A
⇒ A = 2
Comparing the coefficient of x²,
A + B = 0
⇒ B = -A = -2
Comparing the coefficient of constant terms
A – C = 3
⇒ C = A – 3 = 2 – 3 = -1
∴ x + 3 = 2(x² + 1) + (-2x – 1)(x – 1) = 2(x² + 1) – (2x + 1)(x – 1)

Question 4.
\(\int \frac{d x}{\left(x^2+a^2\right)\left(x^2+b^2\right)}\)
Solution:

Question 5.
\(\int \frac{d x}{e^x+e^{2 x}}\)
Solution:

Question 6.
\(\int \frac{d x}{(x+1)(x+2)}\) (Mar. ’12; May ’11)
Solution:

Question 7.
\(\int \frac{1}{e^x-1} d x\)
Solution:

Question 8.
\(\int \frac{1}{(1-x)\left(4+x^2\right)} d x\)
Solution:
Let \(\frac{1}{(1-x)\left(4+x^2\right)}=\frac{A}{1-x}+\frac{B x+C}{x^2+4}\)
∴ 1 = A(x² + 4) + (Bx + C)(1 – x)
When x – 1 then 5A = 1 ⇒ A = \(\frac{1}{5}\)
The coefficient of x² on both sides gives
A – B = 0 ⇒ B = \(\frac{1}{5}\)
Comparing constant terms,

Question 9.
\(\int \frac{2 x+3}{x^3+x^2-2 x} d x\)
Solution:
x³ + x² – 2x = x(x² + x – 2) = x(x – 1)(x + 2)

∴ 2x + 3 = A(x – 1)(x + 2) + Bx(x + 2) + Cx(x – 1)
Put x = 1 we get
5 = 3B ⇒ B = \(\frac{5}{3}\)
Put x = -2 on both sides
-4 + 3 = C(-2) (-2 – 1)
⇒ -1 = 6C
⇒ C = \(-\frac{1}{6}\)
Coefficient of x2 on both sides
A + B + C = 0

II. Evaluate the following integrals.

Question 1.
\(\int \frac{d x}{6 x^2-5 x+1}\)
Solution:
6x² – 5x + 1 = 6x² – 3x – 2x + 1
= 3x(2x – 1) – 1(2x – 1)
= (3x – 1)(2x – 1)

Question 2.
\(\int \frac{d x}{x(x+1)(x+2)}\)
Solution:
Let \(\frac{1}{x(x+1)(x+2)}=\frac{A}{x}+\frac{B}{x+1}+\frac{C}{x+2}\)
∴ 1 = A(x + 1)(x + 2) + Bx(x + 2) + Cx(x + 1)
Put x = -1 then -B = 1 ⇒ B = -1
Coefficient of x2 both sides
A + B + C = 0 and put x = – 2 then
C(-2)(-1) = 1
⇒ C = \(\frac{1}{2}\)
∴ A = -B – C = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)

Question 3.
\(\int \frac{3 x-2}{(x-1)(x+2)(x-3)} d x\)
Solution:
Let \(\frac{3 x-2}{(x-1)(x+2)(x-3)}=\frac{A}{x-1}+\frac{B}{x+2}\) + \(\frac{C}{x-3}\)
∴ 3x – 2 = A(x + 2)(x – 3) + B(x – 1)(x – 3) + C(x – 1)(x + 2)
Put x = 1, then 1 = A(3)(-2) ⇒ A = \(-\frac{1}{6}\)
Put x = -2, then -8 = B(-3)(-5) ⇒ B = \(-\frac{8}{15}\)
Put x = 3, then 7 = C(2)(5) ⇒ C = \(\frac{7}{10}\)

Question 4.
\(\int \frac{7 x-4}{(x-1)^2(x+2)} d x\)
Solution:
Let \(\frac{7 x-4}{(x-1)^2(x+2)}=\frac{A}{x-1}+\frac{B}{(x-1)^2}+\frac{C}{x+2}\)
∴ 7x – 4 = A(x – 1)(x + 2) + B(x + 2) + C(x – 1)²
Put x = 1 both sides 3 = 3B ⇒ B = 1
Put x = -2 both sides -18 = 9C ⇒ C = -2
Comparing the coefficient of x² on both sides
A + C = 0
⇒ A = -C = 2

III. Evaluate the following integrals.

Question 1.
\(\int \frac{1}{(x-a)(x-b)(x-c)} d x\)
Solution:
Let \(\frac{1}{(x-a)(x-b)(x-c)}\) = \(\frac{A}{x-a}+\frac{B}{x-b}+\frac{C}{x-c}\)
Then 1 = A(x – b)(x – c) + B(x – a)(x – c) + C(x – a)(x – b)
Put x = a both sides we get 1 = A(a – b)(a – c)
⇒ A =\(\frac{1}{(a-b)(a-c)}\)
Put x = b both sides we get 1 = B(b – a)(b – c)
⇒ B = \(\frac{1}{(b-a)(b-c)}\)
Put x = c both sides we get 1 = C (c – a)(c – b)
⇒ C = \(\frac{1}{(c-a)(c-b)}\)

Question 2.
\(\int \frac{2 x+3}{(x+3)\left(x^2+4\right)} d x\)
Solution:
Let \(\frac{2 x+3}{(x+3)\left(x^2+4\right)}=\frac{A}{x+3}+\frac{B x+C}{x^2+4}\) ……(1)
∴ 2x + 3 = A(x² + 4) + (Bx + c)(x + 3)
Put x = -3 both sides -6 + 3 = A(9 + 4)
⇒ A = \(-\frac{3}{13}\)
Comparing the coefficient of x² on both sides
A + B = 0
⇒ B = -A = \(\frac{3}{13}\)
and comparing constant terms on both sides
4A + 3C = 3
⇒ 3C = 3 – 4A

Question 3.
\(\int \frac{2 x^2+x+1}{(x+3)(x-2)^2} d x\)
Solution:
Let \(\frac{2 x^2+x+1}{(x+3)(x-2)^2}=\frac{A}{x+3}+\frac{B}{x-2}\) + \(\frac{C}{(x-2)^2}\)
∴ 2x² + x + 1 = A(x – 2)² + B(x – 2)(x + 3) + C(x + 3)
Put x = 2 on both sides
8 + 2 + 1 = C(5)
⇒ C = \(\frac{11}{5}\)
Put x = -3 on both sides
18 – 3 + 1 = A(-5)²
⇒ A = \(\frac{16}{25}\)
Put x = 0 on both sides

Question 4.
\(\int \frac{d x}{x^3+1}\)
Solution:
We have x³ + 1 = (x + 1)(x² – x + 1)
∴ \(\frac{1}{x^3+1}=\frac{1}{(x+1)\left(x^2-x+1\right)}\) = \(\frac{A}{x+1}+\frac{B x+C}{x^2-x+1}\)
∴ 1 = A(x² – x + 1) + (Bx + C)(x + 1) …….(1)
Put x = -1 both sides 1 = A(3)
⇒ A = \(\frac{1}{3}\)
Comparing the coefficient of x² on both sides
A + B = 0
⇒ B = \(-\frac{1}{3}\)
Comparing constant terms we get
A + C = 1
⇒ C = 1 – A
= 1 – \(\frac{1}{3}\)
= \(\frac{2}{3}\)
∴ From(1)

Question 5.
\(\int \frac{\sin x \cos x}{\cos ^2 x+3 \cos x+2} d x\)
Solution:
Let cos x = t then sin x dx = -dt

∴ t = A(t + 1) + B(t + 2)
Put t = -1 then -1 = B(-1 + 2)
⇒ B = -1
and when t = -2 then -2 = A(-1)
⇒ A = 2
∴ \(\int \frac{t}{t^2+3 t+2} d t=\int \frac{2}{t+2} d t-\int \frac{1}{t+1} d t\)
∴ From (1)

= log|t + 1| – 2 log|t + 2|
= log|cos x + 1| – 2 log|cos x + 2| + c

Students must practice this TS Intermediate Maths 2B Solutions Chapter 6 Integration Ex 6(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Exercise 6(b)

I. Evaluate the following integrals.

Question 1.
∫e^2x dx, x ∈ R
Solution:

Question 2.
∫sin 7x dx, x ∈ R
Solution:
Let 7x = t then 7 dx = dt
⇒ dx = \(\frac{1}{7}\) dt
∴ ∫sin 7x dx = \(\frac{1}{7}\) ∫sint dt
= \(-\frac{1}{7}\) cos t
= \(-\frac{1}{7}\) cos 7x + c

Question 3.
\(\int \frac{x}{1+x^2} d x\), x ∈ R
Solution:

Question 4.
∫2x sin(x² + 1) dx, x ∈ R
Solution:
Let x² + 1 = t then 2x dx = dt
∴ ∫2x sin(x² + 1) dx = ∫sin t dt
= -cos t + c
= -cos(x² + 1) + c

Question 5.
\(\int \frac{(\log x)^2}{x} d x\) on I ⊂ (0, ∞).
Solution:

Question 6.
\(\int \frac{e^{Tan^{-1} x}}{1+x^2} d x\) on I ⊂ (0, ∞).
Solution:

Question 7.
\(\int \frac{\sin \left({Tan}^{-1} x\right)}{1+x^2} d x\), x ∈ R
Solution:

Question 8.
\(\int \frac{1}{8+2 x^2} d x\) on R.
Solution:

Question 9.
\(\int \frac{3 x^2}{1+x^6} d x\) on R.
Solution:

Question 10.
\(\int \frac{2}{\sqrt{25+9 x^2}} d x\) on R.
Solution:

Question 11.
\(\int \frac{3}{\sqrt{9 x^2-1}} d x\) on (\(\frac{1}{3}\), ∞).
Solution:

Question 12.
∫sin mx cos nx dx on R, m ≠ n, m and n are positive integers.
Solution:

Question 13.
∫sin mx sin nx dx on R, m ≠ n, m and n are positive integers.
Solution:

Question 14.
∫cos mx cos nx dx on R, m ≠ n, m and n are positive integers.
Solution:

Question 15.
∫sin x sin 2x sin 3x dx on R.
Solution:
Consider sin x sin 2x sin 3x = \(\frac{1}{2}\) (2 sin x sin 2x sin 3x)
= \(\frac{1}{2}\) [cos(3x – 2x) – cos(3x + 2x)] sin x
= \(\frac{1}{2}\) [sin x cos x – sin x cos 5x]
= \(\frac{1}{4}\) [2 sin x cos x – 2 sin x cos 5x]
= \(\frac{1}{4}\) [sin 2x – [sin(5x + x) + sin(x – 5x)]
= \(\frac{1}{4}\) [sin 2x – [sin 6x – sin 4x]]
= \(\frac{1}{4}\) [sin 2x – sin 6x + sin 4x]
∴ ∫sin x sin 2x sin 3x dx = \(\frac{1}{4}\) ∫sin 2x dx – \(\frac{1}{4}\) ∫sin 6x dx + \(\frac{1}{4}\) ∫sin 4x dx
= \(-\frac{1}{8}\) cos 2x + \(\frac{1}{24}\) cos 6x – \(\frac{1}{16}\) cos 4x + c
= \(\frac{1}{4}\left[\frac{\cos 6 x}{6}-\frac{\cos 4 x}{4}-\frac{\cos 2 x}{2}\right]\) + c

Question 16.
\(\int \frac{\sin x}{\sin (a+x)} d x\) on I ⊂ R – {nπ – a : n ∈ Z}.
Solution:

II. Evaluate the following integrals.

Question 1.
\(\int(3 x-2)^{\frac{1}{2}} d x\) on (\(\frac{2}{3}\), ∞)
Solution:

Question 2.
\(\int \frac{1}{7 x+3} d x\) on I ⊂ R – {\(-\frac{3}{7}\)}
Solution:

Question 3.
\(\int \frac{\log (1+x)}{1+x} d x\) on (-1, ∞).
Solution:

Question 4.
∫(3x² – 4)x dx on R.
Solution:

Question 5.
\(\int \frac{d x}{\sqrt{1+5 x}} \text { on }\left(-\frac{1}{5}, \infty\right)\)
Solution:

Question 6.
∫(1 – 2x³) x² dx on R.
Solution:

Question 7.
\(\int \frac{\sec ^2 x}{(1+\tan x)^3} d x\) on I ⊂ R – {nπ – \(\frac{\pi}{4}\) : n ∈ Z}
Solution:

Question 8.
∫x³ sin(x⁴) dx on R.
Solution:

Question 9.
\(\int \frac{\cos x}{(1+\sin x)^2} d x\) on I ⊂ R – {2nπ + \(\frac{3 \pi}{2}\) : n ∈ Z}
Solution:

Question 10.
∫\(\sqrt[3]{\sin x}\) cos x dx on [2nπ, (2n + 1)π], (n ∈ Z).
Solution:

Question 11.
∫2x \(e^{x^2}\) dx on R.
Solution:
Let x² = t then 2x dx = dt
∴ ∫2x \(e^{x^2}\) dx = ∫e^t dt
= e^t + c
= \(e^{x^2}\) + c

Question 12.
\(\int \frac{e^{\log x}}{x} d x\) on (0, ∞).
Solution:

Question 13.
\(\int \frac{x^2}{\sqrt{1-x^6}} d x\) on I ∈ (-1, 1)
Solution:

Question 14.
\(\int \frac{2 x^3}{1+x^8} d x\) on R.
Solution:

Question 15.
\(\int \frac{x^8}{1+x^{18}} d x\) on R. (Mar. ’09)
Solution:

Question 16.
\(\int \frac{e^x(1+x)}{\cos ^2\left(x e^x\right)} d x\) on I ⊂ R – {x ∈ R : cos(xe^x) = 0}. (Mar. ’10, ’04)
Solution:

Question 17.
\(\int \frac{{cosec}^2 x}{(a+b \cot x)^5} d x\) on I ⊂ R – {x ∈ R : a + b cot x = 0}, where a, b ∈ R, b ≠ 0.
Solution:

Question 18.
∫e^x sin e^x dx on R.
Solution:
Let t = e^x then dt = e^x dx
∴ ∫e^x sin e^x dx = ∫sin t dt
= -cos t + c
= -cos(e^x) + c

Question 19.
\(\int \frac{\sin (\log x)}{x} d x\) on (0, ∞).
Solution:
Let log x = t then \(\frac{1}{x}\) dx = dt
∴ \(\int \frac{\sin (\log x)}{x} d x\) = ∫sin t dt
= -cos t + c
= -cos(log x) + c

Question 20.
\(\int \frac{1}{x \log x} d x\) on (1, ∞).
Solution:

Question 21.
\(\int \frac{(1+\log x)^n}{x} d x\) on (e^-1, ∞), n ≠ -1.
Solution:

Question 22.
\(\int \frac{\cos (\log x)}{x} d x\) on (0, ∞).
Solution:
Let log x = t then \(\frac{1}{x}\) dx = dt
∴ \(\int \frac{\cos (\log x)}{x} d x\) = ∫cos t dt
= sin t + c
= sin(log x) + c

Question 23.
\(\int \frac{\cos \sqrt{x}}{\sqrt{x}} d x\) on (0, ∞).
Solution:
Let √x = t then \(\frac{1}{2 \sqrt{x}}\) dx = dt
∴ \(\int \frac{\cos \sqrt{x}}{\sqrt{x}} d x\) = 2 ∫cos t dt
= 2 sin t + c
= 2 sin(√x) + c

Question 24.
\(\int \frac{2 x+1}{x^2+x+1} d x\) on R.
Solution:
Let x² + x + 1 = t then (2x + 1) dx = dt
∴ \(\int \frac{2 x+1}{x^2+x+1} d x=\int \frac{d t}{t}\)
= log|t| + c
= log|x² + x + 1| + c

Question 25.
\(\int \frac{a x^{n-1}}{b x^n+c} d x\) where n ∈ N, a, b, c are real numbers, b ≠ 0 and x ∈ I ⊂ {x ∈ R : xⁿ ≠ \(-\frac{c}{b}\)}
Solution:

Question 26.
\(\int \frac{1}{x \log x[\log (\log x)]} d x\) on (1, ∞).
Solution:

Question 27.
∫coth x dx on R.
Solution:
∫coth x dx = \(\int \frac{\cosh x}{\sinh x} d x\)
Let sinh x = t then cosh x dx = dt
∴ ∫coth x dx = \(\int \frac{\mathrm{dt}}{\mathrm{t}}\)
= log|t| + c
= log|sinh x| + c

Question 28.
\(\int \frac{1}{\sqrt{1-4 x^2}} d x \text { on }\left(-\frac{1}{2}, \frac{1}{2}\right)\).
Solution:

Question 29.
\(\int \frac{d x}{\sqrt{25+x^2}}\) on R.
Solution:

Question 30.
\(\int \frac{1}{(x+3) \sqrt{x+2}}\) on I ⊂ (-2, ∞). (New Model Paper & May ’12)
Solution:

Question 31.
\(\int \frac{1}{1+\sin 2 x} d x\) on I ⊂ R – {\(\frac{n \pi}{2}+(-1)^n \frac{\pi}{4}\) : n ∈ Z}.
Solution:

Question 32.
\(\int \frac{x^2+1}{x^4+1} d x\) on R.
Solution:

Question 33.
\(\int \frac{d x}{\cos ^2 x+\sin 2 x}\) on I ⊂ R / ({(2n + 1)\(\frac{\pi}{2}\) : n ∈ Z} ∪ {2nπ + \({tan}^{-1} \frac{1}{2}\) : n ∈ Z})
Solution:

Question 34.
\(\int \sqrt{1-\sin 2 x} d x\) on I ⊂ [2nπ – \(\frac{3 \pi}{4}\), 2nπ + \(\frac{\pi}{4}\)], n ∈ Z.
Solution:

Question 35.
\(\int \sqrt{1+\cos 2 x} d x\) on I ⊂ [2nπ – \(\frac{\pi}{2}\), 2nπ + \(\frac{\pi}{2}\)], n ∈ Z.
Solution:

Question 36.
\(\int \frac{\cos x+\sin x}{\sqrt{1+\sin 2 x}} d x\) on I ⊂ [2nπ – \(\frac{\pi}{4}\), 2nπ + \(\frac{3 \pi}{4}\)], n ∈ Z.
Solution:

Question 37.
\(\int \frac{\sin 2 x}{(a+b \cos x)^2} d x\) on {R, if |a| > |b|, I ⊂ {x ∈ R : a + b cos x ≠ 0}, if |a| < |b|}.
Solution:

Question 38.
\(\int \frac{\sec x}{(\sec x+\tan x)^2} d x\) on I ⊂ R – {(2n + 1)\(\frac{\pi}{2}\), n ∈ Z}.
Solution:

Question 39.
\(\int \frac{d x}{a^2 \sin ^2 x+b^2 \cos ^2 x}\) on R, a ≠ 0, b ≠ 0.
Solution:

Question 40.
\(\int \frac{d x}{\sin (x-a) \sin (x-b)}\) on I ⊂ R – ({a + nπ : n ∈ Z} ∪ {b + nπ : n ∈ Z}).
Solution:

Question 41.
\(\int \frac{1}{\cos (x-a) \cos (x-b)} \mathbf{d x}\) on I ⊂ R – ({a + \(\frac{(2 n+1) \pi}{2}\) : n ∈ Z} ∪ {b + \(\frac{(2 n+1) \pi}{2}\) : n ∈ Z})
Solution:

III. Evaluate the following integrals.

Question 1.
\(\int \frac{\sin 2 x}{a \cos ^2 x+b \sin ^2 x} d x\) on I ⊂ R – {x ∈ R | a cos²x + b sin²x = 0}
Solution:

Question 2.
\(\int \frac{1-\tan x}{1+\tan x} d x\) for x ∈ I ⊂ R – {nπ – \(\frac{\pi}{4}\) : n ∈ Z}
Solution:

Question 3.
\(\int \frac{\cot (\log x)}{x} d x\), x ∈ I ⊂ (0, ∞) – {e^nπ : n ∈ Z}
Solution:

Question 4.
∫e^x cot e^x dx, x ∈ I ⊂ R – {log nπ : n ∈ Z}
Solution:
Let e^x = t then e^x dx = dt
∴ ∫e^x cot x dx = ∫cot t dt
= log|sin t| + c
= log|sin(e^x)| + c

Question 5.
∫sec(tan x) sec²x dx on I ⊂ {x ∈ E : tan x ≠ \(\frac{(2 k+1) \pi}{2}\) for any k ∈ Z), where E = R – {\(\frac{(2 n+1) \pi}{2}\), n ∈ Z}
Solution:
Let tan x = t, then sec²x dx = dt

Question 6.
\(\int \sqrt{\sin x} \cos x d x\) on [2nπ, (2n + 1)π], (n ∈ Z).
Solution:

Question 7.
∫tan⁴x sec²x dx, x ∈ I ⊂ R – {\(\frac{(2 n+1) x}{2}\) : n ∈ Z}.
Solution:
Let tan x = t then sec²x dx = dt
∴ ∫tan⁴x sec²x dx = ∫t⁴dt
= \(\frac{t^5}{5}\) + c
= \(\frac{\tan ^5 x}{5}\) + c

Question 8.
\(\int \frac{2 x+3}{\sqrt{x^2+3 x-4}} d x\), x ∈ I ⊂ R – [-4, 1]
Solution:

Question 9.
\(\int {cosec}^2 x \sqrt{\cot x} d x\) on (0, \(\frac{\pi}{2}\)].
Solution:

Question 10.
∫sec x log(sec x + tan x) dx on (0, \(\frac{\pi}{2}\)).
Solution:
Let log(sec x + tan x) = t then \(\frac{1}{\sec x+\tan x}\) (sec x tan x + sec²x) dx = dt
⇒ \(\frac{\sec x(\sec x+\tan x) d x}{\sec x+\tan x}\) = dt
⇒ sec x dx = dt
∴ ∫sec x log(sec x + tan x) dx = ∫t dt + c
= \(\frac{\mathrm{t}^2}{2}\) + c
= \(\frac{1}{2}\) [log(sec x + tan x)]² + c

Question 11.
∫sin³x dx on R.
Solution:
sin 3x = 3 sin x – 4 sin³x
⇒ 4 sin³x = 3 sin x – sin 3x
⇒ sin³x = \(\frac{3 \sin x-\sin 3 x}{4}\)
∴ ∫sin³x dx = \(\frac{1}{2}\) ∫(3 sin x – sin 3x) dx
= \(\frac{3}{4}\)∫sin x dx – \(\frac{1}{4}\)∫sin 3x dx
= \(-\frac{3}{4}\) cos x + \(\frac{1}{12}\) cos 3x + c
= \(\frac{1}{12}\) (cos 3x – 9 cos x] + c

Question 12.
∫cos³x dx on R.
Solution:
cos 3x = 4 cos³x – 3 cos x
⇒ 4cos³x = cos 3x + 3 cos x
⇒ cos³x = \(\frac{1}{4}\)(cos 3x + 3 cos x)
∴ ∫cos3x dx = \(\frac{1}{4}\)∫(cos 3x + 3 cos x) dx
= \(\frac{1}{12}\) sin 3x + \(\frac{3}{4}\) sin x dx + c
= \(\frac{1}{12}\) [sin 3x + 9 sin x] + c

Question 13.
∫cos x cos 2x dx on R.
Solution:
We have cos A cos B = \(\frac{1}{2}\) [cos(A + B) + cos(A – B)]
⇒ cos x cos 2x = \(\frac{1}{2}\) [cos 3x + cos x]
∴ ∫cos x cos 2x dx = \(\frac{1}{2}\) [∫cos 3x + ∫cos x] dx
= \(\frac{1}{2}\left(\frac{1}{3}\right)\) sin 3x + \(\frac{1}{2}\) sin x + c
= \(\frac{1}{6}\) sin 3x + \(\frac{1}{2}\) sin x + c
= \(\frac{1}{6}\) [sin 3x + 3 sin x] + c

Question 14.
∫cos x cos 3x dx on R.
Solution:
cos x cos 3x = \(\frac{1}{2}\) [cos 4x + cos 2x]
∴ ∫cos x cos 3x dx = \(\frac{1}{2}\) ∫cos 4x dx + \(\frac{1}{2}\) ∫cos 2x dx
= \(\frac{1}{8}\) sin 4x + \(\frac{1}{4}\) sin 2x + c

Question 15.
∫cos⁴x dx on R.
Solution:

Question 16.
\(\int x \sqrt{4 x+3} d x\) on (\(-\frac{3}{4}\), ∞).
Solution:

Question 17.
\(\int \frac{d x}{\sqrt{a^2-(b+c x)^2}}\) on {x ∈ R : |b + cx| < a}, where a, b, c are real numbers c ≠ 0 and a > 0.
Solution:
Let b + cx = t then c dx = dt
⇒ dx = \(\frac{1}{c}\) dt

Question 18.
\(\int \frac{d x}{a^2+(b+c x)^2}\) on R, where a, b, c are real numbers c ≠ 0 and a > 0.
Solution:

Question 19.
\(\int \frac{d x}{1+e^x}\), x ∈ R.
Solution:

Question 20.
\(\int \frac{x^2}{(a+b x)^2} d x\), x ∈ I ⊂ R – {\(-\frac{a}{b}\)}, where a, b are real numbers, b ≠ 0.
Solution:
Let a + bx = t then b dx = dt
⇒ dx = \(\frac{1}{b}\) dt
Also x = \(\frac{t-a}{b}\)

Question 21.
\(\int \frac{x^2}{\sqrt{1-x}} d x\), x ∈ (-∞, 1).
Solution:

Students must practice this TS Intermediate Maths 2B Solutions Chapter 6 Integration Ex 6(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Exercise 6(a)

I. Evaluate the following integrals.

Question 1.
∫(x³ – 2x² + 3) dx on R.
Solution:

Question 2.
∫2x√x dx on (0, ∞).
Solution:

Question 3.
\(\int \sqrt[3]{2 x^2}\) dx on (0, ∞).
Solution:

Question 4.
\(\int\left(\frac{x^2+3 x-1}{2 x}\right)\) dx, x ∈ I ⊂ R – {0}
Solution:

Question 5.
\(\int \frac{1-\sqrt{x}}{x}\) dx on (0, ∞).
Solution:

Question 6.
\(\int\left(1+\frac{2}{x}-\frac{3}{x^2}\right) d x\) on I ⊂ R – {0}
Solution:

Question 7.
\(\int\left(x+\frac{4}{1+x^2}\right) d x\) on R
Solution:

Question 8.
\(\int\left(e^x-\frac{1}{x}+\frac{2}{\sqrt{x^2-1}}\right) d x\) on I ⊂ R – [-1, 1]
Solution:

Question 9.
\(\int\left(\frac{1}{1-x^2}+\frac{1}{1+x^2}\right) d x\) on (-1, 1)
Solution:

Question 10.
\(\int\left(\frac{1}{\sqrt{1-x^2}}+\frac{2}{\sqrt{1+x^2}}\right) d x\) on (-1, 1). [May ’11]
Solution:

Question 11.
\(\int e^{\log \left(1+\tan ^2 x\right)} d x\) on I ⊂ R – {\(\frac{(2 n+1) \pi}{2}\) : n ∈ Z}
Solution:

Question 12.
\(\int \frac{\sin ^2 x}{1+\cos 2 x} d x\) on I ⊂ R – {(2n ± 1)π : n ∈ Z}.
Solution:

II. Evaluate the following integrals.

Question 1.
∫(1 – x²)³ dx on (-1, 1).
Solution:

Question 2.
\(\int\left(\frac{3}{\sqrt{x}}-\frac{2}{x}+\frac{1}{3 x^2}\right) d x\) on (0, ∞).
Solution:

Question 3.
\(\int\left(\frac{\sqrt{x}+1}{x}\right)^2 d x\) on (0, ∞).
Solution:

Question 4.
\(\int \frac{(3 x+1)^2}{2 x} d x\), x ∈ I ⊂ R – {0}.
Solution:

Question 5.
\(\int\left(\frac{2 x-1}{3 \sqrt{x}}\right)^2 d x\) on (0, ∞).
Solution:

Question 6.
\(\int\left(\frac{1}{\sqrt{x}}+\frac{2}{\sqrt{x^2-1}}-\frac{3}{2 x^2}\right) d x\) on (1, ∞).
Solution:

Question 7.
∫(sec²x – cos x + x²) dx, x ∈ I ⊂ R – {\(\frac{n \pi}{2}\) : n is an odd integer}.
Solution:
∫(sec²x – cos x + x²) dx
= ∫sec²x dx – ∫cos x dx + ∫x² dx
= tan x – sin x + \(\frac{x^3}{3}\) + c

Question 8.
∫(sec x tan x + \(\frac{3}{x}\) – 4] dx, x ∈ I ⊂ R – ({\(\frac{n \pi}{2}\) : n is an odd integer} ∪ {0})
Solution:
∫(sec x tan x + \(\frac{3}{x}\) – 4] dx
= ∫sec x + tan x dx + 3 ∫\(\frac{dx}{x}\) – 4∫dx
= sec x + 3 log|x| – 4x + c

Question 9.
\(\int\left(\sqrt{x}-\frac{2}{1-x^2}\right) d x\) on (0, 1)
Solution:

Question 10.
\(\int\left(x^3-\cos x+\frac{4}{\sqrt{x^2+1}}\right) d x\), x ∈ R
Solution:

Question 11.
\(\int\left(\cosh x+\frac{1}{\sqrt{x^2+1}}\right) d x\), x ∈ R
Solution:

Question 12.
\(\int\left(\sinh x+\frac{1}{\left(x^2-1\right)^{\frac{1}{2}}}\right) d x\), x ∈ I ⊂ (-∞, -1) ∪ (1, ∞).
Solution:

Question 13.
\(\int \frac{\left(a^x-b^x\right)^2}{a^x b^x} d x\), (a > 0, a ≠ 1 and b > 0, b ≠ 1) on R.
Solution:

Question 14.
∫sec²x cosec²x dx on I ⊂ R – ({nx : n ∈ Z} ∪ {(2n + 1)\(\frac{\pi}{2}\) : n ∈ Z}) (May ’09)
Solution:

Question 15.
\(\int\left(\frac{1+\cos ^2 x}{1-\cos 2 x}\right) d x\) on I ⊂ R – {nπ : n ∈ Z} (Mar. ’13)
Solution:

Question 16.
\(\int \sqrt{1-\cos 2 x} d x\) on I ⊂ [2nπ, (2n + 1)π], n ∈ Z. (Mar. ’09)
Solution:

Question 17.
\(\int \frac{1}{\cosh x+\sinh x} d x\) on R.
Solution:
\(\int \frac{1}{\cosh x+\sinh x} d x\)
= \(\int \frac{\cosh x-\sinh x}{\cosh ^2 x-\sinh ^2 x} d x\)
= ∫(cos hx – sin hx) dx (∵ cosh²x – sinh²x = 1)
= ∫cosh x dx – ∫sinh x dx
= sinh x – cosh x + c

Question 18.
\(\int \frac{1}{1+\cos x} d x\) on I ⊂ R – [(2n + 1)π : n ∈ Z].
Solution:
\(\int \frac{1}{1+\cos x} d x\)
= \(\int \frac{1-\cos x}{(1+\cos x)(1-\cos x)} d x\)
= \(\int \frac{1-\cos x}{\sin ^2 x} d x\)
= ∫cosec²x dx – ∫cot x cosec x dx
= -cot x + cosec x + c
= cosec x – cot x + c

Students must practice this TS Intermediate Maths 2B Solutions Chapter 4 Ellipse Ex 4(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 4 Ellipse Exercise 4(b)

I.

Question 1.
Find the equation of the tangent and normal to the ellipse x² + 8y² = 33 at (-1, 2).
Solution:
Given ellipse is x² + 8y² = 33
⇒ \(\frac{x^2}{33}+\frac{y^2}{(33 / 8)}=1\) ……..(1)
Let P(x₁, y₁) = (-1, 2) be a point on (1) then
the equation of tangent at (x₁, y₁) is \(\frac{\mathrm{xx}_1}{33}+\frac{\mathrm{yy}_1}{(33 / 8)}-1=0\)
\(\frac{x(-1)}{33}+\frac{y(2)}{(33 / 8)}=1\)
⇒ -x + 16y = -33
⇒ x – 16y + 33 = 0
Equation of normal at P(-1, 2) on the ellipse

Question 2.
Find the equation of tangent and normal to the ellipse x² + 2y² – 4x + 12y + 14 = 0 at (2, -1).
Solution:
Given equation of ellipse is x² + 2y² – 4x + 12y + 14 = 0
Let P(x₁, y₁) = (2, -1)
Now differentiating w.r.t ‘x’

∴ Slope of the tangent at (2, -1) is \(\frac{d y}{d x}(2,-1)=\frac{2-2}{-2+6}=0\)
∴ The slope of the normal at (2, -1) is ∞.
∴ Equation of the tangent to the given ellipse at P(2, -1) is y + 1 = 0, and the equation of normal at P(2, -1) is x – 2 = 0.

Question 3.
Find the equation of the tangents to 9x² + 16y² = 144, which makes equal intercepts on the coordinate axis.
Solution:
Given the equation of the ellipse is 9x² + 16y² = 144
⇒ \(\frac{x^2}{16}+\frac{y^2}{9}=1\)
Let S ≡ \(\frac{x^2}{16}+\frac{y^2}{9}-1=0\)
Compared with the general equation S = 0 we have
a² = 16, b² = 9
⇒ a = 4, b = 3
∴ Equation of the tangent to the ellipse S = 0 having slope is y = mx ± \(\sqrt{a^2 m^2+b^2}\)

Question 4.
Find the coordinates of the points on the ellipse x² + 3y² = 37 at which the normal is parallel to the line 6x – 5y = 2.
Solution:
Given equation of ellipse is x² + 3y² = 37 …….(1)
⇒ \(\frac{x^2}{37}+\frac{y^2}{\left(\frac{37}{3}\right)}=1\)
Let P(x₁, y₁) be any point on the ellipse (1) then \(\frac{x_1^2}{37}+\frac{y_1^2}{\left(\frac{37}{3}\right)}=1\)
⇒ \(x^2+3 y_1^2=37\)
Given line is 6x – 5y + 2 = 0 …….(2)
Slope of the line = \(\frac{6}{5}\)
∴ Equation of the normal at P(x₁, y₁) to the ellipse S = 0 is


∴ The coordinates of the points on ellipse x² + 7y² = 37 at which the normal is parallel to the line 6x – 5y = 2 are (5, 2), (-5, -2).

Question 5.
Find the value of k if 4x + y + k = 0 is a tangent to the ellipse x² + 3y² = 3.
Solution:
Given ellipse is x² + 3y² = 3
⇒ \(\frac{x^2}{3}+\frac{y^2}{1}=1\)
Hence a² = 3 and b² = 1
The equation of the given line is 4x + y + k = 0.
⇒ y = -4x – k where m = -4, and c = -k
The condition for tangency is c² = a²m² + b²
⇒ k² = 3(16) + 1
⇒ k² = 49
⇒ k = ±7

Question 6.
Find the condition for the line x cos α + y sin β = p to be a tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\).
Solution:
Given equation of ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) ……..(1)
and equation of given line is x cos α + y sin α = p
⇒ y sin α = p – x cos α
⇒ y = -x cot α + p cosec α …….(2)
which is of the form y = mx + c where m = -cot α and c = p cosec α
Condition for tangency is c² = a²m² + b²
⇒ p² cosec²α = a² cot²α + b²
⇒ p² = \(a^2 \frac{\cot ^2 \alpha}{{cosec}^2 \alpha}+\frac{b^2}{{cosec}^2 \alpha}\)
⇒ p² = a² cos²α + b² sin²α which is the required condition.

II.

Question 1.
Find the equations of tangent and normal to the ellipse 2x² + 3y² = 11 at the point whose ordinate is 1.
Solution:
Let P(x₁, y₁) be a given point and given y₁ = 1 and (x₁, y₁) lies on 2x² + 3y² = 11.
⇒ \(2 \mathrm{x}_1^2+3 \mathrm{y}_1{ }^2=11\)
⇒ \(2 \mathrm{x}_1^2+3=11\)
⇒ 2\(\mathrm{x}_1^2\) = 8
⇒ \(\mathrm{x}_1^2\) = 4
⇒ x₁ = ±2
The required points are (2, 1) and (-2, 1) at which the equations of tangent and normal are to be determined.
The equation of tangent at (x₁, y₁) to the ellipse 2x² + 3y² = 11
⇒ \(\frac{x^2}{\left(\frac{11}{2}\right)}+\frac{y^2}{\left(\frac{11}{3}\right)}=1\) is \(\frac{\mathrm{xx}}{\left(\frac{11}{2}\right)}+\frac{\mathrm{yy}}{\left(\frac{11}{3}\right)}=1\)

⇒ -3x – 4y = 2
⇒ 3x + 4y + 2 = 0 ……..(4)
∴ Tangents are 4x + 3y – 11 = 0 and 4x – 3y – 11 = 0
Also the normals are 3x – 4y – 2 = 0 and 3x + 4y + 2 = 0.

Question 2.
Find the equations to the tangents to the ellipse x² + 2y² = 3 drawn from the point (1, 2) and also find the angle between these tangents.
Solution:
Given the equation of the ellipse is x² + 2y² = 3
⇒ \(\frac{x^2}{3}+\frac{y^2}{\left(\frac{3}{2}\right)}=1\) which is of the form \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) where a² = 3 and b² = \(\frac{3}{2}\)
Equation of any tangent to the ellipse is y = mx ± \(\sqrt{a^2 m^2+b^2}\)
If the tangents are drawn from (1, 2) then
2 = m ± \(\sqrt{3 m^2+3 / 2}\)
⇒ 2 – m = \(\pm \sqrt{3 m^2+3 / 2}\)
⇒ m² – 4m + 4 = 3m² + \(\frac{3}{2}\)
⇒ 2m² – 8m + 8 = 6m² + 3
⇒ 4m² + 8m – 5 = 0
⇒ 4m² + 10m – 2m – 5 = 0
⇒ 2m(2m + 5) – 1(2m + 5) = 0
⇒ 2m – 1 = 0 (or) 2m + 5 = 0
⇒ m = \(\frac{1}{2}\) (or) m = \(-\frac{5}{2}\)
The equation of tangents when m = \(\frac{1}{2}\) is

∴ Equations of tangents drawn from the point (1, 2) to the ellipse S = 0 are given by x – 2y + 3 = 0 and 5x + 2y – 9 = 0.
Also, the angle between them is tan^-1(12).

Question 3.
Find the equation of the tangents to the ellipse 2x² + y² = 8 which are
(i) parallel to x – 2y – 4 = 0
(ii) perpendicular to x + y + 2 = 0
(iii) which makes an angle \(\frac{\pi}{4}\) with x-axis.
Solution:
Given the equation of the ellipse is 2x² + y² = 8
⇒ \(\frac{x^2}{4}+\frac{y^2}{8}=1\)
Let S ≡ \(\frac{x^2}{4}+\frac{y^2}{8}-1=0\) ……..(1)
and compare with general equation a² = 4, and b² = 8
⇒ a = 2, b = 2√2
(i) Parallel to x – 2y – 4 = 0:
Given line is x – 2y – 4 = 0 ……..(2)
Equation of any line parallel to x – 2y – 4 = 0 is x – 2y + k = 0 ………(3)
⇒ 2y = x + k
⇒ y = \(\frac{\mathrm{x}}{2}+\frac{\mathrm{k}}{2}\) where m = \(\frac{1}{2}\) and c = \(\frac{k}{2}\)
If (3) is a tangent to (1) them c² = a²m² + b²
⇒ \(\frac{\mathrm{k}^2}{4}=4\left(\frac{1}{4}\right)+8\)
⇒ \(\frac{\mathrm{k}^2}{4}\) = 1 + 8
⇒ k² = 36
⇒ k = ±6
∴ The equation of the required tangent from (3) is x – 2y ± 6 = 0.

(ii) Perpendicular to x + y – 2 = 0:
Given line is x + y – 2 = 0 ………(4)
Equation of any line perpendicular to (4) is x – y + k = 0 ……….(5)
∴ y = x + k and m = 1, c = k
By the condition for tangency c² = a²m² + b²
⇒ k² = 4(1) + 8
⇒ k² = 12
⇒ k = ±2√ 3
∴ Equation of the required line from (5) is x – y ± 2√3 = 0 ………..(6)

(iii) Which makes an angle \(\frac{\pi}{4}\) with x-axis:
If the line makes \(\frac{\pi}{4}\) with x-axis then m = tan\(\frac{\pi}{4}\) = 1.
∴ Equation of the line is y = x + c ………..(7)
If this is a tangent to (1) then c² = a²m² + b²
⇒ c² = 4(1) + 8
⇒ c² = 12
⇒ c = ±2√3
∴ From (7), the equation of the required line is y = x ± 2√3.

Question 4.
A circle of radius 4, is concentric with the ellipse 3x² + 13y² = 78. Prove that a common tangent is inclined to the major axis at an angle \(\frac{\pi}{4}\).
Solution:
Given ellipse is 3x² + 13y² = 78
⇒ \(\frac{x^2}{26}+\frac{y^2}{6}=1\)
Comparing with \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) we have a² = 26, b² = 6,
centre of the ellipse = (0, 0).
The equation of a circle with centre (0, 0) and radius 4 is x² + y² = 16 ……….(2)
Equation of any tangent to the ellipse having slope ‘m’ is y = mx ± \(\sqrt{a^2 m^2+b^2}\)
⇒ mx – y + \(\sqrt{a^2 m^2+b^2}\) = 0 (Taking one tangent as common)
⇒ mx – y + \(\sqrt{26 m^2+6}\) = 0 ………(3)
If (3) is a tangent to (2) then the perpendicular distance from (0, 0) to (3) = Radius of the circle (2)
∴ \(\frac{\sqrt{26 m^2+6}}{\sqrt{m^2+1}}\)
⇒ 26m² + 6 = 16(m² + 1)
⇒ 10m² – 10 = 0
⇒ m² = 1
⇒ m = ±1
If θ is the angle made by the common tangent with the major axis of the ellipse then tan θ = ±1
⇒ θ = ±\(\frac{\pi}{4}\)
Hence common tangent makes an angle \(\frac{\pi}{4}\) with the major axis of the ellipse.

III.

Question 1.
Show that the foot of the perpendicular drawn from the centre on any tangent to the ellipse lies on the curve (x² + y²)² = a²x² + by².
Solution:
Let S ≡ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1=0\) be the equation of ellipse.
Let P(x₁, y₁) be any point on the ellipse.
The equation of the tangent to the ellipse S = 0 having slope m is y = mx ± \(\sqrt{a^2 m^2+b^2}\)
⇒ y – mx = ±\(\sqrt{a^2 m^2+b^2}\) ……..(1)
The equation to the perpendicular from centre on this tangent (1) is y – 0 = \(\frac{-1}{m}\)(x – 0)
⇒ my + x = 0 ……….(2)
Now P(x₁, y₁) is the point of intersection of (1) and (2)
∴ y₁ – mx₁ = ±\(\sqrt{a^2 m^2+b^2}\) ……(3) and my₁ + x₁ = 0 ………(4)
Squaring (3) and (4) and adding

Question 2.
Show that the locus of the feet of the perpendiculars drawn from foci to any tangent of the ellipse is the auxiliary circle.
Solution:
Let S ≡ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1=0\) be the equation of ellipse.

Let P(x₁, y₁) be any point on the locus.
The equation of tangent to the ellipse S = 0 having slope ‘m’ is y = mx ± \(\sqrt{a^2 m^2+b^2}\)
⇒ y – mx = ±\(\sqrt{a^2 m^2+b^2}\) ……..(1)
The equation to the perpendicular from either focus (±ae, 0) on the tangent (1) is
y – 0 = \(\frac{-1}{m}\)(x ± ae)
⇒ my + x = ±ae ………(2)
Since P(x₁, y₁) is a point of intersection of (1) and (2) we have
y₁ – mx₁ = ±\(\sqrt{a^2 m^2+b^2}\) ……..(3)
and my₁ + x₁ = ±ae ……….(4)
Eliminating in from the equation by squaring and adding (3) and (4)
(y₁ – mx₁)² + (my₁ + x₁)² = a²m² + b² + a²e²
= a²m² + a² (1 – e²) + a²e²
= a²m² + a²
= a²(m² + 1)
∴ \(\mathrm{y}_1^2\left(1+\mathrm{m}^2\right)+\mathrm{x}_1^2\left(1+\mathrm{m}^2\right)=\mathrm{a}^2\left(1+\mathrm{m}^2\right)\)
⇒ \(x_1^2+y_1{ }^2=a^2\)
∴ The Locus of P(x₁, y₁) is x² + y² = a² which is the equation of the auxiliary circle of the ellipse.

Question 3.
The tangent and normal to the ellipse x² + 4y² = 4 at a point P(θ) on it meets the major axis in Q and R respectively. If 0 < θ < \(\frac{\pi}{2}\) and QR = 2 then show that θ = \(\cos ^{-1}\left(\frac{2}{3}\right)\). (March 2012)
Solution:
Given ellipse is x² + 4y² = 4
⇒ \(\frac{x^2}{4}+\frac{y^2}{1}=1\)

Let S ≡ \(\frac{x^2}{4}+\frac{y^2}{1}-1=0\) be the given ellipse.
Comparing this with \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1=0\) we get a² = 4, b² = 1
⇒ a = 2, b = 1
The equation of the tangent at P(θ) on the ellipse S = 0 is \(\frac{x}{a} \cos \theta+\frac{y}{b} \sin \theta=1\)
⇒ \(\frac{\mathrm{x}}{2} \cos \theta+\frac{\mathrm{y}}{1} \sin \theta=1\) ……..(1)
The tangent (1) meets the major axis at the Q
∴ y-coordinate of Q = 0; Put y = 0 in (1)


⇒ -3 cos²θ + 4 = 4 cosθ
⇒ 3 cos²θ + 4 cos θ – 4 = 0
⇒ 3 cos²θ + 6 cos θ – 2 cos θ – 4 = 0
⇒ 3 cos θ (cos θ + 2) – 2(cos θ + 2) = 0
⇒ (cos θ + 2) (3 cos θ – 2) = 0
⇒ cos θ + 2 = 0; solution is not admissive (∵ -1 ≤ cos θ ≤ 1)
and 3 cos θ – 2 = 0
⇒ cos θ = \(\frac{2}{3}\)
⇒ θ = \(\cos ^{-1}\left(\frac{2}{3}\right)\)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 5 Hyperbola Ex 5(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 5 Hyperbola Exercise 5(a)

I.

Question 1.
One focus of a hyperbola is located at the point (1, -3) and the corresponding directrix is the line y = 2. Find the equation of the hyperbola if its eccentricity is \(\frac{3}{2}\). (May 2009)
Solution:
Given one focus of hyperbola is at (1, -3)
∴ S = (1, -3) and directrix is y – 2 = 0
Given e = \(\frac{3}{2}\).
Let P(x₁, y₁) be a point on the locus. Then
SP = e . PM
⇒ SP² = e² . PM²

∴ Locus of (x₁, y₁) is the equation of hyperbola 4x² – 5y² – 8x + 60y + 4 = 0.

Question 2.
If the lines 3x – 4y = 12 and 3x + 4y = 12 meets on a hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) then find the eccentricity of the hyperbola.
Solution:
Given the equation of lines are
3x – 4y = 12 …….(1)
3x + 4y = 12 ………(2)
The combined equations of lines (1) and (2) is (3x – 4y) (3x + 4y) = 144
⇒ 9x² – 16y² = 144
⇒ \(\frac{x^2}{16}-\frac{y^2}{9}=1\) which represents a hyperbola of the form \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\).

Question 3.
Find the equations of hyperbola whose foci are (±5, 0); the transverse axis is of length 8.
Solution:
Given foci as (±5, 0)and comparing with the standard equation we get
ae = 5 …….(1)
and the length of the transverse axis is 2a = 8
⇒ a = 4
∴ ae = 5
⇒ e = \(\frac{5}{4}\)
since b² = a²(e² – 1)
⇒ b² = 16\(\left(\frac{25}{16}-1\right)\) = 9
∴ Equation of hyperbola whose foci are (±5, 0) and the transverse axis of length ‘8’ is \(\frac{x^2}{16}-\frac{y^2}{9}=1\)
⇒ 9x² – 16y² = 144

Question 4.
Find the equation of hyperbola whose asymptotes are the straight lines (x + 2y + 3) = 0 and (3x + 4y + 5) = 0 and which passes through the point (1, -1).
Solution:
Given asymptotes are x + 2y + 3 = 0 and 3x + 4y + 5 = 0.
∴ The equation of point of asymptotes is (x + 2y + 3) (3x + 4y + 5) = 0
⇒ 3x² + 6xy + 9x + 4xy + 8y² + 10y + 9x + 12y + 15 = 0
⇒ 3x² + 10xy + 8y² + 14x + 22y + 15 = 0
∴ The equation of hyperbola having the given lines as asymptotes are
3x² + 10xy + 8y² + 14x + 22y + k = 0 ……..(1)
Given (1) is passing through (1, -1) then
3 – 10 + 8 + 14 – 22 + k = 0
⇒ k = 7
∴ From (1) the equation of the required hyperbola is 3x² + 10xy + 8y² + 14x + 22y + 7 = 0

Question 5.
If 3x – 4y + k = 0 is a tangent to x² – 4y² = 5, find the value of k.
Solution:
Given the equation of the hyperbola is x² – 4y² = 5
⇒ \(\frac{x^2}{5}-\frac{y^2}{\left(\frac{5}{4}\right)}=1\)
Comparing with \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
We get a² = 5 and b² = \(\frac{5}{4}\)
Given 3x – 4y + k = 0
⇒ 4y = 3x + 3
⇒ y = \(\frac{3}{4} x+\frac{k}{4}\)

Question 6.
Find the product of lengths of perpendiculars from any point on the hyperbola \(\frac{x^2}{16}-\frac{y^2}{9}=1\) to its asymptotes.
Solution:
Let S ≡ \(\frac{x^2}{16}-\frac{y^2}{9}-1=0\) be the given hyperbola.
Let P = (a sec θ, b tan θ) be any point on S = 0.
The equation of asymptotes of the hyperbola S = 0 are \(\frac{x}{4}+\frac{y}{3}=0\) and \(\frac{x}{4}-\frac{y}{3}=0\)
⇒ 3x + 4y = 0 ………(1) and 3x – 4y = 0 ………(2)
Let PM be the length of the perpendicular drawn from P(4 sec θ, 3 tan θ) to the line (1) then
PM = \(\left|\frac{12 \sec \theta+12 \tan \theta}{\sqrt{9+16}}\right|\) = \(\left|\frac{12 \sec \theta+12 \tan \theta}{5}\right|\)
Let PN be the length of the perpendicular from P(4 sec θ, 3 tan θ) on line (2). Then
PN = \(\frac{|12 \sec \theta-12 \tan \theta|}{\sqrt{9+16}}=\frac{|12 \sec \theta-12 \tan \theta|}{5}\)
∴ Product of perpendiculars = PM . PN
= \(\frac{|12 \sec \theta+12 \tan \theta|}{5} \cdot \frac{|12 \sec \theta-12 \tan \theta|}{5}\)
= \(\frac{144\left(\sec ^2 \theta-\tan ^2 \theta\right)}{25}\)
= \(\frac{144}{25}\)
∴ Product of length of perpendiculars = \(\frac{144}{25}\)

Question 7.
If the eccentricity of a hyperbola is \(\frac{5}{4}\), then find the eccentricity of its conjugate hyperbola. (March 2012, 2013)
Solution:
If S ≡ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}-1=0\) is the equation of hyperbola then S’ ≡ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}+1=0\) is the equation of the conjugate hyperbola.
Let e and e₁ be the eccentricities of the hyperbola and its conjugate respectively,

∴ The eccentricity of the conjugate hyperbola is \(\frac{5}{3}\).

Question 8.
Find the equation of the hyperbola whose asymptotes are 3x = ±5y and the vertices and (±5, 0).
Solution:
The equation of asymptotes is given by 3x – 5y = 0 and 3x + 5y = 0.
∴ The equation of hyperbola is of the form (3x – 5y) (3x + 5y) = k
⇒ 9x² – 25y² = k
If the hyperbola passes through the vertex (±5, 0) then 9(25) = k
⇒ k = 225
Hence the equation of asymptotes of a hyperbola is 9x² – 25y² = 225

Question 9.
Find the equation of normal at θ = \(\frac{\pi}{3}\) to the hyperbola 3x² – 4y² = 12.
Solution:
The given equation of the hyperbola is 3x² – 4y² = 12
⇒ \(\frac{x^2}{4}-\frac{y^2}{3}=1\)
The equation of normal at P(a sec θ, b tan θ) to the hyperbola S = 0 is

Question 10.
If the angle between asymptotes is 30° then find its eccentricity.
Solution:
The angle between asymptotes of the hyperbola

II.

Question 1.
Find the centre, foci, eccentricity, equation of directrices, and length of the latus rectum of the following hyperbolas.
(i) 16y² – 9x² = 144 (June 2010)
Solution:
The given equation of the hyperbola is 16y² – 9x² = 144
⇒ \(\frac{y^2}{9}-\frac{x^2}{16}=1\)
⇒ \(\frac{x^2}{16}-\frac{y^2}{9}=-1\)
Comparing with \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1\) We get
a² = 16 and b² = 9
⇒ a = 4 and b = 3
(i) Centre of the hyperbola = (0, 0)

(ii) x² – 4y² = 4 (May 2011)
Solution:
This can be written as \(\frac{x^2}{4}-\frac{y^2}{1}=1\)
⇒ a² = 4 and b² = 1
⇒ a = 2 and b = 1
(i) Centre = (0, 0)

(iii) 5x² – 4y² + 20x + 8y – 4 = 0 (Mar 2012)
Solution:
The given equation is 5x² – 4y² + 20x + 8y – 4 = 0
⇒ 5x² + 20x – 4y² + 8y = 4
⇒ 5(x² + 4x) – 4(y² – 2y) = 4
⇒ 5(x² + 4x + 4) – 4(y² – 2y + 1) = 20 + 4 – 4 = 20
⇒ 5(x + 2)² – 4(y – 1)² = 20
⇒ \(\frac{\left(\mathrm{x}-(-2)^2\right)}{4}-\frac{(\mathrm{y}-1)^2}{5}=1\)
This is of the form \(\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1\)
Where a² = 4 and b² = 5, h = -2, k = 1
(i) Centre of the hyperbola = C(h, k) = (-2, 1)
(ii) Eccentricity = \(\sqrt{\frac{a^2+b^2}{a^2}}=\sqrt{\frac{4+5}{4}}=\frac{3}{2}\)
(iii) Foci = (h ± ae, k)
= (-2 ± 2(\(\frac{3}{2}\)), 1)
= (1, 1), (-5, 1)
∴ Foci of the hyperbola = (1, 1), (-5, 1)
(iv) Equations of directrices are x = h ± \(\frac{a}{e}\)
= \(-2 \pm \frac{2}{(3 / 2)}=-2 \pm \frac{4}{3}\)
∴ 3x = -6 ± 4
⇒ 3x = -2 and 3x = -10
⇒ 3x + 2 = 0 and 3x + 10 = 0
(v) Length of the latus rectum = \(\frac{2 b^2}{a}=\frac{2 \times 5}{2}\) = 5

(iv) 9x² – 16y² + 72x – 32y – 16 = 0
Solution:
The given equation is 9x² – 16y² + 72x – 32y – 16 = 0
⇒ 9x² + 72x – 16y² – 32y = 16
⇒ 9(x² + 8x) – 16(y² + 2y) = 16
⇒ 9(x² + 8x + 16) – 16(y² + 2y + 1) = 16 + 144 – 16 = 144
⇒ \(\frac{(x-(-4))^2}{16}+\frac{[y-(-1)]^2}{9}=1\)
This is of the form \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\)
Where a² = 16 and b² = 9
⇒ a = 4 and b = 3
(i) Coordinates of centre = C(h, k) = C(-4, -1)
(ii) Eccentricity e = \(\sqrt{\frac{a^2+b^2}{a^2}}=\sqrt{\frac{16+9}{16}}=\frac{5}{4}\)
(iii) Coordinates of foci = (h ± ae, k)
= (-4 ± 4(\(\frac{5}{4}\)), -1)
= (-9, -1), (1, -1)
(iv) Equations of directrices are x = ±\(\frac{a}{e}\)
= \(-4 \pm \frac{4}{(5 / 4)}\)
= \(-4 \pm \frac{16}{5}\)
⇒ x + 4 = ±\(\frac{16}{5}\)
⇒ 5x + 20 = 16 or 5x + 20 = -16
⇒ 5x + 4 = 0 (or) 5x + 36 = 0
(v) Length of the latus rectum = \(\frac{2 b^2}{a}=\frac{2(9)}{4}=\frac{9}{2}\)

Question 2.
Find the equation to the hyperbola whose foci are (4, 2) and (8, 2) and whose eccentricity is 2. (March 2009)
Solution:
Let S = (4, 2) and S’ = (8, 2) be the foci.
Since the Y-coordinate of S and S’ are the same, the hyperbola’s major axis is parallel to the X-axis.
The equation of required hyperbola is \(\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1\)
Centre of Hyperbola C = Midpoint of SS’
= \(\left(\frac{4+8}{2}, \frac{2+2}{2}\right)\)
= (2, 2)
Given that e = 2
Distance between the foci is SS’ = 2ae
∴ 2ae = \(\sqrt{(4-8)^2+(2-2)^2}\) = 4
⇒ ae = 2
⇒ a(2) = 2
⇒ a = 1
But b² = a²(e² – 1) = 1(4 – 1) = 3
The equation of required hyperbola is \(\frac{(x-6)^2}{1}-\frac{(y-2)^2}{3}=1\)
⇒ (x² – 12x + 36) – \(\frac{\left(y^2-4 y+4\right)}{3}\) = 1
⇒ 3x² – y2 – 36x + 4y + 101 = 0
∴ Equation of Hyperbola is 3x² – y² – 36x + 4y + 101 = 0

Question 3.
Find the equation of hyperbola of a given length of transverse axis 6 whose vertex bisects the distance between the centre and the focus.
Solution:
Let C be the centre.
S is the focus and A, A’ are vertices of the required hyperbola.

C = (0, 0), S = (ae, 0);
Given AA’ = 2a = 6
⇒ CA = a = 3; A = (3, 0)
Given that A bisects \(\overline{\mathrm{CS}}\)
∴ A is midpoint of \(\overline{\mathrm{CS}}\)
∴ (\(\frac{ae}{2}\)) = a
⇒ e = 2
But b² = a²(e² – 1)
⇒ b² = a²(4 – 1) = 3a² = 27
∴ The equation of the required hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
⇒ \(\frac{x^2}{9}-\frac{y^2}{27}=1\)
⇒ 3x² – y² = 27

Question 4.
Find the equation of the tangents to the hyperbola x² – 4y² = 4 which are (i) parallel (ii) perpendicular to the line x + 2y = 0. (May 2011)
Solution:
Given the equation of Hyperbola x² – 4y² = 4
⇒ \(\frac{x^2}{4}-\frac{y^2}{1}=1\) ……..(1)
∴ a² = 4, b² = 1
Given line is x + 2y = 0 ……..(2)
(i) Equation of any line parallel to (2) is x + 2y + k = 0
⇒ 2y = -x – k
⇒ y = \(-\frac{x}{2}-\frac{k}{2}\) ……(3)
Condition for (3) to be a tangent to the hyperbola (1) is c² = a²m² – b²
where c = \(-\frac{k}{2}\), m = \(-\frac{1}{2}\)
∴ \(\frac{k^2}{4}=4\left(\frac{1}{4}\right)-1\)
⇒ \(\frac{k^2}{4}\) = 0
⇒ k = 0
The equation of tangent parallel to x + 2y = 0 is x + 2y = 0.
(ii) Equation of line perpendicular to x + 2y = 0 is 2x – y + k = 0.
⇒ y = 2x + k, where m = 2 and c = k
∴ c² = a²m² – b²
⇒ k² = 4(4) – 1 = 15
⇒ k = ±√15
∴ Equation of tangent perpendicular to x + 2y = 0 is 2x – y ± √15 = 0.

Question 5.
Find the equations of tangents drawn to the hyperbola 2x² – 3y² = 6 through (-2, 1).
Solution:
Given equation of hyperbola 2x² – 3y² = 6
⇒ \(\frac{x^2}{3}-\frac{y^2}{2}=1\) …….(1)
Comparing (1) with \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) we get a² = 3, b² = 2
Equation of any tangent to the hyperbola (1) having slope ‘m’ is y = mx ± \(\sqrt{a^2 m^2-b^2}\)
⇒ y = mx ± \(\sqrt{3 m^2-2}\) ……….(2)
If the tangent (2) passes through (-2, 1) then 1 = -2m ± \(\sqrt{3 m^2-2}\)
⇒ (2m + 1)² = 3m² – 2
⇒ 4m² + 4m + 1 = 3m² – 2
⇒ m² + 4m + 3 = 0
⇒ (m + 3) (m + 1) = 0
⇒ m = -1 (or) m = -3
∴ The equations of tangents from (2) are y = -x ± √1 and y = -3x ± √25 = -3x ± 5
∴ x + y ± 1 = 0 and 3x + y ± 5 = 0 are the equations.
But the point (-2, 1) does not satisfy x + y – 1 = 0 and 3x + y – 5 = 0.
Hence the equations of required tangents passing through (-2, 1) are x + y + 1 = 0 and 3x + y + 5 = 0.

Question 6.
Prove that the product of the perpendicular distances from any point on a hyperbola to its asymptotes is constant.
Solution:
Let S ≡ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1=0\) be the given hyperbola.
Let P = (a sec θ, b tan θ) be any point on S = 0.
The equations of asymptotes of hyperbola S = 0 are \(\frac{x}{a}+\frac{y}{b}=0\) and \(\frac{x}{a}-\frac{y}{b}=0\)
⇒ bx + ay = 0 (1) and bx – ay = 0 ………(2)
Let PM be the perpendicular length drawn from P(a sec θ, b tan θ) on line (2).
∴ PM = \(\frac{|b a \sec \theta+a b \tan \theta|}{\sqrt{a^2+b^2}}\)
Let PN be the perpendicular length drawn from P(a sec θ, b tan θ) on line (2).

∴ The product of the perpendicular distances from any point on a hyperbola to its asymptotes is a constant.

III.

Question 1.
Tangents to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) make angles θ1, θ2 with transverse axis of a hyperbola. Show that the point of intersection of these tangents lies on the curve 2xy = k(x² – a²) when tan θ1 + tan θ2 = k.
Solution:
Given hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
The transverse axis of the hyperbola is the x-axis, (i.e., y = 0)
Let P(x₁, y₁) be the point of intersection of the tangents drawn to the given hyperbola.
The equation of any tangent to the hyperbola is of the form y = mx ± \(\sqrt{a^2 m^2-b^2}\)
If this passes through (x₁, y₁) then

This is a quadratic equation in ‘m’ and be m₁, m₂ be the roots which corresponds to the slopes tan θ₁, tan θ₂ of tangents.

∴ Locus of (x₁, y₁) is the curve 2xy = k(x² – a²).

Question 2.
Show that the locus of feet of the perpendiculars drawn from foci to any tangent of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is the auxiliary circle of the hyperbola.
Solution:
Let S ≡ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}-1=0\) be the given hyperbola.
Foci of the hyperbola S = 0 are (±ae, 0).
Equation of any tangent to S = 0 having slope ‘m’ is y = mx ± \(\sqrt{a^2 m^2-b^2}\)
⇒ y – mx = ±\(\sqrt{a^2 m^2-b^2}\) ………(1)
Let P(x₁, y₁) be the locus of feet of the perpendicular form foci of the hyperbola to the tangent (1).
The equation of the perpendicular from either focus (±ae, 0) on the above tangent is
y – 0 = \(-\frac{1}{m}\)(x – (±ae))
⇒ my + x = ±ae …….(2)
P(x₁, y₁) lies on (1) and (2).
y₁ – mx₁ = \(\pm \sqrt{a^2 m^2-b^2}\) …….(3)
and my₁ + x₁ = ±ae ………(4)
Eliminating m from equations (3) and (4)

∴ The Locus of (x₁, y₁) is x² + y² = a² which is the equation of the Auxiliary circle of the Hyperbola.

Question 3.
Show that the equation \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\) represents
(i) an ellipse if ‘c’ is a real constant less than 5.
(ii) a hyperbola if ‘c’ is any real constant between 5 and 9.
(iii) show that each ellipse in (i) and each hyperbola (ii) has foci at the two points (±2, 0), independent of the value of ‘c’.
Solution:
Given equation \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\) ……(1) represents an ellipse
if 9 – c > 0 and 5 – c > 0
⇒ 9 > c and 5 > c
⇒ c < 9 and c < 5
⇒ c < 5 ∴ c is a real constant and less than 5 if (1) represents an ellipse.
(i) The equation of the hyperbola is of the form \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) and the given equation (1) represents a hyperbola
if 9 – c > 0 and 5 – c < 0
⇒ 9 > c and 5 < c
⇒ 5 < c < 9
∴ (1) represents hyperbola if C is a real constant such that 5 < c < 9
(ii) If \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\) represents ellipse then
a² = 9 – c and b² = 5 – c
Eccentricity b² = a²(1 – e²)
⇒ 5 – c = (9 – c) (1 – e²)

Hence each ellipse in (i) and each hyperbola in (ii) has foci at the two points (±2, 0) independent of the value of C.

Question 4.
Show that the angle between the two asymptotes of a hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is \(2 {tan}^{-1}\left(\frac{b}{a}\right)\) (or) 2 sec-1(e). [New Model Paper, May 2012]
Solution:
Let the equation of the hyperbola be \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
The asymptotes of hyperbola are y = ±\(\frac{b}{a}\)x where m1 = \(\frac{b}{a}\) and m2 = \(-\frac{b}{a}\).
If θ is the angle between asymptotes of the hyperbola then

Students must practice this TS Intermediate Maths 2B Solutions Chapter 4 Ellipse Ex 4(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 4 Ellipse Exercise 4(a)

I.

Question 1.
Find the equation of the ellipse with focus at (1, -1), e = \(\frac{2}{3}\) and directrix as x + y + 2 = 0. (Mar. 2001)
Solution:
Given that focus S = (1, -1) and e = \(\frac{2}{3}\) and
equation of directrix is L = x + y + 2 = 0
Let (x₁, y₁) be any point on the ellipse and PM is the perpendicular distance from P to the directrix L = 0.

Question 2.
Find the equation of the ellipse in the standard form whose distance between foci is 2 and the length of latus rectum is \(\frac{15}{2}\).
Solution:
The equation of an ellipse in the standard form is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\), a > b
Given that the length of the latus rectum = \(\frac{15}{2}\)
∴ \(\frac{2 b^2}{a}=\frac{15}{2}\)
⇒ 4b² = 15a
Given that the distance between foci = 2
∴ 2ae = 2
⇒ ae = 1 ……(2)
From (1), 4a²(1 – e²) = 15a (∵ b² = a²(1 – e²))
⇒ 4(a² – a²e²) = 15a
⇒ 4(a² – 1) = 15a (∵ ae = 1)
⇒ 4a² – 15a – 4 = 0
⇒ 4a² – 16a + a – 4 = 0
⇒ 4a(a – 4) + 1(a – 4) = 0
⇒ a = 4 or a = \(-\frac{1}{4}\)
∴ a = 4 (∵ a > 0)
∴ From (1), 4b² = 15(4) = 60
⇒ b² = 15
Hence the required equation of the ellipse is \(\frac{x^2}{16}+\frac{y^2}{15}\) = 1

Question 3.
Find the equation of the ellipse in the standard form such that the distance between foci is 8 and the distance between directrices is 32.
Solution:
Given that the distance between foci = 8
∴ 2ae = 8
⇒ ae = 4 ……(1)
The distance between the directrices is ZZ’ = 32
⇒ 2 \(\frac{a}{e}\) = 32
⇒ \(\frac{a}{e}\) = 16 ……..(2)
From (1) and (2),
(ae) (\(\frac{a}{e}\)) = 4(16)
⇒ a² = 64
⇒ a = 8
b² = a²(1 – e²)
= a² – a²e²
= 64 – 16
= 48
∴ The equation of the required ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
⇒ \(\frac{x^2}{64}+\frac{y^2}{48}=1\)

Question 4.
Find the eccentricity of the ellipse (in standard form), if the length of the latus rectum is equal to half of its major axis.
Solution:
Let the ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Length of the latus rectum of the ellipse = \(\frac{2 b^2}{a}\)
Length of major axis = 2a
∴ \(\frac{2 b^2}{a}\) = a
⇒ 2b² = a2
⇒ 2a²(1 – e²) = a²
⇒ 2(1 – e²) = 1
⇒ 1 – e² = \(\frac{1}{2}\)
⇒ e² = \(\frac{1}{2}\)
⇒ e = \(\frac{1}{\sqrt{2}}\)
∴ The eccentricity of the ellipse is \(\frac{1}{\sqrt{2}}\).

Question 5.
The distance of a point on the ellipse x² + 3y² = 6 from its centre is equal to 2. Find the eccentric angles.
Solution:
Given ellipse is x² + 3y² = 6
\(\frac{x^2}{6}+\frac{y^2}{2}=1\) ……(1)
Comparing with \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\), we have a² = 6, b² = 2.
∴ a = √6, b = √2
The Centre of the ellipse (1) is C = (0, 0)
Let P = (a cos θ, b sin θ) = (√6 cos θ, √2 sin θ) which is a point on the ellipse whose distance from C(0, 0) is equal to 2.
∴ CP = 2
⇒ \(\sqrt{6 \cos ^2 \theta+2 \sin ^2 \theta}\) = 2
⇒ 6 cos²θ + 2 sin²θ = 4
⇒ 6 cos²θ + 2 (1 – cos²θ) = 4
⇒ 4 cos²θ = 2
⇒ cos²θ = \(\frac{1}{2}\)
⇒ cos θ = ±\(\frac{1}{\sqrt{2}}\)
⇒ θ = \(\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4}\)

Question 6.
Find the equation of the ellipse in the standard form, if it passes through the points (-2, 2) and (3, -1).
Solution:
Let the equation of the ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) …….(1)
since (1) passes through (-2, 2) we have \(\frac{4}{a^2}+\frac{4}{b^2}=1\) ……..(2)
since (1) passes through (3, -1) we have \(\frac{9}{a^2}+\frac{1}{b^2}=1\) ……(3)
From (2) and (3)

Question 7.
If the ends of the major axis of an ellipse are (5, 0) and (-5, 0). Find the equation of the ellipse in the standard form if its focus lies on line 3x – 5y – 9 = 0.
Solution:
Let A(5, 0), A’ = (-5, 0) are the ends of the major axis of an ellipse.
Since the Y coordinates of A, A’ is zero,
The major axis is y = 0
⇒ Major axis lies along the x-axis
∴ The equation of the required ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a > b)
Also 2a = AA’ = \(\sqrt{(-5-5)^2}=\sqrt{(-10)^2}\) = 10
⇒ a = 5
Focus is S = (+ae, 0) = (5e, 0).
Given that focus lies on line 3x – 5y – 9 = 0
⇒ 3(5e) – 5(0) – 9 = 0

Question 8.
If the length of the major axis of an ellipse is three times the length of its minor axis then find the eccentricity of the ellipse.
Solution:
Let the ellipse in the standard form be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) ……(1)
The length of the major axis is ‘a’ and the length of the minor axis is ‘b’.
Given that a = 3b
⇒ a² = 9b²
⇒ a² = 9a²(1 – e²)
⇒ 1 – e² = \(\frac{1}{9}\)
⇒ e² = \(\frac{8}{9}\)
⇒ e = \(\frac{2 \sqrt{2}}{3}\)
∴ Eccentricity of the ellipse = \(\frac{2 \sqrt{2}}{3}\)

II.

Question 1.
Find the length of the major axis, minor axis, latus rectum, eccentricity, coordinates of centre, foci, and the equations of directrices of the following ellipse. (New Model Paper)
(i) 9x² + 16y² = 144
Solution:
The given equation of the ellipse is 9x² + 16y² = 144
Writing this in the standard form we get \(\frac{x^2}{16}+\frac{y^2}{9}=1\) and comparing with S = 0.
We get a² = 16, and b² = 9
⇒ a = 4 and b = 3
Here a > b
(i) Length of the major axis = AA’= 2a = 2(4) = 8
(ii) Length of the minor axis is = BB’ = 2b = 2(3) = 6
(iii) Length of the latus rectum = \(\frac{2 b^2}{a}=\frac{2(9)}{4}=\frac{9}{2}\)
(iv) Eccentricity = \(\sqrt{\frac{a^2-b^2}{a^2}}=\sqrt{\frac{16-9}{16}}=\sqrt{\frac{7}{4}}\)
(v) Coordinates of centre = (0, 0)
(vi) Foci = (±ae, 0) = (±√7, 0)
(vii) Equation of directrices are x = \(\pm \frac{a}{e}\)
⇒ x = \(\pm \frac{4}{\frac{\sqrt{7}}{4}}=\pm \frac{16}{\sqrt{7}}\)
⇒ √7x = ±16
⇒ √7x ± 16 = 0

(ii) 4x² + y² – 8x + 2y + 1 = 0 (Mar. ’10, ’11)
Solution:
4x² – 8x + y² + 2y + 1 = 0
⇒ 4x² – 8x + 4 + y² + 2y + 1 = 4
⇒ 4(x² – 2x + 1) + y² + 2y + 1 = 4
⇒ 4 (x – 1)² + (y + 1)² = 4
⇒ \(\frac{(x-1)^2}{1}+\frac{(y+1)^2}{4}=1\)
Comparing with \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\)
Where a² = 1 and b² = 4
⇒ a = 1 and b = 2 and a < b.
(i) Length of the major axis = BB’ = 2b = 2(2) = 4
(ii) Length of the minor axis = AA’ = 2a = 2(1) = 2
(iii) Length of the latus rectum = \(\frac{2 a^2}{b}=\frac{2(1)}{2}\) = 1
(iv) Eccentricity = \(\sqrt{\frac{b^2-a^2}{b^2}}=\sqrt{\frac{4-1}{4}}=\frac{\sqrt{3}}{2}\)
(v) Coordinates of centre = (1, -1)
(vi) foci = (h, k ± be)
= \(\left(1 , -1 \pm 2\left(\frac{\sqrt{3}}{2}\right)\right)\)
= (1, -1 ± √3)
(vii) Equations of directrices is y = k ± \(\frac{b}{e}\) = \(-1 \pm \frac{2}{\left(\frac{\sqrt{3}}{2}\right)}=-1 \pm \frac{4}{\sqrt{3}}\)
⇒ √3y + √3 ± 4 = 0

(iii) x² + 2y² – 4x + 12y + 14 = 0
Solution:
The given equation can be written as x² – 4x + 2y² + 12y = -14
⇒ x² – 4x + 4 + 2(y² + 6y) = -14 + 4
⇒ x² – 4x + 4 + 2(y² + 6y + 9) = -14 + 4 + 18
⇒ (x – 2)² + 2(y + 3)² = 8
⇒ \(\frac{(x-2)^2}{8}+\frac{(y+3)^2}{4}\) = 1 …….(1)
Comparing the given ellipse (1) with \(\frac{(x-h)^2}{a^2}+\frac{(y+k)^2}{b^2}\) = 1, we get
h = 2, k = -3, a² = 8, b² = 4
⇒ a = 2√2, b = 2
Clearly a > b
(i) Length of the major axis = AA’
= 2a
= 2(2√2)
= 4√2
(ii) Length of the minor axis is BB’ = 2b
= 2(2)
= 4
(iii) Length of the latus rectum = \(\frac{2 b^2}{a}\)
= \(\frac{2(4)}{2 \sqrt{2}}\)
= 2√2
(iv) Eccentricity = \(\sqrt{\frac{a^2-b^2}{a^2}}=\sqrt{\frac{8-4}{8}}=\sqrt{\frac{4}{8}}=\frac{1}{\sqrt{2}}\)
(v) Coordinates of centre = (2, -3)
(vi) Foci = (h ± ae, k)
= \(\left(2 \pm 2 \sqrt{2} \cdot\left(\frac{1}{\sqrt{2}}\right),-3\right)\)
= (2 ± 2, -3)
= (4, -3),(0, -3)
(vii) Equation of directrices are x = \(h \pm \frac{a}{e}\)
= \(2 \pm \frac{2 \sqrt{2}}{(1 / \sqrt{2})}\)
= 2 ± 4
∴ x = 6, x = -2 are the equations of directrices.

Question 2.
Find the equation of the ellipse in the form \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}\) = 1, given the following data.
(i) Centre (2, -1), one end of the major axis (2, -5), e = \(\frac{1}{3}\)
Solution:
Centre C(h, k) = (2, -1)
Let one end of the major axis is B = (2, -5)
Since the x-coordinates of C and B are the same and equal to ‘2’,
the major axis of an ellipse is x = 2 which is a line parallel to the y-axis.
The equation of ellipse is \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}\) = 1 where a < b.
CB = b where C = (2, -1) and B = (2, -5)
∴ b = \(\sqrt{(2-2)^2+(-1+5)^2}\) = 4
But a² = b²(1 – e²)
= 16(1 – \(\frac{1}{9}\))
= \(\frac{128}{9}\)
∴ The equation of the required ellipse is \(\frac{(\mathrm{x}-\mathrm{h})^2}{\left(\frac{128}{9}\right)}+\frac{(\mathrm{y}+1)^2}{16}=1\)
⇒ \(\frac{9(x-2)^2}{128}+\frac{(y+1)^2}{16}=1\)
⇒ 9(x – 2)² + 8(y + 1)² = 128

(ii) Centre = (4, -1) one end of the minor axis is (-1, -1) and passes through (8, 0).
Solution:
Given centre C(h, k) = (4, -1) and one ends of the minor axis is (-1, -1).
Let A = (-1, -1)
Since the y-coordinates of C and A are the same and equal to ‘-1’, the minor axis is parallel to the X-axis.
∴ Major axis parallel to Y-axis.
∴ a = CA = \(\sqrt{(4+1)^2+(-1+1)^2}\) = 5
∴ The equation of the required ellipse is \(\frac{(\mathrm{x}-\mathrm{h})^2}{\mathrm{a}^2}+\frac{(\mathrm{y}+\mathrm{k})^2}{\mathrm{~b}^2}=1\)
⇒ \(\frac{(x-4)^2}{25}+\frac{(y+1)^2}{b^2}=1\) ……(1)
Since Ellipse is passing through the point (8, 0) we have \(\frac{(8-4)^2}{25}+\frac{1}{b^2}=1\)

∴ Required equation of ellipse is (x – 4)² + 9(y + 1)² = 25.

(iii) Centre (0, -3), e = \(\frac{2}{3}\), semi minor axis is 5.
Solution:
Given that centre C(h, k) = (0, -3), e = \(\frac{2}{3}\)
Semi minor axis = 5
The equation of the required ellipse is \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\)
Case (1): If a > b then b² = a²(1 – e)²
Given semi-minor axis b = 5

Case (2): If a < b then a² = b²( 1 – e²)
semi minor axis = 5
⇒ a = 5

(iv) Centre (2, -1), e = \(\frac{1}{2}\), length of latus rectum = 4.
Solution:
Given C(h, k) = (2, -1), e = \(\frac{1}{2}\), length of latus rectum = 4
Case (1): Where a > b, we have b² = a²(1 – e²)
and length of latus rectum =


⇒ (x – 2)² + 9(y + 1)² = 64 is the required equation of ellipse.

Question 3.
Find the radius of the circle passing through the foci of an ellipse 9x² + 16y² = 144 and having the least radius.
Solution:
Given the equation of the ellipse is 9x² + 16y² = 144
\(\frac{x^2}{16}+\frac{y^2}{9}=1\)
Compared with the general equation we have
a² = 16, b² = 9
⇒ a = 4 and b = 3
Foci of ellipse = (±ae, 0)
Also since a² > b² we have b² = a²(1 – e²)
⇒ 9 = 16(1 – e²)
⇒ 1 – e² = \(\frac{9}{16}\)
⇒ e² = 1 – \(\frac{9}{16}\) = \(\frac{7}{16}\)
⇒ e = \(\frac{\sqrt{7}}{4}\)
Eccentricity of ellipse (e) = \(\frac{\sqrt{7}}{4}\)
∴ Focus = (±ae, 0)
= \(\left(\pm 4\left(\frac{\sqrt{7}}{4}\right), 0\right)\)
= (±√7, 0)
Now the equation of a circle having (√7, 0) and (-√7, 0) as extremities of diameter is given by
(x – √7 ) (x + √7 ) + (y – 0) (y – 0) = 0
⇒ x² + y² = 7
Hence the least radius of the circle x² + y² = 7 is √7.

Question 4.
A man running on a race course notices that the sum of the distances between the two flag posts is always 10m. and the distance between the flag posts is 8m. Find the equation of the race course traced by the man.
Solution:

Given AA’ = 2a = 10
⇒ a = 5 (Taking flag posts located at A & A’)
Also given the distance between two fixed points S and S’ = 8m
∴ 2ae = 8
⇒ ae = 4
∴ b² = a²(1 – e²)
⇒ a² – a²e² = 25 – 16 = 9
⇒ b² = 9
Hence the equation of ellipse is \(\frac{x^2}{25}+\frac{y^2}{9}\) = 1.

III.

Question 1.
A line of fixed length (a + b) moves so that its ends are always on two fixed perpendicular straight lines. Prove that a marked point on the line, which divides this line into portions of length ‘a’ and ‘b’ describes an ellipse and also finds the eccentricity of the ellipse when a = 8, b = 12.
Solution:

Let AB be a line of fixed length and a + b which moves with its end A, B on the x and y-axis.
AB = a + b
Let P(x₁, y₁) be any point on the line AB and BP = a, and AP = b.
Let M and N be the projections of P on the x and y-axis.
Such that OM = x₁ and ON = y₁

Question 2.
Prove that the equation of the chord joining the points ‘α’ and ‘β’ on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) is \(\frac{{x}}{a} \cos \left(\frac{\alpha+\beta}{2}\right)+\frac{y}{b} \sin \left(\frac{\alpha+\beta}{2}\right)=\cos \left(\frac{\alpha-\beta}{2}\right)\).
Solution:
Let S = \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\) = 0 be the given ellipse
and let P = (a cos α, b sin α) and Q = (a cos β, b sin β) be the two given points on the ellipse S = 0.
The equation of the chord PQ is

Dividing by ‘ab’ on both sides, the equation of the chord joining the points (α, β) on the ellipse S = 0 is \(\frac{{x}}{a} \cos \left(\frac{\alpha+\beta}{2}\right)+\frac{y}{b} \sin \left(\frac{\alpha+\beta}{2}\right)=\cos \left(\frac{\alpha-\beta}{2}\right)\)

Telangana TSBIE TS Inter 2nd Year English Study Material Revision Test-II Exercise Questions and Answers.

TS Inter 2nd Year English Study Material Revision Test-II

Time: 1 1/2 Hrs
Marks : 50

Section – A

Question 1.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) Undoubtedly women in ancient India enjoyed a much higher status than their descendants in the eighteenth and nineteenth centuries.
Answer:
The given lines occur in the informative essay “The Awakening of Women”. This article was composed by a committed writer K.M. Phanikkar. The article deals with the status of women over various periods. Every statement is backed with supporting details.

The essay focuses mainly on the impact the Gandhian Movement had on the progress of women. Yet, the writer states how women’s status was in the past. Women ancient India had a respectable position. It is only in the eighteenth and nineteenth centuries that women’s condition touched a pathetic low. The given lines highlight the fact that writer is balanced but not biased.

b) It was a matter of surprise to the outside world that independence of India should have appointed women to the highest posts so freely, as members of the Cabinet,
Answer:
The given lines occur in the informative essay “The Awakening of Women”. This article was composed by a committed writer, K.M. Phanikkar. The article deals with the status of women’s over various periods. Every statement is backed with supporting details. The position of women started to improve with their active participation in the Gandhian Movement, showed constant progress in all fields.

In pre-independent India, legislation was made in favour of their rights. After India became independent, women were appointed in both key government and administrative posts. This surprised the world. People outside India thought that India was very conservative regarding women’s position. Thus the lines play an important role in clearing certain prejudices.

Question 2.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) He rests at case beneath some pleasant weed.
Answer:
Introduction:
The above line is taken from the sonnet “On the Grasshopper and Cricket” written by John Keats. He denoted his life to the perfection of poverty.

Context and Meaning:
Here the poet expresses his feelings, regarding natures song. The Grasshopper and the Cricket are used as symbols. Seasons may come and go. But Nature never fails to inspire us with its songs. When birds, stop singing in extreme heat, during the summer. The earth is filled with songs of a grasshopper. We can hear the voice of the grasshopper who runs from hedge to hedge. He keeps singing tiredlessly and when he gets tired with fun, he goes under some pleasant weed to take rest.

Critical Comment:
The poet sends the message that nature is beautiful all the line, irrespective of the season.

b) And seems to one in drowsiness half lost, The Grasshopper’s among some grassy hills.
Answer:
Introduction:
These are the conducting lines of the poem “On the Grasshopper and Cricket?? written by John Keats, a Romantic poet. He devoted his life to the perfection of poetry.

Context and Meaning:
John Keats celebrates the music of the Earth. He finds beauty in hot summer as well as in the cold winter. Here, the grasshopper is symbol of hot summer and cricket is symbol of cold winter. During the winter season in the frosty evening, the birds stop singing songs. At that time the cricket begins to sing. He spreads the warmth ofjoy everywhere. The people who are half sleep feel that it is the grasshopper song which is coming from the grassy hills. Thus, he depicts the beauty of Nature.

Critical Comment:
The poet sends the message that nature is beautiful all the time, irrespective of the season. In a similar way, we should be joyful in our life and be happy in all situations.

Question 3.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) But when the movement was actually started, women were everywhere at the forefront. Elaborate.
Answer:
The essay “The Awakening of Women” traces the evolution women’s progress in India over ages. K.M. Panikkar, a multifaceted genius, discusses the theme at length. Facts have been presented in a systematic order. Supporting details have been provided, Gandhiji understood the power of women. He believed that women could be an inexhaustible source of power.

He gave a call to them to participate in his movement. But, he had certain doubts about their readiness. His doubts were proved to be baseless. Women were very active in every area. They picketed liquor shops. They boycotted foreign goods. They took part in civil disobedience. Nowhere were women inferior to men. It was in fact the other way round.

b) Name some legislative reforms mentioned in the essay The Awakening of Women that seek to establish the equality of women.
Answer:
“The Awakening of Women” traces the evolution women’s progress in India over ages. K.M. Panikkar, a multifaceted genius, discusses the theme at length. Facts have been presented in a systematic order. Supporting details have been provided. Women’s active part in the struggle for freedom initiated a positive change in their status.

Even before India attained independence, laws were enacted and enforced in their favour. And that process continued after independence. Rights to property, to freedom of marriage, to education and employment, raising the age of marriage and the prevention of the dedication of women to temple services were some major legislative reforms.

Question 4.
Answer ANYONE of the following questions in about 100 words [1 × 4 = 4]

a) What is the theme of the poem On the Grasshopper and Cricket?
Answer:
The poem “On the Grasshoppers and Cricket’ is written by John Keats, an English Romantic poet. He has devoted his life to the perfection of poetry. In this poem, John Keats depicts the beauty of Nature. He says that the poetry of earth as symbols to praise Nature is never ending beauty. Seasons may come and go but Nature never fails to inspire us with its songs.

When birds stop singing in extreme heat, the earth is filled with the songs of a grasshopper. He sings endlessly, but when tired rests under some pleasant weed. During winter birds stop singing. There is a deathly silence. Frost spreads its blanket over Nature. Regardless, a shrill second cOmes from beneath stones and it is the cricket singing. Its song restores warmth. Thus, the small creatures prove to the world that the poetry of earth never ceases.

b) Discuss the common features between the grasshopper and cricket.
Answer:
The poem “ On the Grasshopper and Cricket” is written by John Keats. He is an English Romantic poet. He has developed his life to the perfections of poetry. In this poem, he depicts the beauty of nature. He says that the poetry of earth never ceases. He uses the Grasshopper and the Cricket as symbol to praise nature’s never ending beauty.

Seasons may come and go. But, nature never fails to inspire us with its songs. Therefore both the grasshopper and the cricket are the representative voices of nature’s music or poetry. Both offer a soothing effect to the extremities of climate. The grasshoppers song balances the extreme heat during the summer by providing music that is comforting and pleasing the cricket does the same during winter.

Question 5.
Answer ANYONE of the following questions in about 100 words. [1 × 4 = 4]

a) “Love, sacrifice and generosity are the essential elements for happy living”. Explain the statement with reference to the story A Gift for Christmas.
Answer:
A Gift for Christmas” is a well-known short story by O. Henry. The original name of the author is William Sydney Porter. This story was first published in 1905. A Gift for Christmas” is a Christmas story, and it functions as a parable about both the nature of love and the true meaning of generosity. Della’s earnest desire to buy a meaningful Christmas gift for Jim drives the plot of the story, and Jim’s reciprocity of that sentiment is shown when he presents Della with the tortoise-shell combs. Both Jim and Della give selflessly, without expectation of reciprocity. Their sole motivation is to make the other person happy. This, combined with the personal meaning imbued in each of the gifts, conveys the story’s moral that true generosity is both selfless and thoughtful.

b) Sketch the character of Jim.
Answer:
A Gift for Christmas” is a well-known short story by O. Henry. The original name of the author is William Sydney Porter. This story was first published in1905. Jim is a thin man of twenty two. He does not have enough income to support his wife. He bears the burden of fulfilling everyday demands of his wife. He is a very punctual person that why he constantly looks at his watch.

Section – B

Question 6.
Read the following passage and answer ANV FIVE questions given below: [5 × 1 = 5]

Della’s white fingers quickly opened the package. And then at first a scream of joy followed by a quick feminine change to tears. For, there lay The Combs — the set of combs, side and back, that Della had seen in a Broadway window and liked so much. They were beautiful combs, so expensive and they were hers now. But alas, the hair in which she was to wear them was sold and gone! She took them up lovingly, smiled through her tears and said, ‘My hair grows so fast, Jim!’

i) Who gave the package to Delia?
Answer:
to sharpen it

ii) What was Della’s reaction at first?
Answer:
We become better persons

iii) How did her joy change?
Answer:
No

iv) What did Della find in the package?
Answer:
the graphite inside

v) Where had she seen the combs earlier?
Answer:
because every action leaves a mark

vi) The combs were inexpensive. Write true or false.
Answer:
True

vii) Write the antonym of the word happy from the passage.
Answer:
exterior

viii) Write he synonym of the word shout from the passage.
an:
sorrows

Question 7.
Study the following advertisement and answer ANY FIVE questions that follow. [5 × 1 = 5]

i) Expand SHIP.
Answer:
Swach Hyderabad Internship Programme

ii) What are the eligibility criteria for participating in the programme?
Answer:
Social responsibility, passion, above 18years of age.

iii) Can very young boys and girls participate in this programme?
Answer:
no

iv) State any two themes of the internship programme.
Answer:
Lake cleanup, plantation

v) Registration is both online and offline. Write true or false.
Answer:
false

vi) When is the programme scheduled to begin?
Answer:
21st January 2022

vii) The number of hours of-the schedule is ___________ . (Fill in the blank.)
Answer:
20

viii) Write the word used in the ad to mean ‘a short term training period for practical experience’.
Answer:
Internship

Question 8.
Study the bar graph below and answer ANT FIVE questions given after it. [5 × 1 = 5]

i) What does the bar graph present?
Answer:
Sales of ice-creams of different flavours

ii) Ice cream of which flavour do people like the most in shop A?
Answer:
Ice-cream of mango flavours

iii) How many ice creams of almond flavour are sold in shop B?
Answer:
65

iv) Find the total number of ice creams of chocolate flavour sold in shop A and shop B.
Answer:
165

v) 30 ice creams of coconut flavour are sold in ___________. (Fill in the blank.)
Answer:
shop B

vi) Ice cream of which flavour do people like more in shop B, Chocolate or Vanilla?
Answer:
Chocolate

vii) How many ice creams of mango flavour are sold in shop A?
Answer:
100

viii) How many ice cream flavours are shown in the graph?
Answer:
5

Section – C

Question 9.
Rewrite the following passage using FIVE punctuation marks wherever necessary- [5 × 1 = 5]

The brahmo samaj led the movement for emancipation the ancient rules of purdah were broken and brahmo women moved freely in society: but this was. but a false dawn as it was far in advance of popular opinion.
Answer:
The Brahmo Samaj led the movement for emancipation. The ancient rules of purdah were broken and Brahmo women moved freely in society: but this was but a false dawn as it was far in advance of popular opinion.

Question 10.
Match the following words in Column ‘A’ with their definitions in Column ‘B’. [5 × 1 = 5]
Column A —– Column B
i) amphibious   ( ) a) lasting for a very short time
ii) antidote       ( ) b) designed to cause death
iii) ephemeral  ( ) c) living on land as well as in water
iv) lethal          ( ) d) someone who has a lot of experience in a field
v) veteran        ( ) e) a substance that can act against the effect of poison
Answer:
i) c
ii) e
iii) a
iv) b
v) d

Telangana TSBIE TS Inter 2nd Year English Study Material Revision Test-I Exercise Questions and Answers.

TS Inter 2nd Year English Study Material Revision Test-I

Time : 1 1/2 Hrs
Marks : 50

Section – A

Question 1.
Annotate ANY ONt of the following in about 100 words. [1 × 4 = 4]

a) If someone maintains that two and two are five or that Iceland is on the equator, you feel pity rather than anger.
Answer:
Introduction:
These beautiful lines are taken from the thought-provoking essay,” How to Avoid Foolish Opinions” written by Bertrand Russell. His clarity of thought and fluency of expression lend beauty to his style.

Context and Meanings:
Russell gives us tips on how to avoid foolish opinions. He says that there are many ways to avoid being dramatic. To avoid foolish opinions, no super human or genius is required. Many matters are less easily brought to the test of experience. If we hear views opposite to our opinions, it makes us angry. It is a sign that we actually have no good reason for our opinion. If someone has very stupid and wrong opinions, we feel pity rather than anger. So, we must carefully reconsider our ideas.

Critical Comment:
Though the article discusses many mistakes mankind is prove to make, it ends with a lively ray of hope.

b) Persecution is used in theology, not in arithmetic because in arithmetic, there is knowledge, but in theology, there is only opinion.
Answer:
Introduction:
These lines are taken from the thought provoking essay, “How to Avoid Foolish Opinion” written by Bertrand Russell. His clarity of thought and fluency of expression lend beauty to his style.

Context and Meanings:
Russell gives us tips on how to avoid foolish opinion. Here, he teas us about controversies. The worst controversies are about matters which have no good evidence either way. If you can not observe an issue, think about any biases you might have about it. This is because belief can go beyond facts. Persecution means annoying others deliberately all the time, the theology is required belief where as arithmetic is require facts and figures. Hence, persecution is not used in arithmetic but in theology – the study of God and religion.

Critical Comment:
The author says that belief can go beyond facts.

Question 2.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) We are meeting today to wish her bon voyage.
Answer:
Reference:
These lines are taken from the satirical and humorous poem “Goodbye party for Miss Pushpa TS” by Nission Ezekid, a.versalite Indo-Anglian poet with a great sense of humour and wit.

Context and Explanation:
It is a farewell speech for miss pushpa, who is leaving the country the poem is a parody of English as used by some indians. The speaker adresses his colleagues as friends and miss pushpa as sister.

Critical Comment:
The lines highlight the speaker’s good nature and good intention. The style is simple and clear.

b) That is showing good spirit. I am always appreciating the good spirit
Answer:
Reference:
These lines are extracted from the satirical and humorous peom “Goodbye party for Miss Pushpa TS” written by Nission Ezhekiel, a versatile Indo-Anglion poet with a great sense of humour and wit. The poem is a parody of English as used by some Indians.

Context and Explanation:
It is a farewell speech for Miss pushpa, who is leaving the country. On the occasion, the speaker is praising the helpful nature of Miss. Pushpa. He praises her good nature. Whenever he asked her to do anything, she was saying that she would do it just now only. This reply from her is showing her good spirit and he is always appreciating the good spirit.

Critical Comment:
This shows her good spirit and her readiness to do any work she is a willing worker.

Question 3.
Answer ANY ONE of the following questions in about 100 words [1 × 4 = 4]

a) How can we prevent developing a dogmatic attitude as per Russell’s suggestion?
Answer:
The thought provoking essay,”How to Avoid Foolish Opinion’s” is written by Bertrand Russell. In this essay, he says that there are many ways to avoid being dogmatic. Making a keen observation where it can settle the bias is the first way. Next to know what other people think.

One has to be aware of what they think. This can be done by going on vacation and talking to people with different ideas. The third is arguing with an imaginary character. The fourth one is to deal with one’s sense of self worth. To overcome conceit, we must remember that we live for a short while on a small planet in vast cosmos.

b) What does Bertrand Russell say about a person getting angry about a difference of opinion?
Answer:
The thought provoking essay,”How to Avoid Foolish Opinions” is wiitten by Bertrand Russell. In this essay, he gives us tips on how to avoid foolish opinions and being dogmatic. He advices us to identify our weak points and reconsider our opinions. when we hear views opposite to our opinions. It makes us angry. It is a clear sign of something wrong with our beliefs, then we must carefully reconsider our ideas. We have to be aware of what other people think. Thus, we can avoid such problem.

Question 4.
Answer ANY ONE of the following questions in about 100 words [1 × 4 = 4]

a) How does the speaker describe Miss Pushpa in the poem?
Answer:
The poem “Goodbye Party for Miss Pushpa T.S.” is written by Nission Ezekiel. He is a versatile poet with a great sense of humor and wit. His present poem is a parody of English as used by some Indians. It is a farewell speach for Miss Push pa, who is going abroad. On this occasion, they have gathered there to hid farewell to her. A person comes and gives a speech. the poet creates humour through the speakers description of Miss Pushpa.

The speaker describes not only her internal but external sweetness. He says that she always ‘smiles’ without reason. He describes her good and amicasle nature. He also refers to her helpful qualities. He appreciates her concern for friends. He says that she always says ‘yes’ to any of their request. Thus, he is trying to exaggesate to show his love and respect for her. But, he doesn’t realize that he is describing her humorously and very lovsely. He doesn’t mind that his English is wrong linguestically. Thus, he describes her humorously with his Babu English.

b) Does the poem bring out the sweetness of Miss Pushpa? Justify your answer.
Answer:
The poem “Goodbye party for Miss Pushpa TS” is written by Nission Ezekiel. He is a versatile poet with a great sense of humour and wit. The poem is an extract from his volume of pems. ‘Hymns in Darkness’. It is an parody of English as used by Some Indians. It is farewell party for Miss. Pushpa, who is going abroad for better prospects. The Speaker announces in the very beginning that they have gathered there to bid farewell to her.

They want to wish her a happy journey. On this occasion, the speaker brings out the sweetness Miss Pushpa. He starts praising her sweetness which is both internal and external. She is beautiful not only because of her charms, but her honesty also. She is a sweet lady with all smile on her face. She smiles without a reason. She belongs to a reputed family. She is very popular among people. She is always ready to do anything for everyone. Thus the poem brings out the sweetness of Miss Pushpa. It appreciates her concern for friends. These are sweet qualities of Miss Pushpa.

Question 5.
Answer ANY ONE of the following questions in about 100 words; [1 × 4 = 4]

a) Describe the character of Arun, the boarding school boy?
Answer:
Ruskin Bond is a well-known contemporary Indian writer of British descent. He wrote many books inspirational children’s books and was honoured with the Sahitya Akademi Award for his literary work. The present short story represent from “The women on plat form No. 8” the main idea of is a story about love and affection that overcomes all sense of belonging barriers.

Arun was a boarding school student. He was returning to school. His parents thought he was old enough to travel alone. So he took a bus from his hometown to Ambala, arriving early in the evening. The train he needed to catch left at 12 a.m. He was waiting for the northbound train on platform 8 at Ambala station. It had been a long time for him. He walked up and down the platform, browsing the book stall and feeding Street dogs biscuits. He stood there watching the trains come and go. Whenever a train arrived, the platform became a center for activity, and it would be quiet after the train had left. He sat down on his suitcase, tired of pacing around the platform, and stare at the railway tracks.

A soft voice asked from behind if he was alone. Arun saw a middle aged woman in white sari, with dark kind eyes leaning over him. There was some kind of dignity about her which made Arun stand up respectfully and answer. He told her that he was alone and that he was going to school. She asked him if his parents had not come to see him off. Arun said that he did not live there and he could travel alone. The lady agreed with him. Arun liked her for her simplicity, her deep soft voice and the serenity of her face.

b) What made Arun call the strange woman ‘mother’ at the end?
Answer:
Ruskin Bond is a well-known contemporary English Indian writer. He wrote a number of inspirational children’s books and was awarded the Sahitya Akademi Award for his literary work. The following is a short story from “The Women on Plat Form No. 8.” This short story’s core concept is about love and affection overcoming all obstacles to belonging.

Arun called the stranger woman ‘mother’ at the end, because she had treated him tenderly and offered him tea and sweets. She listened to him and showed trust in him. He liked her kindness and graceful behaviour. She introduced herself as his mother. She supported Arun against satish’s mother, Arun wanted to repay her kindness by acknowledging her as mother.

Section – B

Question 6.
Read the following passage and answer ANY SIX questions given below: [6 × 1 = 6]

I was going to refuse out of shyness and suspicion, but she took me by the hand. Then I felt it would be silly to pull my hand away. She told a porter to look after my suitcase and then she led me down the platform. Her hand was gentle. She held my hand neither too firmly nor too lightly. I looked up at her again. She was not young, but she was not old.

i) Name the short story from which this passage is taken.
Answer:
The Woman on Platform No. 8

ii) What was Arun going to do?
Answer:
To Refuse out of shyness and suspicion

iii) How did she hold his hand?
Answer:
neighter to firmly nor too lightly

iv) How did Arun feel of taking back his hand away?
Answer:
He felt silly

v) What did she tell a porter?
Answer:
To look after Arun’s suitcase

vi) Pick out the word from the passage which means tender.
Answer:
Gentle

vii) ‘She held my hand neither too firmly nor too lightly.’ Say true or false.
Answer:
True

viii) Rewrite the sentence “She was not young, but she was not old.” using “neither. nor……”.
Answer:
She was neither young nor old.

Question 7.
Read the following passage and answer ANY SIX questions given below: [6 × 1 = 6]

The Warrior Who Broke All Barriers The very word COVID spreads dread worldwide. But, Dr Annam Srinivasa Rao of Khammam stands out as an exception. Putting his life at risk, he served a large number of COVID patients in various ways. His organization served food and extended medical facilities to them while alive. When died, the Foundation arranged for transportation and last rites of hundreds of bodies when their own families abandoned the bodies!

When he was tested positive, he was worried, not of his health, but of the people who needed his service! By looking after hundreds of disabled (both physically and mentally) orphans from far and near for over a decade, his organization – Annam Seva Foundation, Danvaigudem, Khammam – has redefined philanthropy. He was inspired into this service when he himself grew up in an orphanage. His struggles to secure some employment helped him master the art of taking everything in his stride. Thus, he continues his services undeterred by police cases, neighbours’ wrath, financial constraints etc. An admirable spirit indeed!

i) What makes one describe Dr Annam Srinivasa Rao as the warrior who broke all barriers?
Answer:
Has he put his life at risk and served COVID patients also

ii) How does the world respond to the word COVID, according to the passage?
Answer:
Reads the word COVID

iii) Why was Dr Annam Srinivasa Rao worried when he tested positive?
Answer:
Of the people who needed his service and missed it

iv) Name the organization that he founded and its location.
Answer:
Annam Seva Foundation: Danavayagudem, Khammam

v) Why did Dr Annam Srinivasa Rao choose this path?
Answer:
Has he him self growup in a orphanage

vi) Pick out from the passage the one-word substitute that means selfless service out of love for humanity.
Answer:
Phinlanthropy

vii) Find out from the passage the phrasal verb that means taking full care and responsibility of.
Answer:
Looking after

viii) Write the idiom used in the passage that means accepting and dealing with difficulties without letting them worry one too much
Answer:
Taking something in one’s stried

Question 8.
Study the pie-chart below and answer any Six questions given after it. [6 × 1 = 6]

i) What does the pie chart show?
Answer:
favourite beverages of people

ii) How many beverages are taken into account?
Answer:
5

iii) What is the most preferred beverage?
Answer:
Coconut Water (38%)

iv) How many people preferred coffee?
Answer:
15%

v) What is the least preferred beverage?
Answer:
Sugarcane Juice

vi) People who preferred tea are _____________.
Answer:
25%

vii) People who preferred cola are __________.
Answer:
12%

viii) People who preferred Coconut water are 27%. Write true or false.
Answer:
False

Section – C

Question 9.
Rewrite’th6 following passage using SIX of the punctuation marks wherever necessary. [6 × 1 = 6]

It is more difficult to deal with the self-esteem of man as a man because we cannot argue out the matter with some non-human mind, the only way I know of dealing with this general human conceit is to remind ourselves that man is a brief episode in the life of a small planet in a little comer of the universe and that for aught we know other parts of the cosmos may contain beings as superior to ourselves as we are to jellyfish.
Answer:
It is more difficult to deal with the self-esteem of man as a man because we cannot argue out the matter with some non- human mind. The only way I know of dealing with this general human conceit is to remind ourselves that man is a brief episode in the life of a small planet in a little corner of the universe and that, for aught we know, other parts of the cosmos may contain beings as superior to ourselves as we are to jellyfish.

Question 10.
Match the following words in Column ‘A’ with their definitions in Column ‘B’. [6 × 1 = 6]
Column A —- Column B
i) ambidextrous   ( ) a) one who eats excessively
ii) contemporary ( ) b) something which is out of date
iii) glutton           ( ) c) a person walking on a street
iv) invincible       ( ) d) able to use both hands equally well
v) obsolete         ( ) e) living or occurring at the same time
vi) pedestrian     ( ) f) too strong to be defeated
Answer:
i) d
ii) e
iii) a
iv) f
v) b
vi) c

Students must practice this TS Intermediate Maths 2B Solutions Chapter 3 Parabola Ex 3(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Exercise 3(a)

I.

Question 1.
Find the vertex and focus of 4y² + 12x – 20y + 67 = 0.
Solution:
Given equation is 4y² + 12x – 20y + 67 = 0
⇒ 4y² – 20y = -12x – 67
⇒ 4(y² – 5y) = -12x – 67

Question 2.
Find the vertex and focus of x² – 6x – 6y + 6 = 0.
Solution:
The given equation is x² – 6x – 6y + 6 = 0
⇒ x² – 6x = 6y – 6
⇒ x² – 6x + 9 = 6y – 6 + 9 = 6y + 3
⇒ (x – 3)² = \(6\left(y+\frac{1}{2}\right)=6\left(y-\left(-\frac{1}{2}\right)\right)\)
This is of the form (x – h)² = 4a(y – k)
where h = 3, 4a = 6 ⇒ a = \(\frac{3}{2}\) and k = \(\frac{-1}{2}\)
Vertex = (h, k) = (3, \(\frac{-1}{2}\))
Focus = (h, a + k) = (3, \(\frac{3}{2}-\frac{1}{2}\)) = (3, 1)

Question 3.
Find the equations of the axis and directrix of the parabola y² + 6y – 2x + 5 = 0.
Solution:
The given equation is y² + 6y – 2x + 5 = 0
⇒ y² + 6y = 2x – 5
⇒ y² + 6y + 9 = 2x – 5 + 9 = 2x + 4
⇒ (y + 3)² = 2(x + 2)
⇒ [y – (-3)]² = 2[x – (-2)]
This is of the form (y – k)² = 4a(x – h)
where k = -3, 4a = 2 ⇒ a = \(\frac{1}{2}\), h = -2
∴ Axis is y – k = 0 ⇒ y + 3 = 0
and Directrix is x – h + a = 0
⇒ x + 2 + \(\frac{1}{2}\) = 0
⇒ x + \(\frac{5}{2}\) = 0
⇒ 2x + 5 = 0

Question 4.
Find the equations of the axis and directrix of the parabola 4x² + 12x – 20y + 67 = 0.
Solution:
Given equation is 4x² + 12x – 20y + 67 = 0
⇒ 4(x² + 3x) = 20y – 67

Question 5.
Find the equation of a parabola whose focus is S(1, -7) and whose vertex is A(1, -2). (New Model Paper, Mar. ’12)
Solution:
Given that vertex A(h, k) = (1, -2) and focus S = (1, -7).
Since the x coordinates of A and S are equal and equal to 1,
the axis of the parabola is x = 1 and it is a line parallel to the y-axis.
Also, the focus is below the vertex.
∴ The equation of the parabola is (x – h)² = -4a(y – k)
⇒ (x – 1)² = -4a(y + 2) ……..(1)
where a = AS = \(\sqrt{(1-1)^2+(-2+7)^2}\) = 5
∴ From (1) we have (x – 1)² = -20(y + 2)
Which is the equation of the required parabola.

Question 6.
Find the equation of the parabola whose focus is S(3, 5) and vertex is A(1, 3). (E.Q.)
Solution:
Given vertex A = (1, 3) and focus S = (3, 5)

Let the directrix meets the axis of the parabola at Z(x, y), A is the midpoint of SZ.
Hence \(\frac{\mathrm{x}+3}{2}\) = 1 and \(\frac{\mathrm{y}+5}{2}\) = 3
⇒ x = -1 and y = 1
∴ Coordinates of Z = (-1, 1)
Slope of AZ = \(\frac{5-1}{3+1}\) = 1
∴ Slope of directrix = -1 (∵ directrix is perpendicular to \(\overline{\mathrm{AS}}\))
∴ Equation of directrix L = 0 is y – 1 = -1(x + 1)
⇒ x + y = 0
Let P(x₁, y₁) be any point on the parabola and PM is the perpendicular distance from P to the directrix L = 0 is

⇒ \(\mathrm{x}_1^2+\mathrm{y}_1^2\) – 2x₁y₁ – 12x₁ – 20y₁ + 68 = 0
∴ Locus of (x₁, y₁) is the equation of parabola given by x² + y² – 2xy – 12x – 20y + 68 = 0.

Question 7.
Find the equation of the parabola whose latus rectum is the line segment joining points (-3, 2) and (-3, 1). (E.Q.)
Solution:
Given L = (-3, 2) and L’ = (-3, 1) be the two end points of the latus rectum of the parabola.
Since the x coordinates of L and L’ are ‘1’ we have an axis of the parabola parallel to the x-axis.
∴ The equation of the required parabola is (y – k)² = ±4a(x – h)
The length of the latus rectum LL’ = 4a
⇒ 4a = \(\sqrt{(-3+3)^2+(2-1)^2}\) = 1
⇒ a = \(\frac{1}{4}\)
Let S be the focus of the required parabola Then
S = mid point of LL’ = (h, k)

Question 8.
Find the position (Interior or exterior or on) of the following points with respect to the parabola y² = 6x.
(i) (6, -6)
(ii) (0, 1)
(iii) (2, 3)
Solution:
Given the equation of a parabola is y² – 6x = 0
Comparing with y² = 4ax
we have 4a = 6
⇒ a = \(\frac{3}{2}\)
(i) Let P(x₁, y₁) = (6, -6) be the given point.
Then S₁₁ = \(\mathrm{y}_1{ }^2\) – 4ax₁
= (-6)² – 4(\(\frac{3}{2}\))(6)
= 36 – 36
= 0
∴ The point (6, -6) lies on the parabola y² = 6x.
(ii) Let P(x₁, y₁) = (0, 1) and \(\mathrm{y}_1{ }^2\) – 4ax₁
= 1 – 4(\(\frac{3}{2}\))(0)
= 1
∴ S₁₁ > 0 and the point (0, 1) lies outside the parabola y² = 6x.
(iii) Let P(x₁, y₁) = (2, 3) Then S₁₁ = \(\mathrm{y}_1{ }^2\) – 6x₁
= 9 – 6(2)
= -3 < 0
∴ Point (2, 3) lies inside the parabola y² = 6x.

Question 9.
Find the coordinates of the point on the parabola y = 8x whose focal distance is 10. (Mar. ’11)
Solution:
Given y² = 8x and Let P(x₁, y₁) be any point on the parabola y² = 8x
Comparing with y² = 4ax we get
4a = 8
⇒ a = 2
The focal distance of the parabola = x₁ + a = x₁ + 2
Given x₁ + 2 = 10
Since \(\mathrm{y}_1^2\), we have \(\mathrm{y}_1^2\) = 8(8) = 64
⇒ y₁ = ±8
Hence the required points on the parabola y² = 8x are given by (8, 8) and (8, -8).

Question 10.
If (\(\frac{1}{2}\), 2) is one extremity of a focal chord of the parabola y² = 8x. Find the coordinates of the other extremity. (June ’10)
Solution:
The given equation of a parabola is y² = 8x.
Comparing with y² = 4ax we get
4a = 8
⇒ a = 2
Let P(x₁, y₁) = (\(\frac{1}{2}\), 2) be one extremity of the focal chord.
Let Q(x₂, y₂) be the other extremity of the focal chord of the parabola y² = 8x.
∴ x₁x₂ = a² and y₁y₂ = -4a² (standard result)
⇒ \(\frac{1}{2}\)x₂ = 4
⇒ x₂ = 8
and 2y₂ = -4(4)
⇒ y₂ = -8
[∵ P(x₁, y₁) = (\(\frac{1}{2}\), 2)]
∴ The other extremity of the focal chord of the given parabola is (8, -8).

Question 11.
Prove that the point on the parabola y² = 4ax, (a > 0) nearest to the focus is its vertex.
Solution:
Given equation is y² = 4ax …….(1) and focus is S = (a, 0).
Let P(at², 2at) be any point on y² = 4ax.
Let f(t) = SP = \(\sqrt{\left(a t^2-a\right)+4 a^2 t^2}\)
= \(\sqrt{a^2\left[\left(t^2-1\right)^2+4 t^2\right]}\)
= a(t² + 1)
∴ f(t) = 2at and f”(t) = 2a > 0
∴ For f(t) to be minimum or maximum f'(t) = 0 ⇒ t = 0
∴ P = (0, 0).
Hence the f(t) has a minimum at t = 0 and the point on the parabola nearest to its focus is (0, 0).

Question 12.
A comet moves in a parabolic orbit with the sun as the focus. When the comet is 2 × 10⁷ Km. from the sun the line from the sun to it makes an angle \(\frac{\pi}{2}\) with the axis of the orbit. Find how near the comet comes to the sun.
Solution:

Let the equation of the parabolic orbit be y² = 4ax
Let S be the position of the sun (focus) on the axis of the parabola.
Let P be the position of a comet when it is at a distance of 2 × 10⁷ Km from the Sun ‘S’.
∴ SP = 2 × 10⁷
⇒ 2a = 2 × 10⁷ Km
⇒ a = 10⁷ Km
The distance of the comet from the Sun S is minimum when it is at the vertex.
∴ The nearest distance of the comet from the sun S is SA = a = 10⁷ Km.

II.

Question 1.
Find the locus of the point of trisection of the double ordinate of a parabola y² = 4ax, (a > 0).
Solution:

Let P(at², 2at), and P’ = (at², -2at) be the ends of double ordinate PP’ of the parabola y² = 4ax.
Let Q(x₁, y₁) be any point on the locus.
∴ Q(x₁, y₁) is the point of trisection of PP’.
⇒ Q(x₁, y₁) divides PP’ in the ratio 1 : 2.

∴ 9\(\mathrm{y}_1^2\) = 4ax₁ and locus of (x₁, y₁) is 9y² = 4ax.

Question 2.
Find the equation of the parabola whose vertex and focus are on the positive x-axis at a distance ‘a’ and ‘a’ ‘ from the origin respectively.
Solution:
Let A(a, 0) be vertex and S(a’, 0) be the focus
We have

∴ a = AS
∴ a = \(\sqrt{\left(a-a^{\prime}\right)^2}\) = a’ – a
The equation of the required parabola is (y – k)² = 4a(x – h)
⇒ (y – 0)² = 4(a’ – a) (x – a)
⇒ y² = 4(a’ – a) (2 – a)

Question 3.
If L and L’ are the ends of the latus rectum of the parabola x² = 6y, find the equation of OL and OL’ where ‘O’ is the origin. Also, find the angle between them.
Solution:
Given equation of parabola is x² = 6y ……..(1)
Comparing with y² = 4ax we have 4a = 6
⇒ a = \(\frac{3}{2}\)
Given L, L’, and the ends of the latus rectum of the parabola (1).
L = (2a, a) and L’ = (-2a, a)

Question 4.
Find the equation of a parabola whose axis is parallel to the x-axis and which passes through the points (-2, 1), (1, 2), and (-1, 3).
Solution:
Let A = (-2, 1), B = (1, 2), C = (-1, 3) be the given points.
Let the equation of the parabola whose axis is parallel to the x-axis and passing through the points A, B, C be x = ly² + my + n …….(1)
If parabola (1) passes through A(-2, 1) then -2 = l + m + n …….(2)
If (1) passes through B(1, 2) then
1 = 4l + 2m + n ……..(3)
If (1) passes through C(-1, 3) then
-1 = 9l + 3m + n ……..(4)
From (2) and (3),
-3l – m = -3
⇒ 3l + m = 3 ……..(5)
From (3) and (4),
-5l – m = 2
⇒ 5l + m = -2 ………(6)
Solving (5) and (6), we get
-2l = 5
⇒ l = \(\frac{-5}{2}\)
and 5(\(\frac{-5}{2}\)) + m = -2
⇒ m = -2 + \(\frac{25}{2}\) = \(\frac{21}{2}\)
∴ From (2) we have l + m + n = 2
⇒ \(-\frac{5}{2}+\frac{21}{2}\) + n = -2
⇒ n + 8 = -2
⇒ n = -10
Hence the required equation of parabola from (1) is x = \(-\frac{5}{2} y^2+\frac{21}{2} y-10\)
⇒ 5y² + 2x – 21y + 20 = 0

Question 5.
Find the equation of the parabola whose axis is parallel to the y-axis and which passes through the points (4, 5), (-2, 11), and (-4, 21). (Mar. ’12)
Solution:
Let A(4, 5), B(-2, 11) and C(-4, 21) be the given points.
The equation of the parabola whose axis is parallel to the y-axis is
y = lx² + mx + n ………(1)
Since (1) passes through point A(4, 5) we have
5 = 16l + 4m + n ………(2)
Since (1) passes through point B(-2, 11) then
11 = 4l – 2m + n ……..(3)
Also since (1) passes through C(-4, 21) we have
21 = 16l – 4m + n ………(4)
From (2) and (3)
12l + 6m = -6
61 + 3m = -3
2l + m = -1 ……….(5)
From (3) and (4)
-12l + 2m = -10
⇒ -6l + m = -5
⇒ 6l – m = 5 ……….(6)
Solving (5) and (6) we get
8l = 4
⇒ l = \(\frac{1}{2}\)
∴ From (6)
3 – m = 5
⇒ -m = 2
⇒ m = -2
From (2) we have
16l + 4m + n = 5
⇒ 8 – 8 + n = 5
⇒ n = 5
∴ The equation of the required parabola passing through points A, B, C from (1) is
y = \(\frac{1}{2}\)x2 – 2x + 5
⇒ x2 – 4x – 2y + 10 = 0

III.

Question 1.
Find the equation of the parabola whose focus is (-2, 3) and whose directrix is the line 2x + 3y – 4 = 0. Also, find the length of the latus rectum and the equation of the axis of the parabola. (Mar. ’13)
Solution:
Let S = (-2, 3) be the focus and L = 2x + 3y – 4 = 0 be the directrix.
Let P(x₁, y₁) be any point on the parabola and PM be the perpendicular distance from P to the directrix.

∴ The locus of P(x₁, y₁) is the equation of parabola given by 9x² – 12xy + 4y² + 68x – 54y + 153 = 0
The length of the latus rectum = 4a = 2(2a) = 2
The perpendicular distance from focus to the directrix = \(\frac{2|2(-2)+3(3)-4|}{\sqrt{4+9}}=\frac{2}{\sqrt{13}}\) units
Since the axis of the parabola is perpendicular to the directrix and passes through the focus (-2, 3).
The equation of the line passing through (-2, 3) and perpendicular to L = 0 is L(x – x₁) – a(y – y₁) = 0
⇒ 3(x + 2) – 2(y – 3) = 0
⇒ 3x – 2y + 12 = 0
∴ Axis of the parabola is 3x – 2y + 12 = 0.

Question 2.
Prove that the area of the triangle inscribed in the parabola y² = 4ax is \(\frac{1}{8a}\) |(y₁ – y₂) (y₂ – y₃) (y₃ – y₁)| sq. units. where y₁, y₂, y₃ are the ordinates of its vertices. (New Model Paper)
Solution:
Let A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) be the vertices of ∆ABC inscribed in a parabola y² = 4ax.
Then the area of the triangle ABC is ∆ = |\(\frac{1}{2}\)Σx₁(y₂ – y₃)| sq.units
In the parametric form x₁ = \(\mathrm{at}_1{ }^2\) and y₁ = 2at₁
∴ Take A = \(\left(a t_1{ }^2, 2 a t_1\right)\) = (x₁, y₁)
B = \(\left(a t_2{ }^2, 2 a t_2\right)\) = (x₂, y₂)
C = \(\left(a t_3{ }^2, 2 a t_3\right)\) = (x₃, y₃)


∴ LHS = RHS and hence the area of the triangle inscribed in the parabola y² = 4ax is \(\frac{1}{8a}\) |(y₁ – y₂) (y₂ – y₃) (y₃ – y₁)| sq. units.

Question 3.
Find the coordinates of the vertex and focus, the equation of the directrix, and the axis of the following parabolas.
(i) y² + 4x + 4y – 3 = 0
Solution:
The given equation can be written as y² + 4y = -4x + 3
⇒ y² + 4y + 4 = -4x + 3 + 4 = -4x + 7
⇒ (y + 2)² = -4(x – \(\frac{7}{4}\))
⇒ \([y-(-2)]^2=-4\left[x-\left(\frac{7}{4}\right)\right]\)
Which is of the form (y – k)² = -4a(x – h)
Where (h, k) =(\(\frac{7}{4}\), 1) and a = 1,
Vertex = (h, k) = (\(\frac{7}{4}\), -2)
Focus = (h – a, k)
= (\(\frac{7}{4}\) – 1, -2)
= (\(\frac{3}{4}\), -2)
Axis of the parabola = y – k = 0
⇒ y + 2 = 0
Directrix of the parabola is x – h – a = 0
⇒ x – \(\frac{7}{4}\) – 1 = 0
⇒ x – \(\frac{11}{4}\) = 0
⇒ 4x – 11 = 0

(ii) x² – 2x + 4y – 3 = 0
Solution:
The given equation can be written as x² – 2y = -4y + 3
⇒ x² – 2x + 1 = -4y + 3 + 1 = -4y + 4
⇒ (x – 1)² = -4(y – 1)
This is of the form (x – h)² = -4a(y – k) whose a = 1, (h, k) = (1, 1)
Vertex = (h, k) = (1, 1)
Focus = (h, k – a) = (1, 1 – 1) = (1, 0)
Axis is x – h = 0 ⇒ x – 1 = 0
Directrix is y – k – a = 0
⇒ y – 1 – 1 = 0
⇒ y – 2 = 0
⇒ y = 2

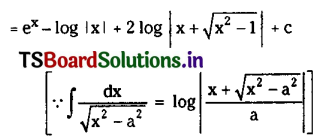
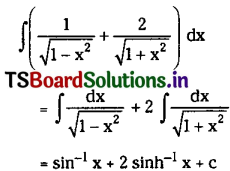
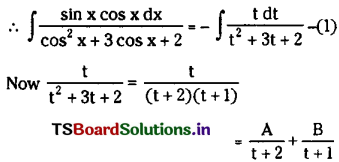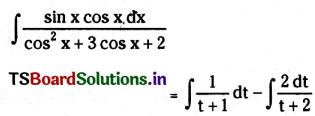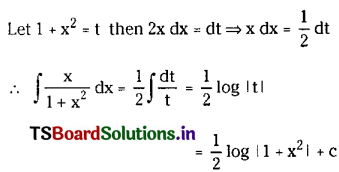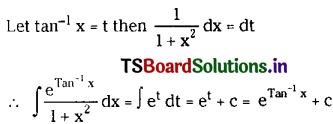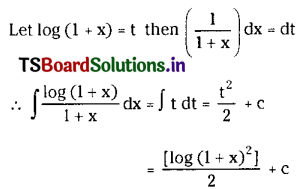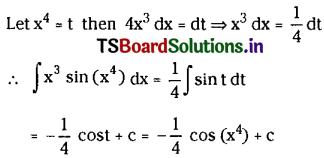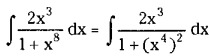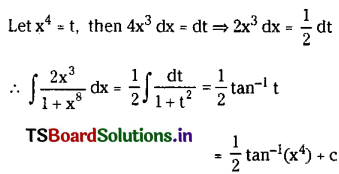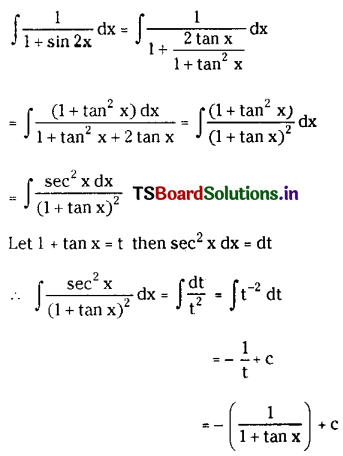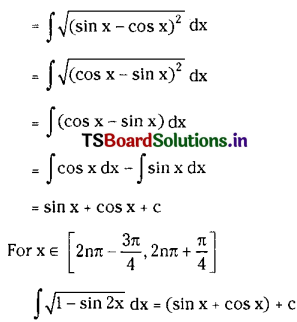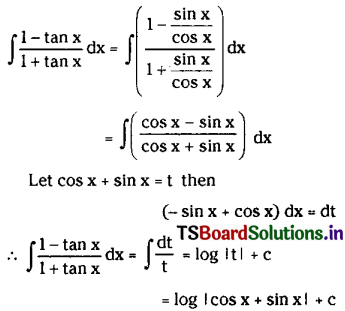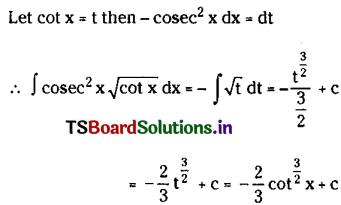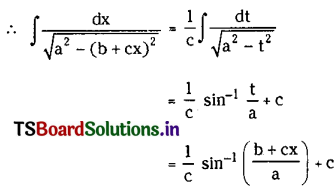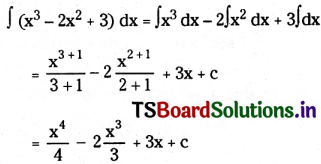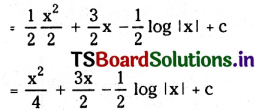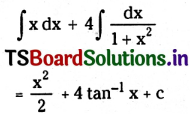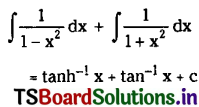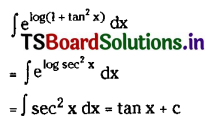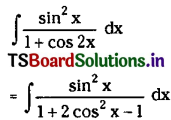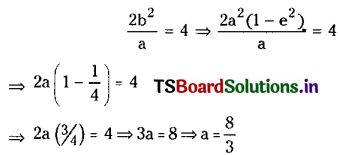Telangana TSBIE TS Inter 2nd Year English Study Material Revision Test-V Exercise Questions and Answers.

TS Inter 2nd Year English Study Material Revision Test-V

Time: 1 1/2 Hrs
Marks : 50

Section – A

Question 1.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) May be the world needs good watchmen as much as it does engineers.
Answer:
We see these words in the one act play’Guilty. It was written by Horace J. Gardiner and Bonneviere Arnaud. This short and sweet play offers readers a pleasant reading experience. It conveys valuable messages. Conversations serve as good examples of everyday English. Jim is the central character in the play. He studied engineering but works as a night watchman. This fact shows the scenario of employment. It also appreciates Jim’s spirit. Mrs Moore says the given words to Ma Ryan, Jim’s mother. She focuses on the value of ‘dignity of labour’. She makes it clear that every job is important. One should respect one’s work. Watchmen are as important as engineers.

b) Ma, you’re talking like someone in a fog, without any sense.
Answer:
We see these words in the one-act play Guilty’. It was written by Horace J. Gardiner and Bonneviere Arnaud. This short and sweet play offers readers a pleasant reading experience, it conveys valuable messages. Conversations serve as good examples of everyday English. Jim says these words to his mother, when she asks him to quickly escape from there. Mother’s advice sounds senseless to the honest and innocent Jim. So, he asks her why she is talking in such a meaningless way. But she sees the ‘robbed’ ornament in Jim’s pocket. She sees a policeman. She puts two and two together and makes four.

Question 2.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]

a) It is said that before entering the sea a river trembles with fear.
Answer:
Introduction:
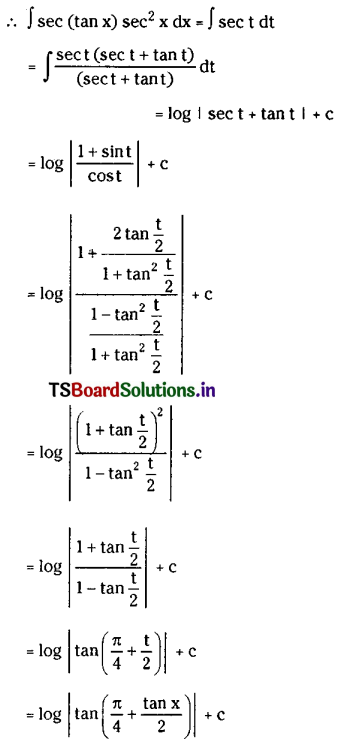
These are the opening lines of the poem, “Fear”, written by Khalil Gibran; a Lebanese-American writer. He became famous for his book, “The Prophet”, a collection of philosophical essays. His writings deal with Spiritual Love and Life Issues.

Context and Meaning:
In the poem, the poet expresses his philosophical understanding of overcoming fear. The speaker thinks of the image of a river flowing into the sea. The poet’s point of view is not wholly his own. He may have heard of the river’s fear and chose to give it some strength through the poetry. The river may have traversed difficult paths before entering the ocean. Yet it themselves with fear at the sight of the vastness of the ocean.

Critical comment:
The poet compares humanity to rivers. Even for a man there is always the fear of the unknown and being lost in it.

b) The river cannot go back. Nobody can go back. To go back is impossible in existence.
Answer:
Introduction:
These spiritual lines are taken from the “Fear”, written by Khalil Gibran, a Lebanese-American writer. He is famous for his book, “The Prophet”, a collection of philosophical essays. His writings, deal with Spiritual Love and Life Issues.

Context and Meaning:
The river travels through mountains and plains to merge with an ocean. The poet talks about her fear directly. He compares humanity to rivers. He discusses the year that human beings encounter too. There is a desire to go back. But, that is impossible in existence. People as well as ‘the river need to accept the fact that there is no other option but to move forward. Thus, people must take risks and believe in themselves.

Critical comment:
The poem shows a variety of themes. The error of moving forward, the anxiety of losing oneself, and the journey life till death are some of the major themes.

Question 3.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) Sketch the character of Jim in the light of Ma Ryan’s comments like. It is the same! But how did it get into Jim’s pocket?
Answer:
“Guilty’, by Horace J Gardiner and Bonneviere Arnaud, is an interesting one-act play. It conveys some significant messages. The playlet exhibits all the properties of a good one-act play. It has a few characters. It observes all the unities. Jim is the lead character in the play. He is an engineering graduate.

Yet, he works as a night watchman. He is a fine, good boy and a hard worker. He is honest to the core. He is NOT the thief as his mother suspects. Jim, in fact, finds the jewel on the road. And he plans to give it back to the rightful owner, Van King. In the excitement, he fails to inform these facts to his mother. So, she makes such comments.

b) “Ma, you are talking like someone in a fog, without any sense.” Are these words from Jim an order or exception? Explain.
Answer:
“Guilty, by Horace J Gardiner and Bonneviere Arnaud, is an Interesting one-act play. It conveys some significant messages The playlet exhibits all the properties of a good one-act play. It has a few characters. It observes all the unities. Ma Ryan suspects that Jim has stolen the jewel. She asks him to escape. Jim is innocent. He, therefore, feels that his mother is confused and talking meaninglessly. Jim asks why his mother is speaking like that day. So, it is clear that his words are an exception. They are not an order. They love each other, They have faith in their good nature. Circumstances make them say so.

Question 4.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) How can one overcome fear? Explain.
Answer:
The poem ”Fear”, is written by Khalil Gibran, a Lebanese – American writer. He is famous for his book, The Prophet”, a collection of Philosophical essays. The poet conveys his philosophical insight about overcoming fear in the poem. He imagines a river that flows into the sea. He refers to the river as ‘She’ to infuse life into the river. He talks about her fear directly. He discusses the fear that human beings encounter too.

The river trembles with fear at the sight of the vastness of the ocean. She looks back at the path she has traversed. But, that is impossible in existence. There is no other option to her. She has to move forward and accept the truth. So, she takes the risk of entering the ocean so that she becomes an ocean. The poet compares humanity to the river. Through the river’s emotions, the poet sends a powerful message to those who fear, losing their identity, death, change, being forgotten in this universe and so on. So, once can overcome fear by taking risks to achieve success.

b) What does the line ‘The river needs to take the risk of entering the ocean’ mean? Discuss.
Answer:
The poem ”Fear”, is written by Khalil Gibran, a Lebanese – American writer. He is famous for his book, The Prophet”, a collection of Philosophical essays. The poet conveys his philosophical insight about overcoming fear in the poem. He imagines a river that flows into the sea. He refers to the river as ‘She’ to infuse life into the river. He talks about her fear directly. He discusses the fear that human beings encounter too.

The river trembles with fear at the sight of the vastness of the ocean. She looks back at the path she has traversed. But, that is impossible in existence. There is no other option to her. She has to move forward and accept the truth. So, she takes the risk of entering the ocean so that she becomes an ocean. The poet compares humanity to the river. Through the river’s emotions, the poet sends a powerful message to those who fear, losing their identity, death, change, being forgotten in this universe and so on. So, once can overcome fear by taking risks to achieve success.

Question 5.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]

a) The narrator thought that his interview was superfluous. Why?
Answer:
Richard Gordon (1921-2017) was an oncologist and doctor from England. He wrote a number of novels as well as screenplays for films and television.

In the present story deals with an interview. Here the poet shares his experience how he faced an interview with Dr Lionel Loftus, the dean of st swithin’s Medical school. He feel very nervously.

He sit at the waiting room and he prepared for an interview number of medical questions himself. Unexpectedly one old man who worked as a secretary of the medical school, and asked him a few questions. After that dean called him and he doesn’t ask any medical questions. He asked him in a general questions about personal actives of life. After completing an interview, the dean announces that he is admitted st swithin’s Medical school. The narrator feel’s that interview was a superfluous.

b) Why do you think the old man visited the waiting room?
Answer:
Richard Gordon (1921-2017) was an oncologist and doctor from England. He wrote a number of novels as well as screenplays for films and television. In the present story deals with an interview. Here the poet shares his experience how he faced an interview, one old man who worked as a secretary of the medical school, he stared examine the questions the narrator critically a very few questions about the narrator ability to pay the fee However and finally he got the admission in the st swithin’s Medical school.

Section – B

Question 6.
Read the following passage and answer ANY FIVE questions given below: [5 × 1 = 5]

‘I am not the Dean,’ he explained. ‘I am the medical school Secretary here long before you were born, my boy. Before your fair probably. I remember well enough when the Dean himself came up admitted.’ He removed his glasses and pointed them at me. I’ve seen thousand of students pass through the school. Some of them have turned out on and some of them bad – it’s just like your own children.’ I nodded heartily, as I was anxious to please everyone.

Now, young feller,’ he went on more briskly, ‘I’ve got some questions to ask you.’ I folded my hands submissively and braced myself mentally. ‘Have you been to a public school?’ he asked. ‘Yes.’ ‘Do you play Rugby football or Association?’ ‘Rugby.’ ‘Do you think you can afford to pay the fees?’ ‘Yes.’ He grunted, and without a word withdrew. Left alone, I diverted my apprehensive mind by running my eye carefully over the line of black-and white pictures of past deans, studying each one in turn. After ten minutes or so the old man returned and led me in to see the living holder of the office.

i) I am not the Dean, he explained. Who does the word ‘I” refer to?
Answer:
The Secretary

ii) How long was the Secretary there in. the college?
Answer:
Since the narrator or even his father was not born.

iii) Name the games mentioned in the passage.
Answer:
Rugby and Association (football).

iv) What was the last question to the speaker?
Answer:
If he could afford to pay the fee

v) How did the narrator divert his apprehensive mind?
Answer:
By running his eye carefully over the line of black-and-white pictures of past deans

vi) Where did the old man take the narrator?
Answer:
Into the office of the Dean

vii) Pick the word, from the passage, which means have enough money to pay.
Answer:
Afford

viii) Pick the antonym of slowly from the passage.
Answer:
Briskly

Question 7.
Read the following passage and answer ANY FIVE questions given below: [5 × 1 = 5]

Giving Pays
“You will die within a year”, highly skilled physicians told John. D. Rockefeller, the first billionaire in the world. By then, he was 53 only. Being the richest man in the world, he could buy anything but could only digest soup and crackers. As he approached death, he awoke one morning with the vague realisation of not being able to take any of his wealth with him into the next world. The man who could control the business world suddenly realised he was not in control of his own life. He was left with only one choice: established a foundation and channelized his assets to Hospitals, Research and Charity work which eventually led to the discovery of Penicillin, cures for Malaria, Tuberculosis and Diphtheria. But the most amazing part of Rockefeller’s story is that the moment he began to give back, his body’s chemistry was altered so significantly that he got better. It looked as if he would die at 53 but he lived to be 98.

i) John Rockefeller died at the age of 53. Write Yes or No.
Answer:
No

ii) What was his speciality?
Answer:
The first billionaire in the world

iii) Substantiate the statement we can’t buy everything with money with a sentence from the passage.
Answer:
He could buy and thing but could only digest soup and crackers

iv) What realization dawned upon him?
Answer:
That he could not take his wealth with him to the next world and the could control his business world but not his own health

v) What was the choice that he was left with?
Answer:
Establishing a charity foundation and channelizing his wealth into it

vi) What do you think actually enhanced Rockefeller’s life?
Answer:
His giving back

vii) Write the synonym of changed.
Answer:
Altered

viii) Write the word used in the passage to mean giving money, food, help etc to people in need.
Answer:
Charity

Question 8.
Study the following advertisement and answer ANY FIVE questions that follow. [5 × 1 = 5]

i) How many habits are mentioned in the advertisement?
Answer:
height

ii) What should one do when things limit productivity?
Answer:
remove the things that limit productivity

iii) What should one do to focus on the important things?
Answer:
ruthlessly cut away the unimportant

iv) What must one do to get inspiration?
Answer:
Tap into one’s inspiration

v) How should we deal with things when they need to be done?
Answer:
set timelines

vi) When should one allocate breaks strategically?
Answer:
when one is tired

vii) Pick the synonym of the word practice from the passage.
Answer:
habit

viii) What must one do to optimize time pockets?
Answer:
making best of every minute

Question 9.
Study the Flow chart below and answer ANY FIVE questions that follow. [5 × 1 = 5]

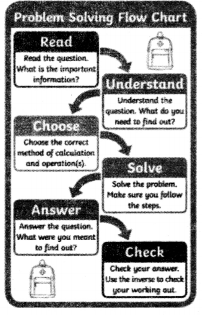
i) What does the flow chart describe?
Answer:
problem solving

ii) How many steps are given in the flow chart?
Answer:
six

iii) What should you do to get important information?
Answer:
read the question

iv) What is the third step?
Answer:
choosing with correct method

v) To solve the problem, what needs to be followed?
Answer:
make sure that all this steps or followed correctly

vi) Calculation and operations are found in __________. (Fill in the blank.)
Answer:
in the third step – choose

vii) What do you need to And out?
Answer:
answer

viii) What is to be checked at the end of solving the problem?
Answer:
answer

Section – C

Question 10.
Write a dialogue between two friends on the choice of career. [3 × 1 = 3]
Answer:
BETWEEN TWO FRIENDS:

Pavani : Hi, Sudha! What do you want to do after Intermediate?

Sudha : Hi, Vani ! We are in MPC group. And our automatic choice is Engineering. The only thing to decide is which branch and which college. Do you have any other ideas?

Pavani : Yes. I’m not interested in Engineering.

Sudha : Very surprising I What else will you do?

Pavani : I’ll pursue B.Sc., course.

Sudha : Are you mad? Joining B.Sc.,?

Pavani : Why are you so excited? I just love Physics. I want to join B.Sc., now and then M.Sc., Physics. Later I want togo for research in Physics, particularly in Nanotechnology.

Sudha : Really, stunning! I don’t know anything about other options. All these days I’ve been under the impression that M.P.C in Intermediate means Engineering afterwards.

Pavani : There are lot many other options Sudha ! You can consult any lecturer, or go through ‘education pages’ of newspapers or even browse the internet. Plenty of courses are available. We have to select the one that we are really interested in.

Sudha : Thank you Vani. You’ve really opened my eyes. That too, at the right time. I’ll follow your guidelines. Bye!

Question 11.
Mark the stress for FIVE of the follow mg words. [5 × 1 = 5]
(i) common
(ii) adopt
(iii) humility
(iv) footprint
(v) understand
Answer:
i) ‘common
ii) a’dopt
iii) hu’mility
iv) ‘footprint
v) under’stand
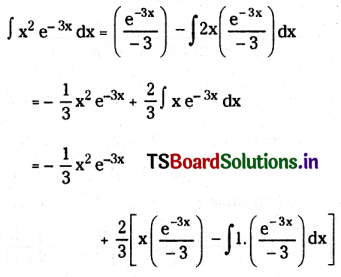
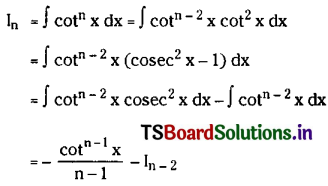