TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Ex 6(f)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 6 Integration Ex 6(f) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Exercise 6(f)

I. Evaluate the following integrals.

Question 1.
∫e^x (1 + x²) dx
Solution:
∫e^x (1 + x²) dx = ∫(e^x + e^x x²) dx
= ∫e^x dx + ∫e^x x² dx
= e^x + x² e^x – ∫2x e^x dx
= e^x + x² e^x – [2x e^x – ∫2e^x dx]
= e^x + x² e^x – 2x e^x + 2e^x + c
= e^x [1 + x² – 2x + 2] + c
= e^x (x² – 2x + 3) + c
[Integration by parts ∫uv dx = u∫v dx – ∫(\(\frac{\mathrm{d}}{\mathrm{dx}}\)(u) ∫v dx) is used]

Question 2.
∫x² e^-3x dx
Solution:
Use integration by parts successively using u = x² and v = e^-3x then

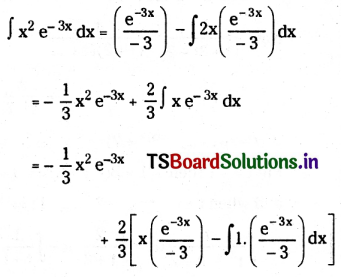
Question 3.
∫x³ e^ax dx
Solution:

II.

Question 1.
Show that ∫xⁿ e^-x dx = -xⁿ e^-x + n ∫x^n-1 e^-x dx
Solution:
∫xⁿ e^-x dx using integration by parts
= xⁿ (e^-x) – ∫n x^n-1 (-e^-x) dx
= -xⁿ e^-x + n∫x^n-1 e^-x dx

Question 2.
If I_n = ∫cosⁿx dx, then show that I_n = \(\frac{1}{n} \cos ^{n-1} x \sin x+\frac{n-1}{n} I_{n-2}\)
Solution:

III.

Question 1.
Obtain the reduction formula for I_n = ∫cotⁿx dx, n being a positive integer, n ≥ 2 and deduce the value of ∫cot⁴x dx. (May ’11)
Solution:

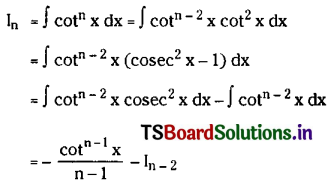
Question 2.
Obtain the reduction formula for I_n = ∫cosecⁿx dx, n being a positive integer, n ≥ 2 and deduce the value of ∫cosec⁵x dx.
Solution:

Question 3.
If I_m,n = ∫sin^mx cosⁿx dx, then show that \(I_{m, n}=-\frac{\sin ^{m-1} x \cos ^{n+1} x}{m+n}+\frac{m-1}{m+n} I_{m-2, n}\) for a positive Integer n and an integer m ≥ 2.
Solution:

Question 4.
Evaluate ∫sin⁵x cos⁴x dx
Solution:
Denote I_5,4 = ∫sin⁵x cos⁴x dx using the above reduction formula

Question 5.
If I_n = ∫(log x)ⁿ dx then show that I_n = x(log x)ⁿ – n I_n-1 and hence find ∫(log x)⁴ dx.
Solution:

Put n = 4, 3, 2, 1 we get
I₄ = x(log x)⁴ – 4I₃
= x(log x)⁴ – 4[x(log x)³ – 3I₂]
= x(log x)⁴ – 4x(log x)³ + 12[x(log x)² – 2I₁]
= x(log x)⁴ – 4x(log x)³ + 12x(log x)² – 24I₁]
= x(log x)⁴ – 4x(log x)³ + 12x(log x)² – 24 ∫log x dx
= x(log x)⁴ – 4x(log x)³ + 12x(log x)² – 24[x log x – x] + c
= x(log x)⁴ – 4x(log x)³ + 12x(log x)² – 24x log x – 24x + c