TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Ex 6(b)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 6 Integration Ex 6(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Exercise 6(b)

I. Evaluate the following integrals.

Question 1.
∫e^2x dx, x ∈ R
Solution:

Question 2.
∫sin 7x dx, x ∈ R
Solution:
Let 7x = t then 7 dx = dt
⇒ dx = \(\frac{1}{7}\) dt
∴ ∫sin 7x dx = \(\frac{1}{7}\) ∫sint dt
= \(-\frac{1}{7}\) cos t
= \(-\frac{1}{7}\) cos 7x + c

Question 3.
\(\int \frac{x}{1+x^2} d x\), x ∈ R
Solution:

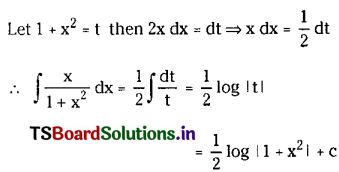
Question 4.
∫2x sin(x² + 1) dx, x ∈ R
Solution:
Let x² + 1 = t then 2x dx = dt
∴ ∫2x sin(x² + 1) dx = ∫sin t dt
= -cos t + c
= -cos(x² + 1) + c

Question 5.
\(\int \frac{(\log x)^2}{x} d x\) on I ⊂ (0, ∞).
Solution:

Question 6.
\(\int \frac{e^{Tan^{-1} x}}{1+x^2} d x\) on I ⊂ (0, ∞).
Solution:

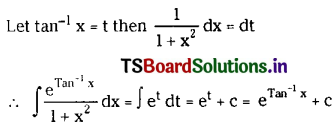
Question 7.
\(\int \frac{\sin \left({Tan}^{-1} x\right)}{1+x^2} d x\), x ∈ R
Solution:

Question 8.
\(\int \frac{1}{8+2 x^2} d x\) on R.
Solution:

Question 9.
\(\int \frac{3 x^2}{1+x^6} d x\) on R.
Solution:

Question 10.
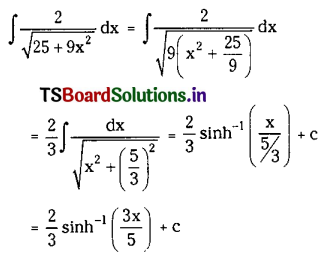
\(\int \frac{2}{\sqrt{25+9 x^2}} d x\) on R.
Solution:

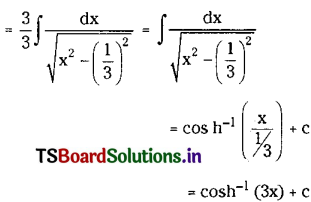
Question 11.
\(\int \frac{3}{\sqrt{9 x^2-1}} d x\) on (\(\frac{1}{3}\), ∞).
Solution:

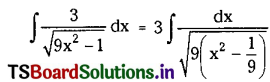
Question 12.
∫sin mx cos nx dx on R, m ≠ n, m and n are positive integers.
Solution:

Question 13.
∫sin mx sin nx dx on R, m ≠ n, m and n are positive integers.
Solution:

Question 14.
∫cos mx cos nx dx on R, m ≠ n, m and n are positive integers.
Solution:

Question 15.
∫sin x sin 2x sin 3x dx on R.
Solution:
Consider sin x sin 2x sin 3x = \(\frac{1}{2}\) (2 sin x sin 2x sin 3x)
= \(\frac{1}{2}\) [cos(3x – 2x) – cos(3x + 2x)] sin x
= \(\frac{1}{2}\) [sin x cos x – sin x cos 5x]
= \(\frac{1}{4}\) [2 sin x cos x – 2 sin x cos 5x]
= \(\frac{1}{4}\) [sin 2x – [sin(5x + x) + sin(x – 5x)]
= \(\frac{1}{4}\) [sin 2x – [sin 6x – sin 4x]]
= \(\frac{1}{4}\) [sin 2x – sin 6x + sin 4x]
∴ ∫sin x sin 2x sin 3x dx = \(\frac{1}{4}\) ∫sin 2x dx – \(\frac{1}{4}\) ∫sin 6x dx + \(\frac{1}{4}\) ∫sin 4x dx
= \(-\frac{1}{8}\) cos 2x + \(\frac{1}{24}\) cos 6x – \(\frac{1}{16}\) cos 4x + c
= \(\frac{1}{4}\left[\frac{\cos 6 x}{6}-\frac{\cos 4 x}{4}-\frac{\cos 2 x}{2}\right]\) + c

Question 16.
\(\int \frac{\sin x}{\sin (a+x)} d x\) on I ⊂ R – {nπ – a : n ∈ Z}.
Solution:

II. Evaluate the following integrals.

Question 1.
\(\int(3 x-2)^{\frac{1}{2}} d x\) on (\(\frac{2}{3}\), ∞)
Solution:

Question 2.
\(\int \frac{1}{7 x+3} d x\) on I ⊂ R – {\(-\frac{3}{7}\)}
Solution:

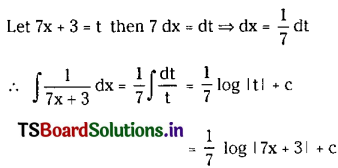
Question 3.
\(\int \frac{\log (1+x)}{1+x} d x\) on (-1, ∞).
Solution:

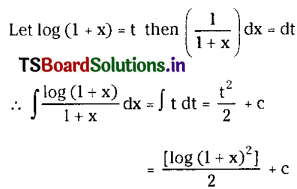
Question 4.
∫(3x² – 4)x dx on R.
Solution:

Question 5.
\(\int \frac{d x}{\sqrt{1+5 x}} \text { on }\left(-\frac{1}{5}, \infty\right)\)
Solution:

Question 6.
∫(1 – 2x³) x² dx on R.
Solution:

Question 7.
\(\int \frac{\sec ^2 x}{(1+\tan x)^3} d x\) on I ⊂ R – {nπ – \(\frac{\pi}{4}\) : n ∈ Z}
Solution:

Question 8.
∫x³ sin(x⁴) dx on R.
Solution:

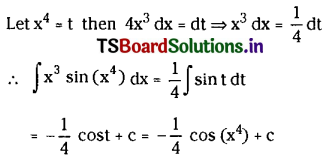
Question 9.
\(\int \frac{\cos x}{(1+\sin x)^2} d x\) on I ⊂ R – {2nπ + \(\frac{3 \pi}{2}\) : n ∈ Z}
Solution:

Question 10.
∫\(\sqrt[3]{\sin x}\) cos x dx on [2nπ, (2n + 1)π], (n ∈ Z).
Solution:

Question 11.
∫2x \(e^{x^2}\) dx on R.
Solution:
Let x² = t then 2x dx = dt
∴ ∫2x \(e^{x^2}\) dx = ∫e^t dt
= e^t + c
= \(e^{x^2}\) + c

Question 12.
\(\int \frac{e^{\log x}}{x} d x\) on (0, ∞).
Solution:

Question 13.
\(\int \frac{x^2}{\sqrt{1-x^6}} d x\) on I ∈ (-1, 1)
Solution:

Question 14.
\(\int \frac{2 x^3}{1+x^8} d x\) on R.
Solution:

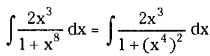
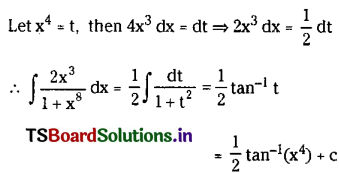
Question 15.
\(\int \frac{x^8}{1+x^{18}} d x\) on R. (Mar. ’09)
Solution:

Question 16.
\(\int \frac{e^x(1+x)}{\cos ^2\left(x e^x\right)} d x\) on I ⊂ R – {x ∈ R : cos(xe^x) = 0}. (Mar. ’10, ’04)
Solution:

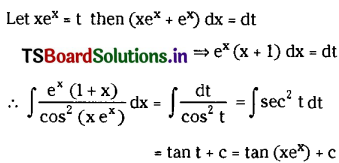
Question 17.
\(\int \frac{{cosec}^2 x}{(a+b \cot x)^5} d x\) on I ⊂ R – {x ∈ R : a + b cot x = 0}, where a, b ∈ R, b ≠ 0.
Solution:

Question 18.
∫e^x sin e^x dx on R.
Solution:
Let t = e^x then dt = e^x dx
∴ ∫e^x sin e^x dx = ∫sin t dt
= -cos t + c
= -cos(e^x) + c

Question 19.
\(\int \frac{\sin (\log x)}{x} d x\) on (0, ∞).
Solution:
Let log x = t then \(\frac{1}{x}\) dx = dt
∴ \(\int \frac{\sin (\log x)}{x} d x\) = ∫sin t dt
= -cos t + c
= -cos(log x) + c

Question 20.
\(\int \frac{1}{x \log x} d x\) on (1, ∞).
Solution:

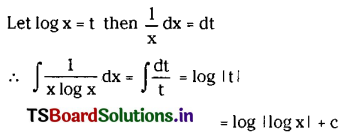
Question 21.
\(\int \frac{(1+\log x)^n}{x} d x\) on (e^-1, ∞), n ≠ -1.
Solution:

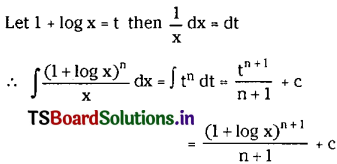
Question 22.
\(\int \frac{\cos (\log x)}{x} d x\) on (0, ∞).
Solution:
Let log x = t then \(\frac{1}{x}\) dx = dt
∴ \(\int \frac{\cos (\log x)}{x} d x\) = ∫cos t dt
= sin t + c
= sin(log x) + c

Question 23.
\(\int \frac{\cos \sqrt{x}}{\sqrt{x}} d x\) on (0, ∞).
Solution:
Let √x = t then \(\frac{1}{2 \sqrt{x}}\) dx = dt
∴ \(\int \frac{\cos \sqrt{x}}{\sqrt{x}} d x\) = 2 ∫cos t dt
= 2 sin t + c
= 2 sin(√x) + c

Question 24.
\(\int \frac{2 x+1}{x^2+x+1} d x\) on R.
Solution:
Let x² + x + 1 = t then (2x + 1) dx = dt
∴ \(\int \frac{2 x+1}{x^2+x+1} d x=\int \frac{d t}{t}\)
= log|t| + c
= log|x² + x + 1| + c

Question 25.
\(\int \frac{a x^{n-1}}{b x^n+c} d x\) where n ∈ N, a, b, c are real numbers, b ≠ 0 and x ∈ I ⊂ {x ∈ R : xⁿ ≠ \(-\frac{c}{b}\)}
Solution:

Question 26.
\(\int \frac{1}{x \log x[\log (\log x)]} d x\) on (1, ∞).
Solution:

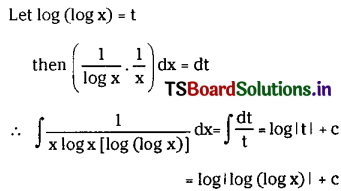
Question 27.
∫coth x dx on R.
Solution:
∫coth x dx = \(\int \frac{\cosh x}{\sinh x} d x\)
Let sinh x = t then cosh x dx = dt
∴ ∫coth x dx = \(\int \frac{\mathrm{dt}}{\mathrm{t}}\)
= log|t| + c
= log|sinh x| + c

Question 28.
\(\int \frac{1}{\sqrt{1-4 x^2}} d x \text { on }\left(-\frac{1}{2}, \frac{1}{2}\right)\).
Solution:

Question 29.
\(\int \frac{d x}{\sqrt{25+x^2}}\) on R.
Solution:

Question 30.
\(\int \frac{1}{(x+3) \sqrt{x+2}}\) on I ⊂ (-2, ∞). (New Model Paper & May ’12)
Solution:

Question 31.
\(\int \frac{1}{1+\sin 2 x} d x\) on I ⊂ R – {\(\frac{n \pi}{2}+(-1)^n \frac{\pi}{4}\) : n ∈ Z}.
Solution:

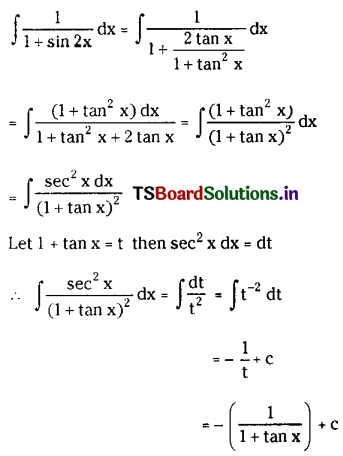
Question 32.
\(\int \frac{x^2+1}{x^4+1} d x\) on R.
Solution:

Question 33.
\(\int \frac{d x}{\cos ^2 x+\sin 2 x}\) on I ⊂ R / ({(2n + 1)\(\frac{\pi}{2}\) : n ∈ Z} ∪ {2nπ + \({tan}^{-1} \frac{1}{2}\) : n ∈ Z})
Solution:

Question 34.
\(\int \sqrt{1-\sin 2 x} d x\) on I ⊂ [2nπ – \(\frac{3 \pi}{4}\), 2nπ + \(\frac{\pi}{4}\)], n ∈ Z.
Solution:

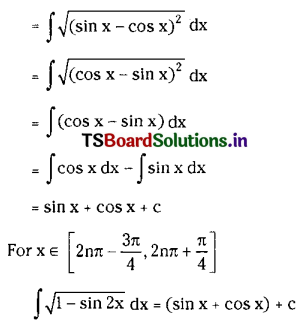
Question 35.
\(\int \sqrt{1+\cos 2 x} d x\) on I ⊂ [2nπ – \(\frac{\pi}{2}\), 2nπ + \(\frac{\pi}{2}\)], n ∈ Z.
Solution:

Question 36.
\(\int \frac{\cos x+\sin x}{\sqrt{1+\sin 2 x}} d x\) on I ⊂ [2nπ – \(\frac{\pi}{4}\), 2nπ + \(\frac{3 \pi}{4}\)], n ∈ Z.
Solution:

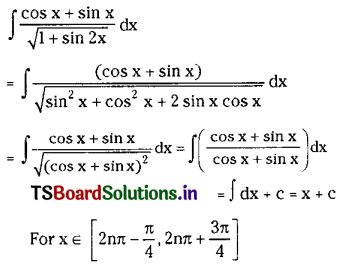
Question 37.
\(\int \frac{\sin 2 x}{(a+b \cos x)^2} d x\) on {R, if |a| > |b|, I ⊂ {x ∈ R : a + b cos x ≠ 0}, if |a| < |b|}.
Solution:

Question 38.
\(\int \frac{\sec x}{(\sec x+\tan x)^2} d x\) on I ⊂ R – {(2n + 1)\(\frac{\pi}{2}\), n ∈ Z}.
Solution:

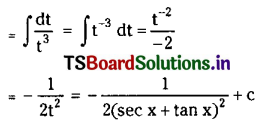
Question 39.
\(\int \frac{d x}{a^2 \sin ^2 x+b^2 \cos ^2 x}\) on R, a ≠ 0, b ≠ 0.
Solution:

Question 40.
\(\int \frac{d x}{\sin (x-a) \sin (x-b)}\) on I ⊂ R – ({a + nπ : n ∈ Z} ∪ {b + nπ : n ∈ Z}).
Solution:

Question 41.
\(\int \frac{1}{\cos (x-a) \cos (x-b)} \mathbf{d x}\) on I ⊂ R – ({a + \(\frac{(2 n+1) \pi}{2}\) : n ∈ Z} ∪ {b + \(\frac{(2 n+1) \pi}{2}\) : n ∈ Z})
Solution:

III. Evaluate the following integrals.

Question 1.
\(\int \frac{\sin 2 x}{a \cos ^2 x+b \sin ^2 x} d x\) on I ⊂ R – {x ∈ R | a cos²x + b sin²x = 0}
Solution:

Question 2.
\(\int \frac{1-\tan x}{1+\tan x} d x\) for x ∈ I ⊂ R – {nπ – \(\frac{\pi}{4}\) : n ∈ Z}
Solution:

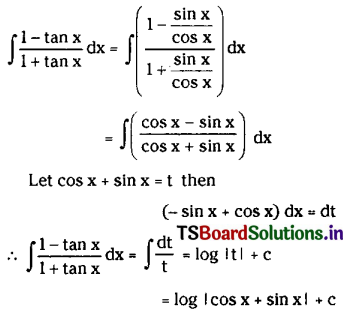
Question 3.
\(\int \frac{\cot (\log x)}{x} d x\), x ∈ I ⊂ (0, ∞) – {e^nπ : n ∈ Z}
Solution:

Question 4.
∫e^x cot e^x dx, x ∈ I ⊂ R – {log nπ : n ∈ Z}
Solution:
Let e^x = t then e^x dx = dt
∴ ∫e^x cot x dx = ∫cot t dt
= log|sin t| + c
= log|sin(e^x)| + c

Question 5.
∫sec(tan x) sec²x dx on I ⊂ {x ∈ E : tan x ≠ \(\frac{(2 k+1) \pi}{2}\) for any k ∈ Z), where E = R – {\(\frac{(2 n+1) \pi}{2}\), n ∈ Z}
Solution:
Let tan x = t, then sec²x dx = dt

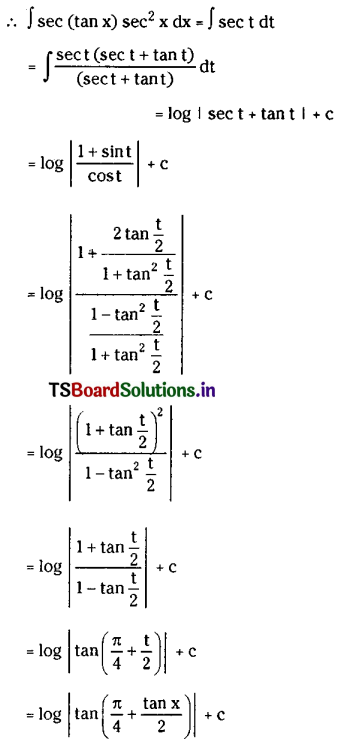
Question 6.
\(\int \sqrt{\sin x} \cos x d x\) on [2nπ, (2n + 1)π], (n ∈ Z).
Solution:

Question 7.
∫tan⁴x sec²x dx, x ∈ I ⊂ R – {\(\frac{(2 n+1) x}{2}\) : n ∈ Z}.
Solution:
Let tan x = t then sec²x dx = dt
∴ ∫tan⁴x sec²x dx = ∫t⁴dt
= \(\frac{t^5}{5}\) + c
= \(\frac{\tan ^5 x}{5}\) + c

Question 8.
\(\int \frac{2 x+3}{\sqrt{x^2+3 x-4}} d x\), x ∈ I ⊂ R – [-4, 1]
Solution:

Question 9.
\(\int {cosec}^2 x \sqrt{\cot x} d x\) on (0, \(\frac{\pi}{2}\)].
Solution:

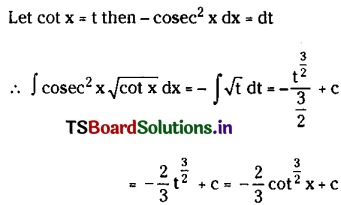
Question 10.
∫sec x log(sec x + tan x) dx on (0, \(\frac{\pi}{2}\)).
Solution:
Let log(sec x + tan x) = t then \(\frac{1}{\sec x+\tan x}\) (sec x tan x + sec²x) dx = dt
⇒ \(\frac{\sec x(\sec x+\tan x) d x}{\sec x+\tan x}\) = dt
⇒ sec x dx = dt
∴ ∫sec x log(sec x + tan x) dx = ∫t dt + c
= \(\frac{\mathrm{t}^2}{2}\) + c
= \(\frac{1}{2}\) [log(sec x + tan x)]² + c

Question 11.
∫sin³x dx on R.
Solution:
sin 3x = 3 sin x – 4 sin³x
⇒ 4 sin³x = 3 sin x – sin 3x
⇒ sin³x = \(\frac{3 \sin x-\sin 3 x}{4}\)
∴ ∫sin³x dx = \(\frac{1}{2}\) ∫(3 sin x – sin 3x) dx
= \(\frac{3}{4}\)∫sin x dx – \(\frac{1}{4}\)∫sin 3x dx
= \(-\frac{3}{4}\) cos x + \(\frac{1}{12}\) cos 3x + c
= \(\frac{1}{12}\) (cos 3x – 9 cos x] + c

Question 12.
∫cos³x dx on R.
Solution:
cos 3x = 4 cos³x – 3 cos x
⇒ 4cos³x = cos 3x + 3 cos x
⇒ cos³x = \(\frac{1}{4}\)(cos 3x + 3 cos x)
∴ ∫cos3x dx = \(\frac{1}{4}\)∫(cos 3x + 3 cos x) dx
= \(\frac{1}{12}\) sin 3x + \(\frac{3}{4}\) sin x dx + c
= \(\frac{1}{12}\) [sin 3x + 9 sin x] + c

Question 13.
∫cos x cos 2x dx on R.
Solution:
We have cos A cos B = \(\frac{1}{2}\) [cos(A + B) + cos(A – B)]
⇒ cos x cos 2x = \(\frac{1}{2}\) [cos 3x + cos x]
∴ ∫cos x cos 2x dx = \(\frac{1}{2}\) [∫cos 3x + ∫cos x] dx
= \(\frac{1}{2}\left(\frac{1}{3}\right)\) sin 3x + \(\frac{1}{2}\) sin x + c
= \(\frac{1}{6}\) sin 3x + \(\frac{1}{2}\) sin x + c
= \(\frac{1}{6}\) [sin 3x + 3 sin x] + c

Question 14.
∫cos x cos 3x dx on R.
Solution:
cos x cos 3x = \(\frac{1}{2}\) [cos 4x + cos 2x]
∴ ∫cos x cos 3x dx = \(\frac{1}{2}\) ∫cos 4x dx + \(\frac{1}{2}\) ∫cos 2x dx
= \(\frac{1}{8}\) sin 4x + \(\frac{1}{4}\) sin 2x + c

Question 15.
∫cos⁴x dx on R.
Solution:

Question 16.
\(\int x \sqrt{4 x+3} d x\) on (\(-\frac{3}{4}\), ∞).
Solution:

Question 17.
\(\int \frac{d x}{\sqrt{a^2-(b+c x)^2}}\) on {x ∈ R : |b + cx| < a}, where a, b, c are real numbers c ≠ 0 and a > 0.
Solution:
Let b + cx = t then c dx = dt
⇒ dx = \(\frac{1}{c}\) dt

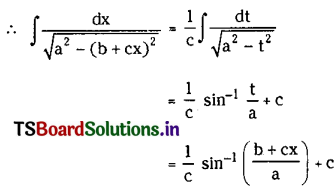
Question 18.
\(\int \frac{d x}{a^2+(b+c x)^2}\) on R, where a, b, c are real numbers c ≠ 0 and a > 0.
Solution:

Question 19.
\(\int \frac{d x}{1+e^x}\), x ∈ R.
Solution:

Question 20.
\(\int \frac{x^2}{(a+b x)^2} d x\), x ∈ I ⊂ R – {\(-\frac{a}{b}\)}, where a, b are real numbers, b ≠ 0.
Solution:
Let a + bx = t then b dx = dt
⇒ dx = \(\frac{1}{b}\) dt
Also x = \(\frac{t-a}{b}\)

Question 21.
\(\int \frac{x^2}{\sqrt{1-x}} d x\), x ∈ (-∞, 1).
Solution: