TS Inter 2nd Year Maths 2B Solutions Chapter 4 Ellipse Ex 4(a)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 4 Ellipse Ex 4(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 4 Ellipse Exercise 4(a)

I.

Question 1.
Find the equation of the ellipse with focus at (1, -1), e = \(\frac{2}{3}\) and directrix as x + y + 2 = 0. (Mar. 2001)
Solution:
Given that focus S = (1, -1) and e = \(\frac{2}{3}\) and
equation of directrix is L = x + y + 2 = 0
Let (x₁, y₁) be any point on the ellipse and PM is the perpendicular distance from P to the directrix L = 0.

Question 2.
Find the equation of the ellipse in the standard form whose distance between foci is 2 and the length of latus rectum is \(\frac{15}{2}\).
Solution:
The equation of an ellipse in the standard form is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\), a > b
Given that the length of the latus rectum = \(\frac{15}{2}\)
∴ \(\frac{2 b^2}{a}=\frac{15}{2}\)
⇒ 4b² = 15a
Given that the distance between foci = 2
∴ 2ae = 2
⇒ ae = 1 ……(2)
From (1), 4a²(1 – e²) = 15a (∵ b² = a²(1 – e²))
⇒ 4(a² – a²e²) = 15a
⇒ 4(a² – 1) = 15a (∵ ae = 1)
⇒ 4a² – 15a – 4 = 0
⇒ 4a² – 16a + a – 4 = 0
⇒ 4a(a – 4) + 1(a – 4) = 0
⇒ a = 4 or a = \(-\frac{1}{4}\)
∴ a = 4 (∵ a > 0)
∴ From (1), 4b² = 15(4) = 60
⇒ b² = 15
Hence the required equation of the ellipse is \(\frac{x^2}{16}+\frac{y^2}{15}\) = 1

Question 3.
Find the equation of the ellipse in the standard form such that the distance between foci is 8 and the distance between directrices is 32.
Solution:
Given that the distance between foci = 8
∴ 2ae = 8
⇒ ae = 4 ……(1)
The distance between the directrices is ZZ’ = 32
⇒ 2 \(\frac{a}{e}\) = 32
⇒ \(\frac{a}{e}\) = 16 ……..(2)
From (1) and (2),
(ae) (\(\frac{a}{e}\)) = 4(16)
⇒ a² = 64
⇒ a = 8
b² = a²(1 – e²)
= a² – a²e²
= 64 – 16
= 48
∴ The equation of the required ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
⇒ \(\frac{x^2}{64}+\frac{y^2}{48}=1\)

Question 4.
Find the eccentricity of the ellipse (in standard form), if the length of the latus rectum is equal to half of its major axis.
Solution:
Let the ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Length of the latus rectum of the ellipse = \(\frac{2 b^2}{a}\)
Length of major axis = 2a
∴ \(\frac{2 b^2}{a}\) = a
⇒ 2b² = a2
⇒ 2a²(1 – e²) = a²
⇒ 2(1 – e²) = 1
⇒ 1 – e² = \(\frac{1}{2}\)
⇒ e² = \(\frac{1}{2}\)
⇒ e = \(\frac{1}{\sqrt{2}}\)
∴ The eccentricity of the ellipse is \(\frac{1}{\sqrt{2}}\).

Question 5.
The distance of a point on the ellipse x² + 3y² = 6 from its centre is equal to 2. Find the eccentric angles.
Solution:
Given ellipse is x² + 3y² = 6
\(\frac{x^2}{6}+\frac{y^2}{2}=1\) ……(1)
Comparing with \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\), we have a² = 6, b² = 2.
∴ a = √6, b = √2
The Centre of the ellipse (1) is C = (0, 0)
Let P = (a cos θ, b sin θ) = (√6 cos θ, √2 sin θ) which is a point on the ellipse whose distance from C(0, 0) is equal to 2.
∴ CP = 2
⇒ \(\sqrt{6 \cos ^2 \theta+2 \sin ^2 \theta}\) = 2
⇒ 6 cos²θ + 2 sin²θ = 4
⇒ 6 cos²θ + 2 (1 – cos²θ) = 4
⇒ 4 cos²θ = 2
⇒ cos²θ = \(\frac{1}{2}\)
⇒ cos θ = ±\(\frac{1}{\sqrt{2}}\)
⇒ θ = \(\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4}\)

Question 6.
Find the equation of the ellipse in the standard form, if it passes through the points (-2, 2) and (3, -1).
Solution:
Let the equation of the ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) …….(1)
since (1) passes through (-2, 2) we have \(\frac{4}{a^2}+\frac{4}{b^2}=1\) ……..(2)
since (1) passes through (3, -1) we have \(\frac{9}{a^2}+\frac{1}{b^2}=1\) ……(3)
From (2) and (3)

Question 7.
If the ends of the major axis of an ellipse are (5, 0) and (-5, 0). Find the equation of the ellipse in the standard form if its focus lies on line 3x – 5y – 9 = 0.
Solution:
Let A(5, 0), A’ = (-5, 0) are the ends of the major axis of an ellipse.
Since the Y coordinates of A, A’ is zero,
The major axis is y = 0
⇒ Major axis lies along the x-axis
∴ The equation of the required ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a > b)
Also 2a = AA’ = \(\sqrt{(-5-5)^2}=\sqrt{(-10)^2}\) = 10
⇒ a = 5
Focus is S = (+ae, 0) = (5e, 0).
Given that focus lies on line 3x – 5y – 9 = 0
⇒ 3(5e) – 5(0) – 9 = 0

Question 8.
If the length of the major axis of an ellipse is three times the length of its minor axis then find the eccentricity of the ellipse.
Solution:
Let the ellipse in the standard form be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) ……(1)
The length of the major axis is ‘a’ and the length of the minor axis is ‘b’.
Given that a = 3b
⇒ a² = 9b²
⇒ a² = 9a²(1 – e²)
⇒ 1 – e² = \(\frac{1}{9}\)
⇒ e² = \(\frac{8}{9}\)
⇒ e = \(\frac{2 \sqrt{2}}{3}\)
∴ Eccentricity of the ellipse = \(\frac{2 \sqrt{2}}{3}\)

II.

Question 1.
Find the length of the major axis, minor axis, latus rectum, eccentricity, coordinates of centre, foci, and the equations of directrices of the following ellipse. (New Model Paper)
(i) 9x² + 16y² = 144
Solution:
The given equation of the ellipse is 9x² + 16y² = 144
Writing this in the standard form we get \(\frac{x^2}{16}+\frac{y^2}{9}=1\) and comparing with S = 0.
We get a² = 16, and b² = 9
⇒ a = 4 and b = 3
Here a > b
(i) Length of the major axis = AA’= 2a = 2(4) = 8
(ii) Length of the minor axis is = BB’ = 2b = 2(3) = 6
(iii) Length of the latus rectum = \(\frac{2 b^2}{a}=\frac{2(9)}{4}=\frac{9}{2}\)
(iv) Eccentricity = \(\sqrt{\frac{a^2-b^2}{a^2}}=\sqrt{\frac{16-9}{16}}=\sqrt{\frac{7}{4}}\)
(v) Coordinates of centre = (0, 0)
(vi) Foci = (±ae, 0) = (±√7, 0)
(vii) Equation of directrices are x = \(\pm \frac{a}{e}\)
⇒ x = \(\pm \frac{4}{\frac{\sqrt{7}}{4}}=\pm \frac{16}{\sqrt{7}}\)
⇒ √7x = ±16
⇒ √7x ± 16 = 0

(ii) 4x² + y² – 8x + 2y + 1 = 0 (Mar. ’10, ’11)
Solution:
4x² – 8x + y² + 2y + 1 = 0
⇒ 4x² – 8x + 4 + y² + 2y + 1 = 4
⇒ 4(x² – 2x + 1) + y² + 2y + 1 = 4
⇒ 4 (x – 1)² + (y + 1)² = 4
⇒ \(\frac{(x-1)^2}{1}+\frac{(y+1)^2}{4}=1\)
Comparing with \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\)
Where a² = 1 and b² = 4
⇒ a = 1 and b = 2 and a < b.
(i) Length of the major axis = BB’ = 2b = 2(2) = 4
(ii) Length of the minor axis = AA’ = 2a = 2(1) = 2
(iii) Length of the latus rectum = \(\frac{2 a^2}{b}=\frac{2(1)}{2}\) = 1
(iv) Eccentricity = \(\sqrt{\frac{b^2-a^2}{b^2}}=\sqrt{\frac{4-1}{4}}=\frac{\sqrt{3}}{2}\)
(v) Coordinates of centre = (1, -1)
(vi) foci = (h, k ± be)
= \(\left(1 , -1 \pm 2\left(\frac{\sqrt{3}}{2}\right)\right)\)
= (1, -1 ± √3)
(vii) Equations of directrices is y = k ± \(\frac{b}{e}\) = \(-1 \pm \frac{2}{\left(\frac{\sqrt{3}}{2}\right)}=-1 \pm \frac{4}{\sqrt{3}}\)
⇒ √3y + √3 ± 4 = 0

(iii) x² + 2y² – 4x + 12y + 14 = 0
Solution:
The given equation can be written as x² – 4x + 2y² + 12y = -14
⇒ x² – 4x + 4 + 2(y² + 6y) = -14 + 4
⇒ x² – 4x + 4 + 2(y² + 6y + 9) = -14 + 4 + 18
⇒ (x – 2)² + 2(y + 3)² = 8
⇒ \(\frac{(x-2)^2}{8}+\frac{(y+3)^2}{4}\) = 1 …….(1)
Comparing the given ellipse (1) with \(\frac{(x-h)^2}{a^2}+\frac{(y+k)^2}{b^2}\) = 1, we get
h = 2, k = -3, a² = 8, b² = 4
⇒ a = 2√2, b = 2
Clearly a > b
(i) Length of the major axis = AA’
= 2a
= 2(2√2)
= 4√2
(ii) Length of the minor axis is BB’ = 2b
= 2(2)
= 4
(iii) Length of the latus rectum = \(\frac{2 b^2}{a}\)
= \(\frac{2(4)}{2 \sqrt{2}}\)
= 2√2
(iv) Eccentricity = \(\sqrt{\frac{a^2-b^2}{a^2}}=\sqrt{\frac{8-4}{8}}=\sqrt{\frac{4}{8}}=\frac{1}{\sqrt{2}}\)
(v) Coordinates of centre = (2, -3)
(vi) Foci = (h ± ae, k)
= \(\left(2 \pm 2 \sqrt{2} \cdot\left(\frac{1}{\sqrt{2}}\right),-3\right)\)
= (2 ± 2, -3)
= (4, -3),(0, -3)
(vii) Equation of directrices are x = \(h \pm \frac{a}{e}\)
= \(2 \pm \frac{2 \sqrt{2}}{(1 / \sqrt{2})}\)
= 2 ± 4
∴ x = 6, x = -2 are the equations of directrices.

Question 2.
Find the equation of the ellipse in the form \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}\) = 1, given the following data.
(i) Centre (2, -1), one end of the major axis (2, -5), e = \(\frac{1}{3}\)
Solution:
Centre C(h, k) = (2, -1)
Let one end of the major axis is B = (2, -5)
Since the x-coordinates of C and B are the same and equal to ‘2’,
the major axis of an ellipse is x = 2 which is a line parallel to the y-axis.
The equation of ellipse is \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}\) = 1 where a < b.
CB = b where C = (2, -1) and B = (2, -5)
∴ b = \(\sqrt{(2-2)^2+(-1+5)^2}\) = 4
But a² = b²(1 – e²)
= 16(1 – \(\frac{1}{9}\))
= \(\frac{128}{9}\)
∴ The equation of the required ellipse is \(\frac{(\mathrm{x}-\mathrm{h})^2}{\left(\frac{128}{9}\right)}+\frac{(\mathrm{y}+1)^2}{16}=1\)
⇒ \(\frac{9(x-2)^2}{128}+\frac{(y+1)^2}{16}=1\)
⇒ 9(x – 2)² + 8(y + 1)² = 128

(ii) Centre = (4, -1) one end of the minor axis is (-1, -1) and passes through (8, 0).
Solution:
Given centre C(h, k) = (4, -1) and one ends of the minor axis is (-1, -1).
Let A = (-1, -1)
Since the y-coordinates of C and A are the same and equal to ‘-1’, the minor axis is parallel to the X-axis.
∴ Major axis parallel to Y-axis.
∴ a = CA = \(\sqrt{(4+1)^2+(-1+1)^2}\) = 5
∴ The equation of the required ellipse is \(\frac{(\mathrm{x}-\mathrm{h})^2}{\mathrm{a}^2}+\frac{(\mathrm{y}+\mathrm{k})^2}{\mathrm{~b}^2}=1\)
⇒ \(\frac{(x-4)^2}{25}+\frac{(y+1)^2}{b^2}=1\) ……(1)
Since Ellipse is passing through the point (8, 0) we have \(\frac{(8-4)^2}{25}+\frac{1}{b^2}=1\)

∴ Required equation of ellipse is (x – 4)² + 9(y + 1)² = 25.

(iii) Centre (0, -3), e = \(\frac{2}{3}\), semi minor axis is 5.
Solution:
Given that centre C(h, k) = (0, -3), e = \(\frac{2}{3}\)
Semi minor axis = 5
The equation of the required ellipse is \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\)
Case (1): If a > b then b² = a²(1 – e)²
Given semi-minor axis b = 5

Case (2): If a < b then a² = b²( 1 – e²)
semi minor axis = 5
⇒ a = 5

(iv) Centre (2, -1), e = \(\frac{1}{2}\), length of latus rectum = 4.
Solution:
Given C(h, k) = (2, -1), e = \(\frac{1}{2}\), length of latus rectum = 4
Case (1): Where a > b, we have b² = a²(1 – e²)
and length of latus rectum =


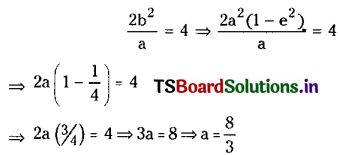
⇒ (x – 2)² + 9(y + 1)² = 64 is the required equation of ellipse.

Question 3.
Find the radius of the circle passing through the foci of an ellipse 9x² + 16y² = 144 and having the least radius.
Solution:
Given the equation of the ellipse is 9x² + 16y² = 144
\(\frac{x^2}{16}+\frac{y^2}{9}=1\)
Compared with the general equation we have
a² = 16, b² = 9
⇒ a = 4 and b = 3
Foci of ellipse = (±ae, 0)
Also since a² > b² we have b² = a²(1 – e²)
⇒ 9 = 16(1 – e²)
⇒ 1 – e² = \(\frac{9}{16}\)
⇒ e² = 1 – \(\frac{9}{16}\) = \(\frac{7}{16}\)
⇒ e = \(\frac{\sqrt{7}}{4}\)
Eccentricity of ellipse (e) = \(\frac{\sqrt{7}}{4}\)
∴ Focus = (±ae, 0)
= \(\left(\pm 4\left(\frac{\sqrt{7}}{4}\right), 0\right)\)
= (±√7, 0)
Now the equation of a circle having (√7, 0) and (-√7, 0) as extremities of diameter is given by
(x – √7 ) (x + √7 ) + (y – 0) (y – 0) = 0
⇒ x² + y² = 7
Hence the least radius of the circle x² + y² = 7 is √7.

Question 4.
A man running on a race course notices that the sum of the distances between the two flag posts is always 10m. and the distance between the flag posts is 8m. Find the equation of the race course traced by the man.
Solution:

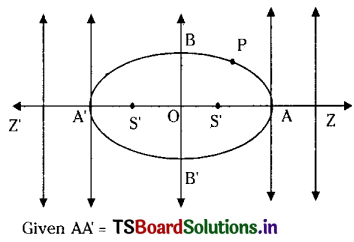
Given AA’ = 2a = 10
⇒ a = 5 (Taking flag posts located at A & A’)
Also given the distance between two fixed points S and S’ = 8m
∴ 2ae = 8
⇒ ae = 4
∴ b² = a²(1 – e²)
⇒ a² – a²e² = 25 – 16 = 9
⇒ b² = 9
Hence the equation of ellipse is \(\frac{x^2}{25}+\frac{y^2}{9}\) = 1.

III.

Question 1.
A line of fixed length (a + b) moves so that its ends are always on two fixed perpendicular straight lines. Prove that a marked point on the line, which divides this line into portions of length ‘a’ and ‘b’ describes an ellipse and also finds the eccentricity of the ellipse when a = 8, b = 12.
Solution:

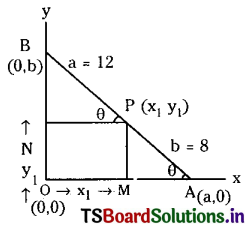
Let AB be a line of fixed length and a + b which moves with its end A, B on the x and y-axis.
AB = a + b
Let P(x₁, y₁) be any point on the line AB and BP = a, and AP = b.
Let M and N be the projections of P on the x and y-axis.
Such that OM = x₁ and ON = y₁

Question 2.
Prove that the equation of the chord joining the points ‘α’ and ‘β’ on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) is \(\frac{{x}}{a} \cos \left(\frac{\alpha+\beta}{2}\right)+\frac{y}{b} \sin \left(\frac{\alpha+\beta}{2}\right)=\cos \left(\frac{\alpha-\beta}{2}\right)\).
Solution:
Let S = \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\) = 0 be the given ellipse
and let P = (a cos α, b sin α) and Q = (a cos β, b sin β) be the two given points on the ellipse S = 0.
The equation of the chord PQ is

Dividing by ‘ab’ on both sides, the equation of the chord joining the points (α, β) on the ellipse S = 0 is \(\frac{{x}}{a} \cos \left(\frac{\alpha+\beta}{2}\right)+\frac{y}{b} \sin \left(\frac{\alpha+\beta}{2}\right)=\cos \left(\frac{\alpha-\beta}{2}\right)\)