TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Ex 6(a)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 6 Integration Ex 6(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Exercise 6(a)

I. Evaluate the following integrals.

Question 1.
∫(x³ – 2x² + 3) dx on R.
Solution:

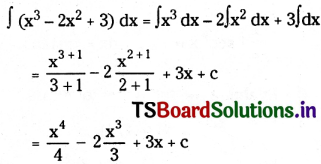
Question 2.
∫2x√x dx on (0, ∞).
Solution:

Question 3.
\(\int \sqrt[3]{2 x^2}\) dx on (0, ∞).
Solution:

Question 4.
\(\int\left(\frac{x^2+3 x-1}{2 x}\right)\) dx, x ∈ I ⊂ R – {0}
Solution:

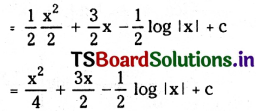
Question 5.
\(\int \frac{1-\sqrt{x}}{x}\) dx on (0, ∞).
Solution:

Question 6.
\(\int\left(1+\frac{2}{x}-\frac{3}{x^2}\right) d x\) on I ⊂ R – {0}
Solution:

Question 7.
\(\int\left(x+\frac{4}{1+x^2}\right) d x\) on R
Solution:

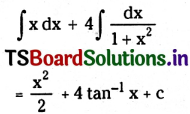
Question 8.
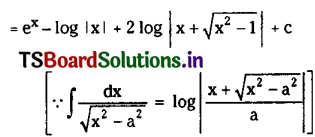
\(\int\left(e^x-\frac{1}{x}+\frac{2}{\sqrt{x^2-1}}\right) d x\) on I ⊂ R – [-1, 1]
Solution:

Question 9.
\(\int\left(\frac{1}{1-x^2}+\frac{1}{1+x^2}\right) d x\) on (-1, 1)
Solution:

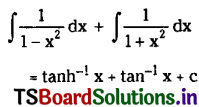
Question 10.
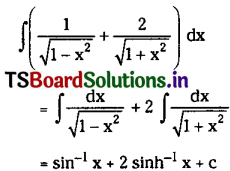
\(\int\left(\frac{1}{\sqrt{1-x^2}}+\frac{2}{\sqrt{1+x^2}}\right) d x\) on (-1, 1). [May ’11]
Solution:

Question 11.
\(\int e^{\log \left(1+\tan ^2 x\right)} d x\) on I ⊂ R – {\(\frac{(2 n+1) \pi}{2}\) : n ∈ Z}
Solution:

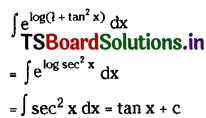
Question 12.
\(\int \frac{\sin ^2 x}{1+\cos 2 x} d x\) on I ⊂ R – {(2n ± 1)π : n ∈ Z}.
Solution:

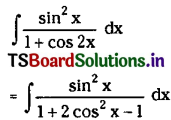
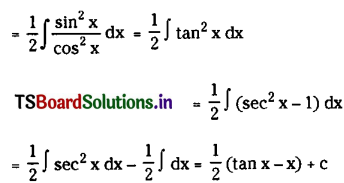
II. Evaluate the following integrals.

Question 1.
∫(1 – x²)³ dx on (-1, 1).
Solution:

Question 2.
\(\int\left(\frac{3}{\sqrt{x}}-\frac{2}{x}+\frac{1}{3 x^2}\right) d x\) on (0, ∞).
Solution:

Question 3.
\(\int\left(\frac{\sqrt{x}+1}{x}\right)^2 d x\) on (0, ∞).
Solution:

Question 4.
\(\int \frac{(3 x+1)^2}{2 x} d x\), x ∈ I ⊂ R – {0}.
Solution:

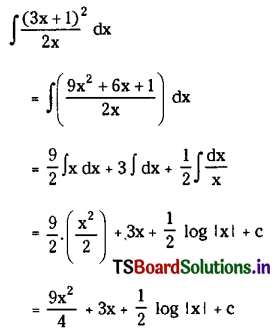
Question 5.
\(\int\left(\frac{2 x-1}{3 \sqrt{x}}\right)^2 d x\) on (0, ∞).
Solution:

Question 6.
\(\int\left(\frac{1}{\sqrt{x}}+\frac{2}{\sqrt{x^2-1}}-\frac{3}{2 x^2}\right) d x\) on (1, ∞).
Solution:

Question 7.
∫(sec²x – cos x + x²) dx, x ∈ I ⊂ R – {\(\frac{n \pi}{2}\) : n is an odd integer}.
Solution:
∫(sec²x – cos x + x²) dx
= ∫sec²x dx – ∫cos x dx + ∫x² dx
= tan x – sin x + \(\frac{x^3}{3}\) + c

Question 8.
∫(sec x tan x + \(\frac{3}{x}\) – 4] dx, x ∈ I ⊂ R – ({\(\frac{n \pi}{2}\) : n is an odd integer} ∪ {0})
Solution:
∫(sec x tan x + \(\frac{3}{x}\) – 4] dx
= ∫sec x + tan x dx + 3 ∫\(\frac{dx}{x}\) – 4∫dx
= sec x + 3 log|x| – 4x + c

Question 9.
\(\int\left(\sqrt{x}-\frac{2}{1-x^2}\right) d x\) on (0, 1)
Solution:

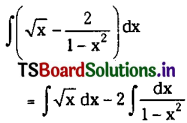
Question 10.
\(\int\left(x^3-\cos x+\frac{4}{\sqrt{x^2+1}}\right) d x\), x ∈ R
Solution:

Question 11.
\(\int\left(\cosh x+\frac{1}{\sqrt{x^2+1}}\right) d x\), x ∈ R
Solution:

Question 12.
\(\int\left(\sinh x+\frac{1}{\left(x^2-1\right)^{\frac{1}{2}}}\right) d x\), x ∈ I ⊂ (-∞, -1) ∪ (1, ∞).
Solution:

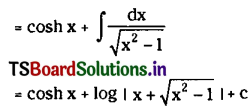
Question 13.
\(\int \frac{\left(a^x-b^x\right)^2}{a^x b^x} d x\), (a > 0, a ≠ 1 and b > 0, b ≠ 1) on R.
Solution:

Question 14.
∫sec²x cosec²x dx on I ⊂ R – ({nx : n ∈ Z} ∪ {(2n + 1)\(\frac{\pi}{2}\) : n ∈ Z}) (May ’09)
Solution:

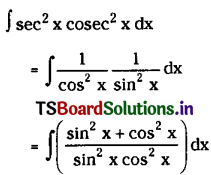
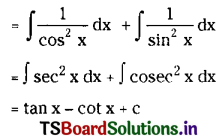
Question 15.
\(\int\left(\frac{1+\cos ^2 x}{1-\cos 2 x}\right) d x\) on I ⊂ R – {nπ : n ∈ Z} (Mar. ’13)
Solution:

Question 16.
\(\int \sqrt{1-\cos 2 x} d x\) on I ⊂ [2nπ, (2n + 1)π], n ∈ Z. (Mar. ’09)
Solution:

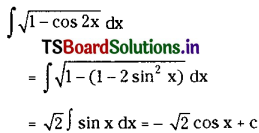
Question 17.
\(\int \frac{1}{\cosh x+\sinh x} d x\) on R.
Solution:
\(\int \frac{1}{\cosh x+\sinh x} d x\)
= \(\int \frac{\cosh x-\sinh x}{\cosh ^2 x-\sinh ^2 x} d x\)
= ∫(cos hx – sin hx) dx (∵ cosh²x – sinh²x = 1)
= ∫cosh x dx – ∫sinh x dx
= sinh x – cosh x + c

Question 18.
\(\int \frac{1}{1+\cos x} d x\) on I ⊂ R – [(2n + 1)π : n ∈ Z].
Solution:
\(\int \frac{1}{1+\cos x} d x\)
= \(\int \frac{1-\cos x}{(1+\cos x)(1-\cos x)} d x\)
= \(\int \frac{1-\cos x}{\sin ^2 x} d x\)
= ∫cosec²x dx – ∫cot x cosec x dx
= -cot x + cosec x + c
= cosec x – cot x + c