TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Ex 6(e)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 6 Integration Ex 6(e) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 6 Integration Exercise 6(e)

I. Evaluate the following integrals.

Question 1.
\(\int \frac{x-1}{(x-2)(x-3)} d x\)
Solution:
\(\int \frac{x-1}{(x-2)(x-3)} d x\)

= x + 2 log|x – 3| – x – log|x – 2| + c
= 2 log|x – 3| – log|x – 2| + c
Alter: Let \(\frac{x-1}{(x-2)(x-3)}=\frac{A}{x-2}+\frac{B}{x-3}\) (Partial fractions method)
∴ x – 1 = A(x – 3) + B(x – 2)
Comparing coefficients of x and constant terms on both sides
A + B = 1 ………(1) and
-3A – 2B = -1
⇒ 3A + 2B = 1 ………(2)
From (1), 2A + 2B = 2
Solving A = -1 and B = 2

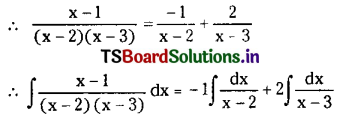
= -log|x – 2| + 2 log|x – 3| + c
= 2 log|x – 3| – log|x – 2| + c

Question 2.
\(\int \frac{x^2}{(x+1)(x+2)^2} d x\)
Solution:
Let \(\frac{x^2}{(x+1)(x+2)^2}=\frac{A}{x+1}+\frac{A}{x+2}+\frac{C}{(x+2)^2}\)
∴ x² = A(x + 2)² + B(x + 1)(x + 2) + C(x + 1)
Put x = -1, then A = 1
Comparing the coefficient of x²,
A + B = 1 ⇒ B = 0
Put x = -2, and we get
4 = C(-1)
⇒ C = -4

Question 3.
\(\int \frac{x+3}{(x-1)\left(x^2+1\right)} d x\)
Solution:
Let \(\frac{x+3}{(x-1)\left(x^2+1\right)}=\frac{A}{x-1}+\frac{B x+C}{x^2+1}\)
∴ x + 3 = A(x² + 1) + (Bx + C)(x – 1)
Put x = 1, then 4 = 2A
⇒ A = 2
Comparing the coefficient of x²,
A + B = 0
⇒ B = -A = -2
Comparing the coefficient of constant terms
A – C = 3
⇒ C = A – 3 = 2 – 3 = -1
∴ x + 3 = 2(x² + 1) + (-2x – 1)(x – 1) = 2(x² + 1) – (2x + 1)(x – 1)

Question 4.
\(\int \frac{d x}{\left(x^2+a^2\right)\left(x^2+b^2\right)}\)
Solution:

Question 5.
\(\int \frac{d x}{e^x+e^{2 x}}\)
Solution:

Question 6.
\(\int \frac{d x}{(x+1)(x+2)}\) (Mar. ’12; May ’11)
Solution:

Question 7.
\(\int \frac{1}{e^x-1} d x\)
Solution:

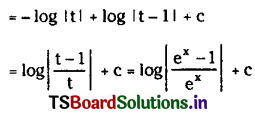
Question 8.
\(\int \frac{1}{(1-x)\left(4+x^2\right)} d x\)
Solution:
Let \(\frac{1}{(1-x)\left(4+x^2\right)}=\frac{A}{1-x}+\frac{B x+C}{x^2+4}\)
∴ 1 = A(x² + 4) + (Bx + C)(1 – x)
When x – 1 then 5A = 1 ⇒ A = \(\frac{1}{5}\)
The coefficient of x² on both sides gives
A – B = 0 ⇒ B = \(\frac{1}{5}\)
Comparing constant terms,

Question 9.
\(\int \frac{2 x+3}{x^3+x^2-2 x} d x\)
Solution:
x³ + x² – 2x = x(x² + x – 2) = x(x – 1)(x + 2)

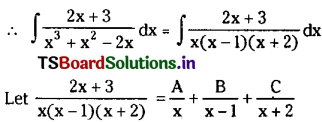
∴ 2x + 3 = A(x – 1)(x + 2) + Bx(x + 2) + Cx(x – 1)
Put x = 1 we get
5 = 3B ⇒ B = \(\frac{5}{3}\)
Put x = -2 on both sides
-4 + 3 = C(-2) (-2 – 1)
⇒ -1 = 6C
⇒ C = \(-\frac{1}{6}\)
Coefficient of x2 on both sides
A + B + C = 0

II. Evaluate the following integrals.

Question 1.
\(\int \frac{d x}{6 x^2-5 x+1}\)
Solution:
6x² – 5x + 1 = 6x² – 3x – 2x + 1
= 3x(2x – 1) – 1(2x – 1)
= (3x – 1)(2x – 1)

Question 2.
\(\int \frac{d x}{x(x+1)(x+2)}\)
Solution:
Let \(\frac{1}{x(x+1)(x+2)}=\frac{A}{x}+\frac{B}{x+1}+\frac{C}{x+2}\)
∴ 1 = A(x + 1)(x + 2) + Bx(x + 2) + Cx(x + 1)
Put x = -1 then -B = 1 ⇒ B = -1
Coefficient of x2 both sides
A + B + C = 0 and put x = – 2 then
C(-2)(-1) = 1
⇒ C = \(\frac{1}{2}\)
∴ A = -B – C = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)

Question 3.
\(\int \frac{3 x-2}{(x-1)(x+2)(x-3)} d x\)
Solution:
Let \(\frac{3 x-2}{(x-1)(x+2)(x-3)}=\frac{A}{x-1}+\frac{B}{x+2}\) + \(\frac{C}{x-3}\)
∴ 3x – 2 = A(x + 2)(x – 3) + B(x – 1)(x – 3) + C(x – 1)(x + 2)
Put x = 1, then 1 = A(3)(-2) ⇒ A = \(-\frac{1}{6}\)
Put x = -2, then -8 = B(-3)(-5) ⇒ B = \(-\frac{8}{15}\)
Put x = 3, then 7 = C(2)(5) ⇒ C = \(\frac{7}{10}\)

Question 4.
\(\int \frac{7 x-4}{(x-1)^2(x+2)} d x\)
Solution:
Let \(\frac{7 x-4}{(x-1)^2(x+2)}=\frac{A}{x-1}+\frac{B}{(x-1)^2}+\frac{C}{x+2}\)
∴ 7x – 4 = A(x – 1)(x + 2) + B(x + 2) + C(x – 1)²
Put x = 1 both sides 3 = 3B ⇒ B = 1
Put x = -2 both sides -18 = 9C ⇒ C = -2
Comparing the coefficient of x² on both sides
A + C = 0
⇒ A = -C = 2

III. Evaluate the following integrals.

Question 1.
\(\int \frac{1}{(x-a)(x-b)(x-c)} d x\)
Solution:
Let \(\frac{1}{(x-a)(x-b)(x-c)}\) = \(\frac{A}{x-a}+\frac{B}{x-b}+\frac{C}{x-c}\)
Then 1 = A(x – b)(x – c) + B(x – a)(x – c) + C(x – a)(x – b)
Put x = a both sides we get 1 = A(a – b)(a – c)
⇒ A =\(\frac{1}{(a-b)(a-c)}\)
Put x = b both sides we get 1 = B(b – a)(b – c)
⇒ B = \(\frac{1}{(b-a)(b-c)}\)
Put x = c both sides we get 1 = C (c – a)(c – b)
⇒ C = \(\frac{1}{(c-a)(c-b)}\)

Question 2.
\(\int \frac{2 x+3}{(x+3)\left(x^2+4\right)} d x\)
Solution:
Let \(\frac{2 x+3}{(x+3)\left(x^2+4\right)}=\frac{A}{x+3}+\frac{B x+C}{x^2+4}\) ……(1)
∴ 2x + 3 = A(x² + 4) + (Bx + c)(x + 3)
Put x = -3 both sides -6 + 3 = A(9 + 4)
⇒ A = \(-\frac{3}{13}\)
Comparing the coefficient of x² on both sides
A + B = 0
⇒ B = -A = \(\frac{3}{13}\)
and comparing constant terms on both sides
4A + 3C = 3
⇒ 3C = 3 – 4A

Question 3.
\(\int \frac{2 x^2+x+1}{(x+3)(x-2)^2} d x\)
Solution:
Let \(\frac{2 x^2+x+1}{(x+3)(x-2)^2}=\frac{A}{x+3}+\frac{B}{x-2}\) + \(\frac{C}{(x-2)^2}\)
∴ 2x² + x + 1 = A(x – 2)² + B(x – 2)(x + 3) + C(x + 3)
Put x = 2 on both sides
8 + 2 + 1 = C(5)
⇒ C = \(\frac{11}{5}\)
Put x = -3 on both sides
18 – 3 + 1 = A(-5)²
⇒ A = \(\frac{16}{25}\)
Put x = 0 on both sides

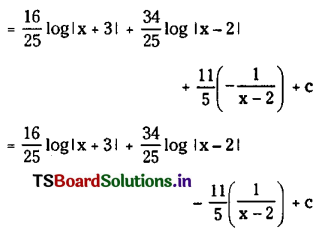
Question 4.
\(\int \frac{d x}{x^3+1}\)
Solution:
We have x³ + 1 = (x + 1)(x² – x + 1)
∴ \(\frac{1}{x^3+1}=\frac{1}{(x+1)\left(x^2-x+1\right)}\) = \(\frac{A}{x+1}+\frac{B x+C}{x^2-x+1}\)
∴ 1 = A(x² – x + 1) + (Bx + C)(x + 1) …….(1)
Put x = -1 both sides 1 = A(3)
⇒ A = \(\frac{1}{3}\)
Comparing the coefficient of x² on both sides
A + B = 0
⇒ B = \(-\frac{1}{3}\)
Comparing constant terms we get
A + C = 1
⇒ C = 1 – A
= 1 – \(\frac{1}{3}\)
= \(\frac{2}{3}\)
∴ From(1)

Question 5.
\(\int \frac{\sin x \cos x}{\cos ^2 x+3 \cos x+2} d x\)
Solution:
Let cos x = t then sin x dx = -dt

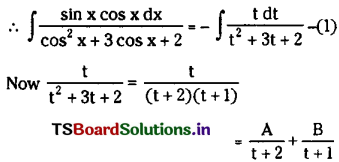
∴ t = A(t + 1) + B(t + 2)
Put t = -1 then -1 = B(-1 + 2)
⇒ B = -1
and when t = -2 then -2 = A(-1)
⇒ A = 2
∴ \(\int \frac{t}{t^2+3 t+2} d t=\int \frac{2}{t+2} d t-\int \frac{1}{t+1} d t\)
∴ From (1)

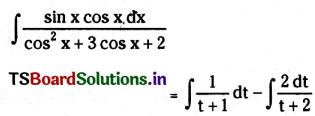
= log|t + 1| – 2 log|t + 2|
= log|cos x + 1| – 2 log|cos x + 2| + c