TS Inter 2nd Year Maths 2B Solutions Chapter 5 Hyperbola Ex 5(a)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 5 Hyperbola Ex 5(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 5 Hyperbola Exercise 5(a)

I.

Question 1.
One focus of a hyperbola is located at the point (1, -3) and the corresponding directrix is the line y = 2. Find the equation of the hyperbola if its eccentricity is \(\frac{3}{2}\). (May 2009)
Solution:
Given one focus of hyperbola is at (1, -3)
∴ S = (1, -3) and directrix is y – 2 = 0
Given e = \(\frac{3}{2}\).
Let P(x₁, y₁) be a point on the locus. Then
SP = e . PM
⇒ SP² = e² . PM²

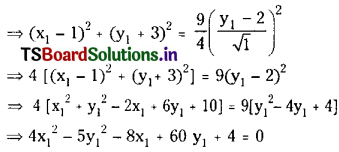
∴ Locus of (x₁, y₁) is the equation of hyperbola 4x² – 5y² – 8x + 60y + 4 = 0.

Question 2.
If the lines 3x – 4y = 12 and 3x + 4y = 12 meets on a hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) then find the eccentricity of the hyperbola.
Solution:
Given the equation of lines are
3x – 4y = 12 …….(1)
3x + 4y = 12 ………(2)
The combined equations of lines (1) and (2) is (3x – 4y) (3x + 4y) = 144
⇒ 9x² – 16y² = 144
⇒ \(\frac{x^2}{16}-\frac{y^2}{9}=1\) which represents a hyperbola of the form \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\).

Question 3.
Find the equations of hyperbola whose foci are (±5, 0); the transverse axis is of length 8.
Solution:
Given foci as (±5, 0)and comparing with the standard equation we get
ae = 5 …….(1)
and the length of the transverse axis is 2a = 8
⇒ a = 4
∴ ae = 5
⇒ e = \(\frac{5}{4}\)
since b² = a²(e² – 1)
⇒ b² = 16\(\left(\frac{25}{16}-1\right)\) = 9
∴ Equation of hyperbola whose foci are (±5, 0) and the transverse axis of length ‘8’ is \(\frac{x^2}{16}-\frac{y^2}{9}=1\)
⇒ 9x² – 16y² = 144

Question 4.
Find the equation of hyperbola whose asymptotes are the straight lines (x + 2y + 3) = 0 and (3x + 4y + 5) = 0 and which passes through the point (1, -1).
Solution:
Given asymptotes are x + 2y + 3 = 0 and 3x + 4y + 5 = 0.
∴ The equation of point of asymptotes is (x + 2y + 3) (3x + 4y + 5) = 0
⇒ 3x² + 6xy + 9x + 4xy + 8y² + 10y + 9x + 12y + 15 = 0
⇒ 3x² + 10xy + 8y² + 14x + 22y + 15 = 0
∴ The equation of hyperbola having the given lines as asymptotes are
3x² + 10xy + 8y² + 14x + 22y + k = 0 ……..(1)
Given (1) is passing through (1, -1) then
3 – 10 + 8 + 14 – 22 + k = 0
⇒ k = 7
∴ From (1) the equation of the required hyperbola is 3x² + 10xy + 8y² + 14x + 22y + 7 = 0

Question 5.
If 3x – 4y + k = 0 is a tangent to x² – 4y² = 5, find the value of k.
Solution:
Given the equation of the hyperbola is x² – 4y² = 5
⇒ \(\frac{x^2}{5}-\frac{y^2}{\left(\frac{5}{4}\right)}=1\)
Comparing with \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
We get a² = 5 and b² = \(\frac{5}{4}\)
Given 3x – 4y + k = 0
⇒ 4y = 3x + 3
⇒ y = \(\frac{3}{4} x+\frac{k}{4}\)

Question 6.
Find the product of lengths of perpendiculars from any point on the hyperbola \(\frac{x^2}{16}-\frac{y^2}{9}=1\) to its asymptotes.
Solution:
Let S ≡ \(\frac{x^2}{16}-\frac{y^2}{9}-1=0\) be the given hyperbola.
Let P = (a sec θ, b tan θ) be any point on S = 0.
The equation of asymptotes of the hyperbola S = 0 are \(\frac{x}{4}+\frac{y}{3}=0\) and \(\frac{x}{4}-\frac{y}{3}=0\)
⇒ 3x + 4y = 0 ………(1) and 3x – 4y = 0 ………(2)
Let PM be the length of the perpendicular drawn from P(4 sec θ, 3 tan θ) to the line (1) then
PM = \(\left|\frac{12 \sec \theta+12 \tan \theta}{\sqrt{9+16}}\right|\) = \(\left|\frac{12 \sec \theta+12 \tan \theta}{5}\right|\)
Let PN be the length of the perpendicular from P(4 sec θ, 3 tan θ) on line (2). Then
PN = \(\frac{|12 \sec \theta-12 \tan \theta|}{\sqrt{9+16}}=\frac{|12 \sec \theta-12 \tan \theta|}{5}\)
∴ Product of perpendiculars = PM . PN
= \(\frac{|12 \sec \theta+12 \tan \theta|}{5} \cdot \frac{|12 \sec \theta-12 \tan \theta|}{5}\)
= \(\frac{144\left(\sec ^2 \theta-\tan ^2 \theta\right)}{25}\)
= \(\frac{144}{25}\)
∴ Product of length of perpendiculars = \(\frac{144}{25}\)

Question 7.
If the eccentricity of a hyperbola is \(\frac{5}{4}\), then find the eccentricity of its conjugate hyperbola. (March 2012, 2013)
Solution:
If S ≡ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}-1=0\) is the equation of hyperbola then S’ ≡ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}+1=0\) is the equation of the conjugate hyperbola.
Let e and e₁ be the eccentricities of the hyperbola and its conjugate respectively,

∴ The eccentricity of the conjugate hyperbola is \(\frac{5}{3}\).

Question 8.
Find the equation of the hyperbola whose asymptotes are 3x = ±5y and the vertices and (±5, 0).
Solution:
The equation of asymptotes is given by 3x – 5y = 0 and 3x + 5y = 0.
∴ The equation of hyperbola is of the form (3x – 5y) (3x + 5y) = k
⇒ 9x² – 25y² = k
If the hyperbola passes through the vertex (±5, 0) then 9(25) = k
⇒ k = 225
Hence the equation of asymptotes of a hyperbola is 9x² – 25y² = 225

Question 9.
Find the equation of normal at θ = \(\frac{\pi}{3}\) to the hyperbola 3x² – 4y² = 12.
Solution:
The given equation of the hyperbola is 3x² – 4y² = 12
⇒ \(\frac{x^2}{4}-\frac{y^2}{3}=1\)
The equation of normal at P(a sec θ, b tan θ) to the hyperbola S = 0 is

Question 10.
If the angle between asymptotes is 30° then find its eccentricity.
Solution:
The angle between asymptotes of the hyperbola

II.

Question 1.
Find the centre, foci, eccentricity, equation of directrices, and length of the latus rectum of the following hyperbolas.
(i) 16y² – 9x² = 144 (June 2010)
Solution:
The given equation of the hyperbola is 16y² – 9x² = 144
⇒ \(\frac{y^2}{9}-\frac{x^2}{16}=1\)
⇒ \(\frac{x^2}{16}-\frac{y^2}{9}=-1\)
Comparing with \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1\) We get
a² = 16 and b² = 9
⇒ a = 4 and b = 3
(i) Centre of the hyperbola = (0, 0)

(ii) x² – 4y² = 4 (May 2011)
Solution:
This can be written as \(\frac{x^2}{4}-\frac{y^2}{1}=1\)
⇒ a² = 4 and b² = 1
⇒ a = 2 and b = 1
(i) Centre = (0, 0)

(iii) 5x² – 4y² + 20x + 8y – 4 = 0 (Mar 2012)
Solution:
The given equation is 5x² – 4y² + 20x + 8y – 4 = 0
⇒ 5x² + 20x – 4y² + 8y = 4
⇒ 5(x² + 4x) – 4(y² – 2y) = 4
⇒ 5(x² + 4x + 4) – 4(y² – 2y + 1) = 20 + 4 – 4 = 20
⇒ 5(x + 2)² – 4(y – 1)² = 20
⇒ \(\frac{\left(\mathrm{x}-(-2)^2\right)}{4}-\frac{(\mathrm{y}-1)^2}{5}=1\)
This is of the form \(\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1\)
Where a² = 4 and b² = 5, h = -2, k = 1
(i) Centre of the hyperbola = C(h, k) = (-2, 1)
(ii) Eccentricity = \(\sqrt{\frac{a^2+b^2}{a^2}}=\sqrt{\frac{4+5}{4}}=\frac{3}{2}\)
(iii) Foci = (h ± ae, k)
= (-2 ± 2(\(\frac{3}{2}\)), 1)
= (1, 1), (-5, 1)
∴ Foci of the hyperbola = (1, 1), (-5, 1)
(iv) Equations of directrices are x = h ± \(\frac{a}{e}\)
= \(-2 \pm \frac{2}{(3 / 2)}=-2 \pm \frac{4}{3}\)
∴ 3x = -6 ± 4
⇒ 3x = -2 and 3x = -10
⇒ 3x + 2 = 0 and 3x + 10 = 0
(v) Length of the latus rectum = \(\frac{2 b^2}{a}=\frac{2 \times 5}{2}\) = 5

(iv) 9x² – 16y² + 72x – 32y – 16 = 0
Solution:
The given equation is 9x² – 16y² + 72x – 32y – 16 = 0
⇒ 9x² + 72x – 16y² – 32y = 16
⇒ 9(x² + 8x) – 16(y² + 2y) = 16
⇒ 9(x² + 8x + 16) – 16(y² + 2y + 1) = 16 + 144 – 16 = 144
⇒ \(\frac{(x-(-4))^2}{16}+\frac{[y-(-1)]^2}{9}=1\)
This is of the form \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\)
Where a² = 16 and b² = 9
⇒ a = 4 and b = 3
(i) Coordinates of centre = C(h, k) = C(-4, -1)
(ii) Eccentricity e = \(\sqrt{\frac{a^2+b^2}{a^2}}=\sqrt{\frac{16+9}{16}}=\frac{5}{4}\)
(iii) Coordinates of foci = (h ± ae, k)
= (-4 ± 4(\(\frac{5}{4}\)), -1)
= (-9, -1), (1, -1)
(iv) Equations of directrices are x = ±\(\frac{a}{e}\)
= \(-4 \pm \frac{4}{(5 / 4)}\)
= \(-4 \pm \frac{16}{5}\)
⇒ x + 4 = ±\(\frac{16}{5}\)
⇒ 5x + 20 = 16 or 5x + 20 = -16
⇒ 5x + 4 = 0 (or) 5x + 36 = 0
(v) Length of the latus rectum = \(\frac{2 b^2}{a}=\frac{2(9)}{4}=\frac{9}{2}\)

Question 2.
Find the equation to the hyperbola whose foci are (4, 2) and (8, 2) and whose eccentricity is 2. (March 2009)
Solution:
Let S = (4, 2) and S’ = (8, 2) be the foci.
Since the Y-coordinate of S and S’ are the same, the hyperbola’s major axis is parallel to the X-axis.
The equation of required hyperbola is \(\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1\)
Centre of Hyperbola C = Midpoint of SS’
= \(\left(\frac{4+8}{2}, \frac{2+2}{2}\right)\)
= (2, 2)
Given that e = 2
Distance between the foci is SS’ = 2ae
∴ 2ae = \(\sqrt{(4-8)^2+(2-2)^2}\) = 4
⇒ ae = 2
⇒ a(2) = 2
⇒ a = 1
But b² = a²(e² – 1) = 1(4 – 1) = 3
The equation of required hyperbola is \(\frac{(x-6)^2}{1}-\frac{(y-2)^2}{3}=1\)
⇒ (x² – 12x + 36) – \(\frac{\left(y^2-4 y+4\right)}{3}\) = 1
⇒ 3x² – y2 – 36x + 4y + 101 = 0
∴ Equation of Hyperbola is 3x² – y² – 36x + 4y + 101 = 0

Question 3.
Find the equation of hyperbola of a given length of transverse axis 6 whose vertex bisects the distance between the centre and the focus.
Solution:
Let C be the centre.
S is the focus and A, A’ are vertices of the required hyperbola.

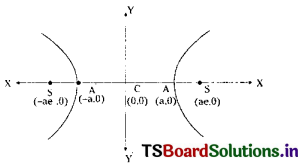
C = (0, 0), S = (ae, 0);
Given AA’ = 2a = 6
⇒ CA = a = 3; A = (3, 0)
Given that A bisects \(\overline{\mathrm{CS}}\)
∴ A is midpoint of \(\overline{\mathrm{CS}}\)
∴ (\(\frac{ae}{2}\)) = a
⇒ e = 2
But b² = a²(e² – 1)
⇒ b² = a²(4 – 1) = 3a² = 27
∴ The equation of the required hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
⇒ \(\frac{x^2}{9}-\frac{y^2}{27}=1\)
⇒ 3x² – y² = 27

Question 4.
Find the equation of the tangents to the hyperbola x² – 4y² = 4 which are (i) parallel (ii) perpendicular to the line x + 2y = 0. (May 2011)
Solution:
Given the equation of Hyperbola x² – 4y² = 4
⇒ \(\frac{x^2}{4}-\frac{y^2}{1}=1\) ……..(1)
∴ a² = 4, b² = 1
Given line is x + 2y = 0 ……..(2)
(i) Equation of any line parallel to (2) is x + 2y + k = 0
⇒ 2y = -x – k
⇒ y = \(-\frac{x}{2}-\frac{k}{2}\) ……(3)
Condition for (3) to be a tangent to the hyperbola (1) is c² = a²m² – b²
where c = \(-\frac{k}{2}\), m = \(-\frac{1}{2}\)
∴ \(\frac{k^2}{4}=4\left(\frac{1}{4}\right)-1\)
⇒ \(\frac{k^2}{4}\) = 0
⇒ k = 0
The equation of tangent parallel to x + 2y = 0 is x + 2y = 0.
(ii) Equation of line perpendicular to x + 2y = 0 is 2x – y + k = 0.
⇒ y = 2x + k, where m = 2 and c = k
∴ c² = a²m² – b²
⇒ k² = 4(4) – 1 = 15
⇒ k = ±√15
∴ Equation of tangent perpendicular to x + 2y = 0 is 2x – y ± √15 = 0.

Question 5.
Find the equations of tangents drawn to the hyperbola 2x² – 3y² = 6 through (-2, 1).
Solution:
Given equation of hyperbola 2x² – 3y² = 6
⇒ \(\frac{x^2}{3}-\frac{y^2}{2}=1\) …….(1)
Comparing (1) with \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) we get a² = 3, b² = 2
Equation of any tangent to the hyperbola (1) having slope ‘m’ is y = mx ± \(\sqrt{a^2 m^2-b^2}\)
⇒ y = mx ± \(\sqrt{3 m^2-2}\) ……….(2)
If the tangent (2) passes through (-2, 1) then 1 = -2m ± \(\sqrt{3 m^2-2}\)
⇒ (2m + 1)² = 3m² – 2
⇒ 4m² + 4m + 1 = 3m² – 2
⇒ m² + 4m + 3 = 0
⇒ (m + 3) (m + 1) = 0
⇒ m = -1 (or) m = -3
∴ The equations of tangents from (2) are y = -x ± √1 and y = -3x ± √25 = -3x ± 5
∴ x + y ± 1 = 0 and 3x + y ± 5 = 0 are the equations.
But the point (-2, 1) does not satisfy x + y – 1 = 0 and 3x + y – 5 = 0.
Hence the equations of required tangents passing through (-2, 1) are x + y + 1 = 0 and 3x + y + 5 = 0.

Question 6.
Prove that the product of the perpendicular distances from any point on a hyperbola to its asymptotes is constant.
Solution:
Let S ≡ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1=0\) be the given hyperbola.
Let P = (a sec θ, b tan θ) be any point on S = 0.
The equations of asymptotes of hyperbola S = 0 are \(\frac{x}{a}+\frac{y}{b}=0\) and \(\frac{x}{a}-\frac{y}{b}=0\)
⇒ bx + ay = 0 (1) and bx – ay = 0 ………(2)
Let PM be the perpendicular length drawn from P(a sec θ, b tan θ) on line (2).
∴ PM = \(\frac{|b a \sec \theta+a b \tan \theta|}{\sqrt{a^2+b^2}}\)
Let PN be the perpendicular length drawn from P(a sec θ, b tan θ) on line (2).

∴ The product of the perpendicular distances from any point on a hyperbola to its asymptotes is a constant.

III.

Question 1.
Tangents to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) make angles θ1, θ2 with transverse axis of a hyperbola. Show that the point of intersection of these tangents lies on the curve 2xy = k(x² – a²) when tan θ1 + tan θ2 = k.
Solution:
Given hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
The transverse axis of the hyperbola is the x-axis, (i.e., y = 0)
Let P(x₁, y₁) be the point of intersection of the tangents drawn to the given hyperbola.
The equation of any tangent to the hyperbola is of the form y = mx ± \(\sqrt{a^2 m^2-b^2}\)
If this passes through (x₁, y₁) then

This is a quadratic equation in ‘m’ and be m₁, m₂ be the roots which corresponds to the slopes tan θ₁, tan θ₂ of tangents.

∴ Locus of (x₁, y₁) is the curve 2xy = k(x² – a²).

Question 2.
Show that the locus of feet of the perpendiculars drawn from foci to any tangent of the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is the auxiliary circle of the hyperbola.
Solution:
Let S ≡ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}-1=0\) be the given hyperbola.
Foci of the hyperbola S = 0 are (±ae, 0).
Equation of any tangent to S = 0 having slope ‘m’ is y = mx ± \(\sqrt{a^2 m^2-b^2}\)
⇒ y – mx = ±\(\sqrt{a^2 m^2-b^2}\) ………(1)
Let P(x₁, y₁) be the locus of feet of the perpendicular form foci of the hyperbola to the tangent (1).
The equation of the perpendicular from either focus (±ae, 0) on the above tangent is
y – 0 = \(-\frac{1}{m}\)(x – (±ae))
⇒ my + x = ±ae …….(2)
P(x₁, y₁) lies on (1) and (2).
y₁ – mx₁ = \(\pm \sqrt{a^2 m^2-b^2}\) …….(3)
and my₁ + x₁ = ±ae ………(4)
Eliminating m from equations (3) and (4)

∴ The Locus of (x₁, y₁) is x² + y² = a² which is the equation of the Auxiliary circle of the Hyperbola.

Question 3.
Show that the equation \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\) represents
(i) an ellipse if ‘c’ is a real constant less than 5.
(ii) a hyperbola if ‘c’ is any real constant between 5 and 9.
(iii) show that each ellipse in (i) and each hyperbola (ii) has foci at the two points (±2, 0), independent of the value of ‘c’.
Solution:
Given equation \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\) ……(1) represents an ellipse
if 9 – c > 0 and 5 – c > 0
⇒ 9 > c and 5 > c
⇒ c < 9 and c < 5
⇒ c < 5 ∴ c is a real constant and less than 5 if (1) represents an ellipse.
(i) The equation of the hyperbola is of the form \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) and the given equation (1) represents a hyperbola
if 9 – c > 0 and 5 – c < 0
⇒ 9 > c and 5 < c
⇒ 5 < c < 9
∴ (1) represents hyperbola if C is a real constant such that 5 < c < 9
(ii) If \(\frac{x^2}{9-c}+\frac{y^2}{5-c}=1\) represents ellipse then
a² = 9 – c and b² = 5 – c
Eccentricity b² = a²(1 – e²)
⇒ 5 – c = (9 – c) (1 – e²)

Hence each ellipse in (i) and each hyperbola in (ii) has foci at the two points (±2, 0) independent of the value of C.

Question 4.
Show that the angle between the two asymptotes of a hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is \(2 {tan}^{-1}\left(\frac{b}{a}\right)\) (or) 2 sec-1(e). [New Model Paper, May 2012]
Solution:
Let the equation of the hyperbola be \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
The asymptotes of hyperbola are y = ±\(\frac{b}{a}\)x where m1 = \(\frac{b}{a}\) and m2 = \(-\frac{b}{a}\).
If θ is the angle between asymptotes of the hyperbola then