TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(a)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 3 Parabola Ex 3(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Exercise 3(a)

I.

Question 1.
Find the vertex and focus of 4y² + 12x – 20y + 67 = 0.
Solution:
Given equation is 4y² + 12x – 20y + 67 = 0
⇒ 4y² – 20y = -12x – 67
⇒ 4(y² – 5y) = -12x – 67

Question 2.
Find the vertex and focus of x² – 6x – 6y + 6 = 0.
Solution:
The given equation is x² – 6x – 6y + 6 = 0
⇒ x² – 6x = 6y – 6
⇒ x² – 6x + 9 = 6y – 6 + 9 = 6y + 3
⇒ (x – 3)² = \(6\left(y+\frac{1}{2}\right)=6\left(y-\left(-\frac{1}{2}\right)\right)\)
This is of the form (x – h)² = 4a(y – k)
where h = 3, 4a = 6 ⇒ a = \(\frac{3}{2}\) and k = \(\frac{-1}{2}\)
Vertex = (h, k) = (3, \(\frac{-1}{2}\))
Focus = (h, a + k) = (3, \(\frac{3}{2}-\frac{1}{2}\)) = (3, 1)

Question 3.
Find the equations of the axis and directrix of the parabola y² + 6y – 2x + 5 = 0.
Solution:
The given equation is y² + 6y – 2x + 5 = 0
⇒ y² + 6y = 2x – 5
⇒ y² + 6y + 9 = 2x – 5 + 9 = 2x + 4
⇒ (y + 3)² = 2(x + 2)
⇒ [y – (-3)]² = 2[x – (-2)]
This is of the form (y – k)² = 4a(x – h)
where k = -3, 4a = 2 ⇒ a = \(\frac{1}{2}\), h = -2
∴ Axis is y – k = 0 ⇒ y + 3 = 0
and Directrix is x – h + a = 0
⇒ x + 2 + \(\frac{1}{2}\) = 0
⇒ x + \(\frac{5}{2}\) = 0
⇒ 2x + 5 = 0

Question 4.
Find the equations of the axis and directrix of the parabola 4x² + 12x – 20y + 67 = 0.
Solution:
Given equation is 4x² + 12x – 20y + 67 = 0
⇒ 4(x² + 3x) = 20y – 67

Question 5.
Find the equation of a parabola whose focus is S(1, -7) and whose vertex is A(1, -2). (New Model Paper, Mar. ’12)
Solution:
Given that vertex A(h, k) = (1, -2) and focus S = (1, -7).
Since the x coordinates of A and S are equal and equal to 1,
the axis of the parabola is x = 1 and it is a line parallel to the y-axis.
Also, the focus is below the vertex.
∴ The equation of the parabola is (x – h)² = -4a(y – k)
⇒ (x – 1)² = -4a(y + 2) ……..(1)
where a = AS = \(\sqrt{(1-1)^2+(-2+7)^2}\) = 5
∴ From (1) we have (x – 1)² = -20(y + 2)
Which is the equation of the required parabola.

Question 6.
Find the equation of the parabola whose focus is S(3, 5) and vertex is A(1, 3). (E.Q.)
Solution:
Given vertex A = (1, 3) and focus S = (3, 5)

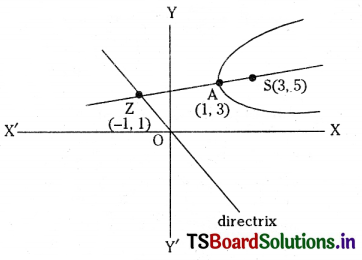
Let the directrix meets the axis of the parabola at Z(x, y), A is the midpoint of SZ.
Hence \(\frac{\mathrm{x}+3}{2}\) = 1 and \(\frac{\mathrm{y}+5}{2}\) = 3
⇒ x = -1 and y = 1
∴ Coordinates of Z = (-1, 1)
Slope of AZ = \(\frac{5-1}{3+1}\) = 1
∴ Slope of directrix = -1 (∵ directrix is perpendicular to \(\overline{\mathrm{AS}}\))
∴ Equation of directrix L = 0 is y – 1 = -1(x + 1)
⇒ x + y = 0
Let P(x₁, y₁) be any point on the parabola and PM is the perpendicular distance from P to the directrix L = 0 is

⇒ \(\mathrm{x}_1^2+\mathrm{y}_1^2\) – 2x₁y₁ – 12x₁ – 20y₁ + 68 = 0
∴ Locus of (x₁, y₁) is the equation of parabola given by x² + y² – 2xy – 12x – 20y + 68 = 0.

Question 7.
Find the equation of the parabola whose latus rectum is the line segment joining points (-3, 2) and (-3, 1). (E.Q.)
Solution:
Given L = (-3, 2) and L’ = (-3, 1) be the two end points of the latus rectum of the parabola.
Since the x coordinates of L and L’ are ‘1’ we have an axis of the parabola parallel to the x-axis.
∴ The equation of the required parabola is (y – k)² = ±4a(x – h)
The length of the latus rectum LL’ = 4a
⇒ 4a = \(\sqrt{(-3+3)^2+(2-1)^2}\) = 1
⇒ a = \(\frac{1}{4}\)
Let S be the focus of the required parabola Then
S = mid point of LL’ = (h, k)

Question 8.
Find the position (Interior or exterior or on) of the following points with respect to the parabola y² = 6x.
(i) (6, -6)
(ii) (0, 1)
(iii) (2, 3)
Solution:
Given the equation of a parabola is y² – 6x = 0
Comparing with y² = 4ax
we have 4a = 6
⇒ a = \(\frac{3}{2}\)
(i) Let P(x₁, y₁) = (6, -6) be the given point.
Then S₁₁ = \(\mathrm{y}_1{ }^2\) – 4ax₁
= (-6)² – 4(\(\frac{3}{2}\))(6)
= 36 – 36
= 0
∴ The point (6, -6) lies on the parabola y² = 6x.
(ii) Let P(x₁, y₁) = (0, 1) and \(\mathrm{y}_1{ }^2\) – 4ax₁
= 1 – 4(\(\frac{3}{2}\))(0)
= 1
∴ S₁₁ > 0 and the point (0, 1) lies outside the parabola y² = 6x.
(iii) Let P(x₁, y₁) = (2, 3) Then S₁₁ = \(\mathrm{y}_1{ }^2\) – 6x₁
= 9 – 6(2)
= -3 < 0
∴ Point (2, 3) lies inside the parabola y² = 6x.

Question 9.
Find the coordinates of the point on the parabola y = 8x whose focal distance is 10. (Mar. ’11)
Solution:
Given y² = 8x and Let P(x₁, y₁) be any point on the parabola y² = 8x
Comparing with y² = 4ax we get
4a = 8
⇒ a = 2
The focal distance of the parabola = x₁ + a = x₁ + 2
Given x₁ + 2 = 10
Since \(\mathrm{y}_1^2\), we have \(\mathrm{y}_1^2\) = 8(8) = 64
⇒ y₁ = ±8
Hence the required points on the parabola y² = 8x are given by (8, 8) and (8, -8).

Question 10.
If (\(\frac{1}{2}\), 2) is one extremity of a focal chord of the parabola y² = 8x. Find the coordinates of the other extremity. (June ’10)
Solution:
The given equation of a parabola is y² = 8x.
Comparing with y² = 4ax we get
4a = 8
⇒ a = 2
Let P(x₁, y₁) = (\(\frac{1}{2}\), 2) be one extremity of the focal chord.
Let Q(x₂, y₂) be the other extremity of the focal chord of the parabola y² = 8x.
∴ x₁x₂ = a² and y₁y₂ = -4a² (standard result)
⇒ \(\frac{1}{2}\)x₂ = 4
⇒ x₂ = 8
and 2y₂ = -4(4)
⇒ y₂ = -8
[∵ P(x₁, y₁) = (\(\frac{1}{2}\), 2)]
∴ The other extremity of the focal chord of the given parabola is (8, -8).

Question 11.
Prove that the point on the parabola y² = 4ax, (a > 0) nearest to the focus is its vertex.
Solution:
Given equation is y² = 4ax …….(1) and focus is S = (a, 0).
Let P(at², 2at) be any point on y² = 4ax.
Let f(t) = SP = \(\sqrt{\left(a t^2-a\right)+4 a^2 t^2}\)
= \(\sqrt{a^2\left[\left(t^2-1\right)^2+4 t^2\right]}\)
= a(t² + 1)
∴ f(t) = 2at and f”(t) = 2a > 0
∴ For f(t) to be minimum or maximum f'(t) = 0 ⇒ t = 0
∴ P = (0, 0).
Hence the f(t) has a minimum at t = 0 and the point on the parabola nearest to its focus is (0, 0).

Question 12.
A comet moves in a parabolic orbit with the sun as the focus. When the comet is 2 × 10⁷ Km. from the sun the line from the sun to it makes an angle \(\frac{\pi}{2}\) with the axis of the orbit. Find how near the comet comes to the sun.
Solution:

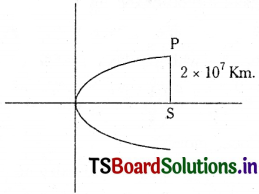
Let the equation of the parabolic orbit be y² = 4ax
Let S be the position of the sun (focus) on the axis of the parabola.
Let P be the position of a comet when it is at a distance of 2 × 10⁷ Km from the Sun ‘S’.
∴ SP = 2 × 10⁷
⇒ 2a = 2 × 10⁷ Km
⇒ a = 10⁷ Km
The distance of the comet from the Sun S is minimum when it is at the vertex.
∴ The nearest distance of the comet from the sun S is SA = a = 10⁷ Km.

II.

Question 1.
Find the locus of the point of trisection of the double ordinate of a parabola y² = 4ax, (a > 0).
Solution:

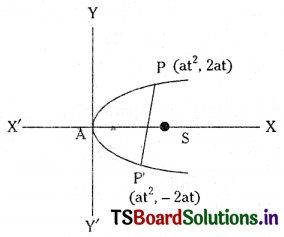
Let P(at², 2at), and P’ = (at², -2at) be the ends of double ordinate PP’ of the parabola y² = 4ax.
Let Q(x₁, y₁) be any point on the locus.
∴ Q(x₁, y₁) is the point of trisection of PP’.
⇒ Q(x₁, y₁) divides PP’ in the ratio 1 : 2.

∴ 9\(\mathrm{y}_1^2\) = 4ax₁ and locus of (x₁, y₁) is 9y² = 4ax.

Question 2.
Find the equation of the parabola whose vertex and focus are on the positive x-axis at a distance ‘a’ and ‘a’ ‘ from the origin respectively.
Solution:
Let A(a, 0) be vertex and S(a’, 0) be the focus
We have

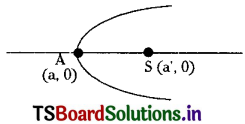
∴ a = AS
∴ a = \(\sqrt{\left(a-a^{\prime}\right)^2}\) = a’ – a
The equation of the required parabola is (y – k)² = 4a(x – h)
⇒ (y – 0)² = 4(a’ – a) (x – a)
⇒ y² = 4(a’ – a) (2 – a)

Question 3.
If L and L’ are the ends of the latus rectum of the parabola x² = 6y, find the equation of OL and OL’ where ‘O’ is the origin. Also, find the angle between them.
Solution:
Given equation of parabola is x² = 6y ……..(1)
Comparing with y² = 4ax we have 4a = 6
⇒ a = \(\frac{3}{2}\)
Given L, L’, and the ends of the latus rectum of the parabola (1).
L = (2a, a) and L’ = (-2a, a)

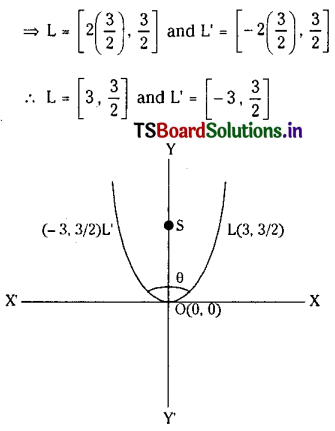
Question 4.
Find the equation of a parabola whose axis is parallel to the x-axis and which passes through the points (-2, 1), (1, 2), and (-1, 3).
Solution:
Let A = (-2, 1), B = (1, 2), C = (-1, 3) be the given points.
Let the equation of the parabola whose axis is parallel to the x-axis and passing through the points A, B, C be x = ly² + my + n …….(1)
If parabola (1) passes through A(-2, 1) then -2 = l + m + n …….(2)
If (1) passes through B(1, 2) then
1 = 4l + 2m + n ……..(3)
If (1) passes through C(-1, 3) then
-1 = 9l + 3m + n ……..(4)
From (2) and (3),
-3l – m = -3
⇒ 3l + m = 3 ……..(5)
From (3) and (4),
-5l – m = 2
⇒ 5l + m = -2 ………(6)
Solving (5) and (6), we get
-2l = 5
⇒ l = \(\frac{-5}{2}\)
and 5(\(\frac{-5}{2}\)) + m = -2
⇒ m = -2 + \(\frac{25}{2}\) = \(\frac{21}{2}\)
∴ From (2) we have l + m + n = 2
⇒ \(-\frac{5}{2}+\frac{21}{2}\) + n = -2
⇒ n + 8 = -2
⇒ n = -10
Hence the required equation of parabola from (1) is x = \(-\frac{5}{2} y^2+\frac{21}{2} y-10\)
⇒ 5y² + 2x – 21y + 20 = 0

Question 5.
Find the equation of the parabola whose axis is parallel to the y-axis and which passes through the points (4, 5), (-2, 11), and (-4, 21). (Mar. ’12)
Solution:
Let A(4, 5), B(-2, 11) and C(-4, 21) be the given points.
The equation of the parabola whose axis is parallel to the y-axis is
y = lx² + mx + n ………(1)
Since (1) passes through point A(4, 5) we have
5 = 16l + 4m + n ………(2)
Since (1) passes through point B(-2, 11) then
11 = 4l – 2m + n ……..(3)
Also since (1) passes through C(-4, 21) we have
21 = 16l – 4m + n ………(4)
From (2) and (3)
12l + 6m = -6
61 + 3m = -3
2l + m = -1 ……….(5)
From (3) and (4)
-12l + 2m = -10
⇒ -6l + m = -5
⇒ 6l – m = 5 ……….(6)
Solving (5) and (6) we get
8l = 4
⇒ l = \(\frac{1}{2}\)
∴ From (6)
3 – m = 5
⇒ -m = 2
⇒ m = -2
From (2) we have
16l + 4m + n = 5
⇒ 8 – 8 + n = 5
⇒ n = 5
∴ The equation of the required parabola passing through points A, B, C from (1) is
y = \(\frac{1}{2}\)x2 – 2x + 5
⇒ x2 – 4x – 2y + 10 = 0

III.

Question 1.
Find the equation of the parabola whose focus is (-2, 3) and whose directrix is the line 2x + 3y – 4 = 0. Also, find the length of the latus rectum and the equation of the axis of the parabola. (Mar. ’13)
Solution:
Let S = (-2, 3) be the focus and L = 2x + 3y – 4 = 0 be the directrix.
Let P(x₁, y₁) be any point on the parabola and PM be the perpendicular distance from P to the directrix.

∴ The locus of P(x₁, y₁) is the equation of parabola given by 9x² – 12xy + 4y² + 68x – 54y + 153 = 0
The length of the latus rectum = 4a = 2(2a) = 2
The perpendicular distance from focus to the directrix = \(\frac{2|2(-2)+3(3)-4|}{\sqrt{4+9}}=\frac{2}{\sqrt{13}}\) units
Since the axis of the parabola is perpendicular to the directrix and passes through the focus (-2, 3).
The equation of the line passing through (-2, 3) and perpendicular to L = 0 is L(x – x₁) – a(y – y₁) = 0
⇒ 3(x + 2) – 2(y – 3) = 0
⇒ 3x – 2y + 12 = 0
∴ Axis of the parabola is 3x – 2y + 12 = 0.

Question 2.
Prove that the area of the triangle inscribed in the parabola y² = 4ax is \(\frac{1}{8a}\) |(y₁ – y₂) (y₂ – y₃) (y₃ – y₁)| sq. units. where y₁, y₂, y₃ are the ordinates of its vertices. (New Model Paper)
Solution:
Let A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) be the vertices of ∆ABC inscribed in a parabola y² = 4ax.
Then the area of the triangle ABC is ∆ = |\(\frac{1}{2}\)Σx₁(y₂ – y₃)| sq.units
In the parametric form x₁ = \(\mathrm{at}_1{ }^2\) and y₁ = 2at₁
∴ Take A = \(\left(a t_1{ }^2, 2 a t_1\right)\) = (x₁, y₁)
B = \(\left(a t_2{ }^2, 2 a t_2\right)\) = (x₂, y₂)
C = \(\left(a t_3{ }^2, 2 a t_3\right)\) = (x₃, y₃)


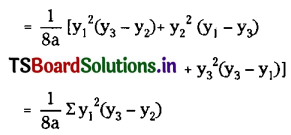
∴ LHS = RHS and hence the area of the triangle inscribed in the parabola y² = 4ax is \(\frac{1}{8a}\) |(y₁ – y₂) (y₂ – y₃) (y₃ – y₁)| sq. units.

Question 3.
Find the coordinates of the vertex and focus, the equation of the directrix, and the axis of the following parabolas.
(i) y² + 4x + 4y – 3 = 0
Solution:
The given equation can be written as y² + 4y = -4x + 3
⇒ y² + 4y + 4 = -4x + 3 + 4 = -4x + 7
⇒ (y + 2)² = -4(x – \(\frac{7}{4}\))
⇒ \([y-(-2)]^2=-4\left[x-\left(\frac{7}{4}\right)\right]\)
Which is of the form (y – k)² = -4a(x – h)
Where (h, k) =(\(\frac{7}{4}\), 1) and a = 1,
Vertex = (h, k) = (\(\frac{7}{4}\), -2)
Focus = (h – a, k)
= (\(\frac{7}{4}\) – 1, -2)
= (\(\frac{3}{4}\), -2)
Axis of the parabola = y – k = 0
⇒ y + 2 = 0
Directrix of the parabola is x – h – a = 0
⇒ x – \(\frac{7}{4}\) – 1 = 0
⇒ x – \(\frac{11}{4}\) = 0
⇒ 4x – 11 = 0

(ii) x² – 2x + 4y – 3 = 0
Solution:
The given equation can be written as x² – 2y = -4y + 3
⇒ x² – 2x + 1 = -4y + 3 + 1 = -4y + 4
⇒ (x – 1)² = -4(y – 1)
This is of the form (x – h)² = -4a(y – k) whose a = 1, (h, k) = (1, 1)
Vertex = (h, k) = (1, 1)
Focus = (h, k – a) = (1, 1 – 1) = (1, 0)
Axis is x – h = 0 ⇒ x – 1 = 0
Directrix is y – k – a = 0
⇒ y – 1 – 1 = 0
⇒ y – 2 = 0
⇒ y = 2