TS Inter 2nd Year Maths 2B Solutions Chapter 4 Ellipse Ex 4(b)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 4 Ellipse Ex 4(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 4 Ellipse Exercise 4(b)

I.

Question 1.
Find the equation of the tangent and normal to the ellipse x² + 8y² = 33 at (-1, 2).
Solution:
Given ellipse is x² + 8y² = 33
⇒ \(\frac{x^2}{33}+\frac{y^2}{(33 / 8)}=1\) ……..(1)
Let P(x₁, y₁) = (-1, 2) be a point on (1) then
the equation of tangent at (x₁, y₁) is \(\frac{\mathrm{xx}_1}{33}+\frac{\mathrm{yy}_1}{(33 / 8)}-1=0\)
\(\frac{x(-1)}{33}+\frac{y(2)}{(33 / 8)}=1\)
⇒ -x + 16y = -33
⇒ x – 16y + 33 = 0
Equation of normal at P(-1, 2) on the ellipse

Question 2.
Find the equation of tangent and normal to the ellipse x² + 2y² – 4x + 12y + 14 = 0 at (2, -1).
Solution:
Given equation of ellipse is x² + 2y² – 4x + 12y + 14 = 0
Let P(x₁, y₁) = (2, -1)
Now differentiating w.r.t ‘x’

∴ Slope of the tangent at (2, -1) is \(\frac{d y}{d x}(2,-1)=\frac{2-2}{-2+6}=0\)
∴ The slope of the normal at (2, -1) is ∞.
∴ Equation of the tangent to the given ellipse at P(2, -1) is y + 1 = 0, and the equation of normal at P(2, -1) is x – 2 = 0.

Question 3.
Find the equation of the tangents to 9x² + 16y² = 144, which makes equal intercepts on the coordinate axis.
Solution:
Given the equation of the ellipse is 9x² + 16y² = 144
⇒ \(\frac{x^2}{16}+\frac{y^2}{9}=1\)
Let S ≡ \(\frac{x^2}{16}+\frac{y^2}{9}-1=0\)
Compared with the general equation S = 0 we have
a² = 16, b² = 9
⇒ a = 4, b = 3
∴ Equation of the tangent to the ellipse S = 0 having slope is y = mx ± \(\sqrt{a^2 m^2+b^2}\)

Question 4.
Find the coordinates of the points on the ellipse x² + 3y² = 37 at which the normal is parallel to the line 6x – 5y = 2.
Solution:
Given equation of ellipse is x² + 3y² = 37 …….(1)
⇒ \(\frac{x^2}{37}+\frac{y^2}{\left(\frac{37}{3}\right)}=1\)
Let P(x₁, y₁) be any point on the ellipse (1) then \(\frac{x_1^2}{37}+\frac{y_1^2}{\left(\frac{37}{3}\right)}=1\)
⇒ \(x^2+3 y_1^2=37\)
Given line is 6x – 5y + 2 = 0 …….(2)
Slope of the line = \(\frac{6}{5}\)
∴ Equation of the normal at P(x₁, y₁) to the ellipse S = 0 is


∴ The coordinates of the points on ellipse x² + 7y² = 37 at which the normal is parallel to the line 6x – 5y = 2 are (5, 2), (-5, -2).

Question 5.
Find the value of k if 4x + y + k = 0 is a tangent to the ellipse x² + 3y² = 3.
Solution:
Given ellipse is x² + 3y² = 3
⇒ \(\frac{x^2}{3}+\frac{y^2}{1}=1\)
Hence a² = 3 and b² = 1
The equation of the given line is 4x + y + k = 0.
⇒ y = -4x – k where m = -4, and c = -k
The condition for tangency is c² = a²m² + b²
⇒ k² = 3(16) + 1
⇒ k² = 49
⇒ k = ±7

Question 6.
Find the condition for the line x cos α + y sin β = p to be a tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\).
Solution:
Given equation of ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) ……..(1)
and equation of given line is x cos α + y sin α = p
⇒ y sin α = p – x cos α
⇒ y = -x cot α + p cosec α …….(2)
which is of the form y = mx + c where m = -cot α and c = p cosec α
Condition for tangency is c² = a²m² + b²
⇒ p² cosec²α = a² cot²α + b²
⇒ p² = \(a^2 \frac{\cot ^2 \alpha}{{cosec}^2 \alpha}+\frac{b^2}{{cosec}^2 \alpha}\)
⇒ p² = a² cos²α + b² sin²α which is the required condition.

II.

Question 1.
Find the equations of tangent and normal to the ellipse 2x² + 3y² = 11 at the point whose ordinate is 1.
Solution:
Let P(x₁, y₁) be a given point and given y₁ = 1 and (x₁, y₁) lies on 2x² + 3y² = 11.
⇒ \(2 \mathrm{x}_1^2+3 \mathrm{y}_1{ }^2=11\)
⇒ \(2 \mathrm{x}_1^2+3=11\)
⇒ 2\(\mathrm{x}_1^2\) = 8
⇒ \(\mathrm{x}_1^2\) = 4
⇒ x₁ = ±2
The required points are (2, 1) and (-2, 1) at which the equations of tangent and normal are to be determined.
The equation of tangent at (x₁, y₁) to the ellipse 2x² + 3y² = 11
⇒ \(\frac{x^2}{\left(\frac{11}{2}\right)}+\frac{y^2}{\left(\frac{11}{3}\right)}=1\) is \(\frac{\mathrm{xx}}{\left(\frac{11}{2}\right)}+\frac{\mathrm{yy}}{\left(\frac{11}{3}\right)}=1\)

⇒ -3x – 4y = 2
⇒ 3x + 4y + 2 = 0 ……..(4)
∴ Tangents are 4x + 3y – 11 = 0 and 4x – 3y – 11 = 0
Also the normals are 3x – 4y – 2 = 0 and 3x + 4y + 2 = 0.

Question 2.
Find the equations to the tangents to the ellipse x² + 2y² = 3 drawn from the point (1, 2) and also find the angle between these tangents.
Solution:
Given the equation of the ellipse is x² + 2y² = 3
⇒ \(\frac{x^2}{3}+\frac{y^2}{\left(\frac{3}{2}\right)}=1\) which is of the form \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) where a² = 3 and b² = \(\frac{3}{2}\)
Equation of any tangent to the ellipse is y = mx ± \(\sqrt{a^2 m^2+b^2}\)
If the tangents are drawn from (1, 2) then
2 = m ± \(\sqrt{3 m^2+3 / 2}\)
⇒ 2 – m = \(\pm \sqrt{3 m^2+3 / 2}\)
⇒ m² – 4m + 4 = 3m² + \(\frac{3}{2}\)
⇒ 2m² – 8m + 8 = 6m² + 3
⇒ 4m² + 8m – 5 = 0
⇒ 4m² + 10m – 2m – 5 = 0
⇒ 2m(2m + 5) – 1(2m + 5) = 0
⇒ 2m – 1 = 0 (or) 2m + 5 = 0
⇒ m = \(\frac{1}{2}\) (or) m = \(-\frac{5}{2}\)
The equation of tangents when m = \(\frac{1}{2}\) is

∴ Equations of tangents drawn from the point (1, 2) to the ellipse S = 0 are given by x – 2y + 3 = 0 and 5x + 2y – 9 = 0.
Also, the angle between them is tan^-1(12).

Question 3.
Find the equation of the tangents to the ellipse 2x² + y² = 8 which are
(i) parallel to x – 2y – 4 = 0
(ii) perpendicular to x + y + 2 = 0
(iii) which makes an angle \(\frac{\pi}{4}\) with x-axis.
Solution:
Given the equation of the ellipse is 2x² + y² = 8
⇒ \(\frac{x^2}{4}+\frac{y^2}{8}=1\)
Let S ≡ \(\frac{x^2}{4}+\frac{y^2}{8}-1=0\) ……..(1)
and compare with general equation a² = 4, and b² = 8
⇒ a = 2, b = 2√2
(i) Parallel to x – 2y – 4 = 0:
Given line is x – 2y – 4 = 0 ……..(2)
Equation of any line parallel to x – 2y – 4 = 0 is x – 2y + k = 0 ………(3)
⇒ 2y = x + k
⇒ y = \(\frac{\mathrm{x}}{2}+\frac{\mathrm{k}}{2}\) where m = \(\frac{1}{2}\) and c = \(\frac{k}{2}\)
If (3) is a tangent to (1) them c² = a²m² + b²
⇒ \(\frac{\mathrm{k}^2}{4}=4\left(\frac{1}{4}\right)+8\)
⇒ \(\frac{\mathrm{k}^2}{4}\) = 1 + 8
⇒ k² = 36
⇒ k = ±6
∴ The equation of the required tangent from (3) is x – 2y ± 6 = 0.

(ii) Perpendicular to x + y – 2 = 0:
Given line is x + y – 2 = 0 ………(4)
Equation of any line perpendicular to (4) is x – y + k = 0 ……….(5)
∴ y = x + k and m = 1, c = k
By the condition for tangency c² = a²m² + b²
⇒ k² = 4(1) + 8
⇒ k² = 12
⇒ k = ±2√ 3
∴ Equation of the required line from (5) is x – y ± 2√3 = 0 ………..(6)

(iii) Which makes an angle \(\frac{\pi}{4}\) with x-axis:
If the line makes \(\frac{\pi}{4}\) with x-axis then m = tan\(\frac{\pi}{4}\) = 1.
∴ Equation of the line is y = x + c ………..(7)
If this is a tangent to (1) then c² = a²m² + b²
⇒ c² = 4(1) + 8
⇒ c² = 12
⇒ c = ±2√3
∴ From (7), the equation of the required line is y = x ± 2√3.

Question 4.
A circle of radius 4, is concentric with the ellipse 3x² + 13y² = 78. Prove that a common tangent is inclined to the major axis at an angle \(\frac{\pi}{4}\).
Solution:
Given ellipse is 3x² + 13y² = 78
⇒ \(\frac{x^2}{26}+\frac{y^2}{6}=1\)
Comparing with \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) we have a² = 26, b² = 6,
centre of the ellipse = (0, 0).
The equation of a circle with centre (0, 0) and radius 4 is x² + y² = 16 ……….(2)
Equation of any tangent to the ellipse having slope ‘m’ is y = mx ± \(\sqrt{a^2 m^2+b^2}\)
⇒ mx – y + \(\sqrt{a^2 m^2+b^2}\) = 0 (Taking one tangent as common)
⇒ mx – y + \(\sqrt{26 m^2+6}\) = 0 ………(3)
If (3) is a tangent to (2) then the perpendicular distance from (0, 0) to (3) = Radius of the circle (2)
∴ \(\frac{\sqrt{26 m^2+6}}{\sqrt{m^2+1}}\)
⇒ 26m² + 6 = 16(m² + 1)
⇒ 10m² – 10 = 0
⇒ m² = 1
⇒ m = ±1
If θ is the angle made by the common tangent with the major axis of the ellipse then tan θ = ±1
⇒ θ = ±\(\frac{\pi}{4}\)
Hence common tangent makes an angle \(\frac{\pi}{4}\) with the major axis of the ellipse.

III.

Question 1.
Show that the foot of the perpendicular drawn from the centre on any tangent to the ellipse lies on the curve (x² + y²)² = a²x² + by².
Solution:
Let S ≡ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1=0\) be the equation of ellipse.
Let P(x₁, y₁) be any point on the ellipse.
The equation of the tangent to the ellipse S = 0 having slope m is y = mx ± \(\sqrt{a^2 m^2+b^2}\)
⇒ y – mx = ±\(\sqrt{a^2 m^2+b^2}\) ……..(1)
The equation to the perpendicular from centre on this tangent (1) is y – 0 = \(\frac{-1}{m}\)(x – 0)
⇒ my + x = 0 ……….(2)
Now P(x₁, y₁) is the point of intersection of (1) and (2)
∴ y₁ – mx₁ = ±\(\sqrt{a^2 m^2+b^2}\) ……(3) and my₁ + x₁ = 0 ………(4)
Squaring (3) and (4) and adding

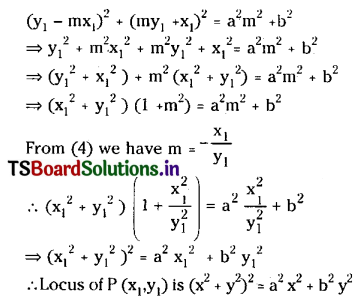
Question 2.
Show that the locus of the feet of the perpendiculars drawn from foci to any tangent of the ellipse is the auxiliary circle.
Solution:
Let S ≡ \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1=0\) be the equation of ellipse.

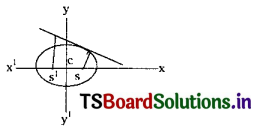
Let P(x₁, y₁) be any point on the locus.
The equation of tangent to the ellipse S = 0 having slope ‘m’ is y = mx ± \(\sqrt{a^2 m^2+b^2}\)
⇒ y – mx = ±\(\sqrt{a^2 m^2+b^2}\) ……..(1)
The equation to the perpendicular from either focus (±ae, 0) on the tangent (1) is
y – 0 = \(\frac{-1}{m}\)(x ± ae)
⇒ my + x = ±ae ………(2)
Since P(x₁, y₁) is a point of intersection of (1) and (2) we have
y₁ – mx₁ = ±\(\sqrt{a^2 m^2+b^2}\) ……..(3)
and my₁ + x₁ = ±ae ……….(4)
Eliminating in from the equation by squaring and adding (3) and (4)
(y₁ – mx₁)² + (my₁ + x₁)² = a²m² + b² + a²e²
= a²m² + a² (1 – e²) + a²e²
= a²m² + a²
= a²(m² + 1)
∴ \(\mathrm{y}_1^2\left(1+\mathrm{m}^2\right)+\mathrm{x}_1^2\left(1+\mathrm{m}^2\right)=\mathrm{a}^2\left(1+\mathrm{m}^2\right)\)
⇒ \(x_1^2+y_1{ }^2=a^2\)
∴ The Locus of P(x₁, y₁) is x² + y² = a² which is the equation of the auxiliary circle of the ellipse.

Question 3.
The tangent and normal to the ellipse x² + 4y² = 4 at a point P(θ) on it meets the major axis in Q and R respectively. If 0 < θ < \(\frac{\pi}{2}\) and QR = 2 then show that θ = \(\cos ^{-1}\left(\frac{2}{3}\right)\). (March 2012)
Solution:
Given ellipse is x² + 4y² = 4
⇒ \(\frac{x^2}{4}+\frac{y^2}{1}=1\)

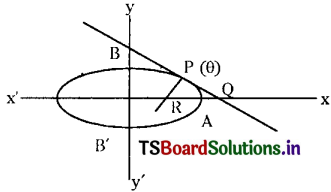
Let S ≡ \(\frac{x^2}{4}+\frac{y^2}{1}-1=0\) be the given ellipse.
Comparing this with \(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1=0\) we get a² = 4, b² = 1
⇒ a = 2, b = 1
The equation of the tangent at P(θ) on the ellipse S = 0 is \(\frac{x}{a} \cos \theta+\frac{y}{b} \sin \theta=1\)
⇒ \(\frac{\mathrm{x}}{2} \cos \theta+\frac{\mathrm{y}}{1} \sin \theta=1\) ……..(1)
The tangent (1) meets the major axis at the Q
∴ y-coordinate of Q = 0; Put y = 0 in (1)


⇒ -3 cos²θ + 4 = 4 cosθ
⇒ 3 cos²θ + 4 cos θ – 4 = 0
⇒ 3 cos²θ + 6 cos θ – 2 cos θ – 4 = 0
⇒ 3 cos θ (cos θ + 2) – 2(cos θ + 2) = 0
⇒ (cos θ + 2) (3 cos θ – 2) = 0
⇒ cos θ + 2 = 0; solution is not admissive (∵ -1 ≤ cos θ ≤ 1)
and 3 cos θ – 2 = 0
⇒ cos θ = \(\frac{2}{3}\)
⇒ θ = \(\cos ^{-1}\left(\frac{2}{3}\right)\)