Class 10

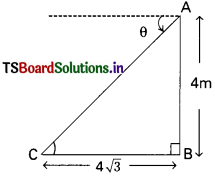
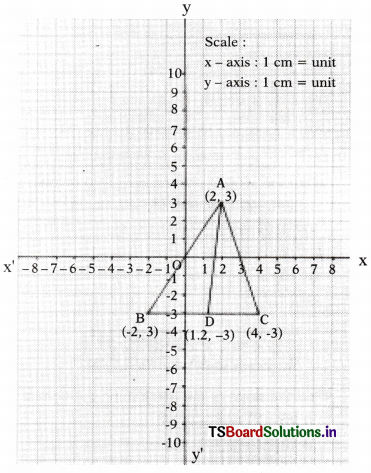
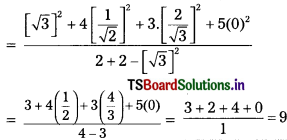
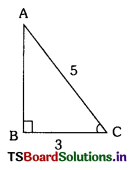
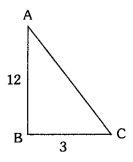
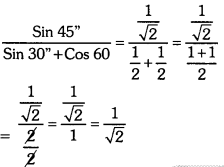
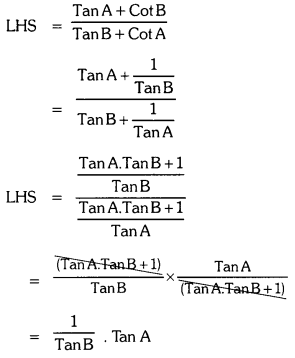
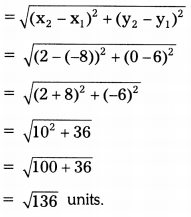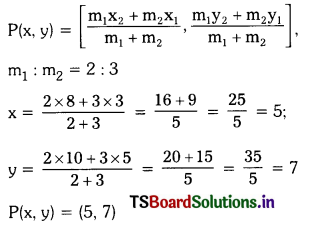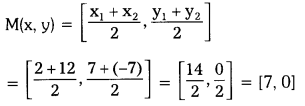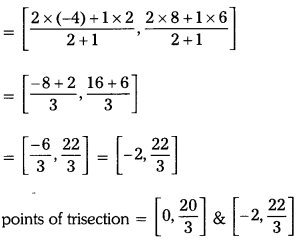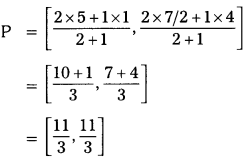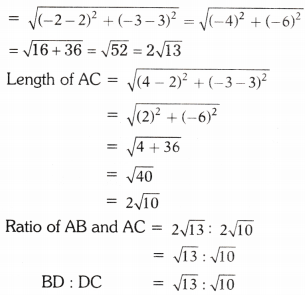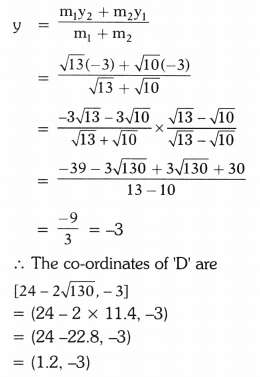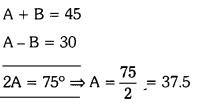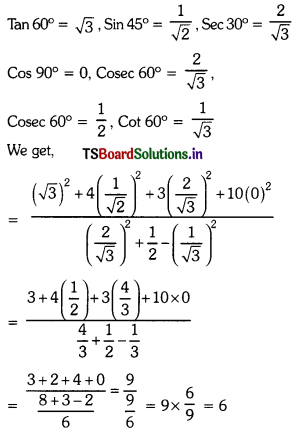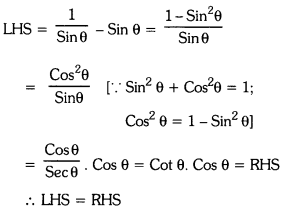Solving these TS 10th Class Maths Bits with Answers Chapter 11 Trigonometry Bits for 10th Class will help students to build their problem-solving skills.

Trigonometry Bits for 10th Class

Question 1.
If sin θ = \(\frac{\mathrm{a}}{\mathrm{b}}\) then tan θ =

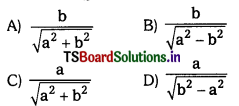
Answer:
(D)

Question 2.
cos² θ + sin² θ is
A) 0
B) 1
C) \(\frac{1}{2}\)
D) θ²
Answer:
B) 1

Question 3.
If sin θ = cos θ, then the value of 2 tan θ + cos²θ
A) 1
B) \(\frac{1}{2}\)
C) \(\frac{5}{2}\)
D) \(\frac{2}{5}\)
Answer:
C) \(\frac{5}{2}\)

Question 4.
If tan θ + sec θ = 8, then sec θ – tan θ is
A) 8
B) \(\frac{1}{8}\)
C) 6
D) 64
Answer:
B) \(\frac{1}{8}\)

Question 5.
The maximum value of sin θ is
A) \(\frac{1}{2}\)
B) \(\frac{\sqrt{3}}{2}\)
C) 1
D) \(\frac{1}{\sqrt{2}}\)
Answer:
C) 1

Question 6.
If tan θ = \(\frac{7}{8}\) then the value of \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
A) \(\frac{7}{8}\)
B) \(\frac{8}{9}\)
C) \(\frac{64}{49}\)
D) \(\frac{49}{64}\)
Answer:
C) \(\frac{64}{49}\)

Question 7.
If 5 tan θ = 4, then the value of \(\frac{5 \sin \theta-3 \cos \theta}{5 \sin \theta+3 \cos \theta}\) is
A) 0
B) 1
C) \(\frac{1}{7}\)
D) \(\frac{2}{7}\)
Answer:
C) \(\frac{1}{7}\)

Question 8.
\(\frac{\sin \theta}{1+\cos \theta}\) is

Answer:
(C)

Question 9.
The value of \(\frac{2 \tan 30}{1+\tan ^2 30}\) =
A) sin 60°
B) cos 60°
C) tan 60°
D) sin 30°
Answer:
A) sin 60°

Question 10.
The value of sin 45° + cos 45° is
A) \(\frac{1}{\sqrt{2}}\)
B) \(\sqrt{2}\)
C) \(\frac{\sqrt{3}}{2}\)
D) 1
Answer:
B) \(\sqrt{2}\)

Question 11.
If tan θ = 1, the value of \(\frac{5 \sin \theta+4 \cos \theta}{5 \sin \theta-4 \cos \theta}\) is
A) 9
B) 46°
C) 1
D) 0
Answer:
A) 9

Question 12.
tan θ is not defined when θ is
A) 90°
B) 60°
C) 30°
D) 0°
Answer:
A) 90°

Question 13.
If sin θ = \(\frac{\mathrm{a}}{\mathrm{b}}\) then cos θ =
A) \(\frac{\sqrt{a^2-b^2}}{b}\)
B) \(\frac{b}{a}\)
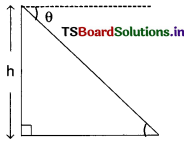
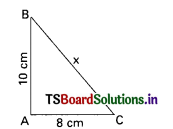
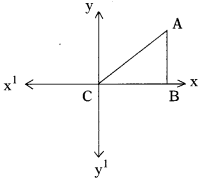
C) \(\frac{\sqrt{b^2-a^2}}{b}\)
D) \(\frac{b-a}{b}\)
Answer:
C) \(\frac{\sqrt{b^2-a^2}}{b}\)

Question 14.
If sin θ = \(\frac{12}{13}\) then tan θ =
A) \(\frac{13}{5}\)
B) \(\frac{5}{12}\)
C) \(\frac{13}{12}\)
D) \(\frac{12}{5}\)
Answer:
D) \(\frac{12}{5}\)

Question 15.
sin θ . sec θ =
A) tan θ
B) cosec θ
C) cot θ
D) sin θ . cos θ
Answer:
A) tan θ

Question 16.
\(\sqrt{1+\cot ^2 \theta}\) =
A) cosec² θ
B) 1 + cot θ
C) sec θ
D) cosec θ
Answer:
D) cosec θ

Question 17.
tan 135° =
A) \(\frac{1}{\sqrt{3}}\)
B) \(\sqrt{3}\)
C) – \(\sqrt{3}\)
D) -1
Answer:
D) -1

Question 18.
\(\sqrt{1+\sin A} \cdot \sqrt{1-\sin A}\) =
A) sin A
B) 1 – sin² A
C) cos A
D) 1
Answer:
C) cos A

Question 19.
sin (90 + θ) =
A) cos θ
B) – cos θ
C) sin θ
D) – sin θ
Answer:
A) cos θ

Question 20.
If tan θ = \(\frac{1}{\sqrt{3}}\), then cos θ =
A) \(\frac{1}{2}\)
B) \(\frac{\sqrt{3}}{2}\)
C) \(\frac{2}{\sqrt{3}}\)
D) \(\sqrt{3}\)
Answer:
B) \(\frac{\sqrt{3}}{2}\)

Question 21.
If cos θ = \(\frac{\sqrt{3}}{2}\) and ‘θ’ is acute, then the value of 4 sin² θ + tan² θ =
A) \(\frac{3}{4}\)
B) 1
C) \(\frac{4}{3}\)
D) \(\frac{5}{3}\)
Answer:
C) \(\frac{4}{3}\)

Question 22.
sin (A – B) = \(\frac{1}{2}\); cos (A + B) = \(\frac{1}{2}\). So, A =
A) 60°
B) 15°
C) 30°
D) 45°
Answer:
D) 45°

Question 23.
sin (-θ) =
A) sin θ
B) cos θ
C) – cos θ
D) – sin θ
Answer:
D) – sin θ

Question 24.
If sin (A – B) = \(\frac{1}{2}\); cos (A + B) = \(\frac{1}{2}\) then B =
A) 15°
B) – sin θ
C) sin θ
D) cos θ
Answer:
A) 15°

Question 25.
If α + β = 90° and α = 2β, then cos² β + sin² β =
A) 1
B) 0
C) \(\frac{1}{2}\)
D) 2
Answer:
A) 1

Question 26.
If tan θ = \(\frac{1}{\sqrt{3}}\) then 7 sin² θ + 3 cos² θ =
A) 1
B) 2
C) 3
D) 4
Answer:
D) 4

Question 27.
cos² 0° + cos² 60° =
A) \(\frac{5}{4}\)
B) \(\frac{2}{\sqrt{3}}\)
C) \(\frac{1}{\sqrt{2}}\)
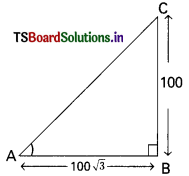
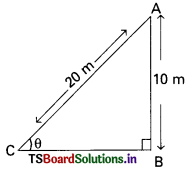
D) \(\frac{\sqrt{3}}{2}\)
Answer:
A) \(\frac{5}{4}\)

Question 28.
cot (270° – θ) =
A) -tan θ
B) tan θ
C) cot θ
D) – cot θ
Answer:
B) tan θ

Question 29.
sin 240° =
A) \(\frac{1}{\sqrt{2}}\)
B) \(\frac{2}{\sqrt{3}}\)
C) – \(\frac{\sqrt{3}}{2}\)
D) \(\frac{\sqrt{3}}{2}\)
Answer:
C) – \(\frac{\sqrt{3}}{2}\)

Question 30.
\(\frac{1-\tan ^2 30}{1+\tan ^2 30}\) =
A) \(\frac{1}{2}\)
B) 1
C) 0
D) 2
Answer:
A) \(\frac{1}{2}\)

Question 31.
If sin (A + B) = \(\frac{\sqrt{3}}{2}\) ; cos B = \(\frac{\sqrt{3}}{2}\) value of A is
A) 45°
B) 60°
C) 30°
D) 90°
Answer:
C) 30°

Question 32.
cos (A – B) = \(\frac{1}{2}\); sin B = \(\frac{1}{\sqrt{2}}\) measure of A =
A) 15°
B) 105°
C) 90°
D) 60°
Answer:
B) 105°

Question 33.
sin² 45° + cos² 45° + tan² 45° =
A) 2
B) 1
C) 3
D) \(\frac{3}{\sqrt{2}}\)
Answer:
A) 2

Question 34.
sin \(\frac{\pi}{6}\) + cos \(\frac{\pi}{3}\) =
A) \(\frac{2}{\sqrt{3}}\)
B) 2
C) \(\frac{1}{2}\)
D) 1
Answer:
D) 1

Question 35.
If sec θ + tan θ = 4; then cos θ =
A) \(\frac{8}{17}\)
B) \(\frac{4}{17}\)
C) \(\frac{15}{17}\)
D) \(\frac{17}{8}\)
Answer:
A) \(\frac{8}{17}\)

Question 36.
tan 0° =
A) 1
Β) α
C) \(\frac{1}{\sqrt{3}}\)
D) 0
Answer:
D) 0

Question 37.
If sin θ = \(\frac{\mathrm{a}}{\mathrm{b}}\); cos θ = \(\frac{\mathrm{c}}{\mathrm{d}}\) then cot θ =
A) \(\frac{\mathrm{ab}}{\mathrm{cd}}\)
B) \(\frac{\mathrm{bc}}{\mathrm{ad}}\)
C) \(\frac{\mathrm{ca}}{\mathrm{bd}}\)
D) \(\frac{\mathrm{ad}}{\mathrm{bc}}\)
Answer:
B) \(\frac{\mathrm{bc}}{\mathrm{ad}}\)

Question 38.
cos(xy) =
A) cos x sin x + cos y sin
B) cos x sin y + cos y sin y
C) sin x cos y + cos x sin y
D) cos x cos y + sin x sin y
Answer:
D) cos x cos y + sin x sin y

Question 39.
\(\frac{\tan \theta}{\sqrt{1+\tan ^2 \theta}}\) =
A) \(\frac{\tan \theta}{1+\tan \theta}\)
B) \(\frac{1}{\tan \theta}\)
C) cot θ
D) sin θ
Answer:
D) sin θ

Question 40.
cos θ:
A) 1 – sin² θ
B) sin² θ + 1
C) \(\frac{\cot \theta}{\ cosec \theta}\)
D) \(\frac{\ cosec \theta}{\ cot \theta}\)
Answer:
C) \(\frac{\cot \theta}{\ cosec \theta}\)

Question 41.
Value of cos 0° + sin 90° + \(\sqrt{3}\) cosec 60° =
A) 2
B) 3
C) 4
D) 1
Answer:
C) 4

Question 42.
π radians =
A) 90°
B) 60°
C) 180°
D) 45°
Answer:
C) 180°

Question 43.
cos⁶θ + sin⁶ θ =
A) 1 + sin³θ cos³ θ
B) 1 – 3sin²θ cos² θ
C) 1 – 3sin³θ cos³ θ
D) 45°
Answer:
C) 1 – 3sin³θ cos³ θ

Question 44.
cos 12 – sin 78 = …………. (A.P. Mar. ’15)
A) 1
B) \(\frac{1}{2}\)
C) 0
D) – 1
Answer:
C) 0

Question 45.
If x = cosec θ + cot θ and y = cosec θ – cot θ, then which of the following is true ………… (A.P Mar.’15)
A) x + y = 0
B) x – y = 0
C) \(\frac{x}{y}\) = 1
D) xy = 1
Answer:
D) xy = 1

Question 46.
cos (A – B) = …… (A.P. Mar.’15)
A) cos A cos B + sin A sin B
B) cos A sin A + cos B sin B
C) sin A sin B – cos A cos B
D) cos A cos B – sin A sin B
Answer:
A) cos A cos B + sin A sin B

Question 47.
cos (90 – θ) = ………….. (A.P. Mar.’15)
A) cos θ
B) sin θ
C) cosec θ
D) tan θ
Answer:
B) sin θ

Question 48.
In ∆ ABC, sin C = \(\frac{3}{5}\) then cos A = (A.P. June’15_
A) \(\frac{3}{5}\)
B) \(\frac{4}{5}\)
C) \(\frac{5}{4}\)
D) \(\frac{5}{3}\)
Answer:
A) \(\frac{3}{5}\)

Question 49.
tan² θ – sec² θ = ………. (A.P. June ’15)
A) 1
B) -1
C) 0
D) α
Answer:
B) -1

Question 50.
sec (90 – A) = …………… (A.P. June
A) cos A
B) cosec A
C) sin A
D) tan A
Answer:
B) cosec A

Question 51.
If cosec θ + cot θ = 5 then cosec θ – cot θ = ………….. (A.P. June ’15)
A) \(\frac{1}{5}\)
B) 5
C) -5
D) – \(\frac{1}{5}\)
Answer:
A) \(\frac{1}{5}\)

Question 52.
If x = 2 sec θ; y = 2 tan θ then x² – y² = ………………. (A.P. June ’15)
A) 0
B) -2
C) 4
D) 2
Answer:
C) 4

Question 53.
If \(\sqrt{3}\) tan θ = 1 then θ = ………. (A.P. June’15)
A) 60°
B) 90°
C) 45°
D) 30°
Answer:
D) 30°

Question 54.
(sec 60) (cos 60) = …………… (A.P. June’15)
A) 1
B) \(\frac{1}{2}\)
C) – 1
D) – \(\frac{1}{2}\)
Answer:
A) 1

Question 55.
sin (60 + 30) = ………………. (A.P. Mar. ’16)
A) 2
B) -2
C) 1
D) 1
Answer:
D) 1

Question 56.
If sin θ + tan θ = \(\frac{1}{2}\), then sin θ – tan θ = …………… (A.P. Mar.’16)
A) 1
B) – 1
C) 2
D) \(\frac{1}{2}\)
Answer:
C) 2

Question 57.
cos (90 – θ) = …………….. (A.P. Mar. ’16)
A) cos θ
B) tan θ
C) cosec θ
D) sin θ
Answer:
D) sin θ

Question 58.
If cot A = \(\frac{5}{12}\) then sin A + cos A = ………… (T.S. Mar. ’15)
A) \(\frac{17}{13}\)
B) \(\frac{12}{13}\)
C) \(\frac{5}{13}\)
D) \(\frac{20}{13}\)
Answer:
A) \(\frac{17}{13}\)

Question 59.
Which of the following is not possible value for sin x ………. (T.S. Mar. ’15)
A) \(\frac{3}{4}\)
B) \(\frac{3}{5}\)
C) \(\frac{4}{5}\)
D) \(\frac{5}{4}\)
Answer:
D) \(\frac{5}{4}\)

Question 60.
If sin cos θ (0 < θ < 90) then tan θ + cot θ = ………….. (T.S Mar. ’16)
A) 2\(\sqrt{3}\)
B) \(\frac{2}{\sqrt{3}}\)
C) 2
D) 1
Answer:
C) 2

Question 61.
If sec θ + tan θ = 3 then sec θ – tan θ = ……………. (T.S. Mar. ’16)
A) \(\frac{1}{3}\)
B) \(\frac{2}{3}\)
C) \(\frac{4}{3}\)
D) \(\frac{5}{3}\)
Answer:
A) \(\frac{1}{3}\)

Question 62.
In ∆ABC, AB = c, BC = a, AC = b and ∠BAC = θ then area of ∆ABC is …………… (θ is acute) (T.S. Mar.’16)
A) \(\frac{1}{2}\) ab sin θ
B) \(\frac{1}{2}\) ca sin θ
C) \(\frac{1}{2}\) bc sin θ
D) \(\frac{1}{2}\) b² sin θ
Answer:
C) \(\frac{1}{2}\) bc sin θ

Question 63.
The value of sin² 60° – sin²30° is ………………..
A) \(\frac{1}{4}\)
B) \(\frac{1}{2}\)
C) \(\frac{3}{4}\)
D) –\(\frac{1}{2}\)
Answer:
B) \(\frac{1}{2}\)

Question 64.
If cosec θ = 2 and cot θ = \(\sqrt{3}\) p, where θ is an acute angle, then the value of ‘p’ is
A) 2
B) 1
C) 0
D) \(\sqrt{3}\)
Answer:
B) 1

Question 65.
The value of \(\left(\frac{11}{\cot ^2 \theta}-\frac{11}{\cos ^2 \theta}\right)\) is
A) 11
B) 0
C) \(\frac{1}{11}\)
D) -11
Answer:
D) -11

Question 66.
If sec 2A = cosec (A – 27°), where 2A is an acute angle, then the measure of ∠A is
A) 35°
B) 37°
C) 39°
D) 21°
Answer:
C) 39°

Question 67.
\(\frac{1-\sec ^2 A}{{cosec}^2-1}\) = ………………….
A) -tan² A
B) -tan⁴ A
C) 1
D) -sec² A
Answer:
B) -tan⁴ A

Question 68.
If sec θ = 3k and tan θ = \(\frac{3}{\mathrm{k}}\) then (k² – \(\frac{1}{\mathrm{k}^2}\)) = …………….
A) 9
B) 3
C) \(\frac{1}{9}\)
D) 1
Answer:
C) \(\frac{1}{9}\)

Question 69.
If P, Q and R are interior angles of a ∆PQR, then tan \(\left(\frac{P+Q}{2}\right)\) equals.
A) sin \(\left(\frac{\mathrm{R}}{2}\right)\)
B) cos \(\left(\frac{\mathrm{R}}{2}\right)\)
C) cot \(\left(\frac{\mathrm{R}}{2}\right)\)
D) \(\left(\frac{\mathrm{R}}{2}\right)\)
Answer:
C) cot \(\left(\frac{\mathrm{R}}{2}\right)\)

Question 70.
If sin (x – 20)° = cos (3x – 10)°, then ‘x’ is
A) 60
B) 30
C) 45
D) 35.5
Answer:
B) 30

Question 71.
Maximum value of \(\frac{1}{\sec \theta}\), 0° ≤ θ ≤ 90° is
A) 1
B) 2
C) \(\frac{1}{2}\)
D) \(\frac{1}{\sqrt{2}}\)
Answer:
A) 1

Question 72.
The value of cos² 17° – sin²73° is
A) 1
B) \(\frac{1}{3}\)
C) 0
D) -1
Answer:
C) 0

Question 73.
If A = 30°, then sin 2A equals…………..
A) \(\frac{1}{2}\)
B) \(\frac{\sqrt{3}}{2}\)
C) \(\frac{1}{\sqrt{2}}\)
D) 1
Answer:
B) \(\frac{\sqrt{3}}{2}\)

Question 74.
In a right angled ∆ABC, right angle at ‘C’ if tan A = \(\frac{8}{15}\), then the value of cosec² A – 1 is
A) 0
B) \(\frac{64}{225}\)
C) \(\frac{225}{64}\)
D) \(\frac{289}{64}\)
Answer:
C) \(\frac{225}{64}\)

Question 75.
If \(\frac{1}{2}\) tan² 45° = sin²A and ‘A’, acute, then the value of A is
A) 60°
B) 45°
C) 30°
D) 15°
Answer:
B) 45°

Question 76.
sin (45° + θ) cos (45 – θ) =
A) 2 sin θ
B) 0
C) 1
D) 2 cos θ
Answer:
B) 0

Question 77.
If cos 2θ sin 40; here 2θ and 4θ are acute angles, then the value of ‘θ’ is
A) 60°
B) 45°
C) 15°
D) 30°
Answer:
C) 15°

Question 78.
If sin x = cos x, 0 ≤ x ≤ 90°, then x =
A) 30°
B) 90°
C) 0°
D) 45°
Answer:
D) 45°

Question 79.
2 sin θ = sin²θ is true for the value of θ is ………….
A) 0°
B) 45°
C) 30°
D) 60°
Answer:
A) 0°

Question 80.
If sin 45°.cos 45° + cos 60° = tan θ, then the value of θ is
A) 0°
B) 30°
C) 45°
D) 60°
Answer:
C) 45°

Question 81.
From the below figure ON= x; PN = y and Op = r; ∆PON = θ and ∆PON = 90°; sin θ =

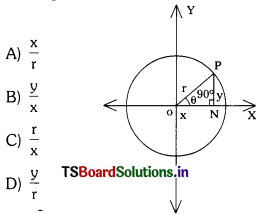
Answer:
(D)

Question 82.
cos θ = …………………..
A) \(\frac{x}{r}\)
B) \(\frac{y}{r}\)
C) \(\frac{r}{x}\)
D) \(\frac{y}{x}\)
Answer:
A) \(\frac{x}{r}\)

Question 83.
tan θ =
A) \(\frac{x}{y}\)
B) \(\frac{y}{x}\)
C) \(\frac{r}{x}\)
D) \(\frac{r}{y}\)
Answer:
B) \(\frac{y}{x}\)

Question 84.
sin θ . cosec θ + cos θ . sec θ + tan θ . cot θ =
A) 3
B) 1
C) sinθ.cosθ.tanθ
D) none
Answer:
A) 3

Question 85.
If sinθ. cosec θ = x; then x =
A) 0
B) 1
C) \(\frac{1}{\sin \theta}\)
D) \(\frac{1}{\ cosec \theta}\)
Answer:
B) 1

Question 86.
If sec θ = \(\frac{13}{12}\), then sin θ =
A) \(\frac{5}{13}\)
B) \(\frac{5}{12}\)
C) \(\frac{12}{5}\)
D) \(\frac{12}{13}\)
Answer:
A) \(\frac{5}{13}\)

Question 87.
sin (90 + θ) =
A) cos θ
B) – cos θ
C) sin θ
D) – sin θ
Answer:
A) cos θ

Question 88.
Value of tan² 30° + 2 cot² 60° =
A) \(\frac{2}{3}\)
B) 2
C) 1
D) \(\frac{4}{3}\)
Answer:
C) 1

Question 89.
sin² 75° + cos² 75° =
A) 75
B) 150
C) tan² 75°
D) 1
Answer:
D) 1

Question 90.
sin⁴θ – cos⁴θ =
A) 1
B) cos²θ – sin²θ
C) 2 sin² θ – 1
D) 2 sin²θ
Answer:
C) 2 sin² θ – 1

Question 91.
(1 + tan θ)² =
A) sec² θ
B) sec²θ + 2 tan θ
C) sec²θ + tan²θ
D) sec²θ + tan θ
Answer:
B) sec²θ + 2 tan θ

Question 92.
Expressing tan θ, interms of sec θ.

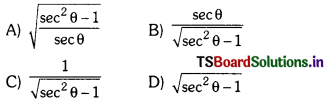
Answer:
(D)

Question 93.
If 5 sin A = 3; then sec² A – tan² A =
A) \(\frac{9}{25}\)
B) 0
C) \(\frac{25}{9}\)
D) 1
Answer:
D) 1

Question 94.
(sin θ + cos θ)² + (sin θ – cos θ)² =
A) 2 sin²θ+ cos²θ
B) 2
C) 2 sin²θ + 4 cos²θ
D) 2 sin²θ
Answer:
B) 2

Question 95.

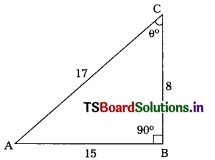
In ∆ABC, ∠B = 90°; ∠C = 0. From the figure, tan θ =
A) \(\frac{8}{17}\)
B) \(\frac{15}{8}\)
C) \(\frac{8}{15}\)
D) \(\frac{17}{15}\)
Answer:
B) \(\frac{15}{8}\)

Question 96.
Value of cos 0° + sin 90° + \(\sqrt{2}\) sin 45°
A) 0
B) 2 + \(\sqrt{2}\)
C) 4
D) 3
Answer:
D) 3

Question 97.
Value of 3 sin² 45° + 2cos² 60° =
A) 2
B) 4
C) 32
D) 1 1/2
Answer:
A) 2

Question 98.
Value of cos 240° =
A) \(\frac{1}{2}\)
B) –\(\frac{\sqrt{3}}{2}\)
C) – \(\frac{1}{2}\)
D) none
Answer:
C) – \(\frac{1}{2}\)

Question 99.
If tan θ + cot θ = 2; then tan²θ + cot²θ =
A) 4
B) 2
C) 6
D) 1
Answer:
B) 2

Question 100.
Value of tan 60° – tan 30°
A) \(\frac{1}{\sqrt{3}}-\sqrt{3}\)
B) \(\frac{1}{\sqrt{3}}\)
C) \(\frac{2 \sqrt{3}}{3}\)
D) \(\frac{\sqrt{3}}{3}\)
Answer:
C) \(\frac{2 \sqrt{3}}{3}\)

Question 101.
If sin θ = cos θ, then θ =
A) 30°
B) 45°
C) 60°
D) 90°
Answer:
B) 45°

Question 102.
(1 + tan² 60°)² =
A) 1
B) 2
C) 4
D) 16
Answer:
D) 16

Question 103.
cos (270° – θ)
A) – cos θ
B) – sin θ
C) sin θ
D) cos θ
Answer:
B) – sin θ

Question 104.
When 0° ≤ θ ≤ 90°; the maximum value of sin θ + cos θ is
A) \(\sqrt{2}\)
B) \(\frac{1}{\sqrt{2}}\)
C) 1
D) 2
Answer:
A) \(\sqrt{2}\)

Question 105.
In right angle ∆ABC; ∠B = 90°; tan C = \(\frac{5}{12}\) then the length of hypotenuse is
A) 16
B) 13
C) 21
D) 17
Answer:
B) 13

Question 106.
If A, B are acute angles; sin (A – B) = \(\frac{1}{2}\) sin A = \(\frac{1}{2}\) then B =
A) \(\frac{\pi}{3}\)
B) \(\frac{\pi}{5}\)
C) \(\frac{\pi}{6}\)
D) \(\frac{\pi}{12}\)
Answer:
D) \(\frac{\pi}{12}\)

Question 107.
In ∆ABC, a = 3; b = 4; c = 5 then cos A =
A) \(\frac{3}{5}\)
B) \(\frac{3}{4}\)
C) \(\frac{5}{3}\)
D) \(\frac{4}{5}\)
Answer:
D) \(\frac{4}{5}\)

Question 108.

If sin C = \(\frac{3}{5}\) then cos A =
A) \(\frac{3}{5}\)
B) \(\frac{4}{5}\)
C) \(\frac{5}{4}\)
D) \(\frac{5}{3}\)
Answer:
A) \(\frac{3}{5}\)

Question 109.
sec A. \(\sqrt{1-\sin ^2 A}\) =
A) cos A
B) sec A
C) 0
D) 1
Answer:
D) 1

Question 110.
cot(270° – θ) =
A) -tan θ
B) tan θ
C) cot θ
D) – cot θ
Answer:
B) tan θ

Question 111.
\(\frac{\sin 18^{\prime \prime}}{\cos 72^{\prime \prime}}\) =
A) 1
B) \(\frac{1}{4}\)
C) 0
D) ∞
Answer:
A) 1

Question 112.
If π < θ < \(\frac{3 \pi}{2}\) then θ lies in
A) first quadrant
B) second quadrant
C) third quadrant
D) fourth quadrant
Answer:
C) third quadrant

Question 113.
If sinθ . cosθ = k; then sin θ + cos θ =
A) K²
B) K² – 1
C) \(\sqrt{2 K^2-1}\)
D) \(\sqrt{1+2 \mathrm{~K}}\)
Answer:
D) \(\sqrt{1+2 \mathrm{~K}}\)

Question 114.
If tan² 60° + 2 tan² 45° = x tan 45°; then x =
A) 0
B) 5
C) 1
D) 2
Answer:
B) 5

Question 115.
sin³θ cos θ . cos³ θ . sin θ =
A) sin θ + cos θ
B) sin θ cos θ
C) sin θ
D) cos θ
Answer:
B) sin θ cos θ

Question 116.
\(\frac{\sqrt{1+\tan ^2 \theta}}{\sqrt{1+\cot ^2 \theta}}\) =
A) sin θ
B) cos θ
C) tan θ
D) cot θ
Answer:
C) tan θ

Question 117.
sin² 47° + sin² 43° =
A) 0
B) ∞
C) 1
D) can not be determined
Answer:
C) 1

Question 118.
sec (360° – θ) =
A) cos θ
B) sec θ
C) cosec θ
D) cot θ
Answer:
B) sec θ

Question 119.
If sin θ + cos θ = \(\sqrt{2}\); then value of θ =
A) 0°
B) 30°
C) 45°
D) 60°
Answer:
C) 45°

Question 120.
(1 + cot²45°)²: =
A) 4
B) 2
C) 1
D) \(\sqrt{2}\)
Answer:
A) 4

Question 121.
\(\frac{{\ cosec}^2 \theta}{\cot \theta}\) – cot θ =
A) cot θ
B) cosec θ
C) sec θ
D) tan θ
Answer:
D) tan θ

Question 122.
If the following, which are in geometric progression ?
A) sin 30°, sin 45°, sin 60°
B) sec 30°, sec 45°, sec 60°
C) tan 30°, tan 45°, tan 60°
D) cos 45°, cos 60°, cos 90°
Answer:
C) tan 30°, tan 45°, tan 60°

Question 123.
\(\sqrt{\frac{\sec x+\tan x}{\sec x-\tan x}}\) =
A) sec x + tan x
B) sec x- tan x
C) 2 tan x
D) 2 sec x
Answer:
A) sec x + tan x

Question 124.
\(\frac{1}{\sec ^2 A}+\frac{1}{{cosec}^2 A}\) =
A) 2
B) 1
C) tan2A + cos2A
D) 0
Answer:
B) 1

Question 125.
If 4 sin 30° . sec 60° = x tan 4°; then x =
A) 0
B) 1
C) 3
D) 4
Answer:
D) 4

Question 126.
Value of sin 60° cos 30° + cos 60°. sin 30°
A) \(\frac{1}{2}\)
B) 1
C) \(\frac{\sqrt{3}}{2}\)
D) \(\frac{2}{\sqrt{3}}\)
Answer:
B) 1

Question 127.
Value of cos 60°. cos 30° + sin 60°. sin 30°
A) \(\frac{\sqrt{3}}{2}\)
B) \(\frac{1}{\sqrt{2}}\)
C) 1
D) \(\frac{2}{\sqrt{3}}\)
Answer:
A) \(\frac{\sqrt{3}}{2}\)

Question 128.
\(\frac{\tan 45^{\prime \prime}}{\ cosec 30^{\prime \prime}}+\frac{\sec 60^{\prime \prime}}{\cot 45^{\prime \prime}}\) =
A) 1 1/2
B) 1
C) 2
D) 2 1/2
Answer:
D) 2 1/2

Question 129.
Value of cos 75° =
A) sin 15°
B) – sin 15°
C) cos 15°
D) \(\frac{\sqrt{3}}{2}\)
Answer:
A) sin 15°

Question 130.
tan θ . cot θ = sec θ . x; then x =
A) cos θ
B) sec θ
C) tan θ
D) cot θ
Answer:
A) cos θ

Question 131.
(1 + tan²A) (1 – sin² A) =
A) sec²A
B) cos²A
C) 1
D) 1 – sin²A + tan²A
Answer:
C) 1

Question 132.
tan 240° =
A) \(\frac{1}{\sqrt{3}}\)
B) \(\sqrt{3}\)
C) –\(\sqrt{3}\)
D) –\(\frac{1}{\sqrt{3}}\)
Answer:
B) \(\sqrt{3}\)

Question 133.
\(\frac{\sin ^4 A-\cos ^4 A}{\sin ^2 A-\cos ^2 A}\) =
A) sin² A – cos² A
B) 1
C) sin² A
D) cos²
Answer:
B) 1

Question 134.
If sin θ = \(\frac{1}{2}\); then cos \(\frac{3 \theta}{2}\)
A) \(\frac{1}{\sqrt{2}}\)
B) \(\frac{\sqrt{3}}{2}\)
C) \(\frac{1}{2}\)
D) \(\frac{2}{\sqrt{3}}\)
Answer:
A) \(\frac{1}{\sqrt{2}}\)

Question 135.
cos \(\left(\frac{3}{2}+\theta\right)\) =
A) cos θ
B) sin θ
C) – sin θ
D) sec θ
Answer:
B) sin θ

Question 136.
\(\frac{\tan \theta \cdot \sqrt{1-\sin ^2 \theta}}{\sqrt{1-\cos ^2 \theta}}\)
A) sin θ
B) cos θ
C) sec θ
D) 1
Answer:
D) 1

Question 137.
If sec θ + tan θ = \(\frac{1}{5}\), then sin θ =
A) \(\frac{5}{13}\)
B) \(\frac{12}{13}\)
C) \(\frac{13}{12}\)
D) \(\frac{5}{13}\)
Answer:
B) \(\frac{12}{13}\)

Question 138.
(sec 45° + tan 45°) (sec 45° – tan 45°) =
A) 1
B) 0
C) 2
D) 2\(\sqrt{2}\)
Answer:
A) 1

Question 139.
If the angle in a triangle are in the ratio of 1 : 2 : 3 then the smallest angle in radius is
A) \(\frac{\pi}{3}\)
B) \(\frac{\pi}{6}\)
C) \(\frac{2\pi}{3}\)
D) \(\frac{\pi}{2}\)
Answer:
B) \(\frac{\pi}{6}\)

Question 140.
\(\sqrt{{\ cosec}^2 \theta-\cot ^2 \theta}\) =
A) cosec θ – cot θ
B) cosec θ + cot θ
C) 1
D) 0
Answer:
C) 1

Question 141.
tan A, in terms of sin A is

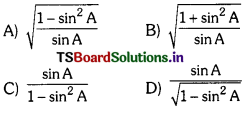
Answer:
(D)

Question 142.
\(\frac{1}{1-\sin \theta}\) + \(\frac{1}{1+\sin \theta}\) =
A) 2 tan² θ
B) 2 sec² θ
C) 2 cosec² θ
D) 2 cot² θ
Answer:
B) 2 sec² θ

Question 143.
If cot² θ = 3; then cosec θ =
A) 4
B) 2
C) 3
D) 1
Answer:
B) 2

Question 144.
If cos θ = – cos θ, then θ is
A) 60°
B) 45°
C) 30°
D) 90°
Answer:
B) 45°

Question 145.
If A is acute and tan A = \(\frac{1}{\sqrt{3}}\); then sin A = ……………….
A) \(\frac{1}{2}\)
B) 1
C) \(\sqrt{2}\)
D) \(\frac{\sqrt{3}}{2}\)
Answer:
A) \(\frac{1}{2}\)

Question 146.
If sin θ = \(\frac{\mathrm{a}}{\mathrm{b}}\); cos θ = \(\frac{\mathrm{c}}{\mathrm{d}}\) ;then tan θ =
A) \(\frac{\mathrm{bc}}{\mathrm{ad}}\)
b) \(\frac{\mathrm{ac}}{\mathrm{bd}}\)
C) \(\frac{\mathrm{ab}}{\mathrm{cd}}\)
D) \(\frac{\mathrm{ad}}{\mathrm{bc}}\)
Answer:
D) \(\frac{\mathrm{ad}}{\mathrm{bc}}\)

Question 147.
If sin A = \(\frac{1}{\sqrt{2}}\) ; then tan A =
A) 3
B) 4
C) 1
D) \(\sqrt{2}\)
Answer:
C) 1

Question 148.
If sec θ = cosec θ; then value of θ =
A) \(\frac{\pi}{2}\)
B) \(\frac{\pi}{4}\)
C) \(\frac{\pi}{6}\)
D) \(\frac{\pi}{3}\)
Answer:
B) \(\frac{\pi}{4}\)

Question 149.
The radius of a circle is ‘r’; an arc of length ‘l’ is making an angle θ, at the centre of the circle, then θ =
A) \(\frac{\mathrm{l}}{\mathrm{r}}\)
B) \(\frac{\mathrm{r}}{\mathrm{l}}\)
C) lr
D) l + r
Answer:
A) \(\frac{\mathrm{l}}{\mathrm{r}}\)

Question 150.
tan (A + B) =

Answer:
(B)

Question 151.
tan(A – B) =

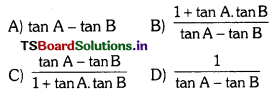
Answer:
(C)

Question 152.
\(\frac{\sqrt{\ cosec^2 \theta-1}}{\ cosec \theta}\) =
A) 1+ sec θ
B) cosec θ + cot θ
C) cos θ
D) tan θ
Answer:
C) cos θ

Question 153.
\(\frac{\sin \theta}{\sqrt{1-\sin ^2 \theta}}\) =
A) tan θ
B) cosec θ
C) cot θ
D) sec θ
Answer:
A) tan θ

Question 154.
\(\frac{\sqrt{\sec ^2 \theta-1}}{\sec \theta}\) =
A) cosec θ
B) sin θ
C) cosec θ – cot θ
D) 2 sec θ
Answer:
B) sin θ

Question 155.
If x = 2 cosec θ; y = 2 cot θ; then x² – y² =
A) 4
B) 0
C) 1
D) 2
Answer:
A) 4

Question 156.
If cos(A + B) = θ, cos B = \(\frac{\sqrt{3}}{2}\); then A is
A) 60°
B) 180°
C) 15°
D) 115°
Answer:
A) 60°

Question 157.
\(\frac{\sqrt{1-\cos ^2 \theta}}{\cos \theta}\) =
A) tan θ
B) cos θ
C) sec θ
D) cot θ
Answer:
A) tan θ

Question 158.
\(\frac{1}{\sqrt{1+\tan ^2 \theta}}\) =
A) sin θ
B) cos θ
C) sec θ
D) cosec θ
Answer:
B) cos θ

Question 159.
cos θ . tan θ =
A) cos θ
B) cot θ
C) sin θ
D) cos² θ
Answer:
C) sin θ

Question 160.
sin 225° =
A) \(\frac{1}{\sqrt{2}}\)
B) –\(\frac{1}{\sqrt{2}}\)
C) \(\frac{\sqrt{3}}{2}\)
D) \(\frac{2}{\sqrt{3}}\)
Answer:
B) –\(\frac{1}{\sqrt{2}}\)

Question 161.
sec² 33° – cot² 57° =
A) 0
B) 1
C) -1
D) \(\frac{1}{2}\)
Answer:
B) 1

Question 162.
sin 180° =
A) 0
B) 1
C) -1
D) ∞
Answer:
A) 0

Question 163.
If cos θ = \(\frac{1}{2}\) ; then cos \(\frac{\theta}{2}\) =
A) \(\frac{1}{4}\)
B) \(\frac{\sqrt{3}}{2}\)
C) \(\frac{1}{2}\)
D) 1
Answer:
B) \(\frac{\sqrt{3}}{2}\)

Question 164.
sin (A + B).cos (A – B) + sin (A – B). cos (A + B) =
A) cos 2A
C) sin 2A
B) cos 2B
D) sin 2B
Answer:
B) cos 2B

Question 165.
Value of cos 60° . cos30° – sin 60° . sin 30° =
A) 1
B) 0
C) \(\frac{1}{4}\)
D) \(\frac{1}{2}\)
Answer:
B) 0

Question 166.
cos 300° =
A) \(\frac{\sqrt{3}}{2}\)
B) 1
C) 0
D) \(\frac{1}{2}\)
Answer:
D) \(\frac{1}{2}\)

Question 167.
If sin (A + B) = 1; sin B = \(\frac{1}{2}\) ; then A =
A) 30°
B) 45°
C) 60°
D) 90°
Answer:
C) 60°

Question 168.
\(\sqrt{\sec ^2 A+\ cosec^2 A}\) =
A) cos A + sin A
B) sec A + cosec A
C) tan A+ cot A
D) 1
Answer:
C) tan A+ cot A

Question 169.
If \(\sqrt{3}\) tan θ = 1; then θ =
A) 30°
B) 45°
C) 60°
D) 90°
Answer:
A) 30°

Question 170.
\(\sqrt{\ cosec ^2 \theta-\sin ^2 \theta-\cos ^2 \theta}\) =
A) cot θ
B) tan θ
C) sec θ
D) cosec θ
Answer:
A) cot θ

Question 171.
sin 750° =
A) \(\frac{1}{\sqrt{2}}\)
B) \(\frac{1}{2}\)
C) 1
D) \(\frac{\sqrt{3}}{2}\)
Answer:
B) \(\frac{1}{2}\)

Question 172.
Cosec 60° × cos 90° =
A) ∞
B) \(\frac{2}{\sqrt{3}}\)
C) 0
D) 3
Answer:
C) 0

Question 173.
sin 81° = ………………
A) cos 9°
B) cos 81°
C) – cos 9°
D) can not be possible to determine without tables
Answer:
A) cos 9°

Question 174.
If sin θ = \(\frac{11}{15}\) ; then cos θ =
A) \(\frac{\sqrt{26}}{7}\)
B) \(\frac{2 \sqrt{26}}{3}\)
C) \(\frac{2 \sqrt{26}}{15}\)
D) none
Answer:
C) \(\frac{2 \sqrt{26}}{15}\)

Question 175.
If tan θ = \(\sqrt{3}\), then sec θ = ……………….
A) 2
B) -2
C) 4
D) 5
Answer:
A) 2

Question 176.
If 3 cot θ = 5, then \(\frac{5 \sin \theta-3 \cos \theta}{5 \sin \theta+3 \cos \theta}\) = ………………..
A) -1
B) 1
C) 7
D) 0
Answer:
D) 0

Question 177.
(1 + tan²θ) cos²θ = …………….
A) 1
B) 0
C) 8
D) 14
Answer:
A) 1

Question 178.
(sec²θ – 1) (1 – cosec²θ) = ………………
A) 2
B) -1
C) 3
D) -4
Answer:
B) -1

Question 179.
cot²θ – \(\frac{1}{\sin ^2 \theta}\)
A) 4
B) -3
C) 2
D) -1
Answer:
D) -1

Question 180.
If cos θ . sin θ = \(\frac{1}{2}\) ; then θ = …………….
A) 1
B) -1
C) 3
D) 4
Answer:
A) 1

Question 181.
If cos θ = -cos θ; then θ in radian measure is ………….
A) π^c
B) \(\frac{\pi^c}{2}\)
C) \(\frac{\pi^c}{3}\)
D) \(\frac{\pi^c}{7}\)
Answer:
C) \(\frac{\pi^c}{3}\)

Question 182.
If sin A = \(\frac{3}{5}\) ; then sin (90 + A) = ………….
A) \(\frac{4}{5}\)
B) \(\frac{5}{4}\)
C) \(\frac{1}{3}\)
D) \(\frac{2}{3}\)
Answer:
A) \(\frac{4}{5}\)

Question 183.
\(\sqrt{(\sec \theta+1)(\sec \theta-1)}\) = ……………..
A) cot θ
B) tan θ
C) cos θ
D) sin θ
Answer:
B) tan θ

Question 184.
\(\sqrt{\sec ^2 \theta-\tan ^2 \theta+\cot ^2 \theta}\) = …………………..
A) -cos θ
B) 1
C) sec θ
D) cosec θ
Answer:
D) cosec θ

Question 185.
cos 150° = …………….
A) –\(\frac{\sqrt{3}}{2}\)
B) – \(\sqrt{3}\)
C) –\(\frac{1}{2}\)
D) none
Answer:
A) –\(\frac{\sqrt{3}}{2}\)

Question 186.
sin² 75° + cos² 75° = ………………..
A) 3
B) 2
C) 4
D) 1
Answer:
D) 1

Question 187.
sin 240° + sin 120° = …………..
A) 0
B) -1
C) 3
D) none
Answer:
A) 0

Question 188.
If cosec θ + cot θ = 2; then cosec θ – cot θ = ………………
A) -1
B) 2
C) \(\frac{1}{2}\)
D) 3
Answer:
C) \(\frac{1}{2}\)

Question 189.
If sec A + tan A = \(\frac{1}{3}\); then sec A – tan A = ……………
A) 4
B) 1
C) -3
D) 3
Answer:
D) 3

Question 190.
sin 30° + cos 60° = ………………
A) 1
B) 4
C) 3
D) none
Answer:
A) 1

Question 191.
(cos A + sin A)² + (cos A – sin A)² = ………………..
A) 1
B) 2
C) 4
D) none
Answer:
B) 2

Question 192.
sin 450° = ……………….
A) 4
B) 2
C) -1
D) none
Answer:
D) none

Question 193.
cos(A + B) = ……………..
A) cos A cos B – sin A sin B
B) cos A sec B – sin A sin B
C) cos A cos B + sin A sec B
D) none
Answer:
A) cos A cos B – sin A sin B

Question 194.
tan(A – B) = ………….
A) tan A – cos B
B) tan B – tan A
C) \(\frac{\tan B-\tan A}{1+\tan A+\tan B}\)
D) none
Answer:
C) \(\frac{\tan B-\tan A}{1+\tan A+\tan B}\)

Question 195.
tan (360 – θ) = ……………….
A) sin θ
B) sec θ
C) tan θ
D) -tan θ
Answer:
D) -tan θ

Question 196.
The value of tan 75° = …………..
A) 2 + \(\sqrt{3}\)
B) 2 – \(\sqrt{3}\)
C) \(\sqrt{3}\) – 1
D) none
Answer:
A) 2 + \(\sqrt{3}\)

Question 197.
cos 110°. cos 70° – sin 110°.sin 70° = ……………..
A) 4
B) 1
C) -1
D) 3
Answer:
C) -1

Question 198.
Express tan θ, interms of sin θ = ………………
A) \(\frac{\cos \theta}{1-\sin \theta}\)
B) \(\frac{\sin \theta}{\sqrt{1-\sin ^2 \theta}}\)
C) \(\frac{\sin \theta}{1+\cos \theta}\)
D) none
Answer:
B) \(\frac{\sin \theta}{\sqrt{1-\sin ^2 \theta}}\)

Question 199.
cosec 60° . sec 60° = ……………….
A) \(\frac{1}{2}\)
B) \(\frac{\sqrt{3}}{4}\)
C) \(\frac{4}{3}\)
D) \(\frac{4}{\sqrt{3}}\)
Answer:
D) \(\frac{4}{\sqrt{3}}\)

Question 200.
sin(A + B) =
A) sin A cos B + cos A sin B
B) sin A – cos B sin B
C) sin A cos B – sin A sin B
D) none
Answer:
A) sin A cos B + cos A sin B

Question 201.
cos (180 – θ) = ……………..
A) – cos θ
B) cos θ
C) sec θ
D) none
Answer:
A) – cos θ

Question 202.
sin 2A = ………………
A) 2 sin A cos A
B) cos A sin A
C) sin² A
D) cos² A
Answer:
A) 2 sin A cos A

Question 203.
\(\sqrt{\ cosec ^2 \theta-\sin ^2 \theta-\cos ^2 \theta}\) = ……………….
A) -tan θ
B) -sin θ
C) sec θ
D) cot θ
Answer:
D) cot θ

Question 204.
(1 – sec²θ) (1 – cosec²θ) = ……………….
A) 3
B) -1
C) 4
D) 1
Answer:
D) 1

Question 205.
If cos θ = \(\frac{3}{5}\); then cos (-θ) = …………….
A) \(\frac{-3}{5}\)
B) \(\frac{3}{5}\)
C) \(\frac{1}{5}\)
D) \(\frac{1}{4}\)
Answer:
B) \(\frac{3}{5}\)

Question 206.
2 sin 45°. cos 45° = …………….
A) 1
B) 4
C) -1
D) none
Answer:
A) 1

Question 207.
If cot = x; then cosec θ = ………….
A) \(\sqrt{2 x+1}\)
B) \(\sqrt{1+x}\)
C) \(\sqrt{x^2+1}\)
D) none
Answer:
C) \(\sqrt{x^2+1}\)

Question 208.
In the figure, AB = ………………

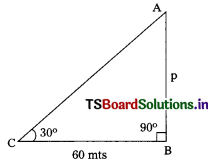
A) 16 \(\sqrt{3}\)
B) 10 \(\sqrt{3}\)
C) 9\(\sqrt{3}\)
D) 20\(\sqrt{3}\)
Answer:
D) 20\(\sqrt{3}\)

Question 209.
sin 45°.cos 45° + \(\sqrt{3}\) sin 60° = ………..
A) 2
B) -2
C) 3
D) none
Answer:
A) 2

Question 210.
\(\frac{\sqrt{\sec ^2 A-1}}{\sec A}\) = ………………
A) sec A
B)-cos A
C) cos A
D) sin A
Answer:
D) sin A

Question 211.
\(\frac{\sqrt{\ cosec ^2 \theta-1}}{\ cosec \theta}\) = …………..
A) -sin θ
B)-cos θ
C) cos θ
D) none
Answer:
C) cos θ

Question 212.
If α + β = 90° and α = 2β; then cos² α + sin² β = ………………
A) \(\frac{-1}{2}\)
B) -1
C) 2
D) \(\frac{1}{2}\)
Answer:
D) \(\frac{1}{2}\)

Question 213.
tan 30° + cot 30° = ………….
A) \(\frac{4}{\sqrt{3}}\)
B) \(\frac{4}{3}\)
C) \(\frac{\sqrt{3}}{4}\)
D) none
Answer:
A) \(\frac{4}{\sqrt{3}}\)

Question 214.
\(\sqrt{\tan ^2 \theta+\cot ^2 \theta+2}\) = ………………..
A) tan θ – cos θ
B) tan θ
C) tan θ + cot θ
D) tan θ – cot θ
Answer:
C) tan θ + cot θ

Question 215.
If sin θ = \(\frac{\mathrm{a}}{\mathrm{b}}\); then tan θ = …………….

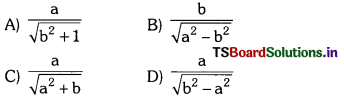
Answer:
(D)

Question 216.
tan θ = \(\frac{1}{\sqrt{3}}\) ; cos θ = ……………
A) \(\frac{\sqrt{3}}{2}\)
B) \(\sqrt{3}\)
C) \(\frac{2}{\sqrt{3}}\)
D) \(\frac{1}{2}\)
Answer:
A) \(\frac{\sqrt{3}}{2}\)

Question 217.
If 5 sin A = 3; sec²A – tan²A = ……………..
A) 3
B) -1
C) 4
D) 1
Answer:
D) 1

Question 218.
sin (-θ) = …………………..
A) cos θ
B) -tan θ
C) sec θ
D) -sin θ
Answer:
D) -sin θ

Question 219.
cos (-θ) = ………………..
A) sec θ
B) -cos θ
C) cos θ
D) 1
Answer:
C) cos θ

Question 220.
sin (180 – θ) = ………………
A) cos θ
B) sin θ
C) tan θ
D) 0
Answer:
B) sin θ

Question 221.
cos (270 – θ)
A) cos θ
B) sin θ
C) – sin θ
D) none
Answer:
C) – sin θ

Question 222.
tan (360 – θ) = ……………
A) -tan θ
B) tan θ
C) sec θ
D) cos θ
Answer:
A) -tan θ

Question 223.
cosec (270 – θ) = ……………..
A) sec θ
B) -sec θ
C) tan θ
D) none
Answer:
C) tan θ

Question 224.
sec (90 + θ) = …….
A) tan θ
B) cosec θ
C) – cos θ
D) – cosec θ
Answer:
D) – cosec θ

Question 225.
cos 240° = ……………..
A) \(\frac{-1}{2}\)
B) -1
C) \(\frac{2}{3}\)
D) -3
Answer:
A) \(\frac{-1}{2}\)

Question 226.
sin 420° = ………….
A) – \(\frac{\sqrt{3}}{2}\)
B) 1
C) \(\frac{\sqrt{3}}{2}\)
D) \(\frac{2}{\sqrt{2}}\)
Answer:
C) \(\frac{\sqrt{3}}{2}\)

Question 227.
tan 750° = ……………..
A) \(\frac{-1}{\sqrt{3}}\)
B) \(\sqrt{3}\)
C) -1
D) \(\frac{1}{\sqrt{3}}\)
Answer:
D) \(\frac{1}{\sqrt{3}}\)

Question 228.
cosec 300° = ………………
A) \(\frac{-2}{\sqrt{3}}\)
B) \(\frac{1}{\sqrt{3}}\)
C) \(\frac{-1}{2}\)
D) –\(\frac{1}{\sqrt{3}}\)
Answer:
A) \(\frac{-2}{\sqrt{3}}\)

Question 229.
sec 240° = …………..
A) 3
B) -1
C) 2
D) -2
Answer:
D) -2

Question 230.
sin² 47° + sin² 43° = ……………
A) 1
B) -1
C) 3
D) none
Answer:
A) 1

Question 231.
If cosec θ – cot θ = 4, then cosec θ + cot θ = ……………….
A) 1
B) \(\frac{1}{2}\)
C) \(\frac{-1}{4}\)
D) \(\frac{1}{4}\)
Answer:
D) \(\frac{1}{4}\)

Question 232.
tan θ in terms of cosec θ = ………………….
A) \(\frac{1}{\sqrt{\ cosec ^2 \theta-1}}\)
B) \(\frac{1}{\sqrt{1+\ cosec \theta}}\)
C) \(\frac{1}{1+\tan ^2 \theta}\)
D) none
Answer:
A) \(\frac{1}{\sqrt{\ cosec ^2 \theta-1}}\)

Question 233.
\(\frac{\ cosec ^2 \theta}{\cot \theta}\) – cot θ = …………………
A) cot θ
B) sec θ
C) tan θ
D) none
Answer:
C) tan θ

Question 234.
\(\frac{1-\tan ^2 30^{\prime \prime}}{1+\tan ^2 30^{\prime \prime}}\) = ………………
A) -2
B) \(\frac{-1}{2}\)
C) 1
D) \(\frac{1}{2}\)
Answer:
D) \(\frac{1}{2}\)

Question 235.
\(\frac{1}{\sec ^2 A}+\frac{1}{\ cosec ^2 A}\) = ………………
A) -1
B) 1
C) 3
D) 4
Answer:
B) 1

Question 236.
tan θ. cot θ = sec θ. x; then x = …………………….
A) cos θ
B) – cos θ
C) tan θ
D) none
Answer:
A) cos θ

Question 237.
If sin (A + B) = \(\frac{\sqrt{3}}{2}\) ; cos B = \(\frac{\sqrt{3}}{2}\) then A = ……………….
A) 70°
B) 45°
C) 60°
D) 30°
Answer:
D) 30°

Question 238.
cos \(\left(\frac{3 \pi}{2}+\theta\right)\) = …………….
A) tan θ
B) cos θ
C) -sin θ
D) sin θ
Answer:
D) sin θ

Question 239.
sec θ + tan θ = \(\frac{1}{2}\); then sin θ = …………….
A) \(\frac{2}{13}\)
B) \(\frac{1}{13}\)
C) \(\frac{12}{13}\)
D) \(\frac{13}{2}\)
Answer:
C) \(\frac{12}{13}\)

Question 240.
If sec = cosec θ; then the value of θ in radians = …………………
A) \(\frac{\pi^c}{2}\)
B) \(\frac{\pi^c}{4}\)
C) \(\frac{\pi^c}{3}\)
D) \(\frac{\pi^c}{12}\)
Answer:
B) \(\frac{\pi^c}{4}\)

Question 241.
Maximum value of sin θ + cos θ = ……………..
A) 3
B) \(\sqrt{3}\)
C) 2
D) \(\sqrt{2}\)
Answer:
D) \(\sqrt{2}\)

Question 242.
Maximum value of cos θ = …………………
A) 1
B) -1
C) 2
D) 0
Answer:
A) 1

Question 243.
Minimum and maximum value of tan θ = ……………
A) (-∞, ∞)
B) (- ∞, 0)
C) (3, 2)
D) (1, -1)
Answer:
A) (-∞, ∞)

Question 244.
\(\frac{\sin ^4 \theta-\cos ^4 \theta}{\sin ^2 \theta-\cos ^2 \theta}\) = ……………….
A) 2
B) -1
C) 1
D) none
Answer:
C) 1

Question 245.
cos 0° + sin 90° + \(\sqrt{3}\) cosec 60° = ………………
A) 0
B) -1
C) 3
D) 4
Answer:
D) 4

Question 246.
\(\left|\begin{array}{l}
\tan \theta \sec \theta \\
\sec \theta \tan \theta
\end{array}\right|\) = …………………
A) -1
B) -4
C) 1
D) none
Answer:
C) 1

Question 247.
If cosec θ + cot θ = 3, then cosec θ – cot θ = …………….
A) \(\frac{1}{2}\)
B) \(\frac{1}{3}\)
C) \(\frac{-1}{3}\)
D) none
Answer:
B) \(\frac{1}{3}\)

Question 248.
\(\frac{\tan \theta}{\sqrt{1+\tan ^2 \theta}}\) = ……………..
A) -cos θ
B) -sin θ
C) sin θ
D) sin² θ
Answer:
C) sin θ

Question 249.
\(\frac{\sqrt{1-\cos ^2 \theta}}{\cos \theta}\) = ……………
A) -cot θ
B) tan θ
C) sec θ
D) none
Answer:
B) tan θ

Question 250.
x = 2 cosec θ; y = 2 cot θ; x² – y² = …………….
A) 4
B) -1
C) -3
D) 2
Answer:
A) 4

Question 251.
\(\sqrt{\sec ^2 A+\ cosec ^2 A}\) = ……………….
A) tan A – cos A
B) tan A + cos A
C) 1
D) tan A + cot A
Answer:
D) tan A + cot A

Question 252.
sin 81° = ……………….
A) cos 9°
B) cos 20°
C) tan 9°
D) none
Answer:
A) cos 9°

Question 253.
\(\frac{\sqrt{\sec ^2 \theta-1}}{\sec \theta}\) = ………………
A) – tan θ
B) cos θ
C) sin θ
D) none
Answer:
C) sin θ

Question 254.
If sin A = \(\frac{1}{\sqrt{2}}\); then tan A = ……………
A) 4
B) 3
C) -1
D) 1
Answer:
D) 1

Question 255.
sin 225° = ………………
A) \(\frac{-1}{\sqrt{2}}\)
B) \(\sqrt{2}\)
C) \(\frac{-1}{2}\)
D) 1
Answer:
A) \(\frac{-1}{\sqrt{2}}\)

Question 256.
cos (x – y) = ………………
A) cos x cos y + sin x sin y
B) cos x – sin x sin y
C) cos x cos y – 1
D) all
Answer:
A) cos x cos y + sin x sin y

Question 257.
\(\frac{1}{1-\sin \theta}+\frac{1}{1+\sin \theta}\) = ………………..
A) sec⁴ θ
B) sec θ
C) \(\frac{\sec ^2 \theta}{2}\)
D) 2 sec² θ
Answer:
D) 2 sec² θ

Question 258.
sin⁴ θ – cos⁴ θ = ………………..
A) 2 sec² θ – 1
B) sec² θ + 1
C) sec² θ – 3
D) none
Answer:
A) 2 sec² θ – 1

Question 259.
tan θ is not defined if θ = ……………..
A) 0°
B) 70°
C) 90°
D) 20°
Answer:
C) 90°

Question 260.
If cosec θ = \(\frac{25}{7}\) ; then cot θ = …………….
A) \(\frac{4}{7}\)
B) \(\frac{7}{24}\)
C) \(\frac{4}{23}\)
D) \(\frac{24}{7}\)
Answer:
D) \(\frac{24}{7}\)

Question 261.
tan 26°. tan 64° = …………..
A) 1
B) -1
C) 3
D) 7
Answer:
A) 1

Question 262.
If tan 2A = cot (A – 18°) where 2A is an acute angle then A = ……………
A) 116°
B) 20°
C) 16°
D) 36°
Answer:
D) 36°

Question 263.
sin(90 – Φ) = ……………
A) cos Φ
B) sin Φ
C) – cos Φ
D) 0
Answer:
A) cos Φ

Question 264.
In ∆ABC, sin \(\left(\frac{B+C}{2}\right)\) = ………………
A) cos \(\frac{A}{2}\)
B) cos \(\frac{C}{2}\)
C) tan \(\frac{A}{2}\)
D) 1
Answer:
A) cos \(\frac{A}{2}\)

Question 265.
\(\frac{\sec 35^{\prime}}{\ cosec 55^{\prime \prime}}\) = …………………
A) -3
B) 8
C) 4
D) 1
Answer:
D) 1

Question 266.
sin \(\frac{\pi^c}{4}\) + cos 45° = ……………….
A) 2
B) \(\sqrt{2}\)
C) -1
D) 0
Answer:
B) \(\sqrt{2}\)

Question 267.
sec 0° = ………………..
A) -1
B) 1
C) 0
D) 7
Answer:
B) 1

Question 268.
sec θ – tan θ = \(\frac{1}{n}\) then sec θ + tan θ = ………………
A) -n
B) -1
C) n
D) none
Answer:
C) n

Question 269.
If 3 tan A = 4 then cos A = ……………..
A) \(\frac{1}{2}\)
B) \(\frac{1}{3}\)
C) \(\frac{1}{7}\)
D) none
Answer:
D) none

Question 270.
From the figure, sin C = …………..

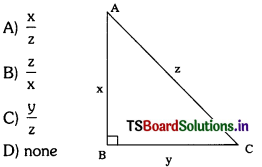
Answer:
(A)

Question 271.
cos² θ = ……………….
A) 1 + sin² θ
B) 1 – sin² θ
C) 1 – sin θ
D) 1 + cos θ
Answer:
B) 1 – sin² θ

Question 272.
sec θ is not defined if θ = …………………
A) 0°
B) 90°
C) 30°
D) 45°
Answer:
B) 90°

Question 273.
(1 + tan² 60)² = ………………..
A) 1
C) 16
B) 10
D) 12
Answer:
B) 10

Question 274.
Reciprocal of cot A = ……………..
A) sin A
B) sin² A
C) sec² A
D) tan A
Answer:
D) tan A

Question 275.
sin A = cos B then A + B = …………….
A) 20°
B) 70°
C) 90°
D) none
Answer:
C) 90°

Question 276.
Trigonometry was introduced by ……………….
A) Cantor
B) Cayley
C) Hipparchus
D) none
Answer:
C) Hipparchus

Question 277.
If tan A = \(\frac{3}{4}\) then sec² A – tan² A = ………………..
A) 4
B) 3
C) -1
D) 1
Answer:
D) 1

Question 278.
tan² Φ sec² Φ = ………………..
A) -1
B) 1
C) 3
D) 0
Answer:
A) -1

Question 279.
In the figure, tan X = ……………..

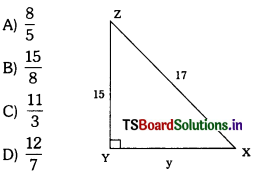
Answer:
(B)

Question 280.
If sin θ = cos 66° then θ = ………………
A) 30°
B) 24°
C) 36°
D) 48°
Answer:
B) 24°

Question 281.
If sec = \(\frac{\mathrm{X}}{\cos \theta}\) then X = ……………….
A) \(\frac{1}{2}\)
B) 0
C) -1
D) 1
Answer:
D) 1

Question 282.
Which of the following is not the value of sin θ ?
A) 1
B) \(\frac{3}{4}\)
C) \(\frac{4}{3}\)
D) \(\frac{1}{2}\)
Answer:
B) \(\frac{3}{4}\), C) \(\frac{4}{3}\)

Question 283.
Which of the following is not correct?
A) cos 0°
B) sin 90° = 0
C) tan 45° = cot 45°
D) both A and B
Answer:
D) both A and B

Question 284.
(sec A + tan A) (1 = sin A) = ……………….
A) sec A
B) sin A
C) cosec A
D) cos A
Answer:
D) cos A

Question 285.
If sec θ + tan θ = X then cosec θ = ……………..

Answer:
(C)

Question 286.
From the adjacent figure, \(\frac{c}{a}=\frac{29}{21}\) represents

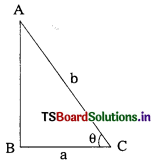
A) cos θ
B) cosec θ
C) cot θ
D) sin θ
Answer:
B) cosec θ

Question 287.
From the adjacent figure, value of ‘sin²A + cos²A’

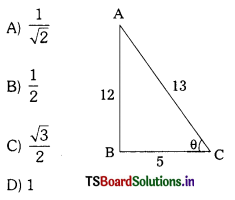
Answer:
(D)

Solving these TS 10th Class Maths Bits with Answers Chapter 2 Sets Bits for 10th Class will help students to build their problem-solving skills.

Sets Bits for 10th Class

Question 1.
The symbol for a null set is
A) ∈
B) ∪
C) ϕ
D) \(\not \subset\)
Answer:
C) ϕ

Question 2.
C = {x : x is a circle in a given plane} is
A) finite set
B) infinite set
C) universal set
D) void set
Answer:
B) infinite set

Question 3.
Which of the following set is infinite?
A) The set of natural numbers ≤ 100
B) The set of even natural numbers between 50 and 100.
C) The set of points on a circle.
D) The set of prime numbers between 10 and 50.
Answer:
C) The set of points on a circle.

Question 4.
The number of elements in the set D = {x : x is a day of the week} is
A) 6
B) 4
C) 5
D) 7
Answer:
D) 7

Question 5.
The symbol for “implies” is
A) ⇒
B) ⇔
C) ⊂
D) \(\supset\)
Answer:
A) ⇒

Question 6.
If A = {1, 2, 3} the number of subsets of A is
A) 3
B) 8
C) 9
D) 6
Answer:
B) 8

Question 7.
Two sets A and B are said to be disjoint if
A) A∪B = ϕ
B) A – B = ϕ
C) B – A = ϕ
D) A ∩ B = ϕ
Answer:
D) A ∩ B = ϕ

Question 8.
For every set A, A ∩ ϕ =
A) ϕ
B) A
C) 0
D) 1
Answer:
A) ϕ

Question 9.
For every set A, A ∩ A =
A) 1
B) 0
C) A
D) ϕ
Answer:
C) A

Question 10.
If A and B are two sets, then x ∈ A ∩ B ⇒
A) x ∈ A or x ∈ B
B) x ∈ A and x ∈ B
C) x ∈ A and x \(\notin\) B
D) x\(\notin\)A and x ∈ B
Answer:
B) x ∈ A and x ∈ B

Question 11.
If A and B are two sets, then x ∈ A∪B ⇒
A) x ∈A and x\(\notin\)B
B) x\(\notin\)A and x∈B
C) x ∈ A or x ∈ B
D) x\(\notin\)A and x\(\notin\)B
Answer:
C) x ∈ A or x ∈ B

Question 12.
If A and B are two sets, then x ∈ A – B ⇒
A) x ∈ A or x ∈ B
B) x ∈ A and x ∈ B
C) x\(\notin\)A and x∈B
D) x\(\notin\)A and x\(\notin\)B
Answer:
D) x\(\notin\)A and x\(\notin\)B

Question 13.
If V = {a, e, i, o, u} and B = {a, i, k, u} then V – B =
A) {a, e, i, o, u}
B) {a, e, o, u}
C) {e, o}
D) {a, e, o}
Answer:
C) {e, o}

Question 14.
The shaded portion in the adjacent figure represents

A) A ∩ B
B) A ∪ B
C) A – B
D) A ⊂ B
Answer:
B) A ∪ B

Question 15.
The shaded portion in the adjacent figure represents

A) A ∩ B
B) A ∪ B
C) A ⊂ B
D) B ⊂ A
Answer:
A) A ∩ B

Question 16.
The shaded portion in the adjacent figure represents
A) A ⊂ B
(B) B ⊂ A
(C) B – A
(D) A – B
Answer:
(C) B – A

Question 17.
Which of the following sets are equal ?
A) E = {1, 0}, H = {a, b)
B) A = {0, a}, C = {b, 0}
C) D = {4, 8, 12}, F = {8, 12, 4}
D) G = {1, 5, 7, 11}, I = {1, 2, 3, 4}
Answer:
C) D = {4, 8, 12}, F = {8, 12, 4}

Question 18.
If A = {1, 3} and B = {1, 5, 9} then A – B =
A) {3}
B) {1}
C) {5, 9}
D) {1, 3, 5, 9}
Answer:
A) {3}

Question 19.
Which of the following sets in infinite ?
A) {x : x ∈ N and (x – 1 )(x – 2) = 0}
B) {x : x ∈ N and x² = 9}
C) {x : x ∈ N and 2x – 1 = 0}
D) {x : x ∈ N and x is odd}
Answer:
D) {x : x ∈ N and x is odd}

Question 20.
Which of the following sets finite ?
A) {x : x ∈ N and x is prime}
B) {x : x ∈ N and x is an even number less than 20}
C) {x : x² = 4 and x is an odd integer}
D) {x : x² is an even prime greater than 2}
Answer:
B) {x : x ∈ N and x is an even number less than 20}

Question 21.
Set of human being that reside on moon is ………
A) finite set
B) null set
C) infinite set
D) universal set
Answer:
B) null set

Question 22.
Which of the following is true in the following venn diagram ……..

A) A ∪B = ϕ
B) A ∪ B = µ
C) A ∩ B = µ
D) A ∩ B = ϕ
Answer:
D) A ∩ B = ϕ

Question 23.
Which of the following is an example for finite set
A) {x / x ∈ N and x² = 9}
B) Set of rational numbers in between 2 and 3
C) Multiples of even primes
D) Set of all primes
Answer:
A) {x / x ∈ N and x² = 9}

Question 24.
The number of subsets of the null set ϕ is ……….
A) 0
B) 1
C) 3
D) 4
Answer:
B) 1

Question 25.
If A = (a, b, c, d), how many subsets does the set ‘A’ have
A) 5
B) 6
C) 16
D) 65
Answer:
C) 16

Question 26.
A = {1, 2, 3, 7, 8}; B = {4, 5, 6, 7} find A ∩ B
A) {1, 2, 3, 4, 5, 6, 7, 8}
B) 7
C) ϕ
D) {7, 8}
Answer:
B) 7

Question 27.
n(A) = 14; n (B) = 11; n(A ∩ B) = 19 then n(A ∪B) = ……
A) 6
B) 16
C) 22
D) 25
Answer:
A) 6

Question 28.
The shaded area in the figure shows.

A) A – B
B) B – A
C) A ∆ B
D) (A ∪ B) (A ∩ B)
Answer:
C) A ∆ B

Question 29.
If ‘A’ and ‘B’ are two sets such that A ⊂ B then A ∪ B =
A) A
B) B
C) A ∩ B
D) None
Answer:
B) B

Question 30.
If ‘A’ and ‘B’ are disjoint sets then n(A ∩ B) = …….
A) 1
B) ϕ
C) 0
D) { }
Answer:
D) { }

Question 31.
Match the following :
Group -1 Group – II

Answer:
A) L → (iii), M → (i), N → (ii), O → (iv)
B) L → (i), M → (ii), N → (iii), O → (iv)
C) L → (iii), M → (i), N → (iv), O → (ii)
D) L → (iii), M → (ii), N → (ii), O → (iv)
Answer:
A) L → (iii), M → (i), N → (ii), O → (iv)

Question 32.
A ∩ ϕ = ………
A) A
B) ϕ
C) ϕ – A
D) { }
Answer:
A) A

Question 33.
Let A = {1, 2, {1}, {1, 2}, 3, 4}, then which of the following is true ?
A) {3} ∈ A
B) {1, 3} ∈ A
C) {1, 2} ∈ A
D) None
Answer:
C) {1, 2} ∈ A

Question 34.
Which of the following is false ?
A) {1} ∈ A
B) {1, 2} ⊆ A
C) {1, 2} ∈ A
D) None
Answer:
D) None

Question 35.
If A = {1, 2, 3, 4}, B = {2, 4,6, 8} then A – B =
A) {6, 8}
B) {1, 2}
C) {1, 3}
D) None
Answer:
C) {1, 3}

Question 36.
If n(A ∪ B) = 8, n (A) = 6, n(B) = 4 then n (A ∩ B) = …….
A) 2
B) 4
C) 6
D) 8
Answer:
A) 2

Question 37.
Let A, B are two sets such that n(A) = 5, n(B) = 7 then the maximum number of elements in A ∪ B is
A) 7
B) 9
C) 12
D) None
Answer:
C) 12

Question 38.
If A = {1, 2, 3, 4 }, then the cardinality of set A is
A) 3
B) 4
C) 5
D) 6
Answer:
B) 4

Question 39.
If A, B are disjoint sets such that n(A) = 4 and n(A∪B) = 7, then n(B) = ……..
A) 4
B) 11
C) 3
D) 20
Answer:
C) 3

Question 40.
An object of a set is called
A) Subject
B) Number
C) Alphabet
D) Element
Answer:
D) Element

Question 41.
The symbol used for ‘belongs to’ is
A) ⊂
B) ⊆
C) ∈
D) \(\notin\)
Answer:
C) ∈

Question 42.
The set of all real numbers is
A) ϕ
B) Finite set
C) Infinite set
D) None
Answer:
C) Infinite set

Question 43.
The number of elements in the empty set is
A) 0
B) ϕ
C) 1
D) ∞
Answer:
A) 0

Question 44.
If A = {1, 2, 2, 1, 3, 4, 3, 4}, then n(A) =
A) 0
B) 4
C) 8
D) 20
Answer:
B) 4

Question 45.
If A ⊂ B, then A ∪ B = ………..
A) ϕ
B) μ
C) A
D) B
Answer:
D) B

Question 46.
A ∩ ϕ = ………
A) ϕ
B) µ
C) A
D) A^c
Answer:
A) ϕ

Question 47.
The German mathematician who developed the theory of sets ………
A) Bhaskara
B) Cayley
C) George Cantor
D) None
Answer:
C) George Cantor

Question 48.
A set is a …….. of objects.
A) well defined collection
B) collection
C) elements
D) none
Answer:
A) well defined collection

Question 49.
The objects in the set are called ……….. of the set.
A) elements
B) members
C) both A & B
D) false
Answer:
C) both A & B

Question 50.
Roster form of the set of natural numbers less then 6 is ……….
A) {4, 5, 6}
B) {1, 2, 3}
C) {2, 3, 4}
D) {1,2, 3, 4, 5}
Answer:
D) {1,2, 3, 4, 5}

Question 51.
The set formed from the letters of the word “SCHOOL” is ……
A) {S, O, H}
B) {H, O, L}
C) {S, C, H}
D) {S, C, H, O, L}
Answer:
D) {S, C, H, O, L}

Question 52.
Roster form is also called ……. form.
A) list
B) set
C) number
D) none
Answer:
A) list

Question 53.
Describing a set by same property common to all its elements is called …….. or ………
A) set builder form
B) rule form
C) both A & B
D) none
Answer:
C) both A & B

Question 54.
A = {2, 4, 6, 8, 10} then its rule form is ……..
A) A = {x² / x ∈ N}
B) A = {2x / x is odd, x ≤ 20}
C) A = {x³ / x ∈ N}
D) A = {x / x is an even number, x ≤ 10}
Answer:
D) A = {x / x is an even number, x ≤ 10}

Question 55.
If B = {1, 7, 2, 0, 6} then n(B) = …….
A) 5
B) 6
C) 7
D) 9
Answer:
A) 5

Question 56.
n (ϕ) = ……….
A) n
B) ϕ
C) 0
D) 9
Answer:
C) 0

Question 57.
Every set is ………. of itself.
A) subset
B) proper set
C) power set
D) none
Answer:
A) subset

Question 58.
If A ⊂ B and A ≠ B then ‘A’ is called the ……… of B.
A) subset
B) proper subset
C) power set
D) none
Answer:
B) proper subset

Question 59.
In set Builder form, the letter x denotes any …….. that belongs to the set.
A) constant
B) element
C) arbitrary element
D) none
Answer:
C) arbitrary element

Question 60.
In the rule form, the sland bar stands for ……….
A) subset
B) such that
C) belongs
D) all
Answer:
B) such that

Question 61.
2 is ……….. of set of natural numbers.
A) power
B) proper
C) subset
D) an element
Answer:
D) an element

Question 62.
-3 is …….. of the set of whole numbers.
A) proper
B) power
C) element
D) not an element
Answer:
D) not an element

Question 63.
0 ……….. to set of whole numbers.
A) does not belong
B) belong
C) subset
D) power set
Answer:
B) belong

Question 64.
A = {1, 2, 7, 10} then 7 …….. A.
A) ⊂
B) ∈
C) \(\notin\)
D) none
Answer:
B) ∈

Question 65.
A = {1, 2, 7,10} then 4 …… A.
A) \(\supset\)
B) ∈
c) ⊂
D) \(\notin\)
Answer:
D) \(\notin\)

Question 66.
“0 does not belong to the set of natural numbers” we write the statement symbolically as ………..
A) 0 \(\notin\) N
B) 0 ∈ N
C) 0 ⊂ N
D) none
Answer:
A) 0 \(\notin\) N

Question 67.
Set builder form of D = {1, \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\), \(\frac{1}{5}\), \(\frac{1}{6}\)} is ………..

Answer:
B) k = {\(\frac{x}{x}\) = \(\frac{1}{n^3}\), n ∈ N}

Question 68.
B = {\(\frac{x}{x}\) + 3 = 6}, B = …………
A) {0, 1, 3}
B) {7, 0}
C) {0, 3}
D) {3}
Answer:
D) {3}

Question 69.
A ……….. is a set with no elements in it.
A) inifinite set
B) finite set
C) null set
D) none
Answer:
C) null set

Question 70.
The null set is sometimes denoted as …………
A) empty set
B) void set
C) both A & B
D) none
Answer:
C) both A & B

Question 71.
Empty set is denoted by ………..
A) {ϕ}
B) {0}
C) N
D) ϕ
Answer:
D) ϕ

Question 72.
{0} is a set contains the element
A) 0
B) ϕ
C) {ϕ}
D) none
Answer:
A) 0

Question 73.
A set with only are element is known as ……. set.
A) Double
B) Singleton
C) Tri
D) None
Answer:
B) Singleton

Question 74.
Number of elements in a singleton set is …….
A) 0
B) 2
C) 7
D) 1
Answer:
D) 1

Question 75.
A = {x/x + 4 = 4} then A = ……
A) {4}
B) {0}
C) {0, 4}
D) {0, 7}
Answer:
B) {0}

Question 76.
B = {x / x ∈ N and x < 1000} is a …….. set.
A) finite
B) infinite
C) singleton
D) empty
Answer:
A) finite

Question 77.
If in two sets A and B, every element of A is in B and every element of B is in A. Then we write it as ………..
A) A ≠ B
B) A < B C) A > B
D) A = B
Answer:
D) A = B

Question 78.
A ≠ B means, set A and B do not contains same elements. This is
A) false
B) true
C) can’t be determined
D) none
Answer:
B) true

Question 79.
The number of elements in a set is called the ……. of the set.
A) cardinal
B) ordinal
C) true
D) all the above
Answer:
A) cardinal

Question 80.
If B = {1, 7, 2, 0, 6} then n(B) = ……..
A) 7
B) 0
C) 6
D) 5
Answer:
D) 5

Question 81.
If every element of A is also an element of B then we write this as ……
A) A < B
B) B < A
C) A ⊂ B
D) B ⊂ A
Answer:
C) A ⊂ B

Question 82.
If A = {1, 2, 3} and B = {1, 2, 3, 4} then we say A is a …… of B.
A) subset
B) superset
C) equal
D) none
Answer:
A) subset

Question 83.
In the above question B is ……… of A.
A) subset
B) superset
C) superset
D) all the above
Answer:
C) superset

Question 84.
A is not a subset of B if A contains ……… which is not in B.
A) equal
B) at least one element
C) 2
D) none
Answer:
B) at least one element

Question 85.
{x/x is a student of your school) is in ………. form.
A) Roster
B) Singleton
C) Set Builder
D) None
Answer:
C) Set Builder

Question 86.
{2, 4, 6, 8, 10} is an example of …….. set.
A) finite
B) infinite
C) singleton
D) two
Answer:
A) finite

Question 87.
{x/x is a natural number} is a ……….. set.
A) finite
B) infinite
C) singleton
D) none
Answer:
B) infinite

Question 88.
{x/x≠x} is a ……. set.
A) empty
B) infinite
C) singleton
D) none
Answer:
A) empty

Question 89.
A = {1, 2, 3}, B = {3, 4, 5} then A ∩ B = ……….
A) 3
B) {1, 2}
C) {4, 5}
D) {3}
Answer:
D) {3}

Question 90.
A = {a, b, c}, B = {c, a, b} then …………
A) A≠B
B) A = B
C) A ⊂ B
D) none
Answer:
B) A = B

Question 91.
A = {1, 2, 7}, B = {2, 1} then ………
A) A ⊂ B
B) B ⊂ A
C) A = B
D) none
Answer:
B) B ⊂ A

Question 92.
A ⊂ B then A – B = ……..
A) ⊂
B) B
C) A
D) ϕ
Answer:
D) ϕ

Question 93.
A – ϕ = ……….
A) A
B) ϕ
C) μ
D) none
Answer:
A) A

Question 94.
A ∪ A’ = ………..
A) A
B) ϕ
C) A
D) A’
Answer:
B) ϕ

Question 95.
μ’ = …………
A) A
B) μ
C) ϕ
D) none
Answer:
C) ϕ

Question 96.
A = {1, 2, 3}, B = {12, 0, 5} then A – B = ………
A) B
B) A
C) {5}
D) none
Answer:
B) A

Question 97.
A ∪ ϕ = ………….
A) A
B) B
C) ϕ
D) μ
Answer:
A) A

Question 98.
ϕ’ = ………..
A) B
B) A
C) μ
D) 0
Answer:
B) A

Question 99.
{2, 6, 10} ∩ {8, 9, 11, 12, 13} = ………..
A) {2}
B) {1, 2}
C) {13, 1}
D) ϕ
Answer:
D) ϕ

Question 100.
n(A) = 4 then n(p(A)) = …….
A) 12
B) 13
C) 15
D) 16
Answer:
D) 16

Question 101.
A – (A – B) = ……….
A) A ∩ B
B) ϕ
C) A ∪ B
D) B
Answer:
A) A ∩ B

Question 102.
(A’)’ = …………
A) A’
B) A
C) ϕ
D) none
Answer:
B) A

Question 103.
If A ⊂ B, then A – B = ………..
A) μ
B) B
C) A
D) ϕ
Answer:
D) ϕ

Question 104.
If A ⊂ B then A ∪ (B – A) = ………
A) B
B) A
C) ϕ
D) none
Answer:
A) B

Question 105.
W – {0} = ……..
A) R
B) A
C) Z
D) Q
Answer:
B) A

Question 106.
If A ⊂ B, B ⊂ C then ………
A) B = C
B) A = B
C) C ⊂ A
D) A ⊂ C
Answer:
D) A ⊂ C

Question 107.
Cardinal number of null set is ……
A) 4
B) ϕ
C) 0
D) none
Answer:
C) 0

Question 108.
A’ – B’ = ……..
A) A – B’
B) A’ – B
C) B – A
D) A – B
Answer:
C) B – A

Question 109.
If A = {1, 2, 3}, B = {3, 4, 5} then A ∆ B = ……….
A) {0}
B) {1, 2}
C) {7}
D) none
Answer:
D) none

Question 110.
A = ϕ, B = ϕ then A ∪ B = …………..
A) μ
B) ϕ
C) cant be determined
D) None
Answer:
B) ϕ

Question 111.
A ∩ B = ϕ then n (A ∩ B) = ………..
A) 7
B) 9
C) 3
D) none
Answer:
D) none

Question 112.
A ∪ B = A ∩ B then ……………….
A) A = B
B) A ≠ B
C) A ⊂ B
D) B ⊂ C
Answer:
A) A = B

Question 113.
μ’ = ϕ is called ……….. law.
A) Identity
B) Associative
C) Inverse
D) Complementary
Answer:
D) Complementary

Question 114.
A’ = B then A ∪ B = …….
A) A
B) μ
C) ϕ
D) none
Answer:
D) none

Question 115.
ϕ ∆ ϕ = ………..
A) μ
B) ϕ
C) {0}
D) none
Answer:
B) ϕ

Question 116.
A ∪ A = A is called ……… law.
A) idempotent
B) inverse
C) complete
D) identity
Answer:
A) idempotent

Question 117.
A ∪ B = B if …………
A) A \(\supset\)
B) A ⊂ B
C) A = B
D) none
Answer:
B) A ⊂ B

Question 118.
A = ϕ, B = ϕ then A ∩ B = ………
A) {6, 1}
B) {0}
C) μ
D) ϕ
Answer:
D) ϕ

Question 119.
n(A) = 10, n(B) = 4, n(A∩B) = 2 then n(A∪B) = ……….
A) 11
B) 16
C) 10
D) 12
Answer:
D) 12

Question 120.
(A ∪ B)’ = ………..
A) A’ ∩ B’
B) A’∪B
C) A’ ∩B
D) A ∩ B
Answer:
A) A’ ∩ B’

Question 121.
(A – B) ∪ {A – C) = ……..
A) (A – B) ∪ C
B) (A – B) ∩ C
C) (A – B) – C
D) none
Answer:
D) none

Question 122.
n(A) = 3 then number of proper subsets of A is ………
A) 10
B) 9
C) 7
D) 8
Answer:
C) 7

Question 123.
A ∩ B = ϕ then B ∩ A’ = ……….
A) μ
B) A
C) ϕ
D) B
Answer:
D) B

Question 124.
A ∪ (B ∩ C) = ……..
A) (A ∪ B) ∩ (A ∪ C)
B) (A∩B)∪(A∩C)
C) (A∪B)∩C
D) none
Answer:
A) (A ∪ B) ∩ (A ∪ C)

Question 125.
A = {all primes less than 20}
B = {all whole numbers less than 10} then
A∩B = ………….
A) {2, 3, 5, 7, 10}
B) {2, 8, 9}
C) {2, 3, 5, 7}
D) {2, 4, 6}
Answer:
C) {2, 3, 5, 7}

Question 126.
In the above problem A – B = ……….
A) {11, 13, 17, 19}
B) {1, 3, 7, 19}
C) {13, 17, 10}
D) none
Answer:
A) {11, 13, 17, 19}

Question 127.
N(A∪B) = 51, n(A) = 20, n(A∩B) = 13, then n(B) =
A) 80
B) 44
C) 40
D) 39
Answer:
B) 44

Question 128.
The identity element under union of sets of ………..
A) μ
B) {0}
C) {ϕ}
D) none
Answer:
C) {ϕ}

Question 129.
μ ∪ ϕ = ………..
A) ϕ
B) {0}
c) {ϕ}
D) μ
Answer:
D) μ

Question 130.

This venn – diagram represents ……..
A) A ∩ B
B) A – B
C) A ∪ B
D) A Δ B
Answer:
A) A ∩ B

Question 131.
N ∩ W = ……
A) Q
B) W
C) N
D) {0}
Answer:
C) N

Question 132.
If A and B are disjoint sets then n (A ∪ B) = ………
A) n(A) – n(B)
B) n(A) + n(B)
C) \(\frac{n(A)}{n(B)}\)
D) none
Answer:
B) n(A) + n(B)

Question 133.
From the venn diagram A ∪ B = ………..

A) {1, 2, 3}
B) {1, 2, 4, 5}
C) {6, 7, 10}
D) none
Answer:
D) none

Question 134.
Identity element under intersection of sets is ………
A) {0}
B) μ
C) ϕ
D) none
Answer:
B) μ

Question 135.
Which of the following is true ?
A) A – B ≠ B – A
B) A ∪ ϕ = A
C) μ’ = μ
D) all
Answer:
A) A – B ≠ B – A

Question 136.
A is the set of factors of 12. Which are of the following is not a member of A ?
A) 9
B) 10
C) 12
D) 5
Answer:
D) 5

Question 137.
If the number of proper subsets of a given set is 31 then the set contains elements.
A) 7
B) 6
C) 5
D) 10
Answer:
C) 5

We are offering TS 10th Class Maths Notes Chapter 2 Sets to learn maths more effectively.

TS 10th Class Maths Notes Chapter 2 Sets

→ A set is a well-defined collection of objects.
E.g.: The collection of instruments in a Mathematics Instrument Box.
The collection of districts in Andhra Pradesh.

→ An object belonging to a set is known as an element of the set.
For example, if B = {1, 2, 3, 4, 5}
1, 2, 3, 4, 5 are the elements of set B.

→ We use upper case letters A, B, C,…., X, Y, Z etc., to denote a set while the elements of a set are represented by small letters a, b, c,…. etc.

→ If ‘x’ is an element of set A.
We say that ‘x’ belongs to ‘A’ and we write xe A.
If Y is not element of set B.
We say that ‘x does not belongs to B’ and we write xg B.

→ A set can be represented in two ways.

• Roster (or) Tabular form
• Set builder form.

→ Roster form :

• In roster form, all the elements of a set are list the elements being separated by commas and are enclosed within braces (curly brackets).
• For example, the set of all even positive integers less than 20 is described in the roaster form as {2, 4, 6, 8, 10,12,14,16,18}.
• The set of all vowels in english alphabet can be written as V = {a, e, i, o, u}
• It may be noted while writing the set in roaster form, an element is not generally repeated.
• For example, the set of letters forming the word ‘FOLLOWER’ is written as {F, O, L, W, E, R}.

→ Set builder form :
In set builder form, we use a symbol x (or any other symbol like the letters y, z etc.,) for the elements of the set. After that we write either a colon or a vertical line. Then we write the characteristic property possessed by the elements of the set. Lastly we enclose the description within braces.
Let A = (2, 3, 5, 7,11,13,17}. This is the set of all prime numbers less than 19. It can be represented in set builder form as {x/x is a prime number less than 19}

→ Null set:
A set which does not contain any element is called the empty set or the null set or the void set. The empty/ null set is denoted by the symbol Φ or {}.
E.g.: Let P = {x : 1 < x < 2 and x e N}
P is an empty set because there is no natural number between 1 and 2.

→ Finite set:
A set is called a finite set if it is possible to count the number of elements in it.
C = {x, y, z} and A = {1, 2, 3, 4, 5}

→ Infinite set:
A set is called an infinite set if the number of elements in it is not finite (i.e.,) we cannot count the number of elements in it.
For example, E = {x : x is a multiple of 3}
0 = {x/x is an odd natural number}

→ Cardinal number of a set:
The number of elements in a set is called the cardinal number of the set.
If A = {1, 2, 3, 4, 5}, n(A) = 5 If B = {5, 6, 7}, n(B) = 3 But n(Φ) = 0

→ Universal set; subset:
If we consider all the students in a school as universal set, then the students in any class of that school will be a subset of it.
The subset is denoted by the symbol: ⊂
A set S is a subset of a set R, if every element of S is an element of R.
i. e., S ⊂ R
S ⊂ R whenever x ∈ S, then x ∈ R.
If U = {a, b, c,…., x, y, z} and V = (a, e, i, o, u}, then V ⊂ U.
If we consider the alphabet in English as universal set, then the set of vowels is a subset of it.

→ Equal sets :
Two sets A and B are said to be equal if every element of A is also an element of B and if every element of B is also an element of A.
In other words, two sets A and B are said to be equal if they have exactly the same elements.
We write A = B
E.g.: A = {5, 8,10,11}, B = {10, 5, 11, 8}
Then A = B

→ Equivalent sets:
Two finite sets A and B are said to be equivalent if they have the same number of elements. We write A = B
For example, let A = {x, y, z} and B = {2, 4, 6} then A and B are equivalent sets.

→ Difference of sets :
Let A and B are two sets. The difference of sets A and B, in the same order, is the set of elements that belong to A but not to B.
We write it as A – B and read as ‘A’ difference B’.
A – B = {x: x ∈ A and x ∉ B}

→ Union of sets :
Let A and B be any two sets. The union of A and B is the set that contains all the elements of A and also the elements of B, the common elements being taken only once.

Symbolically,
A ∪ B = {x : x ∈ A or x ∈ B}
E.g.: If A = {1, 3, 5, 7} and B = {5, 7, 9,11} then A ∪ B = {1, 3, 5, 7, 9,11}
We read A ∪ B as ‘A union B’.

→ Intersection of sets :
Let A and B be any two sets. The intersection of sets A and B is the set of all elements which are common to both A and B.

Symbolically,
A ∩ B = {x : x ∈ A and X ∈ B}
E.g.: If A = {2,4, 6, 8} and B = {6, 8,10,12} then A ∩ B = {6, 8}
We read A ∩ B as ‘A intersection B’.

→ Disjoint sets:
Two sets A and B are said to be disjoint, if A ∩ B = Φ

i. e., there is no common element in the sets.
E.g.: A = {1, 2, 3, 4, 5} and B = {6, 7, 8}
Here, A and B have no elements in common.
∴ A and B are called disjoint sets.

→ Venn diagrams:
Venn diagrams are a convenient way of showing operations between sets. Most of the ideas about sets and their properties can be visualised by means of diagrams. These diagrams are known as venn diagrams because they are named after John Venn. In these diagrams, the universal set is represented by the interior of a rectangle and its subsets are represented by the interior of circles.
(i) n(A) + n(B) – n(A ∪ B) = n(A ∩ B)
(ii) n(A) + n(B) – n(A ∩ B) = n(A ∪ B)
E.g.:
(i) If n(A) = 7, n(B) = 8, n(A ∩ B) = 3, find n(A ∪ B).
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
= 7 + 8 – 3 = 12
(ii) If n(A) = 14, n(B) = 5, n(A ∪ B) = 16, find n(A ∩ B).
n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 14 + 5 – 16
= 19 – 16 = 3

Important Formula:

• Null Set. P = {x: 1 < x < 2 and x ∈ N}
• A set is called Finite Set. If it is possible to count.
• A set is called Infinite Set. If it is not possible to count.
• The number of elements in a set is called the cardinal number of the set.
• Two sets A and B are said to be equal if they have the same elements, i.e A = B
• Symbol of subset is ⊂.

Flow Chat:

George Cantor(1845 – 1918A.D):

• George Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics.
• Cantor established the importance of one-to-one correspondence between the numbers of two sets, defined infinite and well-ordered sets and proved that the real numbers are “more numerous” than the natural numbers.
• He defined the cardinal and ordinal numbers and their arithmetic.
• Cantor’s work is of great philosophical interest, a fact of which he was well aware.

Solving these TS 10th Class Maths Bits with Answers Chapter 4 Pair of Linear Equations in Two Variables Bits for 10th Class will help students to build their problem-solving skills.

Pair of Linear Equations in Two Variables Bits for 10th Class

Question 1.
Which of the following pairs of equations represent inconsistent system ?
A) 2x + 3y = 8
5x – 4y = 3
B) 6x + 3y = 9
x – 8y = 0
C) 2x + 5y = 11
4x + 10 y = 21
D) 3x – 4y = 6
6x – 8y = 12
Answer:
C) 2x + 5y = 11
4x + 10 y = 21

Question 2.
The pair of linear equations 3x + 4y + 5 = 0 and 12x + 16 y + 15 = 0 have ……… solution (s).
A) Unique
B) Many
C) Two
D) No
Answer:
D) No

Question 3.
The pair of linear equations px + 2y = 5 and 3x + y = 1 has unique solutions if
A) p ≠ 6
B) p = 6
C) p = 5
D) p ≠ 5
Answer:
A) p ≠ 6

Question 4.
The lines represented by 8x + 2pγ = 2 and 2x + 5y + 1 = 0 are parallel if p =
A) \(\frac{-5}{4}\)
B) \(\frac{2}{7}\)
C) 10
D) \(\frac{3}{8}\)
Answer:
C) 10

Question 5.
Solution of the equations \(\sqrt{2}\)x + \(\sqrt{3}\)y = 0 and \(\sqrt{3}\)x – \(\sqrt{8}\)y = 0
A) x = 1
y = 0
B) x = 0
y = 1
C) x = 1
y = 1
D) x = 0
y = 0
Answer:
D) x = 0
y = 0

Question 6.
The pair of equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 has a unique solution, then
A) \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{\mathrm{b}_1}{\mathrm{b}_2}\)
B) \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
C) \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
D) \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
Answer:
A) \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{\mathrm{b}_1}{\mathrm{b}_2}\)

Question 7.
If x = 1, then the value of y satisfying the equation \(\frac{5}{x}\) + \(\frac{3}{y}\) = 6
A) 3
B) +\(\frac{1}{3}\)
C) –\(\frac{1}{3}\)
D) 1
Answer:
A) 3

Question 8.
The value of y when \(\frac{x+y}{x y}\) = 2 and \(\frac{x-y}{x y}\) = 6 is
A) \(\frac{1}{4}\)
B) –\(\frac{1}{2}\)
C) –\(\frac{7}{4}\)
D) \(\frac{5}{4}\)
Answer:
A) \(\frac{1}{4}\)

Question 9.
If ax + by = c and px + qy = r has unique solution, then
A) \(\frac{a}{b}\) = \(\frac{p}{q}\)
B) ab = pq
C) \(\frac{a}{q}\) = \(\frac{b}{p}\)
D) aq ≠ bp
Answer:
A) \(\frac{a}{b}\) = \(\frac{p}{q}\)

Question 10.
If 5x + py + 8 =0 and 10x + 15y + 12 = 0 has no solution, then p =
A) 7\(\frac{1}{2}\)
B) 6\(\frac{1}{2}\)
C) 7
D) 4
Answer:
A) 7\(\frac{1}{2}\)

Question 11.
y = 5x is a line
A) parallel to x – axis
B) parallel to y – axis
C) parallel to x = 5y
D) passes through the origin
Answer:
D) passes through the origin

Question 12.
The point (-3,-8) is in the ____ quadrant.
A) Q₁
B) Q₂
C) Q₃
D) Q₄
Answer:
C) Q₃

Question 13.
The point (7, -5) is in the _____ quadrant.
A) I
B) II
C) III
D) IV
Answer:
D) IV

Question 14.
Find the value of x if y = \(\frac{3}{4}\) x and 5x + 8y = 33
A) 2
B) 3
C) 4
D) -3
Answer:
B) 3

Question 15.
\(\frac{120}{x}\) + \(\frac{12}{x}\) = 11, then x =
A) 132
B) 11
C) 12
D) 13
Answer:
C) 12

Question 16.
Which of the following equations is not a linear equation ?
A) x – 3y = 2x + y + 8
B) 4x² – 6y = y + 6
C) 8x – 3 = 5y + 7
D) 3x = 4y
Answer:
B) 4x² – 6y = y + 6

Question 17.
Which of the following number is a solution for the equation 3(7 – 3y) + 4y = 16 ?
A) 0
B) -1
C) 1
D) 2
Answer:
C) 1

Question 18.
When two lines in the same plane may in-tersect ?
A) At two points
B) At many points
C) At only one point
D) None
Answer:
C) At only one point

Question 19.
In the following values of x and y satisfies the equation 4x + 3y = 110
A) (10, 20)
B) (15, 30)
C) (10, 30)
D) (20, 10)
Answer:
D) (20, 10)

Question 20.
3x + 2y – 80 = 0; 4x + 3y – 110 = 0 solution for this linear equations is
A) Unique
B) Infinite
C) Two
D) No
Answer:
A) Unique

Question 21.
x + 2y – 30 = 0; 2x + 4y – 66 = 0 these lines represent
A) Intersecting lines
B) Parallel lines
C) Coincident lines
D) None of these
Answer:
B) Parallel lines

Question 22.
The point of intersection of x + y = 6 and x – y = 4 is ………. (A.P. Mar. 16)
A) (5, 1)
B) (1, 5)
C) (2, 4)
D) (4, 6)
Answer:
A) (5, 1)

Question 23.
A pair of linear equations in two variables are 2x – y = 4 and 4x – 2y = 6. The pair of equations are …….. (T.S. Mar’15)
A) Consistent
B) Dependent
C) Inconsistent
D) Cannot say
Answer:
C) Inconsistent

Question 24.
The value of ‘x’ in the equation 3x – (x – 4) = 3x + 1 is …….. (T.S. Mar’16)
A) -3
B) 0
C) 3
D) 10
Answer:
C) 3

Question 25.
The sum of squares of two consecutive positive even numbers is 340, then the numbers are …… (A.P. Mar. 15)
A) 12, 14
B) 10, 12
C) 14, 16
D) 16, 18
Answer:
A) 12, 14

Question 26.
Length of the dark line given in the; diagram (A.P. Mar. 16)

Answer:
C) \(\sqrt{l^2+\mathrm{b}^2+\mathrm{h}^2}\)

Question 27.
500x + 240y = 8, 130x + 240y = \(\frac{43}{10}\) then x = ………..
A) \(\frac{9}{200}\)
B) \(\frac{7}{20}\)
C) \(\frac{1}{100}\)
D) \(\frac{1}{10}\)
Answer:
C) \(\frac{1}{100}\)

Question 28.
In the above problem y = ……….
A) 1
B) 0
C) 10
D) none
Answer:
D) none

Question 29.
If the equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 are consistent then ……….
A) \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\)
B) \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\)
C) \(\frac{a_1}{a_2}\) = 1
D) none
Answer:
A) \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\)

Question 30.
Sita has pencils and pens which are together 40 in number. If she has 5 less pencils and 5 more pens the number of pens become four times the number of pencils. Represent this situation in a linear equation form.  A) x – y = 40
B) x + y = 40
C) x – y = 7
D) all
Answer:
B) x + y = 40

Question 31.
The lines represented by 5x + 7y – 14 = 0 and 10x + 3y – 8 = 0 are ………. lines.
A) coincident
B) vertical
C) parallel
D) consistent
Answer:
D) consistent

Question 32.
The standard form of a linear equation is ……………
A) xa + y = 0
B) ax + by
C) ax + b = 0
D) ax + by + c = 0
Answer:
D) ax + by + c = 0

Question 33.
The lines 3x + 8y – 13 = 0 and -6x – 16y + 23 = 0 are ………. lines.
A) coincident
B) parallel
C) circular
D) none
Answer:
B) parallel

Question 34.
The lines represented by 5x + 3y – 7 = 0 and 6y + 10x – 14 = 0 are lines.
A) coincident
B) parallel
C) intersecting
D) none
Answer:
A) coincident

Question 35.
The pairs of equations 4x – 2y + 6 = 0 and 2x – y + 8 = 0 has …… solutions(s).
A) 1
B) 12
C) No solution
D) 10
Answer:
C) No solution

Question 36.
The number of solutions to the pair of equations 6x – 7y + 8 = 0 and 12x – 14y + 10 = 0 is
A) 1
B) 20
C) 3
D) infinite
Answer:
D) infinite

Question 37.
The number of solutions to the pair of equations 11x – 7y = 6 and 4x + 9y = 8 is
A) 4
B) 3
C) 7
D) 1
Answer:
D) 1

Question 38.
If the pair of equations kx + 14y + 8 = 0 and 3x + 7y + 6 = 0 has a unique solution then
A) k ≠ 6
B) k = 0
C) k = 7
D) none
Answer:
A) k ≠ 6

Question 39.
a₁x + b₁y₁ + c₁ = 0 and a₂x + b₂y + c₂ = 0 are ……… equations.
A) parallel
B) pair of linear
C) consistent
D) none
Answer:
B) pair of linear

Question 40.
If \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\) then the lines will have …….. solutions.
A) infinite
B) 2
C) 3
D) 7
Answer:
A) infinite

Question 41.
3x – 2y + 6 = 0, 6x – 4y + 8 = 0 represents ……. lines
A) consistent
B) inconsistent
C) circle
D) parallel
Answer:
D) parallel

Question 42.
5x – 2y – 10 = 0,10x – 4y – 20 = 0 these are ……… lines.
A) consistent
B) parallel
C) intersecting
D) none
Answer:
A) consistent

Question 43.
The number of solutions to 4x + 6y – 7 = 0 and 8x + 5y – 8 = 0 is ………..
A) 14
B) 3
C) 4
D) 1
Answer:
D) 1

Question 44.
\(\frac{2}{x}\) + \(\frac{3}{y}\) = 2, \(\frac{12}{x}\) – \(\frac{9}{y}\) = 3 then x = ……….
A) 1
B) 4
C) 2
D) none
Answer:
C) 2

Question 45.
In the above problem y = ………
A) 2
B) -1
C) 7
D) 3
Answer:
D) 3

Question 46.
If 2^x + 3^y = 17 and 2^x+2 – 3^y+1 = 5, then y = ……….
A) 2
B) 3
C) 1
D) 7
Answer:
A) 2

Question 47.
In the above problem x = ………
A) 2
B) 4
C) 3
D) none
Answer:
C) 3

Question 48.
\(\frac{\mathbf{a x}}{\mathbf{b}}\) – \(\frac{\mathbf{b y}}{\mathbf{a}}\) = a + b, ax – by = 2ab then x = ……….
A) 3b
B) \(\frac{-3}{b}\)
C) 1
D) -2a
Answer:
A) 3b

Question 49.
In the above problem y = ………
A) – a
B) 2a
C) -a²
D) 3b – a
Answer:
A) – a

Question 50.
Slope of the line ax + by + c = 0 is ………
A) \(\frac{b}{a}\)
B) \(\frac{1}{a}\)
C) \(\frac{a}{b}\)
D) \(\frac{-a}{b}\)
Answer:
D) \(\frac{-a}{b}\)

Question 51.
The line ax + by + c = 0 does not passes through ………..
A) (0, 0)
B) (a, 0)
C) both A & B
D) none
Answer:
C) both A & B

Question 52.
If x + y = 7, x – y = 1 then 2x = ……….
A) 3
B) 4
C) 7
D) 8
Answer:
D) 8

Question 53.
In the above problem y = ………..
A) 3
B) 7
C) 1
D) 4
Answer:
A) 3

Question 54.
Slope of the line y = x is ………
A) 2
B) – 1
C) 1
D) none
Answer:
C) 1

Question 55.
The line x = 2015 is ……….
A) slope not defined
B) parallel to Y – axis
C) both A & B
D) none
Answer:
C) both A & B

Question 56.
x + \(\frac{6}{y}\) = 6, 3x – \(\frac{8}{y}\) then y = ………..
A) – 2
B) 4
C) 1
D) 2
Answer:
D) 2

Question 57.
In the above problem x = ……….
A) 3
B) 2
C) -1
D) 9
Answer:
A) 3

Question 58.
3x – 5y = -1, – y + x = -1 then (x, y) = ……..
A) (-2, -1)
B) (2, -1)
C) curve
D) none
Answer:
A) (-2, -1)

Question 59.
The value of y in -5x + 10y = 100 at x = 0 is ……….
A) 12
B) 9
C) -10
D) 10
Answer:
D) 10

Question 60.
If x + y = 36, then at y = -1, x = ………..
A) 38
B) 37
C) 80
D) 12
Answer:
B) 37

Question 61.
x + y = 10, x – y = – 4 then x = …………
A) 4
B) 3
C) 5
D) none
Answer:
B) 3

Question 62.
In the above problem y = ……….
A) 9
B) 4
C) 7
D) 13
Answer:
C) 7

Question 63.
Solution to 2x – 2y – 2 = 0,4x – 4y – 5 = 0 is …….
A) (1, 4)
B) (2, -1)
C) (8, –\(\frac{1}{4}\))
D) no solution
Answer:
D) no solution

Question 64.
The two lines 2x + y – 6 = 0 and 4x – 2y – 4 = 0 intersect at ……….
A) (2, 2)
B) (3, 2)
C) (1, -4)
D) (1, 4)
Answer:
A) (2, 2)

Question 65.
Solution to x – y = 1, 2x – 2y = 7 is ……..
A) (1, 1)
B) (1, 9)
C) (8, 4)
D) no solution
Answer:
D) no solution

Question 66.
Perimeter of rectangle = ……..
A) l + b
B) l – b
c) 2(l + b)
D) \(\frac{l+\mathrm{b}}{2}\)
Answer:
c) 2(l + b)

Question 67.
x + y = 2015 has …… number of solutions.
A) 10
B) 2014
C) 20
D) infinite
Answer:
D) infinite

Question 68.
px + 3y – (p – 3) = 0, 12x + py – p = 0 has infinitely many solutions then p = ………..
A) 7
B) 9
C) ± 71
D) ± 6
Answer:
D) ± 6

Question 69.
If 3x + 4y + 2 = 0, 9x + 12y + k = 0 represent coincident lines, then k = ………….
A) 12
B) 9
C) 6
D) 7
Answer:
C) 6

Question 70.
2x + 3y = 1, 3x – y = 7 then (x, y) = ……..
A) (2, -1)
(B) (-2, 1)
(C) (8, \(\frac{1}{4}\))
(D) (0, 3)
Answer:
A) (2, -1)

Question 71.
Slope of the line x = 2y is ………
A) 2
B) -2
C) 1
(D) \(\frac{1}{2}\)
Answer:
B) -2

Question 72.
If 7x – 8y = 9, then y = …………
A) 9 + 7x
B) \(\frac{9-7 x}{8}\)
C) \(\frac{9-7 x}{6}\)
D) none
Answer:
D) none

Question 73.
Slope of X – axis is ……….
A) 0
B) 1
C) -1
D) 2
Answer:
A) 0

Question 74.
Angle between any two parallel lines is …………
A) 70°
B) 0°
C) 100°
D) 180°
Answer:
B) 0°

Question 75.
4m – 2n = 2, 6m – 5n = 9 then n = ………..
A) 5
B) 4
C) 1
D) – 3
Answer:
D) – 3

Question 76.
In the above problem m = …………
A) – 1
B) 4
C) -31
D) 7
Answer:
A) – 1

Question 77.
2u + 3y = 2, 4u – 6y = 0 then y = ……….
A) \(\frac{1}{2}\)
B) 1
C) \(\frac{1}{31}\)
D) \(\frac{1}{3}\)
Answer:
D) \(\frac{1}{3}\)

Question 78.
In Q. No. 77 the value of u = …………
A) \(\frac{1}{21}\)
B) \(\frac{1}{2}\)
C) 2
D) 4
Answer:
B) \(\frac{1}{2}\)

Question 79.
Area of rectangle = ………….
A) l²b
B) \(\frac{l}{b}\)
C) lb
D) none
Answer:
C) lb

Question 80.
\(\frac{x+3}{2}\) – y = 2, \(\frac{x-3}{2}\) + 2y = 4 \(\frac{1}{2}\) then x = ………..
A) 1
B) 4
C) 51
D) none
Answer:
D) none

Question 81.
In the above problem y = ……….
A) 2
B) – 2
C) 7
D) 12
Answer:
A) 2

Question 82.
If ax + b = 0, then x = ………..
A) -b
B) –\(\frac{\mathrm{b}}{\mathrm{a}}\)
C) \(\frac{\mathrm{b}}{\mathrm{a}}\)
D) none
Answer:
B) –\(\frac{\mathrm{b}}{\mathrm{a}}\)

Question 83.
2x – 3y = -12 then at x = 0, y = ……….
A) 4
B) 6
C) 8
D) 12
Answer:
A) 4

Question 84.
Two parallel lines differ by ……….
A) circle
B) triangle
C) constant
D) none
Answer:
C) constant

Question 85.
x = 1 and y = –\(\frac{1}{2}\) then x – y = ………..
A) – 1
B) 1
C) –\(\frac{1}{2}\)
D) 7
Answer:
D) 7

Question 86.
If 99x + 101y = 499, 101x + 99y = 510 then x = ………
A) -1
B) 3
C) 4
D) 2
Answer:
B) 3

Question 87.
In the above problem y = ………
A) 3
B) 4
C) 2
D) 8
Answer:
C) 2

Question 88.
141x + 93y = 189, 93x + 141y = 45 then y = …….
A) – 1
B) 4
C) -2
D) 2
Answer:
A) – 1

Question 89.
In the above problem x = …….
A) 3
B) 4
C) 1
D) 2
Answer:
D) 2

Question 90.
If -x + y = – 10, then x = …………….
A) y – 3
B) y² – 1
C) y – 10
D) y + 10
Answer:
D) y + 10

Question 91.
(-a, -b) ∈ ………..
A) Q₂
B) Q₃
C) Q₁
D) Q₄
Answer:
B) Q₃

Question 92.
(2, 0) lies on ……….
A) Q₁
B) Q₂
C) x axis
D) y axis
Answer:
C) x axis

Question 93.
The line x – y = 8 intersects X – axis at ……….
A) (2, 3)
B) (1, 1)
C) (0, 8)
D) (8, 0)
Answer:
D) (8, 0)

Question 94.
The values of k for which the pair of linear equations 3x – 2y = 7 and 6x + ky + 11 = 0 has a unique solution is
A) all numbers except 4
B) all numbers expect – 4
C) 4
D) – 4
Answer:
B) all numbers expect – 4

Question 95.
The pair of linear equations -3x + 4y = 7 and \(\frac{9}{2}\) x – 6y + \(\frac{21}{2}\) = 0 has ……………….
A) infinite number of solutions
B) no solution
C) two solutions
D) unique solution
Answer:
A) infinite number of solutions

Question 96.
If ad ≠ bc then the pair of linear equations ax + by = p and cx + dy = q has ……….. solutions.
A) no
B) unique
C) 2
D) none
Answer:
C) 2

Question 97.
A line parallel to the line x + 2y + 1 = 0 is ………
A) x + y + 3 = 0
B) 2x + 4y + 1 = 0
C) x – y + 1 = 0
D) all
Answer:
B) 2x + 4y + 1 = 0

Question 98.
The pair of equations x = 3, y = 2 graphi-cally represent lines which ………
A) intersect at (3, 4)
B) intersect at (4, 3)
C) parallel
D) coincident
Answer:
A) intersect at (3, 4)

Question 99.
If the pair of equations 2x + y = 7 and 6x – py – 21 =0 has infinite number of solutions then p = ………..
A) 3
B) 4
C) 5
D) none
Answer:
D) none

Question 100.
The value of k for which the system of equations kx + 3y = 1,12x + ky = 2 has no solution is ………..
A) k = -1
B) k = 3
C) k = 2
D) k = -6
Answer:
D) k = -6

Question 101.
The line 3x + y = 7 intersects X- axis at ………..
A) (\(\frac{7}{2}\), 0)
B) (0, \(\frac{7}{2}\))
C (0, 1)
D) (0, 3)
Answer:
A) (\(\frac{7}{2}\), 0)

Question 102.
For what value of k, 2x + 3y = 4 and (k + 2)x + 6y = 3k + 2 will have infinitely many solutions ?
A) k = -1
B) k = 2
C) k = 7
D) none
Answer:
B) k = 2

Question 103.
\(\frac{x+1}{2}\) + \(\frac{y-1}{3}\) = 9, \(\frac{x-1}{3}\) + \(\frac{y+1}{2}\) = 8 then x =
A) 13
B) 17
C) -3
D) 10
Answer:
A) 13

Question 104.
In the above problem y = ……….
A) 4
B) – 3
C) 9
D) 7
Answer:
D) 7

Question 105.
If the equations (2m – 1)x + 3y – 5 = 0, 3x + (n – 1)y – 2 = 0 has infinite number of solutions then n = …………
A) 1
B) \(\frac{5}{11}\)
C) \(\frac{1}{5}\)
D) \(\frac{11}{5}\)
Answer:
D) \(\frac{11}{5}\)

Question 106.
In the above problem m = ………..
A) \(\frac{17}{4}\)
B) \(\frac{7}{4}\)
C) \(\frac{1}{2}\)
D) \(\frac{8}{3}\)
Answer:
A) \(\frac{17}{4}\)

Question 107.
A fraction becomes \(\frac{9}{11}\) if 2 is added to both numerator and denominator. If 3 is added to both numerator and denominator it be-comes is …………
A) \(\frac{17}{4}\)
B) \(\frac{7}{4}\)
C) \(\frac{1}{2}\)
D) \(\frac{8}{3}\)
Answer:
A) \(\frac{17}{4}\)

Question 108.
The ratio of incomes of two persons is 11:7 and the ratio of their expenditures is 9 : 5. If each of them manages to save ₹ 400 per month then the monthly income of first person is ………..
A) ₹ 2,200
B) ₹ 1,200
C) ₹ 800
D) ₹ 1010
Answer:
A) ₹ 2,200

Question 109.
In the above problem income of second person is ……….
A) ₹ 8,001
B) ₹ 1,100
C) ₹ 1,400
D) ₹ 4,100
Answer:
C) ₹ 1,400

Question 110.
The age of a father 8 years ago was 5 time that of his son 8 years. Hence, his age will be 8 years more than twice the age of his son. Then the present age of father is years. ( )
A) 80
B) 92
C) 24
D) 48
Answer:
D) 48

Question 111.
In the above problem age of son is ……… years.
A) 16
B) 96
C) 12
D) none
Answer:
A) 16

Question 112.
The two lines 2x – y = 1, x + 2y = 13 will intersect at …………
A) (5, 3)
B) (3, 5)
C) (1, 3)
D) (3, 9)
Answer:
B) (3, 5)

Question 113.
Identify parallel lines
A) 2x + 3y = 6, 8x + 12y = 9
B) x + y = 7, x – y = 1
C) 2x + y = 7, x – y = 1 :
D) 2x + y = 7, 3x – y = 7 .
Answer:
A) 2x + 3y = 6, 8x + 12y = 9

Question 114.
Solution to 2x + 3y = 12, 2y – 1 = x is ……….
A) (8, -1)
B) (3, 8)
C) (3, 2)
D) (1, -1)
Answer:
C) (3, 2)

Question 115.
The lines x – y = 1; 2x + y = 8 intersects at ……….
A) (1, 9)
B) (9, 3)
C) (3, 4)
D) none
Answer:
D) none

Question 116.
\(\frac{5}{x-1}\) + \(\frac{1}{y-2}\) = 2, \(\frac{6}{x-1}\) + \(\frac{-3}{y-2}\) = 1 If then x = ……….
A) 4
B) 7
C) -1
D) 3
Answer:
A) 4

Question 117.
In the above problem y = …………
A) 1
B) -1
C) 5
D) 9
Answer:
C) 5

Question 118.
If 2x + 3y = 10 and 2x – 3y = 6 then (x, y) = …………
A) (2, 5)
B) (\(\frac{2}{3}\), 4)
C) (0, 0)
D) (4, \(\frac{2}{3}\))
Answer:
D) (4, \(\frac{2}{3}\))

Solving these TS 10th Class Maths Bits with Answers Chapter 12 Applications of Trigonometry Bits for 10th Class will help students to build their problem-solving skills.

Applications of Trigonometry Bits for 10th Class

Question 1.
If a pole 6 m high casts a shadow 2 \(\sqrt{3}\) m long on the ground, then the sun’s angle of elevation is
A) 60°
B) 45°
C) 30°
D) 90°
Answer:
A) 60°

Question 2.
If the angle of elevation of a tower from a distance of 100 m from its foot is 60°then the height of the tower is …………. m.
A) 100\(\sqrt{3}\)
B) \(\frac{100}{\sqrt{3}}\)
C) 50 \(\sqrt{3}\)
D) \(\frac{50}{\sqrt{3}}\)
Answer:
A) 100\(\sqrt{3}\)

Question 3.
The height of a tower is 10 m. The length of its shadow when Sun’s altitude is 45° is …………….. m.
A) 10
B) 20
C) 10\(\sqrt{3}\)
D) 50
Answer:
A) 10

Question 4.
The length of the shadow of a tower on the plane ground is \(\sqrt{3}\) times the height of the tower, the angle of elevation of sun is
A) 30°
B) 45°
C) 60°
D) 90°
Answer:
A) 30°

Question 5.
The ratio of the length of a rod and it’s shadow is 1 : \(\sqrt{3}\) then the angle of elevation of the Sun is
A) 45°
B) 30°
C) 75°
D) 90°
Answer:
B) 30°

Question 6.
If two towers of height X and Y subtend angles of 30° and 60°respectively at the centre of the line joining their feet, then X : Y is equal to
A) 1 : 3
B) 1 : \(\sqrt{3}\)
C) 3 : 1
D) \(\sqrt{3}\) : 1
Answer:
A) 1 : 3

Question 7.
A wall of 8 m long casts a shadow 5 m long at the same time a tower casts a shadow 50m long, then the height of tower is
A) 20 m
B) 40 m
C) 80 m
D) 200 m
Answer:
C) 80 m

Question 8.
If the Sun’s angle of elevation is 60°, then a pole of height 6 m will cast a shadow of length ………….. m.
A) \(\sqrt{3}\)
B) 5\(\sqrt{3}\)
C) 6\(\sqrt{3}\)
D) 2\(\sqrt{3}\)
Answer:
D) 2\(\sqrt{3}\)

Question 9.
A pole of 12 m high casts a shadow 4\(\sqrt{3}\)m on the ground, then the Sun’s angle of elevation is
A) 60°
B) 120°
C) 45°
D) 30°
Answer:
A) 60°

Question 10.
If the height and length of the shadow of a man are the same then the angle of elevation of the Sun is
A) 60°
B) 45°
C) 90°
D) 120°
Answer:
B) 45°

Question 11.
What is the angle of elevation of the top of a temple of height 10 m at a point whose distance from the base of the tower is 10\(\sqrt{3}\) m ?
A) 30°
B) 60°
C) 45°
D) 90°
Answer:
A) 30°

Question 12.
The length of the shadow of 5m height tree whose angle of elevation of the Sun is 30° is?
A) 5 m
B) \(\sqrt{3}\) m
C) 5\(\sqrt{3}\) m
D) 10 m
Answer:
C) 5\(\sqrt{3}\) m

Question 13.
From the top of a 10m height tree the angle of depression of a point on the ground is 30° then the distance of the point from the foot of the tree is
A) 10 m
B) 10\(\sqrt{3}\) m
C) \(\frac{10}{\sqrt{3}}\) m
D) 5\(\sqrt{3}\) m
Answer:
B) 10\(\sqrt{3}\) m

Question 14.
Ladder ‘x’ meters long is laid against a well making an angle ‘0’ with the ground. If we want to directly find the distance between the foot of ladder and foot of the wall, which trigonometrical ratio should be considered ?
A) sin θ
B) cos θ
C) tan θ
D) cot θ
Answer:
B) cos θ

Question 15.
Top of a building was observed at an angle of elevation ‘α’ from a point, which is at distance ‘d’ meters from the foot of the building. Which trigonometrical ratio should be considered for finding height of buildings.
A) tan α
B) sin α
C) cos α
D) sec α
Answer:
A) tan α

Question 16.
In the given figure, the value of angle θ is

A) 30°
B) 60°
C) 45°
D) 90°
Answer:
A) 30°

Question 17.
The given figure shows the observation of point ‘C’ from point A. The angle of depression from A is

A) 30°
B) 45°
C) 90°
D) 75°
Answer:
A) 30°

Question 18.
If the length of the shadow of a tower is \(\frac{1}{\sqrt{3}}\) times the height of the tower, then the angle of elevation of the sun is ……………..
A) 30°
B) 45°
C) 60°
D) 75°
Answer:
C) 60°

Question 19.
A tower is 50 m high. Its shadow is x m shorter when the sun’s altitude is 45° then when it is 30°, then x = ………… cm
A) 105
B) 20
C) 10
D) 100
Answer:
D) 100

Question 20.
The length of the string of a kite flying at 100 m above the ground with the elevation of 60° is ………….
A) \(\frac{200}{\sqrt{3}}\)
B) \(\frac{20}{\sqrt{3}}\)
C) \(\frac{291}{\sqrt{3}}\)
D) none
Answer:
A) \(\frac{200}{\sqrt{3}}\)

Question 21.
A player sitting on the top of a tower of height 40 m observes the angle of depression of a ball lying on the ground is 60 The distance between the foot of the tower and ball is …………… m.
A) 20
B) \(\frac{80}{\sqrt{61}}\)
C) \(\frac{40}{\sqrt{3}}\)
D) \(\frac{40}{\sqrt{6}}\)
Answer:
C) \(\frac{40}{\sqrt{3}}\)

Question 22.
If the ratio of height of a tower and the length of its shadow on the ground is \(\sqrt{3}\) :1, then the angle of elevation of the sun is ……………….
A) 80°
B) 60°
C) 70°
D) 100°
Answer:
B) 60°

Question 23.
The angle of depression of the top of a tower at a point 100 m from the house is 45°, then the height of the tower is …………. m.
A) 18.1
B) 16.3
C) 36.6
D) 26.7
Answer:
C) 36.6

Question 24.
An object is placed above the observer’s horizontal, we call the angle between the line of sight and observer’s horizontal is ……………..
A) angle of elevation
B) angle of depression
C) point
D) none
Answer:
A) angle of elevation

Question 25.
Angle of elevation of the top of a building from a point on the ground is 30. Then the angle of depression of this point from the top of the building is …………………
A) 65°
B) 60°
C) 70°
D) 30°
Answer:
D) 30°

Question 26.
What change will be observed in the angle of elevation as we move away from the object ?
A) increase
B) decrease
C) can’t be determined
D) none
Answer:
A) increase

Question 27.
An object is placed below the observer’s horizontal, then what is the angle between line of sight and observer’s horizontal ?
A) angle of elevation
B) angle of depression
C) can’t be determined
D) none
Answer:
B) angle of depression

Question 28.
What change will be observed in the angle of elevation as we approach the foot of the tower ?
A) 0
B) 60°
C) Data not correct
D) none
Answer:
D) none

Question 29.
In the figure given below, the imaginary line through the object and eye of the observer is called …………………

A) line of sight
B) angle of depression
C) angle of elevation
D) none
Answer:
A) line of sight

Question 30.
In the figure given below, a man on the top of cliff observers a boat coming towards him. Then 6 represents the angle of …………….

A) depression
B) elevation
C) equal
D) none
Answer:
A) depression

Question 31.
In the figure given below, if AB = 10 m and AC = 20 m, then θ = ………………..

A) 60°
B) 30°
C) 70°
D) none
Answer:
B) 30°

Question 32.
A pole 6 m high casts a shadow 2\(\sqrt{3}\) m long on the ground, then the sun’s elevation is …………….
A) 70°
B) 20°
C) 80°
D) 60°
Answer:
D) 60°

Question 33.
In the figure given below, if AB = CD = 10\(\sqrt{3}\) m then BC = ………………

A) 90
B) 60
C) 40
D) None
Answer:
C) 40

Question 34.
In the figure given below, if AB = 10\(\sqrt{3}\) m, then CD = …………….. (take \(\sqrt{3}\) = 1.732)

A) 7.32
B) 8.14
C) 3.1
D) 1.92
Answer:
A) 7.32

Question 35.
In the figure given below, if AD = 7\(\sqrt{3}\) m, then BC = ………………. m.

A) 13
B) 19
C) 28
D) None
Answer:
C) 28

Question 36.
The length of the shadow of a tree is 7 m high, when the sun’s elevation is …………………..
A) 45°
B) 60°
C) 70°
D) 90°
Answer:
A) 45°

Question 37.
If two tangents inclined at an angle of 60 are drawn to a circle of radius 3 cm, then length of tangent is equal to …………. m.
A) 4\(\sqrt{3}\)
B) 2\(\sqrt{91}\)
C) \(\sqrt{3}\)
D) 3\(\sqrt{3}\)
Answer:
D) 3\(\sqrt{3}\)

Question 38.
The angle formed by the line of sight with horizontal, when the point being viewed is above the horizontal level is called
A) angle of elevation
B) angle of depression
C) point
D) none
Answer:
A) angle of elevation

Question 39.
cot² B – Cosec² B = ………………
A) 0
B) – 1
C) 1
D) 2
Answer:
B) – 1

Question 40.
\(\frac{\tan \theta}{\sec \theta}\) = ……………….
A) – cos θ
B) sin θ
C) – tan θ
D) none
Answer:
B) sin θ

Question 41.
A boy observed the top of an electrical pole to be at angle of elevation of 60° when the observation point is 8 m away from the foot of the pole then the height of the pole is ……………… m.
A) 18\(\sqrt{3}\)
B) 14
C) 7\(\sqrt{3}\)
D) 8\(\sqrt{3}\)
Answer:
D) 8\(\sqrt{3}\)

Question 42.
Suppose you are shooting an arrow from the top of a building at a height of 6 m to a target on the ground at an angle of depression of 60 what is the distance between you and the object ?
A) 9
B) 7\(\sqrt{3}\)
C) 12\(\sqrt{3}\)
D) None
Answer:
D) None

Question 43.
Sin \(\frac{\pi^{\mathrm{c}}}{2}\) = ……………….
A) 4
B) 3
C) 1
D) -1
Answer:
C) 1

Question 44.
Domain of sin θ = ………………..
A) R
B) R – {30°}
C) N
D) None
Answer:
D) None

Question 45.
tan \(\frac{\pi^{\mathrm{c}}}{4}\) = ……………….
A) 2
B) 3
C) -1
D) 1
Answer:

Question 46.
cot 15° = ………………
A) 2 + \(\sqrt{3}\)
B) 2 – \(\sqrt{3}\)
C) \(\sqrt{2}\)
D) \(\sqrt{3}\) – 1
Answer:
A) 2 + \(\sqrt{3}\)

Question 47.
A + B = 180° then cos A + cos B = ………………
A) 4
B) 1
C) 0
D) none
Answer:
C) 0

Question 48.
sin 15° = ……………….
A) \(\frac{\sqrt{3}}{9 \sqrt{2}}\)
B) \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
C) \(\frac{\sqrt{3}+1}{2}\)
D) none
Answer:
B) \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)

Question 49.
tan A = \(\frac{\mathrm{n}}{\mathrm{n}+1}\), tan B = \(\frac{\mathrm{n}}{2\mathrm{n}+1}\), A + B = …………..
A) 4
B) 3
C) -1
D) 1
Answer:
D) 1

Question 50.
The angle of elevation of tower at a point 40 m apart from it is cot^-1 \(\left(\frac{3}{5}\right)\). Obtain the height of the tower.
A) \(\frac{200}{3}\) m
B) \(\frac{100}{3}\) m
C) \(\frac{210}{17}\) m
D) none
Answer:
A) \(\frac{200}{3}\) m

Question 51.
A ladder 20 m long is placed against a vertical wall of height 10 m, then the distance between the foot of the ladder and the wall is …………………. m.
A) 7\(\sqrt{3}\)
B) 20\(\sqrt{3}\)
C) 30\(\sqrt{3}\)
D) none
Answer:
C) 30\(\sqrt{3}\)

Question 52.
sin 18° = ………………
A) \(\frac{\sqrt{5}}{4}\)
B) \(\frac{\sqrt{5}-1}{4}\)
C) \(\frac{1+\sqrt{3}}{2}\)
D) \(\frac{\sqrt{3}-1}{4}\)
Answer:
B) \(\frac{\sqrt{5}-1}{4}\)

Question 53.
In the below figure x = …………………. cm.

A) 10
B) 12
C) 13
D) 19
Answer:
A) 10

Question 54.
cot (90 – A) = ………………
A) 3 tan A
B) sin A
C) cot A
D) tan A
Answer:
D) tan A

Question 55.
cos⁴ A – sin⁴ A = …………….
A) sin² A
B) cos² A
C) cos 2A
D) cos 3A
Answer:
C) cos 2A

Question 56.
If cosec θ + cot θ = k then cos θ ……………..
A) \(\frac{k^2-1}{k^2+1}\)
B) \(\frac{k^2}{k^2-1}\)
C) \(\frac{k^2+1}{k}\)
D) none
Answer:
D) none

Question 57.
x = (sec θ + tan θ), y = (sec θ – tan θ) then xy ………………
A) -1
B) 0
C) 1
D) -2
Answer:
C) 1

Question 58.
tan 15° = ……………..
A) \(\frac{\sqrt{3}}{\sqrt{3}+1}\)
B) \(\frac{\sqrt{3}-1}{\sqrt{3}+1}\)
C) \(\frac{\sqrt{3}-1}{2}\)
D) none
Answer:
B) \(\frac{\sqrt{3}-1}{\sqrt{3}+1}\)

Question 59.
cosec θ = ……………….
A) \(\sqrt{1+\cot ^2 \theta}\)
B) \(\sqrt{\cot ^2 \theta-1}\)
C) \(\sqrt{1+\sin \theta}\)
D) \(\sqrt{\cot \theta-1}\)
Answer:
A) \(\sqrt{1+\cot ^2 \theta}\)

Question 60.
x = a sin θ, y = a cos θ then x² + y² = ………………
A) \(\frac{a}{3}\)
B) \(\frac{a}{2}\)
C) a
D) a²
Answer:
D) a²

Question 61.
Example of a Pythagorean Triplet is ………………
A) 5, 12, 13
B) 5, 10, 11
C) 8, 9, 11
D) none
Answer:
A) 5, 12, 13

Question 62.
sec² A = …………….
A) 1 – tan² A
B) 1 + tan² A
C) cot² A
D) none
Answer:
B) 1 + tan² A

Question 63.
\(\frac{1}{\cos \theta}\) – cos θ = ………………
A) tan θ . sin θ
B) sec θ . cos θ
C) tan θ . cot θ
D) none
Answer:
A) tan θ . sin θ

Question 64.
sin θ = cos θ, θ ∈ Q₁ then θ = …………..
A) \(\frac{\pi^c}{2}\)
B) \(\frac{\pi^c}{3}\)
C) \(\frac{2 \pi^c}{3}\)
D) \(\frac{\pi^c}{4}\)
Answer:
D) \(\frac{\pi^c}{4}\)

Question 65.
72° = …………………
A) \(\frac{\pi^c}{2}\)
B) \(\frac{\pi^c}{3}\)
C) \(\frac{2 \pi^c}{5}\)
D) \(\frac{\pi^c}{5}\)
Answer:
C) \(\frac{2 \pi^c}{5}\)

Question 66.
sin² 105° + cos² 105° = ……………….
A) 1
B) 0
C) 9
D) 10
Answer:
A) 1

Question 67.
sin 45° (cos 45°) = ………………..
A) 1
B) \(\frac{1}{2}\)
C) 3
D) none
Answer:
B) \(\frac{1}{2}\)

Question 68.
cos 40° = 0.76 then sin 50² = ………………..
A) 0.76
B) 7.6
C) 76.6
D) none
Answer:
A) 0.76

Question 69.
At a point 15 m away from the base of a 15 m high pole, the angle of elevation of the top is …………………
A) 30°
B) 45°
C) 60c
D) 90°
Answer:
B) 45°

Question 70.
When the length of the shadow of a person is equal to his height, then the elevation of source of light is …………
A) 15°
B) 30°
C) 45°
D) 60°
Answer:
C) 45°

Question 71.
The angle of elevation of top of a tree is 30. On moving 20 m nearer, the angle of elevation is 60. The height of the tree is
A) 15\(\sqrt{3}\) m
B) 2\(\sqrt{3}\) m
C) 10\(\sqrt{3}\) m
D) 5\(\sqrt{3}\) m
Answer:
C) 10\(\sqrt{3}\) m

Question 72.
The ratio of length of a pole and its shadow is 1 :\(\sqrt{3}\).The angle of elevation is
A) 90°
B) 60°
C) 45°
D) 30°
Answer:
D) 30°

Question 73.
The upper part of a treee is broken by wind and makes an angle of 30° with the ground and at a distance of 21 m from the foot of the tree. Find the total height of the tree.
A) 30\(\sqrt{3}\) m
B) 21 m
C) 30 m
D) 21\(\sqrt{3}\) m
Answer:
D) 21\(\sqrt{3}\) m

Question 74.
From a bridge 25 m high, the angle of depression of a boat is 45°. Find the horizontal distance of the boat from the bridge.
A) 25\(\sqrt{3}\) m
B) 25 m
C) \(\frac{25}{\sqrt{3}}\)
D) 45 m
Answer:
B) 25 m

Question 75.
A tower makes an angle of elevation equal to the angle of depression from the top of a cliff 25 m height. Find the height of the tower.
A) 25 m
B) 75 m
C) 5m
D) 50 m
Answer:
D) 50 m

Question 76.
When the angle of elevation of a pole is 45°, the length of the pole and its shadow are
A) equal
B) length > shadow
C) shadow > length
D) none of the above
Answer:
A) equal

Question 77.
In a rectangle, if the angle between a diagonal and a side is 30, and the length of the diagonal is 6 cm, the area of the rectangle is
A) 18 cm²
B) 9 cm²
C) 18\(\sqrt{3}\) cm²
D) 9\(\sqrt{3}\) cm²
Answer:
D) 9\(\sqrt{3}\) cm²

Question 78.
Two posts are 15 m and 25 m high and the line joining their tops make an angle of 45° with the horizontal. The distance between the two posts is
A) 15 m
B) 25 m
C) 18 m
D) 10 m
Answer:
D) 10 m

Question 79.
An electric pole 20 m high stands up right! on the ground with the help of steel wire to its top and affixed on the ground. If the steel wire makes 60° with the horizontal ground, find the length of steel wire.
A) 60\(\sqrt{3}\) m
B) 20 m
C) 60 m
D) \(\frac{20}{\sqrt{3}}\) m
Answer:
D) \(\frac{20}{\sqrt{3}}\) m

Question 80.
A building casts a shadow of length 50\(\sqrt{3}\) m when the sun is 30° about the horizontal. The height of the building is
A) 30 m
B) 40 m
C) 50 m
D) 60 m
Answer:
C) 50 m

Question 81.
When the angle of elevation of a light! changes from 30° to 45°, the shadow of pole becomes 100\(\sqrt{3}\) m less. The height of the pole is
A) 30 m
B) 120 m
C) 75 m
D) 100 m
Answer:
D) 100 m

Question 82.
From the top of a building 50 m from horizontal, the angle of depression made by a car is 30°. How far is the car from the building ?
A) \(\frac{50}{\sqrt{3}}\)
B) 50\(\sqrt{3}\) m
C) 150 m
D) 30\(\sqrt{3}\) m
Answer:
B) 50\(\sqrt{3}\) m

Question 83.
From the top of a building with height 30°(\(\sqrt{3}\) + 1) m two cars make angles of depression of 45° and 30° due east. What is the distance between two cars ?
A) 30 m
B) 60 m
C) 45 m
D) 75 m
Answer:
B) 60 m

Question 84.
A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60°. When he retires 40 m from the bank, he finds the angle to be 30°. The breadth of the river is
A) 10 m
B) 15 m
C) 20 m
D) 25 m
Answer:
C) 20 m

Question 85.
A ladder of 10 m length touches a wall at a height of 5 m. The angle made by it with the horizontal is
A) 30°
B) 45°
C) 60°
D) 90°
Answer:
A) 30°

Question 86.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance between the top of the tree and the ground is 10 m. Find the height of the tree.
A) 10 m
B) 30\(\sqrt{3}\) m
C) 10\(\sqrt{3}\) m
D) 30 m
Answer:
C) 10\(\sqrt{3}\) m

Question 87.
The angle of elevation of a cloud from a point 200 m above the lake is 30° and the angle of depression of its reflection in the lake is 60°. The height of the cloud above the lake is
A) 100 m
B) 200 m
C) 300 m
D) 400 m
Answer:
D) 400 m

Question 88.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60. After a flight of 10 seconds, its angle of elevation is observed to be 30 from the same point on the ground. Find the speed of the aeroplane.
A) 415.7 km/h
B) 215.3 km/h
C) 700 km/h
D) none of the above
Answer:
A) 415.7 km/h

Question 89.
If AB = 4m, and AC = 8m, then the angle of elevation of A as observed from C is
A) 30°
B) 45°
C) 60°
D) 90°
Answer:
A) 30°

Question 90.
If a pole of height 6 m casts a shadow 2\(\sqrt{3}\) m long on the ground, then the sun’s elevation is
A) 30°
B) 60°
C) 45°
D) 90°
Answer:
B) 60°

Question 91.
Find the elevation of the sun at the moment when the length of the shadow of a tower is just equal to its height.
A) 30°
B) 45°
C) 60°
D) 90°
Answer:
B) 45°

Question 92.
If the shadow of a tree is \(\frac{1}{\sqrt{3}}\) times the height of the tree, then the angle of elevation of the sun is
A) 30°
B) 45°
C) 60°
D) 90°
Answer:
C) 60°

Telangana SCERT 10th Class Physics Study Material Telangana 9th Lesson Electric Current Textbook Questions and Answers.

TS 10th Class Physical Science 9th Lesson Questions and Answers Electric Current

Improve Your Learning
I. Reflections on concepts

Question 1.
Explain how electron flow causes electric current with Lorentz-Orude’s theory of electrons.
Answer:
1. Lorenti and Drude, scientists of 19th Century proposed that conductors like metals contain large number of free electrons while the positive ions are fixed in their locations. The arrangement of the positive ions is aimed lattice.
2. Assume that a conductor is an open circuit. The electrons move randomly in lattice space of a conductor as shown in the following figure.

3. When the electrons are in random motion, they can move in any direction.

4. Hence if we imagine any cross-section as In above figure, the number of electrons, crossing the cross-section of a conductor from left to right in one second is equal to that of electrons passing the cross-section from right to left in one second and the nett charge moving along conductor through any cross-section Is zero when the conductor is in open circuit.

5. When the ends of the conductor are connected to a source (say, battery) through a bulb, the bulb glows because energy transfer takes place from battery to the bulb.

6. As the electrons are responsible for transfer of energy from battery to the bulb, they must have an ordered motion.

7. When the electrons are in ordered motion there will be a net charge crossing any cross-section of the conductor.

8. This ordered motion of electrons Is called electric current.

Question 2.
Write the difference between potential difference and emf.
Answer:

Question 3.
How can you verify that the resistance of a conductor is temperature dependent?
Answer:

1. Take a bulb and measure the resistance of the bulb using a multimeter in open circuit. Note the value of the resistance.
2. Now connect the bulb in a circuit and switch on the circuit.
3. After a few minutes the bulb gets heated.
4. Now measure the resistance of the bulb again with multimeter.
5. The value of resistance of the bulb in second instance is more than the resistance of the bulb in open circuit.
6. Here the increase in temperature of the filament in the bulb is responsible for increase in resistance of the bulb.
7. Thus the value of resistance of a conductor depends on the temperature.

Question 4.
What do you mean by electric shock? Explain how it takes place.
Answer:

• If we touch live wire of 240V which gives 0.0024 A of current flows through the body the function g of organs inside the body gets disturbed.
• This disturbance inside the body is felt as electric shock.
• If the current flow continues further, it damages the tissues of the body which leads to decrease ¡n resistance of the body.
• When this current flows for a longer time, damage to the tissues increases and there by the resistance of human body decreases further.
• Hence, the current through the human body will increase.
• If this current reaches 0.07 A, it affects the functioning of the heart.
• If this current passes through the heart for more than one-second t could be fatal.

Question 5.
Draw a circuit diagram for a circuit in which two resistors A and B are connected in series with a battery and a voltmeter is connected to measure the potential difference across the resistor A.
Answer:
A circuit diagram in which two resistors A and B are connected ¡n series with a battery and a voltmeter is connected to measure the p.d. across the resistor A.

Question 6.
In the below figure, the potential at A is ……………………… when the potential at B is zero.

Answer:
Apply Kirchoff’s loop rule V_A-5 x 1 – 2—V_b=0
V_A-5 – 2-0 =0 ⇒V_A = 7V
The potential at A = 7V when the potential at B = O

Question 7.
How does a battery work? Explain.
Answer:
1. A battery consists of two metal plates (electrodes) and a chemical (electrolyte).
2. This electrolyte consists positive and negative ions which move In opposite directions.
3. This electrolyte exerts a force called chemical force (F_c) to make the ions move in a specified direction.
4. Positive Ions move towards one plate and accumulate on that. As a result this plate becomes positively charged (Anode).

5. Negative Ions move to another plate and accumulate on that. As a result of this the plate becomes negatively charged (Cathode).
6. This accumulation continues till both plates are sufficiently charged.
7. But the ions experience another force called electric force (F_e) when sufficient number of charges accumulated on the plates.
8. The direction of F_e is opposite to F_c and magnitude depends on the amount of charge accumulated on the plates.
9. The accumulation of charges on plates is continuous till F_e becomes equal to F_c Now there will not be any motion due to balance of F_e and F_c.

10. The new battery that we buy from the shop is under the Influence of balanced forces. This Is the reason for the constant RD. between the terminals of a battery.

11. When a conducting wire Is connected to the terminals of the battery, a RD. is created between the ends of the conductor which sets up an electric field through-out the conductor.

12. The large number of electrons In the conductor, near the positive terminal of the battery are attracted by It and start to move towards positive terminal. As a result the amount of positive charge on this plate decreases. So F_e becomes weaker than F_c and F_c pulls negative ions from anode towards cathode.

13. The negative terminal pushes one electron into the conductor because of stronger repulsion between negative terminal and negative ion.

14. Hence. the total number of electrons in the conductor remains constant during the current flow. The above-said process continues till F_e = F_c.

Question 8.
Explain Kirchhoff’s laws with examples.
Answer:
Kirchhoffs laws:
1. The junction law: At any junction point in a circuit where the current can divide, the sum of the currents in the junction must equal to the sum of the currents leaving the junction.
This means that there is no accumulation of electric charges at any junction in a circuit. Eg: ‘P Is the junction
I₁, I_4, and I₆ are the currents into the junction.
I₂, I_3, and I₅ are the currents leaving the junction.
According to Kirchhoff’s junction law
I₁+I₄+I₆ = I₂+I₃+I₅

2) The loop law: The algebraic sum of the increases and decreases in potential difference across various components of a closed circuit loop must be zero.
Eg: For the loop ACDBA
-V₂+I₂R₂-I₁R₁ +V₁=O
For the loop EFDCE
– (I₁ + I₂) R₃ -I₂R₂ + V₂ = O
For the loop EFBAE
-(I₁+I₂)R₃-I₁R₁+V₁=O

Question 9.
Deduce the expression for the equivalent resistance of three resistors connected In series.
Answer:
Two or more resistors are said to be connected in series if the current flowing through one, also flows through the others.
In series combination, we know that
1. The same current passes through the resistors.
2. The potential difference across combination of resistors is equal to the sum of the voltages across the individual resistors.
Connect the circuit as shown n the figure.
The cell connected across the series combination of 3 resistors maintains a potential difference (v) across the combination. The current through the combination is I.


Let us replace the combination of 3 resIstors by a single resistor R_eq such that current does not change.
R_eq is given by Ohm’s law as
R_eq = \( \frac{V}{I}\)
⇒V=IR_eq

The potential differences V₁, V₂, V₃ across the resistors R₁, R₂ and R₃
respectively are given by Ohm’s law as
V₁ = IR₁, V₂ = IR₂, V = IR₃
Since the resistances are connected in series
V= V₁ +V₂+V₃
IR_eq = IR₁ + IR₂ + IR₃
I (R_eq) = I (R₁ + R₂ + R₃)
⇒ R_eq = R₁ + R₂ + R₃
Similarly, for n resistors connected in series,
R_eq = R₁ + R₂ + R₃+ ………………………. +R_n.

Question 10.
Deduce the expression for the equivalent resistance of three resIstors connected In parallel.
Answer:
If resistances are connected in such a way that the same potential difference gets applied across each of them, they are said to be connected In parallel.

For a parallel combination, we know that,

1. The total current flowing Into the combination is equal to the sum of the currents passing through the individual resistors ⇒ I = I₁+ I₂+ I₃
2. The potential difference remains constant V₁ = V₂ = V₃ = V.
   Connect the circuit as shown in the figure.
3. The cell connected across 3 resistors maintains the same potential difference across each resistor.
4. The current I gets divided at A into 3 parts I₁ I₂ and I₃ which flows through R₁, R_2, and R₃ respectively.
5. Let us replace the combination of resistors by an equivalent resistance R_eq such that potential difference across the circuit does not change.
6. The equivalent resistance R_eq = \(\frac{V}{I} \Rightarrow I=\frac{V}{R_{e q}}\)
7. The currents I₁,I₂,I₃ across R₁,R₂ and R3 are given by I₁ = \(\frac{V}{R_1}\), I₂ = \(\frac{V}{R_2} \), I₃ = \(\frac{V}{R_3} \),

Since the resistors are in parallel,

Question 11.
What is the value of 1KWH in joules?
Answer:
1 KWH = (1000 J/s) (60 × 60s) = 3600 × 1000J = 3.6 × 10⁶ So, 1KWH is equal to 3.6 x 10⁶ Joules.

Question 12.
Silver is a better conductor of electricity than copper. Why do we use copper wire for conduction of electricity?
Answer:
Reasons:

• Copper has low resistivity. When electricity is passed through copper wires, the power losses in the form of heat are very small.
• Cost of copper versus that of silver metal, copper is less expensive.
• Copper has flexibility and resistance to breakage.
• Copper is cheaply available than silver.

Application of concepts

Question 1.
Explain overloading of household circuit.
Answer:

1. Electricity enters our homes through two wires called lines. These lines have low resistance and the potential difference between the wires is usually about 240 V.
2. All electrical devices are connected in parallel in our home. Hence, the potential drop across each device is 240 V.
3. Based on the resistance of each electric device, it draws some current from the supply. Total current drawn from the mains is equal to the sum of the currents passing through each device.
4. If we add more devices to the household circuit the current drawn from the mains also increases.
5. This leads to overheating and may cause a fire. This is called “overloading”.

For example:
If we switch on devices, such as heater shown in the figure, from the mains exceeds the maximum limit 20 A.

Question 2.
Why do we use fuses in household circuits?
Answer:

1. The fuse consists of a thin wire of low melting point.
2. To prevent damages due to overloading we connect an electric fuse to the household circuit.
3. When the current in the fuse exceeds 20A, the wire will heat up and melt.
4. The circuit then becomes open and prevents the flow of current into the household circuit. So all the electric devices are saved from damage that could be caused by overload.
5. Thus, we can save the household wiring and devices by using fuses.

Question 3.
Two bulbs have ratings 100W, 220V, and 60W, 220V. Which one has the greater resistance?
Answer:
Resistance of first bulb R₁ = \(\frac{V^2}{P}=\frac{220 \times 220}{100}\) = 484 Ω
Resistance of second bulb R₂ = \(\frac{V^2}{P}=\frac{220 \times 220}{60}=\frac{4840}{6}\) = 806.6Ω
∴ The bulb rated 60W, 220V has higher resistance.

Question 4.
Why don’t we use series arrangement of electrical appliances like bulb, Television, fan and others in domestic circuits?
Answer:

1. We have seen that in a series circuit, the current is constant throughout the electric circuit.
2. But it is obviously impracticable to connect an electric bulb and an electric heater in series because they need currents of widely different values to operate properly.
3. Another major disadvantage of a series circuit is that when one component fails, the circuit is broken and none of the other components works.

Question 5.
Are the headlights of a car connected in series or parallel? Why?
Answer:
The headlights of a car are connected in parallel.
Reason:

• When they are connected in parallel, same voltage (P.D) will be maintained in the two lights.
• If one of the lights damaged, the other will work without any disturbance.

Question 6.
Why should we connect electric appliances in parallel in a household circuit? What happens if they are connected in series?
Answer:
We should connect the electric appliances in parallel to household circuit because

• Each appliance gets the full voltage.
• The parallel circuit divide the current through the appliances. Each appliance gets proper current depending on its resistance.
• If one appliance is switched on/off others are not affected.

If appliances are connected in series the following disadvantages are arised:

• The same current will flow through all the appliances, which is not desired.
• Total resistance becomes large and the current gets reduced.
• We cannot use independently on/off switches with individual appliances.
• All appliances have to be used simultaneously even if we don’t need them.

Question 7.
If the resistance of your body is 10000012, what would be the current that flows in your body when you touch the terminals of a 12V battery?
Answer:
Resistance of the body (R) 1,00,000 Ω
Potential difference of the battery (V) =12V
Current that flows in the body (I) = ?
According to Ohm’s law, \(\frac{V}{I}\) = R
⇒ I = \(\frac{V}{R}=\frac{12}{1,00,000}\) = 0.00012 A

Question 8.
A wire of length 1m and radius 0.1 mm has a resistance of 100W. Find the resistivity of the material.
Answer:
Resistance of wire, R = 100 Ω
Radius of wire, r = 0.1mm = 1 x 10^-4 m
Length of wire, l = 1m
Formula for resistivity of wire: ρ = \(\frac{R A}{l}=\frac{R \pi r^2}{l} \)
Substituting the given values, ρ = \(\frac{22}{7} \times 10^2 \times \frac{10^{-4} \times 10^{-4}}{l} \) = \(\frac{22}{7} \times 10^{-6} \) ohm—meter
= 3.14 × 10^-6 ohm-mt

Question 9.
Why do we consider tungsten as a suitable material for making the filament of a bulb?
(Or)
What is the reason for using tungsten as a filament in electric bulb?
Answer:
Tungsten has a high resistivity value (5.60 ×10^-8 m) and a high melting point (3422°C). So the filament of a bulb is usually made of tungsten. Its high resistivity enables the filament to become red hot soon and then it produces white heat to emit light. Its high melting point keeps it in a solid state and also prevents oxidation.

Question 10.
How can you appreciate the role of a small fuse in house wiring circuit in preventing damage to various electrical appliances connected to the circuit?
Answer:

1. The fuse consists of a thin wire of low melting point. When the current in the fuse exceeds $20 \mathrm{~A}$, the wire will heat up and melt.
2. The circuit then becomes open and prevents the flow of current into the household circuit. So all the electric devices are saved from change that could be caused by overload.
3. Thus we can save the house holding wiring and devices by using fuses.
4. So we should appreciate the role of fuse in preventing damage to electrical appliances in household circuits.

Question 11.
Uniform wires of resistance 100c are melted and recast into wire of length double that of the original. What would be the resistance of the new wire formed?
Answer:
Before recasting,
Resistance R₁ = 100 Ω
length (l₁)= l (say)
After recasting
Resistance R₂ = ?
length (‘l₂) = 2l

We know that R α l,
\(\frac{R_1}{R_2}=\frac{l_1}{l_2}\)

Higher Order Thinking Questions

Question 1.
Imagine that you have three resistors of 30 Ω each. How many resultant resistances can be obtained by connecting these three in different ways. Draw the relevant diagrams.
Answer:
Let R₁ = 30Ω, R₂ = 30Ω, R₃ = 30Ω
We get different resistors by different combinations as shown below.

Question 2.
A house has 3 tube lights, two fans and a Television. Each tube light draws 40W. The fan draws 80W and the Television draws 60W. On the average, all the tube lights are kept on for five hours, two fans for 12 hours and the television for five hours every day. Find the cost of electric energy used in 30 days at the r ate of Rs. 3.00 per Kwh.
Answer:
Power consumption by tube lights in a day = 40W x 3 x 5H = 600 WH
Power consumption by fans in a day = 80W x 2 x 12H = 1920 WH
Power consumption by television in a day = 60W x 1 x 5H = 300 WH
Total power consumption in a day = 600 + 1920 + 300 = 2820 WH
Power consumption for 30 days = 2820 x 30 = 84600 WH

Rate of 1 KWH = Rs 3/- Total consumption = 84.60 x Rs.3 = Rs. 253.80

Question 3.
Observe the circuit and answer the questions given below:
(i) Are resIstors 3 and 4 In series?
(ii) Is the battery in series with any resistor?
(iii) What is the potential drop across the resistor 3?
(iv) What is the total emf in the circuit if the potential drop across resistor 1 is 6V?
Answer:
(i) No. Resistors 3 and 4 are not in series. They are in parallel.
(ii) No.
(iii) As resistors 3 and 4 are in parallel, same potential difference will be allowed
through them. Hence the potential drop across resistor 3 is 8V.
(iv) Total emf=V₁+V₂+V₃+V₄=6V+14V+8V+8V=36V.

Multiple choice questions

Question 1.
A uniform wire of resistance 50 Q is cut into five equal parts. These parts are now connected in parallel. Then the equivalent resistance of the combination is : ( )
(A) 2 Q
(B) 12 Q
(C) 250 Q
(D) 6250 Q
Answer:
(A) 2 Q

Question 2.
A charge is moved from a point A to a point B. The work done to move unit charge during this process is called ( )
(A) potential at A
(B) potential at B
(C) potential difference between A&B
(D) current from A to B
Answer:
(C) potential difference between A&B

Question 3.
Joule / coulomb is the same as ( )
(A) 1-watt
(B) 1-volt
(C) 1 ampere
(D) 1-ohm
Answer:
(B) 1-volt

Question 4.
The resistors of values 2 Ω, 4 Ω, and 6 Ω are connected in series. The equivalent resistance in the circuit is ( )
(A) 2 Ω
(B) 4 Ω
(C) 12 Ω
(D) 6 Ω
Answer:
(C) 12 Ω

Question 5.
The resistors of values 3 Ω, 6 Ω, and 18 Ω are connected in parallel. The equivalent resistance in the circuit is ( )
(A) 12 Ω
(B) 36 Ω
(C) 18 Ω
(D) 1.8 Ω
Answer:
(D) 1.8 Ω

Question 6.
The resistors of values 6 Ω, and 6 Ω are connected in series and 12 Ω are connected in parallel. The equivalent resistance of the circuit is ( )
(A) 24 Ω
(B) 6 Ω
(C) 18 Ω
(D) 2.4 Ω
Answer:
(B) 6 Ω

Question 7.
The current in the wire depends ( )
(A) only on the potential difference applied
(B) only on the resistance of the wire
(C) on both of them
(D) none of them
Answer:
(C) on both of them

Suggested Experiments

Question 1.
State Ohm’s law. Suggest an experiment to verify it and explain the procedure.
Answer:
A. Ohm’s Law: The potenbal difference between the ends of a conductor is directly proportional toe the electric current passing through it at constant temperature.
Verification:
Aim: To verify Ohm’s law or to show that -=Co,,ctani
Materials required: 5 dry cells of 1.5V each, conducting wires, an ammeter,
a voltmeter, Manganin wire of length 10cm, LED and Key.

Procedure:
1. Connect a circuit as shown in figure.
2. Solder the connecting wires to the ends of the Manganin wire.
3. Close the key.
4. Note the readings of current from Baltery Key ammeter and potential difference from volt meter in the following table.

5. Now connect 2 cells (in series) instead of one cell in the circuit. Note the values of ammeter and voltmeter and record them in the above table.
6. Repeat the same for three cells, four cells, five cells respectively.
7. Record the values of V and I corresponding to each case in the table.
8. Find \(\frac{V}{I} \) for each set of values.
9. We notice that \(\frac{V}{I} \)  is a constant.
V ∝ I ⇒ \(\frac{V}{I} \)= Constant
This constant is known as resistance of the conductor, denoted by R.
⇒ \(\frac{V}{I} \) = R
∴ Ohm’s law is verified.

Question 2.
How do you verify that resistance of a conductor is proportional to the length of the conductor for constant cross-section area and temperature?
Answer:
1. Collect Iron spokes of different lengths with the same cross-sectional area.
2. Make a circuit as shown in the figure.
3. Connect one of the iron spokes between P and Q.
4. Measure the value of the current using the ammeter connected to the circuit and note in your notebook.
5. Repeat this for other lengths of the iron spokes. Note the corresponding values of currents in your notebook as shown below.

1. We observe that current decreases as the length of the spoke increases.
2. We also know that resistance increases as current decreases.
3. Hence the resistance of iron spoke increases as its length increases.
4. We conclude that the resistance of a conductor is directly proportional to its length for a constant-potential difference and constant cross-sectional area.

R ∝ l

Suggested Projects

Question 1.
a. Take a battery and measure the potential difference. Make a circuit and measure the potential difference when the battery is connected in the circuit. Is there any difference in potential difference of battery?
Answer:

1. The potential difference across the terminals of a battery when it is not connected in any circuit is called the Electromotive force of battery or emf of battery.
2. As soon as the battery is connected to an external circuit, there will be a current through the battery as well as the external circuit.
3. Due to this current flowing through the battery, there will be a voltage drop inside the battery because of the internal resistance of the battery itself.
4. Hence when external circuit is connected, the voltage appeared across the terminal of the battery is somewhat less than the open circuit voltage of the battery.
5. This is because of voltage drop due to internal resistance ¡nside the battery.

b. Measure the resistance of a bulb (filament) in open circuit with a multimeter. Make a circuit with elements such as bulb, battery of 12V and key in series. Close the key. Then again measure the resistance of the same bulb (filament) for every 30 seconds. Record the Observations in a proper table. What can you conclude from the above results?
Answer:
Materials required: a bulb, 12 v battery, key, and multimeter.

Procedure:

1. Measuretheresistanceofabulb in open circuit.
2. Connect the bulb, battery and a key in series in a circuit as shown in fig.
3. Close the key and measure the resistance of a bulb for every 30 seconds with a multimeter and note down them in the following table.

Observations: Resistance of the bulb in open circuit = 4.3 Q.

Conclusion:

1. From the above observations, it is clear that the resistance of a bulb (filament increases as the time increases.
2. This Is because, as the current passes through the filament of a bulb, filament gets heated up and its temperature increases.
3. As the temperature of the filament increases, its 20 resistance also increases
4. So, the resistance of a conductor depends upon its temperature.

Question 2.
Calculate the resistance of venous bulbs that you use at your home and find which one is having higher / lower resistance value. Write the report on your observations.
Answer:
We are using following types of bulbs in my bouse,

1. In candescent bulb (100 W)
2. Fluorescent tube lights (40 W)
3. CFL lamp (20 W)
4. LED bulb (10 W)

Conclusion:

• From the above observations, it is clear that the LED bulb of low wattage has higher resistance.
• So, it is clear that the resistance of a electrical appliance is more ¡f its wattage is less.

Question 3.
Collect the information and prepare a report on power consumption in your home/school.
Answer:
In my house, we are using the following electric appliances.
Tubelights (40 W) – 3 (Using daily each for 8 hours)
Fans(80 W) – 3 (UsIng daily each for 10 hours)
Television (60 W) – 1 (UsIng daily each for S hours)
Electric heater (1000 W) – 1 (Using daily each for 30 mm)

Calculation of power consumption :

Total electric energy consumed Per Day = 4160 WH

Conclusion:
Total electric energy consumed for one month (30 days) = 4160 x 30 = 1248000
Total electric energy consumed for one month in KWH = \(\frac{124800}{1000} \) = 124.8 KWH
∴ We are consuming nearly 125 KWH (units) of electric energy in my house in a month.

TS 10th Class Physical Science Electric Current Intext Questions

Page 176

Question 1.
What do you mean by electric current?
Answer:
The flow of electrons in a particular direction is called electric current.

Question 2.
Which type of charge (+ve or -ve) flows through an electric wire when it is connected in an electric circuit?
Answer:
Electrons carry nagative charge. So negative charge flows through circuit.

Question 3.
Is there any evidence for the motion of charge in daily life situations?
Answer:

1. Lightning, which is observed in the sky at the time of heavy rain is an evidence for the motion of charge in the atmosphere.
2. When we put the switch of an electric lamp ‘on’, the bulb glows. It is also evidence to motion of charge.

Question 4.
Does motion of charge always lead to electric current?
Answer:
Yes.

Question 5.
What do you notice in activity 1?
Answer:
The bulb glows.

Page 177

Question 6.
Can you predict the reasons for the bulb not glowing in situations 2 & 3?
Answer:

1. In situation 2, the source of current, namely battery is removed from circuit. So the bulb does not glow.
2. In situation 3, nylon wires do not conduct electricity. Nylon is a non-conductor. So the bulb does not glow.

Question 7.
Why do all materials not act as conductors?
Answer:
The materials in which electrons do not move freely do not act as conductors.

Question 8.
How does a conductor transfer energy from source to bulb?
Answer:
The electrons in a conductor move randomly in lattice space of conductor. These electrons transfer energy from source to bulb.

Question 9.
What happens to the motion of electrons when the ends of the conductor are connected to the battery?
Answer:
When the ends of the conductor are connected to the battery, the transfer of charged particles takes place from battery to bulb and again to the battery. As the circuit is complete and closed the bulb glows.

Page 178

Question 10.
Why do electrons move in specified direction?
Answer:
When the conductor Is connected to a battery, a uniform electric field is set up throughout the conductor. This field makes the electrons move towards positive end.

Question 11.
In which direction do the electrons move?
Answer:
The free electrons in the conductor are accelerated by the electric field and move in a direction opposite to the direction of the field.

Question 12.
Do the electrons accelerate continuously?
Answer:
No

Question 13.
Do they move with constant speed?
Answer:
The electrons collide with lattice ions, lose energy and may even come to rest at every collision.

Page 179

Question 14.
Why does a bulb glow immediately when we switch on?
Answer:
When we switch on any electric circuit, irrespective of length of the connecting wire, an electric field is set up throughout the conductor instantaneously, due to the potential difference of the source connected to the circuit. This electric field makes all the electrons move in a specified direction simultaneously. So the bulb glows immediately.

Question 15.
How can we decide the direction electric current?
Answer:
The direction of electric current is determined by the signs of the charge (q) and drift speed (y).

Page 180

Question 16.
How can we measure electric current?
Answer:
We can measure electric current, using an Ammeter.

Question 17.
Where do the electrons get energy for their motion from?
Answer:
The field exerts a force on the charge (electrons) The free charges accelerate the electric field, if the free charges ar electrons, then the direction of electric force on them ‘s opposite to the direction of electric field. It means that the electric field does some work to move free charges in a specified direction.

Question 18.
Can you find the work done by the electric force?
Answer:
Work done by the electric force on a free charge q ‘s given by W = EJ.

Page 181

Question 19.
What Is the direction of electric current In terms of potential difference?
Answer:
In terms of potential difference, the direction of electric current is from positive terminal to the negative terminal.

Question 20.
Do positive charges move In a conductor? Can you give an example of this?
Answer:
In electrolytic positive charges move towards of negative electrode.

Question 21.
How dosas battery maintain a constant potential difference between Ita terminals?
Answer:
The accumulation of charge on plates continues till the electric force F becomes equal to chemical force F, At this situation, the potential difference between the terminals Is maintained constant.

Question 22.
Why does the battery discharge when ita positive and negative terminals are connected through s conductor?
Answer:
When a conducting wire is connected to the terminals of the battery, a potential difference Is created between the ends and it sets up an electric field throughout the conductor. The electrons near the positive terminal of the battery are attracted by it and start moving towards positive terminal. As a result, the amount of positive charge on the plate decreases and the F becomes weaker than F. So the battery becomes discharged.

Page 182

Question 23.
What happens when the battery is connected in a circuit?
Answer:
When a conducting wire is connected to the terminals of the battery, a potential difference is created between the ends of the conductor. This potential difference sets up an electric field throughout the conductor and Its direction is from positive terminal to negative terminal In the conductor.

Page 183

Question 24.
How can we measure potential difference or emf?
Answer:
Generally, a voltmeter s used to measure potential difference or emf.

Page 184

Question 25.
Is there any relation between emf of battery and drift speed of electrons in the conductor connected to a battery?
Answer:
The ratio of emf and drift speed of electrons Is constant for some materials at constant temperatures.

Page 186

Question 26.
Can you guess the reason why the ratio of V and I in case of LED Is not constant?
Answer:
LED (Light Emitting Diode) is made up of semiconducting material. It is non Ohmic material and so the ratio of V and I in case of LED is not constant.

Question 27.
Do all materials obey Ohm’s law?
Answer:
No. Some materials such as silicon, germanium etc. do not obey Ohm’s law.

Question 28.
Can we classify the materials based on Ohm’s law?
Answer:
Yes. Based on Ohms’s law materials are classified into three categories.
They are:

• Ohmic materials,
• Non-Ohmic materials and
• Semiconductors.

Question 29.
What is resistance?
Answer:
Resistance of a conductor is the obstruction to the motion of electrons in a conductor.

Question 30.
Is the value of resistance the same for all materials?
Answer:
No. Silver and copper have least resistance value. Other materials such as iron, aluminum etc. have little higher resistance values. Tungsten has a very high resistance value.

Question 31.
Is there any application of Ohm’s law in daily life?
Answer:
Ohm’s law has a wide application in daily life:

1. We use materials like copper which are ohmic conductors to make household electrical wiring and in Industries.
2. Semiconductors which find an extensive application in modern electronic devices such as TV, DVD, Computers etc., are made up of non-ohmic materials.
3. The fuse, a device which protects household electrical appliances from high-voltage electric currents, is also an application of Ohm’s law.

Question 32.
What causes electric shock in the human body-current or voltage?
Answer:
It Is the electric current that causes electric shock in the human body. When 0.0024 Amperes of current flows through human body the functioning of organs inside the body gets disturbed. This disturbance inside the body Is felt as electric shock. ¡f the current flow continues further, It damages the tissues of the body which leads to decrease in resistance of the body.

Page 187

Question 33.
Do you know the voltage of mains that we use in our household circuits?
Answer:
The voltage of mains that we use in our household circuits is 240V. Usually, it varies between 220V and 240V.

Question 34.
What happens to our body if we touch live wire of 240V?
Answer:
The current passing through our body when we touch a live wire of 240V is given by, I= \(\frac{240}{100000}\) = 0.024 A
When this quantity of current flows through the body the functioning of organs inside the body gets disturbed. This disturbance inside the body is felt as electric shock and damages the tissues of the body.
When this current flows for a longer time, damage to tissues increases and resistance of body decreases.
A current of 0.07A, effects the functioning of heart and it may lead to fatal consequences.

Page 188

Question 35.
Why does not a bird get a shock when it stands on a high-voltage wire?
Answer:

1. There are two parallel transmission lines on electric poles.
2. The p.d. between the two lines is 240 V throughout their lengths.
3. When the bird stands on a high-voltage wire, there is no potential difference between the legs of the bird because it stands on a single wire.
4. If the two lines are connected across by a conducting device, then only current flows between the wires.
5. As the bird stands on a single wire no current passes through its body.
6. So, it does not feel any electric shock.

Page 189

Question 36.
What could be the reason for an increase in the resistance of the bulb when current flows through it?
Answer:

1. As the bulb glows it gets heated.
2. The increase in temperature of the filament in the bulb is responsible for increase in resistance of the bulb since resistance is temperature dependent.

Question 37.
What happens to the resistance of a conductor If we increase its length?
Answer:
The resistance of a conductor increases with the increase in its length.i.e., R α l

Page 190

Question 38.
Does the thickness of a conductor influence its resistance’?
Answer:
Yes. The resistance of a conductor decreases with Increase in Its thickness. i.e., R α\(\frac{1}{A}\) (A = thickness or cross-section area of conductor)

Page 192

Question 39.
How are electric devices connected in circuits?
Answer:
Electric devices are connected in circuits either is series combination or an parallel combination.

Page 193

Question 40.
What do you notice in activity 6?
Answer:
In series connection of resistors, there Is only one path for the flow of current in the circuit. If the current in the entire circuit is I, It Is the same current lin the parts also.

Question 41.
What do you mean by equivalent resistance?
Answer:
If the current drawn by a resistor is equal to the current drawn by the combination of resistors, then the resistor is called as equivalent resistor.

Question 42.
What happens when one of the resistors In series breaks down?
Answer:
When one of the resistors In senes combination breaks down, the circuit becomes open and flow of current cannot take place In the circuit.

Question 43.
Can you guess in what way household wiring has been done?
Answer:
The household wiring has been done in parallel combination because
(i) the equivalent resistance of the parallel combination is less than the resistance of each of the resistors and (ii) through one of the resistors in parallel combination is cut off the other resistors continue to work.

Page 194

Question 44.
How much current is drawn from the battery?
Answer:
Measure the current (1) drawn from the battery using the ammeter and it Is 1.5 amps.

Question 45.
Is it equal to Individual currents drawn by the resistors?
Answer:
Yes, the current drawn from the battery‘s equal to the sum of individual currents drawn by the individual resistors (here bulbs).
That is, I=I₁ +I₂+I₃+ ……………………….. .

Page 199

Question 46.
You might have heard the sentence like “this month we have consumed 100 units of current”. What does unit mean?
Answer:
The electric appliances that we use n our daily life consume electric energy.
This energy Is measured in units.
i.e., 1 unit = 1 K.W,H. (Kilo Watt hour)
⇒ 1 K.W.H = 1000 W.H.

Question 47.
A bulb Is marked “60w and 120V”. What do these values Indicate?
Answer:
60 W and 120 V’ marked on a bulb indicates that If the bulb is connected to 120 volts mains, it will be able to convert 60 Watts of electrical energy into heat or light in one second.

Page 200

Question 48.
What is the energy lost by the charge in 1 Sec?
Answer:
The energy lost by the charge is equal to W/t where W = Work done and ‘t’ is the time in seconds.

Page 201

Question 49.
What do you mean by overload?
Answer:

1. Electricity enters our homes, through two wires called lines.
2. These line wires have low resistance and the p.d. of the wires is usually 240V.
3. These two line wires run throughout the household circuit to which we connect various appliances such as bulbs, fans, TV, refrigerator, air cooler etc.
4. These appliances are connected in parallel combination.
5. It we add more devices to the household circuit the current drawn from the mains abnormally increases. This is called overload.

Question 50.
Why does It cause damage to electric appliances?
Answer:

1. The maximum current that we can draw from the mains is 20A.
2. When the current drawn from the mains Is more than 20A, overheating occurs and may cause a fire.
3. It also causes damage to electrical appliances.

Question 51.
What happens when this current Increases greatly?
Answer:
When the current drawn from the mains is more than 20A, overheating occurs and may cause breaking of fire. This is called overloading and causes the damage of electrical appliances. Sometimes it may lead to fire accidents

Page 202

Question 52.
How can we prevent damage due to overloading?
Answer:
To prevent damage due to overloading an electric fuse is connected in the household circuit.

Think And discuss

Question 1.
What do you mean by short circuit?
Answer:
Short circuit means a connection across an electric circuit with a very low resistance, by an insulation failure etc. Current passes through this by pass.

Question 2.
Why does a short circuit damage electric wiring and devices connected to it?
Answer:
As the current takes short cut, which results in heating or burning which damages the wiring and devices connected to it.

TS 10th Class Physical Science Electric Current Activities

Activity 1

Question 1.
Write an activity to check when a bulb glows in a circuit.
Answer:
Aim: To check when a bulb glows In a circuit.
Materials required:

1. A bulb
2. a battery
3. a switch
4. insulated copper wire

Procedure (1):

• Take a bulb, a battery, a switch and few insulated copper wires.
• Connect the ends of the copper wires to the terminals of the battery through the bulb and switch.
• Now switch on the circuit.

Observation (1): The bulb glow.
Procedure (2):

• Remove the battery from the circuit and connect the remaining components to make a complete circuit.
• Again switch on the circuit and observe the bulb.

Observation (2): The bulb does not glow.
Result: The battery contains charges which glows the buLb.

Lab Activity

Question 2.
State Ohm’s law. Suggest an experiment to verify it and explain the procedure.
Answer:
Aim: To show that the ratio V/I is a constant for a conductor.
Materials required: 5 dry cells of 1.5V each, conducting wires, an ammeter, a voltmeter, thin iron spoke of length 10 cm, LED, and key.

Procedure:

• Connect a circuit as shown in figure.
• Solder the conducting wires to the ends of the iron spoke
• Close the key.
• Note the readings of current (I) from ammeter and potential difference. (V) from voIt meter in the table given below.

• Now connect two cells in the circuit and note the respective readings of ammeter and voltmeter in the above table.
• Repeat the above procedure using three cells and four cells and five cells respectively.
• Record the values of potential difference (V) and current (I) corresponding to each case in the above table.
• Find V/I for each set of values.
• We notice that V/I Is a constant.
• From this experiment, we can conclude that the potential difference between the ends of the iron spoke is directly proportional to the current passing through it.

Activity 2

Question 3.
Conduct an activity to show that the resistance of a conductor is temperature dependent.
Answer:

1. Take a bulb and measure the resistance of the bulb using a multimeter in open circuit. Note the value resistance.
2. Now connect the bulb in a circuit and switch on the circuit.
3. After few minutes the bulb gets heated.
4. Now measure there’s distance of the bulb again with multimeter.
5. The value of resistance of the bulb in second instance Is more than the resistance of the bulb In open circuit.
6. Here the increase in temperature of the filament in the bulb is responsible for increase In resistance of the bulb.
7. Thus the value of resistance of a conductor depends on the temperature.

Activity 3

Question 4.
Show that the resistance of a conductor depends on the material of the conductor.
Answer:

1. Collect different metal rods of the same length and same cross-sectional area like copper, aluminum, iron, etc.
2. Make a circuit as shown in the figure.
3. p and Q are the free ends of the conducting wires Different metal rods are connected between P and Q.
4. Connect one of the metal rods between the ends P and Q.
5. Switch on the circuit.
6. Measure the current using the ammeter connected to the circuit and note it in your notebook.
7. Repeat this with other metal rods and measure electric current In each case.
8. We notice that the values of current are different for different metal rods for a constant potential differences.
9. Hence, we conclude that the resistance of a conductor depends on the material of the conductor.

Activity 4

Question 5.
Conduct an activity to show that resistance of a conductor is proportional to the length of the conductor for constant cross-section area and temperature.
Answer:

1. Collect iron spokes of different lengths with Metal rods at different lengths are connected between P and Q same cross-sectional area
2. Make a circuit leaving gap between P and Q as shown in figure.
3. Connect one of the Iron spokes say 10 cm long between P and Q
4. Measure the value of current using ammeter connected to the circuit and note the value of current.
5. Repeat this experiment for other lengths say 20cm, 30 cm, 40 cm of iron spokes and note the corresponding values of current In each case.
6. We notice that the value of current decreases with increasing in the length of the iron spoke
7. Thus the resistance of iron spoke increases with Increasing in the length i.e R α l
8. From this we conclude that the resistance (R) of a conductor is directly proportional to its length (I) for a constant area of cross-section.

∴ R α l (at constant temperature and cross-sectional area)

Activity 6

Question 6.
Show that the resistance of a conductor is inversely proportional to its cross sectional area.
Answer:

1. Collect iron rods of equal lengths but different cross-section areas.
2. Make a circuit leaving gap between P and Q as shown In figure
3. Connect one of the rods between P and Q and measure the current using ammeter and note values.
4. Repeat this with the other rods and note the corresponding values of current in each case and note them. :
5. You will notice that the current flowing through the rod increases Increase In the cross-section area of the rod.
6. Thus the resistance of the rod decreases with Increase in the cross-section area. From this, we conclude that the resistance (R) of a conductor is inversely proportional to its cross-section area (A)

∴ R α \(\frac{l}{\mathrm{~A}}\) (at constant temperature and length of the conductor)

Activity 7

Question 7.
Conduct an activity to show that potential difference of combination of resistors, connected in series, is equal to sum of the P.D.S of individual resistors.
Answer:

1. Connect three bulbs which act as resistors in series, with a battery, ammeter and a plug key.
2. Now connect a voltmeter In the circuit across AB, close the key and note the voltage (V) across the series combination of resistors. Note the reading As V.
3. Similarly connect the voltmeter across the resistors, one at a time and measure the voltage across them as V₁, V_2, and V₃.
4. You will find that V=V₁ +V₂ + V₃

5. From this we conclude that “the potential difference across a combination of resistors, connected In serles, is equal to the sum of the voltages across the individual resistors”.

Question 8.
Prove that the current drawn from the battery Is equal to the sum of Individual currents drawn by the resistor, when they are connected in parrallel, with an activity.
Answer:

1. Connect three bulbs which act as resistors in parallel combination (see figure).
2. To this combination connect a cell ammeter and a plug key.
3. Close the key and note the ammeter reading, This gives the current ‘1’ In the circuit.
4. Now connect the ammeter in the branch of the circuit that has R, and note the reading. This gives the current I₁ through the branch.
5. Similarly, place the ammeter in the branches containing R₂ and R₃ and measure the currents I₂, and I₃ respectively.
6. You will find that the current ‘I’ gets divided into the branches such that I= I₁+ I₂ + I₃
7. From this activity, we conclude that “The total Current flowing Into the parallel combination is equal to the sum of the currents passing through the individual resistors.”

Solving these TS 10th Class Maths Bits with Answers Chapter 1 Real Numbers Bits for 10th Class will help students to build their problem-solving skills.

Real Numbers Bits for 10th Class

Question 1.
\(\sqrt{4}\) is
A) a rational number
B) an irrational number
C) an odd number
D) none of these
Answer:
A) a rational number

Question 2.
The logarithmic form of 64 = 2⁶ is
A) log₂64 = 6
B) log₆64 = 2
C) log₄64 = 2
D) log₃64 = 6
Answer:
A) log₂64 = 6

Question 3.
The exponential form of \(\log _4 1024\) = 5 is = 5 is
A) 5⁴ =1024
B) 6⁴ = 1024
C) 4⁵ = 1024
D) 2⁸ = 1024
Answer:
C) 4⁵ = 1024

Question 4.
If log₂8 = y, then y =
A) 3
B) 4
C) 6
D) 10
Answer:
A) 3

Question 5.
log₃729 = x, then x =
A) 243
B) 81
C) 9
D) 6
Answer:
D) 6

Question 6.
log 15 =
A) log 1 + log 5
B) log 10 + log 5
C) log 3 + log 5
D) log 3 × log 5
Answer:
C) log 3 + log 5

Question 7.
The HCF of the least prime number and the least composite number is
A) 1
B) 3
C) 4
D) 2
Answer:
A) 1

Question 8.
The L.C.M of 36 and 54 is
A) 18
B) 108
C) 36
D) 54
Answer:
B) 108

Question 9.
The sum of the exponents of the prime factor in the prime factorisation of 108 is
A) 5
B) 6
C) 4
D) 1
Answer:
A) 5

Question 10.
\(1 . \overline{23}\) is
A) a rational number
B) an irrational number
C) an integer
D) a natural number
Answer:
A) a rational number

Question 11.
The HCF of 6, 72 and 120 is
A) 12
B) 15
C) 6
D) 3
Answer:
C) 6

Question 12.
The LCM of 8, 9 and 25 is
A) 200
B) 1800
C) 225
D) 72
Answer:
B) 1800

Question 13.
The rational number in between and \(\sqrt{1}\) and is
(A) \(\frac{9}{4}\)
(B) \(\frac{3}{4}\)
(C) \(\frac{5}{4}\)
(D) \(\frac{5}{4}\)
Answer:
(B) \(\frac{3}{4}\)

Question 14.
Set of Rational and irrational numbers are called
A) Real numbers
B) Natural numbers
C) Whole numbers
D) Integers
Answer:
A) Real numbers

Question 15.
log form of 3⁵ = 243 is …..
A) \(\log _3^{243}\) = 5
B) \(\log _5^{243}\) = 3
C) \(\log _3^{243}\) = 5
D) \(\log _5^{243}\) = 5
Answer:
A) \(\log _3^{243}\) = 5

Question 16.
the symbol of “implies” is ……….
A) ⇔
B) ⇒
C) ∀
D) ∃
Answer:
B) ⇒

Question 17.
The prime factorisation of 729 is ………..
A) 36
B) 35
C) 34
D) 38
Answer:
A) 36

Question 18.
If ‘x’ and ‘y’ are two prime numbers then their HCF
A) 3⁶
B) 3⁵
C) xy
D) x + y
Answer:
B) 3⁵

Question 19.
\(\log _{10}^{0.01}\) = ……..
A) -1
B) 1
C) -2
D) 2
Answer:
C) -2

Question 20.
The number of odd numbers in between O’ and 100 is …. ( )
A) 100
B) 51
C) 49
D) 50
Answer:
D) 50

Question 21.
The exponential form of \(\log _4^8\) = x is …………..
A) x⁸ = 4
B) x⁴ = 8
C) 4^x = 8
D) 8^x = 4
Answer:
C) 4^x = 8

Question 22.
The value of \(\frac{36}{2^3 \times 5^3}\) in decimal form is ………
A) 0.036
B) 0.36
C) 0.0036
D) 3.6
Answer:
A) 0.036

Question 23.
LCM of two numbers is 108 and their HCF is 9 and one of them is 54. So the second one is ( )
A) 9
B) 18
C) 6
D) 12
Answer:
B) 18

Question 24.
The number of prime factors of 36 is
A) 4
B) 3
C) 2
D) 1
Answer:
C) 2

Question 25.
The exponential form of \(\log _{10}^{0.001}\) = – 3 is ……
A) (0.001)¹⁰ = -3
B) (-3)¹⁰ = 0.001
C) 10³ = -0.001
D) 10^-3 = 0.001
Answer:
D) 10^-3 = 0.001

Question 26.
Which of the following in not a rational number …… ( )
A) \(\log _{10}^3\)
B) \(5 . \overline{23}\)
C) 12.123
A) \(\frac{10}{19}\)
Answer:
A) \(\log _{10}^3\)

Question 27.
LCM of 24 and 36 is ……. ( )
A) 24
B) 36
C) 72
D) 864
Answer:
C) 72

Question 28.
H.C.F. of 324 and 360 is …… ( )
A) 9
B) 1
C) 63
D) 36
Answer:
B) 1

Question 29.
\(\log _x \sqrt[3]{x}\) = …… ( )
A) 3
B) \(\frac{1}{3}\)
C) \(0 . \overline{3}\)
D) B and C
Answer:
D) B and C

Question 30.
\(\log _4 8^2\) …………………..
A) 4
B) 8
C) 2
D) 3
Answer:
A) 4

Question 31.
Last digit of 5¹⁰⁰ is ………..
A) 5
B) 6
C) 0
D) Cannot say
Answer:
C) 0

Question 32.
log₁₀0 …….
A) does not exist
B) 1
C) 0
D) exist
Answer:
B) 1

Question 33.
If log 2 = 0.30103, then log 32 = ( )
A) 4.81648
B) 1.50515
C) 9.63296
D) 9.0309
Answer:
A) 4.81648

Question 34.
If log₁₀ 0.00001 = x, then x =
A) 4
B) -4
C) 5
D) -5
Answer:
D) -5

Question 35.
If log_aax² – 5x + 8 = 2, then x = ….
A) 2 or 3
B) 5 or 7
C) -2 or -3
D) 8 or -2
Answer:
D) 8 or -2

Question 36.
log₃x² = 2 then x =
A) 2
B) -2
C) 3
D) -3
Answer:
C) 3

Question 37.
\(\log _9 \sqrt{3 \sqrt{3 \sqrt{3}}}\) = ……….
A) \(\frac{7}{8}\)
B) \(\frac{7}{16}\)
C) \(\frac{7}{16}\)
D) \(\frac{1}{8}\)
Answer:
A) \(\frac{7}{8}\)

Question 38.
log₈128 =
(A) 7/3
(B) 16
(C) 2048
(D) 136
Answer:
(D) 136

Question 39.
Which of the following is an irrational number ? ( )

Answer:
(D) \(\sqrt{25+16}\)

Question 40.
The prime factorization of 144 is ( )
A) 4² × 3²
B) 2⁷ × 3⁴
C) 12 × 12
D) 2⁴ × 3²
Answer:
D) 2⁴ × 3²

Question 41.
L.C.M of the numbers 2⁷ × 3⁴ × 7 and 2³ × 3⁴ × 11 is ( )
A) 2³ × 3⁴
B) 2⁷ × 3⁴
C) 2⁷ × 3⁴ × 7 × 11
D) 2³ × 3⁴ × 7 × 11
Answer:
D) 2³ × 3⁴ × 7 × 11

Question 42.
The H.C.F. of the numbers 3⁷ × 5³ × 2⁴ and 3² × 7⁴ × 2⁸ is
A) 2⁴ × 3²
B) 2⁸ × 3⁷ × 5³ × 7⁴
C) 2⁸ × 3⁷
D) 2 × 3 × 5 × 7
Answer:
C) 2⁸ × 3⁷

Question 43.
The decimal expansion of 0.225 in its rational form is
A) 225
B) \(\frac{225}{10^4}\)
C) \(\frac{225}{10^2}\)
D) \(\frac{9}{40}\)
Answer:
C) \(\frac{225}{10^2}\)

Question 44.
Which of the following is a rational number ?
A) \(\sqrt{3}\)
B) \(\sqrt{5}\)
C) \(\sqrt{7}\)
D) \(\sqrt{9}\)
Answer:
A) \(\sqrt{3}\)

Question 45.
What is the L.C.M of greatest 2 digit num-ber and the greatest 3 digit number ?
A) 99 × 999
B) 999
C) 99 × 9 × 111
D) 9 × 11 × 111
Answer:
B) 999

Question 46.
What is the H.C.F of n and n + 1, where n is a natural number ? ( )
A) n
B) n + 1
C) n/2
D) 1
Answer:
D) 1

Question 47.
What is the L.C.M of least prime and the least composite number ?
A) least prime × least composite
B) 2
C) least composite
D) 6
Answer:
D) 6

Question 48.
The product of L.C.M. and H.C.F. of the least prime and least composite number is ( )
A) 4
B) 6
C) 8
D) 16
Answer:
D) 16

Question 49.
n² – 1 is divisible by 8, if n is ( )
A) an odd number
B) an even number
C) prime number
D) integer
Answer:
B) an even number

Question 50.
If x and y are any two co-primes, then their L.C.M. is ( )
A) x + y
B) x . y
C) x/y
D) x – y
Answer:
C) x/y

Question 51.
If x and y are any two relatively prime numbers, then their H.C.F is ( )
A) x . y
B) x
C) y
D) 1
Answer:
D) 1

Question 52.
If m and n are co-primes, the H.C.F. of m² and n² is ( )
A) m
B) n²
C) m²
D) 1
Answer:
A) m

Question 53.
If n is a natural number, then which of the following expression ends in zero ?
A) (3 × 2)ⁿ
B) (5 × 7)ⁿ
C) (9 × 3)ⁿ
D) (2 × 5)ⁿ
Answer:
A) (3 × 2)ⁿ

Question 54.
The number of prime factors of 72 is
A) 12
B) 2
C) 3
D) 6
Answer:
C) 3

Question 55.
How many prime factors are there in the prime factorization of 240 ? ( )
A) 20
B) 5
C) 3
D) 6
Answer:
B) 5

Question 56.
After how many digits will the decimal expansion of 11/32 terminates ? ( )
A) 5
B) 4
C) 3
D) Never
Answer:
D) Never

Question 57.
p, q are co-primes and q = 2ⁿ.5^m where m > n, then the decimal expansion of p/q terminates after places.
A) m
B) n
C) m . n
D) m + n
Answer:
A) m

Question 58.
The decimal expansion of \(\frac{9}{17}\) is
A) terminating
B) non-terminating & non-repeating
C) non-terminating & repeating
D) none
Answer:
D) none

Question 59.
The decimal expansion of \(\frac{27}{14}\) is ( )
A) \(1 . \overline{9285714}\)
B) \(1.9 \overline{285714}\)
C) 1.9285714
D) \(0.19 \overline{285714}\)
Answer:
A) \(1 . \overline{9285714}\)

Question 60.
\(5.6789 \overline{1}\) is a ……. number ( )
A) prime
B) composite
C) irrational
D) rational
Answer:
C) irrational

Question 61.
0.12112 1112 11112 ….. is …… number
A) irrational
B) rational
C) composite
D) prime
Answer:
C) composite

Question 62.
\(\sqrt{2}\) – 2 is …….. number ( )
A) natural
B) rational
C) whole
D) an irrational
Answer:
D) an irrational

Question 63.
3 × 5 × 7 × 11 + 35 is …… number.
A) composite
B) natural
C) negative
D) none
Answer:
B) natural

Question 64.
The decimal expansion of \(\frac{209}{80}\) terminates after ….. places. ( )
A) 5
B) 6
C) 4
D) 9
Answer:
A) 5

Question 65.
7 × 11 × 17 + 34 is divisible by ………
A) 7 or 10
B) 7 or 19
C) 17 or 79
D) 8 or 231
Answer:
C) 17 or 79

Question 66.
\(\frac{73}{625}\) has a …… decimal expansion.
A) Non-terminal
B) Terminal
C) Non-terminating, repeating
D) None
Answer:
D) None

Question 67.
The number of prime factors of 1024 is ………..
A) 12
B) 9
C) 7
D) 1
Answer:
B) 9

Question 68.
The decimal expansion of \(\frac{199}{99}\) is ……….
A) \(1 . \overline{02}\)
B) \(1 . \overline{07}\)
C) \(1 . \overline{39}\)
D) \(1 . \overline{14}\)
Answer:
D) \(1 . \overline{14}\)

Question 69.
The period of the decimal expansion of \(\frac{19}{21}\) is ……
A) 917461
B) 904761
C) 940761
D) None
Answer:
A) 917461

Question 70.
If a rational number p/q has a terminating decimal, then the prime factorisation q is of the form
A) 3^m5ⁿ
B) 3^m
C) 3^m5ⁿ3^p
D) 2^m5ⁿ
Answer:
C) 3^m5ⁿ3^p

Question 71.
The prime factorisation of 20677 is
A) 13 × 29 × 71
B) 23 × 29 × 31
C) 19 × 23 × 17
D) None
Answer:
C) 19 × 23 × 17

Question 72.
The LCM of 208 and 209 is …..
A) 208 × 109
B) 19 × 218
C) 104 × 20
D) 208 × 209
Answer:
A) 208 × 109

Question 73.
The HCF of 1001 and 1002 is ….
A) 1
B) 7
C) 9
D) 11
Answer:
B) 7

Question 74.
If p₁, p₂, p₃,…… p_n are co-primes then their LCM is …….
A) p₃p₅p₇
B) p₆p₇…. p_n
C) p₁p₂…….. p_n
D) p₂p₄…..p_n
Answer:
C) p₁p₂…….. p_n

Question 75.
In the above problem HCF is ….
A) p₁
B) 9
C) 1
D) 7
Answer:
D) 7

Question 76.
The decimal expansion of \(\frac{7}{16}\) without actual division is …….
A) 0.4375
B) 4.375
C) 43.75
D) 0.0004375
Answer:
C) 43.75

Question 77.
The expansion of \(\frac{87}{625}\) terminates after …. places.
A) 6
B) 4
C) 14
D) 9
Answer:
A) 6

Question 78.
The expansion of \(\frac{123}{125}\) terminates after ……. places.
A) 9
B) 7
C) 3
D) None
Answer:
C) 3

Question 79.
The decimal form of \(\frac{80}{81}\) repeats after …….. places.
A) 16
B) 12
C) 7
D) None
Answer:
D) None

Question 80.
\(\frac{70}{71}\) is a …… decimal.
A) terminating
B) non-terminating
C) non-terminating, repeating
D) none
Answer:
B) non-terminating

Question 81.
\(\frac{123}{125}\) is a … decimal.
A) terminating
B) non-terminating
C) non-terminating, repeating
D) none
Answer:
C) non-terminating, repeating

Question 82.
14.381 may certain the denominator when expressed in p/q form is ….
A) 8³ × 6³
B) 12³ × 4³
C) 2³ × 5³
D) 7³ × 8³
Answer:
C) 2³ × 5³

Question 83.
5\(\sqrt{5}\) + 6\(\sqrt{5}\) – 2 \(\sqrt{5}\) = ……
A) 6 \(\sqrt{5}\)
B) 7 \(\sqrt{5}\)
C) 2 \(\sqrt{5}\)
D) 9 \(\sqrt{5}\)
Answer:
D) 9 \(\sqrt{5}\)

Question 84.
9 \(\sqrt{2}\) × \(\sqrt{2}\) = ……
A) 16
B) 18
C) 19
D) 20
Answer:
D) 20

Question 85.
log₁₀10 = ……………
A) 0
B) -1
C) 1
D) 7
Answer:
D) 7

Question 86.
log_a\(\frac{1}{a}\) = ……
A) 4
B) 3
C) -1
D) 12
Answer:
A) 4

Question 87.
log_ba . log_ab = ……
A) 7
B) 3
C) 4
D) 1
Answer:
A) 7

Question 88.
log₁1 = …………
A) 1
B) -1
C) 0
D) not defined
Answer:
D) not defined

Question 89.
log_0.10.01 = ……..
A) 8
B) 6
C) 9
D) None
Answer:
B) 6

Question 90.
log 2 + log 5 = …….
A) 1
B) 2
C) 9
D) 12
Answer:
A) 1

Question 91.
16 × 64 = 4^k then k = ……..
A) 9
B) 12
C) 5
D) 19
Answer:
C) 5

Question 92.
a + b = b + a is called …….. property.
A) Associative
B) Identity
C) Inverse
D) Commutative
Answer:
B) Identity

Question 93.
log₅125 = ……..
A) 5
B) 3
C) 15
D) 12
Answer:
C) 15

Question 94.
Exponential form of log₄64 = 3 is ……..
A) 4³ = 64
B) 3⁴ = 64
C) 4² = 81
D) None
Answer:
A) 4³ = 64

Question 95.
log 15 = ……..
A) log 5 + log 10
B) log 3 + log 12
C) log 5 + log 3
D) all the above
Answer:
D) all the above

Question 96.
\(\frac{1}{\sqrt{2}}\) is a ………. number.
A) rational
B) an irrational
C) natural
D) whole
Answer:
B) an irrational

Question 97.
Q ∪ Q’ = ………..
A) P
B) C
C) R
D) None
Answer:
A) P

Question 98.
……….. is called the additive identity.
A) 0
B) 1
C) 2
D) None
Answer:
B) 1

Question 99.
\(\sqrt{2}\) = 1.414 then 3 \(\sqrt{2}\) = ………..
A) 2.42
B) 13.42
C) 42.42
D) 4.242
Answer:
D) 4.242

Question 100.
\(\frac{23}{2^3 \cdot 5^2}\) = ……….
A) 11.5
B) 0.115
C) 1.15
D) 115.1
Answer:
A) 11.5

Question 101.
0.9375 = ……….
A) \(\frac{15}{16}\)
B) \(\frac{5}{16}\)
C) \(\frac{16}{15}\)
D) \(\frac{18}{1199}\)
Answer:
A) \(\frac{15}{16}\)

Question 102.
4\(\frac{1}{5}\) = ……….
A) 4.12
B) 4.2
C) 0.42
D) 4.02
Answer:
B) 4.2

Question 103.
\(\frac{5}{11}\) = ……….
A) \(0 . \overline{43}\)
B) \(0 . \overline{44}\)
C) \(0 . \overline{31}\)
D) \(0 . \overline{45}\)
Answer:
D) \(0 . \overline{45}\)

Question 104.
LCM of 12, 15 and 21 is ………
A) 420
B) 440
C) 820
D) 110
Answer:
A) 420

Question 105.
0.4 = ……..
A) \(\frac{2}{5}\)
B) \(\frac{5}{2}\)
C) \(\frac{1}{9}\)
D) None
Answer:
A) \(\frac{2}{5}\)

Question 106.
\(\sqrt{\frac{4}{9}}\) = …………
A) \(\frac{3}{2}\)
B) \(\frac{2}{3}\)
C) \(\frac{\sqrt{2}}{3}\)
D) \(\frac{2}{\sqrt{3}}\)
Answer:
B) \(\frac{2}{3}\)

Question 107.
HCF of 12, 18 is …………
A) 12
B) 9
C) 2
D) 6
Answer:
D) 6

Question 108.
2² × 5 × 7 = ………..
A) 240
B) 144
C) 140
D) 909
Answer:
C) 140

Question 109.
loga_a 1 ……. a > 0
A) a²
B) 2
C) 1
D) 0
Answer:
D) 0

Question 110.
log₂₀₁₅2015 = ………
A) 15
B) 1
C) 5
D) 0
Answer:
B) 1

Question 111.
Multiplicative inverse of 3\(\frac{1}{3}\) is ……..
A) 3\(\frac{1}{3}\)
B) \(\frac{3}{13}\)
c) \(\frac{3}{10}\)
d) \(\frac{3}{14}\)
Answer:
c) \(\frac{3}{10}\)

Question 112.
(ab)c = a(bc) is called …….. property.
A) Associative
B) Inverse
C) Identity
D) None
Answer:
A) Associative

Question 113.
\(\frac{41}{75}\) = ………..

Answer:

Question 114.
log 64 – log 4 = ………..
A) 4
B) 7
C) 1
D) None
Answer:
D) None

Question 115.
LCM of 306 and 657 is …….
A) 22338
B) 23238
C) 11128
D) None
Answer:
A) 22338

Question 116.
\(\frac{1167}{50}\) = ……….
A) 1.675
B) 23.34
C) 81.45
D) None
Answer:
B) 23.34

Question 117.
6ⁿ can not end with ………
A) 6
B) 0
C) 2
D) None
Answer:
B) 0

Question 118.
\(\sqrt{\mathbf{2 0 2 5}}\) = ………..
A) 405
B) 54
C) 45
D) 55
Answer:
C) 45

Question 119.
5⁵ = ……….
A) 1325
B) 1125
C) 3125
D) 1859
Answer:
C) 3125

Question 120.
\(\frac{3}{8}\) = ………
A) 0.375
B) 3.75
C) 8.175
D) None
Answer:
A) 0.375

Question 121.
\(\sqrt{5}\) = ……..
A) 1.414
B) 2.236
C) 1.73
D) 2.998
Answer:
B) 2.236

Question 122.
log₂16 = ………….
A) 2
B) 8
C) 4
D) 12
Answer:
C) 4

Question 123.
2 log 3 + 3 log 5 – 5 log 2 = ………
A) log \(\frac{1125}{32}\)
B) log \(\frac{125}{23}\)
C) log \(\frac{1025}{16}\)
D) None
Answer:
A) log \(\frac{1125}{32}\)

Question 124.
log₂ 1024 = ……….
A) 16
B) 20
C) 19
D) 10
Answer:
D) 10

Question 125.
log₁₈ 324 = ………
A) 2
B) 16
C) 19
D) 12
Answer:
A) 2

Question 126.
log₃ \(\frac{1}{27}\) = ………
A) 3
B) 6
C) -3
D) -7
Answer:
C) -3

Question 127.
log₆ 1 = ………….
A) 12
B) 19
C) 7
D) 0
Answer:
D) 0