We are offering TS 10th Class Maths Notes Chapter 2 Sets to learn maths more effectively.
TS 10th Class Maths Notes Chapter 2 Sets
→ A set is a well-defined collection of objects.
E.g.: The collection of instruments in a Mathematics Instrument Box.
The collection of districts in Andhra Pradesh.
→ An object belonging to a set is known as an element of the set.
For example, if B = {1, 2, 3, 4, 5}
1, 2, 3, 4, 5 are the elements of set B.
→ We use upper case letters A, B, C,…., X, Y, Z etc., to denote a set while the elements of a set are represented by small letters a, b, c,…. etc.
→ If ‘x’ is an element of set A.
We say that ‘x’ belongs to ‘A’ and we write xe A.
If Y is not element of set B.
We say that ‘x does not belongs to B’ and we write xg B.
→ A set can be represented in two ways.
- Roster (or) Tabular form
- Set builder form.
→ Roster form :
- In roster form, all the elements of a set are list the elements being separated by commas and are enclosed within braces (curly brackets).
- For example, the set of all even positive integers less than 20 is described in the roaster form as {2, 4, 6, 8, 10,12,14,16,18}.
- The set of all vowels in english alphabet can be written as V = {a, e, i, o, u}
- It may be noted while writing the set in roaster form, an element is not generally repeated.
- For example, the set of letters forming the word ‘FOLLOWER’ is written as {F, O, L, W, E, R}.
![]()
→ Set builder form :
In set builder form, we use a symbol x (or any other symbol like the letters y, z etc.,) for the elements of the set. After that we write either a colon or a vertical line. Then we write the characteristic property possessed by the elements of the set. Lastly we enclose the description within braces.
Let A = (2, 3, 5, 7,11,13,17}. This is the set of all prime numbers less than 19. It can be represented in set builder form as {x/x is a prime number less than 19}
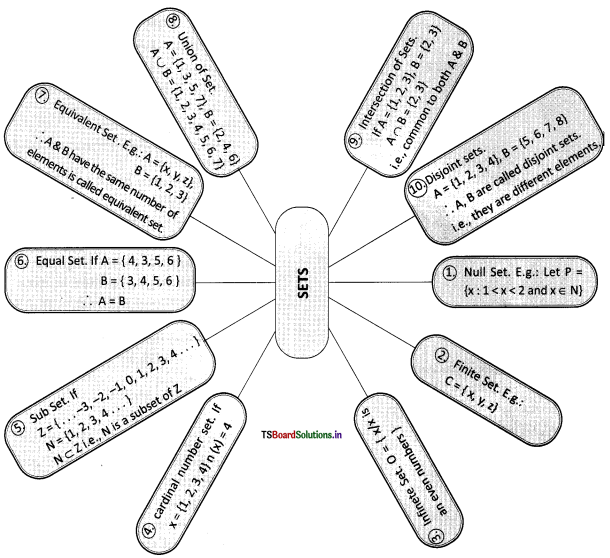
→ Null set:
A set which does not contain any element is called the empty set or the null set or the void set. The empty/ null set is denoted by the symbol Φ or {}.
E.g.: Let P = {x : 1 < x < 2 and x e N}
P is an empty set because there is no natural number between 1 and 2.
→ Finite set:
A set is called a finite set if it is possible to count the number of elements in it.
C = {x, y, z} and A = {1, 2, 3, 4, 5}
→ Infinite set:
A set is called an infinite set if the number of elements in it is not finite (i.e.,) we cannot count the number of elements in it.
For example, E = {x : x is a multiple of 3}
0 = {x/x is an odd natural number}
→ Cardinal number of a set:
The number of elements in a set is called the cardinal number of the set.
If A = {1, 2, 3, 4, 5}, n(A) = 5 If B = {5, 6, 7}, n(B) = 3 But n(Φ) = 0
→ Universal set; subset:
If we consider all the students in a school as universal set, then the students in any class of that school will be a subset of it.
The subset is denoted by the symbol: ⊂
A set S is a subset of a set R, if every element of S is an element of R.
i. e., S ⊂ R
S ⊂ R whenever x ∈ S, then x ∈ R.
If U = {a, b, c,…., x, y, z} and V = (a, e, i, o, u}, then V ⊂ U.
If we consider the alphabet in English as universal set, then the set of vowels is a subset of it.
→ Equal sets :
Two sets A and B are said to be equal if every element of A is also an element of B and if every element of B is also an element of A.
In other words, two sets A and B are said to be equal if they have exactly the same elements.
We write A = B
E.g.: A = {5, 8,10,11}, B = {10, 5, 11, 8}
Then A = B
→ Equivalent sets:
Two finite sets A and B are said to be equivalent if they have the same number of elements. We write A = B
For example, let A = {x, y, z} and B = {2, 4, 6} then A and B are equivalent sets.
![]()
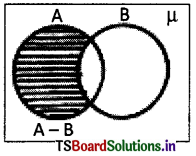
→ Difference of sets :
Let A and B are two sets. The difference of sets A and B, in the same order, is the set of elements that belong to A but not to B.
We write it as A – B and read as ‘A’ difference B’.
A – B = {x: x ∈ A and x ∉ B}
→ Union of sets :
Let A and B be any two sets. The union of A and B is the set that contains all the elements of A and also the elements of B, the common elements being taken only once.
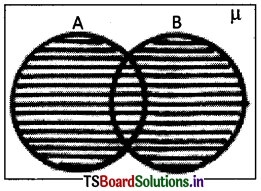
Symbolically,
A ∪ B = {x : x ∈ A or x ∈ B}
E.g.: If A = {1, 3, 5, 7} and B = {5, 7, 9,11} then A ∪ B = {1, 3, 5, 7, 9,11}
We read A ∪ B as ‘A union B’.
→ Intersection of sets :
Let A and B be any two sets. The intersection of sets A and B is the set of all elements which are common to both A and B.
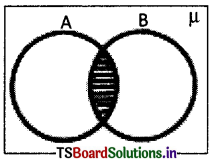
Symbolically,
A ∩ B = {x : x ∈ A and X ∈ B}
E.g.: If A = {2,4, 6, 8} and B = {6, 8,10,12} then A ∩ B = {6, 8}
We read A ∩ B as ‘A intersection B’.
→ Disjoint sets:
Two sets A and B are said to be disjoint, if A ∩ B = Φ
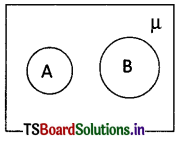
i. e., there is no common element in the sets.
E.g.: A = {1, 2, 3, 4, 5} and B = {6, 7, 8}
Here, A and B have no elements in common.
∴ A and B are called disjoint sets.
→ Venn diagrams:
Venn diagrams are a convenient way of showing operations between sets. Most of the ideas about sets and their properties can be visualised by means of diagrams. These diagrams are known as venn diagrams because they are named after John Venn. In these diagrams, the universal set is represented by the interior of a rectangle and its subsets are represented by the interior of circles.
(i) n(A) + n(B) – n(A ∪ B) = n(A ∩ B)
(ii) n(A) + n(B) – n(A ∩ B) = n(A ∪ B)
E.g.:
(i) If n(A) = 7, n(B) = 8, n(A ∩ B) = 3, find n(A ∪ B).
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
= 7 + 8 – 3 = 12
(ii) If n(A) = 14, n(B) = 5, n(A ∪ B) = 16, find n(A ∩ B).
n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 14 + 5 – 16
= 19 – 16 = 3
![]()
Important Formula:
- Null Set. P = {x: 1 < x < 2 and x ∈ N}
- A set is called Finite Set. If it is possible to count.
- A set is called Infinite Set. If it is not possible to count.
- The number of elements in a set is called the cardinal number of the set.
- Two sets A and B are said to be equal if they have the same elements, i.e A = B
- Symbol of subset is ⊂.
Flow Chat:
George Cantor(1845 – 1918A.D):
- George Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics.
- Cantor established the importance of one-to-one correspondence between the numbers of two sets, defined infinite and well-ordered sets and proved that the real numbers are “more numerous” than the natural numbers.
- He defined the cardinal and ordinal numbers and their arithmetic.
- Cantor’s work is of great philosophical interest, a fact of which he was well aware.