TS 10th Class Maths Solutions Chapter 7 Coordinate Geometry Optional Exercise

Students can practice TS Class 10 Maths Solutions Chapter 7 Coordinate Geometry Optional Exercise to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 7 Coordinate Geometry Optional Exercise

Question 1.
Centre of the circle Q is on the Y-axis. And the circle passes through the points (0, 7) and (0, -1). Circle intersects the positive X-axis at (P, 0). What is the value of P ?
Solution:
Let Q be the centre of the circle. It lies on Y- axis. So, let the co-ordinates of the Q be (0, y). R(0, 7) is a point on the circle.

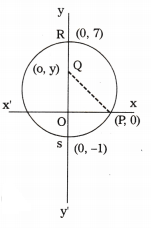
∴ Radius of the circle QR = 7 – y —- (1)
S(0, – 1) is also a point on the circle.
∴ Radius of the circle QS = y + 1 —– (2)
From (1) & (2), we get
y + 1 = 7 – y
⇒ y + y = 7 – 1
⇒ 2y = 6
⇒ y = 6/2 = 3
Hence centre of the circle is (0, 3).
Radius of the circle = 7 – 3 = 4 units —- (3)
PQ denotes the radius of the circle
∴ Distance between (p, 0) and (0, 3)
= \(\sqrt{(0-p)^2+(3-0)^2}\) = \(\sqrt{\mathrm{p}^2+9}\)
From (3), \(\sqrt{\mathrm{p}^2+9}\) = 4
Squaring on both sides,
\(\left(\sqrt{\mathrm{p}^2+9}\right)^2\) = 4²
⇒ P² + 9 = 16
P² = 16 – 9 = 7
Hence p = \(\sqrt{7}\)

Question 2.
The triangle ΔABC is formed by the points A(2, 3), B(-2, -3), C(4, -3). What is the point of intersection of side BC and angular bisector of A ?
Solution:
In ΔABC, AD is the angular bisector of ∠A in-tersecting BC at D. The vertices of A, B and C are (2, 3), (-2, -3) and (4, -3) respectively.
We know that angular bisector of A divides BC in the ratio of the other two sides (i.e)
AB : AC
Length of AB

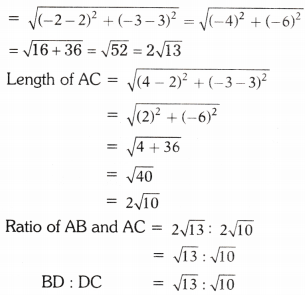
Let the co-ordinates of D be (x, y)

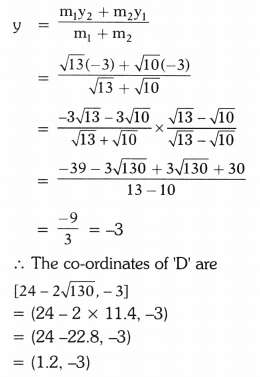
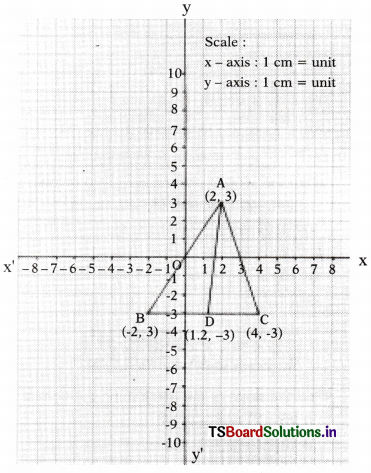
Question 3.
The side of BC of an equilateral triangle ΔABC is parallel to X-axis. Find the slopes of line along sides BC, CA and AB.
Solution:
ΔABC is an equilateral triangle. BC is parallel to X-axis.
The angle made by AB with X-axis is 60°.
∴ Slope of AB = tan θ = tan 60° = \(\sqrt{3}\)
BC is parallel to X-axis
∴ Slope of BC = 0
The angle made by AC with X-axis is 60°
∴Slope of AC = tan 60°= \(\sqrt{3}\)

Question 4.
A right triangle has sides ‘a’ and ‘b’ where a > b. If the right angle is bisected then find the distance between orthocentres of the smaller triangles using coordinate geometry.
Solution:

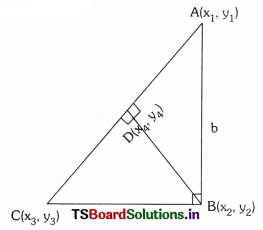
A triangle is formed with a cm hypotenuse (a > b)
∠B = 90°. A line is drawn from B to D the line divides the triangle into two smaller triangles. If we want to determine the distance between orthocentres, we have to find the distance between B and D.
∴ The distance between orthocentres = The distance between the points B and D.
\(\sqrt{\left(x_4-x_2\right)^2+\left(y_4-y_2\right)^2}\)

Question 5.
Find the centroid of the triangle formed by the line 2x + 3y – 6 = 0 with the co-ordinate axis.
Solution:
The given line is 2x + 3y – 6 = 0
If we want to find the X-intersection, we have to substitute (x, 0) in the given line.
2x + 3y – 6 = 0
2x + 3.0 – 6 = 0
2x = 6

∴ x = 3
∴ The intersection point of X-axis = (3, 0)
If we want to find the Y-intersection, we have to substitute (0, y) in the given line
2x + 3y – 6 = 0
2.0 + 3.y – 6 = 0
3y – 6 = 0; 3y = 6

∴ The intersection point of Y-axis = (0, 2)
The coordinates of origin = (0, 0)
∴ Sides of the triangle = (0, 0), (3, 0), (0, 2)
∴ Centroid = \(\left[\frac{\mathrm{x}_1+\mathrm{x}_2+\mathrm{x}_3}{3}, \frac{\mathrm{y}_1+\mathrm{y}_2+\mathrm{y}_3}{3}\right]\)
= \(\left[\frac{0+3+0}{3}, \frac{0+0+2}{3}\right]\) = [1, \(\frac{2}{3}\)]