TS 10th Class Maths Important Questions Chapter 11 Trigonometry

These TS 10th Class Maths Chapter Wise Important Questions Chapter 11 Trigonometry given here will help you to solve different types of questions.

TS 10th Class Maths Important Questions Chapter 11 Trigonometry

Previous Exams Questions

Question 1.
If sin A = cos A then find the value of A. (A.P. Mar. ’15)
Solution:
sin A = cos A (given)
then A + A = 90 ⇒ 2A = 90
⇒ A = \(\frac{90}{2}\) = 45°
∴ A = 45°

Question 2.
If 4 sin² θ – 1 = 0 then find ‘θ’ (θ < 90) also, find the value of θ and the value of cos²θ + tan²θ (AP. Mar. ’15)
Solution:
Given, 4 Sin²θ – 1 = 0
4 Sin²θ = 1
Sin²θ = \(\frac{1}{4}\)
Sinθ = ± \(\sqrt{\frac{1}{4}}\) = ±\(\frac{1}{2}\)
Given θ is less than 90°
∴ Sin θ = \(\frac{1}{2}\)
sinθ = sin 30°
∴ θ = 30°
Cosθ = Cos 30° = \(\frac{\sqrt{3}}{2}\)
Tan θ = Tan 30° = \(\frac{1}{\sqrt{3}}\)
Cos² θ + Tan² θ = Cos² 30° + Tan² 30°
= \(\left(\frac{\sqrt{3}}{2}\right)^2\) + \(\left(\frac{1}{\sqrt{3}}\right)^2\)
= \(\frac{3}{4}\) + \(\frac{1}{3}\) = \(\frac{9+4}{12}\) = \(\frac{13}{12}\)

Question 3.
Show that tan²θ – \(\frac{1}{\cos ^2 \theta}\) = 1 (T.S. Mar. ’15)
Solution:
Method – I : Since \(\frac{1}{\cos ^2 \theta}\) = sec²θ

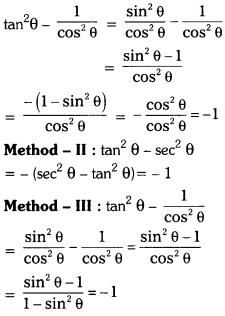
Question 4.
Find the value of (T.S. Mar. ’15)

Solution:

Question 5.
If tan θ = \(\sqrt{3}\) (θ is acute angle) then find the value of 1 + cos θ. (T.S. Mar. ’16)
Solution:
tan θ = \(\sqrt{3}\) = tan 60 (∵ θ is acute)
⇒ θ = 60
⇒ 1 + cos θ = 1 + cos 60 = 1 + \(\frac{1}{2}\) = \(\frac{3}{2}\)
∴ 1 + cos θ = \(\frac{3}{2}\)

Question 6.
Show that \(\sqrt{\frac{1-\sin \theta}{1+\sin \theta}}\) = sec θ – tan θ. (T.S. Mar. ’16)
Solution:
\(\sqrt{\frac{1-\sin \theta}{1+\sin \theta}}\) = \(\sqrt{\frac{(1-\sin \theta)(1-\sin \theta)}{(1+\sin \theta)(1-\sin \theta)}}\)

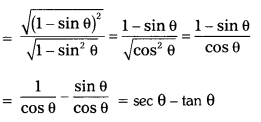
Hence proved

Question 7.
If tan (A + B) = 1, and cos (A – B) = \(\frac{\sqrt{3}}{2}\) 0° < A + B < 90, A > B then find values of A and B. (T.S. Mar. ’16)
Solution:
tan (A + B) = 1 = tan 45°
∴ A + B = 45° ……………. (1)
cos (A – B) = \(\frac{\sqrt{3}}{2}\) = cos 30°
⇒ A – B = 30° ……………… (2)
Solving the equation (1) and (2) we get

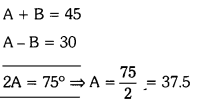
then A + B = 45
37.5 + B = 45 ⇒ B = 45 – 37.5 = 7.5
So, A = 37.5°, B = 7.5°

Question 8.
Find the value of tan² 60 + 4 cos² 45 + 3 sec² 30 + 5 cos² 90 = cosec 30 + sec 60 – cot² 30 (T.S. Mar. ’16)
Solution:
Put the following values in the given problem
tan 60° = \(\sqrt{3}\) , cos 45° = \(\sqrt{2}\), sec 30° = \(\frac{2}{\sqrt{3}}\)
cos 90° = 0, cosec 30° = 2, sec 60° = 2, cot 30° = \(\sqrt{3}\)
We get
tan² 60 + 4 cos² 45 + 3 sec² 30 + 5 cos² 90 = cosec 30 + sec 60 – cot² 30

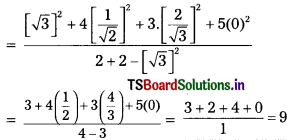
Additional Questions

Question 1.
In a right angled triangle ABC, with right angle at B in which a = 5 units, b = 13 units and ∠BCA = θ, then find sin θ and tan θ.
Solution:
Given a = 5 units = BC
b = 13 units = CA or AC
∠BCA = θ
By pythagoras theorem
AC² = AB² + BC²
⇒ 13² = AB² + 5²
⇒ AB² = 13² – 5² = 169 – 25 = 144
⇒ AB = \(\sqrt{144}\) = 12 units
Now from the figure
Sin θ = \(\frac{\mathrm{AB}}{\mathrm{AC}}\) = \(\frac{12}{13}\)
and Tan θ = \(\frac{\mathrm{AB}}{\mathrm{AC}}\) = \(\frac{12}{5}\)

Question 2.
If Cos c = \(\frac{3}{5}\), then find Sin c and Tan c
Solution:
We have cos c = \(\frac{3}{5}\) = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)

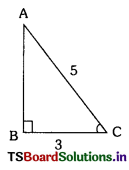
⇒ AC = 5, BC = 3
By Pythagoras theorem
AC² = AB² + BC²
⇒ 5² = AB² + 3²
⇒ 25 = AB² + 9 = 16
⇒ AB = \(\sqrt{16}\) = 4
From Sin c = \(\frac{\mathrm{AB}}{\mathrm{AC}}\) = \(\frac{4}{5}\), Tan c = \(\frac{\mathrm{AB}}{\mathrm{AC}}\) = \(\frac{4}{3}\)

Question 3.
If 12 Tan A = 9, then find Sin A and Cos A.
Solution:
Given 12 Tan A = 9

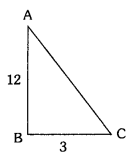
⇒ Tan A = \(\frac{9}{12}\) = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
⇒ BC = 9, AB = 12
By Pythagoras theorem
AC² = AB² + BC²
= 12² + 9²
= 144 + 81
AC² = 225
AC = \(\sqrt{225}\) = 15
Now, sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) = \(\frac{9}{5}\) and cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}\) = \(\frac{12}{15}\)
∴ sin A = \(\frac{9}{15}\) and cos A = \(\frac{12}{15}\)

Question 4.
If 5Cot A = 12, find Cos A and Cosec A.
Solution:
Given Cot A = \(\frac{12}{5}\) = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ AB = 12, BC = 5
By Pythagoras theorem
AC² = AB² + BC²
= 12² + 5²
= 144 + 25
= AC² = 169
AC = \(\sqrt{169}\) = 13
From the figuref ∆ABC,
Cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}\) = \(\frac{12}{13}\), Cosec A = \(\frac{\mathrm{AC}}{\mathrm{BC}}\) = \(\frac{13}{5}\)
∴ Cos A = \(\frac{12}{13}\) and Cosec A = \(\frac{13}{5}\)

Question 5.
Evaluate the following.
i) Sin 60° + Cos 60°
Solution:
Sin 60° + Cos 60° = \(\frac{\sqrt{3}}{2}\) + \(\frac{1}{2}\) = \(\frac{\sqrt{3}+1}{2}\)

ii) \(\frac{{Sin} 45^{\prime \prime}}{{Sin} 30^{\prime \prime}+{Cos} 60}\)
Solution:

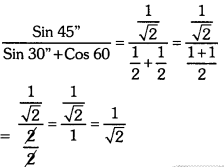
iii) Tan² 30° + Cot² 45° – Cos 60
Solution:
Tan² 30° + Cot² 45° – Cos 60
= \(\left(\frac{1}{\sqrt{3}}\right)^2\) + (1)² – \(\frac{1}{2}\)
= \(\frac{1}{3}\) + \(\frac{1}{1}\) – \(\frac{1}{2}\)
= \(\frac{2+6-3}{6}\)
= \(\frac{5}{6}\)

iv) 2 Tan² 45° + Sin² 60° – Cos² 30°
Sol:
2 Tan² 45° + Sin² 60° – Cos² 30°
= 2(1)² + \(\left(\frac{\sqrt{3}}{2}\right)^2\) – \(\left(\frac{\sqrt{3}}{2}\right)^2\)
= 2 × 1 + \(\frac{3}{4}\) – \(\frac{3}{4}\) = 2

v) Cot² 30° + 4 Sin² 45° + 3 Cosec 60°
Solution:
Cot² 30° + 4 Sin² 45° + 3 Cosec 60°
= (\(\sqrt{3}\))² + 4\(\left(\frac{1}{\sqrt{2}}\right)^2\) + 3\(\left(\frac{2}{\sqrt{3}}\right)^2\)
= 3 + 4 × \(\frac{1}{2}\) + 3 × \(\frac{4}{3}\)
= 3 + 2 + 4
= 9

vi) \(\sqrt{2}\) Sin 45° + Cos 90° + Sin 90°
Solution:
\(\sqrt{2}\) .Sin 45° + Cos 90° + Sin 90°
= \(\sqrt{2}\) . \(\frac{1}{\sqrt{2}}\) + 0 + 1
= 1 + 1
= 2

Question 6.
Evaluate Cos 60°, Cos 30° – Sin 60° Sin 30°
What is the value of Cos (60° + 30°) ? What can you conclude ?
Solution:
Take Cos 60° Cos 30° – Sin 60°. Sin 30°
= \(\frac{1}{2}\) \(\frac{\sqrt{3}}{2}\) – \(\frac{\sqrt{3}}{2}\) . \(\frac{1}{2}\)
= \(\frac{\sqrt{3}}{4}\) – \(\frac{\sqrt{3}}{4}\)
= 0 …………….. (1)
Now take Cos(60° + 30°) = Cos (90°) = 0 ………….. (2)
From equations (1) and (2), I conclude that
Cos(60° + 30°) = Cos 60° . Cos 30° – Sin 60°. Sin 30°
i.e.,Cos(A + B) = Cos A . Cos B – Sin A . Sin B.

Question 7.
Is it right to say Sin (60° – 30°) = Sin 60°. Cos 30° – Cos 60°. Sin 30° ?
Solution:
LHS = Sin(60° – 30°)
= Sin 30° = \(\frac{1}{2}\)
RHS = Sin 60°. Cos 30° – Cos 60°. Sin 30°
= \(\frac{\sqrt{3}}{2}\) . \(\frac{\sqrt{3}}{2}\) – \(\frac{1}{2}\) . \(\frac{1}{2}\)
= \(\frac{3}{4}\) – \(\frac{1}{4}\) = \(\frac{-1}{4}\)
= \(\frac{2}{4}\)
= \(\frac{1}{2}\)
Yes, it is right to say
Sin(60° – 30°) = Sin 60°. Cos 30° – Cos 60°. Sin 30°
i.e., Sin (A – B) = Sin A Cos B – Cos A. Sin B.

Question 8.
Is it right to say that Cos (A + B) = Cos A + Cos B ?
Solution:
Take A = 60°, B = 30°
Then Cos(A + B) = Cos (60° + 30°)
= Cos 90° = 0
Cos A + Cos B = Cos 60° + Cos 30°
= \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\)
= \(\frac{1+\sqrt{3}}{2}\)
∴ Cos (A + B) ≠ Cos A + Cos B
It is not right to say that Cos (A + B) ≠ Cos A + Cos B

Question 9.
i) \(\frac{{Sin} 66^{\prime \prime}}{{Cos} 24 “}\)
ii) \(\frac{{Sin} 18^{\prime \prime}}{{Cos} 72^{\prime \prime}}\)
iii) \(\frac{{Tan} 80^{\prime \prime}}{{Cot} 10^{\prime \prime}}\)
iv) \(\frac{{Sec} 69^{\prime \prime}}{{Cosec} 21 “}\)
v) \(\frac{{Tan} 54 “}{{Cot} 36^{\prime \prime}}\)
Solution:

Question 10.
Find the value of
i) Sin 75° – Cos 15°
ii) Sec 23° – Cosec 67°
iii) Sec 70° – Sec 20°
iv) Tan 68° – Tan 22°
Solution:
i) Given Sin 75° – Cos 15°
= Sin 75° – Cos(90 – 75°)
= Sin 75° – Sin 75°
= 0

ii) Given Sec 23° – Cosec 67°
= Sec 23° – Cosec (90 – 23°)
= Sec 23° – Sec 23°
= 0

iii) Sec 70° Sec 20°
= Sin 70° . \(\frac{1}{\cos 20 “}\) = \(\frac{{Sin} 70^{\prime \prime}}{{Cos}\left(90^{\prime \prime}-70^{\prime \prime}\right)}\)
= \(\frac{{Sin} 70 “}{{Cos}(90 “-70 “)}\) = \(\frac{{Sin} 70^{\prime \prime}}{{Sin} 70^{\prime \prime}}\) = 1

iv) Given Tan 68°. Tan 22°
Tan 68° . Tan(90° – 68°)
Tan 68° . Cot 68°
= \(\frac{{Tan} 68^{\prime \prime}}{{Tan} 68^{\prime \prime}}\) = 1

Question 11.
If Cot 2A = Tan (A – 18), when 2A is an acute angle, find the value of A.
Solution:
Given that Cot 2A = Tan (A – 18°)
⇒ Tan (90° – 2A) = Tan (A – 18°) [∵ Cot θ = Tan (90 – θ)]
⇒ 90 – 2A = A – 18°
⇒ 90 + 18° = A + 2A
⇒ 3A = 108°
⇒ A = \(\frac{108 “}{3}\) = 36°
Hence, the value of A is 36°.

Question 12.
If Cos 4A = Sin(A – 20), when 4A is an acute angle, find the value of A.
Solution:
Given that Cos 4A = Sin(A – 20°)
⇒ Sin(90° – 4A) = Sin(A – 20°)
[∴ Cos 0 = Sin(90 – 0)]
⇒ 90 – 4A = A – 20°
⇒ 90 + 20 = A + 4A
⇒ 110° = 5A
⇒ A = \(\frac{110 “}{15}\) = 22°
Hence, the value of A is 22°.

Question 13.
If Sin θ + Cosec θ = 2, find the value of Sin² θ + Cosec² θ
Solution:
Given Sin θ + Cosec θ = 2
Squaring on both sides
(Sin θ + Cosec)² = 2²
⇒ Sin² θ + Cosec² θ + 2 . Sin θ . Cosec θ = 4
⇒ Sin² θ + Cosec² θ + 2 . Sin θ . \(\frac{1}{{Sin} \theta}\) = 4
⇒ Sin² θ + Cosec² θ + 2 = 4
⇒ Sin² θ + Cosec² θ + 4 – 2
⇒ Sin² θ + Cosec² θ = 2

Question 14.
Show that \(\frac{{Tan} A+{Cot} B}{{Tan} B+{Cot} A}\) = Tan A . Cot B.
Solution:

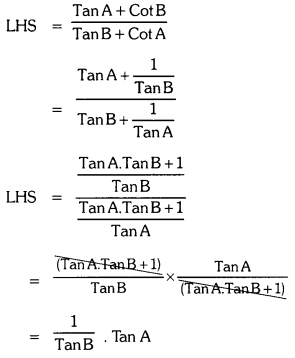
= Cot B . Tan A
= Tan A . Cot B = RHS
LHS = RHS

Question 15.
Show that (Sin θ + Cos θ)² – (Sin θ – Cos θ)² = 4 Sin θ Cos θ
Solution:
LHS = (Sin θ + Cos θ)² – (Sin θ – Cos θ)²
= (Sin² θ + Cos² θ + 2 Sin θ . Cos θ) – (Sin² θ + Cos² θ – 2 Sin θ . Cos θ)
= (2 Sin θ + Cos θ) – (-2 Sin θ . Cos θ)
= 2 Sin θ + Cos θ + 2 Sin θ . Cos θ
= 4 Sin θ . Cos θ
= RHS
∴ LHS = RHS

Question 16.
Find the value of \(\frac{{Tan}^2 60^{\prime \prime}+4 {Sin}^2 45^{\prime \prime}+3 {Sec}^2 30^{\prime \prime}+10 {Cos}^2 90^{\prime \prime}}{{Cosec}^2 60^{\prime \prime}+{Cos} 60^{\prime \prime}-{Cot}^2 60^{\prime \prime}}\)
Solution:
Put the following values in the given problem.

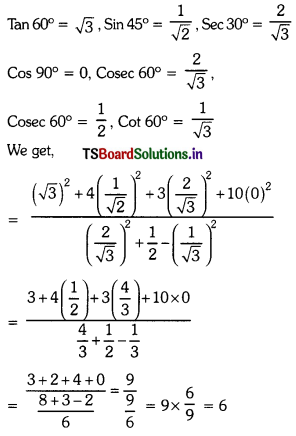
Question 17.
Show that \(\frac{1}{{Sin} \theta}\) – Sin θ = Cot θ. Cos θ
Solution:

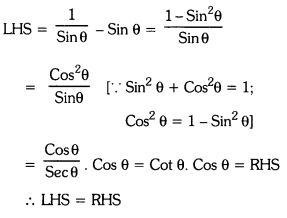
Question 18.
Show that \(\frac{{Tan}^2 q}{1+{Sec} q}=\frac{1-{Cos} q}{{Cos} q}\)
Solution:

∴ LHS = RHS

Question 19.
Evaluate : log₄ (1 + tan² 45°)²
Solution:
∴ log₄ (1 + 1)²
= log₄ = 1

Question 20.
Is it true to say that cos (60°+30°) = cos 60° cos 30° + sin 60° sin 30°
Solution:
Here L.H.S = cos (60° + 30°) = cos 90° = 0
R.H.S – cos 60° cos 30° + sin 60° sin 30°
= \(\frac{1}{2}\) × \(\frac{\sqrt{3}}{2}\) + \(\frac{\sqrt{3}}{2}\) × \(\frac{1}{2}\)
= \(\frac{\sqrt{3}}{4}\) + \(\frac{\sqrt{3}}{4}\)
= \(\frac{\sqrt{3}}{4}\)
= \(\frac{\sqrt{3}}{2}\)
Here L.H.S ≠ R.H.S, so it’s not justify.

Question 21.
In ∆ABC, ∠C = 90° If BC + CA = 17 cm; BC – CA = 7 cm. Find
(i) sin A
(ii) sin B
Solution:
Here, given ∠C = 90°; BC + CA = 7 cm;
BC – CA = 7 cm

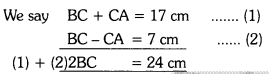
BC = \(\frac{24}{2}\) = 12 cm; figure script pno.4
BC = 12 cm
We apply BC = 12 cm. In BC + CA = 17 cm
Then 12 + CA = 17
CA = 17 – 12 = 5 cm
We know from ∆ABC, AB² = BC² + CA²
AB = \(\sqrt{\mathrm{BC}^2+\mathrm{CA}^2}\)
AB = \(\sqrt{12^2+5^2}\) = \(\sqrt{144+5}\)
AB = \(\sqrt{169}\) = 13
We know = sin A = \(\frac{\mathrm{BC}}{\mathrm{AB}}\) = \(\frac{12}{13}\)
sin B = \(\frac{\mathrm{AC}}{\mathrm{AB}}\) = \(\frac{5}{13}\)

Question 22.
Find the value of cos² 1° + cos² 2° + cos² 3° + ……………. + cos² 90°
Solution:
We know cos² (90° – 89°) + cos² (90° – 88°) + …………… + cos² 89° + cos² 90°
Here total 90° terms is there we know sin²θ + cos²θ = 1
= (sin² 89° + cos² 89) + (sin² 89 + cos² 88) + ………….. 44 terms.
= 44(1) + \(\frac{1}{\sqrt{2}}\) + 1
= 45 + \(\frac{1}{\sqrt{2}}\)

Question 23.
If cosec θ + cot θ = k then prove that cos θ = \(\frac{\mathrm{k}^2-1}{\mathrm{k}^2+1}\).
Solution:
Given cosec θ + cot θ = k ………….. (1)
We know cosec²θ – cot²θ = 1
∴ (cosec θ + cot θ) (cosec θ – cot θ) = 1 k(cosec θ – cot θ) = 1
k(cosec θ – cot θ) = 1
cosec θ – cot θ = …………….. (2)