TS Inter 2nd Year Economics Study Material 10th Lesson తెలంగాణ ఆర్థిక వ్యవస్థ
వ్యాసరూప సమాధాన ప్రశ్నలు:
ప్రశ్న 1.
తెలంగాణ రాష్ట్ర నిర్మితిపై వ్యాసం రాయండి.
జవాబు.
హైదరాబాద్ రాష్ట్రం నిజాం నవాబులచే రెండు శతాబ్దాలకు పైగా (1724-1948) పరిపాలించబడింది. రాష్ట్రానికి స్వంత కరెన్సీ, పరిపాలనా వ్యవస్థ రవాణా మరియు కమ్యూనికేషన్ వ్యవస్థ, స్వంత రైల్వే, పోస్టల్ వ్యవస్థ ఉండేది. ఉర్దూ భాష అధికార భాషగానే కాకుండా ఉర్దూలోనే విద్యాభ్యాసం జరిగేది.
భారత దేశానికి 15 ఆగస్టు, 1947 స్వాతంత్ర్యం వచ్చినపుడు, హైదరాబాద్ రాజ్యపాలకుడు మీర్ ఉస్మాన్ అలీఖాన్, ఏడవ నిజాం రాజు స్వతంత్రంగానే ఉంచాలనుకున్నాడు. కానీ అన్ని సంస్థానాలు, రాజరిక వ్యవస్థలు భారతదేశంలో కలవాలనుకున్నాయి. ఆ సమయం రాష్ట్రంలో అంతర్గత కలహాలు మొదలయ్యాయి. ముఖ్యంగా వ్యవసాయ కూలీలు ఫ్యూడల్ పాలనపై తిరుగుబాటు చేసారు.
తెలంగాణ సాయుధ పోరాటంగా ఈ సంఘటన పిలువబడింది. ఆ పరిస్థితులలో భారత ప్రభుత్వం “సాయుధ బలగాలతో” నిజాం రాజుపై ఒత్తిడి తెచ్చి భారత్లో కలవాలని కోరింది. చరిత్రలో పోలీస్ చర్యగా పిలవబడింది. ఈ ఘటనతో సెప్టెంబర్ 17, 1948 రోజున హైదరాబాద్ రాజ్య విలీనం జరిగింది. 1952వ సంవత్సరంలో సాధారణ ఎన్నికలు జరిగాయి. అందులో డా॥ బూర్గుల రామకృష్ణారావు ముఖ్యమంత్రిగా ప్రజా ప్రభుత్వం ఏర్పాటైంది.
మద్రాసు రాష్ట్రంలో చాలా కాలం భాగంగా ఉన్న ఆంధ్ర ప్రాంతం 1 అక్టోబరు, 1953న ఆంధ్ర రాష్ట్రంగా ఏర్పాటైంది. తెలంగాణ ప్రాంతం ఆంధ్ర రాష్ట్రంలో కలిసింది. ఆంధ్ర ప్రాంతంలో తెలంగాణ ప్రాంతం కలవడం వల్ల ఈ క్రింది ప్రయోజనాలు పొందవచ్చునని భావించారు.
- హైదరాబాద్ను కలుపుకుంటే రాజధాని సమస్య పరిష్కారమవుతుందని భావించారు.
- తీవ్ర ఆర్థిక ఇబ్బందులలో ఉన్న ఆంధ్ర రాష్ట్రానికి, మిగులు బడ్జెట్ నిధులు గల తెలంగాణ ఆదాయం ఉపయోగించుకొనుటకు
- కృష్ణా, గోదావరి నదులపై నియంత్రణ మొదలైనవి.
- ఆంధ్ర రాష్ట్ర ఏర్పాటు సమయంలో చేసుకొన్న వాగ్దానాలు, తెలంగాణ ప్రాంతానికి కల్పించిన రక్షణలు అమలు కాలేదు.
ఆ సమయంలో చేసుకొన్న ముఖ్య ఒప్పందాలు.
- 1956 నాటి పెద్ద మనుషుల ఒప్పందం.
- 1969లో అఖిలపక్ష ఒప్పందం.
- 1969లో 8 అంశాల ఫార్ములా, 1970లో 5 అంశాల ఫార్ములా.
- 972లో సుప్రీంకోర్టు ఇచ్చిన తీర్పు.
- ఆరుసూత్రాల పథకం.
- జీ.వో నెం. (G.O.No.) 610 గిర్ గ్లాని కమీషన్ రిపోర్టు.
పైన పేర్కొన్న అంశాలు అమలుకు నోచుకోకపోవడం వల్ల తెలంగాణ ప్రాంతం, సీమాంధ్ర ప్రాంతాలకంటే అన్ని రంగాలలో వెనుకబడిపోయింది. ఈ పరిస్థితులు తరచూ ఉద్యమాలు చెలరేగడానికి కారణాలైనాయి.
1969లో చెలరేగిన ప్రత్యేక రాష్ట్ర ఉద్యమం నిరంతరం కొనసాగుతూ 2009 నుంచి ప్రత్యేక తెలంగాణ రాష్ట్ర ఉద్యమం ప్రజా ఉద్యమంగా మారింది.
ఉద్యమం వివిధ రూపాలుగా సమ్మెలు, బండ్లు, రైలురోకో, జాతీయ రహదార్ల నిర్బంధం, విద్యార్థుల నిరసనలు, విద్యాసంస్థలు, విశ్వవిద్యాలయాల మూసివేత, సకల జనుల సమ్మెలో ప్రభుత్వ ఉద్యోగులు పాల్గొనడం, ఆర్.టి.సి., సింగరేణి కార్మికుల సమ్మెలు, ఆత్మహత్యలు, శ్రీ కల్వకుంట్ల చంద్రశేఖరరావు (ప్రస్తుత తెలంగాణ ముఖ్యమంత్రి) ఆమరణ నిరాహార దీక్షతో కేంద్ర ప్రభుత్వం తెలంగాణను 29వ రాష్ట్రంగా ప్రకటించింది.
జూన్ 2, 2014న ఆంధ్రప్రదేశ్ రెండు రాష్ట్రాలుగా విడిపోయింది. తెలంగాణలోని 10 జిల్లాలతో తెలంగాణ రాష్ట్ర ఏర్పాటు జరిగింది.

ప్రశ్న 2.
స్థూల రాష్ట్ర ప్రాంతీయోత్పత్తి (GSDP) అనగానేమి ? తెలంగాణాలో స్థూల రాష్ట్ర ప్రాంతీయోత్పత్తి, తలసరి ఆదాయాల ధోరణిని వివరించండి.
జవాబు.
స్థూల రాష్ట్ర ప్రాంతీయోత్పత్తి లేదా రాష్ట్ర ఆదాయం అనేది రాష్ట్ర ఆర్థిక వృద్ధిని కొలవడానికి ముఖ్యమైన సూచిక. “రాష్ట్రంలో ఒక సంవత్సర కాలంలో ఉత్పత్తి అయిన మొత్తం వస్తువుల, సేవల విలువల మొత్తాని లెక్కించడాన్ని (without duplication) స్థూల రాష్ట్ర ప్రాంతీయాదాయం అని నిర్వచించవచ్చు.
ఆర్థిక గణాంక శాఖ సంచాలకులు రాష్ట్రంలో ఉత్పత్తి, ఆదాయ మదింపు పద్ధతుల ద్వారా స్థూల రాష్ట్ర ప్రాంతీయోత్పత్తి (GSDP) ని అంచనా వేస్తున్నారు.
తెలంగాణ ఆర్ధిక వ్యవస్థలో స్థూల రాష్ట్ర ప్రాంతీయ్పోత్తి ధోరణులు :
ఒక రాష్ట్ర ఆర్ధిక వ్యవస్థ పనితీరును స్థూల రాష్ట్ర ప్రాంతీయోత్పత్తిలో వచ్చే వృద్ధి రేటు సూచిస్తుంది. స్థూల రాష్ట్ర ప్రాంతీయోత్పత్తి అధ్యయనం ద్వారా ఒక నిర్దిష్ట కాలంలో ఆర్థిక వ్యవస్థలో వివిధ రంగాల పని తీరును అంచనా వేయవచ్చు.
2011-12 నుంచి 2019-20 మధ్య కాలంలో తెలంగాణ స్థూల రాష్ట్ర ప్రాంతీయోత్పత్తి, భారత్ స్థూల దేశీయోత్పత్తి వార్షిక వృద్ధి రేట్ల ప్రస్తుత, తెలంగాణకు సంబంధించి, స్థూల రాష్ట్ర ప్రాంతీయోత్పత్తి 2011-12 నుండి 2019-20 మధ్య కాలంలో ప్రస్తుత ధరలో రూ. 3.59 లక్షల కోట్ల నుండి రూ. 9.69 లక్షల కోట్లకు పెరగగా, స్థిర ధరలలో రూ. 3.59 లక్షల కోట్ల నుంచి రూ.6.63 కోట్లకు పెరిగింది.
కాగా ఇదే కాలంలో భారత్లో ప్రస్తుత ధరల్లో స్థూల దేశీయోత్పత్తి రూ.87.36 లక్షల కోట్ల నుంచి రూ. 203.8 లక్షల కోట్లకు, స్థిర ధరల్లో రూ.87.36 లక్షల కోట్ల నుంచి రూ. 146.83 లక్షల కోట్లకు పెరిగింది.
ఇక వార్షిక వృద్ధి రేట్లకు సంబంధించి ప్రస్తుత ధరలలో తెలంగాణలో స్థూల రాష్ట్ర ప్రాంతీయోత్పత్తి వృద్ధి రేటు 2011-12లో 11.7 నుంచి 2018-19 నాటి 14.3 శాతం పెరగగా 2019-20లో 12.6 శాతంగా నమోదయింది. కాగా ఇదే కాలంలో భారత్ లో ఇది వరుసగా 13.8 శాతం, 11 శాతం, 7.5 శాతంగా నమోదయింది. 2011-12 నుంచి 2019-20 మధ్య కాలంలో 2012-13, 2013-14 సంవత్సరాలు మినహా తెలంగాణ రాష్ట్ర స్థూల ప్రాంతీయోత్పత్తి రేటు, భారత్ స్థూల దేశీయోత్పత్తి వృద్ధి రేటు కంటే ఎక్కువగా నమోదయింది.
2012-13 నుంచి 2019-20 మధ్య కాలంలో, స్థిర ధరలలో, తెలంగాణ స్థూల రాష్ట్ర ప్రాంతీయోత్పత్తి వార్షిక వృద్ధి రేటు 3 శాతం నుంచి 8.2 శాతానికి పెరగగా, భారత్ స్థూల దేశీయోత్పత్తి వార్షిక వృద్ధి రేటు 2012-13లో 5, 6 శాతం ఉండగా 2016-17 లో 8.3 శాతానికి పెరిగి 2019-20 నాదికి 5 శాతానికి పడిపోయింది.
2011-12 నుంచి 2019-20 మధ్య కాలంలో భారత దేశ స్థూల దేశీయోత్పత్తిలో తెలంగాణ రాష్ట్ర వాటా స్థిర, ప్రస్తుత ధరలలో 4.11 శాతం నుంచి 4.5 శాతం మధ్య ఉన్నది.
తెలంగాణలో భారతదేశంలో ప్రస్తుత ధరలలో తలసరి ఆదాయం :
నిర్దేశిత సంవత్సరంలో రాష్ట్ర నికర ప్రాంతీయోత్పత్తి విలువను రాష్ట్ర జనాభాచే భాగించడం ద్వారా రాష్ట్ర తలసరి ఆదాయాన్ని లెక్కిస్తారు.
తెలంగాణలో 2011-12 లో తలసరి ఆదాయం రూ. 91,121 ఉండగా అది 2019-20 (ముందస్తు అంచనా) నాటికి రూ. 2,28,216 కు పెరిగి 2011-12పై 150 శాతం వృద్ధిని సాధించింది. కాగా భారత్లో తలసరి ఆదాయం 2011-12లో రూ. 63,462 కాగా 2019-20 (ముందస్తు అంచనా) నాటికి రూ. 13,432 కి పెరిగి 2011-12పై 111 శాతం వృద్ధిని సాధించింది. ఈ విధంగా తెలంగాణలో తలసరి ఆదాయం భారత్ తలసరి ఆదాయం కంటే ఎక్కువ.

ప్రశ్న 3.
తెలంగాణ ఆర్థిక వ్యవస్థలో జోడించిన స్థూల రాష్ట్ర ఉత్పత్తి విలువ (GVSA) లో వివిధ రంగాల వాటాపై వ్యాసం వ్రాయండి.
జవాబు.
ఆర్థిక వ్యవస్థలో గల వివిధ రంగాలు ప్రదర్శించిన వృద్ధి రేట్లు ఆ వ్యవస్థ యొక్క వృద్ధి ధోరణిని తెలుపుతాయి. ఆర్థిక వ్యవస్థలో గల వివిధ రంగాలను 16 రంగాలుగా విభజించినప్పటికీ సులభంగా గ్రహించుట కొరకు వీటిని స్థూలంగా మూడు రంగాలుగా వర్గీకరిస్తారు.
అవి : ప్రాథమిక, ద్వితీయ, గౌణ రంగాలు. ఈ రంగాల వృద్ధి రేట్లను ప్రాథమిక ధరలలో జోడించిన స్థూల ఉత్పత్తి విలువ (GVA) తో సూచిస్తారు.
a) ప్రాథమిక రంగం :
ఈ రంగంలో పంటలు, పశుసంపద, అడవులు, మత్స్య పరిశ్రమ, గనులు మొదలైనవి.
b) ద్వితీయ రంగం :
ఇందులో తయారీ రంగం, గ్యాస్, నీటి సరఫరా, ఇతర అనుబంధ సేవలు మొదలైనవి.
c) గౌణ రంగం :
ఇందులో వ్యాపారం రిపేర్ సేవలు, హోటళ్ళు, రెస్టారెంటులు, రవాణా (రైల్వే రోడ్ వే, నౌకాయానం, విమానయానం మొ.||) నిలువ (storage), కమ్యూనికేషన్, బ్రాడ్కాస్టింగ్, ఆర్థిక సేవలు, స్థిరాస్థి రంగం, ప్రభుత్వ పాలన మొదలైనటువంటివి ఉంటాయి.
ఆర్థిక వ్యవస్థలో వివిధ రంగాల విశ్లేషణ ఆ వ్యవస్థలో ఆయా రంగాల పని తీరుని తెలుపుటకు, ఆర్థిక స్థితిగతుల అంచనాకు తోడ్పడుతుంది. అంతేగాక ప్రస్తుత సంవత్సరంలో ఆర్థికవ్యవస్థలో ఆయా రంగాలు ఏ విధమైన పనితీరును కనబరచాయో, రాబోయే కాలంలో ఏ విధంగా పనిచేయగలవో తెలుసుకొనుటకు వీలవుతుంది.
ప్రాథమిక రంగం వృద్ధి రేటు 2012-13లో 21.9 శాతం (స్థిర ధరలో 8.6 శాతం) నుంచి 2015-16 లో కేవలం 2.2 శాతానికి (స్థిర ధరలలో 58 శాతం) తగ్గగా 2016-17 నాటికి 17.1 శాతానికి పెరిగి తిరిగి 2019-20 (AE)లో 15.8 శాతానికి (స్థిర ధరలలో 10.7 శాతం) తగ్గింది.
ఈ విధంగా ప్రాథమిక రంగంలో మిశ్రమ వార్షిక సగటు వృద్ధి రేట్లు నమోదగుటను గమనించవచ్చు. 2012-13, 2014-15 సంవత్సరాలలో ద్వితీయ రంగం రుణాత్మక వృద్ధి రేటును చవిచూడగా 2015-16 లో అత్యధిక వృద్ధి రేటు అనగా 20.3 శాతం (స్థిర ధరలలో 21.4 శాతం) ను నమోదు చేసుకొన్నది.
2019-20 (AE) ప్రకారం ఈ రంగంలో 5.3 శాతం వృద్ధిరేటు నమోదయింది. 2012-13 నుంచి 2019-20 మధ్య కాలంలో గౌణ రంగపు వృద్ధి రేటు 18.4 శాతం నుంచి 14.1 శాతం (స్థిర ధరలలో 8.4 శాతం నుంచి 9.6 శాతం) మధ్య కొనసాగింది. మొత్తానికి తెలంగాణ రాష్ట్ర ఆర్థిక వ్యవస్థలో ప్రస్తుత, స్థిర ధరలలో జోడించిన స్థూల రాష్ట్ర ఉత్పత్తి విలువ వృద్ధి రేటులో మిశ్రమ ధోరణిని చూడవచ్చు.
జోడించిన స్థూల రాష్ట్ర ఉత్పత్తి విలువ (GSVA) లో వివిధ రంగాల వాటా :
GSVA లో గౌణ రంగం లేదా సేవల రంగం వాటా 2011-12లో 52.8 శాతం నుంచి 2019-20 (AE) నాటికి 65.2 శాతానికి పెరగగా, ప్రాథమిక రంగం లేదా వ్యవసాయ రంగం దాని అనుబంధ రంగాల వాటా ఇదే కాలంలో 19.6 శాతం నుంచి 18.6 శాతానికి తగ్గగా, ద్వితీయ రంగం లేదా పారిశ్రామిక రంగం వాటా 27.6 శాతం నుంచి 16.2 శాతానికి తగ్గింది. తెలంగాణ రాష్ట్రపు GSVAలో ప్రాథమిక, ద్వితీయ రంగాల వాటా అస్థిర రూపంలో ఉండగా, గౌణ రంగం లేదా సేవల రంగం వాటా స్థిరంగా ఉండటాన్ని గమనించవచ్చు.

ప్రశ్న 4.
తెలంగాణ రాష్ట్ర జనభా తీరుతెన్నులను విశదీకరించండి.
జవాబు.
ఒక రాష్ట్ర ఆర్థిక వ్యవస్థ అభివృద్ధి ఆ వ్యవస్థలో లభ్యమవుతున్న వనరులపై ఆధారపడి ఉంటుంది. మానవ వనరులు ఉంటే, సహజ వనరులను అభిలషణీయంగా, సమర్థవంతంగా వినియోగపరిచి, రాష్ట్ర ప్రగతికి, అధిక ఉత్పత్తికి కారకులవుతారు. నాణ్యమైన జనాభాతో పాటు మూలధన కల్పన, సాంకేతిక పరమైన మార్పులు ఆర్థిక వ్యవస్థకు చలనత్వాలను కలిగిస్తుంది.
2011 జనాభా లెక్కల ప్రకారం తెలంగాణ జనాభా దాదాపు 42%గా నమోదయింది. భారతదేశమొత్తం భౌగోళిక వైశాల్యంలో తెలంగాణ 3.5% విస్తీర్ణం కల్గి ఉంది. రంగారెడ్డి జిల్లా జనాభాలో అత్యధికంగా 52.97 లక్షల మంది ఉండగా, నిజామాబాద్ జిల్లా జనాభాలో 25.51 లక్షల మందితో చివరి భాగాన ఉంది.
జనసాంద్రత :
ప్రతి చదరపు కిలోమీటరులో నివసించే జనాభాను జనసాంద్రత అంటారు. ఈ జనసాంద్రత జనాభా పెరుగుదల రేటును బట్టి మారుతూ ఉంటుంది. భారతదేశ మొత్తం జనసాంద్రతతో పోలిస్తే తెలంగాణలో జనసాంద్రత పెరుగుదల తక్కువగా ఉంది.
హైదరాబాద్ జిల్లా రాష్ట్ర రాజధాని నగరం కాబట్టి అధిక జనసాంద్రతను కల్గి ఉండి చదరపు కిలోమీటరుకు 18,172 మంది నివసిస్తున్నారు. 2001-2011 జనాభా లెక్కల ప్రకారం తెలంగాణలో జనాభా వృద్ధి రేటు 1.4% భారతదేశ జనాభా వృద్ధి రేటు 1.84% కంటే తక్కువ.
పిల్లల జనాభా :
0-6 సం॥లోపు వారిని పిల్లలు అంటారు. తెలంగాణలో పిల్లల జనాభా శాతం 2001లో 14.2% నుంచి 2011లో 10.5% తగ్గింది. ఈ తగ్గుదలకు కారణం పెరుగుతున్న అక్షరాస్యత, అధిక ఆదాయాలకు తోడు కుటుంబ నియంత్రణ పద్ధతులు అవలంబించడం. అన్ని జిల్లాలలో పిల్లల జనాభా శాతం రాష్ట్ర సగటుకు దగ్గరగా 10.5% గా ఉన్నది. ఒక మహబూబ్ నగర్ జిల్లాలో మాత్రం పిల్లల జనాభా 17.4% గా ఉంది.
కుటుంబ పరిమాణం, ఎస్.సి. & ఎస్.టి. జనాభాలో స్త్రీ, పురుషుల నిష్పత్తి :
జనాభా లెక్కల ప్రకారం కొంతమంది వ్యక్తులు `ఒక దగ్గర కలిసి జీవిస్తూ ఒకే వంటగదిని వాడుకోవడాన్ని కుటుంబం అంటారు. మొత్తం జనాభాను గృహాల సంఖ్యచే భాగించగా కుటుంబ పరిమాణం వస్తుంది. తెలంగాణలో సగటు కుటుంబ పరిమాణం 42% గా ఉంది.
ఎస్.సి/ఎస్.టి. జనాభా :
2011 జనాభా లెక్కల ప్రకారం షెడ్యూల్ కులాల (ఎస్.సి.) జనాభా మొత్తం రాష్ట్ర జనాభాలో 15.44% ఉంది. అదే విధంగా షెడ్యూల్ తెగల (ఎస్.టి.) జనాభా మొత్తం రాష్ట్ర జనాభాలో 9.34% ఉంది. .2011 జనాభా లెక్కల ప్రకారం ఎస్.సి. జనాభా మొత్తం జనాభాలో 54,32,650 మంది ఉన్నారు.
ఎస్.టి. జనాభా 32,86,928 మంది. ఎస్.సి. జనాభా అత్యధిక శాతం కరీంనగర్ జిల్లాలో 18-80%గా నమోదయ్యారు. అత్యల్పం హైదరాబాద్ 6.29%. ఎస్.టి. జనాభా ఖమ్మం జిల్లాలో 27.37%గా ఉంది. అత్యల్పం హైదరాబాద్లో 1.24%గా ఉంది. పట్టణాల కంటే గ్రామాలలోనే అధిక జనాభా వృద్ధి నమోదయింది.
స్త్రీ-పురుష నిష్పత్తి :
1000 మంది పురుషులకు స్త్రీల సంఖ్య ఆధారంగా స్త్రీ, పురుష నిష్పత్తి నిర్ణయించబడుతుంది. 2011 జనాభా లెక్కల ప్రకారం తెలంగాణలో ప్రతి 1,000 మంది పురుషులకు 990 మంది స్త్రీల అనుపాతం ఉంది.
మానవ అభివృద్ధి సూచి :
ఇది మూడు అంశాల వారిగా రూపొందించారు.
- పుట్టిన సమయంలో ఆయుఃప్రమాణం
- శిశుమరణాల రేటు
- అక్షరాస్యతా స్థాయి.
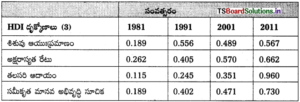
తెలంగాణలో మానవ అభివృద్ధి సూచిక (HDI):
వలసదారుల వాటా :
తెలంగాణలోని పట్టణ జనాభాలో అధిక పెరుగుదలకు ఆంధ్ర ఇతర రాష్ట్రాల నుండి వలసదారులే కారణం. 1961 నుంచి 2011 మధ్య కాలంలో తెలంగాణలో వలసదారుల జనాభా 62 లక్షలు. పట్టణ జనాభాలో రంగారెడ్డి జిల్లా మొదటి స్థానంలో నిలిచింది. 70% జనాభా పట్టణ వాసులే. దీనికి కారణం పట్టణాల అభివృద్ధి మరియు హైదరాబాద్ పరిసరాల అభివృద్ధి.
అక్షరాస్యత :
2011 జనాభా లెక్కల ప్రకారం తెలంగాణలో అక్షరాస్యత శాతం 66%.

ప్రశ్న 5.
తెలంగాణ రాష్ట్రంలో విద్య, ఆరోగ్య రంగాల స్థితిని విశదీకరించండి.
జవాబు.
తెలంగాణలో విద్య :
దేశంలో మానవ వనరులు, ఆర్థికాభివృద్ధి బలోపేతం కావడానికి విద్యను ప్రధాన సాధనంగా భావించాలి. ఉత్పాదక శ్రామిక శక్తిని పెంపొందించడంలో విద్య కీలక పాత్ర పోషిస్తుంది. భారత రాజ్యాంగంలోని 45 వ నిబంధన ప్రకారం 6 నుంచి 14 సంవత్సరాల మధ్య వయస్సు గల బాలబాలికలకు ఉచిత, నిర్బంధ విద్యను అందించడం రాష్ట్రాల బాధ్యత.
తెలంగాణలో అక్షరాస్యత రేటు :
2011 జనాభా లెక్కల ప్రకారం తెలంగాణలో అక్షరాస్యత రేటు 66.54 శాతం. అయితే పట్టణ-గ్రామీణ, అంతర్ జిల్లా, వయస్సు వారీ జనాభా, స్త్రీ-పురుషులు, సామాజిక వర్గాల పరంగా అక్షరాస్యత రేటులో తేడాలున్నాయి. రాష్ట్రంలో విద్యా రంగం స్థితి :
a) నమోదు(Enrollment) :
2017-18 సంవత్సరంలో అన్ని పాఠశాలలు కలిపి 58.71 లక్షల విద్యార్థులు నమోదు చేసుకొన్నారు. ఇందులో 53 శాతం ప్రైవేటు పాఠశాలల నమోదు కాగా మిగితా 47 శాతం ప్రభుత్వ పాఠశాలల నమోదు.
b) స్థూల నమోదు నిష్పత్తి (Gross Enrollment Ration-GER) :
స్థూల నమోదు నిష్పత్తి (GER) విశ్వవిద్యాలయాలు, కళాశాలలు, పాఠశాలలో విద్యార్థుల నమోదు సంఖ్యను నిర్ణయిస్తుంది. GER 2017-18లో ప్రాథమిక పాఠశాలలో బాలురు – 98.76 శాతం, బాలికలు -. 98.05 శాతం కాగా ఉచ్ఛతర ప్రాథమిక పాఠశాలలో బాలురు – 87.32 శాతం, బాలికలు 88.4 శాతం.
c) విద్యార్థి – ఉపాధ్యాయ నిష్పత్తి (Pupil – Teacher Ratio – PTR) :
ఇది ఒక విద్యా సంవత్సరంలో ప్రత్యేక విద్యా స్థాయికి సంబంధించి ఎంత మంది విద్యార్థులకు ఒక ఉపాధ్యాయుడు ఉంటాడనే విషయాన్ని తెలుపుతుంది. PTR, 2018-19లో రాష్ట్రంలో ప్రాథమిక స్థాయిలో 18.90, ఉచ్ఛతర ప్రాథమిక స్థాయి 14.12, సెకండరీ స్థాయిలో 17.85 గా ఉంది. రాష్ట్రం మొత్తానికి 2018-19లో PTR 17.67.
పాఠశాల విద్య :
i) సమగ్ర శిక్షా అభియాన్:
గతంలో కేంద్ర ప్రభుత్వ ప్రాయోజిత పథకాలైన
- సర్వ శిక్షా అభియాన్ (SSA) సార్వత్రిక ప్రాథమిక విద్యను అమలు పరుస్తూండగా
- రాష్ట్రీయ మాధ్యమిక శిక్షా అభియాన్ (RMSA) సెకండరీ విద్యలో సామీప్యత (acess), ప్రమాణం (quality) లో పెంపుదలకు అమలు చేసింది.
ii) కస్తూర్బా గాంధీ బాలికా విద్యాలయం :
వీటిని 2004-05 లో రెసిడెన్షియల్ పాఠశాల సౌకర్యం కల్పించే ఉద్దేశంతో నెలకొల్పారు. నీటిలో ప్రవేశానికి అర్హతలు : SC, ST, BC, మైనారిటీ వర్గాలకు సంబంధించిన
- VI నుంచి VII తరగతులు వారికి,
- అనాధలు,
- బడి మానేసిన ఒంటరి తల్లి/తండ్రి కలిగిన విద్యార్థులు
iii) ఆదర్శ పాఠశాలలు :
194 ఆదర్శ పాఠశాలలు రాష్ట్రంలో 2013-14లో స్థాపించబడ్డాయి. వీటిలో అధిక విద్యార్హతలున్న ఉపాధ్యాయులచే ఇంగ్లీషు మీడియంలో విద్యా బోధన జరుగుతుంది. ఈ వథకం రద్దయినందువలన తెలంగాణ ప్రభుత్వం వీటి బాధ్యత తీసుకొని 2015-16 నుంచి వీటిని కొనసాగిస్తున్నది.
ఇంటర్మీడియట్ విద్య :
ప్రస్తుతం రాష్ట్రంలో 2,558 జూనియర్ కళాశాలలు ఉండగా వాటిలో విద్యార్థుల సంఖ్య 7.18 లక్షలు. 2,558 జూనియర్ కళాశాలలో, 404 ప్రభుత్వ, 4 వొకేషనల్, 41 ప్రైవేట్ ఎయిడెడ్, 1,583 ప్రైవేట్ మరియు ఇతర జూనియర్ కళాశాలలు కాగా 530 ఇతర ప్రభుత్వ సంస్థలు. ఈ బోర్డు ఉపాధిని కల్పించేందుకు వీలయిన 23 వొకేషనల్ కోర్సులను ఇంటర్మీడియట్ స్థాయిలో ప్రవేశపెట్టింది.

ఉన్నత విద్య:
a) కళాశాల విద్య :
కళాశాల విద్య డిపార్ట్ మెంట్ యొక్క ప్రధాన లక్ష్యం ఉన్నత విద్యలో సామీప్యత (access), సమానత (equality), నాణ్యత (quality) ను సాధించుట. ఇందుకోసం కేంద్ర ప్రభుత్వ ప్రాయోజిత పథకమైన రాష్ట్రీయ ఉచ్ఛతర శిక్షా అభియాన్ (RUSA) నుంచి నిధుల సమీకరణకు తెలంగాణ ప్రభుత్వం కృషి చేస్తున్నది.
b) డిగ్రీ ఆన్లైన్ సర్వీసెస్ తెలంగాణ (DOST) :
డిగ్రీ కళాశాలలో బి.ఎ/బి.కాం/బి.యస్సీ/బి.బి.ఎ వండి డీగ్రీ కోర్సులలో ప్రవేశాలను తెలంగాణ ప్రభుత్వం 2016 సంవత్సరం నుంచి DOST ద్వారా కల్పిస్తున్నది. 2018 – 19లో డిగ్రీ కళాశాలలో 2,00,472 మంది విద్యార్థులు ప్రవేశాన్ని పొందగా ఇందులో 42,688 విద్యార్థులు ప్రభుత్వ కళాశాలలో ప్రవేశాన్ని పొందారు.
c) సాంకేతిక విద్య :
సాంకేతిర విద్యా డైరెక్టరేట్ రాష్ట్రంలో పాలిటెక్నిక్, వృత్తి విద్యలను పర్యవేక్షిస్తుంది. ఇది ప్రభుత్వ, ప్రైవేటు, ఎయిడెడ్ రంగాలలలో ప్రవేశాలు, విద్యా బోధనను పర్యవేశిస్తుంది. ప్రస్తుతం రాష్ట్రంలో 820 డిప్లమో డిగ్రీలో యుక్తమైన కళాశాలలు 1,36,805 విద్యార్థులతో పనిచేస్తున్నాయి.
సాంఘిక సంక్షేమ విద్యా సంస్థలు :
SC, ST, BC, మైనారిటీ, వికలాంగ బాలబాలికలక సమీప ప్రాంతాలలో విద్యా సంస్థలు ఉండే విధంగా చూని సాంఘిక సమానత్వ సాధనకు ప్రభుత్వం సాంఘిక సంక్షేమ విద్యా సంస్థలను నెలకొల్పింది. ఈ సంస్థలు రెసిడెన్షియల్ రూపంలో ఉండి విద్యార్థులకు ఉచిత హాస్టల్ వసతితో బాటు పాఠ్యపుస్తరాల పంపిణీ చేస్తాయి.
A) షెడ్యూల్డ్ కులాల రెసిడెన్షియల్ పాఠశాలలు :
తెలంగాణ సాంఘిక సంక్షేమ రెసిడెన్నియల్ విద్యా సంస్థల సొసైటి (TSWREIS) రాష్ట్రంలో 269 రెసిడెన్షియల్ విద్యా సంస్థలను నడుపుచున్నది. ఇందులో 175 బాలికలకు సంబంధించినవి. వీటిలో 5వ తరగతి నుండి డిగ్రీ వరకు షెడ్యూల్డ్ కులాలకు చెందిన విద్యార్థులకు ప్రవేశం కలదు. ప్రస్తుతం 268 విద్యా సంస్థలు ఉండగా అందులో 134 తెలంగాణ ఏర్పడిన తరువాత ప్రారంభించబడ్డాయి.
B) షెడ్యూల్డ్ తెగల రెసిడెన్షియల్ పాఠశాలలు :
a) తెలంగాణ గిరిజన సంక్షేమ రెసిడెన్షియల్ విద్యా సంస్థల సొసైటీ (TTWRESIS) – గురుకులాలు :
రాష్ట్రంలో ఈ గురుకులాలు 175 ఉన్నాయి.
b) ఆశ్రమ పాఠశాలలు :
రాష్ట్రంలో ప్రస్తుతం 321 ఆశ్రమ పాఠశాలలు ఉన్నాయి.
c) ప్రభుత్వ ప్రాథమిక పాఠశాలలు :
గిరిజన సంక్షేమ శాఖ 1,427 ప్రాథమిక పాఠశాలలను నిర్వహిస్తున్నది.
C) వెనుకబడిన తరగతులు సంక్షేమ రెసిడెన్షియల్ పాఠశాలలు :
మహాత్మా జ్యోతిబా పూలే తెలంగాణ వెనకబడిన తరగతుల సంక్షేమ రెసిడెన్షియల్ సంస్థల సొసైటీ (M,JPTBCWREIS) వెనకబడిన తరగతులు, ఆర్థికంగా వెనకబడిన తరగతుల వారికి విద్యను అందించుటకు స్థాపించారు.
ఒక రెసిడెన్షియల్ డిగ్రీ కళాశాలను నడుపుతున్నది. ఈ విద్యా సంస్థలలో దాదాపు 99,360 విద్యార్థులు విద్యను అభ్యసిస్తున్నారు.
D) మైనారిటీ రెసిడెన్షియల్ విద్యా సంస్థలు :
మైనారిటీ వర్గాలకు చెందిన బాలబాలికలకు అధిక నాణ్యతతో కూడిన విద్యను అందించుటకు రాష్ట్ర ప్రభుత్వం తెలంగాణ మైనారిటీల రెసిడెన్షియల్ విద్యా సంస్థల సొసైటీ (TMREIS) ని స్థాపించింది. ప్రస్తుతం రాష్ట్రంలో 216 మైనారిటీ విద్యా సంస్థలు 12 కళాశాలలతో కలిపి 79,424 విద్యార్థులకు విద్యను కల్పిస్తున్నాయి.

II. తెలంగాణలో ఆరోగ్య రంగం :
‘అందరికీ ఆరోగ్యం’ అనే ప్రపంచ ఆరోగ్య సంస్థ (WHO) లక్ష్యాన్ని చేరుకోవడానికి తెలంగాణ ప్రభుత్వం వివిధ కార్యక్రమాలను చేపట్టింది. జాతీయ ప్రసూతి లబ్ది పథకం (National Maternity Benefit Programme), సమగ్ర శిశు అభివృద్ధి పథకం, పిల్లల కోసం బాలికా సమృద్ధి యోజన పథకం, పునరుత్పత్తి కలిగిన మహిళలకు సప్లిమెంటరీ న్యూట్రీషన్ పథకాన్ని అమలు చేస్తున్నది.
‘సామాజిక, ఆర్థిక దృక్పథం 2020’ ప్రకారం తెలంగాణ రాష్ట్రంలో 4,797 ఆరోగ్య ఉప కేంద్రాలు, 633 ప్రాథమిక ఆరోగ్య కేంద్రాలు, 249 పట్టణ ప్రాథమిక ఆరోగ్య కేంద్రాలు, 90 కమ్యూనిటీ ఆరోగ్య కేంద్రాలు, 19 ఏరియా ఆసుపత్రులు, 29 జిల్లా కేంద్ర ఆసుపత్రులు, 9 వైద్య కళాశాల ఆసుపత్రులు, 12 స్పెషాలిటీ ఆసుపత్రులు, 2 సూపర్ స్పెషాలిటీ ఆసుపత్రులు ఉన్నాయి.
ఆరోగ్య రంగంలో తెలంగాణ ప్రభుత్వం అమలు పరుస్తున్న పథకాలు : రాష్ట్రావతరణ అనంతరం తెలంగాణ ప్రభుత్వం ఆరోగ్య రంగంలో అనేక పథకాలను రూపొందించి అమలు పరుస్తున్నది. అందులో ముఖ్యమైనవి.
a) కంటి వెలుగు :
సామాన్యంగా ప్రజలు ప్రత్యేకించి మహిళలు, వృద్ధులు కంటి సమస్యలను వాయిదా వేయడం లేదా ఆ సమస్యలను కొనసాగిస్తూనే జీవనాన్ని గడుపుతుంటారు. ఈ సమస్య నివారణ కోసమే తెలంగాణ ప్రభుత్వం కంటి వెలుగు పథకాన్ని రూపొందించి అమలుపరుస్తున్నది.
b) బస్తీ దవాఖాన :
పట్టణ ప్రాంతాలలో ప్రామాణికతతో కూడిన ఆరోగ్య సేవలు అందించుటకు బస్తీ దవాఖానాలు స్థాపించారు. ప్రతి బస్తీ దవాఖాన 6,000 నుండి 10,000 జనాభా ఉన్న ప్రాంతాలకు సేవలందిస్తుంది. పట్టణ మురికినాడలలో వీటిని స్థాపిస్తారు. రాష్ట్రంలో 104 బస్తీ దవాఖానాలు పనిచేస్తున్నాయి.
c) ఆరోగ్య, వెల్నెస్ కేంద్రాలు :
ఇవి సమగ్ర ఆరోగ్య సేవలతో బాటు ప్రసూతి, చిన్న పిల్లల ఆరోగ్య రక్షణ సేవలను అందిస్తున్నాయి. వైద్య సేవలు, అవసరమైన ఔషధాలను ఇవి ఉచితంగా పంపిణీ చేస్తాయి. రాష్ట్రంలో 636 ప్రాథమిక ఆరోగ్య కేంద్రాలు, 86 ఉపకేంద్రాలు, 104 బస్తీ దవాఖానాలు, 227 పట్టణ ప్రాథమిక ఆరోగ్య కేంద్రాలు ఆరోగ్య వెల్నెస్ కేంద్రాలుగా పనిచేస్తున్నాయి.
d) తెలంగాణ వైద్య విధాన పరిషత్ (TVVP) ఆసుపత్రులు :
తెలంగాణ వైద్య విధాన పరిషత్ ఆధ్వర్యంలో 107 TVVP ఆసుపత్రులు పనిచేస్తున్నాయి. ఇవి ప్రసూతి, చిన్న పిల్లల ఆరోగ్య రక్షణ సేవలు, సాధారణ వైద్య సేవలు, సర్జరీలు, ఆప్తమాలజీ, పీడియాట్రిక్స్, ఆర్థోపెడిక్స్, డెర్మటాలజీ, ENT మొదలైన సేవలను అందిస్తాయి.
e) ఆయుష్ (ఆయుర్వేద, యోగ, నాచురోపతి, యునాని, హోమియోపతి) :
తెలంగాణ ప్రభుత్వం, జాతీయ ఆయుష్ మిషన్ సహకారంతో రాష్ట్రంలో ఆయుష్ పద్ధతి వైద్యాన్ని ప్రోత్సహిస్తున్నది. ఆయుష్ శాఖ కింద రాష్ట్రంలో 860 దవాఖానాలు పనిచేస్తున్నాయి.
f) ఆరోగ్య శ్రీ :
‘ఆరోగ్యశ్రీ ఆరోగ్య రక్షణ ట్రస్టు’ ద్వారా రాష్ట్రంలో ఆరోగ్యశ్రీ అనే ఒక ఏకైక పథకం ఆరోగ్య బీమాతో అమలవుతుంది. దీని ప్రధాన ఆశయం పేదరిక రేఖకు దిగువన ఉన్న వారికి వైద్య సేవలను అందించడం. ఈ పథకం ద్వారా పేద వారికి ఎంపిక చేయబడిన వ్యాధులకు నగదు రహిత సేవలు అందించబడతాయి.
g) KCR కిట్ :
ఈ పథకాన్ని తెలంగాణ ప్రభుత్వం జూన్ 2, 2017 న ప్రారంభించింది. పేదరికపు రేఖకు దిగువన ఉండి ప్రభుత్వ ఆరోగ్య కేంద్రాల నుంచి ఆరోగ్య సేవలు పొందే గర్భిణీ స్త్రీలకు, మగశిశువు జన్మిస్తే రూ. 12,000, ఆడశిశువు జన్మిస్తే రూ. 13,000 సహాయం అందించబడుతుంది.

ప్రశ్న 6.
తెలంగాణ రాష్ట్రంలో నీటిపారుదల సౌకర్యాలను వివరించండి.
జవాబు.
తెలంగాణ ప్రత్యేక రాష్ట్రంగా అవతరించిన నాటి నుంచి నీటి పారుదల సౌకర్యాల అభివృద్ధి పట్ల తెలంగాణ ప్రభుత్వం అత్యధిక ప్రాధాన్యత నిచ్చుచున్నది. నీటిపారుదల సౌకర్యాలను విస్తరించుట ద్వారా రాష్ట్రంలో కనీసం ఒక కోటి ఎకరాలకు నీటి పారుదలను దించాలనే లక్ష్యాన్ని నిర్దేశించుకొన్నది. రాష్ట్రంలో నీటి పారుదల ప్రాజెక్టుల ప్రస్తుత పరిస్థితిని గురించి కింద వివరించవచ్చు.
a) డా॥ బి.ఆర్. అంబేద్కర్ ప్రాణహిత ప్రాజెక్టు:
కుమరం భీం జిల్లాలో గల తుమ్మిడిహట్టి గ్రామం, కౌటాల నుండలం, ప్రాంతంలో పెంగ, వార్ధా నదుల సంగమం వద్ద గల ప్రాణహిత నదిపై ఒక బ్యారేజిని నిర్మించి 20 TMC ల నీటిని మళ్లించి ఉత్తర ఆదిలాబాద్ జిల్లాలో గతంలో నిర్దేశించిన 56,500 ఎకరాలకు బదులు 2 లక్షల ఎకరాలకు నీటిని సమకూర్చడం.
b) కాళేశ్వరం ప్రాజెక్టు :
కాళేశ్వరం దగ్గరలో గల మేడిగడ్డ వద్ద గోదావరి నదిపై ఒక బ్యారేజీ, మేడిగడ్డ (లక్ష్మీ బ్యారేజీ) మరియు అన్నారం వద్ద గల శ్రీపాద యెల్లంపల్లి మరియు అన్నారం వద్ద గల శ్రీపాద యెల్లంపల్లి మరియు సుందిల్ల వద్ద మరో రెండు బ్యారేజీలను నిర్మించడం.
వీటి ద్వారా కాలువలు, టన్నెల్స్, లిఫ్ట్ పద్ధతులు, రిజర్వాయర్లు, నీటి పంపిణీ వ్యవస్థలను ఉపయోగించి కమాండ్ ఏరియాలో గల 7 జిల్లాల (పునర్విభజన వలన 13 జిల్లాలకు) ఆయకట్టు తొలుత ప్రకటించిన 16,40,000 ఎకరాలకు బదులు 18,25,700 ఎకరాలకు నీటిని అందించుటకు నిర్ణయం తీసుకున్నారు.
i) అలీసాగర్ ఎత్తిపోతల పథకం :
ఈ పథకం ద్వారా నిజామాబాద్ జిల్లాలో గల నవీపేట, రెంజల్, ఎడపల్లి, నిజామాబాద్, డిచ్పల్లి, మాక్లూర్ మండలాలలో సుమారు 53,793 ఎకరాలకు నిజాంసాగర్ ఆయకట్టు ద్వారా నీటి పారుదలలో వచ్చిన కొరత తీర్చుటకు అనుబంధంగా నీటి పారుదల కల్పిస్తారు. కోహ్లి గ్రామం వద్ద గోదావరి కుడి కాలువ నుండి 720 క్యూసెక్కుల నీరు ఎత్తిపోయడం ఈ పథకం ప్రతిపాదన.
ii) అర్గుల రాజారాం గుత్ప – ఎత్తిపోతల పథకం :
నిజాంసాగర్ ఆయకట్టు ద్వారా నీటి పారుదలలో వచ్చిన కొరతను తీర్చుటకు నిజామాబాద్ జిల్లాలో సుమారు 38,792 ఎకరాలకు నిజాంసాగర్ యొక్క D74 నుంచి నుంచి D82 డిస్ట్రిబ్యూటరీల ద్వారా నీటిపారుదల ఈ పథకం ద్వారా కల్పించబడుతుంది.
iii) చౌట్పల్లి హన్మంతరెడ్డి ఎత్తిపోతల పథకం :
శ్రీరాంసాగర్ ప్రాజెక్టు – లక్ష్మీ కెనాల్ యొక్క D4 డిస్ట్రిబ్యూటరీ ద్వారా షెట్పల్లి చెరువును నింపి నిజామాబాద్ జిల్లాలోని కమ్మర్పల్లి, మోర్తాడ్ మండలాలలోని 18 గ్రామాలకు 180 క్యూసెక్కుల నీటిని ఎత్తిపోతల ద్వారా 11,625 ఎకరాలకు నీటిపారుదల సౌకర్యం కల్పించుట ఈ పథకం ఉద్దేశం.
iv) లెండ్ అంతర్ రాష్ట్ర ప్రాజెక్టు :
ఇది తెలంగాణ, మహారాష్ట్రలకు సంబంధించిన అంతర్ రాష్ట్ర ప్రధాన ప్రాజెక్టు. దీని ప్రధాన పనులు మహారాష్ట్రలోని నాందేడ్ జిల్లాలో ఉన్నాయి. ఈ ప్రాజెక్టు ద్వారా తెలంగాణలో 27,000 ఎకరాలు, మహారాష్ట్రలో 22,000 ఎకరాలు మొత్తం 49,000 ఎకరాలకు నీటి పారుదల కల్పించాలనేది ప్రతిపాదన.
v) ఎం. బాగారెడ్డి సింగూరు ప్రాజెక్టు :
సంగారెడ్డి జిల్లా, సింగూరు గ్రామం వద్ద గోదావరి ఉపనది అయిన మంజీరా నది వద్ద ఈ ప్రాజెక్టు నిర్మించబడ్డది. దీని స్థూల నీటి నిలువ స్థాయి 29.91 TMCలు.
vi) జె: చొక్కారావు దేవాదుల ఎత్తిపోతల పథకం :
ఈ పథకం ద్వారా జయశంకర్ భూపాలపల్లి జిల్లా, ఏటూరు నాగారం మండలం, గంగారం వద్ద గోదావరి నది నుంచి ఎత్తిపోతల ద్వారా వరంగల్ పట్టణ ప్రాంతంలో గల ఎత్తు ప్రాంత కరువు భూములైన 6.21 లక్షల ఎకరాలకు నీటి పారుదల సౌకర్యం కల్పించడం.
vii) దిగువ పెంగా ప్రాజెక్టు :
ఇది తెలంగాణ, మహారాష్ట్రల ఉమ్మడి ప్రాజెక్టు. ఇది గోదావరి ఉపనది అయిన పెన్గాంగ వద్ద కలదు. ఈ ప్రాజెక్టు నికర నీటి నిలువ అంచనా 42.67 TMCలు, మహారాష్ట్ర, తెలంగాణ ఈ నీటిని 88:12 నిష్పత్తిలో పంచుకొంటాయి.
viii) శ్రీరామ ఎత్తిపోతల పథకం :
తెలంగాణ రాష్ట్రం ఏర్పడిన తరవాత గతంలో ఉన్న రాజీవ్ దుమ్ముగూడెం, ఇందిరా సాగర్ రుద్రంకోట ఆయకట్టులను కలిపి ఈ పథకాన్ని ప్రారంభించింది. భద్రాద్రి కొత్తగూడెం, ఖమ్మం, మహబూబ్ నగర్ జిల్లాలలో లక్షల ఎకరాలకు నీటిపారుదల కల్పించడం దీని లక్ష్యం.
ix) తుపాకుల గూడెం బ్యారేజి (సమ్మక్క బ్యారేజి) :
ప్రభుత్వం ఈ బ్యారేజి స్థలాన్ని కంతనపల్లి గ్రామం నుంచి తుపాకుల గూడెం గ్రామం, వరంగల్ రూరల్కు బదిలీ చేయుటకు అంగీకారం తెలిపింది. ఈ ప్రాజెక్టు ద్వారా పూర్వ వరంగల్, నల్గొండ, ఖమ్మం జిల్లాలు లబ్ది పొందుతాయి. తెలంగాణ ప్రభుత్వం ఈ ప్రాజెక్టు పేరును “సమ్మక్క బ్యారేజి” గా మార్చుటకు ప్రతిపాదించింది.
x) శ్రీ కుమరం భీం ప్రాజెక్టు :
ఇది ఒక మధ్య తరహా నీటిపారుదల ప్రాజెక్టు. దీనిని ఆసిఫాబాద్ జిల్లా, మండలం, అడ గ్రామం వద్ద స్థాపించుటకు ప్రతిపాదించారు. దీని ద్వారా ఆసిఫాబాద్ జిల్లాలోని వాంకిడి, ఆసిఫాబాద్, కాగజ్ నగర్, సిర్పూర్ (IT) మండలాలలో 69 గ్రామాల 45,500 ఎకరాల ఆయకట్టుకు నీటిపారుదల, అందించాలనేది లక్ష్యం.
xi) పాలెం వాగు ప్రాజెక్టు :
ఇది గోదావరి ఉపనది అయిన పాలెంవాగు వద్ద మధ్యతరహా నీటిపారుదల ప్రాజెక్టు రూపంలో ఉన్నది. జయశంకర్ భూపాలపల్లి జిల్లా వెంకటాపురం మండలం మల్లాపురం గ్రామం ప్రాంతంలో ఉన్నది. ఈ ప్రాజెక్టు ఖరీప్ సీజన్లో 4100 హెక్టార్లు (10,132 ఎకరాలు), రబీ సీజన్లో 1250 హెక్టార్ల భూమికి నీటిపారుదల సౌకర్యాన్ని కల్పించుచున్నది.
xii) శ్రీరాం సాగర్ ప్రాజెక్టు :
దీనిని నిజామాబాద్ జిల్లాలో పోచంపాడు వద్ద గోదావరి నదిపై నిర్మించారు. దీని ముఖ్య లక్ష్యం తెలంగాణ రాష్ట్రంలోని 5 పూర్వ జిల్లాలకు అనగా కరీంనగర్, వరంగల్, ఆదిలాబాద్, నల్గొండ, ఖమ్మం జిల్లాలకు త్రాగునీరు, సాగు నీరును అందించడం. ఈ ప్రాజెక్టు కింద సుమారు 4 లక్షల ఎకరాలకు నీరు లభిస్తుంది.
xiii) కడెం ప్రాజెక్టు :
దీనిని పూర్వ ఆదిలాబాద్ జిల్లాలోని కడెం నదిపై నిర్మించారు. దీని ద్వారా ఆదిలాబాద్ జిల్లాలో 25,000 ఎకరాలకు సాగునీరు లభిస్తుంది.
xiv) నిజాంసాగర్ ప్రాజెక్టు :
పూర్వ నిజామాబాద్ జిల్లాలోని అచ్చంపేట, భంజపల్లి గ్రామాల మధ్య గోదావరి నదికి ఉపనది. అయిన మంజీర నదిపై నిర్మించారు. ఈ డ్యామ్ 2.31 లక్షల ఎకరాల భూమికి సాగునీటిని అందిస్తుంది.

B. కృష్ణానది పరివాహక ప్రాంతం :
i) మహార్మాగాంధీ కల్వకుర్తి ఎత్తిపోతల ప్రాజెక్టు :
మహబూబ్ నగర్ జిల్లాలో 4.10 లక్షల ఎకరాలకు నీటిపారుదల సౌకర్యాన్ని కల్పించి ఎత్తు ప్రాంతాలలో కరువు పీడిత ప్రజలకు తాగునీటి సరఫరా చేయడం ఈ పథకం ఉద్దేశం. శ్రీశైలం ప్రాజెక్టు రిజర్వాయర్ నుంచి మూడు దశలలో ఎత్తిపోతల ద్వారా 40 TMC ల నిలువకు ప్రతిపాదన.
ii) రాజీవ్ భీమా ఎత్తిపోతల పథకం :
ఈ పథకం ద్వారా రెండు ప్రాంతాలలో అనగా జూరాల ప్రాజెక్టు వద్ద గల పంచదేవ్పాడ్, ఉకబెట్టివాగు వద్ద గల రామన్పౌడ్ నుంచి ఎత్తిపోతల ద్వారా నీటిపారుదల సౌకర్యాన్ని ఎత్తు ప్రాంతాలలో తీవ్రమైన కరువును చవిచూసిన పూర్వ మహబూబ్ నగర్ జిల్లాలోని 15 మండలాలలో వివిధ ప్రాంతాలకు విస్తరించడం. అంతేగాక ఈ ప్రాంతాలలో గల 196 గ్రామాలకు తాగు నీరును సరఫరా చేయడం ఈ పథకపు లక్ష్యం.
iii) జవహర్ నెట్టంపాడు ఎత్తిపోతల పథకం :
ప్రియదర్శిని జూరాల ప్రాజెక్టు రిజర్వాయర్ నుంచి 21.425 TMCల నీటిని ఎత్తిపోయడం ద్వారా గద్వాల, ఆలంపూర్ నియోజక వర్గాలలోని 8 మండలాలలో గల 148 గ్రామాలలలో 2 లక్షల ఎకరాలకు నీటిపారుదల సౌకర్యం కల్పించడం ఈ పథకం ఉద్దేశం.
iv) ప్రియుదర్శిని జూరాల ప్రాజెక్టు :
ఇది ఒక బహుళార్ధక సాధక ప్రాజెక్టు. జోగులాంబ గద్వాల జిల్లా, రేవులపల్లి గ్రామం వద్ద కృష్ణా నదిపై దీనిని నిర్మించారు. ఈ ప్రాజెక్టు ఎడమ (ఎన్.టి.ఆర్. కాలువ), కుడి (నల్లసోమనాద్రి కాలువ) కాలువల ద్వారా కరువు పీడిత ప్రాంతాలైన వనపర్తి జిల్లాలోని ఆత్మకూరు, కొత్తకోట, పెబ్బేరు మండలాలు, నాగర్ కర్నూల్ జిల్లాలోని వేపగండల, కొల్లాపూర్ మండలాలు, మహబూబ్ నగర్ జిల్లాలోని ఇటిక్యాల్ మానోపాడ్ మండలాలకు సంబంధించి 1.02 లక్షల ఎకరాలకు నీటి పారుదల కల్పించుట.
v) రాజోలిబండ మళ్లింపు పథకం :
ఇది తెలంగాణ, కర్ణాటక రాష్ట్రాల ఉమ్మడి ప్రాజెక్టు. కర్ణాటకలోని రాయచూర్ జిల్లాలో తుంగభద్ర నదిపై నిర్మించిన ఆనకట్టతో యుక్తమైనది ఈ ప్రాజెక్టు. నిజాం రాష్ట్ర పాలన కాలంలో ఈ పథకం మంజూరు చేయబడ్డది. ఈ ఆనకట్ట 1946లో ప్రారంభించబడి 1958లో పూర్తిచేయబడ్డది.
vi) కోయిల్ సాగర్ ఎత్తిపోతల పథకం :
సుహబూబ్ నగర్ జిల్లా, దేవరకద్ర మండలం, బొల్లారం గ్రామం వద్ద 1955లో ఈ ప్రాజెక్టును నిర్మించారు. మహబూబ్ నగర్ జిల్లా అమరచింత నియోజ వర్గంలోని 12,000 ఎకరాల ఆయకట్టుకు నీటిపారుదల ఈ ప్రాజెక్టు ద్వారా జరుగుతుంది.
vii) పాలమూరు – రంగారెడ్డి ఎత్తిపోతల పథకం :
ఎత్తు ప్రాంతంలో గల 12.310 లక్షల ఎకరాల ఆయకట్టుకు నీటిపారుదల సౌకర్యం కల్పించడం ఈ ప్రాజెక్టు లక్ష్యం. ఈ ప్రాజెక్టు ద్వారా నాగర్ కర్నూల్ (1 లక్ష ఎకరాలు), మహబూబ్ నగర్ (4.14 లక్షల ఎకరాలు), రంగారెడ్డి (3.64 లక్షల ఎకరాలు), వికారాబాద్ (3.32 లక్షల ఎకరాలు), నల్గొండ (0, 30 లక్షల ఎకరాలు) జిల్లాలకు నీటి పారుదలతో బాటు సమీప గ్రామాలకు, GHMCకి తాగు నీరు మరియు పారిశ్రామిక అవసరాలకు నీటి సౌకర్యం సమకూర్చాలనేది ప్రభుత్వ ఆశయం.
viii) గట్టు ఎత్తిపోతల పథకం :
జోగులాంబ గద్వాల జిల్లాలోని గట్టు, దరూర్, కె.టి. దొడ్డి మండలాలలోని ఎత్తు ప్రాంతాలలో గల 28,000 ఎకరాలకు నీటి పారుదల సౌకర్యం కల్పించడం ఈ పథకం ముఖ్య లక్ష్యం.
ix) డిండి ఎత్తిపోతల పథకం:
నల్గొండ జిల్లాలోని ఎత్తు ప్రాంతాలు కరువు పీడిత ప్రాంతాలే కాకుండా వీటిలో చాలా ప్రాంతాలు ఫ్లోరైడ్ సమస్యకు గురైనాయి. ఈ సమస్య నివారణకు ఇక్కడి ప్రాంతాలకు ఏకైక మార్గం కృష్ణా నది నీరు. డిండి ప్రాజెక్టు ద్వారా నాగర్ కర్నూల్, నల్గొండ, యాదాద్రి భువనగిరి, రంగారెడ్డి జిల్లాలకు 3.61 లక్షల ఎకరాలకు నీటి పారుదల సౌకర్యాన్ని కల్పించడంతో బాటు తాగు నీటి సౌకర్యాన్ని కల్పించడం జరుగుచున్నది.
x) ఉదయ సముద్రం ఎత్తిపోతల పథకం :
ఎలిమినేటి మాధవ రెడ్డి శ్రీశైలం ఎడమ కాలువ బాలెన్సింగ్ రిజర్వాయర్ అయిన ఉదయ సముద్రం నుంచి ఎత్తిపోతల ద్వారా 6.70 TMC ల నీటిని నల్గొండ జిల్లాలోని నక్రేకల్, నల్గొండ, మునుగోడు, తుంగతుర్తి అసెంబ్లీ నియోజక వర్గాలలో తీవ్రంగా క్షామం, కరువు పీడిత ఎత్తు ప్రాంతాలలో 1 లక్ష ఎకరాలకు నీటిపారుదల సౌకర్యం కల్పించడం ఈ పథకం లక్ష్యం.
xi) నాగార్జున సాగర్ ప్రాజెక్టు :
ఇది ప్రపంచంలోనే అతి పెద్ద బహుళార్థ సాధక ప్రాజెక్టు. దీనిని కృష్ణా నదిపై నల్గొండ,, గుంటూరు జిల్లాల సరిహద్దుల్లో నిర్మించారు. ఈ ప్రాజెక్టు కుడి కాలువ ద్వారా ఆంధ్రాకు 1.11 మిలియన్ హెక్టార్లకు, తెలంగాణకు 0.32 మిలియన్ హెక్టార్లకు నీరు లభిస్తుంది.
xii) శ్రీశైలం ప్రాజెక్టు :
దీనిని కృష్ణా నది పైస మహబూబ్ నగర్, కర్నూలు జిల్లాల సరిహద్దుల్లో నిర్మించారు. దీని ఎడమ కాలువ ద్వారా 4.20 లక్షల ఎకరాల భూమికి సాగు నీరు లభిస్తుంది.

ప్రశ్న 7.
తెలంగాణ రాష్ట్రంలో IT, ITeS వృద్ధి, దృష్టి కోణాన్ని అంచనా వేయండి.
జవాబు.
రాష్ట్ర ఆర్ధిక వ్యవస్థ అభివృద్ధి చెందుతున్నప్పుడు వ్యవసాయాధార వ్యవస్థ నుంచి పారిశ్రామిక ఆర్థిక వ్యవస్థగా రూపాంతరం చెందుతుంది. ఆర్థికాభివృద్ధి ప్లవన దశకు (take off stage) చేరుకున్నప్పుడు సేవా రంగం వృద్ధి త్వరిగతిన జరగడమే కాకుండా పారిశ్రామిక రంగం కంటే ముందుంటుంది.
రాష్ట్ర ఆర్థిక వ్యవస్థలో జోడించిన స్థూల రాష్ట్ర ప్రాంతీయోత్పత్తి విలున (GVSA)లో సేనా రంగం 2018-19 (మొదటి సవరించిన అంచనా) లో స్థిర ధరలలో 64.5 శాతం నాటాను కలిగి ఉండి ముందంజ రంగంగా కొనసాగుతున్నది.
తెలంగాణలో ఇన్ఫర్మేషన్ టెక్నాలజీ (IT), దాని అనుబంధ సేవలు (ITeS) : ఇన్ఫర్మేషన్ టెక్నాలజీ (IT), దాని అనుబంధ సేవల (ITeS) ఉత్పత్తి, ఎగుమతులలో తెలంగాణ రాష్ట్రం ప్రముఖ స్థానాన్ని కలిగి ఉంది. IT రంగం ద్వారా వచ్చిన పెను మార్పులు నూతన అవకాశాలను ప్రత్యేకించి బిగ్ డేటా అనలిటిక్స్, సైబర్ సెక్యూరిటీ, క్లౌడ్ కంప్యూటింగ్, యానిమేషన్ గేమింగ్ వంటి వాటిని కల్పించింది. రాష్ట్ర రాజధాని నగరమైన హైదరాబాద్ ప్రాపంచిక IT హబ్ గా గుర్తింపు పొందింది.
ఇక్కడ చిన్నవి, పెద్దవి కలిపి 1500 IT, ITeS కంపెనీలు ప్రత్యక్షంగా 4.3 లక్షల వృత్తి నైపుణ్యులకు ఉద్యోగిత కల్పించడమే కాకుండా 7 లక్షల మందికి పరోక్ష ఉద్యోగితను కల్పించుచున్నవి. 2014-15 నుంచి IT, ITeS రంగంలో బలమైన వృద్ధి చోటు చేసుకొనుచున్నది. ఈ స్థితిని పట్టిక – 10.7 ద్వారా చూడవచ్చు. 2014-15 నుంచి 2016-17 మధ్య కాలంలో IT, ITeS యూనిట్ల సంఖ్య, ఉద్యోగిత, ఎగుమతులలో శ్రీఘ్రతర వృద్ధి ఏర్పడింది.
2018-19 లో రాష్ట్ర IT సాఫ్ట్వేర్ ఉత్పత్తుల ఎగుమతుల విలువ రూ. 1,09,219 కోట్లు (US$15.6 బిలియన్లు), దేశ IT ఎగుమతులలో తెలంగాణ రాష్ట్ర వాటా 11 శాతం, దేశానికి IT ఎగుమతుల ద్వారా సంక్రమించే రాబడిలో హైదరాబాద్ 2 స్థానాన్ని కలిగి ఉంది.
IT విధానం :
దేశంలో సాంకేతికత పెట్టుబడులకు ప్రధాన కేంద్రంగా మార్చే లక్ష్యంతో IT, ITeS సేవలను పెంపొందించి ఈ రంగాల్లో పెట్టుబడులను ఆకర్షించి ఉద్యోగితను పెంచుట కొరకు తెలంగాణ ప్రభుత్వం ICT (Information and Commu- nication Technology) విధానాన్ని రూపొందించింది.

IT, ITeS ప్రధాన లక్ష్యాలు :
i) IMAGE టవర్ :
అధునాతన అవస్థాపనా సౌకర్యాల కల్పన ద్వారా యానిమేషన్, గేమింగ్, VFX సేవల కల్పనకు IMAGE టవర్ను నెలకొల్పుటకు తెలంగాణ ప్రభుత్వం సంకల్పించింది. దీనిని రుద్రారం గ్రామం, రంగారెడ్డి జిల్లాలో 10 ఎకరాల స్థలంలో రూ. 1,000 కోట్లతో ప్రభుత్వ, ప్రైవేట్ భాగస్వామ్యం (PPP)లో స్థాపించ తలపెట్టింది.
ii) తెలంగాణ ఫైబర్ గ్రిడ్ ప్రాజెక్టు:
ఈ ప్రాజెక్టును తెలంగాణ ప్రభుత్వం 2015లో ప్రారంభించింది. తగిన అవస్థాపనా సౌకర్యాలను కల్పించి 10 జోన్లు (33 జిల్లాలో) గా ‘డిజిటల్ తెలంగాణ’ను సాకారం చేయడం ఈ ప్రాజెక్టు ప్రధాన లక్ష్యం.
iii) ఎలక్ట్రానిక్ నేవల డెలివరీ (ESD) :
రాష్ట్ర ప్రజలకు, వ్యాపారస్థులకు ప్రభుత్వం కల్పించే ఎలక్ట్రానిక్ సేవలలో పారదర్శకత, జవాబుదారీతనం, సామర్థ్యంతో కూడిన డెలివరీలో ESD నోడల్ ఏజెన్సీగా విధులను నిర్వర్తిస్తుంది. డిజిటల్ తెలంగాణ సాధనలో భాగంగా సాంకేతికత ద్వారా ప్రజాకేంద్రక స్మార్ట్ సేవలు అందించుట ESD లక్ష్యం. ESD, 550 పై చిలుకు సేవలను 38 కార్యా లయాల ద్వారా మీ సేవ, T-వాలెట్, T-ఆప్ వంటి వాటి ద్వారా తెలంగాణ రాష్ట్ర ప్రజలకు సేవలను అందించుచున్నది.
iv) నైపుణ్యం, విజ్ఞానాన్నిఅందించే తెలంగాణ అకాడమి (TASK) :
IT, ITeS, జీవశాస్త్రాలు ఆరోగ్యం రక్షణ, ఏరోస్పేస్, బాంకింగ్, ఆర్ధిక, సేవలు వంటి రంగాలకు అవసరమైన శ్రామికశక్తి నైపుణ్యాల పెంపుదల కోసం ఉద్దేశించిన ఏకైక సంస్థ TASK (Telangana Academy for Skill and Knowledge) విద్యా రంగం, పరిశ్రమల భాగస్వామ్యంతో లాభరహిత వ్యవస్థగా TASK నెలకొల్పబడింది.
డిగ్రీ, ఇంజనీరింగ్ విద్యను అభ్యసించిన విద్యార్ధులకు సాంకేతిక, సాంకేతికేతర సాఫ్ట్ స్కిల్స్ అందించి పరిశ్రమలకు పూర్తి తయారీ రూపంలో శ్రామిక శక్తిని అందించుట TASK లక్ష్యం.

ప్రశ్న 8.
తెలంగాణ రాష్ట్ర ప్రభుత్వం చేపట్టిన అభివృద్ధి, సంక్షేమ పథకాలను క్లుప్తంగా వివరించండి.
జవాబు.
తెలంగాణ రాష్ట్రంలో అభివృద్ధి సంక్షేమ పథకాలు :
తెలంగాణ ప్రత్యేక రాష్ట్రంగా అవతరించిన నాటి నుంచి పేద ప్రజల జీవన ప్రమాణ స్థాయిలో పెంపుదల కోసం తెలంగాణ రాష్ట్ర ప్రభుత్వం అనేక పథకాలను రూపొందించింది. వీటిని గురించి కింద వివరించవచ్చు.
a) పౌరులందరికీ సంబంధించిన అభివృద్ధి, సంక్షేమ పథకాలు :
i) ఆసరా పెన్షన్ల పథకం :
సంక్షేమ కార్యక్రమాలు, సాంఘిక భద్రత కల్పనలో భాగంగా పేదవారు గౌరవంగా జీవనాన్ని గడపడానికి వీలుగా తెలంగాణ ప్రభుత్వం ‘ఆసరా పెన్షన్’ల పథకాన్ని ప్రవేశపెట్టింది. సమాజంలో అతి పేదవారికి, బలహీన వర్గాలకు రక్షణ కల్పించుటలో భాగంగా ఎయిడ్స్ రోగులు, వితంతువులు, అశక్తులైన నేత పనివారు, గీత కార్మికులు, పెరుగుతున్న వయస్సుతో జీవన అవసరాలు కోల్పోయిన వారికి ఈ పథకం ద్వారా సహాయం లభిస్తుంది.
నవంబర్ 8, 2014 న ఈ పథకాన్ని పూర్వ మహబూబ్ నగర్ జిల్లాలోని, కొత్తూరులో పథకాన్ని ప్రారంభించారు.
ii) ఆరోగ్యలక్ష్మి :
గర్భిణీ స్త్రీలు, పిల్లలకు పాలిచ్చే తల్లులలో పౌష్టిక, పోషక విలువలు పెంచుట కొరకు ఈ పథకాన్ని రూపొందించారు. తెలంగాణ ప్రభుత్వం ఈ పథకాన్ని అంగన్ వాడి కేంద్రాల ద్వారా పేదరికపు రేఖకు దిగువన ఉన్న గర్భిణీ స్త్రీలు, 6 సంవత్సరాల లోపు వయస్సు గల పిల్లలకు ప్రతిరోజు పోషకాహాన్ని అందిస్తుంది. ఈ పథకాన్ని జనవరి 1, 2015 న ప్రారంభించారు.
iii) అమ్మ ఒడి :
రాష్ట్రంలో మాతా, శిశు మరణాలను తగ్గించుట కొరకు ప్రభుత్వం ఈ పథకాన్ని ప్రవేశపెట్టింది. ఈ పథకం ద్వారా గర్భిణీ స్త్రీలకు ప్రసూతికి ముందు, ప్రసూతి తరవాత ఆర్థిక, రవాణా సహకారం కల్పించబడుతుంది.
iv) మిషన్ భగీరథ :
కృష్ణా, గోదావరి నదుల నీటి సహాయంతో శుద్ధి చేసిన తాగు నీరుసు పైపులైను ద్వారా రాష్ట్ర ప్రజలకు అందుబాటులోకి తేవడం ఈ పథకం ముఖ్య ఆశయం. ఆగష్టు 7, 2016న మెదక్ జిల్లా, గజ్వేల్ నుండలం, కోమటిబండ గ్రామంలో ఈ పథకాన్ని ప్రారంభించారు.
v) పేదవారికి గృహాలు :
ఈ పథకం ద్వారా హైదరాబాద్, ఇతర పట్టణ ప్రాంతాలలో రెండంతస్తుల మూడంతస్తుల భవనాలలో రెండు పడకల గదుల (2 BHK) ప్లాట్లు, గ్రామీణ ప్రాంతాలలో స్వతంత్ర గృహాలు నిర్మించి ఇవ్వాలని ప్రభుత్వం నిర్ణయించింది.
vi) బియ్యం పంపిణీ :
ఈ పథకాన్ని జనవరి, 1, 2015న ప్రారంభించారు. కుటుంబ సభ్యుల సంఖ్యతో సంబంధం లేకుండా ఒక రూపాయికి కిలోగ్రాము చొప్పున 6 కిలోల బియ్యాన్ని తెలంగాణ రాష్ట్ర సివిల్ సప్లయ్ కార్పోరేషన్ చౌక ధరల దుకాణాల ద్వారా సప్లయ్ చేస్తుంది.

B. SC/STs వర్గాల అభివృద్ధి, సంక్షేమ పథకాలు :
i) SC, ST ల ప్రత్యేక అభివృద్ధి నిధి :
SC, ST ల ప్రత్యేక అభివృద్ధి నిధి (SDF) చట్టం, 2017 ననుసరించి తెలంగాణ ప్రభుత్వం రెండు బడ్జెట్ పద్దులను అనగా (i) SC ప్రత్యేక అభివృద్ధి నిధి (SCSDF), (ii) ST ప్రత్యేక అభివృద్ధి నిధి (STSDF) లను రూపకల్పన చేసింది.
ii) షెడ్యూల్డ్ కులాల సంక్షేమం :
తెలంగాణలో షెడ్యూల్డ్ కులాల అభివృద్ధి శాఖ కింద వివరించిన పథకాల అమలును పర్యవేక్షిస్తుంది.
a) SC లకు కల్యాణ లక్ష్మి :
అక్టోబర్, 2, 2014న ఈ పథకాన్ని ప్రభుత్వం ప్రారంభించింది. తెలంగాణకు చెందిన SC వర్గపు 18 సంవత్సరాల వయస్సు పై బడిన బాలిక వివాహ ఖర్చుల కొరకు వధువు కుటుంబానికి రూ. 51,000 ప్రభుత్వం గతంలో ఇచ్చేది. ఇందుకు SC కుటుంబపు తల్లిదండ్రుల ఆదాయ పరిమితి 2 లక్షల రూపాయలు. కాగా కల్యాణ లక్ష్మి గ్రాంటును ప్రభుత్వం 2017లో రూ.75,116 లకు, 2018 లో రూ.1,00,116 లకు పెంచింది.
b) అంబేద్కర్ ఓవర్సీస్ నిధి పథకం :
ఈ గ్రాంటు ద్వారా విద్యార్థులు USA, UK, కెనడా, ఆస్ట్రేలియా, సింగపూర్, ఫ్రాన్స్, జర్మనీ, జపాన్, న్యూజిలాండ్ మరియు సౌత్ కొరియా వంటి దేశాల్లో విద్యను అభ్యసించవచ్చు. 2018-19 సంవత్సరంలో 101 మంది విద్యార్థులు ఈ పథకంలో ఎంపికయ్యారు.
c) భూమి కొనుగోలు పథకం :
నిరుపేద షెడ్యూల్డ్ కులాల మహిళలకు లబ్ధి చేకూర్చుటకు ఈ పథకాన్ని రూపొందించారు. ఈ పధరం కింద 2014-16 నుంచి 2019-20 మధ్య కాలంలో దాదాపు రూ.667.71 కోట్ల వ్యయంతో సుమారు 15,044.35 ఎకరాల భూమిని కొనుగోలు చేయగా 5,930 మందికి పంపిణీ చేశారు.
iii) షెడ్యూల్డ్ తెగల సంక్షేమం :
షెడ్యూల్డ్ తెగల సమగ్రాభివృద్ధి కొరకు తెలంగాణ ప్రభుత్వం కింద తెలిపిన పథకాలను అమలు పరుస్తున్నది.
a) ST లకు కల్యాణ లక్ష్మి :
ఈ పథకాన్ని అక్టోబర్ 2, 2014లో ప్రారంభించారు. ఈ పథకం కింద 18 సంవత్సరాలు నిండిన తెలంగాణకు చెందిన ST యువతి కళ్యాణ ఖర్చుల కోసం రూపాయలు 1,00,116 ఆర్థిక సహాయం ఇవ్వబడుతుంది.
b) ఆర్థిక మద్దతు పథకాలు :
ఈ పథకం ద్వారా వ్యవసాయ రంగం, ఉద్యానవనం, మత్స్య పరిశ్రమ, చిన్న నీటి పారుదల, పశు సంవర్ధకం, స్వయం ఉపాధి వంటి రంగాలలో నిమగ్నమైన గిరిజనులకు ఆర్థిక సహాయం కల్పిస్తారు.
c) అడవి హక్కుల చట్టం, 2006 :
తమ జీవనోపాధి కొరకు కొన్ని యుగాల నుంచి అడవుల పై ఆధారపడి జీవించే గిరిజనులు, ఇతర సంప్రదాయ ఆటవిక జీవులకు తమ జీవనాన్ని కొనసాగించుకొనే రక్షణను అడవి హక్కుల చట్టం 2006 కల్పిస్తుంది. ఈ చట్టం ప్రకారం 93,494 మంది గిరిజనులకు 3,00,092 ఎకరాల భూమిని పంపిణీ చేయడం జరిగింది.

C. వెనకబడిన వర్గాల (BC) అభివృద్ధి, సంక్షేమ పథకాలు :
వెనకబడిన తరగతుల వర్గాల సంక్షేమం కోసం తెలంగాణ ప్రభుత్వం చేపట్టిన పథకాలు :
i) కళ్యాణ లక్ష్మి :
2016-17 సంవత్సరం నుంచి కళ్యాణ లక్ష్మి పథకాన్ని వెనకబడిన తరగతులు (BC), ఆర్థికంగా వెనకబడిన తరగతుల వారికి కూడా వర్తింపజేశారు.
ii) చాలా వెనకబడిన తరగతుల అభివృద్ధి కార్పోరేషన్ :
వెనకబడిన తరగతుల వర్గాలలో సాంఘికంగా, విద్యాపరంగా, ఆర్థికపరంగా చాలా వెనకబడిన తరగతుల (MBC) సంక్షేమంలో మెరుగుదల కొరకు ఈ కార్పోరేషన్ ను 2017లో తెలంగాణ ప్రభుత్వం స్థాపించింది.
D. మైనార్టీల అభివృద్ధి, సంక్షేమ పథకాలు :
తెలంగాణ రాష్ట్రంలో మైనార్టీ వర్గం వారి సాంఘిక, ఆర్థిక స్థితిగతులలో పెంపుదల కోసం తెలంగాణ ప్రభుత్వం చేపట్టిన. కొన్ని ముఖ్యమైన పథకాలను కింద వివరించాం.
a) బ్యాంక్ తో అనుసంధానం చేయబడిన సబ్సిడీ పథకం :
మైనార్టీ వర్గాల వారు స్వయంఉపాధి చేపట్టే వ్యాపారం చేసేవారికి ఈ పథకాన్ని ఉద్దేశించారు. సబ్సిడీతో కూడుకున్న ఆర్థిక సహాయాన్ని బ్యాంకుల ద్వారా మైనార్టీ ఫైనాన్స్ కార్పోరేషన్ కల్పిస్తుంది.
b) శిక్షణ, ఉద్యోగిత, నైపుణ్య అభివృద్ధి :
మైనార్టీల శాఖ మైనార్టీ యువతకు తగిన శిక్షణను ఆ వారు స్వయం ఉపాధి చేపట్టుటకు వీలుగా మైనార్టీ పైనాన్స్ కార్పోరేషన్ ద్వారా ఆర్థిక సహకారాన్ని అందిస్తుంది.
c) షాదీ ముబారక్ పథకం :
ఈ పథకం ప్రకారం అర్హమైన మైనార్టీ వర్గానికి చెందిన యువతి పెళ్ళి ఖర్చులకు రూ.1,00,116 గ్రాంటు రూపంలో ఇవ్వబడుతుంది.

స్వల్ప సమాధాన ప్రశ్నలు:
ప్రశ్న 1.
తెలంగాణ ఆర్థిక వ్యవస్థలో రంగాల వారీ వృద్ధి రేటు ధోరణులను వివరించండి.
జవాబు.
ఆర్థిక వ్యవస్థలో గల వివిధ రంగాలు ప్రదర్శించిన వృద్ధి రేట్లు ఆ వ్యవస్థ యొక్క వృద్ధి ధోరణిని తెలుపుతాయి. ఆర్థిక వ్యవస్థలో గల వివిధ రంగాలను 16 రంగాలుగా విభజించినప్పటికీ సులభంగా గ్రహించుట కొరకు వీటిని స్థూలంగా మూడు రంగాలుగా వర్గీకరిస్తారు.
అవి : ప్రాథమిక, ద్వితీయ, గౌణ రంగాలు. ఈ రంగాల వృద్ధి రేట్లను ప్రాథమిక ధరలలో జోడించిన స్థూల ఉత్పత్తి విలువ (GVA) తో సూచిస్తారు.
a) ప్రాథమిక రంగం :
ఈ రంగంలో పంటలు, పశుసంపద, అడవులు, మత్స్య పరిశ్రమ, గనులు మొదలైనవి.
b) ద్వితీయ రంగం :
ఇందులో తయారీ రంగం, గ్యాస్, నీటి సరఫరా, ఇతర అనుబంధ సేవలు మొదలైనవి.
c) గౌణ రంగం :
ఇందులో వ్యాపారం రిపేర్ సేవలు, హోటళ్ళు, రెస్టారెంటులు, రవాణా (రైల్వే రోడ్ వే, నౌకాయానం, విమానయానం మొ.||) నిలువ (storage), కమ్యూనికేషన్, బ్రాడ్కాస్టింగ్, ఆర్థిక సేవలు, స్థిరాస్థి రంగం, ప్రభుత్వ పాలన మొదలైనటువంటివి ఉంటాయి.
ఆర్థిక వ్యవస్థలో వివిధ రంగాల విశ్లేషణ ఆ వ్యవస్థలో ఆయా రంగాల పని తీరుని తెలుపుటకు, ఆర్థిక స్థితిగతుల అంచనాకు తోడ్పడుతుంది. అంతేగాక ప్రస్తుత సంవత్సరంలో ఆర్థికవ్యవస్థలో ఆయా రంగాలు ఏ విధమైన పనితీరును కనబరచాయో, రాబోయే కాలంలో ఏ విధంగా పనిచేయగలవో తెలుసుకొనుటకు వీలవుతుంది.
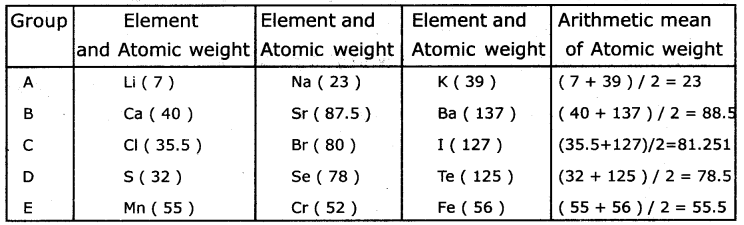
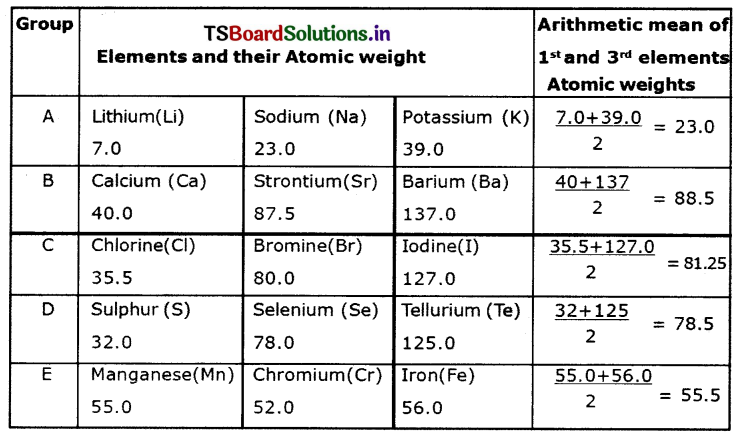
ప్రాథమిక రంగం వృద్ధి రేటు 2012-13లో 21.9 శాతం (స్థిర ధరలో 8.6 శాతం) నుంచి 2015-16 లో కేవలం 2.2 శాతానికి (స్థిర ధరలలో 58 శాతం) తగ్గగా 2016-17 నాటికి 17.1 శాతానికి పెరిగి తిరిగి 2019-20 (AE)లో 15.8 శాతానికి (స్థిర ధరలలో 10.7 శాతం) తగ్గింది.
ఈ విధంగా ప్రాథమిక రంగంలో మిశ్రమ వార్షిక సగటు వృద్ధి రేట్లు నమోదగుటను గమనించవచ్చు. 2012-13, 2014-15 సంవత్సరాలలో ద్వితీయ రంగం రుణాత్మక వృద్ధి రేటును చవిచూడగా 2015-16 లో అత్యధిక వృద్ధి రేటు అనగా 20.3 శాతం (స్థిర ధరలలో 21.4 శాతం) ను నమోదు చేసుకొన్నది.
2019-20 (AE) ప్రకారం ఈ రంగంలో 5.3 శాతం వృద్ధిరేటు నమోదయింది. 2012-13 నుంచి 2019-20 మధ్య కాలంలో గౌణ రంగపు వృద్ధి రేటు 18.4 శాతం నుంచి 14.1 శాతం (స్థిర ధరలలో 8.4 శాతం నుంచి 9.6 శాతం) మధ్య కొనసాగింది. మొత్తానికి తెలంగాణ రాష్ట్ర ఆర్థిక వ్యవస్థలో ప్రస్తుత, స్థిర ధరలలో జోడించిన స్థూల రాష్ట్ర ఉత్పత్తి విలువ వృద్ధి రేటులో మిశ్రమ ధోరణిని చూడవచ్చు.
జోడించిన స్థూల రాష్ట్ర ఉత్పత్తి విలువ (GSVA) లో వివిధ రంగాల వాటా :
GSVA లో గౌణ రంగం లేదా సేవల రంగం వాటా 2011-12లో 52.8 శాతం నుంచి 2019-20 (AE) నాటికి 65.2 శాతానికి పెరగగా, ప్రాథమిక రంగం లేదా వ్యవసాయ రంగం దాని అనుబంధ రంగాల వాటా ఇదే కాలంలో 19.6 శాతం నుంచి 18.6 శాతానికి తగ్గగా, ద్వితీయ రంగం లేదా పారిశ్రామిక రంగం వాటా 27.6 శాతం నుంచి 16.2 శాతానికి తగ్గింది. తెలంగాణ రాష్ట్రపు GSVAలో ప్రాథమిక, ద్వితీయ రంగాల వాటా అస్థిర రూపంలో ఉండగా, గౌణ రంగం లేదా సేవల రంగం వాటా స్థిరంగా ఉండటాన్ని గమనించవచ్చు.
ప్రశ్న 2.
తెలంగాణ ఆర్థిక వ్యవస్థలో రంగాల వారీ వృద్ధి రేటు ధోరణులను వివరించండి.
జవాబు.
ఒక రాష్ట్ర ఆర్థిక వ్యవస్థ అభివృద్ధి ఆ వ్యవస్థలో లభ్యమవుతున్న వనరులపై ఆధారపడి ఉంటుంది. మానవ వనరులు ఉంటే, సహజ వనరులను అభిలషణీయంగా, సమర్థవంతంగా వినియోగపరిచి, రాష్ట్ర ప్రగతికి, అధిక ఉత్పత్తికి కారకులవుతారు. నాణ్యమైన జనాభాతో పాటు మూలధన కల్పన, సాంకేతిక పరమైన మార్పులు ఆర్థిక వ్యవస్థకు చలనత్వాలను కలిగిస్తుంది.
2011 జనాభా లెక్కల ప్రకారం తెలంగాణ జనాభా దాదాపు 42%గా నమోదయింది. భారతదేశమొత్తం భౌగోళిక వైశాల్యంలో తెలంగాణ 3.5% విస్తీర్ణం కల్గి ఉంది. రంగారెడ్డి జిల్లా జనాభాలో అత్యధికంగా 52.97 లక్షల మంది ఉండగా, నిజామాబాద్ జిల్లా జనాభాలో 25.51 లక్షల మందితో చివరి భాగాన ఉంది.
జనసాంద్రత :
ప్రతి చదరపు కిలోమీటరులో నివసించే జనాభాను జనసాంద్రత అంటారు. ఈ జనసాంద్రత జనాభా పెరుగుదల రేటును బట్టి మారుతూ ఉంటుంది. భారతదేశ మొత్తం జనసాంద్రతతో పోలిస్తే తెలంగాణలో జనసాంద్రత పెరుగుదల తక్కువగా ఉంది.
హైదరాబాద్ జిల్లా రాష్ట్ర రాజధాని నగరం కాబట్టి అధిక జనసాంద్రతను కల్గి ఉండి చదరపు కిలోమీటరుకు 18,172 మంది నివసిస్తున్నారు. 2001-2011 జనాభా లెక్కల ప్రకారం తెలంగాణలో జనాభా వృద్ధి రేటు 1.4% భారతదేశ జనాభా వృద్ధి రేటు 1.84% కంటే తక్కువ.
పిల్లల జనాభా :
0-6 సం॥లోపు వారిని పిల్లలు అంటారు. తెలంగాణలో పిల్లల జనాభా శాతం 2001లో 14.2% నుంచి 2011లో 10.5% తగ్గింది. ఈ తగ్గుదలకు కారణం పెరుగుతున్న అక్షరాస్యత, అధిక ఆదాయాలకు తోడు కుటుంబ నియంత్రణ పద్ధతులు అవలంబించడం. అన్ని జిల్లాలలో పిల్లల జనాభా శాతం రాష్ట్ర సగటుకు దగ్గరగా 10.5% గా ఉన్నది. ఒక మహబూబ్ నగర్ జిల్లాలో మాత్రం పిల్లల జనాభా 17.4% గా ఉంది.
కుటుంబ పరిమాణం, ఎస్.సి. & ఎస్.టి. జనాభాలో స్త్రీ, పురుషుల నిష్పత్తి :
జనాభా లెక్కల ప్రకారం కొంతమంది వ్యక్తులు `ఒక దగ్గర కలిసి జీవిస్తూ ఒకే వంటగదిని వాడుకోవడాన్ని కుటుంబం అంటారు. మొత్తం జనాభాను గృహాల సంఖ్యచే భాగించగా కుటుంబ పరిమాణం వస్తుంది. తెలంగాణలో సగటు కుటుంబ పరిమాణం 42% గా ఉంది.
ఎస్.సి/ఎస్.టి. జనాభా :
2011 జనాభా లెక్కల ప్రకారం షెడ్యూల్ కులాల (ఎస్.సి.) జనాభా మొత్తం రాష్ట్ర జనాభాలో 15.44% ఉంది. అదే విధంగా షెడ్యూల్ తెగల (ఎస్.టి.) జనాభా మొత్తం రాష్ట్ర జనాభాలో 9.34% ఉంది. .2011 జనాభా లెక్కల ప్రకారం ఎస్.సి. జనాభా మొత్తం జనాభాలో 54,32,650 మంది ఉన్నారు.
ఎస్.టి. జనాభా 32,86,928 మంది. ఎస్.సి. జనాభా అత్యధిక శాతం కరీంనగర్ జిల్లాలో 18-80%గా నమోదయ్యారు. అత్యల్పం హైదరాబాద్ 6.29%. ఎస్.టి. జనాభా ఖమ్మం జిల్లాలో 27.37%గా ఉంది. అత్యల్పం హైదరాబాద్లో 1.24%గా ఉంది. పట్టణాల కంటే గ్రామాలలోనే అధిక జనాభా వృద్ధి నమోదయింది.
స్త్రీ-పురుష నిష్పత్తి :
1000 మంది పురుషులకు స్త్రీల సంఖ్య ఆధారంగా స్త్రీ, పురుష నిష్పత్తి నిర్ణయించబడుతుంది. 2011 జనాభా లెక్కల ప్రకారం తెలంగాణలో ప్రతి 1,000 మంది పురుషులకు 990 మంది స్త్రీల అనుపాతం ఉంది.
మానవ అభివృద్ధి సూచి :
ఇది మూడు అంశాల వారిగా రూపొందించారు.
- పుట్టిన సమయంలో ఆయుఃప్రమాణం
- శిశుమరణాల రేటు
- అక్షరాస్యతా స్థాయి.
తెలంగాణలో మానవ అభివృద్ధి సూచిక (HDI):

వలసదారుల వాటా :
తెలంగాణలోని పట్టణ జనాభాలో అధిక పెరుగుదలకు ఆంధ్ర ఇతర రాష్ట్రాల నుండి వలసదారులే కారణం. 1961 నుంచి 2011 మధ్య కాలంలో తెలంగాణలో వలసదారుల జనాభా 62 లక్షలు. పట్టణ జనాభాలో రంగారెడ్డి జిల్లా మొదటి స్థానంలో నిలిచింది. 70% జనాభా పట్టణ వాసులే. దీనికి కారణం పట్టణాల అభివృద్ధి మరియు హైదరాబాద్ పరిసరాల అభివృద్ధి.
అక్షరాస్యత :
2011 జనాభా లెక్కల ప్రకారం తెలంగాణలో అక్షరాస్యత శాతం 66%.
ప్రశ్న 3.
తెలంగాణ వ్యవసాయ రంగాన్ని చర్చించండి.
జవాబు.
తెలంగాణలో వ్యవసాయ రంగం : వ్యవసాయం ప్రధానంగా వర్షాధారంపై ఆధారపడి, అధిక భాగం భూగర్భ జలాల (ground water) ద్వారా సాగు చేయబడుతుంది. దాదాపు నేటికి 55.49% మంది ప్రజలు జీవనోధారం కోసం వ్యవసాయ పనుల పైననే ఆధారపడుతున్నారు.
విలువతో కూడిన స్థూల రాష్ట్ర ప్రాంతీయోత్పత్తి (GSVA) లో వ్యవసాయ రంగం వాటా 2018-19 (మొదట సవరించిన అంచనా) లో ప్రస్తుత ధరలలో 18.1 శాతం (స్థిర ధరలలో 15.6 శాతం) కాగా 2019-20 (ముందస్తు అంచనా) లో ఇది ప్రస్తుత ధరలలో 18,6 శాతం (సిర ధరలలో 16 శాతం).
భారతదేశ భౌగోళిక వైశాల్యంలో తెలంగాణ 12వ అతిపెద్ద రాష్ట్రం. తెలంగాణ రాష్ట్ర మొత్తం భూమి వైశాల్యం 112.08 లక్షల హెక్టారులు. ఇందులో 60 శాతం భూమి వ్యవసాయ యోగ్యమైనది. 2018-19లో 48.98 లక్షల హెక్టార్ల భూమి నికర పంట భూమి కాగా 60.59 లక్షల హెక్టార్ల భూమి స్థూల పంటల భూమి.
కాగా రాష్ట్ర భౌగోళిక వైశాల్యంలో అడవుల కింద గల భూవిస్తీర్ణం 26.98 లక్షల హెక్టార్లు, దాదాపుగా 24.07 శాతం. ఇక వ్యవసాయేతర భూవిస్తీర్ణం 8.34 లక్షల హెక్టారులు, 15.78 లక్షల హెక్టార్లు తడి భూమి, వ్యవసాయానికి పనికి రాని భూమి 6.07 లక్షల హెక్టార్లు, 5.94 లక్షల హెక్టార్ల భూమి పచ్చిక భూమి.
నికర, స్థూల పంటసాగు భూమి :
తెలంగాణ రాష్ట్రంలో గల వివిధ జిల్లాలలో 2018-19లో భౌగోళిక వైశాల్య పరంగా పంటలు పండించిన నికర భూమి 46. 60 లక్షల హెక్టార్లు (41.5 శాతం).
తెలంగాణలో ఆహార, ఆహారేతర పంటల సాగు భూవిస్తీర్ణం :
ధాన్యాలు, చిరుధాన్యాలు, పప్పు దినుసులు వంటివి ఆహార పంటలు. కాగా పత్తి, నూనెగింజలు, పూలు వంటివి ఆహారేతర పంటలు. 2017-18 సంవత్సరంలో 37.14 లక్షల హెక్టార్ల భూమిలో ఆహార పంటలు సాగు చేయబడ్డాయి. రాష్ట్రంలో పత్తి, నూనెగింజలు, పూలు, పొగాకు, పశుగ్రాసం వంటి ఆహారేతర పంటలు సాగు చేయబడ్డాయి.
నీటి పారుదల తక్కువ మోతాదులో ఉన్న ప్రాంతాలలో ఖరీఫ్ (యాసంగి) కాలంలో ఆహారేతర పంటలలో పత్తి ప్రముఖంగా సాగుచేయబడుతుంది. 2017-18లో 23.45 లక్షల హెక్టార్లలో ఆహారేతర పంటలు సాగుచేయబడ్డాయి.
2018 – 19లో ఆహార, ఆహారేతర పంటల సాగుభూమి :
తెలంగాణలో 2018-19 సంవత్సరంలో ఖరీఫ్, రబీ కాలంలో సాగులో ఉన్న స్థూల పంట సాగు భూమి 57.75 లక్షల హెక్టార్లు. ఖరీఫ్ కాలంలో సాగుచేయబడిన 45 లక్షల హెక్టార్ల భూమిలో 2018-19 సంవత్సరంలో 53, 9 శాతం ఆహార పంటలు కాగా 46.1 శాతం ఆహారేతర పంటలు. అయితే రబీ సీజన్ లో మాత్రం సాగుచేసిన భూమి 12.75 లక్షల హెక్టారులలో ఆహార పంటల భూవిస్తీర్ణం 11.07 లక్షల హెక్టార్లు (87 శాతం).
మనుగడలో లేదా అమలులో ఉన్న భూకమతాలు :
తెలంగాణ రాష్ట్రంలో 2010-11లో మనుగడలో గల సగటు కమతం పరిమాణం 1.12 హెక్టార్లు కాగా ఇది 2015-16 నాటికి 1.00 హెక్టారు (2.47105 ఎకరాలు). గమనించదగ్గ విషయమేమిటంటే మనుగడలో గల మొత్తం కమతాలలో ఉపాంత, చిన్న కమతాలు మొత్తం కమతాలలో 80 శాతం. అయితే 2010-11ని 2015– 16తో పోల్చగా 2015-16 లో మాధ్యమిక, పెద్ద కమతాల పరిమాణం తగ్గింది.

వ్యవసాయ రంగానికి సంబంధించి తెలంగాణ ప్రభుత్వ ప్రధాన పథకాలు :
a) రైతు బంధు :
రుణ భారం నుంచి విముక్తి కల్పిచేందుకు వీలుగా ఒక పెట్టుబడి రూపంలో సహకారాన్ని అందించి రైతుల సాధికారితను పెంచే ఉద్దేశంతో తెలంగాణ ప్రభుత్వం రూపొందించిన పథకమే రైతు బంధు. 2018, మే 10వ తేదిన ఈ పథకం ప్రారంభించబడ్డది.
2019-20 సంవత్సరం నుంచి తెలంగాణ ప్రభుత్వం ఈ రకమైన పెట్టుబడి సహకారాన్ని ప్రతి సీజను రూ. 4,000 ఎకరం నుంచి రూ.5,000 లకు పెంచింది.
b) రైతు బీమా :
2018, ఆగష్టు 15న తెలంగాణ ప్రభుత్వం ఈ పథకాన్ని ప్రారంభించింది. రోగగ్రస్తుడైన రైతు మరణిస్తే, అతని కుటుంబ సభ్యులు లేదా అతనిపై ఆధారపడిన వారికి ఆర్థికపరమైన భద్రతను కల్పించడం ఈ పథకం ప్రధాన ఉద్దేశం. ఈ పథకం కింద ప్రతి రైతుకు రూపాయలు 5 లక్షల బీమా కవరేజి ఉంటుంది.
ప్రశ్న 4.
తెలంగాణ పారిశ్రామికాభివృద్ధిని వివరిచండి.
జవాబు.
తెలంగాణలో పారిశ్రామిక రంగం :
దేశంలో గల ప్రధాన పారిశ్రామిక రాష్ట్రాలలో ఒకటిగా తెలంగాణ అరన స్థానాన్ని, జోడించిన స్థూల దేశీయోత్పత్తి విలువలో 8వ స్థానాన్ని కలిగియున్నది. జోడించిన స్థూల రాష్ట్ర ప్రాంతీయోత్పత్తి విలువలో పారిశ్రామిక రంగం వాటా 2018-19 (మొదటి సవరించిన అంచనా) ప్రస్తుత ధరలలో 17.4% (స్థిర ధరలలో 19.9 శాతం) కాగా 2019- 20 (ముందస్తు అంచనా) లో 16.2 శాతం (స్థిర ధరలలో 18.7 శాతం).
పరిశ్రమల వార్షిక సర్వే (Annual Survey of Industries) దత్తాంశం ప్రకారం, తెలంగాణ రాష్ట్రంలో 2008-09 లో . పరిశ్రమల సంఖ్య 7,357 కాగా ఈ సంఖ్య 2012-13లో 10,279 కి, 2013-14లో 11,068 కి 2014-15 లో 11,995 కి, 2015-16 లో 12,353 కి పెరిగింది.
తెలంగాణలో సూక్ష్మ, చిన్న, మధ్యతరహా పరిశ్రమలు (MSME) :
సూక్ష్మ, చిన్న, మధ్య మిక పరిశ్రమలు (Micro, Small and Medium Enterprises – MSME), పెద్ద తరహా పరిశ్రమలకు అవసరమైన ఉత్పాదకాలను సప్లయ్ చేసే అనుషంగిక పరిశ్రమలుగా పనిచేస్తూ రాష్ట్రంలో సంతులిత ప్రాంతీయాభివృద్ధికి, సమ్మిళిత వృద్ధికి తోడ్పడతాయి. తక్కువ మూలధనం, తక్కువ స్థాయి నైపుణ్యంగల పారిశ్రామిక యూనిట్ల ద్వారా ఉద్యోగ కల్పనలో కీలక పాత్రను కలిగి ఉంటాయి.
తెలంగాణ ప్రత్యేక రాష్ట్రంగా అవతరించిన నాటి నుంచి MSME యూనిట్ల స్థాపనలో గణనీయ పెరుగుదల సంభవించింది. జనవరి 2015 నాటికి MSME లు 8,435 కు పెరిగి రూ. 11,847 కోట్లతో 1.59 లక్షల మందికి ఉద్యోగావకాశాలు కల్పించాయి.
తెలంగాణ రాష్ట్ర నూతన పారిశ్రామిక విధానం:
దేశ 29 వ రాష్ట్రంగా అవతరించిన అనంతరం తెలంగాణ ప్రభుత్వం తన “పారిశ్రామిక విధానం-2014” ను ప్రకటించింది. ఇందులో రాష్ట్రంలో పారిశ్రామికీకరణకు ఒక నినాదాన్ని తన విజన్ గా ప్రకటించింది. ఆ నినాదం : “పరిశోధన సుంచి నవకల్పన, నవకల్పన నుంచి పరిశ్రమ, పరిశ్రమ నుంచి సౌభాగ్యం”. ఒక్క మాటలో చెప్పాలంటే ఈ నినాదపు ముఖ్య లక్ష్యం – “ఆవిష్కరించు, ఆరంభించు, సంలీనించు”.
అవస్థాపనా సౌకర్యాలను కల్పిస్తూ. ఎలాంటి ఇబ్బందులు కలగకుండా తగిన సౌకర్యాల కల్పన ద్వారా తెలంగాణలో పెట్టుబడులకు అనువైన వాతావరణాన్ని కల్పించి సులభ రీతిలో వ్యాపారం కొనసాగించే విధంగా చర్యలు చేపట్టడం ఈ విధానపు ప్రధాన లక్ష్యం.

ప్రశ్న 5.
TS GENCO, TS TRANSCO లపై వ్యాఖ్యానించండి.
జవాబు.
(a) తెలంగాణ రాష్ట్ర విద్యుత్ ఉత్పత్తి కార్పోరేషన్ TSGENCO : 1.7, 2019 నాటికి తెలంగాణలో TSGENCOతో కలిపి విద్యుత్ కాంట్రాక్టెడ్ కెపాసిటీ 16,201 MM. ఇందులో ప్రైవేటు రంగం వాటా 7,739 MW, రాష్ట్ర వాటా 5,826 MW, కేంద్ర రంగం వాటా 2,536 MW, అంతర్రాష్ట్ర 76 MW, ఉమ్మడి రంగ వాటా 25 MW, TSGENCO కెపాసిటీ అయిన 5,825 MW లలో థర్మల్ విద్యుత్తు 3,382. 50MW, హైడల్ విద్యుత్తు 2,441.76 MV, సోలార్ విద్యుత్తు 1 MW.
తెలంగాణలో విద్యుత్తు డిమాండ్లో పెరుగుదలను దృష్టిలో ఉంచుకొని TSGENC0, 5,080 MW లతో రెండు కొత్త ధర్మల్ యూనిట్లను ప్రతిపాదించింది. అవి : భదాద్రి థర్మల్ పవర్ సెక్షన్ 4 × 270 MW ; యాదాద్రి ధర్మల్ పవర్ స్టేషన్ – 5 × 800 MW.
(b) విద్యుత్ ప్రసారం, పంపిణీ :
తెలంగాణ ప్రత్యేక రాష్ట్రంగా అవతరించిన తరవాత విద్యుత్తు ప్రసారం, పంపిణీ కొరకు TS TRANSCO ను నెలకొల్పింది. ప్రస్తుతం 112 FIT స్టేషన్లు, 833, 33/11 KVA ఉప కేంద్రాలు, 2.54 లక్షల పంపిణీ ట్రాన్స్ఫార్మర్లు. రాష్ట్రంలో ఉన్నాయి.
తెలంగాణ రాష్ట్రంలో గల ప్రధాన విద్యుదుత్పత్తి కేంద్రాలు :
నేషనల్ థర్మల్ పవర్ కార్పోరేషన్ (NTPC), కరీంనగర్ జిల్లాలోని రామగుండంలో ఉంది. కొత్తగూడెం థర్మల్ పవర్ కార్పోరేషన్ (KTPC) పాల్వంచ, ఖమ్మం జిల్లాలో, కాకతీయ థర్మల్ పవర్ కార్పోరేషన్ భూపాలపల్లిలో ఉండగా కొన్ని హైడల్ విద్యుత్తు ఉత్పత్తి కేంద్రాలు నాగార్జున సాగర్, పోచంపాడు, సింగూర్, నిజాం సాగర్, పులిచింతలలలో ఉన్నాయి. 2013-14లో రాష్ట్రంలో 2,482 MW విద్యుత్తు కొరత ఉండేది.
విద్యుత్తు డిమాండ్ 47,428 MW కాగా అందుబాటులో ఉన్నది 44,946 MW. 2014-15లో విద్యుత్తు డిమాండ్ 50,916 MW కాగా అందుబాటులో ఉండింది 48,788 MW.
విద్యుచ్ఛక్తి పంపిణీకి సంబంధించి తెలంగాణలో రెండు కంపెనీలు పనిచేస్తున్నాయి. అవి :
తెలంగాణ రాష్ట్ర దక్షిణ ప్రాంత విద్యుత్ పంపిణీ కంపెనీ లిమిటెడ్ (TSSPDCL), తెలంగాణ రాష్ట్ర ఉత్తర ప్రాంత విద్యుత్ పంపిణీ లిమిటెడ్ (TSNPDCL). 1.12.2019 నాటికి రాష్ట్రంలో 1.53 కోట్ల విద్యుత్ కనెక్షన్లు ఉన్నాయి. ఇందులో 73 శాతం విద్యుత్ వినియోగం గృహ వినియోగం
రూపంలో కలదు.

ప్రశ్న 6.
రాష్ట్రంలో విద్యతీరు తెన్నులను క్లుప్తంగా వ్యాఖ్యానించండి.
జవాబు.
తెలంగాణలో విద్య :
దేశంలో మానవ వనరులు, ఆర్థికాభివృద్ధి బలోపేతం కావడానికి విద్యను ప్రధాన సాధనంగా భావించాలి. ఉత్పాదక శ్రామిక శక్తిని పెంపొందించడంలో విద్య కీలక పాత్ర పోషిస్తుంది. భారత రాజ్యాంగంలోని 45 వ నిబంధన ప్రకారం 6 నుంచి 14 సంవత్సరాల మధ్య వయస్సు గల బాలబాలికలకు ఉచిత, నిర్బంధ విద్యను అందించడం రాష్ట్రాల బాధ్యత.
తెలంగాణలో అక్షరాస్యత రేటు :
2011 జనాభా లెక్కల ప్రకారం తెలంగాణలో అక్షరాస్యత రేటు 66.54 శాతం. అయితే పట్టణ-గ్రామీణ, అంతర్ జిల్లా, వయస్సు వారీ జనాభా, స్త్రీ-పురుషులు, సామాజిక వర్గాల పరంగా అక్షరాస్యత రేటులో తేడాలున్నాయి. రాష్ట్రంలో విద్యా రంగం స్థితి :
a) నమోదు(Enrollment) :
2017-18 సంవత్సరంలో అన్ని పాఠశాలలు కలిపి 58.71 లక్షల విద్యార్థులు నమోదు చేసుకొన్నారు. ఇందులో 53 శాతం ప్రైవేటు పాఠశాలల నమోదు కాగా మిగితా 47 శాతం ప్రభుత్వ పాఠశాలల నమోదు.
b) స్థూల నమోదు నిష్పత్తి (Gross Enrollment Ration-GER) :
స్థూల నమోదు నిష్పత్తి (GER) విశ్వవిద్యాలయాలు, కళాశాలలు, పాఠశాలలో విద్యార్థుల నమోదు సంఖ్యను నిర్ణయిస్తుంది. GER 2017-18లో ప్రాథమిక పాఠశాలలో బాలురు – 98.76 శాతం, బాలికలు -. 98.05 శాతం కాగా ఉచ్ఛతర ప్రాథమిక పాఠశాలలో బాలురు – 87.32 శాతం, బాలికలు 88.4 శాతం.
c) విద్యార్థి – ఉపాధ్యాయ నిష్పత్తి (Pupil – Teacher Ratio – PTR) :
ఇది ఒక విద్యా సంవత్సరంలో ప్రత్యేక విద్యా స్థాయికి సంబంధించి ఎంత మంది విద్యార్థులకు ఒక ఉపాధ్యాయుడు ఉంటాడనే విషయాన్ని తెలుపుతుంది. PTR, 2018-19లో రాష్ట్రంలో ప్రాథమిక స్థాయిలో 18.90, ఉచ్ఛతర ప్రాథమిక స్థాయి 14.12, సెకండరీ స్థాయిలో 17.85 గా ఉంది. రాష్ట్రం మొత్తానికి 2018-19లో PTR 17.67.
పాఠశాల విద్య :
i) సమగ్ర శిక్షా అభియాన్:
గతంలో కేంద్ర ప్రభుత్వ ప్రాయోజిత పథకాలైన
- సర్వ శిక్షా అభియాన్ (SSA) సార్వత్రిక ప్రాథమిక విద్యను అమలు పరుస్తూండగా
- రాష్ట్రీయ మాధ్యమిక శిక్షా అభియాన్ (RMSA) సెకండరీ విద్యలో సామీప్యత (acess), ప్రమాణం (quality) లో పెంపుదలకు అమలు చేసింది.
ii) కస్తూర్బా గాంధీ బాలికా విద్యాలయం :
వీటిని 2004-05 లో రెసిడెన్షియల్ పాఠశాల సౌకర్యం కల్పించే ఉద్దేశంతో నెలకొల్పారు. నీటిలో ప్రవేశానికి అర్హతలు : SC, ST, BC, మైనారిటీ వర్గాలకు సంబంధించిన
- VI నుంచి VII తరగతులు వారికి,
- అనాధలు,
- బడి మానేసిన ఒంటరి తల్లి/తండ్రి కలిగిన విద్యార్థులు
iii) ఆదర్శ పాఠశాలలు :
194 ఆదర్శ పాఠశాలలు రాష్ట్రంలో 2013-14లో స్థాపించబడ్డాయి. వీటిలో అధిక విద్యార్హతలున్న ఉపాధ్యాయులచే ఇంగ్లీషు మీడియంలో విద్యా బోధన జరుగుతుంది. ఈ వథకం రద్దయినందువలన తెలంగాణ ప్రభుత్వం వీటి బాధ్యత తీసుకొని 2015-16 నుంచి వీటిని కొనసాగిస్తున్నది.
ఇంటర్మీడియట్ విద్య :
ప్రస్తుతం రాష్ట్రంలో 2,558 జూనియర్ కళాశాలలు ఉండగా వాటిలో విద్యార్థుల సంఖ్య 7.18 లక్షలు. 2,558 జూనియర్ కళాశాలలో, 404 ప్రభుత్వ, 4 వొకేషనల్, 41 ప్రైవేట్ ఎయిడెడ్, 1,583 ప్రైవేట్ మరియు ఇతర జూనియర్ కళాశాలలు కాగా 530 ఇతర ప్రభుత్వ సంస్థలు. ఈ బోర్డు ఉపాధిని కల్పించేందుకు వీలయిన 23 వొకేషనల్ కోర్సులను ఇంటర్మీడియట్ స్థాయిలో ప్రవేశపెట్టింది.

ఉన్నత విద్య:
a) కళాశాల విద్య :
కళాశాల విద్య డిపార్ట్ మెంట్ యొక్క ప్రధాన లక్ష్యం ఉన్నత విద్యలో సామీప్యత (access), సమానత (equality), నాణ్యత (quality) ను సాధించుట. ఇందుకోసం కేంద్ర ప్రభుత్వ ప్రాయోజిత పథకమైన రాష్ట్రీయ ఉచ్ఛతర శిక్షా అభియాన్ (RUSA) నుంచి నిధుల సమీకరణకు తెలంగాణ ప్రభుత్వం కృషి చేస్తున్నది.
b) డిగ్రీ ఆన్లైన్ సర్వీసెస్ తెలంగాణ (DOST) :
డిగ్రీ కళాశాలలో బి.ఎ/బి.కాం/బి.యస్సీ/బి.బి.ఎ వండి డీగ్రీ కోర్సులలో ప్రవేశాలను తెలంగాణ ప్రభుత్వం 2016 సంవత్సరం నుంచి DOST ద్వారా కల్పిస్తున్నది. 2018 – 19లో డిగ్రీ కళాశాలలో 2,00,472 మంది విద్యార్థులు ప్రవేశాన్ని పొందగా ఇందులో 42,688 విద్యార్థులు ప్రభుత్వ కళాశాలలో ప్రవేశాన్ని పొందారు.
c) సాంకేతిక విద్య :
సాంకేతిర విద్యా డైరెక్టరేట్ రాష్ట్రంలో పాలిటెక్నిక్, వృత్తి విద్యలను పర్యవేక్షిస్తుంది. ఇది ప్రభుత్వ, ప్రైవేటు, ఎయిడెడ్ రంగాలలలో ప్రవేశాలు, విద్యా బోధనను పర్యవేశిస్తుంది. ప్రస్తుతం రాష్ట్రంలో 820 డిప్లమో డిగ్రీలో యుక్తమైన కళాశాలలు 1,36,805 విద్యార్థులతో పనిచేస్తున్నాయి.
సాంఘిక సంక్షేమ విద్యా సంస్థలు :
SC, ST, BC, మైనారిటీ, వికలాంగ బాలబాలికలక సమీప ప్రాంతాలలో విద్యా సంస్థలు ఉండే విధంగా చూని సాంఘిక సమానత్వ సాధనకు ప్రభుత్వం సాంఘిక సంక్షేమ విద్యా సంస్థలను నెలకొల్పింది. ఈ సంస్థలు రెసిడెన్షియల్ రూపంలో ఉండి విద్యార్థులకు ఉచిత హాస్టల్ వసతితో బాటు పాఠ్యపుస్తరాల పంపిణీ చేస్తాయి.
A) షెడ్యూల్డ్ కులాల రెసిడెన్షియల్ పాఠశాలలు :
తెలంగాణ సాంఘిక సంక్షేమ రెసిడెన్నియల్ విద్యా సంస్థల సొసైటి (TSWREIS) రాష్ట్రంలో 269 రెసిడెన్షియల్ విద్యా సంస్థలను నడుపుచున్నది. ఇందులో 175 బాలికలకు సంబంధించినవి. వీటిలో 5వ తరగతి నుండి డిగ్రీ వరకు షెడ్యూల్డ్ కులాలకు చెందిన విద్యార్థులకు ప్రవేశం కలదు. ప్రస్తుతం 268 విద్యా సంస్థలు ఉండగా అందులో 134 తెలంగాణ ఏర్పడిన తరువాత ప్రారంభించబడ్డాయి.
B) షెడ్యూల్డ్ తెగల రెసిడెన్షియల్ పాఠశాలలు :
a) తెలంగాణ గిరిజన సంక్షేమ రెసిడెన్షియల్ విద్యా సంస్థల సొసైటీ (TTWRESIS) – గురుకులాలు :
రాష్ట్రంలో ఈ గురుకులాలు 175 ఉన్నాయి.
b) ఆశ్రమ పాఠశాలలు :
రాష్ట్రంలో ప్రస్తుతం 321 ఆశ్రమ పాఠశాలలు ఉన్నాయి.
c) ప్రభుత్వ ప్రాథమిక పాఠశాలలు :
గిరిజన సంక్షేమ శాఖ 1,427 ప్రాథమిక పాఠశాలలను నిర్వహిస్తున్నది.
C) వెనుకబడిన తరగతులు సంక్షేమ రెసిడెన్షియల్ పాఠశాలలు :
మహాత్మా జ్యోతిబా పూలే తెలంగాణ వెనకబడిన తరగతుల సంక్షేమ రెసిడెన్షియల్ సంస్థల సొసైటీ (M,JPTBCWREIS) వెనకబడిన తరగతులు, ఆర్థికంగా వెనకబడిన తరగతుల వారికి విద్యను అందించుటకు స్థాపించారు.
ఒక రెసిడెన్షియల్ డిగ్రీ కళాశాలను నడుపుతున్నది. ఈ విద్యా సంస్థలలో దాదాపు 99,360 విద్యార్థులు విద్యను అభ్యసిస్తున్నారు.
D) మైనారిటీ రెసిడెన్షియల్ విద్యా సంస్థలు :
మైనారిటీ వర్గాలకు చెందిన బాలబాలికలకు అధిక నాణ్యతతో కూడిన విద్యను అందించుటకు రాష్ట్ర ప్రభుత్వం తెలంగాణ మైనారిటీల రెసిడెన్షియల్ విద్యా సంస్థల సొసైటీ (TMREIS) ని స్థాపించింది. ప్రస్తుతం రాష్ట్రంలో 216 మైనారిటీ విద్యా సంస్థలు 12 కళాశాలలతో కలిపి 79,424 విద్యార్థులకు విద్యను కల్పిస్తున్నాయి.

II. తెలంగాణలో ఆరోగ్య రంగం :
‘అందరికీ ఆరోగ్యం’ అనే ప్రపంచ ఆరోగ్య సంస్థ (WHO) లక్ష్యాన్ని చేరుకోవడానికి తెలంగాణ ప్రభుత్వం వివిధ కార్యక్రమాలను చేపట్టింది. జాతీయ ప్రసూతి లబ్ది పథకం (National Maternity Benefit Programme), సమగ్ర శిశు అభివృద్ధి పథకం, పిల్లల కోసం బాలికా సమృద్ధి యోజన పథకం, పునరుత్పత్తి కలిగిన మహిళలకు సప్లిమెంటరీ న్యూట్రీషన్ పథకాన్ని అమలు చేస్తున్నది.
‘సామాజిక, ఆర్థిక దృక్పథం 2020’ ప్రకారం తెలంగాణ రాష్ట్రంలో 4,797 ఆరోగ్య ఉప కేంద్రాలు, 633 ప్రాథమిక ఆరోగ్య కేంద్రాలు, 249 పట్టణ ప్రాథమిక ఆరోగ్య కేంద్రాలు, 90 కమ్యూనిటీ ఆరోగ్య కేంద్రాలు, 19 ఏరియా ఆసుపత్రులు, 29 జిల్లా కేంద్ర ఆసుపత్రులు, 9 వైద్య కళాశాల ఆసుపత్రులు, 12 స్పెషాలిటీ ఆసుపత్రులు, 2 సూపర్ స్పెషాలిటీ ఆసుపత్రులు ఉన్నాయి.
ఆరోగ్య రంగంలో తెలంగాణ ప్రభుత్వం అమలు పరుస్తున్న పథకాలు : రాష్ట్రావతరణ అనంతరం తెలంగాణ ప్రభుత్వం ఆరోగ్య రంగంలో అనేక పథకాలను రూపొందించి అమలు పరుస్తున్నది. అందులో ముఖ్యమైనవి.
a) కంటి వెలుగు :
సామాన్యంగా ప్రజలు ప్రత్యేకించి మహిళలు, వృద్ధులు కంటి సమస్యలను వాయిదా వేయడం లేదా ఆ సమస్యలను కొనసాగిస్తూనే జీవనాన్ని గడుపుతుంటారు. ఈ సమస్య నివారణ కోసమే తెలంగాణ ప్రభుత్వం కంటి వెలుగు పథకాన్ని రూపొందించి అమలుపరుస్తున్నది.
b) బస్తీ దవాఖాన :
పట్టణ ప్రాంతాలలో ప్రామాణికతతో కూడిన ఆరోగ్య సేవలు అందించుటకు బస్తీ దవాఖానాలు స్థాపించారు. ప్రతి బస్తీ దవాఖాన 6,000 నుండి 10,000 జనాభా ఉన్న ప్రాంతాలకు సేవలందిస్తుంది. పట్టణ మురికినాడలలో వీటిని స్థాపిస్తారు. రాష్ట్రంలో 104 బస్తీ దవాఖానాలు పనిచేస్తున్నాయి.
c) ఆరోగ్య, వెల్నెస్ కేంద్రాలు :
ఇవి సమగ్ర ఆరోగ్య సేవలతో బాటు ప్రసూతి, చిన్న పిల్లల ఆరోగ్య రక్షణ సేవలను అందిస్తున్నాయి. వైద్య సేవలు, అవసరమైన ఔషధాలను ఇవి ఉచితంగా పంపిణీ చేస్తాయి. రాష్ట్రంలో 636 ప్రాథమిక ఆరోగ్య కేంద్రాలు, 86 ఉపకేంద్రాలు, 104 బస్తీ దవాఖానాలు, 227 పట్టణ ప్రాథమిక ఆరోగ్య కేంద్రాలు ఆరోగ్య వెల్నెస్ కేంద్రాలుగా పనిచేస్తున్నాయి.
d) తెలంగాణ వైద్య విధాన పరిషత్ (TVVP) ఆసుపత్రులు :
తెలంగాణ వైద్య విధాన పరిషత్ ఆధ్వర్యంలో 107 TVVP ఆసుపత్రులు పనిచేస్తున్నాయి. ఇవి ప్రసూతి, చిన్న పిల్లల ఆరోగ్య రక్షణ సేవలు, సాధారణ వైద్య సేవలు, సర్జరీలు, ఆప్తమాలజీ, పీడియాట్రిక్స్, ఆర్థోపెడిక్స్, డెర్మటాలజీ, ENT మొదలైన సేవలను అందిస్తాయి.
e) ఆయుష్ (ఆయుర్వేద, యోగ, నాచురోపతి, యునాని, హోమియోపతి) :
తెలంగాణ ప్రభుత్వం, జాతీయ ఆయుష్ మిషన్ సహకారంతో రాష్ట్రంలో ఆయుష్ పద్ధతి వైద్యాన్ని ప్రోత్సహిస్తున్నది. ఆయుష్ శాఖ కింద రాష్ట్రంలో 860 దవాఖానాలు పనిచేస్తున్నాయి.
f) ఆరోగ్య శ్రీ :
‘ఆరోగ్యశ్రీ ఆరోగ్య రక్షణ ట్రస్టు’ ద్వారా రాష్ట్రంలో ఆరోగ్యశ్రీ అనే ఒక ఏకైక పథకం ఆరోగ్య బీమాతో అమలవుతుంది. దీని ప్రధాన ఆశయం పేదరిక రేఖకు దిగువన ఉన్న వారికి వైద్య సేవలను అందించడం. ఈ పథకం ద్వారా పేద వారికి ఎంపిక చేయబడిన వ్యాధులకు నగదు రహిత సేవలు అందించబడతాయి.
g) KCR కిట్ :
ఈ పథకాన్ని తెలంగాణ ప్రభుత్వం జూన్ 2, 2017 న ప్రారంభించింది. పేదరికపు రేఖకు దిగువన ఉండి ప్రభుత్వ ఆరోగ్య కేంద్రాల నుంచి ఆరోగ్య సేవలు పొందే గర్భిణీ స్త్రీలకు, మగశిశువు జన్మిస్తే రూ. 12,000, ఆడశిశువు జన్మిస్తే రూ. 13,000 సహాయం అందించబడుతుంది.
ప్రశ్న 7.
తెలంగాణ రాష్ట్రంలో రెసిడెన్షియల్ విద్యాసంస్థల స్థితిని, అవకాశాలను చర్చించండి.
జవాబు.
ఆర్థిక వ్యవస్థలో గల వివిధ రంగాలు ప్రదర్శించిన వృద్ధి రేట్లు ఆ వ్యవస్థ యొక్క వృద్ధి ధోరణిని తెలుపుతాయి. ఆర్థిక వ్యవస్థలో గల వివిధ రంగాలను 16 రంగాలుగా విభజించినప్పటికీ సులభంగా గ్రహించుట కొరకు వీటిని స్థూలంగా మూడు రంగాలుగా వర్గీకరిస్తారు.
అవి : ప్రాథమిక, ద్వితీయ, గౌణ రంగాలు. ఈ రంగాల వృద్ధి రేట్లను ప్రాథమిక ధరలలో జోడించిన స్థూల ఉత్పత్తి విలువ (GVA) తో సూచిస్తారు.
a) ప్రాథమిక రంగం :
ఈ రంగంలో పంటలు, పశుసంపద, అడవులు, మత్స్య పరిశ్రమ, గనులు మొదలైనవి.
b) ద్వితీయ రంగం :
ఇందులో తయారీ రంగం, గ్యాస్, నీటి సరఫరా, ఇతర అనుబంధ సేవలు మొదలైనవి.
c) గౌణ రంగం :
ఇందులో వ్యాపారం రిపేర్ సేవలు, హోటళ్ళు, రెస్టారెంటులు, రవాణా (రైల్వే రోడ్ వే, నౌకాయానం, విమానయానం మొ.||) నిలువ (storage), కమ్యూనికేషన్, బ్రాడ్కాస్టింగ్, ఆర్థిక సేవలు, స్థిరాస్థి రంగం, ప్రభుత్వ పాలన మొదలైనటువంటివి ఉంటాయి.
ఆర్థిక వ్యవస్థలో వివిధ రంగాల విశ్లేషణ ఆ వ్యవస్థలో ఆయా రంగాల పని తీరుని తెలుపుటకు, ఆర్థిక స్థితిగతుల అంచనాకు తోడ్పడుతుంది. అంతేగాక ప్రస్తుత సంవత్సరంలో ఆర్థికవ్యవస్థలో ఆయా రంగాలు ఏ విధమైన పనితీరును కనబరచాయో, రాబోయే కాలంలో ఏ విధంగా పనిచేయగలవో తెలుసుకొనుటకు వీలవుతుంది.
ప్రాథమిక రంగం వృద్ధి రేటు 2012-13లో 21.9 శాతం (స్థిర ధరలో 8.6 శాతం) నుంచి 2015-16 లో కేవలం 2.2 శాతానికి (స్థిర ధరలలో 58 శాతం) తగ్గగా 2016-17 నాటికి 17.1 శాతానికి పెరిగి తిరిగి 2019-20 (AE)లో 15.8 శాతానికి (స్థిర ధరలలో 10.7 శాతం) తగ్గింది.
ఈ విధంగా ప్రాథమిక రంగంలో మిశ్రమ వార్షిక సగటు వృద్ధి రేట్లు నమోదగుటను గమనించవచ్చు. 2012-13, 2014-15 సంవత్సరాలలో ద్వితీయ రంగం రుణాత్మక వృద్ధి రేటును చవిచూడగా 2015-16 లో అత్యధిక వృద్ధి రేటు అనగా 20.3 శాతం (స్థిర ధరలలో 21.4 శాతం) ను నమోదు చేసుకొన్నది.
2019-20 (AE) ప్రకారం ఈ రంగంలో 5.3 శాతం వృద్ధిరేటు నమోదయింది. 2012-13 నుంచి 2019-20 మధ్య కాలంలో గౌణ రంగపు వృద్ధి రేటు 18.4 శాతం నుంచి 14.1 శాతం (స్థిర ధరలలో 8.4 శాతం నుంచి 9.6 శాతం) మధ్య కొనసాగింది. మొత్తానికి తెలంగాణ రాష్ట్ర ఆర్థిక వ్యవస్థలో ప్రస్తుత, స్థిర ధరలలో జోడించిన స్థూల రాష్ట్ర ఉత్పత్తి విలువ వృద్ధి రేటులో మిశ్రమ ధోరణిని చూడవచ్చు.
జోడించిన స్థూల రాష్ట్ర ఉత్పత్తి విలువ (GSVA) లో వివిధ రంగాల వాటా :
GSVA లో గౌణ రంగం లేదా సేవల రంగం వాటా 2011-12లో 52.8 శాతం నుంచి 2019-20 (AE) నాటికి 65.2 శాతానికి పెరగగా, ప్రాథమిక రంగం లేదా వ్యవసాయ రంగం దాని అనుబంధ రంగాల వాటా ఇదే కాలంలో 19.6 శాతం నుంచి 18.6 శాతానికి తగ్గగా, ద్వితీయ రంగం లేదా పారిశ్రామిక రంగం వాటా 27.6 శాతం నుంచి 16.2 శాతానికి తగ్గింది. తెలంగాణ రాష్ట్రపు GSVAలో ప్రాథమిక, ద్వితీయ రంగాల వాటా అస్థిర రూపంలో ఉండగా, గౌణ రంగం లేదా సేవల రంగం వాటా స్థిరంగా ఉండటాన్ని గమనించవచ్చు.
ప్రశ్న 8.
తెలంగాణ రాష్ట్ర ఆరోగ్య రంగ కార్యక్రమాలను విశదీకరించండి.
జవాబు.
తెలంగాణలో ఆరోగ్య రంగం : ‘అందరికీ ఆరోగ్యం’ అనే ప్రపంచ ఆరోగ్య సంస్థ (WHO) లక్ష్యాన్ని చేరుకోవడానికి తెలంగాణ ప్రభుత్వం వివిధ కార్యక్రమాలను చేపట్టింది. జాతీయ ప్రసూతి లబ్ది పథకం (National Maternity Benefit Programme), సమగ్ర శిశు అభివృద్ధి పథకం, పిల్లల కోసం బాలికా సమృద్ధి యోజన పథకం, పునరుత్పత్తి కలిగిన మహిళలకు సప్లిమెంటరీ న్యూట్రీషన్ పథకాన్ని అమలు చేస్తున్నది.
”సామాజిక, ఆర్థిక దృక్పథం – 2020′ ప్రకారం తెలంగాణ రాష్ట్రంలో 4,797 ఆరోగ్య ఉప కేంద్రాలు, 633 ప్రాథమిక ఆరోగ్య కేంద్రాలు, 249 పట్టణ ప్రాథమిక ఆరోగ్య కేంద్రాలు, 90 కమ్యూనిటీ ఆరోగ్య కేంద్రాలు, 19 ఏరియా ఆసుపత్రులు, 29 జిల్లా కేంద్ర ఆసుపత్రులు, 9 వైద్య కళాశాల ఆసుపత్రులు, 12 స్పెషాలిటీ ఆసుపత్రులు, 2 సూపర్ స్పెషాలిటీ ఆసుపత్రులు ఉన్నాయి.
ఆరోగ్య రంగంలో తెలంగాణ ప్రభుత్వం అమలు పరుస్తున్న పథకాలు :
రాష్ట్రావతరణ అనంతరం తెలంగాణ ప్రభుత్వం ఆరోగ్య రంగంలో అనేక పథకాలను రూపొందించి అమలు పరుస్తున్నది. అందులో ముఖ్యమైనవి.
a) కంటి వెలుగు :
సామాన్యంగా ప్రజలు ప్రత్యేకించి మహిళలు, వృద్ధులు కంటి సమస్యలను వాయిదా వేయడం లేదా ఆ సమస్యలను కొనసాగిస్తూనే జీవనాన్ని గడుపుతుంటారు. ఈ సమస్య నివారణ కోసమే తెలంగాణ ప్రభుత్వం కంటి వెలుగు పథకాన్ని రూపొందించి అమలుపరుస్తున్నది.
b) బస్తీ దవాఖాన :
పట్టణ ప్రాంతాలలో ప్రామాణికతతో కూడిన ఆరోగ్య సేవలు అందించుటకు బస్తీ దవాఖానాలు స్థాపించారు. ప్రతి బస్తీ దవాఖాన 6,000 నుండి 10,000 జనాభా ఉన్న ప్రాంతాలకు సేవలందిస్తుంది. పట్టణ మురికినాడలలో వీటిని స్థాపిస్తారు. రాష్ట్రంలో 104 బస్తీ దవాఖానాలు పనిచేస్తున్నాయి.
c) ఆరోగ్య, వెల్నెస్ కేంద్రాలు :
ఇవి సమగ్ర ఆరోగ్య సేవలతో బాటు ప్రసూతి, చిన్న పిల్లల ఆరోగ్య రక్షణ సేవలను అందిస్తున్నాయి. వైద్య సేవలు, అవసరమైన ఔషధాలను ఇవి ఉచితంగా పంపిణీ చేస్తాయి. రాష్ట్రంలో 636 ప్రాథమిక- ఆరోగ్య కేంద్రాలు, 86 ఉపకేంద్రాలు, 104 బస్తీ దవాఖానాలు, 227 పట్టణ ప్రాథమిక ఆరోగ్య కేంద్రాలు ఆరోగ్య వెల్నెస్ కేంద్రాలుగా పనిచేస్తున్నాయి.
d) తెలంగాణ వైద్య విధాన పరిషత్ (TVVP) ఆసుపత్రులు :
తెలంగాణ వైద్య విధాన పరిషత్ ఆధ్వర్యంలో 107 TVVP ఆసుపత్రులు పనిచేస్తున్నాయి. ఇవి ప్రసూతి, చిన్న పిల్లల ఆరోగ్య రక్షణ సేవలు, సాధారణ వైద్య సేవలు, సర్జరీలు, ఆప్తమాలజీ, పీడియాట్రిక్స్, ఆర్థోపెడిక్స్, డెర్మటాలజీ, ENT మొదలైన సేవలను అందిస్తాయి.
e) ఆయుష్ (ఆయుర్వేద, యోగ, నాచురోపతి, యునాని, హోమియోపతి) :
తెలంగాణ ప్రభుత్వం, జాతీయ ఆయుష్ మిషన్ జంలో ఆయుష్ పద్ధతి వైద్యాన్ని ప్రోత్సహిస్తున్నది. ఆయుష్ శాఖ కింద రాష్ట్రంలో 860 దవాఖానాలు పనిచేస్తున్నాయి.
f) ఆరోగ్య శ్రీ :
ఆరోగ్యశ్రీ ఆరోగ్య రక్షణ ట్రస్టు’ ద్వారా రాష్ట్రంలో ఆరోగ్యశ్రీ అనే ఒక ఏకైక పథకం ఆరోగ్య బీమాతో అమలవుతుంది. దీని ప్రధాన ఆశయం పేదరిక రేఖకు దిగువన ఉన్న వారికి వైద్య సేవలను అందించడం, ఈ పథకం ద్వారా పేద వారికి ఎంపిక చేయబడిన వ్యాధులకు నగదు రహిత సేవలు అందించబడతాయి.
g) KCR కిట్ :
ఈ పథకాన్ని తెలంగాణ ప్రభుత్వం జూన్ 2, 2017 న ప్రారంభించింది. పేదరికపు రేఖకు దిగువన ఉండి ప్రభుత్వ ఆరోగ్య కేంద్రాల నుంచి ఆరోగ్య సేవలు పొందే గర్భిణీ స్త్రీలకు, మగశిశువు జన్మిస్తే రూ.12,000, ఆడశిశువు జన్మిస్తే రూ. 13,000 సహాయం అందించబడుతుంది.

ప్రశ్న 9.
తెలంగాణలో పేదరికం, నిరుద్యోగిత స్థితిగతులను విశ్లేషించండి.
జవాబు.
పేదరికం బహుముఖ దృగ్విషయం. ఇది సాంఘిక, ఆర్థిక, రాజకీయ, కొంతమేరకు బహిర్గత కారణాలచే ప్రభావితమౌతుంది. పేదరికమనేది ఒక సాంఘిక దృగ్విషయం. సమాజంలో గల ఒక వర్గం పౌరులు తను జీవనాన్ని గడుపుటకు కనీస అవసరాలు కూడా తీర్చుకోలేని స్థితిని సేవలికంగా నిర్వచించవచ్చు.
(a) టెందూల్కర్ నిపుణుల కమిటీ పేదరికం అంచనాలు :
1993-94లో తెలంగాణలో పేదరికపు అంచనాల కొరకు సాలుసలి తలసరి ఆదాయం గ్రామీణ ప్రాంతాలకు రూ. 11,244, పట్టణ ప్రాంతాలకు రూ. 11,282 గా ప్రమేయం చేయబడ్డది.
అదే విధంగా 2011-12 లో పేదరికపు అంచనా కొరకు సాలునరి తలసరి ఆదాయం గ్రామీణ ప్రాంతాలకు రూ.860గా పట్టణ ప్రాంతాలకు రూ.1,009 గా భావించడం జరిగింది. కమిటీ అంచనాల ప్రకారం 1993-94 నుండి 2011-12 మధ్య కాలంలో తెలంగాణలో గ్రామీణ, పట్టణ పేదరికం వరుసగా 49 శాతం, 30.5 శాతంగా ఉంది.
(b) రంగరాజన్ కమిటీ రిపోర్టు పేదరికం అంచనాలు :
పేదరికంపై రంగరాజన్ కమిటీ రిపోర్టు అంచనాల ప్రకారం 2011-12లో తెలంగాణలో పేదరికపు స్థాయి దేశం మొత్తం పేదరికపు స్థాయి కంటే చాలా తక్కువ. ఈ రిపోర్టు ప్రకారం గ్రామీణ ప్రాంతాలలో పేదరికపు స్థాయి తెలంగాణలో 9.3 శాతం కాగా దేశం మొత్తంలో అది 30.9 శాతంగా ‘అలాగే పట్టణ ప్రాంతాలలో పేదరికపు స్థాయి 11.1 తాతం కాగా దేశం మొత్తంలో అది 26.4 శాతంగా ఉంది.
తెలంగాణ రాష్ట్రంలో నిరుద్యోగిత రేట్లు :
అమలులో ఉన్న వేతనం వద్ద ఒక వ్యక్తి శారీరకంగా, మానసికంగా పనిచేయడానికి సిద్ధంగా ఉన్నప్పటికీ అతనికి ఉద్యోగ అవకాశం లభ్యం కాకపోవడాన్ని నిరుద్యోగితగా నిర్వచించవచ్చు. ఇంకొక విధంగా చెప్పాలంటే ఇది దేశంలో నిరుద్యోగుల సంఖ్య కంటే ఉద్యోగ అవకాశాల సంఖ్య తక్కువగా ఉండే స్థితిని సూచిస్తుంది.
తెలంగాణ రాష్ట్రంతో బాటు భారతదేశంలో నిరుద్యోగిత రేటు 2011-12లో తెలంగాణలో నిరుద్యోగిత రేటు భారతదేశ నిరుద్యోగిత రేటు కంటే తక్కువ. మొత్తానికి రాష్ట్రంలో పురుషులతో పోల్చినప్పుడు స్త్రీలలోనే నిరుద్యోగిత రేటు ఎక్కువ. పట్టణ, గ్రామీణ ప్రాంతాల నిరుద్యోగిత రేట్లలో కూడా ఇంచుమించు ఇదే పరిస్థితి ఉన్నది.
ప్రశ్న 10.
కాళేశ్వరం ప్రాజెక్టు ప్రాముఖ్యతను చర్చించండి.
జవాబు.
కాళేశ్వరం ప్రాజెక్టు :
కాళేశ్వరం దగ్గరలో గల మేడిగడ్డ వద్ద గోదావరి నదిపై ఒక బ్యారేజీ, మేడిగడ్డ (లక్ష్మీ బ్యారేజీ) మరియు అన్నారం వద్ద గల శ్రీపాద యెల్లంపల్లి మరియు సుందిల్ల వద్ద మరో రెండు బ్యారేజీలను నిర్మించడం.
వీటి ద్వారా కాలువలు, టన్నెల్స్, లిఫ్ట్ పద్ధతులు, రిజర్వాయర్లు, నీటి పంపిణీ వ్యవస్థలను ఉపయోగించి కమాండ్ ఏరియాలో గల 7 జిల్లాల (పునర్విభజన వలన 13 జిల్లాలకు) ఆయకట్టు తొలుత ప్రకటించిన 16,40,000 ఎకరాలకు బదులు 18,25,700 ఎకరాలకు నీటిని అందించుటకు నిర్ణయం.
దీనితో బాటు స్టేజి-1, స్టేజి-II, సింగూరు, నిజాంసాగర్ ప్రాజెక్టుల స్థిరీకరణ ద్వారా మరో 18,82,970 ఎకరాలకు (18,25,700 + 18,82,970 = 37,08,670 ఎకరాలు) నీరును అందించుట తెలంగాణ ప్రభుత్వ ధ్యేయం. వీటితో బాటు జంట నగరాలకు 20 TMC లు, నదీ పరీవాహక గ్రామాలకు 10 TMCల తాగు నీరు, పారిశ్రామిక అవసరాలకు 16 TMCల నీరు అందించాలని ప్రభుత్వం ప్రతిపాదించింది. కాళేశ్వరం ప్రాజెక్టు యొక్క మొత్తం అంచనా వ్యయం 80,000 కోట్ల రూపాయలు కాగా 31.7.2019 నాటికి 51,434 కోట్ల రూపాయలు వ్యయం చేయడం జరిగింది.

ప్రశ్న 11.
తెలంగాణలో ఇంధన మార్గాలు గురించి వ్రాయండి.
జవాబు.
తెలంగాణలో ఇంధన (శక్తి) రంగం : తెలంగాణ ఆర్ధిక వ్యవస్థ వ్యవసాయాధారితం అయినందున ఇతర రాష్ట్రాలతో పోల్చితే విద్యుచ్ఛక్తి వినియోగం ఎక్కువ తెలంగాణ రాష్ట్రంలో 2017-18 లో రాష్ట్ర తలసరి విద్యుచ్ఛక్తి వినియోగం 1,727 యూనిట్లతో 13.62 శాతం వినియోగ వృద్ధి రేటును నమోదు చేసుకొన్నది.
2018-19లో భారత్ లో సగటు విద్యుత్తు వినియోగం 1,181 యూనిట్లు, ఈ వివరాల ప్రకారం తెలంగాణలో విద్యుత్తు సగటు వినియోగం, దేశ వినియోగం కంటే ఎక్కువగా ఉండటమే కాకుండా దేశంలో మొదటి స్థానంలో ఉన్నది.
2016-17లో తెలంగాణలో విద్యుత్తు వినియోగం 53,017 మిలియన్ యూనిట్లు (MU) కాగా ఇది 2017-18 లో 60,237 MUకు పెరిగింది. అదేవిధంగా విద్యుత్తు తలసరి వినియోగం 2016-17 లో 1,551 యూనిట్లు 2017-18 లో 1,727 యూనిట్లకు పెరిగింది.
ఆవిభాజ్య ఆంధ్రప్రదేశ్లో గల విద్యుత్తు స్థాపిత శక్తి (installed capacity)ని రాష్ట్ర విభజనానంతరం తెలంగాణకు 53.89 శాతం, ఆంధ్రకు 46.11 శాతంగా నిర్దేశించబడ్డది.
తదనుగుణంగా డిసెంబర్ 2016 నాటికి తెలంగాణ రాష్ట్ర స్థాపిత శక్తి కేంద్ర, రాష్ట్ర ప్రైవేటు రంగాలన్నింటిని కలిపి మొత్తం 12,295.75 MW. ‘Power Sector, జనవరి 2018, రిపోర్టు ప్రకారం 31.1.2018 నాటికి తెలంగాణ రాష్ట్ర విద్యుత్తు స్థాపిత శక్తి 14.689.46 MW; ఇందులో రాష్ట్రం వాటా 7572.65 MW, కేంద్రం వాటా 2036.85 MW, ప్రైవేటు రంగం వాటా 5079.96 MW.
ప్రశ్న 12.
తెలంగాణలో SC/ST వర్గాల సంక్షేమ పథకాల గురించి రాయండి.
జవాబు.
SC/STs వర్గాల అభివృద్ధి, సంక్షేమ పథకాలు :
i) SC, ST ల ప్రత్యేక అభివృద్ధి నిధి :
SC, ST ల ప్రత్యేక అభివృద్ధి నిధి (SDF) చట్టం, 2017 ననుసరించి తెలంగాణ ప్రభుత్వం రెండు బడ్జెట్ పద్దులను అనగా (i) SC ప్రత్యేక అభివృద్ధి నిధి (SCSDF), (ii) ST ప్రత్యేక అభివృద్ధి నిధి (STSDF) లను రూపకల్పన చేసింది.
ii) షెడ్యూల్డ్ కులాల సంక్షేమం :
తెలంగాణలో షెడ్యూల్డ్ కులాల అభివృద్ధి శాఖ కింద వివరించిన పథకాల అమలును పర్యవేక్షిస్తుంది.
a) SC లకు కళ్యాణ లక్ష్మి :
అక్టోబర్, 2, 2014న ఈ పథకాన్ని ప్రభుత్వం ప్రారంభించింది. తెలంగాణకు చెందిన SC వర్గపు 18 సంవత్సరాల వయస్సు పై బడిన బాలిక వివాహ ఖర్చుల కొరకు వధువు కుటుంబానికి రూ.51,000 ప్రభుత్వం గతంలో ఇచ్చేది. ఇందుకు SC కుటుంబపు తల్లిదండ్రుల ఆదాయ పరిమితి 2 లక్షల రూపాయలు. కాగా కల్యాణ లక్ష్మి గ్రాంటును ప్రభుత్వం 2017లో రూ.75,116 లకు, 2018 లో రూ.1,00,116 లకు పెంచింది.
b) అంబేద్కర్ ఓవర్సీస్ నిధి పథకం :
ఈ గ్రాంటు ద్వారా విద్యార్థులు USA, UK, కెనడా, ఆస్ట్రేలియా, సింగపూర్, ఫ్రాన్స్, జర్మనీ, జపాన్, న్యూజిలాండ్ మరియు సౌత్ కొరియా వంటి దేశాల్లో విద్యను అభ్యసించవచ్చు. 2018-19 సంవత్సరంలో 101 మంది విద్యార్థులు ఈ పథకంలో ఎంపికయ్యారు.
c) భూమి కొనుగోలు పథకం :
నిరుపేద షెడ్యూల్డ్ కులాల మహిళలకు లబ్ధి చేకూర్చుటకు ఈ పథకాన్ని రూపొందించారు. ఈ పధరం కింద 2014-16 నుంచి 2019-20 మధ్య కాలంలో దాదాపు రూ.667.71 కోట్ల వ్యయంతో సుమారు 15,044.35 ఎకరాల భూమిని కొనుగోలు చేయగా 5,930 మందికి పంపిణీ చేశారు.
iii) షెడ్యూల్డ్ తెగల సంక్షేమం :
షెడ్యూల్డ్ తెగల సమగ్రాభివృద్ధి కొరకు తెలంగాణ ప్రభుత్వం కింద తెలిపిన పథకాలను అమలు పరుస్తున్నది.
a) ST లకు కల్యాణ లక్ష్మి :
ఈ పథకాన్ని అక్టోబర్ 2, 2014లో ప్రారంభించారు. ఈ పథకం కింద 18 సంవత్సరాలు నిండిన తెలంగాణకు చెందిన ST యువతి కళ్యాణ ఖర్చుల కోసం రూపాయలు 1,00,116 ఆర్థిక సహాయం ఇవ్వబడుతుంది.
b) ఆర్థిక మద్దతు పథకాలు :
ఈ పథకం ద్వారా వ్యవసాయ రంగం, ఉద్యానవనం, మత్స్య పరిశ్రమ, చిన్న నీటి పారుదల, పశు సంవర్ధకం, స్వయం ఉపాధి వంటి రంగాలలో నిమగ్నమైన గిరిజనులకు ఆర్థిక సహాయం కల్పిస్తారు.
c) అడవి హక్కుల చట్టం, 2006 :
తమ జీవనోపాధి కొరకు కొన్ని యుగాల నుంచి అడవుల పై ఆధారపడి జీవించే గిరిజనులు, ఇతర సంప్రదాయ ఆటవిక జీవులకు తమ జీవనాన్ని కొనసాగించుకొనే రక్షణను అడవి హక్కుల చట్టం – 2006 కల్పిస్తుంది. ఈ చట్టం ప్రకారం 93,494 మంది గిరిజనులకు 3,00,092 ఎకరాల భూమిని పంపిణీ చేయడం జరిగింది.
C. వెనకబడిన వర్గాల (BC) అభివృద్ధి, సంక్షేమ పథకాలు :
వెనకబడిన తరగతుల వర్గాల సంక్షేమం కోసం తెలంగాణ ప్రభుత్వం చేపట్టిన పథకాలు :
i) కళ్యాణ లక్ష్మి :
2016-17 సంవత్సరం నుంచి కళ్యాణ లక్ష్మి పథకాన్ని వెనకబడిన తరగతులు (BC), ఆర్థికంగా వెనకబడిన తరగతుల వారికి కూడా వర్తింపజేశారు.
ii) చాలా వెనకబడిన తరగతుల అభివృద్ధి కార్పోరేషన్ :
వెనకబడిన తరగతుల వర్గాలలో సాంఘికంగా, విద్యాపరంగా, ఆర్థికపరంగా చాలా వెనకబడిన తరగతుల (MBC) సంక్షేమంలో మెరుగుదల కొరకు ఈ కార్పోరేషన్ ను 2017లో తెలంగాణ ప్రభుత్వం స్థాపించింది.
D. మైనార్టీల అభివృద్ధి, సంక్షేమ పథకాలు :
తెలంగాణ రాష్ట్రంలో మైనార్టీ వర్గం వారి సాంఘిక, ఆర్థిక స్థితిగతులలో పెంపుదల కోసం తెలంగాణ ప్రభుత్వం చేపట్టిన కొన్ని ముఖ్యమైన పథకాలను కింద వివరించాం.
a) బ్యాంక్తో అనుసంధానం చేయబడిన సబ్సిడీ పథకం : మైనార్టీ వర్గాల వారు స్వయంఉపాధి చేపట్టే వ్యాపారం చేసేవారికి ఈ పథకాన్ని ఉద్దేశించారు. సబ్సిడీతో కూడుకున్న ఆర్థిక సహాయాన్ని బ్యాంకుల ద్వారా మైనార్టీ ఫైనాన్స్ కార్పోరేషన్ కల్పిస్తుంది.
b) శిక్షణ, ఉద్యోగిత, నైపుణ్య అభివృద్ధి : మైనార్టీల శాఖ, మైనార్టి యువతకు తగిన శిక్షణను ఆ వారు స్వయం ఉపాధి చేపట్టుటకు వీలుగా మైనార్టీ ఫైనాన్స్ కార్పోరేషన్ ద్వారా ఆర్థిక సహకారాన్ని అందిస్తుంది.
c) షాదీ ముబారక్ పథకం : ఈ పథకం ప్రకారం అర్హమైన మైనార్టీ వర్గానికి చెందిన యువతి పెళ్ళి ఖర్చులకు రూ. 1,00,116 గ్రాంటు రూపంలో ఇవ్వబడుతుంది.

అతిస్వల్ప సమాధాన ప్రశ్నలు:
ప్రశ్న 1.
స్థూల జిల్లా ప్రాంతీయోత్పత్తి
జవాబు.
ఒక నిర్దిష్ట కాలం లేదా ఒక సంవత్సర కాలంలో ఒక జిల్లా యొక్క భౌగోళిక సరిహద్దులలో ఒక సంవత్సర కాలంలో ఒకటి. కంటే ఎక్కువసార్లు లెక్కించకుండా ఉత్పత్తి చేయబడిన వస్తుసేవల విలువను తెలిపేదే స్థూల, జిల్లా ప్రాంతీయోత్పత్తి (GDDP). ఈ GDDP అంచనా, ఒక జిల్లాను ఇతర జిల్లాలతో పోల్చుట ద్వారా ఆ జిల్లా యొక్క అభివృద్ధి స్థాయి వివరణకు తోడ్పడుతుంది.
ఈ వివరాల ప్రకారం తెలంగాణ రాష్ట్రంలో GDDP లో హైదరాబాదు జిల్లా ప్రథమ స్థానంలో ఉండగా, రంగారెడ్డి, మేడ్చల్-మల్కాజిగిరి, సంగారెడ్డి జిల్లాలు వరుసగా రెండవ, మూడవ, నాల్గవ స్థానాల్లో నిలిచాయి.
ప్రశ్న 2.
తలసరి ఆదాయం.
జవాబు.
ఒక దేశ జాతీయాదాయాన్ని ఆ దేశపు జనాభాతో భాగించగా వచ్చే మొత్తాన్ని తలసరి ఆదాయం అని అంటారు. ఈ భావనను క్రింది విధంగా వివరించవచ్చును.
తలసరి ఆదాయం = జాతీయాదాయం / జనాభా.
ప్రశ్న 3.
పిల్లల జనాభా.
జవాబు.
పిల్లల జనాభా (Child Population) :
0-6 సంవత్సరాల లోపు వారిని పిల్లలు (Children) గా భావించాలి. తెలంగాణలో పిల్లల జనాభా శాతం 2001 లో 14.2% నుంచి, 2011 లో 10.5%కు తగ్గింది. ఈ తగ్గుదలకు కారణం పెరుగుతున్న అక్షరాస్యత, అధిక ఆదాయాలకు తోడుగా కుటుంబ నియంత్రణ పద్ధతులు అవలంభించడం.
అన్ని జిల్లాలలో పిల్లల జనాభా శాతం, రాష్ట్ర సగటుకు దగ్గరగా 10.5%గా ఉన్నది. కేవలం ఒక మహబూబ్ నగర్ జిల్లాలో మాత్రం పిల్లల జనాభా 17.4% గా ఉంది.

ప్రశ్న 4.
ఆహార, ఆహారేతర పంటలు.
జవాబు.
ధాన్యాలు, చిరుదాన్యాలు, పప్పుదినుసులు వంటివి ఆహార పంటలు. ప్రత్తి, నూనెగింజలు, పూలు వంటివి ఆహారేతర పంటలు. 2017-18 సంవత్సరంలో 37.14 లక్షల హెక్టార్ల భూమిలో ఆహారపంటలు సాగుచేయబడ్డాయి. ఇదే కాలంలో 23-45 లక్షల హెక్టార్లలో ఆహారేతర పంటలు సాగుచేయబడ్డాయి.
ప్రశ్న 5.
మనుగడలో ఉన్న కమతం.
జవాబు.
ఈ రకమైన వ్యవసాయ భూకమతాల సమాచార సేకరణ కోసం భారత ప్రభుత్వం ప్రతి 5 సం॥లకు ఒకసారి గణన నిర్వహిస్తుంది. ఈ గణన ప్రకారం మనుగడలో ఉన్న కమతాలు, ఉపాంత, చిన్న, మాధ్యమిక పెద్ద కమతాలు రూపంలో ఉన్నాయి. తెలంగాణలో 2010-11లో మనుగడలో గల సగటు కమతం పరిమాణం 1.12 హెక్టారులు. 2015-16 నాటికి ఇది 1.00 హెక్టారు (2.47 ఎకరాలు)గా ఉంది.
ప్రశ్న 6.
రైతుబంధు.
జవాబు.
రుణ భారం నుంచి విముక్తి కల్పిచేందుకు వీలుగా ఒక పెట్టుబడి రూపంలో సహకారాన్ని అందించి రైతుల సాధికారితను పెంచే ఉద్దేశంతో తెలంగాణ ప్రభుత్వం రూపొందించిన పథకమే రైతు బంధు. 2018, మే 10వ తేదిన ఈ పథకం ప్రారంభించబడ్డది.
2019-20 సంవత్సరం నుంచి తెలంగాణ ప్రభుత్వం ఈ రకమైన పెట్టుబడి సహకారాన్ని ప్రతి సీజను రూ.4,000 ఎకరం నుంచి రూ.5,000 లకు పెంచింది.
ప్రశ్న 7.
రైతు బీమా.
జవాబు.
2018, ఆగష్టు 15న తెలంగాణ ప్రభుత్వం ఈ పథకాన్ని ప్రారంభించింది. రోగగ్రస్తుడైన రైతు మరణిస్తే, అతని కుటుంబ సభ్యులు లేదా అతనిపై ఆధారపడిన వారికి ఆర్థికపరమైన భద్రతను కల్పించడం ఈ పథకం ప్రధాన ఉద్దేశం. ఈ పథకం కింద ప్రతి రైతుకు రూపాయలు 5 లక్షల బీమా కవరేజి ఉంటుంది.

ప్రశ్న 8.
సూక్ష్మ, చిన్న మధ్య తరహా పరిశ్రమలు (MSME).
జవాబు.
ఈ పరిశ్రమలు పెద్దతరహా పరిశ్రమలకు అవసరం అయిన ఉత్పాదకాలను సప్లయ్ చేసే అనుషంగిక పరిశ్రమలుగా పనిచేస్తూ రాష్ట్రంలో సంతులిత ప్రాంతీయాభివృద్ధికి, సమ్మిళిత వృద్ధికి తోడ్పడతాయి. ఇవి తక్కువ మూలధనం, తక్కువ స్థాయి నైపుణ్యం గల పారిశ్రామిక యూనిట్ల ద్వారా ఉద్యోగ కల్పనలో కీలక పాత్రను కలిగి ఉంటాయి.
ప్రశ్న 9.
TS-ipass.
జవాబు.
తెలంగాణ రాష్ట్ర పారిశ్రామిక విధాన నినాదం “ఆవిష్కరించు, వృద్ధిపరచు, సంవిలీనించు”. తెలంగాణ రాష్ట్ర ప్రభుత్వం ”తెలంగాణ రాష్ట్ర పారిశ్రామిక ప్రాజెక్ట్ అనుమతి సొంత ధ్రువీకరణ (సర్టిఫికేషన్) విధానాన్ని (TS-ipass) రూపొందించి, పెట్టుబడిదారుల అనుకూల విధానాన్ని ప్రవేశపెట్టి, పెట్టుబడులను ఆకర్షించి పారిశ్రామిక ప్రగతికి బాటలు వేసింది”.
ప్రశ్న 10.
ఇమేజ్ టవర్.
జవాబు.
అధునాతన అవస్థాపనా సౌకర్యాల కల్పన ద్వారా యానిమేషన్, గేమింగ్, VFX సేవల కల్పనకు IMAGE టవర్ను నెలకొల్పుటకు తెలంగాణ ప్రభుత్వం సంకల్పించింది. దీనిని రుద్రారం గ్రామం, రంగారెడ్డి జిల్లాలో 10 ఎకరాల స్థలంలో రూ. 1,000 కోట్లతో ప్రభుత్వ, ప్రైవేట్ భాగస్వామ్యం (PPP)లో స్థాపించ తలపెట్టింది.
ప్రశ్న 11.
ఆసరా పెన్షన్ పథకం
జవాబు.
ప్రభుత్వం సాంఘిక భద్రత, సంక్షేమం దృష్ట్యా ఈ పథకాన్ని ప్రారంభించింది. ఆసరా పథకం క్రింద వృద్ధులు, వితంతువులు, వికలాంగులు, నేత కార్మికులు, కల్లుగీత కార్మికులు, ఉపాధిని కోల్పోయిన వారికి నెలకు 1000/- వికలాంగులకు 1,500/- ఆర్థిక సహాయం అందించే కార్యక్రమాన్ని అమలు చేస్తున్నది. దీనిని బీడి కార్మికులకు కూడా వర్తింపజేసింది.

ప్రశ్న 12.
తెలంగాణ ఫైబర్ గ్రిడ్.
జవాబు.
ఈ ప్రాజెక్టును తెలంగాణ ప్రభుత్వం 2015లో ప్రారంభించింది. తగిన అవస్థాపనా సౌకర్యాలను కల్పించి 10 జోన్లు (33 జిల్లాలో) గా ‘డిజిటల్ తెలంగాణ’ను సాకారం చేయడం ఈ ప్రాజెక్టు ప్రధాన లక్ష్యం.
ప్రశ్న 13.
మిషన్ కాకతీయ.
జవాబు.
వ్యవసాయాన్ని పునరుత్తేజం చేసేందుకు దీర్ఘకాలిక చర్యగా నూతన ప్రభుత్వం “మిషన్ కాకతీయ” అనే ఒక బృహత్తర కార్యక్రమాన్ని ప్రారంభించింది. దీని ప్రధాన ఆశయం “మన ఊరు మన చెరువు”.
ఈ కార్యక్రమం క్రింద సంప్రదాయ చెరువులు, చిన్న నీటిపారుదల వనరులను పునరుద్ధరించడం, ఉపరితల భూగర్భ జలాలను మెరుగుపర్చడం ద్వారా 46,531 చెరువులను రానున్న 5 సంవత్సరాలలో దశల వారీగా పునరుద్ధరించాలని ప్రతిపాదించడం జరిగింది.
ప్రశ్న 14.
తెలంగాణలో స్త్రీ,పురుషుల నిష్పత్తి.
జవాబు.
వెయ్యిమంది పురుషులకు స్త్రీల సంఖ్య ఆధారంగా స్త్రీ-పురుష నిష్పత్తి నిర్ణయించబడుతుంది. 2011 జనాభా లెక్కల ప్రకారం తెలంగాణలో ప్రతి 1000 మంది పురుషులకు 988 మంది స్త్రీల అనుపాతం ఉంది. భారతదేశంలో ఈ అనుపాతం 1,000 మంది పురుషులకు 943 మంది స్త్రీలు ఉన్నారు. కాబట్టి తెలంగాణ రాష్ట్రంలో స్త్రీలు ఇండియాలో గల సగటు స్త్రీల సంఖ్య కంటే అధికంగా ఉన్నారని తెలుస్తుంది.
ప్రశ్న 15.
స్థూల నమోదు నిష్పత్తి (GER).
జవాబు.
స్థూల నమోదు నిష్పత్తి (GER) విశ్వవిద్యాలయాలు, కళాశాలలు, పాఠశాలలో విద్యార్థుల నమోదు సంఖ్యను నిర్ణయిస్తుంది. GER 2017-18లో ప్రాథమిక పాఠశాలలో బాలురు – 98.76 శాతం, బాలికలు – 98.05 శాతం కాగా ఉచ్ఛతర ప్రాథమిక పాఠశాలలో బాలురు – 87.32 శాతం, బాలికలు 88.4.

ప్రశ్న 16.
షెడ్యూల్డ్ కులాల రెసిడెన్షియల్ పాఠశాలలు.
జవాబు.
తెలంగాణా సాంఘికసంక్షేమ రెసిడెన్షియల్ విద్యాసంస్థల సొసైటీ రాష్ట్రంలో 269 రెసిడెన్షియల్ విద్యాసంస్థలను నడుపుతుంది. ఇందులో 175 బాలికలకు సంబంధించినవి. వీటిలో 5వ తరగతి నుండి డీగ్రీ వరకు షెడ్యూల్డ్ కులాలకు చెందిన ప్రవేశం కలదు.
ప్రశ్న 17.
కంటి వెలుగు,
జవాబు.
సామాన్యంగా ప్రజలు ప్రత్యేకించి మహిళలు, వృద్ధులు కంటి సమస్యలను వాయిదా వేయడం లేదా ఆ సమస్యలను కొనసాగిస్తూనే జీవనాన్ని గడుపుతుంటారు. ఈ సమస్య నివారణ కోసమే తెలంగాణ ప్రభుత్వం కంటి వెలుగు పథకాన్ని రూపొందించి అమలుపరుస్తున్నది.
ప్రశ్న 18.
మానవ అభివృద్ధి సూచిక.
జవాబు.
ఈ సూచికలో మూడు అంశాలు ఉంటాయి. అవి
ఎ) తలసరి ఆదాయం
బి) ఆయుర్ధాయం, ఆరోగ్య ప్రామాణికతలు,
సి) అక్షరాస్యత, విద్య.
ప్రశ్న 19.
ఆరోగ్య లక్ష్మి.
జవాబు.
గర్భిణీ స్త్రీలు, పిల్లలకు పాలిచ్చే తల్లులలో పౌష్టిక, పోషక విలువలు పెంచుట కొరకు ఈ పథకాన్ని రూపొందించారు. తెలంగాణ ప్రభుత్వం ఈ పథకాన్ని అంగన్ వాడి కేంద్రాల ద్వారా పేదరికపు రేఖకు దిగువన ఉన్న గర్భిణీ స్త్రీలు, 6 సంవత్సరాల లోపు వయస్సు గల పిల్లలకు ప్రతిరోజు పోషకాహాన్ని అందిస్తుంది. ఈ పథకాన్ని జనవరి 1, 2015 న ప్రారంభించారు.

ప్రశ్న 20.
నిరుద్యోగిత.
జవాబు.
అమలులో ఉన్న వేతన రేటు వద్ద ఒక వ్యక్తి శారీరకంగా, మానసికంగా పనిచేయడాన్ని సిద్ధంగా ఉన్నప్పటికి అతనికి ఉద్యోగ అవకాశం లభ్యం కాకపోవడాన్ని నిరుద్యోగితగా చెబుతారు. ఈ భావన దేశంలో నిరుద్యోగుల సంఖ్య కంటే ఉద్యోగావకాశాల సంఖ్య తక్కువగా ఉండే స్థితిని సూచిస్తుంది.
ప్రశ్న 21.
కళ్యాణ లక్ష్మి.
జవాబు.
ఆర్థికంగా వెనుకబడిన ఎస్.సి., ఎస్.టి. కుటుంబాలలో పెళ్ళి చేసుకొనే అమ్మాయిలకు ఒకేసారి 51 వేల రూపాయల ఆర్థిక సహాయాన్ని అందించే కార్యక్రమాన్ని అక్టోబరు 2, 2014 నుంచి ప్రారంభించింది.
ప్రశ్న 22.
మిషన్ భగీరథ.
జవాబు.
కృష్ణ, గోదావరి నదుల నీటి సహాయంతో శుద్ధి చేసిన త్రాగునీరును పైపులైను ద్వారా రాష్ట్ర ప్రజలకు అందుబాటులోకి తేవడం ఈ పథకం ముఖ్య ఆశయం. ఈ పథకాన్ని 7 ఆగస్టు, 2016లో కోమటిబండ, మెదక్ జిల్లాలో ప్రారంభించారు. గ్రామ ప్రజలకు 100 లీటర్లు, మున్సిపాలిటీ వాసులకు 135 లీటర్లు కార్పొరేషన్ వారికి 150 లీటర్లు అందించాలనేది లక్ష్యం.
ప్రశ్న 23.
B.C సంక్షేమ పథకాలు.
జవాబు.
వెనకబడిన తరగతుల వర్గాల సంక్షేమం కోసం తెలంగాణ ప్రభుత్వం చేపట్టిన పథకాలు :
i) కళ్యాణ లక్ష్మి :
2016-17 సంవత్సరం నుంచి కళ్యాణ లక్ష్మి పథకాన్ని వెనకబడిన తరగతులు (BC), ఆర్థికంగా వెనకబడిన తరగతుల వారికి కూడా వర్తింపజేశారు.
ii) చాలా వెనకబడిన తరగతుల అభివృద్ధి కార్పోరేషన్ :
వెనకబడిన తరగతుల వర్గాలలో సాంఘికంగా, విద్యాపరంగా, ఆర్థికపరంగా చాలా వెనకబడిన తరగతుల (MBC) సంక్షేమంలో మెరుగుదల కొరకు ఈ కార్పోరేషన్ ను 2017లో తెలంగాణ ప్రభుత్వం స్థాపించింది.

ప్రశ్న 24.
మైనారిటీల సంక్షేమ పథకాలు.
జవాబు.
తెలంగాణ రాష్ట్రంలో మైనార్టీ వర్గం వారి సాంఘిక, ఆర్థిక స్థితిగతులలో పెంపుదల కోసం తెలంగాణ ప్రభుత్వం చేపట్టిన కొన్ని ముఖ్యమైన పథకాలను కింద వివరించాం.
a) బ్యాంక్ తో అనుసంధానం చేయబడిన సబ్సిడీ పథకం :
మైనార్టీ వర్గాల వారు స్వయంఉపాధి చేపట్టే వ్యాపారం చేసేవారికి ఈ పథకాన్ని ఉద్దేశించారు. సబ్సిడీతో కూడుకున్న ఆర్థిక సహాయాన్ని బ్యాంకుల ద్వారా మైనార్టీ ఫైనాన్స్ కార్పోరేషన్ కల్పిస్తుంది.
b) శిక్షణ, ఉద్యోగిత, నైపుణ్య అభివృద్ధి :
మైనార్టీల శాఖ, 3 యువతకు తగిన శిక్షణను ఆ వారు స్వయం ఉపాధి చేపట్టుటకు వీలుగా మైనార్టీ పైనాన్స్ కార్పోరేషన్ ద్వారా ఆర్థిక సహకారాన్ని అందిస్తుంది.
c) షాదీ ముబారక్ పథకం :
ఈ పథకం ప్రకారం అర్హమైన మైనార్టీ వర్గానికి చెందిన యువతి పెళ్ళి ఖర్చులకు రూ.1,00,116 గ్రాంటు రూపంలో ఇవ్వబడుతుంది. కళ్యాణ లక్ష్మి. మిషన్ భగీరథ.
TS Inter 2nd Year Economics Study Material
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()