TS 10th Class Maths Important Questions Chapter 2 Sets

These TS 10th Class Maths Chapter Wise Important Questions Chapter 2 Sets given here will help you to solve different types of questions.

TS 10th Class Maths Important Questions Chapter 2 Sets

Previous Exams Questions

Question 1.
Write roster and builder form of “The set of all natural numbers which divide 42”. (T.S. Mar. ’15)
Solution:
Factors of 42 = 1, 2, 3, 6, 7, 14, 21, 42
So roster form = {1, 2, 3, 6, 7, 14, 21, 42}
The builder form = (x/x ∈ N, x is a factor of 42 }

Question 2.
Write A = {1, 2, 3, 4} in set builder form. (A.P. June ’15)
Solution:
The given set A = {1, 2, 3, 4}
The set builder form is A = {x/x ∈ N, x < 5 }

Question 3.
Let A = { x/x is an even number }
B = { x/x is an odd number}
C = { x/x is a prime number}
D = { x/x is a multiple of 5 }
Find (A.P. June’15)
i) A ∪ B
ii) A ∩ B
iii) C – D
iv) A ∩ C
Solution:
A = { x : x is an even number }
= {2, 4, 6, 8, 10}
B = { x : x is an odd number}
= {1, 3, 5, 7, 9 }
C = { x : x is a prime number}
= { 2, 3, 5, 7, 11}
D = { x : x is a multiple of 5}
= { 5, 10, 15, 20, 25}

i) A ∪ B = { 2, 4, 6, 8, 10, ……..} ∪ {1, 3, 5, 7, 9, …….}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …………}

ii) A ∩ B = { 2, 4, 6, 8, 10, ……….} ∩ {1, 3, 5, 7, 9, ………… }
= { } = Φ

iii) C – D = {2, 3, 5, 7, 11, ……….} – { 5, 10, 15, 20, 25, ………}
= {2, 3, 7, 11, …….}

iv) A ∩ C = { 2, 4, 6, 8, 10, ………….} ∩ {2, 3, 5, 7, 11, ……….}
= {2}

Question 4.
Write all the subsets of B = {p, q} (A.P. Mar ’16)
Solution:
{p}, {q}, {p, q} and { } are the subsets of the given set B = (p, q}
As then n(B) = 2 then number of all subsets = 2ⁿ = 2² = 4.

Question 5.
Write the roster form of the set A. (A.P. Mar. ’16)
A = {x : x = 2n + 1 ∀ n ∈ N}
Solution:
If n = 1 then 2n + 1 = 2(1) + 1
= 2 + 1 = 3
If n = 2 then 2n + 1 = 2(2) + 1
=4 + 1 = 5
If n = 3 then 2n + 1 = 2(3) + 1
= 6 + 1 = 7
So {3, 5, 7, 9, ………..} is the roster form of given set.

Question 6.
If A = {1, 2, 3, 4} and B = (1, 2, 3, 5, 6} then find
(i) A ∩ B
(ii) B ∩ A
(iii) A – B and
(iv) B – C then comment on the above. (A.P. Mar. ’16)
Solution:
Given A = {1, 2, 3, 4} and B = { 1, 2, 3, 5, 6} then
i) A ∩ B = {1, 2, 3, 4} ∩ { 1, 2, 3, 5, 6}
= {1, 2, 3}

ii) B ∩ A = {1, 2, 3, 5, 6} ∩ { 1, 2, 3, 4}
= {1, 2, 3}
So A ∩ B = B ∩ A

iii) A – B = {1, 2, 3, 4} – { 1, 2, 3, 5, 6}
= {4}

iv) B – A = { 1, 2, 3, 5, 6} – {1, 2, 3, 4}
= {5, 6}
So A – B ≠ B – A

Question 7.
Write the Set builder form of A – B where A = { x : x ∈ N and x < 20 } and B = { x : x ∈ N and x ≤ 5 } (T.S. Mar. ’16)
Solution:
Given A = { x : x ∈ N and x < 20 } is
A = {1, 2, 3, …….. 17, 18, 19} and
for B = {x : x ∈ N and x ≤ 5}
B = { 1, 2, 3, 4, 5} then
A – B = {1, 2, 3, ……… 17, 18, 19} – {1, 2, 3, 4, 5}
= {6, 7, 8, …… 18, 19} (T.S. Mar ’15)
The builder form of above A – B is
A – B = {x/x ∈ N and 6 ≤ x ≤ 19}
Or
A – B = {x : x ∈ N and 5 < x < 20}

Question 8.
If A = {x / x ∈ N, x < 6 } and B = { x : x ∈ N, 3 < x < 8} then show that A – B ≠ B – A with the help of venn – diagram.
Solution:
A = {x : x ∈ N, x < 6}
A = {1, 2, 3, 4, 5}
B = {x : x ∈ N, 3 < x < 8}
B = {4, 5, 6, 7}
∴ A – B = {1, 2, 3, 4, 5} – {4, 5, 6, 7}
= {1, 2, 3}

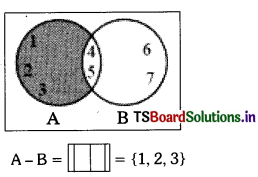
and
B – A = {4, 5, 6, 7} – {1, 2, 3, 4, 5}
= {6, 7}

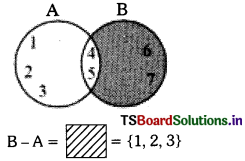
∴ A – B ≠ B – A

Question 9.
Write the set builder form of A = {1, \(\frac{1}{4}\), \(\frac{1}{9}\), \(\frac{1}{16}\), \(\frac{1}{25}\)} (T.S. Mar. ’16)
Solution:
{\(\frac{1}{1}\), \(\frac{1}{4}\), \(\frac{1}{9}\), \(\frac{1}{16}\), \(\frac{1}{25}\)} are in the form of \(\frac{1}{\mathrm{p}^2}\) whereas p < 6
So, A = { x : x = \(\frac{1}{\mathrm{p}^2}\), p ∈ N, and p < 6} is the set builder form.

Question 10.
If x is set of all factors of 24 and y is set all factors of 36 then find X ∪ Y and X ∩ Y using venn – diagrams. Comment. (T.S. Mar. ’16)
Solution:
X = Set of all factors of 24
= {1, 2, 3, 4, 6, 8, 12, 24}
Y = Set of all factors of 36
= {1, 2, 3, 4, 6, 9, 12, 18, 36}
Venn diagram of X ∪ Y
i)

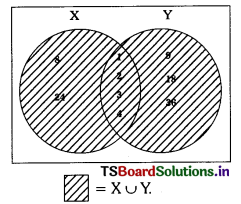
∴ X ∪ Y = {1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36}

ii)

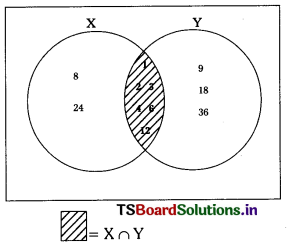
∴ X ∩ Y = {1, 2, 3, 4, 6, 12}
∴ It is clear X ∪ Y ≠ X ∩ Y

Additional Questions

Question 1.
Which of the following are sets ? Justify your answer.
i) The collection of all months of a year beginning with letter ‘M’
ii) A team of eleven best cricket players of the world.
iii) The collection of all girls in your class.
iv) The collection of all odd integers.
Solution:
i) The months of a year which begin with the letter ‘M’ are March and May.
The required set is {March, May}.
∴ It is a well defined collection of objects.
So, it is a set.
ii) It is not a set, because we cannot determine the eleven best cricket players of the world.
iii) It is a set, because we can divide whether he / she belongs to the given set or not.
iv) It is a set, because we can divide whether the number belongs to the given set or not.

Question 2.
If A = (1, 2, 3, 4} B = (5, 6, 7} and C = (p, q, r, s}, then fill the appropriate symbol, ∈ or ∉ in the blanks.
i) 2 ………… A
ii) 6 …………. C
iii) 4 ………… B
iv) q …………. C
v) 5 …………. B
vi) 8 …………. A
Solution:
i) 2 ∈ A
ii) 6 ∉ C
iii) 4 ∉ B
iv) q ∈ C
v) 5 ∈ B
vi) 8 ∉ A

Question 3.
Express the following statements using symbols.
i) The element p does not belong to ‘A’
ii) ‘q’ is an element of the set ‘B’
iii) 4 belongs to the set of Natural numbers N
iv) 5 belongs to the set prime numbers P
Solution:
i) p ∉ A
ii) q ∈ B
iii) 4 ∈ N
iv) 5 ∈ p

Question 4.
Write the following sets in roaster form.
i) A = (x : x is a natural number less than 8}
ii) B = (x : x is a two digital natural number such that the sum of its digits is 5}
iii) C = (x : x is a prime number which is a divisor of 30}
iv) D = { the set of all letters in the word CRICKET}
Solution:
i) A = (1, 2, 3, 4, 5, 6, 7}
ii) B = (14, 41, 23, 32}
iii) C = (2, 3, 5}
iv) D = { C, E, I, K, R, T}

Question 5.
Write the following sets in the set-builder form.
i) A = {5, 10, 15, 20}
ii) B = {3, 9, 27, 81}
iii) C = {4, 16, 64, 256}
iv) D = {1, 8, 27, 64, 125, ……….. 1000}
Solution:
i) A = {x : x is a multiple of 5 and less than 21}
ii) B = {x : x is a power of 3 and x is less than 5}
iii) C = {x : x is a power of 4, and x is less than 5}
iv) D = {x : x is a cube of natural numbers and not greater than 10}

Question 6.
Match the roaster form with set builder
i) {1, 2, 4, 8} (a) (x : x is an even natural number less than 11}
ii) {3, 5} (b) (x : x is a natural number and divisor of 8}
iii) {L, E, T, R} (c) (x : x is a prime number and a divisor of 15}
iv) (2, 4, 6, 8, 10}(d) (x : x is a letter of the word ‘LETTER’}
Solution:
i) b
ii) c
iii) d
iv) a

Question 7.
If A = {1, 2, 3, 4, 5}; B = {3, 4, 5, 6}, then find A ∪ B and A ∩ B.
Solution:
Given A = {1, 2, 3, 4, 5}, B = {3, 4, 5, 6}
A ∪ B = {1, 2, 3, 4, 5, 6}
A ∩ B = {3, 4, 5}.

Question 8.
If A = {4, 5, 6, 7, 8}; B = {7, 8, 9, 10, 11} then find A – B and B – A.
Solution:
Given A = {4, 5, 6, 7, 8},
B = {7, 8, 9, 10, 11}
A – B = {4, 5, 6}
B – A = {9, 10, 11}

Question 9.
Which of the following pairs of sets are disjoint ?
i) A = {3, 4, 5, 6}; B = {4, 6}
ii) A = {a, e, i, o, u}; B = {i, j, k}
iii) A = {5, 10, 15, 20}; B = {8, 16, 24}
iv) A = {1, 3, 5, 7};B = {2, 4, 6, 8}
Solution:
Disjoint sets: Two sets are said to be disjoint sets when they have no elements in common.
i) A and B are not disjoint sets (∵ 4, 6 are common)
ii) A and B are not disjoint sets (∵ i is common)
iii) A and B are disjoint sets (∵ No elements in common)
iv) A and B are disjoint sets (∵ No elements in common)

Question 10.
If A = {3, 4, 5, 6, 7}, B = {2, 4, 6, 8} then find n (A ∪ B).
Solution:
n(A) = 5 (∵ A contains 5 elements)
n(B) = 4 (∵ B contains 4 elements)
But A ∪ B = {2, 3, 4, 5, 6, 7, 8}
Now n(A ∪ B) = 7 (∵ A ∪ B contains 7 elements)

Question 11.
If A and B are two sets and n(A) – 15, n(B) = 25 and n(A ∩ B) = 10, find n (A ∪ B)
Solution:
We Know that n (A ∪ B) = n (A) + n (B) – n(A ∩ B)
∴ n(A ∪ B) = 15 + 25 – 10
n(A ∪ B) = 40 – 10 = 30

Question 12.
Which of the following sets are equal ?
i) A = {3, 4, 5, 6}, B = {7, 8, 9, 10}
ii) C = {a, b, c, d}, D = {d, c, a, b} :
iii) E = {2, 4, 6, 8}, F = {x : x is a positive even number < 10}
iv) G = {5, 10, 15, 20, . . . }, H = {x : x is a multiple of 5}
Solution:
i) A and B are not equal sets
ii) C and D are equal sets
iii) E and F are equal sets
iv) G and H are equal sets

Question 13.
State the reason for the following.
i) {4, 5,6, ……….. 12} ≠ {x : x ∈ N and 4 < x < 12}
ii) {2, 4, 6, 8, 10} ≠ {x : x = 2n + 1 and x ∈ N}
iii) {3, 6, 9, 12} ≠ {x : x is a multiple of 6}
iv) {1, 3, 5, 7, 9} ≠ {x : x is an even number}
Solution:
The first set is {4, 5, 6, … ,12}
Writing the second set in roaster form is {5, 6, 7, …,11}
The 1st and 2nd set have not exactly the same elements.
i) ∴ {4, 5, 6, . . . , 12} ≠ {x : x ∈ N and 4 < x < 12}

ii) The first set is {2, 4, 6, 8, 10}
Writing the 2nd set in roaster form is {3, 5, 7, 9}
∴ {2, 4, 6, 8, 10} ≠ {3, 5, 7, 9}

iii) The first set is {3, 6, 9, 12}
Writing the 2nd set is roaster form is {6, 12, 18, 24, … }
∴ {3, 6, 9, 12} ≠ {6, 12, 18, 24,. . .}

iv) The first set is {1, 3, 5, 7, 9}
Writing the 2nd set in roaster form is {2, 4, 6, 8}
∴ {1, 3, 5, 7, 9} ≠ {2, 4, 6, 8,…}

Question 14.
List all the subsets of the following :
i) A = {a, b}
ii) B = {p, q, r}
iii) {1, 2, 3}
Solution:
i) {a}, {b}, {a, b}, {Φ}
ii) {p}, {q}, {r}, {p, q}, {p, r}, {q, r}, {p, q, r}, {Φ}
iii) {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1,2, 3}, {Φ}

Question 15.
State which of the following sets are empty.
i) Set of integers which lie between 5 and 6.
ii) Set of even natural numbers divisible by 2.
iii) The set of lines which are parallel to the Y-axis.
iv) {x : x is a natural number, x < 6 and x > 8}
Solution:
i) It is empty set, because there is no integer lying between 5 and 6
ii) It is not empty set, because there are even natural numbers which are divisible by 2.
iii) It is not empty set, because there are number of lines parallel to the Y-axis is infinite.
iv) It is empty set, because there is no natural number satisfying this condition.

Question 16.
Which of the following set is finite or infinite ?
i) A = {x : x ∈ N and x < 50}
ii) B = {x : x ∈ N and x ≤ 10}
iii) C = {1³, 2³, 3³, ……}
iv) D = {x : x ∈ N and x is even}
Solution:
i) A = {1,2, 3, 4,…. 49}
This set is finite, because there are 49 numbers possible to count

ii) B = {1, 2, 3, 4, . . . , 10}
This set is finite, because there are 10 numbers possible to count

iii) C = {1³, 2³, 3³, . . . }
This set is infinite, because there are infinite numbers.

iv) D = {2, 4, 6, 8, . . . }
This set is infinite, because there are infinite even numbers.

Question 17.
If A = {1, 2, 3, 4, 5}; B = {4, 5, 6, 7} then find B – A.
Solution:
Given A = {1, 2, 3, 4, 5}; B = {4, 5, 6, 7}
B – A = {4, 5, 6, 7} – {1, 2, 3, 4, 5}
B – A = {6, 7}

Question 18.
If A = {0, 1, 2} and B = {2, 4} then find n (A ∪ B)
Solution:
Given A = {0, 1, 2}, B = {2, 4}
A ∪ B = {0, 1, 2, 4}
∴ n(A ∪ B) = 4

Question 19.
If A’ is the set of all primes below ‘5’ and ‘B’ is the set of all prime factors of ’30’, then is A – B = B – A?
Solution:
Given A = Set of all primes below 5 = {2, 3}
B = Set of all prime factors of 30 = {2, 3, 5}
A – B = { } and B – A = { 5 }
∴ A – B ≠ B – A

Question 20.
Represent the following through Venn- diagram.
i) A – B
ii) B – A
iii) A ∪ B
iv) A ∩ B
Solution:
i) Venn-diagram of A – B is

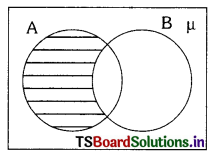
ii) Venn-diagram of B – A is

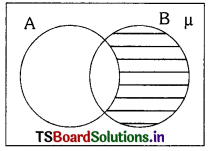
iii) Venn-diagram of A ∪ B is

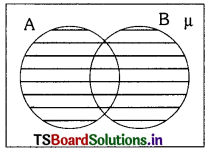
iv) Venn-diagram of A ∩ B is

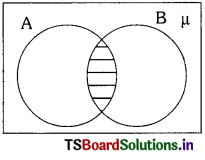
Question 21.
If A = (x : Y is a Natural number below 10}
B = {x : Y is an even number below 10}
C = {x : Y is an odd number below 10}then
find (i) A – B
(ii) A – C
(iii) B ∪ C
(iv) Also mention the Mutually disjoint sets among (i), (ii) and (iii).
Solution:
Given A = {1, 2, 3, 4, 5, 6, 7, 8, 9}
B = {2, 4, 6, 8}
C = {1, 3, 5, 7, 9}
i) A – B = {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 4, 6, 8}
= {1, 3, 5, 7, 9}

ii) A – C = {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 3, 5, 7, 9}
= {2, 4, 6, 8}

iii) B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8, 9}

iv) (i) and (ii) are disjoint sets because there is no element in common.
(ii) and (iii) are not disjoint sets because there are 2, 4, 6, 8 common elements.
(i) and (iii) are not disjoint sets because there are 1, 3, 5, 7, 9 common elements.

Question 22.
If A = {1, 4, 9, 16, 25, . . . } then write it in set builder form.
Solution:
A = {1, 4, 9, 16, 25, ……..}
= {1², 2², 3², 4², 5², . . . . }
= {x²/ x ∈ N}

Question 23.
If A = {x / x is a prime number and x < 20} then B = {x / 2x + 1, x ∈ w and x < 9} then Find
(i) A ∩ B
(ii) B ∩ A
(iii) A – B
(iv) B – A. What do you observe ?
Solution:
A = {x / x is a prime number and x < 20}
B = {2x + 1, x ∈ w and x < 9}
∴ A = {2, 3, 5, 7, 11, 13, 17, 19}
B = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
1) A ∩ B = {2, 3, 5, 7, 11, 13, 17, 19} ∩ (1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
= {3, 5, 7, 11, 13, 17, 19}

2) B ∩ A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19} ∩ {2, 3, 5, 7, 11, 13, 17, 19}
= {3, 5, 7, 11, 13, 17, 19}

3) A – B = {2, 3, 5, 7, 11, 13, 17, 19} – {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
= {2}

4) B – A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19} – {2, 3, 5, 7, 11, 13, 17, 19}
= {1, 9, 15}
Note : i) A ∩ B = B ∩ A
ii) A – B ≠ B – A