TS 10th Class Maths Solutions Chapter 8 Similar Triangles InText Questions

Students can practice TS Class 10 Maths Solutions Chapter 8 Similar Triangles InText Questions to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 8 Similar Triangles InText Questions

Do This

Question 1.
Fill in the blanks with similar / not similar. (AS₃) (Page No : 194)
i) All squares are …………..
Solution:
similar

ii) All equilateral triangles are …………….
Solution:
similar

iii) All isosceles triangles are ……………
Solution:
similar

iv) Two polygons with same number of sides are ……………. if their corresponding angles are equal and corresponding sides are equal.
Solution:
similar

v) Reduced and Enlarged photographs of an object are ……………
Solution:
similar

vi) Rhombus and squares are …………….. to each other.
Solution:
not similar

Question 2.
Write the True / False for the following statements. (AS₃) (Page No : 194)
i) Any two similar figures are congruent.
Solution:
False

ii) Any two congruent figures are similar.
Solution:
True

iii) Two polygons are similar if their corresponding angles are equal.
Solution:
False

Question 3.
Give two different examples of pair of (AS₃) (Page No : 194)
i) Similar figures
ii) Non-similar figures
Solution:
i) Similar figures :
a) Any two circles
b) Any two squares
c) Any two equilateral triangles

ii) Non – similar figures :
a) A square and a rhombus
b) A square and a rectangle

Question 4.
What value(s) of x will make DE//AB, in the given figure ?
AD = 8x + 9, CD = x + 3, (AS₁)
BE = 3x + 4, CE = x (Page No : 200) (A.P. Mar. ’16, ’15)

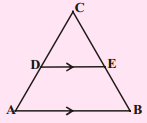
Solution:
Given : In ∆ABC, DE // AB
AD = 8x + 9, CD = x + 3,
BE = 3x + 4, CE = x
By Basic Proportional theorem,
If DE // AB then we should have
\(\frac{\mathrm{CD}}{\mathrm{DA}}\) = \(\frac{\mathrm{CE}}{\mathrm{EB}}\)
∴ \(\frac{x+3}{8 x+9}\) = \(\frac{x}{3 x+4}\)
⇒ (x + 3) (3x + 4) = x(8x + 9)
⇒ x(3x + 4) + 3(3x + 4) = 8x² + 9x
⇒ 3x² + 4x + 9x + 12 = 8x² + 9x
⇒ 8x² + 9x – 3x² – 4x – 9x – 12 = 0
⇒ 5x² – 4x – 12 = 0
⇒ 5x² – 10x + 6x – 12 = 0
⇒ 5x(x – 2) + 6(x – 2) = 0
⇒ (5x + 6) (x – 2) = 0
⇒ 5x + 6 = 0 (or) x – 2 = 0 – 6
⇒ x = \(\frac{-6}{5}\) (or) x = 2
∴ The value of x = 2 will make DE // AB.

Question 5.
In ∆ABC, DE // BC. AD = x, DB = x – 2, AE = x + 2 and EC = x – 1. Find the value of x. (AS₁) (Page No : 200)

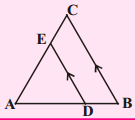
Solution:
Given : In ∆ABC, DE // BC
By Basic Proportionality theorem,
we have
\(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)
⇒ \(\frac{x}{x-2}\) = \(\frac{x+2}{x-1}\)
⇒ x(x – 1) = (x + 2) (x – 2)
⇒ x² – x = x² – 4
⇒ – x = – 4
∴ x = 4

Try This

Question 1.
E and F are points on the sides PQ and PR respectively of ∆PQR. For each of the fol-lowing, state whether. EF || QR or not ? (AS₂) (Page No : 197)
i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
Solution:

Hence, EF is not parallel to QR.

ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
Solution:
Here, \(\frac{\mathrm{PE}}{\mathrm{EQ}}\) = \(\frac{4}{4.5}\) = \(\frac{0.8}{0.9}\) = \(\frac{8}{9}\)
\(\frac{\mathrm{PE}}{\mathrm{RF}}\) = \(\frac{8}{9}\)
\(\frac{\mathrm{PE}}{\mathrm{EQ}}\) = \(\frac{\mathrm{PE}}{\mathrm{RF}}\)
∴ EF // QR
Hence, EF is parallel to QR.

iii) PQ = 1.28 cm, PR = 2.56 cm, PE =1.8 cm and PF = 3.6 cm
Solution:

Given, PQ = 1.28 cm, PE = 1.8 cm
⇒ EQ = PE – PQ = 1.8 – 1.28
⇒ EQ = 0.52 cm
Also, PR = 2.56 cm, PE = 3.6 cm
FR = PF – PR = 3.6 cm – 2.56 cm
FR = 1.04 cm
Now
\(\frac{\mathrm{PE}}{\mathrm{EQ}}\) = \(\frac{1.8}{0.52}\) = \(\frac{0.9}{0.26}\)
\(\frac{\mathrm{PF}}{\mathrm{FR}}\) = \(\frac{3.6}{1.04}\) = \(\frac{0.9}{0.26}\)
\(\frac{\mathrm{PE}}{\mathrm{EQ}}\) = \(\frac{\mathrm{PF}}{\mathrm{FR}}\)
∴ EF // QR (By converse of Basic proportionality theorem)
Hence, EF is parallel to QR.

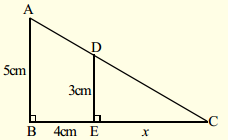
Question 2.
In the following figures DE || BC.
i) Find EC (AS₁) (Page No : 198)

Solution:
\(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)
⇒ \(\frac{1.5}{3}\) = \(\frac{\mathrm{1}}{\mathrm{EC}}\)
∴ EC = \(\frac{3}{1.5}\) = 2 cm

ii) Find AD

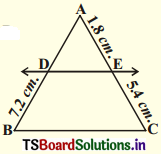
Solution:
\(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)
⇒ \(\frac{\mathrm{AD}}{7.2}\) = \(\frac{1.8}{5.4}\)
∴ AD = \(\frac{1.8}{5.4}\) × 7.2 = latex]\frac{12.96}{5.4}[/latex] = 2.4 cm.

Think – Discuss

Question 1.
Can you give some more examples from your daily life where scale factor is used ? (AS₃) (Page No : 192)
Solution:
Scale factor is used in drawing maps, designing machines and in sculpture, etc.

Question 2.
Can you say that a square and a rhombus are similar ? Discuss with your friends. Write why the conditions are not sufficient. (AS₂) (Page No : 193)
Solution:
A square ☐ ABCD and a rhombus
▱ PQRS are not similar.
Though the ratio of their corresponding sides are equal, the corresponding angles are not equal.

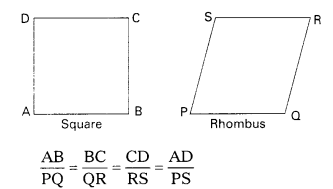
But ∠A ≠ ∠P; ∠B ≠ ∠Q, ∠C ≠ ∠R; ∠D ≠ ∠S

Try This

Question 1.
Are the triangles formed in each figure similar ? If so, name the criterion of similarity. Write the similarity relation in symbolic form. (AS₃) (Page No : 207)
i)

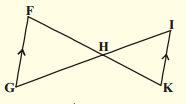
!! ∠G = ∠I alt.int.angles for the ∠F = ∠K parallel lines GF // KI
Solution:
∆GHF and ∆lKH are similar by ASA similarity rule.
∆GHF ~ ∆lKH

ii)

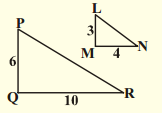
Solution:
∆PQR and ∆LMN
\(\frac{\mathrm{LM}}{\mathrm{PQ}}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
\(\frac{\mathrm{MN}}{\mathrm{QR}}\) = \(\frac{4}{10}\) = \(\frac{2}{5}\)
\(\frac{\mathrm{LM}}{\mathrm{PQ}}\) ≠ \(\frac{\mathrm{MN}}{\mathrm{QR}}\)
∆PQR is not similar to ∆LMN

iii)

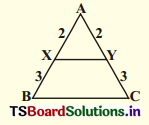
Solution:
∠A = ∠A (Common)
\(\frac{\mathrm{AX}}{\mathrm{XB}}\) = \(\frac{2}{3}\) ; \(\frac{\mathrm{AY}}{\mathrm{YC}}\) = \(\frac{2}{3}\)
\(\frac{\mathrm{AX}}{\mathrm{XB}}\) = \(\frac{\mathrm{AY}}{\mathrm{YC}}\)
∆ABC and ∆AXY are similar by SAS similarity condition.
∆ABC ~ ∆AXY

iv)

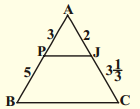
Solution:
\(\frac{\mathrm{AP}}{\mathrm{PB}}\) = \(\frac{3}{5}\) ; \(\frac{\mathrm{AJ}}{\mathrm{JC}}\) = \(\frac{2}{3 \frac{1}{3}}\)
= \(\frac{2}{10 / 3}=\frac{2 \times 3}{10}=\frac{6}{10}=\frac{3}{5}\)
\(\frac{\mathrm{AP}}{\mathrm{PB}}\) = \(\frac{\mathrm{AJ}}{\mathrm{JC}}\)
∆ABC and ∆APJ are similar.

v)

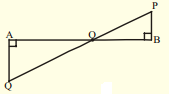
Solution:
∆AOQ and ∆BOP are similar by AA criterion. ∆AOQ ~ ∆BOP

vi)

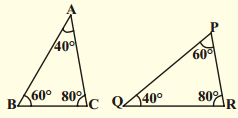
Solution:
∆ABC and ∆PQR are similar AAA Similarity condition
∆ABC ~ ∆QPR

vii)

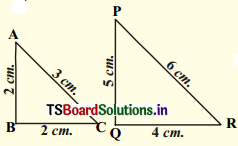
Solution:

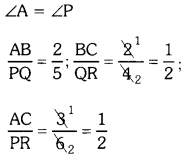
∆ABC and ∆PQR are not similar.

viii)

Solution:
∆ABC and ∆PQR are not similar.

Question 2.
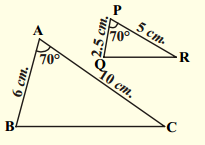
If pairs of the triangles are similar and then find the value of x. (AS₁, AS₂) (Page No : 207)
i)

Solution:
Gwen : In ∆PQR and ∆LTS
∠Q = ∠T
∠R = ∠S
∴ ∠P = ∠T
(by angle sum property of triangles)
Hence, ∆PQR ~ ∆LTS [∵ AAA]
Then \(\frac{\mathrm{PQ}}{\mathrm{LT}}\) = \(\frac{\mathrm{QR}}{\mathrm{TS}}\) = \(\frac{\mathrm{PR}}{\mathrm{LS}}\)
∴ \(\frac{3}{4.5}\) = \(\frac{5}{\mathrm{x}}\)
3x = 5 × 4.5
⇒ x = \(\frac{5 \times 4.5}{3}\) = 5 × 1.5 = 7.5

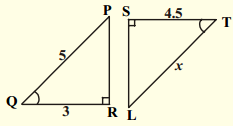
ii)

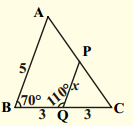
Solution:
Given : In ∆ABC and ∆PQC
∠B = ∠Q
[∵ ∠PQC = 180° – 110° = 70° – linear pair of angles]
∠C = ∠C [∵ common]
∴ ∠A = ∠P
[ ∵ Angle sum property of triangles]
∴ ∆ABC ~ ∆PQC (by AAA similarity condition).
Then the ratio of their corresponding sides are equal.
∴ \(\frac{\mathrm{AB}}{\mathrm{PQ}}\) = \(\frac{\mathrm{BC}}{\mathrm{QC}}\) = \(\frac{\mathrm{AC}}{\mathrm{PC}}\)
\(\frac{5}{\mathrm{x}}\) = \(\frac{6}{3}\)
⇒ x = \(\frac{5 \times 3}{6}\) = 2.5

ii)

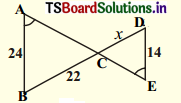
Solution:
Given : In ∆ABC and ∆ECD
∠A = ∠E
∠ACB = ∠ECD [∵ Vertically opposite angles]
∴ ∠B = ∠D [∵ Angles um property of triangles]
∴ ∆ABC ~ ∆ECD by AAA rule.
Hence, \(\frac{\mathrm{AB}}{\mathrm{ED}}\) = \(\frac{\mathrm{BC}}{\mathrm{CD}}\) = \(\frac{\mathrm{AC}}{\mathrm{EC}}\)
\(\frac{24}{14}\) = \(\frac{22}{\mathrm{x}}\)
⇒ x = \(\frac{22 \times 14}{24}\) = 12.83

iv)

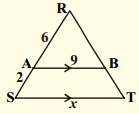
Solution:
Given : In ∆RAB and ∆RST
∠R = ∠R (common)
∠A = ∠S and ∠B = ∠T [∵ Pair of corresponding angles for AB // ST]
∴ ∆RAB ~ ∆RST [∵ AAA similarity]
∴ \(\frac{\mathrm{RA}}{\mathrm{RS}}\) = \(\frac{\mathrm{AB}}{\mathrm{ST}}\) = \(\frac{\mathrm{RB}}{\mathrm{RT}}\)
\(\frac{6}{8}\) = \(\frac{9}{\mathrm{x}}\)
[from the figure, RS = 6 + 2 = 8]
⇒ x = \(\frac{9 \times 8}{6}\) = 12

v)

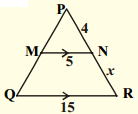
Solution:
Given: In ∆PQR and ∆PMN
∠P = ∠P (∵ Common)
∠Q = ∠M
(∵ Pair of corresponding angles for MN // OR]
∠R = ∠N
∴ ∆PQR ~ ∆PMN [∵ AAA similarity]
∴ \(\frac{\mathrm{PQ}}{\mathrm{PM}}\) = \(\frac{\mathrm{QR}}{\mathrm{MN}}\) = \(\frac{\mathrm{PR}}{\mathrm{PN}}\)
\(\frac{15}{5}\) = \(\frac{4+x}{4}\)
[From the figure, PR = 4 + x]
⇒ 3 × 4 = 4 + x
∴ x = 12 – 4 = 8

vi)

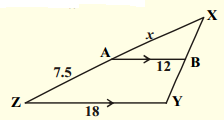
Solution:
Given : In ∆XYZ and ∆XBA
∠X = ∠X (∵ Common)
∠B = ∠Y [∵ Pair of corresponding angles for AB // ZY]
∴ ∆XYZ ~ ∆XBA [∵ AAA similarity]
Hence, \(\frac{\mathrm{XY}}{\mathrm{XB}}\) = \(\frac{\mathrm{YZ}}{\mathrm{BA}}\) = \(\frac{\mathrm{XZ}}{\mathrm{XA}}\)
\(\frac{18}{12}\) = \(\frac{7.5+x}{x}\)
[from the figure, XZ = 7.5 + X]
\(\frac{3}{2}\) = \(\frac{7.5+x}{x}\)
3x = 15 + 2x
3x – 2x = 15
x = 15

vii)

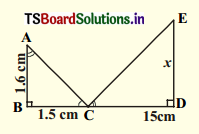
Solution:
Given : With the given conditions, we can’t find the value of x.
Note: If it is given that ∠A = ∠E then we can say that
∆ABC ~ ∆ EDC (by A.A.A rule)
and \(\frac{\mathrm{AB}}{\mathrm{ED}}\) = \(\frac{\mathrm{BC}}{\mathrm{CD}}\) = \(\frac{\mathrm{AC}}{\mathrm{EC}}\)
⇒ \(\frac{1.6}{\mathrm{x}}\) = \(\frac{1.5}{15}\)
⇒ x = \(\frac{1.6 \times 15}{1.5}\) = 16

viii)

Solution:
Given : Data not sufficient.

Think – Discuss

Question 1.
Discuss with your friends that In what way similarity of triangles is different from similarity of other polygons? (AS₃) (Page No. 203)
Answer:
In two triangles if the corresponding angles are equal then they are similar, whereas in two polygons if the corresponding angles are equal, they may not be similar.
i.e., In triangles,
(Pairs of corresponding angles are equal) ⇔ (Ratio of corresponding sides are equal).
But this is not so with respect to polygons.

Do This

Question 1.
In ∆ACB, ∠C = 90° and CD ⊥ AB. Prove that \(\frac{\mathrm{BC}^2}{\mathrm{AC}^2}\) = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) (AS₂) (Page No. 218)

Solution:
Proof : ∆ADC and ∆CDB are similar
∴ \(\frac{\Delta \mathrm{ADC}}{\Delta \mathrm{CDB}}\) = \(\frac{\frac{1}{2} \times \mathrm{AD} \times \mathrm{DC}}{\frac{1}{2} \times \mathrm{BD} \times \mathrm{DC}}\) = \(\frac{\mathrm{AD}}{\mathrm{BD}}\)
⇒ \(\frac{\Delta \mathrm{CDB}}{\Delta \mathrm{ADC}}\) = \(\frac{\mathrm{BC}}{\mathrm{AD}}\) ……………. (1)
(or) \(\frac{\Delta \mathrm{CDB}}{\Delta \mathrm{ADC}}\) = \(\frac{\mathrm{BC}^2}{\mathrm{AC}^2}\) ………….. (2)
[Ratio of areas of similar triangles is equal to the ratio of squares of their corresponding sides.]
From (1) and (2),
\(\frac{\mathrm{BC}}{\mathrm{AD}}\) = \(\frac{\mathrm{BC}^2}{\mathrm{AC}^2}\) (Q.E.D)

Question 2.
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street. (AS₄) (Page No : 218)
Solution:

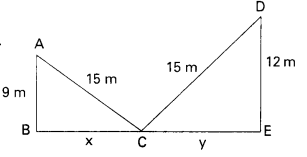
Let A and D be the windows on the either sides of the street.
From Pythagoras theorem,
AC² = AB² + BC²
15² = 9² + BC²
BC² = 225 – 81
BC = \(\sqrt{144}\) = 12 ……………… (1)
Also,
CD² = DE² + CE²
15² = 12² + CE²
CE² = 225 – 144
CE = \(\sqrt{81}\) = 9
∴ BE = BC + CE
= 12 + 9 = 21
∴ Width of the street = 21 m

Question 3.
In the given fig. if AD ⊥ BC, prove that AB² + CD² = BD² + AC². (AS₂) (Page No : 219)

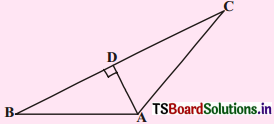
Solution:
Given : In ∆ABC, AD ⊥ BC
R.T.P. : AB² + CD² = BD² + AC²
Proof : ∆ABD is a right angled triangle.
AB² – BD² = AD² …………….. (1)
∆ACD is a right angle triangle.
AC² – CD² = AD² ……………. (2)
From (1) and (2)
AB² – BD² = AC² – CD²
AB² + CD² = BD² + AC²

Think – Discuss

Question 1.
For a right angled triangle with integer sides atleast one of its measurements must be an even number. Why ? Discuss with your friends and teachers. (AS₃) (Page No : 215)
Solution:
Given : A right triangle with integer sides.
To discuss : At least one measurement must be an even number.
Case – (i) : If the measurements of the sides are 3, 4, 5 – Primitive Pythagorean tripplet then one measurement ‘4’ is even and the given statement is true.

Case – (ii) : If the measurements are an integer multiple of primitive i.e., 3n, 4n and 5n then also ‘4n’ is even [irrespective of n-even / odd]
∴ Given statement is true.

Case – (iii) : If one measurement ‘n’ is odd, then n, \(\frac{\mathrm{n}^2+1}{2}\) and \(\frac{\mathrm{n}^2-1}{2}\) are the measurements of the sides, then also \frac{\mathrm{n}^2-1}{2} is even. [∵ n = 2k + 1]
n² = (2k + 1)² = 4k² + 4k + 1
n² – 1 = 4k² + 4k + 1 – 1
= 4(k² + k)
= 2(2k² + 2k) [even]
∴ In any case the given statement is true.