TS 10th Class Maths Important Questions Chapter 8 Similar Triangles

These TS 10th Class Maths Chapter Wise Important Questions Chapter 8 Similar Triangles given here will help you to solve different types of questions.

TS 10th Class Maths Important Questions Chapter 8 Similar Triangles

Previous Exams Questions

Question 1.
Construct a triangle of sides 4.2 cm, 5.1 cm and 6 cm. Then construct a triangle similar to it, whose sides are \(\frac{2}{3}\) of corresponding sides of the first triangle. (A.P. Mar. ’15)
Solution:

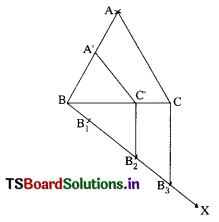
1. Draw a triangle ABC, with sides AB = 4.2 cm, BC = 5.1 cm, CA = 6 cm.
2. Draw a ray BX making an acute angle with BC on the side opposite to vertex A.
3. Locate 3 points B₁, B₂, B₃ on BX so that BB₁ = B₁B₂ = B₂B₃
4. Join B₃, C and draw a line through B₂ parallel to B₃C intersecting BC and C¹.
5. Draw a line through C¹ parallel to CA intersect AB at A¹.
6. ∆A¹BC¹ is required triangle.

Question 2.
Is a square similar to a rectangle ? Justify your answer. (A.P. Mar.’15)
Solution:
In a square and rectangle, the corresponding angles are equal. But the corresponding sides are not proportional.

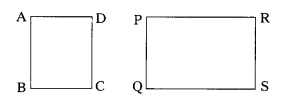
∴ A square and a rectangle are not similar.

Question 3.
In a ∆DEF, A, B and C are mid points of EF, FD and DE respectively. If the area of ∆DEF is 14.4 cm² then find the area of ∆ABC. (T.S. Mar. ’15)
Solution:
Area of ∆ABC = 1/4 of area of ∆DEF
= 1/4 (14.4) = 3.6 cm²

Question 4.
Observe the below diagram and find the values of x and y. (T.S. Mar. ’15)

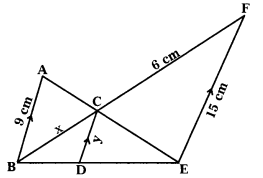
Solution:
∆ABC ~ AEFC
\(\frac{\mathrm{x}}{6}\) = \(\frac{9}{15}\)
x = \(\frac{9 \times 6}{15}\) = \(\frac{18}{5}\) = 3.6 cm.
∆BDC ~ ABEF
\(\frac{\mathrm{x}}{9.6}\) = \(\frac{\mathrm{y}}{15}\)
⇒ y = \(\frac{3.6 \times 15}{9.6}\) = \(\frac{45}{8}\) = 5.625 cm

Question 5.
Observe the figure given below in ∆FQR if XY // PQ, \(\frac{\mathrm{PX}}{\mathrm{XR}}\) = \(\frac{5}{3}\) and QR = 7.2. Then find the length of RY. (T.S. Mar. ’15)

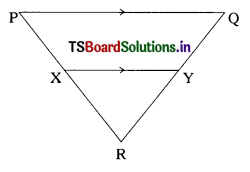
Solution:
XY || PQ
⇒ \(\frac{\mathrm{PX}}{\mathrm{XR}}\) = \(\frac{\mathrm{QY}}{\mathrm{YR}}\)
⇒ \(\frac{5}{3}\) + 1 = \(\frac{\mathrm{QY}}{\mathrm{RY}}\) + 1
⇒ \(\frac{8}{3}\) = \(\frac{\mathrm{QR}}{\mathrm{RY}}\)
⇒ RY = 7.2 × \(\frac{3}{8}\) = 2.7 cm.

Question 6.
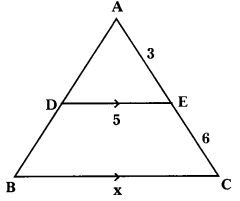
Find the value of ‘x’ in the given figure where ∆ ABC ~ ∆ ADE. (T.S. Mar. ’15)

Solution:
∆ABC ~ ∆ADE
∴ \(\frac{\mathrm{AB}}{\mathrm{AD}}\) = \(\frac{\mathrm{BC}}{\mathrm{DE}}\) = \(\frac{\mathrm{AC}}{\mathrm{AE}}\) ;
BC = x, DE = 5, AE = 3, AC = 9
By substituting \(\frac{\mathrm{BC}}{\mathrm{DE}}\) = \(\frac{\mathrm{AC}}{\mathrm{AE}}\)
∴ \(\frac{\mathrm{x}}{5}\) = \(\frac{9}{3}\) ⇒ x = \(\frac{9 \times 5}{3}\) = 15
∴ x = 15 cm

Question 7.
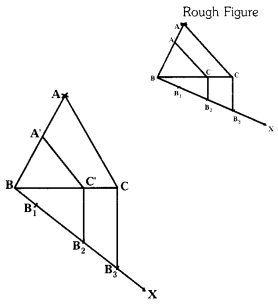
Construct a triangle of sides 5 cm, 6 cm, and 7 cm then construct a triangle similar to it, whose sides are \(\frac{2}{3}\) of the corresponding sides of the triangle. (T.S. Mar. ’15)

Solution:
Construction steps :

1. Draw a triangle ∆ABC with sides AB = 5 cm, BC = 6 cm and CA = 7 cm.
2. Draw a ray \(\overrightarrow{\mathrm{BX}}\) making an acute angle with BC on the side opposite to vertex A.
3. Locate 3 points B₁, B₂, B₃ on BX. So that BB₁ = B₁B₂ = B₂B₃.
4. Join B₃, C and draw a line through B₂ parallel to B₃ C intersecting BC at C’.
5. Draw a line through C’ parallel to CA intersect AB at A’.
6. ∆A’B’C’ is required triangle.

Additional Questions

Question 1.
In a ∆ ABC, DE || BC and AD = \(\frac{1}{3}\) BD. If BC = 5.6 cm, find DE.
Solution:
Given DE || BC, AD = \(\frac{1}{3}\) BD, BC = 5.6 cm

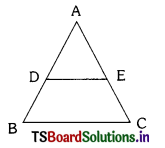
AD = \(\frac{1}{3}\) BD ⇒ BD = 3 AD …………… (1)
From similar triangles, ABC and ADE
We have \(\frac{\mathrm{AD}}{\mathrm{AB}}\) = \(\frac{\mathrm{DE}}{\mathrm{BC}}\)
⇒ \(\frac{\mathrm{AD}}{\mathrm{AD}+\mathrm{DB}}\) = \(\frac{\mathrm{DE}}{5.6}\)
⇒ \(\frac{\mathrm{AD}}{\mathrm{AD}+3\mathrm{DB}}=\) = \(\frac{\mathrm{DE}}{5.6}\)
[∵ from (1) DB = BD = 3AD]
⇒ \(\frac{\mathrm{AD}}{4 \mathrm{AD}}\) = \(\frac{\mathrm{DE}}{5.6}\)
⇒ \(\frac{1}{4}\) = \(\frac{\mathrm{DE}}{5.6}\)
⇒ DE = \(\frac{5.6}}{4\)
∴ DE = 1.4 cm

Question 2.
In the adjacent figure ∆ABC ~ ∆AHK. If AK = 8 cm, BC = 4.5 cm and HK = 9 cm find AC.
Solution:

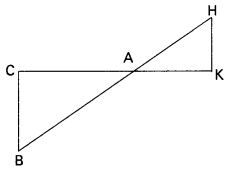
Given AK = 8 cm, BC 4.5 cm, HK from similar ∆les, ABC and AHK
We have \(\frac{\mathrm{AC}}{\mathrm{AK}}\) = \(\frac{\mathrm{BC}}{\mathrm{HK}}\)
AC = \(\frac{\mathrm{AK} \times \mathrm{BC}}{\mathrm{HK}}\)
= \(\frac{8 \times 4.5}{9}\)
= 8 × 0.5 = 4
∴ AC = 4 cm

Question 3.
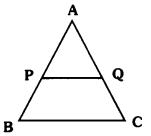
In the below given figure P and Q are points on the sides AB and AC respectively of ∆ABC such that AQ = 3 cm, QC = 5 cm and PQ || BC. Find the ratio of areas of ∆APQ and ∆ABC.

Solution:
Given AQ = 3 cm, QC = 5 cm and PQ || BC.
We know that by theorem,
Ratio of the areas of two similar triangles = Ratio of the squares of their corresponding sides
Now AC = AQ + QC = 3 + 5 = 8 cm
By Theorem \(\frac{\text { area of } \triangle \mathrm{APQ}}{\text { area of } \triangle \mathrm{ABC}}\) = \(\frac{(\mathrm{AQ})^2}{(\mathrm{AC})^2}\)
= \(\frac{3^2}{8^2}\)
= \(\frac{9}{64}\)
∴ Ratio of areas of ∆APQ and ∆ABC = 9 : 64

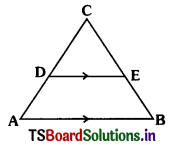
Question 4.
What value of (5) of x will make DE || AB, in the given figure ?
AD = 5x + 5, CD = x + 2 BE = 3x + 3, CE = x

Solution:
Given in ∆ ABC, DE || AB
AD = 5x + 5, CD = x + 2
BE = 3x + 3, CE = x
y Basic proportional theorem,
If DE || AB, then we have
\(\frac{\mathrm{CD}}{\mathrm{DA}}\) = \(\frac{\mathrm{CE}}{\mathrm{EB}}\)
⇒ \(\frac{x+2}{5 x+5}\) = \(\frac{x}{3 x+3}\)
⇒ (5x + 5) x = (x +2) (3x + 3)
⇒ 5x² + 5x = 3x² + 3x + 6x + 6
⇒ 5x² – 3x² + 5x – 3x – 6x – 6 = 0
⇒ 2x² – 4x – 6 = 0
⇒ 2x² – 6x + 2x – 6 = 0
⇒ 2x (x – 3) + 2(x – 3) = 0
⇒ (x – 3) + (2x + 2) = 0
⇒ x-3 = 0 or 2x + 2 = 0
⇒ x = 3 or 2x = -2
⇒ x = –\(\frac{2}{2}\) = -1
∴ The value of x = 3 will make DE || AB.

Question 5.
∆ABC ~ ∆PQR and their areas are respectively 81 cm² and 144 cm². If QR = 16cm then find BC.
Solution:
\(\frac{\text { area of } \triangle \mathrm{ABC}}{\text { area of } \triangle \mathrm{DEF}}\) = \(\left(\frac{\mathrm{BC}}{\mathrm{QR}}\right)^2\)
⇒ \(\frac{81}{144}\) = \(\left(\frac{\mathrm{BC}}{16}\right)^2\)
⇒ \(\frac{9}{12}\) = \(\frac{\mathrm{BC}}{16}\)
⇒ BC = \(\frac{9}{12}\) × 16 = \(\frac{144}{12}\) = 12
∴ BC = 12 cm.

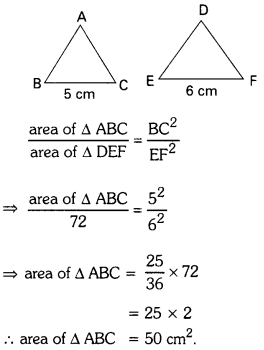
Question 6.
∆ABC ~ ∆DEF, BC = 5 cm, EF = 6 cm and area of ∆DEF = 72 cm². Determine the area of ∆ABC.
Solution:
Given ∆ABC ~ ∆DEF
and BC = 5cm, EF = 6cm
Area of ∆DEF = 72 cm²
We know that areas of two similar triangles are in the ratios of the squares of the corresponding sides.

Question 7.
A ladder 13m long reaches a window of building 12cm above the ground. Determine the distance of the foot of the ladder from the building.
Solution:
In ∆ ABC, B = ∠90°
⇒ AC² = AB² + BC² (By Pythagoras theorem)
Let AC = 13m, AB = 12m, BC = ?

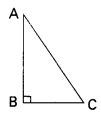
⇒ 13² = 12² + BC²
⇒ 169 = 144 + BC²
⇒ BC² = 169 – 144 = 25
⇒ BC = \(\sqrt{25}\) = 5m
Hence, the foot of the ladder from the building is at a distance of 5m.

Question 8.
The hypotenuse of a right angled triangle is 3 m more than twice of the shortest side. If the third side is 1 m less than the hypotenuse find the sides of the triangle.
Solution:

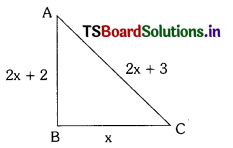
Let the shortest side = x m = BC
Then hypotenuse = 2x + 3 m = AC
The third side = (2x + 3) – 1
= (2x + 2) m = AB
By phythagoras theorem, we have
AC² = AB² + BC²
⇒ (2x + 3)² = (2x + 2)² + x²
⇒ 4x² + 9 + 12x = 4x² + 4 + 8x + x²
⇒ x² + 8x – 12x + 4 – 9 = 0
⇒ x² – 4x – 5 = 0
⇒ x² – 5x + x – 5 = 0
⇒ x (x – 5) + 1 (x – 5) = 0
⇒ (x – 5) (x + 1) = 0
⇒ x – 5 = 0 or x + 1 = 0
⇒ x = 5 or x = -1
But x can’t be negative x = 5
Hence, the sides of the triangle are
x, 2x + 3, 2x + 2
⇒ x = 5, 2 × 5 + 3, 2 × 5 + 2
= 5, 10 + 3, 10 + 2
i.e. 5, 13, 12

Question 9.
A ladder 25 m long reaches a window which is 15 m above the ground an one side of the road. Keeping its foot at the same point, the ladder is turned to other side of the road to reach a window 20 m high. Find the width of the road.
Solution:

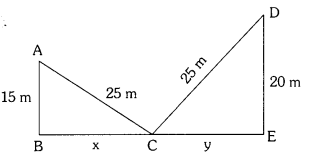
Let A and D be the windows on the either sides of the road
From phythagoras theorem,
AC² = AB² + BC²
⇒ 25² = 15² + BC²
⇒ BC² = 25² – 15² = 625 – 225 = 400
BC = \(\sqrt{400}\) = 20m ……………. (1)
Also CD² = CE² + DE²
25² = CE² + 20²
CE² = 25² – 20² = 625 – 400 = 225
CE = \(\sqrt{225}\) = 15m
Width of the road = BE = BC + CE
= 20 + 15
= 35 m

Question 10.
In the given figure below, If AD ⊥ BC, prove that AB² – BD² = AC² – CD².

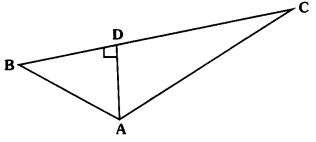
Solution:
Given in ∆ ABC, AD ⊥ BC
R.T.P : AB² – BD² = AC² – CD²
Proof : ∆ ABD is a right angled triangle.
We have AB² = AD² + BD² (By pythagaros theorem)
⇒ AB² – BD² = AD² ……………… (1)
∆ ACD is a right angled triangle.
We have AC² = AD² + CD²
⇒ AC² – CD² = AD² ………………. (2)
From (1) and (2), we have
AB² – BD² = AC² – CD²

Question 11.
In an equilateral triangle ABC, if AD is the altitude prove that 3AB² = 4 AD².
Solution:

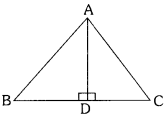
Given ABC is an equilateral triangle.
Here, AD ⊥ BC and AB = BC = CA
In triangles ADB and ADC
∠ADB = ∠ADC = 90°
Hypotenuse AB = Hypotenuse AC
AD is common
∴ ∆ ADB ≅ ∆ ADC
∴ BD = DC
In ∆ ADB, ∠ADB = 90°(By Phythagoras theorem)
AB² = AD² + BD²
= AD² + \(\left(\frac{\mathrm{BC}}{2}\right)^2\) (∵ BD = CD)
= AD² + \(\frac{\mathrm{BC}^2}{4}\)
AB² = \(\frac{4 A D^2+B C^2}{4}\)
⇒ 4AB² = 4AD² + BC²
⇒ 4AB² – BC² = 4AD²
⇒ 4AB² – AB² = 4AD² (∵ BC = AB)
∴ 3AB² = 4AD²

Question 12.
A wire attached to a vertical pole of height 15 m is 25 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut ?
Solution:

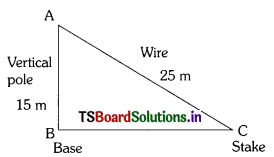
Let AB = Vertical pole
AC = Wire
B = Base
C = Stake
By Pythagoras theorem
AC² = AB² + BC²
25² = 15² + BC²
BC² = 25² – 15²
BC² = 62² – 225 = 400
BC = \(\sqrt{400}\) = 20 m
∴ The stake should be driven 20 m for the base of the pole so that the wire will be taut.

Question 13.
The larger of two complimentary angles is double the smaller. Find the angles.
Solution:
Let first complementary angle = x
Second complementary angle = 2x
Sum of the two complementary angles = 90°
∴ x + 2x = 90
3x = 90
x = \(\frac{90}{3}\)
x = 30
First angle = 30°, second angle = 60°.

Question 14.
In ∆ ABC, DE || BC and \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{3}{5}\). If AE = 2.1 cm, then find AC.
Solution:
Here, Given DE || BC and \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{3}{5}\)
AE = 2.1
∴ \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{CE}}\)
\(\frac{3}{5}\) = \(\frac{2.1}{\mathrm{CE}}\)

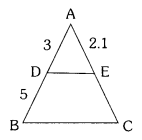
CE = \(\frac{5 \times 2.1}{3}\)
CE = \(\frac{10.5}{3}\) = 3.5
CE = 3.5
Then AC = AE + CE
AC = 2.1 + 3.5
AC = 5.6

Question 15.
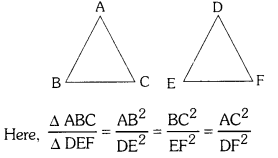
What can you say about the ratio of areas of two similar triangles ?
Solution:
The ratio of areas of two similar triangles is( equal to the ratio of the squares of their corresponding sides.
Here

Question 16.
Construct an isosceles triangle whose base is 8 cm and altitude is 4 cm. Then, draw another similar triangle whose side are 1 \(\frac{1}{2}\) times the corresponding sides of the isosceles triangle.
Solution:

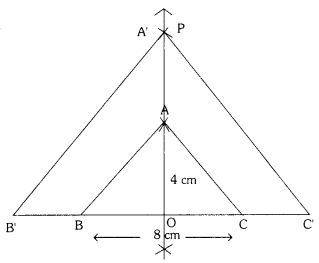
1. Draw a lines segment BC = 8 cm
2. Draw the perpendicular bisector PQ of BC intersecting BC at ‘O’
3. Mark a point ‘A’ on PQ such that \(\overline{\mathrm{OA}}\) = 4 cm
4. Join AB and AC to the isosceles triangle ABC
5. Extend BC on either side O’C’ = 1 \(\frac{1}{2}\) times; BC = 12 times.
6. Similarly extend OA So that OA’ = 1 \(\frac{1}{2}\) times A = \(\frac{12}{2}\) = 6
7. Join A’ B’ and A’ C’
8. Now A’ B’ C’ – The required triangle

Question 17.
Give two different examples of pair of 3 similar figures and non similar figures.
Solution:
Similar figures :

1. Any two circles
2. Any two squares

Non-similar figures :

1. A square and a rhombus
2. A square and a rectangle

Question 18.
∆ ABC ~ ∆ DEF and their areas are respectively 64 cm² and 121 cm². If EF = 15.4 cm then find BC.
Solution:
Given area of ∆ABC = 64 cm²
area of ∆DEF = 121 cm²
EF = 15.4 cm, BC = ?
We know that \(\frac{\text { area of } \triangle \mathrm{ABC}}{\text { area of } \triangle \mathrm{DEF}}\)=\(\frac{\mathrm{BC}^2}{\mathrm{EF}^2}\)
⇒ \(\frac{64}{121}\) = \(\frac{\mathrm{BC}^2}{(15.4)^2}\)
⇒ BC² = \(\frac{64}{121}\) × (15.4)²
= \(\frac{64}{121}\) × 15.4 × 15.4
BC² = 125.44
∴ BC = \(\sqrt{125.44}\) = 11.2 cm.

Question 19.
In D ABC, DE || BC and \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{3}{5}\) ; AC = 5.6 find AE.
Solution:

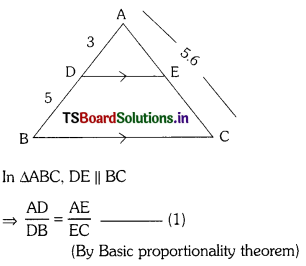
But \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{3}{5}\) , So \(\frac{\mathrm{AE}}{\mathrm{EC}}\) = \(\frac{3}{5}\)
given AC = 5.6
from (1) \(\frac{3}{5}\) = \(\frac{\mathrm{AE}}{\mathrm{AC – AE}}\)
\(\frac{3}{5}\) = \(\frac{\mathrm{AE}}{5.6-\mathrm{AE}}\) (By cross-multiplication)
5 AE = 3 (5.6 – AE)
5 AE = 3 × 5.6 – 3AE
5AE + 3 AE = 3 × 5.6
8AE = 16.8
AE = \(\frac{16.8}{8}\) = 2.1 cm

Question 20.
State and prove basic proportionality theorem.
Solution:
Preposition : If a line is drawn parallel to one side of the triangle to intersect the other sides in distinct points, then the other two sides are divided in the same ratio.

Given : A triangle ABC in which DE || BC and DE intersects AB in D and AC in E.
To Prove : \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)

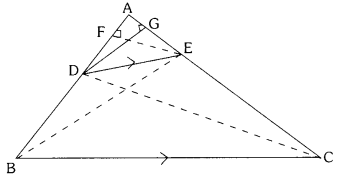
Construction : Join BE, CD and draw EF ⊥ AB. DG ⊥ AC.
Proof: In ∆ EAD and ∆ EDB, Here as EF ⊥ AB
therefore EF is the height for both of triangles EAD and EDB.
Now, Area of ∆ EAD = \(\frac{1}{2}\) (base × height)
= \(\frac{1}{2}\) × AD × EF
Area of EDB = \(\frac{1}{2}\) (base × height)
= \(\frac{1}{2}\) × DB × EF

∴ ∆ DBF, ECD are on the same base DE and between the same parallels DE || BC,
We have area of ∆DBE = area of ∆ECD
Hence (1) = (2)
i.e, \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\) (Q.E.D)

Question 21.
Construct a triangle of sides 4 cm, 5 cm and 6 cm then construct a triangle. Similar to it. Whose sides are \(\frac{2}{3}\) of the corresponding sides of the first triangle.
Solution:

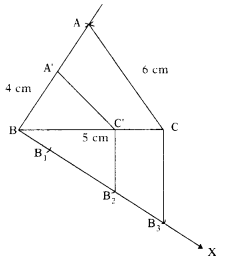
Steps of construction :

1. Draw ∆ ABC with AB = 4 cm, BC = 5 cm and CA = 6 cm.
2. Draw a Ray \(\overrightarrow{\mathrm{BX}}\) making an acute angle with BC on the side opposite to vertex A.
3. Mark three points B₁, B₂ and B₃ on \(\overrightarrow{\mathrm{BX}}\) Such that BB₁ = B₁B₂ = B₂B₃.
4. Join B₃, C.
5. Draw a line parallel B₃, C through B₂ meeting BA at A’.
6. ∆ A’ BC’ is required triangle.