TS 10th Class Maths Important Questions Chapter 10 Mensuration

These TS 10th Class Maths Chapter Wise Important Questions Chapter 10 Mensuration given here will help you to solve different types of questions.

TS 10th Class Maths Important Questions Chapter 10 Mensuration

Previous Exams Questions

Question 1.
Find the volume and total surface area of a hemisphere whose radius is 35 cm ?
Solution:
Radius of the hemisphere (r) = 35 cm.
Volume of the hemisphere = \(\frac{2}{3}\) πr³
= \(\frac{2}{3}\) × \(\frac{22}{7}\) × 35 × 35 × 35
= \(\frac{269500}{3}\) cm³ = 89833 \(\frac{1}{3}\) cm³
Total surface area = 3πr²
= 3 × \(\frac{22}{7}\) × 35 × 35 = 11550 cm²

Question 2.
The radius of a conical tent is 5m and its height is 12m. Calculate the length of the canvas used in making the tent if width of canvas is 2 cm.
Solution:
Radius of the conical tent (r) = 5 m.
Height of the tent (h) = 12 m.
Slant height of the cone
(l) = \(\sqrt{r^2+h^2}\)
= \(\sqrt{5^2+12^2}\)
= \(\sqrt{25+144}\) = \(169\) = 13 m
Now, surface area of the tent = πrl
= \(\frac{22}{7}\) × 5 × 13 = \(\frac{1430}{7}\) m
Area of the canvas used = \(\frac{1430}{7}\) m
It is given that the width of the canvas = 2 m
Length of the canvas used = \(\frac{\text { Area }}{\text { Width }}\)
= \(\frac{1430}{7}\) × \(\frac{1}{2}\) = 102.14 m

Question 3.
If a cylinder and cone are of the same radius and height, then how many cones full of milk can fill the cylinder ? Answer with reasons. (Mar. ’15 (T.S)
Solution:
Volume of the cylinder is three times to the volume of the cone if they have same radius and height.

Question 4.
A medicine capsule is in the shape of a cylinder with two hemispheres stock to each of its ends. If the length of cylinder) part is 14mm and the diameter of hemi-sphere is 6 mm, then find the volume of medicine capsule. (Mar. ’15 (T.S)
Solution:
Volume of the capsule.

= volume of the cylinder + 2x volume of the hemisphere
= πr²h + 2 × (\(\frac{2}{3}\) πr³)
= \(\frac{22}{7}\) × 3² × 14 + \(\frac{4}{3}\) × \(\frac{22}{7}\) × 3²
= \(\frac{22}{7}\) × 16
= 16π cubic millimetre.

Question 5.
State the relation between r and l (slant height) of a cone.
Solution:
Slant height (l) = \(\sqrt{r^2+h^2}\)

Question 6.
The radius of a spherical balloon in creases from 7 cm to 14 cm as air is pumped into it. Find the ratio of volumes of balloon before and after pumping thef air. (Mar. ’15 (T.S.))
Solution:
Radius of radius = r₁ : r₂ = 7 : 14 = 1 : 2
Ratio of volumes = r₁³ : r₂³ = 1³ : 2³ = 1 : 8

Question 7.
A conical solid block is exactly fitted inside the cubical box of side ‘a’ then the volume of conical solid block is \(\frac{4}{3}\)πa³. Is this statement true. Justify. (Mar. ’16 (T.S))
Solution:
The cone is exactly fitted inside the cubical box.

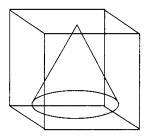
So height of cone = a = side of cube a
Radius of cone = \(\frac{\mathrm{a}}{2}\)
Volume of cone = \(\frac{1}{3}\)πr² h
= \(\frac{1}{3}\) . π . \(\left(\frac{\mathrm{a}}{2}\right)^2\) . a = \(\frac{1}{3}\) . π . \(\frac{\mathrm{a}^2}{4}\) . a
= \(\frac{1}{3} \frac{\pi a^3}{4}\) = \(\frac{1}{12}\) πa³
But to say \(\frac{4}{3}\) πa³ is not correct.

Question 8.
If the surface area of a hemisphere is ‘S’ then express ‘r’ interms of ‘s’. (Mar. ’16 (T.S))
Solution:
The surface area of a hemisphere = 2πr² = S
⇒ r² = \(\frac{S}{2 \pi}\)
∴ r = \(\sqrt{\frac{5}{2 \pi}}\)

Question 9.
Find the volume and surface area of a sphere of radius 42 cm.
Solution:
Radius of the sphere (r) = 42 cm
Curved surface area (A) = 4πr²
= 4 × \(\frac{22}{7}\) × 42 × 42 = 22,176 cm²
Volume of sphere V = \(\frac{4}{3}\) πr²
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × 42 × 42 × 42
= 3,10,464 cm²

Question 10.
A solid metallic ball of volume 64 cm3 is melted and made into a solid cube. Find the side of solid cube. (Mar. ’16 (T.S))
Solution:
Volume of solid metal = volume of cube
= 64 cm³
∴ Volume of cube = s³ = 64 cm
S = \(\sqrt[3]{64}\) = 4 cm
So side of the cube = 4 cm

Question 11.
DWACRA is supplied cuboidal shaped wax block with measurements 88 cm x 42 cm x 35 cm. From this how many number of cylinderical candles of 2.8 cm diametre and 8 cm of height can be prepared ? (Mar. ’16 (T.S))
Solution:
Shape of wax block = cuboid
Its length (l) = 88 cm
breath (b) =42 cm
height (h) = 35 cm
Then the volume of wax present in block
= lbh = 88 × 42 × 35 cm³ ………….. (1)
Shape of candle = cylinder
Diameter of candle = (d) = 2.8 cm
⇒ radius = r = \(\frac{2.8}{2}\) = 1.4 cm
height (h) = 8 cm
Volume of wax required to make one candle
V = πr²h
= \(\frac{22}{7}\) × 1.4 × 1.4 × 8 cm³
∴ Total number of candles that can be
Total volume of block made = \(\frac{\text { Total volume of block }}{\text { Volume of each candle }}\)
= \(\frac{88 \times 42 \times 35}{\frac{22}{7} \times 1.4 \times 1.4 \times 8}\) = 2625
So, 2625 candles can be made with given measurements.

Additional Questions

Question 1.
A company wants to manufacture 500 hemi-spherical basins from a copper sheet. If the radius of basin is 14 cm, find the area of copper sheet to manufacture the above hemi-spherical basins.
Solution:
Radius of the hemi-spherical basin = r = 14 cm
Surface area of hemi-spherical basin = 2πr²
= 2 × \(\frac{22}{7}\) × 14 × 14
= 1232 cm²
Hence, area of the copper sheet required for one basin = 1232 cm²
∴ Total area of copper sheet required for 500 basins
= 1232 × 500
= 616000 cm²
= 61.6 m²

Question 2.
A toy is in the form of right circular cone whose base radius 5 cm and height is 12cm. Find the area of sheet required to make 10 such toys.
Solution:
Radius of the toy = r = 5 cm
Height of the toy = h = 12 cm
Slant height of the toy = l = \(\sqrt{r^2+h^2}\)
= \(\sqrt{5^2+12^2}\)
= \(\sqrt{25+144}\)
= \(\sqrt{169}\)
= 13 cm
Lateral surface area of the toy = πrl
L.S.A = \(\frac{22}{7}\) × 5 × 13 = 204.28 cm²
∴ Area of the sheet required for 10 caps
= 10 204.28 = 2041.8 cm²

Question 3.
The shape of solid iron rod is a cylindrical. Its height is 20cm and base diameter is 14 cm. Then find the total volume of 60 such rods.
Solution:
Diameter of the cylinder = d = 14 cm
∴ Radius of the base = r = \(\frac{\mathrm{d}}{2}\) = \(\frac{14}{2}\) = 7 cm
Height of the cylinder = h = 20 cm.
Volume of the cylinder = v = πr²h
= \(\frac{22}{7}\) × 7 × 7 × 20
= 3.080 cm³
∴ Total volume of 60 rods = 60 × 3080
= 1,84,800 cm³

Question 4.
A heap of rice is in the form of a cone of diameter 10 m and height 12m. Find its volume. How much Canvas cloth is required to cover the heap ?
Solution:
Diameter of the heap = d = 10 m
∴ Radius = r = \(\frac{\mathrm{d}}{2}\) = \(\frac{10}{2}\) = 5 m
Height of the cone = h = 12 cm
Slant height = l = \(\sqrt{r^2+h^2}\)
= \(\sqrt{5^2+12^2}\)
= \(\sqrt{25+144}\)
= \(\sqrt{169}\)
= 13 cm
Volume of the heap of rice = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 5 × 5 × 12
= 314.29 m³
Canvas cloth required to cover the cap = surface area of the conical heap = πrl
= \(\frac{22}{7}\) × 5 × 13
= 204.29 m²

Question 5.
The curved surface area of a cone is 5170 cm² and its diameter is 84 cm. What is its slant height ?
Solution:
Diameter of the base of the cone = d = 84 cm
∴ Radius of the base = r = \(\frac{\mathrm{d}}{2}\) = \(\frac{84}{2}\) =42 cm
Curved surface area of the cone = πrl
By problem, πrl = 5170
\(\frac{22}{7}\) × 42 × l = 5170
⇒ l = \(\frac{5170 \times 7}{22 \times 42}\) = 39.16cm.
Hence, the slant height of the cone = 39.16 cm.

Question 6.
A cone of height 32 cm and radius 8 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere.
Solution:
Given Height of the cone = h = 32 cm.
radius of the cone = r = 8 cm.
Let R = Radius of the sphere.
Since cone resphaes in the form of a sphere Volume of the cone = volume of the sphere
⇒ \(\frac{1}{3}\) πr²h = \(\frac{4}{3}\) πR³
⇒ \(\frac{1}{3}\) × \(\frac{22}{7}\) × 8 × 8 × 32 = \(\frac{4}{3}\) × \(\frac{22}{7}\) × R³
⇒ 8 × 8 × 8 = R³
⇒ R³ = 8³
⇒ R = 8
Hence the radius of the sphere = R = 8 cm.

Question 7.
A metallic sphere of radius 4.9 cm is melted and recast in to the shape of a cylinder of radius 7 cm. Find the height of the cylinder.
Solution:
Let height of cylinder = h
Given radius of sphere = R = 4.9 cm
and Radius of cylinder = r = 7 cm
since sphere is melted in to the shape of a cylinder.
volume of the sphere = volume of the cylinder
⇒ \(\frac{4}{3}\) πR³ = πr²h
⇒ \(\frac{4}{3}\) × \(\frac{22}{7}\) × (4.9)³ = \(\frac{22}{7}\) × 7² × h
⇒ h = \(\frac{4}{3}\) x \(\frac{4.9 \times 4.9 \times 4.9}{7 \times 7}\)
h = 3.2 cm.
Hence the height of the cylinder = h = 3.20 cm

Question 8.
The rain water from a roof of 33m × 30m drains into a cylindrical vessel having diameter of base 4m and height 4.2m. If the vessel is just full, find the rain fall in cm.
Solution:
Dimensions of the roof = 33m × 30m
Diameter of cylindrical vessel = d = 4m
∴ Radius = r = \(\frac{\mathrm{d}}{2}\) = \(\frac{4}{2}\) = 2m
and height of vessel = h = 4.2 m. :
Let H = height of the rain fall
Now, volume of the rain fall = volume of the drained water in the cylindrical vessel
33 × 30 × H = πr²h
⇒ 33 × 30 × H = \(\frac{22}{7}\) × 2 × 2 × 4.2
⇒ H = \(\frac{22}{7}\) × \(\frac{2 \times 2 \times 4.2}{33 \times 30}\)
= 0.053 cm
H = 5.3 cm
∴ Rain fall = 5.3 cm

Question 9.
The radii of the internal and external surfaces of a hollow spherical shell are 2 cm and 4 cm respectively. If it is melted and: recast in to a solid cylinder of radius 2\(\sqrt{2}\) cm. find the height of the cylinder.
Solution:
Given radii of the hollow spherical shell = 2 cm and 4 cm
Let r₁ = 4 cm, r₂ = 2 cm and h = height solid! cylinder and Radius of solid cylinder = r =1
2\(\sqrt{2}\) cm. since hollow spherical shell melt and recast in to solid cylinder.
∴ volume of the follow spherical shell = volume of the solid cylinder
⇒ \(\frac{4 \pi}{3}\) (r₁³ – r₂³) = π – r²h
⇒ \(\frac{4}{3}\) (r₁³ – r₂³) = r²h
⇒ \(\frac{4}{3}\) (4³ – 2³) = (2\(\sqrt{2}\))²h
⇒ \(\frac{4}{3}\) (64 – 8) = 4 × 2 × h
⇒ \(\frac{4}{3}\) × 56 = 8 × h
⇒ h = \(\frac{4}{3}\) × \(\frac{56}{8}\) = \(\frac{28}{3}\) cm
∴ Height of the cylinder = h = \(\frac{28}{3}\) cm

Question 10.
A cylindrical bucket, 36 cm high and with radius of base 16 cm is filled with rice. This bucket is emptied out on the ground and a conical heap of rice is formed. If the height of the comical heap is 27 cm. find the radius d slant height of the heap.
Solution:
Given height of cylindrical bucket = 36 cm = h
and radius = 16 cm = r
Let height of conical heap = 27cm = H
and Radius of conical heap = R
slant height of the heap = I
Since the rice is carried and emptied by cylindrical bucket to form a conical heap,
Volume of cylindrical bucket = volume of conical heap.

Hence, Radius of heap = R = 32 cm
and slant height of the heap = l = 41.86 m

Question 11.
Find the total surface area of a hemi-sphere of radius 2.8 cm.
Solution:
Given radius of hemi-sphere = 2.8 cm
= 3 × \(\frac{22}{7}\) × (2.8)²
= 3 × \(\frac{22}{7}\) × 2.8 × 2.8
= 73.92 cm²

Question 12.
A cone of height 16 cm and radius of base 4 cm is made up modeling clay. A child u9 reshapes it into a sphere find the radius of the sphere.
Solution:
Given height of the cone = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) π × (4)² × 16
= \(\frac{1}{3}\) π × 4 × 4 × 16
Since, the volume of the clay is in the form of the cone and the sphere remains the same, we have
volume of sphere = volume of the cone
\(\frac{4}{3}\) πr³ = \(\frac{1}{3}\) π × 4 × 4 × 16
r³ = \(\frac{1}{3}\) × 4 × 4 × 16 × \(\frac{3}{4}\)
r³ = 64 = 4³
∴ r = 4
∴ The radius of the sphere = 4

Question 13.
A storage tank consists of a circular cylinder with a hemi-sphere stuck on either end. If the external diameter of the cylinder be 1.4 m and its length be 8 m find the cost of painting it on the out side at rate of ₹ 20 per m².
Solution:
Total surface area of the tank
= 2 × C.S.A of the hemisphere +C.S.A of cylinder

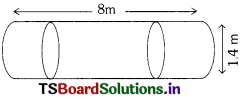
Hemisphere :
Radius (r) = \(\frac{\text { diamater }}{2}\)
= \(\frac{1.4}{2}\) = 0.7 m
C.S.A of hemi-sphere = 2 πr²
= 2 × \(\frac{22}{7}\) × 0.7 × 0.7
= 3.08 m²
2 × C.S.A = 2 × 3.08 m² = 6.16 m²
Cylinder : Radius (r) = \(\frac{\text { diamater }}{2}\) = \(\frac{1.4}{2}\) = 0.7 m
Height (h) = 8 m
C.S.A. of cylinder = 2πrh
= 2 × \(\frac{22}{7}\) × 0.7 × 8 = 35.2 m²
∴ Total surface area of the cylinder storage tank = 35.2 + 6.16 = 41.36 m²
cost of painting its surface area @ 20 per sq.m is = 41.36 × 20 = ₹ 827.2

Question 14.
How many spherical balls can be made out of a solid cube of lead whose edge measures 44 cm and each ball being 4 cm in diameter.
Solution:
Side of lead cube = 44 cm
Radius of spherical balls = \(\frac{4}{2}\) cm = 2 cm

Now, volume of spherical ball = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × 2³ cm³
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × 8 cm³
Volume of x spherical balls = \(\frac{4}{3}\) × \(\frac{22}{7}\) × 8 × x cm³
It is clear that volume of x spherical balls = volume of lead cube.
⇒ \(\frac{4}{3}\) × \(\frac{22}{7}\) × 8 × x = 44 × 44 × 44
⇒ x = \(\frac{44 \times 44 \times 44 \times 3 \times 7}{4 \times 22 \times 8}\)
x = 2541
Hence, total number of spherical balls = 2541

Question 15.
Explain the terms in the formula
V = l × b × h
Solution:
Given V = l × b × h
when v = volume
l = length
b = breath
h = height

Question 16.
Self help group wants to manufacture Joker’s caps (conical caps) of 6 cm radius and 8 cm hight. If the available colour paper sheet is 1000 cm² then how many caps can be manufactured from that paper.
Solution:
Radius of Joker’s cap = r = 6 cm
height of Joker’s cap = h = 8 cm
Now l = \(\sqrt{r^2+h^2}\) = \(\sqrt{6^2+8^2}\)
= \(\sqrt{36+64}\) = \(\sqrt{100}\) = 10 cm
Now, surface area of one cap = πrl
= \(\frac{22}{7}\) × 6 × 10 = 188.57 cm²
But area of available colour paper sheet = 1000 cm²
Number of caps Manufactured from that colour paper = \(\frac{\text { Area of colour paper sheet }}{\text { Surface area of are cap }}\)
= \(\frac{1000}{188.57}\) = 5.303 = 5

Question 17.
A cone of height 24 cm and radius of base 6 cm is made up modelling clay. A child reshapes it into a sphere. Find the radius of the sphere.
Solution:
Volume of cone = \(\frac{1}{3}\) π × 6 × 6 × 24 cm³
If r is the radius of the sphere, then its volume is \(\frac{4}{3}\) πr³
Since the volume of clay in the form of the cone and the sphere remains the same, we have
\(\frac{4}{3}\) πr³ = \(\frac{1}{3}\) π × 6 × 6 × 24
r³ = 3 × 3 × 24 = 3 × 3 × 3 × 8
r³ = 3³ × 2³
r = 3 × 2 = 6
Therefore the radius of the sphere is 6 cm.

Question 18.
A rectangular park is to be designed. Its breadth is 3m less than its length. Its area is to be 4 square meters more than the area of park that has already been made in the shape of an isosceles triangle with base as the breadth of the rectangular park and altitude 12m. Find the length and breadth.
Solution:
Let the breadth of the rectangular park be x m.
So, its length = (x + 3) m.
Therefore, the area of the rectangular park
= x(x + 3)m² = (x² + 3x)m².
Now, base of the isosceles triangle = x m.

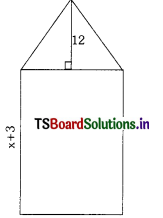
Therefore, its area = \(\frac{1}{2}\) × x × 12
= 6x m²
According to our requirements,
x² – 3x = 6x + 4
i.e., x² – 3x – 4 = 0
Using the quadratic formula, we get
x = \(\frac{3 \pm \sqrt{25}}{2}\) = \(\frac{3+5}{2}\) = 4 or -1.
But x ≠ -1. Therefore, x = 4.
So, the breadth of the park = 4m and its length will be x + 3 = 4 + 3 = 7m.
Verification :
Area of rectangular park = 28 m²
Area of triangular park = 24 m² = (28 – 4) m².

Question 19.
To calculate the quantity of milk inside a bottle, we need to find out …………… [ ]
a) Area
b) Volume
c) Density
d) Total surface area

Question 20.
The height of right angle triangle is 7 cm less than the base, the length of the diagonal is 17cm, then the length of remaining two sides are …………. [ ]
a) 15cm, 8 cm
b) 12 cm, 5 cm
c) 24 cm, 17 cm
d) All above