TS 10th Class Maths Important Questions Chapter 9 Tangents and Secants to a Circle

These TS 10th Class Maths Chapter Wise Important Questions Chapter 9 Tangents and Secants to a Circle given here will help you to solve different types of questions.

TS 10th Class Maths Important Questions Chapter 9 Tangents and Secants to a Circle

Previous Exams Questions

Question 1.
What do we call the part a and b in the below circle ? (A.P. June ’15)

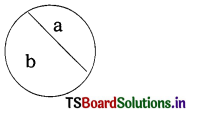
Solution:
a is minor segment and ‘b’ is major segment.

Question 2.
How many tangents can be drawn to a circle from a point on the same circle, Why? (T.S. Mar. ’15)
Solution:
The number of tangents that can be drawn to a circle from a point on it is one. This is as per concept of tangents.

Question 3.
Draw a circle with radius 3 cm and construct a pair of tangents from a point 8 cam away from the centre. (T.S. Mar. ’15)
Solution:

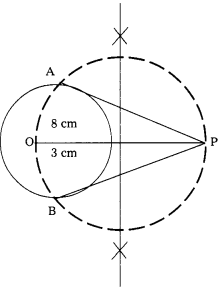
AP, BP are joining rays

Question 4.
Construct and measure the length of a pair ? of tangents that are drawn from a point at a distance of 8 cm whose radius is 5 cm. (T.S. Mar. ’16)
Solution:
Steps of construction :

1. Construct a circle with a radius of 5 cm.
2. Take the point ‘p’ in the exterior of the circle which is at a distance of ‘8’ cm from its centre.
3. Construct a perpendicular bisector to OP which meets at M.
4. The draw a circle with a radius of MP or MO from the point M. This circle cuts the previous circle drawn from the centre ‘O’ at the points A and B.
5. Now join the points PA and then PB.
6. PA, PB are the required tangents which are measured 6.2 cm long.
   

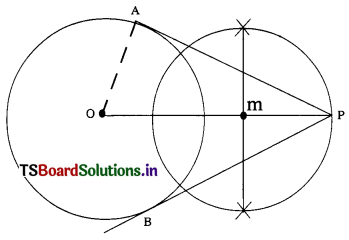
OA = 5 cm
OP = 8 cm
AP = PB = 6.2 cm.

Additional Questions

Question 1.
Calculate the length of Tangent from a point 13 cm away from the centre of a circle of radius 5 cm.
Solution:
In ∆OTR ∠OTP = 90°
OT = 5 cm, OP = 13 cm
By Pythagoras theorem

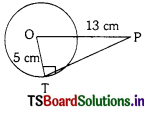
OP² = OT² + PT²
13² = 5² + PT²
⇒ PT² = 13² – 5²
= 169 – 25 = 144
PT = \(\sqrt{144}\) = 12 cm
∴ Length of the required tangent = PT = 12 cm

Question 2.
Two concentric circles of radii 25 cm and 24 cm are drawn. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:
Given two circles of radii 25 cm and 24 cm with common centre.
Let AB be the tangent to the inner circle and chord to the larger circle. Let ‘P’ be the point of contact.

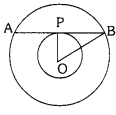
In the figure ∠OPB = 90°
OP = 24 cm, OB = 25 cm
Now OB² = OP² + PB²
25² = 24² + PB²
⇒ 625 = 576 + PB²
⇒ PB2 = 625 – 576 = 49
PB = \(\sqrt{49}\) = 7 cm
Now AB = 2 × PB = 2 × 7 = 14 cm
∴ Length of the chord to the larger circle = AB = 14 cm

Question 3.
Find the area of a quadrant of a circle whose circumference is 88 cm.
Solution:
Given circumference of a circle = 88 cm
Let r = Radius of the circle
Now 2πr = 88
⇒ r = \(\frac{88}{2 \pi}\) = \(\frac{88}{2 \times \frac{22}{7}}\)
= \(\frac{88 \times 7}{2 \times 22}\) = 14 cm
Area of the circle = πr² = \(\frac{22}{7}\) × (14)²
= \(\frac{22}{7}\) × 14 × 14
Area of the quadrant of a circle = \(\frac{1}{4}\) (πr²)
= \(\frac{1}{4}\) × \(\frac{22}{7}\) × 14 × 14
= 154 cm²

Question 4.
The length of the minute hand of a clock is 21 cm. Find the area swept by the volume by the minute hand in 20 minutes.
Solution:
Angle made by minute hand in 1 min = \(\frac{360^{\circ}}{60^{\circ}}\)
= 6°
Angle made by minute hand in 20 min
= 20 × 6° = 120°
The area swept by minute hand is in the shape of a sector with radius.
r = 21 cm and angle x = 120°
Area (A) = \(\frac{\mathbf{x}^{\circ}}{360^{\circ}}\) × πr²
= \(\frac{120^{\circ}}{360^{\circ}}\) × \(\frac{22}{7}\) × 21 × 21
= 462 cm²
∴ Area swept by minute hand in 20 minutes = 462 cm².

Question 5.
Two circle touch internally. The sum of their area is 125π cm² and distance between their centre is 5 cm. Find the radii of the circles.
Solution:
Let r₁ and r₂ be the radii of the given circles.
Sum of the areas of two circles
⇒ πr₁² + πr₂² = 125 π
⇒ π(r₁² + r₂²) = 125 π
⇒ r₁² + r₂² = 125 …………………… (1)
Distance between the centres = r₁ – r₂ (r₁ > r₂)
= 5 cm
Now (r₁ – r₂)² = (r₁² + r₂²) – 2r₁r₂
(5)² = 125 – 2r₁r₂ from (1)
⇒ 2r₁r₂ = 125 – 25
2r₁r₂ = 100 …………….. (2)
Then (r₁ + r₂)² = r₁² + r₂² + 2r₁r₂
= 125 + 100 (∵ from (1) and (2))
(r₁ + r₂)² = 225
⇒ r₁ + r₂ = \(\sqrt{225}\) = 15

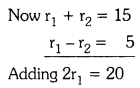
and r₁ – r₂ = 5
10 – r₂ = 5
⇒ r₂ = 10 – 5 = 5 cm
⇒ r₁ = \(\frac{10}{2}\) = 10 cm
∴ r₁ = 10 cm and r₂ = 5 cm

Question 6.
Find the area of the shaded region in the figure, given in which two circles with centres A and B touch each other at the point P. If AP = 10 cm and AB = 5 cm.
Solution:
AP denotes the radius of the bigger circle, i.e.,
AP = 10 cm
= r₁ (say)

AB denotes the distance between the centres of two circles i.e
A – B = 5 cm
BP denotes the radius of the smaller Circle i.e.,
BP = AP – AB
= 10 – 5 = 5 cm = r₂ (say)
The area of the shaded region = Area of the bigger circle – Area of the smaller area
= πr₁² – πr₂²
= π(r₁² – r₂²)
= π(10² – 5²2)
= π(100 – 25)
= π(75)
= \(\frac{22}{7}\) × 75
= 235.71 cm²

Question 7.
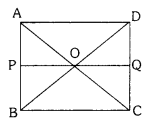
O is any point inside a rectangle ABCD prove that OB² + OD² = OA² + OC².
Solution:
Here PQ || BC so that
‘P’ is on AB; Q is on CD
If PQ || BC then
PQ ⊥ AB and PQ ⊥ CD
∴ ∠B = ∠C = 90°
∠BPQ = 90°
∠CQP = 90°

So that BPQC and APQD are the rectangles.
From ∆OPB, OB² = BP² + OP² ……………. (1)
and ∆OQD, OD² = OQ² + DQ² ………………. (2)
From ∆OQC, OC² = OQ² + CQ² ……………. (3)
From ∆OAR, OA² = AP² + OP² …………….. (4)
(1) + (2) OB² = BP² + OP²
OD² = OQ² + DQ²
OB² + OD² = BP² + OQ² + OP² + DQ²
From figure BP = CQ and DQ = AP
∴ OB² + OD² = CQ² + OQ² + OP² + AP²
From (3) & (4)
OQ² + CQ² = OC²; AP² + OP² = OA²
∴ OB² + OD² = OC² + OA²