Mahesh

Students must practice these TS Inter 1st Year Maths 1B Study Material Chapter 8 Limits and Continuity Ex 8(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Limits and Continuity 8(a)

I. Compute the following limits. (V.S.A.Q.)

Question 1.
\(\lim _{x \rightarrow a}\left(\frac{x^2-a^2}{x-a}\right)\) (V.S.A.Q.)
Answer:

Question 2.
\(\lim _{x \rightarrow 1}\) (x² + 2x + 3) (V.S.A.Q.)
Answer:
\(\lim _{x \rightarrow 1}\) (x² + 2x + 3) = 1² + 2(1) + 3 = 6

Question 3.
\(\lim _{x \rightarrow 0}\left(\frac{1}{x^2-3 x+2}\right)\) (V.S.A.Q.)
Answer:

Question 4.
\(\lim _{x \rightarrow 3}\left(\frac{1}{x+1}\right)\) (V.S.A.Q.)
Answer:

Question 5.
\(\lim _{x \rightarrow 1}\left(\frac{2 x+1}{3 x^2-4 x+5}\right)\) (V.S.A.Q.)
Answer:

Question 6.
\(\lim _{x \rightarrow 1}\left(\frac{x^2+2}{x^2-2}\right)\) (V.S.A.Q.)
Answer:

Question 7.
\(\lim _{x \rightarrow 2}\left(\frac{2}{x+1}-\frac{3}{x}\right)\) (V.S.A.Q.)
Answer:

Question 8.
\(\lim _{x \rightarrow 0}\left(\frac{x-1}{x^2+4}\right)\) (V.S.A.Q.)
Answer:

Question 9.
\(\lim _{x \rightarrow 0}\) x^3/2 (x > 0) (V.S.A.Q.)
Answer:
\(\lim _{x \rightarrow 0}\) x^3/2 = 0^3/2 = 0

Question 10.
\(\lim _{x \rightarrow 0}\) (√x + x^5/2), (x > 0) (V.S.A.Q.)
Answer:
\(\lim _{x \rightarrow 0}\) (√x + x^5/2) = √0 + 0^5/2 = 0 + 0 = 0

Question 11.
\(\lim _{x \rightarrow 0}\) x² cos \(\left(\frac{2}{x}\right)\) (V.S.A.Q.)
Answer:
\(\lim _{x \rightarrow 0}\) x² \(\lim _{x \rightarrow 0}\) cos \(\left(\frac{2}{x}\right)\) = 0 . (l) = 0 where |l| ≤ 1.

Question 12.
\(\lim _{x \rightarrow 3} \frac{x^2-9}{x^3-6 x^2+9 x+1}\) (V.S.A.Q.)
Answer:

Question 13.
\(\lim _{x \rightarrow 1}\left[\frac{x-1}{x^2-x}-\frac{1}{x^3-3 x^2+2 x}\right]\) (V.S.A.Q.)
Answer:
Note: The problem shall be designed as

Question 14.
\(\lim _{x \rightarrow 3}\left(\frac{x^4-81}{2 x^2-5 x-3}\right)\) (V.S.A.Q.)
Answer:

Question 15.
\(\lim _{x \rightarrow 3}\left(\frac{x^2-8 x+15}{x^2-9}\right)\) (V.S.A.Q.)
Answer:

Question 16.
If f(x) = – \(\sqrt{25-x^2}\) then find
\(\lim _{x \rightarrow 1}\left(\frac{f(x)-f(1)}{x-1}\right)\)
Answer:

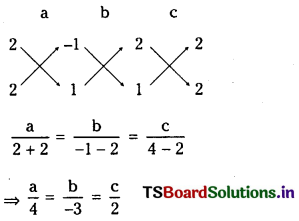
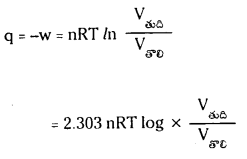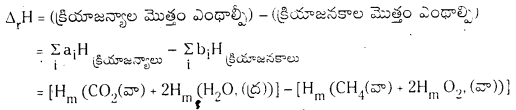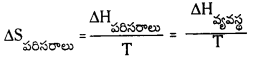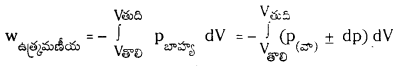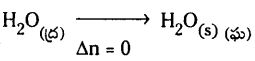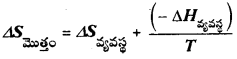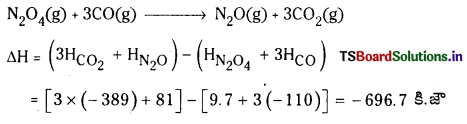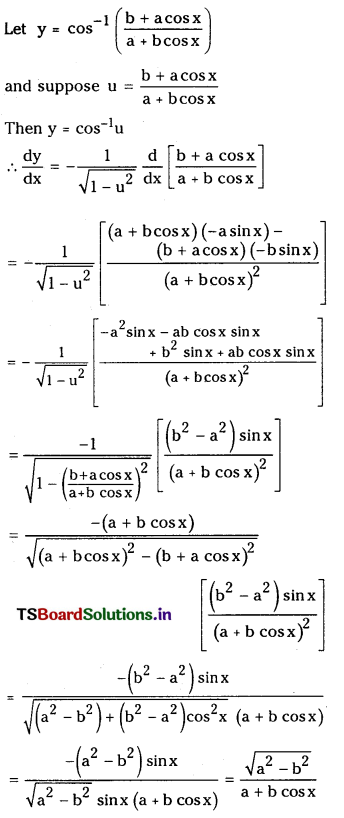Telangana TSBIE TS Inter 1st Year Chemistry Study Material 6th Lesson ఉష్ణగతిక శాస్త్రం Textbook Questions and Answers.

TS Inter 1st Year Chemistry Study Material 6th Lesson ఉష్ణగతిక శాస్త్రం

అత్యంత లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఉష్ణగతిక శాస్త్రం అనే పదం ఏమి తెలియజేస్తుంది ?
జవాబు:
రసాయన, భౌతిక రసాయన, జీవరసాయన ప్రక్రియలలో ‘ఉష్ణానికీ, ఇతర రూపాలలోని ‘శక్తుల’కూ మధ్య ఉండే పరిమాణాత్మక సంబంధాలను గురించి రసాయనశాస్త్రంలో ఉండే ఈ విభాగాన్ని ఉష్ణగతికశాస్త్రము అంటారు.
ముఖ్యముగా ఉష్ణగతికశాస్త్రం అంటే “ఉష్ణం ప్రవహించడం”.

ప్రశ్న 2.
ఉష్ణగతికశాస్త్రం నియమాలకు, సమతాస్థితికి మధ్య సంబంధమేమిటి ?
జవాబు:
ఒక వ్యవస్థ సమతాస్థితిలో ఉన్నప్పుడు లేదా ఒక సమతాస్థితి నుంచి వేరొక సమతాస్థితికి మారుతున్నపుడు మాత్రమే ఉష్ణగతిక శాస్త్ర నియమాలు అనువర్తిస్తాయి.
గతిక సమతాస్థితి వద్ద గిబ్స్ శక్తి అత్యల్పంగా ఉంటుంది. గిబ్స్ శక్తి మార్పు Δ_r.\(\mathrm{G}^{\ominus}\)కు, సమతాస్థితి స్థిరాంకం ‘K’ కు ఉన్న సంబంధము
O = Δ_r.\(\mathrm{G}^{\ominus}\) + 7T ln K
లేదా Δ_r.\(\mathrm{G}^{\ominus}\) = – RT ln K
లేదా Δ_r.\(\mathrm{G}^{\ominus}\) = -2.303 RT log K.

ప్రశ్న 3.
వ్యవస్థను నిర్వచించండి. ఉదాహరణ ఇవ్వండి.
జవాబు:
ఉష్ణగతికశాస్త్ర అధ్యయనానికి ఎంచుకున్న విశ్వంలోని లఘుభాగాన్ని వ్యవస్థ అంటారు.
ఉదా : బీకరులో తీసుకొన్న నీరు, ఒక సిలిండర్లో ఉన్న వాయువు.

ప్రశ్న 4.
స్థిరోష్ణక గోడ ఉంది 4U = w Vact వ్యవస్థపరంగా ఉష్ణం, పని అంటే ఏమి అర్థమయింది ?
జవాబు:
వ్యవస్థ నుంచి పరిసరాలకు లేదా పరిసరాల నుంచి వ్యవస్థకు ఎలాంటి ఉష్ణశక్తి వినిమయమూ జరగని ప్రక్రియను స్థిరోష్ణక ప్రక్రియ అంటారు. ఈ ప్రక్రియలో పని జరిగినపుడు వ్యవస్థ యొక్క అంతరికశక్తి పెరుగుతుంది.
w_ad = U₂ – U₁ = ΔU
వ్యవస్థపై పని జరిగినపుడు, w_ad = ధనాత్మకం
వ్యవస్థ పనిచేసినపుడు, w_ad = ఋణాత్మకం.

ప్రశ్న 5.
వ్యవస్థ మీద పని ఏమీ జరగలేదు. వ్యవస్థ ‘q’ పరిమాణంలో ఉష్ణం కోల్పోయింది. ఈ వ్యవస్థ ఎలాంటి గోడను కలిగి ఉంది ?
జవాబు:
వ్యవస్థ ఉష్ణ వాహక గోడను కలిగి ఉంది. ఉష్ణవాహక గోడల ద్వారా ఉష్ణం బదిలీ అయితే, ΔU = q = T_B – T_A.
ఇచ్చట T_A, T_B లు ఉష్ణోగ్రతలు, q = బదిలీ అయిన ఉష్ణరాశి, ΔU = ఆంతరిక శక్తిలో మార్పు.

ప్రశ్న 6.
వ్యవస్థకు ‘q’ పరిమాణంలో ఉష్ణం అందించబడింది, వ్యవస్థ పనిచేసింది. ఈ వ్యవస్థ ఏ రకంపై ఎలాంటిదై ఉంటుంది ?
జవాబు:
‘W’ పరిమాణంలో వ్యవస్థ ద్వారా పని జరిగి, ‘q’ పరిమాణంలో ఉష్ణశక్తి వ్యవస్థకు ఇవ్వబడినపుడు, ΔU = q – W. ఇది సంవృత వ్యవస్థ. అంటే వ్యవస్థ నుండి పరిసరాలకు, లేదా పరిసరాల నుండి వ్యవస్థకు శక్తి మార్పిడి జరుగుతుంది. కాని ద్రవ్యమార్పు జరగదు.

ప్రశ్న 7.
ఒక ఆదర్శ వాయువు స్వేచ్ఛా వ్యాకోచంలో ఉత్ర్కమణీయ, అనుత్రమణీయ ప్రక్రియల్లో వాయువు చేసే పని ఏమిటి ?
జవాబు:
స్వేచ్ఛావ్యాకోచంలో (P_{బాహ్య} = 0) కాబట్టి పని ఏమీ జరగదు. ఈ వ్యాకోచం ఉత్రమణీయం కావచ్చు. లేదా అనుత్రమణీయం కావచ్చు.

ప్రశ్న 8.
సమీకరణం ΔU = q – p_exΔV నుంచి ఘనపరిమాణం స్థిరంగా ఉన్నప్పుడు ΔU విలువ ఎంత ?
జవాబు:
ΔU = q-p_ex × ΔV సమీకరణంలో, ప్రక్రియను స్థిరఘనపరిమాణములో జరిపించినపుడు (ΔV = 0) అప్పుడు
ΔU = q అవుతుంది. అంటే అంతరిక శక్తిలో మార్పు = అందించబడిన ఉష్ణం.

ప్రశ్న 9.
సమోష్ణ స్వేచ్ఛా వ్యాకోచం ప్రక్రియలో ఒక ఆదర్శ వాయువు q, ΔU విలువలు ఎంత ?
జవాబు:
q, ΔU ల మధ్య సంబంధం ఈ క్రింది విధంగా ఉంటుంది. ΔU = q + w, సమోష్ణ స్వేచ్ఛా వ్యాకోచ ప్రక్రియలో w = 0, q = 0, ∴ ΔU = 0. కాబట్టి సమోష్ణ స్వేచ్ఛా వ్యాకోచ ప్రక్రియలో q, ΔU ల విలువలు శూన్యం (0) గా ఉంటాయి.

ప్రశ్న 10.
సమోష్ణ అనుత్రమణీయ ప్రక్రియ మార్పులో ఆదర్శవాయువుకు ‘q’ విలువ ఎంత ?
జవాబు:
ΔU = q + W సమీకరణాన్ని, సమోష్టక అనుత్రమణీయ మార్పులకు అన్వయిస్తే, అప్పుడు
q = – w = p_{బాహ్య} × (V_తుది – V_తొలి)

ప్రశ్న 11.
ఆదర్శ వాయువు సమోష్ణ ఉత్రమణీయ మార్పులో ‘q’ విలువ ఎంత ?
జవాబు:
ఆదర్శ వాయువు సమోష్ణ ఉత్ర్కమణీయ మార్పులకు ‘q’ విలువ

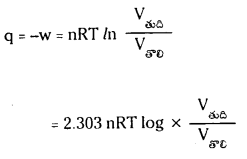
ప్రశ్న 12.
ఆదర్శ వాయువు స్థిరోష్ణక మార్పులో ΔU, w_(adiabatic) ల సంబంధమేమిటి ?
జవాబు:
ΔU, W ల సంబంధం క్రింది విధంగా ఉంటుంది.
ΔU = q + w
ఆదర్శ వాయువు స్థిరోష్ణక మార్పుకు q = 0
అపుడు ΔU = w_{“స్థిరోష్ణక}

ప్రశ్న 13.
ఉష్ణగతికశాస్త్రం మొదటి నియమం ఇవ్వండి.
జవాబు:
“శక్తిని సృష్టింపలేము, నశింపచెయ్యలేము. ఒక రూపములోని శక్తిని వేరొక రూపంలోకి మార్చగలము.” (లేదా) “మొదటి రకం సతతచలన యంత్రనిర్మాణము అసాధ్యం”. (లేదా)
“చక్రీయ ప్రక్రియలో వ్యవస్థ శక్తి మార్పు శూన్యం”.

ప్రశ్న 14.
వ్యవస్థ చేసిన పనికి, వ్యవస్థపై జరిగిన పనికి సంప్రదాయ గుర్తులు ఏమిటి ?
జవాబు:
ఒక వ్యవస్థ ద్వారా జరిగిన పనిని – pΔV తో సూచిస్తారు. అంటే వ్యవస్థ పనిచేస్తే దానిని ఋణ గుర్తుతో సూచిస్తారు. ఒక వ్యవస్థపై పని జరగడానికి + pΔV తో సూచిస్తారు. అంటే వ్యవస్థపై జరిగిన పనిని ధన గుర్తుతో సూచిస్తారు.

ప్రశ్న 15.
ఘనపరిమాణం (V), పీడనం (P), ఉష్ణోగ్రత (T) లు స్థితిప్రమేయాలు. ఇలా చెప్పడం సరైందా ?
జవాబు:
ఒక వ్యవస్థను ప్రభావితం చేసే అంశాలయిన పీడనం, ఘనపరిమాణం, ఉష్ణోగ్రత మొదలైన వాటి మీద ఆధారపడే ఉష్ణగతిక ప్రమేయాలను స్థితి ప్రమేయాలు అంటారు. ఇవి చర్యామార్గంపై ఆధారపడవు. కేవలం స్థితిపై ఆధారపడతాయి. కాబట్టి V, P, T లు స్థితి ప్రమేయాలే.

ప్రశ్న 16.
ఉష్ణం పరిసరాల నుంచి వ్యవస్థకు, వ్యవస్థ నుంచి పరిసరాలకు మారినపుడు దాని సంప్రదాయక గుర్తులు ఏమిటి ?
జవాబు:
పరిసరాల నుంచి వ్యవస్థకు, వ్యవస్థ నుంచి పరిసరాలకు ఉష్ణరాశి మార్పును ΔH తో సూచిస్తారు. ఒక చర్యలో వ్యవస్థ పరిసరాల నుంచి ఉష్ణం గ్రహిస్తే ΔH విలువ ధన గుర్తుతో సూచిస్తారు. అదే వ్యవస్థ పరిసరాలకు ఉష్ణం విడుదల చేస్తే ΔH విలువ ఋణ గుర్తుతో సూచిస్తారు.

ప్రశ్న 17.
పరిసరాల నుంచి వ్యవస్థ ఎలాంటి ఉష్ణం గ్రహించలేదు. అయితే వ్యవస్థ మీద పని జరిగింది. వ్యవస్థకు ఎలాంటి సరిహద్దు గోడ ఉంది ?
జవాబు:
వ్యవస్థపై పని జరుగుతుంది. కాని వ్యవస్థ ఉష్ణశక్తిని గ్రహించదు. ఈ వ్యవస్థ గోడను స్థిరోష్ణక గోడ అంటారు.
ΔU = w_{స్థిరోష్ణక}

ప్రశ్న 18.
వ్యవస్థ మీద పని ఏమీ జరగలేదు. అయితే ‘q’ ఉష్ణం వ్యవస్థ నుంచి పరిసరాలకు మారింది. వ్యవస్థకు ఎలాంటి సరిహద్దు గోడ ఉంది ?
జవాబు:
వ్యవస్థ మీద పని జరగదు కానీ ‘q’ పరిమాణంలో వ్యవస్థ ఉష్ణశక్తిని పరిసరాలకు కోల్పోతే దానిని ఉష్ణవాహక గోడలు
అంటారు.
అప్పుడు ΔU = -q.

ప్రశ్న 19.
వ్యవస్థ పనిచేసింది, వ్యవస్థకు ‘q’ ఉష్ణం కూడా ఇవ్వబడింది. ఇది ఎలాంటి వ్యవస్థ ?
జవాబు:
‘w’ పరిమాణంలో వ్యవస్థ ద్వారా పని జరిగి ‘q’ పరిమాణంలో ఉష్ణశక్తి వ్యవస్థకు ఇవ్వబడినపుడు, ΔU = q – w. ఇది సంవృత వ్యవస్థ.

ప్రశ్న 20.
q = w = – P_ext (υ_f – υ_i). ఇది అనుత్ప్ర్కమణీయ …… మార్పు.
జవాబు:
q = w = -P_{బాహ్య} (v_తుది – v_తొలి) అనేది అనుత్రమణీయ సమోష్ణక మార్పు.

ప్రశ్న 21.
q = – w = nRT ln (v_f/v_i). సమోష్ఠీయ …….. మార్పు.
జవాబు:
q = – w= nRT ln (v_తుది /v_తొలి) సమోష్ఠీయ ఉత్రమణీయ మార్పు.

ప్రశ్న 22.
1H కి ఉష్ణమోచక, ఉష్ణగ్రాహక చర్యల్లో సాంప్రదాయిక గుర్తులు ఏమిటి ?
జవాబు:
ఉష్ణమోచక చర్యలకు, AH విలువ ఋణాత్మకం.
ఉష్ణగ్రాహక చర్యలకు, AH విలువ ధనాత్మకం.

ప్రశ్న 23.
విస్తార (extensive), గహన (intensive) ధర్మాలంటే ఏమిటి ?
జవాబు:
పదార్థపు పరిమాణంపై ఆధారపడియుండే ధర్మాలను విస్తార ధర్మాలు అంటారు.
ఉదా : ద్రవ్యరాశి, ఘనపరిమాణము, అంతరికశక్తి, ఎంథాల్పీ మొదలగునవి. పదార్థం పరిమాణంతో సంబంధం లేని ధర్మాలను గహన ధర్మాలు అంటారు.
ఉదా : ఉష్ణోగ్రత, సాంద్రత, పీడనం మొదలగునవి.

ప్రశ్న 24.
సమీకరణం q = c · m · ΔT లో ΔT ఉష్ణోగ్రత మార్పు ‘m’ పదార్థం ద్రవ్యరాశి ‘q’ కావలసిన ఉష్ణం. అయితే ‘c’ ఏమిటి ?
జవాబు:
‘c’ ని ఉష్ణధారణ అంటారు.
“ఒక గ్రామ్ పదార్థం యొక్క ఉష్ణోగ్రతను 1°C పెంచుటకు అవసరమైన ఉష్ణాన్ని ఉష్ణధారణ అంటారు.
c = \(\frac{\mathrm{q}}{\Delta \mathrm{T}}\)

ప్రశ్న 25.
ΔU, ΔH ల సంబంధం తెలిపే సమీకరణం వ్రాయండి.
జవాబు:
ΔU, ΔH ల మధ్య సంబంధం సూచించే సమీకరణం
ΔH = ΔU + ΔnRT
ΔH = ఎంథాల్పీలోని మార్పు
ΔU = అంతరికశక్తులలో మార్పు
Δn = n_p – n_R
[n_p = క్రియాజన్యాల మొత్తం మోల్ల సంఖ్య
n_R = క్రియాజనకాల మొత్తం మోల్ల సంఖ్య].
R = సార్వత్రిక వాయు స్థిరాంకం
T = పరమ ఉష్ణోగ్రత.

ప్రశ్న 26.
C_p, C_υ ల మధ్య సంబంధం ఏమిటి ?
జవాబు:
ఒక ఆదర్శ వాయువుకు స్థిర ఘనపరిమాణం దగ్గర ఉష్ణధారణను C_Vగాను, స్థిర పీడనం దగ్గర ఉష్ణధారణను C_p గాను సూచిస్తే అప్పుడు వాటి మధ్య సంబంధం
C_P – C_V = R
R = వాయు స్థిరాంకం.

ప్రశ్న 27.
బాంబ్ కెలోరిమీటర్ ఆక్సిజన్ సమక్షంలో 298k, 1 atm పీడనంలో 1 gm గ్రాఫైట్ ఇచ్చిన సమీకరణం ప్రకారం దహనం చెందింది.
C_(graphite) + O₂(వా) → CO₂(వా)
చర్య జరగడం వల్ల ఉష్ణోగ్రత 298K నుండి 299K కు పెరిగింది. బాంబ్ కెలోరిమీటర్ ఉష్ణధారణ 20.7 kJK^-1, పై చర్యకు 298K, 1 atm పీడనం వద్ద ఎంథాల్పీ మార్పు ఎంత ?
జవాబు:
దత్తాంశం : C_p = 20.7 kJ
ΔT = 299 – 298 = 1k
సమీకరణం : ΔH = C_p × ΔT
ΔH = 20.7 × 1 = 20.7 kJ

ప్రశ్న 28.
పై చర్యకు అంతరిక శక్తి మార్పు ΔU ఎంత ?
జవాబు:
ΔU = ΔH – RΔT
= 20.7 – 8.314 × 10^-3 (ΔT = 1)
= 20.7 – 0.08314
= 20.617 kJ.

ప్రశ్న 29.
CH₄ (వా) + 2O₂(వా) → CO₂(వా) + 2H₂O(ద్ర) చర్యకు క్రియాజనకాలు, క్రియాజన్యాల మోలార్ ఎంథాల్పీల ఆధారంగా చర్యోష్టం Δ_rH ఎంత ?
జవాబు:

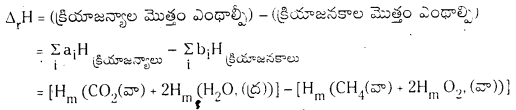
H_m = ఆయా పదార్ధాల మోలార్ ఎంథాల్పీల సంకేతం

ప్రశ్న 30.
కేవలం ఎంథాల్పీ తగ్గుదల మాత్రమే చర్య అయత్నీకృతానికి కారణం కాదు. ఎందువల్ల ?
జవాబు:
ఎంథాల్పీ తగ్గుదల (ΔH = ఋణాత్మకం) అయత్నీకృత ప్రక్రియకు కారణం కావచ్చు. కాని అన్ని సందర్భాలలో ఇది నిజం కాదు. ఎందులకనగా

1. ΔH = ధనాత్మకంగా గల కొన్ని చర్యలు [\(\frac{1}{2}\)N₂ (వా) + O₂ (వా) → NO₂ (వా), ΔH° = + 33.2 కి.జౌ. మోల్] అయత్నీ కృత చర్యలు
2. ΔH = 0 అయినప్పటికి కొన్ని చర్యలు కూడా అయత్నీకృతంగా ఉన్నాయి.
3. అయత్నీకృత చర్య ΔG అనే మరో అంశం మీద కూడా ఆధారపడి ఉంటుంది.

ప్రశ్న 31.
కేవలం ఎంట్రోపీ పెరుగుదల చర్య అయత్నీకృతానికి కారణం కాదు. ఎందువల్ల ?
జవాబు:
ఎంట్రోపీలో పెరుగుదల చర్య అయత్నీకృతం అవడానికి కారణం అనేది సరియైనది కాదు. ఎందుకంటే ఎంట్రోపీలో తగ్గుదల (ΔG = -ve) వల్ల కూడా చర్య అయత్నీకృతం అవుతుంది.

ప్రశ్న 32.
గిబ్స్ శక్తి మార్పు ΔG కు, సమతాస్థితి స్థిరాంకం ‘K’ కు మధ్య సంబంధం తెలపండి.
జవాబు:
గిబ్స్ సమీకరణము
Δ_r\(G^{\ominus}\) = -RT lnK
Δ_r\(G^{\ominus}\) = -2.303 RT log K.

ప్రశ్న 33.
Δ\(H^{\ominus}\), Δ\(S^{\ominus}\) లు తెలిస్తే Δ\(G^{\ominus}\) గణించవచ్చు. ఇది నిజమా ? కాదా ? ఎందువల్ల ?
జవాబు:
గిబ్స్ హెల్మ్హోల్ట్ సమీకరణము ప్రకారం
Δ\(G^{\ominus}\) = Δ\(H^{\ominus}\) – TΔ\(S^{\ominus}\)
ప్రమాణ ఉష్ణోగ్రత 298 k వద్ద ప్రమాణవిలువలు Δ\(H^{\ominus}\), Δ\(S^{\ominus}\) మరియు Δ\(G^{\ominus}\) గణించవచ్చు.
Δ\(H^{\ominus}\) మరియు Δ\(S^{\ominus}\) కనుగొనుట సాధ్యమైతే Δ\(G^{\ominus}\) ను కూడా పై సమీకరణం ద్వారా లెక్కించవచ్చు. కాబట్టి ఇవ్వబడిన ప్రతిపాదన నిజమే.

ప్రశ్న 34.
సమతాస్థితి స్థిరాంకం ‘K’ ని ప్రయోగశాలలో ఇచ్చిన ఉష్ణోగ్రత వద్ద ఖచ్చితంగా కొలిస్తే Δ\(G^{\ominus}\) ని వేరే ఏ ఉష్ణోగ్రత వద్దనన్నా కొలవవచ్చా ? ఎట్లా ?
జవాబు:
సమతాస్థితి స్థిరాంకం (K) మరియు Δ\(G^{\ominus}\) లు ఒకదానితో ఒకటి క్రింది విధంగా సంబంధితమై ఉంటాయి.
Δ\(G^{\ominus}\) = -2.303 RT log K.
ఇచ్చిన ఉష్ణోగ్రత వద్ద Kను నిర్ణయిస్తే, ఏ ఉష్ణోగ్రత వద్దనైనా పై సమీకరణం ఉపయోగించి Δ\(G^{\ominus}\) ను నిర్ణయించవచ్చును.

ప్రశ్న 35.
NO(వా) ఉష్ణగతిక స్థిరత్వాన్ని క్రింది చర్యల ఆధారంగా వివరించండి.
\(\frac{1}{2}\)N₂(వా) + \(\frac{1}{2}\)O₂(వా) → NO(వా), Δ_r\(H^{\ominus}\) = 90 kJ/mol^-1
NO(వా) + \(\frac{1}{2}\)O₂(వా) → NO₂(వా), Δ_r\(H^{\ominus}\) = -74kJ/mol^-1
జవాబు:
ఉష్ణమోచక పదార్థాలు స్థిరంగా వుంటాయి. అలాగే ఉష్ణగ్రాహ పదార్థాలు అస్థిరంగా వుంటాయి.
NO అనేది ఉష్ణగ్రాహ పదార్థం కాబట్టి అస్థిరంగా వుంటుంది.
NO₂ అనేది ఉష్ణమోచక పదార్థం కాబట్టి స్థిరంగా వుంటుంది.

ప్రశ్న 36.
1.00 మోల్ H₂O(ద్ర) ప్రమాణ పరిస్థితుల్లో ఏర్పడితే పరిసరాల ఎంట్రోపి మార్పు ఎంత ?
Δ_f\(H^{\ominus}\) H₂O(l)] = -286 kJ/mol^-1
జవాబు:
పరిసరాల ఎంట్రోపీ మార్పు

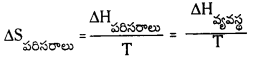
పరిసరాల ఎంథాల్పీ ఎంత పెరుగుతుందో వ్యవస్థ ఎంథాల్పీ అంతే తగ్గుతుంది.
= \(\frac{-286}{298}\) = \(\frac{286 \times 10^3}{298}\) -J/k = 1.0476 కి.జౌ. మోల్^-1

ప్రశ్న 37.
ఒక చర్యకు సమతాస్థితి స్థిరాంకం విలువ 10. Δ\(G^{\ominus}\) విలువ ఎంత ?
R = 8.314 JK^-1mol^-1, T = 300 K.
జవాబు:
Δ\(G^{\ominus}\) = -2.303 RT log K
= -2.303 × 8.314 × 300 log 10
= – 2.303 × 8.314 × 300 × 1 = -5.744 Jk^-1

ప్రశ్న 38.
ఉష్ణగతికశాస్త్రం మూడో నియమం ఏమిటి ?
జవాబు:
“పరిపూర్ణ శుద్ధ స్ఫటిక పదార్థాల ఎంట్రోపి విలువ పరమశూన్య ఉష్ణోగ్రత (0 K లేదా 273°C) సమీపించేకొద్దీ శూన్య విలువకు సమీపిస్తుంది”.

లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 39.
వివృత (open), సంవృత (closed), వివిక్త (isolated) వ్యవస్థలంటే ఏమిటి ? ఒక్కొక్కదానికి ఒక ఉదాహరణ ఇవ్వండి.
జవాబు:

1. వివృత (లేదా) తెరచిన వ్యవస్థ : పరిసరాల నుంచి వ్యవస్థకు లేదా వ్యవస్థ నుంచి పరిసరాలకు శక్తి, ద్రవ్యం రెండూ మార్పిడి జరిగితే అటువంటి దానిని వివృత వ్యవస్థ అంటారు.
   ఉదా : తెరచి ఉంచిన బీకరులో తీసుకున్న ద్రవం
2. సంవృత (లేదా) మూసిన వ్యవస్థ : వ్యవస్థ నుంచి పరిసరాలకు (లేదా) పరిసరాల నుంచి వ్యవస్థకు శక్తి మార్పిడి మాత్రమే జరిగితే అటువంటి వ్యవస్థను సంవృత వ్యవస్థ అంటారు.
   ఉదా : మూసి ఉంచిన వాహక పాత్ర (రాగి లేదా స్టీలు పాత్ర)లో తీసుకున్న ద్రవం
3. వివిక్త (లేదా) బంధిత వ్యవస్థ : వ్యవస్థకు, పరిసరాలకు మధ్య శక్తి గానీ, ద్రవ్యం గానీ ఏదీ కూడా వినిమయం చెందని వ్యవస్థను వివిక్త వ్యవస్థ అంటారు.
   ఉదా : థర్మాస్ ఫ్లాస్క్

ప్రశ్న 40.
స్థితిప్రమేయాలు (state functions), స్థితి చరాంశాలు (state variables) వీటిని నిర్వచించండి. ఉదాహరణ ఇవ్వండి.
జవాబు:
స్థితి ప్రమేయాలు : ఏ ధర్మాలు వ్యవస్థ యొక్క తొలి మరియు తుది స్థితులపై ఆధారపడి ఆ చర్య నడిచే మార్గముపై ఆధారపడవో వాటిని స్థితి ప్రమేయాలు అంటారు.
ఉదా : శక్తి, ఎంథాల్పీ, గిబ్స్ శక్తి
స్థితి చరాంశాలు : వ్యవస్థ గురించిన పూర్తి వివరణ ఇచ్చుటకు ఉపయోగపడే చరరాశులైన P, V, T లను స్థితి చరాంశాలు అంటారు.

ప్రశ్న 41.
“అంతరిక శక్తి ఒక స్థితి ప్రమేయం” వివరించండి.
జవాబు:
ఒక రసాయన వ్యవస్థలో మార్పు జరిగినప్పుడు ఎంత శక్తి విడుదలవుతుంది లేదా గ్రహించబడుతుందీ తెలుసుకోవడానికి
ఆ వ్యవస్థ మొత్తం శక్తిని తెలిపే పరిమాణాన్ని అంతరిక శక్తి అంటారు. దీనిని ‘U’ తో సూచిస్తారు.

ఈ క్రింది మార్పులు జరిగినపుడు వ్యవస్థ అంతరిక శక్తి ‘U’ లో మార్పు వస్తుంది.

1. వ్యవస్థ పని చేసినప్పుడు లేదా వ్యవస్థపై పని జరిగినప్పుడు
2. ఉష్ణశక్తి వ్యవస్థ నుంచి బయటకు లేదా బయట నుండి వ్యవస్థకు ప్రవహించినప్పుడు
3. ద్రవ్యం వ్యవస్థ నుండి బయటకు లేదా బయట నుండి వ్యవస్థకు చేరేటప్పుడు
4. అంతరిక శక్తి ‘U’ లో మార్పు వ్యవస్థ అనుసరించిన మార్గం మీద ఆధారపడదు. ఇది స్థితి ప్రమేయం. తొలి మరియు తుది స్థితులపై ఆధారపడి ఉంటుంది. కాబట్టి అంతరిక శక్తి స్థితి ప్రమేయం.

ప్రశ్న 42.
“పని స్థితి ప్రమేయం కాదు” వివరించండి.
జవాబు:
ఒక వ్యవస్థ ఒక స్థితి నుండి వేరొక స్థితికి మారినపుడు పని జరుగుతుంది. వ్యవస్థలో జరిగే ఈ స్థితి మార్పు వివిధ మార్గాలలో జరుగవచ్చు. కాబట్టి పని పరిమాణం వివిధ రకాలుగా ఉంటుంది. అన్ని మార్గాలలో జరిగే పని ఒకే విధంగా ఉండదు. అంటే జరిగే పని పరిమాణం వ్యవస్థ అనుసరించే మార్గం మీద ఆధారపడి ఉంటుంది. ఇది స్థితి ప్రమేయం కాదు. మార్గ ప్రమేయం.

ప్రశ్న 43.
ఉష్ణం అంటే ఏమిటో వివరించండి.
జవాబు:
భిన్న ఉష్ణోగ్రతల వద్ద ఉండే రెండు వస్తువుల మధ్య పరివర్తనం చెందే శక్తిని ఉష్ణం అంటారు.
ఉష్ణం అనేది శక్తి ఒక రూపం. ఇది మార్గ ప్రమేయం. స్థితి ప్రమేయం కాదు. దీనిని కెలోరి లేదా జౌళ్ళలో కొలుస్తారు. 1 కెలోరి = 4.18 జౌల్స్. దీనిని ‘q’ తో సూచిస్తారు. వ్యవస్థ నుండి పరిసరాలకు ఉష్ణం వినిమయం అయితే అపుడు ‘q’ విలువ ఋణాత్మకం. పరిసరాల నుండి వ్యవస్థ ఉష్ణం గ్రహించినపుడు ‘q’ విలువ ధన్మాతకం.

ప్రశ్న 44.
సమోష్ణక ఉత్రమణీయ చర్యకు ‘W_rev‘ ను ఉత్పాదించండి.
జవాబు:
-ఉత్రమణీయ పరిస్థితులలో పనిని P_(వా) ను ఉపయోగించి క్రింది విధంగా వ్రాయవచ్చు.

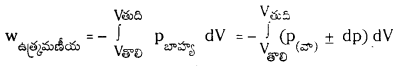
dp, dV విలువలు చాలా తక్కువ. అందువల్ల dp xdV ఇంకా తక్కువ కాబట్టి ఉపేక్షణీయం అవుతుంది.

ప్రశ్న 45.
10 atm పీడనం వద్ద 2L ఆదర్శ వాయువు సమోష్ణక విధానంలో 20L కు శూన్యంలోకి వ్యాకోచం చెందుతుంది. ఈ వ్యాకోచంలో ఎంత ఉష్ణం గ్రహించబడుతుంది ? ఎంత పని జరుగుతుంది ?
జవాబు:
వాయువు శూన్యంలోకి స్వేచ్ఛగా వ్యాకోచించింది. అప్పుడు పీడనం (P) = 0
V_తుది = 20L, V_తొలి = 2L
q = – w = p(V_తుది – V_తొలి)
= 0 (20 – 2) = 0
అంటే పని ఏమీ జరగదు. అదేవిధంగా ఉష్ణం ఏమీ గ్రహించబడదు.

ప్రశ్న 46.
పై సమస్యలోని ఆదర్శ వాయువులు 1 atm స్థిరపీడనానికి వ్యతిరేకంగా వ్యాకోచిస్తే ‘q’ విలువ ఎంత ?
జవాబు:
q = – w = P_{బాహ్య}(V₂ – V₁)
= 1 (20 – 2)
= 18 L. atm.

ప్రశ్న 47.
పై 45వ ప్రశ్నలోని ఆదర్శ వాయువు 10L ఘనపరిమాణానికి ఉత్రమణీయంగా వ్యాకోచం చెందితే ‘q’ విలువ ఎంత ?
జవాబు:
ఆదర్శ వాయువుకి PV = nRT
P = 10 atm.
V = 2L
10 × 2 = nRT
nRT = 20 L. atm
q = -w= 2.303 nRT log \(\frac{V_2}{V_1}\)
= 2.303 × 20 log \(\frac{20}{2}\)
= 46.06 L. atm

ప్రశ్న 48.
స్థితి ప్రమేయం ‘H’ ను వివరించండి. ΔU, ΔH ల మధ్య సంబంధం ఏమిటి ?
జవాబు:

1. స్థిరపీడనం, ఉష్ణోగ్రతల వద్ద ఒక వ్యవస్థ పరిసరాలతో వినిమయం చేసుకొన్న ఉష్ణరాశి పరిమాణాన్ని ఎంథాల్పీ (H) అంటారు.
2. ఒక ప్రక్రియను స్థిరపీడనం దగ్గర జరిపిస్తే, వ్యవస్థ ఘనపరిమాణం మారుతుంది. జరిగిన పని పీడనం – ఘ.ప పని అయితే w ను pΔV తో సూచిస్తారు.
3. మొదటి నియమము ప్రకారము
   ΔU = q_p – pΔV = q_p – p(V₂ – V₁)
   U₂ – U₁ = q_p – p (V₂ – V₁)
   ‘q_p‘ స్థిరపీడనం దగ్గర గ్రహించిన ఉష్ణరాశి (U + pV) ను ఎంథాల్పీ అంటారు.
   H = U + pV
   q_p = (U₂ + pV₂) – (U₁ + pV₁)
4. గ్రీకు పదం ఎంథాల్పీన్ అంటే వేడిచేయటం (లేదా) అంతర్గత ఉష్ణం.
   q_p = H₂ – H₁ = ΔH గా వ్రాయవచ్చు.
5. స్థిరపీడనం, స్థిర ఉష్ణోగ్రత వద్ద కలిగే శక్తి మార్పును ఎంథాల్పీ మార్పు (ΔH) అంటారు.
6. ఎంథాల్పీ మాత్రం U, P, V ల మీద ఆధారపడి ఉంటుంది. ఇవన్నీ స్థితి ప్రమేయాలు. కాబట్టి ‘ΔH’ కూడా స్థితి ప్రమేయమే.
   q_p కూడా ప్రక్రియ మార్గంపై ఆధారపడదు.
   q_p స్థితి ప్రమేయం.
   స్థిరపీడనం వద్ద పరిమితమైన మార్పులకు
   ΔH = ΔU + ΔpV, ‘p’ స్థిరం కాబట్టి
   ΔH = ΔU + pΔV

ప్రశ్న 49.
ΔH = ΔU + Δn (వా) RT ను ఉత్పాదించండి.
జవాబు:
ఒక చర్యలో వాయు క్రియాజనకాలు మాత్రమే పాల్గొంటే, క్రియాజనక వాయువుల మొత్తం ఘనపరిమాణం V_A అనుకొనుము. చర్య జరిగిన తరువాత వచ్చిన వాయు క్రియాజన్యాలు మొత్తం ఘనపరిమాణం V_B అనుకొనుము.
n_A = వాయు క్రియాజనకాల మొత్తం మోల్లు
n_B = క్రియాజన్యాల మోత్ల సంఖ్య
అపుడు pV_A = n_ART, pV_B = n_BRT అగును.
pV_B – pV_A = n_BRT – n_ART = (n_B – n_A) RT
(లేదా) p(V_B – V_A) = (n_B – n_A) RT
(లేదా) pΔV = Δn/_gRT
Δn = n_B – n_A
pΔV విలువను ΔH = ΔV + pΔV సమీకరణంలో ప్రతిక్షేపిస్తే
ΔH = ΔU + ΔnRT అవుతుంది.

ప్రశ్న 50.
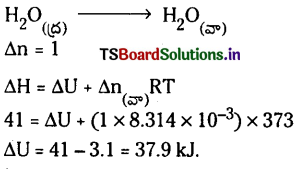
1 మోల్ నీటిని 1 bar పీడనం, 100°C వద్ద ఆదర్శ వాయువులా ప్రవర్తించే నీటిబాష్పం ఏర్పరిస్తే ఆ చర్యలో మోలార్ బాష్పీకరణ ఎంథాల్పీ 41 kJ/mol^-1 క్రింది వాటికి అంతరికశక్తి మార్పును లెక్కకట్టండి.
a) 1 mole నీరు 1 bar, 100°C వద్ద బాష్పీకరణం చెందినప్పుడు
b) 1 mole నీరు ద్రవస్థితి నుంచి మంచుగా మారినప్పుడు
జవాబు:
a)

b)

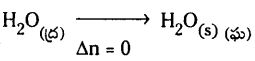
ఈ మార్పులో ఘనపరిమాణం మార్పు అతిస్వల్పం, పరిగణించదగింది కాదు. కాబట్టి
pΔV = Δn, RT ≈ 0 కాబట్టి
ΔH ≈ ΔU కాబట్టి ΔU = 41.00 kJ/mole

ప్రశ్న 51.
గహన, విస్తార ధర్మాలు వివరించండి.
జవాబు:
పదార్థ పరిమాణంపై ఆధారపడని ధర్మాలను గహన ధర్మాలు అంటారు.
ఉదా : పీడనం, సాంద్రత, బాష్పీభవన, ద్రవీభవన స్థానాలు, బాష్పపీడనం. పదార్థ పరిమాణంపై ఆధారపడు ధర్మాలను విస్తార ధర్మాలు అంటారు.
ఉదా : ఎంట్రోపి, ద్రవ్యరాశి, ఘనపరిమాణం, అంతరశక్తి, ఎంథాల్పీ, గిబ్స్ స్వేచ్ఛాశక్తి.

ప్రశ్న 52.
ఉష్ణధారణ అంటే ఏమిటి ? C_p – C_v = Rను ఉత్పాదించండి.
జవాబు:
ఒక పదార్థపు ఉష్ణోగ్రతను 1°C పెంచుటకు కావల్సిన ఉష్ణరాశిని ఉష్ణధారణ సామర్థ్యము అంటారు. దీనిని గణితం ప్రకారం క్రింది విధంగా సూచిస్తారు.
C = \(\frac{\mathrm{q}}{\mathrm{dT}}\)
C_p – C_v = R ఉత్పాదన :
ఆదర్శ వాయువుకు, H = E + pV
ఉష్ణోగ్రతాపరంగా అవకలనం చేస్తే

ప్రశ్న 53.
ΔU ను ప్రయోగపూర్వకంగా కెలోరిమెట్రిక్ విధానంలో ఏ విధంగా నిర్ణయిస్తారు ?
జవాబు:
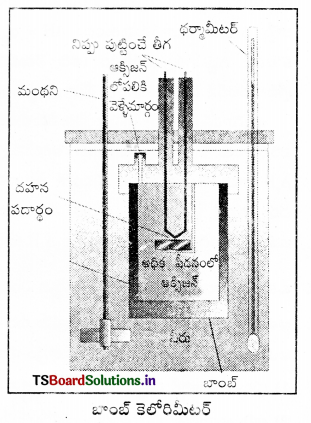
అంతరికశక్తి మార్పు ΔU కొలిచే సాధనం : రసాయన చర్యల్లో స్థిర ఘనపరిమాణం వద్ద గ్రహించబడిన ఉష్ణాన్ని బాంబ్ కెలోరిమీటర్లో కొలుస్తారు. బాంబ్ కెలోరిమీటర్ ఒక దృఢమైన గోడలు గల ఉక్కుపాత్ర. ఇది ఒక జల పతాకంలో ముంచబడి వుంటుంది. ఈ మొత్తం పాత్రల అమరికనే కెలోరిమీటర్ అంటారు. తేలికగా దహనం చెందే పదార్థాన్ని ఉక్కు బాంబులో వుంచి ఆక్సిజన్ను కలిపి దహనం చేస్తారు.

చర్య ఉష్ణమోచకమై ఉష్ణం వెలువడుతుంది. ఇది కెలోరిమీటర్ ఉష్ణోగ్రతను పెంచుతుంది. బాంబ్ కెలోరిమీటర్ ఉష్ణబంధకం చేయబడి వుంటుంది. అందువల్ల కెలోరిమీటర్ నుంచి పరిసరాలకు ఉష్ణ వినిమయం జరగదు. బాంబ్ కెలోరిమీటర్ చర్య జరిగేటపుడు పూర్తిగా మూసివుంచబడి వుంటుంది. కాబట్టి దాని ఘనపరిమాణంలో మార్పు ఉండదు. అంటే చర్యలో శక్తి మార్పులు స్థిర ఘనపరిమాణంలో జరిగిన వాటిగా అనుకొని కొలతలు చేయాలి. స్థిర ఘనపరిమాణం అంటే ΔU = 0,

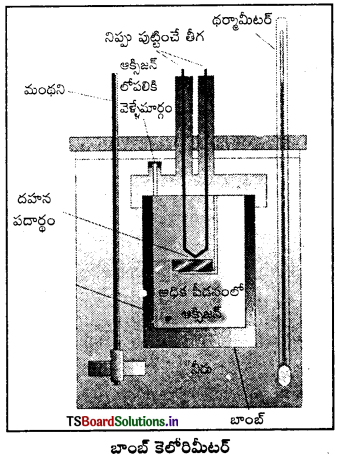
W = p ΔU = 0, అంటే చర్యలో పని ఏమీ జరగదు. చర్యలో వాయు పదార్థాలున్నప్పటికీ ఘనపరిమాణంలో మార్పురాదు. చర్య వల్ల కెలోరిమీటర్ పెరిగిన ఉష్ణోగ్రతను ఉపయోగించి కెలోరిమీటర్ ద్రవ్యరాశి, దాని ఉష్ణధారణ విలువల ద్వారా వెలువడిన ఉష్ణాన్ని (q₁) క్రింది సమీకరణం ఉపయోగించి గణించవచ్చు.
విశిష్టోష్టణం × ద్రవ్యరాశి = ఉష్ణధారణ
q = C × m × ΔT = C × ΔT ఇచ్చట c × m = C

ప్రశ్న 54.
ΔH ను ప్రయోగపూర్వకంగా కెలోరిమెట్రిక్ విధానంలో ఏ విధంగా నిర్ణయిస్తారు ?
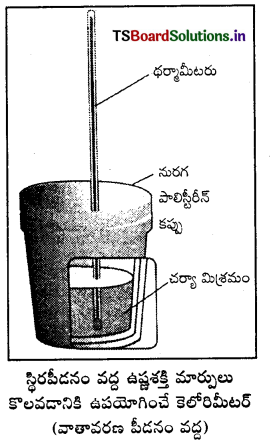
జవాబు:
స్థిరపీడనం వద్ద ఉష్ణశక్తి ΔH ని కొలవడం : మూత లేకుండా తెరచి వున్న కెలోరిమీటర్ సాధారణంగా వాతావరణ పీడనం దగ్గర వుంటుంది. వాతావరణ పీడనం స్థిరంగా వుంటుంది కాబట్టి కెలోరిమీటర్లో చర్య వల్ల వచ్చిన ఉష్ణ మార్పు స్థిరపీడనం వద్ద కొలిచిందిగా భావించవచ్చు. దీనిని రాస్తే ΔH కు సమానమవుతుంది. ΔH = q_p. కాబట్టి స్థిరపీడనం వద్ద కొలిచిన ఉష్ణమార్పు చర్యోష్ణం (అది వెలువడిన ఉష్ణం కావచ్చు లేదా గ్రహించబడిన ఉష్ణం కావచ్చు.) లేదా చర్యా ఎంథాల్పి Δ_rH అవుతుంది.

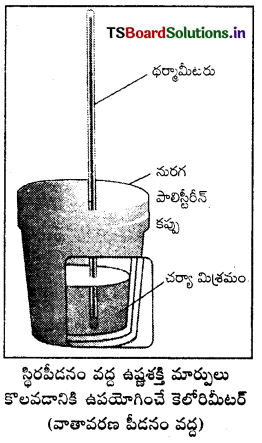
ఉష్ణమోచక చర్యలో ఉష్ణం వెలువడుతుంది. అంటే వ్యవస్థ నుంచి పరిసరాలకు ఉష్ణం ఇవ్వబడుతుంది. అందువల్ల q_p రుణాత్మకమవుతుంది. Δ_rH కూడా రుణాత్మకం. అదేవిధంగా ఉష్ణగ్రాహక చర్యలో వ్యవస్థ లేదా చర్య ఉష్ణం గ్రహిస్తుంది. అంటే పరిసరాల నుంచి చర్యకు ఉష్ణం ఇవ్వబడుతుంది. దీనికి q_p ధనాత్మకం Δ_rH కూడా ధనాత్మకమే.

ప్రశ్న 55.
చర్యా ఎంథాల్పీ అంటే ఏమిటి ? ప్రమాణ చర్యా ఎంథాల్పీని వివరించండి.
జవాబు:
చర్యా ఎంథాల్పీ-చర్యా ఎంథాల్పీ మార్పు Δ_rH : ఒక రసాయన చర్యలో క్రియాజనకాలు క్రియాజన్యాలుగా మారతాయి.
క్రియాజనకాలు → క్రియాజన్యాలు
స్థాయికియోమెట్రిక్ సమీకరణం ప్రకారం క్రియాజనకాల మోల్లు చర్యలో పాల్గొన్నప్పుడు జరిగే ఎంథాల్పీ మార్పునే చర్యా ఎంథాల్పీ అంటారు. ఒక చర్య ఎంథాల్పీ మార్పును Δ_rH సంకేతంతో చూపిస్తారు.
ప్రమాణ చర్యా ఎంథాల్పీలు : చర్యలో పాల్గొన్న అన్ని పదార్థాలు ప్రమాణ స్థితుల్లో వుంటే అప్పుడు ఆ చర్యా ఎంథాల్పీని ప్రమాణ చర్యా ఎంథాల్పీ అంటాం. ప్రమాణ చర్యా ఎంథాల్పీని Δ\(\mathrm{H}^{\ominus}\) గా అంటే ΔH సంకేతానికి తలమీద కుడిపైన గుర్తు రాస్తారు. 1 బార్ పీడనాన్ని ప్రమాణ పీడనంగాను, 298K ఉష్ణోగ్రతను ప్రమాణ ఉష్ణోగ్రతగాను తీసుకుంటారు.

ప్రశ్న 56.
“సంఘటనోష్ణం”ను నిర్వచించండి. ఒక ఉదాహరణ ఇవ్వండి.
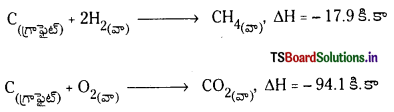
జవాబు:
సంఘటనోష్ణం : స్థిర ఉష్ణోగ్రత వద్ద ప్రమాణస్థితిలో ఒక మోల్ సమ్మేళనం దాని అనుఘటక మూలకాల నుంచి (ప్రమాణ స్థితిలో) ఏర్పడినపుడు వెలువడే లేదా ఉద్గారించబడే ఉష్ణరాశిని సంశ్లేషణ ఉష్ణం అంటారు.
అనుఘటకాల నుంచి ఉష్ణం ఉద్గారం అయ్యే చర్యలో ఏర్పడే సమ్మేళనాలను ఉష్ణమోచక సమ్మేళనాలంటారు. అనుఘటకాల నుంచి సమ్మేళనం ఉష్ణగ్రాహక చర్య ద్వారా ఏర్పడినపుడు ఉష్ణగ్రాహక సమ్మేళనాలు అంటారు. అనుఘటక పదార్థాలు కూడా ప్రమాణస్థితిలో ఉంటే దానిని ప్రమాణ సంశ్లేషనోష్ణం అంటారు.
ఉదా :

ప్రశ్న 57.
ప్రావస్థ మార్పు ఎంథాల్పీని నిర్వచించి వివరించండి.
జవాబు:
ఒక ప్రావస్థ ఇంకొక ప్రావస్థకు మారినప్పుడు శక్తిని వ్యవస్థ గ్రహించడమో లేదా శక్తి పరిసరాలకు విడుదల కావడమో జరుగుతుంది. ఉదాహరణకు మంచును కరిగించి నీరుగా మార్చాలంటే ఉష్ణాన్ని మంచుకు ఇవ్వాలి. ఇది 273K వద్ద స్థిర పీడనం వద్ద జరుగుతుంది.
H₂O(S) → H₂O(l) : ∆_fus\(\mathrm{H}^{\ominus}\) = 6.00 kJ mol^-1
ఇక్కడ ∆_{ద్రవీభవన} \(\mathrm{H}^{\ominus}\) ప్రమాణస్థితుల్లో ద్రవీభవన ఎంథాల్పీ. అదే 273K, 1 అట్మాస్ఫియర్ పీడనంలో నీరు ఘనీభవించి మంచుగా మారే ఉత్రమణీయ ప్రక్రియలో అదే ప్రమాణంలో ఉష్ణం పరిసరాలకు విడుదల అవుతుంది.

ప్రశ్న 58.
ద్రవీభవన ఎంథాల్పీ (మోలార్ ద్రవీభవన ఎంథాల్పీ)ని నిర్వచించి వివరించండి.
జవాబు:
ఒక మోల్ ఘనపదార్థాన్ని ప్రమాణ పరిస్థితుల్లో ద్రవీకరించినప్పుడు చెందే ఎంథాల్పీ మార్పును ప్రమాణ ద్రవీభవన మోలార్ ఎంథాల్పీ అంటారు. దీనిని ∆_fus Hగా రాస్తారు.
H₂(ఘ) → H₂O_(వా) ; ∆_fus H° = 6.0 kJ

ప్రశ్న 59.
బాష్పీభవన ఎంథాల్పీ (మోలార్ బాష్పీభవన ఎంథాల్పీ)ని నిర్వచించి వివరించండి.
జవాబు:
ప్రమాణ స్థితిలో ఉన్న ఒక మోల్ ఘనపదార్థాన్ని ద్రవీభవనం చేయడానికి అవసరమయ్యే ఎంథాల్పీ మార్పును మోలార్ ద్రవీభవన ఎంథాల్పీ అంటారు.
ఉదా : H₂O(ద్ర) → H₂O(వా); ∆_vap \(\boldsymbol{H}^{\ominus}\) = + 40.79 కి.జౌ. మోల్^-1.

ప్రశ్న 60.
ప్రమాణ ఉత్పతన ఎంథాల్పీని నిర్వచించి వివరించండి.
జవాబు:
ప్రమాణ పీడనం మరియు స్థిర ఉష్ణోగ్రత వద్ద ఒక మోల్ ఘనపదార్థం ఉత్పతనం చెందినపుడు కలిగే ఎంథాల్పీ మార్పును ప్రమాణ ఉత్పతన ఎంథాల్పీ అంటారు.
ఉదా : CO_{2 (ఘ)} → CO_{2(బాష్పం)}, ∆H° = + 25.2 కి.జౌ. మోల్^-1

ప్రశ్న 61.
ప్రమాణ సంఘటనోష్ణం (సంశ్లేషణోష్ఠం) (∆_r\(\boldsymbol{H}^{\ominus}\)) ను నిర్వచించి వివరించండి.
జవాబు:
ఒక మోల్ సంయోగపదార్థం దాని అత్యంత స్థిరమైన స్థితిలో, సంఘటిత మూలకాల నుంచి ఏర్పడినప్పుడు వచ్చే ప్రమాణ ఎంథాల్పీ మార్పునే ఆ సంయోగ పదార్థపు ప్రమాణ మోలార్ సంఘటన ఎంథాల్పీ లేదా ప్రమాణ మోలార్

సంఘటనోష్ణం అంటారు. దీనికి సంకేతం ∆_f\(\boldsymbol{H}^{\ominus}\). అత్యంత స్థిరమైన సంఘటిత స్థితినే నిర్దేశ లేదా ప్రమాణ స్థితి అంటారు. ఒక మూలకం నిర్దేశ లేదా ప్రమాణ స్థితి అంటే ఆ మూలకపు అత్యంత స్థిరమైన 25°C వద్ద 1 బార్ పీడనం వద్ద వున్న సంఘటిత స్థితి. ప్రమాణస్థితిలో హైడ్రోజన్, ఆక్సిజన్, కార్బన్లు, వరుసగా H₂(g) O₂ (g) C(graphite) గా వుంటాయి.
C(graphite) + O₂(g) → CO₂(g); ∆H = -393.5 kJ

ప్రశ్న 62.
హెస్ స్థిరోష్ణ నియమాన్ని నిర్వచించి వివరించండి. (March 2013)
జవాబు:
ఒక రసాయన చర్య ఒక దశలో జరిగినా లేక అనేక దశల్లో జరిగినా ఆ చర్యలో జరిగే మొత్తం ఎంథాల్పీ మార్పు సమానంగా ఉంటుంది.
A అనే పదార్థం రెండు విభిన్న మార్గాల ద్వారా చర్య జరిపి D అనే పదార్థాన్ని ఇచ్చినదని అనుకోండి.
ఏకదశ : A → D; ∆H = Q
అనేక దశలు :
A → B; ∆H₁ = q₁
B → C; ∆H₂ = q₂
C → D; ∆H₃ = q₃
∆H₁ + ∆H₂ + ∆H₃ = q₁ + q₂ + q₃
హెస్ నియమం ప్రకారం Q = q₁ + q₂ + q₃

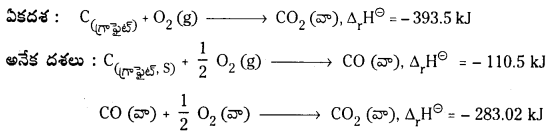
ఉదా : CO₂ (వా) ను C (గ్రా), O₂ (వా) నుండి రెండు విధాలుగా పొందవచ్చు.
అనేకదశలలో మొత్తం ఎంథాల్పీ మార్పు = – 392.52 కి.జౌ
ఏకదశలో మరియు అనేక దశలలో ఎంథాల్పీ మార్పు సమానంగా ఉంది కాబట్టి ఈ ఉదాహరణ హెస్ నియమానికి అనుగుణంగా ఉన్నది.

ప్రశ్న 63.
దహనచర్య ఎంథాల్పీ (∆<sub.c\(H^{\ominus}\)) ను నిర్వచించి వివరించండి.
జవాబు:
ఒక మోల్ పదార్థం ప్రమాణస్థితుల్లో అధిక ఆక్సిజన్ సమక్షంలో దహనం చెంది పూర్తిగా ఆక్సీకరణం చెందినప్పుడు వచ్చిన క్రియాజన్యాలు కూడా ప్రమాణస్థితుల్లో వున్నప్పుడు ఆ దహన చర్యలో వెలువడిన ఉష్ణాన్ని ఆ చర్య యొక్క ప్రమాణ దహనచర్య ఎంథాల్పీ అంటారు.
ఉదా : C₄H₁₀ (వా) + \(\frac{13}{2}\)O₂ (వా) → 4CO₂ (వా) + 5H₂O (ద్ర); ∆_c\(H^{\ominus}\) = -2658.0 kJ mol^-1

ప్రశ్న 64.
∆_a\(H^{\ominus}\) , పరమాణీకరణ ఎంథాల్పీని నిర్వచించి వివరించండి.
జవాబు:
నిర్వచనం : అణువుల్లోని ఒక మోల్ బంధాలను పూర్తిగా విడగొట్టి తటస్థ పరమాణువులను ఏర్పరచేటప్పుడు కలిగే ఎంథాల్పీ మార్పును పరమాణీకరణ ఎంథాల్పీ అంటారు.
ఉదా : H -H బంధాల విచ్ఛిత్తి వల్ల హైడ్రోజన్ పరమాణువులు ఏర్పడుతున్నాయి. ఈ చర్యలో వచ్చే ఎంథాల్పీ మార్పును పరమాణీకరణ ఎంథాల్పీ, ∆_a\(H^{\ominus}\) అంటారు.
H_2(వా) → 2H_(వా) ; ∆_a\(H^{\ominus}\) = 435.0 kJ mol^-1.

ప్రశ్న 65.
బంధ ఎంథాల్పీ (∆_bond\(H^{\ominus}\)) నిర్వచించి వివరించండి.
జవాబు:
నిర్వచనం : వాయుస్థితిలో వున్న ఒక సమయోజనీయ పదార్థంలోని ఒక మోల్ సమయోజనీయ బంధాలను విచ్ఛిత్తిచేసి వాయుస్థితిలో వున్న క్రియాజన్యాలను ఇచ్చినప్పుడు జరిగిన ఎంథాల్పీ మార్పును బంధ నియోజన ఎంథాల్పీ అంటారు.
ఉదా : H₂(g) → 2H (g); ∆_H-H\(H^{\ominus}\) = 435.0 kJ mol^-1
ఈ చర్యలో జరిగిన ఎంథాల్పీ మార్పు H – H బంధపు బంధ వియోజన ఎంథాల్పీ.

ప్రశ్న 66.
CH₄ లోని C-H బంధ ఎంథాల్పీని వివరించండి.
జవాబు:
మీథేన్, (CH₄) లో నాలుగు C – H బంధాలున్నాయి. ఇవన్నీ బంధ ధైర్ఘ్యం, బంధశక్తులకు సంబంధించి సమాన విలువలు కలిగి ఉంటాయి. అయితే బంధాల్ని ఒక్కొక్కటిగా విచ్ఛిత్తి చేస్తుంటే బంధశక్తి విలువలు మారతాయి.
CH₄ (వా) → C (వా) + 4H; ∆a\(H^{\ominus}\) = 1665 kJ. mol^-1
CH₄ (వా) → CH₃ (వా) + H; ∆_bond\(H^{\ominus}\) = 427 kJ mol^-1.
CH₃ (వా) → CH₂ (వా) + H; ∆_bond\(H^{\ominus}\) = +439 kJ mol^-1.
CH₂ (వా) → CH (వా) + H; ∆_bond\(H^{\ominus}\) = +452 kJ mol^-1.
CH (వా) → C (వా) + H; ∆_bond\(H^{\ominus}\) = +347 kJ mol^-1.
కాబట్టి;
CH₄ (వా) → C (వా) + 4H (వా) ; ∆_a\(H^{\ominus}\) = 1665 kJ mol^-1.
ఇలాంటి పరిస్థితుల్లో సగటు బంధశక్తి తీసుకోవాలి.
ఉదా : CH₄, ∆_C-H\(H^{\ominus}\) కు సగటు బంధశక్తి
∆_C-H\(H^{\ominus}\) = 1/4(∆_a\(H^{\ominus}\) = 1/4(1665 kJ mol^-1) = 416 kJ mol^-1

ప్రశ్న 67.
ద్రావణోష్ణం (∆_sol\(H^{\ominus}\)), విలీన ప్రక్రియ ఉష్ణం (∆_sol\(H^{\ominus}\)) లను నిర్వచించి వివరించండి.
జవాబు:
1. మోల్ ద్రావితాన్ని అధిక ద్రావణిలో సంపూర్ణంగా కరిగించినప్పుడు విడుదలైన లేదా గ్రహించబడ్డ ఉష్ణరాశి ప్రమాణమును ద్రావణోష్ణం అంటారు.
ఉదా : MgSO₄ + నీరు → MgSO₄ జ|| ద్రా.
స్థిర ఉష్ణోగ్రతా పీడనాల వద్ద 1 మోల్ ద్రావితం కరిగి వున్న ద్రావణానికి అధిక ద్రావణి కలిపి విలీనం చేసినపుడు జరిగే ఎంథాల్పీ మార్పును విలీనోష్ణం అంటారు.
ద్రావణి పరిమాణం మీద ఆధారపడి ద్రావణ ప్రక్రియలో ఎంథాల్పీ మార్పు ఉంటుంది. ఇంకా, ఇంకా ఎక్కువ ద్రావణి కలిపిన కొద్ది ఎంథాల్పీలో మార్పు ఏమీ ఉండదు.
ఉదా : HCl(వా) ను విలీన ప్రక్రియ చేసినపుడు ఎంథాల్పీ మార్పు
ΔH_(40H2O) – ΔH_(25H2O) = ΔH_{‘విలీనం}
Δ_{విలీనం} = [-72.79 -(-72.03)] kJ/mol = -0.76 kJ/mol.

ప్రశ్న 68.
అయొనైజేషన్ ఎంథాల్పీ, ఎలక్ట్రాన్ స్వీకరణ ఎంథాల్పీలను నిర్వచించండి.
జవాబు:
అయొనైజేషన్ ఎంథాల్పీ వాయుస్థితిలో ఉన్న ఒంటరి తటస్థ పరమాణువు బాహ్యకర్పరం నుండి ఒక ఎలక్ట్రాన్ను తొలగించి అయాన్ మార్చే సందర్భంలో కలిగే ఎంథాల్పీ మార్పును అయొనైజేషన్ ఎంథాల్పీ అంటారు.
ఉదా : Na (వా) → Na⁺ (వా) + ఎలక్ట్రాన్ ∆₁\(H^{\ominus}\) = 496 కి.జౌ/మోల్
ఎలక్ట్రాన్ స్వీకరణ ఎంథాల్పీ : వాయుస్థితిలో ఉన్న ఒంటరి తటస్థ పరమాణువు అదనంగా ఒక ఎలక్ట్రాన్ను కలిగినపుడు కలిగే ఎంథాల్పీ మార్పును ఎలక్ట్రాన్ స్వీకరణ ఎంథాల్పీ (లేక) ఎలక్ట్రాన్ ఎఫినిటి అంటారు.
ఉదా : Cl(వా) + ఎలక్ట్రాన్ → Cl^– (వా)
∆_(eg)\(H^{\ominus}\) = – 348.6 కి.జౌ/మోల్

ప్రశ్న 69.
ఒక ప్రక్రియ అయత్నీకృతాన్ని వివరించండి.
జవాబు:
బాహ్యకారక ప్రమేయం లేకుండా చర్య స్వచ్ఛందంగా జరిగే ప్రక్రియను అయిత్నీకృతం అంటారు. ఇది అద్విగత చర్య. అన్ని సహజ ప్రక్రియలు అయత్నీకృత చర్యలే. ఎంథాల్పీలో తగ్గుదల అయత్నీకృత చర్యలకు ఒక అంశం. కాని ఇది అన్ని సందర్భాలలో నిజం కాదు. అయత్నీకృత చర్యలలో ఎంట్రోపీ పెరుగుతుంది. అయత్నీకృత చర్యలకు క్రింది మూడు నిశ్చిత పరిస్థితులు కావాలి.

1. ΔH° = – (ఎంథాల్పీ మార్పు ఋణాత్మకం)
2. ΔS° = + (ఎంట్రోపీలో మార్పు ధన్మాతకం)
3. ΔG° = – (స్వేచ్ఛాశక్తిలో మార్పు ఋణాత్మకం).

అయత్నీకృత చర్యల యొక్క నిబంధనను వివరించడానికి గిబ్స్ ఒక ఉష్ణగతిక ప్రమేయాన్ని ప్రవేశపెట్టాడు. దీనిని గిబ్స్ శక్తి అంటారు. గిబ్స్ సమీకరణం ప్రకారం, ΔG = ΔH – TΔS
అయత్నీకృత చర్యలు-నిబంధనలు :
చర్యల స్వచ్ఛందత లేదా అయత్నీకృతంపై ఉష్ణోగ్రత ప్రభావం

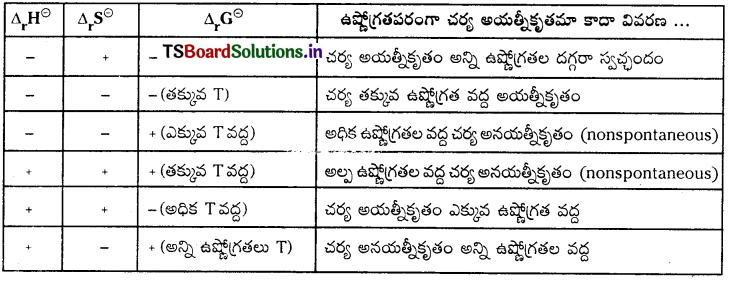
ప్రశ్న 70.
ఒక అయత్నీకృత ప్రక్రియకు కారణం ఎంథాల్పీ తగ్గుదల మాత్రమే కారణమా ? వివరించండి.
జవాబు:
ఎంథాల్పీలో తగ్గుదల, ∆H = -Ve, అనేది అయత్నీకృత చర్యలకు తోడ్పడే ఒక అంశమే గాని అన్ని సందర్భాలలో అది నిజం కాదు. ఎందుకంటే ఎంథాల్పీలో పెరుగుదల, ∆H =
Ve, ఉన్న కొన్ని చర్యలు అయత్నీకృతాలుగా ఉంటాయి.

ఉదా : \(\frac{1}{2}\) N₂ (వా) + O₂ (వా) → NO₂ (వా) ∆<sub.rH° = + 33.2 కి.జౌ.
గిబ్స్ ప్రకారం, అయత్నీకృత చర్యలకు ∆G విలువ ఋణాత్మకంగా ఉండాలి. కాబట్టి అయతికృత చర్యలకు ఎంథాల్పీ తగ్గుదల మాత్రమే కారణం కాదు.

ప్రశ్న 71.
ఎంట్రోపీ అంటే ఏమిటి ? ఉదాహరణలతో వివరించండి.
జవాబు:
ఎంటోపి : ఒక వ్యవస్థలోని అణువుల క్రమరాహిత్యాన్ని తెలియచేసే దానిని ఎంట్రోపి అంటారు. వ్యవస్థలోని అణువుల క్రమరాహిత్యం పెరిగే కొలది ఎంట్రోపి పెరుగుతుంది. ఇది స్థితి ప్రమేయం ఒక వివిక్త వ్యవస్థలో జరిగే అయత్నీకృత ప్రక్రియకు ఎంట్రోపి మార్పు (∆S) ధనాత్మకంగా వుంటుంది.

ప్రశ్న 72.
ఎంట్రోపీ పెరుగుదలే అయత్నీకృత ప్రక్రియకు కారణం. వివరించండి.
జవాబు:
అయత్నీకృత చర్యకు ఎంట్రోపీలో పెరుగుదల అనేది ఒక అంశం మాత్రమే. అన్ని సందర్భాలలో కాదు. ఎంట్రోపీలో తగ్గుదల (∆S = – ve) ఉన్నపుడు తిరోగామి చర్య అయత్నీకృతంగా ఉంటుంది. ఎంట్రోపీలో మార్పు సున్న (∆S = 0) అయితే ఆ వ్యవస్థ సమతాస్థితిలో ఉంటుంది. ∆H = – ve, ∆S = + ve, ∆G = -ve అయితే అన్ని ఉష్ణోగ్రతల వద్ద చర్య అయత్నీకృతంగా ఉంటుంది.

ప్రశ్న 73.
∆U, ∆S ఉత్రమణీయ, అనుత్రమణీయ ప్రక్రియలను వివరించగలుగుతాయా ? వివరించండి.
జవాబు:
∆U అనేది అంతరికశక్తిలో మార్పు. ∆S అనేది ఎంటోపిలో మార్పు.
ఉష్ణమోచక చర్యలలో పురోగామి ప్రక్రియలో ∆U లో తగ్గుదల ఉంటుంది. ఈ సందర్భంలో ∆U అనే చర్య అయత్నీకృతకు అనుకూలం. ద్విగత చర్యలలో ∆U లో తగ్గుదల ఉండే దిశ చర్యకు అనుకూలంగా ఉంటుంది.
∆S విషయంలో ∆S = + ve అయితే చర్య అయత్నీకృతం.
∆S = -ve అయితే తిరోగామి చర్య అయత్నీకృతం, ∆S = 0 అయితే చర్య సమతాస్థితిలో ఉంటుంది.
∆U లేదా ∆H = -ve, ∆S = + ve, ∆G = -ve అయితే అన్ని ఉష్ణోగ్రతల వద్ద చర్య అయత్నీకృతం.

ప్రశ్న 74.
4Fe (ఘ) + 3O₂ (వా) → 2Fe₂O₃ (ఘ) అనే ఐరన్ ఆక్సీకరణ చర్యకు 298K వద్ద ఎంట్రోపీ మార్పు -549.45 JK^-1 mol^-1, దీనికి రుణాత్మక ఎంట్రోపీ ఉన్నా చర్య అయత్నీకృతంగా జరుగుతుంది. ఎందువల్ల ?
జవాబు:
∆G = ∆H – T∆S
= 1648 × 10³ J mol^-1 – 298 (-549.45) = 1648 × 10³ + 163 × 10³ = -1485 × 10³
∆G ఋణాత్మకం. అందువల్ల ఎంట్రోపీ మార్పు ఋణాత్మకంగా ఉన్నప్పటికీ చర్య అయత్నీకృతంగా జరుగుతుంది.

ప్రశ్న 75.
కింది వాటిల్లో ఏ ఫార్ములాలు సరైనవి ?
a) G = H – TS
b) ∆G_{వ్యవస్థ} = ∆H_{వ్యవస్థ} – T∆S_{వ్యవస్థ}
c)

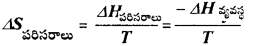
d)

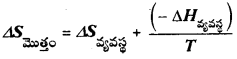
e)
T∆S_{మొత్తం} = T∆S_{వ్యవస్థ} – ∆H_{వ్యవస్థ}
జవాబు:

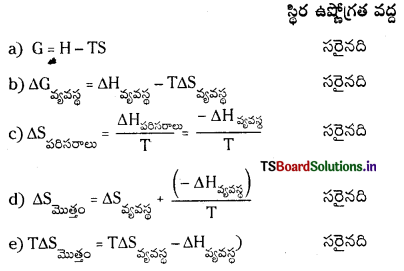
ప్రశ్న 76.
ఆక్సిజన్ను ఓజోన్గా మార్చడానికి ∆_r\(\boldsymbol{G}^{\ominus}\) ను 298K వద్ద గణించండి. చర్య Kp విలువ 2.43 × 10^-29.
జవాబు:
∆_r\(\boldsymbol{G}^{\ominus}\) = -2.303 RT log K_p
K_p = 2.43 × 10^-29
∆_r\(\boldsymbol{G}^{\ominus}\) = -2.303 × 8.314 × 298 (log 2.43 × 10^-24)
∆_r\(\boldsymbol{G}^{\ominus}\) = 163 kJ

ప్రశ్న 77.
ఉష్ణగతికశాస్త్రం రెండో నియమాన్ని నిర్వచించి వివరించండి.
జవాబు:
క్లాసియస్ నిర్వచనం : విశ్వం యొక్క ఎంట్రోపీ గరిష్ఠంగా మారే దిశలో చర్చిస్తుంది.
లేదా
ఉష్ణశక్తి స్వచ్ఛందంగా చల్లని వస్తువు నుంచి వేడిగా గల వస్తువుకు ప్రసరించదు.
లేదా
పనిని పూర్తిగా ఉష్ణరాశిగా మార్చవచ్చు కానీ ఉష్ణరాశిని 100% పనిగా మార్చడం అసాధ్యం.
లేదా
అన్ని స్వచ్ఛంద చర్యల్లో ఎంట్రోపీ మార్పు ధనాత్మకం లేదా రెండోరకం సతతచలన యంత్ర నిర్మాణం అసాధ్యం.

ప్రశ్న 78.
ఉష్ణగతికశాస్త్రం మూడో నియమాన్ని నిర్వచించండి. దీనిని గురించి మీకు ఏమి తెలిసింది ?
జవాబు:
మూడవ నియమం:
పరిపూర్ణ శుద్ధ స్ఫటిక పదార్థాల ఎంట్రోపి విలువ పరమశూన్య ఉష్ణోగ్రత వద్ద శూన్యవిలువను కలిగి ఉంటుంది.
S_T = \(\int_0^T \frac{C_p}{T} \cdot d T\) – సమీకరణం ఉపయోగించి, ఇవ్వబడిన ఉష్ణోగ్రత వద్ద C_p విలువ తెలిస్తే ఎంట్రోపి (S) విలువను లెక్కగట్టవచ్చు.

ప్రాముఖ్యత :

1. ఈ నియమం సాయంతో చర్యల్లో ఎంట్రోపీ మార్పును నిర్ణయించవచ్చు.
2. ఈ నియమం ప్రకారం ఏ స్వచ్ఛంద చర్యల్లో అయినా మొత్తం మీద ఎంట్రోపీ మార్పు ధనాత్మకంగా ఉండును.
3. ఈ నియమం ఎంట్రోపి అవధిని గురించి తెలుపుతుంది.

ప్రశ్న 79.
ఎంట్రోపీ భావనను వివరించండి.
జవాబు:
ఎర్రటోపి : ఒక వ్యవస్థలోని అణువుల క్రమరాహిత్యాన్ని తెలియచేసే దానిని ఎంట్రోపి అంటారు. వ్యవస్థలోని అణువుల క్రమరాహిత్యం పెరిగే కొలది ఎంట్రోపి పెరుగుతుంది. ఇది స్థితి ప్రమేయం ఒక వివిక్త వ్యవస్థలో జరిగే అయత్నీకృత ప్రక్రియకు ఎంట్రోపి మార్పు (ΔS) ధనాత్మకంగా వుంటుంది.

ప్రశ్న 80.
గిబ్స్ శక్తిపరంగా ప్రక్రియ అయత్నీకృత మార్పును వివరించండి.
జవాబు:
గిబ్స్ శక్తి : ఇది ఉష్ణగతిక ప్రమేయం. దీనిలో ఎంథాల్పీ, ఎంట్రోపీ ప్రమేయాలు ఇమిడి వుంటాయి. ఒక చర్య స్వచ్ఛంద
చర్య ఔనో, కాదో తెలుసుకొనుటకు ఇది తగినంత, అవసర సమాచారాన్ని ఇస్తుంది. ఇది స్థితి ప్రమేయం.
గిబ్స్ సమీకరణం ప్రకారం
ΔG = ΔH – TΔS
ఇచ్చట ΔG = గిబ్స్ శక్తిలో మార్పు
ΔH = ఎంథాల్పీ మార్పు
TΔS = ఉష్ణోగ్రతతో ఎంట్రోపీ మార్పు.
ΔG, ఋణాత్మకమయిన స్వచ్ఛంధ చర్య. (ΔG < 0) GΔ, ధనాత్మకమైన అస్వచ్ఛంద చర్య. (ΔG > 0)
ΔG = 0, చర్య సమతాస్థితిలో ఉంటుంది.
ΔG = + ve, ΔS = + ve అయితే – ప్రక్రియ అయత్నీకృతం (TΔS > ΔH గా ఉండాలి.)
ΔG = – ve, ΔS = + ve, ΔH = – ve అయితే చర్య అన్ని ఉష్ణోగ్రతల వద్ద అయత్నీకృతం.

ప్రశ్న 81.
గిబ్స్ శక్తి మార్పు విలువ, గుర్తుల ఆధారంగా ఒక రసాయనిక చర్య అయత్నీకృత మార్పును, దాని నుంచి లభించే ఉపయోగకరమైన పనిని తెలుసుకోవచ్చు. దీన్ని వివరించండి.
జవాబు:
ఒక స్వచ్ఛంద చర్యకు “ΔG” గిబ్స్ శక్తి మార్పు విలువ ఋణాత్మకంగా ఉండవలెను. భిన్న చర్యల ΔH, ΔS మరియు ΔG విలువలు క్రింది విధంగా ఉండును.

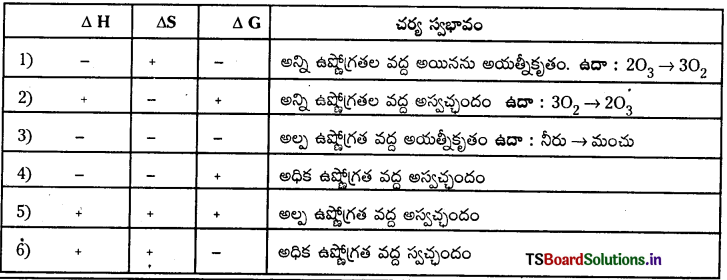
గిబ్స్ శక్తిలో మార్పుకు, సమతాస్థితి స్థిరాంకం ‘K’ కు గల సంబంధాన్ని క్రింది సమీకరణం సూచిస్తుంది.
Δ_r\(\mathrm{G}^{\ominus}\) = Δ_r\(\mathrm{H}^{\ominus}\) – TΔ_r\(\mathrm{S}^{\ominus}\) = -RTlnK.
ఉష్ణగ్రాహక చర్యలకు Δ_rH విలువ అధికంగా ఉండాలి మరియు ధనాత్మకంగా ఉండాలి (K < 1)
ఉష్ణమోచక చర్యలకు Δ_r° విలువ అధికంగా ఉండాలి మరియు ఋణాత్మకంగా ఉండాలి. (K > 1)

ప్రశ్న 82.
ఒక ప్రక్రియలో 701 J ల ఉష్ణం వ్యవస్థ గ్రహించగా వ్యవస్థ 394J పనిని చేసింది. వ్యవస్థ అంతరిక శక్తి మార్పు ఎంత ?
జవాబు:
dq = dU – dW
701 = dU – (- 394 J)
dU = 701 – 394 = 307 J
వ్యవస్థ అంతరిక శక్తి మార్పు = 307 J

ప్రశ్న 83.
సయనమైడ్ NH₂CN, డైఆక్సిజన్ల మధ్య బాంబ్ కెలోరిమీటర్ 298K వద్ద చర్య జరిగితే ΔU = – 742.7 kJ mol^-1. ఇదే ఉష్ణోగ్రత వద్ద ఎంథాల్పీ మార్పు ఎంత ?
NH₂CN (వా) + \(\frac{3}{2}\) O₂(వా) → N₂(వా) + CO₂(వా) + H₂O(ద్ర)
జవాబు:
NH₂CN (వా) + \(\frac{3}{2}\) O₂(వా) → N₂(వా) + CO₂(వా) + H₂O(ద్ర)
మొత్తం వాయుస్థితిలో ఉన్న క్రియాజనకాల మోత్ల సంఖ్య = 1 + 1.5 = 2.5
మొత్తం వాయుస్థితిలో ఉన్న క్రియాజన్యాల మోల్ల సంఖ్య = 1 + 1 + 0 = 2
Δn = 2 – 2.5 = – 0.5
ΔΗ = ΔU + ΔnRT
= – 742.7 + (0.5 × 8.314 × 10^-3 × 298)
= -743.9 kJ

ప్రశ్న 84.
60g అల్యూమినియం ఉష్ణోగ్రతను 35°C నుంచి 55°C కు మార్చడానికి ఎన్ని KJ ఉష్ణం కావాలి ? అల్యూమినియం మోలార్ ఉష్ణధారణ = 24 J mol^-1K^-1.
జవాబు:
q = msdT
q = విడుదలయిన ఉష్ణం
m = అల్యూమినియం యొక్క ద్రవ్యరాశి
s = అల్యూమినియం మోలార్ ఉష్ణధారణ
dT = ఉష్ణోగ్రతలో వ్యత్యాసం
q = \(\frac{60}{27}\) × 24 × 20 = 1.067 కి.జౌ

ప్రశ్న 85.
1.0 mol నీటిని 10°C నుంచి మంచుగా – 10°C కు మార్చడానికి ఎంత ఎంథాల్పీ మార్పు తేవాలి ?
Δ_fus = 6.03 kJ mol^-1 at 0°C 38.
C_p[H₂O(ద్ర)] = 75.3J mol^-1K^-1
C_p[H₂O(ఘ)] = 36.8 J mol^-1K^-1
జవాబు:

1st step ఉష్ణం విడుదలయినది ΔH = nC_pdT = – 75.3 × 10 = – 753 J
2nd step ఉష్ణం విడుదలయినది ΔH = -6.0312 J
3rd step ఉష్ణం విడుదలయినది ΔH = nC_pdT = + 36.8 × 10 = + 368 J
∴ ΔH = -6.03 + (−0.753) + (+ 0.368) = – 6.415 kJ

ప్రశ్న 86.
C(ఘ) ను CO₂గా మార్చడానికి దహనక్రియ ఎంథాల్పీ – 393.5 kJ mol^-1. కార్బన్, డై ఆక్సిజన్ వాయువు నుంచి 35.2 g CO₂ ఏర్పడినప్పుడు విడుదలయ్యే ఉష్ణశక్తి ఎంత ?
జవాబు:
C (వా) + O₂ (వా) → CO₂ (వా), ΔH = -393.5 కి.జౌ
1 మోల్ CO₂ (44 గ్రా) CO₂ ఏర్పడేటపుడు విడుదలయ్యే ఉష్ణం = – 393.5 కి.జౌ
35.2 గ్రా. CO₂ ఏర్పడేటపుడు విడుదలయ్యే ఉష్ణం =\(\frac{35.2}{44}\) × -393.5 = -314.8 జౌ.

ప్రశ్న 87.
CO(వా), CO₂(వా), N₂O(వా), N₂O₄(వా)ల సంఘటన ఎంథాల్పీలు వరుసగా 9.7 kJ mol^-1. కింది చర్య Δ_rH విలువ కనుక్కోండి.
N₂O₄ (వా) + 3CO(వా) → N₂O(వా) + 3CO₂(వా)
జవాబు:

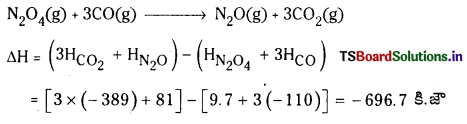
ప్రశ్న 88.
N₂(వా) + 3H₂(వా) → 2NH₃(వా) ; Δ_r\(\mathrm{H}^{\ominus}\) = – 92.4 kJ mol, అయితే అమ్మోనియా ప్రమాణ సంఘటన ఎంథాల్పీ ఎంత ?
జవాబు:
ఉష్ణం యొక్క చర్య Δ_r \(\mathrm{H}^{\ominus}\) is – 92.4 kJ mol^-1
పైన పేర్కొన్న సమీకరణం 2 మోల్స్ యొక్క అమ్మోనియా ఏర్పడటానికి అవసరమయిన ఉష్ణశక్తి.
ఒక్క మోల్ అమ్మోనియా ప్రమాణ సంఘటన ఎంథాల్పీ
NH₃ = \(\frac{-92.4}{2}\) = – 46.2 kJ
∴ అమ్మోనియా ప్రమాణ సంఘటన ఎంథాల్పీ = – 46.2 kJ

ప్రశ్న 89.
CH₃OH (ద్ర) ప్రమాణ సంఘటన ఎంథాల్పీని కింది చర్యల ద్వారా గణించండి.
CH₃OH (ద్ర) + \(\frac{3}{2}\)O₂(వా) → 2H₂O(ద్ర); Δ_r\(\boldsymbol{H}^{\ominus}\) = -726 kJ mol^-1
C(గ్రాఫైట్) + O₂(వా) → CO₂(వా) ; Δ_c\(\boldsymbol{H}^{\ominus}\) = -393 kJ mol^-1
H₂(వా) + \(\frac{1}{2}\)O₂(వా) → H₂O(ద్ర); Δ_f\(\boldsymbol{H}^{\ominus}\) = -286 kJ mol^-1
జవాబు:
ఇచ్చిన దత్తాంశం నుండి

1. CH₃OH (ద్ర) + \(\frac{3}{2}\)O₂(వా) → CO₂(వా) + 2H₂O(ద్ర); Δ_r\(\mathrm{H}^{\ominus}\) = -726 kJ mol^-1
2. C (graphite) + O₂(వా) → CO₂(వా); Δ_c\(\mathrm{H}^{\ominus}\) = – 393 kJ mol^-1
3. H₂(వా) + \(\frac{1}{2}\)O₂(వా) → H₂O(ద్ర); Δ_f\(\mathrm{H}^{\ominus}\) = – 286 kJ mol^-1

1ని ఉత్రమణీయం చేస్తే,

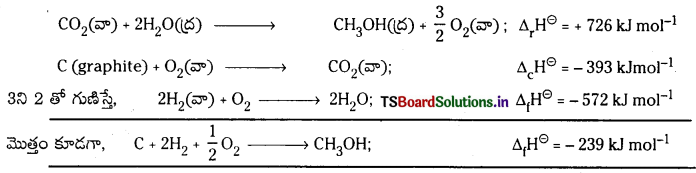
ప్రశ్న 90.
CCl₄(వా) → C(వా) + 4 Cl(వా) చర్యకు ఎంథాల్పీ మార్పు గణించండి.
CCl₄ లోని C – C బంధానికి బంధ ఎంథాల్పీ ఎంత ?
Δ_vap\(H^{\ominus}\)(CCl₄) = 30.5 kJ mol^-1.
Δ_r\(H^{\ominus}\) (CCl₄) = − 135.5 kJ mol^-1.
Δ_a\(H^{\ominus}\)(C) = 715.0 kJ mol^-1, ఇక్కడ Δ_a\(H^{\ominus}\) అనేది పరమాణీకరణ ఎంథాల్పీ,
Δ_a\(H^{\ominus}\)(Cl₂) = 242 kJ mol^-1
జవాబు:
C(s) + 2Cl₂(వా) → CCl₄(ద్ర)
Δ_rH° = [ΔH ఉత్పన్నాలు] – [ΔH క్రియాజనకాలు]
= 715 + 484 + 135.5 – 30.5
= 1334.5 – 30.5 = 1304 కి.జౌ.
∴ C – Cl బంధ ఎంథాల్పీ = \(\frac{1304}{4}\) = 326 కి.జౌ.

ప్రశ్న 91.
ఒక వివిక్త వ్యవస్థ ΔU = 0 అయితే ΔS ఏమవుతుంది ?
జవాబు:
ఇవ్వబడిన వివిక్త వ్యవస్థకు ΔU = 0
ΔH = ΔU + ΔnRT
∴ ΔH = ΔnRT
ΔS = \(\frac{\Delta \mathrm{H}}{\mathrm{T}}\) = \(\frac{\Delta \mathrm{nRT}}{\mathrm{T}}\)
∴ ΔS > 0 (లేక) ΔS = + ve

ప్రశ్న 92.
298 K వద్ద 2A + B → C చర్యకు ΔH = 400 kJ mol^-1‍ ΔS = 0.2 kJ K^-1 mol^-1 ఉష్ణోగ్రతా విస్తృతిలో ΔH, ΔS లు స్థిరంగా ఉంటాయనుకొంటే ఏ ఉష్ణోగ్రత వద్ద చర్య అయత్నీకృతం అవుతుంది ?
జవాబు:
సమతాస్థితి వద్ద ΔG = 0
T_equi = \(\frac{\Delta \mathrm{H}}{\Delta \mathrm{S}}\) = \(\frac{400}{0.2}\) = 2000 K
2000 °K వద్ద ప్రక్రియ అయత్నీకృతం అవుతుంది.

ప్రశ్న 93.
2Cl(వా) → Cl₂(వా) చర్యకు ΔH, ΔS ల గుర్తులు ఇవ్వండి.
జవాబు:
బంధం ఏర్పడినప్పుడు శక్తి విడుదలవుతుంది.
∴ ΔH = – ve
ఈ ప్రక్రియలో 2 క్లోరిన్ ఆటమ్స్ కలిసి ఒక Cl₂ అణువుగా ఏర్పడతాయి. ఇది ఉష్ణమోచక చర్య ఎంట్రోపీ తగ్గుతుంది.
∴ ΔS = – ve

ప్రశ్న 94.
2A (వా) + B(వా) → 2D(వా) చర్యకు 4\(U^{\ominus}\) = -10.5 kJ, Δ\(S^{\ominus}\) = – 44.1 JK^-1 చర్యకు 25°C వద్ద Δ\(\boldsymbol{G}^{\ominus}\) విలువ ఎంత ? చర్య అయత్నీకృతమా, కాదా ?
జవాబు:
ΔH = ΔU + Δn_gRT
ΔH = -10.5 + (-1) × 8.314 × 10^-3 × 298
= -12.97 kJ
ΔG = ΔH – TΔS
= -12.97 – 298 (-44.1 × 10^-3) = 0.164 kJ
ΔG = ధనాత్మకం (ΔG > 0 ). కావున చర్య అయత్నీకృతం కాదు.

ప్రశ్న 95.
ఒక చర్యకు 300K సమతాస్థితి స్థిరాంకం 10. దీనికి Δ\(\boldsymbol{G}^{\ominus}\) విలువ ఎంత ? R = 8.314 JK^-1mol^-1.
జవాబు:
Δ\(\boldsymbol{G}^{\ominus}\) = -2.303 RT log K_p
= -2.303 × 8.314 × 300 × 1 = – 5.744 kJ/mol

ప్రశ్న 96.
ఉష్ణగతికశాస్త్రం ప్రథమ నియమం నిర్వచించండి. దాని గణితరూప సమీకరణం రాయండి.
జవాబు:
ఉష్ణగతికశాస్త్ర ప్రథమ నియమం : “శక్తిని సృష్టింపలేము నశింపచెయ్యలేము. ఒక రూపములోని శక్తిని వేరొక రూపంలోకి మార్చగలము”.
లేదా
“మొదటిరకం సతతచలన యంత్ర నిర్మాణం అసాధ్యం”
లేదా
“చక్రీయ ప్రక్రియలో వ్యవస్థ శక్తి మార్పు శూన్యం”
ఒక వ్యవస్థ తొలి అంతరశక్తి E_A అని వ్యవస్థ గ్రహించిన ఉష్ణరాశి Q అని, వ్యవస్థ చేసిన పని “w”, అని దాని తుది అంతరికశక్తి E_B అని అంతరిక శక్తిలోని మార్పు ΔE అని అనుకుంటే
ΔE = E_B – E_A = Q – w
⇒ Q = ΔE + w
దీనినే ఉష్ణగతిక శాస్త్ర ప్రథమ నియమపు గణితాత్మక రూపం అంటారు.

ప్రశ్న 97.
ఉష్ణగతికశాస్త్రం రెండో నియమానికి ఏవైనా రెండు వేరువేరు నిర్వచనాలు ఇవ్వండి.
జవాబు:
క్లాసియస్ నిర్వచనం : విశ్వం యొక్క ఎంట్రోపీ గరిష్ఠంగా మారేదిశలో చలిస్తుంది.
లేదా
ఉష్ణశక్తి స్వచ్ఛందంగా చల్లని వస్తువు నుంచి వేడిగా గల వస్తువుకు ప్రసరించదు.
లేదా
పనిని పూర్తిగా ఉష్ణరాశిగా మార్చవచ్చు కానీ ఉష్ణరాశిని 100% పనిగా మార్పులు అసాధ్యం.
లేదా
అన్ని స్వచ్ఛంద చర్యలో ఫలిత ఎంట్రోపీ మార్పు ధనాత్మకం లేదా రెండోరకం సతతచలన యంత్ర నిర్మాణం అసాధ్యం.

ప్రశ్న 98.
గిబ్స్ శక్తిని వివరించండి.
జవాబు:
గిబ్స్ శక్తి : ఇది ఉష్ణగతిక ప్రమేయం. వీనిలో ఎంథాల్పీ ఎంట్రోపీ ప్రమేయాలు ఇమిడి వుంటాయి. ఒక చర్య స్వచ్ఛంద చర్య ఔనో, కాదో తెలుసుకొనుటకు ఇది తగినంత, అవసర సమాచారాన్ని ఇస్తుంది. ఇది స్థితి ప్రమేయం.

ప్రశ్న 99.
చర్య అయత్నీకృతాన్ని గిబ్స్ శక్తితో వివరించండి.
జవాబు:
ఒక స్వచ్ఛంద చర్యకు “ΔG” గిబ్స్ శక్తి మార్పు విలువ ఋణాత్మకంగా ఉండవలెను. భిన్న చర్యల ΔH, ΔS మరియు ΔG విలువలు క్రింది విధంగా ఉండును.

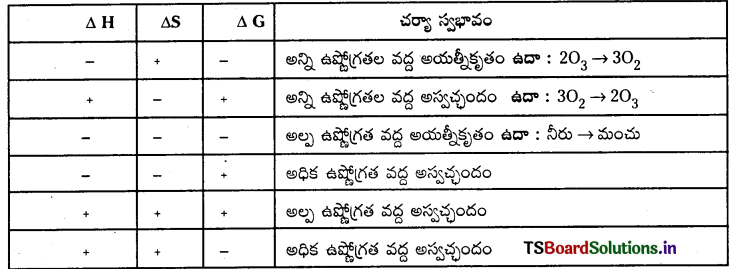
గిబ్స్ శక్తి మార్పు. (ΔG) కు, ఎంథాల్పీ మార్పు (ΔH) కు గల సంబంధం ఈ క్రింది విధంగా రాస్తారు.
ΔG = ΔH – TΔS
ΔG = + ve అయితే (ΔG > 0) ఆ చర్య అయత్నీకృత చర్య
AG = – ve అయితే (ΔG – 0) ఆ చర్య అనయత్నీకృత చర్య
ΔG = 0 అయితే ఆ చర్య సమతాస్థితిలో ఉంటుంది.
ΔG = + ve, ΔS = + ve అయితే – ప్రక్రియ అయత్నీకృతం (TΔS > ΔH గా ఉండాలి.)
ΔG = – ve, ΔS = + ve, ΔH = – ve అయితే ఆ చర్య అన్ని ఉష్ణోగ్రతల వద్ద అయత్నీకృతం.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 100.
హెస్ స్థిర ఉష్ణ సంకలనం నియమం నిర్వచించి వివరించండి. ఉదాహరణ ఇవ్వండి.
జవాబు:
ఒక రసాయన చర్య ఒక దశలో జరిగినా లేక అనేక దశల్లో జరిగినా ఆ చర్యలో జరిగే మొత్తం ఎంథాల్పీ మార్పు సమానంగా ఉంటుంది.
A అనే పదార్థం రెండు విభిన్న మార్గాల ద్వారా చర్య జరిపి అనే పదార్థాన్ని ఇచ్చినదని అనుకోండి.
ఏకదశ : A→ D; ΔH = Q
అనేక దశలు :
A → B; ΔH₁ = q₁
B → C; ΔH₂ = q₂
C → D; ΔH₃ = q₃
ΔH₁ + ΔH₂ + ΔH₃ = q₁ + q₂ + q₃
హెన్ నియమం ప్రకారం Q = q₁ + q₂ + q₃
ఏకదశ : C_{(గ్రాఫైట్)} + O₂ (g) → CO₂ (వా), Δ_r\(\mathrm{H}^{\ominus}\) = -393.5 kJ
అనేక దశలు : C_{(గ్రాఫైట్, S)} + \(\frac{1}{2}\)O₂ (g) → CO(వా), Δ_r\(\mathrm{H}^{\ominus}\) = -110.5 kJ
CO(వా) + \(\frac{1}{2}\) O₂ (వా) → CO₂ (వా), Δ_r\(\mathrm{H}^{\ominus}\) = -282.02 kJ
ఉదా : CO₂ (వా) ను C (గ్రా), O₂ (వా) నుండి రెండు విధాలుగా పొందవచ్చు.
అనేకదశలలో మొత్తం ఎంథాల్పీ మార్పు = – 392.52 కి.జౌ
ఏకదశలో మరియు అనేక దశలలో ఎంథాల్పీ మార్పు సమానంగా ఉంది కాబట్టి ఈ ఉదాహరణ హెస్ నియమానికి అనుగుణంగా ఉన్నది.

ఉపయోగాలు :

1. ప్రయోగం ద్వారా నిర్ణయించడానికి వీలుకాని సమ్మేళనాల సంఘటనోష్టాలను ఈ నియమం ద్వారా పరోక్షంగా లెక్కించవచ్చు.
2. నెమ్మదిగా జరిగే చర్యల చర్యోష్ణాన్ని నిర్ణయించవచ్చు.
3. అయానిక పదార్థాల స్ఫటిక జాలకశక్తిని నిర్ణయించవచ్చు.
4. కొన్ని మూలకాల ఎలక్ట్రాన్ ఎఫినిటి విలువలను పరోక్ష పద్ధతిలో కనుగొనవచ్చు.

ప్రశ్న 101.
ప్రయోగపూర్వకంగా ఒక ప్రక్రియలో అంతరిక శక్తి మార్పు కొలిచే విధానం వివరించండి.
జవాబు:
అంతరిక శక్తి : స్థిర ఉష్ణోగ్రత పీడనాల వద్ద ఒక పదార్థంలో నిల్వ ఉంచబడిన మొత్తం శక్తిని అంతరిక శక్తి అంటారు. ఇది స్థితి ప్రమేయం-మరియు విస్తార ధర్మం.
అంతరిక శక్తిలో మార్పు (ΔU) = U_p – U_R
U = క్రియాజన్యాల అంతరికశక్తి; Up – క్రియాజనకాల అంతరికశక్తి.
ΔU = Q – w;
Q = ఉష్ణం;
W = పని

అంతరికశక్తి మార్పు ΔU కొలిచే సాధనం : రసాయన చర్యల్లో స్థిర ఘనపరిమాణం వద్ద గ్రహించబడిన ఉష్ణాన్ని బాంబ్ కెలోరిమీటర్లో కొలుస్తారు. బాంబ్ కెలోరిమీటర్ ఒక దృఢమైన గోడలు గల ఉక్కుపాత్ర. ఇది ఒక జల పతాకంలో ముంచబడి వుంటుంది. ఈ మొత్తం పాత్రల అమరికనే కెలోరిమీటర్ అంటారు. తేలికగా దహనం చెందే
పదార్థాన్ని ఉక్కు బాంబులో వుంచి ఆక్సిజన్ను కలిపి దహనం చేస్తారు. చర్య ఉష్ణమోచకమై ఉష్ణం వెలువడుతుంది. ఇది కెలోరిమీటర్ ఉష్ణోగ్రతను పెంచుతుంది. బాంబ్ కెల్ రెమీటర్ ఉష్ణబంధకం చేయబడి వుంటుంది. అందువల్ల కెలోరిమీటర్ నుంచి పరిసరాలకు ఉష్ణ వినిమయం జరగదు.

బాంబ్ కెలోరిమీటర్ చర్య జరిగేటపుడు పూర్తిగా మూసివుంచబడి వుంటుంది. కాబట్టి దాని ఘనపరిమాణంలో మార్పు ఉండదు. అంటే చర్యలో శక్తి మార్పులు స్థిర ఘనపరిమాణంలో జరిగిన వాటిగా అనుకొని కొలతలు చేయాలి. స్థిర ఘనపరిమాణం అంటే ΔU = 0, w = p ΔU = 0, అంటే చర్యలో పని ఏమీ జరగదు. చర్యలో వాయు పదార్థాలున్నప్పటికీ ఘనపరిమాణంలో మార్పురాదు. చర్య వల్ల కెలోరిమీటర్ పెరిగిన ఉష్ణోగ్రతను ఉపయోగించి కెలోరిమీటర్ ద్రవ్యరాశి, దాని ఉష్ణధారణ విలువల ద్వారా వెలువడిన ఉష్ణాన్ని (q₁) క్రింది సమీకరణం ఉపయోగించి గణించవచ్చు.
విశిష్టోష్టణం × ద్రవ్యరాశి = ఉష్ణధారణ
q = C × m × ΔT = C × ΔT ఇచ్చట c × m = C

ప్రశ్న 102.
ప్రయోగ పూర్వకంగా ఒక ప్రక్రియలో ఎంథాల్పీ మార్పు కొలిచే విధానం వివరించండి.
జవాబు:
ఎంథాల్పీ (H) స్థిర పీడనం మరియు ఉష్ణోగ్రత వద్ద వ్యవస్థకు, పరిసరాలకు మధ్య మార్పిడి జరిగే ఉష్ణపరిమాణాన్ని ఎంథాల్పీ (H) అంటారు.
ఎంథాల్పీ మార్పు (ΔH) = ΔU + PΔU (లేక) ΔH + ΔnRT
ΔU = అంతరికశక్తి మార్పు,
P = పీడనం,
ΔV = ఘనపరిమాణంలో మార్పు.
ఎంథాల్పీ స్థితి ప్రమేయం మరియు విస్తార ధర్మం.

ఎంథాల్పీ మార్పు (ΔH) = H_{క్రియాజన్యాలు} – H_{క్రియాజనకాలు}
స్థిరపీడనం వద్ద ఉష్ణశక్తి ΔH ని కొలవడం : మూత లేకుండా తెరచి వున్న కెలోరిమీటర్ సాధారణంగా వాతావరణ పీడనం దగ్గర వుంటుంది. వాతావరణ పీడనం స్థిరంగా వుంటుంది కాబట్టి కెలోరిమీటర్లో చర్య వల్ల వచ్చిన ఉష్ణ మార్పు స్థిరపీడనం వద్ద కొలిచిందిగా భావించవచ్చు. దీనిని రాస్తే ΔH కు సమానమవుతుంది. ΔH = q_p. కాబట్టి స్థిరపీడనం వద్ద కొలిచిన ఉష్ణమార్పు చర్యోష్ణం (అది వెలువడిన ఉష్ణం కావచ్చు లేదా గ్రహించబడిన ఉష్ణం కావచ్చు. లేదా చర్యా ఎంథాల్పి Δ_rH అవుతుంది.

ఉష్ణమోచక చర్యలో ఉష్ణం వెలువడుతుంది. అంటే వ్యవస్థ నుంచి పరిసరాలకు ఉష్ణం ఇవ్వబడుతుంది. అందువల్ల q_p రుణాత్మకమవుతుంది. Δ_rH కూడా రుణాత్మకం. అదేవిధంగా ఉష్ణగ్రాహక చర్యలో వ్యవస్థ లేదా చర్య ఉష్ణం గ్రహిస్తుంది. అంటే పరిసరాల నుంచి చర్యకు ఉష్ణం ఇవ్వబడుతుంది. దీనికి q_p ధనాత్మకం Δ_rH కూడా ధనాత్మకమే.

ప్రశ్న 103.
ఒక చర్య అయత్నీకృతమా కాదా అన్నది ఎంథాల్పీ, ఎంట్రోపీ, గిబ్స్ శక్తులు ఉపయోగించి వివరించండి.
జవాబు:
అయత్నీకృత చర్య : బాహ్యకారకం ప్రమేయం లేకుండా స్వచ్ఛందంగా జరిగే చర్యను అయత్నీకృత చర్య అంటారు. అయత్నీకృత చర్యలు అన్నీ ఉష్ణగతిక శాస్త్రం ప్రకారం, “అద్విగత చర్యలే”.

1. ప్రకృతిలో జరిగే చర్యలు అన్నీ అయత్నీకృత చర్యలే
2. అన్ని అయత్నీకృత చర్యలలో ఎంట్రోపీలో పెరుగుదల ఉంటుంది.
3. అయత్నీకృత చర్యలలో, ఎంథాల్పీ మార్పు (ΔS) = + ve
4. అయత్నీకృత చర్యలలో, ఎంథాల్పీ మార్పు (ΔH) = – ve
5. అయత్నీకృత చర్యల యొక్క నిబంధనను వివరించడానికి “గిబ్స్” ఒక ఉష్ణగతిక ప్రమేయాన్ని ప్రవేశపెట్టాడు. దానినే గిబ్స్ శక్తి అంటారు. ఈ గిబ్స్ శక్తికి, ఎంథాల్పీకి, ఎంట్రోపికి సంబంధం క్రింది విధంగా ఉంటుంది.

G = H – TS. దీనినే గిబ్స్ సమీకరణం అంటారు. అన్ని అయత్నీకృత చర్యలను
ΔG = – ve స్థిర ఉష్ణోగ్రత, మరియు పీడనం వద్ద జరిగే మార్పును గిబ్స్ సమీకరణాన్ని క్రింది విధంగా రాస్తారు.
ΔG = ΔH – TΔS
ΔS = + ve అయితే ప్రక్రియ అయత్నీకృతం
ΔS = – ve అయితే తిరోగామి చర్య అయత్నీకృతం
ΔS = 0, అయితే ప్రక్రియ సమతాస్థితితో ఉంటుంది.

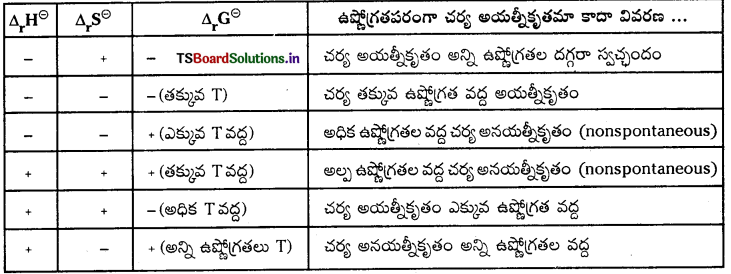
అయత్నీకృత చర్యలు – నిబంధనలు :

చర్యల స్వచ్ఛందత లేదా అయత్నీకృతంపై ఉష్ణోగ్రత ప్రభావం

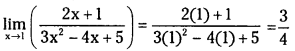
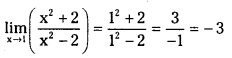
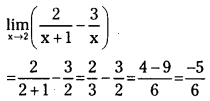
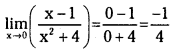
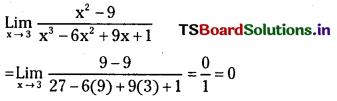
Students must practice these TS Inter 1st Year Maths 1B Study Material Chapter 9 Differentiation Ex 9(b) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Differentiation 9(b)

I.
Question 1.
Find the derivatives of the following functions. (V.S.A.Q.)
(i) cotⁿx
Answer:
Let y = cotⁿx
Then \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = – n cot^{n – 1}x (cosec²x)
= – n cot^n-1 x (cosec²x)
(∵ \(\frac{\mathrm{d}}{\mathrm{dx}}\) (cot x) = – cosec² x)

(ii) cosec⁴x
Answer:
Let y = cosec⁴x
Then \(\frac{d y}{d x}\) = 4 cosec³x \(\frac{\mathrm{d}}{\mathrm{d} x}\) (cosec x)
= 4 cosec³x (- cosec x cot x)
= – 4 cosec⁴x cot x

(iii) tan (e^x)
Answer:
Let y = tan (e^x)
Then \(\frac{d y}{d x}\) = sec² (e^x) \(\frac{d}{d x}\) (e^x)
= e^x.sec²(e^x)

(iv) \(\frac{1-\cos 2 x}{1+\cos 2 x}\)
Answer:
Let y = \(\frac{1-\cos 2 x}{1+\cos 2 x}=\frac{2 \sin ^2 x}{2 \cos ^2 x}\) = tan² x
∴ \(\frac{d y}{d x}\) = 2 tan x \(\frac{\mathrm{d}}{\mathrm{dx}}\) (tan x)
= 2 tan x sec²x

(v) sin^mx cosⁿx
Answer:
Let y = sin^mx cosⁿx
Then \(\frac{d y}{d x}\) = sin^mx \(\frac{d}{d x}\) (cosⁿx) + cosⁿ\(\frac{d y}{d x}\)(sin^mx)
= sin^mx n cos^{n – 1}x (- sin x) + cosⁿx (m sin^{m – 1}x) cos x
= m cos^{n + 1}x sin^{m – 1}x – n sin^{m + 1}x cos^{n – 1}x

(vi) sin mx . cos nx
Answer:
Let y = sin mx cos nx
Then \(\frac{d y}{d x}\) = sin mx . \(\frac{d}{d x}\) (cos nx) + cos nx \(\frac{d}{d x}\) (sin mx)
= sin mx (- n sin nx) + cos nx (m cos mx)
= – n sin mx sin nx + m cos nx cos mx

(vii) x . tan^-1 x
Answer:
Let y = x . tan^-1x

(viii) sin^-1 (cos x)
Answer:
Let y = sin^-1 (cos x)

(ix) log (tan 5x)
Answer:
Let y = log (tan 5x)

(x) sinh^-1 \(\left(\frac{3 x}{4}\right)\)
Answer:

(xi) tan^-1 (log x)
Answer:
Let y = tan^-1 (log x)

(xii) log\(\left(\frac{x^2+x+2}{x^2-x+2}\right)\) (May 2006)
Answer:

(xiii) log [sin^-1 (e^x)]
Answer:
Let y = log [sin^-1 (e^x)]

(xiv) (sin x)² (sin^-1x)²
Answer:
Let y = (sin x)² (sin^-1x)²

(xv) \(\frac{\cos x}{\sin x+\cos x}\)
Answer:

(xvi) \(\frac{x\left(1+x^2\right)}{\sqrt{1-x^2}}\)
Answer:

(xvii) e^sin-1x
Answer:
Let y = e^sin-1x

(xviii) cos (log x + e^x
Answer:
Let y = cos (log x + e^x
\(\frac{d y}{d x}\) = – sin(log x + e^x) \(\frac{\mathrm{d}}{\mathrm{dx}}\) (log x + e^x)
= – sin (log x + e^x) (\(\frac{1}{x}\) + e^x)

(xix) \(\frac{\sin (x+a)}{\cos x}\)
Answer:

(xx) cot^-1 (cosec 3x)
Answer:
Let y = cot^-1 (cosec 3x)

Question 2.
Find the derivatives of the following functions. (V.S.A.Q.)
(i) x = sin h²y
Answer:

(ii) x = tanh²y
Answer:

(iii) x = e^{sinh y}
Answer:
\(\frac{\mathrm{dx}}{\mathrm{dy}}\) = e^{sin hy} \(\frac{\mathrm{d}}{\mathrm{dy}}\) (sin hy)
= e^sinhy cos hy = x cos hy

(iv) x tan (e^-y)
Answer:
\(\frac{\mathrm{dx}}{\mathrm{dy}}\) = sec²(e^-y) \(\frac{d}{d y}\) (e^-y)
= – sec²(e^-y) (e^-y)
= – e^-y (1 + tan² (e^-y)) = – e^-y(1 + x²)

(v) x = log (1 + sin²y)
Answer:

(vi) x = log(1 + √y)
Answer:
1 + √y = e^x
√y = e^x – 1
y = (e^x – 1)²
∴ \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 2(e^x – 1) . \(\frac{\mathrm{d}}{\mathrm{dx}}\) (e^x
= 2(e^x – 1) e^x
= 2√y (√y + 1) = 2(y + √y)

II. Find the derivatives of the following functions. (V.S.A.Q.)

(i) cos [log (cot x)]
Answer:
y = cos [log (cot x)]
Let cot x = u, log u = v, so that y = cos v

(ii) sin h^-1
Answer:

(iii) log [cot (1 – x²)]
Answer:
y = log [cot (1 – x²)]
Let 1 – x² = u, cot u = v, and y = log v

(iv) sin [cos (x²)]
Answer:
y = sin [cos (x²)]
Let x² = u, v = cos u and y = sin v
\(\frac{d y}{d x}=\frac{d y}{d v} \cdot \frac{d v}{d u} \cdot \frac{d u}{d x}\)
= cos v(- sin u) (2x)
= – 2x cos (cos u) sin u
= – 2x cos [(cos (x²)] sin (x²)

(v) sin [tan^-1 (e^x)]
Answer:
y = sin [tan^-1 (e^x)]
Let e^x = u, tan^-1u = v and y = sin v

(vi) \(\frac{\sin (a x+b)}{\cos (c x+d)}\)
Answer:

(vii) tan^-1 (tanh \(\frac{x}{2}\))
Answer:

(viii) sin x (tan^-1x)
Answer:
Let y = sin x (tan^-1x)²

III. Find the derivatives of the following functions.

Question 1.
sin^-1\(\left(\frac{b+a \sin x}{a+b \sin x}\right)\) (a > o, b > 0) (E.Q.)
Answer:

Question 2.
cos^-1\(\left(\frac{b+a \cos x}{a+b \cos x}\right)\) (a > 0, b > 0) (E.Q.)
Answer:

Question 3.
tan^-1 \(\left(\frac{\cos x}{1+\cos x}\right)\)
Answer:

Here students can locate TS Inter 1st Year Economics Notes Chapter 5 Market Analysis to prepare for their exam.

TS Inter 1st Year Economics Notes Chapter 5 Market Analysis

→ Market: The market is a mechanism where the activities of selling and purchasing of goods and services take place.

→ Perfect Competition: Perfect competition is a market where a large number of buyers and sellers exist. All goods are homogeneous and sold at the same price.

→ Monopoly: A monopoly is a market with a single producer and the product will not have any close substitutes.

→ Monopolistic Competition: It is a market where several firms will produce the same commodity with small differences. Here advertisement takes place.

→ Product differentiation: Small differences exist between the products of different firms. Their cross elasticity of demand is more.

→ Selling Costs: Firms will spend on advertisements to increase their sales. These expenses are called selling costs.

→ Oligopoly: Oligopoly is a market where a few firms produce the goods. The price of a good is decided independently or collectively by the firms.

→ Duopoly: Duopoly is a market where only two producers exist in the market. It is a limited form of oligopoly.

→ Equilibrium Price: Equilibrium Price is that price where demand and supply are equal in the market.

→ Equilibrium of a Firm: A firm is said to be in equilibrium at a point where it has no desire either to expand or to contract its output.

TS Inter 1st Year Economics Notes Chapter 5 మార్కెట్ విశ్లేషణ

→ వస్తు సేవల కొనుగోళ్ళు, అమ్మకాలు జరిగే ప్రదేశాన్ని మార్కెట్ అంటారు.

→ మార్కెట్ను విస్తీర్ణం, కాలవ్యవధి, పోటీని బట్టి వివిధ రకాలుగా వర్గీకరించవచ్చును.

→ విస్తీర్ణం ఆధారంగా మార్కెట్ను స్థానిక మార్కెట్, జాతీయ మార్కెట్, అంతర్జాతీయ మార్కెట్ అని మూడు రకాలుగా విభజిస్తారు.

→ కాల వ్యవధి ఆధారంగా మార్కెట్ను అతిస్వల్పకాలిక మార్కెట్, స్వల్పకాలిక మార్కెట్, దీర్ఘకాలిక మార్కెట్గా విభజిస్తారు.

→ పోటీ ఆధారంగా పరిపూర్ణ పోటీ మార్కెట్, అపరిపూర్ణ పోటీ మార్కెట్ అని రెండు రకాలుగా మార్కెట్ను విభజిస్తారు.

→ అనేకమంది అమ్మకందార్లు, కొనుగోలుదార్లు ఉండటం, సజాతీయమైన వస్తువు ఉత్పత్తి, సంస్థల స్వేచ్ఛా ప్రవేశం, నిష్క్రమణ, ఉత్పత్తి కారకాల గమనశీలత, రవాణా ఖర్చులు లేకుండుట, మార్కెట్లో ఒకే ధర ఉండటం అనేవి పరిపూర్ణ పోటీ లక్షణాలు.

→ కొనుగోలుదార్ల మధ్యకాని, అమ్మకందార్ల మధ్యకాని సంపూర్ణ పోటీ లేనటువంటి దానిని అసంపూర్ణ పోటీ అంటారు. దీనిలో ధర విచక్షణ ఉంటుంది.
ఈ అపరిపూర్ణ పోటీ మార్కెట్ ముఖ్యంగా నాలుగు రకాలు:

1. ఏకస్వామ్యం
2. ద్విస్వామ్యం
3. పరిమితస్వామ్యం
4. ఏకస్వామ్య పోటీ మార్కెట్

Here students can locate TS Inter 1st Year Economics Notes Chapter 4 Production Analysis to prepare for their exam.

TS Inter 1st Year Economics Notes Chapter 4 Production Analysis

→ Production: Production is the process that converts inputs into output. By using resources in the production process consumption goods or capital goods will be produced.

→ Production function: The production function shows the relationship between the inputs used and the output produced by a firm.

→ Factors of production: Factors that help in the production are called factors of production. These are land, labour, capital and organization.

→ Short period: Short period is a period in which a producer can’t change land, capital and organization. Labour can be changed.

→ Long period: It is a period in which all factors of production can be changed by the producer to increase or decrease output.

→ Average product: Average product can be obtained by dividing total product by the number of labourers.

→ Marginal product: Marginal product is the additional production by employing an additional unit of a labourer.

→ Fixed factors: Land, capital and entrepreneurship are the fixed factors of production in the short run. We cannot change them.

→ Variable factors: Factors of production which can be changed. Labour is a variable factor in the short run. In the long run all the factors of production are variable.

→ Change in the scale of Production: Change in the scale of production relates to the changes in the production due to the changes in the combination of factors of production in long run.

→ Internal economies: Internal economies refer to the benefits accrued to individual firms due to the expansion of their production activity.

→ External economies: These refer to the returns accrued to all thb firms in the industry as a result of the expansion of the industry as a whole.

→ Supply: Supply is the quantity of a good offered by the producer for sale at the given prices during a certain period.

→ Supply function: Supply function shows the relationship between the determinants of supply and the supply of a good.

→ Opportunity cost: It denotes the foregone production when a factor is shifted from one use to another use.

→ Total cost: Total cost can be obtained by adding the payments made to the fixed and variable factors in the short run.

→ Fixed costs: Fixed costs are payments made to the fixed factors by a firm in the short run. These costs are fixed and will not change along with the changes in the output.

→ Variable costs: Variable costs are the payments made to the variable factors in the short run. These will change along with the changes in the output.

→ Average cost: Production cost per unit of a good production can be obtained by dividing the total cost by the total number of goods.

→ Marginal cost: Marginal cost is the change in total cost when we produce an additional unit of a commodity.

→ Total revenue: Total revenue is the amount earned by a firm by selling goods in the market. By multiplying the price by the number of goods sold, we get the total revenue.

→ Average revenue: Average revenue can be obtained by dividing the total revenue by number of goods sold.

→ Marginal revenue: Marginal revenue is the additional revenue earned by selling an additional unit of the good.

TS Inter 1st Year Economics Notes Chapter 4 ఉత్పత్తి విశ్లేషణ

→ ఉత్పత్తి అనగా ప్రయోజనాల సృష్టి.

→ ఉత్పత్తిలో పాల్గొనే కారకాలను ఉత్పత్తి కారకాలంటారు. అవి నాలుగు: 1. భూమి. 2. శ్రమ. 3. మూలధనం 4. వ్యవస్థాపన.

→ భౌతిక ఉత్పత్తి సాధనాలకు, భౌతిక ఉత్పత్తికి మధ్య గల సంబంధంను ఉత్పత్తి ఫలం అంటారు.

→ స్వల్పకాలం అనగా ఉత్పత్తి ప్రక్రియలో చర సాధనాలను మాత్రమే మార్చి, ఉత్పత్తిలో మార్పులు చేపట్టగలిగే కాలపరిధి.

→ చరానుపాత సూత్రం స్వల్ప కాలానికి చెందినది. ఈ సూత్రం ప్రకారం కొన్ని ఉత్పత్తి కారకాలను స్థిరంగా ఉంచి చర ఉత్పత్తి సాధనం పరిమాణంలో మార్పు చేస్తూ ఉన్నప్పుడు ఉత్పత్తి ఏ అనుపాతంలో మారుతుందో తెలియజేస్తుంది.

→ దీర్ఘకాలంలో అన్ని ఉత్పత్తి సాధనాలు చర అనుపాతంలో మారినపుడు ఉత్పత్తి ఏ అనుపాతంలో మార్పు చెందుతుందో తెలియజేసే దానిని తరహాననుసరించి ప్రతిఫలాలు అంటారు.

→ ఒక నిర్ణీత ధర వద్ద, నిర్ణీతకాలంలో, మార్కెట్లో విక్రయానికి సిద్ధంగా ఉన్న వస్తు పరిమాణాన్ని సప్లయ్ అంటారు. ఇతర పరిస్థితులు మారనంత వరకు ఒక వస్తువు ధర తగ్గితే సప్లయ్ తగ్గుతుంది. ధర పెరిగితే సప్లయ్ పెరుగుతుంది.

→ ఒక ఉత్పత్తిదారుడు ఉత్పత్తికి వెచ్చించే మొత్తాన్ని “ఉత్పత్తి వ్యయం” అంటారు. వ్యయాలు రెండు రకాలు:

1. సాధారణ వ్యయాలు
2. ఆర్థిక వ్యయాలు.

Here students can locate TS Inter 1st Year Economics Notes Chapter 3 Demand Analysis to prepare for their exam.

TS Inter 1st Year Economics Notes Chapter 3 Demand Analysis

→ Demand: The desire backed up by willingness and ability to pay a sum of money for some quantity of a good or service.

→ Demand function: It is the functional relationship between the quantity demanded for a good and all the quantitative factors which determine the demand.

→ Demand schedule: It is the table that shows the relation between the prices and quantities demanded.

→ Individual demand: It is the quantity demanded by a single consumer in the market.

→ Market demand: It is the total demand for the commodities in the market.

→ Substitute goods: Substitutes are those goods that satisfy the same want.

→ Complementary goods: Complementaries are those goods that satisfy the same want jointly.

→ Price demand: It refers to the functional relationship between the price of the good and the quantity demanded.

→ Superior goods: In case of superior goods, quantity demanded increases when there is an increase in the income of consumers. There exists a positive relationship between income and quantity demanded.

→ Inferior goods: Quantity demanded of inferior goods decreases with the increase in income of the consumers. There exists an inverse relationship between income and quantity demanded.

→ Elasticity: Elasticity is the ratio between the proportional change of one variable and the proportional change of another variable.

→ Price Elasticity of demand: It Is the percentage or proportional change in quantity demanded of a commodity as a result of percentage change in price of that commodity; other things like income, tastes, prices of related goods etc., remain constant.

→ Income elasticity of demand: It is the percentage change in the quantity demanded of a commodity as a result of the percentage change in the income of the consumer.

→ Cross elasticity of demand: It is the percentage change in the quantity demanded of a commodity as a result of a proportional change in the price of a related commodity.

→ Unitary elastic demand: In such case, the elasticity of demand is equal to one and the demand curve will be in the shape of a ‘rectangular hyperbola’.

TS Inter 1st Year Economics Notes Chapter 3 డిమాండ్ విశ్లేషణ

→ ఒక నిర్ణీత కాలంలో, నిర్ణీతమైన ధర వద్ద కొనుగోలుకు సిద్ధంగా ఉన్న వస్తువు పరిమాణాన్ని ఆ వస్తువుకు ఉన్న డిమాండ్ అంటారు.

→ ఒక వస్తువు డిమాండ్ పరిమాణానికి, దానిని నిర్ణయించే కారకాలకు మధ్యగల సంబంధాన్ని తెలియజేసేది డిమాండ్ ఫలం. దీనిని D_x = f(P_x, P_y, ………….. P_x-1, Y, T) అనే సమీకరణం ద్వారా తెలియజేయవచ్చు.

→ ఒక వస్తువు ధర, వినియోగదారుని ఆదాయాలు, వినియోగదారుల అలవాట్లు, అభిరుచులు మొదలైన అంశాలు వస్తువు డిమాండ్ను నిర్ణయిస్తాయి.

→ ఇతర పరిస్థితులు మారకుండా స్థిరంగా ఉన్నప్పుడు ఒక నిర్ణీత కాలంలో ఒక వస్తువు ధర తగ్గితే డిమాండ్ పెరుగుతుంది. ధర పెరిగితే డిమాండ్ తగ్గుతుందని డిమాండ్ సూతం నిర్వచించును.

→ ఇతర అంశాలు స్థిరంగా ఉన్నప్పుడు ధర పెరిగితే డిమాండ్ తగ్గుతుంది, ధర తగ్గితే డిమాండ్ పెరుగుతుంది. ధరకు, డిమాండ్కు మధ్య ఉన్న సంబంధాన్ని తెలిపేది ధర డిమాండ్.

→ ఆదాయానికి, కొనుగోలు చేసే వస్తు పరిమాణానికి మధ్య ఉన్న సంబంధాన్ని ఆదాయ డిమాండ్ అంటారు. ఇతర అంశాలు స్థిరంగా ఉండి ఆదాయం పెరిగితే డిమాండ్ పెరుగుతుంది, ఆదాయం తగ్గితే డిమాండ్ తగ్గుతుంది. ఆదాయ డిమాండ్ను బట్టి వస్తువులను మేలురకం మరియు నాసిరకం వస్తువులుగా గుర్తించవచ్చు.

→ ప్రత్యామ్నాయ పూరక వస్తువుల ధరకు, ఒక వస్తువు డిమాండ్కు మధ్య ఉన్న సంబంధాన్ని జాత్యంతర డిమాండ్ అంటారు.

→ ఒక వస్తువు ధరలో మార్పు కలిగినప్పుడు ఏ మేరకు డిమాండ్లో ప్రతిస్పందన వస్తుందో తెలియజేసేదే డిమాండ్ వ్యాకోచత్వం.

→ వ్యాకోచత్వాలు మూడు రకాలు. 1) ధర డిమాండ్ వ్యాకోచత్వం 2) ఆదాయ డిమాండ్ వ్యాకోచత్వం 3) జాత్యంతర డిమాండ్ వ్యాకోచత్వం.

→ ధర డిమాండ్ వ్యాకోచత్వం ఐదు రకాలు.

1. పూర్తి వ్యాకోచత్వం
2. పూర్తి అవ్యాకోచత్వం
3. ఏకత్వ వ్యాకోచత్వం
4. సాపేక్ష వ్యాకోచత్వం
5. సాపేక్ష అవ్యాకోచత్వం.

→ ఆదాయంలో వచ్చే మార్పు వల్ల వస్తువు డిమాండ్లో వచ్చే పరిమాణాత్మక మార్పును ఆదాయ డిమాండ్ వ్యాకోచత్వం అంటారు.

→ ఒక వస్తువు ధరలో వచ్చిన మార్పు వల్ల దాని పత్యామ్నాయ లేదా పూరక సంబంధమైన వస్తువు డిమాండ్లో వచ్చిన పరిమాణాత్మకమైన మార్పును తెలియజేసేది జాత్యంతర డిమాండ్ వ్యాకోచత్వం.

Here students can locate TS Inter 1st Year Economics Notes Chapter 2 Theories of Consumer Behaviour to prepare for their exam.

TS Inter 1st Year Economics Notes Chapter 2 Theories of Consumer Behaviour

→ Utility means wanting satisfying power of a thing, measurement of utility can be two types: 1. Cardinal utility 2. Ordinal utility.

→ Cardinal utility was developed by Alfred Marshall. According to the cardinal utility approach, a utility can be measured in terms of numbers like 1, 2, 3, 4 etc.

→ Ordinal utility approach was developed by R.J.D. Hicks & Allen. According to this approach, utility is subjective. So, it is not possible to measure in terms of numbers. They are ranked 1st, 2nd, 3rd etc.

→ The law of Diminishing marginal utility was developed by H.H. Gossen in 1854 and later it was popularised by Marshall. This law shows the relationship between the quantity of a thing consumed and its marginal utility. If a consumer goes on consuming a commodity then the satisfaction that derives from its additional units declines.

→ The law of Equi-Marginal Utility explains as to how a consumer distributes his limited income among various commodities to get maximum satisfaction. The consumer will be in equilibrium when the following condition is satisfied :

→ Indifference curve is a technique based on the ordinal utility approach. Ic represents the satisfaction of a consumer from two goods.

→ MRS is the rate at which an individual exchanges successive units of one commodity for another.

→ A set of indifference curves drawn for different income levels is called as an indifference map.

→ Consumer equilibrium is a point where the consumer gets maximum satisfaction from two goods.

TS Inter 1st Year Economics Notes Chapter 2 ప్రవర్తనా సిద్ధాంతాలు

→ ఒక వస్తువుకు ఉండే మానవుని కోరికను తీర్చగలిగే శక్తిని ప్రయోజనం అంటారు.

→ వివిధ వస్తువుల నుంచి పొందే ప్రయోజనాలను యుటిల్స్ అనే ఊహాత్మక యూనిట్ల ద్వారా కొలవడానికి వీలుంది. దీనిని అభివృద్ధిపరచినది మార్షల్. 1, 2, 3 మొదలగు సంఖ్యలను కార్డినల్ సంఖ్యలు అంటారు. వీటి ద్వారా వినియోగదారుని ప్రయోజనమును కొలవవచ్చు.

→ వస్తువు అన్ని యూనిట్ల వినియోగం ద్వారా పొందగలిగే మొత్తం తృప్తిని మొత్తం ప్రయోజనం అంటారు.

→ వినియోగదారుడు అదనంగా వస్తువు యూనిట్ను ఉపయోగించడం వల్ల మొత్తం ప్రయోజనంలో కలిగే మార్పు MO = ΔTU/ΔQ

→ క్షీణోపాంత ప్రయోజన సూత్రంను గాసెన్ మొదటి సూత్రం అంటారు. ఇది వస్తు పరిమాణానికి, ప్రయోజనానికి మధ్య ఉన్న సంబంధాన్ని గూర్చి తెలుపును. ఒకే రకమైన వస్తువును వినియోగదారుడు క్రమంగా ఎక్కువగా వినియోగిస్తూ ఉంటే, మొత్తం ప్రయోజనం ఒక దశ వరకు పెరిగి, ఆ తరువాత తగ్గుతుంది.

→ సమోపాంత ప్రయోజన సూత్రాన్ని గాసెన్ ద్వితీయ సూత్రం అని కూడా అంటారు. వినియోగదారుడు తన పరిమితమైన ఆదాయాన్ని ఖర్చుచేసి ఏ విధంగా గరిష్ట ప్రయోజనం పొందుతాడో తెలియజేసేది.

→ కార్డినల్ విశ్లేషణలో ప్రయోజనం అనేది మానసికపరమైంది. అందువల్ల దాన్ని సంఖ్యా రూపంలో కొలవడానికి సాధ్యం కాదు. అందువల్ల R.J.D. హిక్స్ మరియు అలెన్ ఆర్డినల్ విశ్లేషణ ద్వారా వినియోగదారుని ప్రవర్తనను తెలియజేశారు. ఈ విశ్లేషణలో వినియోదారు తనకు లభ్యమైన వివిధ వస్తు సముదాయాలకు ర్యాంకులు 1, 2, 3 మొదలైనవి ఇవ్వడం ద్వారా వాటన్నిటిని క్రమ పద్ధతిలో ఏర్పరచుకుంటారు.

→ వినియోగదారుడు కొనుగోలు చేసే రెండు వస్తువుల వివిధ సమ్మేళనాలను తెలియజేసే బిందువులను కలుపగా ఏర్పడే రేఖలను “ఉదాసీనతా వక్రరేఖ” అంటారు. దీని ద్వారా కూడా వినియోగదారుని ప్రయోజనాన్ని కొలవవచ్చు.

Here students can locate TS Inter 1st Year Economics Notes Chapter 1 Introduction to Economics to prepare for their exam.

TS Inter 1st Year Economics Notes Chapter 1 Introduction to Economics

→ Economics is a social science. It explains how an economy and different individuals behave while managing their economic activities.

→ The term Economics is originated from greek words ‘OIKOS’ and ‘Nemein’.

→ Economic problem is concerned with economizing scarce resources. Wants, efforts and satisfaction constitute the essence of economics.

1. Wealth definition – Adam Smith
2. Welfare definition – Alfred Marshall
3. Scarcity definition – Lionel Robbins
4. Growth definition – Samuelson

→ Modern economists have divided economic theory into two parts,

• Micro Economics
• Macro Economics.

The two terms were first coined and used by ‘Ragnar Frisch’ in 1933. Micro Economics was popularised by Alfred Marshall, and J.M. Keynes popularised Macro Economics. Both approaches are essential for a proper understanding of a problem. The two approaches are interdependent.

→ The method of studying economic phenomena by taking assumptions and deducing conclusions from assumptions is called deduction.

→ Inductive method is the process in which one can arrive generalization on the basis of observed facts.

→ Economic static – analysis where establishing the functional relationship between two variables whose values are related to the same point of time.

→ Economic dynamics is the study of in relation to the preceding and succeeding events.

→ A positive science may be defined as a body of systematized knowledge concerning ‘What it is’.

→ A normative science may be defined as a body of systematized knowledge relating to the object of “What ought to be”?

→ Anything which satisfies human want is good.

→ Goods can be divided into two types: i) Free goods ii) Economic goods.
Economic goods are again divided into three types: i) Consumer goods ii) Capital goods iii) Intermediary Goods.
Semi-finished and under-finished products are called intermediary goods.

→ Wealth means money but in Economics all economic goods including land is treated as wealth. Wealth has three characters.

1. Utility
2. Exchange value
3. Transferability
4. Scarcity

→ Income is a flow over a period of time. Income flow is circular in character. There are two types of income, i) Money income ii) Real income.

→ Wants satisfying capacity of good is called utility. There are four types of utilities,

1. Form utility
2. Place utility
3. Time utility
4. Service utility.

→ Value means the exchange value of goods in economics. A good has value in use and value in exchange.

→ The value of a good expressed in terms of money is its price.

→ Human wants are starting points of all economic activities. They are unlimited, competitive, complementary, and recur. Wants are classified into necessities, comforts, and luxuries.

→ In Economics welfare means utility of satisfaction. Welfare indicates better living conditions of people in society. Wealth and welfare are closely related to one another.

TS Inter 1st Year Economics Notes Chapter 1 అర్థశాస్త్ర పరిచయం

→ అర్థశాస్త్రం అనే పదం గ్రీకు భాషలోని “Okinomickos” అనే పదం నుంచి ఆవిర్భవించింది.

→ ఆడమ్ స్మిత్ అభిప్రాయం ప్రకారం అర్థశాస్త్రం ప్రధానంగా “సంపదను” గూర్చి చర్చిస్తుంది.

→ మార్షల్ అర్థశాస్త్రంలో సంపద కన్నా శ్రేయస్సుకు ఎక్కువ ప్రాధాన్యత ఇచ్చాడు.

→ రాబిన్స్ ప్రకారం ఆర్థిక సమస్యలన్నింటికి మూలకారణం ‘కొరత’,

→ శామ్యూల్సన్ తన నిర్వచనములో ప్రస్తుత వినియోగానికే కాక భవిష్యత్ వినియోగానికి కూడా ప్రాధాన్యతను ఇచ్చాడు.

→ జేకబ్ వైనర్ ప్రకారం ఆర్థికవేత్తల ప్రశ్నలు వాటికి సంబంధించిన చర్చల ద్వారా అర్థశాస్త్రంను అర్థం చేసుకోవచ్చును.

→ రాగ్నార్ ఫ్రిష్ మొట్టమొదటిసారిగా 1933 సం॥లో సూక్ష్మ స్థూల అర్థశాస్త్రం అనే పదాలను ఉపయోగించడం జరిగింది.

→ సూక్ష్మ అర్థశాస్త్రం వైయుక్తిక యూనిట్లను పరిశీలిస్తుంది. దీనిని ‘ధరల సిద్ధాంతం’ అని కూడా అంటారు.

→ స్థూల అర్థశాస్త్రం ఆర్థిక వ్యవస్థ మొత్తాన్ని ఒకే యూనిట్గా పరిశీలిస్తుంది. దీనిని ‘ఆదాయ ఉద్యోగిత’ సిద్ధాంతం అని కూడా అంటారు.

→ నిగమన పద్ధతి సార్వత్రిక ప్రతిపాదనల నుంచి ఆరంభమై ప్రత్యేక ప్రతిపాదనలకు దారితీస్తుంది.

→ ఆగమన పద్ధతిలో ప్రత్యేక ప్రతిపాదనల నుంచి సార్వజనీన ప్రతిపాదనలు రూపొందిస్తారు.

→ ఆర్థిక నిశ్చలత్వం అనగా కాలంతో సంబంధం లేకుండా ఆర్థిక కార్యకలాపాలను పరిశీలించడం.

→ ఆర్థిక చలనత్వం అనగా కాలంతో పాటు మార్పు చెందే వివిధ చలాంకాల మధ్య ఉన్న సంబంధాన్ని అధ్యయనం చేయడం.

→ ఉనికిలో ఉన్న విషయాలను గురించి ఒక క్రమబద్ధమైన అధ్యయనం చేయడాన్ని నిశ్చయాత్మక అర్థశాస్త్రం అంటారు.

→ ‘ఎలా ఉండాలి’ అనే విషయాన్ని గురించి క్రమబద్ధమైన పద్ధతిలో అధ్యయనం చేసేది నిర్ణయాత్మక శాస్త్రం.

→ అర్థశాస్త్రంలో మానవ కోరికను సంతృప్తిపరచగలిగే భౌతిక, అభౌతికాంశాలన్నింటిని వస్తువులుగా పరిగణిస్తారు.

→ ప్రకృతి నుండి ఉచితంగా లభించే వస్తువులను ఉచిత వస్తువులంటారు.

→ మానవులచే ఉత్పత్తి చేయబడే వస్తువులన్నింటిని ఆర్థిక వస్తువులంటారు.

→ మానవ కోరికలను ప్రత్యక్షంగా సంతృప్తిపరిచే వస్తువులన్నింటిని వినియోగ వస్తువులంటారు.

→ ఉత్పత్తి చేయబడిన ఉత్పత్తి కారకాన్ని ఉత్పాదక వస్తువులంటారు.

→ ఉత్పత్తి ప్రక్రియలో పూర్తిగా తయారు కాకుండా ఉన్న ముడి సరుకులను మాధ్యమిక వస్తువులంటారు.

→ అర్థశాస్త్ర పరిభాషలో భూమితోపాటుగా ఆర్థిక వస్తువులన్నింటిని కలిపి సంపదగా పరిగణిస్తారు.

→ ఆదాయం ఒక ప్రవాహం వంటిది. ఈ ప్రవాహానికి మూలం సంపద.

→ మానవుని కోర్కెలను తీర్చగలిగే వస్తు సేవల యొక్క శక్తినే ప్రయోజనం అంటారు. ఇది నాలుగు రకాలు.

1. ఆకార ప్రయోజనం
2. స్థాన ప్రయోజనం
3. కాల ప్రయోజనం
4. సేవా ప్రయోజనం.

→ అర్థశాస్త్రంలో విలువ భావనను రెండు రకాలుగా వివరిస్తారు.

1. వినియోగపు విలువ
2. మారకపు విలువ.

→ వస్తువు యొక్క విలువను ద్రవ్య రూపంలో తెలియజేయటాన్ని ‘ధర’ అంటారు.

→ మానవుని కోర్కెలు అనంతాలు. వనరులు పరిమితం, మానవుని కోర్కెలు ఆర్థిక కార్యకలాపములకు మూలం.

→ ఆర్థికపరమైన ఒక విరామస్థితిని సమతౌల్యం అంటారు.

→ ఒక వ్యక్తి లేదా సమాజం సంపద నుండి పొందే సంతృప్తిని తెలియజేస్తుంది సంక్షేమం.

Here students can locate TS Inter 1st Year Economics Notes Chapter 6 Theories of Distribution to prepare for their exam.

TS Inter 1st Year Economics Notes Chapter 6 Theories of Distribution

→ Land: Land is a free gift of nature. In economics, land refers to the soil, forests, water, minerals, atmosphere etc.

→ Contract Rent: Contract rent is the reward paid for the services of land, buildings etc., according to an agreement made earlier.

→ Piece Wage: Piece wage is the amount paid for labourers according to the volume of work done by them.

→ Time Wage: Time wage is the amount paid to labourers for a fixed period of work, i.e., daily, weekly and monthly etc.

→ Money Wage: Money wage is the reward received by a labourer in cash for his labour.

→ Real Wage: Real wage is the purchasing power of money wages in terms of goods and services.

→ Capital: Capital is that part of wealth other than land which is used for further production.

→ Net Interest: Net interest is the reward for the service of the capital alone.

→ Normal Profit: No profit no loss situation. In this situation, both the firm and industry will be in equilibrium.

→ Supernormal Profit: Supernormal Profit is the total revenue of the firm will be more than the total cost. Only in the short run firm gets these profits.

TS Inter 1st Year Economics Notes Chapter 6 పంపిణీ సిద్ధాంతాలు

→ మొత్తం ఉత్పత్తి విలువ నాలుగు ఉత్పత్తి కారకాల మధ్య ఏవిధంగా పంపిణీ చేయబడుతుందో తెలియ జేసేది పంపిణీ.

→ పంపిణీని ఆదాయ పంపిణీ, వైయక్తిక ఆదాయ పంపిణీ అని రెండు విధాలుగా పరిశీలించవచ్చును.

→ నిశ్చల పరిస్థితిలో ఉద్యమదారునితో సహా ప్రతి ఉత్పత్తి కారకము దాని ఉపాంత ఉత్పాదనకు సమానంగా ప్రతిఫలం పొందుతుందని జె.బి. క్లార్క్ ఉపాంత ఉత్పాదకత సిద్ధాంతాన్ని తెలిపెను.

→ ఉత్పత్తి కారకంగా భూమి అందించే సేవలకు లభించే ప్రతిఫలం భాటకం. భూమికున్న సహజమైన నశింపులేని శక్తులను ఉపయోగించుకున్నందుకుగాను రైతు తన పంటలో భూస్వామికి చెల్లించే భాగం భాటకం.

→ శ్రామికుల సేవలకు ఒప్పందం ప్రకారం, యజమాని ప్రతిఫలంగా ఇచ్చే మొత్తం ద్రవ్యాన్ని వేతనం అంటారు. వేతనాలు నాలుగు రకాలు.

1. ద్రవ్యవేతనం
2. వాస్తవిక వేతనం
3. పనినిబట్టి వేతనం
4. కాలాన్నిబట్టి వేతనం.

→ ద్రవ్యత్వాభిరుచిని వీడినందుకుగాను ఋణగ్రహీత, ఋణదాతకు చెల్లించే ప్రతిఫలం వడ్డీ అని కీన్స్ అభిప్రాయం.

→ ఋణగ్రహీత నుండి ఋణదాత పొందే మొత్తం వడ్డీని స్థూలవడ్డీ అంటారు. కేవలం మూలధనం సేవకిచ్చే ప్రతిఫలం నికర వడ్డీ.

→ ఉత్పత్తిలో అనిశ్చితత్వం భరించినందుకు వ్యవస్థాపనకు వచ్చే ప్రతిఫలం లాభమని ప్రొ నైట్ అభిప్రాయం.

→ మొత్తం రాబడి నుండి వ్యయాన్ని తీసివేస్తే వచ్చేది స్థూలలాభం. కేవలం వ్యవస్థాపకుని సేవకు లభించే ప్రతిఫలం నికర లాభం.

Students must practice these TS Intermediate Maths 1B Solutions Chapter 7 The Plane Ex 7(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B The Plane 7(a)

I.
Question 1.
Find the equation of the plane if the foot of the perpendicular from origin to the plane is (1, 3, – 5). (V.S.A.Q.)
Answer:

OP is the normal to the plane and plane is passing through P (1, 3, – 5).
Dr’s of normal OP are (1 – 0, 3 – 0, – 5 – 0)
= 1, 3, – 5
Hence equation of the plane is
⇒ a (x – x₁) + b (y – y₁) + c (z – z₁) = 0
⇒ 1(x – 1) + 3(y – 3) – 5(z + 5) = 0
⇒ x + 3y – 5z – 35 = 0

Question 2.
Reduce the equation x + 2y – 3z – 6 = 0 of the plane to the normal form. (V.S.A.Q.)
Answer:
Equation of the plane is x + 2y – 3z – 6 = 0
⇒ x + 2y – 3z = 6
Dividing both sides by
\(\sqrt{1^2+2^2+(-3)^2}\) = \(\sqrt{1+4+9}\) = √14
We get
\(\left(\frac{1}{\sqrt{14}}\right) x+\left(\frac{2}{\sqrt{14}}\right) y+\left(\frac{-3}{\sqrt{14}}\right) z=\frac{6}{\sqrt{14}}\)

Question 3.
Find the equation of the plane whose intercepts on X, Y, Z – axes are 1,2,4 respectively. (S.A.Q.) (May 2014)
Answer:
Equation of the plane in the intercepts form x y z is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1, given a = 1, b = 2, c = 4
We have \(\frac{x}{1}+\frac{y}{2}+\frac{z}{4}\) = 1
⇒ 4x + 2y + z = 4

Question 4.
Find the intercepts of the plane 4x + 3y- 2z + 2 = 0 on the co-ordinate axes. (V.S.A.Q.)
Answer:
Given 4x + 3y – 2z = – 2
⇒ – 2x – \(\frac{3}{2}\)y + z = 1
⇒ \(\frac{x}{-\left(\frac{1}{2}\right)}+\frac{y}{-\left(\frac{2}{3}\right)}+\frac{z}{(1)}\)
∴ x – intercept = – \(\frac{1}{2}\), y – intercept = – \(\frac{2}{3}\) and z – intercept = 1.

Question 5.
Find the d.c’s of the normal to the plane x + 2y + 2z – 4 = 0. (V.S.A.Q.) [Mar. ’13, May ’12]
Answer:
Equation of the plane is x + 2y + 2z – 4 = 0
D.r’s of the normal = 1, 2, 2
∴ \(\sqrt{a^2+b^2+c^2}\) = \(\sqrt{1+4+4}\) = 3
∴ D.c’s of the normal are \(\frac{1}{3}, \frac{2}{3}, \frac{2}{3}\)

Question 6.
Find the equation of the plane passing through the point (-2, 1, 3), and having (3, -5, 4) as d.r’s of its normal. (V.S.A.Q.)
Answer:
D.r’s of normal are 3, -5, 4 and since the plane passes through (- 2, 1, 3), we have equation of the plane is
3(x + 2) – 5 (y – 1) + 4 (z – 3) = 0
⇒ 3x + 6-5y + 5 + 4z – 12 = 0
⇒ 3x – 5y + 4z – 1 = 0

Question 7.
Write the equation of the plane 4x – 4y + 2z + 5 = 0 in the intercept form. (V.S.A.Q.) [March 2012]
Answer:
Equation of the plane is
4x – 4y + 2z + 5 = 0
∴ 4x – 4y + 2z = – 5

Question 8.
Find the angle between the planes
x + 2y + 2z – 5 = 0 and 3x + 3y + 2z – 8 = 0. (V.S.A.Q.)
Answer:
Equations of the planes are
x + 2y + 2z-5 = 0 ………………. (1)
and 3x + 3y + 2z – 8 = 0 ………………. (2)
If θ is the angle between the planes then by the formula,

II.
Question 1.
Find the equation of the plane passing through the point (1, 1, 1) and parallel to the plane x + 2y + 3z – 7 = 0. (V.S.A.Q.) [May 2011]
Answer:
Equation of the plane parallel to the given plane x + 2y + 3z – 7 = 0 is of the form x + 2y + 3z + k = 0
If this passes through the point (1, 1, 1) then
1 + 2 + 3 + k = 0 k = – 6
So, the equation of the required plane is
x + 2y + 3z – 6 = 0

Question 2.
Find the equation of the plane passing through (2, 3, 4) and perpendicular to X-axis. (V.S.A.Q.)
Answer:
If the plane is perpendicular to X-axis then X-axis is a normal to the plane and d.c’s of X-axis are 1, 0, 0.
∴ Equation of the plane is of the form x = k.
Since this passes through (2, 3, 4) we have k = 2.
∴ Equation of the required plane is x = 2.

Question 3.
Show that 2x + 3y + 7 = 0 represents a plane perpendicular to XY-plane. (V.S.A.Q.)
Answer:
Equation of the given plane is 2x + 3y + 7 = 0
Equation of the plane perpendicular to XY plane is z = 0
i. e., 0.x + 0.y + 1.z = 0
Since the two planes are perpendicular by the condition a₁a₂ + b₁b₂ + c₁c₂ = 0 we have 2(0) + 3(0) + 0(1) = 0
∴ Plane 2x + 3y + 7 = 0 is perpendicular to XY – plane.

Question 4.
Find the constant k so that the planes x – 2y + kz = 0 and 2x + 5y – z = 0 are at right angles. Find the equation of the plane through (1, -1,-1) and perpendicular to these planes. (S.A.Q.)
Answer:
Equations of the given planes are x – 2y + kz = 0 and 2x + 5y – z = 0
If the planes are perpendicular then
1(2) + (- 2) (5) + k (-1) = 0
⇒ 2 – 10 – k = 0 ⇒ k = – 8
Equation of the plane is
x – 2y – z = 0 …………….. (1)
and 2x + 5y – z = 0 ………………….. (2)
Equation of the plane passing through (1, – 1, – 1) is of the form
a (x – 1) + b (y + 1) + c (z + 1) = 0 …………………. (3)
If this plane is perpendicular to (1) and (2) then a – 2b – 8c = 0 and 2a + 5b – c = 0
Solving

∴ From (3), equation of the required plane is 42 (x – 1) – 15 (y + 1) + 9 (z + 1) = 0
⇒ 42x – 15y + 9z – 48 = 0

Question 5.
Find the equation of the plane through (- 1, 6, 2) and perpendicular to the join of (1, 2, 3) and (- 2, 3, 4). (S.A.Q.)
Answer:

Let A (1, 2, 3) and B (-2, 3, 4) be the given points.
D.r’s of AB are 3, -1,-1.
The line AB is perpendicular to the plane and passing through the point P (- 1, 6, 2).
Then equation of the plane is
3(x + 1) – 1 (y – 6) – 1 (z – 2) = 0
⇒ 3x – y – z + 11 = 0

Question 6.
Find the equation of the plane bisecting the line segment joining (2, 0, 6) and (-6, 2, 4) and perpendicular to it. (S.A.Q.)
Answer:

Let A (2, 0, 6) and B(- 6, 2, 4) be the two points.
Then mid point of AB
= \(\left(\frac{2-6}{2}, \frac{0+2}{2}, \frac{6+4}{2}\right)\) = (- 2, 1, 5)
Equation of the plane is perpendicular to AB.
∴ Dr’s of normal to the plane are
2 + 6, 0 – 2, 6 – 4 = 8, – 2, 2
Equation of the required plane is
8(x + 2) – 2(y – 1) + 2 (z – 5) = 0
⇒ 8x – 2y + 2z + 8 = 0

Question 7.
Find the equation of the plane passing through (0,0, – 4) and perpendicular to the line joining the points (1, – 2, 2) and (- 3, 1, – 2). (S.A.Q.)
Answer:
Let A (1, -2, 2) and B (-3, 1, -2) be the given points.
D.r’s of normal to the plane are
(1 + 3, -2 – 1, 2 + 2) = (4, -3, 4)
Equation of the required plane passing through (0, 0 -4) is
4(x – 0) – 3 (y – 0) + 4 (z + 4) = 0
⇒ 4x – 3y + 4z + 16 = 0

Question 8.
Find the equation of the plane through (4, 4, 0) and perpendicular to the planes 2x + y + 2z + 3 = 0 and 3x + 3y + 2z – 8 = 0. (S.A.Q.)
Answer:
The equation of the plane passing through the point (4, 4, 0) is of the form
a (x – 4) + b (y – 4) + c (z – 0) = 0 ………………. (1)
If this is perpendicular to 2x + y + 2z + 3 = 0 and 3x + 3y + 2z – 8 = 0
Then 2a + b + 2c = 0 ……………… (2)
and 3a + 3b + 2c = 0 ……………… (3)
Solving (2) and (3)

∴ From (1) equation of the required plane is
– 4 (x – 4) + 2 (y – 4) + 3 (z – 0) = 0
⇒ – 4x + 2y + 3z + 8 = 0
⇒ 4x – 2y – 3z – 8 = 0

III.
Question 1.
Find the equation of the plane through the points (2, 2, – 1), (3, 4, 2), (7, 0, 6). (E.Q.)
Answer:
Equation of the plane passing through (2, 2, – 1) is
a (x – 2) + b (y – 2) + c (z + 1) = 0 ………………. (1)
If this passes through (3, 4, 2) then
a (3 – 2) + b (4 – 2) + c (2 + 1) = 0
⇒ a + 2b + 3c = 0 …………………. (2)
Similarly if the plane passing through (7, 0. 6) is
a (7 – 2) + b (0 – 2) + c (6 + 1) = 0
⇒ 5a – 2b + 7c = 0 ………………… (3)
Solving (2) and (3) we get

∴ From (1) equation of the required plane is
5 (x – 2) + 2 (y – 2) – 3 (z +1) = 0
⇒ 5x + 2y – 3z – 17 = 0

Question 2.
Show that the points (0, – 1, 0), (2, 1, – 1), (1, 1, 1), (3, 3, 0) are coplanar. (E.Q.)
Answer:
Equation of the plane passing through (0, -1, 0) will be of the form
a (x – 0) + b (y + 1) + c (z – 0) = 0 …………………… (1)
If this passes through (2, 1, – 1) then a (2 – 0) + b (1 + 1) + c (- 1 – 0) = 0
⇒ 2a + 2b – c = 0 …………………… (2)
Similarly if the plane passes through (1, 1, 1) then
a (1 – 0) + b (1 + 1) + c (1 – 0) = 0
⇒ a + 2b + c = 0 ………………….. (3)
Solving (2) and (3),

∴ Equation of the plane passing through (0, -1, 0), (2, 1,-1) and (1, 1, 1) is
4 (x – 0) – 3 (y + 1) + 2 (z – 0) = 0 [From (1)]
⇒ 4x – 3y + 2z – 3 = 0 ………………….. (4)
If it passes through (3, 3, 0), then
4(3) – 3(3) + 2 (0) – 3 = 0
Hence the point (3,3,0) also passes through (4) and hence the given points are coplanar.

Question 3.
Find the equation of the plane through (6, -4, 3), (0, 4, -3) and cutting of intercepts whose sum is zero. (E.Q.)
Answer:
Equation of the plane in the intercepts form is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1.
Given a + b + c = 0
⇒ c = – (a + b)
The plane passes through the points A(6, – 4, 3) and B (0, 4, -3)
Hence, \(\frac{6}{a}-\frac{4}{b}+\frac{3}{c}\) = 1 ……………………. (1)
If this passes through B(0, 4, – 3), then
\(\frac{4}{b}-\frac{3}{c}\) = 1 ……………………….. (2)
Adding (1) and (2); \(\frac{6}{a}\) = 2 ⇒ a = 3
From (2),
\(\frac{4}{b}-\frac{3}{c}\) = 1 ⇒ 4c – 3b = bc
⇒ – 4 (a + b) – 3b = – b (a + b)
⇒ – 4a – 4b – 3b = – ab – b²
⇒ 4a + 7b = ab + b²
Since a = 3 we have 12 + 7b = 3b + b²
⇒ b² – 4b – 12 = 0 ⇒ (b – 6) (b + 2) = 0

Case – (i): b = 6, then c = -(3 + 6) = – 9
Equation of the plane is \(\frac{x}{3}+\frac{y}{6}-\frac{z}{9}\) = 1
⇒ 6x + 3y – 2z = 18

Case – (ii): b = – 2, then c = -(3 – 2) = – 1
Equation of the plane is \(\frac{x}{3}-\frac{y}{2}+\frac{z}{-1}\) = 1
⇒ \(\frac{x}{3}-\frac{y}{2}+\frac{z}{-1}\) = 1 ⇒ 2x – 3y – 6z = 6

Question 4.
A plane meets the co-ordinate axes in A, B, C. If the centroid of ∆ABC is (a, b, c). Show that the equation to the plane is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 3. (E.Q.)
Answer:
Suppose α, β, γ be the intercepts of the plane ABC.
Equation of the plane in the intercept form is
\(\frac{x}{\alpha}+\frac{y}{\beta}+\frac{z}{\gamma}\) = 1 ……………… (1)

Co-ordinates of A = (α, 0, 0), B = (0, β, 0) and C = (0, 0, γ)
G is the centroid of ∆ABC.

Question 5.
Show that the plane through (1, 1, 1), (1, – 1, 1) and (- 7, – 3, – 5) is parallel to Y – axis. (S.A.Q.)
Answer:
Equation of the plane through A (1, 1, 1) is
a (x – 1) + b (y – 1) + c (z – 1) = 0 ………………… (1)
This plane passes through B (1, – 1, 1) then
0 – 2b + 0 = 0 0 ⇒ b = 0
Equation of XZ plane is y = 0
∴ 0 . x + 1 . y + 0 . z = 0
The required plane is perpendicular to XZ plane and hence parallel to Y – axis.

Question 6.
Show that the equations ax + by + r = 0, by + cz + p = 0, cz + ax + q = 0 represent planes perpendicular to XY, YZ, ZX planes respectively. (S.A.Q.)
Answer:
Let the equation of the plane be ax + by + c = 0
The d.r’s of normal to the plane are a, b, c Equation of XY plane is z = 0 .-. D.r’s of normal are (0, 0, 1)
∴ a (0) + b (0) + 0 (1) = 0
∴ ax + by + r = 0 represent a plane perpendicular to XY – plane.
Similarly by + cz + p = 0 and cz + ax + q = 0 represent planes perpendicular to YZ – plane, ZX planes respectively.

Here students can locate TS Inter 1st Year Accountancy Notes Chapter 10 Preparation of Final Accounts to prepare for their exam.

TS Inter 1st Year Accountancy Notes Chapter 10 Preparation of Final Accounts

1. To find out the net profit and true financial position, all expenses relating to the current year whether paid or not, all incomes received or to be received should be taken into account. Some of the income and expenses relating to next year should not include in the current year. The amount to be adjusted in the books is called an adjustment.

2. Types of adjustments:

1. Adjustment for closing stock.
2. Adjustment for outstanding expenses.
3. Adjustment for prepaid expenses.
4. Adjustment for income receivable.
5. Adjustment for income received in advance.
6. Adjustment for depreciation.
7. Adjustment for interest on capital.
8. Adjustment for interest on drawings,
9. Adjustment for bad debts and Reserve for bad debts.

TS Inter 1st Year Accountancy Notes Chapter 10 ముగింపు లెక్కల తయారీ

1. ఒక వ్యాపార సంస్థ సంవత్సరానికి నికర లాభము / నష్టము, ఆర్థిక పరిస్థితిని తెలుసుకోవడానికి ప్రస్తుత సంవత్సరానికి సంబంధించిన ఖర్చులను చెల్లించినా, చెల్లించవలసినా, అదే విధముగా స్వీకరించిన, రావలసిన ఆదాయాలను లెక్కలోకి తీసుకోవాలి. రాబోయే సంవత్సరానికి చెందిన ఆదాయాలు గాని, వ్యయాలు గాని ప్రస్తుత సంవత్సరములో చేర్చకూడదు. అంకణాలో ఇచ్చిన మొత్తాలకు సంబంధిత మొత్తాలను సర్దుబాటు చేయడాన్ని సర్దుబాట్లు అంటారు.

2. సర్దుబాట్లలో రకాలు:

1. ముగింపు సరుకునకు సంబంధించిన సర్దుబాట్లు
2. చెల్లించవలసిన వ్యయాలకు సర్దుబాట్లు
3. ముందుగా చెల్లించిన వ్యయాలకు సర్దుబాట్లు
4. రావలసిన ఆదాయాలకు సర్దుబాట్లు
5. ముందుగా వచ్చిన ఆదాయాలకు సర్దుబాట్లు
6. స్థిరాస్తులపై తరుగుదలకు సర్దుబాట్లు
7. మూలధనముపై వడ్డీకి సర్దుబాట్లు
8. సొంతవాడకాలపై వడ్డీకి సర్దుబాట్లు
9. రాని బాకీలకు సర్దుబాట్లు
10. రాని, సంశయాత్మక బాకీల నిధికి సర్దుబాట్లు