TS Inter 1st Year Maths 1B Solutions Chapter 8 Limits and Continuity Ex 8(a)

Students must practice these TS Inter 1st Year Maths 1B Study Material Chapter 8 Limits and Continuity Ex 8(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Limits and Continuity 8(a)

I. Compute the following limits. (V.S.A.Q.)

Question 1.
\(\lim _{x \rightarrow a}\left(\frac{x^2-a^2}{x-a}\right)\) (V.S.A.Q.)
Answer:

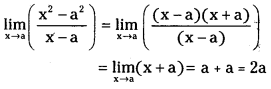
Question 2.
\(\lim _{x \rightarrow 1}\) (x² + 2x + 3) (V.S.A.Q.)
Answer:
\(\lim _{x \rightarrow 1}\) (x² + 2x + 3) = 1² + 2(1) + 3 = 6

Question 3.
\(\lim _{x \rightarrow 0}\left(\frac{1}{x^2-3 x+2}\right)\) (V.S.A.Q.)
Answer:

Question 4.
\(\lim _{x \rightarrow 3}\left(\frac{1}{x+1}\right)\) (V.S.A.Q.)
Answer:

Question 5.
\(\lim _{x \rightarrow 1}\left(\frac{2 x+1}{3 x^2-4 x+5}\right)\) (V.S.A.Q.)
Answer:

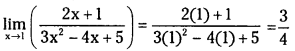
Question 6.
\(\lim _{x \rightarrow 1}\left(\frac{x^2+2}{x^2-2}\right)\) (V.S.A.Q.)
Answer:

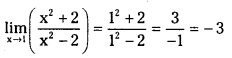
Question 7.
\(\lim _{x \rightarrow 2}\left(\frac{2}{x+1}-\frac{3}{x}\right)\) (V.S.A.Q.)
Answer:

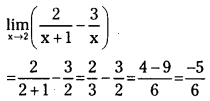
Question 8.
\(\lim _{x \rightarrow 0}\left(\frac{x-1}{x^2+4}\right)\) (V.S.A.Q.)
Answer:

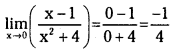
Question 9.
\(\lim _{x \rightarrow 0}\) x^3/2 (x > 0) (V.S.A.Q.)
Answer:
\(\lim _{x \rightarrow 0}\) x^3/2 = 0^3/2 = 0

Question 10.
\(\lim _{x \rightarrow 0}\) (√x + x^5/2), (x > 0) (V.S.A.Q.)
Answer:
\(\lim _{x \rightarrow 0}\) (√x + x^5/2) = √0 + 0^5/2 = 0 + 0 = 0

Question 11.
\(\lim _{x \rightarrow 0}\) x² cos \(\left(\frac{2}{x}\right)\) (V.S.A.Q.)
Answer:
\(\lim _{x \rightarrow 0}\) x² \(\lim _{x \rightarrow 0}\) cos \(\left(\frac{2}{x}\right)\) = 0 . (l) = 0 where |l| ≤ 1.

Question 12.
\(\lim _{x \rightarrow 3} \frac{x^2-9}{x^3-6 x^2+9 x+1}\) (V.S.A.Q.)
Answer:

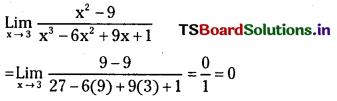
Question 13.
\(\lim _{x \rightarrow 1}\left[\frac{x-1}{x^2-x}-\frac{1}{x^3-3 x^2+2 x}\right]\) (V.S.A.Q.)
Answer:
Note: The problem shall be designed as

Question 14.
\(\lim _{x \rightarrow 3}\left(\frac{x^4-81}{2 x^2-5 x-3}\right)\) (V.S.A.Q.)
Answer:

Question 15.
\(\lim _{x \rightarrow 3}\left(\frac{x^2-8 x+15}{x^2-9}\right)\) (V.S.A.Q.)
Answer:

Question 16.
If f(x) = – \(\sqrt{25-x^2}\) then find
\(\lim _{x \rightarrow 1}\left(\frac{f(x)-f(1)}{x-1}\right)\)
Answer: