TS Inter 1st Year Maths 1B Solutions Chapter 9 Differentiation Ex 9(b)

Students must practice these TS Inter 1st Year Maths 1B Study Material Chapter 9 Differentiation Ex 9(b) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Differentiation 9(b)

I.
Question 1.
Find the derivatives of the following functions. (V.S.A.Q.)
(i) cotⁿx
Answer:
Let y = cotⁿx
Then \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = – n cot^{n – 1}x (cosec²x)
= – n cot^n-1 x (cosec²x)
(∵ \(\frac{\mathrm{d}}{\mathrm{dx}}\) (cot x) = – cosec² x)

(ii) cosec⁴x
Answer:
Let y = cosec⁴x
Then \(\frac{d y}{d x}\) = 4 cosec³x \(\frac{\mathrm{d}}{\mathrm{d} x}\) (cosec x)
= 4 cosec³x (- cosec x cot x)
= – 4 cosec⁴x cot x

(iii) tan (e^x)
Answer:
Let y = tan (e^x)
Then \(\frac{d y}{d x}\) = sec² (e^x) \(\frac{d}{d x}\) (e^x)
= e^x.sec²(e^x)

(iv) \(\frac{1-\cos 2 x}{1+\cos 2 x}\)
Answer:
Let y = \(\frac{1-\cos 2 x}{1+\cos 2 x}=\frac{2 \sin ^2 x}{2 \cos ^2 x}\) = tan² x
∴ \(\frac{d y}{d x}\) = 2 tan x \(\frac{\mathrm{d}}{\mathrm{dx}}\) (tan x)
= 2 tan x sec²x

(v) sin^mx cosⁿx
Answer:
Let y = sin^mx cosⁿx
Then \(\frac{d y}{d x}\) = sin^mx \(\frac{d}{d x}\) (cosⁿx) + cosⁿ\(\frac{d y}{d x}\)(sin^mx)
= sin^mx n cos^{n – 1}x (- sin x) + cosⁿx (m sin^{m – 1}x) cos x
= m cos^{n + 1}x sin^{m – 1}x – n sin^{m + 1}x cos^{n – 1}x

(vi) sin mx . cos nx
Answer:
Let y = sin mx cos nx
Then \(\frac{d y}{d x}\) = sin mx . \(\frac{d}{d x}\) (cos nx) + cos nx \(\frac{d}{d x}\) (sin mx)
= sin mx (- n sin nx) + cos nx (m cos mx)
= – n sin mx sin nx + m cos nx cos mx

(vii) x . tan^-1 x
Answer:
Let y = x . tan^-1x

(viii) sin^-1 (cos x)
Answer:
Let y = sin^-1 (cos x)

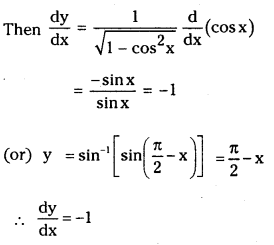
(ix) log (tan 5x)
Answer:
Let y = log (tan 5x)

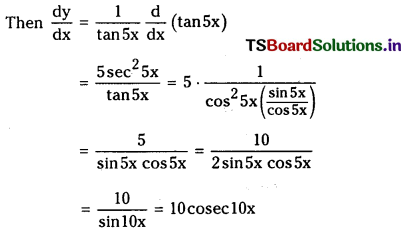
(x) sinh^-1 \(\left(\frac{3 x}{4}\right)\)
Answer:

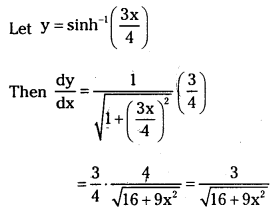
(xi) tan^-1 (log x)
Answer:
Let y = tan^-1 (log x)

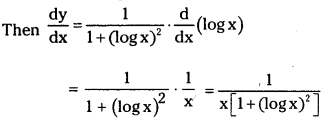
(xii) log\(\left(\frac{x^2+x+2}{x^2-x+2}\right)\) (May 2006)
Answer:

(xiii) log [sin^-1 (e^x)]
Answer:
Let y = log [sin^-1 (e^x)]

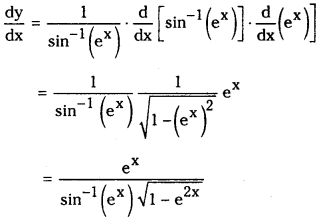
(xiv) (sin x)² (sin^-1x)²
Answer:
Let y = (sin x)² (sin^-1x)²

(xv) \(\frac{\cos x}{\sin x+\cos x}\)
Answer:

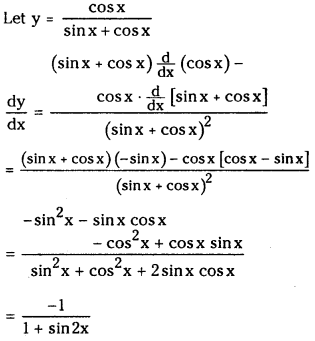
(xvi) \(\frac{x\left(1+x^2\right)}{\sqrt{1-x^2}}\)
Answer:

(xvii) e^sin-1x
Answer:
Let y = e^sin-1x

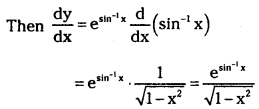
(xviii) cos (log x + e^x
Answer:
Let y = cos (log x + e^x
\(\frac{d y}{d x}\) = – sin(log x + e^x) \(\frac{\mathrm{d}}{\mathrm{dx}}\) (log x + e^x)
= – sin (log x + e^x) (\(\frac{1}{x}\) + e^x)

(xix) \(\frac{\sin (x+a)}{\cos x}\)
Answer:

(xx) cot^-1 (cosec 3x)
Answer:
Let y = cot^-1 (cosec 3x)

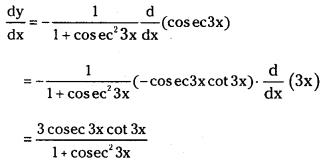
Question 2.
Find the derivatives of the following functions. (V.S.A.Q.)
(i) x = sin h²y
Answer:

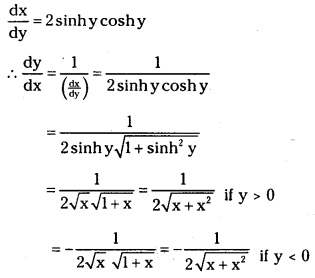
(ii) x = tanh²y
Answer:

(iii) x = e^{sinh y}
Answer:
\(\frac{\mathrm{dx}}{\mathrm{dy}}\) = e^{sin hy} \(\frac{\mathrm{d}}{\mathrm{dy}}\) (sin hy)
= e^sinhy cos hy = x cos hy

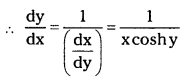
(iv) x tan (e^-y)
Answer:
\(\frac{\mathrm{dx}}{\mathrm{dy}}\) = sec²(e^-y) \(\frac{d}{d y}\) (e^-y)
= – sec²(e^-y) (e^-y)
= – e^-y (1 + tan² (e^-y)) = – e^-y(1 + x²)

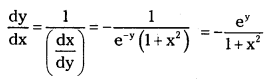
(v) x = log (1 + sin²y)
Answer:

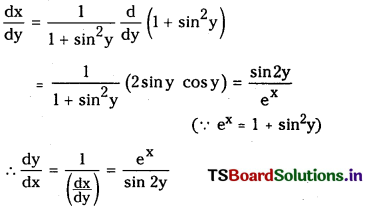
(vi) x = log(1 + √y)
Answer:
1 + √y = e^x
√y = e^x – 1
y = (e^x – 1)²
∴ \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 2(e^x – 1) . \(\frac{\mathrm{d}}{\mathrm{dx}}\) (e^x
= 2(e^x – 1) e^x
= 2√y (√y + 1) = 2(y + √y)

II. Find the derivatives of the following functions. (V.S.A.Q.)

(i) cos [log (cot x)]
Answer:
y = cos [log (cot x)]
Let cot x = u, log u = v, so that y = cos v

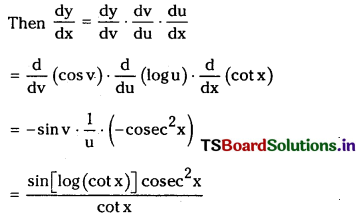
(ii) sin h^-1
Answer:

(iii) log [cot (1 – x²)]
Answer:
y = log [cot (1 – x²)]
Let 1 – x² = u, cot u = v, and y = log v

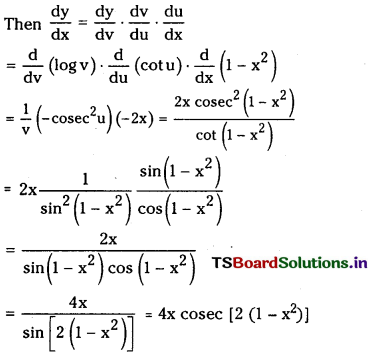
(iv) sin [cos (x²)]
Answer:
y = sin [cos (x²)]
Let x² = u, v = cos u and y = sin v
\(\frac{d y}{d x}=\frac{d y}{d v} \cdot \frac{d v}{d u} \cdot \frac{d u}{d x}\)
= cos v(- sin u) (2x)
= – 2x cos (cos u) sin u
= – 2x cos [(cos (x²)] sin (x²)

(v) sin [tan^-1 (e^x)]
Answer:
y = sin [tan^-1 (e^x)]
Let e^x = u, tan^-1u = v and y = sin v

(vi) \(\frac{\sin (a x+b)}{\cos (c x+d)}\)
Answer:

(vii) tan^-1 (tanh \(\frac{x}{2}\))
Answer:

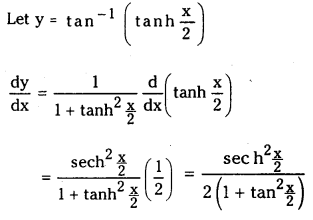
(viii) sin x (tan^-1x)
Answer:
Let y = sin x (tan^-1x)²

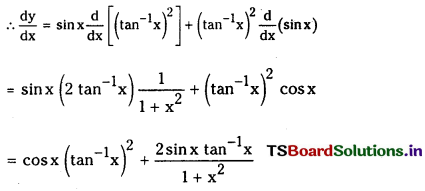
III. Find the derivatives of the following functions.

Question 1.
sin^-1\(\left(\frac{b+a \sin x}{a+b \sin x}\right)\) (a > o, b > 0) (E.Q.)
Answer:

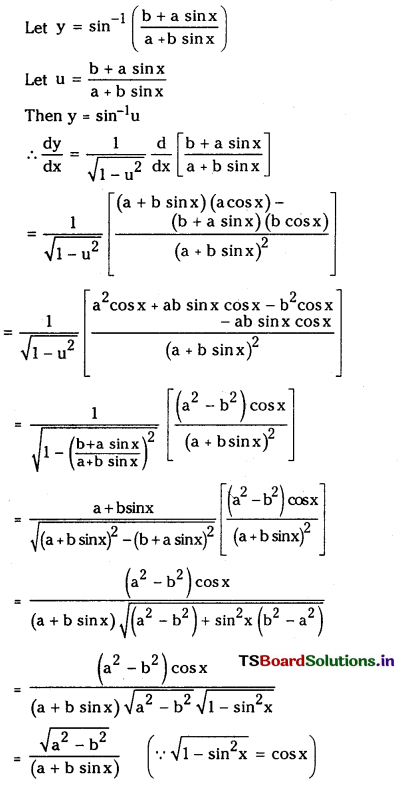
Question 2.
cos^-1\(\left(\frac{b+a \cos x}{a+b \cos x}\right)\) (a > 0, b > 0) (E.Q.)
Answer:

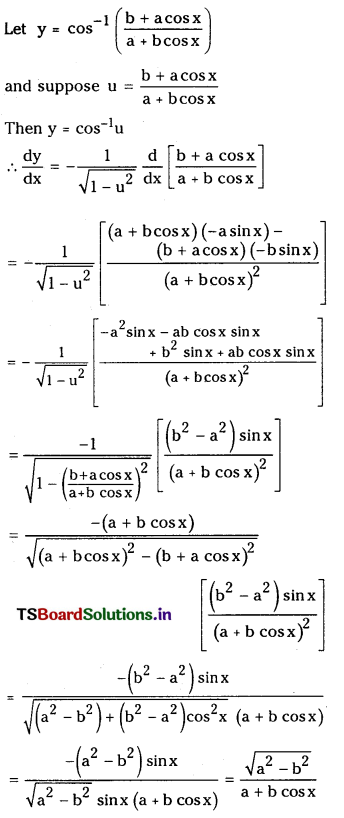
Question 3.
tan^-1 \(\left(\frac{\cos x}{1+\cos x}\right)\)
Answer: