Telangana TSBIE TS Inter 2nd Year Sanskrit Study Material 5th Poem रुद्रमदेवी Textbook Questions and Answers.
TS Inter 2nd Year Sanskrit Study Material 5th Poem रुद्रमदेवी
निबन्ध प्रश्नाः (వ్యాసరూప సమాధాన ప్రశ్నలు) (Essay Questions)
1. रुद्रामदेव्याः विजयं संक्षिपता?
(రుద్రమదేవి యొక్క విజయాన్ని సంక్షిప్తంగా వివరించండి.)
2. देवगिरिनाथः महादेवः रुद्रमाम्बया कथं पराजितः?
(దేవగిరినాథుడు రుద్రమదేవిచేత ఏ విధముగా ఓడింపబడెను ?)
జవాబు:
‘రుద్రమదేవి’ అనే పాఠ్యభాగాన్ని శ్రీ దురిశేటి వెంకట రమణాచార్యులు రచించారు. వీరు రచించిన ‘శిల్పశ్రీ’ అనే కావ్యం నుండి ఈ పాఠ్యభాగం స్వీకరింపబడింది. ఇందులో రుద్రమదేవి పరాక్రమాన్ని, ధైర్యాన్ని చక్కగా వర్ణించారు. కాకతిరాజ్య రాణిగా ఆమె సాధించిన విజయాలను చక్కగా ఆవిష్కరించారు.
కాకతీయ చక్రవర్తులలో గణపతిదేవుడు ప్రసిద్ధుడు. అతడు తన పరాక్రమంతో రాజ్యాన్ని చాలాకాలం పాలించాడు. అతని కుమార్తె రుద్రమదేవి. యుద్ధ విద్యలో ప్రావీణ్యాన్ని సాధించింది. వృద్ధాప్యంతో గణపతిదేవుడు రాజ్యాన్ని పరిపాలించలేకపోతున్నారు. ఇది గమనించిన అతని మంత్రి ఒకరోజు రాజును సమీపించి “రాజా ! తమ కుమార్తె అయిన రుద్రమదేవిని రాణిగా పట్టాభిషేకం చేయండి. తమ సర్వశక్తి సమన్వయురాలు. రాజ్యాన్ని పాలించగల సమర్థురాలు, ఆమె తన పాదాలను శత్రువుల శిరస్సులపై ఉంచి శత్రువులను అణచివేయగల సమర్థురాలు. అందువల్ల మీరు రుద్రమదేవిని రాణిగా పట్టాభిషేకం చేయండి. ప్రజలంతా సంతోషిస్తారు.” అని పలికాడు.
“निजधरां मुदितां कुरु सप्रजाम्”
గణపతిదేవుడు తన మంత్రి మాటలను శ్రద్ధగా విన్నాడు. చాలా సంతోషించాడు. వెంటనే తన రాజ్యంలోని ప్రజలకు తన నిర్ణయాన్ని ప్రకటించాడు. అంతట చాటింపు వేశాడు. ఒక మంచి ముహూర్తంలో పుణ్యనదీజలాలతోను, వేద మంత్రాలతోను, వేద పండితుల ఆశీర్వచనాలతోను రుద్రమదేవికి వైభవంగా పట్టాభిషేకం జరిపించాడు.
రుద్రమదేవి పరాక్రమం తెలిసిన సామంతులందరు ఆమెకు నమస్కరించారు. ఆమె సామ్రాజ్యాధిపత్యాన్ని అంగీకరించారు. సకాలంలో పన్నులు కట్టారు. కాని దేవగిరి రాజ్యాన్ని పరిపాలిస్తున్న హరిహర, మురారి దేవులు మాత్రం రుద్రమదేవి ఆధిపత్యాన్ని అంగీకరించలేదు. ఒక స్త్రీ తమపై పెత్తనం చెలాయించడం ఏమిటని తిరుగుబాటు చేయాలనుకున్నారు. వీరిద్దరు రుద్రమదేవిని ఎదిరించడానికి పన్నాగాలు పన్నారు. చతురంగ బలాలతో యుద్ధానికి బయలుదేరారు. ఆ సమయంలో రుద్రమదేవి పరమేశ్వరుడిని సేవించడానికి బయలుదేరింది. అదనుచూచి శత్రుమూకలు రాజ్యంపై దాడిచేశారు.
समभियान्त्यथ्यो विभियोधियः
తన రాజ్యం శత్రుహస్తగతమైనదనే విషయాన్ని రుద్రమదేవి తెలుసుకుంది. కోపంతో కన్నులు ఎర్రబడినాయి. వెంటనే రుద్రమదేవి పరిమిత సైన్యంతో అపరకాళికవలె, శత్రుసైన్యంపై ఎదురుదాడి చేసింది. సామంతులందరు రుద్రమదేవిని అనుసరించారు. యుద్ధరంగంలో శంఖనాదం చేసింది. శత్రువుల గుండెల్లో భయాన్ని పుట్టించింది. క్షణాల్లో రుద్రమదేవి వీర ఖడ్గాన్ని చేపట్టింది. పగపట్టిన నాగు పామువలె బుసలు కొట్టింది. శత్రువుల తలలను నరుకుతూ యుద్ధరంగంలో వీరవిహారం చేసింది. శత్రుసైన్యం విలవిలలాడారు. దేవాద్రినాథుడిని చూచింది. వెంటనే అంకుశాన్ని ధరించి మదగజంపై ఉన్న మావటివాడిని చంపింది. రథాన్ని ఎక్కి ధనస్సుతో బాణవర్షం కురిపించింది. రథాన్ని నడుపుతున్న సారధిని చంపింది. ఆతని గుర్రాలను చంపింది. చివరకు అతని రథాన్ని, పతాకాన్ని ఖండించింది. శత్రురాజు విరథునిగా చేసింది.
“नृपाणी तं विरथं चकार ”
చివరకు మహేంద్రుడు దిక్కుతోచని స్థితిలో పడ్డారు. తన పరాజయాన్ని అంగీ కరించాడు. శత్రుసైన్యాలు యుద్ధం నుండి పారిపోయారు. స్త్రీలు బలహీనులు అనే మాట తప్పని గ్రహించాడు. గతిలేక మహాదేవుడు కూడా యుద్ధరంగం నుండి పారిపోయాడు. ఈ రకంగా రుద్రమదేవి అసమాన పరాక్రమం చూపించి వీరనారిగా గుర్తింపు పొందింది.
Introduction : The lesson Rudrama Devi was written by Sri D. Venkataramacharya. It is taken from the author’s poem Silpasri. The present lesson describes Rudrama’s victory over Mahadeva, the ruler of Devagiri.
Queen of Kakati Kingdom : When the king of Kakati kingdom became old, his minister advised him to install his daughter Rudrama as the queen. It would make the kingdom along with the subjects pleased. निजधरां मुदितां कुरु सप्रजाम् ।
The king felt happy at that suggestion, and made announcement to that effect. On an auspicious day, Rudrama was made the queen while the priests chanted mantras, and water from holy rivers and oceans was sprinkled on her. The pious queen became successful as people and feudatory lords paid their taxes willingly.
The Jealous Enemies: However, Harihara and Muran became jealous of her success. The king of Devagiri lured them by his crooked ways. He said that a weak woman insulted them. The ruler of Devagiri. who was proud of his army attacked Rudrama.
समभियान्त्यरयो विभियोऽधियः ।
At that time, Rudrama went to worship Siva. On getting the news that the city was under siege, she returned with limited forces to the city. When she blew her conch, the soldiers and feudatory kings understood that it was their queen, and blew their conches.
The Warrior Queen: The queen and her soldiers attacked the enemy from opposite sides. Rudrama threw her sword and killed the mahout of Mahadevas elephant. The king of Devagiri jumped in to another chariot. Rudrama killed the charioteer and the horses, and broke his string and flag. नृपाणी तंविश्यं चकार । The Devagiri ruler and his followers ran away from the battle field. He understood that women were not weak.
सन्दर्भवाक्यानि (సందర్భ వాక్యాలు) (Annotations)
1. निजधरां मुदितां कुरु सप्रजाम् ।
परिचय : एतत् वाक्यं रुद्रमदेवी इति पाठ्यभागात् स्वीकृतम् । अस्य रचयिता श्री डी. वेङ्कटरामाचार्यः ।
सन्दर्भ : काकतीयराजः वृद्धः अभवत् । पलितकेशं तं तस्य सचिवः अवदत् यत् रुद्रमदेवी राज्यं कर्तुम् अर्हति । ताम् अभषेचय । प्रजाः तोषय इति ।
भाव : निजराज्यं प्रजाः च तोषय ।
2. समभियान्त्यरयो विभियोऽधियः ।
परिचय : एतत् वाक्यं रुद्रमदेवी इति पाठ्यभागात् स्वीकृतम् । अस्य रचयिता श्री डी. वेङ्कटरामाचार्यः ।
सन्दर्भ : काकतीयराजः स्वपुत्रीं रुद्रमदेवीम् राज्ये अभिषिक्तवान् । -तदसहमानाः देवगिरिराजादयः वयम् अबलया अवमानिताः इति संचिन्त्य ताम् -अभिययौ ।
भाव : भयहीनाः मूर्खाः शत्रवः अभिद्रवन्ति ।

3. नृपाग्रणीं तं विरथं चकार ।
परिचय : एतत् वाक्यं रुद्रमदेवी इति पाठ्यभागात् स्वीकृतम् । अस्य रचयिता श्री डी. वेङ्कटरामाचार्यः ।
सन्दर्भ : रुद्रमदेवी रणे देवगिरिराजस्य हस्तिपकं अहनत् । तदनु तस्य सारथिम्, अश्वान् च हत्वा तं विरथं चकार ।
भाव : सा चक्रवर्तिनं तं रथहीनम् अकारयत् ।
एकपद समाधान प्रश्नाः (ఏక పద సమాధాన ప్రశ్నలు) (One Word Questions)
पश्न 1.
कस्य वचः निशम्य नृपतिः मुदम् अवाप ?
समादान:
सचिवस्य वचः
पश्न 2.
रुद्रमां का सफलां चकार ?
समादान:
शिवदेववाक्
पश्न 3.
रुद्रमया प्रयुक्तः खड्गः कं जघान ?
समादान:
देवगिरिराजस्य हस्तिपकं
कठिन शब्दार्द (కఠిన పదాలు – అర్ధాలు)
1. जरठः = वृध्दः, ముసలివాడు ,
2. धरणीभुक् = राजा, రాజు
3. पुरोधाः = पुरोहितः, పురోహితుడు
4. शत्रुवरुथिनी = शत्रुसेना, శత్రుసేన
5. वाहिनी = सेना, సేన
6. वृषा = इन्द्रः, ఇంద్రుడు
7. उज्ज्वलप्रथनदुर्गमवर्त्म = प्रकाशयुक्तः विस्तृतः दुष्प्राप्यमार्गः ప్రవేశింప వీలుగాని మార్గం
8. पृथुभण्डनपण्डिताः = दुष्टकर्मकुशलाः, చెడుపనులు చేయువారు
9. समीकम् = युद्धम्, యుద్ధము
10. विगतत्रपा = निर्लज्जाः, సిగ్గులేనివారు
11. विभियः = निर्भीकाः, భయంలేనివారు
12. अधियः = मूढाः, మూడులు
13. निकृताः = शठाः, శఠులు
14. अपसमंज्ञा = अपमानः, అవమానం
15. हस्तिपकः = गजनियन्ता, మావటివాఁడు
16. उन्मदद्विपः = मदगजः, మదగజము
17. तुरङ्गः = अश्व:, గుర్రం
18. व्याली = सर्पिणी, పాము

19. परीतम् = आक्रान्तम्, ఆక్రమణ
20. पराक्तम् = पराक्रान्तम्, ఇతరులచే పొందబడిన
21. अरातिसैन्यम् = शत्रुसैन्यम्, శత్రుసైన్యం
22. ईक्षा = दृक्, చూపు
23. जिघांसुः = हन्तुम् इच्छति इति जिघांसुः, చంపాలనే కోరిక
24. शरौघम् = शराणां समूहः, బాణాల సమూహం
25. तुमुलम् = कोलाहलमयम्, కోలాహలము
26. परिपन्थिनः = शत्रवः, శత్రువులు
व्याकरणाश (వ్యాకరణాంశాలు)
सन्धयः (సంధులు)
1. सितनिजातपवारणतः + अभितः = सितनिजातपवारणतोऽभितः – विसर्गसन्धिः
2. जरठः + अभवत् = जरठोऽभवत् – विसर्गसन्धिः
3. सचिवः + अवदत् = सचिवोऽवदत् – विसर्गसन्धिः
4. अभूत् + वलयन् = अभूद्वलयन् – जश्त्वसन्धिः
5. निगममन्त्रवचोभिः + अषिच्यत = निगममन्त्रवचोभिरषिच्यत – विसर्गसन्धिः
6. विधिवत् + निजकाम्यया = विधिवन्निजकाम्यया – अनुनासिकसन्धिः
7. हरिहरः + च = हरिहरश्च – श्चुत्व सन्धिः
8. यत् + अभिवीक्ष्य = यदभिवीक्ष्य – जश्त्वसन्धिः
9. पतिः + उज्वलप्रथनदुर्गमवर्त्मनि = पतिरुज्ज्वलप्रथनर्दुर्गमवर्त्मनि – विसर्गसन्धिः
10. विभियः + अधियः = विभियोऽधियः – विसर्गसन्धिः
समासाः (సమాసాలు)
1. पलिताः केशाः यस्य सः – पलितकेशः – बहुव्रीहि
2. शत्रुणां शिरांसि – शत्रुशिरांसि तेषु शत्रुशिरस्सु – षष्ठीतत्पुरुष
3. मित्राणि च ते जनाश्च मित्रजनाः – विशेषणपूर्वपदकर्मधारय
4. सकलाश्च ते मित्रजनाश्च – सकलमित्रजनाः तेषु सकलमित्रजनेषु – विशेषणपूर्वपदकर्मधारयः
5. भयं करोतीति भयङ्करी – उपपदतत्पुरुष
6. निजस्य धरा निजधरा तां निजधराम् – षष्ठीतत्पुरुष
7. प्रजाभिः सह वर्तते इति सप्रजा तां सप्रजाम् – बहुव्रीहि
8. पुलकैः सहितं यथा स्यात् तथा सपुलकं – अव्ययीभाव
9. धरणीं भुङ्क्ते इति धरणीभुक् तेन धरणीभुजा – उपपदतत्पुरुष
10. तनोः जायते इति तनुजा – उपपदतत्पुरुष
11. विगतं मलं यस्याः सा विमला – बहुव्रीहि
12. अविद्यमानं कलुषं यस्याः सा अकलुषा ताम् अकलुषाम् – बहुव्रीहि
13. निजस्य काम्या निजकाम्या – षष्ठीतत्पुरुष
14. मह्याः पतिः महीपतिः – षष्ठीतत्पुरुष
अर्थतात्पर्याणि (Meanings & Substances) (తాత్పర్యములు)
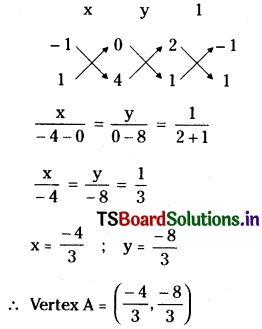
1. अथ स काकतिराजपुरन्दरः सितनिजातपवारणतोऽभितः ।
पटुपराक्रमभानुमरीचिना चिरमुवास भुवं परिपालयन् ॥
అథ స కాకతిరాజ పురందరః సితనిజాతపవాణతో భితః |
పటుపరాక్రమభానుమరీచినా చిరమువాస భువం పరిపాలయన్ ॥
पदच्छेदः – अथ, स, काकतिराजपुरन्दरः, सितनिजातपवारणतः, अभितः, पदुपराक्रमभानुमरीचिना, चिरं, उवास भुवं पालयन् ।
अन्वयक्रमः – अथ, काकतिराजपुरन्दरः, सः, पटुपराक्रमभानुमरीचिना, सितनिजातपवारणतः, भुवं अभितः, पालयन्, चिरं, उवास ।
अर्थाः-
अथ = పిమ్మట
काकतिराजपुरन्दरः = కాకతి రాజ్యమునకు రాజు
सः = ఆ గణపతిదేవుడు;
पटुपराक्रमभानुमरीचिना = పటిష్టమైన పరాక్రమం అనే సూర్యకిరణాలతో;
सितनिजातपवारणतः = తెల్లనైన తన యొక్క గొడుగుతో;
भुवं अभितः = భూమినంతా;
पालयन्, = పాలిస్తూ;
चिरं = చాలాకాలం;
उवास = గడిపాడు.
भावः-
కాకతీయ సామ్రాజ్య చక్రవర్తులలో శ్రేష్ఠుడైన ఆ గణపతి దేవుడు తన పటిష్ఠమైన పరాక్రమంతో, తెల్లనైన తన ఛత్రంతో భూమినంతా చాలా కాలం పాలించాడు.
The king of Kakati lived a long time ruling the earth with his rays of valour spreading on all sides of his royal umbrella.

2. बहुतिथे समये सति गच्छति प्रियपिनाकभुजो जरठोऽभवत् ।
पलितकेशममुं शिथिलीभवत्पटुनिजावयवं सचिवोऽवदत् ॥
బహుతిథే సమయే సతీ గచ్ఛతి ప్రియపినాకభుజో జరఠో భవత్ |
పలితకేశమముం శిథిలీభవత్పటునిజావయవం సచివోకెవదత్ ||
पदच्छेदः – बहुतिये, समये, सति, गच्छति, प्रियपिनाक भुजो, जरठः, अभवत्, पलितकेशम्, अमुं शिथिलीभवत्, पटुनिजावयवं सचिवः अवदत् ।
अन्वयक्रमः – बहुतिये समयः गच्छति सति, प्रियपिनाकभुजः, जरठः, अभवत्, पलितकेशम्, शिधिलीभवत्पटुनिजावयवं अमुं, सचिवः अवदत् ।
अर्थाः-
बहुतिये समयः = చాలా కాలము;
गच्छति सति = గడవగానే
प्रियपिनाकभुजः = రాజ్యభారమును వహిస్తున్నవాడైన రాజు;
जरठः = ముసలివాడు,
अभवत् = అయ్యాడు;
पलितकेशम् = తెల్లబడిన కేశములుగల;
शिथिलाभवत्पटु निजावयवम् = శిధిలమైన తన శరీర అవయవములుగల;
अमुम् = ఈ గణపతిదేవిని గూర్చి;
सचिवः = మంత్రి;
अवदत् = పలికాడు.
भावः-
చాలా కాలం గడిచింది. రాజైన గణపతి దేవుడు ముసలివాడుగా అయ్యాడు జుట్టు తెల్లబడింది. అవయవాలు శిథిలమైనాయి. అటువంటి ఈ గణపతి దేవుడిని ఉద్దేశించి అతని మంత్రి పలికాడు.
As many days passed, the king became old. On seeing the king whose hair turned grey and limbs lost their strength, the minister said to him.
3. अयि महन् दुहिता तव रुद्रमा निखिलकाकतिराज्यरमेश्वरी ।
भवितुमर्हति शत्रुशिरस्सु या कृतवती चरणं कमलारुणाम् ॥
అయిమహాన్ దుహితా తవ రుద్రమా నిఖిలకాకతి రాజ్యరమేశ్వరీ |
భువితుమర్హతి శత్రుశిరస్సు యా కృతవతీ చరణం కమలారుణామ్ ||
पदच्छेदः – अयि, महान्, दुहिता, तव, रुद्रमा, निखिलकाकति राज्यरमेश्वरी भवितुं अर्हति, शतृशिरस्सु, सा कृतवती, चरणं, कमलारुणाम् ।
अन्वयक्रमः – अयि महन् तव, दुहिता, रुद्रमा निखिलकाकतिराज्यरमेश्वरी, भवितुं अर्हति, या, शतृशिरस्सु, कमलारुणाम्, चरणं, कृतवती ।
अर्थाः-
अयि महन् = అయ్యా మహానుభావా !;
तव दुहिता = నీ కుమార్తె అయిన;
रुद्रमा = రుద్రమదేవి;
निखिलकाकतिराज्यरमेश्वरी = సమస్త కాకతీయ సామ్రాజ్య లక్ష్మిగా;
भवितुं = రాణిగా అగుటకు;
अर्हति = తగియున్నది;
या = ఏ రుద్రమదేవి ;
शतृशिरस्सु = శత్రువుల శిరస్సులందు;
कमलारुणाम् = కమలమువలె ఎర్రనైన;
चरणं = పాదమును;
कृतवती = ఉంచగలదు.
भावः-
ఓ మహారాజ ! నీ కుమార్తె అయిన రుద్రమదేవి సమస్త కాకతి రాజ్యలక్ష్మిగా అగుటకు యోగ్యురాలుగా ఉంది. ఆమె శత్రురాజుల శిరస్సులపై కమలములవలె ఎర్రనైన తన పాదాలను ఉంచగలదు.
4. सकलमित्रजनेष्वभयङ्करीं निखिलशत्रुजनेषु भयङ्करीम् ।
शिवपरामभिषेचय रुद्रमां निजधरां मुदितां कुरु सप्रजाम् ।
సకల మిత్రజనేష్వభయంకరీ నిఖిల శత్రుజనేషు భయంకరీం |
శివపరామభిషేచయ రుద్రమాం నిజధరాం ముదితాం కురుసప్రజామ్ ॥
पदच्छेदः सकलमित्रजनेषु, अभयंकरी, निखिलशतृजनेषु, भयंकरी, शिवपराम् अभिषेचय, रुद्रमाम्, निजधरां, सप्रजाम्, मुदितां, कुरु
अन्वयक्रमः – सकलमित्रजनेषु, अभयंकरी, निखिलजनेषु भयंकरी, शिवपराम्, रुद्रमां अभिषेचय, स प्रजाम् निजधरां, मुदितां, कुरु
अर्थाः-
सकलमित्रजनेषु = సమస్త మిత్రు జనులయందు;
अभयंकरी = భయంలేనిదిగాను;
निखिलजनेषु = సకల శత్రుజనులయందు;
भयंकरी = భయంకరి అయిన;
शिवपराम् = శివశక్తి సమన్వయరాలైన;
रुद्रमां = రుద్రమదేవిని;
अभिषेचय = అభిషేకించి;
शिवपराम् = ప్రజలతోకూడిన;
सप्रजाम् = నీ భూమిని;
मुदितां = సంతోషించినదానినిగా;
कुरु = చేయుము.
भावः-
రాజా ! ఆశ్రితుల పట్ల అభయాన్ని కల్గించేదియును, శత్రుజనులపట్ల భయాన్ని కల్గించే, శివశక్తి సంపన్నురాలైన రుద్రమదేవిని రాణిగా పట్టాభిషేకం చేయండి. దాంతో రాజ్యమంతా మిక్కిలి ఆనందిస్తుంది.
Crown Rudrama, the devotee of Siva, who removes the fear of all her friends, but who. frightens her enemies. Make the kingdom and the people happy.”
5. इति निशम्य वचः सचिवस्य तन्नृपतिराप मुदं परमां तदा ।
जनपदेषु पुरेषु च घोषणाध्वनिरभूद्वलयन् विदिशो दिशः ॥
ఇతి నిశమ్య వచః సచివస్య తన్నృపతి రాపముదం పరమాం తదా ।
జనపదేషు పురేషు చ ఘోషణా ధ్వనిరభూద్వలయన్ విదిశోదిశః ||
पदच्छेदः – इति, निशम्य वचः अचिवस्य, तत्, नृपतिः, आप, मुदं परमां, तदा, जनपदेषु परेषु, च, घोषणाध्वनिः, अभूत्, वलयन्, विदिशो दिशः
अन्वयक्रमः – इति, सचिवस्य, वचः, निशम्य, नृपतिः, तदा परमां, मुदां, आप, जनपदेषु, च, पुरेषु, दिशः, विदिशः, घोषणाद्वनि:, अभूत्
अर्थाः-
इति = ఈ విధంగా;
सचिवस्य = మంత్రి యొక్క;
वचः = మాటలను;
निशम्य = విని;
नृपतिः = రాజు;
तदा = అప్పుడు;
परमां = మిక్కిలి;
मुदां = ఆనందాన్ని;
आप = పొందాడు;
जनपदेषु = గ్రామాలయందు;
पुरेषु = నగరాలయందు;
दिशः विदिशः = అన్ని దిక్కుల యందు;
घोषणाद्वनि: = చాటింపు;
अभूत् = జరిగెను.
भावः-
గణపతిదేవ మహారాజు తన మంత్రిమాటలను విని మిక్కిలి ఆనందించాడు. రుద్రమదేవి రాణి కాబోతుందన్న విషయాన్ని గ్రామాల్లోను, నగరాల్లోను, అన్ని దిక్కులయందు చాటింపు వేశాడు.
On hearing those words of the minister, the king became happy. Announcement to that effect was made in towns and villages, echoing in the quarters.
6. महितपुण्यसमुद्रनदीजलैः शुभदिने महतां च पुरोधसाम् ।
सपुलकं तनुजा धरणीभुजा निगममन्त्रवचोभिरषिच्यत ॥
మహితపుణ్యసముద్రనదీజలైః శుభదినే మహతాం చ పురోధసాం ।
సపులకం తనుజా ధరణీభుజా నిగమమంత్రవచోభిరషిచ్యత
पदच्छेदः – महितपुण्यसमुद्रनदीजलैः, शुभदिने, महताम्, च, पुरोधसाम् सपुलकं, तनूजा, धरणीभुजा निगममन्त्रवचोभिः अभिषिच्यत ।
अन्वयक्रमः – महितपुण्यसमुद्रनदीजलैः, निगममन्त्रवर्चाभिः महतां, पुरोधसाम्, शुभदिने, धरणीभुजा, सपुलकं तनूजा अभिषित्यत ।
अर्थाः-
महितपुण्यसमुद्रनदीजलैः = మహిమాన్వితమైన పుణ్యప్రదములైన సముద్రనదీ జలాలతోను;
महतां = మహాత్ములైన;
पुरोधसाम् = పురోహితులయొక్క;
निगम-मन्त्रवचोभिः = వేదమంత్రాలతో;
धरणीभुजा = రాజైన గణపతిదేవుడు;
सपुलकं = పులకరించినవాడై;
शुभदिने = శుభదినమందు;
अभिषित्यत = అభిషేకింపచేశాడు.
भावः-
గణపతిదేవుడు ఒక శుభముహూర్తంలో మహిమాన్వితమైన పుణ్యప్రదమైన సముద్రనదీ జలాలలోను, మహాత్ములైన వేదమంత్రాలతోను తన కుమార్తెను కాకతీయ రాణిగా పట్టాభిషేకం చేశాడు.
On an auspicious day, as the priests chanted the Vedic mantras, she was sprinkled with the waters of the holy oceans and rivers.
7. प्रियहिता विमला शिवदेववागकलुषां सफलां च चकार ताम् ।
नतमहीपतयो जनता च यत् करमदुः विधिवन्निजकाम्यया ॥
ప్రియహితా విమలా శివదేవవాగకలుషాం సఫలాం చ చకార తామ్ ।
నతమహీపతయో జనతా చ యత్ కరముదుః విధివన్నిజకామ్యయా ॥
पदच्छेदः प्रियहिता, विमला, शिवदेववाक् तां, अकलुषां, सफलां, च, चकार, ताम्, नतमहीपतयः, जनता, च, यत्, करमदुः, विधिवत्, निजकाम्यया
अन्वयक्रमः प्रियहिता, विमला, शिवदेववाक् तां, अकलुषां, सफलां, चकार, नतमहीपतयः, च, जनता विधिवत्, निजकाम्यया करं, अदुः |
अर्थाः-
प्रियहिता = ప్రియహితకరమైన;
विमला = స్వచ్ఛమైన;
शिवदेववाक् = మంత్రి శివదేవుని వాక్కు;
तां = ఆ రుద్రమదేవిని;
अकलुषां = కలుషత్వం లేనిదానిని గాను;
च = మరియు;
जनता = ప్రజలు;
विधिवत्, = శాస్త్ర విధానాన్ని అనుసరించి;
निजकाम्यया = పూర్తి ఇష్టంతో;
करं = పన్నును;
अदुः = సమర్పించారు.
भावः-
గణపతిదేవుని మంత్రి అయిన శివ దేవుని ప్రియహితమైన, స్వచ్ఛమైన వాక్కు ఆ రుద్రమదేవిని సఫలురాలిగాను, కల్మషంలేనిదానినిగాను చేసింది. సామంత రాజుల, ప్రజలు శాస్త్ర విధానాన్ని అనుసరించి పూర్తి ఇష్టంతో తమ పన్నులను కట్టాడు.
The blessing of Siva made her pious and accomplished. Kings and people payed taxes willingly.

8. हरिहरश्च मुरारिमहीपतिः यदभिवीक्ष्य नितान्तमसूयया ।
कलुषितौ चकितौ च तथाभवत् निखिलराष्ट्रमनन्तसमृद्धिमत् ॥
హరిహరశ్చ మురారి మహీపతిః యదభివీక్ష్య నితాంతమసూయసా ।
కలుషీతౌ చకితౌ చ తథాభవత్ నిఖిల రాష్ట్ర మనంత సమృద్ధిమత్
पदच्छेदः – हरिहरः च मुरारिमहीपतिः, यत् अभिवीक्ष्य, नितान्तं, असूयया, कलुषितौ चकितौ च तथाः अभवत् निखिलराष्ट्रम् अनन्तसमृद्विमत् ।
अन्वयक्रमः – हरिहरः, च, मुरारिमहीपतिः, नितान्तं, असूयया, यत् अनन्तसमृद्धिमत्, निखिल राष्ट्र, अभिवीक्ष्य, कलुषितौ चकितौ, तथा, अभवत् ।
अर्थाः-
हरिहरः = హరిహరుడు;
च = మరియు;
मुरारिमहीपतिः = మురారిరాజు;
यत् अनन्तसमृद्धिमत् = మిక్కిలి సమృద్ధితో కూడిన;
निखिलराष्ट्रम् = సమస్త రాష్ట్రాన్ని;
अभिवीक्ष्य = చూచి;
कलुषितौ = కలుషితులుగాను;
चकितौ = ఆశ్చర్యం పొందే విధంగాను;
तथा = ఆ విధంగా;
अभवत् = అయింది.
भावः-
హరిహరుడు మరియు మురారి మిక్కిలి సమృద్ధితో కూడిన కాకతీయ రాష్ట్రాన్ని మిక్కిలి అసూయతో చూడసాగారు. వారు కలుషులు అయ్యే విధంగాను, ఆశ్చర్యం పొందే విధంగాను ఆ రాష్ట్రం మొత్తం అభివృద్ధిని పొందింది.
Harihara and Murari, having enviously observed that the kingdom was prosperous, became scared and frightened.
9. अथ च देवगिरेः पतिरुज्ज्वलप्रथनदुर्गमवर्त्मनि पण्डितः ।
हरिहरं च मुरारिमलोभयत् कुटिलनीतिजितात्महितावुभौ ॥
అథ చ దేవగిరేః పతిరుజ్జ్వల ప్రథన దుర్గమ వర్త్మని, పండితః,
హరిహరం చ మురారిమలోభయత్ కుటిల నీతి జితాత్మాహితావుభౌ
पदच्छेदः – अथ, च, देवगिरेः, पतिज्वलप्रथनदुर्गम वर्त्मनि, पण्डिताः, हरिहरं च, मुरारिम्, अलोभयत्; कुटिलनीतिजितात्महितौ, अभौ ।
अन्वयक्रमः – अथ, देवगिरेः, पतिः, उज्वल प्रथनदुर्गमवर्त्मनि पण्डितः हरिहरं, च, मुरारि, कुटिलनीतिजितात्महितौ उभौ, अलोभयत् ।
अर्थाः-
अथ = పిమ్మట;
उज्वलप्रथनदुर्गमवर्त्मनि = ప్రకాశవంతమైన, విస్తృతమైన ప్రవేశించుటకు యోగ్యముగాని మార్గరచనయందు;
पण्डिताः = నిపుణుడైన;
देवगिरेः पतिः = దేవగిరిరాజు;
हरिहरं = హరిహరుడిని;
च = మరియు;
मुरारिम् = మురారిని ;
कुटिलनीतिजितात्महितौ = కుటిలమైన నీతి చేత జయింపబడిన ఆత్మహితులైన;
उभौ = ఆ ఇద్దరిని;
अलोभयत् = ప్రలోభపెట్టారు.
भावः-
పిమ్మట ప్రకాశవంతమైన, విస్తృతమైన ప్రవేశించుటకు యోగ్యముకాని మార్గమును రచించుటయందు నైపుణ్యంగల దేవగిరిరాజు హరిహరుడిని, మురారిని తన కుటిలనీతితో ప్రలోభపెట్టాడు.
Then the king of Devagiri, the master in bad ways, lured them, who let their welfare won over by crooked mind.
10. अबलया च कयाचिदिमे वयं सुबलिनो बलिनो विगतत्रपाः ।
कलुषिता निकृताः परिपूरिताः मलिनयाऽसितयाऽपसमझया ||
అబలయా చ కయాచిదిమే వయం సుబలినో బలినో విగతత్రపాః ।
కలుషితా నికృతాః పరిపూరితాః మలినయా కాసితయాపసమజ్ఞయా ॥
पदच्छेदः – अबलया, च, कयाचित् इमे वयं सुबलिनः, बलिनः, विगतत्रपाः, कलुषिताः, निकृताः, परिपूरिताः, मलिनया, असितया, असमज्ञया ।
अन्वयक्रमः – सुबलिनः, बलिनः, इमे, चयं, विगतत्रपाः, अबलया, मलिनया, कलुषिताः, असितया निकृताः, असमज्ञया परिपू
अर्थाः-
सुबलिनः = గొప్పబలయుక్తమైన సైన్యబలం కలిగిన;
बलिनः = బలవంతులమైన;
इमे चयं = ఈ మనం;
कयाचित् अबलया = ఒకానొక స్త్రీ చరిత్ర;
विगतत्रपाः = సిగ్గులసహారిమై;
मलिनया = మాలిన్యంతో;
कलुषिताः = కల్మషం పొందినారు;
असितया = నల్లదనముచే, పాపముచే;
निकृताः = కుత్సితులమైనారు;
असमज्ञया = అనాలోచనతో;
परिपूरिताः = పూర్తిగా నిండినవారు అయ్యారు.
भावः-
బలసంపన్నమై సైన్యంతో బలవంతులమైన మనం ఒకానొక స్త్రీచేత సిగ్గువిడినవారం అయినాము. అంతేకాదు వారు మాలిన్యంతో కలుషితులైనారు. నల్లనైన పాపంతో కుత్సితులైనారు. అనాలోచనతో పూర్తిగా మునిగిపోయారు.
‘We, the powerful and fearless, having great army, are sullied with insult by some woman.”
11. इति स देवगिरेः पतिरुन्मदद्विपतुरङ्गमसैनिक गर्वितः ।
अभिययौ पटुकाकतिवाहिनीं शिवबलामबलामिति रुद्रमाम् ॥
ఇతి స దేవగిరేః పతిరున్మదద్విపతురంగమసైనిక గర్వితః |
అభియయౌ పటుకాకతివాహినీం శివబలామబలామితి రుద్రమామ్ ॥
पदच्छेदः – इति, सः, देवगिरेः पतिः, उन्मदद्विपतुरङ्गम सैनिकगर्वितः, अभिययौ, पटुकाकतिवाहिनीम् शिवबलाम्, अबलाम् इति, रुद्रमाम् ।
अन्वयक्रमः – इति, देवगिरेः पतिः, सः, रुन्मदद्विपतुरङ्गम सैनिकगर्वितः, पटुकाकतिवाहिनीं, शिवबलाम् रुद्रमाम्, अबलां, अभिययौ ।
अर्थाः-
इति = అని;
देवगिरेः पतिः = దేవగిరి ప్రభు;
उन्मद = బాగా మదించిన;
द्विपतुरंगम सैनिकगणितः = ఏనుగులు, గుర్రాలు, సైనికుల బలంతో గర్వించినవాడై;
पटुकाकतिवाहिनीं = పటిష్టమైన కాకతీయ సైన్యముగల;
शिवबलाम् = శివబలశక్తితో కూడిన;
रुद्रमाम् = రుద్రమదేవిని;
अबलां = అబలగా భావించి;
अभिययौ = ఎదుర్కొన్నారు ఆక్రమించాడు.
भावः-
బాగా మదించిన గజతురగ సైనిక బలంతో గర్వించిన ఆ దేవగిరి రాజు పటిష్టమైన సైన్య సంపత్తి కలిగిన, శివబల సమన్వితురాలైన రుద్రమదేవిని అబలగా భావించి ఎదుర్కొనడానికి సిద్ధపడినాడు.
Thus, the ruler of Devagiri, proud of his intoxicated elephants, horses and soldiers, attacked the Kakati army thinking that Rudrama, who was blessed by Siva was weak.
12. शशिकलाभरणे निखिलेश्वरे भजनकामनया खलु रुद्रमा ।
गतवती पृथुभण्डनपण्डिताः समभियान्त्यरयो विभियोऽधियः ॥
శశికలాభరణే నిఖిలేశ్వరే భజనకామనయా ఖలు రుద్రమా |
గతవతీ పృధుభండనపండితాః సమభియాంత్యరయో విభియోథియః ॥
पदच्छेदः -. शशिकलाभरणे, निखिलेश्वरे, भजनकामनया, खलु, रुद्रमा, गतवती, पृथुभण्डनपण्डिताः, समभियान्ति, अरयः, विभियः, अधियः ।
अन्वयक्रमः – निखिलेश्वरे, शशिकलाभरणे, भजकामनया, रुद्रमा, गतवती, पृथुभण्डनपण्डिताः, विभियः, अधियः, अरयः समभियान्ति ।
अर्थाः-
निखिलेश्वरे = నిఖిలేశ్వరుడైన;
शशिकलाभरणे, = పరమేశ్వరుడిని;
भजकामनया = సేవింపదలచినదైన;
रुद्रमा = రుద్రమదేవి;
गतवती = వెళ్ళింది;
पृथुभण्डनपण्डिताः = ప్రవేశించడానికి ‘ యోగ్యముగా మార్గమును తెరిసిన;
विभियः = భయములేని ;
अधियः = బుద్ధిలేనివారై;
समभियान्ति = ఆక్రమించారు.
भावः-
రుద్రమదేవి నిఖిలేశ్వరుడైన పరమేశ్వరుడిని సేవించడానికి వెళ్ళింది. ఆ సమయంలో ప్రవేశించడానికి వీలుగాని మార్గమును తెలిసిన, శత్రువులు భయంలేనివారై, బుద్ధిహీనులై నగరాన్ని ఆక్రమించారు.
While Rudrama went to worship the cres-cent ornamental Siva, the foolish enemies, who were experts in wrong deeds attacked.
13. उदन्तमासाद्य नितान्तरोषकषायितारक्तमुखाऽरुणाक्षी ।
निवर्त्य सैन्येन मितेन वेगात् रुद्राम्बिका प्राप पुरं पराक्तम् ॥
ఉదంతమాసాద్య నితాంతరోషకషాయితారక్తముఖాుణాక్షి |
నిర్వర్త్య సైన్యేన మితేన వేగాత్ రుద్రాంబికా ప్రాప పురం పరాక్తమ్ ॥
पदच्छेदः – उदन्तम्, आसाद्य, नितान्तरोषकषायितारक्तमुखी, अरुणाक्षी, निवर्त्य, सैन्येन, मितेन, वेगात्, रुद्राम्बिका, प्राप, पुरं, पराक्तम्
अन्वयक्रमः – उदन्तं, आसाद्य, नितान्तरोषकषायितारक्तमुखी, अरणाक्षी, रुद्रांबिका, मितेन, सैन्येन निर्वर्त्य, वेगात् पराक्तम्, पुरं प्राप
अर्थाः-
उदन्तं = జరిగిన వృత్తాంతాన్ని,
आसाद्य = తెలుసుకొని,
नितान्त = మిక్కిలి;
रोषकषायिता = కోపంతో ఎర్రబడిన;
रक्तमुखी = ఎరుపెక్కిన ముఖము గలదైన;
अरणाक्षी = ఎర్రబారిన కన్నులు గల;
रुद्रांबिका = రుద్రమదేవి ;
मितेन = పరిమితమైన;
सैन्येन = సైన్యంతో;
निर्वर्त्य = వెనుదిరిగి;
वेगात् = వేగంగా;
पराक्तम् = శత్రువులతో ఆక్రమింపబడిన;
पुरं = నగరాన్ని;
प्राप = చేరుకుంది. (పొందింది)
भावः-
రుద్రమదేవి జరిగిన విషయమంతా తెలుసుకుంది. దాంతో ఆమె మిక్కిలి కోపాన్ని పొందింది. ముఖం ఎర్రబడింది. కన్నులు ఎర్రబడినాయి. వెంటనే పరిమిత సైన్యంతో శివాలయం నుండి వెనుదిరిగి, శత్రువులతో ఆక్రమింపబడిన నగరాన్ని చేరుకుంది.
On getting the news, Rudrama, whose eyes and face reddened with great anger, turned back and with limited force approached the city that was under attack.

14. व्यालीव निश्वस्य परैः परीतं पुरं समुदीक्ष्य समीपमेत्य ।
दध्मौ स्वशङ्खं युधि चण्डिकेव जिघांसुरीक्षाभिररातिसैन्यम् ॥
వ్యలీవ నిశ్శ్వస్య పరైః పరీతం పురం సముద్వీక్ష్య సమీపమేత్య ।
దధ్మౌ స్వశంఖం యుధి చండికేవ జిఘాంసురీక్షాభిరరాతిసైన్యం ॥
पदच्छेदः – व्यलीव, निश्वस्य, परैः परीतं, पुरं, समुद्वीक्ष्य, समीपं, एत्य, दध्मौ, स्वशंखं, युधि, चण्डिकेव, जिघांसुः, ईक्षाभिः, अरातिसैन्यम् |
अन्वयक्रमः – परैः, परीतं, पुरं, ईक्षाभिः, अरातिसैन्यं, समुद्वीक्ष्य, व्यलीव, निश्वस्य जिघांसुह चण्डिकेव, युधि, स्वशंखं दध्मौ ।
अर्थाः-
परैः = శత్రువుల చేత;
परीतं = ఆక్రమింపబడిన,
पुरं = నగరాన్ని,
ईक्षाभिः = చూపులతో;
समुद्वीक्ष्य = బాగుగా చూచి;
व्यलीव = పామువలె;
निश्वस्य = నిట్టూర్చి;
अरातिसैन्यं = శత్రుసైన్యాన్ని;
जिघांसुह = జయింపదలచినదై;
चण्डिकेव = చండికాదేవి వలె;
स्वशंखं = తన శంఖాన్ని;
युधि = యుద్ధంలో;
दध्मौ = పూరించెను.
भावः-
రుద్రమదేవి శత్రువులతో ఆక్రమింపబడిన నగరాన్ని తన కన్నులతో చూచింది. వారిని సమీపించింది. పామువలె కోపంతో బుసలు కొట్టింది. వారిని జయింప దలచినదై యుద్ధరంగంలో చండికవలె ధ్వని శంఖాన్ని పూరించింది.
Hissing like a serpent, she reached the city under siege of the enemies, and blew her conch, desiring to kill the armies of the enemy like Chandika.
15. आध्मातशंखामधिगम्य राज्ञीं रुद्राम्बिकां दुर्गगता हि योधाः ।
सामन्तभूपाश्च विवृद्धमोदसमृद्धयो दध्मुरतोऽविलम्बम् ॥
ఆధ్మాతశంఖామధిగమ్య రాజ్జీం రుద్రాంబికాం దుర్గగతా హి యోధాః ।
సామంతభూపాశ్చ వివృద్ధమోదసమృద్ధయొ దధ్మురతో కవిలంబమ్ ॥
पदच्छेदः – आध्मातशंखाम्, अधिगम्य, राज्ञीं, रुद्रांबिकां, दुर्गगता, हि, योधाः, सामन्तभूपाः, विवृद्धमोदसमृद्धयः दध्मुः, अतः अविलम्बम्
अन्वयक्रमः – राज्ञीं, रुद्रांबिकां, आध्मातशंखां, अधिगम्य, दुर्गगताः, योधाः, च, सामन्तभूपाः, विवृद्धमोदसमृद्धयः, अविलम्बं, अतः, दध्मुः
अर्थाः-
राज्ञीं = రాణి అయిన,
रुद्रांबिकां = రుద్రమ దేవి,
अधिगम्य = తెలుసుకొని;
दुर्गगताः = దుర్గంలోని;
योधाः = వీరులు;
च = మరియు;
सामन्तभूपाः = సామంత రాజులు;
विवृद्धमोदसमृद्धयः = మిక్కిలి ఆనందముతో కూడినవారై;
अविलम्बं = వెంటనే;
अतः = అక్కడి నుండి;
दध्मुः = శంఖాన్ని పూరించారు.
भावः-
రుద్రమదేవి చేసిన శంఖ ధ్వనిని విని దుర్గంలోని వీరులు మరియు సామంతరాజులు మిక్కిలి ఆనందాన్ని పొందినవారై వెంటనే శంఖాన్ని పూరించారు.
Having understood that it was their queen Rudrama, who blew the conch, the feudatory kings and the soldiers in the city became overjoyed, and they blew their conches.
16. अन्योन्यसंज्ञामधिगम्य सर्वे जजृम्भिरे शत्रुवरूथिनीनाम् ।
पश्चात्पुरस्ताच्च महाभटास्ते दवानला वा चटुलाटवीनाम् ।
అన్యోన్యసంజ్ఞామధిగమ్య సర్వే జజృంభిరే శత్రువరూధినీనామ్ ।
పశ్చాత్పురస్తాచ్చ మహాభటాస్తే దవానలా వా చటులాటవీనామ్ ||
पदच्छेदः – अन्योन्यसंज्ञां, अधिगम्य, सर्वे, जजृंभिरे, शतृवरूथिनीनाम्, पश्चात्, पुरस्तात्, च, महाभटाः, ते, दवानला, वा चतुलाटवीनाम् ।
अन्वयक्रमः – सर्वे, महाभटाः, अन्योन्यसंज्ञां, अधिगम्य, चटुलाटवीनां, दवानला वा, शतृवरूथिनीनाम्, पश्चात्, पुरस्तात्, जजृम्भिरे ।
अर्थाः-
सर्वे ते महाभटाः = ఆ సైనికులందరు;
अन्योन्यसंज्ञां = పరస్పర సంజ్ఞలతో;
अधिगम्य = తెలుసుకొని;
चटुलाटवीनां = చంచలమైన అడవియందు పుట్టిన;
दवानला वा = కారుచిచ్చు వలె;
शतृवरूथिनीनाम् = శత్రుసైన్యముల యొక్క;
पश्चात् = వెనుక ;
पुरस्तात् = ముందు భాగమందు;
जजृम्भिरे = చుట్టుముట్టారు.
भावः-
రుద్రమదేవి సైనికులందరు పరస్పర సంజ్ఞలతో శత్రుసైనికులు వచ్చారనే విషయాన్ని తెలుసుకొని అరణ్యంలో ఏర్పడిన కారుచిచ్చువలె శత్రుసైన్యానికి ముందు, వెనుక భాగాలను చుట్టుముట్టారు.
Receiving signals from one another, they attacked the enemy forces from front and back, just as a forest fire would spread from both ends of a forest.
17. क्षणात्ततो रुद्रमया प्रयुक्तः खड्गः सपक्षश्च फणीव वेगात् ।
देवाद्रिनाथस्य गजे निषण्णं धृताङ्कुशं हस्तिपकं जघान ॥
క్షణాత్తతో రుద్రమయా ప్రయుక్తః ఖడ్గః సపక్షశ్చ ఫణీవ వేగాత్ |
దేవాద్రినాథస్య గజే విషణ్ణం ధృతాంకుశం హస్తిపకం జఘాన ॥
पदच्छेदः – क्षणात्, ततः, रुद्रमया, प्रयुक्तः, खड्गः, सपक्षः, च, फणीव, वेगात्, देवाद्रिनायस्य, गजे, विषण्णं, धृतांकुशं हस्तिपकं जघान ।
अन्वयक्रमः – ततः, रुद्रमया, क्षणात् प्रयुक्तः, स्वइमः, सपक्षः, फणीव, वेगात्, देवाद्रिनाथस्य, गजे, निषण्णं, धृतांकुशं हस्तिपकं, जघान ।
अर्थाः-
ततः = పిమ్మట,
रुद्रमया क्षणात् = క్షణకాలంలో,
प्रयुक्तः = ప్రయోగింపబడిన;
खड्गः = ఖడ్గము;
वेगात् = వేగంగా;
सपक्षः = రెక్కలుగల;
फणीव = పామువలె ;
देवाद्रिनाथस्य = దేవాద్రి ప్రభువు యొక్క,
गजे = ఏనుగు మీద;
विषण्णम् = కూర్చొనియున్న;
धृतांकुशं = అంకుశాన్ని ధరించిన;
हस्तिपकं = మావటివాడిని;
जघान = చంపెను.
भावः-
పిమ్మట రుద్రమదేవి క్షణకాలంలో తన ఖడ్గాన్ని ప్రయోగించింది. అది వేగంగా రెక్కలున్న పామువలె మహేంద్రనాధుని ఏనుగుపై అంకుశాన్ని ధరించియున్న మావటివాడిని చంపింది.
In a flash, like a serpent, the sword thrown by Rudrama killed the Devagiri ruler’s mahout who sat on the elephant holding the hook.
18. पादाभिघातात् कुपितः फणीव श्वसन् महादेवनृपः सवेगम् ।
आरुह्य कस्यापि रथं सचापो वृषेव वर्षं व्यसृजच्छरौघम् ।
పాదాభిఘాతాత్ కుపితః ఫణీవ శ్వసన్ మహాదేవనృపః సవేగమ్ |
ఆరుహ్య కస్యాపి రథం సచాపో వృషేవ వర్షం వ్యసృజచ్ఛరౌఘమ్ ||
पदच्छेदः – पादाभिधातात्, कुपितः, फणीव श्वसन्, महादेवनृपः, सवेगम् आरुह्य, कस्यापि, रथं, सयापः, वृषेव, वर्षं, ज्यसृजत्, शरौधम् ।
अन्वयक्रमः – महादेवनृपः पादाभिघातात्, कुपितः, फणीव, श्वसन्, सवेगम्, कस्यापि, रथं, आरुह्य, सचापः, वृषेव, शरौधं, व्यसृजत् ।
अर्थाः-
महादेवनृपः = మహా దేవరాజు,
पादाभिघातात् = కాలితో తొక్కబడిన,
कुपितः = కోపగించిన;
फणीव = పామువలె;
श्वसन् = నిట్టూర్పు విడుచుచు;
सवेगम् = వేగంగా;
कस्यापि, रथं = ఒకానొక రధాన్ని;
आरुह्य = ఎక్కి;
सचापः = ధనస్సును ధరించినవాడై;
वृषेव = ఇంద్రునివలె;
शरौधं = బాణముల సముదాయాన్ని;
व्यसृजत् = ప్రయోగించాడు.
भावः-
మహాదేవుడు పాదాలచే తొక్కబడిన పామువలె కోపగించినవాడై బుసలు కక్కుతూ, మరొక రథాన్ని ఎక్కి దేవేంద్రునివలె బాణవర్షాన్ని కురిపించాడు.
Angered like a serpent stamped by foot, the king of Devagiri got into someone’s chariot and rained arrows just as Indra would cause showers.
19. निवार्य तं सूतमिषुद्वयेन, षड्भिस्तुरङ्गौ, गुणकेतने च ।
एकैकबाणेन निपात्य, शत्रुं नृपाग्रणीं तं विरथं चकार ॥
నివార్య తం, సూతమిషుద్వయేన, షడ్భిస్తురంగౌ, గుణకేతనే చ |
ఏకైకభాణేన నిపాత్య, శత్రుం నృపాగ్రణీం తం విరథం చకార ||
पदच्छेदः – निवार्य, तं, सूतम्, इक्षुद्वयेन षड्भिः, तुरंगौ गुणकेतने, च, एकैकबाणेन, निपात्य, शतॄं, नृपाग्रणी, तं विरथं, चकार ।
अन्वयक्रमः – तं निवार्य, सूतं, इषुद्वयेन, षट्भिः, तुरंगौ, च, एकैकबाणेन, गुणकेतने, निपात्य, नृपाग्रणीं तं विरथं चकार ।
अर्थाः-
तं = అతడిని;
निवार्य = అడ్డగించి,
सूतं = సారధిని,
इषुद्वयेन = రెండు బాణములతో;
षट्भिः = ఆరు బాణాలతో;
तुरंगौ = గుర్రాలను;
च = మరియు;
एकैकबाणेन = ఒక్కొక్క బాణంతో;
गुणकेतने = అల్లెత్రాడును, పతాకాన్ని;
निपात्य = పడగొట్టి;
शतॄं = శత్రువైన;
तं नृपाग्रणीं = ఆ రాజశ్రేష్ఠుడిని;
विरथं चकार = రథహీనుడిగా చేశాడు.
भावः-
రుద్రమదేవి సారధిని రెండు బాణములతోను, ఆరు బాణములతో గుర్రాలను, ఒక్కొక్క బాణంతో అల్లెత్రాడును, జెండాను పడగొట్టింది. పిమ్మట తన శత్రువైన ఆ రాజును కూడా రథంలేని వాడినిగా చేసింది.
Stopping him, killing the charioteer with two arrows, the two horses with six arrows, and felling the string and the flag with one arrow each, she made him devoid of his chariot.
20. कर्तव्यतामूढमतिस्स राजा ब्रीडाभिभूतं स्वबलं च कुर्वन् ।
पराजितात्माऽपगतः समीकात् स्त्रियोऽबला इत्यनृतं विजज्ञे ॥
కర్తవ్యతామూఢమతిస్స రాజా వ్రీడాభిభూతం స్వబలం చ కుర్వన్ |
పరాజితాత్మాక పగతః సమీకాత్ స్త్రియోక్బలా ఇత్యనృతం విజజ్ఞే ॥
पदच्छेदः – कर्तव्यतामूढमतिः सः, राजा, ब्रीडाभिभूतम्, स्वबलम्, च, कुर्वन्, पराजिततात्मा, अपगतः, समीकात्, स्त्रियः, अबला, इति, अनृतं विजज्ञे ।
अन्वयक्रमः – कर्तव्यतामूढमतिः सः, राजा, स्वबलं, व्रीडाभिभूतं, कुर्वन्, पराजितात्मा, समीकात् अपगतः, स्त्रियः, अबला, इति, अनुतं, विजज्ञे ।
अर्थाः-
कर्तव्यतामूढमतिः = కర్తవ్యమునందు మూఢమైన మనస్సుగల,
सः राजा = ఆ రాజు;
स्वबलं = తన బలమును;
व्रीडाभिभूतं = సిగ్గుపడేదిగా చేసి;
पराजितात्मा = ఓడిపోయినవాడై;
समीकात् = యుద్ధము నుండి;
अपगतः = తొలగిపోయాడు ;
स्त्रियः = స్త్రీలు;
अबला: = బలంలేనివారు;
अनृतं इति = అసత్యము;
इति = అని;
विजज्ञे = తెలుసుకున్నాడు.
भावः-
ఏమిచేయాలో తెలియని మనస్సుగల ఆ రాజు తన సైన్యాన్ని సిగ్గుపడే దానిగా చేశాడు. గత్యంతరం లేక పరాజయాన్ని పొంది యుద్ధం నుండి పారిపోయాడు. అబలలు అనేది అసత్యమని గ్రహించాడు.
Not knowing what to do, the defeated king causing shame to his army ran away from the battlefield. He realized that it was false to say that women were weak.
21. विजृम्भितेऽस्मिन् तुमुले समीके रुद्राम्बया रुद्रबलात्तशक्त्या ।
जिता हि सर्वे परिपन्थिनस्ते पलायनं चक्रुरहो विचित्रम् ॥
విజృంభితేకాస్మిన్ తుములే సమీకే రుద్రాంబయా రుద్రబలాత్తశక్త్యా |
జీతా హి సర్వే పరిపంథినస్తే పలాయనం చక్రురహో విచిత్రమ్ ||
पदच्छेदः – विजृम्भिते, अस्मिन् तुमुले, समीके, रुद्राम्बया, रुद्रबलात्तशक्त्या जिता, हि, सर्वे, परिपन्थिनः, ते पलायनं चक्रुः, अहो, विचित्रम् |
अन्वयक्रमः – विजृम्भिते अस्मिन् तुमुले, समीके रुद्रबलात्तशक्त्या, रुद्राम्बया, सर्वे, परिपन्थिनः, जिता, ते पलायनं चक्रुः, अहो, विचित्रं ।
अर्थाः-
विजृम्भिते = బాగా విజృంభించిన ,
तुमुले अस्मिन् समीके = భీకరయుద్ధమందు;
रुद्रबलात्तशक्त्या = రుద్రబలసంపత్తిగల;
रुद्राम्बया = రుద్రమదేవి చేత;
सर्वे परिपन्थिनः = సమస్త శత్రువులు;
जिता = జయింపబడ్డారు;
पलायनं चक्रुः = పారిపోయారు;
ते = వారు;
अहो = ఆహా !;
विचित्रं = ఆశ్చర్యము.
भावः-
భయంకరంగా జరిగిన ఈ యుద్ధంలో రుద్రశక్తితో కూడిన రుద్రమదేవి . శత్రువులందరిని జయించింది. దాంతో ఈ శత్రువులంతా పలాయనం చేశారు. ఆహా ! ఎంత ఆశ్చర్యము.
In that tumultuous battle, Rudramba, who received strength from Rudra, defeated her enemies, and they ran away.
रुद्रमदेवी Summary in Sanskrit
कवि परिचयः
‘रुद्रमदेवी’ इत्याख्यः पाठ्यभागोऽयं श्री दुरिशेटि वेङ्कटरामाचार्य – कविना रचितात् ” शिल्पश्रीः ” काव्यात् गृहीतः । श्री मङ्गाम्बा कनकाचार्ययोः सुतोऽयं कविपण्डितः साहित्यविद्याप्रवीणपरीक्षायाम् सर्वप्रथमस्थानम् अलभत । संस्कृतभाषानिबद्धानां काव्यानां पठने पाठने च श्रद्धावान् अयं कविपुङ्गवः तेलुगु- भाषायां ‘“अनार्कलि, अथर्वणाचार्युडु’ इति द्वे काव्ये अरचयत् । कालिदास- रघुवंशकाव्यस्य तेलुगुभाषया “अनार्कलि, अथर्वणाचार्युडु’ इति द्वे काव्ये अरचयत् कालिदास- रघुवंशकाव्यस्य तेलुगुभाषया अनुवादम् अकरोत् । अपि च “शिल्पश्रीः ” इति पञ्चसर्गात्मकं लघुकाव्यमरचयत् । अस्मिन् काव्ये सः काकतीयराजस्य गणपतिदेवस्य, तस्य पुत्र्याः वीरवनितायाः महाराज्ञ्याः रुद्रमाम्बायाः तेलंगाणाराज्ये अत्यन्तं प्रसिद्धस्य रामप्पदेवालयस्य निर्मातुः शिल्पिशिरोमणेः रामोजु पण्डितस्य च चरितम् अवर्णयत् ।
कथा सारांश
काकतिराजपुरन्दरः गणपतिदेवः प्रधानसचिवस्य शिवय्यदेवस्य अभिमत मनुसृत्य स्वपुत्र युद्धविद्यायां प्रजापरिपालने च कुशलिनीं रुद्रमां स्वराज्यस्य परिपालयित्रीं चकार । एतदसहमानौ हरिहरदेव – मुरारिदेवौ अपि च देवगिरिपालको यादवराजा महादेवः अनया सह योद्धुं समागतः । निशम्येदं नितान्तरोषकषायिता रक्तमुखा अरुणाश्री रुद्रमा मितेनैव सैन्येन वेगात् तैस्सह अभियोध्दुं जगाम । राज्ञ्या कृतां शङ्खध्वनिम् अनुसृत्य पराक्रमशीला नैके योधाः सामन्तभूपाश्च शत्रून् पराजेतुं युद्धभूमिं प्रति गताः । युद्धभूमौ शक्तिस्वरूपिण्याः रुद्रमायाः पराक्रमेण भीताः शत्रवः सर्वे पराजयम् अङ्गीकृत्य पलायनं कृतवन्तः ।

रुद्रमदेवी Summary in Telugu
కవి పరిచయం
‘రుద్రమదేవి’ అనే పాఠ్యభాగాన్ని శ్రీ దురిశేటి వెంకట రామాచార్యులు రచించారు. వీరు రచించిన ‘శిల్పశ్రీ’ అనే కావ్యం నుండి ఈ పాఠ్యభాగం స్వీకరింపబడింది. వీరి తల్లి పేరు ముగాంబ. తండ్రి పేరు కనకాచార్యులు. వీరు సాహిత్య విద్యా ప్రవీణయందు ప్రథమ శ్రేణిలో కృతార్థులయ్యారు. వీరు సంస్కృతభాషలోని వ్యాసములను చదువుట యందు మిక్కిలి ఆసక్తిని చూపేవారు. వీరు తెలుగు భాషలో “అనార్కలి, అధర్వణాచార్యుడు’ అనే రెండు గ్రంథాలను రచించారు. కాళిదాసు రచించిన ‘రఘువంశం’ అనే కావ్యాన్ని తెలుగులో అనువదించారు. మరియు వీరు రచించిన ‘శిల్పశ్రీః, అనే కావ్యంలో ఐదు సర్గలు ఉన్నాయి. ఇది ఒకే లఘుకావ్యము. ఈ కావ్యంలో కాకతి రాజైన గణపతి దేవుని యొక్క కుమార్తె అయిన రుద్రమదేవి పరాక్రమం గురించి వర్ణింపబడింది. అంతేగాక రామప్పదేవాలయాన్ని నిర్మించిన శిల్పి శిరోమణి అయిన రామోజు పండితుని యొక్క చరిత్రను కూడా వర్ణించాడు.
కథా సారాంశము
కాకతిరాజైన గణపతిదేవుని ప్రధానమంత్రి అయిన శివయ్యదేవుడు వచ్చి రుద్రమను రాణిగా పట్టాభిషేకం చేయమని సూచించాడు. అతని కోరికను అనుసరించి రుద్రమదేవిని రాణిగా పట్టాభిషేకం చేయించాడు. దీన్ని హరిహరదేవుడు, మురారి దేవుడు అనే ఇద్దరు సామంత రాజులు సహించలేకపోయారు. దేవగిరి రాజైన మహాదేవునితో కలసి రుద్రమ దేవితో యుద్ధం చేయడానికి వచ్చారు. ఈ వృత్తాంతాన్ని రుద్రమదేవి గ్రహించింది. కోపంతో ఎర్రబడిన కన్నులతో వేగంగా పరిమిత సైన్యంతో శత్రుసైన్యంపై తిరుగుబాటు చేసింది. కత్తిపట్టి యుద్ధరంగంలో వీరవిహారం చేసింది. శత్రుసైన్యాన్ని ఓడించింది. శత్రువులందరు యుద్ధరంగం నుండి పారిపోయారు. అందరు తమ పరాజయాన్ని అంగీకరించారు. స్త్రీలు అబలలు అనే మాట నిజం కాదని గ్రహించారు.
కాకతీయ రాజులో గణపతిదేవుడు ప్రసిద్ధుడు. అతని కుమార్తె రుద్రమదేవి. గణపతి దేవునికి వృద్ధాప్యం వచ్చింది. రాజపాలన చేయలేకపోతున్నారు. ఆ సమయంలో అతని మంత్రి ఒకరోజు రాజును సమీపించి రుద్రమదేవిని రాణిగా చేయమని సూచిస్తాడు. మంత్రి సలహాను అనుసరించి గణపతిదేవుడు ఒక మంచి సుముహూర్తంలో రుద్రమదేవిని రాణిగా పట్టాభిషేకం చేస్తాడు. సామంతులందరు రుద్రమదేవి నాయకత్వాన్ని అంగీకరిస్తారు. కాని సామంతులలో హరిహర, మురారి దేవులు మాత్రం రుద్రమను అబలగా తలచి ఆమె ఆధిపత్యాన్ని అంగీకరించలేరు. వారిద్దరు కుటిల పన్నాగం పన్నుతారు.
ఒకరోజు రుద్రమదేవి శివాలయానికి వెళ్ళింది. అదే సమయంలో వీరిద్దరు రాజ్యాన్ని ఆక్రమించుకోవాలని ప్రయత్నించి దుర్గంలోకి ప్రవేశించారు. ఈ వార్తను విన్న రుద్రమదేవి మిక్కిలి కోపగించింది. పరిమిత సైన్యంతో వారిద్దరిని ఎదుర్కొంది. భీకర యుద్ధంలో శత్రుపక్షాల సైన్యాన్ని చీల్చి చెండాడింది. దాంతో భయపడిన మహాదేవుడు పరాజయంతో కూడిన అవమానంతో యుద్ధరంగం నుండి పలాయనం చేశాడు.
रुद्रमदेवी Summary in English
Introduction of the Poet
The lesson Rudramadevi is an extract from the poem Silpasri written by Sri D. Venkataramacharya. Silpasri is a poem with five cantos. It describes the story of Queen Rudrama Devi of the Kakatiya Dynasty. Sri Ramacharya authored two kavyas in Telugu namely Anarkali and Atharva Chanakyudu. He translated Raghu- vamsa of Kalidasa into Telugu.
The present lesson describes how Rudrama Devi defeated the king of Devagiri.
![]()
![]()