Mahesh

Here students can locate TS Inter 1st Year Political Science Notes Chapter 9 Secularism to prepare for their exam.

TS Inter 1st Year Political Science Notes Chapter 9 Secularism

→ Secularism is an important social and political phenomenon.

→ “Secularism is an ideology which provides a theory of life and conduct as against one provided in religion”. – ERIC.S.Waterhouse

→ Secular State is neither religious nor irreligious.

→ Secular State gives equal freedom to all religions.

→ Religion of citizens has nothing to do with secular matters in secularism.

→ Secularism strongly opposes the existence, continuance and survival of authoritarian religious leaders and institutions.

→ It is vehemently opposed to the supporting of religion in public matters.

→ Theocracy technically means rule by God.

→ There will be a particular religion, which is declared as the official religion in a Theocratic State.

→ Religious priests and spiritual heads will be given special significance in Theocratic States.

→ Secularism enables individuals to enjoy their religious freedom to their full extent.

→ The word ‘secular’ was included in the Indian Constitution in the year 1976 through 42nd Constitutional Amendment Act.

TS Inter 1st Year Political Science Notes Chapter 9 లౌకికవాదం

→ మతం, రాజ్యం వేరు వేరు అని లౌకికవాదం విశ్వసిస్తుంది.

→ సెక్యులర్ అనే ఆంగ్ల పదానికి లాటిన్ భాషలో ‘ఇహలోకం’ (This world) అని అర్థం.

→ “మతంలో పేర్కొన్న దానికంటే భిన్నమైన జీవనం, ప్రవర్తనలకు సంబంధించిన సిద్ధాంతాన్ని ప్రతిపాదించే ఒకానొక ఆదర్శమే” లౌకికవాదమని వాటర్హిస్ (Water house) మహాశయుడు పేర్కొన్నాడు.

→ లౌకిక రాజ్యం అన్ని మతాలవారికి సమానమైన స్వేచ్ఛా, స్వాతంత్ర్యాలను ప్రసాదిస్తుంది.

→ లౌకిక రాజ్యం ఒక మతానికి అనుకూలం కాదు. మరొక మతానికి వ్యతిరేకం కాదు. మత విషయాలలో తటస్థంగా ఉంటుంది.

→ స్వేచ్ఛ, ప్రజాస్వామ్యానికి లౌకికవాదం అత్యంత ఆవశ్యకమైనది.

→ లౌకికవాదం సమ సమాజానికి పాత్రిపదిక. అన్ని మతాల వారిని సమానంగా పరిగణిస్తుంది. మానవులు సృష్టించిన అసమానతలను గుర్తించదు.

→ మతస్వామ్యం (Theocracy) అనే పదాన్ని ప్రథమంగా ‘జోసెఫస్’ అనే యూదు చరిత్రకారుడు యూదు మతగ్రంథమైన ‘థోరా’లో పేర్కొన్నాడు.

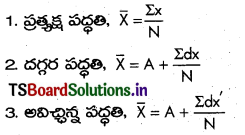
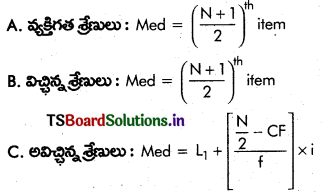
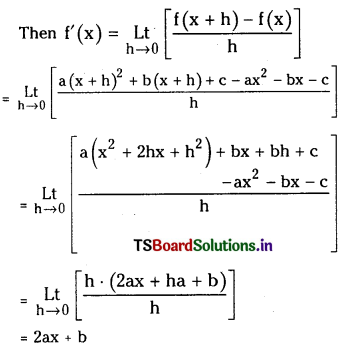
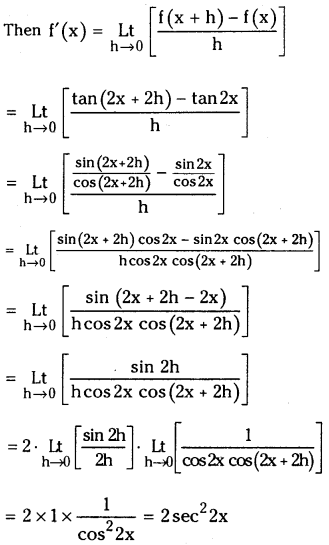
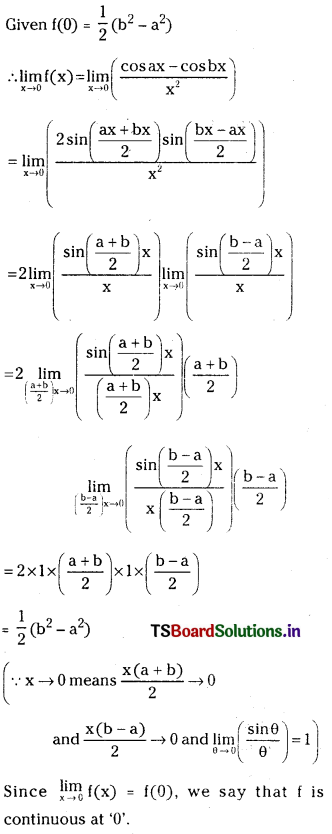
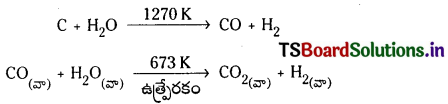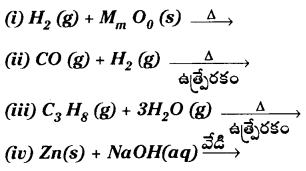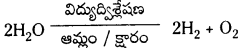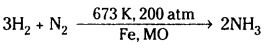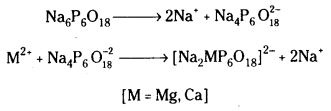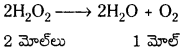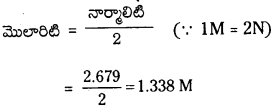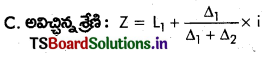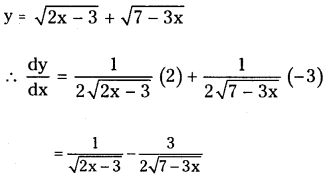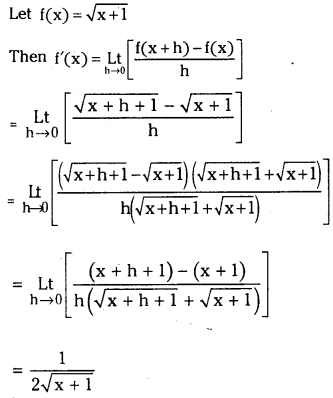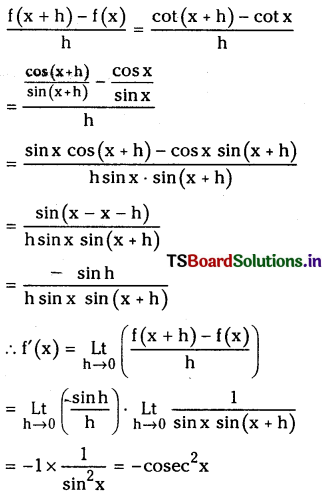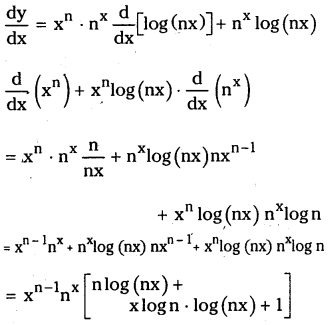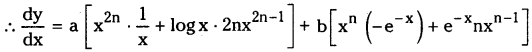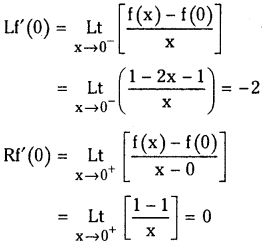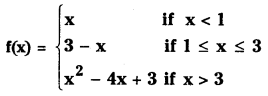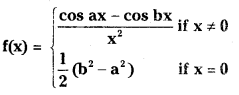Telangana TSBIE TS Inter 1st Year Chemistry Study Material 8th Lesson హైడ్రోజన్ – దాని సమ్మేళనాలు Textbook Questions and Answers.

TS Inter 1st Year Chemistry Study Material 8th Lesson హైడ్రోజన్ – దాని సమ్మేళనాలు

అత్యంత లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 1.
హైడ్రోజన్ ఐసోటోపులు మూడు వాటి చర్యావేగాల్లో భేదపడతాయి. కారణాలు తెలపండి.
జవాబు:

1. హైడ్రోజన్ మూడు రకాల ఐసోటోపులు కలిగి ఉంటుంది. అవి
   1. ప్రోటియమ్ (¹H₁)
   2. డ్యుటీరియమ్ (²H₁)
   3. ట్రైటియమ్ (³H₁).
2. ఈ మూడు ఐసోటోపులలో వరుసగా 0, 1, 2 న్యూట్రాన్లు ఉంటాయి. ట్రిటియం రేడియోధార్మికత కలిగి ఉంటుంది. ఈ హైడ్రోజన్ ఐసోటోపులు వాటి చర్యావేగాల్లో విభేదిస్తాయి. వీటి చర్యాశీలత క్రింది క్రమంలో ఉంటుంది.
   H > D > T.
3. ఈ ఐసోటోపులు ఒకే ఎలక్ట్రాన్ విన్యాసం కలిగి ఉండటం వల్ల వాటికి సారూప్యరసాయన ధర్మాలు ఉంటాయి.

ప్రశ్న 2.
అధిక ద్రవీభవన స్థానాలున్న లోహాలను వెల్డింగ్ చేయడానికి డైహైడ్రోజను ఎందుకు వాడతారు ?
జవాబు:
డ్రైహైడ్రోజన్ వియోగం చెంది పరమాణు హైడ్రోజన్ను ఇస్తుంది. ఈ పరమాణు హైడ్రోజన్ మండి 4000K ఉష్ణోగ్రతను ఇస్తుంది. కావున ఈ ఉష్ణోగ్రత జ్వాల సహాయంతో అధిక ద్రవీభవన స్థానాలున్న లోహాలను వెల్డింగ్ చేయటానికి డై హైడ్రోజను వాడతారు.

ప్రశ్న 3.
అత్యంత శుద్ధమైన డైహైడ్రోజనన్ను తయారుచేయడానికి ఒక పద్ధతిని వివరించండి.
జవాబు:
నికెల్ ఎలక్ట్రోడ్లతో వెచ్చని సజల బేరియమ్ హైడ్రాక్సైడ్ (Ba(OH)₂]ను విద్యుద్విశ్లేషణ చేసి అత్యంత శుద్ధమయిన హైడ్రోజన్ ను పొందవచ్చు. ఈ ప్రక్రియలో 99.95% శుద్ధమైన H₂, ఏర్పడును.

ప్రశ్న 4.
“సినా గ్యాస్” పదాన్ని వివరించండి.
జవాబు:
CO, H₂ ల మిశ్రమాన్ని వాటర్ గ్యాస్ లేదా సిన్ గ్యాస్ అని అంటారు. దీనిని మిథనోల్ మరియు ఇతర హైడ్రోకార్బన్లను సంశ్లేషణం చేయటానికి వాడతారు.
తయారీ :

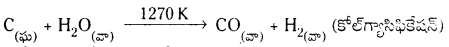
ప్రశ్న 5.
“కోల్ గాసిఫికేషన్” అంటే ఏమిటి ? దానిని సరైన తుల్య సమీకరణంతో వివరించండి.
జవాబు:
కోలన్ను ఉపయోగించి 1270K ఉష్ణోగ్రత వద్ద నుంచి సిన్ గ్యాస్ ను తయారు చేయటాన్ని కోల్ గాసిఫికేషన్ అంటారు.

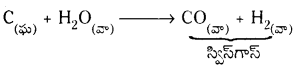
ప్రశ్న 6.
హైడ్రైడ్ అంటే నిర్వచనం చెప్పండి. ఎన్ని రకాల హైడ్రేడ్లున్నాయి ? వాటి పేర్లను చెప్పండి.
జవాబు:
హైడ్రోజన్ ఇతర మూలకాలతో ఏర్పరచే ద్విగుణాత్మక సమ్మేళనాలను హైడ్రైడ్లు అంటారు. ఇవి మూడు రకాలు.

1. అయానిక లేదా సెలైన్ లేదా ఆవరణ సదృశ హైడ్రైడ్లు. ఉదా || NaH, CaH₂ మొ||
2. కోవలెంట్ లేదా అణు హైడ్రైడ్లు. ఉదా || B₂H₆, CH₄ మొ||వి.
3. లోహ లేదా నాన్ – స్టాయికియోమెట్రిక్ హైడ్రైడ్లు. ఉదా || PdH

ప్రశ్న 7.
ద్రవీకృత ప్రావస్థలో నీటికి అసాధారణ లక్షణం ఉంటుంది. అది నీటి అధిక భాష్పీభవనోష్టానికి దారితీస్తుంది. ఆ ధర్మం ఏమిటి ?
జవాబు:
నీటి అణువుల మధ్య అంతరణుక హైడ్రోజన్ బంధాలు ఉండటం వలన ద్రవీకృత ప్రావస్థలో నీటికి అసాధారణ లక్షణం ఉంటుంది. దీని వలన నీటికి అధిక భాష్పీభవన స్థానం ఉంటుంది.

ప్రశ్న 8.
కిరణజన్య సంయోగక్రియ జరుగుతున్నప్పుడు నీరు గా ఆక్సీకరణం చెందుతుంది. అయితే ఏ మూలకం క్షయకరణం చెందుతుంది ?
జవాబు:
కిరణజన్య సంయోగక్రియను ఈ విధంగా వ్రాస్తారు. 6CO₂ + 6H₂O → C₆H₁₂O₆ + 6O₂.
ఈ చర్యలో నీరు, O₂ గా ఆక్సీకరణం చెందుతుంది. కార్బన్ క్షయకరణం చెందుతుంది. (కార్బన్ యొక్క ఆక్సీకరణ స్థితి +4 నుంచి ‘0’ కు తగ్గుతుంది.)

ప్రశ్న 9.
“స్వయం ప్రోటోలసిస్” అంటే మీకేమి తెలుస్తుంది ? నీటి స్వయం ప్రోటోలసిసికి సమీకరణాన్ని రాయండి.
జవాబు:
నీరు ఆమ్లంగాను, క్షారంగాను పనిచేయగల ద్విస్వభావ పదార్థంగా పనిచేస్తుంది. ఈ విధంగా నీరు స్వయం అయనీకరణం చెందే ధర్మాన్ని ‘స్వయం ప్రొటోలసిస్’ అంటారు. నీటి స్వయం ప్రొటోలసిస్ చర్యను క్రింది విధంగా వ్రాయవచ్చు.

ప్రశ్న 10.
బ్రాన్ స్టెడ్ సిద్ధాంతపరంగా నీరు ద్విస్వభావం గల పదార్థం. దానిని మీరు ఎట్లా వివరిస్తారు ?
జవాబు:
బ్రానెడ్ సిద్ధాంతం ప్రకారం ప్రోటాన్ దాత ఆమ్లంగాను, ప్రోటాన్ స్వీకర్త క్షారంగాను పనిచేస్తాయి. నీరు NH₃ కు ప్రోటాను దానం చేసి ఆమ్లంగా పనిచేస్తుంది.

నీరు H₂S నుంచి ప్రోటాన్ ను స్వీకరించి క్షారంగా పనిచేస్తుంది.

కావున నీరు ద్విస్వభావం గల పదార్ధం.

లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 11.
NH₃, H₂O, HF ల బాష్పీభవన స్థానాలు, ఆయా గ్రూపుల్లో వాటి తరవాత మూలకాల హైడ్రైడ్ల బాష్పీభవన స్థానాలకంటే ఎక్కువగా ఉంటాయి. మీ కారణాలు చెప్పండి.
జవాబు:
NH₃, H₂O, HF ల బాష్పీభవన స్థానాలు, అయా గ్రూపుల్లో వాటి తరువాత మూలకాల హైడ్రైడ్ల బాష్పీభవన స్థానాలకంటే ఎక్కువగా ఉంటాయి. కారణం,

1. NH₃, H₂O, HF లలో హైడ్రోజన్ అధిక ఋణ విద్యుదాత్మకత గల N, O, F లతో బంధించబడి ఉంటుంది.
2. అందువలన ఈ హైడ్రేడ్లలో హైడ్రోజన్ బంధాలు ఏర్పడతాయి.
3. ఈ హైడ్రోజన్ బంధాలు ఏర్పడుట వలన ఈ హైడ్రైడ్లకు అధిక భాష్పీభవన స్థానాలుంటాయి.

ప్రశ్న 12.
ఆవర్తన పట్టికలో హైడ్రోజన్ స్థానాన్ని దాని ఎలక్ట్రాన్ విన్యాసపరంగా చర్చించండి.
జవాబు:
ఆవర్తన పట్టికలో హైడ్రోజన్ యొక్క స్థానం చర్చనీయాంశం. హైడ్రోజన్ IA గ్రూపులోని క్షార లోహాలతోను, VIIA గ్రూపులోని హాలోజన్లతోను పోలికలు కలిగి ఉంటుంది.

హైడ్రోజన్ను IA గ్రూపు మూలకాలతో చేర్చుటకు కారణాలు

1. హైడ్రోజన్ యొక్క ఎలక్ట్రాన్ విన్యాసం (1s¹) క్షార లోహాల బాహ్య ఎలక్ట్రాన్ విన్యాసంను (ns¹) పోలి ఉంటుంది.
2. క్షార లోహలవలె హైడ్రోజన్ ఒక ఎలక్ట్రాన్ను పోగొట్టుకొని ఏకమాత్ర ధనావేశిత అయాన్ ను ఏర్పచగలదు. (H⁺)

హైడ్రోజన్ ను VII A గ్రూపు మూలకాలతో చేర్చుటకు కారణాలు :

1. హైడ్రోజన్ హాలోజన్లవలె ద్విపరమాణుక అణువులను ఏర్పరుస్తుంది.
2. హైడ్రోజన్ హాలోజన్లవలె ఒక ఎలక్ట్రాన్ను పొంది ఏకమాత్ర ఋణావేశిత అయాన్లను ఏర్పరుస్తుంది. (H^–) హైడ్రోజన్ యొక్క స్థానాన్ని దాని ఎలక్ట్రాన్ విన్యాసాన్ని 1s¹ మాత్రమే పరిగణలోనికి తీసికుని 1A గ్రూపు మూలకాలతో కలిపారు.

ప్రశ్న 13.
హైడ్రోజన్ ఎలక్ట్రాన్ విన్యాసం దాని రసాయన ధర్మాలకు ఎట్లా అనువుగా ఉంటుంది ?
జవాబు:
హైడ్రోజన్ యొక్క ఎలక్ట్రాన్ విన్యాసం 1s¹. కావున

1. హైడ్రోజన్ ఒక ఎలక్ట్రాను కోల్పోయి చర్యలలో పాల్గొని H⁺ ను ఏర్పరచును.
   ఉదా : HF + H₂O → H₃O⁺ + F^–
2. హైడ్రోజన్ ఒక ఎలక్ట్రాను గ్రహించి చర్యలలో పాల్గొని HP ను ఏర్పరుస్తుంది.
   ఉదా : 2Na + H₂ → 2NaH [Na⁺ H^–]
3. హైడ్రోజన్ ఒక ఎలక్ట్రాను పంచుకొని సమయోజనీయ బంధాలను ఏర్పరచును.
   ఉదా : H : Cl.

ప్రశ్న 14.
(a) క్లోరిన్ (b) సోడియం లోహంతో డైహైడ్రోజన్ చర్య జరిపితే ఏమవుతుంది ? వివరించండి.
జవాబు:
a) క్లోరిన్తో డైహైడ్రోజన్ చర్య : డై హైడ్రోజన్ క్లోరిన్తో చర్య జరిపి హైడ్రోజన్ క్లోరైడ్ను ఏర్పరచును.
H₂ + Cl₂ → 2HCI.
b) డై హైడ్రోజన్ Na లోహంతో చర్య : డై హైడ్రోజన్ Na లోహంతో చర్య జరిపి సోడియం హైడ్రైడన్ను ఏర్పరుస్తుంది.
2Na + H₂ → 2NaH

ప్రశ్న 15.
భారజలం పై ఒక వ్యాఖ్యను రాయండి.
జవాబు:
డ్యుటీరియం ఆక్సైడ్ (D₂O) ను భారజలం అంటారు. \(\frac{\mathrm{N}}{2}\) NaOH ద్రావణంతో క్షారయుతం చేసిన నీటిని ఎక్కువ కాలం పాటు విద్యుద్విశ్లేషణ జరిపి భారజలాన్ని తయారుచేస్తారు.

(1) న్యూక్లియర్ రియాక్టర్లలో మోడరేటర్గాను,
(2) చర్యా విధానాల అధ్యయనంలో వినిమయ కారకంగాను భారజలాన్ని ఉపయోగిస్తారు.

ఇతర డ్యుటీరియమ్ సమ్మేళనాలను తయారుచేయటానికి D₂O ను ఉపయోగిస్తారు.
CaC₂ + 2D₂O → C₂D₂ + Ca(OD)₂
SO₃ + D₂O → D₂SO₄
Al₄ C₃ + 12D₂O → 3 CD₄ + 4 Al(OD)₃
ఈ చర్యలను డ్యుటిరాలసిస్ చర్యలు అంటారు.

ప్రశ్న 16.
హైడ్రోజన్ ఐసోటోపుల పేర్లను తెలపండి. ఈ ఐసోటోపుల ద్రవ్యరాశుల నిష్పత్తి ఏమిటి ?
జవాబు:
హైడ్రోజన్కు మూడు ఐసోటోపులున్నాయి.

1. హైడ్రోజన్ \({ }_1^1 \mathrm{H}\)
2. డ్యుటీరియమ్ \({ }_1^2 \mathrm{H}\) లేదా \({ }_1^2 \mathrm{D}\)
3. ట్రైటియమ్ \({ }_1^3 \mathrm{H}\) లేదా \({ }_1^3 \mathrm{~T}\)
   ఈ ఐసోటోపుల ద్రవ్యరాశుల నిష్పత్తి
   H : D : T = 1 : 2 : 3

ప్రశ్న 17.
“వాటర్ గ్యాస్ షిఫ్ట్” చర్య అంటే ఏమిటి ? ఈ చర్యతో హైడ్రోజన్ తయారీని ఎట్లా పెంచగలరు ?
జవాబు:
CO, H₂ ల మిశ్రమాన్ని వాటర్గా గ్యాస్ లేదా సిన్ గ్యాస్ అంటారు.
వాటర్గాస్ షిప్ట్ చర్య : H₂ యొక్క ఉత్పత్తి పెంచటానికి సిన్గ్యాస్ మిశ్రమంలోని కార్బన్ మోనాక్సైడ్ను ఐరన్ క్రోమోట్ ఉత్ప్రేరకం సమక్షంలో నీటి ఆవిరితో చర్యనొందిస్తారు. ఈ చర్యను “వాటర్ గ్యాస్ షిఫ్ట్ చర్య” అంటారు.

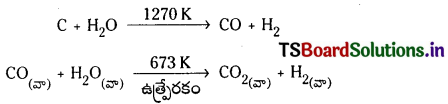
సోడియం ఆర్మినైట్ ద్రావణంలో మార్జనం చేసి CO₂ ను తొలగించవచ్చు.

ప్రశ్న 18.
కింది చర్యలను పూర్తిచేసి, తుల్యం చేయండి.

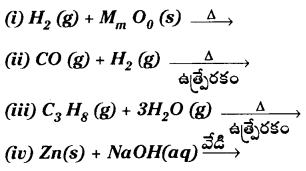
జవాబు:

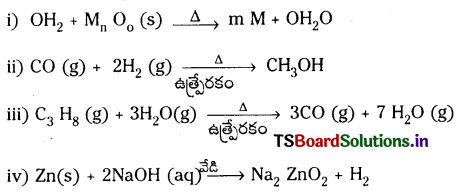
ప్రశ్న 19.
13వ గ్రూపు మూలకాలు ఏర్పరచే హైడ్రైడ్ల స్వభావం ఏమిటి ?
జవాబు:
13వ గ్రూపు మూలకాలు p – బ్లాకు చెందుతాయి. ఇవి కోవలెంట్ హైడ్రైడ్లను ఏర్పరుస్తాయి. ఈ హైడ్రైడ్లు మూడు రకాలు

1. ఎలక్ట్రాన్ న్యూనతగల సమ్మేళనాలు.
2. ఎలక్ట్రాన్ ఖచ్చిత హైడ్రైడ్లు
3. ఎలక్ట్రాన్ అధిక హైడ్రైడ్లు. ఇవి లూయీ ఆమ్లాలుగా పనిచేస్తాయి. ఉదా : B₂H₆
   బోరాన్ ఏర్పరచే హైడ్రైడ్లను బోరేన్లు అంటారు.

ప్రశ్న 20.
సంశ్లేషిత రెజిన్ పద్ధతి, అయాన్ వినిమయ రెజిన్ పద్ధతుల్లో జలకాఠిన్యతను తొలగించడానికి ఉపయోగించే సూత్రాన్ని, పద్ధతిని చర్చించండి.
జవాబు:
i) సంశ్లేషిత రెజిన్ల పద్దతి : ఈ పద్దతిలో అయాన్లను తొలగించడం రెండు రకాలుగా జరుగుతుంది. అన్ని రకాల లవణాలు తొలగించబడిన నీటిని అయాన్ విరహిత జలం అంటారు.

1. కాటయాను తొలగించుట : కాటయాన్ వినిమయ రెజిన్ ను కలిగి ఉన్న ట్యాంక్ గుండా కఠినజలాన్ని పంపుతారు. అపుడు Ca⁺² మరియు Mg⁺² అయాన్లు H⁺ అయాన్లతో స్థానభ్రంశం చెందించబడతాయి.
2RCOOH + Ca⁺² → (R COO)₂ + 2H⁺

2. ఆనయాన్లను తొలగించుట : ఆ తర్వాత నీటిని ఆనయాన్ వినిమయ రెజిన్ ట్యాంక్ ద్వారా పంపుతారు. అపుడు నీటిలోని ఆనయాన్లు రెజిన్లోని OH^– అయాన్లతో స్థానభ్రంశం చెందించబడతాయి.

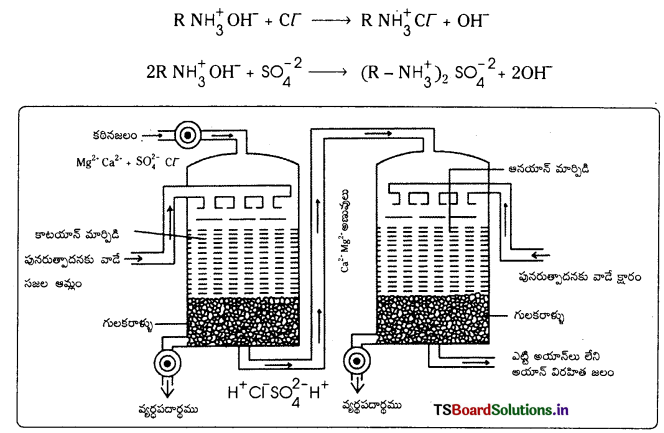
H⁺ మరియు OH^– అయాన్లు ఏకమై అయాన్ విరహిత జలాన్ని ఏర్పరుస్తాయి.
కొంత కాలానికి రెజిన్లు తమ వినిమయ సామర్థ్యాన్ని కోల్పోతాయి. అందువలన వాటిని మరల ఉద్ధరించాలి. `కాటయాన్ రెజిన్ గుండా విలీన H₂SO₄ ప్రసరింపచేయడం ద్వారా పునరుద్ధరిస్తారు. ఆనయాన్ రెజిన్ గుండా కాస్టిక్ సోడా ప్రసరింపచేయడం ద్వారా పునరుద్ధరిస్తారు.

ii) అయాన్ వినిమయ పద్ధతి: ఈ పద్ధతిని జియొలైట్ లేదా పెరుటిట్ ప్రక్రియ అని కూడా అంటారు. ఆర్థ సోడియమ్ అల్యూమినియమ్ సిలికేట్ (Na A/SiO₄) ను జియొలైట్ లేదా పెరుటిట్ అంటారు. దీనిని కఠిన జలానికి కలిపినపుడు వినిమయ చర్యలు జరుగుతాయి.

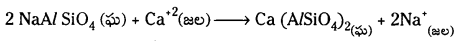
జియొలైట్లో ఉన్న సోడియమ్ అంతా ఖర్చు అయిపోయినపుడు అది వ్యయమైపోయింది అని అంటారు. దాన్ని సజల NaCl ద్రావణంతో అభిచర్యని జరిపి పునరుత్పత్తి చేస్తారు.

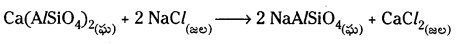
ప్రశ్న 21.
ఇంధనంగా హైడ్రోజన్ ఉపయోగాన్ని గురించి కొన్ని వాక్యాలు రాయండి. (March 2013)
జవాబు:
హైడ్రోజన్ అధిక మండు ఉష్ణోగ్రతలను కలిగి ఉంటుంది. అందువలననే, దీనిని పారిశ్రామిక ఇంధనంగా విరివిగా ఉపయోగిస్తారు.

1. ఆక్సీ హైడ్రోజన్ బ్లోటార్చ్ : పరిశుద్ధ H₂ మరియు O₂ వాయువుల మిశ్రమాన్ని అత్యధిక ఉష్ణోగ్రత (3000°C సుమారుగా) వద్ద మండిస్తే ఆక్సీ హైడ్రోజన్ బ్లోటార్చ్ ఏర్పడుతుంది. ఈ జ్యాలను వెల్డింగ్ మరియు కరిగించే ప్రక్రియలలో ఉపయోగిస్తారు.
2. వాటర్ గ్యాస్ : CO మరియు H₂ ల మిశ్రమాన్ని వాటర్ గ్యాస్ అంటారు. వేడిగా ఉన్న ఎర్రని కోక్ మీదుగా నీటి ఆవిరిని పంపి దీనిని తయారుచేస్తారు. దీనిని పారిశ్రామిక ఇంధనంగా వాడతారు.
3. సెమివాటర్ గ్యాస్ : హైడ్రోజన్, కార్బన్ మోనాక్సైడ్, కార్బన్ డై ఆక్స్డ్, నైట్రోజన్ మరియు మిథేన్ల మిశ్రమాన్ని సెమివాటర్ గ్యాస్ అంటారు. స్టీల్ పరిశ్రమలలో దీనిని ఇంధనంగా ఉపయోగిస్తారు.
4. హైడ్రోజన్ ను, ఇంధన ఘటాలలో విద్యుత్ శక్తిని ఉత్పత్తి చేయుటకు ఉపయోగిస్తారు.

ప్రశ్న 22.
1% H₂O₂ ద్రావణాన్ని మీకు ఇచ్చాం. దాని నుంచి శుద్ధ H₂O₂ ని తయారుచేయడానికి మీరు ఏమి చర్యలను తీసుకుంటారు ?
జవాబు:
ఇవ్వబడిన 1% H₂O₂ నుండి శుద్ధ H₂O₂ ను క్రింది విధంగా పొందవచ్చు.

1. 1% H₂O₂ ద్రావణాన్ని మొదట నీటితో నిష్కర్షించి. దానిని తగ్గించిన పీడనం వద్ద స్వేదనానికి గురిచేస్తారు. అప్పుడు H₂O₂ ఏర్పడుతుంది.
2. 30% గాఢత గల H₂O₂ ద్రావణాన్ని అల్ప పీడనాల వద్ద జాగ్రత్తగా స్వేదనం చేస్తే గాఢత ఇంకా పెరిగి 85% అవుతుంది.
3. పై దశలోని H₂O₂ ను ఘనీభవనంచేస్తే శుద్ధ H₂O₂ ఏర్పడుతుంది.

ప్రశ్న 23.
ఆధునిక కాలంలో H₂O₂ వలన కలిగే ఏవైనా మూడు ఉపయోగాలను చెప్పండి.
జవాబు:

1. గృహ పారిశ్రామిక వ్యర్థ పదార్థాల కాలుష్య నివారణ అభిచర్యలో వాడతారు.
2. సయనైడ్ల ఆక్సీకరణలో వాడతారు.
3. మురుగు కాల్వల వ్యర్థాలకు ఏరోబిక్ స్థితులను పునర్వవస్థీకరించడానికి దీనిని వాడతారు.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 24.
వ్యాపార సరళిలో డైహైడ్రోజనిని తయారుచేయడంపై ఒక వ్యాసం రాయండి. తుల్య సమీకరణాలను ఇవ్వండి.
జవాబు:
వ్యాపార సరళిలో డైహైడ్రోజన్ ను ఈ క్రింది పద్ధతులలో తయారు చేస్తారు.

i) ప్లాటినమ్ ఎలక్ట్రోడ్లను ఉపయోగించి ఆమ్లీకృత లేదా క్షారయుత జలాన్ని విద్యుద్విశ్లేషణ చేస్తే డై హైడ్రోజన్ ఏర్పడుతుంది.

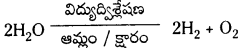
ii) నెల్సన్ పద్దతిలో బ్రైన్ ద్రావణాన్ని విద్యుత్ విశ్లేషణ చేసి డై హైడ్రోజన్ ను తయారు చేస్తారు.
Nacl → Na⁺ + Cl^–
H₂O → H⁺ + OH^–
ఆనోడ్ వద్ద 2Cl^– → Cl₂ + 2e^–
కాథోడ్ వద్ద 2H⁺ + 2e^– → H₂
2Na⁺ + 20H^– → 2NaOH

iii) ఉత్ప్రేరకం సమక్షంలో, అధిక ఉష్ణోగ్రతల వద్ద హైడ్రోకార్బన్ల పై నీటి ఆవిరి చర్య ఫలితంగా డై హైడ్రోజన్

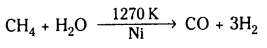
iv)ఎర్రగా కాల్చిన కోక్ మీదుగా నీటి ఆవిరిని పంపినపుడు డై హైడ్రోజన్ ఏర్పడుతుంది.

CO, H₂ మిశ్రమాన్ని సిన్గ్యాస్ అంటారు. దీనిలోని CO ను ఐరన్ క్రోమేట్ ఉత్ప్రేరకం సమక్షంలో నీటి ఆవిరితో చర్యనొందించి H₂ ను అధికంగా ఉత్పత్తి చేస్తారు. దీనినే వాటర్ గ్యాస్ షిఫ్ట్ చర్య అంటారు.

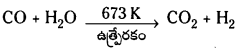
సోడియం ఆర్శినైట్ ద్రావణంతో మార్జనం చేసి CO₂ ను తొలగిస్తారు.

ప్రశ్న 25.
i) N₂
ii) లోహ అయాన్లు, లోహ ఆక్సైడ్లు
iii) కర్బన సమ్మేళనాలు.
వీటితో చర్యలను బట్టి డైహైడ్రోజన్ రసాయనశాస్త్రాన్ని వివరించండి.
జవాబు:
i) నైట్రోజన్ చర్య: నైట్రోజన్ హైడ్రోజన్ చర్య జరిపి అమ్మోనియాను ఇస్తుంది.

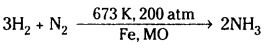
అమ్మోనియాను భారీగా తయారుచేయటానికి హాబర్ విధానంలో ఈ చర్యనే వాడతారు.

ii) a) లోహ అయాన్లతో చర్య : హైడ్రోజన్, లోహ అయానులను జల ద్రావణంలో లోహాలుగా క్షయకరణం చెందించును.

b) లోహ ఆక్సైడ్లతో చర్య : హైడ్రోజన్ లోహ ఆక్సైడ్ ను లోహాలుగా క్షయకరణం చెందించును.
H₂ + CuO → Cu + H₂O

iii) కర్బన సమ్మేళనాలతో చర్య ఉత్ప్రేరకాల సమక్షంలో హైడ్రోజన్ వివిధ రకాల కర్బన సమ్మేళనాలతో చర్య
జరుపుతుంది.
a) వృక్షజనితమయిన నూనెలను నికెల్ ఉత్ప్రేరక సమక్షంలో హైడ్రోజనీకరణం చేస్తే తినే కొవ్వును ఇస్తుంది.
b) ఓలిఫిన్లతో హైడ్రో ఫార్మైలేషన్ జరిపితే ఆల్డిహైడ్లు వస్తాయి. అవి మళ్ళీ క్షయకరణం చెంది ఆల్కహల్లను ఇస్తాయి.
H₂C = CH₂ + CO + H₂ → CH₃ CH₂ CHO
CH₃ CH₂ CHO + H₂ → CH₃ CH₂ CH₂ OH

ప్రశ్న 26.
కింది వాటిని సరైన ఉదాహరణలతో వివరించండి.
i) ఎలక్ట్రాన్ కొరత గల హైడ్రైడ్లు
ii) ఎలక్ట్రాన్లు కచ్చితంగా ఉన్న హైడ్రైడ్లు
iii) ఎలక్ట్రాన్లు అధికంగాగల హైడ్రైడ్లు
జవాబు:
i) ఎలక్ట్రాన్ కొరత గల హైడ్రైడ్లు : 13వ గ్రూపు మూలకాలన్ని ఎలక్ట్రాన్ కొరత గల హైడ్రైడ్లను ఏర్పరుస్తాయి. లూయీ నిర్మాణాన్ని సాంప్రదాయ పద్దతిలో రాయటానికి కావలసిన ఎలక్ట్రాన్ల కన్నా తక్కువ ఎలక్ట్రాన్లు ఉంటాయి. ఇవి లూయీ ఆమ్లాలుగా పనిచేస్తాయి. ఉదా : B₂H₆

ii) ఎలక్ట్రాన్లు కచ్చితంగా ఉన్న హైడ్రైడ్లు: 14వ గ్రూపు మూలకాలు ఎలక్ట్రాన్లు కచ్చితంగా ఉన్న హైడ్రైడ్లను ఏర్పరుస్తాయి. లూయీ నిర్మాణాన్ని సాంప్రదాయక పద్ధతిలో రాయటానికి కావలసిన ఎలక్ట్రాన్లు ఉంటాయి.
ఉదా : CH₄, SiH₄

iii) ఎలక్ట్రాన్లు అధికంగా గల హైడ్రైడ్లు: 15 – 17 గ్రూపు మూలకాలు ఎలక్ట్రాన్లు అధికంగాగల హైడ్రైడ్లను ఏర్పరుస్తాయి. లూయీ నిర్మాణాన్ని సాంప్రదాయక పద్దతిలో రాయటానికి కావలసిన ఎలక్ట్రాన్ల కన్నా ఎక్కువ ఎలక్ట్రాన్లు ఉంటాయి. ఎక్కువయిన ఈ ఎలక్ట్రాన్లు ఒంటరి జంటలుగా ఉంటాయి. ఇవి లూయీ క్షారాలుగా పనిచేస్తాయి.
ఉదా : NH₃, H₂O

ప్రశ్న 27.
i) అయానిక హైడ్రైడ్లు
ii) అల్పాంతరాళ హైడ్రైడ్ల గూర్చి క్లుప్తంగా రాయండి.
జవాబు:
i) అయానిక హైడ్రైడ్లు లేదా సెలైన్ హైడ్రైడ్లు :
– అధిక ధన విద్యుదాత్మకత కల s – బ్లాక్ మూలకాలు అయానిక హైడ్రేడ్లను ఏర్పరుస్తాయి.
– LiH, BeHz, MgH, వంటి హైడ్రైడ్లలో కొంత సమయోజనీయ లక్షణం కనిపిస్తుంది.
– తయారీ : లోహాన్ని నేరుగా H₂ తో సంయోగం ద్వారా వీటిని పొందవచ్చు.

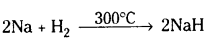
– ఘన స్థితిలో అయానిక హైడ్రైడ్లు స్పటిక, అభాష్పశీల, అవాహక పదార్థాలు. అయినా వీటి ద్రవాలు విద్యుత్ వాహకాలు. వాటి విద్యుత్ విశ్లేషణలో ఆనోడ్ వద్ద హైడ్రోజన్ వాయువు ఏర్పడుతుంది. దీనిని బట్టి H^– అయాన్ ఉంటుందని నిర్ధారణ అవుతుంది.

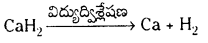
– సెలైన్ హైడ్రైడ్లు నీటితో చర్య జరిపి H₂ వాయువును ఇస్తాయి.
NaH + H₂O → NaOH + H₂

ii) అల్పాంతరాళ హైడ్రైడ్లు: d – బ్లాకు, f బ్లాకు మూలకాలు హైడ్రోజన్తో సంయోగం చెంది అల్పాంతర లేదా నాన్-స్టాయికియోమెట్రిక్ హైడ్రైడ్లను ఏర్పరుస్తాయి. ఉదా : CrH, CrH₂, ZnH₂
అయితే 7, 8, 9 గ్రూపు లోహలు హైడ్రైడ్లను ఇవ్వవు. ఇవి నాన్-స్టాయికియోమెట్రిక్ సమ్మేళనాలు.
ఇంతకు ముందు కాలంలో, ఈ హైడ్రైడ్లలోని హైడ్రోజన్ లోహ జాలకంలోని అల్పాంతరాళాల్లో ఆక్రమించుకొని, జాలక రకంలో మార్పు లేకుండా దానిని వికృతి చెందిస్తుందని భావించారు. అయితే ఇటీవల అధ్యయనాలు Ni, Pd, Ce, AC హైడ్రైడ్లు మినహా మిగిలిన ఈ తరగతి హైడ్రైడ్లన్నింటి జాలకాలు వాటి మాతృ లోహల జాలకాల కంటే భిన్నంగా ఉంటాయని చూపాయి.

pd, pt వంటి లోహాలు చాలా ఎక్కువ ఘనపరిమాణంలో హైడ్రోజనన్ను తమలో ఇముడ్చుకోగలవు. అందుకని హైడ్రోజనన్ను నిల్వచేసే మాధ్యమాలుగా వాటిని ఉపయోగిస్తారు.

ప్రశ్న 28.
నీటి రసాయన ధర్మాలను ఏ నాలుగింటినైనా విశదీకరించండి.
జవాబు:
i) ద్విస్వభావ ప్రవృత్తి : నీరు ఆమ్లంగాను, క్షారంగాను పనిచేయగల సామర్థ్యాన్ని చూపుతుంది. అంటే ద్విస్వభావ పదార్థంగా పనిచేస్తుంది. బ్రాన్టెడ్ సిద్ధాంతపరంగా అది NH₃ తో ఆమ్లంగా పనిచేస్తుంది. H₂S తో నీరు క్షారంగా పనిచేస్తుంది.
H₂O + NH₃ ⇌ OH^– + \(\mathrm{NH}_4^{+}\)
H₂O + H₂S ⇌ H₃O⁺ + HS^–

ii) లోహలతో చర్య : అధిక ధనవిద్యుదాత్మకత గల లోహాలు నీటిని క్షయీకరించి డై హైడ్రోజన్గా మార్చగలవు.
2H₂O + 2Na → 2NaOH + H₂

iii) జలవిశ్లేషణ చర్య : కొన్ని సమయోజనీయ పదార్థాలు, కొన్ని అయానిక పదార్థాలు నీటిలో జలవిశ్లేషణ చెందుతాయి.
P₄O₁₀ + 6H₂O → 4 H₃PO₄
SiCl₄ + 2H₂O → SiO₂ + 4HCl

iv) ఆర్ద్ర లవణాలు ఏర్పడడం : జల ద్రావణాల నుంచి చాలా లవణాలు ఆర్ధ లవణాలుగా స్ఫటికీకరణం చెందగలవు.

a) సమన్వయ సమయోజనీయ జలం : ఉదా : [Cr(H₂O)₆]³⁺ 3Cl^–
b) అల్పాంతరాళ జలం : ఉదా : BaCl₂. 2H₂O
c) హైడ్రోజన్ బంధిత జలం : ఉదా : [Cu (H₂O)₄]²⁺ \(\mathrm{SO}_4^{2-}\) . H₂O ఇది CuSO₄ . 5H₂O లో ఉంటుంది.

ప్రశ్న 29.
కఠినజలం, మృదుజలం అంటే వివరించండి.
i) `అయాన్ – వినిమయ పద్ధతి
ii) కాల్గన్ పద్ధతులను నీటి కఠినత్వాన్ని తొలగించడానికి వాడకంపై వ్యాఖ్యను రాయండి.
జవాబు:
కఠిన జలం : సబ్బుతో త్వరగా నురుగును ఇవ్వని నీటిని కఠిన జలం అంటారు.

• నీటిలో Ca మరియు Mg లవణాల వలన కఠినత్వం వస్తుంది.
• Ca, Mg బై కార్బోనేట్ల వల్ల అశాశ్వత కాఠిన్యత వస్తుంది.
• Ca, Mg క్లోరైడ్ లు, సల్ఫేట్ల వల్ల శాశ్వత కాఠిన్యత వస్తుంది.

మృదుజలం : సబ్బుతో త్వరగా నురుగును ఏర్పరచే నీటిని మృదుజలం అంటారు.

i) అయాన్ – వినిమయ పద్ధతి : ఈ పద్ధతిని జియొలైట్ లేదా పెరుటిట్ ప్రక్రియ అని కూడా అంటారు. ఆర్థ సోడియమ్ అల్యూమినియమ్ సిలికేట్ (Na AlSiO₄) ను జియొలైట్ లేదా పెరుటిట్ అంటారు. దీనిని కఠిన జలానికి కలిపినపుడు వినిమయ చర్యలు జరుగుతాయి.

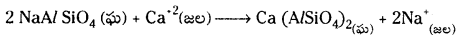
జియొలైట్లో ఉన్న సోడియమ్ అంతా ఖర్చు అయిపోయినపుడు అది వ్యయమైపోయింది అని అంటారు. దాన్ని సజల NaCl ద్రావణంతో అభిచర్యని జరిపి పునరుత్పత్తి చేస్తారు.

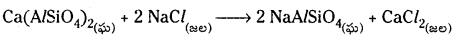
ii) కాల్గన్ పద్ధతి : సోడియమ్ హెక్సా మెటాఫాస్ఫేట్ (Na₆P₆O₁₈) ని వ్యాపార సరళిలో కాల్గన్ అంటారు. దీనిని కఠిన జలానికి కలిపినపుడు కింది చర్యలు జరుగుతాయి.

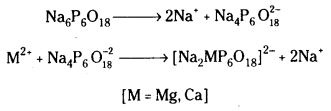
సంక్లిష్ట Mg⁺², Ca⁺² అయాన్లు ద్రావణంలో ఉంటాయి. ఇవి సబ్బుతో చర్య నొందవు. కావున ఈ నీరు సబ్బుతో నురగను ఇస్తుంది.

ప్రశ్న 30.
హైడ్రోజన్ పెరాక్సైడ్ ఆక్సీకరణిగాను, క్షయకరణిగాను పనిచేయగలదు అనడానికి రసాయన చర్యలను రాసి సమర్ధించండి.
జవాబు:
ఆమ్ల, క్షార యానకాలు రెండింటిలోను హైడ్రోజన్ పెరాక్సైడ్ ఆక్సీకరణిగాను, క్షయకరణిగాను పనిచేస్తుంది.

i) ఆమ్ల యానకంలో ఆక్సీకరణ చర్య :
2Fe⁺² + 2H⁺ + H₂O → 2Fe⁺³ + 2H₂O
Pbs + 4H₂O₂ → PbSO₄ + 4H₂O

ii) ఆమ్ల యానకంలో క్షయకరణ చర్య :
2 Mn\(\mathrm{O}_4^{-}\) + 6H⁺ + 5H₂O₂ → 2Mn⁺² + 8H₂O + O₂
HOCl + H₂O₂ → H₃O⁺ + O₂

iii) క్షార యానకంలో ఆక్సీకరణ చర్య :
2Fe⁺² + H₂O₂ → 2Fe⁺³ + 2OH^–
Mn⁺² + H₂O₂ → Mn⁺⁴ + 2OH^–

iv) క్షార యానకంలో క్షయకరణ చర్య :
I₂ + H₂O₂ + 2OH^– → 2I^– + 2H₂O + O₂
2 Mn\(\mathrm{O}_4^{-}\) + 3H₂O₂ → 2MnO₂ + 3O₂ + 2H₂O + 20H^–

ప్రశ్న 31.
క్రింది రసాయన చర్యలను పూర్తి చేసి తుల్యం చేయండి.
i) Pbs (ఘ) + H₂O₂ (జల) →
ii) Mn\(O_4^{-}\) (జల) + H₂O₂ (జల) →
iii) CaO (ఘ) + H₂O (వా) →
iv) Ca₃N₂ (ఘ) + H₂O (ద్ర) →
పై చర్యలను
a) జలవిశ్లేషణ,
b) ఆక్సీకరణ-క్షయకరణ,
c) హైడ్రేషన్ చర్యలుగా వర్గీకరించండి.
జవాబు:

1. Pbs + 4H₂O₂ → PbSO₄ + 4H₂O
   ఈ చర్య రిడాక్స్ చర్య Pbs ఆక్సీకరణం చెందుతుంది. H₂O₂ క్షయకరణం చెందుతుంది.
2. 2 Mn\(\mathrm{O}_4^{-}\) + 6H⁺ + 5H₂O₂ → 2Mn⁺² + 8H₂O + 5O₂
   ఈ చర్య రిడాక్స్ చర్య. Mn\(\mathrm{O}_4^{-}\) క్షయకరణం చెందుతుంది. H₂O₂ ఆక్సీకరణం చెందుతుంది.
3. CaO + H₂O → Ca(OH)₂
   ఈ చర్య హైడ్రేషన్ చర్య
4. Ca₃N₂ + H₂O → 3 Ca(OH)₂ + 2NH₃
   ఈ చర్య జలవిశ్లేషణ చర్య.

ప్రశ్న 32.
హైడ్రోజన్ పెరాక్సైడిని తయారుచేయడానికి వివిధ పద్ధతులను వాటికి అనువైన రసాయన సమీకరణాలతో చర్చించండి. వీటిలో ఏ పద్ధతి H₂O₂ ని తయారుచేయడానికి ఉపయోగపడుతుంది ?
జవాబు:

1. బెరీయం పెరాక్సైడు చల్లని విలీన H₂SO₄ ను కలపడం ద్వారా H₂O₂ ను తయారుచేయవచ్చు.
   BaO₂. 8H₂O (s) + H₂SO₄ (aq) → BaSO₄ + H₂O₂ (aq) 8H₂O
2. 50% H₂SO₄ ద్రావణాన్ని విద్యుద్విశ్లేషణ చేయడం ద్వారా పెరాక్సో డై సల్ఫ్యూరిక్ ఆమ్లాన్ని తయారుచేస్తారు. దీనిని జలవిశ్లేషణ చేస్తే H₂O₂ ఏర్పడుతుంది.
   2HS\(\mathrm{O}_4^{-}\) → H₂ S₂ O₈ + 2e^–
   H₂S₂O₈ + 2H₂O → 2H₂SO₄ + H₂O₂
3. పారిశ్రామికంగా H₂O₂ ను 2 – ఆల్మెన్ ఆంత్రా క్వినోల్ను స్వయం ఆక్సీకరణం చేసి తయారుచేస్తారు.
   

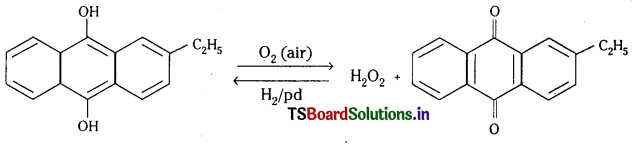
ప్రశ్న 33.
H₂O₂ గాఢతని ఎన్ని రకాలుగా మీరు చెప్పగలరు ? 15 ఘనపరిమాణ H₂O₂ గాఢతని gL^-1 లలో లెక్కగట్టండి. ఈ గాఢతను నార్మాలిటీ, మొలారిటీలలో తెలియజేయండి.
జవాబు:
i) H₂O₂ ద్రావణ గాఢతను ఘనపరిమాణాలలో సూచిస్తారు.
ఉదా : 10 ఘ.ప H₂O₂, 20 ఘ.ప H₂O₂ మరియు 100 ఘ.ప H₂O₂
20 ఘ.ప H₂O₂ అనగా 1 మి.లీ ద్రావణం STP వద్ద 20 మి.లీ. O₂ ను విడుదలచేస్తుంది.
∵ 10 మి.లీ 20 ఘ.ప H₂O₂ STP వద్ద 200 మి.లీ. O₂ విడుదల చేస్తుంది.
10 ఘ.ప H₂O₂ ద్రావణం అనగా 1 మి.లీ. ద్రావణం STP వద్ద 10 మి.లీ. O₂ వాయువును విడుదలచేస్తుంది.

ii) H₂O₂ గాఢతను భారశాతంలో చెప్పడం : H₂O₂ ఈ క్రింది విధంగా విఘటనం చెందుతుంది.

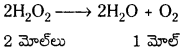
2 మోల్ల H₂O₂ నుండి 1 మోల్ O₂ వాయువు వెలువడుతుంది. ∴ 2 × 34 గ్రా. H₂O₂ నుండి 22.4 లీ O₂ వెలువడుతుంది.
STP వద్ద 10 లీ O₂ వాయువును ఇచ్చే H₂O₂ భారం
1 లీ|| ద్రావణంలో H₂O₂ భారం = \(\frac{2 \times 34 \times 10}{22.4}\) = 30.36 %
30.36%(W/V) 100 మి.లీ ద్రావణం H₂O భారాన్ని సూచిస్తుంది.
∵ H₂O₂ శక్తి = 30.36 (W/V)
∵ H₂O₂ మొలారిటి : ∵ H₂O₂ ద్రావణపు మొలారిటి = \(\frac{30.36}{34}\) = 0.893 M
H₂O₂ నార్మాలిటి : నార్మాలిటి అనగా 1లీ ద్రావణంలో గల ద్రావితపు తుల్యభారాల సంఖ్య.
∴ నార్మాలిటి = \(\frac{30.36}{17}\) = 1.786 N
15 ఘ.ప H₂O₂ శక్తి :
10 ఘ.ప H₂O₂ అనగా 3% W/V
15 ఘ.ప H₂O₂ అనగా \(\frac{15 \times 3}{10}\) = 4.5 gm / 100 మి.లీ.
1 litre H₂O₂ భారం = 45 gm/Litre
10 ఘ.ప H₂O₂ నార్మాలిటి – 1.786
15 ఘ.ప H₂O₂ నార్మాలిటి = \(\frac{15 \times 1.786}{10}\) = 2.679 N

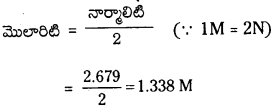
Here students can locate TS Inter 1st Year Political Science Notes Chapter 8 Democracy to prepare for their exam.

TS Inter 1st Year Political Science Notes Chapter 8 Democracy

→ Democracy is not only a form of government but also a way of life.

→ The term ‘Democracy’ is originated from two Greek words ‘Demos’ and ‘Kratos’ which means people and rule or authority.

→ “Democracy is the government of the people, by the people and for the people”. – Abraham Lincoln.

→ “Democracy is a government in which everyone has a share.” – J.R.Seeley

→ Democracy is classified into two types, namely, Direct democracy and Indirect democracy.

→ Referendum, initiative, plebiscite, and recall are said to be the devices of direct democracy.

→ Direct democracy is followed in some cantons of Switzerland.

→ Indirect democracy is also known as representative democracy.

→ The term ‘referendum’ literally means ‘refer to’.

→ Initiative ensures popular sovereignty.

→ The term ‘plebiscite’ is derived from two Latin words ‘plebis’ and ‘scitum’ which means people and decree respectively.

→ Recall is an important direct democratic device that allows the voters to call back their elected representatives on their failures.

→ The future of Democracy totally depends on how citizens perceive and play their role in public affairs.

TS Inter 1st Year Political Science Notes Chapter 8 ప్రజాస్వామ్యం

→ ప్రజాస్వామ్యాన్ని ఆంగ్లంలో ‘డెమోక్రసీ (Democracy)’ అంటారు. ఈ పదము ‘డెమోస్ (Demos)’ మరియు’ క్రటోస్ (Kratos)’ అను రెండు గ్రీకు పదముల నుండి గ్రహించబడింది. డెమోస్ అంటే ‘ప్రజలు’, క్రటోస్ అంటే ”అధికారం’ లేదా ‘పాలనా’ అని అర్థం.’

→ ప్రజాస్వామ్యం ఒక ప్రభుత్వ విధానమే కాదు ఒక జీవన విధానం కూడా.

→ “ప్రజాస్వామ్యం అంటే ప్రజల యొక్క, ప్రజల చేత, ప్రజల కొరకు పరిపాలించే, నిర్వహించబడే ప్రభుత్వం” కి అబ్రహాం లింకన్ మహాశయుడు పేర్కొన్నాడు.

→ “పరిపాలనలో, ప్రభుత్వంలో ప్రతి ఒక్కరికి భాగస్వామ్యం కల్పించే ప్రభుత్వమే ప్రజాన మహాశయుడు పేర్కొన్నాడు.

→ ప్రజాస్వామ్య వ్యవస్థలో ప్రజలంతా సంపూర్ణ స్వేచ్ఛా, స్వాతంత్య్రాలను కలిగి ఉంటారు.

→ ప్రజాస్వామ్యం రెండు రకాలుగా ఉంటుంది. అవి : 1) ప్రత్యక్ష ప్రజాస్వామ్యం 2) పరోక్ష ప్రజాస్వామ్యం.

→ ప్రత్యక్ష ప్రజాస్వామ్యం నాలుగు పద్ధతుల ప్రాతిపదికగా పనిచేస్తుంది. అవి :

1. ప్రజాభిప్రాయ సేకరణ
2. ప్రజాభిప్రాయ నివేదన
3. ప్రజాభిప్రాయ నిర్ణయం
4. పునరాయనం.

→ పరోక్ష ప్రజాస్వామ్యాన్నే పాత్రినిధ్య ప్రజాస్వామ్యమని కూడా అంటారు.

→ పత్యక్ష ప్రజాస్వామ్య పద్ధతి స్విట్జర్లాండ్ లోని కొన్ని కాంటన్ (రాష్ట్రాలు) లలో అమలులో ఉన్నది.

→ పునరాయనం అనగా ఎన్నికైన ప్రతినిధులు తమ విధులను నిర్వర్తించటంలో విఫలమైతే ఓటర్లచేత వెనుకకు పిలవబడతారు.

→ ప్రజాభిప్రాయ సేకరణ ప్రజల సార్వభౌమాధికారాన్ని ప్రతిబింబిస్తుంది.

Here students can locate TS Inter 1st Year Political Science Notes Chapter 7 Citizenship to prepare for their exam.

TS Inter 1st Year Political Science Notes Chapter 7 Citizenship

→ Citizenship is a privilege of individuals residing in democratic states.

→ Persons, who possess citizenship are known as citizens.

→ Citizen is a person who has shared in deliberative functions of the state – Aristotle.

→ One’s capacity to rule and to be ruled is citizenship -Aristotle.

→ The persons who reside in other states are known as Aliens.

→ According to Jus Sanguinis, citizenship is acquired on the basis of blood relationship.

→ According to Jus Soli, citizenship is acquired by the principle of the place of Birth.

→ Natural citizenship is acquired by the persons on the grounds of birth or residence.

→ Naturalised citizenship is conferred by a state to the Aliens.

→ Ignorance, illiteracy, poverty, and selfishness are hindrances to good citizenship.

TS Inter 1st Year Political Science Notes Chapter 7 పౌరసత్వం

→ పౌరసత్వం ప్రజాస్వామ్య రాజ్యాలలో నివసించే వ్యక్తుల ప్రత్యేక హక్కు.

→ రాజ్య వ్యవహారాలలో ప్రత్యక్షంగా, చురుకైన పాత్ర కలిగిన వ్యక్తియే పౌరుడిగా పరిగణించాలని అరిస్టాటిల్ పేర్కొన్నాడు.

→ రాజ్యంలో పౌరుడు శాశ్వత ప్రాతిపదికగా నివసిస్తాడు.

→ రాజ్యంలో విదేశీయులు తాత్కాలిక ప్రాతిపదికన నివసిస్తారు.

→ పౌరసత్వం రెండు పద్ధతుల ద్వారా సంక్రమిస్తుంది.
అవి :

1. సహజ పౌరసత్వం
2. సహజీకృత లేదా సంపాదిత పౌరసత్వం.

→ సహజ పౌరసత్వం మూడు అంశాల ప్రాతిపదికగా లభిస్తుంది. అవి :

1. జస్ సోలి (భూమి లేదా జన్మస్థలం)
2. జస్ సాంగ్వినీస్ (బంధుత్వం లేదా రక్తసంబంధం)
3. మిశ్రమ సూత్రం.

→ సహజ పౌరసత్వం లేని వ్యక్తి సహజీకృత పద్ధతి ద్వారా రాజ్య పౌరసత్వాన్ని పొందేందుకు నిర్ణీత కాలం పాటు నివసించాలి.

→ విదేశీ పురుషుడిని వివాహం చేసుకొన్న మహిళ తన స్వదేశీ పౌరసత్వాన్ని కోల్పోయి, తన భర్తకు చెందిన రాజ్య పౌరసత్వాన్ని పొందుతుంది.

→ సైన్యం నుండి పారిపోయినా, రాజ్యానికి వ్యతిరేకంగా కుట్రలు, కుతంత్రాలకు పాల్పడినా, వారి పౌరసత్వాన్ని కొన్ని దేశాలు రద్దు చేస్తాయి.

→ మంచి పౌరుడు మంచి ప్రవర్తనను కలిగి ఉండాలి.

→ మంచి పౌరసత్వానికి అజ్ఞానం, నిరక్షరాస్యతలనేవి ప్రధాన ఆటంకాలుగా పరిగణించబడతాయి.

Here students can locate TS Inter 1st Year Political Science Notes Chapter 6 Rights and Duties to prepare for their exam.

TS Inter 1st Year Political Science Notes Chapter 6 Rights and Duties

→ Rights are essential for the all-round development of the individual and the progress of society.

→ Every individual must recognize and respect the rights of l1 fellow individuals.

→ Rights are broadly classified into three categories namely Natural (ii) Moral and (iii) Legal.

→ Legal Rights are of three types, (i) Civil Rights (ii) Political Rights (iii) Economic Rights.

→ Civil life is possible through civil rights, whereas political life is possible through political rights and economic life is possible through economic rights.

→ Civil rights include the right to life, right to liberty, right to equality, right to property, right to family, right to religion, the right to contract, right to education, right form associations and unions, and right to constitutional remedies.

→ Political rights include the right to vote, the right to contest in elections, the right to hold public offices, the right to petition and the right to criticism.

→ Economic rights include the right to work, the right to adequate wages, the right to reasonable hours of work, the right to compensation and the right to self-government in industry.

→ Safeguards of rights include democratic rule, written and rigid constitution, constitutional incorporation, separation of powers, decentralization of powers, rule of law, independent and impartial judiciary, independent press, social and economic equalities, and eternal vigilance.

→ Human rights are the amenities required for the basic existence of human beings.

→ Magna Carta in England is the First step towards the realization of human rights.

→ Human rights are broadly classified into two categories (i) Civil and Political Rights (ii) Economic, Social and Cultural rights.

→ The Constitution of India incorporated many of the human rights, mentioned in the U.N. declaration of human Rights. Especially articles 19 to 28 of part – III on fundamental rights are in consonance with the human rights of individuals.

→ Responsibilities are the obligations of individuals towards others residing in society.

→ Responsibilities are moral, legal, positive, and negative.

TS Inter 1st Year Political Science Notes Chapter 6 హక్కులు – విధులు

→ రాజనీతిశాస్త్ర అధ్యయనంలో హక్కుల భావనకు చాలా ప్రాముఖ్యత ఉంది.

→ వ్యక్తుల సంపూర్ణ వికాసానికి అత్యంత అవసరమైన నియమాలే హక్కులు.

→ ‘వ్యక్తులు ఆదర్శవంతమైన, బాధ్యతాయుతమైన పౌరులుగా తీర్చిదిద్దబడటానికి అవసరమైన పరిస్థితులను శ్రద్ధతో కల్పించేవే హక్కులు’ అని లాస్కీ మహాశయుడు పేర్కొన్నాడు.

→ మానవులు జన్మతః అనుభవించే హక్కులే సహజ హక్కులు. “నైతిక హక్కులు” సమాజంలోని నైతిక సూత్రాల ప్రాతిపదికగా రూపొందింపబడినాయి.

→ రాజ్యం చేత గుర్తించబడి ప్రభుత్వం ద్వారా అమలయ్యే వాటిని ‘చట్టబద్ధమైన హక్కులు’ అంటారు.

→ నాగరిక సమాజానికి పౌరహక్కులు అత్యంత అవసరం.

→ రాజ్యానికి సంబంధించిన రాజకీయ వ్యవహారాలలో పాల్గొనేందుకు పౌరులకు అవకాశాలు కల్పించే హక్కులను ‘రాజకీయ హక్కులు’ అంటారు.

→ వ్యక్తులు ఆర్థిక వ్యవహారాలలో పాల్గొనేందుకు తోడ్పడే హక్కులను ‘ఆర్థిక హక్కులు’ అంటారు.

→ ‘పౌర హక్కులన్నింటిలో ప్రాణరక్షణ హక్కు అత్యంత ప్రధానమయినది అని టి.హెచ్. గ్రీన్ మహాశయుడు పేర్కొన్నాడు.

→ సమాజంలోని నివసించే వ్యక్తులు ఇతర వ్యక్తుల పట్ల నిర్వర్తించే అంశాలనే బాధ్యతలు అంటారు.

→ ప్రతి పౌరుడు తాను నివసించే రాజ్యం పట్ల, ప్రభుత్వం పట్ల, చట్టాల పట్ల సంపూర్ణ విశ్వాసాన్ని, విధేయతను కలిగి ఉండాలి.

Here students can locate TS Inter 1st Year Economics Notes Chapter 10 Basic Statistics for Economics to prepare for their exam.

TS Inter 1st Year Economics Notes Chapter 10 Basic Statistics for Economics

→ Economics is that branch of social science that studies the economic behavior of human beings.

→ In Economics, measures are known as policies. So a number of analyses of economic problems would be possible without data.

→ Statistics means numerical facts systematically collected.

→ Statistics is used in finding the relationship between the cause and effect of an economic problem.

→ Collection of data is classified into two types.

1. Primary data
2. Secondary data

→ There are various kinds of diagrams in common use.

1. Geometric diagram
2. Frequency diagram
3. Line graphs diagram

→ ‘Bar’ diagram and ‘Pie’ diagram come in the category of geometric diagrams.

→ The Bar diagrams are of three types:

1. Simple bar diagram 2. Multiple bar diagram 3. Subdivided bar diagram.

→ Height and length rectangular bars for each class of data.

→ It is used for comparing two or more sets of data.

→ These diagrams are used to represent various parts of the total.

→ The circle is divided into as many parts as components by drawing straight lines from the centre.

→ The measures of central tendency is a way of summarizing the data in the form of typical values. There are three most commonly used averages:

1. Arithmetic Mean
2. Median
3. Mode

→ It is the quotient of the sum of all the items divided by the number of items.

→ Mean calculation: under ungrouped data

→ Mean calculating under grouped data:

Using the symbol S for summation we get

→ Shortcut or Step deviation method for a mean of grouped data:

→ Median is the middle element when the data set is arranged in order of magnitude.

→ Mode is the most frequently observed value in the data with the highest frequency is called the mode of data.

→ Relationship among Mean, Median, and Mode:
There exist an empirical relation among mean, median, and mode.
So, Mode = 3 Median – 2 Mean

TS Inter 1st Year Economics Notes Chapter 10 అర్థశాస్త్రంలో ప్రాథమిక గణాంక శాస్త్ర భావనలు

→ గణాంక శాస్త్రాన్ని ఆంగ్లంలో ‘స్టాటిస్టిక్స్’ అని పిలుస్తారు. దీనిని రెండు అర్థాలలో వాడుతారు. ఏకవచనంలో దీనిని ‘గణాంక శాస్త్రం’ అంటారు. బహువచనంలో “సాంఖ్యా దత్తాంశం” అంటారు.

→ గణాంకశాస్త్ర పరిధిలోకి ముఖ్యంగా వచ్చే అంశాలు దత్తాంశాన్ని సేకరించడం, సమర్పించడం, విశ్లేషణ చేయడం, విపులీకరించడం మొదలగునవి.

→ అర్థశాస్త్ర అధ్యయనంలో గణాంక శాస్త్ర పరిజ్ఞానం అవసరమని J.S. మిల్, జీవాన్స్, కీన్స్ లాంటి వారు పేర్కొన్నారు. అర్థశాస్త్ర విశ్లేషణ అంతా గణాంక దత్తాంశంపై పూర్తిగా ఆధారపడి ఉంటుంది. పేదరికం, నిరుద్యోగం, ధరలు మొదలగువాటి స్వరూప, స్వభావాలు తెలుసుకొనుటకు దీనిని ఉపయోగిస్తారు.

→ గణాంక ఫలితాలు తేలికగా అవగాహన చేసుకొనుటకు చిత్రపటాలు ఉపయోగపడతాయి. అవి. ముఖ్యంగా 5 రకాలు.

1. ఏకపరిమాణ చిత్రాలు
2. ద్విపరిమాణ చిత్రాలు
3. త్రిపరిమాణ చిత్రాలు
4. పిక్టోగ్రాములు
5. కార్టోగ్రాములు

→ i) సాధారణ బార్ చిత్రాన్ని ఒక చలనరాశిలో మార్పు చూపడానికి ఉపయోగిస్తారు.
ii) ఉప విభాజిత బార్పటం మొత్తం దత్తాంశంలోని భాగాలు బార్లో చూపించవచ్చు.
iii) బహుళ బారటం అంతర సంబంధమున్న దత్తాంశం ఒక పటంలో చూపడానికి ఉపయోగిస్తారు.
iv) దత్తాంశంలో మార్పులు సులభంగా గమనించడానికి శాతపు బార్ ఉపయోగిస్తారు.

→ శ్రేణులలో ఉన్న అంశాల మొత్తాన్ని అంశాల సంఖ్యతో భాగిస్తే ఉత్పన్నమయ్యే సంఖ్య అంకమధ్యమం.
A. వ్యక్తిగత శ్రేణుల మూడు పద్ధతులు:

B. విచ్చిన్న శ్రేణులు:

C. అవిచ్చిన్న శ్రేణులు:

→ విభాజనాన్ని ఏ విలువ రెండు సమభాగాలుగా విభజిస్తుందో దానిని “మధ్యగతం” అంటారు.

→ శ్రేణులలో ఉన్న అంశాలలో ఏ విలువ అతి తరచుగా వస్తుందో ఆ విలువను బాహుళకం అంటారు.
A. వ్యక్తిగత శ్రేణి: Z = ఎక్కువ పర్యాయాలు వచ్చేది.
B. విచ్ఛిన్న శ్రేణి : Z = ఎక్కువ పర్యాయాలు వచ్చేది.

Students must practice these TS Inter 1st Year Maths 1B Study Material Chapter 9 Differentiation Ex 9(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Differentiation 9(a)

I.
Question 1.
Find the derivatives of the following functions f(x). (V.S.A.Q.)
(i) √x + 2x^3/4 + 3x^5/6 (x > 0)
Answer:

(ii) \(\sqrt{2 x-3}+\sqrt{7-3 x}\)
Answer:

(iii) (x² – 3) (4x³ + 1)
Answer:
y = (x² – 3) (4x³ + 1)
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = (x² – 3) \(\frac{\mathrm{d}}{\mathrm{dx}}\) (4x³ + 1) + (4x³ + 1) \(\frac{\mathrm{d}}{\mathrm{dx}}\) (x² – 3)
= (x² – 3) (12x²) + (4x³ + 1) (2x)
= 12x⁴ – 36x² + 8x⁴ + 2x = 20x⁴ – 36x² + 2x

(iv) (√x – 3x) (x + \(\frac{1}{x}\))
Answer:

(v) (√x + 1) (x² – 4x + 2) (x > 0)
Answer:
y = (√x + 1) (x² – 4x + 2)
\(\frac{d y}{d x}\) = (√x + 1) \(\frac{d}{d x}\) (x² – 4x + 2) + (x² – 4x + 2) \(\frac{d}{d x}\) (√x + 1)
= (√x + 1) (2x – 4) + (x² – 4x + 2) \(\left(\frac{1}{2 \sqrt{x}}\right)\)
= (√x + 1) (2x – 4) + \(\frac{x^2-4 x+2}{2 \sqrt{x}}\)

(vi) (ax + b)ⁿ (cx + d)^m
Answer:
Let y = (ax + b)ⁿ (cx + d)^m
\(\frac{d y}{d x}\) = (ax + b)ⁿ . m(cx + d)^{m – 1}(c) + (cx + d)^m n (ax + b)^{n – 1} (a)
= (ax + b)ⁿ (cm (cx + d)^{m – 1}] + (cx + d)^m [an(ax + b)^{n – 1}]
= (ax + b)^{n – 1} (cx + d)^{m – 1} [cm (ax + b) + an(cx + d)]
= (ax + b)ⁿ (cx + d)^m \(\left[\frac{a n}{a x+b}+\frac{c m}{c x+d}\right]\)

(vii) 5 sin x + e^x log x
Answer:
y = 5 sin x + e^x log x

(viii) 5^x + log x + x³ e^x
Answer:
y = 5^x + log x + x³ e^x
∴ \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 5^x log 5 + \(\frac{1}{x}\) + [x³e^x + 3x²e^x]

(ix) e^x + sin x cos x
Answer:
y = e^x + sin x cos x
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = e^x + sin x (- sin x) + cos x (cos x) dx
= e^x + cos² x – sin² x = e^x + cos 2x

(x) \(\frac{p x^2+q x+r}{a x+b}\) (|a| + |b| ≠ 0)
Answer:

(xi) log₇(log x) (x > 0)
Answer:
y = log₇(log x)

(xii) \(\frac{1}{a x^2+b x+c}\) (|a| + |b| + |c| ≠ 0)
Answer:

(xiii) e^2x log (3x + 4) (x > – 4/3)
Answer:
y = e^2x log (3x + 4) (x > – 4/3)

(xiv) (4 + x²) e^2x
Answer:
y = (4 + x²) e^2x
∴ \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = (4 + x²) \(\frac{\mathrm{d}}{\mathrm{dx}}\) (e^2x) + e^2x . \(\frac{\mathrm{d}}{\mathrm{dx}}\) (4 + x²)
= (4 + x²) (2e^2x) + e^2x (2x)
= 2e^2x (x² + x + 4)

(xv) \(\frac{a x+b}{c x+d}\) (|c| + |d| ≠ 0) (May 2022)
Answer:
y = \(\frac{a x+b}{c x+d}\)

(xvi) a^x.e^x2 (Board New Model Paper)
Answer:
y = a^x.e^x2
Then
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = a^x . \(\frac{\mathrm{d}}{\mathrm{dx}}\) (e^x2) + \(\frac{\mathrm{d}}{\mathrm{dx}}\) (a^x)
= a^x (2x) e^x2 + e^x2 . a^x log_ea
= a^x e^x2 (2x + log_e^a)
= y (2x + log_e^a)

Question 2.
If f(x) = (1 + x + x² + …… + x¹⁰⁰) then find f ‘(1). (V.S.A.Q.)
Answer:
f(x) = (1 + x + x² + ……. + x¹⁰⁰)
Then f(x) = 1 + 2x+ 3x² + …………….. + 100x⁹⁹
and f’(1) = 1 + 2 + 3 + ………………. + 100
= \(\frac{100(100+1)}{2}\) = 101 × 50 = 5050
(∵ Σn = \(\frac{\mathrm{n}(\mathrm{n}+1)}{2}\))

Question 3.
If f(x) = 2x + 3x – 5 then prove that f ‘(0) + 3f ‘( -1) = 0. (V.S.A.Q.)
Answer:
Given f(x) = 2x² + 3x – 5
Then f'(x) = 4x + 3
∴ f(0) + 3f (- 1) = 3 + 3 [4 (- 1) + 3] = 3 – 3 = 0

II.
Question 1.
Find the derivatives of the following functions from the first principle. (S.A.Q.)
(i) x³
Answer:
Let f(x) = x³ then

(ii) x⁴ + 4
Answer:
let f(x) = x⁴ + 4

(iii) ax² + bx + c
Answer:
Let f(x) = ax² + bx + c

(iv) √x + 1
Answer:
Let f(x) = √x + 1

(v) sin 2x (Board New Model Paper)
Answer:
Let f(x) = sin 2x

(vi) cos ax (May 2014, March 2013, 2011)
Answer:
Let f(x) = cos ax

(vii) tan 2x (March 2014, May 2011)
Answer:
Let f(x) = tan 2x

(viii) cot x
Answer:
let f(x) = cot x
then

(ix) sec 3x
Answer:
Let f(x) = sec 3x
then

(x) x sin x
Answer:
Let f(x) = x sin x
Then f(x + h) – f(x) = (x + h) sin (x + h) – x sin x
= x [sin(x + h) – sin x] + h sin (x + h)

= x cos x × 1 + sin x
= x cos x + sin x

(xi) cos²x
Answer:
Let f(x) = cos²x
Then f (x + h) – f(x) = cos² (x + h) – cos²x
= [1 – sin²(x + h)] – (1 – sin²x)
= sin²x – sin²(x + h)
= sin (x + x + h) sin (x – x – h)
= sin (2x + h) sin (- h)

= – sin 2x × 1 = – sin 2x

Question 2.
Find the derivatives of the following functions. (S.A.Q.)
(i) \(\frac{1-x \sqrt{x}}{1+x \sqrt{x}}\) (x > 0)
Answer:

(ii) xⁿ n^x log (nx), (x > 0, n ∈ N)
Answer:
Let y = xⁿ n^x log (nx)
Then

(iii) ax²ⁿ log x + bxⁿ e^-x
Answer:
Let y = ax²ⁿ log x + bxⁿ e^-x

= a [x^{2n – 1} + 2nx^{2n – 1} log x] + b [- xⁿ e^-x + ne^-x x^{n – 1}]
= ax^{2n – 1} + 2anx^{2n – 1} log x – bxⁿe^-x + bne^-x x^{n – 1}

(iv) \(\left(\frac{1}{x}-x\right)^3\) e^x
Answer:

Question 3.
Show that the function f(x) = | x | + | x – 1| x ∈ R is differentiable for all real numbers except for 0 and 1. (S.A.Q.)
Answer:
f(x) = |x| + |x – 1| ∀ x ∈ R
then f(x) = x + x – 1 = 2x – 1, x ≥ 1
= x – (x – 1) = x – x + 1 = 1, 0 < x < 1
= – x – (x – 1)
= – x – x + 1 = 1 – 2x; x ≤ 0
∴ f(x) = 2x – 1, x ≥ 1
= 1, 0 < x < 1 = 1 – 2x; x ≤ 0 If x > 1, then f(x) = 2x – 1 which is a polynomial differentiable for all x > 1.
If 0 < x ≤ 1, then f(x) = 1 = Constant which is differentiable.

Case (i): Differentiability at x = 0:

∵ Lf'(0) ≠ Rf'(0), the function f is not differentiable at x = 0.

Case (i): Differentiability at x = 1:

∵ Lf'(1) ≠ Rf'(1) we say that f(x) is not differentiable at x = 1.
∴ f(x) is differentiable for all real x except zero and one.

Question 4.
Verify whether the following function is differentiable at 1 and 3. (S.A.Q.)

Answer:
Case (i):

Case (ii):

Since Lf'(3) ≠ Rf'(3), f(x) is not differentiable at x = 3.

Question 5.
Is the following function f differentiable at 2 ? Justify. (S.A.Q.)

Answer:

Since Lf'(2) ≠ Rf'(2), we say f(x) is not differentiable at x = 2.

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Mean Value Theorems Important Questions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Mean Value Theorems Important Questions

Question 1.
Verify Rolle’s theorem for the function y = f(x) = x² + 4 in [-3, 3]. [Mar. ’19 (TS); Mar. ’17 (AP), ’15 (TS); B.P.; May ’15 (TS)]
Solution:
f is a polynomial function that is continuous and differentiable in [-3, 3]
Given f(x) = x² + 4
∴ f(-3) = (-3)² + 4 = 13
and f(3) = 3² + 4 = 13
∴ f(-3) = f(3).
Hence the function satisfies the conditions of Rolle’s theorem and f'(x) = 2x
∴ f'(c) = 2c = 0
c = 0 ∈ (-3, 3)
Thus Roll’s theorem is verified.

Question 2.
Verify Rolle’s theorem for the following function x² – 1 on [-1, 1]. [Mar. ’14; May ’13]
Solution:
Let f(x) = x² – 1 defined on [-1, 1].
Since the function f(x) is a polynomial, it is continuous on [-1, 1] and differentiable on (-1, 1).
Also f(1) = 1 – 1 = 0,
f(-1) = (-1)² – 1 = 0
f(-1) = f(1).
Hence f satisfies all conditions of Rolle’s theorem.
Now we have to find a point c ∈ (-1, 1) such that f'(c) = 0, f'(x) = 2x
and f'(c) = 0
2c = 0
c = 0 ∈ (-1, 1)
Hence Rolle’s theorem is verified.

Question 3.
Let f(x) = (x – 1) (x – 2) (x – 3). Prove that there is more than one ‘c’ in (1, 3) such that f'(c) = 0. [Mar. ’13]
Solution:
f is a polynomial in x which is continuous over [1, 3] and derivable over (1, 3).
Given f(x) = (x – 1) (x – 2) (x – 3)
We have f'(x) = (x – 1) (x – 2) + (x – 2) (x – 3) + (x – 1) (x – 3)
= x² – 3x + 2 + x² – 5x + 6 + x² – 4x + 3
= 3x² – 12x + 11
f'(c) = 0
3c² – 12c + 11 = 0
c = \(\frac{12 \pm \sqrt{144-132}}{6}\) = 2 ± \(\frac{1}{\sqrt{3}}\)
2 + \(\frac{1}{\sqrt{3}}\) ∈ (1, 3) and 2 – \(\frac{1}{\sqrt{3}}\) ∈ (1, 3)
∴ There exists more than one ‘c’ in (1, 3) such that f'(c) = 0.

Question 4.
Verify Rolle’s theorem for the function f(x) = x(x + 3) \(\mathrm{e}^{-\mathrm{x} / 2}\) in [-3, 0]. [Mar. ’18 (AP)]
Solution:
f is continuous in [-3, 0] and differentiable in (-3, 0).
Also f(-3) = (-3) (-3 + 3) e^3/2 = 0
f(0) = 0 (0 . 3) e^3/2 = 0
∴ f(-3) = f (0)
So f satisfies the conditions of Rolle’s theorem.
Given f(x) = x(x + 3) e^3/2
Then f'(x) = x(x + 3) \(\left(\frac{-1}{2}\right) \mathrm{e}^{-\mathrm{x} / 2}\) + \(x\left(e^{\frac{-x}{2}}\right)+(x+3) e^{\frac{-x}{2}}\)

f'(e) = 0
-e² + e + 6 = 0
e = -2 or 3
Now -2 ∈ (- 3, 0) and c = -2
∴ Rolle’s theorem was verified.

Question 5.
Verify Lagrange’s mean value theorem for the function f(x) = x² on [2, 4].
Solution:
Being a polynomial function
(i) f(x) = x² is continuous on [2, 4] and
(ii) differentiable in (2, 4)
By Lagrange’s theorem there should exist c ∈ (2, 4) such

Hence Lagrange’s theorem is verified.

Question 6.
On the curve y = x², find a point at which the tangent is parallel to the chord joining (0, 0) and (1, 1).
Solution:
The slope of the chord joining (0, 0) and (1, 1) is
m₁ = \(\frac{1-0}{1-0}\) = 1
Given curve is y = x²
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 2x
∴ The slope of the tangent at any point on the curve is m₂ = 2x
If the tangent is parallel to the chord, then m₁ = m₂
2x = 1
x = \(\frac{1}{2}\)
Now, y = x² = \(\left(\frac{1}{2}\right)^2=\frac{1}{4}\)
∴ The required point on the curve is \(\left(\frac{1}{2}, \frac{1}{4}\right)\)

Question 7.
Verify Rolle’s Theorem for the following function sin x – sin 2x on [0, π].
Solution:
Let f(x) = sin x – sin 2x defined over [0, π].
f is continuous over [0, π] and differentiable over (0, π).
Also f(0) = 0 and f(π) = sin π – sin 2π = 0
f(0) = f(π) = 0
Hence f satisfies the conditions of Rolle’s theorem.
Also f'(x) = cos x – 2 cos 2x and f'(c) = 0
cos c – 2 cos 2c = 0
cos c = 2(2 cos²c – 1)
4 cos²c – cos c – 2 = 0

Hence conditions of Rolle’s theorem are verified.

Question 8.
Show that there is no real number k, for which the equation x² – 3x + k = 0 has two distinct roots in [0, 1].
Solution:
Let f(x) = x² – 3x + k and suppose there exist two different roots α, β (α < β).
Since f is a polynomial in x, it is continuous over [0, 1] and differentiable in (0, 1).
f is continuous over [α, β] and differentiable in (α, β).
Also f(α) = α² – 3α + k = 0 and
f(β) = β² – 3β + k = 0
∴ f(α) = f(β) = 0
∴ f satisfies the conditions of Rolle’s theorem.
Also f'(c) = 0
3c² – 3 = 0
c² = 1
c = ±1
This is a contradiction since 0 < α < c < β < 1
Hence there do not exist roots α, β in (0, 1).
So, there is no real number k for which the equation x² – 3x + k = 0 has two distinct roots in [0, 1].

Question 9.
Find a point on the graph of the curve y = (x – 3)² where the tangent is parallel to the chord joining (3, 0) and (4, 1).
Solution:
Let the points be A(3, 0) and B(4, 1)
Slope of chord AB = \(\frac{1-0}{4-3}\) = 1
Given y = (x – 3)²
\(\frac{d y}{d x}\) = 2(x – 3)
Slope of the chord 2(x – 3) = 1
2x = 7
x = \(\frac{7}{2}\)
∴ y = (x – 3)²
= \(\left(\frac{7}{2}-3\right)^2=\frac{1}{4}\)
∴ The point on the curve = \(\left(\frac{7}{2},\frac{1}{4}\right)\)

Question 10.
Find a point on the graph of the curve y = x³ where the tangent is parallel to the chord joining (1, 1) and (3, 27).
Solution:
Let the points be A(1, 1) and B(3, 27)

Question 11.
Find ‘c’ so that f'(c) = \(\frac{\mathbf{f}(\mathbf{b})-\mathbf{f}(\mathbf{a})}{b-\mathbf{a}}\) where f(x) = e^x; a = 0, b = 1.
Solution:

Question 12.
Verify Rolle’s theorem for the function (x² – 1) (x – 2) on [-1, 2]. Find a point in the interval where the derivative vanishes.
Solution:
Let f(x) = (x² – 1) (x – 2) = x³ – 2x² – x + 2 defined over [-1, 2].
f being a polynomial in ‘x’, it is continuous over [-1, 2] and differentiable over (-1, 2).
f(-1) = 0, f(2) = 0
∴ f(-1) = f(2)
∴ f satisfies all the conditions of Rolle’s theorem.
f(x) = 3x² – 4x – 1 and f'(c) = 0
3c² – 4c – 1 = 0

∴ Rolle’s theorem is verified.

Question 13.
Verify the conditions of Lagrange’s mean value theorem for the function x² – 1 on [2, 3]. [Mar. ’18 (TS); Mar. ’16 (AP)]
Solution:
Let f(x) = x² – 1 defined over [2, 3]. This is a polynomial in x, continuous on [2, 3] and differentiable over (2, 3).
So by Lagrange’s mean value theorem, there exists a point ‘c’ ∈ (2, 3) such that
f'(c) = \(\frac{\mathrm{f}(3)-\mathrm{f}(2)}{3-2}\)
f'(x) = 2x
f'(c) = 2c
f(3) = 8, f(2) = 3
∴ 2c = \(\frac{8-3}{1}\) = 5
c = \(\frac{5}{2}\) ∈ (2, 3)

Question 14.
Verify the conditions of Lagrange’s mean value theorem for the function sin x – sin 2x on [0, π].
Solution:
Let f(x) = sin x – sin 2x defined over [0, π].
This is continuous on [0, π] and differentiable over (0, π)
since f'(x) = cos x – 2 cos 2x exists for all x ∈ (0, π).
So by Lagrange’s mean value theorem
f'(c) = \(\frac{\mathrm{f}(\pi)-\mathrm{f}(0)}{\pi-0}\), f(π) = 0, f(0) = 0
∴ cos c – 2 cos 2c = \(\frac{0}{\pi}\) = 0
cos c – 2 cos 2c = 0
cos c – 2(2 cos²c – 1) = 0
4cos²c – cos c – 2 = 0
cos c = \(\frac{1 \pm \sqrt{1+32}}{8}=\frac{1 \pm \sqrt{33}}{8}\)
c = \(\cos ^{-1}\left(\frac{1+\sqrt{33}}{8}\right)\) ∈ (0, π)

Question 15.
Verify the conditions of Lagrange’s mean value theorem for the function log x on [1, 2].
Solution:
Let f(x) = log x defined over [1, 2].
This is continuous over [1, 2] and differentiable over (1, 2) since
f'(x)= \(\frac{1}{x}\) ∀ x ∈ (1, 2)

Hence Lagrange’s mean value theorem is satisfied.

Question 16.
Verify Rolle’s theorem for the function f : [-3, 8] → R be defined by f(x) = x² – 5x + 6. [Mar. ’17 (TS)]
Solution:
Given f(x) = x² – 5x + 6 defined on [-3, 8].
Since the function f(x) is a polynomial,
it is continuous on [-3, 8] and differentiable on [-3, 8)
Also f(-3) = (-3)² – 5(-3) + 6
= 9 + 15 + 6
= 30
f(8) = (8)² – 5(8) + 6
= 64 – 40 + 6
= 30
∴ f(-3) = f(8)
Hence f satisfies all conditions of Rolle’s theorem.
Now we have to find a point C ∈ (-3, 8) such that f'(C) = 0
f'(x) = 2x – 5 and f'(c) = 0
2C – 5 = 0
C = \(\frac{5}{2}\) ∈ (-3, 8)
Hence Rolle’s theorem is verified.

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Rate Measure Important Questions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Rate Measure Important Questions

Question 1.
The distance-time formula for the motion of a particle along a straight line is s = t³ – 9t² + 24t – 18. Find when and where the velocity is zero. [Mar. ’19 (AP); Mar. ’12; May ’96]
Solution:
Given, s = t³ – 9t² + 24t – 18
Velocity, v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\)
= 3t² – 9(2t) + 24(1) – 0
= 3t² – 18t + 24
Given, the particle comes to rest then the velocity = 0
3t² – 18t + 24 = 0
t² – 6t + 8 = 0
t² – 4t – 2t + 8 = 0
t(t – 4) – 2(t – 4) = 0
(t – 4) (t – 2) = 0
t – 4 = 0 (or) t – 2 = 0
t = 4 (or) t = 2
t = 2, 4
The velocity is zero when t = 2 sec and 4 sec.
Case 1:
If t = 2 sec, then s = t³ – 9t² + 24t – 18
= (2)³ – 9(2)² + 24(2) – 18
= 8 – 36 + 48 – 18
= 2 units
Case 2:
If t = 4 sec, then s = (4)³ – 9(4)² + 24(4) – 18
= 64 – 144 + 96 – 18
= 160 – 162
= -2 units
∴ The particles are at a distance of two units from the starting point ‘0’ on either side.

Question 2.
The displacement s of a particle travelling in a straight line in ‘t’ seconds is given by s = 45t + 11t² – t³, finding the time when the particle comes to rest. [May ’13 (Old), ’06; Mar. ’07]
Solution:
Given, s = 45t + 11t² – t³
Velocity, v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\)
= 45(1) + 11(2t) – 3t²
= 45 + 22t – 3t²
The particle comes to rest then velocity, v = 0
45 + 22t – 3t² = 0
3t² – 22t – 45 = 0
3t² – 27t + 5t – 45 = 0
3t(t – 9) + 5(t – 9) = 0
(t – 9) (3t + 5) = 0
t – 9 = 0 (or) 3t + 5 = 0
t = 9 (or) t = \(\frac{-5}{3}\)
t = 9 Since t is positive then t = 9
∴ The particle comes to rest when t = 9 sec.

Question 3.
A particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line given by s = f(t) = 8t + t³. Find
(i) the velocity at time t = 2 sec [Mar. ’17, ’15 (AP)]
(ii) the initial velocity
(iii) acceleration at t = 2 sec [May ’12; B.P.]
Solution:
The distance s and time t are connected by the relation s = f(t) = 8t + t³
Velocity, v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\)
= 8(1) + 3t²
= 8 + 3t²
(i) Velocity at t = 2 sec, then,
v = \(\left(\frac{\mathrm{ds}}{\mathrm{dt}}\right)_{\mathrm{t}=2}\)
= 8 + 3(2)²
= 8 + 12
= 20 cm/sec
acceleration, a = \(\frac{\mathrm{dv}}{\mathrm{dt}}\)
= 0 + 3(2t)
= 6t
(ii) Initial velocity (t = 0) is v = \(\left(\frac{\mathrm{ds}}{\mathrm{dt}}\right)_{\mathrm{t}=0}\)
= 8 + 3(0)²
= 8 cm/sec
(iii) The acceleration at t = 2 sec, then
a = \(\left(\frac{\mathrm{dv}}{\mathrm{dt}}\right)_{\mathrm{t}=2}\)
= 6(2)
= 12 cm/sec²

Question 4.
A container is in the shape of an inverted cone and has a height of 8 cm and a radius of 6 m at the top. If it is filled with water at the rate of 2 m³/minute, how fast height of the water change when the level is 4m? [Mar. ’19 (TS): May ’13. ’11, ’09; Mar. ’08, ’06]
Solution:
Let h be the height, r be the radius of the water level and V be the volume of the water in the container at the time ‘t’.
Given that, \(\frac{d v}{d t}\) = 2m3/min.


∴ The height of the water changes at a rate of \(\frac{2}{9 \pi}\) m/min.

Question 5.
The volume of a cube is increasing at a rate of 9 cubic centimeters per second. How fast is the surface area increasing when the length of the edge is 10 centimeters? [Mar. ’17 (TS), ’16 (AP), ’13; May ’15 (TS)]
Solution:
Let x be the length of the edge of the cube.
V is its volume and S is its surface area.
Given that rate of change of volume
\(\frac{\mathrm{dv}}{\mathrm{dt}}\) = 9 cm³/sec
x = 10 cm
The volume of a cube, V = x³
Differentiating v with respect to ‘t’, we get

Question 6.
A point P is moving on the curve y = 2x². The x coordinate of P is increasing at the rate of 4 units per second. Find the rate at which the y-coordinate is increasing when the point is at (2, 8). [Mar. ’16 (TS), ’13; May ’08]
Solution:
Let P(x, y) be any point on the curve y = 2x²
Given, \(\frac{\mathrm{dx}}{\mathrm{dt}}\) = 4 units/sec
Given point (x, y) = (2, 8)
Now, y = 2x²
Differentiating on both sides with respect to ‘t’
\(\frac{\mathrm{dy}}{\mathrm{dt}}=2(2 \mathrm{x}) \cdot \frac{\mathrm{dx}}{\mathrm{dt}}\)
= 4(2) . 4
= 32 units/sec
∴ The y-coordinate is increasing at the rate of 32 units/sec.

Some More Maths 1B Rate Measure Important Questions

Question 7.
A container in the shape of an inverted cone has a height of 12 cm and a radius of 6 cm at the top. If it is filled with water at the rate of 12 cm³/sec. What is the rate of change in the height of the water level when the tank is filled 8 cm?
Solution:
Let h be the height, r be the radius of the water level and v be the volume of water in the container at a time ‘t’.

Given, \(\frac{\mathrm{dV}}{\mathrm{dt}}\) = 12 cm³/sec
height, h = 8 cm
In triangle OAB, OCD are similar, then


Hence the rate of change of water level is \(\frac{3}{4 \pi}\) cm/sec when the water level of the tank is 8 cm.

Question 8.
The volume of a cube is increasing at the rate of 8 cm3/sec. How fast is the surface area increasing when the length of an edge is 12 cm?
Solution:
Let x be the length of the edge of the cube, V be its volume and S be its surface area.
Given that, the rate of change in volume \(\frac{\mathrm{dV}}{\mathrm{dt}}\) = 8 cm³/sec
x = 12 cm
The volume of a cube V = x³
Differentiating V on with respect to ‘t’, we get

Question 9.
A particle moving along straight has the relation s = t³ + 2t + 3, connecting the distance s described by the particle in time t. Find the velocity and acceleration of the particle at t = 4 seconds.
Solution:
Given, s = t³ + 2t + 3
velocity, v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\)
= 3t² + 2 + 0
= 3t² + 2
velocity at t = 4 sec, then, v = \(\left(\frac{\mathrm{ds}}{\mathrm{dt}}\right)_{t=4}\)
= 3(4)² + 2
= 50 units/sec
acceleration, a = \(\frac{\mathrm{dv}}{\mathrm{dt}}\)
= 3(2t) + 0
= 6t
acceleration at t = 4, then
a = \(\left(\frac{\mathrm{dv}}{\mathrm{dt}}\right)_{\mathrm{t}=4}\)
= 6(4)
= 24 units/sec²

Question 10.
A particle is moving along a line according to s = f(t) = 4t³ – 3t² + 5t – 1 where s is measured in metres and t is measured in seconds. Find the velocity and acceleration at time t. At what time the acceleration is zero? [Mar. ’18 (AP); Mar. ’18, ’15 (TS)]
Solution:
Given, s = f(t) = 4t³ – 3t² + 5t – 1
velocity, v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\)
= 4(3t²) – 3(2t) + 5(1) – 0
= 12t² – 6t + 5
acceleration, a = \(\frac{d v}{d t}\)
= 12(2t) – 6(1) + 0
= 24t – 6
∴ Acceleration is 0 if 24t – 6 = 0
24t = 6
t = \(\frac{1}{4}\) sec
∴ Acceleration of particle is 0 at t = \(\frac{1}{4}\) sec

Question 11.
A stone is dropped into a quiet lake and ripples move in circles at speed of 5 cm/sec. At the instant when the radius of the circular ripple is 8 cm, how fast is the enclosed area increased?
Solution:
Let A be the area of the circle with radius ‘r’.
Given, radius, r = 8 cm
\(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 5 cm/sec
Area of the circle, A = πr²
Differentiating on A with respect to ‘t’
\(\frac{\mathrm{dA}}{\mathrm{dt}}=\pi .2 \mathrm{r}, \frac{\mathrm{dr}}{\mathrm{dt}}\)
= 2π (8) (5)
= 80π cm2/sec

Question 12.
The radius of a circle is increasing at the rate of 0.7 cm/sec. What is the rate of increase in its circumference?
Solution:
Let r be the radius and P be the circumference of a circle.
Given, \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 0.7 cm/sec
Circumference of a circle, P = 2πr
Differentiating P on both sides with respect to ‘t’
\(\frac{\mathrm{dp}}{\mathrm{dt}}=2 \pi \cdot \frac{\mathrm{dr}}{\mathrm{dt}}\)
= 2π(0.7)
= 1.4π cm/sec
∴ Rate of increase of circumference of circle = 1.4π cm/sec.

Question 13.
A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic cm of gas per sec. Find the rate at which the radius of the balloon increases when the radius is 15 cm.
Solution:
Let r be the radius and V be the volume of the spherical balloon.
Given, \(\frac{\mathrm{dV}}{\mathrm{dt}}\) = 900 cu.cm/sec
radius, r = 15 cm
Volume of the spherical balloon, V = \(\frac{4}{3} \pi r^3\)
Differentiating on both sides with respect to ‘t’

∴ Rate of increase of radius of the balloon \(\frac{\mathrm{dr}}{\mathrm{dt}}=\frac{1}{\pi}\) cm/sec

Question 14.
The radius of an air bubble is increasing at the rate of \(\frac{1}{2}\) cubic. cm/sec. At what rate is the volume of the bubble increasing when the radius is 1 cm?
Solution:
Let r be the radius and V be the volume of an air bubble.
Given, \(\frac{\mathrm{dr}}{\mathrm{dt}}=\frac{1}{2}\) cm/sec
radius, r = 1 cm
Volume of a air bubble, V = \(\frac{4}{3} \pi r^3\)
Differentiating on both sides with respect to ‘t’

∴ The volume of the air bubble increasing at r = 1 cm is 2π cu. cm/sec.

Question 15.
Let a kind of bacteria grow in such a way that at time t sec. There are \(\mathbf{t}^{3 / 2}\) bacteria. Find the rate of growth at time t = 4 hours.
Solution:
Let g be the amount of growth of bacteria at t sec.
Let g(t) = \(\mathbf{t}^{3 / 2}\)

Question 16.
Let a kind of bacteria grow by t³ (t in sec). At what time the rate of growth of the bacteria is 300 bacteria per sec?
Solution:
Let g be the amount of growth of bacteria at t sec.
Then g(t) = t³
Now, the growth rate at time ‘t’ is g'(t) = 3t²
Given, the rate of growth of the bacteria is 300 per sec.
3t² = 300
t² = 100
t = 10 sec.
∴ After t = 10 sec, the growth rate of bacteria should be 300 bacteria/sec.

Question 17.
Suppose we have a rectangular aquarium with dimensions of length 8m, width 4m, and height 3m. Suppose we are filling the tank with water at a rate of 0.4 m³/sec. How fast is the height of water changing when the water level is 2.5 m?
Solution:
Let h be the height of the water level in the aquarium at the time t.
Given that length, l = 8 m
breadth (or) width, b = 4 cm
height, h = 3 m
Volume of the aquarium, V = lbh
V = 8 . 4 . 3 = 96 cu.m.
Given, \(\frac{\mathrm{dV}}{\mathrm{dt}}\) = 0.4 cu.m/sec
height, h = 2.5 m
volume of aquarium, V = lbh
log V = log(lbh)
log V = log l + log b + log h
Differentiating with respect to ‘t’


(Or)
Let h be the height of the water level in the aquarium at the volume of the aquarium,
V = lbh = 8 . 4 . h = 32h …….(1)
Given that, \(\frac{\mathrm{dV}}{\mathrm{dt}}\) = 0.4 cu.cm/sec
height, h = 2.5 m
Differentiating on both sides with respect to ‘t’

The weight of water changes at the rate of \(\frac{1}{80}\) m.sec.

Question 18.
The total cost c(x) in rupees associated with the production of x units of an item is given by c(x) = 0.007x³ – 0.003x² + 15x + 4000. Find the marginal cost when 17 units are produced.
Solution:
Let M represent the marginal cost.
Given, c(x) = 0.007x³ – 0.003x² + 15x + 4000
The rate of change of total cost is M = \(\frac{\mathrm{dc}}{\mathrm{dx}}\)
= (0.007)(3x²) – 0.003(2x) + 15(1) + (0)
= 0.021x² – 0.006x + 15
∴ The marginal cost at x = 17 is \(\left(\frac{d c}{d x}\right)_{x=17}\)
= (0.021)(17)² – 0.006(17) + 15
= (0.021)(289) – 0.102 + 15
= 20.967

Question 19.
The total cost c(x) in rupees associated with the production of x units of an item is given by c(x) = 0.005x³ – 0.02x² + 30x + 500. Find the marginal cost when 3 units are produced (marginal cost is the rate of change of total cost). [May ’15 (AP)]
Solution:
Given relation c(x) = 0.005x³ – 0.02x² + 30x + 500
\(\frac{\mathrm{dc}}{\mathrm{dx}}\) = (0.005)(3x²) – 0.02(2x) + 30(1)
= (0.015)x² – 0.04x + 30
∴ Marginal cost = \(\left(\frac{\mathrm{dc}}{\mathrm{dx}}\right)_{\mathrm{x}=3}\)
= (0.015) (3)² – 0.04(3) + 30
= (0.015) (9) – 0.04 (3) + 30
= 0.135 – 0.12 + 30
= 30.015

Students must practice these TS Inter 1st Year Maths 1B Study Material Chapter 8 Limits and Continuity Ex 8(e) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Limits and Continuity 8(e)

Question 1.
Is the function f, defined by

continuous on R? (V.S.A.Q.) (May 2011)
Answer:

The function is continuous at ‘1’ hence at continuous on R.

Question 2.
Is f defined by

continuous at ‘0’ (V.S.A.Q.) (May 2012)
Answer:
Given f(0) = 1

Hence f is continuous at ‘0’.

Question 3.
Show that the function
f(x) = [cos(x¹⁰ + 1)]^{\(\frac{1}{3}\)}; x ∈ ℛ is a continuous function. (V.S.A.Q.)
Answer:
Since cos x is continuous for every x ∈ R, we have f(x) = [cos (x¹⁰ + 1)]^1/3 is also continuous over R.

II.
Question 1.
Check the continuity of the following function at 2. (S.A.Q.)

Answer:
Given f(2) = 0

Hence f(x) is not continuous at x = 2.

Question 2.
Check the continuity of f given by (S.A.Q.) (Mar. ’14, ’13)

Answer:
Given f(3) = 1.5 and

Since \(\lim _{x \rightarrow 3}\) f(x) = f(3) we have f is continuous at the point ‘3’.

Question 3.
Show that f given by f(x) = \(\frac{\mathbf{x}-|\mathbf{x}|}{\mathbf{x}}\) (x ≠ 0) is continuous on R – {0}. (S.A.Q.)
Answer:

In both the cases \(\lim _{x \rightarrow a}\) f(x) = f(a)
But if a = 0 then f(0) is not defined f(x) is not continuous at ‘0’.
Hence f(x) is continuous on R – {0}

Question 4.
If f is a function defined by (S.A.Q.)

then discuss the continuity of f.
Answer:

Question 5.
If f is given by

is a continuous function on R, then find the values of ‘k’. (S.A.Q.)
Answer:

Given that f is continuous on R, then it is continuous at ‘1’.
∴ k² – k = 2 ⇒ k² – k – 2 = 0
⇒ (k – 2) (k + 1) = 0
⇒ k = 2 or k = – 1

Question 6.
Prove that the function ‘sin x’ and ‘cos x’ are continuous on R. (S.A.Q.)
Answer:
(i) Let f(x) = sin x
If f is continuous at a point ‘a’ then
\(\lim _{x \rightarrow \mathrm{a}}\) f(x) = f(a)
∴ \(\lim _{x \rightarrow \mathrm{a}}\) (sin x) = sin a = f(a)
(or) by definition we have for ∈ > 0, ∃ a δ > 0
such that |sin x – sin a| < E for |x – a| < δ

Hence f(x) = sin x is continuous at ‘a’
Hence f is continuous over R.

(ii) f(x) = cos x
Let a ∈ R,
∴ \(\lim _{x \rightarrow a}\) f(x) = \(\lim _{x \rightarrow a}\) (cos x) = cos a = f(a)
∴ f is continuous at ‘a’
Hence f is continuous over R.

III.
Question 1.
Check the continuity of f given by

at the point 0, 1 and 2.
Answer:

Question 2.
Find real constants a, b so that the function f given by

is continuous on R
Answer:
Given f is continuous over R ⇒ f is continuous at 0, 1 and 3.
If f is continuous at ‘0’ then

∴ In all cases if f is continuous at 0, 1, 3 and continuous over R.
The values are a = 0,
b = – 2.

Question 3.
Show that

where a and b are real constants, is continuous at ‘0’. (Board New Model Paper) (E.Q.)
Answer:

Students must practice these TS Inter 1st Year Maths 1B Study Material Chapter 8 Limits and Continuity Ex 8(d) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Limits and Continuity 8(d)

Compute the following limits.

Question 1.
\(\lim _{x \rightarrow 3}\left(\frac{x^2+3 x+2}{x^2-6 x+9}\right)\) (V.S.A.Q.)
Answer:

Question 2.
\(\lim _{x \rightarrow 1}\left(\frac{1+5 x^3}{1-x^2}\right)\) (V.S.A.Q.)
Answer:

Question 3.
\(\lim _{x \rightarrow \infty}\left(\frac{3 x^2+4 x+5}{2 x^3+3 x-7}\right)\) (V.S.A.Q.)
Answer:

Question 4.
\(\lim _{x \rightarrow \infty}\left(\frac{6 x^2-x+7}{x+3}\right)\) (V.S.A.Q.)
Answer:

Question 5.
\(\lim _{x \rightarrow \infty}\) (e^-x2 (V.S.A.Q.)
Answer:

Question 6.
\(\lim _{x \rightarrow \infty}\left(\frac{\sqrt{x^2+6}}{2 x^2-1}\right)\) (V.S.A.Q.)
Answer:

II.
Question 1.
\(\lim _{x \rightarrow \infty} \frac{8|x|+3 x}{3|x|-2 x}\) (S.A.Q.) [March 2012]
Answer:

Question 2.
\(\lim _{x \rightarrow \infty}\left(\frac{x^2+5 x+2}{2 x^2-5 x+1}\right)\) (May 2014) (S.A.Q.)
Answer:

Question 3.
\(\lim _{x \rightarrow-\infty}\left(\frac{2 x^2-x+3}{x^2-2 x+5}\right)\) (S.A.Q.)
Answer:

Question 4.
\(\lim _{x \rightarrow \infty}\left(\frac{11 x^3-3 x+4}{13 x^3-5 x^2-7}\right)\) (V.S.A.Q.)
Answer:

Question 5.
\(\lim _{x \rightarrow 2}\left(\frac{1}{x-2}-\frac{4}{x^2-4}\right)\) (S.A.Q.)
Answer:

Question 6.
\(\lim _{x \rightarrow-\infty} \frac{5 x^3+4}{\sqrt{2 x^4+1}}\) (S.A.Q.)
Answer:

Question 7.
\(\lim _{x \rightarrow \infty}\) (√x + 1 – √x) (S.A.Q.)
Answer:

Question 8.
\(\lim _{x \rightarrow \infty}\) (\(\sqrt{x^2+x}\) – x) (S.A.Q.) [March 2011]
Answer:

III.
Question 1.
\(\lim _{x \rightarrow-\infty}\left(\frac{2 x+3}{\sqrt{x^2-1}}\right)\) (S.A.Q.)
Answer:

Question 2.
\(\lim _{x \rightarrow \infty}\left(\frac{2+\sin x}{x^2+3}\right)\) (E.Q.)
Answer:
\(\lim _{x \rightarrow \infty} \frac{2+\sin x}{x^2+3}\)
We have – 1 ≤ sin x ≤ 1
⇒ 2 – 1 ≤ 2 + sin x ≤ 2 + 1
⇒ 1 ≤ 2 + sin x ≤ 3

Question 3.
\(\lim _{x \rightarrow \infty}\left(\frac{2+\cos ^2 x}{x+2007}\right)\) (E.Q.)
Answer:

Question 4.
\(\lim _{x \rightarrow \infty}\left(\frac{6 x^2-\cos 3 x}{x^2+5}\right)\) (V.S.A.Q.)
Answer:

Question 5.
\(\lim _{x \rightarrow \infty}\left(\frac{\cos x+\sin ^2 x}{x+1}\right)\) (E.Q.)
Answer:
We know that – 1 ≤ cos x ≤ 1 and 0 ≤ sin² x ≤ 1
∴ – 1 + 0 ≤ cos x + sin² x ≤ 2