TS Inter 1st Year Maths 1B Solutions Chapter 8 Limits and Continuity Ex 8(e)

Students must practice these TS Inter 1st Year Maths 1B Study Material Chapter 8 Limits and Continuity Ex 8(e) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Limits and Continuity 8(e)

Question 1.
Is the function f, defined by

continuous on R? (V.S.A.Q.) (May 2011)
Answer:

The function is continuous at ‘1’ hence at continuous on R.

Question 2.
Is f defined by

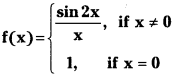
continuous at ‘0’ (V.S.A.Q.) (May 2012)
Answer:
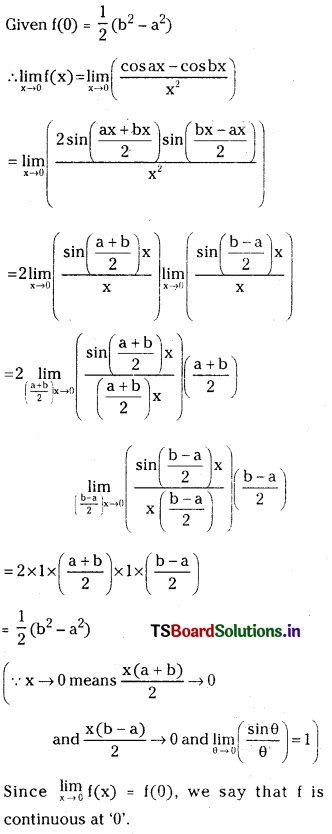
Given f(0) = 1

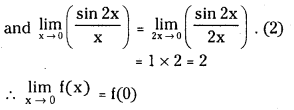
Hence f is continuous at ‘0’.

Question 3.
Show that the function
f(x) = [cos(x¹⁰ + 1)]^{\(\frac{1}{3}\)}; x ∈ ℛ is a continuous function. (V.S.A.Q.)
Answer:
Since cos x is continuous for every x ∈ R, we have f(x) = [cos (x¹⁰ + 1)]^1/3 is also continuous over R.

II.
Question 1.
Check the continuity of the following function at 2. (S.A.Q.)

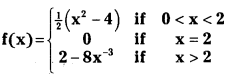
Answer:
Given f(2) = 0

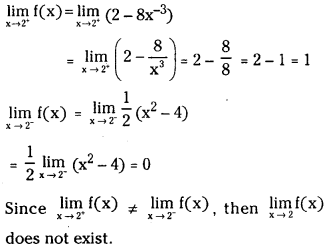
Hence f(x) is not continuous at x = 2.

Question 2.
Check the continuity of f given by (S.A.Q.) (Mar. ’14, ’13)

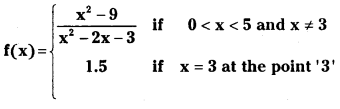
Answer:
Given f(3) = 1.5 and

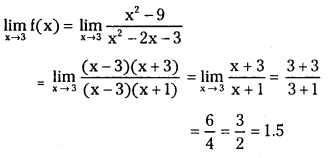
Since \(\lim _{x \rightarrow 3}\) f(x) = f(3) we have f is continuous at the point ‘3’.

Question 3.
Show that f given by f(x) = \(\frac{\mathbf{x}-|\mathbf{x}|}{\mathbf{x}}\) (x ≠ 0) is continuous on R – {0}. (S.A.Q.)
Answer:

In both the cases \(\lim _{x \rightarrow a}\) f(x) = f(a)
But if a = 0 then f(0) is not defined f(x) is not continuous at ‘0’.
Hence f(x) is continuous on R – {0}

Question 4.
If f is a function defined by (S.A.Q.)

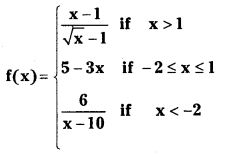
then discuss the continuity of f.
Answer:

Question 5.
If f is given by

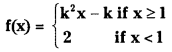
is a continuous function on R, then find the values of ‘k’. (S.A.Q.)
Answer:

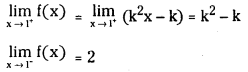
Given that f is continuous on R, then it is continuous at ‘1’.
∴ k² – k = 2 ⇒ k² – k – 2 = 0
⇒ (k – 2) (k + 1) = 0
⇒ k = 2 or k = – 1

Question 6.
Prove that the function ‘sin x’ and ‘cos x’ are continuous on R. (S.A.Q.)
Answer:
(i) Let f(x) = sin x
If f is continuous at a point ‘a’ then
\(\lim _{x \rightarrow \mathrm{a}}\) f(x) = f(a)
∴ \(\lim _{x \rightarrow \mathrm{a}}\) (sin x) = sin a = f(a)
(or) by definition we have for ∈ > 0, ∃ a δ > 0
such that |sin x – sin a| < E for |x – a| < δ

Hence f(x) = sin x is continuous at ‘a’
Hence f is continuous over R.

(ii) f(x) = cos x
Let a ∈ R,
∴ \(\lim _{x \rightarrow a}\) f(x) = \(\lim _{x \rightarrow a}\) (cos x) = cos a = f(a)
∴ f is continuous at ‘a’
Hence f is continuous over R.

III.
Question 1.
Check the continuity of f given by

at the point 0, 1 and 2.
Answer:

Question 2.
Find real constants a, b so that the function f given by

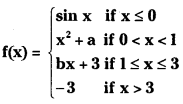
is continuous on R
Answer:
Given f is continuous over R ⇒ f is continuous at 0, 1 and 3.
If f is continuous at ‘0’ then

∴ In all cases if f is continuous at 0, 1, 3 and continuous over R.
The values are a = 0,
b = – 2.

Question 3.
Show that

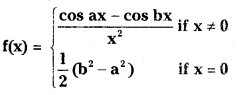
where a and b are real constants, is continuous at ‘0’. (Board New Model Paper) (E.Q.)
Answer: