TS Inter 1st Year Maths 1B Rate Measure Important Questions

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Rate Measure Important Questions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Rate Measure Important Questions

Question 1.
The distance-time formula for the motion of a particle along a straight line is s = t³ – 9t² + 24t – 18. Find when and where the velocity is zero. [Mar. ’19 (AP); Mar. ’12; May ’96]
Solution:
Given, s = t³ – 9t² + 24t – 18
Velocity, v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\)
= 3t² – 9(2t) + 24(1) – 0
= 3t² – 18t + 24
Given, the particle comes to rest then the velocity = 0
3t² – 18t + 24 = 0
t² – 6t + 8 = 0
t² – 4t – 2t + 8 = 0
t(t – 4) – 2(t – 4) = 0
(t – 4) (t – 2) = 0
t – 4 = 0 (or) t – 2 = 0
t = 4 (or) t = 2
t = 2, 4
The velocity is zero when t = 2 sec and 4 sec.
Case 1:
If t = 2 sec, then s = t³ – 9t² + 24t – 18
= (2)³ – 9(2)² + 24(2) – 18
= 8 – 36 + 48 – 18
= 2 units
Case 2:
If t = 4 sec, then s = (4)³ – 9(4)² + 24(4) – 18
= 64 – 144 + 96 – 18
= 160 – 162
= -2 units
∴ The particles are at a distance of two units from the starting point ‘0’ on either side.

Question 2.
The displacement s of a particle travelling in a straight line in ‘t’ seconds is given by s = 45t + 11t² – t³, finding the time when the particle comes to rest. [May ’13 (Old), ’06; Mar. ’07]
Solution:
Given, s = 45t + 11t² – t³
Velocity, v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\)
= 45(1) + 11(2t) – 3t²
= 45 + 22t – 3t²
The particle comes to rest then velocity, v = 0
45 + 22t – 3t² = 0
3t² – 22t – 45 = 0
3t² – 27t + 5t – 45 = 0
3t(t – 9) + 5(t – 9) = 0
(t – 9) (3t + 5) = 0
t – 9 = 0 (or) 3t + 5 = 0
t = 9 (or) t = \(\frac{-5}{3}\)
t = 9 Since t is positive then t = 9
∴ The particle comes to rest when t = 9 sec.

Question 3.
A particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line given by s = f(t) = 8t + t³. Find
(i) the velocity at time t = 2 sec [Mar. ’17, ’15 (AP)]
(ii) the initial velocity
(iii) acceleration at t = 2 sec [May ’12; B.P.]
Solution:
The distance s and time t are connected by the relation s = f(t) = 8t + t³
Velocity, v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\)
= 8(1) + 3t²
= 8 + 3t²
(i) Velocity at t = 2 sec, then,
v = \(\left(\frac{\mathrm{ds}}{\mathrm{dt}}\right)_{\mathrm{t}=2}\)
= 8 + 3(2)²
= 8 + 12
= 20 cm/sec
acceleration, a = \(\frac{\mathrm{dv}}{\mathrm{dt}}\)
= 0 + 3(2t)
= 6t
(ii) Initial velocity (t = 0) is v = \(\left(\frac{\mathrm{ds}}{\mathrm{dt}}\right)_{\mathrm{t}=0}\)
= 8 + 3(0)²
= 8 cm/sec
(iii) The acceleration at t = 2 sec, then
a = \(\left(\frac{\mathrm{dv}}{\mathrm{dt}}\right)_{\mathrm{t}=2}\)
= 6(2)
= 12 cm/sec²

Question 4.
A container is in the shape of an inverted cone and has a height of 8 cm and a radius of 6 m at the top. If it is filled with water at the rate of 2 m³/minute, how fast height of the water change when the level is 4m? [Mar. ’19 (TS): May ’13. ’11, ’09; Mar. ’08, ’06]
Solution:
Let h be the height, r be the radius of the water level and V be the volume of the water in the container at the time ‘t’.
Given that, \(\frac{d v}{d t}\) = 2m3/min.


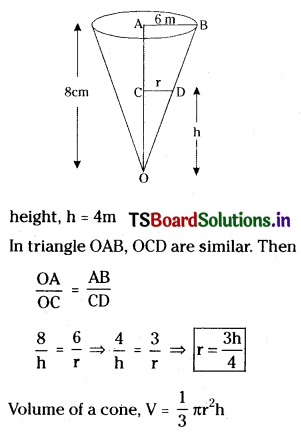
∴ The height of the water changes at a rate of \(\frac{2}{9 \pi}\) m/min.

Question 5.
The volume of a cube is increasing at a rate of 9 cubic centimeters per second. How fast is the surface area increasing when the length of the edge is 10 centimeters? [Mar. ’17 (TS), ’16 (AP), ’13; May ’15 (TS)]
Solution:
Let x be the length of the edge of the cube.
V is its volume and S is its surface area.
Given that rate of change of volume
\(\frac{\mathrm{dv}}{\mathrm{dt}}\) = 9 cm³/sec
x = 10 cm
The volume of a cube, V = x³
Differentiating v with respect to ‘t’, we get

Question 6.
A point P is moving on the curve y = 2x². The x coordinate of P is increasing at the rate of 4 units per second. Find the rate at which the y-coordinate is increasing when the point is at (2, 8). [Mar. ’16 (TS), ’13; May ’08]
Solution:
Let P(x, y) be any point on the curve y = 2x²
Given, \(\frac{\mathrm{dx}}{\mathrm{dt}}\) = 4 units/sec
Given point (x, y) = (2, 8)
Now, y = 2x²
Differentiating on both sides with respect to ‘t’
\(\frac{\mathrm{dy}}{\mathrm{dt}}=2(2 \mathrm{x}) \cdot \frac{\mathrm{dx}}{\mathrm{dt}}\)
= 4(2) . 4
= 32 units/sec
∴ The y-coordinate is increasing at the rate of 32 units/sec.

Some More Maths 1B Rate Measure Important Questions

Question 7.
A container in the shape of an inverted cone has a height of 12 cm and a radius of 6 cm at the top. If it is filled with water at the rate of 12 cm³/sec. What is the rate of change in the height of the water level when the tank is filled 8 cm?
Solution:
Let h be the height, r be the radius of the water level and v be the volume of water in the container at a time ‘t’.

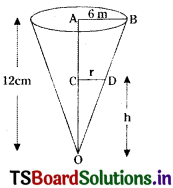
Given, \(\frac{\mathrm{dV}}{\mathrm{dt}}\) = 12 cm³/sec
height, h = 8 cm
In triangle OAB, OCD are similar, then


Hence the rate of change of water level is \(\frac{3}{4 \pi}\) cm/sec when the water level of the tank is 8 cm.

Question 8.
The volume of a cube is increasing at the rate of 8 cm3/sec. How fast is the surface area increasing when the length of an edge is 12 cm?
Solution:
Let x be the length of the edge of the cube, V be its volume and S be its surface area.
Given that, the rate of change in volume \(\frac{\mathrm{dV}}{\mathrm{dt}}\) = 8 cm³/sec
x = 12 cm
The volume of a cube V = x³
Differentiating V on with respect to ‘t’, we get

Question 9.
A particle moving along straight has the relation s = t³ + 2t + 3, connecting the distance s described by the particle in time t. Find the velocity and acceleration of the particle at t = 4 seconds.
Solution:
Given, s = t³ + 2t + 3
velocity, v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\)
= 3t² + 2 + 0
= 3t² + 2
velocity at t = 4 sec, then, v = \(\left(\frac{\mathrm{ds}}{\mathrm{dt}}\right)_{t=4}\)
= 3(4)² + 2
= 50 units/sec
acceleration, a = \(\frac{\mathrm{dv}}{\mathrm{dt}}\)
= 3(2t) + 0
= 6t
acceleration at t = 4, then
a = \(\left(\frac{\mathrm{dv}}{\mathrm{dt}}\right)_{\mathrm{t}=4}\)
= 6(4)
= 24 units/sec²

Question 10.
A particle is moving along a line according to s = f(t) = 4t³ – 3t² + 5t – 1 where s is measured in metres and t is measured in seconds. Find the velocity and acceleration at time t. At what time the acceleration is zero? [Mar. ’18 (AP); Mar. ’18, ’15 (TS)]
Solution:
Given, s = f(t) = 4t³ – 3t² + 5t – 1
velocity, v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\)
= 4(3t²) – 3(2t) + 5(1) – 0
= 12t² – 6t + 5
acceleration, a = \(\frac{d v}{d t}\)
= 12(2t) – 6(1) + 0
= 24t – 6
∴ Acceleration is 0 if 24t – 6 = 0
24t = 6
t = \(\frac{1}{4}\) sec
∴ Acceleration of particle is 0 at t = \(\frac{1}{4}\) sec

Question 11.
A stone is dropped into a quiet lake and ripples move in circles at speed of 5 cm/sec. At the instant when the radius of the circular ripple is 8 cm, how fast is the enclosed area increased?
Solution:
Let A be the area of the circle with radius ‘r’.
Given, radius, r = 8 cm
\(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 5 cm/sec
Area of the circle, A = πr²
Differentiating on A with respect to ‘t’
\(\frac{\mathrm{dA}}{\mathrm{dt}}=\pi .2 \mathrm{r}, \frac{\mathrm{dr}}{\mathrm{dt}}\)
= 2π (8) (5)
= 80π cm2/sec

Question 12.
The radius of a circle is increasing at the rate of 0.7 cm/sec. What is the rate of increase in its circumference?
Solution:
Let r be the radius and P be the circumference of a circle.
Given, \(\frac{\mathrm{dr}}{\mathrm{dt}}\) = 0.7 cm/sec
Circumference of a circle, P = 2πr
Differentiating P on both sides with respect to ‘t’
\(\frac{\mathrm{dp}}{\mathrm{dt}}=2 \pi \cdot \frac{\mathrm{dr}}{\mathrm{dt}}\)
= 2π(0.7)
= 1.4π cm/sec
∴ Rate of increase of circumference of circle = 1.4π cm/sec.

Question 13.
A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic cm of gas per sec. Find the rate at which the radius of the balloon increases when the radius is 15 cm.
Solution:
Let r be the radius and V be the volume of the spherical balloon.
Given, \(\frac{\mathrm{dV}}{\mathrm{dt}}\) = 900 cu.cm/sec
radius, r = 15 cm
Volume of the spherical balloon, V = \(\frac{4}{3} \pi r^3\)
Differentiating on both sides with respect to ‘t’

∴ Rate of increase of radius of the balloon \(\frac{\mathrm{dr}}{\mathrm{dt}}=\frac{1}{\pi}\) cm/sec

Question 14.
The radius of an air bubble is increasing at the rate of \(\frac{1}{2}\) cubic. cm/sec. At what rate is the volume of the bubble increasing when the radius is 1 cm?
Solution:
Let r be the radius and V be the volume of an air bubble.
Given, \(\frac{\mathrm{dr}}{\mathrm{dt}}=\frac{1}{2}\) cm/sec
radius, r = 1 cm
Volume of a air bubble, V = \(\frac{4}{3} \pi r^3\)
Differentiating on both sides with respect to ‘t’

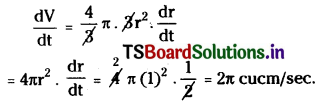
∴ The volume of the air bubble increasing at r = 1 cm is 2π cu. cm/sec.

Question 15.
Let a kind of bacteria grow in such a way that at time t sec. There are \(\mathbf{t}^{3 / 2}\) bacteria. Find the rate of growth at time t = 4 hours.
Solution:
Let g be the amount of growth of bacteria at t sec.
Let g(t) = \(\mathbf{t}^{3 / 2}\)

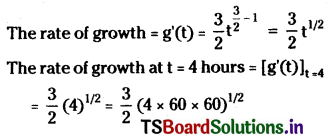
Question 16.
Let a kind of bacteria grow by t³ (t in sec). At what time the rate of growth of the bacteria is 300 bacteria per sec?
Solution:
Let g be the amount of growth of bacteria at t sec.
Then g(t) = t³
Now, the growth rate at time ‘t’ is g'(t) = 3t²
Given, the rate of growth of the bacteria is 300 per sec.
3t² = 300
t² = 100
t = 10 sec.
∴ After t = 10 sec, the growth rate of bacteria should be 300 bacteria/sec.

Question 17.
Suppose we have a rectangular aquarium with dimensions of length 8m, width 4m, and height 3m. Suppose we are filling the tank with water at a rate of 0.4 m³/sec. How fast is the height of water changing when the water level is 2.5 m?
Solution:
Let h be the height of the water level in the aquarium at the time t.
Given that length, l = 8 m
breadth (or) width, b = 4 cm
height, h = 3 m
Volume of the aquarium, V = lbh
V = 8 . 4 . 3 = 96 cu.m.
Given, \(\frac{\mathrm{dV}}{\mathrm{dt}}\) = 0.4 cu.m/sec
height, h = 2.5 m
volume of aquarium, V = lbh
log V = log(lbh)
log V = log l + log b + log h
Differentiating with respect to ‘t’


(Or)
Let h be the height of the water level in the aquarium at the volume of the aquarium,
V = lbh = 8 . 4 . h = 32h …….(1)
Given that, \(\frac{\mathrm{dV}}{\mathrm{dt}}\) = 0.4 cu.cm/sec
height, h = 2.5 m
Differentiating on both sides with respect to ‘t’

The weight of water changes at the rate of \(\frac{1}{80}\) m.sec.

Question 18.
The total cost c(x) in rupees associated with the production of x units of an item is given by c(x) = 0.007x³ – 0.003x² + 15x + 4000. Find the marginal cost when 17 units are produced.
Solution:
Let M represent the marginal cost.
Given, c(x) = 0.007x³ – 0.003x² + 15x + 4000
The rate of change of total cost is M = \(\frac{\mathrm{dc}}{\mathrm{dx}}\)
= (0.007)(3x²) – 0.003(2x) + 15(1) + (0)
= 0.021x² – 0.006x + 15
∴ The marginal cost at x = 17 is \(\left(\frac{d c}{d x}\right)_{x=17}\)
= (0.021)(17)² – 0.006(17) + 15
= (0.021)(289) – 0.102 + 15
= 20.967

Question 19.
The total cost c(x) in rupees associated with the production of x units of an item is given by c(x) = 0.005x³ – 0.02x² + 30x + 500. Find the marginal cost when 3 units are produced (marginal cost is the rate of change of total cost). [May ’15 (AP)]
Solution:
Given relation c(x) = 0.005x³ – 0.02x² + 30x + 500
\(\frac{\mathrm{dc}}{\mathrm{dx}}\) = (0.005)(3x²) – 0.02(2x) + 30(1)
= (0.015)x² – 0.04x + 30
∴ Marginal cost = \(\left(\frac{\mathrm{dc}}{\mathrm{dx}}\right)_{\mathrm{x}=3}\)
= (0.015) (3)² – 0.04(3) + 30
= (0.015) (9) – 0.04 (3) + 30
= 0.135 – 0.12 + 30
= 30.015