TS Inter 1st Year Maths 1B Mean Value Theorems Important Questions

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Mean Value Theorems Important Questions to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Mean Value Theorems Important Questions

Question 1.
Verify Rolle’s theorem for the function y = f(x) = x² + 4 in [-3, 3]. [Mar. ’19 (TS); Mar. ’17 (AP), ’15 (TS); B.P.; May ’15 (TS)]
Solution:
f is a polynomial function that is continuous and differentiable in [-3, 3]
Given f(x) = x² + 4
∴ f(-3) = (-3)² + 4 = 13
and f(3) = 3² + 4 = 13
∴ f(-3) = f(3).
Hence the function satisfies the conditions of Rolle’s theorem and f'(x) = 2x
∴ f'(c) = 2c = 0
c = 0 ∈ (-3, 3)
Thus Roll’s theorem is verified.

Question 2.
Verify Rolle’s theorem for the following function x² – 1 on [-1, 1]. [Mar. ’14; May ’13]
Solution:
Let f(x) = x² – 1 defined on [-1, 1].
Since the function f(x) is a polynomial, it is continuous on [-1, 1] and differentiable on (-1, 1).
Also f(1) = 1 – 1 = 0,
f(-1) = (-1)² – 1 = 0
f(-1) = f(1).
Hence f satisfies all conditions of Rolle’s theorem.
Now we have to find a point c ∈ (-1, 1) such that f'(c) = 0, f'(x) = 2x
and f'(c) = 0
2c = 0
c = 0 ∈ (-1, 1)
Hence Rolle’s theorem is verified.

Question 3.
Let f(x) = (x – 1) (x – 2) (x – 3). Prove that there is more than one ‘c’ in (1, 3) such that f'(c) = 0. [Mar. ’13]
Solution:
f is a polynomial in x which is continuous over [1, 3] and derivable over (1, 3).
Given f(x) = (x – 1) (x – 2) (x – 3)
We have f'(x) = (x – 1) (x – 2) + (x – 2) (x – 3) + (x – 1) (x – 3)
= x² – 3x + 2 + x² – 5x + 6 + x² – 4x + 3
= 3x² – 12x + 11
f'(c) = 0
3c² – 12c + 11 = 0
c = \(\frac{12 \pm \sqrt{144-132}}{6}\) = 2 ± \(\frac{1}{\sqrt{3}}\)
2 + \(\frac{1}{\sqrt{3}}\) ∈ (1, 3) and 2 – \(\frac{1}{\sqrt{3}}\) ∈ (1, 3)
∴ There exists more than one ‘c’ in (1, 3) such that f'(c) = 0.

Question 4.
Verify Rolle’s theorem for the function f(x) = x(x + 3) \(\mathrm{e}^{-\mathrm{x} / 2}\) in [-3, 0]. [Mar. ’18 (AP)]
Solution:
f is continuous in [-3, 0] and differentiable in (-3, 0).
Also f(-3) = (-3) (-3 + 3) e^3/2 = 0
f(0) = 0 (0 . 3) e^3/2 = 0
∴ f(-3) = f (0)
So f satisfies the conditions of Rolle’s theorem.
Given f(x) = x(x + 3) e^3/2
Then f'(x) = x(x + 3) \(\left(\frac{-1}{2}\right) \mathrm{e}^{-\mathrm{x} / 2}\) + \(x\left(e^{\frac{-x}{2}}\right)+(x+3) e^{\frac{-x}{2}}\)

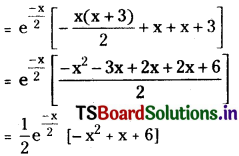
f'(e) = 0
-e² + e + 6 = 0
e = -2 or 3
Now -2 ∈ (- 3, 0) and c = -2
∴ Rolle’s theorem was verified.

Question 5.
Verify Lagrange’s mean value theorem for the function f(x) = x² on [2, 4].
Solution:
Being a polynomial function
(i) f(x) = x² is continuous on [2, 4] and
(ii) differentiable in (2, 4)
By Lagrange’s theorem there should exist c ∈ (2, 4) such

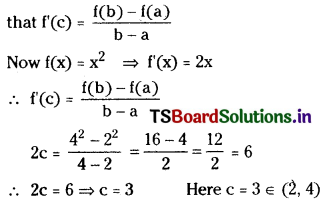
Hence Lagrange’s theorem is verified.

Question 6.
On the curve y = x², find a point at which the tangent is parallel to the chord joining (0, 0) and (1, 1).
Solution:
The slope of the chord joining (0, 0) and (1, 1) is
m₁ = \(\frac{1-0}{1-0}\) = 1
Given curve is y = x²
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 2x
∴ The slope of the tangent at any point on the curve is m₂ = 2x
If the tangent is parallel to the chord, then m₁ = m₂
2x = 1
x = \(\frac{1}{2}\)
Now, y = x² = \(\left(\frac{1}{2}\right)^2=\frac{1}{4}\)
∴ The required point on the curve is \(\left(\frac{1}{2}, \frac{1}{4}\right)\)

Question 7.
Verify Rolle’s Theorem for the following function sin x – sin 2x on [0, π].
Solution:
Let f(x) = sin x – sin 2x defined over [0, π].
f is continuous over [0, π] and differentiable over (0, π).
Also f(0) = 0 and f(π) = sin π – sin 2π = 0
f(0) = f(π) = 0
Hence f satisfies the conditions of Rolle’s theorem.
Also f'(x) = cos x – 2 cos 2x and f'(c) = 0
cos c – 2 cos 2c = 0
cos c = 2(2 cos²c – 1)
4 cos²c – cos c – 2 = 0

Hence conditions of Rolle’s theorem are verified.

Question 8.
Show that there is no real number k, for which the equation x² – 3x + k = 0 has two distinct roots in [0, 1].
Solution:
Let f(x) = x² – 3x + k and suppose there exist two different roots α, β (α < β).
Since f is a polynomial in x, it is continuous over [0, 1] and differentiable in (0, 1).
f is continuous over [α, β] and differentiable in (α, β).
Also f(α) = α² – 3α + k = 0 and
f(β) = β² – 3β + k = 0
∴ f(α) = f(β) = 0
∴ f satisfies the conditions of Rolle’s theorem.
Also f'(c) = 0
3c² – 3 = 0
c² = 1
c = ±1
This is a contradiction since 0 < α < c < β < 1
Hence there do not exist roots α, β in (0, 1).
So, there is no real number k for which the equation x² – 3x + k = 0 has two distinct roots in [0, 1].

Question 9.
Find a point on the graph of the curve y = (x – 3)² where the tangent is parallel to the chord joining (3, 0) and (4, 1).
Solution:
Let the points be A(3, 0) and B(4, 1)
Slope of chord AB = \(\frac{1-0}{4-3}\) = 1
Given y = (x – 3)²
\(\frac{d y}{d x}\) = 2(x – 3)
Slope of the chord 2(x – 3) = 1
2x = 7
x = \(\frac{7}{2}\)
∴ y = (x – 3)²
= \(\left(\frac{7}{2}-3\right)^2=\frac{1}{4}\)
∴ The point on the curve = \(\left(\frac{7}{2},\frac{1}{4}\right)\)

Question 10.
Find a point on the graph of the curve y = x³ where the tangent is parallel to the chord joining (1, 1) and (3, 27).
Solution:
Let the points be A(1, 1) and B(3, 27)

Question 11.
Find ‘c’ so that f'(c) = \(\frac{\mathbf{f}(\mathbf{b})-\mathbf{f}(\mathbf{a})}{b-\mathbf{a}}\) where f(x) = e^x; a = 0, b = 1.
Solution:

Question 12.
Verify Rolle’s theorem for the function (x² – 1) (x – 2) on [-1, 2]. Find a point in the interval where the derivative vanishes.
Solution:
Let f(x) = (x² – 1) (x – 2) = x³ – 2x² – x + 2 defined over [-1, 2].
f being a polynomial in ‘x’, it is continuous over [-1, 2] and differentiable over (-1, 2).
f(-1) = 0, f(2) = 0
∴ f(-1) = f(2)
∴ f satisfies all the conditions of Rolle’s theorem.
f(x) = 3x² – 4x – 1 and f'(c) = 0
3c² – 4c – 1 = 0

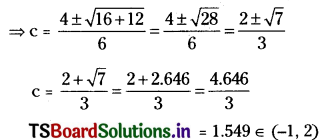
∴ Rolle’s theorem is verified.

Question 13.
Verify the conditions of Lagrange’s mean value theorem for the function x² – 1 on [2, 3]. [Mar. ’18 (TS); Mar. ’16 (AP)]
Solution:
Let f(x) = x² – 1 defined over [2, 3]. This is a polynomial in x, continuous on [2, 3] and differentiable over (2, 3).
So by Lagrange’s mean value theorem, there exists a point ‘c’ ∈ (2, 3) such that
f'(c) = \(\frac{\mathrm{f}(3)-\mathrm{f}(2)}{3-2}\)
f'(x) = 2x
f'(c) = 2c
f(3) = 8, f(2) = 3
∴ 2c = \(\frac{8-3}{1}\) = 5
c = \(\frac{5}{2}\) ∈ (2, 3)

Question 14.
Verify the conditions of Lagrange’s mean value theorem for the function sin x – sin 2x on [0, π].
Solution:
Let f(x) = sin x – sin 2x defined over [0, π].
This is continuous on [0, π] and differentiable over (0, π)
since f'(x) = cos x – 2 cos 2x exists for all x ∈ (0, π).
So by Lagrange’s mean value theorem
f'(c) = \(\frac{\mathrm{f}(\pi)-\mathrm{f}(0)}{\pi-0}\), f(π) = 0, f(0) = 0
∴ cos c – 2 cos 2c = \(\frac{0}{\pi}\) = 0
cos c – 2 cos 2c = 0
cos c – 2(2 cos²c – 1) = 0
4cos²c – cos c – 2 = 0
cos c = \(\frac{1 \pm \sqrt{1+32}}{8}=\frac{1 \pm \sqrt{33}}{8}\)
c = \(\cos ^{-1}\left(\frac{1+\sqrt{33}}{8}\right)\) ∈ (0, π)

Question 15.
Verify the conditions of Lagrange’s mean value theorem for the function log x on [1, 2].
Solution:
Let f(x) = log x defined over [1, 2].
This is continuous over [1, 2] and differentiable over (1, 2) since
f'(x)= \(\frac{1}{x}\) ∀ x ∈ (1, 2)

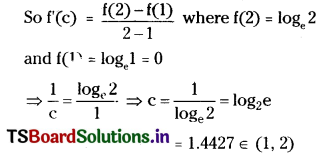
Hence Lagrange’s mean value theorem is satisfied.

Question 16.
Verify Rolle’s theorem for the function f : [-3, 8] → R be defined by f(x) = x² – 5x + 6. [Mar. ’17 (TS)]
Solution:
Given f(x) = x² – 5x + 6 defined on [-3, 8].
Since the function f(x) is a polynomial,
it is continuous on [-3, 8] and differentiable on [-3, 8)
Also f(-3) = (-3)² – 5(-3) + 6
= 9 + 15 + 6
= 30
f(8) = (8)² – 5(8) + 6
= 64 – 40 + 6
= 30
∴ f(-3) = f(8)
Hence f satisfies all conditions of Rolle’s theorem.
Now we have to find a point C ∈ (-3, 8) such that f'(C) = 0
f'(x) = 2x – 5 and f'(c) = 0
2C – 5 = 0
C = \(\frac{5}{2}\) ∈ (-3, 8)
Hence Rolle’s theorem is verified.