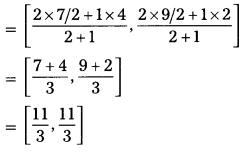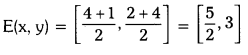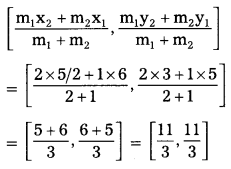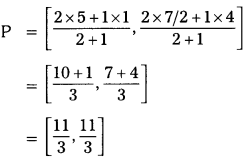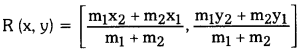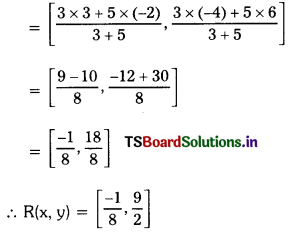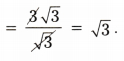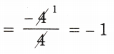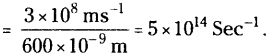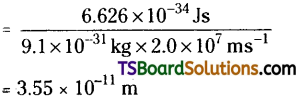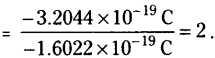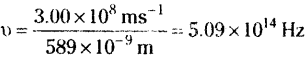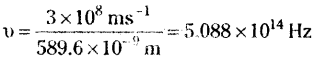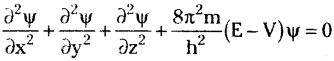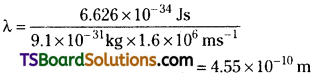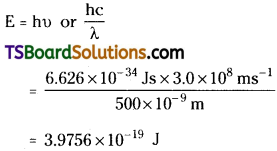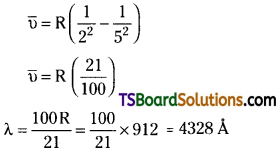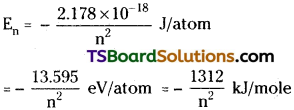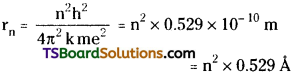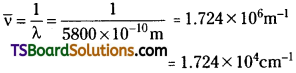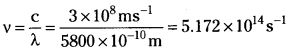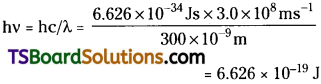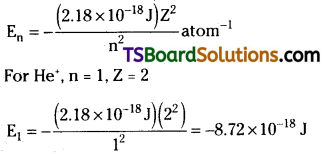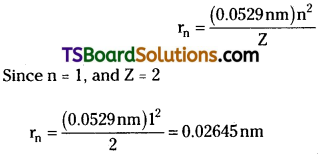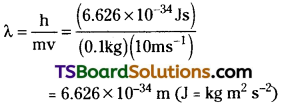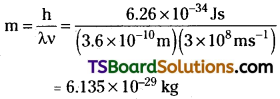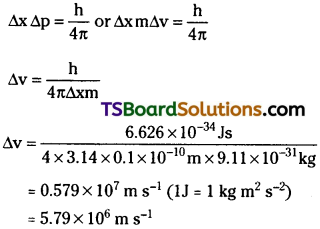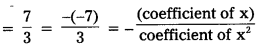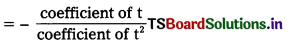Telangana TSBIE TS Inter 1st Year Chemistry Study Material 1st Lesson Atomic Structure Textbook Questions and Answers.
TS Inter 1st Year Chemistry Study Material 1st Lesson Atomic Structure
Very Short Answer Type Questions
Question 1.
What is the charge, mass and charge to mass ratio of an electron?
Answer:
i) Charge on electron
= – 1.602 × 10-19 coulomb or
– 4.8 × 10-10 e.s.u.
ii) Mass of electron
= 0.0005485 amu or
– 9.1 × 10-31 kg
iii) Charge-to-mass ratio
= -1.76 × 108 coulomb/gm or
= – 5.28 × 1017 e.s.u/gm
Question 2.
Calculate the charge of one mole of electrons.
Answer:
Charge of one mole of electrons
= 1.602 × 10-19 × 6.023 × 1023 coulomb
= 96500 coulomb
= 1 Faraday.
Question 3.
Calculate the mass of one mole of electrons.
Answer:
Mass of one mole of electrons
= 9.1 × 10-31 × 6.023 × 1023 kg
= 5.48 × 10-7 kg
Question 4.
Calculate the mass of one mole of protons.
Answer:
Mass of one mole of protons
= 1.672 × 10-27 × 6.023 × 1023 kg
= 1.007 × 10-3 kg
Question 5.
Calculate the mass of one mole of neutrons.
Answer:
Mass of one mole of neutrons = 1.675 × 10-27 × 6.023 × 1023
= 1.00885 × 10-3 kg

Question 6.
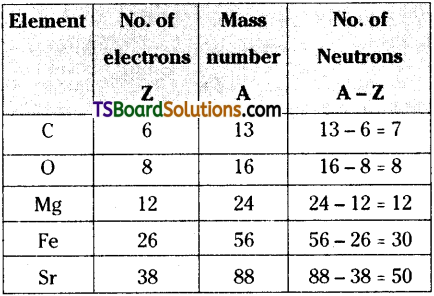
How many neutrons and electrons are present in the nuclei of

Answer:
Number of electrons is equal to atomic number Z.
Number of neutrons = Mass number (A) – Atomic number (Z).
Question 7.
What is a black body?
Answer:
The ideal body, which emits and absorbs all frequencies of radiations is called a black body’.
Question 8.
Which part of electromagnetic spectrum does Balmer series belong?
Answer:
The series of lines formed when electron jumps from higher orbits i.e., 3, 4, 5, …………… to the second orbit, is called Balmer series. This series belongs to visible region.
Question 9.
What is an atomic orbital?
Answer:
The three-dimensional region of the space around the nucleus in an atom where the probability of finding an electron is maximum is called atomic orbital’.
Question 10.
When an electron is transferred in hydrogen atom from n = 4 orbit to n = 5 orbit to which spectral series does this belong?
Answer:
When electronic transition tatkes place between 4th to n = 5 orbit, the absorbed frequency is in far I.R. region. It is called, Brackett series.
Question 11.
How many p – electrons are present in sulphur atom?
Answer:
Sulphur, S (Z = 16) 1s²2s²2p63s²3p4
Total no. of ‘p’ electrons is 6 + 4 = 10
Question 12.
What are the values of principal quantum number (n) and azimuthal quantum number (l) for a 3d electron?
Answer:
For a 3d electron, n = 3 and l = 2.

Question 13.
What is the complete symbol for the atom with the given atomic number (Z) and atomic mass (A) ?
I) Z = 4, A = 9 II) Z = 17, A = 35 III) Z = 92, A = 233.
Answer:
I) 94Be
II) 3517Cl
III) 23392U
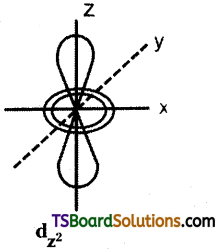
Question 14.
Draw the shape of dz² orbital.
Answer:
Question 15.
Draw the shape of dx²-y² orbital.
Answer:

Question 16.
What is the frequency of radiation of wavelength 600 nm?
Answer:
Frequency υ = \(\frac{c}{\lambda}\)
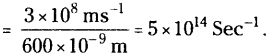
Question 17.
What is Zeeman effect?
Answer:
The splitting of spectral lines into a number of closely-spaced lines under the influence of strong magnetic field is called ‘Zeeman effect’.
Question 18.
What is Stark effect?
Answer:
The splitting of spectral lines into a number of closely spaced lines under the influence of strong electric field is called Stark effect’.
Question 19.
To which element does the following electronic configuration correspond?
I) 1s²2s²2p63s²3p¹
II) 1s²2s²2p63s²3p6
III) 1s²2s²2p5
IV) 1s²2s²2p².
Answer:
I) Aluminium
II) Argon
III) Fluorine
IV) Carbon.
Question 20.
Electrons are emitted with zero velocity from a metal surface when it is exposed to radiation of wavelength 4000 Å. What is the threshold frequency (υ0)?
Answer:
Velocity of electron is ‘Zero’ means KE = 0,
∴ hυ = hυ0 (or) υ = υ0

Question 21.
Explain Pauli’s exclusion principle. [Mar. ’19(AP)]
Answer:
Pauli’s exclusion principle :
“No two electrons in an atom can have the same set of four quantum numbers.”
This principle implies that “an orbital can accommodate a maximum of two electrons” with opposite spins

Question 22.
What is Aufbau principle? [Mar. ’19(AP)]
Answer:
In the ground state of the atoms,
“The orbitals are filled up with electrons in the increasing order of their energy.”
The relative order of energy of various orbitals is
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f ………..
Question 23.
What is Hund’s rule?
Answer:
Hund’s rule :
“Pairing up of electrons takes place only when all the available degenerate orbitals in a given sub-shell are filled with one electron each.”
Question 24.
Explain Heisenberg’s uncertainty principle.
Answer:
Heisenberg’s uncertainty principle:
“It is not possible to determine simultaneously and accurately both the position and men mentum (or velocity) of a microscopic moving particle like electron, proton etc.”
Mathematically it can be expressed as,
∆x × ∆p ≥ \(\frac{h}{4 \pi}\)
where
∆x = uncertainty involved in the position
∆p = uncertainty in momentum and h = Planck’s constant.
Question 25.
What is the wavelength of an electron moving with a velocity of 2.0 × 107 ms-1?
Answer:
λ = \(\frac{h}{mv}\)
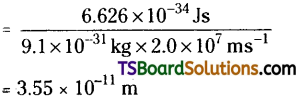
Question 26.
An atomic orbital has n = 2, what are the possible values of l and ml?
Answer:
The atomic orbital having n value may be 2s and 2p.
For 2s orbital l = 0, ml = 0.
For 2p orbital l = 1, ml = -1, 0, +1
Question 27.
Which of the following orbitals are possible? (2s, 1p, 3f, 2p)
Answer:
2s and 2p are possible.
1p is not possible because first orbit contains only s-orbital but no p – orbital.
3f is not possible because third orbit contains three orbitals only. They are 3s, 3p and 3d.
Question 28.
The static electric charge on the oil drop is -3.2044 × 10-19C. How many electrons are present on it?
Answer:
Charge on each electron = – 1.6022 × 10-19C
Charge on oil drop = – 3.2044 × 10-19C
∴ Number of electrons
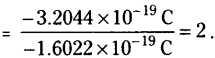
Question 29.
Arrange the following type of radiation in increasing order of frequency:
(a) X – rays (b) visible radiation (c) micro-wave radiation and (d) radiation from radio waves.
Answer:
The order of frequencies is
Radio waves < microwaves < visible radiation < X – rays.

Question 30.
How many electrons in an atom may have n = 4 and in ms = +\(\frac{1}{2}\)?
Answer:
If n = 4 the number of electrons in 4th orbit is 2n² = 2(4)² = 32.
Number of electrons with ms = +\(\frac{1}{2}\) in fourth orbit =16.
Question 31.
How many sub-shells are associated with in = 5?
Answer:
n = 5 orbit contains five sub-shells s, p, d, f and g. i.e., when n = 5; l = 0, 1, 2, 3, 4.
Question 32.
Explain the particle nature of electromagnetic radiations.
Answer:
Electromagnetic radiations contain energy packets (particles) called quantum. The energy associated with each particle is given by
E = hυ
where
h = Planck’s constant
υ = frequency of electromagnetic radiation
The particle nature of electromagnetic radiation is proved by photoelectric effect.
Question 33.
Explain the significance of Heisenberg’s uncertainty principle.
Answer:
Significance of uncertainty principle :
- This principle applies for motion of microscopic objects and not so for macroscopic objects.
- For massive bodies, the uncertainties have no practical importance.
- Microscopic bodies like electrons cannot have fixed paths of motion, according to this principle.
Question 34.
What series of lines are observed in hydrogen spectra?
Answer:
1) Lyman 2) Balmer 3) Paschen 4) Bracket and 5) Pfund series of lines are observed in hydrogen spectra.
Short Answer Questions
Question 1.
What is the wavelength of light emitted when the electron in a hydrogen atom undergoes transition from an energy level with n = 5 to an energy level with n = 3?
Answer:

Question 2.
An atom of an element contains 29 electrons and 35 neutrons. Deduce (I) the number of protons and (ii) the electronic configuration of the element.
Answer:
Since the atom contains 29 electrons, the atomic number of element is 29.
∴ The number of protons is also 29.
The element is copper.
Its electronic configuration is 1s²2s²2p63s²3p63d104s¹
Question 3.
Explain giving reasons, which of the following sets of quantum numbers are not possible.
a) n = 0, l = 0, ml = 0, m2 = +\(\frac{1}{2}\)
b) n= 1, l = 0, ml = 0, m2 = –\(\frac{1}{2}\)
c) n = 1, l = 1, ml = 0, m2 = +\(\frac{1}{2}\)
d) n = 2, l = 1, ml = 0, m2 = +\(\frac{1}{2}\)
e) n = 3, l = 3, ml = – 3, m2 = +\(\frac{1}{2}\)
f) n = 3, l = 1, ml = 0, m2 = +\(\frac{1}{2}\)
Answer:
Set (a) is not possible, because zero value is not permissible for n.
Set (c) is not possible, because for n = 1, possible value of l is zero only.
Set (e) is not possible, because for n = 3, permissible values for l are 0, 1, 2 only.
Question 4.
Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de-Broglie wavelength associated with the electron revolving around the orbit.
Answer:
According to Bohr’s model

So the circumference of the Bohr orbit (2πr) must be equal to an integral (n) multiple of the de-Broglie wavelength (λ).
Question 5.
The longest wavelength doublet absorption transition is observed at 589.0 and 589.6 nm. Calculate the frequency of each transition and energy difference between two excited states.
Answer:
Frequency υ = \(\frac{c}{\lambda}\)
For the radiation having wavelength 589.0 nm the frequency
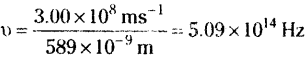
For the radiation having wavelength 589.6 nm the frequency
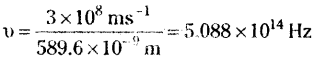
Energy of radiation having wavelength 589.0 nm is
E = hυ or h\(\frac{c}{\lambda}\)
h is Planck’s constant 6.626 × 10-34 Js
= 6.626 × 10-34 Js × 5.09 × 1014 Hz
= 33.73 × 10-20 J
Energy of the radiation having wavelength 589.6 is
E = hυ = h\(\frac{c}{\lambda}\)
= 6.626 × 10-34 Js × 5.088 × 1014 Hz
= 33.71 × 10-20 J
The energy difference between two excited states
= 33.73 × 10-20 J – 33.71 × 10-20 J
= 2 × 10-22J

Question 6.
What are the main features of quantum mechanical model of an atom?
Answer:
Quantum mechanical model of atom explains the motion of very minute particles which possess both particle and wave nature. Schrodiriger’s equation applies to these type of particles and it is given by
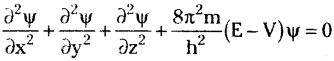
Salient features of the quantum mechanical model of atom:
- The energy of an electron in an atom is quantised. It means, the electron can have only certain values of energy.
- The energy levels in an atom are quantised, which are the allowed solutions of Schrodinger wave equation, applied for electron wave.
- All the information about the orbiting electron in atom is contained in the orbital wave function, Ψ.
- The exact path of an electron cannot be determined accurately. We can only find the probability of the electron at different points in an atom.
- Ψ² is the probability density, which is always positive. From the value of Ψ² at different points within the atom, it is possible to find the orbital’ of electron.
Orbital is the three-dimensional space around the nucleus of an atom, where there is high probability of finding the electron.
Question 7.
What is a nodal plane? How many nodal planes are possible for 2p- and 3d- orbitals?
Answer:
The probability to find the electron at a point within the nucleus in an atom is negligible. This point is called nodal point’. ‘The plane passing through this point is called ‘nodal plane’ (or angular node). So nodal plane is the plane of zero electron density.
The number of nodal planes for an orbital is equal to its Azimuthal quantum number 1 value.
Thus,
No. of nodal planes for s – orbital (l = 0) is zero.
No. of nodal planes for p – orbital (l = 1) isl.
No. of nodal planes for d – orbital (l = 2) is 2.
No. of nodal planes for f – orbital (l = 3) is 3.
Question 8.
The Lyman series occurs between 91.2 nm and 121.6 nm, the Balmer series occurs between 364.7 nm and 656.5 nm and the Paschen series occurs between 820.6 nm and 1876 nm. Identify the spectral regions to which these wavelengths correspond.
Answer:
| Name of series | Spectral Region |
| 1) Lyman | Ultra Violet |
| 2) Balmer | Visible |
| 3) Paschen | Near infrared |

Question 9.
How are the quantum numbers n, 1, m, for hydrogen atom are obtained?
Answer:
Atomic number (Z) of hydrogen atom = 1.
Its electron configuration is 1s¹. From this configuration, it is evident that the electron in ‘H’ atom involves in 1st orbit with n = 1. For an ‘S’ orbital l = 0, m = 0.
∴ The four quantum number values for ‘H’ atom are n = 1, l = 0, m = 0, s = + ½.
Queestion 10.
A line in Lyman series of hydrogen atom has a wavelength of 1.03 × 107 m. What is the initial energy level of the electron?
Answer:

Hence by trial and error method, we found, n2 = 3
So the electron belongs to 3rd energy level (M = 3) originally.
Question 11.
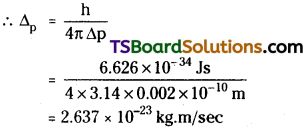
If the position of the electron is measured within an accuracy of ± 0.002 nm, calculate the uncertainty in the momentum of the electron.
Answer:
According to Heisenberg’s uncertainty principle
∆x ∆p = \(\frac{h}{4 \pi}\)
∆x is uncertainty in position
∆p is uncertainty in momentum
Question 12.
If the velocity of the electron is 1.6 × 106 ms-1, calculate the de-Broglie wavelength associated with this electron.
Answer:
According to de-Broglie equation λ = \(\frac{h}{mv}\)
λ = wavelength of electron
h = Planck’s constant 6.626 × 10-34 Js
m = mass of electron 9.1 × 10-31 kg
v = velocity of electron 1.6 × 106 ms-1
Substituting these values in de-Broglie equation
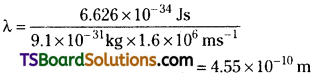
Question 13.
Explain the difference between emission and absorption spectra. (AP ’15)
Answer:
| Emission spectra | Absorption spectra |
| 1) The spectra is formed when electron jumps from higher orbits to lower orbits. | 1) The spectra is formed when electron jumps from lower orbit to higher orbit. |
| 2) It is formed due to emission of energy in quanta. | 2) It is formed due to absorption of energy in quanta. |
| 3) It contains bright lines on dark background. | 3) It contains dark lines on bright background. |
| 4) It can be continuous or discontinuous. | 4) It is always dis-continuous. |

Question 14.
The quantum numbers of electrons are given below. Arrange them in order of increasing energies. Do any of these combinations have same energy?
a) n = 4, l = 2, ml = – 2, ms = + ½
b) n = 3, l = 2, ml = – 1, ms = – ½
c) n = 4, l = 1, ml = 0, ms = + ½
d) n = 3, l = 1, ml = – 1, ms = – ½
Answer:
Rule :
- The relative energy of an electron is given by its (n + l) value, m and s contributions are very little.
- If two electrons have the same (n + l) value, electron with lower n value has lower energy.
a) n = 4, l = 2 (n + l) value = 6
b) n = 3, l = 2 (n + l) value = 5
c) n = 4, l = 1 (n + 0 value = 5
d) n = 3, l = 1 (n + 0 value = 4
Increasing order of energies of electrons is : (4) < (2) < (3) < (1)
Question 15.
The work function for Cesium atom is 1.9 eV. Calculate the threshold frequency of the radiation. If the Cesium element is irradiated with a wavelength of 500 nm, calculate the kinetic energy of the ejected photoelectron.
Answer:
The energy (E) of a 300 nm photon is given by.
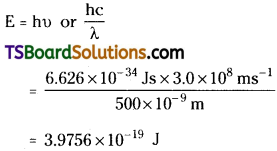
Threshold energy = 1.9 eV × 1.6022 × 10-19
= 3.044 × 10-19 J
Kinetic energy of electron = Energy of photon – Threshold energy
= 3.976 × 10-19 J – 3.044 × 10-19 J
= 9.32 × 10-20 J
Question 16.
Calculate the wavelength for the emission transition if it starts from the orbit having radius 1.3225 nm and ends at 211.6 pm. Name the series to which this transition belongs and the region of the spectrum.
Answer:
Radius of the orbit = 1.3225 nm
= 1.3225 × 10sup>-7 cm = 13.225 × 10-8 cm
∵ The radius of the orbit = 0.529 × n² = 13.225
∴ n = \(\sqrt{\frac{13.225}{0.529}}\) = 5
Radius of the second orbit = 211.6 pm
= 2.116 × 10-8 cm
0.529 × n² = 2.116
or n = 2
The electron transition takes place 5 to 2. So, transition belongs to Balmer series.
It is in the visible region.
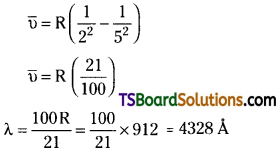
∴ The wavelength of the radiation = 4328 Å
Question 17.
Explain the difference between orbit and orbital.
Answer:
| Orbit | Orbital |
| 1. It is the circular path around the nucleus in which the electron revolves. | 1. It is the region of the space around the nucleus where theprobability of finding the electron is maximum. |
| 2. It represents planar motion of electron. | 2. It represents three dimensional motion of electron. |
| 3. Orbits are non- directional. Hence they cannot explain shape of molecules. | 3. Orbitals (except S – orbital) have directional character. Hence they can account for shapes of molecules. |
| 4. The maximum no. of electrons in an orbit is given by 2n². | 4. An orbital can accommodate a maximum of 2 electrons with opposite spins. |

Question 18.
Explain the photoelectric effect.
Answer:
Photoelectric effect :
J.J. Thomson and P. Lenard showed that “when a beam of light of suitable wavelength is allowed to fall on the surface of a metal, the electrons are emitted from the surface of the metal”. This phenomenon is called, photoelectric effect.
Explanation of photoelectric effect by Einstein:
Einstein (1905) explained photo-electric effect with the help of Planck’s quantum theory of radiation.
According to quantum theory of radiation, a photon of light of frequency, υ is associated with energy equal to hυ. When a photon of light of frequency υ (υ is higher than threshold frequency) falls on a metal, some of the energy associated with the photon is consumed to separate the electron from the surface and the remaining energy is imparted to the ejected electron, to give it certain velocity, say, equal to v. Due to this velocity, the emitted electron gains kinetic energy equal to \(\frac{1}{2}\)mv². The proton of energy which is consumed to separate the electron is equal to the binding energy of the electron.
This energy is called threshold energy’ or work function’ and is equal to the product of h and threshold frequency (υ0) of a photon of radiation falling on the metal surface. Thus this energy is equal to hu0. This is the minimum energy associated with the photon (of frequency υ0) of the incident radiation which is consumed to separate one electron from the metal surface. The above discussion shows that hυ is equal to the sum of \(\frac{1}{2}\)mv² (K.E. of one electron) and hυ0
i.e., hυ = hυ0 + \(\frac{1}{2}\)mv²
Long Answer Questions
Question 1.
Explain Rutherford’s nuclear model of an atom. What are its drawbacks?
Answer:
In 1910, Rutherford proposed a model of the atom to explain the results of his experiment. It is called, Planetary model or Nuclear model of atom. The main features of the model are given below.
- Atom is spherical and mostly hollow.
- The positive charge and the mass of the atom is concentrated in a small region at the centre of the atom. The region is called, ‘Nucleus’.
- The electrons present outside the nucleus (called, extra-nuclear electrons) are equal in number to the protons inside the nucleus.
- Just as the planets revolve around the Sun, the electrons revolve around the nucleus.
- The revolving electron is under the in-fluence of two forces – i) The centripetal force of attraction towards nucleus and ii) the centrifugal force directed away from the orbiting path. These two forces being equal and opposite, balance each other and the electron continues to move in its orbit.
Drawbacks in Rutherford’s Model:
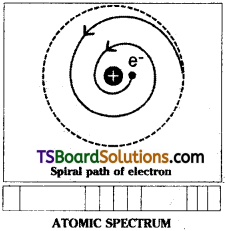
- According to electrodynamics, any charged particle moving under the influence of opposite charge should lose energy continuously, come closer and closer to the nucleus in a spiral path and ultimately fall in the nucleus as shown in figure. Then the atom shall collapse due to the merging of electrons with the nucleus. But it is not happening.
- If the electrons lose energy continuously, the atomic spectrum should have a continuous band. But the atomic spectrum of the elements are found to contain discrete lines.
Question 2.
Explain briefly the Planck’s quantum theory.
Answer:
Planck’s Quantum Theory:
- The emission of radiation is due to vibrations of charged particles (electrons) in the body.
- The emission of radiation is not continuous, but in discrete packets of energy called ‘quanta’. This emitted radiation propagates in the form of waves.
- The energy associated with each quantum (E) is given by E = hυ, where υ is the frequency of radiation and h is Planck’s constant (h = 6.63 × 10-27 ergs)
- A body can emit or absorb either one quantum (hυ) of energy or some whole number multiples of it.
Success of Planck’s Quantum Theory :
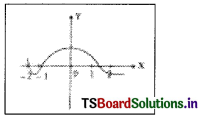
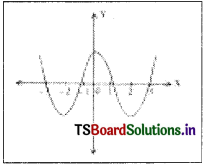
This theory successfully explains the black body radiations. A black body is a perfect absorber and also a perfect radiator of radiations.
Explanation of Graph:
The radiations emitted by a hot black body, when passed through a prism, produce a spectrum of different wavelengths.
A plot of the ‘intensity of radiation’ against wavelength’ gives a curve. Such curves obtained at different temperatures of a black body are shown in the graph.
The following conclusions can be drawn from a study of the shapes of the curves.
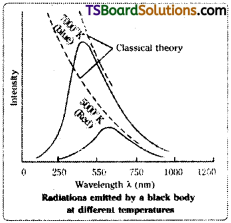
- At a given temperature, the intensity of radiation increases with wavelength, reaches a maximum and then decreases.
- As the temperature increases, the peak of the curve (maximum point in curve) shifts to lower wavelengths.
The wave theory of light’ could not explain the above experimental results, satisfactorily.
Question 3.
What are the postulates of Bohr’s model of hydrogen atom? Discuss the importance of this model to explain various series of line spectra in hydrogen atom. [AP 17, 15; TS 16; IPE 14, 13, Mar. ’19 (AP); Mar.18 (AP & TS)]
Answer:
A) Postulates of Bohr’s theory:
1) Electrons revolve around the nucleus in certain, definite circular paths, called orbits. They are also known as energy levels or shells.
2) Each orbit is associated with a definite amount of energy. Hence these orbits are called energy orbits or energy levels or energy shells.
3) As the value of n increases, the size and energy of the orbit increases.
4) As long as the electrons revolve in the circular orbits, they neither emit nor absorb energy. Hence, these orbits are also called stationary orbits.
5) More than one stationary orbit is possible for any electron and the angular momentum of the revolving electron is quantized. That is, the electrons revolve in those circular orbits in which the angular momentum of the revolving electron is an integral multiple of h/2π.
This can be expressed as mvr = n × \(\frac{h}{2 \pi}\)
where m = mass of the electron;
v = velocity of the electron
r = radius of the orbit;
h – Planck’s constant,
n – Principal quantum number.
6) The energy of electron changes when the electron jumps from one orbit to another orbit. When the electron jumps from a lower orbit to a higher orbit, energy is absorbed. Similarly when the electron jumps from a higher orbit to a lower orbit, energy is emitted. The energy emitted or absorbed is given by the equation, ∆E = E2 – E1 = hυ
where
E1 = Energy of lower orbits;
E2 = Energy of higher orbits;
∆E = Difference in energy;
h = Planck’s constant;
υ = Frequency.
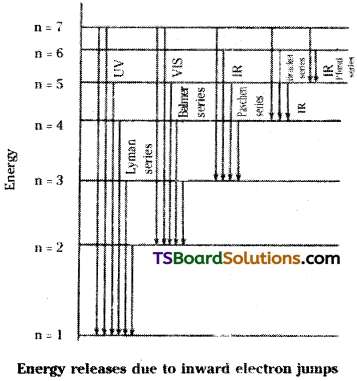
B) Explanation of formation of different lines in various series of Hydrogen atomic spectrum :
Hydrogen atom has only one electron and it revolves around the nucleus in the first orbit. When certain amount of hydrogen gas containing a large number of electrons, is heated or exposed to light energy or is subjected to electric discharge, the different electrons absorb different amount of energy and get excited to different higher orbits. But, they do not stay there for longer periods. Hence, they try to come back to lower orbits (de-excitation). This de-excitation need not necessarily be the same for all the atoms. Some excited electrons may come back from any of the higher energy levels to lower energy level n = 1. Then Lyman series is formed in the U.V. region. Some excited electrons may come back from any of the higher energy levels to lower energy level n = 2. Then
Balmer series is formed in the visible region. Similarly, when the excited electron comes back, from any of the higher energy levels to lower levels 3, 4 & 5, we get Paschen, Bracket and Pfund series respectively in the I.R. region.
The de-excitation process from higher energy level to lower energy level also may take place in a single step or in different steps. For example, the de-excitation process of an electron from 4th energy level to 1st energy level can be as shown below.
Direct step : From 4th level to 1st (i.e.,) 4 → 1
Different steps : 4 → 3 → 2 1; 4 → 3 1; 4 → 2 → 1.
For each electronic transition one line is formed in the spectrum. Thus we get a large number of lines in a given series.
Question 4.
Explain the success of Bohr’s theory for hydrogen atom.
Answer:
The main success of Bohr’s model:
1. Bohr’s model could explain the stability of an atom:
According to Bohr’s model, an electron revolving in a particular orbit cannot lose energy. An electron will absorb energy when it jumps from lower energy level to higher energy level or lose energy when it jumps from higher energy level to lower energy level. When there is no vacant lower energy level the electron keeps revolving in the same orbit without losing energy and thus explains the stability.
2. Bohr theory helped to calculate the energy of an electron in an orbit:
Basing on Bohr’s model a mathematical relation can be developed to calculate the energy of an electron in nth orbit.
En = \(\frac{-\mathrm{k}^2 2 \pi^2 m \mathrm{e}^4}{\mathrm{n}^2 \mathrm{~h}^2}\)
where m = Mass of electron
e = Charge on electron
h = Planck’s constant
k = Coulombs constant 9.0 × 109 Jm/C²
Substituting the values of m, e, h, π and k in the above expression we get
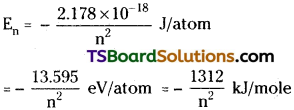
Using Bohr’s model the radius of an orbit in hydrogen atom can be calculated
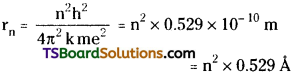
3. Bohr’s model could explain the atomic spectrum of hydrogen :
The different spectral lines in hydrogen spectrum is due to the emission of energy in the form of light when the electron jumps to lower energy level. When hydrogen gas is supplied from some external source, the electrons in different atoms absorb energy and excited to higher energy levels. When the electron returns back to lower energy levels it gives out energy in the form of quantum equal to the difference of energies between the two energy levels.
E2 – E1 = hυ or υ = \(\frac{E_2-E_1}{h}\)
where E1 is the energy of lower energy level, E2 is the energy of high energy level and h is Planck’s constant.
According to Bohr’s model, in a hydro gen atom (or in any other atom) E2 and E1 can have only certain definite values. From this, it follows that u can have only certain fixed values. Thus Bohr’s model explains why there are certain discrete lines in the spectrum of hydrogen.

Question 5.
What are the consequences that lead to the development of quantum mechanical model of an atom?
Answer:
In 1923 Louis de-Broglie proposed that like light matter also has dual character. It exhibits wave as well as particle nature. He derived an equation to calculate the wavelength (λ) of the wave associated with a particle of mass m, moving with velocity v and it is given by
λ = \(\frac{h}{mv}\) (or) λ = \(\frac{h}{p}\)
‘h’ is Planck’s constant and P is momentum of the particle. It may be noted that wave character has significance only in the case of sub-microscopic particles such as electrons.
The precise location of a wave cannot be predicted as a wave is not located at a particular point but extends in space. Thus the wave nature of electron puts some restriction in finding the position precisely. W. Heisenberg put forward this limitation in the form of uncertainty principle. According to Heisenberg,
“It is not possible to determine simultaneously and accurately both the position and momentum of a small moving particle, such as electron.”
It can be expressed mathematically as,
∆x × ∆p ≥ \(\frac{h}{4 \pi}\)
∆x × m ∆v ≥ \(\frac{h}{4 \pi}\)
where ∆x = uncertainty in position
∆p = uncertainty in momentum
m = mass of particle
∆v = uncertainty in velocity
h = Planck’s constant.
The uncertainty principle is due to the direct consequence of dual nature of matter.
A microscopic object such as electron has both observable wave-like and particle-like properties. The behaviour of such particles cannot be explained on the basis of classical mechanics which is based on Newton’s laws of motion. In order to explain the behaviour of electrons a new branch of science called quantum mechanical model of atom was developed. Quantum mechanics is a theoretical science that takes into account the dual nature of matter.
Question 6.
Explain the salient features of quantum mechanical model of an atom.
Answer:
Quantum mechanical model of atom explains the motion of very minute particles which possess both particle and wave nature. Schrodiriger’s equation applies to these type of particles and it is given by
Salient features of the quantum mechanical model of atom:
- The energy of an electron in an atom is quantised. It means, the electron can have only certain values of energy.
- The energy levels in an atom are quantised, which are the allowed solutions of Schrodinger wave equation, applied for electron wave.
- All the information about the orbiting electron in atom is contained in the orbital wave function, Ψ.
- The exact path of an electron cannot be determined accurately. We can only find the probability of the electron at different points in an atom.
- Ψ² is the probability density, which is always positive. From the value of Ψ² at different points within the atom, it is possible to find the orbital’ of electron.
Orbital is the three-dimensional space around the nucleus of an atom, where there is high probability of finding the electron.
Question 7.
What are the limitations of Bohr’s model of an atom? [AP ’15; ’13]
Answer:
Bohr’s model of atom could explain the
i) stability of atom ii) the line spectrum of hydrogen atom and ions with a single electron (He+, Li2+, Be3+ ……………)
But this model could not explain the following observations.
- Bohr’s model cannot explain the spectra of atoms or ions having more than one electron.
- When the spectrum of hydrogen was taken with a spectroscope of high resolving power, it was observed that each line is actually a group of fine lines’. Bohr’s model cannot explain this fine structure in the atomic spectra.
- It cannot explain Zeeman effect (splitting of spectral lines in the presence of magnetic field) and stark effect (splitting of spectral lines in an electric field).
- It also cannot explain the ability of atoms to form molecules by chemical bonds.
- It failed to explain the dual nature of electrons and also the geometry and shapes of molecules.
Question 8.
What are the evidences in favour of dual behaviour of electron?
Answer:
The particle nature of electron can be explained by the photoelectric effect and Planck’s Quantum Theory.
When light falls on the surface of a metal, electrons are ejected from the surface with some kinetic energy by absorbing energy in the form of quantum. The kinetic energy of photo electrons is directly proportional to frequency. Kinetic energy of photoelectrons is independent of intensity because increase energy does not affect the energy of photons rather it simply increases the number of photons falling on the surface of metal and hence the number of photoelectrons. This proves the particle nature of electrons.
The wave nature of electrons was verified experimentally by Davisson and Germer by carrying out diffraction experiments with a beam of fast moving electrons. This wave nature of electrons is utilised in the construction of electron microscope.
From the evidences of photoelectric effect in favour of particle nature and also from the evidences of experiments conducted by Davisson and Germer in favour of wave nature, we can conclude that electron has dual nature.
Question 9.
How are the quantum numbers n, l and ml arrived? Explain the significance of these quantum numbers. [AP & TS ’15, ’16 TS Mar. ’19, ’17) (IPE ’14, ’13, ’10, ’06, ’04]
Answer:
To describe an electron completely four quantum numbers were predicted.
They are
- Principal quantum number, n
- Azimuthal quantum number, l
- Magnetic quantum number, ml and
- Spin quantum number, ms.
a) Principal Quantum Number:
- This was proposed by Neils Bohr.
- It is denoted by the letter ‘n’.
- It represents the circular orbits around the nucleus.
- As the value of n increases the size and energy of the orbit increases.
- According to number method n has the values 1, 2, 3, ……… According to letter method ‘n’ can be represented by the letters K, L, M, ………
- In any orbit, the number of sub-orbits = n,
number of orbitals = n² ;
number of electrons =2n². - This Quantum number describes the size and energy of the orbit.
b) Azimuthal Quantum Number:
- This was proposed by Sommerfeld.
- It is also known as Angular momentum quantum number.
- It is denoted by the letter ‘l’.
- This quantum number represents the sub-levels present in the main levels.
- The sub-levels are s, p, d and f.
- The l values of s, p, d and f sub-levels are 0, 1, 2 and 3 respectively.
- The first main level contains only one sub-level and it is s. The second main level contains s, p sub-levels. The third main level contains s, p, d sub-levels. The fourth main level contains s, p, d and f sub-levels.
| Main level | Sub-levels | Sub-sub-levels |
| 1 | s | 1s |
| 2 | s | 2s |
| p | 2p |
| 3 | s | 3s |
| p | 3p |
| d | 3d |
| 4 | s | 4s |
| p | 4p |
| d | 4d |
| f | 4f |
8) The relative energy values of Is, 2s, 2p etc., can be calculated by adding up their n and 1 values.
Ex :1. Energy value of Is =1+0 = 1
2. Energy value of 2p = 2 + 1 = 3
3. Energy value of 3d = 3 + 2 = 5
4. Energy value of 4f =4 + 3 = 7

9) This Quantum number describes the shape of the orbital.
| Sub-level | Shape |
| s | spherical |
| p | dumb-bell |
| d | double dumb-bell |
| f | four fold dumb-bell |
c) Magnetic Quantum Number:
- This was proposed by Lande.
- It is denoted by the letter ‘m’.
- This quantum number describes the sub – sub levels or orbitals present in a given sub – level.
- ‘ml‘ has values from -l to +l through ‘0’.
- The total number of ‘m’ values for a given value of T is ( 2l + 1).
- All the orbitals present in a given sublevel possesses the same energy values, because they possess the same n and l values.
- This quantum number describes the orientation of the orbitals in space.
d) Spin Quantum Number:
- Uhlenbeck and Goudsmit proposed it.
- It is denoted by ms.
- This quantum number describes the spin of the revolving electron.
- ‘ms‘ value of clockwise electron is +½ and that of anticlockwise electron is -½.
- Clockwise revolving electron is represented by +½ and anticlockwise revolving electron is represented by -½ .
- This quantum number describes the direction of spin of the revolving electron.

Question 10.
Explain the dual behaviour of matter. Discuss its significance to microscopic particles like electrons.
Answer:
de-Broglie’s hypothesis:
The light is found to exhibit wave nature as well as particle nature (dual nature). Based on this idea of dual nature of light’, de Broglie in 1924 proposed that “all micro-particles including the electron moving with high velocity are associated with dual nature (i.e.,) both particle and wave nature.
De-broglie derived an expression for the wavelength of the moving electron.
Expression for de-Broglie wavelengths:
According to ’Planck’s quantum theory’, energy of a photon,
E = hυ; But υ = \(\frac{c}{\lambda}\)
∴ E = h.\(\frac{c}{\lambda}\) ………… (1)
Einstein’s mass-energy equivalence equation is E = mc² ………….. (2)
combining eqns. (1) and (2),
\(\frac{h.c}{\lambda}\) = mc² or λ = \(\frac{h}{mc}=\frac{h}{p}\)
(p = me = momentum)
This equation is applicable to photons as well as to all microparticles, moving with high speed.
∴ We can write in general, λ = \(\frac{h}{p}=\frac{h}{mv}\)
where m = mass of the microparticle and v = its velocity
‘λ’, is called, de-Broglie wavelength or material wavelength.
Significance of de-Broglie’s concept:
According to Bohr’s theory, electron revolves in an orbit in which its angular momentum (mvr) is an integral multiple of \(\frac{h}{2 \pi}\). Bohr assumed electron as a particle. Hence his equation can be taken as mvr = n(\(\frac{h}{2 \pi}\)) where n = a whole number.
According to de Broglie, electron behaves as a standing (or stationary) wave which extends round the nucleus in a circular orbit. If the ends of the electron wave meet to give a regular series of crests and troughs, the electron wave is said to be in phase’. It means, there is constructive interference of electron waves and the electron motion has a character of standing wave or nonenergy radiating motion. Always it is a necessary condition to get an electron wave in phase’ such that the circumference of the Bohr’s orbit (= 2πr) is equal to the whole number of multiples of the wavelength (λ) of the electron wave.
nλ = 2πr
λ = \(\frac{2 \pi r}{n}\)
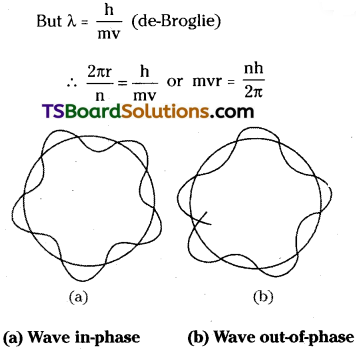
This is Bohr’s equation which stipulates that “the angular momentum of an electron moving round the nucleus is an integral multiple of \(\frac{h}{2 \pi r}\)“. This shows that, de-Broglie’s theory and Bohr’s theory are in agreement with each other.

Question 11.
What are various ranges of electromagnetic radiation? Explain the characteristics of electromagngtic radiation.
Answer:
According to Maxwell, “electromagnetic radiation”, is made up of electromagnetic waves. An electromagnetic wave propagating through space is a combination of two components, one is varying electric field and the other is the varying magnetic field. These two fields are perpendicular to each other and are also perpendicular to the direction of propagation of wave.
Characteristics of electromagnetic radiations :
1) These are produced by oscillating charged particles in a body.
2) The radiations can pass through vacuum also. So medium for transmission is not required.

3) The wavelength (λ) is the distance between two neighbouring crests or troughs of the wave. Unit for λ is cm, m, nm, Å.
4) Frequency of the wave (υ) is the number of waves which cross a particular point in one second.
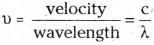
Unit of frequency is cycles per sec (cps) or hertz (Hz)
(1 Hz = 1 cps).
The frequency is inversely proportional to its wavelength.
υ ∝ \(\frac{1}{\lambda}\)
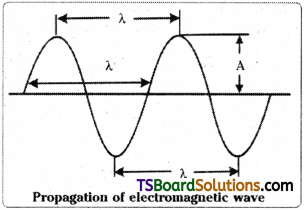
5) Velocity (c) of a wave is the distance travelled by the wave in one second.
Velocity = wavelength × frequency
⇒ c = λ × υ. Velocity of all electromagnetic radiations in space or in vacuum is the same and is equal to 3 × 1010 cm/s.
6) Wave number (\(\overline{\mathrm{υ}}\)) is the number of wavelengths per centimeter. It is reciprocal of wavelength.
\(\overline{\mathrm{υ}}\) = \(\frac{1}{\lambda}\) Unit of \(\overline{\mathrm{υ}}\) is cm-1.
7) Amplitude (A) is the height of the crest or depth of trough of a wave. It determines the intensity or brightness of the light.
8) Electromagnetic spectrum is the spectrum which shows the wavelengths or frequencies or wave numbers of various regions of electromagnetic radiations.

Question 12.
Define atomic orbital. Explain the shapes of s, p and d orbitals with the help of diagrams.
Answer:
Atomic orbital :
The three-dimensional space around the nucleus in an atom where the probability of finding an electron is maximum is called an atomic orbital.
Shapes of s, p and d orbitals :
The shapes of the orbitals are the angular distribution curves’, obtained as one of the solutions of Schrodinger wave equation.
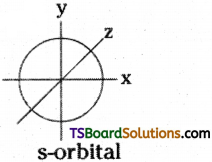
1) Shape of s – orbital:
i) s orbital is spherical in shape.
ii) As the value of principal quantum number increases, size of s orbital increases. Thus, sizes are : 1s < 2s < 3s …………
iii) An ‘s’ orbital has no directional property. s-orbital
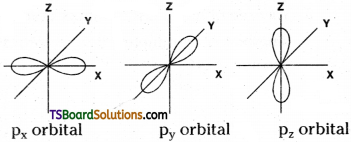
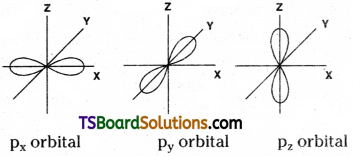
2) Shape of p-orbital :
Shape of p-orbital is dumb-bell. There are three p – orbitals. They are px, py and pz orbitals. Each orbital has two lobes. These lobes are oriented along their respective axes. Each p-orbital has one nodal plane.
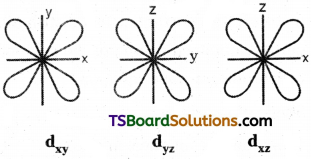
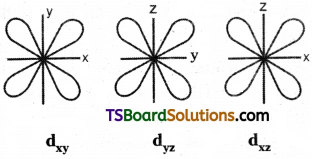
3) Shape of d – orbital :
d – orbital has double dumb-bell shape. There are five d – orbitals. They are dxy, dyz, dxz, dx²-y² and dz² – Each d orbital has 4 lobes. In dxy, orbital, the lobes are placed in – between the x and y axes, similar is the case with other orbitals, dyz and dxz. In dz² orbital, two lobes lie along z axis and there is a ring of electron-cloud around the centre. In dx²-y² orbital, the lobes lie along x and y-axes. Each d orbital has two nodal planes.
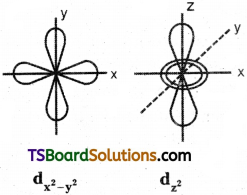
Question 13.
Explain the boundary surfaces for three 2p orbitals and five 3d orbitals diagrammatically.
Answer:
Shape of p – orbital:
Shape of p – orbital is dumb-bell. There are three 2p – orbitals. They are 2px, 2py and 2pz orbitals. Each orbital has two lobes. These lobes are oriented along their respective axes. Each p orbital has one nodal plane.
Shape of d – orbital:
d – orbital has double dumb-bell shape. There are five d – orbitals. They are dxy, dyz, dxz, dx²-y² and z². Each d orbital has 4 lobes. In dxy orbital, the lobes are placed in – between the x and y axes, similar is the case with other orbitals, dyz and dxz. In dz² orbital, two lobes lie along z axis and there is a ring of electron-cloud around the centre. Inx²-y², orbital, the lobes lie along x and y-axes. Each d orbital has two nodal planes.
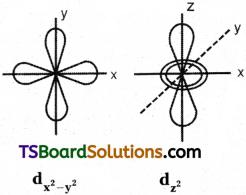
Question 14.
Illustrate the reasons for the stability of completely filled and half-filled subshells.
Answer:
The completely filled and half filled orbitals give stability to the atoms due to following reasons.
1. Completely filled and half filled orbitals give spherical symmetry to the atoms.
2. Also they give more number of Coulom- bic exchange energies.
These can be explained by taking the electronic configurations of Chromium and Copper as examples.
The expected configurations for Cr and Cu are :
Cr (Z = 24) 1s²2s²2p63s²3p64s²3d4
Cu (Z = 29) 1s²2s²2p63s²3p64s²3d9.
The two sub-shells 4s and 3d differ slightly in their energies. Then the electron shifts from a sub-shell of lower energy (4s) to a sub-shell of higher energy (3d), provided such a shift results in all orbitals of the same sub-shell of higher energy (here, 3d) getting either completely filled or half- filled. So the electronic configuration of Cr and Cu are
Cr (Z = 24) 1s²2s²2p63s²3p64s¹3d5
Cu (Z = 29) 1s²2s²2p63s²3p64s¹3d10
These configurations are more stable.
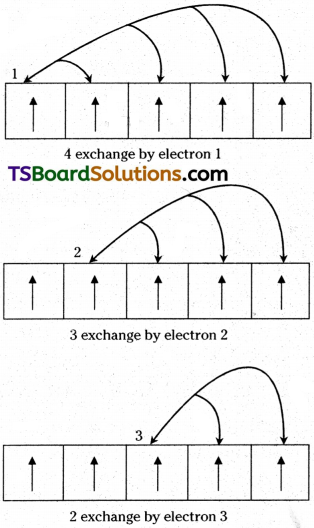
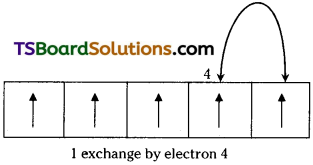
The completely filled and half-filled subshells are more stable for the following reasons:
1) There is symmetrical distribution of electrons in the sub-shells. So they are more stable.
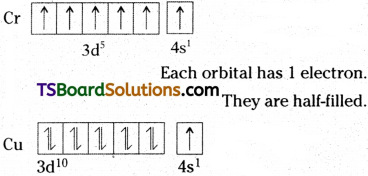
The 3d orbitals are completely filled.
2) When two or more electrons with the same spin are present in the degenerate orbitals, these electrons exchange their positions. Then some energy is released, called exchange energy’. Then the energy of the atom decreases and it becomes more stable. The more the number of ‘exchange pair’ of electrons, the greater would be the decrease of energy and hence the greater is the stability of the atom. In the above configurations of Cr and Cu, there are more ‘exchange pairs’ than in their previous configurations.
Possible exchange for a d5 configuration

Question 15.
Explain emission and absorption spectra. Discuss the general description of line spectra in hydrogen atom.
Answer:
1) Emission spectrum:
The spectrum produced by emitted radiation is called emission spectrum. This spectrum contains bright lines on dark background. This spectrum is of two types. They are (a) Continuous spectrum (b) Discontinuous spectrum.
a) Continuous spectrum :
This spectrum contains a continuous band of colours like rainbow. This spectrum is given by molecules and is also known as Molecular spectrum.
b) Discontinuous spectrum :
This spectrum consists of sharp, distinct lines. This spectrum is given by atoms and is also known as atomic spectrum.
Absorption spectrum:
The spectrum produced by absorbed radiation is known as absorption spectrum. This spectrum contains dark lines on bright background.
The position of the lines or bands in both emission and absorption spectra is same.
2) Explanation of formation of different lines in various series of Hydrogen atomic spectrum :
Hydrogen atom has only one electron and it revolves around the nucleus in the first orbit. When certain amount of hydrogen gas containing a large number of electrons, is heated or exposed to light energy or is subjected to electric discharge, the different electrons absorb different amount of energy and get excited to different higher orbits. But, they do not stay there for longer periods. Hence, they try to come back to lower orbits (de-excitation). This de-excitation need not necessarily be the same for all the atoms. Some excited electrons may come back from any of the higher energy levels to lower energy level n = 1. Then Lyman series is formed in the U.V. region. Some excited electrons may come back from any of the higher energy levels to lower energy level n = 2. Then
Balmer series is formed in the visible region. Similarly, when the excited electron comes back, from any of the higher energy levels to lower levels 3, 4 & 5, we get Paschen, Bracket and Pfund series respectively in the I.R. region.
The de-excitation process from higher energy level to lower energy level also may take place in a single step or in different steps. For example, the de-excitation process of an electron from 4th energy level to 1st energy level can be as shown below.
Direct step : From 4th level to 1st (i.e.,) 4 → 1
Different steps : 4 → 3 → 2 1; 4 → 3 1; 4 → 2 → 1.
For each electronic transition one line is formed in the spectrum. Thus we get a large number of lines in a given series.
Additional Questions & Answers
Question 1.
Calculate the number of protons, neutrons and electrons in 8035Br.
Answer:
In this case, 8035Br , Z = 35, A = 80, species is neutral.
Number of protons = number of electrons = Z = 35
Number of neutrons = A – Z = 80 – 35 = 45.
Question 2.
The number of electrons, protons and neutrons in a species are equal to 18, 16 and 16 respectively. Assign the proper symbol to the species.
Answer:
The atomic number is equal to number of protons = 16. The element is sulphur (S).
Atomic mass number = number of protons + number of neutrons = 16 + 16 = 32
Species is not neutral as the number of protons is not equal to electrons. It is anion (negatively charged) with charge equal to excess electrons = 18 – 16 = 2. Symbol is 3216S2-.

Question 3.
The Vividh Bharati station of All India Radio, Delhi, broadcasts on a frequency of 1,368 kHz (kilo hertz). Calculate the wavelength of the electromagnetic radiation emitted by transmitter. Which part of the electromagnetic spectrum does it belong to?
Answer:
The wavelength, λ, is equal to c/v, where c is the speed of electromagnetic radiation in vacuum and v is the frequency. Substituting the given values, we have

This is a characteristic radiowave wavelength.
Question 4.
The wavelength range of the visible spectrum extends from violet (400 nm) to red (750 nm). Express these wavelengths in frequencies (Hz), (1nm = 10-9m)
Answer:
Frequency of violet light

The range of visible spectrum is from 4.0 × 1014 to 7.5 × 1014 Hz in terms of frequency units.

Question 5.
Calculate (a) wave number and (b) frequency of yellow radiation having wavelength 5800 A.
Answer:
a) Calculation of wave number (\(\overline{\mathrm{ν}}\))
λ = 5800Å = 5800 × 10-8cm = 5800 × 1010 m
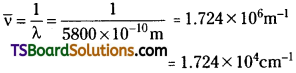
b) Calculation of the frequency (v)
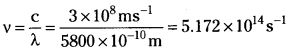
Question 6.
Calculate energy of one mole of photons of radiation whose frequency is 5 × 1010 Hz.
Answer:
Energy (E) of one photon is given by the expression
E = hυ
h = 6.626 × 10-34 J s
V = 5 × 1014 s-1 (given)
E = (6.626 × 10-34 J s) (5 × 1014 s-1)
= 3.313 × 10-19 J
Energy of pne mole of photons
= (3.313 × 10-19 J) × (6.022 × 1023 mol-1)
= 199.51 kJ mol-1
Question 7.
A 100 watt bulb emits monochromatic light of wavelength 400 nm. Calculate the number of photons emitted per second by the bulb.
Answer:
Power of the bulb = 100 watt = 100 J s-1
Energy of one photon E = hν = hc/λ

Question 8.
When electromagnetic radiation of wavelength 300 nm Calls on the surface of sodium, electrons are emitted with a kinetic energy of 1.68 × 105 J mol-1. What is the minimum, energy needed to remove an electron from sodium? What is the maximum wavelength that will cause a photoelectron to be emitted?
Answer:
The energy (E) of a 300 nm photon is given by
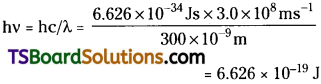
The energy of one mole of photons
= 6.626 × 10-19 J × 6.022 × 1023 mol-1
= 3.99 × 105 J mol-1
The minimum energy needed to remove a mole of electrons from sodium
= (3.99-1.68)105J mol-1
= 2.31 × 105 J mol-1
The minimum energy for one electron

(This corresponds to green light)
Question 9.
The threshold frequency ν0 for a metal is 7.0 × 1014s-1. Calculate the kinetic energy of an electron emitted when radiation of frequency ν = 1.0 × 1015 s-1 hits the metal.
Answer:
According to Einstein’s equation Kinetic energy = \(\frac{1}{2}\)mev² = h(ν – ν0)
= (6.626 × 10-34 Js) (1.0 × 1015 s-1 – 7.0 × 1014 s-1)
= (6.626 × 10-34 Js) (10.0 × 1014 s-1 – 7.0 × 1014 s-1)
= (6.626 × 10-34 Js) (3.0 × 1014 s-1)
= 1.988 × 10-19 J
Question 10.
What are the frequency and wavelength of a photon emitted during a transition from n = 5 state to the n = 2 state in the hydrogen atom?
Answer:
Since ni = 5 and nf = 2, this transition gives rise to a spectral line in the visible region of the Balmer series.
∆E = 2.18 × 10-18 J (\(\frac{1}{5^2}-\frac{1}{2^2}\))
= -4.58 × 10-19 J
It is an emission energy The frequency of the photon (taking energy in terms of magnitude) is given by

Question 11.
Calculate the energy associated with the first orbit of He+. What is the radius of this orbit?
Answer:
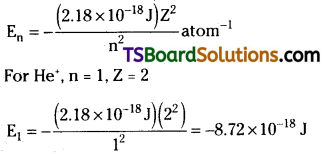
The radius of the orbit is given by
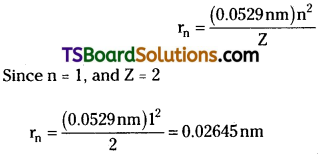
Question 12.
What will be the wavelength of a ball of mass 0.1 kg moving with a velocity of 10 m s-1?
Answer:
According to de Brogile equation
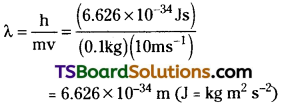
Question 13.
The mass of an electron is 9.1 × 10-31 kg. If its K.E. is 3.0 × 10-25 J, calculate its wavelength.
Answer:
Since K. E. = \(\frac{1}{2}\) mv²


Question 14.
Calculate the mass of a photon with wavelength 3.6 Å.
Answer:
λ = 3.6 Å = 3.6 × 10-10m
Velocity of photon = velocity of light
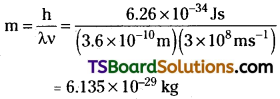
Question 15.
A microscope using suitable photons is employed to locate an electron in an atom within a distance of 0.1 Å. What is the uncertainty involved in the measurement of its velocity?
Answer:
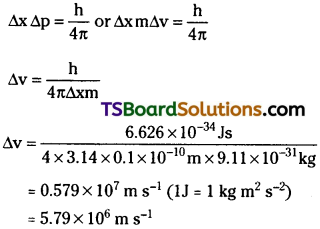
Question 16.
A golf ball has a mass of 40g, and a speed of 45 m/s. If the speed can be measured within accuracy of 2%, calculate the uncertainty in the position.
Answer:
The uncertainty in the speed is 2%, i.e.,

This is nearly ~ 1018 times smaller than the diameter of a typical atomic nucleus. As mentioned earlier for large particles, the uncertainty principle sets no meaningful limit to the precision of measurements.
Question 17.
What is the total number of orbitals associated with the principal quantum number n = 3?
Answer:
For n = 3, the possible values of l are 0, 1 and 2. Thus there is one 3s orbital (n = 3, l = 0 and ml = 0); there are three 3p orbitals (n = 3, l = 1 and m; = -1, 0, +1); there are five 3d orbitals (n = 3, l = 2 and ml = -2, -1, 0, +1, +2).
Therefore, the total number of orbitals is 1 +3 + 5 = 9
The same value can also be obtained by using the relation;
number of orbitals = n², i.e., 3² = 9.

Question 18.
Using s, p, d, f notations, describe the orbital with the following quantum numbers
(a) n = 2, l = 1,
(b) n = 4, l = 0,
(c) n = 5, 1 = 3,
(d) n = 3, l = 2
Answer:

![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()


![]()
![]()
![]()
![]()
![]()