TS 10th Class Maths Important Questions Chapter 3 Polynomials

These TS 10th Class Maths Chapter Wise Important Questions Chapter 3 Polynomials given here will help you to solve different types of questions.

TS 10th Class Maths Important Questions Chapter 3 Polynomials

Previous Exams Questions

Question 1.
Find p(3) if p(x) = x² – 5x + 6 is given.
Solution:
p(x) = x² – 5x + 6 (given)
then p(3) = 3² – 5(3) + 6
= 9 – 15 + 6 = 15 – 15 = 0
∴ p(3) = 0.

Question 2.
Find p(3) if p (x) = x² – 5x – 6 is given. (A.P.Mar.’16)
Solution:
p(x) = x² – 5x + 6 (given)
p (3) = 3² – 5(3) + 6
= 9 – 15 + 6 = 15 – 15 = 0
∴ p(3) = 0.

Question 3.
Find the quotient \(\frac{x^5+x^4+x^3+x^2}{x^3+x^2+x+1}\) when x ≠ 1.
Solution:
\(\frac{x^5+x^4+x^3+x^2}{x^3+x^2+x+1}\)
= \(\frac{x^2\left(x^3+x^2+x+1\right)}{\left(x^3+x^2+x+1\right)}\)
= x²
So the quotient is [x²]

Question 4.
We can write a trinomial having degree 7^th. Justify the given statement by giving one example. (T.S. Mar.15)
Solution:
Since the required is a trinomial, it should have 3 terms. As its degree is 7 the highest exponent (power) of the variable is 7. So the required will be
1) x⁷ – x⁶ + x⁵ (or) x⁷ – x + 10 (or) x⁷ – x⁵ – x (or) x⁷ + 5x⁶ + 6x⁵ or …

Question 5.
If we multiply or divide both sides of a linear equation by a non zero number, then the roots of linear equation will remain the same. Is it true ? If so justify with an example. (T.S. Mar. ’15)
Solution:
Let linear equation be 2x + 8 = 11
Its solution is 2x = 11 – 8 ⇒ 2x = 3
So x = \(\frac{3}{2}\)
Then 2x + 8 = 11 linear equation is divided by 10 on both sides.
\(\frac{2 x+8}{10}\) = \(\frac{11}{10}\) = 20x + 80 = 110
⇒ 20x = 110 – 80 = 30
then x = \(\frac{30}{2}\) = \(\frac{3}{2}\)
So its solution doesn’t change.
So the given statement is true.

Question 6.
Laxmi does not want to disclose the l, b, h of a cuboid of her project. She has constructed a polynomial x³ – 6x² + 11x – 6 by taking the values of l, b, h as its zeros. Can you open the secret ? (T.S. Mar. 15)
Solution:
P(x) = x³ – 6x² + 11x – 6
P(1) = (1)³ – 6(1)² + 11 (1) – 6
= 1 – 6 + 11 – 6
= 12 – 12 = 0
∴ for P(x), (x – 1) is a factor

x² – 5x + 6 = x² – 3x – 2x + 6
= x (x – 3) – 2(x – 3)
= (x – 3) (x – 2)
P(x) = (x – 1) (x – 2) (x – 3)
P(x) zeroes of the polynomial are 1, 2,3
∴ Measurements of the cuboid are 1,2 and 3 units.
Its solution doesn’t change
So it is true.

Question 7.
Draw a graph for the polynomial p(x) = x² + 3x – 4 and find its zeros from the graph.
Solution:
p(x) = x² + 3x – 4


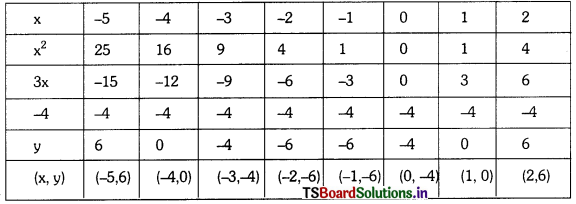
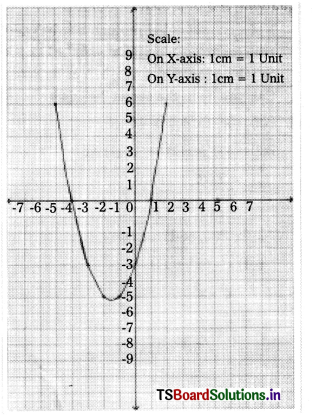
∴ Zeroes of polynomial are -4 and 1

Question 8.
Given an example for a quadratic polynomial which has no zeroes.
Solution:
A quadratic polynomial is in the form of ax² + bx + c. As this has no zeroes. Its discriminant will not be a real number.
So b² – 4ac < 0
So we can choose certain a, b, c values where
b² – 4ac < 0
For examples a = 1, b = 4 and c = 9
So ax² + bx + c = 0
⇒ x² + 4x + 9 = 0 will not have zeroes.

Question 9.
The length of a rectangle is 5 more than its breadth. So express its perimeter in the form of polynomial.
Solution:
Let the breadth of rectangle = xm and its
length = x + 5m.
So the perimeter = 2(l + b)
= 2(x + 5 + x)
= 2(2x + 5)
= 4x + 10m

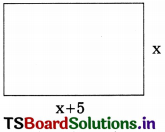
4x + 10 is the polynomial which represents the perimeter of above rectangle.

Question 10.
Draw the graph of polynomial
p(x) = x² – 3x + 2 and find its zeros.
Sol, let y = p(x) = x² – 3x + 2
If x = 0 then p(0) = 0 – 0 + 2
= 2 So (0, 2)
x = 1 then p(1) = 1² – 3(1) + 2
= 1 – 3 + 2
= 0 So (1, 0)
x = 2 then p(2) = 2² – 3(2) + 2
= 4 – 6 + 2
= 0 So (2, 0)
x = 3 then p(3) = 3² – 3(3) + 2
= 9 – 9 + 2
= 2 So (3, 2)
and if x = -1 then p(-1)
= (-1)² – 3(-1) + 2
= 1 + 3 + 2
= 6 So (-1, 6)
x = -2 then p(-2) = (-2)² – 3(2) + 2
= 4 + 6 + 2 = 12 So (-2, 12)
that means the graph of the polynomial
p(x) = x² – 3x + 2 passes through the points. (0, 2), (1, 0) (2, 0) (3, 2) (-1, 6) and (-2, 12)

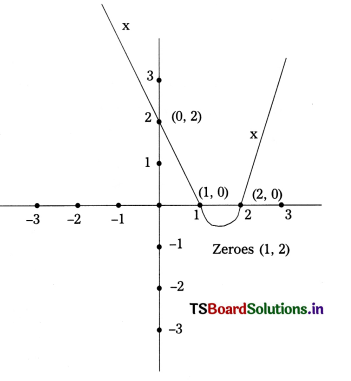
So 1 and 2 are zeroes of the given polynomial.

Question 11.
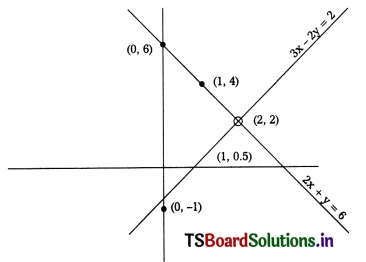
Draw the graphs of the following two linear equations and find their solution.
Solution:
First we have to recognise the points through which the line 3x – 2y = 2 passes then after 2x + y = 6 pass. Let us find the points
3x – 2y = 2
So y = \(\frac{3 x-2}{2}\) —- (1)
Put x = 0 in above equation
∴ y = \(\frac{3(0)-2}{2}\) = \(\frac{0-2}{2}\) = 1
So (0, 1)
Now x = 1 then
y = \(\frac{3(1)-2}{2}\) = \(\frac{3-2}{2}\) = \(\frac{1}{2}\) So(1, \(\frac{1}{2}\))
Now x = 2 then
y = \(\frac{3(2)-2}{2}\) = \(\frac{6-2}{2}\) = \(\frac{4}{2}\) So(2, 2)
that means the line 3x – 2y = 2 passes through the points (0, -1), (1, \(\frac{1}{2}\)) and (2, 2)
Similarly
2x + y = 6
⇒ y = 6 – 2x —– (2)
Put x = 0 in the above equation (2) we get
y = 6 – 2(0) = 6 – 0 = 6 So(0, 6)
and x = 1 ⇒ y = 6 – 2(1) = 6 – 2 = 4
So(1, 4)
and x = 2 ⇒ y = 6 – 2(2) = 6 – 4 = 2
So (2, 2)
So the line 2x + y = 6 passes through the points (0, 6) (1, 4) and (2, 2)
Here we observe (2, 2) is the common point.
That means they intersert at (2, 2)
So x = 2 and y = 2 will be the solution of above the equations.

Additional Questions

Question 1.
If p(x) = 6x⁷ – 2x⁵ + 4x – 8, find
(i) coefficient of x⁵
(ii) degree of p(x)
(iii) constant term. (Each 1 Mark)
Solution:
If p(x) = 6x⁷ – 2x⁵ + 4x – 8,

i) coefficient of x⁵ = – 2
ii) degree of p(x) = highest degree of x – 7
iii) constant term = – 8

Question 2.
If p(t) = 3t³ + 4t – 5, find the values of p(1), p(-1), P(0), p(2), p(-2).
Solution:
given p(t) = 3t³ + 4t – 5
∴ p(1) = 3(1)³ + 4(1) – 5 = 3 + 4 – 5 = 2
p(-1) = 3(-1)³ + 4(-1) – 5 = -3 – 4 – 5 = -12
p(0) = 3(0)³ + 4(0) – 5 = 0 + 0 – 5 = -5
p(2) = 3(2)³ + 4(2) – 5 = 3(8) + 8 – 5
= 24 + 8 – 5 = 27
p(-2) = 3(-2)³ + 4 (-2) – 5
= – 24 – 8 – 5 = – 37

Question 3.
Check whether – 4 and 4 are the zeroes of the polynomial x⁴ – 256.
Solution:
given p(x) = x⁴ – 256
p(-4) = (-4)⁴ – 256 = 256 – 256 = 0
p(4) = (4)⁴ – 256 = 256 – 256 = 0
yes, -4 and 4 are zeroes of the given polynomial

Question 4.
Check whether 5 and -4 are the zeroes of the polynomial p(x) when p(x) = x² – x – 20
Solution:
given p(x) = x² – x – 20
p(5) = (5)² – 5 – 20 = 25 – 5 – 20 = 25 – 25 = 0
P(-4) = (-4)² – (-4) – 20
= 16 + 4 – 20 = 20 – 20 = 0
yes, 5 and – 4 are the zeroes of the polynormial
p(x) = x² – x – 20.

Question 5.
Check whether 3 and – 7 are the zeroes of the polynomial p(x) = x² + 4x – 21.
Solution:
given p(x) = x² + 4x – 21
p(3) = 3² + 4(3) – 21
= 9 + 12 – 21 = 21 – 21 = 0
p(-7) = (-7)² + 4(-7) – 21
= 49 – 28 – 21 = 49 – 49 = 0
yes, 3 and – 7 are the zeroes of the polynomial p(x) = x² + 4x – 21.

Question 6.
Find the zeroes of the given polynomials.
i) p(x) = 4x
ii) p(x) = x² – 9x + 20
iii) p(x) = (x + 5) (x + 6)
iv) p(x) = x⁴ – 81
Solution:
i) p(x) = 4x
p(0) = 4 × 0 = 0
∴ The zero of p(x) = 4x is 0.

ii) p(x) = x² – 9x + 20
= x² – 4x – 5x + 20
= x (x – 4) -5 (x – 4)
= (x – 4) (x – 5)
To find zeroes, let p(x) = 0
⇒ (x – 4) (x – 5) = 0
⇒ x – 4 = 0 or x – 5 = 0
⇒ x = 4 or x = 5
∴ The zeroes of x² – 9x + 20 are 4 nd 5.

iii) p(x) = (x + 5) (x + 6)
To find zeroes, let p(x) = 0
⇒ (x + 5) (x + 6) = 0
⇒ x + 5 = 0 or x + 6 = 0
⇒ x = -5 or x = -6
∴ The zeroes of (x + 5) (x + 6) are – 5 and – 6

iv) p(x) = x⁴ – 81.
To find zeroes, let p(x) = 0
⇒ x⁴ – 81 = 0
⇒ (x²)² – (9)² = 0
⇒ (x² + 9) (x² – 9) = 0
⇒ x² + 9 = 0 or x² – 9 = 0
x² = -9 or (x + 3) (x – 3) = 0
x = ±\(\sqrt{-9}\) = 9 or x + 3 = 0 or x – 3 = 0
x = -3 or x = 3
∴ The zeroes of the polynomial x⁴ – 81 are -3, 3 and ± \(\sqrt{-9}\).

Question 7.
Find the zeroes of the given polynomials.
i) p(x) = x² – x – 12
ii) p(x) = x² – 6x + 9
iii) x² p(x) = x² – 4x + 5
iv) p(x) = x² + 3x – 4
Solution:
i) p(x) = x² – x – 12
To find zeroes, let p(x) = 0
⇒ x² – x – 12 = 0
x² – 4x + 3x – 12 = 0
x(x – 4) + 3 (x – 4) = 0
(x – 4) (x + 3) = 0
⇒ x – 4 = 0 or x + 3 = 0
∴ The zeroes of x² – x – 12 are 4 and – 3

ii) p(x) = x² – 6x + 9
To find zeroes, let p(x) = 0
x² – 6x + 9 = 0
x² – 3x – 3x + 9 = 0
x(x – 3) – 3 (x – 3) = 0
⇒ (x – 3) (x – 3) = 0
⇒ x – 3 = 0 or x – 3 = 0
⇒ x = 3 or x = 3
∴ The zeroes of x² – 6x + 9 is 3.

iii) p(x) = x² – 4x – 5
To find zeroes, let p(x) = 0
x² – 4x – 5 = 0
x² – 5x + x – 5 = 0
⇒ x (x – 5) + 1(x – 5) = 0
⇒ (x – 5) (x + 1) = 0
⇒ x – 5 = 0 or x + 1 = 0
⇒ x = 5 or x = -1
∴ The zeroes of x² – 4x – 5 are 5 and – 1

iv) p(x) = x² + 3x – 4
To find zeroes, let p(x) = 0
x² + 3x – 4 = 0
⇒ x² + 4x – x – 4 = 0
⇒ x(x + 4) – 1(x + 4) = 0
⇒ (x + 4) (x – 1) = 0
⇒ x + 4 = 0 or x – 1 = 0
⇒ x = -4 or x = 1
∴ The zeroes of x² + 3x – 4 are -4 and 1.

Question 8.
Why are \(\frac{1}{3}\) and -2 zeroes of polynomial
p(x) = 3x² + 5x – 2 ?
Solution:
p(x) = 3x² + 5x – 2
Now p(\(\frac{1}{3}\)) = 3(\(\frac{1}{3}\))² + 5(\(\frac{1}{3}\)) – 2
= \(\frac{1}{3}\) + \(\frac{5}{3}\) – 2
= \(\frac{1+5-6}{3}\) = \(\frac{6-6}{3}\) = \(\frac{0}{3}\) = 0
p(-2) = 3 (-2)² + 5(-2) – 2
= 3(4) – 10 – 2
= 12 – 12 = 0
since p(\(\frac{1}{3}\)) and p(-2) are equal to zero
–\(\frac{1}{3}\) and – 2 are zeroes of the polynomial.

Question 9.
Find the zeroes of the following quadratic polynomial and verify the relationship between the zeroes and coefficients.
i) x² – 5x + 6
ii) 3x² – 7x + 4
iii) 5x² + 10x
iv) t² – 12
Solution:
i) Let p(x) = x² – 5x + 6
= x² – 3x – 2x + 6
= x(x – 3) -2 (x – 3)
= (x – 3) (x – 2)
To find zeroes, let p(x) = 0
Hence the zeroes of p(x) are 3 and 2
sum of the zeroes = 3 + 2 = 5 = –\(\frac{(-5)}{1}\)

Product of zeroes = 3 × 2 = 6 = \(\frac{6}{1}\) constant term

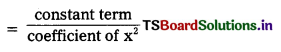
ii) 3x² – 7x + 4
Let p(x) = 3x² – 7x + 4
= 3x² – 3x – 4x + 4
= 3x (x – 1) -4 (x – 1)
= (x – 1) (3x – 4)
To find zeroes, let p(x) = 0
⇒ (x – 1) (3x – 4) = 0
x = 1 or x = 4/3
Hence, the zeroes of p(x) are 1 and \(\frac{4}{3}\).
sum of the zeroes = 1 + \(\frac{4}{3}\) = \(\frac{3+4}{3}\) = \(\frac{7}{3}\)

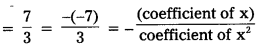
product of zeroes = 1 × \(\frac{4}{3}\) = \(\frac{4}{3}\)

iii) Let p(x) = 5x² + 10x
= 5x (x + 2)
To find zeroes, Let p(x) = 0
⇒ 5x (x + 2) = 0
⇒ x = 0 or x + 2 = 0
⇒ x = 0 or x = -2
Hence the zeroes of p(x) are 0 and -2.
sum of the zeroes = 0 + (-2) = -2

coefficient of x Product of zeroes = 0 x – 2 = 0

iv) t² – 12
let p(t) = t² – 12
to find zeroes, let p(t) = 0
⇒ t² – 12 = 0
⇒ t² = 12 ⇒ t = ±\(\sqrt{12}\) = \(\sqrt{12}\) and –\(\sqrt{12}\)
Hence the zeroes of p(t) are \(\sqrt{12}\) and –\(\sqrt{12}\)
sum of zeroes = \(\sqrt{12}\) + (-\(\sqrt{12}\))
= \(\sqrt{12}\) – \(\sqrt{12}\) = 0 = \(\frac{0}{1}\)

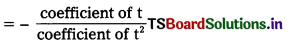
product of zeroes = \(\sqrt{12}\) × (-\(\sqrt{12}\))
= -12 = \(-\frac{12}{1}\)

Question 10.
Find the quadratic polynomial in each case, with the given numbers as the sum and product of its zeroes.
i) \(\frac{1}{3}\), -2
ii) 0, \(\sqrt{3}\)
iii) 3, 5
iv) –\(\frac{1}{2}\), \(\frac{1}{2}\)
Solution:
i) \(\frac{1}{3}\), -2
Let α, β be the zeroes of the quadratic polynomial sum of zeroes = α + β = \(\frac{1}{3}\)
product of zeroes = αβ = -2
The required quadratic polynomial will be
k [x² – x(α + β) + αβ] when k is a constant
⇒ k[x² – \(\frac{x}{3}\) – 2]
If k = 3, then the polynomial will be
3[x² – \(\frac{x}{3}\) – 2] = 3x² – x – 6

ii) 0, \(\sqrt{3}\)
Let α, β be the zeroes of quadratic polynomial.
sum of the zeroes = α + β = 0
product of the zeroes = αβ = \(\sqrt{3}\)
The required quadratic polynomial will be k[x² – x(α + β) + αβ] where k is a constant.
⇒ k [x² – x(0) + \(\sqrt{3}\))
⇒ k [x² – 0 + \(\sqrt{3}\)] ⇒ k[x² + \(\sqrt{3}\)
If k = 1, then the polynomial will be 1[x² + \(\sqrt{3}\)] = x² + \(\sqrt{3}\).

iii) 3, 5
Let α, β be the zeroes of quadratic polynomial.
sum of the zeroes = α + β = 3
product of the zeroes = αβ = 5
The required quadratic polynomial will be k[x² – x(α + β) + αβ] where k is a constant
⇒ k [x² – x(3) + 5]
⇒ k [x² – 3x + 5]
If k = 1, then the polynomial will be
1[x² – 3x + 5] = x² – 3x + 5

iv) –\(\frac{1}{2}\), \(\frac{1}{2}\)
Let α, β be the zeroes of quadratic polynomial sum of the zeroes = α + β
= –\(\frac{1}{2}\)
product of the zeroes αβ = \(\frac{1}{2}\)
The required quadratic polynomial will be k[x² – x(α + β) + αβ] when k is a constant
k[x² – x(-\(\frac{1}{2}\)) + \(\frac{1}{2}\)]
⇒ k[x² + \(\frac{x}{2}\) + \(\frac{1}{2}\)]
If k = 2, then the polynomial will be 2[x² + \(\frac{x}{2}\) + \(\frac{1}{2}\)] = 2x² + x + 1

Question 11.
Find the quadratic polynomial the zeroes α, β given in each case

i) 4, -3
ii) \(\sqrt{5}\) – \(\sqrt{5}\)
iii) \(\frac{1}{3}\), \(\frac{5}{3}\)
Solution:
i) 4, -3
Let the quadratic polynomial be ax² + bx + c, a ≠ 0,
and its zeroes be a and b.
then α = 4, β = – 3
sum of the zeroes = a + b = 4 – 3 = 1
product of the zeroes = a . b = 4 × -3
= -12
The requiral quadratic polynomial is k [x² – x (α + β) + αβ] where k is a constant
⇒ k[x² – x(1) + (-12)]
⇒ k[x² – x – 12]
When k = 1, the quadratic polynomial will be x² – x – 12.

ii) \(\sqrt{5}\) – \(\sqrt{5}\)
Let the quadratic polynomial be
ax² + bx + c, a ≠ 0 and its zeroes be a and b, Here α = \(\sqrt{5}\), β = –\(\sqrt{5}\)
sum of the zeroes = α + β = \(\sqrt{5}\) – \(\sqrt{5}\) = 0
product of the zeroes = α . β
= \(\sqrt{5}\) × –\(\sqrt{5}\) = -5
The required quadratic polynomial is
k² [x – x (α + β) + αβ] where k is a constant
⇒ k² [x² – x(0) + (-5)]
⇒ k[x² – 5]
wherek k = 1, the quadratic polynomial will be x² – 5

iii) \(\frac{1}{3}\), \(\frac{5}{3}\)
Let the quadrate polynomial be
ax² + bx + c, a ≠ 0 and its zeroes be α and β.
Then α = \(\frac{1}{3}\) and β = \(\frac{5}{3}\)
sum of the zeroes = α + β = \(\frac{1}{3}\) + \(\frac{5}{3}\)
= \(\frac{6}{3}\) = 2
Product of the zeroes = αβ = \(\frac{1}{3}\) . \(\frac{5}{3}\)
= \(\frac{5}{9}\)
The required quadratic polynomial is
k[x² – x(α + β) + αβ] where k is a constant
⇒ k[x² – x(2) + \(\frac{5}{9}\)]
⇒ k[x² – 2x + \(\frac{5}{9}\)]
Where k = 9, the quadratic polynomial will be a [x² – 2x + \(\frac{5}{9}\)] = 9x² – 18x + 5

Question 12.
Verify that 1, -2 and -3 are the zeroes of the cubic polynomial x³ + 4x² + x – 6 and check the relationship between zeroes and the coefficients.
Solution:
The given polynomial is x³ + 4x² + x – 6.
Comparing the given polynomial with
ax³ + bx² + cx + d, we get
a = 1, b = 4, c = 1, d = – 6
Let p(x) = x³ + 4x² + x – 6
p(1) = (1)³ + 4(1)² + 1 – 6
= 1 + 4 + 1 – 6 = 6 – 6 = 0
p(-2) = (-2)³ + 4(-2)² + (-2) – 6
= – 8 + 4(4) – 2 – 6
= – 8 + 16 – 2 – 6 = 16 – 16 = 0
p(-3) =(-3)³ + 4(-3)² + (-3) – 6
= – 27 + 4(9) – 3 – 6
= 36 – 36 = 0
∴ 1, -2 and – 3 are the zeroes of given polynomial. So, α = 1, β = -2, ∝= – 3

Question 13.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following.

i) p(x) = x³ + 4x² + 5x + 6, g(x) = x² + 3
ii) p(x) = x⁴ + 3x² – 4x + 8
g(x) = x² + 2 – x
Solution:
i) p(x) = x³ + 4x² + 5x + 6,
g(x) = x² + 3

The degree of x² + 3 is 2. The degree of 2x – 6 is 1
Since degree of (2x – 6)² < degree of (x² + 3)
∴ we stop here.
So, the quotient is x + 4 and the remainder is 2x – 6.

ii) p(x) = x⁴ + 3x² – 4x + 8
g(x) = x² + 2 – x = x² – x + 2
(∴ writing it in standard form)

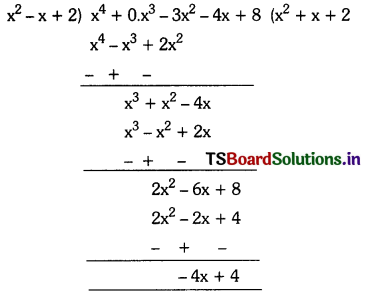
since degree of (-4x + 4) < degree of x² – x + 2
∴ we stop here
So, the quotient is x² + x + 2 and the remainder is (-4x + 4).

Question 14.
Check in each case the first polynomial is a factor of the second polynomial.
i) x² – 2, 2x⁴ – 3x³ – 3x² + 6x – 2
ii) x² – x + 1, x⁴ – 3x² + 4x – 3
Solution:
Hint : If the remainder is zero, then the first polynomial is a factor of the second one

i) x² – 2, 2x⁴ – 3x³ – 3x² + 6x – 2
The given polynomials are in standard form.

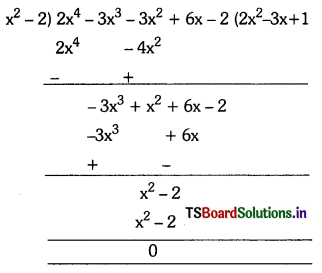
Since the remainder is zero, x² – 2 is the factor of 2x⁴ – 3x³ – 3x² + 6x – 2.

ii) x² – x + 1, x⁴ – 3x² + 4x – 3
The given polynomials is standard form.

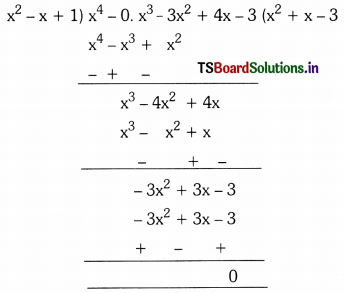
Since the remainder is zero, x² – x + 2 is the factor of x⁴ – 3x² + 4x – 3.

Question 15.
Draw the graph of the polynomial x² + x – 6 and mark the zeroes by the …….
Solution:
given that y = x² + x – 6
= x² + x – 6


zeroes of the polynomial x² + x – 6 are the x – co-ordinates of the points on the – 3 and 2 are the zeroes of the given polynomial on graph.

Question 16.
Check whether \(\frac{1}{2}\) is the zero of the polynomial 2x² + x – 1 or not. (AP-SA-II : 2016)
Solution:
Let p(x) = 2x² + x – 1
we have p(\(\frac{1}{2}\)) = 2(\(\frac{1}{2}\))² + \(\frac{1}{2}\) – 1
= 2 × \(\frac{1}{4}\) + \(\frac{1}{2}\) – 1
= \(\frac{1}{2}\) + \(\frac{1}{2}\) – 1 = 1 – 1
= 0
∴\(\frac{1}{2}\) is the zero of the polynomial.

Question 17.
Verify the relationship between the zeroes and the coefficient of x² – 25 by finding its zeroes. (AP-SA-II : 2016)
Solution:
Given polynomial is x² – 25
we have x² – 25 = 0
⇒ (x + 5) (x – 5) = 0
⇒ x = -5 or x = 5
∴ The zeroes of x² – 25 are – 5 and 5
∴ The sum of zeroes = -5 + 5 = 0 coefficient of x

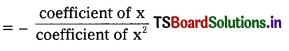
= –\(\frac{0}{1}\) = 0
And product of the zeroes = (-5) × (5) = – 25

= –\(\frac{25}{1}\) = -25
Hence verified.

Question 18.
Give two examples of the polynomials p(x) and g(x) satisfying division algori-tham. (AP-SA-II : 2016)
Solution:
Using division alogaritham,
We have p(x) = q(x) × g(x) + r(x)
Example (1) : on dividing 12x² + 8x + 24 by 3x² + 2x + 6, we get

Here p(x) = 12x² + 8x + 24
g(x) = 3x² + 2x + 6
g(x) = 4
r(x) = 0

Example – 2 : an dividing 3x³ + 6x² + 18x by x² + 2x + 6

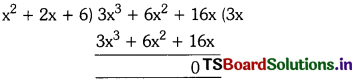
Here p(x) = 3x² + 6x² + 18x
g(x) = x² + 2x + 6
g(x) = 3x
r(x) = 0

Question 19.
Verify that 4, -1, –\(\frac{1}{4}\) are the zeroes of the cubic polynomial 4x³ – 11x² – 19x – 4 and check. (AP-SA-II: 2016)
Solution:
Given polynomial is 4x³ – 11x² – 19x – 4
p(x) comparing the given polynomial with
ax³ + bx² + cx + d, we get
a = 4, b = – 11, c = -19, d = – 4
Further p(4) = 4(4)³ – 11(4)² – 19(4) – 4
= 4 × 64 – 11(16) – 19(4) – 4
= 256 – 176 – 76 – 4
= 256 – 256 = 0
p(-1) = 4(-1)³ – 11(-1)² – 19(-1) – 4
= 4(-1) – 11(1) + 19-4
= -4 – 11 + 19 – 4
= -19 + 19 = 0


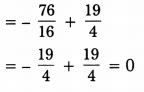
Therefore 4, -1, –\(\frac{1}{4}\) are the zeroes of
4x³ – 11x² – 19x – 4.
We take α = 4, β = – 1 and γ = –\(\frac{1}{4}\)
now α + β + γ = 4 – 1 – \(\frac{1}{4}\) = 3 – \(\frac{1}{4}\) = \(\frac{11}{4}\)
= \(\frac{-(-11)}{4}\) = –\(\frac{b}{a}\)

Question 20.
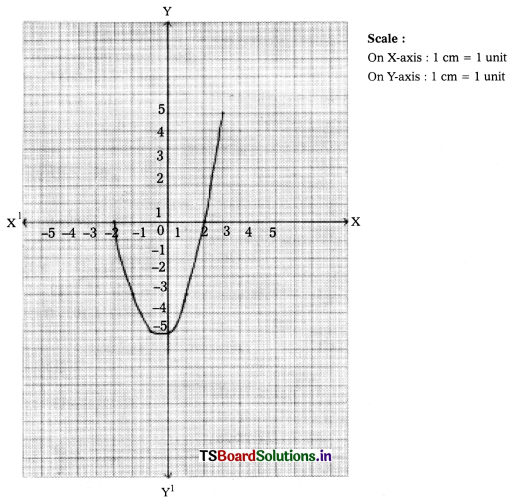
Draw the graph of the polynomial x² + x – 6 and mark the zeroes of the polynomial
Solution:
Given that y = x² + x – 6


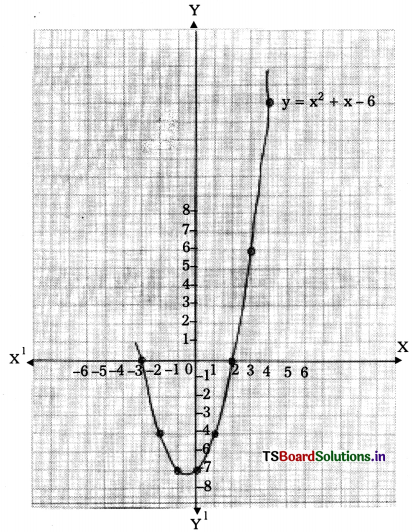
Scale : On X-axis :1 cm = 1 unit
On Y-axis :1 cm = 1 unit
Zeroes of the polynomial x² + x – 6 are the x – coordinates of the points on the x – axis.
-3 and 2 are the zeroes of the given polynomial on graph.

Question 21.
If α, β are zeroes of the polynomial 2x² + 7x + 5, find the value of α + β + αβ? (AP New SCERT Model Paper) Solution:
2x² + 7x + 5
α + β = \(\frac{-b}{a}\) = \(\frac{-7}{2}\)
α.β = \(\frac{\mathrm{c}}{\mathrm{a}}\) = \(\frac{5}{2}\)
∴ α + β + α.β = \(\frac{-7}{2}\) + \(\frac{5}{2}\) = \(\frac{-2}{2}\) = -1

Question 22.
If a, b and c are the zeroes of a polynomial of degree 3, then give the relations between the zeroes and the coefficients of the polynomial. (AP New SCERT Model Paper)
Solution:
α + β + γ = \(\frac{-b}{a}\)
αβ + βγ + γα = \(\frac{c}{a}\)
αβγ = \(\frac{-d}{a}\)

Question 23.
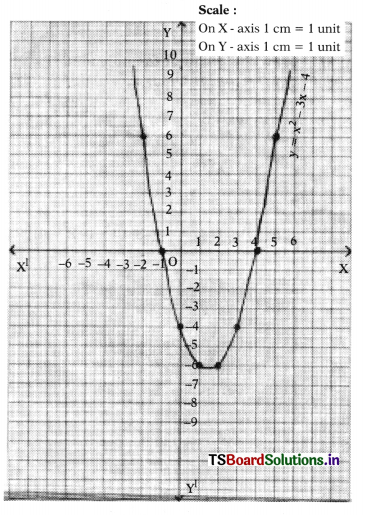
Solve the quadratic polynomial x² – 3x – 4 graphically. (AP New SCERT Model Paper)
Solution:
Let y = x² – 3x – 4

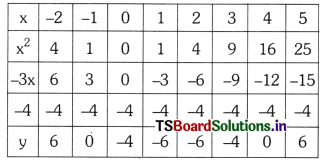
o.p. = (-2, 6), (-1, 0), (0, -4), (1, -6), (2, -6) (3, -4), (4, 0), (5, 6)
Scale : On X-axis 1 cm = 1 unit
On Y-axis 1 cm = 1 unit
The graph of y = x² – 3x – 4 intersects X-axis at (-1, 0) and (4, 0).
Hence the zeroes of p(x) are -1 and 4.