TS 10th Class Maths Important Questions Chapter 7 Coordinate Geometry

These TS 10th Class Maths Chapter Wise Important Questions Chapter 7 Coordinate Geometry given here will help you to solve different types of questions.

TS 10th Class Maths Important Questions Chapter 7 Coordinate Geometry

Previous Exams Questions

Question 1.
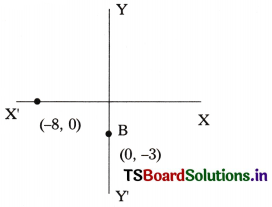
Where do the points (0, -3) and (-8, 0) lie on co-ordinate axis ? (A.P. June ’15)
Solution:
The point (0, -3) lie on OY’
∴ Its X-co-ordinate is zero and Y-co-ordinate is negative and the point (-8, 0) lie on OX’
∵ Its Y-co-ordinate is zero and X-co-ordinate is negative.

Question 2.
Find the centroid triangle whose vertices are (3, 4) (-7, -2) and (10, -5). (T.S. Mar. 15)
Solution:
Centroid of the triangle whose vertices are (x₁, y₁) (x₂, y₂) (x₃, y₃)
= \(\left[\frac{X_1+X_2+X_3}{3}, \frac{Y_1+Y_2+Y_3}{3}\right]\)
Here x₁ = 3, y₁ = 4, x₂ = -7, y₂ = -2, and x₃ = 10, y₃ = -5
Now G = \(\left(\frac{3-7+10}{3}, \frac{4-2-5}{3}\right)\)
= \(\left(\frac{6}{3}, \frac{3}{3}\right)\) = (2, 1)

Question 3.
Show that the points A = (4, 2), B (7, 5) and C (9, 7) are collinear. (A.P. Mar. 15)
Solution:
To show that three points are collinear the area formed by the triangle is zero. Area of triangle
Δ = \(\frac{1}{2}\) |x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)|
Here x₁ = 4, y₁ = 2, x₂ = 7, y₂ = 5,
x₃ = 9, y₃ = 7
Now Δ = \(\frac{1}{2}\) |4(5 – 7) + 7(7 – 2) + 9(2 – 5)|
= \(\frac{1}{2}\)|4(-2) + 7(5) + 9(-3)|
= \(\frac{1}{2}\)|-8 + 35 – 27|
= \(\frac{1}{2}\)|-35 + 35| = \(\frac{1}{2}\) |0| = 0
So the above three are collinear.

Question 4.
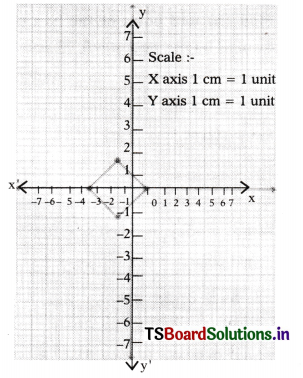
Name the type of the quadrilateral formed by joining the points A (-1, -2), B (1, 0) C (-1, 2) and D (-3, 0) are graph paper, justify your answer. (A.P. Mar. 15)
Solution:
Given points are A (-1, -2); B (1, 0); C (-1, 2) and D (-3, 0)

Distance between the two points

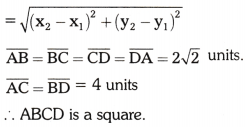
∴ ABCD is a square.
(OR)

From (1) and (2) ABCD is a square.
(OR)
From the graph
1) Diagonals are equal \(\overline{\mathrm{AC}}\) = \(\overline{\mathrm{BD}}\) = 4 units
2) Also diagonals \(\overline{\mathrm{AC}}\) and \(\overline{\mathrm{BD}}\) bisect each other. \(\overline{\mathrm{BD}}\) is a part of X-axis and \(\overline{\mathrm{AC}}\) is parallel to Y-axis.
∴ \(\overline{\mathrm{BD}}\) ⊥ \(\overline{\mathrm{AC}}\)
From (i), (ii) and (iii) ABCD is a square.

Question 5.
Find the mid point of the line segment formed by the points (-5, 5) and (5, -5) (A.P. Mar. 16)
Solution:
Formula for the mid points of line segment formed by (x₁, y₁) and (x₂, y₂) is
\(\left[\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right]\)
here x₁ = -5, y₁ = 5 and x₂ = 5, y₂ = -5
∴ mid point
= \(\left[\frac{-5+5}{2}, \frac{5-5}{2}\right]\) = \(\left[\frac{0}{2}, \frac{0}{2}\right]\) = [0, 0]

Question 6.
Show that the points A(-3, 3) B (0, 0) C(3, -3) are collinear. (T.S.Mar. 16)
Solution:
To show them as collinear the area formed by the triangle should be zero. Formula for area of triangle
∆ = \(\frac{1}{2}\)|x₁(y₂ – y₃) + x₂(y₃ – y₁ + x₃(y₁ – y₂)|
Here x₁ = -3, y₁ = 3; x₂ = 0, y₂ = 0 and x₃ = 3, y₃ = -3
So ∆ = \(\frac{1}{2}\) | (-3) (3 – 0) + 0 (-3 – 3) + 3(3 – 0) |
= \(\frac{1}{2}\) |(-3)(3) + 0(-6) + 3(3) |
= \(\frac{1}{2}\) |-9 + 0 + 9|
= \(\frac{1}{2}\) |0| = 0 sq. units
Hence the above three points are collinear.

Question 7.
Find the trisection points of the line segment joined by the points (-3, 3) and (3, -3). (A.P. Mar. ’16)
Solution:
The points which divide the line segment by 1:2 and 2:1 ratio (internally) are called trisection points.
Formula for the points of trisection of the line segment joined by (x₁, y₂) and (x₂, y₂) are
= \(\left[\frac{\mathrm{mx}_2+\mathrm{nx}_1}{\mathrm{~m}+\mathrm{n}}, \frac{\mathrm{my}_2+\mathrm{ny}_1}{\mathrm{~m}+\mathrm{n}}\right]\)
Where m = 2 and n = 1.
Here x₁ = -3, y₁ = 3 and x₂ = 3, y₂ = -3, then the point in the ratio 2 : 1 is

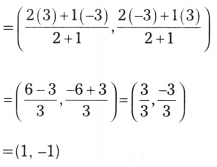
So (1, -1) is one trisection point. The point which is at 1 : 2 ratio is another trisection point.
So m = 1, n = 2.
Here x₁ = -3, = 3, x₂ = 3 and y₂ = -3
then \(\left[\frac{1(-3)+2(3)}{1+2}, \frac{1(-3)+2(3)}{1+2}\right]\)
= \(\left[\frac{-3+6}{3}, \frac{-3+6}{3}\right]\) = \(\left[\frac{3}{3}, \frac{3}{3}\right]\)
= (1, 1) is another trisection point.

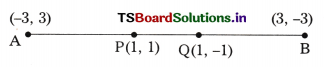
P, Q are trisection points.

Additional Questions

Question 1.
Find the distance between the following pairs of points. (Each 1 Mark)

i) (3, 4) and (6, 2)
ii) (-4, 6) and (0, 2)
iii) (-a, b) and (a, -b)

i) (3, 4) and (6, 2)
Solution:
Distance = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
= \(\sqrt{(6-3)^2+(2-4)^2}\)
= \(\sqrt{9+4}\) = \(\sqrt{13}\) Units

ii) (-4, 6) and (0, 2)
Solution:
Distance = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
= \(\sqrt{(0+4)^2+(2-6)^2}\)
= \(\sqrt{16+(-4)^2}\)
= \(\sqrt{16+16}\) = \(\sqrt{32}\)
= \(\sqrt{16 \times 2}\)
= \(\sqrt{16}\) × \(\sqrt{2}\) = 4\(\sqrt{2}\) Units

iii) (-a, b) and (a, -b)
Solution:
Distance = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
= \(\sqrt{(a+a)^2+(-b-b)^2}\)
= \(\sqrt{(2 a)^2+(-2 b)^2}\)
= \(\sqrt{4 a^2+4 b^2}\) = \(\sqrt{4\left(a^2+b^2\right)}\)
= \(\sqrt{4} \sqrt{a^2+b^2}\) = \(2 \sqrt{a^2+b^2}\) Units

Question 2.
Verify Whether the points A(1, 3), B(3, 5) and C(-4, 2) are collinear or not.
Solution:
Given A = (1, 3), B = (3, 5) and C = (-4, 2)
Slope of AB = m₁ = \(\frac{\mathrm{y}_2-\mathrm{y}_1}{\mathrm{x}_2-\mathrm{x}_1}\)
= \(\frac{5-3}{3-1}\) = \(\frac{2}{2}\) = 1
Slope of BC = m₂ = \(\frac{2-5}{-4-3}\) = \(\frac{-3}{-7}\) = \(\frac{3}{7}\)
Since m₁ ≠ m₂
∴ A, B, C are not collinear.

Question 3.
Show that (5, 3), (1, 2) and (-3, 1) are the vertices of an isosceles triangle.
Solution:
Let A = (5, 3), B = (1, 2) and C = (-3, 1)
Distance = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

Since AB = BC
∴ ΔABC is an isosceles triangle.
Hence given points are the vertices of an isos- celes triangle.

Question 4.
Show that the points (0, -2), (3, 2), (0, 6) and (-3, 2) are the vertices of a square.
Solution:
Let A = (0, -2), B = (3,2), C = (0,6), D = (-3, 2)
Distance = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)


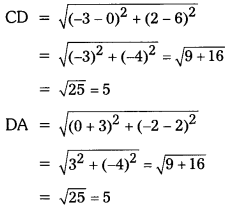
Sin AB = BC = CD = DA
∴ Given vertices form a square.

Question 5.
Show that the points (2, 4), (3, 7), (6, 8) and (5, 5) are the vertices of a Rhombus.
Solution:
Let A = (2, 4), B = (3, 7), C = (6, 8) and D = (5, 5)
Distance = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

Since AB = BC = CD = DA = \(\sqrt{10}\) and AC ≠ BD
∴ Given points form a Rhombus.

Question 6.
Find the co-ordinates of the point which divides the line segment joining the points (-2, 6) and (3, -4) in the ratio 3 : 5.
Solution:
Given points P (-2, 6) and Q (3, -4)
Let R be the required point which divides \(\overline{\mathrm{PQ}}\) in the ratio 3 : 5, then

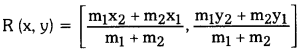
Here P = (-2, 6) = (x₁, y₁),
Q = (3, -4) = (x₂, y₂)
and m₁ : m₂ = 3 : 5
Then R (x, y)

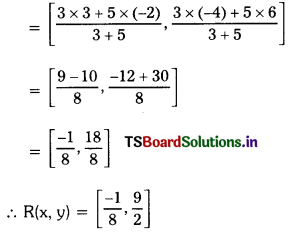
Question 7.
Find the ratio in which the X-axis divides the line segment joining the points (6, -2) and (4, 1) also find the point of intersection.
Solution:
Let the ratio be k : 1
given points are A = (6, -2) and B = (4, 1)
Then by section formula, the co-ordinates of the point which divide AB in the ratio k : 1 are
\(\left(\frac{\mathrm{k} \times 4+1 \times 6}{\mathrm{k}+1}, \frac{\mathrm{k} \times 1+1 \times-2}{\mathrm{k}+1}\right)\)
i.e., \(\left(\frac{4 k+6}{k+1}, \frac{k-2}{k+1}\right)\) ……. (1)
Since the point lies on the X-axis
∴ Its Y-co-ordinate is zero
i.e., \(\frac{k-2}{k+1}\) = 0 ⇒ k – 2 = 0 ⇒ k = 2
∴ The ratio is k : 1 = 2 : 1 ⇒ k = 2
Putting k = 2 in (1), we get, the point of intersection
= \(\left(\frac{4 \times 2+6}{2+1}, \frac{2-2}{2+1}\right)\)
= \(\left(\frac{8+6}{3}, \frac{0}{3}\right)\)
= \(\left(\frac{14}{3}, 0\right)\)

Question 8.
Find the ratio in which the Y-axis divides the line segment joining the points (9, -4) and (3, -2). Also find the point of intersection.
Solution:
Let the ratio be k : 1
Given points are A = (9, -4) and B = (3, -2)
Then by section formula, the co-ordinates of the point which divides AB in the ratio k : 1 are
\(\left(\frac{\mathrm{k} \times 3+1 \times 9}{\mathrm{k}+1}, \frac{\mathrm{k} \times(-2)+1 \times(-4)}{\mathrm{k}+1}\right)\)
i.e., \(\left(\frac{3 k+9}{k+9}, \frac{-2 k-4}{k+1}\right)\) —– (1)
Since the point lies on the Y-axis
∴ Its abscissa = 0
i.e., \(\frac{3 \mathrm{k}+9}{\mathrm{k}+9}\) = 0 ⇒ 3k + 9 = 0 ⇒ 3k = -9
⇒ k = \(\frac{-9}{3}\) = -3
∴ The ratio is k : 1 = -3 : 1 ⇒ k = -3
Putting k = -3 in (1), we get, the point of intersection
= \(\left(\frac{3 \times(-3)+9}{-3+9}, \frac{-2(-3)-4}{-3+1}\right)\)
= \(\left(\frac{-9+9}{6}, \frac{6-4}{-2}\right)\)
= \(\left(\frac{0}{6}, \frac{2}{-2}\right)\)
= (0, -1)

Question 9.
Find the centroid of the triangle whose vertices are given below.
i) (1, 6), (7, 4), (1, 5)
ii) (1, 0), (-3, -3), (-4, -3)

i) (1, 6), (7, 4), (1, 5)
Solution:
Given A = (1, 6) = (x₁, y₁)
B = (7, 4) = (x₂, y₂)
C = (1, 5) = (x₃, y₃)
Centroid of the triangle
= \(\left(\frac{\mathrm{x}_1+\mathrm{x}_2+\mathrm{x}_3}{3}, \frac{\mathrm{y}_1+\mathrm{y}_2+\mathrm{y}_3}{3}\right)\)
∴ Centroid of the triangle
= \(\left(\frac{1+7+1}{3}, \frac{6+4+5}{3}\right)\)
= \(\left(\frac{9}{3}, \frac{15}{3}\right)\) = (3, 5)

ii) (1, 0), (-3, -3), (-4, -3)
Solution:
Given A = (1, 0), B = (-3, -3), C = (-4, -3)
Centroid of the triangle
= \(\left(\frac{\mathrm{x}_1+\mathrm{x}_2+\mathrm{x}_3}{3}, \frac{\mathrm{y}_1+\mathrm{y}_2+\mathrm{y}_3}{3}\right)\)
= \(\left(\frac{1-3-4}{3}, \frac{0-3-3}{3}\right)\)
= \(\left(\frac{-6}{3}, \frac{-6}{3}\right)\)
= (-2, -2)

Question 10.
Find the area of the triangle whose vertices are
i) (3, 4), (0, 1), (3, -3)
ii) (2, 10), (4, 7), (0, -1)
iii) (3, 4), (0, 1), (3, -3)
Solution:
i)
Given A = (3, 4) = (x₁, y₁)
B = (0, 1) = (x₂, y₂)
C = (3, -3) = (x₃, y₃)
are the vertices of ∆ABC.
Area of ∆ABC
= \(\frac{1}{2}\)|x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)|
= \(\frac{1}{2}\)|3(1 + 3) + 0(-3 – 4) + 3(4 – 1)|
= \(\frac{1}{2}\)|3(4) + 0(-7) + 3(3)|
= \(\frac{1}{2}\)|12 + 0 + 9|
= \(\frac{1}{2}\)|21|
= \(\frac{21}{2}\) sq. units

ii) (2, 10), (4, 7), (0, -1)
Solution:
Given A = (2, 10), B = (4, 7), C = (0, -1)
Area of ∆ ABC
= \(\frac{1}{2}\)|x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)|
= \(\frac{1}{2}\)|(7 + 1) + 4(-1 – 10) + 0(10 – 7)|
= \(\frac{1}{2}\)|2(8) + 4(-11) + 0(3)|
= \(\frac{1}{2}\)|16 – 44 + 0|
= \(\frac{1}{2}\)|-28| = |-14|
= 14sq. units

Question 11.
Find the value of k’ for which the points are collinear.
i) (k, 9), (7, 7), (1, 5)
ii) (6, -1), (k, -6), (0, -7)
iii) (k, k), (1, 2), (3, -2)

i) (k, 9), (7, 7), (1, 5)
Solution:
Given A(k, 9) = (x₁, y₁)
B(7, 7) = (x₂, y₂)
C(1, 5) = (x₃, y₃) are collinear
∴ Area of Δ ABC = 0
⇒ \(\frac{1}{2}\) x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂) = 0
⇒| \(\frac{1}{2}\)|k(7 – 5) + 7(5 – 9) + 1(9 – 7)| = 0
⇒ |k(2) + 7(-4) + 1(2)| = 0
⇒ 2k – 28 + 2 = 0
⇒ 2k – 26 = 0
⇒ 2k = 26
k = \(\frac{26}{2}\) = 13
∴ k = 13

ii) (6, -1), (k, -6), (0, -7)
Solution:
Given A(6, -1), B(k, -6), C(0, -7) are collinear
∴ Area of Δ ABC = 0
⇒ \(\frac{1}{2}\)|6(-6 + 7) + k(-7 + 1) + 0(-1 + 6)| = 0
⇒ |6(1) + k(-6) + 0(5)| = 0
⇒ 6 – 6k + 0 = 0
⇒ -6k = -6
⇒ k = \(\frac{-6}{-6}\) = 1
∴ k = 1

iii) (k, k), (1, 2), (3, -2)
Solution:
Given A = (k, k), B(1, 2), C(3, -2) are collinear
∴ Area of Δ ABC = 0
⇒ \(\frac{1}{2}\)|k(2 + 2) + 1(-2 – k) + 3(k – 2)| = 0
⇒ \(\frac{1}{2}\)|k(4) + 1(-2 – k) + 3(k – 2)| = 0
⇒ 4k – 2 – k + 3k – 6 = 0
⇒ 6k – 8 = 0
⇒ 6k = 8
⇒ k = \(\frac{8}{6}\) = \(\frac{4}{3}\)
∴ k = \(\frac{4}{3}\)

Question 12.
Find the slope of the line joining the points.
i) (7, -5) and (8, 1)
ii) (4a, 6b) and (a, -b)
iii) (5, -1) and (-8, 0)

i) (7, -5) and (8, 1)
Solution:
Given A(7, -5) = (x₁, y₁)
B(8, 1) = (x₂, y₂)
Slope of line AB = \(\frac{y_2-y_1}{x_2-x_1}\)
= \(\frac{1-(-5)}{8-7}\)
= \(\frac{1+5}{1}\) = \(\frac{6}{1}\) = 6

ii) (4a, 6b) and (a, -b)
Solution:
Given A(4a, 6b), B(a, -b)
Slope of line AB = \(\frac{-b-6 b}{a-4 a}\) = \(\frac{7 b}{3 a}\)

iii) (5, -1) and (-8, 0)
Solution:
Given A(5, -1) and B(-8, 0)
Slope of line AB = \(\frac{0-(-1)}{-8-5}\)
= \(\frac{0+1}{-13}\) = \(\frac{-1}{13}\)

Question 2.
Find the slope of a line whose inclination is

i) 60°
ii) 135°
iii) 120°
iv) 135°

i) 60°
Solution:
Given 60° = θ
Slope of the line = m
= tan θ = tan 60° = \(\sqrt{3}\)

ii) 135°
Solution:
Given 135° = θ
Slope of the line = m = tan θ = tan 135°
= tan (90° + 45°)
= -cot 45° = -1

iii) 120°
Solution:
Given 120° = θ
Slope of the line = m = tan θ = tan 120°
= tan (90° + 30°)
= -cot 30°
= –\(\sqrt{3}\)

iv) 135°
Slope of the line = m = tan θ = tan 135°
= tan (90° + 45°)
= -cot 45°
= -1

Question 3.
If (6, 7) is the mid point of the line segment joining A(7, 6) and B(5, y), find ‘y’.
Solution:
Given Mid point = (6, 7) = m and
A(7, 6) = (x₁, y₁)
B(5, y) = (x₂, y₂)
Mid point of A and B = (6, 7)
⇒ \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\) = (6, 7)
⇒ \(\left(\frac{7+5}{2}, \frac{6+y}{2}\right)\) = (6, 7)
Equations Y-co-ordìnate on both sides
⇒ \(\frac{6+\mathrm{y}}{2}\) = 7 ⇒ 6 + y = 2 × 7
⇒ 6 + y = 2 × 7
⇒ 6 + y = 14
⇒ y = 14 – 6
y = 8
∴ y = 8