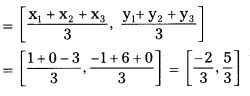Students can practice TS Class 10 Maths Solutions Chapter 7 Coordinate Geometry Ex 7.2 to get the best methods of solving problems.
TS 10th Class Maths Solutions Chapter 7 Coordinate Geometry Exercise 7.2
Question 1.
Find the co-ordinates of the point which divides the line segment joining the points (-1, 7) and (4, -3) in the ratio 2 : 3.
(A.P. Mar. 16)
Solution:
Given points P(-1, 7) and Q (4, -3).
Let ‘R’ be the required point which divides \(\overline{\mathrm{PQ}}\) in the ratio 2 : 3 then
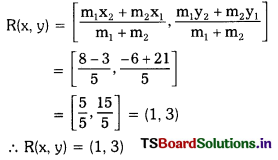
Question 2.
Find the co-ordinates of the points of tri-section of the line segment joining (4, -1) and (-2, -3). (A.P.June ’15)
Solution:
Given points A(4, -1) and B(-2, -3)
Let P and Q be the points of trisection of \(\overline{\mathrm{AB}}\), then AP = PQ = QB
![]()
∴P divides AB internally in the ratio 1:2.
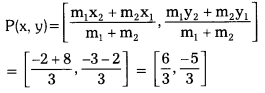
P(x, y) = (2, -5/3)
Also, Q divides \(\overline{\mathrm{AB}}\) in the ratio 2 : 1 internally.
Q(x, y) = \(\left[\frac{-4+4}{3}, \frac{-6-1}{3}\right]\) = (0, -7/3)
Q(x, y) = (0, -7/3)
![]()
Question 3.
Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).
Solution:
Given : A(-3, 10) and B(6, -8)
Let P(-1, 6) divides \(\overline{\mathrm{AB}}\) in the ratio k : 1 internally.
By section formula
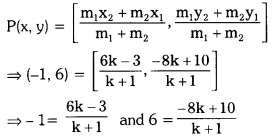
6k – 3 = -k – 1 and -8k + 10 = 6k + 6
-7k = – 2 and 14k = 4 4 14
∴ The ratio is 2/7 : 1 or 2 : 7
Question 4.
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Solution:
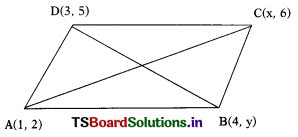
Given : ![]() ABCD is a parallelogram where
ABCD is a parallelogram where
A(1, 2), B(4, y), C(x, 6) and D(3, 5).
In a parallelogram, diagonals bisect each other, i.e., the mid points of the diagonals coincide with each other.
i.e., mid point of AC = mid point of BD
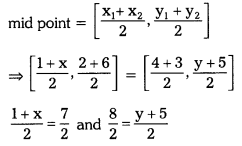
1 + x = 7 and ⇒ 8 = y + 5
x = 6 and y = 8 – 5 = 3
∴ x = 6 and y = 3.
Question 5.
Find the co-ordinates of a point A, where AB is the diameter of a circle. Whose centre is (2, -3) and B is (1, 4).
Solution:
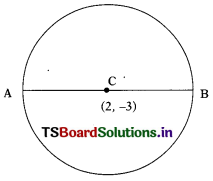
Given : A circle with centre ‘C’ (2, -3)
\(\overline{\mathrm{AB}}\) is diameter where B = (1, 4); A = (x, y)
∴ C is the mid point of AB
[∵ centre of a circle is the midpoint of the diameter].

![]()
Question 6.
If A and B are (-2, -2) and (2, -4) respectively. Find the co-ordinates of such that AP = \(\frac{3}{7}\) AB and P lies on the segment AB.
Solution:
Given : A(-2, -2) and B(2, -4)
P lies on AB such that AP = \(\frac{3}{7}\) AB
![]()
⇒ \(\frac{A P}{A B}\) ⇒ \(\frac{3}{7}\) = \(\frac{A P}{P B}\) = \(\frac{3}{7-3}\) = \(\frac{3}{4}\)
i.e., P divides \(\overline{\mathrm{AB}}\) in the ratio 3 : 4 By section formula.
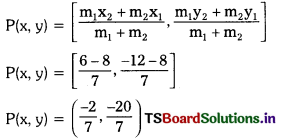
Question 7.
Find the co-ordinates of points which divide the line segment joining A(-4, 0) and B(0, 6) into four equal parts.
Solution:
Given, A(-4, 0) and B(0, 6)
Let R Q and R be the points which divide \(\overline{\mathrm{AB}}\) into four equal parts.
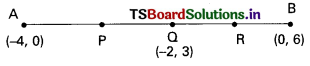
P divides \(\overline{\mathrm{AB}}\) in the ratio 1 : 3
Q → 1 : 1 and R → 3 : 1 use section formula to find P, Q and R.
The Q is the mid point of \(\overline{\mathrm{AB}}\)
P is the midpoint of \(\overline{\mathrm{AQ}}\)
R is the midpoint of \(\overline{\mathrm{QB}}\)

Question 8.
Find the co-ordinates of the points which divide the line segment joining A(-2, 2) and B(2, 8) into four equal parts.
Solution:
Given : A(-2, 2) and B(2, 8)
Let P, Q and R be the points which divide AB into four equal parts.
![]()
Then Q is the midpoint of \(\overline{\mathrm{AB}}\)
P is the midpoint of \(\overline{\mathrm{AQ}}\)
R is the midpoint of \(\overline{\mathrm{QB}}\)

Question 9.
Find the co-ordinates of the point which divide the line segment joining the points (a + b, a – b) and (a – b, a + b) in the ratio 3 : 2 internally.
Solution:
Given : A(a + b, a – b) and B(a – b, a + b)
let P(x, y) divides \(\overline{\mathrm{AB}}\) in the ratio 3 : 2 inter¬nally.
By using section formula,
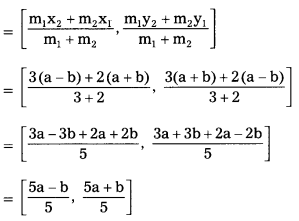
![]()
Question 10.
Find the co-ordinates of centroid of the triangle with vertices following.
i) (-1, 3), (6, -3) and (-3, 6).
Solution:
Given : ΔABC in which A(-1, 3), B(6, -3) and C(-3, 6).
Centroid

ii) (6, 2), (0, 0) and (4, -7).
Solution:
Given : The three vertices of a triangle are A(6, 2), B(0, 0) and C(4, -7)
Centroid (x, y)
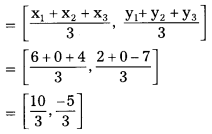
iii) (1, -1) (0, 6) and (-3, 0)
Solution:
Given: (1, -1), (0, 6) and (-3, 0) are the vertices of a triangle.
Centroid (x. y)