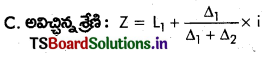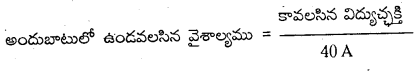Telangana TSBIE TS Inter 1st Year Physics Study Material 5th Lesson గమన నియమాలు Textbook Questions and Answers.
TS Inter 1st Year Physics Study Material 5th Lesson గమన నియమాలు
అతిస్వల్ప సమాధాన ప్రశ్నలు
ప్రశ్న 1.
జడత్వం అంటే ఏమిటి ? జడత్వ కొలతను ఏది ఇస్తుంది (మార్చి 2014)
జవాబు:
జడత్వం అంటే మార్పుకు నిరోధం. వస్తువు తనంతట తానుగా తన స్థితిని మార్చుకోజాలని వస్తు ధర్మాన్ని జడత్వం అంటారు. వస్తువు జడత్వాన్ని ద్రవ్యరాశి ‘m’ తో కొలుస్తారు.
ప్రశ్న 2.
న్యూటన్ మూడవ గమన నియమం ప్రకారం ప్రతి బలం సమానం, వ్యతిరేక బలాలతో కూడా ఉన్నప్పుడు గమనం అనేది ఏ విధంగా సాధ్యమవుతుంది?
జవాబు:
న్యూటన్ మూడవ నియమం ప్రకారము బలాలు ఎప్పుడూ జంటగానే ఏర్పడతాయి. చర్య = – ప్రతిచర్య.
సాధారణంగా చర్య, ప్రతిచర్యలు వేరు వేరు వ్యవస్థలపై పని చేయడం వల్ల చలనం సాధ్యపడుతుంది.
ప్రశ్న 3.
ఒక తుపాకి నుంచి బుల్లెట్ను పేల్చినప్పుడు, తుపాకినీ వెనుకకు నెట్టివేసినట్లు అనిపిస్తుంది. వివరించండి.
జవాబు:
తుపాకి పేల్చటం అంతర్గత చర్య. అంతర్గత బలాలు వస్తువు ద్రవ్యవేగాన్ని మార్చలేవు. కావున m1u1 + m2u2 = 0. (తుపాకి పేలకముందు అవి విరామస్థితిలో ఉన్నవి కావున)
∴ m1u1 = -m2u2 కావున తుపాకి గుండు ముందుకు, తుపాకి వెనుకకు పోవడం ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారం జరుగుతుంది.

ప్రశ్న 4.
ఒకే గుళ్లను ఉపయోగించినా బరువుగా ఉన్న రైఫిల్ తేలిక రైఫిల్ కంటే తక్కువ వేగంతో వెనకకు వస్తుంది. ఎందువల్ల?
జవాబు:
తుపాకి వెనుకకు తన్నే వేగం v1 = \(\frac{\mathrm{mv}}{\mathrm{M}}\) తుపాకి వేగము బులెట్ ద్రవ్యవేగానికి (mv), తుపాకి బరువుకు గల నిష్పత్తి. mv స్థిరంగా ఉన్నప్పటికి తుపాకి బరువు తగ్గితే దాని వెనుకకు తన్నే వేగం పెరుగుతుంది.
ప్రశ్న 5.
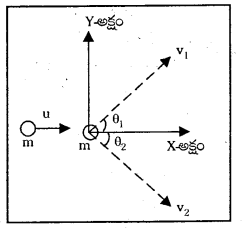
విరామస్థితిలో ఉన్న ఒక బాంబు రెండు ముక్కలుగా పేలితే దాని ముక్కలు వ్యతిరేకదిశలో చలిస్తాయి. వివరించండి.
జవాబు:
విరామ స్థితిలో ఉన్న బాంబుకు తొలి ద్రవ్యవేగం m1v1 + m2v2 = 0 బాంబు పేలిన తరువాత దాని ముక్కల ద్రవ్యవేగాల మొత్తం (ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారం ‘సున్న.)
∴ m1u1 + m2u2 = 0 లేదా m1v1 + m2v2 (- గుర్తు వ్యతిరేక దిశ) అనగా ఆ రెండు ముక్కలు వ్యతిరేక దిశలో చలిస్తాయి.
ప్రశ్న 6.
బలాన్ని నిర్వచించండి. ప్రకృతిలోని ప్రాథమిక బలాలను పేర్కొనండి.
జవాబు:
ఒక వస్తువు యొక్క స్థితిని మార్చునది లేక మార్చుటకు ప్రయత్నించే భౌతికరాశిని బలంగా నిర్వచించారు. ఇది సదిశరాశి.
ప్రకృతిలో ప్రాథమిక బలాలు : 1) గురుత్వాకర్షణ బలాలు, 2) విద్యుదయస్కాంత బలాలు, 3) ప్రబల కేంద్రక బలాలు, 4) దుర్బల కేంద్రక బలాలు.
ప్రశ్న 7.
ఘర్షణ గుణకం విలువ ఒకటి కంటె ఎక్కువగా ఉంటుందా ?
జవాబు:
అవును. సాధారణంగా ఘర్షణ గుణకం ఒకటి కంటే తక్కువగా ఉంటుంది. కాని కొన్ని ప్రత్యేక సందర్భాలలో ‘i’ కంటె ఎక్కువగా ఉండవచ్చు.

ప్రశ్న 8.
గాలి నిండిన టైర్లు ఉన్న కారు కంటే గాలి లేని టైర్లు ఉన్న కారు తొందరగా ఆగుతుంది. ఎందుకు ?
జవాబు:
టైర్లలోని గాలి తక్కువగా ఉన్నపుడు అవి ఎక్కువ భాగము సమాంతరముగా మారి భూమిని తాకుతాయి. దానివలన ఘర్షణ బలం పెరుగుతుంది. దొర్లుడు ఘర్షణ బలం వస్తువుల మధ్య ఉన్న స్పర్శతలం వైశాల్యంపై ఆధారపడుతుంది. కాబట్టి కారు త్వరగా నిశ్చల స్థితికి వస్తుంది.
ప్రశ్న 9.
గుర్రం చలనంలో ఉన్నప్పటికంటే, అది బయలుదేరడం ప్రారంభించే సమయంలో ఎక్కువ బలాన్ని ఎందుకు ఉపయోగిస్తుంది ?
జవాబు:
వస్తువు చలనంలోనికి రావటానికి సీమాంత ఘర్షణ బలాన్ని అధిగమించాలి. (Fs = μsmg). కాని ఒకసారి చలనములోనికి ఉండ వచ్చిన తరువాత గతిక ఘర్షణ బలం పనిచేస్తుంది. గతిక ఘర్షణ బలం సీమాంత ఘర్షణ బలం కంటే తక్కువ. కావున వలన చలనం ఆరంభంలో గుర్రం ఎక్కువ బలంతో బండిని లాగవలసి ఉంటుంది.
ప్రశ్న 10.
వస్తువు భారాన్ని రెట్టింపు చేస్తే ఘర్షణ గుణకం ఏమవుతుంది ? (మే 2014)
జవాబు:
వస్తువు భారాన్ని రెట్టింపు చేసినప్పటికి ఘర్షణ గుణకం విలువ మారదు. ఎందుకనగా ఘర్షణ బలం లంబ ప్రతిచర్య కావున భారం రెండింతలైన, లంబ ప్రతిచర్య, ఘర్షణ బలం కూడా రెట్టింపు అవుతాయి. కాని ఘర్షణ గుణకం విలువ మారదు.
స్వల్ప సమాధాన ప్రశ్నలు
ప్రశ్న 1.
0.1 kg ద్రవ్యరాశి ఉన్న ఒక రాయిని నిలువుగా పైకి విసిరారు. కింది సందర్భాలలో రాయిపై పనిచేసే నికర బలం పరిమాణం, దిశను తెలపండి. ఎ) నిలువుగా పైకి ప్రయాణిస్తున్నప్పుడు, బి) క్రిందికి ప్రయాణిస్తున్నప్పుడు, సి) గరిష్ఠ ఎత్తు వద్ద, (ఎక్కడైతే క్షణం పాటు రాయి విరామస్థితికి వస్తుందో)
జవాబు:
రాయి ద్రవ్యరాశి m = 0.1 kg.
ఎ) రాయి పైకి పోవునపుడు దానిపై పనిచేసే బలం గురుత్వాకర్షణ బలము.
∴ F = mg = 0.1 × 9.8 = 0.98 న్యూ.
బి) రాయి క్రిందికి పడునపుడు దానిపై పనిచేసే బలం F = గురుత్వాకర్షణ బలము
∴ F = mg = 0.1 ×: 9.8 = 0.98 .న్యూ.
సి) రాయి గరిష్టోన్నతి స్థానం వద్ద ఉన్నపుడు దాని వేగం సున్న కాని అధోదిశలో గురుత్వాకర్షణ బలం పనిచేస్తుంది.
∴ ఫలిత బలము = mg = 0.1 × 9.8 = 0.98 న్యూ.
గమనిక : రాయి యొక్క మొత్తం ప్రయాణమార్గంలో గురుత్వాకర్షణ బలం అధోదిశలోనే పనిచేస్తుంది.

ప్రశ్న 2.
ద్రవ్యవేగం, ప్రచోదనాలను నిర్వచించండి. రేఖీయ ద్రవ్యవేగ నిత్యత్వ నియమాన్ని నిర్వచించి, వివరించండి. ఉదాహరణలు ఇవ్వండి.
జవాబు:
ద్రవ్యవేగం (\(\overline{\mathrm{p}}\)) : వస్తువు యొక్క ద్రవ్యరాశిని దాని వేగంతో గుణించగా వచ్చు లబ్ధాన్ని ద్రవ్యవేగంగా నిర్వచించినారు.
ద్రవ్యవేగం (\(\overline{\mathrm{p}}\)) = ద్రవ్యరాశి × వేగము ∴ \(\overline{\mathrm{p}}\) = mv. ఇది సదిశరాశి.
ప్రమాణము : కి.గ్రా. మీ/సె.; మితిఫార్ములా : MLT-1
ప్రచోదనము (J): వస్తువుపై ఎక్కువ బలం స్వల్పకాలంపాటు పనిచేస్తే బలము మరియు కాలముల లబ్దాన్ని ప్రచోదనము అంటారు.
ప్రచోదనము (J) = F × t, ఇది సదిశరాశి. ప్రమాణము : న్యూటన్ – సెకను; మితిఫార్ములా : MLT-1
ప్రచోదనము = ద్రవ్యవేగంలో మార్పు అని చూపుట :
నిర్వచనం ప్రకారము ప్రచోదనము (J) = బలము × కాలము = F × t
కాని బలము F = ma ఇందులో a = \(\left(\frac{\mathrm{v}-\mathrm{u}}{\mathrm{t}}\right)\)
ప్రచోదనము J = m\(\left(\frac{\mathrm{v}-\mathrm{u}}{\mathrm{t}}\right)\) × t = mv – mu. = ద్రవ్యవేగంలోని మార్పు.
అనగా ప్రచోదనము J = mv – mu ద్రవ్యవేగంలో మార్పు.
ప్రశ్న 3.
మోటారు సైకిళ్ళు, కార్లకు షాక్ అబ్సార్బర్లను ఎందుకు ఉపయోగిస్తారు ?
జవాబు:
వాహనాలు వేగంగా చలించేటపుడు రోడ్డుపై గల ఎగుడు దిగుడు గుంటలపై గుండా వెళ్ళినపుడు అవి ప్రచోదనానికి లోనవుతాయి.
ద్రవ్యవేగంలో మార్పు సమానమైనప్పటికి కాలవ్యవధి ఎక్కువ ఐతే ప్రచోదనం దుష్ప్రభావం చూపదు. ప్రచోదనము
J = F.dt = (mv – mu). బలము F = \(\frac{m v-m u}{\Delta t}\) ఇందులో ∆t చిన్నదైతే ద్రవ్యవేగంలో మార్పు సమానమైనప్పటికి బలము ఎక్కువ, కాలవ్యవధి ∆t పెద్దదైతే బలము F విలువ తక్కువ. కావున కాలవ్యవధి పెరిగితే ఒకే విధమైన ప్రచోదనానికి మనపై పనిచేసే బలం తక్కువ. ప్రచోదనంలో కాలవ్యవధిని పెంచడానికి వాహనాలకు షాక్ అబ్జార్బర్లు వాడతారు.
షాక్ అబ్జార్బర్లు ప్రచోదనం వల్ల వచ్చిన బలం ఉపయోగించుకొని వాటిలో గల స్ప్రింగ్లను సంపీడనం చెందిస్తాయి. ఈ స్ప్రింగ్లకు కాలస్థిరాంకము ఎక్కువగా ఉండేటట్లు చేయడం వల్ల స్ప్రింగ్ గ్రహించిన బలాన్ని నిదానంగా విడుదల చేస్తుంది. ఫలితంగా మనపై ప్రచోదన ప్రభావం తగ్గటం వల్ల ప్రయాణం సుఖవంతంగా ఉంటుంది.

ప్రశ్న 4.
సీమాంత ఘర్షణ, గతిక ఘర్షణ, దొర్లుడు ఘర్షణలను వివరించండి.
జవాబు:
స్థితిక ఘర్షణ : విరామ స్థితిలో గల వస్తువుల మధ్య ఘర్షణను స్థితిక ఘర్షణ లేదా సీమాంత ఘర్షణ అంటారు. ఇది వస్తువుల మధ్య జరగబోయే చలనాన్ని వ్యతిరేకిస్తుంది.
వస్తువుపై అనువర్తిత బలం ప్రయోగించినపుడు మాత్రమే స్థితిక ఘర్షణ బలం పనిచేయడం ప్రారంభిస్తుంది. ఈ బలాలు అనువర్తిత బలంతో పాటు ఒక సీమాంత విలువ వరకు పెరుగుతాయి. గరిష్ఠ స్థితిక ఘర్షణ (fs) విలువ అభిలంబ ప్రతిచర్య (N) కు అనులోమానుపాతంలో ఉంటుంది.
(fs) max = μkN
గతిక ఘర్షణ : గమనంలోకి వచ్చిన తరువాత స్పర్శ తలాల మధ్య సాపేక్ష చలనాన్ని నిరోధించే బలాన్ని గతిక ఘర్షణ
బలం అంటారు.
fk = μkN
గతిక ఘర్షణ గుణకం μk విలువ స్థితిక ఘర్షణ గుణకం μs కన్నా తక్కువ.
దొర్లుడు ఘర్షణ : వస్తువుల మధ్య దొర్లుడు చలనం ఉన్నపుడు దొర్లుడు చలనాన్ని వ్యతిరేకిస్తూ స్పర్శ తలాలకు సమాంతరంగా పనిచేసే బలాన్ని దొర్లుడు ఘర్షణ అంటారు.
ఘర్షణ బలాలన్నింటిలో కన్న దొర్లుడు ఘర్షణ బలం విలువ అతి తక్కువ.
ప్రశ్న 5.
ఘర్షణ వల్ల కలిగే లాభాలు, నష్టాలను వివరించండి.
జవాబు:
లాభాలు :
- ఘర్షణ బలాలు మన నిత్యజీవనంలో ముఖ్యమైన పాత్రను పోషిస్తాయి. నడిచేటప్పుడు భూమికి, చెప్పులకు మధ్య గల ఘర్షణ బలం జారిపడిపోకుండా ఆపుతుంది.
- ఘర్షణ బలాలు యంత్రాలలో చలనాన్ని ఒక చక్రము నుండి రెండవ దానికి బెల్టుల ద్వారా అందించుటలో ఉపయోగపడతాయి.
- బ్రేకులు వేసినపుడు వాహనాలు నిశ్చలస్థితికి రావటానికి ఘర్షణ బలాలు అవసరం.
- ఘర్షణ బలాలు లేకున్నచో తాడుతో వస్తువులను బంధించలేము.
- ఘర్షణ బలాలు కారణంగానే మేకులు, బోల్టులు చెక్కలను కలిపి ఉంచుతాయి.
నష్టాలు :
- ఘర్షణ వలన చాలా శక్తి వృధా అవుతుంది.
- యంత్ర భాగాలు త్వరగా అరిగిపోతాయి.
- ఘర్షణ వలన ఉష్ణం జనించి, యంత్ర పదార్థాల బలం తగ్గిపోతుంది

ప్రశ్న 6.
ఘర్షణను తగ్గించే పద్ధతులను పేర్కొనండి. (మార్చి 2014, మే 2014)
జవాబు:
ఘర్షణను తగ్గించు పద్ధతులు:
- నునుపు చేయుట :.ఘర్షణ ముఖ్యముగా తలములోని హెచ్చుతగ్గుల వలన వస్తుంది. కాబట్టి తలములను నునుపు చేయుట ద్వారా ఘర్షణ తగ్గించవచ్చు. కాని బాగా ఎక్కువగా నునుపు చేసినచో మరల ఘర్షణ పెరుగుతుంది.
- స్నేహకాలు ఉపయోగించుట : గ్రీజు, నూనె మొదలగు పదార్థములను ఉపయోగించి యంత్ర భాగాల మధ్య ఘర్షణను తగ్గించవచ్చు.
- బాల్ బేరింగులు ఉపయోగించుట : చిన్నవి, గుండ్రనైన ఇనుపగోళాలు ఉపయోగించి రెండు తలాల మధ్య గల జారుడు చలనాన్ని దొర్లుడు చలనంగా మార్చవచ్చు. ఇలా చేయుట వలన ఘర్షణ తగ్గుతుంది.
- స్ట్రీమ్ లైనింగ్ : గాలిలో ప్రయాణించే విమానాలకు, గాలి వలన ఘర్షణ ఉంటుంది. అదే విధంగా నీటిలో ప్రయాణించే ఓడలకు, నీటికి మధ్య ఘర్షణ ఉంటుంది. ఈ రకమైన ఘర్షణను తగ్గించటాన్కి, విమానాలు, ఓడలు ఒక ప్రత్యేకమైన ఆకారంలో తయారుచేస్తారు. దీనిని స్ట్రీమ్ లైనింగ్ అంటారు.
ప్రశ్న 7.
దొర్లుడు ఘర్షణ నియమాలను తెలపండి.
జవాబు:
ఒక వస్తువు వేరొక తలంపై దొర్లుతున్నపుడు, వాటి మధ్య గల ఘర్షణను దొర్లుడు ఘర్షణ అంటారు.
దొర్లుడు ఘర్షణ గుణకం

దొర్లుడు ఘర్షణ సూత్రాలు :
- దొర్లుడు ఘర్షణ విలువ స్పర్శలోనున్న తలాల వైశాల్యంపై ఆధారపడుతుంది.
- దొర్లే వస్తువు, దొర్లుతున్న తలం ఆకారాన్ని మార్పు చేస్తుంది. అందువలన తలంలోని పదార్థం దొర్లుడును వ్యతిరేకిస్తుంది.
- దొర్లుడు ఘర్షణ, దొర్లుతున్న వస్తువు వ్యాసార్ధముపై ఆధారపడుతుంది. వ్యాసార్ధము ఎక్కువైన దొర్లుడు ఘర్షణ తక్కువగా ఉంటుంది. fr ∝ \(\frac{1}{r}\)
- దొర్లుడు ఘర్షణ, లంబ ప్రతిచర్యకు అనులోమానుపాతంలో ఉంటుంది Fr ∝ R.

ప్రశ్న 8.
లాన్ రోలర్ను నెట్టడం కంటే లాగడం తేలిక. ఎందుకు ?
జవాబు:
గడ్డిని చదునుచేయు రోలరు లేదా రోడ్డు రోలరును F అనే బలం క్షితిజ సమాంతరంతో ‘θ’ కోణం చేస్తూ ముందుకు లాగుతున్నదనుకొనుము. ఈ బలమును రెండు లంబ అంశములుగా విడదీయవచ్చు.
- క్షితిజ సమాంతర అంశ F cos θ – ఇది రోలరును లాగుటకు ఉపయోగపడుతుంది.
- లంబ అంశ F sin θ – ఇది భారానికి వ్యతిరేకంగా పనిచేస్తూ, లంబ ప్రతిచర్యను తగ్గిస్తుంది.
∴ లంబ ప్రతిచర్య R = mg – F sin θ
ఘర్షణ బలం f = μ . R
= [μ (mg – F sin θ)] ………………. (1)
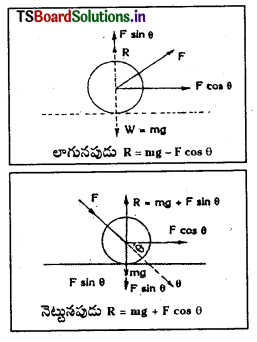
కాని రోలరును ‘F’ బలము క్షితిజంతో ‘θ’ కోణం చేస్తూ నెట్టుచున్నచో ఈ సందర్భంలో పటములో చూపినట్లు లంబ అంశము ‘F sin θ’ భారం వలెనే కిందకు పని చేయుచూ లంబ ప్రతిచర్య విలువను పెంచుతుంది. అనగా R = mg + F sin θ
కావున ఘర్షణ బలం f = μ (mg + F sin θ) ………………. (2)
(1) మరియు (2) ల నుండి నెట్టుటలో ఘర్షణ బలం ఎక్కువగా నున్నది కావున నెట్టుట, లాగుట కంటే కష్టము.
దీర్ఘ సమాధాన ప్రశ్నలు
ప్రశ్న 1.
ఎ) న్యూటన్ రెండవ గమన నియమాన్ని తెలపండి. దాని నుంచి గమన సమీకరణం F= ma ను రాబట్టండి. బి) ఒక వస్తువు వృత్త పథంలో ఎప్పుడూ సమవడితో చలిస్తూ ఉంటే దాని మీద బలం పనిచేస్తుందా ?
జవాబు:
న్యూటన్ రెండవ నియమము: వస్తువు ‘ద్రవ్యవేగంలోని మార్పురేటు వస్తువుపై ప్రయోగించిన బాహ్యబలానికి అనులోమానుపాతంలో ఉండి, బాహ్యబలం పనిచేసే దిశలోనే పనిచేస్తుంది.
అనగా \(\frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{d} \mathrm{t}}\) ∝ F లేదా F = k . \(\frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{d} \mathrm{t}}\) లేదా F = k.ma
ఇందులో k విలువ ఒకటి అగునట్లుగా బలప్రమాణాన్ని నిర్వచించినారు.
కావున F = \(\frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{d} \mathrm{t}}\) లేదా F = ma
F = ma సమీకరణ ఉత్పాదన :
న్యూటన్ రెండవ నియమం నుండి ఏదైనా వస్తువు యొక్క ద్రవ్యవేగంలోని మార్పురేటు బాహ్యబలానికి అనులోమానుపాతంలో ఉంటుంది.
అనగా \(\frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{d} \mathrm{t}}\) ∝ F లేదా F= k . \(\frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{d} \mathrm{t}}\) ఇందులో \(\overline{\mathrm{p}}\) = వస్తువు ద్రవ్యవేగము = mv.
∴ F = k . \(\frac{\mathrm{d}}{\mathrm{dt}}(\mathrm{m} \overline{\mathrm{v}})\)
⇒ k.m. \(\frac{\mathrm{dv}} {\mathrm{dt}}\)
కాని \(\frac{\mathrm{dv}} {\mathrm{dt}}\) = వస్తువు వేగంలోని మార్పురేటు. దీనిని త్వరణము ‘a’ అంటారు.
∴ F = k . m. a ఇందులో k ఒక స్థిరాంకము.
ప్రమాణ బలము (Unit force) : ప్రమాణ ద్రవ్యరాశి గల వస్తువులో ప్రమాణ త్వరణం కలిగించడానికి కావలసిన బలాన్ని ప్రమాణ బలంగా నిర్వచించినారు.
అనగా ద్రవ్యరాశి m = 1 యూనిట్, త్వరణము a = 1 యూనిట్ ఐతే బలము F = 1 యూనిట్ అవుతుంది.
∴ F = kma లో m = 1, a = 1, F = 1 అని వ్రాస్తే k = 1 అవుతుంది.
ప్రమాణబలం నిర్వచనం ప్రకారము F = kma = ma
∴ F = ma
ఒక వస్తువు వృత్త పథంలో ఎప్పుడూ సమవడితో చలిస్తుంటే దాని మీద బలం : m ద్రవ్యరాశి గల ఒక వస్తువు ‘r’ వ్యాసార్ధం గల వృత్తాకార మార్గంలో సమవడితో చలించుచున్నదనుకొనుము. ఏదైనా బిందువు వద్ద వృత్తానికి గీసిన స్పర్శరేఖ వస్తువుకు ఆ బిందువు వద్ద గల వేగాన్ని తెలుపుతుంది. వస్తువుకు గల వేగదిశ అనుక్షణం మారుతుండటం వల్ల వస్తువుకు త్వరణం ఉంటుంది. వృత్తకేంద్రం వైపు పనిచేసే ఈ త్వరణాన్ని అభిలంబత్వరణము అంటారు.

ప్రశ్న 2.
ఘర్షణ కోణం, విశ్రామ కోణాలను నిర్వచించండి. గరుకు వాలుతలం విషయంలో ఘర్షణ కోణం, విశ్రామ కోణానికి సమానమని చూపండి. గరుకు క్షితిజ సమాంతర తలంపై 4కి.గ్రా. ద్రవ్యరాశి ఉన్న ఒక చెక్క దిమ్మె విరామస్థితిలో కలదు. దిమ్మెపై 30 N క్షితిజ సమాంతర బలాన్ని ప్రయోగిస్తే అది కదలడానికి సిద్ధం అయ్యింది. g = 10 m/s2 అయితే, దిమ్మెపై ఆ తలం ప్రయోగించే మొత్తం స్పర్శా బలాన్ని కనుక్కోండి.
జవాబు:
గరుకు వాలుతలంపై ‘m’ ద్రవ్యరాశి గల వస్తువును ఉంచినారనుకొనుము. వాలుతలం క్షితిజ సమాంతరంతో చేసే కోణం ‘θ’ ను పెంచుతూ పోతే, ఒక ప్రత్యేక కోణం θ = α వద్ద దానిపై ఉంచిన వస్తువు త్వరణం లేకుండా తలం వెంబడి కిందకు జారటం మొదలవుతుంది. వాలుతలం చేసే ఈ కోణంను ప్రశాంతత కోణం అంటారు. ఈ విధంగా జారుతున్నపుడు వస్తువు త్వరణం ‘సున్న’ ఉంటుంది.
వస్తువు భారం ‘mg’ నిలువుగా కిందకు పని చేస్తుంది. దీనిని రెండు లంబ అంశాలుగా విడదీయవచ్చు.
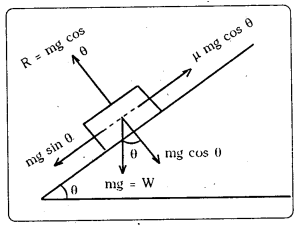
1) ‘mg sin θ’ వాలుతలం వెంబడి కిందకు పనిచేస్తూ వస్తువు కిందకు జరుగునట్లు చేస్తుంది. కాని దీని విలువ, ఘర్షణ బలం fk కు సమానంగా ఉంటుంది.
∴ fk = mg sin θ
2) రెండవ అంశ ‘mg cos θ’ తలానికి లంబంగా పనిచేస్తుంది. దీనికి సమానంగా వ్యతిరేక దిశలో లంబ ప్రతిచర్య పనిచేస్తుంది.
∴ R = mg sin θ
∴ గతిక ఘర్షణ గుణకం μk = \(\frac{\mathrm{f}_{\mathrm{k}}}{\mathrm{R}}=\frac{\mathrm{mg} \sin \theta}{\mathrm{mg} \cos \theta}\) = tan θ
కాని ఇందులో θ = α
∴ μk = tan α
కావున ప్రశాంతత కోణం టాంజెంట్ విలువ ఘర్షణ గుణకంనకు సమానం.
లెక్క ; క్షితిజ సమాంతర తలంపై విరామ స్థితిలో ఉన్న వస్తువుపై పనిచేయు బలాలు
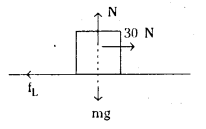
- అభిలంబ చర్య (N)
- వస్తువు భారము (mg)
- క్షితిజ సమాంతర దిశలో బాహ్యబలము (30N)
- స్థితిక ఘర్షణ బలము fs
సమతా స్థితిలో అభిలంబ బలమును వస్తువు భారం తుల్యం చేస్తుంది.
బాహ్యబలము f విలువ స్థితిక ఘర్షణ బలానికి సమానమైతే అది సమతాస్థితిలో ఉంటుంది.
కావున క్షితిజ సమాంతర దిశలో స్పర్శబలము = ఘర్షణ బలం = 30 న్యూ.

లెక్కలు
ప్రశ్న 1.
ఒక కణం రేఖీయ ద్రవ్యవేగం, కాలం (t) ప్రమేయంగా p = a + bt గా ఇచ్చారు. a, b లు ధనాత్మక స్థిరాంకాలు అయితే, కణంపై పనిచేసే బలం ఏమిటి ?
సాధన:
వస్తువు ద్రవ్యవేగము \(\overline{\mathrm{p}}\) = a + bt
వస్తువుపై బలము \(\overline{\mathrm{F}}=\frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{dt}}=\frac{\mathrm{d}}{\mathrm{dt}}\) (a + bt)
∴ F = \(\frac{\mathrm{d}}{\mathrm{dt}}\) (a) + \(\frac{\mathrm{d}}{\mathrm{dt}}\) (bt) = 0 + b
∴ వస్తువుపై బలము = b
ప్రశ్న 2.
10 kg ద్రవ్యరాశి ఉన్న వస్తువు వేగంలో 2 m/s మార్పు కలిగించడానికి 5N బలాన్ని ఎంత కాలం ప్రయోగించాలి ?
సాధన:
బలము F = 5 న్యూ;
వేగంలో మార్పు = v – u = 2 మీ/సె.
ద్రవ్యరాశి m = 10 kg
బలము F = ma, కాలము t = ?
బలము F = m \(\frac{(v-u)}{t}\)
⇒ t = \(\frac{\mathrm{m}(\mathrm{v}-\mathrm{u})}{\mathrm{F}}=\frac{10 \times 2}{5}\) = 4 సె.
ప్రశ్న 3.
m ద్రవ్యరాశి ఉన్న ఒక బంతిని భూమిపై నుంచి నిట్టనిలువుగా పైకి విసిరితే అది క్షణకాలంపాటు విరామస్థితికి వచ్చేలోపు ‘h’ ఎత్తుకు చేరుకొంది. గురుత్వ త్వరణం ‘g’ అనుకోండి. బంతి తన ప్రయాణ కాలంలో గురుత్వాకర్షణ బలం వల్ల పొందే ప్రచోదనం ఎంత ? (గాలి నిరోధాన్ని విస్మరించండి)
సాధన:
ప్రచోదనము J = బలము × కాలము = F × t; వస్తువుపై బలము = భారము = mg
పైకి విసిరిన వస్తువు గాలిలో ఉన్న కాలము t = \(\frac{2 \mathrm{u}}{\mathrm{g}}\). ఇందులో u = \(\sqrt{2 \mathrm{gh}}\)
∴ J = mg × \(\frac{2 \mathrm{u}}{\mathrm{g}}\) = mg × \(\frac{2 \times \sqrt{2 \mathrm{gh}}}{\mathrm{g}}\) = \(\sqrt{8 \mathrm{~m}^2 \mathrm{gh}}\)

ప్రశ్న 4.
ఒక స్థిర బలాన్ని 3.0 kg ద్రవ్యరాశి ఉన్న వస్తువుపై 25 s కాలంపాటు ప్రయోగిస్తే, ఆ వస్తువు వేగం 2.0 m s-1 నుంచి 3.5 m s-1 కు మారింది. వస్తువు వేగ దిశలో మాత్రం ఎలాంటి మార్పు లేదు. బలం పరిమాణాన్ని, బలఁ ప్రయోగించిన దిశను కనుక్కోండి.
సాధన:
వస్తువు ద్రవ్యరాశి m = 3 kg; తొలి వేగము t = 2.0 మీ/సె.;
కాలము t = 25 సె. ;
తుదివేగము v = 3.5 మీ/సె.
బలము F = ma = \(\frac{\mathrm{m}(\mathrm{v}-\mathrm{u})}{\mathrm{t}}=\frac{3(3.5-2)}{25}\) = 0.18 న్యూ.
ప్రశ్న 5.
ఒక లిఫ్ట్ గురుత్వ త్వరణంలో 1/3వ వంతు ఏకరీతి త్వరణంతో పైకి చలిస్తున్నప్పుడు లిఫ్ట్ లో ఉన్న వ్యక్తి దృశ్య భారం. W. అదే లిఫ్ట్ గురుత్వ త్వరణంలో 1/2వ వంతు ఏకరీతి త్వరణంతో కిందికి చలిస్తున్నప్పుడు అతడి దృశ్యభారం ఎంత?
సాధన:
మనిషి దృశ్యభారము = W, త్వరణము = a = \(\frac{\mathrm{g}}{3}\)
వైకి పోవునపుడు లిఫ్ట్లో దృశ్యభారము W = m (g + a) = m(g + \(\frac{\mathrm{g}}{3}\)) = \(\frac{4}{3}\) mg = \(\frac{4}{3}\) N [∵ N = mg]
లేదా అభిలంబ చర్య N = \(\frac{3}{4}\) W
లిఫ్ట్ కిందికి దిగునపుడు త్వరణము a = g/2
కిందికి దిగునపుడు దృశ్యభారము W1 = m (g – a) = m (g – g/2) = m \(\frac{\mathrm{g}}{2}\)
∴ కిందికి దిగునపుడు దృశ్యభారము = W1 = \(\frac{\mathrm{mg}}{2}=\frac{3}{4} \frac{1}{2} \mathrm{~W}=\frac{3 \mathrm{~W}}{8}\)
ప్రశ్న 6.
ఒక తెరచిన ట్రక్కు వెనుక వైపు 200 kg ద్రవ్యరాశి ఉన్న ఒక పెద్ద పెట్టె విరామస్థితిలో కలదు. ట్రక్కు 1.5 m/s2 త్వరణంతో ప్రయాణిస్తున్నప్పుడు ట్రక్కులోని పెట్టె జారిపోకుండా ఉండటానికి ట్రక్కు తలానికి, పెట్టెకు మధ్య ఉండవలసిన కనిష్ఠ స్థితిక ఘర్షణ గుణకం ఎంత ?
సాధన:
పెట్టె బరువు m = 200 kg;
ట్రక్కు త్వరణము a = 1.5 మీ/సె2
పెట్టెలో కలిగిన త్వరణము స్థితిక ఘర్షణ వలన కావున ma = fs ≤ μsN = μsmg (పెట్టె విరామంలో ఉంది కావున)
⇒ a ≤ μsg లేదా μs = \(\frac{\mathrm{a}}{\mathrm{g}}=\frac{1.5}{9.8}\) = 0.153

ప్రశ్న 7.
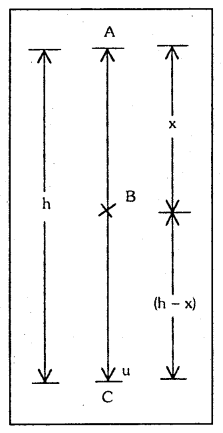
భూమికి 40 m ఎత్తున తొలుత విరామస్థితిలో ఉన్న ఒక బాంబు అకస్మాత్తుగా పేలి, సర్వసమానం అయిన రెండు ముక్కలుగా పేలింది. వాటిలో ఒకటి 10m/s తొలి వేగంతో నిట్టనిలువుగా కిందికి చలిస్తున్నది. బాంబు పేలిన 2 సెకన్ల తరువాత ఆ రెండు ముక్కల మధ్య దూరం ఎంత? (గురుత్వ త్వరణం 10m/s2).
సాధన:
బాంబు రెండు సర్వసమానమైన ముక్కలుగా విభజింపబడటం వల్ల రెండు ముక్కలకు వేగం సమానము. మొదటి ముక్క అధో దిశలో చలిస్తే రెండవది అదే సరళరేఖ వెంబడి ఊర్ధ్వ దిశలో చలిస్తుంది.
కాలము t = 2 సె.
గురుత్వ త్వరణము g = 10 మీ/సె2
1) క్రిందకు చలించిన ముక్క స్థానభ్రంశము s = ut + \(\frac{1}{2}\) gt2
తొలి వేగము u = 20 మీ/సె
∴ s1 = 10 × 2 + \(\frac{1}{2}\) × 10 × 2 × 2 = 40 మీ.
2) ఊర్ధ్వ దిశలో చలించిన ముక్క స్థానభ్రంశము s2 = ut – \(\frac{1}{2}\) gt2 ; తొలివేగం u = 10 మీ/సె
∴ s2 = 10 × 2 – \(\frac{1}{2}\) × 10 × 2 × 2 = 0
ఆ రెండు ముక్కల మధ్య దూరము d – s1 – s2 = 40 – 0 = 40 మీ.
ప్రశ్న 8.
స్థిరంగా బిగించిన ఒక నునుపైన కప్పీ మీదుగా తేలికైన దారాన్ని అమర్చి, దారానికి ఒక వైపు 4 kg ద్రవ్యరాశి, మరొక వైపు 3 kg ద్రవ్యరాశిని వేలాడదీశారు. ఈ 3 kg ద్రవ్యరాశికి మరొక తేలిక దారంతో అదనంగా మరో 3 kg ద్రవ్యరాశి వేలాడదీశారు. విరామస్థితి నుంచి ఆ వ్యవస్థను లాగి వదిలితే, ఆ వ్యవస్థ ఉమ్మడి త్వరణం ఎంత ? (g = 10 m/s2)
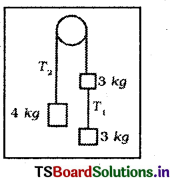
సాధన:
ఒక వైపు మొత్తం ద్రవ్యరాశి m1 = 3 + 3 = 6 kg
రెండవవైపు ద్రవ్యరాశి m2 = 4 kg; g = 10 మీ/సె2
ఆ వ్యవస్థ త్వరణము a = \(\left(\frac{m_1-m_2}{m_1+m_2}\right) g=\left(\frac{6-4}{6+4}\right)\) × 10 = 2 మీ/సె2
ప్రశ్న 9.
క్షితిజ సమాంతర తలంతో 30° కోణం చేస్తున్న ఒక వాలుతలంపై 2 kg ద్రవ్యరాశి ఉన్న దిమ్మె జారుతుంది. దిమ్మెకు, వాలు తలానికి మధ్య ఘర్షణ గుణకం \(\frac{\sqrt{3}}{2}\).
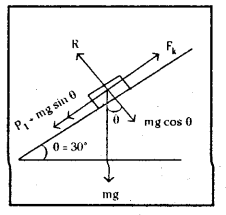
ఎ) దిమ్మె ఎలాంటి త్వరణం లేకుండా కిందికి కదలాలంటే, దిమ్మెపై ఎంత బలాన్ని ప్రయోగించాలి ?
బి) దిమ్మె ఎలాంటి త్వరణం లేకుండా పైకి కదలాలంటే, దిమ్మెపై ఎంత బలాన్ని ప్రయోగించాలి ?
జవాబు:
దిమ్మె ద్రవ్యరాశి m = 2 కి.గ్రా.; వాలు కోణము θ = 30°
వాలు తలము, దిమ్మెల మధ్య ఘర్షణ గుణకము u = \(\frac{\sqrt{3}}{2}\)
1) వాలుతలంపై త్వరణం లేకుండా దిమ్మె క్రిందికి దిగటానికి కావలసిన బలం
F = mg (sin θ – μk cos θ) = 2 × 9.8 (sin 30° – \(\frac{\sqrt{3}}{2}\) × cos 30°)
= 2 × 9.8 \(\left(\frac{1}{2}-\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}\right)\) = 4.9 న్యూ
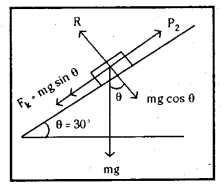
2) దిమ్మను వాలుతలంపైకి త్వరణం లేకుండా లాగడానికి కావలసిన బలం
F = mg (sin θ + μk cos θ)
F = 2 × 9.8 (sin 30° + \(\frac{\sqrt{3}}{2}\) cos 30°)
= 2 × 9.8 \(\left(\frac{1}{2}-\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}\right)\) = 24.5 న్యూ

ప్రశ్న 10.
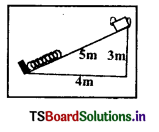
y = x2/20 అదే సమీకరణం సూచించే పరావలయ ఆకారంలో ఉన్న ఒక నునుపు తలంపై పటంలో చూపినట్లు ఒక దిమ్మెను ఉంచారు. μs = 0.5 అయితే, ఆ దిమ్మె జారిపోకుండా ఉండాలంటే, భూమి నుంచి ఎంత ఎత్తులో ఆ దిమ్మెను నునుపు తలంపై అమర్చాలి ? (tan θ = μk = \(\frac{\mathrm{dy}}{\mathrm{dx}}\))
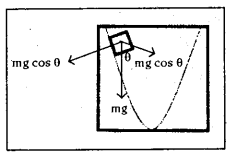
సాధన:
దత్తాంశం నుండి y = \(\frac{x^2}{20}\) ;
∴ వాలు \(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{d}}{\mathrm{dt}}\left(\frac{\mathrm{x}^2}{20}\right)=\frac{2 \mathrm{x}}{10}\)
tan θ = వాలు \([latex]\frac{\mathrm{dy}}{\mathrm{dx}}\)=\frac{x}{10}[/latex] కాని \([latex]\frac{\mathrm{dy}}{\mathrm{dx}}\)[/latex] = tan θ = μs = 0.5 దత్తాంశం నుండి
∴ x = 10 tan θ = 10 μ = 10 × 0.5 = 5
వస్తువు జారకుండా వీలైనంత గరిష్ఠ ఎత్తు వద్ద ఉంచాలంటే
x = 5 అయినపుడు y లెక్కగట్టాలి.
∴ y = \(\frac{x^2}{20}=\frac{5 \times 5}{20}=\frac{25}{20}\) = 1.25 మీ.
ప్రశ్న 11.
ఒక క్షితిజ సమాంతర టేబుల్పై 2 kg ద్రవ్యరాశి ఉన్న ఒక లోహపు దిమ్మెను ఘర్షణలేని కప్పి మీదుగా అమర్చిన దారం సహాయంతో 0.45 kg మరొక ద్రవ్యరాశికి కలిపారు. 0.45 kg ల ద్రవ్యరాశి కిందపడటం వల్ల లోహపు దిమ్మెపై క్షితిజ సమాంతర బలం పనిచేస్తుంది. టేబుల్, దిమ్మెకు మధ్య గతిక ఘర్షణ గుణకం 0.2 అయితే,
ఎ) తొలి త్వరణం, బి) దారంలో తన్యత, సి) దిమ్మె కదిలిన 2 సెకన్ల తరువాత దారం తెగిపోతే, దారం తెగిన తరువాత దిమ్మె కదిలే దూరం కనుక్కోండి.
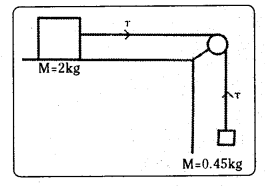
సాధన:
మొదటి దిమ్మె ద్రవ్యరాశి m1 = 0.45 కి.గ్రా.;
రెండవ దిమ్మె ద్రవ్యరాశి m2 = 2 కి.గ్రా.
బల్ల, దిమ్మెల మధ్య ఘర్షణ గుణకము μ = 0.2
ఎ) తొలి త్వరణము a = \(\left(\frac{m_1-\mu m_2}{m_1+m_2}\right) g\) (చలనానికి ముందు μs లెక్కలోకి తీసుకోవాలి.)
∴ a = \(\left(\frac{0.45-2 \times 0.2}{0.45+2}\right) \times 9.8=\frac{0.05 \times 9.8}{2.45}\) = a = 0.2 మీ/సె2

బి) దారంలో తన్యత = T; పటం నుండి T – f = m = a
బలము f = μsmg = 0.2 × 2 × 9.8 = 3.92 న్యూ
∴ T – 3.92 = 2 × 0.2 (లేదా) T = 0.4 + 3.92 = 4.32 న్యూ
సి) కదిలిన తరువాత దారం తెగటానికి పట్టిన కాలము t = 2 సె.
తొలివేగం u = 0 ; త్వరణము a = 0.2 మీ/సె2
తుదివేగము v = u + at = 0 + 0.2 × 2 = 0.4 మీ/సె.
దిమ్మె ప్రయాణించిన దూరము s = \(\frac{\mathrm{v}^2-\mathrm{u}^2}{2 \mu \mathrm{g}}=\frac{0.4 \times 0.4-0}{2 \times 0.2 \times 9.8}\)
∴ s = \(\frac{0.16}{0.4 \times 9.8}\) = 0.0408 మీ. లేదా 4.1 సెం.మీ.
ప్రశ్న 12.
ఒక నునుపైన క్షితిజ సమాంతర తలం మీద 10 కి.గ్రా. ద్రవ్యరాశి ఉన్న A అనే దిమ్మెను ఉంచారు. 5 కి.గ్రా. ద్రవ్యరాశి ఉన్న B అనే మరొక దిమ్మెను పటంలో చూపినట్లు A దిమ్మెపై ఉంచారు. రెండు దిమ్మెల మధ్య ఘర్షణ గుణకం 0.4. కింది దిమ్మెపై 30 N క్షితిజ సమాంతర బలం ప్రయోగించారు. రెండు దిమ్మెల మధ్య ఉన్న ఘర్షణ బలం కనుక్కోండి. (g = 10 m/s2 గా తీసుకోండి)
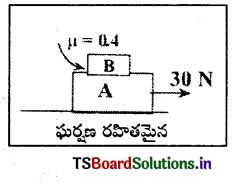
సాధన:
దిమ్మె A ద్రవ్యరాశి mA = 10 కి.గ్రా.
దిమ్మె B ద్రవ్యరాశి mB = 5 కి.గ్రా.; g = 10 మీ/సె2
బలము F = 30 న్యూ; ఘర్షణ గుణకము μ = 0.4
AB ల మధ్య ఘర్షణ బలము f = μmg = 0.4 × 5 × 10 = 20 న్యూ
దిమ్మె B పై ఫలిత బలము = F – f = 30 – 20 = 10 న్యూ.
ముఖ్యమైన అదనపు లెక్కలు
ప్రశ్న 1.
క్రింది వాటిపై పనిచేసే నికర బలం పరిమాణం, దిశను తెలపండి.
ఎ) స్థిర వడితో కిందికి పడుతున్న ఒక వర్షపు బిందువు
బి) నీటిలో తేలియాడుతున్న 10 గ్రా. ద్రవ్యరాశి ఉన్న కార్క్
సి) ఆకాశంలో నైపుణ్యంతో విరామస్థితిలో ఉంచిన గాలిపటం
డి) ఒక గరుకు రోడ్డుపై 30 km/h వేగంతో ప్రయాణిస్తున్న కారు
ఇ) అన్ని ద్రవ్యాత్మక వస్తువులకు చాలా దూరంగా, విద్యుత్ అయస్కాంత క్షేత్రాల ప్రభావానికి లోనుకాకుండా అంతరాళంలో అత్యధిక వేగంతో చలిస్తున్న ఎలక్ట్రాన్
సాధన:
ఎ) స్థిర వడితో పడునపుడు a = 0 కావున బలం F = ma = 0.
బి) కార్కు నీటిపై తేలుతున్నది అనగా అది సమతా స్థితిలో ఉంది. సమతా స్థితిలో ఫలిత బలం F = 0.
సి) ఆకాశంలో స్థిరంగా ఉన్న గాలిపటం మీద ఫలిత బలం F= 0.
డి) స్థిర వడితో ప్రయాణిస్తున్న కారుకు త్వరణం a = 0 కావున బలం F = 0.
ఇ) అన్ని బలాలకు దూరంగా అనగా దానిపై బాహ్యబల ప్రభావం లేదు కావున F = 0.
ప్రశ్న 2.
0.05కి.గ్రా. ద్రవ్యరాశి ఉన్న ఒక గులకరాయిని నిట్టనిలువుగా పైకి విసిరారు. ఆ గులకరాయిపై పనిచేసే నికర బలం పరమాణాన్ని, దిశను కింది సందర్భాలలో తెలియచేయండి.
ఎ) నిలువుగా పైకి ప్రయాణిస్తున్నప్పుడు
బి) కిందికి ప్రయాణిస్తున్నప్పుడు
సి) గరిష్ఠ ఎత్తువద్ద క్షణకాలంపాటు విరామస్థితిలో ఉన్నప్పుడు. ఒకవేళ గులకరాయిని క్షితిజ సమాంతర దిశతో 45° కోణంలో విసిరితే, మీ సమాధానాలు మారతాయా ? (గాలి నిరోధాన్ని విస్మరించండి)
సాధన:
రాయి ఎ) నిలువుగా పైకి వెళుతున్నపుడు బి) క్రిందికి ప్రయాణిస్తున్నపుడు సి) గరిష్ఠ ఎత్తు వద్ద విరామంలో ఉన్నపుడు. ఈ అన్ని సందర్భాలలోను దాని త్వరణం a = g అధోదిశలో ఉంటుంది.
కావున దానిపై బలం F = mg = 0.05 × 10 = 0.5 న్యూ.
రాయిని గాలిలోనికి 45° కోణంతో విసిరినప్పటికి ఈ మూడు స్థానాలలో దానిపై పనిచేసే బలం పరిమాణం మారదు. ఎందుకనగా భారం (mg) ఎల్లపుడు అధో దిశలోనే ఉంది. కావున.

ప్రశ్న 3.
0.1కి.గ్రా. ద్రవ్యరాశి ఉన్న ఒక రాయిపై పనిచేసే నికర బలం పరిమాణం, దిశను కింది సందర్భాలలో తెలపండి.
ఎ) విరామస్థితిలో ఉన్న రైలు కిటికీ నుంచి బయటికి విసిరిన వెంటనే
బి) 36 km/h స్థిర వేగంతో ప్రయాణిస్తున్న రైలు కిటికీ నుంచి బయటికి విసిరిన వెంటనే
సి) 1 ms-2 త్వరణంతో ప్రయాణిస్తున్న రైలు కిటికీ నుంచి బయటికి విసిరిన వెంటనే
డి) 1 ms-2 త్వరణంతో ప్రయాణిస్తున్న రైలు అడుగు తలంపై ఉన్నప్పుడు. రైలుతో సాపేక్షంగా రాయి విరామస్థితిలో ఉంది.
పై అన్ని సందర్భాలలో గాలి నిరోధాన్ని విస్మరించండి.
సాధన:
దత్తాంశం నుండి m = 0.1 కి.గ్రా.; g = 10 మీ/సె2
ఎ) కిటికీలోనుంచి వదలిన వెంటనే F = mg = 0.1 × 10 = 1 న్యూ.
బి) రైలు స్థిరవేగం 36 k.mpH తో చలిస్తుంటే దాని త్వరణము a = 0 కావున కిటికీ నుంచి రాయిని జారవిడిస్తే
F = mg = 0.1 × 10 = 1 న్యూ.
సి) రైలు 1 మీ/సె2 త్వరణంతో చలిస్తున్నా కిటికీ నుంచి జారవిడిస్తే దానిపై రైలు త్వరణం ప్రభావం ఉండదు.
∴ రాయిపై బలము F = mg = 0.1 × 10 = 1 న్యూ.
డి) రైలు అడుగుభాగంలో రాయి ఆనుకొని ఉంటే దానిపై బలము
F = ma ‘a’ రైలు త్వరణము = 1 మీ/సె2
∴ బలము F = 0.1 × 1 = 0.1 న్యూ.
ప్రశ్న 4.
నునుపైన క్షితిజ సమాంతర బల్ల మీద l పొడవున్న దారం ఒక చివర m ద్రవ్యరాశి ఉన్న కణాన్ని, మరొక చివర చిన్న మేకుకు కలిపారు. కణం v వడితో వృత్తాకార మార్గంలో చలిస్తే, ఆ కణంపై పనిచేసే నికర బలం (వృత్తకేంద్రంవైపు పని చేసే బలం)
(i) T,
(ii) T – \(\frac{m v^2}{l}\)
(iii) T + \(\frac{m v^2}{l}\)
(iv) 0
T దారంలోని తన్యత. సరైన సమాధానాన్ని ఎంచుకోండి.
సాధన:
వస్తువు వృత్తాకార మార్గంలో చలించడానికి కావలసిన బలం దారంలోని తన్యత T వలన లభిస్తుంది. కావున (i) సరియైనది.
ప్రశ్న 5.
20 కి.గ్రా. ద్రవ్యరాశి కలిగి, 15 మీ/సె-1 తొలి వేగంతో ప్రయాణిస్తున్న వస్తువుపై 50 N స్థిర అపత్వరణ బలాన్ని ప్రయోగిస్తే, ఎంత కాలం తర్వాత అది ఆగిపోతుంది ?
సాధన:
ద్రవ్యరాశి m = 20 కి.గ్రా.
తొలివేగము u = 15 మీ/సె2
తుది వేగము υ = 0
బలము F = -50 న్యూ.
త్వరణము a = \(\frac{F}{m}=-\frac{50}{20}\) = -2.5 మీ/సె2
v = u + at నుండి 0 = 15 + (-2.5) t
కాలము t = \(\frac{15}{2.5}\) = 6 సె.

ప్రశ్న 6.
ఒక స్థిర బలాన్ని 3.0 కి. గ్రా. ద్రవ్యరాశి ఉన్న వస్తువుపై 25 సెకన్లపాటు ప్రయోగిస్తే, ఆ వస్తువు వేగం 2.0 మీ/సె నుంచి 3.5 మీ/సె-1 మారింది. వస్తువు వేగదిశలో మాత్రం ఎలాంటి మార్పులేదు. బలం పరిమాణాన్ని, బలం ప్రయోగించిన దిశను కనుక్కోండి.
సాధన:
ద్రవ్యరాశి m = 300 కి.గ్రా.;
తొలివేగము u = 2 మీ. సె.
తుది వేగము υ = 3.5 మీ/సె.
కాలము t = 25 సె.; F = ?
బలము F = ma = \(\frac{\mathrm{m}(\mathrm{v}-\mathrm{u})}{\mathrm{t}}=\frac{3(3.5-2)}{25}=\frac{3 \times 1.5}{25}\)
F = \(\frac{4.5}{25}\) = 0.18 న్యూ.
ప్రశ్న 7.
ఒకదానికి ఒకటి లంబంగా ఉన్న 8N, 6N పరిమాణం గల రెండు బలాలను 5 కి.గ్రా. ద్రవ్యరాశి ఉన్న వస్తువుపై ప్రయోగించారు. వస్తువు త్వరణం పరిమాణాన్ని, దిశను తెలపండి.
సాధన:
ద్రవ్యరాశి = m
F1 = \(\overrightarrow{\mathrm{OA}}\) = 8 న్యూ.
F2 = \(\overrightarrow{\mathrm{OB}}\) = 6 న్యూ.
OA, OB లు లంబాలు కావున ఫలిత బలం FR = \(\sqrt{\mathrm{F}_1^2+\mathrm{F}_2^2}=\sqrt{64+36}\)
∴ F = \(\sqrt{100}\) = 10 న్యూ.
ప్రశ్న 8.
ఒక ఆటో డ్రైవర్ రోడ్డు మధ్యలో ఉన్న బాలుని చూసి, ఆ బాలుణ్ణి కాపాడటానికి 36 km/h వేగంతో పోతున్న తన ఆటోకు బ్రేకులు వేస్తే 4.0 s కాలంలో ఆగింది. ఆటోపై ప్రయోగించిన సరాసరి నిరోధ బలం ఎంత ? ఆటో ద్రవ్యరాశి 400 కి.గ్రా. డ్రైవర్ ద్రవ్యరాశి 65 కి.గ్రా.
సాధన:
తొలివేగము u = 36 kmph = 36 × \(\frac{5}{18}\) = 10 మీ/సె.
తుదివేగము V = 0; కాలము t = 4 సె.
ఆటో ద్రవ్యరాశి m1 = 400 కి.గ్రా., డ్రైవర్ ద్రవ్యరాశి m2 = 65 కి.గ్రా.
మొత్తం ద్రవ్యరాశి m = m1 + m2 = 400 + 65 = 465 కి.గ్రా.
నిరోధక బలం F = ma = \(\frac{\mathrm{m}(\mathrm{v}-\mathrm{u})}{\mathrm{t}}=\frac{465(0-10)}{4}\) = – 1162.5 న్యూ.
ప్రశ్న 9.
20,000 కి.గ్రా. ద్రవ్యరాశి ఉన్న ఒక రాకెట్ను ఊర్ధ్వ దిశలో పేల్చితే అది 5.0 మీ/సె2 తొలి త్వరణంతో ఆకాశంలోకి వెళ్ళిపోయింది. పేల్చినప్పుడు ప్రయోగించిన తొలి అభిబలం కనుక్కోండి.
సాధన:
రాకెట్ ద్రవ్యరాశి m = 20,000 కి.గ్రా.
తొలి త్వరణము a = 5 మీ/సె2 ఊర్ధ్వ దిశలో
నికర త్వరణం = g + a = 9.8 + 5 = 14.8
ఆరంభ బలం F = ma = 20,000 × 14.8 = 2.96 × 105 న్యూ.

ప్రశ్న 10.
ప్రారంభంలో 10 మీ/సె-1 స్థిరవేగంతో ఉత్తరం దిశలో ప్రయాణిస్తున్న 0.40 కి.గ్రా. ద్రవ్యరాశి ఉన్న వస్తువుపై 8.0 న్యూ స్థిరబలాన్ని దక్షిణం దిశలో 30 సెకన్లపాటు ప్రయోగించారు. బలం ప్రయోగించిన క్షణ కాలం వద్ద t = 0 అని, ఆ క్షణకాలం వద్ద వస్తువు స్థానం .x = 0 అని అనుకోండి. t = – 5s, 25s, 100s ల వద్ద వస్తువు స్థానాన్ని
ఊహించండి.
సాధన:
ద్రవ్యరాశి m = 0.4 కి.గ్రా.;
తొలివేగము u = 10 మీ/సె. ఉత్తర దిశలో
బలము F = -8 న్యూ (- గుర్తు వ్యతిరేక దిశ)
త్వరణము a = \(\frac{\mathrm{F}}{\mathrm{m}}=\frac{-8.0}{0.4}\) = -20 మీ/సె2 (0 ≤ t ≤ 30 సె. అయినపుడు)
1) కాలము t = -5 సె. అయినపుడు స్థానభ్రంశము s = ?
ఆరంభంలో స్థిరవేగము అనగా t = 0 వద్ద t = -5 కావున (t = -5 నుండి t = 0 వరకు) వేగము స్థిరము.
∴ s = ut = 5 × (-10) = -50 మీ.
2) కాలము t = 25 సె. వద్ద స్థానభ్రంశము s = ut + \(\frac{1}{2}\) at2 నుండి
s = 10 × 25 + \(\frac{1}{2}\) (-20) × 252 = 250 – \(\frac{20}{2}\) × 25 × 25
= -6000 మీ.
3) t = 100 సె. అయినపుడు బలము 30 సెకనులు పనిచేసింది.
కావున 30 సె. తరువాత వస్తువుకు స్థిరవేగం ఉంటుంది.
∴ S = s1 + s2 ఇందులో s1 కు ut1 + \(\frac{1}{2}\) at12 మరియు
s2 = vt2 వాడాడు.
ఇందులో t2 = 30 సె., t2 = 70 సె., v = u + at నుండి
v = 10 + (-20) × 30 = 10 – 600 = – 590 మీ/సె
S1 = ut1 + \(\frac{1}{2}\) at12 నుండి S1 = 10 × 30 + \(\frac{1}{2}\) (-20) × 30 × 30
S1 = 300 – \(\frac{1}{2}\) × 20 × 30 × 30 = 300 – 9000 = -8700 మీ.
S2 = vt2 = -590 × 70 = -41300 మీ.
మొత్తం స్థానభ్రంశము = S = s1 + s2 = -8700 – 41300 = -50000 మీ. = 50 కి.మీ.
ప్రశ్న 11.
ఒక ట్రక్ విరామస్థితితో నుంచి బయలుదేరి 2.0 మీ/సె2 ఏకరీతి త్వరణంతో ప్రయాణిస్తుంది. t = 10 సె. తరువాత ట్రక్ పై కప్పుపై నిల్చొని ఉన్న వ్యక్తి ఒక రాయిని జారవిడిచాడు. (ట్రక్ పైకప్పు భూమి నుంచి 6 మీ.ల ఎత్తులో కలదు). 11 సె. వద్ద ఆ రాయి ఎ) వేగం, బి) త్వరణం కనుక్కోండి. (గాలి నిరోధాన్ని విస్మరించండి.)
సాధన:
తొలివేగము u = 0, త్వరణము a = 2 మీ/సె2,
కాలము t = 10 సె.
రాయి వేగము (జారవిడచిన క్షణంలో) v = u + at
v = 0 + 2 × 10 = 20 మీ/సె.
రాయి క్షితిజ సమాంతర వేగము vx = v = 20 మీ/సె ……………… (1)
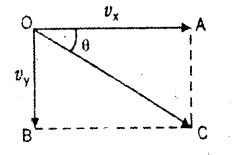
క్షితిజ లంబ దిశలో uy = 0, a = g = 10 మీ/సె2
t = 11 సెకనులు అనగా y దిశలో ప్రయాణించిన కాలము t2 = 11 – 10 = 1 సె.
0°.vy = gt = 10 × 1 = 10 మీ/సె ……………. (2)
11వ సెకనులో వేగము v = \(\sqrt{v_x^2+v_y^2}=\sqrt{20^2+10^2}=\sqrt{500}\) = 22.4 మీ/సె2.
బి) రాయిని జారవిడచిన తరువాత దానిమీద త్వరణము గురుత్వ త్వరణము g = 10 మీ/సె2

ప్రశ్న 12.
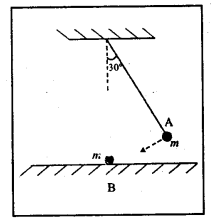
0.1కి.గ్రా. ద్రవ్యరాశి ఉన్న ఒక గోళాన్ని 2 మీ. పొడవు ఉన్న దారంతో ఒక గదిలోని లోకప్పుకు వేలాడదీశారు. గోళం డోలనాలు చేయడం ప్రారంభిస్తే, మాధ్యమిక స్థానం వద్ద గోళం వడి 1 ms-1. ఒకవేళ దారాన్ని తెంపితే గోళం ప్రయాణించే పథం కింది సందర్భాలలో ఎలా ఉంటుంది ? ఎ) ఏదైనా ఒక గరిష్ఠ స్థానం వద్ద, బి) మాథ్యమిక స్ధానం వద్ద.
సాధన:
ఎ) గరిష్ఠ స్థానం వద్ద గోళం వేగము v = 0. ఇక్కడ దారాన్ని తెంపితే అది గురుత్వాకర్షణ బలం వల్ల నిట్టనిలువుగా కిందికి పడుతుంది.
బి) మాధ్యమిక స్థానం వద్ద వేగము v = 1 మీ/సె. ఇక్కడ దారాన్ని తెంపితే లోలకం మాధ్యమిక స్థానం వద్ద గీసిన స్పర్శ రేఖ వెంబడి వేగం ఉంటుంది. గోళం క్షితిజ సమాంతర ప్రక్షేపకం వలె పరావలయ పదాన్ని కలిగి ఉంటుంది.
ప్రశ్న 13.
ఒక వ్యక్తి ద్రవ్యరాశి 70 కి.గ్రా. ఇతడు లిఫ్ట్లో అమర్చిన బరువులు తూచే యంత్రంపై నిల్చొని ఉన్నాడు. ఆ లిఫ్ట్
ఎ) 10 ms-1 ఏకరీతి వేగంతో పైకి,
బి) 5 ms-2 ఏకరీతి త్వరణంతో కిందికి,
సి) 5 ms-2 ఏకరీతి త్వరణంతో పైకి చలిస్తుంది. ప్రతీ సందర్భంలో యంత్రం చూపే రీడింగ్ ఎంత ?
డి) ఒకవేళ లిఫ్ట్ను నడిపే యంత్రం పనిచేయక, భూమ్యాకర్షణ బలం వల్ల స్వేచ్ఛగా కిందికి పడిపోయినట్లయితే యంత్రం చూపే రీడింగ్ ఎంత ?
సాధన:
వ్యక్తి ద్రవ్యరాశి m = 70 కి.గ్రా., గురుత్వ త్వరణము g = 10 మీ/సె2
ఎ) 10 m/s ఏకరీతి వేగంతో చలిస్తుంటే త్వరణము a = 1
∴ దృశ్యభారము వాస్తవ భారము W = mg కి సమానము.
∴ W = mg = 70 × 10 = 700 న్యూ.
b) 5 మీ/సె2 ఏకరీతి త్వరణంతో కిందికి దిగితే
దృశ్యభారము W1 = m(g – a) = 70(10 – 5) = 350 న్యూ.
c) 5 మీ/సె2 ఏకరీతి త్వరణంతో పైకి వెళుతుంటే
దృశ్యభారము . W1 = m (g + a) = 70 (10 + 5) = 1050 న్యూ.
d) లిఫ్ట్ స్వేచ్ఛగా కిందికి పడిపోతే a = g కావున
దృశ్యభారము W = m (g – a) = m(g – g) = 0

ప్రశ్న 14.
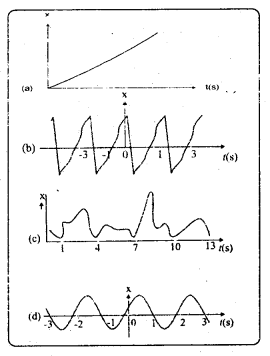
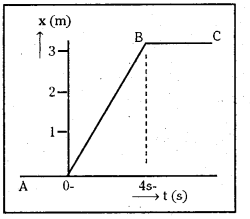
4కి.గ్రా. ద్రవ్యరాశి ఉన్న ఒక కణం స్థానం – కాలం వక్రం పటంలో చూపడమైంది.
ఎ) t < 0, t > 4s, 0 < t < 4s కాలాల వద్ద కణంపై పనిచేసే బలం ఎంత ?
బి) t = 0, t = 4 s ల వద్ద ప్రచోదనం ఎంత ? (ఏకమితీయ గమనం మాత్రమే తీసుకోండి)
సాధన:
ఎ)
- ఇచ్చిన రేఖాపటం నుండి t < 0 వద్ద స్థానభ్రంశము A = 0 నిశ్చలంగా ఉంది కావున బలం F = 0.
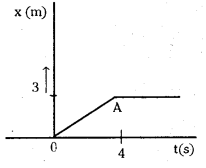
- t > 4 సె అయినపుడు వస్తువు స్థానభ్రంశ – వక్రరేఖ x సమాంతరము. ఇది నిశ్చలస్థితిని చూపిస్తుంది కావున a = 0 మరియు బలము F= 0.
- 0 < t < 4 సెకనుల వద్ద వస్తువు స్థానభ్రంశ-కాల వక్రము OB సరళరేఖ దీని వాలు వస్తువు సమవేగాన్ని ఇస్తుంది.
∴ a = 0 కావున బలము F = ma = 0
బి)
- t < 0 తొలి వేగము u = 0 కావున ప్రచోదనము = 0
- t > 4 సె. వద్ద వస్తువు వేగము సున్న. ప్రచోదనము J = 0
- 0 < t < 4 సెకనుల వద్ద వస్తువుకు సమవేగము ఉంది.
తొలి వేగము u = 0 ;
తుదివేగము v = \(\frac{3}{4}\) మీ/సె. (గ్రాఫ్ నుండి)
ద్రవ్యరాశి m = 4కి.గ్రా.
∴ ప్రచోదనము J = mv – mu = 4(\(\frac{3}{4}\) – 0) = 4 కి.గ్రా. – మీ/సె.
ప్రశ్న 15.
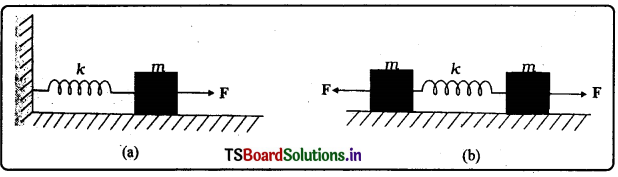
నునుపైన క్షితిజ సమాంతర తలంపై 10 కి.గ్రా., 20 కి.గ్రా. ద్రవ్యరాశులు ఉన్న A, B అనే రెండు వస్తువులను వరుసగా అమర్చి రెండింటిని తేలికైన దారంతో కలిపారు. F= 600 N క్షితిజ సమాంతర బలాన్ని దారం వెంబడి i) A, ii) B ల మీద ప్రయోగించారు. ప్రతీ సందర్భంలో దారంలో తన్యత ఎంత ?
సాధన:
బలము F = 600 న్యూ. A ద్రవ్యరాశి m1 = 10కి.గ్రా., B ద్రవ్యరాశి m2 = 20 కి.గ్రా.
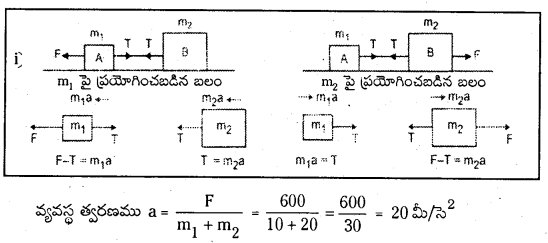
- బలం Aమీద ప్రయోగిస్తే తన్యత T = m2a = 20 × 20 = 400 న్యూ
- బలం B మీద ప్రయోగిస్తే తన్యత T = m1a = 10 × 20 = 200 న్యూ.

ప్రశ్న 16.
8 కి.గ్రా., 12 కి.గ్రా. ద్రవ్యరాశులను ఘర్షణ లేని కప్పి మీదుగా అమర్చిన తేలికైన, సాగని దారం సహాయంతో కలిపారు. ఆ వస్తువులను వదిలినప్పుడు ఆ వస్తువుల త్వరణాలను, దారంలోని తన్యతను కనుక్కోండి.
సాధన:
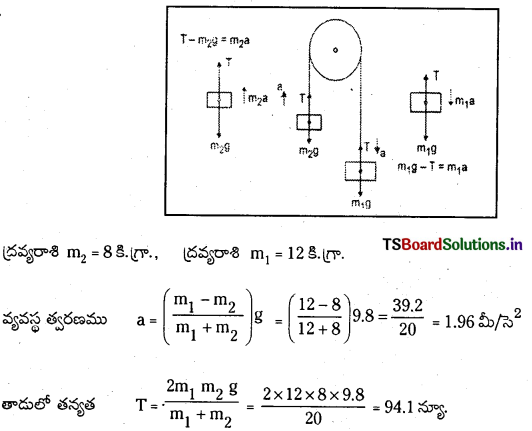
ప్రశ్న 17.
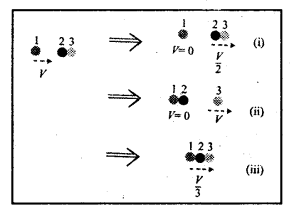
ప్రయోగశాల నిర్దేశ చట్రంలో ఒక కేంద్రకం విరామస్థితిలో కలదు. ఒకవేళ ఆ కేంద్రకం రెండు చిన్న కేంద్రకాలుగా విఘటనం చెందితే, ఆ రెండు కేంద్రకాలు వ్యతిరేక దిశలలో ప్రయాణిస్తాయని చూపండి.
సాధన:
కేంద్రకం విభజించబడటం వల్ల వచ్చిన ముక్కల ద్రవ్యరాశులు m1, m2 మరియు వేగాలు v1, v2 అనుకోండి. పేలకముందు వ్యవస్థ మొత్తం ద్రవ్యవేగము ‘0’ ఎందుకనగా కేంద్రకం విరామంలో ఉంది కావున.
∴ ద్రవ్యవేగ నిత్యత్వ నియమం నుండి m1v1 + m2v2 = 0
లేదా m1v1 = – m2v2 – గుర్తు వ్యతిరేక దిశను తెలియజేస్తుంది. కావున కేంద్రక విచ్ఛిత్తి తరువాత
ఆ ముక్కలు వ్యతిరేక దిశలలో చలిస్తాయి.
ప్రశ్న 18.
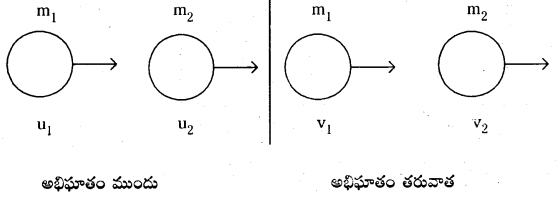
0.05కి.గ్రా. ద్రవ్యరాశి ఉన్న రెండు బిలియర్డ్స్ బంతులు 6 ms-1 వేగంతో వ్యతిరేక దిశలలో ప్రయాణిస్తూ అభిఘాతం చెంది, ఆ తరువాత అంతే వేగంతో వెనుకకు తిరిగి వచ్చాయి. ప్రతి బంతికి, రెండవ బంతి వల్ల అందే ప్రచోదనం కనుక్కోండి.
సాధన:
ఒక్కొక్క బంతి ద్రవ్యరాశి m = 0.05కి.గ్రా.
వేగము v1 = 6 మీ/సె; వేగము v2 = -6 మీ/సె. (వ్యతిరేక దిశ)
అభిఘాతం పిమ్మట వ్యతిరేక దిశలో వెనుదిరిగితే అభిఘాతం వల్ల ఒక్కొక్కదాని ద్రవ్యవేగంలో మార్పు J = m(v – u)
= 0.05 (-6 – 6) = -0.05 × 12 = -0.6కి.గ్రా. -మీ/సె.

ప్రశ్న 19.
100 కి.గ్రా. ద్రవ్యరాశి ఉన్న తుపాకీని పేల్చినప్పుడు 0.020కి.గ్రా. ద్రవ్యరాశి ఉన్న బుల్లెట్ బయటికి వెలువడింది. తుపాకీ గొట్టం నుంచి బుల్లెట్ 80 ms-1 వడితో వెలువడితే, ఆ తుపాకి ప్రత్యావర్తన వడి ఎంత ?
సాధన:
బుల్లెట్ ద్రవ్యరాశి m = 0.02 కి.గ్రా.
వేగము vB = 80 మీ/సె.
తుపాకి బరువు m = 100 కి.గ్రా.
తుపాకి వెనుకకు మరలు వేగము vG = ?
పేలకముందు వ్యవస్థ మొత్తం ద్రవ్యవేగము = 0
ద్రవ్యవేగ నిత్యత్వ నియమం నుండి mvB + MvG = 0
∴ vG = –\(\frac{\mathrm{m} \cdot \mathrm{v}_{\mathrm{B}}}{\mathrm{M}}=\frac{0.02 \times 80}{100}\) = 0.016 మీ/సె.
ప్రశ్న 20.
ఒక బ్యాట్స్మన్ 54 km/h తొలి వేగంతో ప్రయాణిస్తున్న బంతిని 45 కోణంతో తొలి వడిలో మార్పు లేకుండా అనువర్తనం చెందించాడు. బంతికి అందిన ప్రచోదనం ఎంత ? (బంతి ద్రవ్యరాశి 0.15 కి.గ్రా.)
సాధన:
బంతి ద్రవ్యరాశి m = 0.15కి.గ్రా.
వేగము = 54 km/h = 54 × \(\frac{5}{18}\) = 15 మీ/సె.
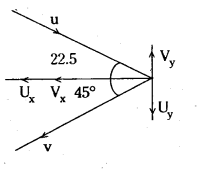
అభిఘాతం పిమ్మట బంతి దిశలో మార్పు θ = 45°
బంతి వేగాన్ని x, y దిశలలో విభజించగా
ux = u. cos θ, vx = -u.cos θ
y దిశలో uy = u sin θ, vy = v sin θ
y దిశలో అంశలు పరస్పరం రద్దు చేసుకుంటాయి.
∴ ఫలితము = 0
∴ బంతిపై ప్రచోదనం = mv – mu
m(-ux cos θ – ux cos θ) = 0.15 (-2ux cos θ) = 0.15 (-2 × 15 cos 22.5°)
బంతి ప్రచోదనము J = 0.15 × 30 × 0.9239 = 4.16కి.గ్రా.మీ/సె.
ప్రశ్న 21.
0.25 కి.గ్రా. ద్రవ్యరాశి ఉన్న రాయిని దారం ఒక చివర కట్టి, 1.5 మీ.ల వ్యాసార్ధం ఉన్న క్షితిజ సమాంతర వృత్తాకార పథంలో 40 rev./min వడితో తిప్పారు. దారంలో ఏర్పడే తన్యత ఎంత ? దారం భరించగల గరిష్ఠ తన్యత 200 N అయితే, రాయిని ఎంత గరిష్ఠ వడితో తిప్పగలం ?
సాధన:
ద్రవ్యరాశి m = 0.25 కి.గ్రా.,
భ్రమణాల సంఖ్య n = 40 r.p.m.
వ్యాసార్ధము r = 1.5 మీ.
కోణీయ వేగము ω = \(\frac{40 \times 2 \pi}{60}=\frac{4}{3} \pi\) రే/సె
గరిష్ఠ తన్యత T = 200 న్యూ
దారంలో తన్యత T = m ω2r = 0.25 × \(\frac{4}{3}\) × \(\frac{4}{3}\)π2 × 1.5 = 6.6 న్యూ
బి) గరిష్ఠ తన్యత T = 200 న్యూ = \(\frac{m v_{\max }^2}{r}\)
∴ vmax2 = \(\frac{200 \times 1.5}{0.25}\) = 1200
⇒ v = \(\sqrt{1200}\) = 34.6 మీ/సె.

ప్రశ్న 22.
ఒకవేళ, పై లెక్కలో రాయి వేగాన్ని గరిష్ఠ వేగాన్ని అధిగమించేటట్లు పెంచితే, హఠాత్తుగా దారం తెగుతుంది. దారం తెగిన తరువాత, కింది వాటిలో ఏది రాయి ప్రయాణించే పథాన్ని తెలియచేస్తుంది ?
ఎ) రాయి వ్యాసార్ధం వెంబడి వెలుపలికి ప్రయాణిస్తుంది.
బి) దారం తెగిన క్షణంలో, స్పర్శారేఖ దిశలో రాయి ఎగిరిపోతుంది.
సి) స్పర్శా రేఖకు కొంత కోణంలో ఎగిరిపోతుంది. ఆ కోణం పరిమాణం రాయి వడిపై ఆధారపడి ఉంటుంది.
సాధన:
పై లెక్కలో (21లో) రాయి వేగము గరిష్ఠ వేగాన్ని మించితే తీగ తెగిపోతుంది. తీగ తెగిన క్షణంలో ద్రవ్యరాశి ఆ బిందువు వద్ద గీసిన స్పర్శరేఖ వెంబడి ఎగిరిపోతుంది.
కావున ‘బి’ సరయిన జవాబు.
ప్రశ్న 23.
ఎందుకో వివరించండి.
ఎ) శూన్యాంతరాళంలో గుర్రం బండిని లాగలేదు, పరిగెత్తలేదు.
బి) వేగంగా ప్రయాణిస్తున్న బస్సును హఠాత్తుగా ఆపితే, బస్సులో కూర్చున్న ప్రయాణీకులు, వాళ్ళు కూర్చున్న స్థలం నుంచి ముందుకు తూలుతారు.
సి) లాన్ రోలర్ను నెట్టడం కంటె లాగడం తేలిక.
డి) క్రికెటర్ బంతిని క్యాచ్ పట్టుకొనేటప్పుడు తన చేతులను వెనుకకు లాగుతాడు.
సాధన:
ఎ) శూన్యంలో గుర్రంబండి ప్రతిచర్య జరిపే అవకాశం లేదు. అందువల్ల చర్య కూడా సాధ్యపడదు. అందువల్ల గుర్రం బండిని లాగలేదు.
బి) వేగంగా వెళుతున్న బస్సును హఠాత్తుగా ఆపితే ప్రయాణీకులు ముందుకు పడటానికి కారణం నిశ్చలస్థితిలోని జడత్వము.
సి) లాన్ రోలర్ను నెట్టినపుడు ప్రయోగించిన బలం (F) లోని ఒక అంశ F sin θ రోలర్ను భూమివైపుకి బలంగా నెట్టుతుంది. కాని అదే బలం F తో లాగితే బల అంశ F sin 9θ రోలర్ను గురుత్వాకర్షణకు వ్యతిరేక దిశలో పైకి లాగుతుంది. అందువల్ల లాన్ రోలర్ను నెట్టడం కన్నా తోయడం తేలిక.
డి) బంతిని క్యాచ్ పట్టుకునేందుకు చేతిని వెనుకకు లాగడం వల్ల బంతి ఆగిపోవడానికి పట్టిన కాలం పెరుగుతుంది. ఫలితంగా చేయి మీద ప్రచోదన ప్రభావం తగ్గును.
ప్రశ్న 24.
0.04 కి.గ్రా. ద్రవ్యరాశి ఉన్న ఒక వస్తువు స్థానం-కాలం వక్రం పటంలో ఇవ్వడమైంది. ఈ గమనానికి తగిన భౌతిక సందర్భాన్ని సూచించండి. వస్తువు పొందిన రెండు వరుస ప్రచోదనాల మధ్య కాలం ఎంత ? ప్రతీ ప్రచోదనం పరిమాణం ఎంత ?
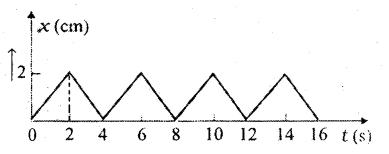
సాధన:
వస్తువు ద్రవ్యరాశి m = 0.04 కి.గ్రా.
పటం నుండి వస్తువు 2 సెకన్లలో ‘0’ నుండి 2 సెం.మీ. వరకు స్థానభ్రంశం పొందింది.
∴ వస్తువు వేగము = వాలు \(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{2}{2}\)
= 1 సెం.మీ./సె. = 10-2 మీ/సె.
మరల తరువాత రెండు సెకన్లలో 2 నుంచి ‘0’ కి స్థానభ్రంశం పొందింది. ఈ దిశలో వేగము v = -1 సెం.మీ/సె.
వస్తువు రెండు సెకనులకొకసారి వేగ దిశ మార్చుకోవడానికి దానిపై కొంత ప్రచోదనబలం పనిచేయాలి.
ప్రచోదనం J = m(v – u) = 0.04 (-1-1) × 10-2 = -0.08 × 10-2
= 8 × 10-4 కి.గ్రా. మీ/సె.

ప్రశ్న 25.
పటంలో చూపినట్లు 1 ms-2 త్వరణంతో తిరుగుతున్న క్షితిజ సమాంతర కన్వేయర్ బెల్ట్ప ఒక వ్యక్తి. బెల్ట్కు సాపేక్షంగా విరామస్థితిలో నిల్చొని ఉన్నాడు. ఆ వ్యక్తిపై నికర బలం ఎంత ? వ్యక్తి బూట్లకు, బెల్ట్కు మధ్య నైతిక ఘర్షణ గుణకం 0.2 అయితే, బెల్ట్ త్వరణం ఏ విలువ వరకు బెల్ట్కు సాపేక్షంగా ఆ వ్యక్తి అదే విధంగా విరామస్థితిలో కొనసాగుతాడు ?
(వ్యక్తి ద్రవ్యరాశి = 65కి.గ్రా.)
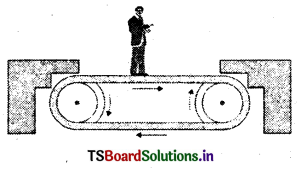
సాధన:
ఎ) బెల్టు త్వరణము a = 1 మీ/సె2
కన్వేయర్ బెల్ట్ పరంగా మనిషి స్థిరంగా ఉండటం వల్ల అతని త్వరణము a = 1 మీ/సె.
మనిషి ద్రవ్యరాశి m = 65 కి.గ్రా.; నికరబలం F = ma = 65 × 1 = 65 న్యూ.
బి) సీమాంత ఘర్షణ బలం μmg ఇందులో μ – 0.2
∴ F = 0.2 mg
మనిషి కదలకుండా ఉండటానికి గరిష్ఠ త్వరణము a’ = \(\frac{\mu \mathrm{mg}}{\mathrm{m}}\)
a’ = μg = 0.2 × 9.8 = 1.96 మీ/సె2
ప్రశ్న 26.
దారం ఒక చివర కట్టిన m ద్రవ్యరాశి ఉన్న రాయి R వ్యాసార్ధం ఉన్న నిలువు వృత్త పథంలో పరిభ్రమిస్తుంది. ఆ వృత్త నిమ్నతమ, ఊర్ధ్వతమ బిందువుల వద్ద నిట్టనిలువుగా కిందికి పనిచేసే నికర బలాలు (సరియైన సమాధానం ఎన్నుకోండి)

T1, v1 లు నిమ్నతమ బిందువు వద్ద తన్యత, వడిని సూచిస్తాయి. T2, v2 లు ఊర్ధ్వతమ బిందువు వద్ద తన్యత, వడిని సూచిస్తాయి.
సాధన:
నిమ్నతమ బిందువు (L) వద్ద ఫలిత బలము FL = (mg – T1),
గరిషోన్నతి బిందువు (H) వద్ద ఫలిత తన్యత FH = mg + T2
కావున (a) సరియైన ఎంపిక.
ప్రశ్న 27.
100 కి.గ్రా. ద్రవ్యరాశి ఉన్న ఒక హెలికాప్టర్ 15 ms-2 నిలువు త్వరణంతో పైకిలేస్తుంది. హెలికాప్టర్ నడిపే వ్యక్తి, అందులోని ప్రయాణీకుల భారం 300 కి.గ్రా. కింది వివిధ సందర్భాలలో పనిచేసే బలం పరిమాణాన్ని, దిశను తెలియచేయండి.
ఎ) హెలికాప్టర్ నడిపే వ్యక్తి, ప్రయాణీకుల వల్ల హెలికాప్టర్ అడుగు తలంపై పనిచేసే బలం
బి) హెలికాప్టర్ రోటర్ దాని పరిసరాలలోని గాలిపై జరిపే చర్య
సి) పరిసరాలలో ఉన్న గాలి, హెలికాప్టర్పై ప్రయోగించే బలం.
సాధన:
హెలికాప్టర్ ద్రవ్యరాశి m = 1000 కి.గ్రా.
ప్రయాణీకులు + సిబ్బంది బరువు m2 = 300 కి.గ్రా.
∴ మొత్తం బరువు M = 1000 + 300 = 1300 కి.గ్రా.
ఊర్ధ్వదిశలో త్వరణము a = 15 మీ/సె2, g = 10 మీ/సె2
ఎ) హెలికాప్టర్ నేలపై సిబ్బంది వల్ల బలము F = m (g + a)
F = 300 (10 + 15) = 300 × 25 = 7500 న్యూ.
బి) రోటరు బ్లేడ్ల వల్ల పరిసరాలపై ప్రతిచర్య అధో దిశలో ఉంటుంది. (హెలికాప్టర్ పైకి వెళ్ళింది కనుక) పైకి లేవడానికి హెలికాప్టర్ రోటర్ ల వల్ల మొత్తం బలం
F = (m1 + m2) (g + a)
F= 1300 (10 + 15) = 32500 న్యూ.
సి) పరిసరాల గాలివల్ల హెలికాప్టర్పై ప్రతిచర్య = హెలికాప్టర్
ఇంజన్ పరిసరాలపై ప్రయోగించిన బలము = 32500 న్యూ.
(చర్య = – ప్రతిచర్య కావున)

ప్రశ్న 28.
10-2m2 మధ్యచ్ఛేద వైశాల్యం ఉన్న ఒక పైపు ద్వారా నీటి ప్రవాహం 15 ms-1 వేగంతో క్షితిజ సమాంతరంగా ప్రయాణిస్తూ బయటకు చిమ్మి, దగ్గరగా ఉన్న నిలువు గోడను తాకింది. గోడపై పతనం అయిన నీరు వెనుకకు తిరిగి రాదని భావిస్తే నీటి వల్ల గోడపై కలిగే బలం ఎంత ?
సాధన:
నీటివేగము u = 15 మీ/సె. ;
సెకనులో బయటకు వచ్చిన గొట్టం అడ్డుకోత a1 = 10-2 మీ2
నీటి పరిమాణము = a1 × v1 = 10-2 × 15 మీ3/సె
నీటి వేగము v1 = 15 మీ/సె.
నీటి సాంద్రత d = 1000 కి.గ్రా./మీ3
1 సెకన్లో గోడను తాకిన నీటి ద్రవ్యరాశి a1 v1 d
= 10-2 × 15 × 1000 = 150 కి.గ్రా.
నీరు వెనుకకు మరల లేదని భావిస్తే నీటి వల్ల గోడపై బలము F = \(\frac{\mathrm{d} \overline{\mathrm{p}}}{\mathrm{dt}}=\frac{\mathrm{mu}}{\mathrm{t}}=\frac{150 \times 15}{1}\) = 2250 న్యూ.
ప్రశ్న 29.
రూపాయి నాణేలను పదింటిని ఒకదానిమీద ఒకటిగా ఒక బల్లపై ఉంచారు. ప్రతి నాణెం ద్రవ్యరాశి m. కింది ప్రతి సందర్భంలో ‘బల పరిమాణం, దిశను తెలపండి.
ఎ) క్రింది నుంచి 7వ నాణెం మీద, పైనున్న నాణేల వల్ల బల పరిమాణం, దిశ
బి) 8వ నాణెం వల్ల 7వ నాణెం మీద పనిచేసే బలపరిమాణం, దిశ
సి) 6వ నాణెం వల్ల 7వ నాణెం మీద ప్రతిచర్య పరిమాణం, దిశ
సాధన:
ఎ) 7వ నాణెంపై బలము = దానిపై గల 3 నాణెముల భారము
∴ F = 3 mg న్యూ
బి) 8వ నాణెంపై ప్రతిచర్య 8వ నాణెం 7వ నాణెంపై ప్రయోగించిన బలానికి సమానము.
∴ F = 3 mg
వివరణ : 8వ నాణెం భారము mg, దానిపై గల 9, 10 నాణెంల భారము 2 mg. మొత్తం 3 mg. ఈ మొత్తం భారాన్ని 8వ నాణెం 7వ నాణెంపై ప్రయోగిస్తుంది.
ప్రశ్న 30.
ఒక విమానం 720 km/h వడితో క్షితిజ సమాంతర వలయం ఆకారంలో ప్రయాణించింది. విమానం రెక్కల గట్టు కోణం 15°. ఆ వలయం వ్యాసార్ధం ఎంత ?
సాధన:
రెక్కల గట్టు కోణము θ = 15°;
వేగము v = 720 kmph = 720 × \(\frac{5}{18}\) = 200మీ/సె
g = 9.8 మీ/సె2
గట్టు కట్టినపుడు tan θ = \(\frac{\mathrm{v}^2}{\mathrm{rg}}\)
∴ వంపు వ్యాసార్ధము r = \(\frac{\mathrm{v}^2}{\mathrm{~g} \tan \theta}=\frac{200 \times 200}{9.8 \times \tan 15^{\circ}}\)
= 15232 మీ. లేదా 15.232 కి.మీ.

ప్రశ్న 31.
ఒక రైలు 54 km/h వడితో 30 మీ. వ్యాసార్ధం ఉన్న గట్టుకట్టని వృత్తాకార రైలు మార్గం గుండా ప్రయాణిస్తుంది. రైలు ద్రవ్యరాశి 106 కి.గ్రా. ఇంజన్, బోగీలు ఈ రెండింటిలో ఏది రైలుకు కావలసిన అభికేంద్ర బలాన్ని సమకూరుస్తుంది. పట్టాలు అరిగిపోకుండా ఉండాలంటే, ఎంత కోణంలో గట్టు కట్టాలి ?
సాధన:
వ్యాసార్ధము r = 30 మీ.
వడి = v = 54 kmph = 54 × \(\frac{5}{18}\) = 15 మీ/సె.
రైలు ద్రవ్యరాశి m = 106 కి.గ్రా.
రైలుకు కావలసిన అభికేంద్ర బలాన్ని ఎత్తుగా నిర్మించిన వెలుపలి పట్టా అందజేస్తుంది. గట్టు కట్టకపోతే ఈ పట్టాకు అరుగుదల ఎక్కువ.
ఏటవాలు గట్టుకోణము tan θ = \(\frac{\mathrm{v}^2}{\mathrm{rg}}=\frac{15 \times 15}{30 \times 9.8}\) = 0.76
∴ tan θ = 0.76 ⇒ θ = tan-1 0.76 = 37.4°
ప్రశ్న 32.
సర్కస్ గ్లోబులో మోటారు సైకిల్ను నిలువు వృత్తంలలో వివిధ రకాల భంగిమలలో అబ్బురపరిచే విన్యాసాలను అతి సులువుగా ప్రదర్శించడం మనం చూస్తూనే ఉంటాం. (ఆ గ్లోబు గోళాకారంగా ఉండి, బయట నుంచి మనం చూడటానికి వీలుగా రంధ్రాలు కలిగి ఉంటుంది) గ్లోబులో మోటారు సైకిల్పై నిలువు వృత్తంలో పరిభ్రమించే ప్రదర్శకునికి కింది నుంచి ఎలాంటి ఆధారం లేకున్నా ఊర్ధ్వతమ బిందువు వద్ద ఉన్నప్పుడు పడిపోకుండా ఉండటానికి కారణమేమిటో వివరించండి. నిలువు వృత్తంలో ఊర్ధ్వతమ స్థానం వద్ద మోటారు సైకిల్పై గమనం పూర్తిచేయడానికి, నిమ్నతమ బిందువు వద్ద ఉండవలసిన కనిష్ఠ వేగం ఎంత ? గ్లోబు వ్యాసార్ధం 25 మీ.
సాధన:
ఊర్ధ్వతమ బిందువు వద్ద R + mg = \(\frac{\mathrm{mv}^2}{\mathrm{r}}\) ఇందులో R. మోటారిస్ట్ అభిలంబచర్య
R = 0 అయితే అతని వేగము అతి తక్కువ
∴ mg = \(\frac{\mathrm{mv}^2}{\mathrm{r}}\) లేదా బావిలో అతని కనిష్ఠ వేగము v = \(\sqrt{\mathrm{gr}}\)
∴ v = \(\sqrt{10 \times 25}=\sqrt{250}\) = 15.8 మీ/సె.

ప్రశ్న 33.
3 మీ. వ్యాసార్ధం ఉన్న ఒక బోలు స్థూపాకార డ్రమ్ దాని నిలువు అక్షంపరంగా, 200 rev/min వడితో పరిభ్రమిస్తుంది. 70 కి.గ్రా. ద్రవ్యరాశి ఉన్న ఒక వ్యక్తి డ్రమ్ లోపలి గోడలకు తాకుతూ నిల్చొని ఉన్నాడు. వ్యక్తి బట్టలకు, డ్రమ్ గోడకు మధ్య ఘర్షణ గుణకం 0.గత్. అడుగు తలాన్ని హఠాత్తుగా తొలగించినప్పుడు, ఆ వ్యక్తి లోపలి గోడలకు అదే విధంగా తాకుతూ పడిపోకుండా ఉండాలంటే స్థూపాకార డ్రమ్కు ఉండాల్సిన కనిష్ఠ భ్రమణ వడి
ఎంత?
సాధన:
ద్రవ్యరాశి m = 70 కి.గ్రా.
వ్యాసార్ధము r = 3 మీ.
n = 200 r.p.m. = \(\frac{200}{60}\) × r.p.s.; ఘర్షణ గుణకము μ = 0.15; మనిషి పడిపోకుండా ఉండటానికి డ్రమ్కు ఉండవలసిన కనీస భ్రమణ వడి w = ?
ఈ సందర్భంలో మనిషి భారము mg = μ.mrw2 కావలెను
w2 = \(\frac{\mathrm{mg}}{\mu \mathrm{mr}} \Rightarrow \mathrm{w}=\sqrt{\frac{\mathrm{g}}{\mu \mathrm{r}}}=\sqrt{\frac{10}{0.15 \times 3}}\) = 4.7 రేడియన్/సె.
![]()
![]()
![]()

![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()