TS Inter 1st Year Physics Study Material Chapter 8 డోలనాలు

Telangana TSBIE TS Inter 1st Year Physics Study Material 8th Lesson డోలనాలు Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 8th Lesson డోలనాలు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
డోలనాత్మకం కాని ఆవర్తన చలనాలకు రెండు ఉదాహరణలు ఇవ్వండి.
జవాబు:

1. గడియారములో సెకనుల ముల్లు చలనము.
2. స్థిరకోణీయ వడితో తిరుగుతూ ఉన్న ఫ్యాన్ రెక్కలు.

ఈ రెండు సందర్భాలలో అవి స్థిర కోణీయ వడితో తిరుగుచున్నవి. అవి ఆవర్తన చలనాలు. వీటి కంపన పరిమితి కాలంతో మారదు. కావున వీటిని సరళహరాత్మక చలనముగా తీసుకొనబడవు.

ప్రశ్న 2.
సరళ హరాత్మక చలన స్థానభ్రంశాన్ని y = a sin (20t + 4) తో సూచించారు. కాలాన్ని \(\frac{2 \pi}{\omega}\) పెంచితే దాని స్థానభ్రంశం ఎంత ?
జవాబు:
సరళ హరాత్మక చలన స్థానభ్రంశం y = a sin (20t + 4) తో సూచిస్తే అందులోని sin ప్రమేయంలో గల ఆర్గ్యుమెంట్ 20t. ఇది \(\frac{2 \pi}{\omega}\) అనగా ఆవర్తనకాలము (T) తో ఆవర్తనం చెందితే దాని స్థానభ్రంశంలో మార్పు ఉండదు.
వివరణ : (20t + 4) ను θ అనుకోండి. \(\frac{2 \pi}{\omega}\) = T. Tకాలంలో స్థానభ్రంశము 2π (ఆవర్తన చలనానికి)
y = sin θ మరియు Ꭹ₁ = sin (θ + 2π) అవుతాయి. కాని sin θ = sin (θ + 2π) కావున y₁ = y అవుతుంది.

ప్రశ్న 3.
ఒక బాలిక ఊయలలో కూర్చొని ఊగుతుంది. బాలిక ఊయలలో నిలబడితే దాని డోలన పౌనఃపున్యం ఏవిధంగా మారుతుంది ?
జవాబు:
బాలిక ఊయలలో నిలబడితే ఆమె ద్రవ్యరాశి కేంద్రం ఆధారానికి దగ్గరగా జరగడంవల్ల లోలకం పొడవు తగ్గును.
ఫలితంగా ఆవర్తన కాలము (T = 2π \(\sqrt{\frac{l}{g}}\)) తగ్గుతుంది.
కాబట్టి ఊయల పౌనఃపున్యం పెరుగును.

ప్రశ్న 4.
లఘులోలకం గుండు నీటితో నిండిన ఒక బోలు గోళం. గోళం నుంచి నీరు కారిపోతుంటే దాని డోలనావర్తన కాలం ఏవిధంగా మారుతుంది ?
జవాబు:
బోలు గోళం నుండి నీరు కారిపోతుంటే ద్రవ్యరాశి కేంద్రం గోళ కేంద్రం నుండి కిందికి జరుగును. కావున లోలకం పొడవు పెరిగి ఆవర్తన కాలం తగ్గును. ఈ ప్రక్రియ ద్రవం గోళంలో సగం వరకు కారేదాకా జరుగును.
గోళంలో ద్రవం సగాని కన్న కిందికి దిగునపుడు మరల ద్రవ్యరాశి కేంద్రం పైకి జరుగును. అంటే లోలకం పొడవు తగ్గడం మొదలై ఆవర్తనకాలం ‘T’ పెరుగును.
గోళం పూర్తిగా ఖాళీ అయితే డోలనావర్తనకాలంలో తొలి విలువను చేరును.

ప్రశ్న 5.
లఘులోలకానికి కట్టిన చెక్క గుండుకు బదులు దాన్ని పోలి ఉండే అల్యూమినియం గుండును ఉపయోగిస్తే దాని ఆవర్తన కాలం ఏవిధంగా మారుతుంది ?
జవాబు:
లోలకంలో చెక్క గుండుకు బదులుగా దానిని పోలిన అల్యూమినియం గుండును వాడితే దాని డోలనావర్తనకాలం మారదు.
డోలనావర్తనకాలం గోళం ద్రవ్యరాశిపై ఆధారపడదు.

ప్రశ్న 6.
లోలక గడియారాన్ని పర్వతంపైకి తీసుకొని వెళితే అది సమయాన్ని పొందుతుందా ? కోల్పోతుందా ?
జవాబు:
పర్వతం పైన g విలువ తక్కువ. లోలక గడియారాన్ని పర్వతం పైకి తీసుకొనిపోతే ఆవర్తనకాలం పెరుగుతుంది. లోలకం ఆవర్తనకాలము T = 2π\(\sqrt{\frac{l}{g}}\) కావున ‘g’ తగ్గితే T పెరుగును.

ప్రశ్న 7.
భూమధ్యరేఖ వద్ద సరైన సమయాన్ని చూపే లోలక గడియారాన్ని ధ్రువాల వద్దకు తీసుకొనిపోతే అది సమయాన్ని పొందుతుందా ? కోల్పోతుందా ? అయితే ఎందుకు ?
జవాబు:
భూమధ్యరేఖ వద్ద సరియైన కాలము చూపు లోలక గడియారమును ధృవాల వద్దకు తీసుకొనిపోయిన ఇది కాలంలో ‘g’ పెరిగిన యెడల T లాభం పొందును. ధృవాల వద్ద గురుత్వ త్వరణము అధికము. ఆవర్తనకాలము T = 2π\(\sqrt{\frac{l}{g}}\). ‘g’ తగ్గును. కావున ఇచ్చిన సమయములో అది చేయు డోలనాల సంఖ్య పెరుగును. కావున గడియారము వేగంగా కదలటం వల్ల కాలాన్ని ఎక్కువగా చూపిస్తుంది.

ప్రశ్న 8.
సరళ హరాత్మక చలనం చేసే కణం స్థానభ్రంశం కంపన పరిమితిలో సగానికి సమానమైనప్పుడు, దాని మొత్తం శక్తిలో K.E, వంతు ఎంత ?
జవాబు:
సరళ హరాత్మక డోలకం మొత్తం శక్తి E = \(\frac{1}{2}\) mω²A²
స్థానభ్రంశం X = \(\frac{\mathrm{A}}{2}\) అయితే P.E. = \(\frac{1}{2}\) mω²x² = \(\frac{1}{2}\) mω² \(\frac{A^2}{4}\)
∴ గతిజశక్తి KE =\(\frac{1}{2}\) mω²A² – \(\frac{1}{2}\) mω²\(\frac{A^2}{4}\) = \(\frac{3}{4}\) \(\frac{1}{2}\) mω²A²
గతిజశక్తి KE = మొత్తం శక్తి × \(\frac{3}{4}\) = మొత్తం శక్తిలో 75%

ప్రశ్న 9.
సరళ హరాత్మక డోలకం కంపన పరిమితిని రెట్టింపు చేస్తే దాని శక్తి ఏవిధంగా మారుతుంది ?
జవాబు:
స.హ.చ. డోలకం మొత్తము శక్తి E = \(\frac{1}{2}\) mω²A²; కొత్త కంపన పరిమితి A₁ = 2A
∴ E₁ = \(\frac{1}{2}\) mω² (2A)² = 4 . \(\frac{1}{2}\) mω²A² ⇒ E₁ = 4E
కంపన పరిమితిని రెట్టింపు చేసిన మొత్తము శక్తి నాలుగు రెట్లు అగును.

ప్రశ్న 10.
కృత్రిమ ఉపగ్రహంలో లఘులోలకాన్ని ఉపయోగించవచ్చా ?
జవాబు:
కృత్రిమ ఉపగ్రహాలలో లఘులోలకాన్ని ఉపయోగించరాదు. కృత్రిమ ఉపగ్రహాలు భారరహిత స్థితిలో ఉంటాయి. అనగా g = 0. ఈ స్థితిలో లోలకం డోలనాలు చేయడానికి కావలసిన టార్క్ τ = L mg sin 6 = θ కావున లోలకం కదలదు.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
సరళ హరాత్మక చలనాన్ని నిర్వచించండి. రెండు ఉదాహరణలు ఇవ్వండి.
జవాబు:
సరళ హరాత్మక చలనం : డోలన చలనం యొక్క సరళమైన రూపాన్ని సరళ హరాత్మక చలనం అంటారు. ఈ చలనం కాల ప్రమేయము (f(t)) తో ఆవర్తనంగా ఉంటుంది.
సరళ హరాత్మక చలనాన్ని f(t) = A cos ωt లేదా A sin ωt వంటి అతిసరళమైన సమీకరణంతో సూచిస్తారు.
ఉదా :

1. సమవృత్తాకార గమనములోని వస్తువు లంబపాదము దాని వ్యాసముపై చలనము.
2. తక్కువ కంపన పరిమితితో చేయు కంపనాలు.
3. భారగ్రస్త స్ప్రింగ్ చేయు కంపనాలు.
4. గొట్టములోని ద్రవము చేయు కంపనాలు.

ప్రశ్న 2.
సరళ హరాత్మక చలనం చేసే కణం స్థానభ్రంశం, వేగం, త్వరణాలు కాలం దృష్ట్యా మారే విధానాన్ని గ్రాఫ్ ద్వారా సూచించండి.
జవాబు:
S.H.M లో ఉన్న కణం స్థానభ్రంశం X = A cos (ωt + Φ)
వేగము v = Aω sin (ωt + Φ)
త్వరణము a = – ω²A cos (ωt + Φ) అను ప్రమేయాలతో సూచిస్తారు. కాలము (t) ని x – అక్షం మీద స్థానభ్రంశము (X), వేగము (v) మరియు త్వరణము (a) లను y – అక్షం మీద తీసుకొని గీసిన రేఖాపటాలు ఈ క్రింది విధంగా ఉంటాయి.

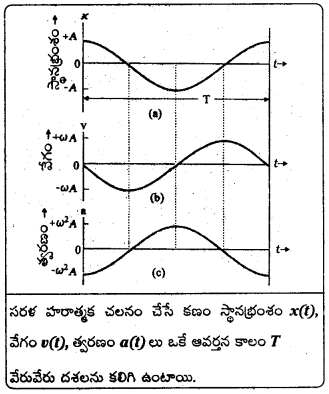
a) స్థానభ్రంశ కాలవక్రము cosine ప్రమేయపు జ్యా వక్రీయ రేఖ. దీని విలువ t = 0 వద్ద గరిష్ఠంగా మొదలవుతుంది. కంపన పరిమితి – A నుండి A వరకు మారును.

b) వేగము ‘v’ sine ప్రమేయంగా మారుతుంది. t = 0 వద్ద వేగము సున్నగా ఉంటూ దీని విలువ -ωA నుండి + ωA వరకు మారును.

c) త్వరణము ‘a’ cosine ప్రమేయంగా మారుతుంది. t = 0 వద్ద – ω²A వద్ద ప్రారంభమై -ω²A నుండి ω²A వరకు మారుతుంది. ఇది స్థానభ్రంశ కాల వక్రాన్ని పోలి ఉండి \(\frac{\pi}{2}\) స్థిర దశాభేదంతో ఉంటుంది.

ప్రశ్న 3.
దశ అంటే ఏమిటి ? సరళ హరాత్మక చలనంలో స్థానభ్రంశం, వేగం, త్వరణాల మధ్య దశా సంబంధాన్ని చర్చించండి.
జవాబు:
స.హ.చ. లో ఉన్న కణము ఏదైనా సమయములో మాధ్యమిక బిందువు నుండి దాని ప్రయాణదిశను, దాని స్థానమును తెలుపు భౌతికరాశిని దశ అందురు.
ప్రావస్థ లేక దశ (Φ) : ఆవర్తన చలన ప్రారంభంలో t = 0 వద్ద ωt + Φ = Φ అవుతుంది. t = 0 వద్ద గల స్థానభ్రంశాన్ని ప్రావస్థ లేదా దశ ”Φ’ అంటారు.
ఆరంభదశ : స.హ.చ. లో ఉన్న కణము స్థానభ్రంశము Y = A cos (ωt – Φ)
వేగము V = A sin (ωt – Φ)
స్థానభ్రంశము మరియు వేగముల మధ్య దశాభేదము 90° ఉండును.
స్థానభ్రంశము, త్వరణముల మధ్య దశాకోణము :
స.హ.చ.లో త్వరణము ‘a’ = -ω² Y లేదా Y = A cos ωt మరియు a = -ω²A cos ωt
– ఋణగుర్తు స్థానభ్రంశము, త్వరణము వ్యతిరేకదిశలలో ఉండుటను సూచించును. వాటి మధ్య దశాభేదము 180° .

ప్రశ్న 4.
k బలస్థిరాంకం గల స్ప్రింగ్కు m ద్రవ్యరాశిని తగిలించారు. స్ప్రింగ్ వ్యవస్థ చేసే దోలన పౌనఃపున్యానికి సమీకరణం రాబట్టండి.
జవాబు:
భారగ్రస్త స్ప్రింగ్ డోలనావర్తనకాలం :
విస్మరించతగినంత తక్కువ ద్రవ్యరాశి గల స్ప్రింగుని ఒక చివర దృఢమైన ఆధారం నుండి వ్రేలాడదీశామనుకుందాము. దాని రెండవ చివర m ద్రవ్యరాశి గల వస్తువు ఉంది. ఈ వస్తువుని నిలువుగా క్రిందికి X దూరం లాగి వదిలామనుకోండి. అపుడు ఆ వస్తువు నిలువు తలంలో డోలనాలు చేస్తుంది.

ఇక్కడ X = మాధ్యమిక స్థానం నుండి వస్తువు స్థానంశం. వస్తువుపై పనిచేసే పునఃస్థాపక బలం స్థానభ్రంశంకి వ్యతిరేక దిశలో ఉంటూ, స్థానభ్రంశంకి అనులోమానుపాతంలో ఉంటుంది.

∴ F ∝ – x లేదా F = -kx. ఇక్కడ k, స్ప్రింగు యొక్క స్ప్రింగు స్థిరాంకం. (- గుర్తు వ్యతిరేక దిశను తెలియజేయును)
∴ వస్తువు త్వరణం = \(\frac{\mathrm{F}}{\mathrm{m}}=-\frac{\mathrm{kx}}{\mathrm{m}}\) = a
త్వరణం, స్థానభ్రంశంకి అనులోమానుపాతంలో ఉంది కనుక వస్తువు సరళ హరాత్మక చలనంలో ఉంటుంది.
సరళహరాత్మక చలనంలో గల వస్తువు ఆవర్తనకాలము

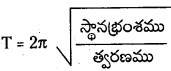
కనుక T = 2π \(\sqrt{\frac{x}{a}}\)
కాని స్ప్రింగ్లలో \(\frac{x}{a}=\frac{m}{y}\)
∴ స్ప్రింగ్ ఆవర్తన కాలము T = 2π \(\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\)

ప్రశ్న 5.
సరళ హరాత్మక డోలకానికి గతిజ, స్థితిజ శక్తులకు సమీకరణాలను రాబట్టండి.
జవాబు:
గతిజశక్తికి సమీకరణమును ఉత్పాదించుట :
సరళహరాత్మక చలనంలో గల వస్తువు స్థానభ్రంశమును x = A cos ωt తో సూచింపవచ్చును. ఇందులో A = కంపన పరిమితి; ωt = θ = కోణీయ స్థానభ్రంశము. స్థానభ్రంశములోని మార్పురేటును వేగం(v)గా నిర్వచించినారు.
వేగం = v = \(\frac{\mathrm{dx}}{\mathrm{dt}}=\frac{\mathrm{d}}{\mathrm{dt}}\) (A cos ωt) = – Aω sin ωt
∴ గతిజశక్తి = \(\frac{1}{2}\) mv² = \(\frac{1}{2}\) mA² ω²sin² ωt = \(\frac{1}{2}\) mA²ω² (1 – cos² ωt) = \(\frac{1}{2}\)mω² (A² – x²)
∴ ఏదైనా స్థానంలో గతిజశక్తి = \(\frac{1}{2}\) mω² (A² – x²
స్థానభ్రంశం x = 0 వద్ద K.E_max = \(\frac{1}{2}\) mω² A²

స్థితిజశక్తికి సమీకరణమును ఉత్పాదించుట :
m ద్రవ్యరాశి గల ఒక వస్తువు ‘O’ అను మధ్యబిందువు ఆధారంగా సరళహరాత్మక చలనంలో ఉన్నది అనుకొనుము. దీని కంపన పరిమితి ‘A’ అనుకొనుము.
సరళ హరాత్మక చలనంలో గల వస్తువు చలనాన్ని y = a cos ωt అను సమీకరణం సూచిస్తుంది.
S.H.M లో గల వస్తువుకు త్వరణము a = – ω²x;
∴ బలము F = mω²x
వస్తువును దాని స్థానం (x) నుండి కొంచెం దూరము dx ప్రక్కకు జరుపుటకు చేసిన పని = dw = F:dx = ఈ పని వస్తువులో స్థితిశక్తి రూపంలో నిలవ ఉంటుంది.
∴ స్థితిశక్తి P.E. = mω²x.dx
మొత్తం పని w = \(\int d w=\int_0^x m \omega^2 x \cdot d x\) దీనిని సమాకలనం చేయగా
మొత్తం పని = స్థితిశక్తి P.E. = \(\frac{1}{2}\) mω²x² …………… (5)

ప్రశ్న 6.
డోలనాలు చేసే లఘులోలకం ఒక అంత్యస్థానం నుంచి మరో అంత్యస్థానానికి చలించే సమయంలో శక్తి ఏవిధంగా మారుతుంది ?
జవాబు:
లఘు లోలకము : సాగదీయడానికి వీలులేని ద్రవ్యరాశి లేనటువంటి పొడవు గల దారానికి ఒక చిన్న లోహపు గుండును తగిలించి దృఢమైన ఆ దారానికి కడితే దానిని లఘు లోలకము అంటారు.
కంపన పరిమితి తక్కువగా గల లఘు లోలకం చేసే డోలనాలు సరళ హరాత్మక చలనాలు.
లోలకం పొడవు వెంబడి నికర వ్యాసార్ధము బలం mg cos θ.
ఇది దారంతో తన్యత T ని తుల్యం చేస్తుంది.
లోలకం డోలనాలు చేయడానికి కావలసిన టార్క్ τ ను
స్పర్శీయ బలం mg sin θ ఇస్తుంది.
లోలకం డోలనాలకు కావలసిన టార్క్ τ = – L mg sin θ
లోలకం కోణీయ త్వరణము α = \(\frac{-\mathrm{mgL}}{\mathrm{I}}\) θ
లోలకం జడత్వ భ్రామకం I = mL²
లోలకం ఆవర్తన కాలము T = 2π \(\sqrt{\frac{\mathrm{I}}{\mathrm{ms} \mathrm{L}}}=2 \pi \sqrt{\frac{\mathrm{L}}{\mathrm{g}}}\)
లఘు లోలకంలో T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{L}{g}}\) అనగా ω = \(\sqrt{\frac{g}{L}}\)
లఘు లోలకం మొత్తం శక్తి E = \(\frac{1}{2}\) mω²A² = \(\frac{1}{2}\) Iω² = \(\frac{1}{2} \mathrm{I} \frac{\mathrm{g}}{\mathrm{L}}\)

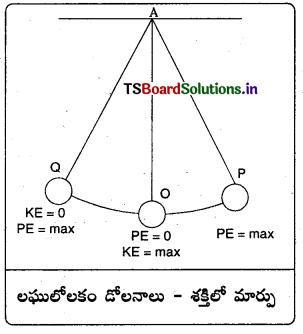
S.H.M లో గల వస్తువుకు సగటు స్థానం వద్ద గతిజశక్తి గరిష్ఠంగాను, గరిష్ఠ స్థానభ్రంశ బిందువువద్ద స్థితిశక్తి గరిష్ఠంగాను ఉంటుంది. కావున లోలకం ఒక అంత్య స్థానం నుండి మరొక అంత్య స్థానానికి మారులోపల సగటు స్థానం వద్ద దాని శక్తి స్థితిజశక్తి నుండి మొత్తం గతిజశక్తి మారుతుంది. సగటు స్థానం నుండి మరల అంత్య బిందువు చేరేసరికి మొత్తం గతిజశక్తి, స్థితిజశక్తిగా మారుతుంది. కాని లఘులోలకం మొత్తం శక్తి విలువ మారదు.

ప్రశ్న 7.
సరళ హరాత్మక చలనం చేసే కణం స్థానభ్రంశం, వేగం, త్వరణాలకు సమాసాలను ఉత్పాదించండి.
జవాబు:
సరళ హరాత్మక చలనంలో గల వస్తువు స్థానభ్రంశము X = A cos (ωt + Φ) అన్న సమీకరణంతో సూచిస్తారు.
a) t = 0 వద్ద స్థానభ్రంశము ‘A’, ωt + Φ = 90° అయిన చోట స్థానభ్రంశము X = 0. ఏదైనా కాలము t వద్ద స్థానభ్రంశము
x = A cos (ωt + Φ) అవుతుంది.

b) S.H.M లో గల వస్తువు వేగము V = \(\frac{\mathrm{d}}{\mathrm{dt}}\) A cos (ωt + Φ) = -ω \(\sqrt{A^2-x^2}\)
= – Aw sin (ωt + Φ)
t = 0 వద్ద వస్తువు వేగము ‘0’ ; (ωt + Φ) = 90° అయినచోట వేగము గరిష్ఠంగా – ωA ను చేరుతుంది.

c) త్వరణము a = \(\frac{d v}{d t}=\frac{d}{d t}\) [- Aw sin (ωt + Φ)] = – Aω² cos ωt + Φ) = -ω²x
గరిష్ఠ త్వరణము a_max = -ω²A

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
సరళ హరాత్మక చలనాన్ని నిర్వచించండి. ఏకరీతి వృత్తాకార చలనం చేసే కణం విక్షేపం (ఏదైనా) వ్యాసంపై సరళ హరాత్మక చలనం చేస్తుందని చూపండి. (మే 2014)
జవాబు:
సరళ హరాత్మక చలనం : డోలన చలనం యొక్క సరళమైన రూపాన్ని సరళ హరాత్మక చలనం అంటారు. ఈ చలనం కాల ప్రమేయము (f(t)) తో ఆవర్తనంగా ఉంటుంది.
సరళ హరాత్మక చలనాన్ని f(t) = A cos ωt లేదా A sin ωt వంటి అతిసరళమైన సమీకరణంతో సూచిస్తారు.

సమవృత్తాకార చలనము మరియు సరళ హరాత్మక చలనముల మధ్య సంబంధము :
‘O’ కేంద్రము, ‘ వ్యాసార్ధం గల ఒక వృత్త పరిధి పై P అను ఒక వస్తువు లేదా కణము అపసవ్యదిశలో ”’ అను సమకోణీఁ వేగంతో చలిస్తున్నది అనుకొనుము. t అను స్వల్ప కాలము తరువాత వస్తువు స్థానము ‘P’ అనుకొనుము.

P నుండి X – – అక్షము మరియు y – అక్షముల మీదకు లంబములను గీయగా ON మరియు OM లు x, y అక్షమ విూద లంబపాదములను సూచించును.
t కాలంలో వస్తువు కోణీయ స్థానభ్రంశము θ = ωt
OPM త్రిభుజం నుండి x అక్షము మీద లంబపాదము
ON = OP cos θ కాని OP = కంపన పరిమితి = OY = r వ్యాసార్ధము
θ = ωt
∴ ఇచ్చిన క్షణంలో X అక్షంపై స్థానభ్రంశము = r cos ωt …………….. (1)

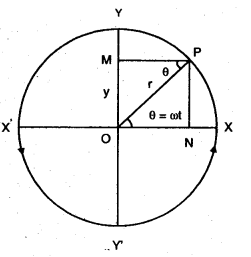
ఇదే విధంగా OPM లంబకోణ త్రిభుజం నుండి y అక్షము మీద లంబపాదము OM = OP sin θ (కాని OP = వ్యాసార్ధము, = కంపన పరిమితి, θ = ωt)
∴ ఇచ్చిన క్షణంలో y – అక్షము మీద స్థానభ్రంశము y = r sin ωt …………… (2)
వస్తువు వృత్తము ఒక భ్రమణము పూర్తిచేయుసరికి లంబపాదములు
ON, OM లు xox’ మరియు yoy’ ల మధ్య ఒక కంపనాన్ని పూర్తిచేస్తాయి.
ఏ క్షణంలోనైనా P బిందువు స్థానభ్రంశాన్ని OP² = ON² + OM² ద్వారా లెక్కగట్టవచ్చును. ఇందులో (ON = r cos ωt, OM = r sin ωt)
కావున సమవృత్తాకారచలనాన్ని పరస్పర లంబదిశలలో గల రెండు సరళ హరాత్మక చలనముల కలయికగా భావించవచ్చును.

ప్రశ్న 2.
లఘులోలకం చలనం సరళ హరాత్మకం అని చూపి, దాని డోలనావర్తన కాలానికి సమీకరణం ఉత్పాదించండి. సెకండ్ల లోలకం అంటే ఏమిటి ? (మార్చి 2014)
జవాబు:
లఘు లోలకము : సాగదీయడానికి వీలులేని ద్రవ్యరాశి లేనటువంటి ఓ పొడవు గల దారానికి ఒక చిన్న లోహపు గుండును తగిలించి దృఢమైన ఆధారానికి కడితే దానిని లఘు లోలకము అంటారు.
కంపన పరిమితి తక్కువగా గల లఘు లోలకం చేసే డోలనాలు సరళ హరాత్మక చలనాలు.

లోలకం పొడవు వెంబడి నికర వ్యాసార్ధియ బలం mg cos θ.
ఇది దారంతో తన్యత Tని తుల్యం చేస్తుంది.
లోలకం డోలనాలు చేయడానికి కావలసిన టార్క్ τ ను
స్పర్శీయ బలం mg sin θ ఇస్తుంది.
లోలకం డోలనాలకు కావలసిన టార్క్ τ = – L mg sin θ
లోలకం కోణీయ త్వరణము α = \(\frac{-m g L}{I} \theta \Rightarrow \frac{\theta}{\alpha}=\frac{I}{m g L}\)
లోలకం జడత్వ భ్రామకం I = mL²
లోలకం ఆవర్తన కాలము T = 2π\(\sqrt{\frac{\mathrm{I}}{\mathrm{mgL}}}=2 \pi \sqrt{\frac{\mathrm{ML}^2}{\mathrm{mgL}}}=2 \pi \sqrt{\frac{\mathrm{L}}{\mathrm{g}}}\)
లఘు లోలకంలో కోణీయ త్వరణము α = \(\frac{-\mathrm{mgL}}{\mathrm{I}}\) θ
అనగా త్వరణము α ∝ – θ (కోణీయ స్థానభ్రంశము) మరియు ఆవర్తన కాలము T = 2π\(\sqrt{\frac{L}{g}}\) ఈ రెండు లక్షణాలు వస్తువు సరళ హరాత్మక చలనంలో ఉండటానికి కావలసిన నిబంధనలు. కావున లఘులోలకం చలనం సరళ హరాత్మక చలనము.
సెకండ్ల లోలకం : డోలనావర్తన కాలం రెండు సెకనులు గల లోలకాన్ని సెకండ్ల లోలకం అంటారు. సెకన్ల లోలకం ఆవర్తన కాలము T = 2సెకనులు.

ప్రశ్న 3.
సరళ హరాత్మక డోలకం గతిజ, స్థితిజ శక్తులకు సమీకరణాలను ఉత్పాదించండి. సరళ హరాత్మక చలనంలోని కణం పథంపై అన్ని బిందువుల వద్ద మొత్తం శక్తి స్థిరం అని చూపండి.
జవాబు:
సరళ హరాత్మక చలనం చేసే కణం స్థానభ్రంశాన్ని x = A cos (ωt + Φ) అని రాస్తారు.

లేదా స్ప్రింగ్ పై బలం F = – Kx. ఇది కాలంతో పాటు మారే నిత్యత్వ బలం కాబట్టి స్థితిశక్తి
U = –\(\frac{1}{2}\) Kx . x = – \(\frac{1}{2}\) Kx²
∴ స్థితిశక్తి U = – \(\frac{1}{2}\) K.A² cos² (ωt + Φ)
S.H.M లో గల వస్తువుకు లేదా కణంకు ఏదైనా బిందువు వద్ద గల మొత్తం శక్తి KE + PE
∴ మొత్తం శక్తి E = \(\frac{1}{2}\) mω² (A² – x²) + \(\frac{1}{2}\) mω² x² (సమీకరణములు 1, 2 ల నుండి)
∴ E = \(\frac{1}{2}\) ω² A² S.H.M లో గల వస్తువుపై పనిచేయు బలాలు నిత్యత్వ బలాలు. ఇవి శక్తి నిత్యత్వ నియమం పాటిస్తాయి. అందువల్ల S.H.M లో గల వస్తువుకు అన్ని బిందువుల వద్ద మొత్తం శక్తి స్థిరము.

లెక్కలు

ప్రశ్న 1.
బోలుగా ఉండే ఇత్తడి గోళంతో ఒక లోలకం గుండును తయారుచేశారు. దాన్ని పూర్తిగా నీటితో నింపితే దాని డోలనావర్తన కాలం ఏమవుతుంది ? ఎందువల్ల ?
జవాబు:
బోలుగా ఉన్న ఇత్తడి గోళంలో పూర్తిగా నీటిని నింపితే దాని ద్రవ్యరాశి కేంద్రస్థానంలో మార్పురాదు. కావున డోలనా వర్తనకాలం మారదు. లోలకం డోలనావర్తన కాలం గోళం ద్రవ్యరాశిపై ఆధారపడదు.

ప్రశ్న 2.
k బల స్థిరాంకం గల రెండు సర్వసమానమైన స్ప్రింగ్లను శ్రేణిలో (ఒకదాని కొనకు మరొకటి) కలిపితే సంయుక్త స్ప్రింగ్ ప్రభావాత్మక బల స్థిరాంకం ఎంత ?
జవాబు:
స్ప్రింగులను శ్రేణిలో కలిపిన ఫలిత స్ప్రింగ్ స్థిరాంకము k_s = \(\frac{\mathrm{k}_1 \mathrm{k}_2}{\mathrm{k}_1+\mathrm{k}_2}\)
k₁ = k₂ = k అయిన k_s = \(\frac{k k}{k+k}=\frac{k^2}{2 k}=\frac{k}{2}\)
శ్రేణిసంధానములో ఫలితస్ప్రింగ్ స్థిరాంకము తగ్గును.

ప్రశ్న 3.
సరళ హరాత్మక చలనంలో మాధ్యమిక స్థానం వద్ద ఏయే భౌతికరాశులు గరిష్ఠ విలువను కలిగి ఉంటాయి ?
జవాబు:
సరళ హరాత్మక చలనంలో మాధ్యమిక స్థానం వద్ద వేగము గరిష్ఠము. కావున గతిజశక్తి కూడా గరిష్ఠము.

ప్రశ్న 4.
సరళ హరాత్మక చలనంలో ఉన్న కణం గరిష్ఠ వేగం, గరిష్ఠ త్వరణంలో సంఖ్యాత్మకంగా సగం ఉంది. దాని డోలనావర్తన కాలం ఎంత?
జవాబు:
గరిష్ఠవేగము V_max = \(\frac{1}{2}\) గరిష్ఠ త్వరణము (a_max) ; కాని V_max = Aω మరియు a_max = ω²A
∴ Aω = \(\frac{1}{2}\) Aω² = ω = 2
∴ ఆవర్తన కాలము T = \(\frac{2 \pi}{\omega}=\frac{2 \pi}{2}\) = π సెకనులు.

ప్రశ్న 5.
బల స్థిరాంకం 260 Nm^-1 గల స్ప్రింగ్కు 2 kg ద్రవ్యరాశిని వేలాడదీశారు. అది 100 డోలనాలు చేయడానికి పట్టే కాలం ఎంత ?
జవాబు:
వ్రేలాడదీసిన ద్రవ్యరాశి m = 2 kg
బలస్థిరాంకము k = 260 N/m
∴ T = 2 × 3.142 × 0.0877 = 0.551 sec
100 డోలనాలకు పట్టుకాలము = 100 × 0.551 = 55.1 sec

ప్రశ్న 6.
నిశ్చలంగా ఉన్న లిఫ్ట్లోని లఘులోలకం డోలనావర్తన కాలం T. లిఫ్ట్ (1) సమవేగంతో పైకి వెళుతున్నప్పుడు (ii) సమవేగంతో కిందికి వెళుతున్నప్పుడు (iii) సమత్వరణం a తో పైకి వెళుతున్నప్పుడు (iv) సమత్వరణం 4 తో కిందికి వెళుతున్నప్పుడు (v) గురుత్వం వల్ల స్వేచ్ఛగా కిందికి పడుతున్నప్పుడు లోలకం డోలనావర్తన కాలం ఏవిధంగా మారుతుంది ?
జవాబు:
i) లిఫ్ట్ సమవేగంతో పైకి వెళుతుంటే దాని త్వరణము a = 0. లోలకంపై ఫలిత త్వరణము = g కావున లోలకం డోలనా వర్తన కాలము మారదు.

ii) సమవేగంతో కిందికి దిగునపుడు దాని త్వరణము a = 0 లోలకంపై ఫలిత త్వరణము a = g కావున దాని ఆవర్తన కాలం మారదు.

iii) లిఫ్ట్ ‘a’ సమత్వరణముతో పైకి పోతుంటే లోలకంపై ఫలిత త్వరణము = (a + g),
ఆవర్తన కాలము T = 2π \(\sqrt{\frac{l}{(g+a)}}\) కావున ఆవర్తన కాలం తగ్గును.

iv) లిఫ్ట్ ‘a’ అను సమత్వరణంతో కిందికి దిగుతుంటే లోలకంపై ఫలిత త్వరణము = g – a కావున లోలకం ఆవర్తన కాలం పెరుగును.

v) లిఫ్ట్ స్వేచ్ఛగా కిందికి పడుతుంటే a = g. లోలకంపై ఫలిత త్వరణం = 0. ∴ ఆవర్తన కాలము అనంతము.

ప్రశ్న 7.
సరళ హరాత్మక చలనంలో ఉండే కణం కంపన పరిమితి 4 సెం.మీ. అది మాధ్యమిక స్థానం నుంచి 1 సెం.మీ. దూరంలో ఉన్నప్పుడు త్వరణం 3 cm s^-2. మాధ్యమిక స్థానం నుంచి 2 సెం.మీ. దూరంలో ఉన్నప్పుడు దాని వేగం ఎంత ?
జవాబు:
కంపన పరిమితి A = 4 cm = 4 × 10^-2m
త్వరణము a = 3cm/s² = 3 × 10^-2 m/s² ; స్థానభ్రంశము Y = 1cm = 10^-2m
∴ కోణీయ వేగం ω = \(\sqrt{\frac{a}{Y}}=\sqrt{\frac{3}{1}}=\sqrt{3}\)
స్థానభ్రంశము 2 సెం.మీ. వద్ద వేగము V = ω \(\sqrt{A^2-Y^2}\), y = 2 సెం.మీ. కావున
∴ V = \(\sqrt{3} \sqrt{(16-4) 10^{-4}}=\sqrt{3} \times \sqrt{12} \cdot 10^{-2}=\sqrt{3} 2 \sqrt{3} \times 10^{-2}=\) = 6 × 10^-2 m/sec = 6 cm/sec

ప్రశ్న 8.
సరళ హరాత్మక డోలకం డోలనావర్తనం కాలం 2s. డోలకం మాధ్యమిక స్థానాన్ని దాటిన 0.25s తరువాత దాని దశలో కలిగే మార్పు ఎంత ?
జవాబు:
ఆవర్తన కాలము T = 2 sec
కాలము t = 0.25 sec
దశాభేదము = Φ = \(\frac{\mathrm{t}}{\mathrm{T}}\) × 2π = \(\frac{0.25}{2}\) × 2π = \(\frac{\pi}{4}\) = 45°
అది మాధ్యమిక బిందువు నుండి \(\frac{\pi}{4}\) దూరములో ఉండును. అనగా దశలో మార్పు \(\frac{\pi}{4}\) రేడియ

ప్రశ్న 9.
సరళ హరాత్మక చలనం చేసే వస్తువు కంపన పరిమితి 5 cm, డోలనావర్తన కాలం 0.2s. వస్తువు స్థానభ్రంశం
(a) 5 cm (b) 3 cm (c) 0 cm వద్ద దాని త్వరణం, వేగాలను కనుక్కోండి.
జవాబు:
కంపన పరిమితి A = 5 సెం.మీ. ; డోలనా వర్తనకాలం T = 0.2 సె
a) స్థానభ్రంశం x = 5 సెం.మీ. అనగా x = A గరిష్ఠము
గరిష్ఠ త్వరణము a = – ω²A కాని ω = \(\frac{2 \pi}{T}=\frac{2 \pi}{0.2}\) = 2π
∴ a = (-10π)² × 5 = 500π² m/s = 5π² మీ/సె
వేగము V = 0 (గరిష్ఠ స్థానభ్రంశం వద్ద V = 0 కావున)

b) స్థానభ్రంశం 3 సెం.మీ. వద్ద
త్వరణం a = – ω²x = – (- 10π)² × 3 = – 100π² × 3
= -30π² సెం.మీ./సె²
= – 3π² మీ/సె
వేగము V = – ω\(\sqrt{A^2-x^2}\) = – 10π\(\sqrt{25-9}\) = 10π\(\sqrt{16}\) సెం.మీ./సె
= 40π సెం.మీ./సె’ = 0.4π మీ/సె

c) స్థానభ్రంశము x = 0 అయిన అనగా మధ్య బిందువు వద్ద
త్వరణము a = -ω²x = 0
వేగము V = – ω\(\sqrt{A^2-x^2}\) = – ωA = 10π × 5 = 50π సెం.మీ./సె
= 0.5π మీ/సె

ప్రశ్న 10.
ఒక గ్రహం ద్రవ్యరాశి, వ్యాసార్థాలు భూమి ద్రవ్యరాశి, వ్యాసార్థాల కంటే రెట్టింపు. భూమిపై లఘులోలకం డోలనావర్తన కాలం T అయితే గ్రహంపై లోలకం డోలనావర్తన కాలం ఎంత ?
జవాబు:
గ్రహము ద్రవ్యరాశి M_p = 2 M_e;
గ్రహము వ్యాసార్ధము R_p = 2 R_e
భూమిపై లోలకము ఆవర్తన కాలము = T
గ్రహముపై ఆవర్తన కాలము T’ = ? g_e = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\)
g_p = \(\frac{\mathrm{G} \cdot 2 \mathrm{M}}{(2 \mathrm{R})^2}=\frac{\mathrm{GM}}{2 \mathrm{R}^2}=\frac{\mathrm{g}_{\mathrm{e}}}{2}\) ; భూమి మీద, T = 2π \(\sqrt{\frac{l}{\mathrm{~g}_{\mathrm{e}}}}\) ; గ్రహము మీద T’ = 2π \(\sqrt{\frac{l}{\mathrm{~g}_{\mathrm{p}}}}\)
∴ \(\frac{T^{\prime}}{T}=\sqrt{\frac{g_e}{g_p}}=\sqrt{2}\) T = \(\sqrt{2}\)T

ప్రశ్న 11.
1 m పొడవు ఉండే లఘులోలకం డోలనావర్తన కాలం 2s నుండి 1.5s కు మారితే పొడవులో వచ్చే మార్పును లెక్కించండి.
జవాబు:
సెకండ్ల లోలకమునకు T₁ = 2 sec; పొడవు l₁ = 1 m.
కొత్త ఆవర్తన కాలము T₂ = 1.5 sec; పొడవు 1₂ = ?
T = 2π \(\sqrt{\frac{l}{\mathrm{~g}}}\); సెకండ్ల లోలకమునకు 2 = 2π \(\sqrt{\frac{l}{\mathrm{~g}}}\)
2వ సందర్భంలో 1.5 = 2π \(\sqrt{\frac{l}{\mathrm{~g}}}\)
∴ \(\frac{2}{1.5}=\frac{1}{\sqrt{l}}=\frac{4}{3}\) ⇒ l = \(\frac{9}{16}\) m
∴ పొడవులో తగ్గుదల = 1 – \(\frac{9}{16}\) = \(\frac{7}{16}\) m = 0.4375 m

ప్రశ్న 12.
ఒక గ్రహంపై 8m ఎత్తు నుంచి వస్తువు స్వేచ్ఛగా కిందికి పడేందుకు 2s తీసుకొంటుంది. ఆ గ్రహంపై లోలకం డోలనావర్తన కాలం 7TS అయితే లోలకం పొడవును లెక్కించండి.
జవాబు:
ఎత్తు, h = 8m ; గ్రహతలమును చేరుటకు పట్టుకాలము t = 2 sec
స్వేచ్ఛగా వదలిన వస్తువుకు t = \(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}\) ⇒ 2 = \(\sqrt{\frac{16}{\mathrm{~g}}}\)
∴ గ్రహముపైన g = \(\frac{16}{4}\) = 4m/s²
లోలకము డోలనావర్తన కాలము T = 2π \(\sqrt{\frac{l}{\mathrm{~g}}}\) = π ⇒ 2 \(\sqrt{\frac{l}{\mathrm{~g}}}\) = 1 లేదా \(\frac{l}{g}=\frac{1}{4}\) ⇒ l = \(\frac{g}{4}\)
ఆ గ్రహముపైన లోలకము పొడవు = \(\frac{4}{4}\) = 1m = 100 సెం.మీ.

ప్రశ్న 13.
ఒక లఘులోలకం పొడవును 0.6m పెంచినప్పుడు, డోలనావర్తన కాలం 50% పెరగడాన్ని గమనించడమైనది. g = 9.8 ms^-2 ఉన్న ప్రదేశంలో దాని తొలి పొడవు, తొలి డోలనావర్తన కాలాలను లెక్కించండి.
జవాబు:
a) లోలకము పొడవులో పెరుగుదల = 0.6m ; ఆవర్తన కాలములో పెరుగుదల = 50% = 1.5T
లోలకము యథార్థ పొడవు = l అనుకొనుము;
యథార్థ ఆవర్తన కాలము = T;
గురుత్వ త్వరణము g = 9.8 m/s²
మొదటి సందర్భానికి 9.8 = 4π² \(\frac{l}{\mathrm{~T}^2}\) ……………… (1)
రెండవ సందర్భానికి l₁ = (l + 0.6), T₁ = 1.5 T; ∴ 9.8 = 4π² \(\frac{l_1}{\mathrm{~T}_1^2}\) …………….. (2)
2ని 1చే భాగించగా 1 = \(\frac{l_1}{l} \cdot \frac{\mathrm{T}^2}{\mathrm{~T}_1^2} \Rightarrow \frac{l_1}{l}=\frac{\mathrm{T}_1^2}{\mathrm{~T}^2}\) 2.25 ⇒ l₁ = 2.25 1; కాని l₁ = l + 0.6;
∴ l + 0.6 = 2.25 l ⇒ 0.6 = 1.25 l ;
∴ లోలకము పొడవు l = \(\frac{0.6}{1.25}\) = 0.48 m

b) ఆవర్తన కాలము T = 2π \(\sqrt{\frac{l}{\mathrm{~g}}}\) = 2 × 3.142 \(\sqrt{\frac{0.48}{9.8}}\) = 6.284 × 0.2213 = 1.391 sec.

ప్రశ్న 14.
సెకండ్ల లోలకంతో నియంత్రితమైన (regulated) ఒక గడియారం సరైన సమయాన్ని చూపిస్తూ ఉంది. ‘వేసవి కాలంలో లోలకం పొడవు 1.02 m లకు పెరిగినట్లైతే గడియారం ఒక రోజులో ఎంత కాలాన్ని పొందుతుంది లేదా కోల్పోతుంది ?
జవాబు:
సెకండ్ల లోలకము ఆవర్తనకాలము, T = 2 sec
సెకండ్ల లోలకము పొడవు, l = g² / 4π² = 0.9927 m
వేసవిలో సెకండ్ల లోలకము పొడవు = 1.02 m
∴ పొడవులో దోషము = ∆l = 1.02 – 1 = 0.0273
లోలకమునందు T ∝ \(\sqrt{\mathrm{l}}\). దోషముల వ్యాపన నియమము నుండి \(\frac{\Delta \mathrm{T}}{\mathrm{T}}=\frac{1}{2} \frac{\Delta l}{l}=\frac{1}{2} \quad \frac{0.0273}{0.9927}\)
∴ ఒక దినమునకు కాలములో దోషము = 86,400 × \(\frac{1}{2} \frac{0.0273}{0.9927}\) = 1188 sec.

ప్రశ్న 15.
స్ప్రింగ్కు వేలాడదీసిన వస్తువు ఆవర్తన కాలం T. ఆ స్ప్రింగ్ను రెండు సమాన భాగాలుగా చేసి (i) వస్తువును ఒక భాగానికి వేలాడదీసినప్పుడు (ii) రెండు భాగాలకు (సమాంతరంగా) ఒకేసారి వస్తువును వేలాడదీసినప్పుడు డోలనావర్తన కాలాలను లెక్కించండి.
జవాబు:
స్ప్రింగ్ ఆవర్తన కాలము T = 2π \(\sqrt{\frac{\mathrm{m}}{\mathrm{K}}}\)
స్ప్రింగు రెండు సమానభాగాలుగా కత్తిరించిన ఒక్కొక్క భాగము
స్ప్రింగ్ స్థిరాంకము K₁ = 2K

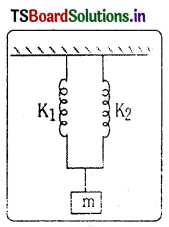
i) ఇచ్చిన ప్రదేశమునకు T = 2π \(\sqrt{\frac{\mathrm{m}}{\mathrm{K}_1}}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{K}}} \frac{1}{\sqrt{2}}=\frac{\mathrm{T}}{\sqrt{2}}\)

ii) రెండు స్ప్రింగులను సమాంతరముగా కలిపి వాటికి ఒకేసారి ద్రవ్యరాశిని వ్రేలాడదీసిన ఫలిత స్ప్రింగ్ స్థిరాంకము
K_p = K₁ + K₂ = 4K
ఆవర్తన కాలము T = 2π \(\sqrt{\frac{m}{K_p}}=2 \pi \sqrt{\frac{m}{4 \cdot K}}=2 \pi \sqrt{\frac{m}{K}} \cdot \frac{1}{2}=\frac{T}{2}\)

ముఖ్యమైన ఉదాహరణ లెక్కలు

ప్రశ్న 1.
మానవ గుండె, సగటు స్పందన రేటు నిమిషానికి 75. గుండె పౌనఃపున్యం, ఆవర్తన కాలాలను లెక్కించండి.
జవాబు:
గుండె స్పందన పౌనఃపున్యం = 75 / (1 min) = 75/(60s) = 1.25 s^-1 = 1.25 Hz = 75 min
ఆవర్తన కాలం, T = 1/(1.25s^-1) = 0.8s

ప్రశ్న 2.
కింది కాల ప్రమేయాల్లో ఏది (a) సరళ హరాత్మక చలనం (b) ఆవర్తన చలనమే కాని సరళ హరాత్మక చలనం కాదు. రెండు సందర్భాల్లో ఆవర్తన కాలాలను తెలపండి.
a) sin ωt – cot ωt
b) sin² ωt
జవాబు:
a) sin ωt – cos ωt = sin ωt – sin (π/2 – ωt)
= 2 cos (π/4) sin (ωt – π/4)
= \(\sqrt{2}\) sin (ωt – π/4)
పై సమీకరణం ఆవర్తన కాలం T = 2 π/ω, దశా కోణం (−π/4) లేదా (π/4) తో ఉండే సరళ హరాత్మక చలనాన్ని సూచిస్తుంది.

b) sin²ωt = 1/2 – 1/2 cos 2ωt
ఇది ఆవర్తన కాలం T = π/ω తో ఉండే ఆవర్తన చలనాన్ని సూచిస్తుంది. ఇది 0 వద్ద కాక 1/2 వద్ద సమతాస్థితి స్థానాన్ని కలిగి ఉండే హరాత్మక చలనాన్ని కూడా సూచిస్తుంది.

ప్రశ్న 3.
కింద ఇచ్చిన సమీకరణా (SI ప్రమాణాలలో) నికి అనుగుణంగా ఒక వస్తువు సరళ హరాత్మక చలనం చేస్తుంది.
x = 5 cos [2πt + π/4]
t = 1.58 వద్ద వస్తువు (a) స్థానభ్రంశం, (b) వడి, (c) త్వరణాలను లెక్కించండి.
జవాబు:
వస్తువు కోణీయ పౌనఃపున్యం ω = 2πs^-1,
ఆవర్తన కాలం T = 1s
t = 1.5s వద్ద
a) స్థానభ్రంశం = (5.0m) cos [(2πs^-1) × 1.5s + π/4]
= (5.0 m) cos [(3π + π/4)]
= – 5.0 × 0.707 m = – 3.535 m

b) సమీకరణం v(t) = – ωA sin (ωt + Φ) ని ఉపయోగించి, వస్తువు వడి
= – (5.0m) (2πs^-1) sin ((2πs^-1) × 1.5s + π/4]
= – (5.0m) (2πs^-1) sin [(3π + π/4]
= 10π × 0.707 ms^-1 = 22 ms^-1

c) సమీకరణం v(t) = \(\frac{\mathrm{d}}{\mathrm{dt}}\) x(t) = \(\frac{\mathrm{d}}{\mathrm{dt}}\) [A cos (ωt + Φ)] ని ఉపయోగించి, వస్తువు త్వరణం
= – (2πs^-1)² × స్థానభ్రంశం
= – (2πs^-1)² × (-3.535 m) = 140 ms^-2

ప్రశ్న 4.
500 Nm^-1 బల స్థిరాంకం గల స్ప్రింగ్కు 5kg ద్రవ్యరాశి గల లోహ కంకణాన్ని (ring) బిగించారు. క్షితిజ సమాంతరంగా ఉండే కడ్డీపై ఘర్షణ లేకుండా కంకణం జారుతుంది. మాధ్యమిక స్థానం నుంచి కంకణాన్ని 10.0 cm లాగి వదిలారు. అయితే కంకణం a) డోలనావర్తన కాలం 5) గరిష్ఠ వడి c) గరిష్ఠ త్వరణాలను లెక్కించండి.
జవాబు:
a) సమీకరణం T = 2π \(\) నుంచి డోలనావర్తన కాలం
T = 2π \(\sqrt{\frac{5.0 \mathrm{~kg}}{500 \mathrm{Nm}^{-1}}}\)
= (2π/10)s = 0.63s

b) సరళ హరాత్మక చలనం చేసే కంకణం వేగం v(t) = – Aω sin (ωt + Φ)
గరిష్ఠ వడి
v_m = Αω
= 0.1 × \(\sqrt{\frac{\mathrm{k}}{\mathrm{m}}}\)
= 0.1 × \(\sqrt{\frac{500 \mathrm{Nm}^{-1}}{5 \mathrm{~kg}}}\) = 1 ms^-1
x = 0 వద్ద గరిష్ఠ వడి ఉంటుంది.

c) మాధ్యమిక స్థానం నుంచి x(t) స్థానభ్రంశం వద్ద కంకణం త్వరణం
a(t) = -ω²x(t)
= – \(\frac{\mathrm{k}}{\mathrm{m}}\) x(t)
గరిష్ఠ త్వరణం, a_max = ω²A
= \(\frac{500 \mathrm{Nm}^{-1}}{5 \mathrm{~kg}}\) × 0.1 m = 10 ms^-2
ఇది అంత్య స్థానాల వద్ద ఉంటుంది.

ప్రశ్న 5.
సెకండులను టిక్చేసే లఘులోలకం పొడవు ఎంత ?
జవాబు:
లఘులోలకం డోలనావర్తన కాలం
T = 2π \(\sqrt{\frac{\mathrm{L}}{\mathrm{g}}}\)
దీని నుంచి కింది విధంగా రాయవచ్చు.
L = \(\frac{\mathrm{g} \mathrm{T}^2}{4 \pi^2}\)
సెకండ్లను టిక్ చేసే లఘులోలకం డోలనావర్తన కాలం 2s.
∴ g = 9.8 ms^-2, T = 2s విలువలకు
L = \(\frac{9.8\left(\mathrm{~ms}^{-2}\right) \times 4\left(\mathrm{~s}^2\right)}{4 \pi^2}\) = 1 m

ముఖ్యమైన అదనపు లెక్కలు

ప్రశ్న 1.
కింది వాటిలో ఏవి ఆవర్తన చలనాలను సూచిస్తాయి ?
a) చెరువు ఒక ఒడ్డు నుంచి అవతలి ఒడ్డుకు, తిరిగి అవతలి ఒడ్డు నుంచి మొదటి ఒడ్డుకు ఒక ఈతగాడు పూర్తి చేసే ట్రిప్.
b) స్వేచ్ఛగా వేలాడదీసిన దండాయస్కాంతాన్ని NS దిశ నుంచి కదిల్చి వదిలితే అది చేసే చలనం.
c) తన ద్రవ్యరాశి కేంద్రం చుట్టూ భ్రమణం చెందే హైడ్రోజన్ అణువు.
d) ధనుస్సు (విల్లు) నుంచి విడుదలైన బాణం.
జవాబు:
a) ఈతగాడు ఈ ఒడ్డు నుండి ఆ ఒడ్డుకు మరల మొదటి వైపుకు వస్తే అది సంవృత చలనమే గాని ఆవృత చలనం కాదు. కారణం ఈ చలనము నియమిత కాలవ్యవధిలో పునరావృతం కాదు.
b) స్వేచ్ఛగా వేలాడదీసిన దండాయస్కాంత కంపనాలు ఆవృత చలనాలు.
c) ఇది ఆవృత చలనము. కారణం వస్తువు పరిభ్రమణంలో ఉంది.
d) విల్లు నుంచి వచ్చిన బాణం ఒకే దిశలో ముందుకు పోతుంది. ఇది ఆవృత చలనం కాదు.

ప్రశ్న 2.
కింది ఉదాహరణలలో ఏవి దాదాపు సరళ హరాత్మక చలనాలు, ఏవి సరళ హరాత్మకం కాని ఆవర్తన చలనాలను సూచిస్తాయి ?
a) తన అక్షం పరంగా భూమి చేసే భ్రమణ చలనం
b) U – గొట్టంలో డోలనం చేసే పాదరస స్తంభం చలనం
c) నునుపైన వక్రత గల లోతు గిన్నెలో సమతాస్థితి స్థానం కంటే కొద్దిగా ఎగువన వదిలిన ఇనుప గుండు చలనం
d) తన సమతాస్థితి స్థానం పరంగా బహుపరమాణుక అణువు చేసే సాధారణ కంపనాలు
జవాబు:
a) భూమి తన అక్షం చుట్టూ చేసే భ్రమణం ఆవృత చలనము. ఇది S.H.M కాదు.
b) U – గొట్టంలో ద్రవం చేసే డోలనాలు సరళ హరాత్మక చలనాలు.
c) సమతాస్థితి నుంచి ఇనుప గుండును స్థానభ్రంశం చెందిస్తే అది నునుపు తలంపై సరళ హరాత్మక చలనం చేస్తుంది.
d) సగటు స్థానం నుండి బహుపరమాణుక అణువు కంపనాలు ఆవర్తన చలనాలు కావు.

ప్రశ్న 3.
దిగువన ఇవ్వబడిన పటం కణం రేఖీయ చలనానికి x – t ల మధ్య గీచిన గ్రాఫ్లను సూచిస్తుంది. వీటిలో ఏవి ఆవర్తన చలనాన్ని సూచిస్తాయి ? సూచిస్తే వాటి డోలనావర్తన కాలం ఎంత ?

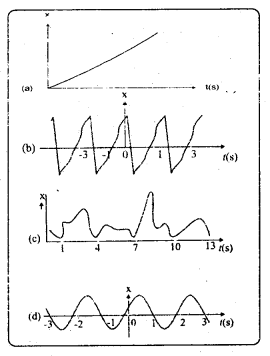
జవాబు:
a) ఈ రేఖాపటము కాలంతో పాటు ఒకే దిశలో స్థానభ్రంశంలో మార్పు సూచిస్తుంది. కావున ఆవృత చలనం కాదు.
b) ఇది ఆవృత చలనాన్ని సూచిస్తుంది. దీని ఆవర్తన కాలము 2 సెకనులు.
c) ఈ చలన వక్రంలోని ఆకారం నియమిత కాలం తరువాత పునరావృతం కాలేదు. అందువల్ల ఇది ఆవృత చలనం కాదు.
d) ఇది ఆవృత చలనము. ఆవర్తన కాలము 2 సెకనులు.

ప్రశ్న 4.
కింది వాటిలో ఏ కాల ప్రమేయాలు a) సరళ హరాత్మక, b) ఆవర్తనమే కానీ సరళ హరాత్మకం కాని, c) ఆవర్తనం కాని చలనాలను సూచిస్తాయి. ప్రతి ఆవర్తన చలనం సందర్భంలో ఆవర్తన కాలాన్ని తెలియచేయండి. (ఎ ఏదైనా ధన స్థిరాంకం)
a) sin ωt – cos ωt
(b) sin³ ωt
(c) 3 cos\(\left(\frac{\pi}{4}-2 \omega t\right)\)
(d) cos ωt + cos 3ωt + cos 5ωt
(e) exp (- ω²t²)
(f) 1 + ωt + ω²t².
జవాబు:

1. ఒక చలనం ఆవృత చలనం కావాలంటే దాని చలనం ఒకే విధంగా ఉండి నిర్ణీత కాలవ్యవధి తరువాత పునరావృతం కావాలి.
2. వస్తువు చలనం S.H.M కావాలంటే దాని చలనం cos (ωt + Φ) లేదా sin (ωt + Φ) వంటి రూపంలో ఉండాలి.

a) sin ωt – cos ωt = \(\sqrt{2}\left[\frac{1}{\sqrt{2}} \sin \omega \mathrm{t}-\frac{1}{\sqrt{2}} \cos \omega \mathrm{t}\right]=\sqrt{2}\left[\cos \frac{\pi}{4} \sin \omega \mathrm{t}-\sin \frac{\pi}{4} \cos \omega \mathrm{t}\right]\)
= \(\sqrt{2} \sin \left(\omega t-\frac{\pi}{4}\right)\)
ఇది S.H.M లో గల వస్తువు సమీకరణాన్ని సూచిస్తుంది. కావున సరళ హరాత్మక చలనము.

b) sin³ ωt = \(\frac{1}{4}\) [3 sin ωt – sin 3ωt]
ఇందులో sin ωt మరియు sin 3ωt లు ఆవృత చలనాలు. ఆవర్తన కాలము 2π/ω. కాని ఈ రెంటి కలయిక సరళ హరాత్మక చలనం కాదు. కేవలం ఆవృత చలనం మాత్రమే.

c) 3 cos \(\left(\frac{\pi}{4}-2 \omega t\right)\) = 3 cos (2ωt – \(\frac{\pi}{4}\)); [∵ cos – θ = cos θ]
కావున ఇది సరళ హరాత్మక చలనము.

d) cos ωt + cos 3ωt + cos 5ωt లలో ప్రతి పదము ఆవర్తన చలనాన్ని కలిగి ఉంది. వీటి అన్నింటి ఫలితంగా వచ్చిన చలనం సరళ హరాత్మక చలనం కాదు.

e) e^-ω2t2 వంటి ఘాతాంక ప్రమేయాలు ఒకే దిశలో పెరుగుతాయి. వీటి ప్రవర్తన పునరావృతం కాదు. అందువల్ల ఇవి ఆవృత చలనాలు లేదా S.H.M లు కావు.

f) 1 + ωt + ω²t² వంటి సమీకరణాల పరిమాణాలు కాలంతో పాటు పునరావృతం కావు. అందువల్ల ఇవి ఆవృత చలనాలు లేదా S.H.M లు కావు.

ప్రశ్న 5.
10 cm ఎడంతో ఉండే రెండు బిందువులు A, B ల మధ్య ఒక కణం రేఖీయ సరళ హరాత్మక చలనం చేస్తుంది. A నుంచి B కి దిశను ధన దిశగా తీసుకొని, కింద ఇచ్చిన స్థానాల వద్ద కణం ఉన్నప్పుడు వేగం, త్వరణం, బలం
దిశలను తెలపండి.
a) A
b) B
c) A, B ల మధ్య బిందువు వద్ద A వైపు వెళ్ళేటప్పుడు,
d) B నుంచి 2 cm దూరంలో, A వైపు వెళ్ళేటప్పుడు,
e) A నుంచి 3 cm దూరంలో, B వైపు వెళ్ళేటప్పుడు,
f) B నుంచి 4 cm దూరంలో, A వైపు వెళ్ళేటప్పుడు.
జవాబు:
a) A బిందువు వద్ద స్థానభ్రంశం గరిష్ఠము. కావున వేగం V = 0 త్వరణము, బలము గరిష్ఠము. వీటి దిశ A నుండి B వైపు ఉంటుంది.

b) B బిందువు వద్ద స్థానభ్రంశం గరిష్ఠము కావున V త్వరణము, బలము గరిష్ఠము. వీటి దిశ B నుండి A వైపు ఉంటుంది.

c) మధ్యబిందువు ‘C’ వద్ద స్థానభ్రంశము సున్న వేగము గరిష్ఠము. ఇది x -ve దిశలో ఉంటుంది. త్వరణము, బలముల పరిమాణము సున్న.

d) B నుండి 2 cm దూరంలో A వైపు చలిస్తే ఇవి x -ve వైపు చలించే ప్రవృత్తి కలిగి ఉన్నాయి. కావున వేగము, త్వరణము, బలం అన్నీ ఋణాత్మకమే.

e) A నుండి 3 cm దూరంలో B వైపు చలిస్తుంటే కణం గమన దిశ x ‘+ve’ వైపు ఉంది. కావున వేగం, త్వరణము మరియు బలముల దిశ ధనాత్మకము.

f) B నుండి 4 cm దూరంలో A వైపు చలిస్తుంటే వేగం x -ve వైపు ఉంది కావున ఋణాత్మకము, త్వరణము మధ్య బిందువు వైపు ఉంది. కావున త్వరణము, బలము ధనాత్మకము.

ప్రశ్న 6.
కణం త్వరణం a, స్థానభ్రంశం x ల మధ్య సంబంధాన్ని తెలిపే కింది సమీకరణాల్లో ఏవి సరళ హరాత్మక చలనాన్ని కలిగి ఉన్నాయి ?
a) a = 0.7 x
b) a = – 200 x²
c) a = – 10x
d) a = 100 x³
జవాబు:
a) ఇది S.H.M కాదు
b) S.H.M కాదు
c) a = – 10x ఇది a = – ω²y రూపంలో ఉంది కావున సరళ హరాత్మక చలనం (S.H.M) ను సూచిస్తుంది.
d) ఇది S.H.M కాదు.
గమనిక : S.H.M లో గల వస్తువు త్వరణము a = – ω²y రూపంలో ఉండాలి. ω = స్థిరపదము (విలువ స్థిరము).

ప్రశ్న 7.
స్ప్రింగ్ త్రాసు స్కేలుపై 0 నుంచి 50 kg వరకు రీడింగ్లు కలవు. స్కేలు పొడవు 20 cm. ఈ త్రాసుకు వేలాడదీసిన వస్తువును లాగి వదిలితే అది 0.6s డోలనావర్తన కాలంతో డోలనాలు చేస్తుంది. అయితే వేలాడదీసిన వస్తువు భారం ఎంత ?
జవాబు:
దత్తాంశం నుండి m₁ = 50 కి.గ్రా లకు సాగుదల y = 20 సెం.మీ. = 0.2 మీ; కాలము T = 0.6 సె
గరిష్ఠ బలం F = mg = 50 × 9.8 = 490 N
బలస్థిరాంకము K = \(\frac{\mathrm{F}}{\mathrm{y}}=\frac{490}{0.2}\) = 2450 న్యూ
ఆవర్తన కాలము T = 2π\(\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\) ⇒ m = \(\frac{\mathrm{KT}^2}{4 \pi^2}\)
m = \(\frac{2450 \times 0.6 \times 0.6}{4 \times(3.14)^2}\) = = 22.56 kg
వస్తువు భారము w = mg = 22.56 × 9.8 = 221.1 న్యూ

ప్రశ్న 8.
పటంలో చూపిన విధంగా 1200 Nm^-1 స్ప్రింగ్ స్థిరాంకం గల స్ప్రింగ్ను క్షితిజ సమాంతరంగా ఉండే బల్లపై అమర్చారు. స్ప్రింగ్ స్వేచ్ఛా చివరకు 3 kg ద్రవ్యరాశిని తగిలించారు. ద్రవ్యరాశిని 2.0 cm దూరం పక్కకు లాగి వదిలారు. i) డోలనాల పౌనఃపున్యం, ii) ద్రవ్యరాశి గరిష్ఠ త్వరణం, iii) ద్రవ్యరాశి గరిష్ఠ వేగాలను కనుక్కోండి.
జవాబు:
దత్తాంశం నుండి k = 1200 Nm^-1; m = 3.0 kg; a = 2 cm = 0.02 m

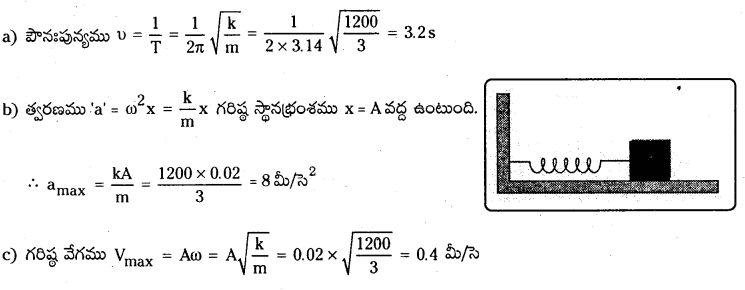
ప్రశ్న 9.
పై అభ్యాసంలో స్ప్రింగ్ సాగదీయనప్పుడు ద్రవ్యరాశి స్థానం x = 0 అని, ఎడమ నుంచి కుడికి ధనాత్మక x – అక్షం అని తీసుకోండి. t = 0 వద్ద స్టాప్ వాచ్ను మొదలు పెట్టినట్లైతే, డోలనాలు చేస్తున్న ద్రవ్యరాశి కింది స్థానాల వద్ద ఉన్నప్పుడు t ప్రమేయంగా x విలువను తెలపండి.
a) మాధ్యమిక స్థానం
b) గరిష్టంగా సాగిన స్థానం
c) గరిష్ఠంగా సంపీడనం (నొక్కిన) చెందిన స్థానం
పై సరళ హరాత్మక చలన ప్రమేయాలు పౌనఃపున్యం, కంపన పరిమితి, తొలి దశల్లో ఒకదానితో ఒకటి ఏవిధంగా విభేదిస్తాయో తెలపండి.
జవాబు:
కంపన పరిమితి A = 2 సెం.మీ; ω = \(\sqrt{\frac{\mathrm{k}}{\mathrm{m}}}=\sqrt{\frac{1200}{3}}\) = 20 రే/సె
a) మాధ్యమిక స్థానం వద్ద x = A sin ωt నుండి x = 2 sin 2ω t

b) గరిష్ఠంగా సాగిన స్థానం వద్ద x = A అనగా Φ = \(\frac{\pi}{2}\) మూల సమీకరణం నుండి
x = A sin (ωt + Φ) నుండి x = 2 sin (20t + \(\frac{\pi}{2}\)) = 2 cos (20t)

c) గరిష్ఠ సంపీడన స్థానం వద్ద x = – A. కావున Φ = \(\frac{3\pi}{2}\) మూల సమీకరణం
x = A sin (ωt + Φ) నుండి x = – 2 sin (20t + \(\frac{3\pi}{2}\)) = -2 cos 20t.

ప్రశ్న 10.
పటం రెండు వృత్తాకార చలనాలను సూచిస్తుంది. వృత్త వ్యాసార్ధం, భ్రమణ కాలం, తొలిస్థానం, తిరిగే దిశ (సవ్య లేదా అపసవ్య) మొదలైన అంశాలు పటంలో చూపించడమైంది.

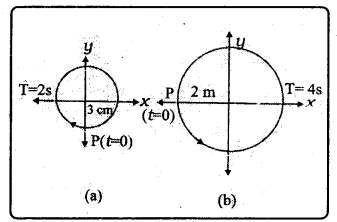
పై రెండు సందర్భాలలో భ్రమణం చెందే కణం P యొక్క వ్యాసార్ధ సదిశ x – అక్ష విక్షేపం యొక్క సహచలనాలను రాబట్టండి.
జవాబు:
పటము (a) నుండి T = 2సె; కంపన పరిమితి A = 3 సెం.మీ. ;
t = 0 వద్ద ‘OP’ x – అక్షంతో చేసిన కోణము \(\frac{\pi}{2}\) = 90° సవ్యదిశ
∴ S.H.M లో గల వస్తుసమీకరణం x = A cos \(\left(\frac{2 \pi \mathrm{t}}{\mathrm{T}}+\phi\right)\) = 3 cos \(\left(\frac{2 \pi \mathrm{t}}{2}+\frac{\pi}{2}\right)\) = 3 cos \(\left(\pi \mathrm{t}+\frac{\pi}{2}\right)\) సెం.మీ.

b) పటము (b) నుండి కాలము T = 4 సె ; కంపన పరిమితి A = 2 మీ.
t = 0 వద్ద x – అక్షంతో P చేయు కోణము Φ = π. (సవ్యదిశలో)
∴ S.H.M లో గల వస్తు సమీకరణం
x = A cos \(\left(\frac{2 \pi t}{T}+\phi\right)\) = 2 cos \(\left(\frac{2 \pi \mathrm{t}}{4}+\pi\right)\) = -2 cos \(\left(\frac{\pi}{2} t\right)\)

ప్రశ్న 11.
పటం (a)లో చూపించిన విధంగా బల స్థిరాంకం గల స్ప్రింగ్ ఒక చివరను దృఢంగా బిగించి, రెండో స్వేచ్ఛా చివరకు ద్రవ్యరాశి m ని బిగించారు. స్వేచ్ఛా చివర ప్రయోగించిన బలం Fవల్ల స్ప్రింగ్ కొంత సాగుతుంది. పటం (b)లో చూపించిన విధంగా అదే స్ప్రింగ్ రెండు స్వేచ్ఛా చివరలను m ద్రవ్యరాశి గల రెండు దిమ్మెలకు అనుసంధానం చేసి, రెండు చివరలా అంతే బలం F ప్రయోగించి స్ప్రింగ్ను సాగదీశారు.

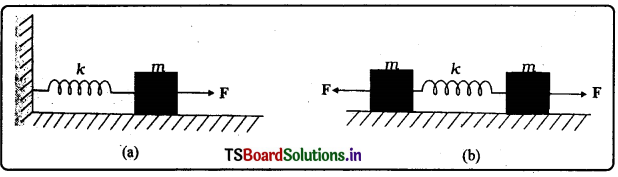
(a) రెండు సందర్భాల్లో స్ప్రింగ్ పొందే గరిష్ఠ సాగుదల ఎంత ?
(b) పటం (a) లో ద్రవ్యరాశిని, పటం (b) లో రెండు ద్రవ్యరాశులను వదిలిపెడితే ప్రతి సందర్భంలో స్ప్రింగ్ చేసే డోలనావర్తన కాలం ఎంత ?
జవాబు:
రెండు సందర్భాలలోను స్ప్రింగ్లో గరిష్ఠ సాగుదల_x = F/k
పటం ‘a’ నుండి స్ప్రింగ్ను సాగదీసిన స్థానం వద్ద బరువును వదలివేస్తే పునఃస్థాపక బలం F = – kx లేదా F ∝ x
ఆవర్తన కాలము T = 2π \(\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\) స్ప్రింగ్లలో
m = తగిలించిన ద్రవ్యరాశి ; k = స్ప్రింగ్ స్థిరాంకము
పటము ‘b’ నుండి రెండు ద్రవ్యరాశులను శ్రేణి పద్ధతిలో కలిపితే స్ప్రింగ్ స్థిరాంకము k అయినపుడు ఫలిత ద్రవ్యరాశి
μ = \(\frac{\mathrm{m} \times \mathrm{m}}{\mathrm{m}+\mathrm{m}}=\frac{\mathrm{m}}{2}\)
ఆవర్తన కాలము T= 2π \(\sqrt{\frac{\mu}{k}}\) = 2π \(\sqrt{\frac{\mathrm{m}}{2 \mathrm{k}}}\)

ప్రశ్న 12.
ఒక వాహన ఇంజన్లోని సిలిండర్లో గల ముషలకం 1.0m (కంపన పరిమితికి రెట్టింపు) ఘాతం (stroke) ను ఇస్తుంది. ఒకవేళ ముషలకం 200 rad/min పౌనఃపున్యంతో సరళ హరాత్మక చలనం చేస్తున్నట్లైతే, దాని గరిష్ఠ వడి ఎంత ?
జవాబు:
కంపన పరిమితి A = \(\frac{1}{2}\) మీ.,
ω = 200 R.P.M
గరిష్ఠ వేగము V_max = A . ω = \(\frac{1}{2}\) × 200 = 100 మీ/నిమిషము

ప్రశ్న 13.
చంద్రుడిపై గురుత్వ త్వరణము విలువ 1.7 ms^-2. భూమిపై 3.58 డోలనావర్తన కాలం గల లఘులోలకాన్ని చంద్రుడిపైకి తీసుకొనిపోతే అక్కడ దాని డోలనావర్తన కాలం ఎంత ? (భూమిపై g విలువ 9.8 ms^-2)
జవాబు:
చంద్రునిపై గురుత్వ త్వరణము g_m = 1.7 మీ/సె^-2 ; భూమిపై g = 9.8 మీ/సె²
భూమిపై లోలకం ఆవర్తన కాలము T_e = 3.5 సె ;
చంద్రునిపై ఆవర్తన కాలం T_m = ?
T_e = 2π \(\sqrt{\frac{l}{g_e}}\)
T_m = 2π \(\sqrt{\frac{l}{g_m}}\)
∴ \(\frac{T_m}{T_e}=\sqrt{\frac{g_e}{g_m}\)
చంద్రునిపై ఆవర్తన కాలం T_m = T_e \(\sqrt{\frac{9.8}{1.7}}\) = 8.4 s

ప్రశ్న 14.
Mద్రవ్యరాశి గల గుండును కలిగి ఉన్న ! పొడవు గల లఘులోలకాన్ని కారులో వేలాడదీశారు. కారు R వ్యాసార్ధం గల వృత్తాకార మార్గంపై సమవడితో చలిస్తోంది. లోలకం వ్యాసార్ధ దిశలో సమతాస్థితి స్థానం పరంగా స్వల్ప డోలనాలను చేస్తే, దాని ఆవర్తన కాలం ఎంత ?
జవాబు:
అభిలంబ త్వరణము a_c = \(\frac{v^2}{\mathrm{R}}\) ఇది క్షితిజ సమాంతరంగా పనిచేస్తుంది.
గురుత్వ త్వరణము ‘g’ క్షితిజ లంబంగా పనిచేస్తుంది.
ఫలిత గురుత్వ త్వరణము g’ = \(\sqrt{g^2+a_c^2}=\sqrt{g^2+\frac{v^4}{R^2}}\)
ఆవర్తన కాలము T = 2π \(\sqrt{\frac{l}{g^{\prime}}}\) = 2π \(\sqrt{\frac{l}{g^2 \quad v^4 / R^2}}\)

ప్రశ్న 15.
10 kg ద్రవ్యరాశి గల వృత్తాకార లోహపలక కేంద్రం వద్ద తీగతో కట్టి పలకను వేలాడదీశారు. తీగను మెలి తిప్పి వదిలితే పలక చేసే విమోటన డోలనాల ఆవర్తన కాలం 1.58 పలక వ్యాసార్ధం 15 cm అయితే తీగ విమోటన స్ప్రింగ్ స్థిరాంకం విలువను కనుక్కోండి. (విమోటన స్ప్రింగ్ స్థిరాంకం aను J = – α θ తో నిర్వచిస్తారు. ఇక్కడ J పునఃస్థాపక టార్క్, θ పురి తిప్పిన కోణం).
జవాబు:
దత్తాంశం నుండి m = 10 కి.గ్రా; R = 15 సెం.మీ. = 0.15 మీ; T = 1.5 సె
బిళ్ళ జడత్వ భ్రామకము I = \(\frac{\mathrm{MR}^2}{2}\) = \(\frac{1}{2}\) × 10 × (0.15)² = 0.1125 kg m²
ఆవర్తన కాలము T = 2π \(\sqrt{\frac{\mathrm{I}}{\alpha}}\)
లేదా α = \(\frac{4 \pi^2 \mathrm{I}}{\mathrm{T}^2}\) = 4 × (3.14)² × \(\frac{1}{2}\) × \(\frac{0.1125}{(1.5)^2}\) = 1.97 Nm/Rad

ప్రశ్న 16.
5 cm కంపన పరిమితి, 0.2s డోలనావర్తన కాలంతో ఒక వస్తువు సహచ చేస్తుంది. వస్తువు స్థానభ్రంశాలు (a) 5 cm (b) 3 cm (c) 0 cm అయినప్పుడు దాని త్వరణం, వేగాలను కనుక్కోండి.
జవాబు:
దత్తాంశం నుండి A = 5 సెం.మీ. = 0.05 మీ; T = 0.2 సె
కోణీయ వేగము ω = \(\frac{2 \pi}{T}=\frac{2 \times 3.14}{0.2}\) = 10π
a) స్థానభ్రంశము x = 5 cm ⇒ x = A వద్ద
త్వరణము A = – ω²A = 10π × 10π × \(\frac{5}{100}\) = 5π² = 49.3 మీ/సె²
వేగము V = 0 (x = A అయినపుడు)

b) స్థానభ్రంశము x = 3 సెం.మీ.= \(\frac{3}{100}\) మీ.
త్వరణము a = – ω²x = 10π × 10π × \(\frac{3}{100}\) = 29.58 మీ/సె²
వేగము V = ω \(\sqrt{\mathrm{A}^2-\mathrm{x}^2}=10 \pi \sqrt{\left(\frac{5}{100}\right)^2-\left(\frac{3}{100}\right)^2}=\frac{10 \pi}{100} \sqrt{25-9}\)
= \(\frac{\pi}{10} \cdot \sqrt{16}=\frac{4 \pi}{10}\) = 1.256 మీ/సె

c) స్థానభ్రంశము x = 0 వద్ద, త్వరణము a = ω²x = 0
వేగము V గరిష్ఠము
∴ V_max = Aω = \(\frac{5}{100}\) × 10π = \(\frac{\pi}{2}\) = 1.57 మీ/సె

ప్రశ్న 17.
క్షితిజ సమాంతరంగా ఉండే స్ప్రింగ్ స్వేచ్ఛా చివరన కట్టిన ద్రవ్యరాశి, తలంపై ఎలాంటి ఘర్షణ లేదా అవరోధం లేనప్పుడు » కోణీయ వేగంతో డోలనాలు చేస్తుంది. t = 0 కాలం వద్ద ద్రవ్యరాశిని x₀ దూరం లాగి కేంద్రం వైపు V₀ వేగంతో నెట్టినప్పుడు కలిగే ఫలిత డోలనాల కంపన పరిమితిని ω, x₀, V₀ పదాలలో కనుక్కోండి.
(సూచన : x = a cos (ωt + θ) సమీకరణంతో ప్రారంభించండి. తొలి వేగం రుణాత్మకం అని గమనించండి.)
జవాబు:
దత్తాంశం నుండి కాలము t = 0 వద్ద x = x₀ మరియు \(\frac{\mathrm{dx}}{\mathrm{dt}}\) = -V₀
S.H.M సమీకరణం x = A cos (ωt + Φ) నుండి x₀ = A cos ωt …………….. (1)
కాని \(\frac{\mathrm{dx}}{\mathrm{dt}}\) = V₀ = -ω A sin ωt
⇒ A sin ωt = \(\frac{V_0}{\omega}\) ………………. (2)
1, 2 సమీకరణాలను వర్గీకరించి కలుపగా
x₀² + \(\frac{\mathrm{V}_0^2}{\omega^2}\) = A² (sin²ωt + cos²ωt) లేదా A² = x₀² + \(\frac{\mathrm{V}_0^2}{\omega^2}\)
∴ కంపన పరిమితి A = \(\sqrt{\mathrm{x}_0^2+\frac{\mathrm{V}_0^2}{\omega^2}}\)