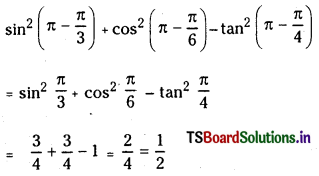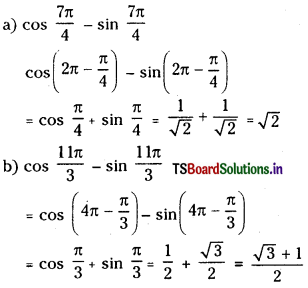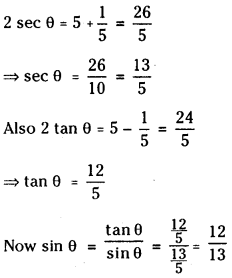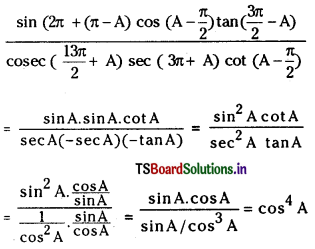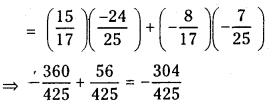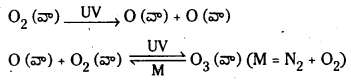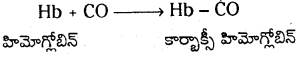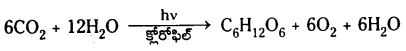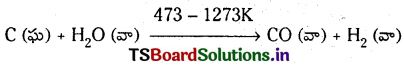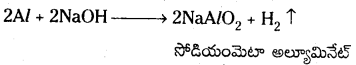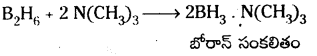TS Inter 1st Year

Telangana TSBIE TS Inter 1st Year Physics Study Material 9th Lesson గురుత్వాకర్షణ Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 9th Lesson గురుత్వాకర్షణ

అతిస్వల్ప సమాధాన ప్రశ్నలు (2 మార్కులు)

ప్రశ్న 1.
విశ్వ గురుత్వ స్థిరాంకం (G) ప్రమాణాలను, మితులను తెలపండి.
జవాబు:
విశ్వ గురుత్వ స్థిరాంకము G కి ప్రమాణాలు న్యూటన్ – మీటరు²/కి.గ్రా.², మితిఫార్ములా M^-1L³T^-2.

ప్రశ్న 2.
న్యూటన్ గురుత్వాకర్షణ నియమాన్ని సదిశా రూపంలో వ్యక్తీకరించండి.
జవాబు:
న్యూటన్ విశ్వగురుత్వాకర్షణ బలము సదిశా సమీకరణము \(\overline{\mathrm{F}}=\frac{\mathrm{Gm}_1 \mathrm{~m}_2 \overline{\mathrm{r}}}{\overline{\mathrm{r}}^3}\)

ప్రశ్న 3.
చంద్రునిపై భూమి గురుత్వాకర్షణ బలం F అయితే, భూమిపై చంద్రుని గురుత్వాకర్షణ బలం ఎంత ? ఈ బలాలు చర్య – ప్రతిచర్య జంటను ఏర్పరుస్తాయా ?
జవాబు:
భూమి, చంద్రుడు మరియు చంద్రుడు, భూమిల మధ్య గురుత్వాకర్షణ బలాలు సమానము. కావున F_EM = -F_ME రెండు వస్తువుల మధ్య గురుత్వాకర్షణ బలాలను చర్య – ప్రతిచర్య బలాలుగా తీసుకొనవచ్చును.

ప్రశ్న 4.
భూమి ద్రవ్యరాశిని స్థిరంగా ఉంచుతూనే, భూమి వ్యాసార్ధం 2% తగ్గిస్తే, దాని ఉపరితలం వద్ద గురుత్వ త్వరణం విలువ (g) లో వచ్చే మార్పు ఎంత ఉంటుంది ?
జవాబు:
గురుత్వ త్వరణము g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\)
ద్రవ్యరాశిని స్థిరంగా ఉంచి వ్యాసార్ధమును 2% తగ్గిస్తే \(\frac{\Delta \mathrm{R}}{\mathrm{R}}\) × 100 = -2
దోష విభాజన నియమము ప్రకారము \(\frac{\Delta \mathrm{g}}{\mathrm{g}}\) × 100 = -2 \(\frac{\Delta \mathrm{R}}{\mathrm{R}}\) × 100
‘g’ లో మార్పు శాతము = – 2 × 2 = – 4% అనగా R తగ్గితే ‘g’ పెరుగును.

ప్రశ్న 5.
మనం ఒక గ్రహం నుంచి మరొక గ్రహానికి మారుతూ ఉంటే వస్తువు a) ద్రవ్యరాశి b) భారం ఎలా మారుతుంటాయి ?
జవాబు:
ఒక “గ్రహము నుండి వేరొక గ్రహమునకు పోయినపుడు ద్రవ్యరాశి మారదు. వస్తువు ద్రవ్యరాశి స్థిరము.
ఒక గ్రహము నుండి వేరొక గ్రహానికి పోవుకొలది కొంత దూరము వరకు భారము క్రమముగా తగ్గును.
శూన్యంలో g = 0 వద్ద భారము సున్న.
మరలా వేరొక గ్రహమును సమీపించు కొలది భారము క్రమముగా పెరుగును.

ప్రశ్న 6.
ఒక లఘులోలకం పొడవును స్థిరంగా ఉంచినప్పుడు, అన్ని గ్రహాల మీద దాని డోలనావర్తన కాలం సమానంగా ఉంటుందా ? కారణంతో సహా మీ సమాధానాన్ని సమర్థించండి.
జవాబు:
లోలకము పొడవును స్థిరంగా ఉంచిన డోలనావర్తనకాలము ఒక గ్రహము నుండి వేరొక గ్రహానికి మారును. లోలకము డోలనావర్తన కాలము T = 2π \(\sqrt{\frac{l}{\mathrm{~g}}}\) ‘T’ ఆ గ్రహము ‘g’ పై ఆధారపడి ఉండును. గురుత్వ త్వరణము g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\) ఒక గ్రహము నుండి వేరొక గ్రహానికి మారును.
కావున లోలకము పొడవు స్థిరంగా ఉన్నప్పటికి ఆవర్తన కాలము గ్రహాన్ని బట్టి మారును.

ప్రశ్న 7.
భూఉపరితలం నుంచి d లోతులో ఉన్న బిందువు వద్ద గురుత్వ త్వరణానికి సమీకరణాన్ని తెలపండి. భూకేంద్రం వద్ద g విలువ ఎంత ?
జవాబు:
భూమి ఉపరితలము నుండి ‘d’ లోతు వద్ద గురుత్వ త్వరణము g_d = g(1 – \(\frac{D}{R}\))
భూమి కేంద్రము వద్ద గురుత్వ త్వరణము విలువ సున్నా.

ప్రశ్న 8.
g విలువను భూమధ్య రేఖ వద్ద కనిష్ఠంగా, ధ్రువాల వద్ద గరిష్ఠంగా ఉండే విధంగా చేసే అంశాలేమిటో తెలపండి.
జవాబు:
గురుత్వత్వరణము భూమధ్యరేఖ వద్ద కనిష్ఠము కారణము,

1. భూమి భూమధ్యరేఖా వ్యాసార్ధము గరిష్ఠము g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\). ‘R’ గరిష్ఠము కావున ‘g’ కనిష్ఠము.
2. భూమధ్యరేఖ వద్ద అపకేంద్రబలము గరిష్ఠము. ఇది గురుత్వాకర్షణ బలమును వ్యతిరేకించును. భూమధ్యరేఖ వద్ద అపకేంద్ర బలము గరిష్ఠము. g విలువ కనిష్ఠము.

భూమి ధ్రువాల పరంగా వ్యాసార్ధము కనిష్ఠము. g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\), కావున g విలువ ధ్రువాల వద్ద గరిష్ఠము. ధ్రువాల వద్ద భ్రమణపరంగా అపకేంద్రబలము సున్నా. కావున g విలువ ధ్రువాల వద్ద గరిష్ఠము.

ప్రశ్న 9.
“హైడ్రోజన్ సూర్యుని చుట్టూ పుష్కలంగా ఉంది. కాని భూమి చుట్టూ అంత పుష్కలంగా లేదు.” వివరించండి.
జవాబు:
హైడ్రోజన్ అణువుల పలాయన వేగంతో పోలిస్తే సూర్యుని పై పలాయన వేగం చాలా ఎక్కువ. సుమారు 620 కి.మీ/సె. అందువలన హైడ్రోజన్ అణువులు అత్యధిక ఆకర్షణ బలానికి లోనయి, సూర్యుని చుట్టూ ఉండిపోతాయి.
భూమి మీద g విలువ సూర్యునితో పోలిస్తే తక్కువ. ఆకర్షణ బలం తక్కువ. అందువలన హైడ్రోజన్, సూర్యుని చుట్టూ బంధింపబడినట్లు భూమిపై బంధింపబడదు. అందువలన సూర్యుని చుట్టూ హైడ్రోజన్ సమృద్ధిగా ఉంటుంది.

ప్రశ్న 10.
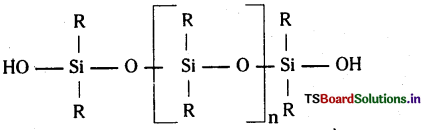
ఒక భూస్థావర ఉపగ్రహం పరిభ్రమణావర్తన కాలం ఎంత ? అది పశ్చిమం నుంచి తూర్పుకి లేదా తూర్పు నుంచి పశ్చిమానికి తిరుగుతుందా ?
జవాబు:
భూస్థావర ఉపగ్రహము ఆవర్తన కాలము 24 గంటలు.
భూస్థావర ఉపగ్రహము భూమి చుట్టూ పడమర నుండి తూర్పు వైపుకు భూమధ్యరేఖా తలములో తిరుగుచుండును.

ప్రశ్న 11.
ధ్రువీయ ఉపగ్రహాలు అంటే ఏమిటి ?
జవాబు:
ఇవి అల్ప ఉన్నతాంశ ఉపగ్రహాలు. ఈ ధ్రువీయ ఉపగ్రహాల పరిభ్రమణావర్తనకాలం 100 నిమిషాలు. అందువల్ల ఇవి రోజులో అనేక సార్లు భూమి చుట్టూ పరిభ్రమిస్తూ కొద్దిపాటి ప్రాంతాన్ని ఎక్కువ పృధక్కరణ (Resolution) తో ఫోటోలు తీస్తాయి. ఈ ఉపగ్రహాలు భూమి ధృవాల చుట్టూ ఉత్తర, దక్షిణ దిశలలో పరిభ్రమిస్తాయి.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
కెప్లర్ గ్రహ గమన నియమాలను పేర్కొనండి.
జవాబు:
కెప్లర్ గ్రహగమన నియమాలు :

1. కక్ష్యల నియమము : గ్రహాలన్నీ సూర్యుని చుట్టూ దీర్ఘ వృత్తాకార కక్ష్యలలో తిరుగుతుంటాయి. ఆ దీర్ఘ వృత్తం ఒకానొక నాభి వద్ద సూర్యుడు ఉంటాడు.
2. వైశాల్యాల నియమము : సూర్యుని నుంచి ఏదైనా గ్రహాన్ని కలిపే సరళరేఖ సమానకాలవ్యవధులలో సమాన వైశాల్యం ఉన్న క్షేత్రాలను చిమ్ముతుంది. అనగా గ్రహాలు సూర్యునికి దగ్గరగా ఉన్నప్పటికంటే దూరంగా ఉన్నపుడు తక్కువ వేగంతో చలిస్తాయి.
3. ఆవర్తన కాలాల నియమము : ఒక గ్రహం పరిభ్రమణ ఆవర్తన కాలవర్గం (T²), ఆ గ్రహ దీర్ఘ వృత్తాకారకక్ష్య అర్ధగురు అక్షం పొడవు ఘనాని (R³)కి అనులోమానుపాతంలో ఉంటుంది.
   T² ∝ R³ లేదా \(\frac{\mathrm{T}^2}{\mathrm{R}^3}\) = స్థిరరాశి

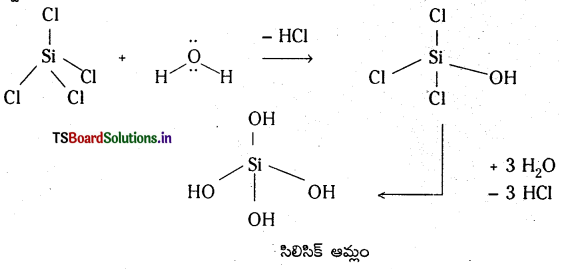
ప్రశ్న 2.
ఒక గ్రహం ఉపరితలంపై గురుత్వ త్వరణం విలువ (g), విశ్వ గురుత్వ స్థిరాంకం (G) ల మధ్య సంబంధాన్ని రాబట్టండి.
జవాబు:
గురుత్వ త్వరణము ‘g’ మరియు విశ్వ గురుత్వ స్థిరాంకము ‘G’ ల మధ్య సంబంధము : ప్రతి వస్తువును భూమి కొంత బలంతో తన కేంద్రంవైపు ఆకర్షిస్తుంది. భూమి వస్తువులపై చూపే ఈ ఆకర్షణ బలాన్నే వస్తువు భారము అంటారు. వస్తువు భారము W = mg ……………… (1)
న్యూటన్ గురుత్వాకర్షణ నియమం ప్రకారము ప్రతి రెండు వస్తువుల మధ్య పనిచేయు ఆకర్షణ బలం F = \(\frac{\mathrm{G} \cdot \mathrm{m} \cdot \mathrm{M}}{\mathrm{R}^2}\) సమానము. ఇందులో R భూమి వ్యాసార్ధము, M భూమి ద్రవ్యరాశి.
∴ వస్తువుల మధ్య ఆకర్షణ బలం F = \(\frac{\mathrm{GmM}}{\mathrm{R}^2}\) …………….. (2)
1, 2 సమీకరణాలు ఒకే భౌతికరాశి అయిన వస్తువుల మధ్య ఆకర్షణ బలాన్ని కొలుస్తున్నాయి. కాబట్టి ఆ రెండు సమీకరణాలు సమానమే.
∴ mg = \(\frac{\mathrm{GmM}}{\mathrm{R}^2}\) లేదా g =\(\frac{\mathrm{GM}}{\mathrm{R}^2}\)
కావున ‘g’ మరియు ‘G’ ల మధ్య సంబంధము g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\)

ప్రశ్న 3.
సమాన విలువలు కలిగిన ఎత్తు (h), లోతు (d) లకు గురుత్వ త్వరణం విలువ ఏ విధంగా మారుతుంది ?
జవాబు:
భూమి నుండి ‘h’ ఎత్తుకు పోతే అక్కడ గురుత్వ త్వరణము ‘g’ విలువ తగ్గుతుంది. గురుత్వ త్వరణము g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\) కాని R2 . ‘h’ ఎత్తుకు వెళ్ళినపుడు భూమి కేంద్రం నుండి ఎత్తు R + h అవుతుంది. కాని భూమి ద్రవ్యరాశి M విలువలో మార్పులేదు.

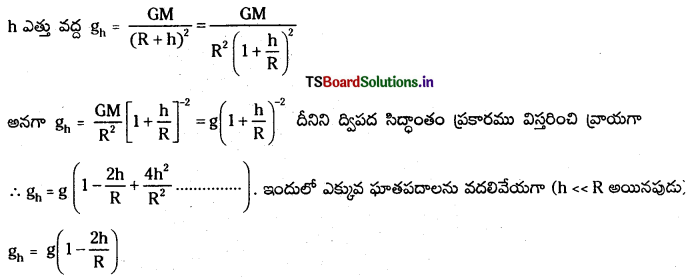
కావున భూమి నుండి పైకి పోయినకొలది గురుత్వ త్వరణము ‘g’ విలువ తగ్గును.

గురుత్వ త్వరణం’g’ పై భూమి ఉపరితలం నుండి లోతు ప్రభావం : భూమి నుండి లోతుకు పోయిన కొలది గురుత్వ త్వరణం ‘g’ విలువ తగ్గుతుంది.

భూమి లోపల ‘d’ అను లోతుకు వెళ్ళినామనుకొనుము. అక్కడ ఉన్న వస్తువుపై భూమి కేంద్రం నుండి ఆ బిందువు వరకుగల భూమి ద్రవ్యరాశి మాత్రమే ఆకర్షణ చూపుతుంది. అనగా భూమి ఫలిత వ్యాసార్ధము (R- d) గా తీసుకోవాలి.
‘d’ లోతు, గురుత్వ త్వరణము g_d = \(\frac{4}{3}\) πρG (R – d) (∵ d = \(\frac{4}{3}\) πρGR కావున)
లేదా g_d = \(\frac{4}{3}\) πρGR (1 – \(\frac{\mathrm{d}}{\mathrm{R}}\)) లేదా g_d = g (1 – \(\frac{\mathrm{d}}{\mathrm{R}}\)) కావున భూమి నుండి లోతుకు పోతే ‘g’ విలువ తగ్గును.
ఎత్తు h = లోతు g అయిన సందర్భంలో g_h < g_d అవుతుంది.

ప్రశ్న 4.
కక్ష్యా వేగం అంటే ఏమిటి ? దానికి సమీకరణాన్ని ఉత్పాదించండి. (మార్చి 2014, మే 2014)
జవాబు:
కక్ష్యా వేగము (V₀) : కక్ష్యలో పరిభ్రమించు వస్తువు లేదా ఉపగ్రహానికి గల వేగాన్ని కక్ష్యా వేగము Vo అంటారు. కక్ష్యా వేగానికి సమీకరణం : ‘m’ ద్రవ్యరాశి గల ఒక ఉపగ్రహం భూమి నుండి ‘h’ ఎత్తులో గల ఒక వృత్తాకార కక్ష్యలో పరిభ్రమిస్తుంది అని అనుకోండి.
కక్ష్యా వ్యాసార్ధము = R + h (ఇందులో R = భూమి వ్యాసార్ధము)
వస్తువులు కక్ష్యలో పరిభ్రమించాలంటే వాటిపై పనిచేయు అపకేంద్ర, అభికేంద్ర బలాలు సమానం కావాలి.
వస్తువుపై అపకేంద్రబలం = \(\frac{\mathrm{mV}^2}{\mathrm{r}}=\frac{\mathrm{mV}_0^2}{\mathrm{R}+\mathrm{h}}\) …………….. (1)
(ఇందులో V = V₀ వస్తువు కక్ష్యావేగము; R + h = కక్ష్యా వ్యాసార్ధము.)
భూమికి ఉపగ్రహానికి మధ్యగల గురుత్వాకర్షణబలం, అభికేంద్ర బలానికి సమానము.
∴ ఉపగ్రహంపై అభికేంద్రబలం = \(\frac{\text { GMm }}{(\mathrm{R}+\mathrm{h})^2}\) …………… (2)

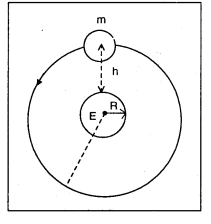
కక్ష్యలో పరిభ్రమించటంలో గల నియమం ప్రకారము
\(\frac{\mathrm{mV}_0^2}{(\mathrm{R}+\mathrm{h})}=\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})^2}\)
∴ V₀² = \(\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}}\) లేదా V₀ = \(\sqrt{\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}}}\)
Rతో పోల్చితే భూమి నుండి ఎత్తు ‘h’ చాలా చిన్నదైనపుడు కక్ష్యా వేగము V₀ = \(\sqrt{\frac{\mathrm{GM}}{\mathrm{R}}}=\sqrt{\mathrm{gR}}\)
దీనిని భూమి సమీప కక్ష్యా వేగము అంటారు. సమీప కక్ష్యా వేగము V₀ = 7.92 కి.మీ./సెకను.

ప్రశ్న 5.
పలాయన వడి అంటే ఏమిటి ? దానికి సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
పలాయన వేగము (V_e) : ఏదైనా వస్తువును గురుత్వాకర్షణ పరిధి దాటి అనంత దూరం పంపడానికి ఆ వస్తువుకు భూమి లేక ఇచ్చిన గ్రహంపై ఉండవలసిన కనీస తొలివేగాన్ని పలాయన వేగంగా నిర్వచించినారు.
పలాయన వేగము V_e = \(\sqrt{2 \mathrm{gR}}=\sqrt{2 \frac{\mathrm{GM}}{\mathrm{R}}}\)
పలాయన వేగానికి సమీకరణమును ఉత్పాదించుట : ‘m’ ద్రవ్యరాశి గల ఒక వస్తువును భూమి కేంద్రం నుండి గురుత్వాకర్షణ బలాలను ఎదురించుతూ భూమి ఉపరితలం వద్దకు తెచ్చినామనుకొనుము.
వస్తువుకు భూమికి మధ్య గురుత్వాకర్షణ బలం F = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\) …………… (1)
వస్తువును భూమి కేంద్రం నుండి ఉపరితలానికి తెచ్చుటలో జరిపిన పని W = F. R …………… (2)
ఈ పని భూమి ఉపరితలం వద్ద గల వస్తువులో స్థితిశక్తి రూపంలో నిలవ ఉంటుంది.
∴ వస్తువుకు ఉపరితలం వద్ద గల స్థితి శక్తి P.E. = \(\frac{\mathrm{GMm}}{\mathrm{R}}\) …………… (3)
భూమి గురుత్వాకర్షణ పరిధి దాటి వస్తువును బయటకు పంపవలెనంటే దానికి ఉండవలసిన కనీస గతిశక్తి భూమి ఉపరితలం వద్ద గల స్థితిశక్తికి సమానం కావలెను.
∴ \(\frac{1}{2}\) mV_e² = \(\frac{\mathrm{GMm}}{\mathrm{R}}\) లేదా V_e² = \(\frac{\mathrm{2GM}}{\mathrm{R}}\)
∴ పలాయన వేగము V_e = \(\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}=\sqrt{2 \mathrm{gR}}\) (∵ g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\))
భూమిపై పలాయన వేగం V_e = 11.2 కి.మీ/సె.
పలాయన వేగము (V_e) మరియు కక్ష్యా వేగము V₀ ల మధ్య సంబంధము V_e = \(\sqrt{2}\)V₀

ప్రశ్న 6.
భూస్థావర ఉపగ్రహం అంటే ఏమిటి ? వాటి ఉపయోగాలను తెలపండి.
జవాబు:
భూస్థావర ఉపగ్రహం : కృత్రిమ ఉపగ్రహం పరిభ్రమణ ఆవర్తన కాలం భూమి పరిభ్రమణ ఆవర్తన కాలానికి సమానంగా ఉండి అది భూమధ్యరేఖపై భూమి ఆత్మ భ్రమణ దిశలో చలిస్తుంటే, ఆ ఉపగ్రహం భూమి దృష్ట్యా స్థిరంగా ఉంటుంది. ఇటువంటి ఉపగ్రహాలను భూస్థావర ఉపగ్రహాలు అంటారు.
భూస్థావర కక్ష్య భూమి నుండి 35,800 కి.మీ. ఎత్తులో ఉంది.
ఉపయోగాలు :

1. వాతావరణంలోని పై పొరలను అధ్యయనం చేయుటకు,
2. వాతావరణంలో సంభవించే మార్పులను ముందుగా తెలుసుకోవడానికి,
3. భూమిలోపల ఉన్న ఖనిజ సంపద గురించి తెలుసుకోవడానికి,
4. టెలివిజన్, టెలిఫోన్, రేడియో ప్రసారాలకు, అంతరిక్ష వస్తువులపై పరిశోధనలు చేయడానికి,
5. భూమి ఆకారము, పరిమాణములను తెలుసుకొనుటకు,
6. భూమి మీద మనము చేరలేని ప్రాంతాల గురించి తెలుసుకోవడానికి ఈ ఉపగ్రహాలు ఉపయోగపడతాయి.

ప్రశ్న 7.
సరాసరి సముద్ర మట్టం నుంచి రెండు ప్రదేశాలు ఒకే ఎత్తులో ఉన్నాయనుకొందాం. ఒకటి పర్వతం మీద ఉంది. మరొకటి గాలిలో ఉంది. ఎక్కడ g ఎక్కువగా ఉంటుంది ? మీ సమాధానానికి కారణం తెలపండి.
జవాబు:
భూమి ఉపరితలంపైన, లోపల గురుత్వ త్వరణము :
1. భూమి ఉపరితలంపై ‘h’ ఎత్తు ఉన్న బిందు ద్రవ్యరాశి m పై బలము F_h = \(\frac{\mathrm{GM}_e \mathrm{~m}}{(\mathrm{R}+\mathrm{h})^2}\) R భూమి వ్యాసార్ధము
g_h = \(\frac{\mathrm{F}_{\mathrm{h}}}{\mathrm{m}}=\frac{\mathrm{Gm}_{\mathrm{e}}}{(\mathrm{R}+\mathrm{h})^2}\) = g(1 + h/R)^-2 = g( 1 – \(\frac{2 \mathrm{~h}}{\mathrm{R}}\))

2. భూమి నుండి ‘d’ లోతులో గల బిందువు వద్ద గురుత్వాకరణ బలం (R – d) మందంగల కర్పరం వల్ల పనిచేసిన బలానికి సమానము. ఇచ్చిన బిందువుపైనగల ‘d’ మందపు కర్పరం వల్ల ఆకర్షణ బలం సున్న.
∴ F_d = \(\frac{\mathrm{GM}_e \mathrm{~m}}{(\mathrm{R}-\mathrm{d})^2}\) ; g_d = \(\frac{F_d}{m}=\frac{G_e}{(R-d)^2}\) = g(1 – d/R)
గమనిక : భూమి నుండి పైకి వెళ్ళినా లేక భూమిలోపలికి వెళ్ళినా గురుత్వ త్వరణం ‘g’ తగ్గును. ‘g’ లో తగ్గుదల లోతుకు వెళ్ళిన దాని కన్న భూమిపైకి వెళితే (‘g’ విలువ) ఎక్కువగా తగ్గుతుంది.

ప్రశ్న 8.
ఒక వస్తువు భారం భూమధ్య రేఖ వద్ద కంటే ధ్రువాల వద్ద ఎక్కువగా ఉంటుంది. ఒకే బరువుకు ఈ రెండు ప్రదేశాల్లో ఎక్కడ ఎక్కువ చక్కెర (sugar) వస్తుంది ? మీ సమాధానానికి కారణం తెలపండి.
జవాబు:
పంచదారను తూచటానికి సాధారణ త్రాసును ఉపయోగిస్తే ధ్రువాల వద్ద తూచినా, భూమధ్య రేఖ వద్ద తూచినా ఒకే పరిమాణంగల పంచదార వస్తుంది. దీనిని కారణం సాధారణ త్రాసులో వస్తువును తూయడానికి రెండు పళ్ళెముల మీద గురుత్వ ఆకర్షణ బలాన్ని సమానం చేయడం.

స్ప్రింగ్ త్రాసును ఉపయోగించి పంచదారను తూస్తే ధ్రువాలవద్ద పంచదార పరిమాణం తక్కువగాను, భూమధ్య రేఖవద్ద పంచదార పరిమాణం ఎక్కువగాను ఉంటుంది. కారణం స్ప్రింగ్ త్రాసు వస్తువు భారము W నిర్ణయిస్తుంది. పంచదార భారం W స్థిరంగా ఉన్నా ధ్రువాల వద్ద ‘g’ విలువ ఎక్కువ కావడం వల్ల తక్కువ ద్రవ్యరాశి ‘m’ గల పంచదార తూయబడుతుంది. భూమధ్య రేఖ వద్ద ‘g’ విలువ తక్కువ కావున అదే భారానికి పంచదార ద్రవ్యరాశి ‘m’ ఎక్కువ.

ప్రశ్న 9.
భూమి చుట్టూ తిరుగుతున్న ఒక కృత్రిమ ఉపగ్రహం చీల (nut) వదులై దాని నుంచి వేరయిపోతే అది భూమి వైపు కిందకు పడుతుందా ? లేదా భూమి చుట్టూ తిరుగుతుందా ? మీ సమాధానానికి కారణం తెలపండి.
జవాబు:
కక్ష్యలో తిరుగు ఉపగ్రహం నుండి ఒక చీల (nut) వదులై దాని నుండి విడిపోతే అది ఉపగ్రహము వెంబడి అంతే వేగంతో అదే కక్ష్యలో చలిస్తుంది. కాని భూమి మీదపడదు. ఎందుకనగా ఉపగ్రహం నుండి వేరైన మేకు ఉపగ్రహం నుండి వేరైన సందర్భంలో ఉపగ్రహానికి గల వేగం ఉంటుంది. కక్ష్యలో తిరిగే వస్తువులపై గురుత్వాకర్షణ బలం (అభిలంబ బలము) మరియు అపకేంద్ర బలాలు సమానం కావడంవల్ల అది భార రహిత స్థితిలో ఉంటుంది. ఈ స్థితిలో దానిపై గల ఫలిత బలం సున్న కాబట్టి వస్తువు అదే వేగంతో అదే కక్ష్యలో పరిభ్రమిస్తుంది.

ప్రశ్న 10.
ఒక వస్తువును 11.2 km s వేగంతో లేదా అంతకంటే ఎక్కువ వేగంతో ప్రక్షిప్తం చేసినప్పుడు అది తిరిగి . భూమికి చేరుకోలేదు. కారణాలతో వివరించండి.
జవాబు:
భూమిపై పలాయన వేగము 11.2 కి.మీ/సె. ఏదైనా వస్తువుకు 11.2 కి.మీ./సె. లేదా అంతకన్నా ఎక్కువ వేగం ఉంటే దాని గతిజశక్తి భూమిపై గల వస్తువుల గురుత్వ పొటెన్షియల్ శక్తి కన్నా ఎక్కువ. కావున అటువంటి వస్తువుల గమనాన్ని భూమి నిరోధించలేదు. అనగా 11.2 కి.మీ/సె. లేదా అంతకన్న ఎక్కువ వేగం గల వస్తువులు భూమి గురుత్వాకర్షణ క్షేత్రాన్ని ఛేదించుకొని అనంత దూరం వెళ్తాయి.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
గురుత్వ స్థితిజ శక్తిని నిర్వచించండి. m₁, m₂, ద్రవ్యరాశులు ఉన్న రెండు కణాలకు సంబంధించిన గురుత్వ స్థితిజ శక్తికి సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
గురుత్వ స్థితిజ శక్తి : గురుత్వాకర్షణ బలం వల్ల ఒక వస్తువులో ఉత్పన్నమయ్యే శక్తిని గురుత్వ స్థితిజ శక్తి అంటారు. గురుత్వ స్థితిజ
శక్తి G.P.E = – GMm \(\left(\frac{1}{r_2^2}-\frac{1}{r_1^2}\right)\) ఇందులో r₁ మరియు r₂ లు
భూమి కేంద్రం నుండి వస్తువు దూరాలు.

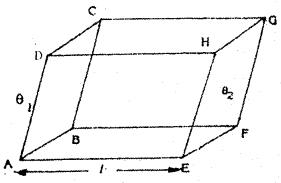
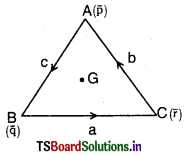
m₁, m₂ ద్రవ్యరాశులుగల రెండు వస్తువులు పటంలో చూపిన విధంగా O, P బిందువుల వద్ద ఉన్నాయనుకోండి. వాటి మధ్య దూరము ‘X’ అనుకోండి.
గురుత్వాకర్షణ నియమం ప్రకారం వాటి మధ్య గల బలం F = \(\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{x}^2}\) కి సమానము వస్తువు m₂ ను A నుండి B వైపుకు స్వల్పదూరం ‘dx’ జరపడానికి చేయవలసిన పని dW = F. dx వస్తువును A నుండి B కి జరపటంలో జరిగిన
మొత్తం పని W అనుకుంటే W =\(\int \mathrm{dW}=\int \frac{G m_1 \mathrm{~m}_2}{\mathrm{x}^2}\) dx. దీని అవధులు r, ∝. స్థితిశక్తి నిర్వచనం ప్రకారం అనంత దూరం ∝ నుండి ఒక వస్తువును ఇచ్చిన బిందువు (మూలబిందువు ‘O’ నుండి దూరం ‘r’) వరకు జరపడంలో చేసిన పని కావున
∴ W = \(\int_{\infty}^r \frac{G m_1 m_2}{x^2} d x=G m_1 m_2 \int_{\infty}^r x^{-2} d x=-G m_1 m_2\left[\frac{1}{\dot{x}}\right]_{\infty}^r=-\frac{G m_1 m_2}{r}\)
– గుర్తు ఆకర్షణ బలానికి వ్యతిరేకంగా పని జరగడాన్ని తెలుపుతుంది. వస్తువును జరపడంలో చేసిన పని ఆ వస్తువులో స్థితిశక్తి రూపంలో (U) నిలువ ఉంటుంది. కావున m, m, ద్రవ్యరాశుల మధ్య దూరం ‘r’ (మూలబిందువు నుండి)గా భావిస్తే వాటి మధ్య గల గురుత్వ స్థితిజశక్తి U = – \(\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{r}}\) కి సమానము.

ప్రశ్న 2.
గురుత్వ త్వరణం a) భూమి ఉపరితలంపైన, b) భూమి ఉపరితలం లోపల ఎలా మారుతుందో తెలిపే సమీకరణాలను ఉత్పాదించండి.
జవాబు:
ఒక గ్రహం ఉపరితలం నుండి ‘h’ ఎత్తులో గురుత్వ త్వరణానికి సమీకరణం ఉత్పాదన : ఏదైనా గ్రహంపై గురుత్వ త్వరణము g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\). ఒక గ్రహానికి సంబంధించినంత వరకు ‘g’ విలువ స్థిరంగా ఉండాలి. కాని భూమిపై గురుత్వ త్వరణము ప్రదేశాన్ని బట్టి మారుతున్నది. దీనికి కారణం భూమి నుండి ఎత్తు, భూమి నుండి లోతు వంటి అంశాలు. ఉన్నతాంశము (ఎత్తు) వలన ‘g’ లో మార్పు : భూమి నుండి ‘h’ ఎత్తుకు పోతే అక్కడ గురుత్వ త్వరణము ‘g’ విలువ తగ్గుతుంది. గురుత్వ త్వరణము g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\) కాని ‘h’ ఎత్తుకు వెళ్ళినపుడు భూమి కేంద్రం నుండి ఎత్తు R + h అవుతుంది.
కాని భూమి ద్రవ్యరాశి M విలువలో మార్పులేదు.

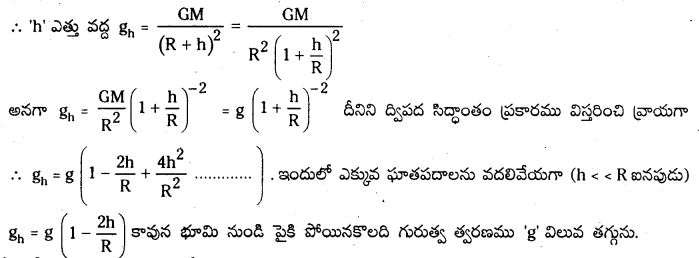
d లోతులో గురుత్వ త్వరణానికి సమీకరణం ఉత్పాదన :
గురుత్వ త్వరణం ‘g’ పై భూమి ఉపరితలం నుండి d లోతు ప్రభావం : భూమి నుండి లోతుకు పోయిన కొలది గురుత్వ త్వరణం ‘g’ విలువ తగ్గుతుంది.

భూమి లోపల ‘d’ అను లోతుకు వెళ్ళినామనుకొనుము. అక్కడ ఉన్న వస్తువుపై భూమి కేంద్రం నుండి ఆ బిందువు వరకుగల భూమి ద్రవ్యరాశి మాత్రమే ఆకర్షణ చూపుతుంది. అనగా భూమి ఫలిత వ్యాసార్ధము (R- d) గా తీసుకోవాలి.
`d’ లోతు వద్ద గురుత్వ త్వరణము g_d = \(\frac{4}{3}\) πρG (R – d) (∵ g = \(\frac{4}{3}\) πρGR) కావున
లేదా g_d = \(\frac{4}{3}\) πρGR (1 – \(\frac{\mathrm{d}}{\mathrm{R}}\)) లేదా g_d = g(1 – \(\frac{\mathrm{d}}{\mathrm{R}}\))
కావున భూమి నుండి లోతుకు పోతే g విలువ తగ్గును.

ప్రశ్న 3.
న్యూటన్ విశ్వ గురుత్వాకర్షణ నియమాన్ని పేర్కొనండి. కావెండిష్ పద్ధతి ద్వారా విశ్వగురుత్వ స్థిరాంకం (G) విలువను ఎలా కనుక్కొంటారో వివరించండి.
జవాబు:
న్యూటన్ విశ్వ గురుత్వాకర్షణ నియమము : ఈ విశ్వంలో ప్రతి వస్తువు మరొక ఇతర వస్తువును ఆకర్షిస్తుంది. ఈ ఆకర్షణ బలం ఆ వస్తువుల ద్రవ్యరాశుల లబ్ధానికి అనులోమాను పాతంలో ఉంటుంది. వాటి మధ్య దూరం వర్గానికి విలోమానుపాతంలో ఉంటుంది.
F ∝ m₁m₂ మరియు F ∝ \(\frac{1}{\mathrm{~d}^2}\) లేదా లేదా F ∝ \(\frac{m_1 m_2}{d^2}\) లేదా F = \(\frac{G m_1 m_2}{d^2}\). ఇందులో G విశ్వ గురుత్వ స్థిరాంకము. గురుత్వాకర్షణ బలం ఎప్పుడూ ఒక ఆకర్షణ బలం. ఇది వస్తువులను కలిపే సరళ రేఖ వెంబడి ఉంటుంది.

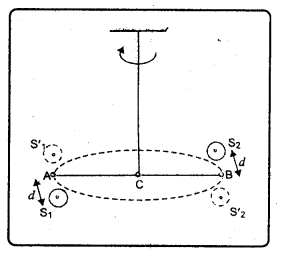
గురుత్వ స్థిరాంకం కనుగొనడానికి కేవెండిష్ ప్రయోగము : కేవెండిష్ ప్రయోగంలో ఒక పొడవాటి కడ్డీ (AB) చివరల రెండు చిన్న సీసం గోళాలను (m) అమర్చినాడు. దీనిని అతి సన్నని తీగ సహాయంతో ఆధారం నుంచి వ్రేలాడదీసినాడు. రెండు పెద్ద సీసం గోళాలను (M) చిన్నగోళం m వద్దకు తెచ్చినపుడు ఆ రెండు చిన్న ద్రవ్యరాశుల మీద సమానమైన గురుత్వాకర్షణ బలం పనిచేయడం వల్ల ఫలితబలం సున్న. చిన్న గోళానికి, పెద్ద గోళానికి మధ్య గురుత్వాకర్షణ బలం F = \(\frac{\mathrm{GMm}}{\mathrm{d}^2}\)
కడ్డీ రెండు చివరల సమానము, వ్యతిరేకమైన బలాలు పనిచేయడం వల్ల కడ్డీ AB పై కొంత టార్క్ ప్రయోగించబడింది. ఫలితంగా అది ఆధారం వెంబడి భ్రమణం చెందుతుంది. కడ్డీ పక్కకు జరిగిన పురికోణం ‘θ’ (Angle of twist) అనుకుంటే తీగలోని పునఃస్థాపక టార్క్ (τ) పురి కోణానికి అనులోమానుపాతంలో ఉంటుంది. τ ∝ θ.
కడ్డీపై టార్క్ τ = బలము × కడ్డీ పొడవు (L)
∴ τ = \(\frac{\mathrm{G} \mathrm{Mm}}{\mathrm{d}^2}\) .L ………….. (1) (గురుత్వ బలయుగ్మము)
కడ్డీపై పునస్థాపక బలయుగ్మము = τθ …………….. (2)
∴ τθ = \(\frac{\mathrm{G} \mathrm{Mm}}{\mathrm{d}^2}\) L లేదా G = \(\frac{\tau \theta \cdot \mathrm{d}^2}{\mathrm{MmL}}\)
MmL
ఈ ప్రయోగంలో θ విలువను కొలవడం వల్ల G విలువను లెక్కగట్టవచ్చును.
G ప్రామాణిక విలువ = 6.67 × 10^-11 N – m² / kg²

లెక్కలు

ప్రశ్న 1.
ఒక్కొక్కటి 1 kg ద్రవ్యరాశులు ఉన్న రెండు గోళాకార బంతుల్ని 1 cm దూరంలో ఉంచారు. వాటి మధ్య ఉండే గురుత్వాకర్షణ బలాన్ని కనుక్కోండి.
జవాబు:
ఒక్కొక్క బంతి ద్రవ్యరాశి m = 1 kg
బంతుల మధ్యదూరము r = 1 cm = 10^-2 m
గురుత్వాకర్షణ బలము F = \(\frac{\mathrm{Gmm}}{\mathrm{r}^2}=\frac{6.67 \times 10^{-11} \times 1 \times 1}{\left(10^{-2}\right)^2}\)
= 6.67 × 10^-11 × 10⁴ = 6.67 × 10^-7 N

ప్రశ్న 2.
ఒక బంతి ద్రవ్యరాశి వేరొక బంతి ద్రవ్యరాశికి 4 రెట్లు ఉంది. ఈ బంతులను 10 cm దూరంలో ఉంచినప్పుడు వాటి మధ్య గురుత్వాకర్షణ బలం 6.67 × 10^-7 N అయితే ఆ బంతుల ద్రవ్యరాశులను కనుక్కోండి.
జవాబు:
మొదటి బంతి ద్రవ్యరాశి m; రెండవ బంతి ద్రవ్యరాశి = 4m.
బంతుల మధ్య దూరము r = 10 cm = 0.1 m
గురుత్వాకర్షణ బలము F = 6.67 × 10^-7 N.
బంతి ద్రవ్యరాశి m = ?
గురుత్వాకర్షణ బలము F = \(\frac{\mathrm{G} \cdot \mathrm{m} \cdot 4 \mathrm{~m}}{\mathrm{r}^2}\) ⇒ 6.67 × 10^-7 = \(\frac{6.67 \times 10^{-11} 4 \mathrm{~m}^2}{0.1 \times 0.1}\) ⇒ 10^-7 = 10^-9 . 4m²
∴ m² = \(\frac{10^{-7}}{4 \times 10^{-9}}=\frac{100}{4}\) = 25 ⇒ m = 5
∴ బంతుల ద్రవ్యరాశులు : 5 kg, 20 kg.

ప్రశ్న 3.
1 m భుజం పొడవు కలిగిన ఒక సమబాహు త్రిభుజం మూడు శీర్షాల వద్ద 1kg, 2kg, 3kg ల ద్రవ్యరాశులు కలిగిన గోళాకార బంతులను ఉంచారు. 1kg ద్రవ్యరాశిపై 2kg, 3kgల ద్రవ్యరాశులు ప్రయోగించే గురుత్వాకర్షణ బలాన్ని గణించండి.
జవాబు:
సమబాహు త్రిభుజము భుజము a = 1m.
మూడు శీర్షాల వద్ద ద్రవ్యరాశులు = 1 kg, 2 kg, 3 kg.
1 kg, 2 kg ల మధ్య బలము F₁ = G. \(\frac{2 \times 1}{1^2}\) = 2 G
1 kg, 3 kg ల మధ్య బలము F₂ = G. \(\frac{3 \times 1}{1^2}\) = 3 G

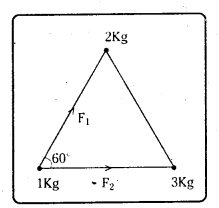
F₁, F₂ లు ఒకదానికొకటి 60° కోణముతో పనిచేయును.
∴ ఫలితబలము F_R = \(\sqrt{F_1^2+F_2^2+2 F_1 F_2 \cos \theta}=\sqrt{4 G^2+9 G^2+2 \times 2 \times 3 G^2 \times \frac{1}{2}}\)
= G\(\sqrt{4+9+6}\) = \(\sqrt{19}\) G

ప్రశ్న 4.
భూఉపరితలం నుంచి ఒక నిర్ణీత ఎత్తులో గురుత్వ త్వరణం భూఉపరితలంపై ఉన్న విలువలో 4% ఉంది. అయితే ఆ ఎత్తు ఎంత ?
జవాబు:
h ఎత్తులో గురుత్వత్వరణము g_h = g విలువలో 4 శాతము.
∴ g_h = \(\frac{4 \mathrm{~g}}{100}\) కాని g_h = \(\frac{g \cdot R^2}{\left(1+\frac{h}{R}\right)^2}\) ఇందులో భూమి వ్యాసార్ధము R = 6400 K.M. = 6.4 × 10⁶ m.
\(\frac{4}{100} g=\frac{g}{(1+h / R)^2} \Rightarrow\left(1+\frac{h}{R}\right)^2=\frac{100}{4}\) (రెండు వైపుల వర్గమూలము చేయగా)
1 + \(\frac{\mathrm{h}}{\mathrm{R}}\) = \(\frac{10}{2}\) = 5 ⇒ 1 + \(\frac{\mathrm{h}}{\mathrm{R}}\) = 5 ⇒ \(\frac{\mathrm{h}}{\mathrm{R}}\) = 5 – 1 = 4
∴ h = 4R = 6400 × 4 = 25.600 k.m.

ప్రశ్న 5.
ఒక కృత్రిమ ఉపగ్రహం 1000 km ఎత్తులో భూమి చుట్టూ తిరుగుతున్నది. దాని కక్ష్యా వడి ఎంత ?
జవాబు:
భూమి వ్యాసార్ధము R = 6,400 km = 6.4 × 10⁶ m.
ఉపగ్రహము ఎత్తు h = 1000 km; G = 6.67 × 10¹¹ N – m² / kg²
భూమి ద్రవ్యరాశి M = 6 × 10²⁴
కక్ష్యా వేగము V_o = \(\sqrt{\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}}}\)
∴ V_o= \(\sqrt{\frac{6.67 \times 10^{-11} \times 6 \times 10^{24}}{6400+1000}}=\sqrt{\frac{6.67 \times 6 \times 10^{13}}{7.4 \times 10^6}}=\sqrt{\frac{40.02 \times 10^7}{7.4}}\) = 7354 m = 7.354 km.

ప్రశ్న 6.
భూ వ్యాసార్ధానికి సమానమైన ఎత్తులో ఒక కృత్రిమ ఉపగ్రహం భూమి చుట్టూ తిరుగుతున్నది. దాని
i) కక్ష్యావడి,
ii) పరిభ్రమణావర్తన కాలాలను కనుక్కోండి.
జవాబు:
భూమి వ్యాసార్ధము R = 6400k.m. ; భూమి నుండి ఎత్తు h = R.
భూమి ద్రవ్యరాశి M = 6 × 10²⁴ ; G = 6.67 × 10^-11 N – m²/kg²
i) కక్ష్యావేగము V_o = \(\sqrt{\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})}}=\sqrt{\frac{\mathrm{GM}}{2 \mathrm{R}}}\)
∴ V_o = \(\sqrt{\frac{6.67 \times 10^{-11} \times 6 \times 10^{24}}{2 \times 6.4 \times 10^6}}=\sqrt{\frac{40.02 \times 10^{13}}{12.8 \times 10^6}}=\sqrt{\frac{40.02 \times 10^7}{12.8}}\)
= 5592 m/s = 5.592 కి. మీ. / సె.

ii) ఆవర్తన కాలము T = \(\frac{2 \pi(2 R)}{V}=\frac{2 \times 3.142 \times 6.4 \times 10^6 \times 2}{5592}\)
= 14, 380 sec. = 3.994h = 4 గంటలు.

ప్రశ్న 7.
రెండు వస్తువుల మధ్య ఉన్న దూరాన్ని 4m పెంచితే, వాటి మధ్య ఉన్న గురుత్వాకర్షణ బలం 36% తగ్గింది. వాటి మధ్య ఉన్న తొలి దూరం ఎంత ?
జవాబు:
వస్తువుల మధ్య బలము F; వస్తువుల మధ్య దూరము = r.
రెండవ సందర్భమునకు r₁ = (r + 4); కాని కొత్త బలము Fకన్నా 36% తక్కువ.
⇒ F₁ = F (1 – \(\frac{36}{100}\)) = \(\frac{64}{100}\) F
∴ \(\frac{\text { G.m.m. }}{(r+4)^2}=\frac{64}{100} \frac{\text { G.m.m }}{r^2}\)
⇒ 100 r² = 64 (r + 4)² రెండువైపుల వర్గమూలము చేయగా
⇒ 10 r = 8 (r + 4) ⇒ 10 r = 8r + 32
∴ (10 – 8) r = 2r = 32 లేదా ∴ r = 16 m.

ప్రశ్న 8.
a భుజం ఉన్న ఒక చతురస్రం ప్రతి శీర్షం వద్ద సర్వసమానమైన ద్రవ్యరాశులు m లను ఉంచారు. ఒక ద్రవ్యరాశిపై మిగతా మూడు ద్రవ్యరాశులు ప్రయోగించే గురుత్వబలాన్ని గణించండి.
జవాబు:
అన్ని ద్రవ్యరాశులు సమానము అని ఇవ్వబడినవి.
∴ m₁ = m₂ = m₃ = m₄
m₁, m₄ ద్రవ్యరాశుల మధ్య బలము F₁ = \(\frac{\mathrm{G} \cdot \mathrm{m}^2}{\mathrm{a}^2}\) …… (1)
m₄, m₃ ద్రవ్యరాశుల మధ్య బలము F₂ = \(\frac{\mathrm{G} \cdot \mathrm{m}^2}{\mathrm{a}^2}\) ……….. (2)

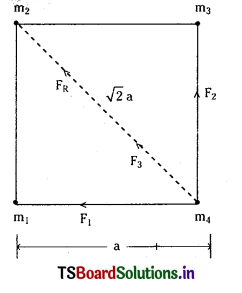
F₁ మరియు F₂ లు పరస్పరము లంబాలు మరియు పరిమాణములో సమానము.
సమాంతర చతుర్భుజ బల నియమము నుండి
∴ F_R = \(\sqrt{2 \mathrm{~F}}=\sqrt{2} \cdot \frac{\mathrm{Gm}^2}{\mathrm{a}^2}\) ………… (3)
(సమాంతర చతుర్భుజ బల నియమము నుండి)
m₄, m₂ ల మధ్య బలము F₃ = \(\frac{\mathrm{Gm}^2}{(\sqrt{2} a)^2}=\frac{\mathrm{Gm}^2}{2 a^2}\) (F₃ అనుకొనుము) …………. (4)
F_R మరియు F₃ లు పరస్పరము సమాంతరము కావున వాటి ఫలిత బలము వాటి మొత్తానికి సమానము.
m₄ వద్ద అన్ని ద్రవ్యరాశుల వలన మొత్తము బలము = \(\sqrt{2} \frac{G m^2}{a^2}+\frac{G m^2}{2 a^2}=\frac{G m^2}{a^2}\left(\sqrt{2}+\frac{1}{2}\right)\)

ప్రశ్న 9.
1kg, 4kg ద్రవ్యరాశులు ఉన్న రెండు గోళాకార బంతుల మధ్య దూరం 12cm. 1kg ద్రవ్యరాశి నుంచి ఎంత దూరంలో ఉన్న బిందువు వద్ద ఏ ద్రవ్యరాశి మీదనైనా పనిచేసే గురుత్వాకర్షణ బలం శూన్యం అవుతుంది ?
జవాబు:
ద్రవ్యరాశి m₁ = 1 kg ; ద్రవ్యరాశి m₂ = 4 kg
మధ్యదూరము d = 12 cm
మూడవ వస్తువు ద్రవ్యరాశి m₃ = ?
m₃ ద్రవ్యరాశిపై ఏ బలమూ పనిచేయకుండుటకు

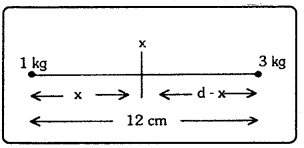
m₁, m₃ ల మధ్య బలము = m₂, m₃ ల మధ్య బలము.
∴ \(\frac{\mathrm{G}_1 \times \mathrm{m}_3}{\mathrm{x}^2}=\frac{\mathrm{G} \times 4 \mathrm{~m}_3}{(\mathrm{~d}-\mathrm{x})^2}\) ⇒ (d – x)² = 4x². రెండు వైపుల వర్గమూలము తీసుకొనగా
d – x = 2x + d = 3x లేదా x = \(\frac{12}{3}\) = 4 cm
∴ 1 kg ద్రవ్యరాశి నుండి దూరము = 4 cm

ప్రశ్న 10.
ఒక్కొక్కటి ద్రవ్యరాశి m, వ్యాసార్ధం R ఉన్నట్టి మూడు ఏకరీతి గోళాలను, అందులో ప్రతి ఒకటి మిగతా రెండింటిని తాకే విధంగా అమర్చారు. వాటిలో ఏ ఒక్క గోళం పైనైనా మిగతా రెండు గోళాల వల్ల కలిగే గురుత్వాకర్షణ బల పరిమాణాన్ని లెక్కించండి.
జవాబు:
ద్రవ్యరాశి m, వ్యాసార్ధము R లు అన్ని గోళాలకు సమానము.
1, 3 గోళాల మధ్య బలము F₁ = \(\frac{\mathrm{G} \cdot \mathrm{m}^2}{(2 \mathrm{R})^2}\)
1, 2 గోళాల మధ్య బలము F₂ = \(\frac{\mathrm{G} \cdot \mathrm{m}^2}{(2 \mathrm{R})^2}\)

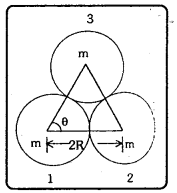
F₁, F₂ లు ఒకదానికొకటి 60° కోణముతో పనిచేయును. సమాంతర చతుర్భుజ బలనియమము ప్రకారము ఫలిత బలము
F = \(\sqrt{F_1^2+F_2^2+2 F_1 F_2 \cos \theta}=\sqrt{F^2+F^2+2 F^2 \frac{1}{2}}=\sqrt{3} F\)
∴ మొదటి గోళముపై మిగిలిన రెండు గోళాల వలన బలము = \(\frac{\sqrt{3} \cdot \mathrm{Gm}^2}{4 \mathrm{R}^2}\)

ప్రశ్న 11.
రెండు కృత్రిమ ఉపగ్రహాలు వేరువేరు ఎత్తులలో భూమి చుట్టూ పరిభ్రమిస్తున్నాయి. వాటి కక్ష్యా వడుల నిష్పత్తి 2: 1. అందులో ఒకటి 100 km ఎత్తులో ఉంటే, మరొకటి ఎంత ఎత్తులో ఉంటుంది ?
జవాబు:
భూమి ద్రవ్యరాశి m = 6 × 10²⁰ kg ; G = 6.67 × 10^-11 N-m² / kg²
కక్ష్యావేగముల నిష్పత్తి V₀₁ : V₀₂ = 2 : 1;
ఒక ఉపగ్రహం ఎత్తు h = 100 k.m
V_o = \(\sqrt{\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}}}\)
∴ \(\sqrt{\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}_1}}=\frac{1}{2} \sqrt{\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}_2}}\)
ఇరువైపులా వర్గము చేయగా \(\frac{\mathrm{Gm}}{\mathrm{R}+\mathrm{h}_1}=\frac{1}{4} \frac{\mathrm{Gm}}{\mathrm{R}+\mathrm{h}_2}\) ⇒ 4 (R + h₂) = R + h₁
4R + 4h₂ = R + h₁ = 3R + 4h₂, h₂ = 100 km ప్రతిక్షేపించగా
∴ h₁ = 3 × 6400 + 400 = 19600 km.

ప్రశ్న 12.
గురుత్వ త్వరణం విలువ 8 ms^-2 ఉన్నటువంటి ఒక ఎత్తు వద్ద ఒక కృత్రిమ ఉపగ్రహం 8 m s^-1 వడితో వృత్తాకార కక్ష్యలో తిరుగుతున్నది. భూఉపరితలం నుంచి ఉపగ్రహం ఎంత ఎత్తులో ఉన్నట్లు ? (గ్రహం వ్యాసార్ధం = 6000 km)
జవాబు:
ఉపగ్రహము కక్ష్యావేగము V_o = 8 km/s. = 8 × 10³ m/s.
ఆ కక్ష్యలో గురుత్వత్వరణము g = 8 m/s²
కక్ష్యా వేగము V = \(\sqrt{\mathrm{gR}}\) ఇందులో R = కక్ష్యా వ్యాసార్ధము, g = ఆ కక్ష్యలో గురుత్వ త్వరణము
∴ R = V²/g = \(\frac{8 \times 8 \times 10^6}{8}\) = 8 × 10⁶m = 8000 km.
ఉపగ్రహము ఎత్తు = 8000 – భూమి వ్యాసార్ధము;
భూమి వ్యాసార్ధము = 6000km.
భూ ఉపరితలము నుండి ఉపగ్రహము ఎత్తు = 8000 – 6000 = 2000 km.

ప్రశ్న 13.
(a) భూఉపరితలం నుంచి ఒక వస్తువు పలాయన వడిని కనుక్కోండి. (b) ఒక వేళ భూమి కర్రతో గనుక తయారై ఉంటే, దాని ద్రవ్యరాశి భూమి ప్రస్తుత ద్రవ్యరాశిలో 10% ఉండేది. భూమి కర్రతో తయారై ఉండి ఉంటే, పలాయన వడి ఎంత ?
జవాబు:భ
భూమి వ్యాసార్ధం, R = 6400 km = 6.4 × 10⁶.m
భూమి ద్రవ్యరాశి, M = 6 × 10²⁴ kg ; g = 9.8 ms^-2
a) పలాయన వడి, V_e = \(\sqrt{2 g R}\)
∴ V_e = \(\sqrt{2 \times 9.8 \times 6.4 \times 10^6}\) = 11.2 km/s

b) భూమి కర్రతో తయారై ఉండి ఉంటే, M₁ = ద్రవ్యరాశిలో 10% = 6 × 10²³
పలాయన వడి, V_e = \(\sqrt{\frac{2 \mathrm{Gm}}{\mathrm{R}}}=\sqrt{\frac{2 \times 6.67 \times 10^{-11} \times 6 \times 10^{23}}{6.4 \times 10^6}}=\sqrt{\frac{2 \times 40.02 \times 10^{12}}{6.4 \times 10^6}}\)
∴ V_e = \(\sqrt{12.51 \times 10^{16}}\)= 3.537 km/s.

ముఖ్యమైన ఉదాహరణ లెక్కలు

ప్రశ్న 1.
భుజం పొడవు గా ఉన్న ఒక చతురస్రం యొక్క ప్రతీ శీర్షం వద్ద ఒక్కో కణాన్ని ఉంచితే, ఆ నాలుగు కణాల వ్యవస్థ మొత్తం స్థితిజశక్తిని కనుక్కోండి. ఆ చతురస్ర కేంద్రం వద్ద పొటెన్షియల్ను కూడా గణించండి.
సాధన:
భుజం పొడవు l ఉన్నటువంటి ఒక చతురస్రం ప్రతీ శీర్షం వద్ద m ద్రవ్యరాశి ఉన్న ఒక్కో కణాన్ని ఉంచామనుకోండి. పటంని పరిశీలిస్తే, l దూరంలో నాలుగు ద్రవ్యరాశుల జతలు, \(\sqrt{2}\) l దూరంలో కర్ణాల పరంగా రెండు ద్రవ్యరాశుల జతలూ మనకు కనిపిస్తాయి. కాబట్టి,

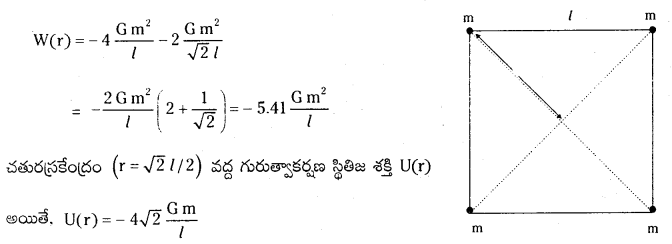
ప్రశ్న 2.
కుజ గ్రహానికి ఫోబోస్ (phobos), డెల్మోస్ (delmos) అనే రెండు ఉపగ్రహాలు ఉన్నాయి. (i) ఫోబోస్ కక్ష్యావర్తన కాలం 7 గం. 39 నిమిషాలు. దాని కక్ష్యా వ్యాసార్ధం 9.4 × 10³ km. కుజుని ద్రవ్యరాశిని కనుక్కోండి. (ii) భూమి, కుజుడూ సూర్యుని చుట్టూ వృత్తాకార కక్ష్యల్లో, కుజుని కక్ష్యా వ్యాసార్ధం భూకక్ష్యా వ్యాసార్ధానికి 1.52 రెట్లు ఉండే విధంగా తిరుగుతున్నాయనుకొందాం. అప్పుడు ఒక కుజ సంవత్సరంలో ఎన్ని రోజులుంటాయి ?
సాధన:
i) సమీకరణం T² = k (R_E + h)³ (k = 4π² / GM_E) లో భూమి ద్రవ్యరాశికి బదులుగా కుజుని ద్రవ్యరాశి M_m ను ప్రతిక్షేపిస్తే,
T² = \(\frac{4 \pi^2}{\mathrm{GM}_{\mathrm{m}}}\) R³ ; M_m = \(\frac{4 \pi^2}{G} \frac{P^3}{T^2}\)
M_m = \(\frac{4 \times(3.14)^2 \times(9.4)^3 \times 10^{18}}{6.67 \times 10^{-11} \times(459 \times 60)^2}=\frac{4 \times(3.14)^2 \times(9.4)^3 \times 10^{18}}{6.67 \times(459 \times 60)^2 \times 10^{-5}}\)
∴ కుజుని ద్రవ్యరాశి = 6.48 × 10²³ kg

ii) కెప్లర్ మూడవ నియమం ప్రకారం,
\(\frac{\mathrm{T}_{\mathrm{M}}^2}{\mathrm{~T}_{\mathrm{E}}^2}=\frac{\mathrm{R}_{\mathrm{MS}}^3}{\mathrm{R}_{\mathrm{ES}}^3}\)
ఇక్కడ RMS కుజునికి, సూర్యునికి మధ్య దూరం, R_ES భూమికి, సూర్యునికి మధ్య దూరం.
∴ TM = (1.52)^3/2 × 365 = 684 రోజులు.

ప్రశ్న 3.
భూమిని తూచడం (Weighing the Earth) : కింది సమాచారాన్ని మీకిచ్చారు :
g = 9.81 ms^-2, R_E = 6.37 × 10⁶ m, చంద్రునికి ఉన్న దూరం R = 3.84 × 10⁸ m, చంద్రుని పరిభ్రమణావర్తన కాలం 27.3 రోజులు. భూమి ద్రవ్యరాశి M_E ని రెండు విభిన్న పద్ధతుల్లో రాబట్టండి.
సాధన:
పద్ధతి -1 : దత్తాంశం నుండి g = 9.81 మీ/సె ; R_E = 6.37 × 10⁶ మీ ; M_E = భూమి ద్రవ్యరాశి
M_E = \(\frac{\mathrm{gR}_{\mathrm{E}}^2}{\mathrm{G}}=\frac{9.81 \times\left(6.37 \times 10^6\right)^2}{6.67 \times 10^{-11}}\) = 5.97 × 10²⁴ kg.
పద్ధతి – 2 : చంద్రుడు భూమికి ఉపగ్రహం. కెప్లర్ మూడవ నియమం ఉత్పాదన నుంచి
(సమీకరణం T² = k (R_E + h)³ (k = 4π²/GM_E) ప్రకారం)
T² = \(\frac{4 \pi^2 R^3}{\mathrm{GM}_{\mathrm{E}}}\) ⇒ M_E = \(\frac{4 \pi^2 R^3}{\mathrm{GT}^2}\)
= \(\frac{4 \times 3.14 \times 3.14 \times(3.84)^3 \times 10^{24}}{6.67 \times 10^{-11} \times(27.3 \times 24 \times 60 \times 60)^2}\) = 6.02 × 10²⁴ kg
రెండు పద్ధతుల ద్వారా దాదాపు ఒకే ఫలితం వచ్చింది. ఆయా పద్ధతుల ద్వారా వచ్చిన విలువల్లో తేడా 1% కంటే తక్కువగానే ఉంది.

ముఖ్యమైన అదనపు లెక్కలు

ప్రశ్న 1.
కింది వాటికి సమాధానాలు రాయండి :
a) ఒక విద్యుదావేశాన్ని ఒక బోలు వాహకంలోపల ఉంచడం ద్వారా దానిపై విద్యుత్ బలం పనిచేయకుండా రక్షణ కల్పించవచ్చు. ఒక వస్తువును ఒక బోలు గోళం లోపల ఉంచడం ద్వారా లేదా మరే ఇతర పద్ధతిలోనైనా దానికి దగ్గరలో ఉన్న ద్రవ్యం యొక్క గురుత్వాకర్షణ బలం నుంచి రక్షించవచ్చా ?
b) భూమి చుట్టూ తిరుగుతున్న ఒక చిన్న వ్యోమ నౌకలోని వ్యోమగామి గురుత్వాకర్షణ బలం ఉనికిని గుర్తించలేదు. భూమి చుట్టూ తిరుగుతున్న వ్యోమనౌక చాలా పెద్దదిగా ఉంటే, గురుత్వాకర్షణ బలం ఉనికిని గుర్తించగలనని అతడు ఆశించవచ్చా ?
c) సూర్యుని మూలంగా భూమిపై కలిగే గురుత్వ త్వరణం, చంద్రుని మూలంగా భూమిపై కలిగే గురుత్వ త్వరణాలను పోల్చినప్పుడు చంద్రుని ఆకర్షణకంటే సూర్యుని ఆకర్షణ ఎక్కువగా ఉంటుందని స్పష్టమవుతుంది. (తరువాతి అభ్యాసాలలో లభ్యమయ్యే సమాచారాన్ని వినియోగించుకొని మీరీ విషయాన్ని స్వయంగా సరిచూసుకోవచ్చు). అయితే, చంద్రుని ఆకర్షణ వల్ల సముద్రపు అల ఎగిసిపడే ప్రభావం కంటే తక్కువ. ఎందుకు ?
జవాబు:
a) గురుత్వాకర్షణ బలాల నుండి ఒక వస్తువును రక్షించడం సాధ్యంకాదు ఎందుకంటే వస్తువుల మధ్యగల గురుత్వాకర్షణ బలాలు యానకం స్వభావంపై ఆధారపడవు. ఇవి ద్రవ్యరాశిగల అన్ని వస్తువుల మధ్య పనిచేస్తాయి.
విద్యుదావేశ బలాలు వాటి మధ్యగల యానకం పెర్మిటివిటి మరియు పదార్థ స్వభావం మీద ఆధారపడటం వల్ల విద్యుత్ బలం నుండి రక్షణ కల్పించవచ్చు.

b) అవును. .అంతరిక్ష నౌక పరిమాణం చాలా పెద్దదయితే కక్ష్యలో తిరుగుతున్న అంతరిక్ష నౌకలోని వ్యోమగామి గురుత్వ త్వరణంలో మార్పు గుర్తించగలడు.

c) అలలపై బలం ప్రభావం, దూరము యొక్క ఘనానికి (cube) విలోమానుపాతంలో ఉంటుంది. కాని గురుత్వాకర్షణ బలం దూరం యొక్క వర్గానికి విలోమానుపాతంలో ఉంటుంది. చంద్రునికన్నా సూర్యుని దూరం చాలా ఎక్కువ కావటం వల్ల సూర్యుని గురుత్వాకర్షణ ప్రభావం అలలపై చాలా తక్కువ. చంద్రుని ఆకర్షణ తక్కువ అయినప్పటికీ భూమి, చంద్రుల మధ్య దూరం చిన్నది కావడం వల్ల అలలపై చంద్రుని ప్రభావం ఎక్కువ.

ప్రశ్న 2.
సరియైన ప్రత్యామ్నాయాన్ని ఎంచుకోండి :
a) ఉన్నతాంశం పెరుగుతున్నకొద్దీ గురుత్వ త్వరణం పెరుగుతుంది / తగ్గుతుంది.
b) లోతు పెరుగుతున్న కొద్దీ గురుత్వ త్వరణం పెరుగుతుంది / తగ్గుతుంది (భూమిని ఏకరీతి సాంద్రత కలిగిన గోళంగా పరిగణించండి).
c) భూమి ద్రవ్యరాశి / వస్తువు ద్రవ్యరాశిపై గురుత్వ త్వరణం ఆధారపడి ఉండదు.
d) భూకేంద్రం నుంచి r₁, r₂ దూరాలలో ఉన్న రెండు బిందువుల మధ్య స్థితిజ శక్తి భేదానికి సూత్రం -G Mm(1/r₂ – 1/r₁) అనేది సూత్రం mg(r₂ – r₁) కంటే ఎక్కువ / తక్కువ.
జవాబు:
a) తగ్గుతుంది
b) తగ్గుతుంది
c) వస్తువు ద్రవ్యరాశి
d) ఎక్కువ

ప్రశ్న 3.
సూర్యుని చుట్టూ భూమి కంటే రెండు రెట్లు ఎక్కువ వడితో తిరిగే ఒక గ్రహం ఉందనుకొందాం. భూమితో పోల్చినప్పుడు దాని కక్ష్యా పరిమాణం (orbital size) ఎంత ఉంటుంది ?
జవాబు:
దత్తాంశం నుండి T_e = = 1 సం||;
T_p = \(\frac{T_e}{2}=\frac{1}{2}\) సం|| r_e = 1 A.U.; r_p = ?
కెప్లర్ సిద్ధాంతం నుండి
r_p = r_e \(\left(\frac{\mathrm{T}_{\mathrm{p}}}{\mathrm{T}_{\mathrm{e}}}\right)^{2 / 3}=1\left(\frac{\frac{1}{2}}{1}\right)^{2 / 3}\) = 0.63 A.U.

ప్రశ్న 4.
బృహస్పతి గ్రహానికి ఉన్న ఒకానొక ఉపగ్రహం ఇయో (I₀) కక్ష్యావర్తన కాలం 1.769 రోజులు, కక్ష్యావ్యాసార్ధం 4.22 × 10⁸m అయితే బృహస్పతి ద్రవ్యరాశి, సూర్యుని ద్రవ్యరాశిలో దాదాపు వెయ్యవ వంతు ఉంటుందని చూపండి.
జవాబు:
జూపిటర్ ఉపగ్రహం ఆవర్తన కాలము T₁ = 1.769 రోజులు = 1.769 × 24 × 60 × 60 s
ఉపగ్రహం కక్ష్యా వ్యాసార్ధము r = 4.22 × 10⁸ m

ప్రశ్న 5.
ఒక్కొక్కటి సౌర ద్రవ్యరాశికి సమానమైన ద్రవ్యరాశి ఉన్న 2.5 × 10¹¹ నక్షత్రాలు మన నక్షత్ర మండలం (galaxy) లో ఉన్నాయని ఊహిద్దాం. నక్షత్ర మండల కేంద్రం నుంచి 50,000 కాంతి సంవత్సరాల దూరంలో ఉన్న ఒక నక్షత్రం ఒక పూర్తి పరిభ్రమణానికి ఎంతకాలం తీసుకొంటుంది ? మన నక్షత్ర మండలమైన పాలపుంత వ్యాసం 10⁵ ly (ly = light year = కాంతి సంవత్సరం)గా తీసుకోండి.
జవాబు:
దత్తాంశం నుండి r = 50,000 కాంతి సంవత్సరాలు = 50,000 × 9.46 × 10¹⁵ m = 4.73 × 10²⁰ m
M = 2.5 × 10¹¹ సౌరద్రవ్యరాశి = 2.5 × 10¹¹ × (2 × 10³⁰) kg = 5.0 × 10⁴¹ kg
కాని M = \(\frac{4 \pi^2 r^3}{\mathrm{GT}^2}\) లేదా T = \(\left(\frac{4 \pi^2 r^3}{\mathrm{GM}}\right)^{1 / 2}=\left[\frac{4 \times(22 / 7)^2 \times\left(4.73 \times 10^{20}\right)^3}{\left(6.67 \times 10^{-11}\right) \times\left(5.0 \times 10^{41}\right)}\right]^{1 / 2}\)
= 1.12 × 10¹⁶ s

ప్రశ్న 6.
సరియైన ప్రత్యామ్నాయాన్ని ఎంచుకోండి :
a) స్థితిజ శక్తి శూన్య విలువను అనంత దూరం వద్ద తీసుకొంటే, పరిభ్రమిస్తున్న ఉపగ్రహం మొత్తం శక్తి దాని గతిజశక్తి / స్థితిజ శక్తికి ఋణాత్మకం.
b) పరిభ్రమిస్తున్న ఒక కృత్రిమ ఉపగ్రహాన్ని భూమ్యాకర్షణ ప్రభావానికి ఆవల వరకు సంధించడానికి అవసరమయ్యే శక్తి కృత్రిమ ఉపగ్రహం ఉన్న ఎత్తులోనే నిశ్చలంగా ఉన్న ఒక ప్రక్షేపకాన్ని భూమ్యాకర్షణ ప్రభావాన్నుంచి ప్రక్షిప్తం చెయ్యడానికి అవసరమయ్యే శక్తి కంటే ఎక్కువ / తక్కువ.
జవాబు:
a) గతిజశక్తి
b) తక్కువ

ప్రశ్న 7.
భూమి నుంచి ఒక వస్తువు పలాయన వడి ఈ అంశాలపై ఆధారపడుతుందా ? a) వస్తువు ద్రవ్యరాశి, b) వస్తువు ప్రక్షిప్తం చేసిన స్థానం, c) ప్రక్షిప్తం చేసిన దిశ, d) వస్తువును ప్రక్షేపించిన స్థానం ఎత్తు.
జవాబు:
పలాయన వడి ద్రవ్యరాశిపై ఆధారపడదు.
పలాయన వడి ప్రక్షేపస్థానం వద్దగల గురుత్వ పొటెన్షియల్ పై ఆధారపడును. ఇది భూమి కేంద్రం నుండి దూరము, (ఎత్తు) ఇచ్చిన బిందు స్థానము మరియు ప్రక్షేప దిశలపై ఆధారపడును.

ప్రశ్న 8.
ఒక తోక చుక్క సూర్యుని చుట్టూ ఒక అత్యధిక అర్థగురు అక్షంగల దీర్ఘవృత్తాకార కక్ష్యలో తిరుగుతున్నది. ఈ తోకచుక్క కక్ష్య యావత్తు ఈ రాశులు స్థిరంగా ఉంటాయా ? a) రేఖీయ వడి, b) కోణీయ వడి, c) కోణీయ ద్రవ్యవేగం, d) గతిజ శక్తి, e) స్థితిజ శక్తి, f) మొత్తం యాంత్రిక శక్తి. తోకచుక్క సూర్యునికి దగ్గరగా వచ్చినప్పుడు అది ఏమైనా ద్రవ్యరాశిని కోల్పోతే ఆ ద్రవ్యరాశిని ఉపేక్షించండి.
జవాబు:
సూర్యుని చుట్టూ దీర్ఘ వృత్తాకార కక్ష్యలో పరిభ్రమిస్తున్న తోకచుక్కకు కోణీయ ద్రవ్యవేగము మరియు మొత్తం శక్తులు మాత్రమే స్థిరము. మిగిలిన రాశులు స్థానం బట్టి మారుతాయి.

ప్రశ్న 9.
ఈ లక్షణాలలో ఏది రోదసిలోని వ్యోమగామికి హాని కలిగించవచ్చు ? a) కాళ్ళ వాపు, b) ముఖం వాపు, c) తల నొప్పి, d) దిగ్విన్యాస (orientational problem) సమస్య.
జవాబు:
వ్యోమగామి భార రహిత స్థితిలో ఉంటాడు. కావున గురుత్వ త్వరణ ప్రభావం అతని మీద ఉండదు.
a) కాళ్ళు బరువు మోయవలసిన అవసరం లేనందున కాళ్ళనొప్పులు రావు:

b) ముఖానికి రక్త ప్రసరణ ఎక్కువగా జరగడం వల్ల ముఖం వాపు వస్తుంది. (ముఖభాగాలు ఉబ్బడం అధిక పీడనంతో రక్త ప్రసరణం వల్ల)

c) అధికమైన మానసిక ఒత్తిడివల్ల తలనొప్పి వస్తుంది. ఇది భూమి మీద ఉన్నా రావచ్చు, అంతరిక్షంలోను రావచ్చు.

d) అంతరాళానికి కూడా దిగ్విన్యాసం ఉంటుంది. కాబట్టి దిగ్విన్యాస సమస్యలు కలుగుతాయి.

ప్రశ్న 10.
ఈ దిగువ ఉన్న రెండు అభ్యాసాల్లో ఇచ్చిన వాటి నుంచి సరియైన సమాధానాన్ని ఎంచుకోండి.

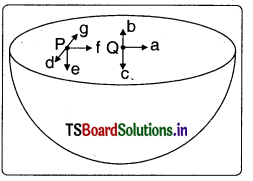
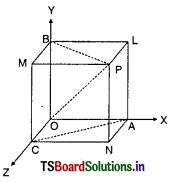
ఏకరీతి ద్రవ్యరాశి సాంద్రత (mass density) కలిగిన ఒక అర్ధగోళాకార కర్పరం కేంద్రం దగ్గర ఉండే గురుత్వాకర్షణ తీవ్రత దిశ పటంలో బాణం గుర్తు సూచించిన విధంగా ఉంది. (i) a, (ii) b, (iii) c, (iv) 0.
జవాబు:
ఏకరీతి సాంద్రతగల అర్ధగోళాకార కర్పరం మీద అన్ని బిందువుల వద్ద గురుత్వాకర్షణ బలం ఒకే విధంగా ఉంటుంది. కావున గురుత్వాకర్షణ తీవ్రత \(\frac{\mathrm{dv}}{\mathrm{dt}}\) = 0 కావున గోళం లోపలగల అన్ని బిందువుల వద్ద గురుత్వాకర్షణ తీవ్రత సున్నా.

గోళం ఒక అర్ధభాగాన్ని తొలగిస్తే అంటే ఇచ్చిన అర్ధగోళంలో కేంద్రము Q లేదా ఇతర బిందువు P వద్ద గురుత్వాకర్షణ అధోదిశలో ఉండటం వల్ల గురుత్వాకర్షణ తీవ్రత కూడా అధోదిశలోనే (C) ఉంటుంది. కావున ఇచ్చిన వాటిలో (iii) ‘c’ సరియైన సమాధానము.

ప్రశ్న 11.
పై సమస్యలో ఒకానొక యాదృచ్ఛిక బిందువు P వద్ద ఉండే గురుత్వాకర్షణ తీవ్రత దిశను బాణం గుర్తుతో సూచించడమైంది. (i) d, (ii) e, (iii) f, (iv) g.
జవాబు:
పైన ఇచ్చిన వివరణ 10వ లెక్కలో ఇచ్చిన వివరణ ప్రకారం P వద్ద గురుత్వాకర్షణ తీవ్రత అధోదిశలో ఉంటుంది. కావున ఇచ్చిన వాటిలో ii) ‘e’ సరియైన సమాధానము.

ప్రశ్న 12.
భూమి నుంచి సూర్యుని వైపు దూసుకెళ్లే విధంగా ఒక రాకెట్ను పేల్చారు. భూ కేంద్రం నుంచి ఎంత ఎత్తులో రాకెట్పై పనిచేసే గురుత్వాకర్షణ బలం శూన్యమవుతుంది ? సూర్యుని ద్రవ్యరాశి = 2 × 10³⁰ kg, భూమి ద్రవ్యరాశి = 6 × 10²⁴ kg. మిగతా ఉపగ్రహాల ప్రభావాన్ని ఉపేక్షించండి. (కక్ష్యా వ్యాసార్ధం = 1.5 × 10¹¹ m).
జవాబు:
దత్తాంశం నుండి M_s = 2 × 10³⁰ kg; M_e = 6 × 10²⁴ kg ; r =
= 1.5 × 10¹¹ m.
రాకెట్ మీద సూర్యుడు, భూమి వల్ల గురుత్వాకర్షణ బలం సమానంగా గల బిందువు భూమి నుండి ‘x’ దూరంలో ఉందనుకోండి. సూర్యుని నుండి దూరము (r – x) అవుతుంది.

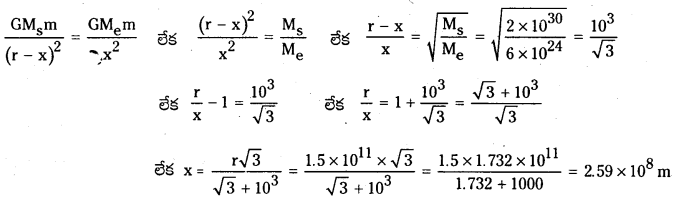
ప్రశ్న 13.
సూర్యుని ఎలా తూచుతారు ? అంటే దాని ద్రవ్యరాశిని అంచనావేయండి. సూర్యుని చుట్టూ భూమి సరాసరి కక్ష్యా వ్యాసార్ధం 1.5 × 10⁸ km.
జవాబు:
సూర్యుని ద్రవ్యరాశి లెక్కించడానికి మనకు భూమి పరిభ్రమణ కాలం T సూర్యుని నుండి గల సగటు కక్ష్యా వ్యాసార్ధము R మరియు భూమి ద్రవ్యరాశి M_e కావలెను.
సూర్యుని వల్ల భూమిపై గురుత్వాకర్షణ F = \(\frac{\mathrm{GM}_{\mathrm{s}} \cdot \mathrm{M}_{\mathrm{e}}}{\mathrm{r}^2}\)
భూమి సూర్యునిచుట్టూ () అను స్థిరవడితో చలిస్తుంటే భూమిపై అభికేంద్ర బలం F’ = M_erω² = M_er\(\frac{4 \pi^2}{\mathrm{~T}^2}\)
అభికేంద్రబలం భూమి, సూర్యుల మధ్య గురుత్వాకర్షణ వల్ల కలుగుతుంది.
\(\frac{\mathrm{GM}_{\mathrm{s}} \mathrm{M}_{\mathrm{e}}}{\mathrm{r}^2}=\mathrm{M}_{\mathrm{e}} \mathrm{r} \frac{4 \pi^2}{\mathrm{~T}^2}\) లేక M_s = \(\frac{4 \pi^2 r^3}{\mathrm{GT}^2}\)
r, T మరియు M విలువలు తెలిస్తే సూర్యుని ద్రవ్యరాశి లెక్కగట్టవచ్చు.
దత్తాంశం నుండి r = 1.5 × 10⁸ km = 1.5 × 10¹¹ m;
T = 365 days = 365 × 24 × 60 ×60 s
M_s = \(\frac{4 \times(22 / 7)^2 \times\left(1.5 \times 10^{11}\right)^3}{\left(6.67 \times 10^{-11}\right) \times(365 \times 24 \times 60 \times 60)^2}\) ≈ 2 × 10³⁰kg

ప్రశ్న 14.
శని సంవత్సరం భూసంవత్సరానికి 29.5 రెట్లు ఉంటుంది. సూర్యుని నుంచి భూమి 1.50 × 10⁸ km దూరంలో ఉన్నట్లయితే సూర్యుని నుంచి శనిగ్రహం దూరం ఎంత ?
జవాబు:
దత్తాంశం నుండి T_s = 29.5 T_e; R_e = 1.5 × 10⁸ km; R_s = ?
\(\frac{\mathrm{T}_{\mathrm{s}}^2}{\mathrm{R}_{\mathrm{s}}^3}=\frac{\mathrm{T}_{\mathrm{e}}^2}{\mathrm{R}_{\mathrm{e}}^3}\) అను సమీకరణం నుండి
లేక R_s = R_e \(\left(\frac{\mathrm{T}_{\mathrm{s}}}{\mathrm{T}_{\mathrm{e}}}\right)^{2 / 3}\) = 1.5 × 10⁸ \(\left(\frac{29.5 \mathrm{~T}_{\mathrm{e}}}{\mathrm{T}_{\mathrm{e}}}\right)^{2 / 3}\) = 1.43 × 10⁹ km.

ప్రశ్న 15.
భూఉపరితలంపై ఒక వస్తువు 63 N బరువు ఉంటుంది. భూవ్యాసార్ధానికి సగం ఎత్తులో భూమి పరంగా ఆ వస్తువుపై పనిచేసే గురుత్వాకర్షణ బలం ఎంత ?
జవాబు:
వస్తువు భారము = mg = 63 N
‘h’ ఎత్తు వద్ద గురుత్వ త్వరణము, g’ = \(\frac{g R^2}{(R+h)^2}=\frac{g R^2}{(R+R / 2)^2}=\frac{4}{9} g^2\)
h ఎత్తు వద్ద వస్తువుపై గురుత్వాకర్షణ బలం F = mg’ = m × \(\frac{4}{9}\) g = \(\frac{4}{9}\) mg = \(\frac{4}{9}\) × 63 = 28 N

ప్రశ్న 16.
భూమిని ఒక ఏకరీతి ద్రవ్యరాశి సాంద్రత గల గోళంగా పరిగణిస్తే, భూఉపరితలంపై 250 N భారం కలిగిన వస్తువు భూకేంద్రంవైపు పోతున్నప్పుడు కేంద్రానికి సగం దూరంలో ఎంత భారం కలిగి ఉంటుంది ?
జవాబు:
d లోతు వద్ద వస్తువు భారము = mg’ = m × g(1 – \(\frac{\mathrm{d}}{\mathrm{R}}\)) = 250\(\left(1-\frac{\frac{\mathrm{R}}{2}}{\mathrm{R}}\right)\) = 125 N

ప్రశ్న 17.
భూఉపరితలం నుంచి ఒక రాకెట్ను 5 km s^-1 వడితో నిట్టనిలువుగా పేల్చారు. భూమికి తిరిగి వచ్చేలోగా అది భూమి నుంచి ఎంత దూరం పోతుంది ? భూమి ద్రవ్యరాశి = 6.0 × 10²⁴ kg;భూమి సగటు వ్యాసార్ధం 6.4 × 10⁶ m; G = 6.67 × 10^-11 Nm²kg^-2
జవాబు:
రాకెట్ను భూమి మీద వేగంతో పైకి పంపినామనుకొనుము అది చేరగల గరిష్ఠ ఎత్తు h అనుకొనుము.
భూమిపై మొత్తం శక్తి = K.E. + P.E = \(\frac{1}{2}\) mv² + \(\left(\frac{-\mathrm{GMm}}{\mathrm{R}}\right)\)
గరిష్ఠ ఎత్తు వద్ద v = 0, K.E = 0 మరియు P.E = – \(\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}\)
మొత్తం శక్తి = K.E + P.E = 0 + \(\left(\frac{-\mathrm{GMm}}{\mathrm{R}+\mathrm{h}}\right)=-\frac{\mathrm{GMm}}{\mathrm{R}+\mathrm{h}}\)
శక్తి నిత్యత్వ నియమం నుండి

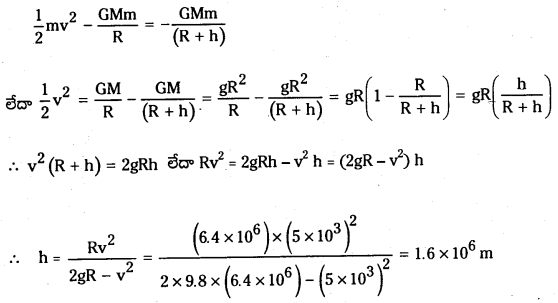
ప్రశ్న 18.
భూఉపరితలంపై ఒక ప్రక్షేపకం పలాయనవడి 11.2 km s^-1 దీనికి మూడు రెట్లు వేగంతో ఒక వస్తువును ప్రక్షిప్తం చేశారు. భూమి నుంచి సుదూరంలో (అంటే అనంత దూరంలో) వస్తువు వడి ఎంత ? సూర్యుడు, ఇతర గ్రహాల ఉనికిని విస్మరించండి.
జవాబు:
దత్తాంశం నుండి v_e = 11.2 kms^-1; ప్రక్షేప వేగము V = 3v_e గురుత్వాకర్షణ పరిధి దాటిన తరువాత వస్తువు ద్రవ్యరాశి m₀, దాని వేగము V₀ అనుకొనుము.
\(\frac{1}{2}\) mv₀² = \(\frac{1}{2}\) mv² – \(\frac{1}{2}\)mv_e² (శక్తి నిత్యత్వ నియమం నుండి)
లేదా v₀ = \(\sqrt{v^2-v_{\mathrm{e}}^2}=\sqrt{\left(3 \mathrm{v}_{\mathrm{e}}\right)^2-\mathrm{v}_{\mathrm{e}}^2}=\sqrt{8} \mathrm{v}_{\mathrm{e}}=\sqrt{8} \times 11.2\) = 31.68 kms^-1 ·

ప్రశ్న 19.
భూ ఉపరితలం నుంచి 400km ఎత్తున ఒక కృత్రిమ ఉపగ్రహం పరిభ్రమిస్తుంది. భూమి గురుత్వాకర్షణ ప్రభావం నుంచి కృత్రిమ ఉపగ్రహాన్ని తప్పించడానికి ఎంత శక్తిని వెచ్చించాలి ? కృత్రిమ ఉపగ్రహం ద్రవ్యరాశి = 200kg; భూమి ద్రవ్యరాశి = 6.0 × 10²⁴ kg; భూ వ్యాసార్ధం = 6.4× 10⁶ m; G = 6.67 × 10^-11Nm² kg^-2.
జవాబు:
h ఎత్తులోగల ఉపగ్రహం మొత్తం శక్తి
= \(-\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}+\frac{1}{2} \mathrm{mv} v^2=-\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}+\frac{1}{2} \mathrm{~m} \frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})}=\frac{-\mathrm{GMm}}{2(\mathrm{R}+\mathrm{h})}\)
ఉపగ్రహాన్ని గురుత్వాకర్షణ క్షేత్రం నుండి దాటించడానికి రాకెట్ ఖర్చుపెట్టిన శక్తి = – కక్ష్యలో గల ఉపగ్రహం మొత్తం శక్తి
= \(\frac{\mathrm{GMm}}{2(\mathrm{R}+\mathrm{h})}=\frac{\left(6.67 \times 10^{-11}\right) \times\left(6 \times 10^{24}\right) \times 200}{2\left(6.4 \times 10^6+4 \times 10^5\right)}\) = 5.9 × 10⁹ J

ప్రశ్న 20.
ఒక్కొక్కటి సూర్యుని ద్రవ్యరాశి (= 2 × 10³⁰ kg) కి సమానమైన ద్రవ్యరాశి కలిగిన రెండు నక్షత్రాలు ముఖాముఖీ అభిఘాతం చెందే విధంగా పరస్పరం సమీపిస్తున్నాయి. వాటి మధ్య దూరం 10⁹ km గా ఉన్నప్పుడు వాటి వడులు విస్మరింపదగినవిగా ఉన్నాయి. అవి ఏ వడితో అభిఘాతం చెందుతాయి ? ప్రతి నక్షత్రం వ్యాసార్ధం 10⁴ km. పరస్పరం అభిఘాతం చెందేంత వరకు అవి విరూపణ చెందకుండా ఉంటాయని అనుకొందాం. (తెలిసిన G విలువ ఉపయోగించండి).
జవాబు:
నక్షత్రం ద్రవ్యరాశి M = 2 × 10³⁰ kg
నక్షత్రముల మధ్య తొలి దూరం r = 10⁹ km = 10¹² m
వ్యవస్థ తొలి స్థితి శక్తి = – \(\frac{\mathrm{GMM}}{\mathrm{R}}\)
నక్షత్రాల మొత్తం గతిజశక్తి = \(\frac{1}{2}\) Mv² + \(\frac{1}{2}\)mv² = Mv²
అభిఘాతం ముందు నక్షత్రాల వేగం ‘v’ మరియు వాటి మధ్య దూరము r = 2R.
రెండు నక్షత్రాల మొత్తం స్థితిశక్తి = – \(\frac{\mathrm{GMM}}{2 \mathrm{R}}\)
K.E. లో పెరుగుదల P.E. లో తరుగుదల వల్ల సాధ్యము

ప్రశ్న 21.
ఒక క్షితిజ సమాంతర బల్లపై ఒక్కొక్కటి 100 kg ద్రవ్యరాశి, 0.10 m వ్యాసార్ధం ఉన్న రెండు బరువైన గోళాలు 1.0 m దూరంలో ఉన్నాయి. ఆ గోళ కేంద్రాలను కలిపే రేఖ మధ్య బిందువు వద్ద గురుత్వాకర్షణ బలం, పొటెన్షియల్ ఎంత ఉంటాయి ? ఆ బిందువు వద్ద ఉంచిన వస్తువు సమతాస్థితిలో ఉంటుందా ? ఒకవేళ ఉంటే, ఆ వస్తువు స్థిర సమతాస్థితిలో ఉంటుందా ? అస్థిర సమతాస్థితిలో ఉంటుందా ?
జవాబు:
గోళములను కలుపు రేఖ మధ్య బిందువు వద్ద గురుత్వ క్షేత్రము = \(\frac{\mathrm{GM}}{(\mathrm{r} / 2)^2}(-\hat{\mathrm{r}})+\frac{\mathrm{GM}}{(\mathrm{r} / 2)} \hat{\mathrm{r}}\) = 0
గోళాలను కలుపు రేఖ మధ్య బిందువు వద్ద గురుత్వ పొటెన్షియల్
V = \(-\frac{\mathrm{GM}}{\mathrm{r} / 2}+\left(\frac{-\mathrm{GM}}{\mathrm{r} / 2}\right)=\frac{-4 \mathrm{GM}}{\mathrm{r}}=\frac{-4 \times 6.67 \times 10^{-11} \times 100}{1.0}\) = -2.7 × 10^-8 J/kg
మధ్య బిందువు వద్ద ఫలిత బలము సున్నా కావున వస్తువు సమతా స్థితిలో ఉంది. దాని స్థానాన్ని కొంచెం పక్కకు జరిపితే ఒక గోళం వల్ల ఆకర్షణ పెరిగి అది సమతా స్థితి కోల్పోతుంది. కావున ఆ వస్తువు అస్థిర నిశ్చల స్థితిలో ఉండును.

ప్రశ్న 22.
మీరు నేర్చుకున్నట్లుగా, ఒక భూస్థావర ఉపగ్రహం భూమి ఉపరితలం నుంచి 36,000 km ఎత్తులో ఉన్న కక్ష్యలో భూమి చుట్టూ పరిభ్రమిస్తుంది. ఉపగ్రహం ఉన్న ప్రదేశంలో భూమి గురుత్వం మూలంగా కలిగే పొటెన్షియల్ ఎంత ? (అనంత దూరం వద్ద పొటెన్షియల్ సున్నాగా తీసుకోండి) భూమి ద్రవ్యరాశి = 6.0 × 10²⁴ kg, భూ వ్యాసార్ధం = 6400 km.
జవాబు:
భూమి నుండి h ఎత్తులో గురుత్వ పొటెన్షియల్
V = – \(\frac{\mathrm{GM}}{(\mathrm{R}+\mathrm{h})}=\frac{-6.67 \times 10^{-11} \times\left(6 \times 10^{24}\right)}{\left(6.4 \times 10^6+36 \times 10^6\right)}\) = -9.4 × 10⁶ J/kg

ప్రశ్న 23.
సూర్యుని ద్రవ్యరాశికి 2.5 రెట్లు ద్రవ్యరాశిని కలిగి, 12 km పరిమాణానికి కుంచించుకుపోయిన ఒక నక్షత్రం సెకనుకు 1.2 పరిభ్రమణాల వడితో తిరుగుతుంది. (ఈ రకమైన నక్షత్రాలను ‘న్యూట్రాన్ నక్షత్రాలు’ అంటారు. Pulsars అని పిలవబడే కొన్ని ఖగోళ వస్తువులు ఈ కోవకు చెందినవే). ఆ నక్షత్ర మధ్యరేఖ (equator) పై ఉంచిన వస్తువు గురుత్వాకర్షణ వల్ల దానికే అతుక్కొనిపోతుందా ? (సూర్యుని ద్రవ్యరాశి = 2 × 10³⁰ kg)
జవాబు:
వస్తువు నక్షత్రానికి అతుక్కొని ఉండాలంటే నక్షత్రంపై గురుత్వ త్వరణము వస్తువు భ్రమణం వల్ల కలిగిన అపకేంద్ర త్వరణము (rω²) కన్న ఎక్కువ ఉండాలి.
గురుత్వ త్వరణము g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}=\frac{6.67 \times 10^{-11} \times 2.5 \times 2 \times 10^{30}}{(12000)^2}\) = 2.3 × 10¹² ms^-2
అభిలంబ త్వరణము = rω² = r (2πv)² = 12000 (2π × 1.5)² = 1.1 × 10⁶ ms^-2
g > rω² కావడం వల్ల వస్తువు నక్షత్రం ఉపరితలంపై అతుక్కొని ఉంటుంది.

Telangana TSBIE TS Inter 1st Year English Study Material Revision Test-I Exercise Questions and Answers.

TS Inter 1st Year English Study Material Revision Test-I

Time: 1 1/2Hrs.
Marks: 50

Section – A

Question 1.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]
a) Education is not what a person is able to hold in his head, so much as it is what a person is able to find.
Answer:
Introduction :
This beautiful sentence is taken from the character building speech. ‘Two Sides of Life” delivered by Booker T Washington. This speech is extracted from his popular book ‘Character Building’.

Context & Explanation :
The writer gives very forceful explanation of character building. He inspires teacher tranies how they should be in their profession. He tells them to be honest. If they don’t know anything, they have to accept it frankly and honestly. Their students will respect them for it. it is because education is not possible to hold in one’s head. It is what a person is able to find. It is not the correct notion that the teacher should know everything.

Critical Comment :
Here, the writer addresses the teacher trainees and advises them to have the character of frankness and honesty.

b) Do not be satisfied until you have put yourselves into that atmosphere where you can seize and hold on to the very highest and most beautiful things that can be got out of life.
Answer:
Introduction :
There motivational lines are at the concluding lines taken from the essay ‘Two Sides of Life’ written by Booker T Washington. Lt is a speech taken from his popular book Character Building.

Context & Explanation : The writer concludes his speech by inspiring his students to be positive in life. He advises them to cultive positive thought, positive attitude to become the strong individual. He tells them to be the best people in life. He warns them not satisfy with the second hand things in life. He inspires them to be in the highest position in the life by achieving great and beautiful things in life.

Critical Comment :
He advises his students to see the happier side and spread cheer all round.

Question 2.
Annotate ANY ONE of the following in about 100 words. [1 × 4 = 4]
a) I asked the professors who teach the meaning of life to tell me what happiness is.
Answer:
Introduction :
This line is taken from the poem ‘Happiness’ written by Carl Sandburg. He is a famous American poet. The poem is extracted from his collection of poems, ‘Chicago Songs.

Context & Explanation :
It depicts the narrator’s experience. He wants to know what happiness is. First, he consults the professors for the answer. They represent the intelligence and success. But, they can’t answer it They claim that they teach the meaning of life. Finally, he finds the real meaning of happiness from a crowd of Hungarians with their women and children under a tree.

Critical Comment :
Here the line describes the narrators experience. He asks the professors about the meaning of happiness.

b) And I saw a crowd of Hungarians under the trees with their women and children and a keg of beer and an accordion.
Answer:
Introduction : These lines are taken from the poem ‘Happiness’ written by Cari Sandburg, a famous American poet. The poem is extracted from his collection of poems, ‘Chicago Songs’.

Context & Explanation :
The poet wants to know the meaning of happiness. He asks professors and top executives to help him on this regard. But, they express their inability. At last he sees a group of Hungarians under the trees with their women and children. They do not have money, intelligence or success. They are spending happy moments under the tree.
They are the symbol of real meaning of happiness. The poet at once understands what happiness is.

Critical Comment :
Here the poet describes how he came across a group of Hungarians, beside a river and beneath the tree.

Question 3.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]
a) How do the two types of persons react to an overcast morning ?
Answer:
Booker T Washington’s addresses are very forceful explanations of character building. In his speech Two Sides of Life he describes how people react to an overcast morning. To a person who constantly looks at the dark side of things in life, the morning appears gloomy, dull and the streets full of muddy water. Everything looks disagreeable to him. Whereas for a person who always looks at the bright side of things in life, the morning appears beautiful in all aspects. He speaks of the beauties in the rain drops, of the freshness in the newly bathed flowers, shrubs and trees.

b) Why does the speaker feel it unfortunate about the students in assessing the personality of their teachers ?
Answer:
Bgoker T Washington is a world-famous Afro-American writer, activist and educator. His collection of speeches comes in the form of Character Building. A selection from that celebrated book is our present lesson. It discusses the two sides of life. It recommends the positive side. Washington lists some mistakes students make about their teachers. He makes it clear that every teacher makes mistakes at times. It is human to err. He advises students to ignore such mistakes. He asks them to see the positive aspects of the lesson as well as the teacher. He emphasises the need to see the good and forget the bad. Good advice indeed!

Question 4.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]
a) Explain the narrator’s experience in finding out what happiness is.
Answer:
The poem ‘Happines& is written by Carl Sandburg. It conveys a beautiful message. It is extracted from his collection of poems. Chicago songs. The poem is an expression of the narrators search for the meaning of happiness and his ultimate realization.

The narrator seeks to know what happiness is. He enquires with many professors but in vain. Even, the top executives are consulted, but to no avail. One Sunday afternoon, he wanders along a river. There, he sees a group of Hungarians with their women and children under the trees. They are spending happy moments there. He at once understands what happiness is. Happiness is living in the present. It is not wealth or success or fame.

b) Seeing helps one better in understanding than listening to. Justify the statement in view of the narrator’s experience in the poem, Happiness.
Answer:
Carl Sandburg’s poem, ‘Happiness’ conveys a beautiful message. True happiness’ It is extracted from his collection, Chicago songs. It shows how the narrator tries to find out the real meaning of happiness and his ultimate realization.

This seems like a more light hearted poem. The poet depicts the narrator’s experience. He asks people what they think of happiness. The first two he asks are the people who should know what happiness is. But, both look at him as if he is trying to fool them. He then ventures out to observe some of the lower class. He examplifies, what he sees, his image of happiness. The poem centers around the difference between the lower and the upper class. He favours the lower class for their simplicity. They value the things in their lives. It is proved in the lives of Hungarians. They show him what happiness is. They enjoy then food, drink, music and fun. At last, seeing Hungarians helps the narrator in understanding how they spend happy moments under a tree. Then he realizes what happiness is. Even if they are not very well educated or wealthy, they stand as a symbol of sharing and helping mentality people.

Question 5.
Answer ANY ONE of the following questions in about 100 words. [1 × 4 = 4]
a) Narrate the feelings of Alan for not being able to reach the ground in time after meeting the old man on his way.
Answer:
?laying the Game”, from the pen of Arthur Mee, pictures the humane angle of Alan. Alan was studying in a school. He got his long-awaited chance to play cricket in his school team. He was excited. On that important day, he started early. But on his way, he saw an old, lean and weak man. That old man was walking with difficulty. The man in Alan woke up. He helped the old man walk with his support. So, he couldn’t reach the ground in time. His chance to play was given to another boy. Alan felt bad. He bit his lips. His sorrow knew no bounds. He couldn’t even express his inability to go there in time. He walked back home slowly in disappointment.

b) Helping the old is as good as playing the game. Elucidate with reference to the story.
Answer:
Arthur Mee is known for his humanism. He expresses it artistically. “Playing the Game” exhibits that rare quality Alan is the central character. He loved cricket. Once, he got a chance to represent his school in cricket. On the scheduled day, Alan started for the ground early. But on the way, he noticed an old man struggling to walk. He was move. He held his helping hand to that aged man. Hence, he couldn’t reach the ground in time. He missed the much-awaited opportunity. He felt sad. But for this kind act, his parents presented him with his favourite bicycle. His classmates cheered him. The story proves, thus, that helping the old is better than playing the game.

Question 6.
Read the following passage carefully and answer ANY FIVE questions given below in a word or a sentence each. [5 × 1 = 5]

“Bravo, Alan,” he said, patting his little son on the back.
“But; Daddy,” began Alan. But his father interrupted him.
“It’s all right, Old man,” he said. ‘You see, I came up behind that policeman and he told me what had happened. So I knew you were playing the game although it wasn’t on the cricket-pitch. So I went back into the High Street and bought the bicycle I promised you. It’s a beauty. And, Alan, we’re proud of you, your Mother and I.”

Questions:
i) Who is the writer of the story from which this passage is taken ?
Answer:
Arthur Henry Mee

ii) Why did Alan’s father pat on his back ?
Answer:
to encourage and to appreciate what Alan had done

iii) How did Alan’s father come to know what had happened ?
Answer:
through the policeman behind whom Alan’s father came

iv) I came up behind that policeman. Did Alan’s father go to the spot where Alan helped the old man ?
Answer:
Yes.

v) Alan’s father says, ” ………… although it wasn’t on the cricket-pitch.” Where did Alan play the game ?
Answer:
in the real world-in life-on the meadow

vi) Why did Alan’s father buy the bicycle ?
Answer:
to support and appreciate Alan’s service activities

vii) Why were they proud of Alan ?
Answer:
because Alan ‘played the game’ in its true sense

viii) When would you use the expression, bravo ?
Answer:
When we want to appreciate someone’s achievement we use the word bravo’.

Question 7.
Read the following passage carefully and answer ANY FIVE questions given below in a word or a sentence each. [5 × 1 = 5]

Small is Beautiful
Be it a big task or tough problem, make it into smaller units and see its impact ! Break down an unthought desire into its components and allow the child to decide. The Mac Donald’s Happy Meal comes with a burger, a drink, some fries and a small toy. My kid wanted it at age five. I could buy it but broke down the decision for her – “you don’t like fries, the burger is not the kind you really like, and the drink on its own costs far less. Are we buying because they are selling or we really like the deal ? If we do so, sure, let us get it.” At age five, she walked from the deal. And from many others after that.

Questions:
i) Break down an unthought desire into components. How would this help one ?
Answer:
that helps one in taking proper decisions

ii) What does the Happy Meal include ?
Answer:
It includes a burger, a drink, some fries and a small toy.

iii) Who asked for the Happy Meal and when ?
Answer:
The narrator’s kid wanted it at age five.

iv) The narrator could buy it. Yet he/she didn’t. What did he/she do ?
Answer:
The narrator broke down the decision for her.

v) What should be the deciding factor to buy something, according to the narrator ?
Answer:
Whether we really like the deal should be the deciding factor.

vi) The five-year-old kid did not cry when her desire was not fulfilled. Why ?
Answer:
The broken down decision helped the girl understand that the deal was not what she really liked.

vii) The passage extends a valuable piece of advice to parents. Say true or false.
Answer:
true

viii) ” ………… the drink on its own ………… ” Write the Part of speech of drink.
Answer:
‘drink’-noun

Section – B

Question 8.
Match ANY EIGHT of the following words in Column-A with their meanings in Column B. [8 × 1/2 = 4]

Column A – Column – B
i) dwell upon – a) repeatedly, all the time
ii) consideration – b) very unhappy or uncomfortable
iii) excellence – c) depressed, nervous
iv) frankness – d) the mixture of gases that surrounds the earth
v) charming – e) the act of thinking process
vi) miserable – f) slightly wet, often in a way that is unpleasant
vii) constantly – g) openness, truthfulness
viii) damp – h) to think or talk a lot about something
ix) atmosphere – i) very pleasant or attractive
x) moody – j) superiority, distinction
Answer:
i) – h
ii) – e
iii) – j
iv) – g
v) – i
vi) – b
vii) – a
viii) – f
ix) – d
x) – c

Question 9.
Identify the parts of speech of ANY EIGHT of the following underlined words. [8 × 1/2 = 4]

No teacher (1) knows everything about (2) every (3) subject. A good (4) teacher will say (5) frankly and (6) clearly (7), “I(8) don’t know. I cannot answer (9) that question (10).”
Answer:
1) teacher – noun
2) about – preposition
3) every – adjective
4) good – adjective
5) will say – verb
6) and – conjuction
7) clearly – adverb
8) I – pronoun
9) answer – verb
10) question – noun

Question 10.
Fill ANY EIGHT of the following blanks with a, an or the. [8 × 1/2 = 4]

i) When you meet ____________ (1) fellow student, ___________ (2) teacher, or anybody, or when
you write letters home, get into ___________ (3) habit of calling attention to ________ (4) bright things of life that you have seen, the things that are beautiful, __________ (5) things that are charming.
ii) ________ (6) apple ________ (7) day builds immunity!
iii) It rained a little during _________ (8) night.
iv) I interviewed ________ (9) M.P. in ________ (10) evening.
Answer:
i)) 1 – a
2 – a
3 – the
4 – the
5 – the

ii) 6 – An
7 – a

iii) 8 – the

iv) 9 – an
10 – the

Question 11.
Supply the missing letters to ANY EIGHT of the following words. [8 × 1/2 = 4]

i) sch _ _ l
ii) enc _ _ raging
iii) app _ _ ranee
iv) exce _ _ ent
v) sp _ _ k
vi) a _ _ ention
vii) p _ _ pie
viii) kno _ _ edge
ix) di _ _ ipline
x) a _ _ ord
Answer:
i) school
ii) encouraging
iii) appearance
iv) excellent
v) speak
vi) attention
vii) people
viii) knowledge
ix) discipline
x) afford

Question 12.
Identify the silent consonant letters in ANY EIGHT of the following words. [8 × 1/2 = 4]

i) bright
ii) doubt
iii) hour
iv) neighbour
v) wrong
vi) handsome
vii) knee
viii) calm
ix) listen
x) dawn
Answer:
i) bright – h
ii) doubt – b
iii) hour – h
iv) neighbour – gh
v) wrong – w
vi) handsome – d
vii) knee – k
viii) calm – l
ix) listen – t
x) dawn – w

Students must practice these TS Inter 1st Year Maths 1A Study Material Chapter 6 Trigonometric Ratios upto Transformations Ex 6(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Trigonometric Ratios upto Transformations Solutions Exercise 6(a)

I.
Question 1.
Convert the following into simplest form
(i) tan (θ – 14π)
Answer:
tan (θ – 14π) = tan [- (14π – θ)]
= – tan (14π – θ)
= – tan [ 2(7π) – θ)
= – tan (-θ) = tan θ

(ii) cot (\(\frac{21 \pi}{2}\) – θ)
Answer:
cot (\(\frac{21 \pi}{2}\) – θ) = cot[10π + (\(\frac{\pi}{2}\) – θ)]
= cot (\(\frac{\pi}{2}\) – θ) = tan θ

(iii) cosec (5π + θ)
Answer:
cosec (5π + θ) = cosec [4π + (π + θ)]
= cosec(π + θ) = – cosec θ

(iv) sec (4π – θ)
Answer:
sec (4π – θ) = sec [2(2π) – θ]
= sec (- θ) = sec θ

Question 2.
Find the values of each of the following
(i) sin (-405°)
Answer:
sin (-405°) = -sin 405° = -sin (360°+45°)
= – sin 45° = \(-\frac{1}{\sqrt{2}}\)

(ii) cos \(\left(-\frac{7 \pi}{2}\right)\)
Answer:
cos \(\left(-\frac{7 \pi}{2}\right)\) = cos \(\frac{7 \pi}{2}\) = cos (630°)
= cos (360 + 270°) = cos 270°
= cos (180 + 90) = -cos 90 = 0
(or) cos \(\left(-\frac{7 \pi}{2}\right)\) = 0 (∵ cos(2n + 1)\(\frac{\pi}{2}\) = 0)

(iii) sec (2100°)
Sol. sec (2100°) = sec [5 × 360° + 300°]
= sec 300° = sec (360° – 60°)
= sec 60° = 2

(iv) cot (-315°)
Answer:
cot (-315°) = – cot 315° = – cot (270 + 45°)
= cot 45° = 1

Question 3.
Evaluate
(i) cos² 45° + cos² 135° + cos² 225° + cos² 315°
Answer:
cos 45° = \(\frac{1}{\sqrt{2}}\), cos 135° = cos (180 – 45°)
= – cos 45° = \(-\frac{1}{\sqrt{2}}\)

cos 225° = cos (180 + 45°)
= – cos 45° = –\(\frac{1}{\sqrt{2}}\)

cos 315° = cos(360 – 45°)
= cos 45° = \(\frac{1}{\sqrt{2}}\)

∴ cos² 45° + cos² 135° + cos² 225° + cos² 315°
= \(\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}\) = 2

(ii) sin²\(\frac{2 \pi}{3}\) + cos²\(\frac{5 \pi}{6}\) – tan²\(\frac{3 \pi}{4}\)
Answer:

(iii) cos 225° – sin 225° + tan 495° – cot 495°
Answer:
cot (180 + 45) – sIn (180 + 45) + tan (360 + 135) – cot (360 + 135)
= – cot 45° + sin 45° + tan 135 – cot 135°
= – cos 45° + sin 45° +tan(180 – 45) – cot(180 – 45)
= – cos 45° + sin 45° – tan 45° + cot 45°
= \(-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\) – 1 + 1 = 0

(iv) (cos θ – sin θ) if
(a) θ = \(\frac{7 \pi}{4}\)
(b) θ = \(\frac{11 \pi}{4}\)
Answer:

Question 4.
(i) If sin θ = –\(\frac{1}{3}\) and 0 does not lie in the third 3 quadrant, find the values of (a) cos θ and (b) cot θ. (March 2013)
Answer:
sin θ = –\(\frac{1}{3}\) and sin θ is negative and does not lie in third quadrant,
⇒ θ lies in fourth quadrant. In IVth quadrant cos θ is positive and cot θ is negative.
a) cos θ = \(\sqrt{1-\sin ^2 \theta}=\sqrt{1-\frac{1}{9}}=\frac{2 \sqrt{2}}{3}\)
b) cot θ = \(\frac{\cos \theta}{\sin \theta}\) = -2√2

(ii) If cos θ = t (0 < t < 1) and θ does not lie in the first quadrant, find the values of a) sin θ b) tan θ
Answer:
cos θ = t, (0 < t < 1)
⇒ cos θ is positive and 0 does not lie in first quadrant
⇒ θ lies in IVth quadrant
a) sin θ = \(-\sqrt{1-\cos ^2 \theta}=-\sqrt{1-t^2}\)
b) tan θ = \(\frac{\sin \theta}{\cos \theta}=-\frac{\sqrt{1-t^2}}{t}\)

(iii) Find the value of sin 330°. cos 120° + cos 210°. sin 300°
Answer:
sin 330° cos 120° + cos 210° sin 300°
= sin (360 – 30) cos (180 – 60) + cos ( 180 + 30) sin (360 – 60)
= (-sin 30°) (-cos 60°) + (-cos 30°) (- sin 60°)
= sin 30 cos 60 + cos 30 sin 60 = sin (30 + 60)
= sin 90° = 1

(iv) If cosec θ + cot θ = \(\frac{1}{3}\), find cos θ and determine the quadrant in which θ lies.
Answer:
we have coses²θ – cot² θ = 1
⇒ (cosec θ + cot θ) (cosec θ – cot θ) = 1

∴ sin θ is positive and cos θ is negative,
⇒ θ lies in IInd quadrant.

Question 5.
(i) If sin α + cosec α= 2, find the value of sinⁿ α + cosecⁿ α; n ∈ Z.
Answer:
Given sin α + cosec α = 2
Squaring both sides
sin² α = cosec² α + 2 = 4
⇒ sin α + cosec α = 2
cubing on both sides
sin³ α + cosec³ α + 3 sin α cosec α (sin α + cosec α) = 8
sin³ α + cosec³ α + 3 (2) = 8
⇒ sin³ α + cosec³ α = 2
In the same way sinⁿ α + cosecⁿ α = 2 (n ∈ z)

(ii) If sec θ + tan θ = 5, find the quadrant in which θ lies and find the value of sin θ
Answer:
We have sec² θ – tan² θ = 1
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1
Also given sec θ + tan θ = 5 ………….(2)

Adding (1) and (2)

tan θ is +ve, sec θ is + ve
⇒ θ lies is first quadrant.

II.
Question 1.
Prove that
(i) \(\frac{\cos (\pi-A) \cot \left(\frac{\pi}{2}+A\right) \cos (-A)}{\tan (\pi+A) \tan \left(\frac{3 \pi}{2}+A\right) \sin (2 \pi-A)}\) = cos A
Answer:

(ii) \(\frac{\sin (3 \pi-A) \cos \left(A-\frac{\pi}{2}\right) \tan \left(\frac{3 \pi}{2}-A\right)}{{cosec}\left(\frac{13 \pi}{2}+A\right) \sec (3 \pi+A) \cot \left(A-\frac{\pi}{2}\right)}\)
Answer:

(iii) sin 780°. sin 480° + cos 240°. cos 300° = \(\frac{1}{2}\)
Answer:
sin [2 × 360 + 60] sin [360 + 120] + cos [180 + 60] cos [360-60]
= sin 60 sin 120 – cos 60 cos 60
= sin 60 sin 60 – cos 60. cos 60
= \(\frac{\sqrt{3}}{2} \frac{\sqrt{3}}{2}-\frac{1}{2} \cdot \frac{1}{2}=\frac{3}{4}-\frac{1}{4}=\frac{1}{2}\)

(iv) \(\frac{\sin 150^{\circ}-5 \cos 300^{\circ}+7 \tan 225^{\circ}}{\tan 135^{\circ}+3 \sin 210^{\circ}}\) = -2
Answer:

(v) cot\(\left(\frac{\pi}{20}\right)\). cot\(\left(\frac{3 \pi}{20}\right)\). cot\(\left(\frac{5 \pi}{20}\right)\). cot\(\left(\frac{7 \pi}{20}\right)\). cot\(\left(\frac{9 \pi}{20}\right)\) = 1
Answer:
cot\(\left(\frac{\pi}{20}\right)\). cot\(\left(\frac{3 \pi}{20}\right)\). cot\(\left(\frac{5 \pi}{20}\right)\). cot\(\left(\frac{7 \pi}{20}\right)\). cot\(\left(\frac{9 \pi}{20}\right)\)
= cot 9°. cot 27°. cot 45°. cot 63°. cot 81°
= cot 9°. cot 27°. 1.cot (90 – 27) . cot (90 -9)
= cot 9°. cot 27°. 1. tan 27°. tan 9°
= 1

Question 2.
(i) Simplify \(\frac{\sin \left(-\frac{11 \pi}{3}\right) \tan \left(\frac{35 \pi}{6}\right) \sec \left(-\frac{7 \pi}{3}\right)}{\cot \left(\frac{5 \pi}{4}\right) {cosec}\left(\frac{7 \pi}{4}\right) \cos \left(\frac{17 \pi}{6}\right)}\)
Answer:

(ii) If tan 20 ° = p, prove that
\(\frac{\tan 610^{\circ}+\tan 700^{\circ}}{\tan 560^{\circ}-\tan 470^{\circ}}=\frac{1-p^2}{1+p^2}\)
Answer:
Given that tan 20° = p then

(iii) If α, β are complementary angles such that b sin α = a, then find the value of (sin α cos β – cos α sin β)
Answer:
Given α, β are complementary angles α + β = 90°
⇒ β = 90° – α
∴ sin α cos β – cos α sin β
= sin (α – β)
= sin[α – (90 – α)]
= sin [2α – 90°]
= -sin[90 – 2α]
= -cos 2α
= -(1 – 2sin²α) = -1 + 2sin²α
= -1 + 2\(\left(\frac{a^2}{b^2}\right)\)
= \(\frac{2 a^2-b^2}{b^2}\)

Question 3.
(i) If cos A = cos B = – \(\frac{1}{2}\), A does not lie in the second quadrant and B does not lie in third quadrant, then find the value of \(\frac{4 \sin B-3 \tan A}{\tan B+\sin A}\)
Answer:
cos A = –\(\frac{1}{2}\) and A does not lie in second quadrant
⇒ A lies in third quadrant
cos B = –\(\frac{1}{2}\) and B does not lie in third quadrant
⇒ B lies in second quadrant
cos A = –\(\frac{1}{2}\) and A lie in third quadrant
⇒ A = 240°
cos B = –\(\frac{1}{2}\) and B lies in second quadrant.
⇒ B = 120°

(ii) If 8 tan A = -15 and 25 sin B = -7 and neither A nor B is in the fourth quadrant, then show that sin A cos B + cos A sin B = \(\frac{-304}{425}\)
Answer:
8 tan A = -15 25 sin B = -7
⇒ tan A = \(\frac{-15}{8}\) ⇒ sin B = \(\frac{-7}{25}\)
Given neither A nor B is in the fourth quadrant, clearly A is in second quadrant and B is in third quadrant,
sin A cos B + cos A sin B

(iii) If A, B, C, D are angle of a cyclic quadrilateral then prove that
a) sin A – sin C = sin D – sin B
b) cos A + cos B + cos C + cos D = 0
Answer:
A, B, C, D are angles of a cyclic quadrilateral
⇒ A + C = 180°, and B + D = 180° ……………(1)
C = 180 – A and D = 180° – B
a) LHS = sin A – sin C
= Sin A – sin (180 – A) = 0
RHS = sin D – sin B
= sin (180 – B) – sin B
= sin B – sin B = 0
LHS = RHS

b) LHS cos A + cos B + cos C + cos D
= cos A + cos B + cos (180 – A) + cos (180 – B)
= cos A + cos B – cos A – cos B = 0
= RHS

Question 4.
If a cos θ – b sin θ = c, then show that a sin θ + b sin θ = ±\(\sqrt{a^2+b^2-c^2}\)
Answer:
Given a cos θ – b sin θ = c
and let a sin θ + b cos θ = x
squaring and adding, we get
⇒ (a cos θ – b sin θ)² + (a sin θ + b cos θ)²
= c² + x²
a² (cos² θ + sin² θ)² + b² (sin² θ + cos² θ)
= c² + x²
⇒ a² + b² + c² + x² ⇒ x² = a² + b² + c²
⇒ x = ±\(\sqrt{a^2+b^2-c^2}\)

(ii) If 3 sin A + 5 cos A = 5, then show that 5 sin A – 3 cos A = ± 3
Answer:
Given that 3 sin A + 5 cos A = 5
Let 5 sin A – 3 cos A = x
squaring and adding, we get
(3 sin A + 5 cos A)² + (5 sin A – 3 cos A)²
= 5² + x²
⇒ 9 (sin² A + cos² A) + 25 (cos² A + sin² A)
⇒ 34 = 25 + x² ± ⇒ x² = 9 ⇒ x = ±3
∴ 5 sin A – 3 cos A = ± 3

(iii) If tan² θ = (1 – e²), show that sec θ + tan³ θ. cosec θ = (2 – e²)^3/2.
Answer:
Given tan²θ = 1 – e²
⇒ sec² θ= 1 + tan² θ = 1
LHS = sec θ + tan³ θ. cosec θ
= sec θ + \(\frac{\sin ^3 \theta}{\cos ^3 \theta} \cdot \frac{1}{\sin \theta}\)
= sec θ + tan² θ sec θ = ( 1 + tan² θ) sec θ
= sec² θ sec θ
= (2 – e²) \(\sqrt{2-\mathrm{e}^2}\)
= (2 – e²)^3/2 = RHS

III.
Question 1.
Prove that following
(i) \(\frac{\tan \theta+\sec \theta-1}{\tan \theta-\sec \theta+1}=\frac{1+\sin \theta}{\cos \theta}\)
Answer:

(ii) prove that
(1 + cot θ – cosec θ) (1 + tan θ + sec θ) = 2
Answer:
(1 + cot θ – cosec θ) (1 + tan θ + sec θ)

(iii) 3 (sin θ – cos θ)⁴ + 6 (sin θ + cos θ)² + 4 (sin⁶ θ + cos⁶ θ) = 13
Answer:
(sin θ – cos θ)² = sin² θ + cos² θ – 2 sin θ cos θ
= 1 – 2sin θ cos θ (sin θ – cos θ)⁴
= (1 – 2 sin θ cos θ)²
= 1 – 4 sin θ cos θ + 4 sin² θ cos² θ (sin θ + cos θ)²
= sin² θ + cos² θ + 2 sin θ cos θ
= 1 + 2 sin θ cos θ
sin⁶ θ + cos⁶ θ = (sin² θ)³ + (cos² θ)³
= (sin² θ + cos² θ) ( sin⁴ θ + cos⁴ θ + sin² θ cos² θ)
= 1 [(sin²θ + cos²θ)² – 2 sin²θ cos²θ + sin²θ cos²θ]
= [1 – sin² θ cos² θ]
LHS = 3 (sin θ – cos θ)⁴ + 6 (sin θ + cos θ)² + 4(sin⁶θ + cos⁶θ)
= 3 [ 1 – 4 sin θ cos θ + 4 sin² θ cos² θ] + 6 [1 + 2sin θ cos θ] + 4 [ 1 – sin² θ cos² θ]
= 3 + 6 + 4 = 13 = RHS

Question 2.
(i) Prove that (sin θ + cosec θ)² + (cos θ + sec θ)² – (tan² θ + cot² θ) = 7
Answer:
(sin θ + cosec θ)² + (cos θ + sec θ)² – (tan²θ + cot²θ)
= sin² θ + 2 + cosec² θ + cos² θ + 2 + sec² θ – tan² θ cot² θ
= sin² θ + 2 + 1 + cot² θ + cos² θ+ 2 + 1 + tan² θ – tan² θ – cot² θ
= (sin² θ + cos² θ) + 2 + 1 + 2 + 1
= 1 + 2 + 1 + 2 + 1 = 7

(ii) cos⁴α + 2 cos²α(1 – \(\frac{1}{\sec ^2 \alpha}\)) = 1 – sin²α
Answer:
cos⁴α + 2 cos²α(1 – cos²α)
= cos⁴α + 2 cos²α sin²α
= cos²α[cos²α + 2sin²α]
= (1 – sin²α)[cos²α + sin²α + sin²α]
= (1 – sin²α)(1 + sin²α) = 1 – sin⁴α

(iii) \(\frac{(1+\sin \theta-\cos \theta)^2}{(1+\sin \theta+\cos \theta)^2}=\frac{1-\cos \theta}{1+\cos \theta}\)
Answer:

(iv) If \(\frac{2 \sin \theta}{(1+\cos \theta+\sin \theta)}\) = x, then find the value of \(\frac{1-\cos \theta+\sin \theta}{1+\sin \theta}\)
Answer:

Question 3.
Eliminate θ from the following
(i) x = a cos³ θ, y = b sin³ θ
Answer:

(ii) x = a cos⁴ θ, y = b sin⁴ θ
Answer:

(iii) x = a (sec θ + tan θ), y = b(sec θ – tan θ)
Answer:
\(\frac{x}{a}\) = sec θ + tan θ, \(\frac{y}{b}\) = sec θ – tan θ
⇒ \(\left(\frac{x}{a}\right)\left(\frac{y}{b}\right)\) = (sec θ + tan θ)(sec θ – tan θ)
= sec²θ – tan²θ = 1
⇒ xy = ab

(iv) x = cot θ + tan θ, y = sec θ – cos θ
Answer:
x = cot θ + tan θ
⇒ x² = (cot θ + tan θ)²
= cot²θ + tan²θ + 2
= (1 + cot²θ) + (1 + tan²θ)
= cosec²θ + sec²θ
= \(\frac{1}{\sin ^2 \theta}+\frac{1}{\cos ^2 \theta}\)
= \(\frac{\sin ^2 \theta+\cos ^2 \theta}{\sin ^2 \theta \cos ^2 \theta}=\frac{1}{\sin ^2 \theta \cos ^2 \theta}\)
∴ x² = sec²θ cosec²θ …………..(1)
y = sec θ – cos θ
⇒ y² = sec² θ + cos² θ – 2
= -1 + sec² θ – 1 + cos² θ
= tan² θ – sin² θ

Telangana TSBIE TS Inter 1st Year Chemistry Study Material 12th Lesson పర్యావరణ రసాయన శాస్త్రం Textbook Questions and Answers.

TS Inter 1st Year Chemistry Study Material 12th Lesson పర్యావరణ రసాయన శాస్త్రం

అత్యంత లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 1.
వాతావరణం, జీవావరణం పదాలను వర్ణించండి.
జవాబు:
వాతావరణం : భూగోళాన్ని చుట్టుకొని ఉండే వాయుస్థితిలోని రక్షక పొరను వాతావరణం అంటారు. వాతావరణంలో అధికభాగం నైట్రోజన్ మరియు ఆక్సిజన్ స్వల్ప పరిమాణంలో కార్బన్ డై ఆక్సైడు, నీటిఆవిరి ఉంటాయి. దీనిలో నాలుగు ఖండాలు ఉన్నాయి. ఇవి భూఉపరితలం నుంచి 500 కి.మీ. ఎత్తు వరకు వ్యాపించి ఉన్నాయి. ఇవి ట్రోపోవరణం, స్ట్రాటోవరణం, మిసోవరణం, థెర్మోవరణం.
జీవావరణం : జీవరాశులు అన్నీ అంటే మొక్కలు, జంతువులు, మానవులను ఉమ్మడిగా జీవావరణం అంటారు.

ప్రశ్న 2.
శిలావరణం, జలావరణం పదాలను వివరించండి.
జవాబు:
శిలావరణం : ఖనిజాలు, మట్టి (భూసారం)తో నిండి ఉన్న ఘనస్థితి భూమి బాహ్య పొరను శిలావరణం అంటాం. భూ ఉపరితలంలో శిలావరణం 5వ వంతు ఉంటుంది. భూమి లోపలి పొరలలో ఖనిజాలు ఉంటాయి. మరింత లోతుగా సహజ వాయువు మరియు చమురు నిక్షేపాలు ఉంటాయి. ఇవన్నీ మరియు కొండలు, పర్వతాలు కూడా శిలావరణంగానే పరిగణించబడతాయి.

జలావరణం : అన్ని రకాల సహజ నీటివనరులు, జలావరణంగా పరిగణించబడతాయి. మహాసముద్రాలు, సముద్రాలు, నదులు, జలాశయాలు, నీటి కాలువలు, రిజర్వాయర్లు, పోలార్ ప్రాంతంలోని మంచు శిఖరాలు, భూగర్భ జలాలు, అనే అన్ని రకాల నీటి వనరులు ఈ ఆవరణ పరిధిలోకే వస్తాయి.

ప్రశ్న 3.
భూకాలుష్యం నిర్వచించండి.
జవాబు:
భూమి అనేది అనేక సహజపదార్థాలు పోగుపడిన ఒక పొర. దీనిలో ఖనిజాలు మరియు మట్టి ఉంటాయి. ఈ పొర పరిశ్రమల వల్ల వచ్చే వృధా పదార్థాలతోను, నగరాలలో వచ్చే వ్యర్థ పదార్థాలతోను, వ్యవసాయదారులు ఉపయోగించే క్రిమినాశకాలు, చీడల నాశకాలు మరియు జీవసంబంధ కారకాలతో కలుషితం అవుతుంది. దీనినే భూమి కాలుష్యం
అంటారు.
క్రిమిసంహారక మందులు, ఆర్గానోఫాస్ఫేట్లు, పెస్టిసైడ్లు, హెర్బిసైడ్లు, ఫంగిసైడ్లు, రొడెంటిసైడ్లు మొదలగు రసాయనాలు కూడా మట్టిని కాలుష్యానికి గురిచేస్తాయి.

ప్రశ్న 4.
రసాయన ఆక్సిజన్ అవసరం (COD) అంటే ఏమిటి ?
జవాబు:
రసాయనిక ఆక్సిజన్ అవసరం (COD) : కలుషిత నీటిలో కరిగి ఉన్న కర్బన రసాయన పదార్థాలను ఆక్సీకరణం చెందించడానికి అవసరమయ్యే ఆక్సిజన్ పరిమాణాన్ని రసాయనిక ఆక్సిజన్ అవసరం అంటాం. నీటిలో ఉండే కర్బన రసాయన పదార్థాల పరిమాణాన్ని తెలిపే ముఖ్య సూచిక ఇది. కర్బన రసాయన పదార్థాలను (50%) ఆమ్లీకృత (H₂SO₄ పొటాషియం డైక్రోమేటు ద్రావణం ద్వారా ఆక్సీకరణం చేసి COD ని నిర్ణయిస్తారు.

ప్రశ్న 5.
జీవరసాయన ఆక్సిజన్ అవసరం (BOD) అంటే ఏమిటి ?
జవాబు:
నీటిలో ఉండే కొన్ని ప్రత్యేక సూక్ష్మజీవులు 20°C వద్ద 5 రోజుల కాలంలో ఉపయోగించుకొనే ఆక్సిజన్ పరిమాణాన్ని జీవరసాయన ఆక్సిజన్ అవసరం అంటారు. శుద్ధనీటి BOD విలువ సుమారు 5pm. 17 ppm కంటే ఎక్కువ BOD విలువ గరిష్ఠ కాలుష్యాన్ని తెలుపుతుంది.

ప్రశ్న 6.
ట్రోపోవరణం, స్ట్రాటోవరణం అంటే ఏమిటి ?
జవాబు:
ట్రోపోవరణం : మానవులు, వారితో సహజీవనం చేసే ఇతర జీవులు మనుగడ సాగించే వాతావరణంలోని మిక్కిలి కింది ప్రదేశాన్ని ట్రోపోవరణం అంటారు. సముద్రమట్టం నుంచి 10 కి.మీ. ఎత్తు వరకు ఇది వ్యాప్తిచెంది ఉంటుంది.
స్ట్రాటోవరణం : ట్రోపోవరణంకు పైభాగంలో స్ట్రాటోవరణం ఉంటుంది. సముద్రమట్టం నుంచి 10-50 కి.మీ. ఎత్తులో స్ట్రాటోవరణం ఉంటుంది. సూర్యుని నుంచి వెలువడే హానికరమైన అతినీలలోహిత కిరణాలను భూ ఉపరితలాన్ని చేరకుండా స్ట్రాటోవరణంలోని ఓజోన్ పొర అడ్డుకుంటుంది.

ప్రశ్న 7.
ట్రోపోవరణంలో ఉండే ప్రధాన కణస్థితి కాలుష్యాలను పేర్కొనండి.
జవాబు:
కణస్థితి కాలుష్యాలు : ఇవి దుమ్ము, పలచని పొగమంచు, ధూమాలు, పొగ, స్మాగ్ మొదలైనవి.

ప్రశ్న 8.
కాలుష్య గాలిలో ఉండే నాలుగు వాయుస్థితి కాలుష్యాలను పేర్కొనండి.
జవాబు:

1. సల్ఫర్ యొక్క ఆక్సైడ్లు SO₂ మరియు SO,₂
2. నైట్రోజన్ యొక్క ఆక్సైడ్లు NO₂
3. కార్బన్ యొక్క ఆక్సైడ్లు CO మరియు CO₂
4. హైడ్రోకార్బన్లు.

ప్రశ్న 9.
గ్రీన్హౌస్ ఫలితం ……, …… వాయువుల ద్వారా కలుగుతుంది.
జవాబు:
గ్రీన్ హౌస్ ఫలితం కార్బన్ డై ఆక్సైడ్ మరియు మీథేన్, ఓజోన్, నీటి ఆవిరి వాయువుల వల్ల కలుగుతుంది.

ప్రశ్న10.
ఆక్సైడ్లు ఆమ్ల వర్షానికి కారణంగా ఉన్నాయి ? దీని pH విలువ ఎంత ? (March 2013)
జవాబు:
SO₂, NO₂ లు ఆమ్ల వర్షాన్ని కలుగజేస్తాయి. SO₂, NO₂ లు ఆక్సీకరణం చెంది నీటితో చర్య జరిపిన తరువాత ఆమ్ల వర్షానికి ప్రధాన కారకాలుగా పనిచేస్తాయి.
2SO₂(వా) + O₂ (వా) + 2H₂O(ద్ర) → 2H₂SO₄ (జల)
4NO₂(వా) + O₂ (వా) + 2H₂O(ద్ర) → 4HNO₃ (జల)
వర్షపు నీరు pH విలువ 5.6 కంటే దిగువకు పడిపోతే దానిని ఆమ్ల వర్షం అంటారు.

ప్రశ్న11.
ఆమ్ల వర్షం కలిగించే రెండు చెడు ప్రభావాలను తెలపండి.
జవాబు:

1. నేలలోని pH విలువ తగ్గి, భూసారం క్షీణించిపోతుంది.
2. కట్టడాల జీవితకాలం అనూహ్యంగా తగ్గిపోతుంది.
3. చలువరాళ్ళతో కట్టిన తాజ్మహల్ గాజులా ఉండే నునుపు స్వభావం ఆమ్ల వర్ష ప్రభావానికి లోనవుతున్నది.

ప్రశ్న12.
పొగ, పలుచని పొగ అంటే ఏమిటి ?
జవాబు:
కర్బన ద్రవ్యాలు దహనం చెందినప్పుడు ఏర్పడిన ఘనస్థితి కణాలను లేదా ఘనద్రవస్థితి మిశ్రమ కణాలను పొగ అనవచ్చు. సిగరెట్ పొగ, శిలాజ జాతి ఇంధనాలు, చెత్తా చెదారం, ఎండిన ఆకులు, తైలాలు మండినప్పుడు ఏర్పడు పొగలు వీటికి ఉదాహరణలు.

పలుచని పొగ : పిచికారీ ద్రవాలలోని కణాల ద్వారాను, గాలిలోని బాష్పాలు ద్రవీకరణం చెందడం ద్వారాను మిస్ట్లు (పలచని పొగమంచులు) ఏర్పడతాయి. ఉదాహరణకు సల్ఫ్యూరిక్ ఆమ్లం ఏర్పరిచే పొగమంచు, కలుపు మొక్కల నాశకాలు, క్రిమినాశకాలు వాటి లక్ష్యాల గురితప్పి గాలిలో ప్రయాణించేటప్పుడు పలుచని పొగలను (మిస్ట్) ఏర్పరుస్తాయి.

ప్రశ్న13.
సంప్రదాయక స్మాగ్ అంటే ఏమిటి ? దాని రసాయన స్వభావం ఏమిటి ? (ఆక్సీకరణ / క్షయీకరణ)
జవాబు:
స్మోక్ (పొగ), ఫాగ్ (మంచు) పదాల నుంచి స్మాగ్ అనే పదం వచ్చింది. శీతల (ఆర్ద్ర) శీతోష్ణస్థితులలో చోటుచేసుకుంటుంది. ఇది పొగ, మంచు, సల్ఫర్ డై ఆక్సైడ్ మిశ్రమం. రసాయనికంగా ఇది క్షయీకరణ స్వభావం ఉన్న మిశ్రమం. కాబట్టి దీనిని క్షయీకరణ సామర్థ్య స్మాగ్ అంటాం.

ప్రశ్న14.
కాంతి రసాయన స్మాగ్ ని సాధారణ అనుఘటకాలను తెలపండి.
జవాబు:
ఇది వేడి, తడిలేని సౌర శీతోష్ణస్థితిలో ఏర్పడుతుంది. ఆటోమొబైల్లు (రవాణా వాహనాలు), కర్మాగారాల నుంచి వెలువడే అసంతృప్త హైడ్రోకార్బన్లు, నైట్రోజన్ ఆక్సెడ్ పై సూర్యకాంతి చర్యలో కాంతి రసాయన స్మాగ్ ఏర్పడుతుంది. కాంతిరసాయన స్మాగ్ ఆక్సీకరణ కారకాలు అధిక గాఢతలలో ఉంటాయి. ఈ కారణంగా దీనిని ఆక్సీకరణ సామర్థ్యం గల స్మాగ్ అంటాం. దీనిలో ఫార్మాల్ డిహైడ్, ఎక్రోలిన్, పెరాక్సీ ఎసిటైల్ నైట్రేటు వంటి పదార్థాలు ఉంటాయి.

ప్రశ్న15.
PAN అంటే ఏమిటి ? దీని ప్రభావం ఏమిటి ?
జవాబు:
PAN అనగా పేరాక్సీ ఎసిటైల్ నైట్రేట్. ఇది కాంతి రసాయన స్మాగ్లో ఉంటుంది. దీని ప్రభావం వల్ల కంటి ప్రకోపాలు కలుగుతాయి. లోహాలు, రాళ్ళు, నిర్మాణ వస్తువులు, రబ్బరు, రంగు పూయబడిన ఉపరితలాల క్షీణతను ఇది కలిగిస్తుంది.

ప్రశ్న16.
స్ట్రాటోవరణంలో ఓజోను ఎలా ఏర్పడుతుంది ?
జవాబు:
స్ట్రాటోవరణంలో డై ఆక్సిజన్ (O₂) అణువులపై UV వికిరణాల చర్య ద్వారా ఏర్పడిన క్రియాజన్యమే ఓజోను. అణు ఆక్సిజన్ ను, UV వికిరణాలు, స్వేచ్ఛా స్థితిలో ఉండే ఆక్సిజన్ పరమాణువులు (0) గా వియోగిస్తాయి. ఈ ఆక్సిజన్ పరమాణువులు అణు ఆక్సిజన్తో సంకలనం చెంది ఓజోన్ ను ఏర్పరుస్తాయి.

ప్రశ్న17.
CF₂ Cl₂ ద్వారా ఓజోను తరుగుదల ప్రాప్తించే చర్యలో ఇమిడి ఉండే అంతర్గత రసాయన సమీకరణాలు తెలపండి.
జవాబు:
స్ట్రాటోవరణంలోకి చేరిన క్లోరో ఫ్లోరోకార్బన్ సమ్మేళనాలు UV వికిరణాలచే వియోగం చెందించబడి క్లోరిన్ స్వేచ్ఛా ప్రాతిపదికను విడుదల చేస్తాయి.

ప్రశ్న18.
ఓజోను రంధ్రం అంటే ఏమిటి ? దీనిని తొలిసారిగా ఎక్కడ గమనించారు ?
జవాబు:
స్ట్రాటోవరణంలోని ఓజోన్ పొర తరుగుదలను ఓజోన్ రంధ్రం అంటారు. దీనిని అంటార్కిటికాలోని దక్షిణ ధ్రువప్రాంతంలో మొదటిసారిగా కనుగొన్నారు.

ప్రశ్న19.
చల్లని శుద్ధ నీటిలో కరిగి ఉండే ఆక్సిజన్ పరిమాణం తెలపండి.
జవాబు:
చల్లని శుద్ధనీటిలో కరిగి ఉండే ఆక్సిజన్ పరిమాణం 4-6 మి.గ్రా/లీ.

ప్రశ్న20.
శుద్ధ నీరు, కలుషిత నీరు వీటి BOD విలువలను తెలపండి.
జవాబు:
శుద్ధనీటి BOD విలువ సుమారు 5 ppm. పురపాలక మురుగు నీటి BOD 100 – 4000 ppm విలువ కలిగి ఉంటుంది. 17 ppm కంటే ఎక్కువ BOD విలువ గరిష్ఠ కాలుష్యాన్ని తెలుపుతుంది.

ప్రశ్న21.
నీటిని కాలుష్యానికి గురిచేసే మూడు పారిశ్రామిక రసాయన పదార్థాలను తెలపండి.
జవాబు:

1. పాలిక్లోరినేటెడ్ బైఫినైల్, డిటర్జెంట్లు మరియు ఎరువులు.
2. పరిశ్రమల నుంచి లోహవ్యర్థాలు కూడా నీటిలో చేరవచ్చు.
   అవి కాడ్మియం, మెర్క్యురీ, నికెల్ మొదలైన భారలోహ అయాన్లు.

ప్రశ్న22.
నీటి కాలుష్యానికి కారణమైన వ్యవసాయరంగ రసాయన పదార్థాలను తెలపండి.
జవాబు:

1. ఫాస్ఫేటును కలిగిన ఎరువులు
2. కలుపు మొక్కల నాశనులు
3. మలాథియాన్ వంటి పురుగుమందులు
4. ఎలుకల నివారణకు వాడే ఫాస్ఫైడ్లు.

లఘు సమాధాన ప్రశ్నలు

ప్రశ్న23.
భూవాతావరణంలోని భిన్న భాగాలను తెలపండి.
జవాబు:
వాతావరణాన్ని నాలుగు భాగాలుగా విభజించారు. అవి :

1) ట్రోపో ఆవరణం (0-11 కి.మీ)
2) స్ట్రాటో ఆవరణం (11-50 కి.మీ.)
3) మిసో ఆవరణం (50-85 కి.మీ.)
4) థెర్మో ఆవరణం (85-500 కి.మీ.)

1) ట్రోపో ఆవరణం : ఇది భూ ఉపరితలానికి అతి దగ్గరగా ఉంటుంది. వాతావరణ ద్రవ్యరాశిలో సుమారు 70% ఇది కలిగి ఉంటుంది.
2) స్ట్రాటో ఆవరణం : ఈ ఆవరణం ఓజోన్ పొరను కలిగి ఉంటుంది. సూర్యుని నుంచి వచ్చే అతినీలలోహిత కాంతిని ఇది శోషించుకుంటుంది. తద్వారా భూమిపై అతినీలలోహిత కిరణాలు పడకుండా చేస్తుంది.
3) మిసో ఆవరణం : ఈ ఆవరణం అల్ప మొత్తంలో O₃ ను కలిగి ఉంటుంది.
4) థెర్మో ఆవరణం : ఈ ఆవరణంలో అల్ప సాంద్రతలు, అల్పపీడనాలు ఉంటాయి. O₂, NO మొదలయిన వాయువులు ఈ ఆవరణంలో ఉంటాయి.

ప్రశ్న 24.
సింక్, COD, BOD, TLV పదాలను వివరించండి. (March 2013)
జవాబు:
సింక్ : చాలా కాలం నిలిచి ఉండే కాలుష్యాన్ని తనలో నిలుపుకొని దానితో అన్యోన్య చర్య జరిపే మాధ్యమాన్ని సింక్ అంటారు. ఉదా : వాతావరణ కార్బన్ డై ఆక్సైడుకు సముద్రాలు సింక్లుగా ఉంటాయి.
COD (Chemical Oxygen Demand] : కలుషిత నీటిలో కరిగి ఉన్న కర్బన రసాయన పదార్థాలను ఆక్సీకరణం చెందించడానికి అవసరమయ్యే ఆక్సిజన్ పరిమాణాన్ని రసాయనిక ఆక్సిజన్ అవసరం అంటారు.
BOD (Biochemical Oxygen Demand] : నీటిలో ఉండే కొన్ని ప్రత్యేక సూక్ష్మజీవులు, ) 20°C వద్ద అయిదురోజుల కాలవ్యవధిలో ఉపయోగించుకొనే ఆక్సిజన్ పరిమాణాన్ని జీవరసాయన ఆక్సిజన్ అవసరం అంటారు. శుద్ధనీటి BOD విలువ సుమారు 5 ppm.

ఆరంభ అవధి విలువ : TLV (Threshold Limit Value)
ఆరోగ్యవంతుడైన పారిశ్రామిక కార్మికుడు తన ఎనిమిది గంటల పనికాలంలో వాతావరణంలోని విష స్వభావ కాలుష్యానికి గురైనప్పటికి, తాను ఎటువంటి హానికర ప్రభావానికి గురికాకుండా ఉండటానికి ఆమోదించబడిన విష కాలుష్య కనిష్ఠ పరిమాణాన్ని ఆరంభ అవధి విలువ అంటారు.

ప్రశ్న 25.
గాలిలో చోటు చేసుకొని ఉన్న వాయుస్థితి కాలుష్యాలను తెలిపి, అవి ఎలా ఏర్పడతాయో వివరించండి.
జవాబు:
1) సల్ఫర్ ఆక్సైడులు : SO₂, SO₃
2) నైట్రోజన్ ఆక్సెడులు : NO, NO₂
3) హైడ్రోకార్బన్లు
4) కార్బన్ ఆక్సైడులు : CO, CO₂

1) సల్ఫర్ ఆక్సైడులు : సల్ఫర్ అనుఘటకంగా గల శిలాజ జాతి ఇంధనాలు మండినప్పుడు సల్ఫర్ ఆక్సైడ్లు ఏర్పడతాయి. వీటిలో సర్వ సాధారణంగా ఉండే రసాయన పదార్థం సల్ఫర్ డై ఆక్సైడ్ వాయుస్థితిలో ఉంటుంది.
S + O₂ → SO₂ (వా)
సల్ఫర్ డై ఆక్సైడ్ ఆక్సీకరణం చెంది సల్ఫర్ ట్రై ఆక్సైడ్గా ఆక్సీకరణం చెందుతుంది.
2SO₂ (వా) + O₂ (వా) → 2SO₃ (వా)

2) నైట్రోజన్ ఆక్సైడులు : ఎత్తైన ప్రదేశాలలో మెరుపులు సంభవించినప్పుడు గాలిలోని N₂, O₂ లు చర్యనొంది NO ఏర్పడుతుంది.
N₂ + O₂ → 2NO (వా)
2NO (వా) + O₂ → 2NO₂ (వా)

3) హైడ్రోకార్బన్లు : ఆటోమొబైల్లో వాడే ఇంధనాలు అసంపూర్ణంగా మండినప్పుడు ఇవి ఏర్పడతాయి.

4) కార్బన్ మొనాక్సైడ్ : కార్బన్ అసంపూర్ణ దహనచర్యకు గురైనప్పుడు కార్బన్ మోనాక్సైడ్ (CO) ఏర్పడుతుంది. పూర్తిగా దహనం చెందినప్పుడు కార్బన్ డైఆక్సైడ్ (CO₂) ఏర్పడుతుంది.
C (ఘ) + \(\frac{1}{2}\)O₂ (వా) → CO (వా)
C (ఘ) + O₂ (వా) → CO₂ (వా)

ప్రశ్న 26.
గ్రీన్ హౌస్ ఫలితం అంటే ఏమిటి ? ఇది ఎలా కలుగుతుంది ?
జవాబు:
కార్బన్ డై ఆక్సైడ్, క్లోరోఫ్లోరో కార్బన్లు, నైట్రిక్ ఆక్సైడ్ మరియు నీటిఆవిరులు పరారుణకాంతిని శోషించుకొని మరల భూమిపైకి ఉద్గారం చేస్తాయి. ఈ క్రియ వల్ల భూమి ఉపరితలం వేడెక్కుతుంది. ఈ దృగ్విషయాన్ని భూమి వేడెక్కడం లేదా భౌగోళిక తాపనం అంటారు. ఈ తాపనానికి కారణమయ్యే వాయువులను హరితగృహ వాయువులు అంటారు.

హరితగృహ ప్రభావం యొక్క దుష్ప్రభావాలు :

1. వాతావరణంలో 1°C ఉష్ణోగ్రత పెరిగితే, ధ్రువ ప్రాంతాలలోని మంచు శిఖరాలు కరిగి సముద్రపు నీటిమట్టం పెరుగుతుంది. దీనివల్ల అనేక తీరప్రాంతాలు ముంపునకు గురయ్యే అవకాశం అధికంగా ఉన్నది.
2. భూగోళం వేడెక్కడం వలన సముద్రాలు, నదులు, సరస్సులలోని నీటి బాష్పీభవనం రేటు కూడా పెరుగుతుంది. దీని కారణంగా అకాల వర్షాలు, తుపానులు వచ్చే అవకాశం ఉన్నది.
3. ఉపరితల నీరు వేగంగా బాష్పీభవనం చెందటం వల్ల వ్యవసాయరంగం కూడా దుష్ప్రభావానికి గురి అవుతుంది. వ్యవసాయరంగానికి నీటికొరత అధికమవుతుంది.
   చెట్లను, అడవులను పెంచటం, CFC తయారీని నిలుపుచేయటం మొదలగు చర్యల వల్ల భౌగోళిక తాపనాన్ని నివారించవచ్చు.

ప్రశ్న 27.
ఆమ్ల వర్షం ఏర్పడే విధానాన్ని తెలుపుతూ దానిలోని అంతర్గత రసాయన సమీకరణాలను వివరించండి.
జవాబు:
నైట్రోజన్ మరియు సల్ఫర్ యొక్క ఆక్సెడ్లు (రవాణా మరియు పారిశ్రామికరంగాల నుండి విడుదల చేయబడినవి) వాతావరణంలోకి చేరుతాయి. అంతేకాక ఇవి నీటిలో కరిగి HNO₃ మరియు H₂SO₄ లను తయారుచేస్తాయి. ఈ ఆమ్లాలు నీటిలో కరిగి ఆమ్ల వర్షాలుగా భూమిని చేరుతాయి.
2SO₂ (వా) + O₂ (వా) + 2H₂O (ద్ర) → 2H₂SO₄ (జల)
4NO₂ (వా) + O₂ (వా) + 2H₂O (ద్ర) → 4HNO₃ (జల)

ప్రశ్న 28.
ఆమ్ల వర్షం ద్వారా కలిగే చెడు ప్రభావాలను వివరించండి.
జవాబు:
ఆమ్లవర్షం వల్ల కలిగే చెడు ప్రభావాలు :

1. నేలలో pH విలువ తగ్గి, భూసారం క్షీణించిపోతుంది.
2. కట్టడాల జీవితకాలం అనూహ్యంగా తగ్గిపోతుంది.
3. చలువరాళ్ళతో కట్టిన తాజ్మహల్ యొక్క గాజులా ఉండే నునుపు స్వభావం ఆమ్లవర్ష ప్రభావానికి లోనవుతున్నది.

ప్రశ్న 29.
కాంతి రసాయన స్మాగ్ ఎలా ఏర్పడుతుంది ? ఇది కలుగజేసే చెడు ప్రభావాలు ఏమిటి ?
జవాబు:
కాంతి రసాయన స్మాగ్ ఏర్పడటం : శిలాజ జాతి ఇంధనాలు మండినప్పుడు భిన్న రకాల కాలుష్యాలు భూగోళ ట్రోపోవరణంలోకి ఉద్గారించబడతాయి. ఉద్గారించబడిన కాలుష్యాలలో హైడ్రోకార్బన్లు (మండనటువంటి ఇంధనాలు), నైట్రిక్ ఆక్సైడ్ (NO) లు రెండూ కాలుష్యాలుగా ఉన్నాయి. ఈ కాలుష్యాల గాఢతలు అధిక స్థాయిలకు చేరినప్పుడు అవి సౌరకాంతితో పరస్పర చర్యలో పాల్గొని, ఒక గొలుసు చర్యను జరుపుతాయి. ఈ గొలుసు చర్యలో NO నైట్రోజన్ ఆక్సైడ్గా (NO₂) మారుతుంది. ఈ NO₂ తిరిగి సౌరకాంతి నుంచి శక్తిని గ్రహించి నైట్రిక్ ఆక్సైడ్గాను, స్వేచ్ఛాస్థితిలో ఉండే ఆక్సిజన్గాను విడిపోతుంది.

ఆక్సిజన్ పరమాణువులు రసాయనికంగా చాలా చురుకైనవి. ఇవి గాలిలోని O₂తో సంకలనం చెంది ఓజోన్ ను ఏర్పరుస్తాయి.
O (వా) + O₂ (వా) ⇌ O₃ (వా)

NO, ఓజోన్ తో చర్య జరిపి NO₂ ను తిరిగి ఏర్పరుస్తుంది. NO₂ బ్రౌన్ రంగు వాయువు. ఇది సరైన అధిక గాఢతల వద్ద “మసకత్వం” (chaze) ఏర్పడటానికి దారితీస్తుంది.
NO (వా) + O₃ (వా) → NO₂ (వా) + O₂ (వా)

ఓజోన్ విషవాయువు. NO₂, O₃ లు రెండూ బలమైన ఆక్సీకరణులు. ఇవి కాలుష్య గాలిలో మండే చర్యకు గురి కాకుండా మిగిలి ఉన్న హైడ్రోకార్బన్లతో చర్యజరిపి, ఫార్మాల్డిహైడ్, ఎక్రోలీన్, పెరాక్సీ ఎసిటైల్ నైట్రేట్ (PAN) వంటి రసాయన పదార్థాలను ఏర్పరుస్తాయి. దీనినే కాంతి రసాయన స్మాగ్ అంటారు.

ప్రశ్న 30.
వాతావరణంలో ఓజోన్ పొర తరుగుదల ఎలా ఏర్పడుతుంది ? ఈ ఓజోన్ పొర తరుగుదల వల్ల ప్రాప్తించే హానికరమైన ప్రభావాలను పేర్కొనండి.
జవాబు:
స్ట్రాటోవరణంలో ఉండే ఓజోను సూర్యుని నుంచి వెలువడే అపాయకరమైన అతినీలలోహిత కిరణాల నుంచి మనల్ని రక్షిస్తుంది. దీనిని ఓజోన్ పొర అంటారు. క్లోరోఫ్లోరో కార్బన్లు వాతావరణంలోనికి విడుదల కావడం ఓజోన్ పొర తరుగుదలకు ముఖ్యకారణం.

స్ట్రాటోవరణంలోని UV వికిరణాలచే CFC లు వియోగం చెందించబడి, క్లోరిన్ స్వేచ్ఛాప్రాతిపదికను విడుదల చేస్తాయి.

క్లోరిన్ స్వేచ్ఛా ప్రాతిపదిక స్ట్రాటోవరణంలోని ఓజోన్తో చర్యజరిపి, క్లోరిన్ మోనాక్సైడ్ ప్రాతిపదికలను అణు ఆక్సిజన్ ను విడుదలచేస్తుంది.

క్లోరిన్ మోనాక్సైడ్ ప్రాతిపదిక, పరమాణు స్థితిలో ఉండే ఆక్సిజన్తో చర్యజరిపి అధిక సంఖ్యలో క్లోరిన్ ప్రాతిపదికలను ఏర్పరుస్తుంది.

క్లోరిన్ ప్రాతిపదికలు నిరంతరంగా ఏర్పడి ఓజోను అణువు వియోగచర్యను జరుపుతాయి. కాబట్టి క్లోరిన్ ప్రాతిపదికలను నిరంతరంగా ఉత్పత్తి చేసి, స్ట్రాటోవరణంలోకి చేర్చడానికి CFC లు రవాణా కారకాలుగా పనిచేస్తాయి. ఇవి ఓజోన్ పొరను నాశనం చేస్తాయి. ఒక CFC అణువు, సుమారు ఒక లక్ష O₃ అణువులను నాశనం చేస్తుంది.

ఓజోన్ పొర తరుగుదల ప్రభావాలు :

1. UV కిరణాలు అధిక పరిమాణంలో ట్రోపోవరణంలోకి చేరతాయి.
2. UV కిరణాల వల్ల చర్మం వడిలిపోతుంది.
3. కంటిలో శుక్లాలు ఏర్పడతాయి.
4. చర్మంపై బొబ్బలు వస్తాయి.
5. చర్మక్యాన్సర్ వస్తుంది.
6. చేపల ఉత్పత్తికి నష్టం కలుగుతుంది.

ప్రశ్న 31.
నీటి కాలుష్యానికి కారణమైన పారిశ్రామిక వ్యర్థాలను పేర్కొనండి. త్రాగేనీటి అంతర్జాతీయ ప్రమాణాలను పేర్కొనండి.
జవాబు:

1. పారిశ్రామిక రసాయన పదార్థాలను పాలిక్లోరినేటెడ్ బై ఫినైల్ను ఉపయోగించే పరిశ్రమల నుండి వెలువడే వ్యర్థాల వల్ల నీటికాలుష్యం జరుగుతుంది.
2. ఎరువుల పరిశ్రమల నుండి వెలువడే ఫాస్ఫేటులు నీటిలోకి చేరితే ఆల్గేల అభివృద్ధి జరుగుతుంది. అవి నీటిలోని ఆక్సిజన్ గాఢతను తగ్గించేస్తాయి.
3. చాలా నీటివనరులను పెట్రోలియం ఉత్పన్నాలు కాలుష్యానికి గురిచేస్తున్నాయి.
4. పేపరు మరియు బట్టల మిల్లుల నుండి వెలువడే వ్యర్థాల వల్ల నీటికాలుష్యం జరుగుతుంది.
5. ఆమ్లాలు, క్షారాలు, డిటర్జెంట్లు, ప్రేలుడు పదార్థాలు, అద్దకాలు, చీడ నాశినులు, ఎరువులు, సిలికోనులు, ప్లాస్టిక్ లు తయారుచేసే పరిశ్రమల నుండి వెలువడే వ్యర్థాలు నీటికాలుష్యానికి కారణభూతాలవుతున్నాయి.

త్రాగునీటి అంతర్జాతీయ ప్రమాణాలు :

ఫ్లోరైడ్ : 1 ppm నైట్రేటు – 50 ppm
సల్ఫేటు : < 500 ppm లెడ్ – 50 ppb

ప్రశ్న 32.
పర్యావరణ కాలుష్యాన్ని నివారించడానికి అవలంబించే హరిత రసాయనశాస్త్రంలోని ప్రణాళికలను సవివరంగా తెలపండి.
జవాబు:
రసాయనశాస్త్రం మరియు ఇతర శాస్త్ర విభాగాలను ఉపయోగించి వాటి అవగాహన, సూత్రాలతో సాధ్యమైనంతవరకు పర్యావరణంలో కాలుష్యం రాకుండా చూడడం గురించి చెప్పేదే హరిత రసాయనశాస్త్రం.
పరిశ్రమలలో వ్యర్థ పదార్థాలు ఏర్పడకుండా లేదా అతికొద్ది మాత్రంలో ఏర్పడే చర్యలను హరిత రసాయన చర్యలు అంటారు. ఈ దిశగా ఆలోచించి హరిత రసాయనశాస్త్రానికి కొన్ని సూత్రాలను ఏర్పరిచారు. అవి :

1. వ్యర్థ అనుజనిత పదార్థాల పరిమాణాన్ని కనిష్ఠ స్థాయికి తగ్గించాలి.
2. విషరహిత, ప్రమాదరహిత క్రియాజనకాలను ఎన్నుకోవాలి.
3. అత్యధిక దిగుబడి వచ్చే విధంగా చర్యాపరిస్థితులను స్థిరీకరించాలి.
4. కాలుష్యరహిత మరియు సురక్షితమైన ద్రావణిని ఉపయోగించాలి.
5. వీలైనచోట సాధారణ వేడిచేసే పద్ధతులు బదులు మైక్రోతరంగాలతో గాని, అతిధ్వనులతో గాని వేడిచేయాలి. ఎందుకంటే ఆ పద్ధతిలో రసాయన చర్యలు హరిత చర్యలుగా జరపబడతాయి.

దైనందిన జీవితంలో హరిత రసాయనశాస్త్రం :

1. వస్త్రాల నిర్జల శుద్ధిక్రియ (Dry Cleaning) : నిర్జల పద్ధతిలో వస్త్రాలను శుభ్రంచేసే ప్రక్రియలో టెట్రాక్లోరో ఈథేన్ ను (Cl₂ C = CCl₂) ఉపయోగించేవారు. ఈ పదార్ధం భూగర్భజలాలను మలినం చేస్తుంది. అంతేకాక క్యాన్సర్ కారకం. దీనికి బదులు ప్రస్తుతం ద్రవరూపంలో ఉన్న కార్బన్ డై ఆక్సైడ్కు డిటర్జెంటును కలిపి ఏర్పడిన మిశ్రమం ద్వారా శుభ్రంచేసే ప్రక్రియను జరుపుతున్నారు.
2. వస్త్రాలను వివర్ణం చేయడానికి, లాండ్రి ప్రక్రియలలో హైడ్రోజన్పరాక్సైడ్ను (H₂O₂) వాడుతున్నారు.
3. కాగితాలను వివర్ణం చేయడం : కాగితాలను వివర్ణం చేయడానికి పూర్వం క్లోరిన్ వాయువును ఉపయోగించేవారు. ఈ రోజుల్లో హైడ్రోజన్ పెరాక్సైడును, హైడ్రోజన్ పెరాక్సైడ్ వివర్ణ సామర్థ్యాన్ని పెంచే ఉత్ప్రేరకాన్ని దానితో కలిపి వాడుతున్నారు. ‘
4. రసాయన పదార్థాల సంశ్లేషణం : 90% దక్షతతో జలమాధ్యమంలో అయానిక ఉత్ప్రేరకం సమక్షంలో ఈథేన్ ను ఏక అంచె ఆక్సీకరణం చర్యకు గురిచేసి ఇథనాల్ (ఎసిటాల్డిహైడ్, (CH₃CHO) ను తయారుచేస్తున్నారు.
   

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 33.
పర్యావరణ కాలుష్యం అంటే ఏమిటి ? ఈ కాలుష్యం ఎన్ని రకాలు ?
జవాబు:
మొక్కలు, జంతువులు, మానవులపై హానికరమైన ప్రభావం ప్రదర్శిస్తూ పరిసరాలలో చోటుచేసుకొని ఉండే, అవాంఛనీయ మార్పులు ప్రదర్శించే ప్రభావాన్నే పర్యావరణ కాలుష్యం అంటారు.
పారిశ్రామికీకరణ కారణంగాను, జనాభా పెరుగుదల కారణంగాను ఎన్నో వ్యర్థ పదార్థాలు పర్యావరణంలోనికి ప్రవేశించుటవలన పర్యావరణం కాలుష్యం అవుతోంది.

పర్యావరణ కాలుష్యానికి కారణాలు :

1. జనాభా పెరుగుదల, సహజ వనరుల తరుగుదల
2. పారిశ్రామికీకరణ
3. అడవులను నరికివేయుట
4. పట్టణీకరణ

కాలుష్య రకాలు :

1. వాయు కాలుష్యం
2. జల కాలుష్యం
3. భూమి కాలుష్యం
4. ధ్వని కాలుష్యం
5. రేడియోధార్మిక కాలుష్యం

వాయు కాలుష్యం :

సల్ఫర్ ఆక్సైడులు : సల్ఫర్ అనుఘటకంగా గల శిలాజ జాతి ఇంధనాలు మండినప్పుడు సల్ఫర్ ఆక్సైడ్లు ఏర్పడతాయి.

SO₂ వాయుస్థితిలో ఉంటుంది. శ్వాసకోశ వ్యాధులు, కళ్ల వెంబడి నీరు కారడం, కళ్లు ఎర్రబడటం వంటివి, సల్ఫర్ డైఆక్సైడ్ కళ్లకు కలిగించిన ప్రకోపనం ద్వారా వస్తుంది.

S (ఘ) + O₂ (వా) → SO₂ (వా) ;
2 SO₂ (వా) + O₂ (వా) → SO₃ (వా)
SO₂ (వా) + O₃ (వా) → SO₃ (వా) + O₂ (వా)
SO₂ (వా) + H₂O₂ (ద్ర) → H₂SO₄ (ద్ర)

నైట్రోజన్ ఆక్సైడ్లు : రవాణా వాహనాలలో శిలాజ జాతి ఇంధనాలు మండించినప్పుడు, నైట్రిక్ ఆక్సైడ్ ఏర్పడుతుంది.

N₂ (వా) + O₂ (వా) → 2NO (వా)
NO తక్షణమే ఆక్సిజన్తో చర్య జరిపి NO₂ ను ఏర్పరుస్తుంది.
స్ట్రాటో ఆవరణంలో నైట్రిక్ ఆక్సైడ్ ఓజోన్ తో చర్య జరిపినపుడు NO₂ ఏర్పడుతుంది.
2NO (వా) + O₃ (వా) → NO₂ (వా) + O₂ (వా)
2NO (వా) + O₂ (వా) → 2NO₂ (వా)
అధిక పరిమాణాలలో ఉండే NO₂ మొక్కల ఆకులను పాడుచేసి, కిరణజన్య సంయోగక్రియ రేటును తగ్గిస్తుంది.

కార్బన్ మోనాక్సైడ్ : కార్బన్ అసంపూర్ణ దహనచర్యకు గురైనప్పుడు CO ఏర్పడుతుంది. ఆటోమొబైల్ల నుంచి వెలువడే బహిష్కృతాల ద్వారా ఇది గాలిలోకి చేరుకుంటుంది. ఇది రక్తంలోని హీమోగ్లోబిన్ తో బంధించబడి కార్బాక్సీ హీమోగ్లోబిన్ ను ఏర్పరుస్తుంది. రక్తం యొక్క ఆక్సిజన్ రవాణా సామర్ధ్యం విపరీతంగా తగ్గిపోతుంది.

కార్బన్ డై ఆక్సైడ్ : అడవులను నరికివేయడం, శిలాజ జాతి ఇంధనాలను మండించడం మొదలైన చర్యల ద్వారా వాతావరణంలో CO₂స్థాయి పెరిగి, వాతావరణ సమతుల్యత లోపిస్తుంది. గాలిలో పెరిగిన CO₂ పరిమాణం కారణంగా భూగోళం వేడెక్కడం జరుగుతుంది.

నీటి కాలుష్యం : మానవ కార్యకలాపాల ద్వారా నీటి కాలుష్యం ఏర్పడుతుంది. భిన్నమార్గాల ద్వారా నీటి కాలుష్యం ఉపరితల నీటి వనరులను, భూగర్భ నీటివనరులను చేరుతుంది. COD, BOD విలువల ద్వారా నీటి కాలుష్య పరిమాణాన్ని నిర్ణయించవచ్చు.

ప్రశ్న 34.
కింది వాటిని వివరంగా తెలపండి.
(a) భూగోళం వేడెక్కడం
(b) ఓజోను తరుగుదల
(c) ఆమ్ల వర్షం
(d) యూట్రోఫికేషన్
జవాబు:
(a) భూగోళం వేడెక్కడం కార్బన్ డై ఆక్సైడ్, క్లోరోఫ్లోరో కార్బన్లు, నైట్రిక్ ఆక్సైడ్ మరియు నీటిఆవిరులు పరారుణ కాంతిని శోషించుకొని మరల భూమిపైకి ఉద్గారం చేస్తాయి. ఈ క్రియ వల్ల భూమి ఉపరితలం వేడెక్కుతుంది. ఈ దృగ్విషయాన్ని భూమి వేడెక్కడం లేదా భౌగోళిక తాపనం అంటారు. ఈ తాపనానికి కారణమయ్యే వాయువులను హరిత గృహ వాయువులు అంటారు.

హరిత గృహ ప్రభావం యొక్క దుష్ప్రభావాలు :

1. వాతావరణంలో 1°C ఉష్ణోగ్రత పెరిగితే, ధ్రువ ప్రాంతాలలోని మంచు శిఖరాలు కరిగి, సముద్రపు నీటి మట్టం పెరుగుతుంది. దీనివల్ల అనేక తీర ప్రాంతాలు ముంపునకు గురయ్యే అవకాశం అధికంగా ఉన్నది.
2. భూగోళం వేడెక్కడం వలన సముద్రాలు, నదులు, సరస్సులలోని నీటి బాష్పీభవనం రేటు కూడా పెరుగుతుంది. దీని కారణంగా అకాల వర్షాలు, తుపానులు వచ్చే అవకాశం ఉన్నది.
3. ఉపరితల నీరు వేగంగా బాష్పీభవనం చెందటం వల్ల వ్యవసాయరంగం కూడా దుష్ప్రభావానికి గురవుతుంది. వ్యవసాయ రంగానికి నీటి కొరత అధికమౌతుంది.
   చెట్లను, అడవులను పెంచటం, CFC తయారీని నిలుపుచేయటం మొ॥గు చర్యల వల్ల భౌగోళిక తాపనాన్ని నివారించవచ్చు.

(b) ఓజోను తరుగుదల : క్లోరోఫ్లోరో కార్బన్లు త్వరితంగా వాతావరణంలోని పైపొరను చేరుకొని, అక్కడి UV వికిరణాన్ని శోషించుకొని, విఘటనం చెంది క్లోరిన్ పరమాణువులను ఇస్తాయి.

స్వేచ్ఛా స్థితిలోని Cl^* పరమాణువు ఓజోన్ ను విఘటనం చెందించి O₂ ను ఇస్తుంది.

దీనివల్ల ఓజోన్ సాంద్రతలో క్షీణత కనిపిస్తుంది. ఈ క్షీణత కారణంగా ఓజోన్ పొరకు రంధ్రాలు ఏర్పడతాయి. ఈ రంధ్రాల ద్వారా అతినీలలోహిత కిరణాలు భూమిని చేరి, మానవులకు అనేక సమస్యలను సృష్టిస్తున్నాయి. కంటిలో శుక్లాలు, చర్మ క్యాన్సర్ వంటి అనారోగ్యాలను కలుగచేస్తాయి.

(c) ఆమ్ల వర్షం : నైట్రోజన్ మరియు సల్ఫర్ యొక్క ఆక్సైడ్లు (రవాణా మరియు పారిశ్రామిక రంగాల నుండి విడుదల చేయబడినవి) వాతావరణంలోకి చేరుతాయి. అంతేకాక ఇవి నీటిలో కరిగి HNO₃ మరియు H₂SO₄లను తయారు చేస్తాయి. ఈ ఆమ్లాలు నీటిలో కరిగి, ఆమ్ల వర్షాలుగా భూమిని చేరుతాయి.
2SO₂ (వా) + O₂ (వా) + 2H₂O (ద్ర) → 2H₂SO₄ (జల)
4NO₂ (వా) + O₂ (వా) + 2H₂O (ద్ర) → 4HNO₃ (జల)

ఆమ్ల వర్ష ప్రభావాలు :

1. నేలలోని pH విలువ తగ్గి, భూసారం క్షీణించిపోతుంది.
2. కట్టడాల జీవితకాలం అనూహ్యంగా తగ్గిపోతుంది.
3. చలువ రాళ్ళతో కట్టిన తాజ్మహల్ గాజులా ఉండే నునుపు స్వభావం ఆమ్ల వర్ష ప్రభావానికి లోనవుతున్నది.

(d) యూట్రోఫికేషన్ : నీటి వనరులైన సరస్సులు, చెరువులలోకి వ్యవసాయ, పారిశ్రామిక రంగాల నుంచి వచ్చిన కర్బన రసాయన పదార్థాలు చేరితే ఆ నీటికి పోషక గుణం పెరుగుతుంది. ఇది విపరీతంగా ఆల్గే పెరుగుదలకు దోహదం చేస్తుంది. ఇలా పోషక గుణం పెరిగిన సరస్సును “యూట్రోఫిక్ సరస్సు” అనీ, ఈ దృగ్విషయాన్ని “యూట్రోఫికేషన్” అని అంటారు.

ప్రశ్న 35.
హరిత రసాయనశాస్త్రం పర్యావరణ కాలుష్యాన్ని నివారిస్తుంది. వివరించండి.
జవాబు:
పర్యావరణానికి ఏ మాత్రం హాని కలుగకుండా రసాయన పదార్థాలను సంశ్లేషించుటనే హరిత రసాయనశాస్త్రం అంటారు.
పాల్.టి. అనస్టాస్ కృషి ఫలితంగా రసాయనశాస్త్రానికి సంబంధించి కొన్ని ప్రాథమిక నియమాలు ఏర్పరచబడినాయి. ఈ నియమాలను పాటిస్తే కాలుష్యాన్ని నివారించవచ్చు.

1. వ్యర్థ పదార్థాలను నివారించాలి లేదా కనిష్ఠ స్థాయికి తగ్గించాలి.
   రసాయన సంశ్లేషణను వ్యర్థ అనుజనిత పదార్థం ఏర్పడని విధంగా సూత్రీకరించాలి. లేదా అట్టి పదార్థం కనిష్ఠ స్థాయిలో ఏర్పడే విధంగా సూత్రీకరించాలి.
2. క్రియాజనకాలను, కారకాలను గరిష్ఠ స్థాయిలో ఉత్పన్నాలుగా మార్చాలి.
   ఉదా : డీల్స్ – ఆల్డర్ చర్య.
3. ఆరోగ్యానికి హానికర లేదా ప్రమాదకర ఉత్పన్నాలను నిరోధించాలి.
4. తక్కువశక్తితో (వేడి . మొ॥) మరియు తక్కువ సమయంలో సంశ్లేషణ పూర్తి అయ్యే విధంగా రసాయన చర్యను ఎన్నుకోవాలి.
5. సంశ్లేషణలో బాష్పశీల మరియు కర్బన ద్రావణులను వీలైనంత వరకు నివారించాలి. ఎందుకంటే ఇట్టి ద్రావణులు తక్కువ ఉష్ణోగ్రత వద్ద ఆవిరై వాతావరణాన్ని కలుషితం చేస్తాయి. బెంజీన్ వంటి కొన్ని ద్రావణులైతే క్యాన్సర్ కారకాలు. అందుకే నీటిలో జరిపే చర్యలు చాలా క్షేమకరం.

కొన్నిసార్లు అసలు ద్రావణమే లేకుండా ఘనస్థితిలో రసాయనచర్యలు జరపగలిగి ఉంటాయి. ఆ విధమైన సంశ్లేషణత హరిత సంశ్లేషణత అవుతుంది.
ఈ నియమాలను పాటిస్తే కాలుష్యం నివారించబడుతుంది.

అదనపు ప్రశ్నలు

ప్రశ్న 1.
నీటిలో ఫ్లోరైడ్ ఉండటం వల్ల ఏం జరుగుతుంది ?
జవాబు:
త్రాగేనీటిలో ఫ్లోరైడ్ గాఢత 2 ppm మించకుండా ఉంటే అది హానికరం కాదు. అదే గాఢత 2 ppm దాటితే ఆరోగ్యానికి హానికరం. ఒకవేళ ఫ్లోరైడ్ గాఢత అధికంగా కలిగిన నీటిని త్రాగితే అందులోని F^– అయానులు మన శరీరంలోని ఎముకలు, దంతాలలోని కాల్షియంతో చర్య జరిపి కాల్షియం ఫ్లోరైడులను తయారుచేస్తాయి.
Ca + F₂ → CaF₂
ఈ చర్య వలన దంతాలు పసుపు వర్ణంలోకి మారతాయి. అంతేకాక శరీరంలోని ఎముకలు బలహీనపడతాయి.

ప్రశ్న 2.
నీటిలో ఫ్లోరైడులను తొలగించే నల్గొండ పద్ధతిని వ్రాయండి.
జవాబు:
నల్గొండ పద్ధతి : ఈ పద్ధతిలో విరంజనచూర్ణం, సున్నం, పటిక ఇదే క్రమంలో నీటిలో కలిపి ఆ నీటిని కొంతకాలం నిలవ ఉంచుతారు. నీటిలోని ఫ్లోరైడ్ అయాన్లు కాల్షియం అమోనియం ఫ్లోరైడ్ అని సంక్లిష్టంగా అవక్షేపం చెందుతాయి. దీనిని వడపోస్తారు. ఏర్పడ్డ శుద్ధ నీటిని అవసరాలకు ఉపయోగిస్తారు.

ప్రశ్న 3.
పారిశ్రామిక వ్యర్థాలు గురించి వ్రాయండి.
జవాబు:
పారిశ్రామిక ఘనస్థితి వ్యర్థపదార్థాలను జీవవిచ్ఛిన్నశీలత గల పదార్థాలుగాను, జీవ విచ్ఛిన్నశీలతలేని వ్యర్థపదార్థాలుగాను వర్గీకరిస్తారు.
పత్తిమిల్లులు, ఆహారపదార్థాలను తయారుచేసే యూనిట్లు, కాగితపు మిల్లులు జీవవిచ్ఛిన్నశీలత గల వ్యర్థపదార్థాలను ఉత్పన్నం చేస్తాయి.

విద్యుత్ను ఉత్పత్తి చేయడంలో ఫ్లై బూడిదను విడుదల చేసే యంత్రాగారాలు, బ్లాస్ట్ బల్బు నుంచి వెలువడే లోహమలం, జీవవిచ్ఛిన్నశీలత లేని వ్యర్థపదార్థం.
జీవవిచ్ఛిన్నశీలతలేని పారిశ్రామిక ఘనస్థితి వ్యర్థపదార్థాలను సరైన క్రమమైన పద్ధతుల ద్వారా పరిష్కరించకపోతే అవి పర్యావరణానికి ప్రమాదాన్ని కల్గిస్తాయి.

ప్రశ్న 4.
కొన్ని సేంద్రియ కాలుష్య కారకాలు తెలపండి.
జవాబు:
మలాథియాన్, DDT, క్లోరోఫినాక్స్ వర్ణసమ్మేళనాలు, ఫినైల్ మెర్క్యురీ ఎసిటేట్ మొ||నవి..

ప్రశ్న 5.
పర్యావరణాన్ని కాలుష్యం నుంచి ఎలా కాపాడుకోవచ్చు ?
జవాబు:
పర్యావరణం కలుషితం కాకుండా ఉండాలంటే ఈ క్రింది జాగ్రత్తలు తీసుకోవాలి.

1. వ్యర్థ పదార్థాల నిర్వహణ.
2. క్రిమిసంహారక మందులు, తెగుళ్ళ మందులు తయారుచేసే పరిశ్రమలలో వెలువడే వ్యర్థ పదార్థాలను జీవ పతనం చెందించాలి.
3. హరిత రసాయనశాస్త్రాన్ని విస్తరింపచేయటం.
4. అడవులను పెంచాలి.
5. సంప్రదాయ ఇంధనాలకు బదులుగా సంప్రదాయేతర ఇంధనాల ఉత్పత్తిని, వాడుకను ఎక్కువ చేయాలి. సౌరశక్తిని నిలువచేసే విధానాలపై దృష్టి సారించాలి.
6. ప్లాస్టిక్లను జీవపతనం చెందించాలి.
7. అధిక జనాభాను అరికట్టాలి.
8. మామూలు రసాయన పద్ధతులకు బదులుగా జీవసాంకేతిక పద్ధతులను పరిశ్రమలలో ఉపయోగించాలి.
9. ప్రజలకు పర్యావరణ కాలుష్యం వల్ల జరిగే నష్టాలను తెలియజేయడం, పర్యావరణాన్ని పరిశుభ్రంగా ఉంచాల్సిన అవసరం తెలియజేయడం.

Students must practice these TS Intermediate Maths 1A Solutions Chapter 9 Hyperbolic Functions Ex 9(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Hyperbolic Functions Solutions Exercise 9(a)

I.
Question 1.
If sinh x = \(\frac{3}{4}\) find cosh (2x) and sinh (2x). (May 2014, Mar.’14, ’12)
Answer:
Given sinh x = \(\frac{3}{4}\)
and we have cosh² x – sinh² x = 1

Question 2.
If sinhx = 3, then show that
x = log_e(3 + √10) (Board New Model Paper).
Answer:
Given sin hx = 3
⇒ x = sinh^-1 3 = log_e (3 + \(\sqrt{3^2+1}\))
= log_e (3 + √10)
(∵ sinh x = log (x + \(\sqrt{x^2+1}\)) ∀ x ∈ R)

Question 3.
Prove that
(i) tanh (x – y) = \(\frac{\tanh x-\tanh y}{1-\tanh x \tanh y}\)
Answer:

(ii) coth (x – y) = \(\frac{{coth} x \cdot {coth} y-1}{{coth} y-{coth} x}\)
Answer:

Question 4.
Prove that
(i) (cosh x – sinh x)ⁿ
= cosh (nx) – sinh (nx) for any n ∈R.
Answer:

(ii) (cosh x + sinh x)ⁿ = cosh (nx) + sinh (nx) for any n ∈ R.
Answer:

Question 5.
Prove that
\(\frac{\tanh x}{{sech} x-1}+\frac{\tanh x}{{sech} x+1}\) = -2cosechx for x ≠ 0.
Answer:

Question 6.
Prove that \(\frac{\cosh x}{1-\tanh x}+\frac{\sinh x}{1-{coth} x}\) = sinhx + coshx for x ≠ 0.
Answer:

Question 7.
For any x ∈ R, prove that cosh⁴ x – sinh⁴ x = cosh 2x.
Answer:
cosh⁴ x – sinh⁴ x
= (cosh² x)² – (sinh² x)²
= (cosh² x + sinh² x) (cosh² x – sinh² x)
= cosh 2x (1) = cosh 2x

Question 8.
If u = log_e \(\left\{\tan \left(\frac{\pi}{4}+\frac{\theta}{2}\right)\right\}\) and if cos θ > 0 then prove that cosh u = sec θ
Answer:

Telangana TSBIE TS Inter 1st Year Chemistry Study Material 11th Lesson P బ్లాక్ మూలకాలు – 14వ గ్రూప్ Textbook Questions and Answers.

TS Inter 1st Year Chemistry Study Material 11th Lesson P బ్లాక్ మూలకాలు – 14వ గ్రూప్

అత్యంత లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 1.
గ్రూపు 14 మూలకాల ఆక్సీకరణ స్థితులలో మార్పును చర్చించండి.
జవాబు:
14వ గ్రూపు మూలకాల బాహ్యతమ కర్పరంలో 4 ఎలక్ట్రానులు ఉన్నాయి. ఈ మూలకాలు కనబరచే సాధారణ ఆక్సీకరణ స్థితులు +4, + 2. కార్బన్ ఋణ ఆక్సీకరణ స్థితుల్ని కూడా చూపుతుంది.
+ 4 ఆక్సీకరణ స్థితిలో ఉన్న సమ్మేళనాలు సమయోజనీయ స్వభావం కలవిగా ఉంటాయి. భారతర మూలకాలలో +2 ఆక్సీకరణ స్థితిని చూపే ప్రవృత్తి పెరిగే క్రమం Ge < Sn < Pb. కార్బన్, సిలికాన్లు తరచుగా +4 ఆక్సీకరణ స్థితిని చూపుతాయి. జెర్మేనియం స్థిర సమ్మేళనాలను +4 స్థితిలో ఏర్పరుస్తుంది. టిన్ రెండు (+2, +4) ఆక్సీకరణ. స్థితులలోను సమ్మేళనాలను ఏర్పరుస్తుంది. లెడ్ సమ్మేళనాలు +2 స్థితిలో స్థిరమైనది.

ప్రశ్న 2.
క్రింది సమ్మేళనాలు నీటితో ఎలా ప్రవర్తిస్తాయి.
a) BCl₃
b) CCl₄
జవాబు:
a) BCl₃ నీటితో చర్య పొంది H₃BO₃ ను ఏర్పరుస్తుంది.
BCl₃ + 3 H₂O → H₃BO₃ + 3HCl
b) CCl₄ నీటితో చర్య పొందదు. నీటిలో కరుగదు. వేరే ప్రావస్థగా వుంటుంది.

ప్రశ్న 3.
BCl₃, SiCl₄ ఎలక్ట్రాన్ కొరత ఉన్న సమ్మేళనాలా ? వివరించండి.
జవాబు:
BCl₃ లో బోరాన్ బాహ్య కర్పరంలో ఎలక్ట్రాన్ అష్టకం లేదు. కనుక అది ఎలక్ట్రాన్ కొరత గల సమ్మేళనం.
SiCl₄ లోని Si కు బాహ్య కర్పరంలో ఎలక్ట్రాన్ అష్టకం ఉన్నది. అది ఎలక్ట్రాన్ కొరత గల సమ్మేళనం కాదు.

ప్రశ్న 4.
క్రింది వాటిలో కార్బన్ సంకరీకరణాన్ని సూచించండి.
a) C\(\mathrm{O}_3^{-2}\)
b) వజ్రం
c) గ్రాఫైట్
d) పుల్లరీన్
జవాబు:
a) C\(\mathrm{O}_3^{-2}\) : …….. sp² సంకరీకరణం
b) వజ్రం : ………… sp³ సంకరీకరణం
c) గ్రాఫైట్ : ……… sp² సంకరీకరణం
d) పుల్లరీన్ : …….. sp² సంకరీకరణం

ప్రశ్న 5.
CO ఎందుకు విషపూరితమైనది ? (March 2013)
జవాబు:
CO విషపూరితమైనది. అది రక్తంలోని హిమోగ్లోబిన్ తో కలిసి స్థిరమైన సంక్లిష్టం ఏర్పరుస్తుంది. అందువల్ల హీమోగ్లోబిన్

కార్బాక్సీ హిమోగ్లోబిన్ ఆక్సీహిమోగ్లోబిన్ కన్నా 300 రెట్లు అధిక స్థిరమైనది.

ప్రశ్న 6.
రూపాంతర (allotropy) అంటే ఏమిటి ? స్పటిక రూపంలోని కార్బన్ భిన్న రూపాంతరాలను తెలపండి. (March 2013)
జవాబు:
ఒకే మూలకం భిన్న భౌతిక రూపాలలో లభించుటను రూపాంతరత అంటారు.
కార్బన్ మూడు స్ఫటిక రూపాంతరాలలో లభిస్తోంది. అవి వజ్రం, గ్రాఫైట్, ఫుల్లరిన్.

ప్రశ్న 7.
కింది ఆక్సెడులను తటస్థ, ఆమ్ల, క్షార, ద్విస్వభావం గల వాటిగా వర్గీకరించండి.
a) CO
b) B₂O₃
c) SiO₂
d) CO₂
e) Al₂O₃
f) PbO₂
g) Tl₂O₃
జవాబు:
a) CO – తటస్థ
b) B₂O₃ – ఆమ్ల
c) SiO₂ – ఆమ్ల
d) CO₂ – ఆమ్ల
e) Al₂O₃ – ద్విస్వభావ
f) PbO₂ – ద్విస్వభావ
g) Tl₂O₃ – క్షార
e) Al₂O₃ – ద్విస్వభావ
f) PbO₂ – ద్విస్వభావ
g) Tl₂O₃ – క్షార

ప్రశ్న 8.
మనిషి (కృత్రిమంగా) తయారుచేసిన ఏవైనా రెండు సిలికేట్ల పేర్లు రాయండి.
జవాబు:

1. గాజు
2. సిమెంట

ప్రశ్న 9.
గ్రూపు 14 మూలకాల బాహ్య ఎలక్ట్రాన్ విన్యాసాన్ని రాయండి.
జవాబు:
గ్రూపు 14 మూలకాలు కార్బన్ (C); సిలికాన్ (Si); జెర్మేనియం (Ge); టిన్ (Sn) మరియు లెడ్ (Pb).
వాటి ఎలక్ట్రాన్ విన్యాసాలు :
కార్బన్ : 1s²2s²2p² (Z = 6)
సిలికాన్ : 1s²2s²2p⁶3s²3p² (Z = 14)
జెర్మేనియం : 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p² (Z = 32)
టిన్ : 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁶4d¹⁰5s²5p² (Z = 50)
లెడ్ : 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁶4d¹⁰4f¹⁴5s²5p⁶5d¹⁰6s²6p² (Z = 82)
గ్రూపు 14 మూలకాల సాధారణ ఎలక్ట్రాన్ విన్యాసం ns²np².

ప్రశ్న 10.
గ్రాఫైట్ కందెనలాగా ఎట్లా పనిచేస్తుంది ?
జవాబు:
గ్రాఫైట్ ద్వి జ్యామితీయ పొరల నిర్మాణం కలిగి ఉంటుంది. అంతేగాక ఈ పొరలు ఒకదానిపై ఒకటి జారుతూ ఉంటాయి. అందుకనే గ్రాఫైట్ కందెనగా పనిచేస్తుంది.

ప్రశ్న 11.
గ్రాఫైట్ మంచి వాహకం – వివరించండి.
జవాబు:
గ్రాఫైట్ ప్రతి కార్బన్ పరమాణువు వద్ద సంకరీకరణంలో పాల్గొనని p – ఆర్బిటాల్లో ఎలక్ట్రాన్ ఉంది. దీనినే స్వేచ్ఛా ఎలక్ట్రాన్ అంటారు. ఒక్కొక్క కార్బన్ పరమాణువు మూడు ఆసన్న కార్బన్ sp² సంకర ఆర్బిటాల్లను ఉపయోగించుకొని మూడు సిగ్మా బంధాలను ఏర్పరుస్తుంది. నాలుగవ ఎలక్ట్రాన్ π బంధాన్ని ఏర్పరుస్తుంది. ఈ ఎలక్ట్రాన్లు మొత్తం పొర అస్థానీకృతం అవుతాయి. ఈ ఎలక్ట్రానులు చలనంలో ఉంటాయి. అందువల్ల గ్రాఫైట్ మంచి విద్యుద్వాహకం.

ప్రశ్న 12.
సిలికా నిర్మాణాన్ని వివరించండి.
జవాబు:
సిలికాన్ డై ఆక్సైడును సిలికా అంటారు. సిలికాన్ డై ఆక్సైడ్ సమయోజనీయ, త్రిమితీయ అల్లిక గల ఘనం. ఇందులో సిలికాన్ పరమాణువు సమయోజనీయ బంధంతో టెట్రా హెడ్రల్ రీతిలో నాలుగు ఆక్సిజన్ పరమాణువులతో కలిసి ఉంటుంది. ప్రతి ఆక్సిజన్ పరమాణువు ఇంకొక సిలికాన్ పరమాణువుతో సమయోజనీయ బంధంతో ఉంటుంది. మొత్తం స్ఫటికాన్ని బృహత్ అణువుగా భావించవచ్చు.

ప్రశ్న 13.
“సంశ్లేషణ వాయువు” అంటే ఏమిటి ?
జవాబు:
వేడిగానున్న కోక్ మీదకు నీటి ఆవిరిని పంపడం ద్వారా వ్యాపార పద్ధతిలో CO, H₂ ల మిశ్రమాన్ని తయారుచేస్తారు. ఏర్పడిన CO, H₂ ల మిశ్రమాన్ని సంశ్లేషణ వాయువు అంటారు.

ప్రశ్న 14.
“ప్రొడ్యూసర్ వాయువు” అంటే ఏమిటి ?
జవాబు:
CO, N₂ ల మిశ్రమాన్ని ప్రొడ్యూసర్ గ్యాస్ అంటారు. దీని సంఘటనం CO = 33%, N₂ = 64%, CO₂ మరియు
H₂ = 2.5%

ప్రశ్న 15.
వజ్రానికి అధిక ద్రవీభవన ఉష్ణోగ్రత ఉంటుంది. వివరించండి.
జవాబు:
వజ్రం త్రిజ్యామితీయ బృహదణు నిర్మాణం కలిగి ఉంటుంది. ప్రతి కార్బన్ sp³ సంకరీకరణం చెందుతుంది. ప్రతి కార్బన్ నాలుగు ఇతర కార్బన్ పరమాణువులతో sp³ సంకర ఆర్బిటాళ్ళతో బంధాలను ఏర్పరుస్తుంది. ఈ నిర్మాణం ప్రాదేశికంగా వ్యాపించి కార్బన్ పరమాణువులతో దృఢమైన త్రిమితీయ అల్లికను ఏర్పరుస్తుంది. ఇలా వ్యాపించి ఉన్న సమయోజనీయ బంధాలను విచ్ఛిన్నం చేయడం చాలా శక్తితో కూడుకున్న పని. అందువల్ల వజ్రానికి అధిక ద్రవీభవన ఉష్ణోగ్రత ఉంటుంది.

ప్రశ్న 16.
కిరణజన్య సంయోగ క్రియలో CO₂ పాత్ర ఏమిటి ?
జవాబు:
కిరణజన్య సంయోగక్రియ ద్వారా పచ్చటి చెట్లు వాతావరణంలోని కార్బన్ డై ఆక్సైడ్ను గ్లూకోజ్ వంటి కార్బోహైడ్రేటులుగా మారుస్తాయి.

ప్రశ్న 17.
హరిత గృహ ప్రభావాన్ని ఏ విధంగా CO₂ పెంచుతుంది ?
జవాబు:
శిలాజ ఇంధనాల దహనం పెరగడం, సిమెంట్ను ఉత్పత్తి చేయడానికి ఇటీవలి కాలంలో లైమ్ స్టోన్ వినియోగం బాగా పెరగడం వల్ల వాతావరణంలో CO₂ భాగం పెరుగుతోంది. దీనివల్ల హరితగృహ ఫలితం పెరుగుతోంది.

ప్రశ్న 18.
సిలికోన్లు అంటే ఏమిటి ?
జవాబు:
సిలికోన్లు ఆర్గానో సిలికాన్ సమ్మేళనాలు. వీటిలో సిలికాన్ కు ఆక్సిజన్, కార్బన్లు బలంగా బంధింపబడి ఉంటాయి.

ప్రశ్న 19.
సిలికోన్ల ఉపయోగాలు వ్రాయండి.
జవాబు:
సిలికోన్ల ఉపయోగాలు :

1. వాటర్ ఫ్రూఫ్ బట్టలు, కాగితాలను తయారుచేయడానికి వాడతారు.
2. సిలికోన్ రబ్బరు ఉత్తమ విద్యున్నిరోధకం. అందువల్ల ఎలక్ట్రికల్ మోటార్లలో ఉపయోగిస్తారు.
3. వీటికి రసాయన జడత్వం ఉన్నది. అందువలన అధిక ఉష్ణోగ్రతలను తట్టుకుంటాయి. ఈ కారణంగా వాటిని పెయింట్లలోనూ, పింగాణీలలోనూ ఉపయోగిస్తారు.
4. ద్రవ సిలికోన్ల స్నిగ్ధత ఉష్ణోగ్రతతో మారదు. -40°C వద్ద కూడ ఇవి గడ్డ కట్టవు. అందువలన వీటిని విమానాలలో కందెనగా వాడతారు.
5. సిలికోన్ నూనెలు అధిక స్థిరత్వం కలిగి ఉంటాయి. వేడిచేసినా కూడా ఆవిరి చెందవు. అందువలన వాటిని అధిక ఉష్ణోగ్రతల వద్ద ఆయిల్ బాథ్ మరియు అధిక శూన్యత పంపులలోనూ వాడతారు.

ఈ విధంగా ఆధునిక యుగంలో సిలికోన్లను అన్ని రంగాలలో వాడతారు.

ప్రశ్న 20.
తగరం (టిన్) మీద నీటి ప్రభావం ఏమిటి ?
జవాబు:
టిన్ నీటి ఆవిరిని వియోగం చెందించి డై ఆక్సైడు, డై హైడ్రోజన్లను ఏర్పరుస్తుంది.

ప్రశ్న 21.
SiCl₄ గురించి వ్రాయండి.
జవాబు:
సిలికాన్ టెట్రా క్లోరైడును సిలికాన్పై క్లోరిన్ చర్యవల్ల ఏర్పడుతుంది.
Si + 2Cl₂ – SiCl₄
SiCl₄ బాష్పశీలి ద్రవం. నీటి అణువు ఇచ్చే ఒంటరి ఎలక్ట్రాన్ జంటను Si లోని d ఆర్బిటాల్ స్వీకరించి Si(OH)₄ ఏర్పడుతుంది.

ప్రశ్న 22.
CO₂ వాయువు కానీ SiO₂ ఘనపదార్థం – వివరించండి.
జవాబు:
సిలికాన్ డై ఆక్సైడ్ త్రిమితీయ బృహదణు నిర్మాణం కలిగి ఉంటుంది. ప్రతి సిలికాన్ పరమాణువు నాలుగు ఆక్సిజన్ పరమాణువులతో చతుర్ముఖీయంగా నాలుగు సమయోజనీయ బంధాలతో బంధింపబడి ఉంటుంది. అందువలన SiO₂ ఘనపదార్థంగా ఉంటుంది.

CO₂ రేఖీయ అణువు. ఈ అణువులు విడివిడిగా ఉంటాయి. ఈ అణువుల మధ్య వాన్ డర్వాల్ బలాలు ఉంటాయి. అందువలన CO₂ వాయువుగా ఉంటుంది.

ప్రశ్న 23.
ZSM – 5 ఉపయోగం వ్రాయండి.
జవాబు:
జియొలైట్లను ఉత్ప్రేరకాలుగా వాడతారు. ZSM-5 అనే జియోలైట్ను ఆల్కహాల్లను నేరుగా గాసోలిన్ మార్చడానికి ఉపయోగిస్తారు.

ప్రశ్న 24.
పొడి మంచు ఉపయోగం ఏమిటి ?
జవాబు:
ఘన CO₂ ను పొడి మంచు అంటారు. ఐస్క్రీమ్, అతిశీతలమైన ఆహారపదార్థాల కోసం ప్రశీతకంగా ఉ పయోగిస్తున్నారు. బరువైనదీ, దహనానికి దోహదపడేదీ కనుక దీనిని మంటలను ఆర్పడానికి వాడతారు.

ప్రశ్న 25.
జలవాయువు (Water gas) ను ఎలా తయారుచేస్తారు ?
జవాబు:
వేడిగా నున్న కోక్ మీదకు నీటి ఆవిరిని పంపుట ద్వారా వ్యాపార పద్ధతిలో జలవాయువును తయారుచేస్తారు.

ప్రశ్న 26.
ప్రొడ్యూసర్ వాయువును ఎలా తయారుచేస్తారు ?
జవాబు:
కొలిమిని కోక్తో నింపి, దాని అడుగు భాగం నుండి వేడి గాలిని పంపుతారు. మొదట CO₂ వాయువు ఏర్పడుతుంది.
CO₂ కోల్ బెడ్ మీదుగా ప్రయాణించి CO గా క్షయకరణం చెందుతుంది.
CO, N₂ ల మిశ్రమం బయటకు వస్తుంది.
C + O₂ → CO₂
C + O₂ → 2CO

ప్రశ్న 27.
గ్రాఫైట్లో C − C బంధ దూరం, వజ్రంలో C – C బంధ దూరం కంటే తక్కువ – వివరించండి.
జవాబు:
గ్రాఫైట్ కార్బన్ C – C బంధ దూరం 141.5 pm గ్రాఫైట్లో కార్బన్ sp² సంకరీకరణం చెంది ఉంటుంది. అందువల్ల మూడు సిగ్మా బంధాలను ఏర్పరుస్తుంది. నాల్గవ ఎలక్ట్రాన్ 7 బంధాన్ని ఏర్పరుస్తుంది. ద్విబంధ స్వభావం వల్ల C – C బంధ దూరం తక్కువ.
వజ్రంలో కార్బన్ sp³ ఆర్బిటాళ్ళతో C – C ఏకబంధాలను మాత్రమే ఏర్పరుస్తుంది. అందువల్ల C – C బంధ దూరం 154 pm.

ప్రశ్న 28.
వజ్రాన్ని అమూల్యమైన రాయిగా వాడతారు – వివరించండి.
జవాబు:
వజ్రానికి వక్రీభవన గుణకం గరిష్ఠంగా 2.45 ఉన్నది. కాంతి పతనమైనపుడు అధిక వక్రీభవన గుణకం వల్ల సంపూర్ణాంతర పరావర్తనం జరుగుతుంది. అందువల్ల వజ్రం కాంతి పడినపుడు ప్రకాశిస్తుంది. అందువల్ల వజ్రాన్ని అమూల్య రాయిగా వాడతారు.

ప్రశ్న 29.
కార్బన్ సంయోజకత నాలుగు కంటే ఎక్కువ ఎప్పుడూ చూపించదు. కానీ ఆ కుటుంబంలో మిగతా మూలకాలు
సంయోజకత ఆరు వరకు చూపిస్తాయి – వివరించండి.
జవాబు:
కార్బన్ బాహ్య కర్పరం 2వ కర్పరం. దీనిలో d ఆర్బిటాళ్ళు ఉండవు. అందువల్ల బాహ్య కర్పరంలో నాలుగు ఎలక్ట్రానులను ఉపయోగించుకొని నాలుగు బంధాలను మాత్రమే ఏర్పరుస్తుంది. కావున కార్బన్ సంయోజకత నాలుగుకు మించదు. మిగిలిన 14వ గ్రూపు మూలకాలు బాహ్య స్థాయిలో ఖాళీ d ఆర్బిటాళ్ళు అందుబాటులో ఉన్నాయి. అందువల్ల అవి ఎలక్ట్రాన్ జంటలను స్వీకరించగలవు. అధిక సమన్వయ సంఖ్యను చూపించగలవు.

ప్రశ్న 30.
ప్రొడ్యూసర్ వాయువు, జల వాయువు కంటె తక్కువ సామర్థ్యం గల ఇంధనం – వివరించండి.
జవాబు:
ప్రొడ్యూసర్ వాయువులో 33% CO మరియు 65% N₂ ఉన్నాయి. నైట్రోజన్ దహనశీలి కాదు. అందువల్ల దాని కెలోరిఫిక్ విలువ 5439 కి.జౌ./మీ³.
జలవాయువులో CO మరియు H₂ లు దహనశీలి వాయువులు. అందువల్ల జలవాయువులో దహనం చెందగల వాయువుల శాతం ఎక్కువ. దాని కెలోరిఫిక్ విలువ 13,000 కి.జౌ./మీ³.

ప్రశ్న 31.
Si\(F_6^{-2}\) తెలుసు కాని SiC\(l_6^{-2}\) తెలియదు వివరించండి.
జవాబు:

1. Si⁺ అయాన్ సైజు పరిమితి వల్ల దాని చుట్టూ ఆరు పెద్ద క్లోరైడు అయాన్లకు సరిపడినంత చోటు లేకపోవుట.
2. క్లోరైడు అయాన్ ఒంటరి జంట, si⁴⁺ ల మధ్య అన్యోన్య చర్య బలహీనమైనది.

లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 32.
నిర్మాణాల ఆధారంగా వజ్రం, గ్రాఫైట్ల ధర్మాలలో తేడాలను వివరించండి.
జవాబు:
గ్రాఫైట్ :

1) గ్రాఫైట్ మృదువుగా వుండి, జారుడు స్వభావం కలిగి ఉంటుంది. కందెనగా ఉపయోగించవచ్చు.
కారణం : గ్రాఫైట్ ని ప్రంతి కార్బన్ (0 సంకరీకరణం చగ్రాఫైట్ పొరల నిర్మాణం కలిగి ఉండి, ఆ పొరలు ఒకదానిపై ఒకటి బలహీన వాండర్ వాల్ బలాలచే బంధించబడి ఉంటాయి. అందువల్లనే, ఒత్తిడి కలుగచేసినపుడు ఆ పొరలు ఒకదానిపై ఒకటి జారుతాయి. అందువలననే గ్రాఫైట్ మృదువుగా ఉంటుంది. కందెనగా ఉపయోగిస్తారు.

2) గ్రాఫైట్ ఉత్తమ ఉష్ణ వాహకం.
కారణం : గ్రాఫైట్లో స్వేచ్ఛా ఎలక్ట్రాన్ ఉంది. అది π బంధాన్ని ఏర్పరుస్తుంది. ఈ ఎలక్ట్రానులు మొత్తం పొర అంతా అస్థానీకృతం అవుతాయి. ఈ ఎలక్ట్రానులు చలనంలో ఉంటాయి. అందువల్ల గ్రాఫైట్ మంచి విద్యుద్వాహకం.

వజ్రం :

1) వజ్రం కఠినంగా ఉండి అరగదీసే రాయిగా పనిచేస్తుంది.
కారణం : వజ్రంలోని ప్రతి కార్బన్ sp³ సంకరీకరణం చెంది వుంటుంది. ప్రతి కార్బన్ నాలుగు ఇతర కార్బన్లతో sp³ – sp³ అతిపాతాల ద్వారా బలమైన బంధాలను ఏర్పరచడం వల్ల త్రిమితీయ బృహదణు నిర్మాణాన్ని పొందుతుంది. ఈ బంధాలను ఛేదించుట కష్టం. అందువల్ల వజ్రం కఠినం.

2) వజ్రం ఉష్ణ వాహకం కాదు.
కారణం : వజ్రంలోని కార్బన్ల వద్ద స్వేచ్ఛా ఎలక్ట్రానులు లేవు.
డైమండ్ మరియు గ్రాఫైట్ మధ్య భేదాలు :

ప్రశ్న 33.
క్రింది వాటిని వివరించండి.
a) PbCl₂, Cl₂ తో చర్య జరిగి, PbCl₄ ఇస్తుంది
b) PbCl₄ ఉష్ణ అస్థిర పదార్ధం
c) లెడ్ PbI₄ ను ఏర్పరచదు
జవాబు:
a) PbCl₂ లో Pb + 2 ఆక్సీకరణ స్థితిలో ఉన్నది. Cl₂ బలమైన ఆక్సీకారిణి. అందువల్ల అది Pb⁺² ను Pb⁺⁴ గా
ఆక్సీకరణం చేస్తుంది. కనుక PbCl₂ ను Cl₂, PbCl₄ గా ఆక్సీకరణం చేస్తుంది.

b) జడ ఎలక్ట్రాన్ జంట ప్రభావం కారణంగా Pb⁺⁺, Pb⁺⁺⁺⁺ కన్నా స్థిరమైనది. అంటే PbCl₂, PbCl₄ కన్నా స్థిరమైనది. అందువల్ల వేడి చేసినపుడు PbCl₄ ను వేడి చేస్తే Cl₂ ను కోల్పోయి PbCl₂ గా మారుతుంది.
c) Pb⁺⁴ జడ ఎలక్ట్రాన్ జంట ప్రభావం కారణంగా అస్థిరం. అందువల్ల Pb⁺⁴ మంచి ఆక్సీకారిణి. I^– మంచి క్షయకారిణి. అందువల్ల Pb⁺⁴ ను Pb⁺² గా క్షయీకరిస్తుంది. అందువల్ల PbI₄ ఏర్పడదు.

ప్రశ్న 34.
క్రింది వాటిని వివరించండి.
a) సిలికాన్ను మిథైల్ క్లోరైడ్తో కాపర్ సమక్షంలో అత్యధిక ఉష్ణోగ్రత వద్ద వేడి చేయబడింది.
b) SiO₂ ను HF తో చర్య జరపడం
c) గ్రాఫైట్ కందెనగా పనిచేస్తుంది
d) వజ్రం అపఘర్షకంగా ఉంటుంది.
జవాబు:
a) 573K వద్ద కాపర్ ఉత్ప్రేరకం సమక్షంలో మిథైల్ క్లోరైడ్ను సిలికాన్ పైకి పంపితే అనేక రకాలైన మిథైల్ ప్రతిక్షేపిత క్లోరో సైలేనులు, Me SiCl₃, Me₂, SiCl₂, Me₃, SiCl చాలా తక్కువ పరిమాణంలో Me₄ Si ఏర్పడతాయి.

b) SiO_n ను HF తో చర్య జరపడం
SiO₂ + 4HF → SiF₄ + 2H₂O
సిలికా HF లో కరిగి Silicon టెట్రా ఫ్లోరైడ్ను ఏర్పరుస్తుంది.

c) గ్రాఫైట్ ద్విజ్యామితీయ పొరల నిర్మాణం కలిగి ఉంటుంది. అంతేగాక, ఈ పొరలు ఒకదానిపై ఒకటి జారుతూ ఉంటాయి. అందుకనే గ్రాఫైట్ కందెనగా పనిచేస్తుంది.

d) వజ్రం త్రిజ్యామితీయ బృహదణు నిర్మాణం కలిగి ఉంటుంది. దీనిలో ప్రతి కార్బన్ పరమాణువు నాలుగు వేరు వేరు కార్బన్లతో బలమైన ఏకబంధాలతో బంధింపబడి ఉంటుంది. అందువల్ల వజ్రం కఠిన పదార్థం. అందువల్ల అపఘర్షకంగా ఉంటుంది.

ప్రశ్న 35.
మీరేమి అర్ధం చేసుకొన్నారు :
a) రూపాంతరత
b) జడజంట ప్రభావం
c) శృంఖలత్వం (catination)
జవాబు:
a) రూపాంతరత : ఒకే మూలకం రెండు లేక అంతకన్నా ఎక్కువ భౌతిక రూపాలలో లభించడాన్ని రూపాంతరత అంటారు.
డైమండ్, గ్రాఫైట్లు, కార్బన్ స్ఫాటిక రూపాంతరాలు. కోక్, కోల్, అస్ఫాటిక రూపాంతరాలు.

b) జడజంట ప్రభావం : బాహ్య కర్పరంలో ns² ఎలక్ట్రాన్ జంట. బంధాలు ఏర్పరచడంలో పాల్గొనకపోవడాన్ని జడజంట ప్రభావం అంటారు. ఈ ప్రభావం కారణంగా తక్కువ విలువ గల ఆక్సీకరణ స్థితి అధిక ఆక్సీకరణ స్థితి కన్నా స్థిరమైనదిగా ఉంటుంది. ఒక గ్రూపు మూలకాలలో పైనుండి క్రిందకు, అల్ప ఆక్సీకరణ స్థితి స్థిరత్వం
పెరుగుతుంది.
13వ గ్రూపు మూలకాలలో +3 సాధారణ ఆక్సీకరణ స్థితి కాగా Tl లో +1 స్థితి స్థిరమైనది. అదే విధంగా 14వ గ్రూపు మూలకాలలో +4 సాధారణ ఆక్సీకరణ స్థితి కాగా Pb లో +2 స్థితి స్థిరమైనది.

c) శృంఖలత్వం :
ఏదేని మూలక పరమాణువులు తమలో తాము గొలుసుకట్టుగా ఏర్పడే స్వభావాన్ని శృంఖలత్వం అంటారు. ఈ ధర్మం కార్బన్కు అధికం. అందువల్ల కార్బన్ గొలుసులు, వలయాలు ఏర్పడతాయి.

ప్రశ్న 36.
సిలికోన్ల తయారీలో RSiCl₃ ప్రారంభ పదార్థంగా వాడితే తయారైన క్రియాజన్యాల నిర్మాణాలను రాయండి.
జవాబు:
R SiCl₃ + 3H₂O → R Si (OH)₃
జలవిశ్లేషణ ఉత్పన్నం సంఘననం చెందితే త్రిజ్యామితీయ సిలికోన్ ఏర్పడుతుంది.

ప్రశ్న 37.
జియొలైట్ల మీద సంక్షిప్తంగా రాయండి.
జవాబు:
అల్యూమినియం సిలికేటులను జియొలైట్లు అంటారు. త్రిమితీయంగా అల్లిక గల సిలికాన్ డై ఆక్సైడ్లో కొన్ని సిలికాన్ పరమాణువులను అల్యూమినియం పరమాణువులు స్థానభ్రంశం చేస్తే అల్యూమినియం సిలికేట్లు ఏర్పడతాయి. దీనికి రుణావేశం ఉంటుంది. Na⁺, K⁺ లేదా Ca⁺⁺ కేటయాన్లు రుణావేశాన్ని తుల్యం చేస్తాయి.

ఉదా : ఫెల్డ్స్పర్ జియొలైటులు. పెట్రో కెమికల్ పరిశ్రమల్లో హైడ్రోకార్బన్లను భంజనం చేయడానికి, వాటి సాదృశీకరణ చర్యలకు జియొలైట్లను ఉత్ప్రేరకాలుగా విస్తృతంగా వాడతారు. ఉదా : ZSM-5 ఆల్కహాల్లను నేరుగా గాసోలీన్ గా మార్చడానికి ఉపయోగిస్తారు. కఠినజలం కఠినత్వాన్ని తగ్గించడానికి ఆర్ద్ర జియొలైట్లను అయాన్ వినిమయాలుగా ఉపయోగిస్తారు.

ప్రశ్న 38.
సిలికేట్ల మీద సంక్షిప్తంగా వ్రాయండి.
జవాబు:
సిలికేట్ల మూల నిర్మాణాత్మక యూనిట్ Si\(\mathrm{O}_4^{4-}\). ఇందులో సిలికాన్ పరమాణువు నాలుగు ఆక్సిజన్ పరమాణువులతో టెట్రాహెడ్రల్ రీతిలో బంధంలో కలిసి ఉంటాయి. సిలికేట్లలో ఆక్సిజన్ పరమాణువులను ఇతర యూనిట్లతో పంచుకోవడం ద్వారా శృంఖల, వలయ, షీట్ లేదా త్రిమితీయ నిర్మాణాలు ఏర్పడవచ్చు.

సిలికేట్ యూనిట్లలో రుణావేశం ధనావేశం గల లోహ అయానులతో తటస్థీకరించబడుతుంది. ఒకవేళ, యూనిట్ యొక్క నాలుగు మూలలు ఇతర టెట్రాహెడ్రల్ యూనిట్లతో పంచుకుంటే త్రిమితీయ అల్లిక నిర్మాణాన్ని పొందుతుంది.

ప్రశ్న 39.
సిలికోన్లు అంటే ఏమిటి ? అవి ఏ విధంగా పొందుతారు ?
జవాబు:

1. సిలికోన్లు ఆర్గానో సిలికాన్ తరగతికి చెందిన అణుపుంజాలు.
2. సిలికోన్లలో అనేక పర్యాయాలు పునరావృతమయ్యే R₂SiO – యూనిట్ ఉంది.
3. సిలికోన్ల తయారీకి ఆల్కైల్ లేదా ఎరైల్ ప్రతిక్షేపిత సిలికాన్ క్లోరైడులు R_n SiCl_(4-n) ప్రారంభ పదార్థాలు. ఇందులో R ఆల్కైల్ లేదా ఎరైల్ సమూహం.
4. 573 K వద్ద కాపర్ ఉత్ప్రేరకం సమక్షంలో మిథైల్ క్లోరైడును సిలికాన్ పైకి పంపితే అనేక రకాలైన మిథైల్ ప్రతిక్షేపిత క్లోరో సినులు ఏర్పడతాయి.
5. డైమిథైల్ క్లోరో సిలేన్ (CH₃)₂ SiCl₂ జలవిశ్లేషణం చెందగా ఏర్పడిన ఉత్పన్నాలు సంఘననం చెంది పొడవైన గొలుసుల అణుపుంజాలు ఇస్తాయి.

అణుపుంజీకరణం వల్ల గొలుసు ఏర్పడుతుంది.

ఉపయోగాలు :

1. వీటిని సీల్ వేసే పదార్థాలుగా, గ్రీజులుగా, విద్యుత్ బంధకాలుగాను
2. బట్టలపై జలనిరోధకంగా ఉపయోగిస్తారు.
3. శస్త్ర చికిత్స సంబంధమైన, సౌందర్య సాధన ద్రవ్యాల తయారీ పరిశ్రమలలో వాడతారు.

ప్రశ్న 40.
ఫుల్లరీన్ మీద సంక్షిప్తంగా వ్రాయండి.
జవాబు:
ఫుల్లరీన్ కార్బన్ స్ఫాటిక రూపాంతరం
తయారుచేయుట : జడవాయువులైన హీలియం లేదా ఆర్గాన్ల సమక్షంలో గ్రాఫైట్ను విద్యుచ్ఛాపంతో వేడి చేసిన ఫుల్లరీన్ తయారవుతుంది.

బాష్పీభవనం చెందిన C_n చిన్న అణువులు ఘనీభవించడం వల్ల వచ్చిన మసిలాంటి పదార్థంలో ముఖ్యంగా C₆₀ తక్కువ పరిమాణంలో C₇₀ ఉంటాయి. కార్బన్ పరమాణువులు 350 ఆ పైన ఫుల్లరిన్లు లేశమాత్రం ఉంటాయి.

ఫుల్లరీన్లు పంజరాన్ని పోలిన అణువులు. C₆₀ అణువుకు సాకర్ బంతిని పోలిన నిర్మాణం ఉండటం వల్ల దీనిని బక్ మినిష్టర్ ఫుల్లరీన్ అంటారు. దీనిలో ఆరు కార్బన్లున్న వలయాలు ఇరవై, ఐదు కార్బన్లున్న వలయాలు పన్నెండు ఉంటాయి. ఆరు కార్బన్ల వలయం ఆరు కార్బన్ల వలయం లేదా అయిదు కార్బన్ల వలయంతో సంలీనం చెందుతాయి. కానీ అయిదు కార్బన్ల వలయాలు ఆరు కార్బన్ల వలయాలతో మాత్రమే సంలీనం చెందుతాయి. అన్ని కార్బన్లు sp² సంకరీకరణం చెంది ఉంటాయి.

ప్రతి కార్బన్ ఆసన్న కార్బన్లతో మూడు సిగ్మా బంధాలను ఏర్పరుస్తుంది. మిగిలిన ఎలక్ట్రాన్ అణు ఆర్బిటాల్ తో అస్థానీకృతమయి అణువుకు ఎరోమాటిక్ స్వభావం చేకూరుస్తుంది. ఈ బంతి ఆకృతి గల అణువుకు 60 శీర్షాలు ఉన్నాయి. ప్రతి శీర్షంను ఒక కార్బన్ పరమాణువు ఆక్రమించి ఉంటుంది. ఈ కార్బన్లకు ఏక, ద్విబంధాలు రెండు ఉండి C – C బంధ దూరాలు 143.5 pm, 138.3 pm లు ఉంటాయి.

ప్రశ్న 41.
SiO₂ నీటిలో ఎందుకు కరగదు ?
జవాబు:
సిలికాన్ డై ఆక్సెడ్ సమయోజనీయ, త్రిమితీయ అల్లిక గల ఘనం. ఇందులో సిలికాన్ పరమాణువు సమయోజనీయ బంధంతో టెట్రాహెడ్రల్ రీతిలో నాలుగు ఆక్సిజన్ పరమాణువులతో కలిసి ఉంటుంది.
సాధారణ స్థితిలో సిలికా దాదాపు చర్యాశీలత లేనిది. ఎందుకంటే Si – O బంధ ఎంథాల్పీ చాలా ఎక్కువ. అందువల్లనే అది నీటిలో కరగదు.

ప్రశ్న 42.
వజ్రం కఠినంగా ఎందుకు వుంటుంది ?
జవాబు:
డైమండ్ ప్రతి కార్బన్ sp³ సంకరీకరణం చెందుతుంది. ప్రతి కార్బన్ నాలుగు ఇతర కార్బన్ పరమాణువులతో sp³ సంకర ఆర్బిటాల్లను టెట్రా హెడ్రల్ రీతిలో ఉపయోగించుకొని బంధాలను ఏర్పరుస్తుంది. ఈ నిర్మాణం ప్రాదేశికంగా వ్యాపించి కార్బన్ పరమాణువులతో దృఢమైన త్రిమితీయ అల్లికను ఏర్పరుస్తుంది. ఇలా వ్యాపించి వున్న సమయోజనీయ బంధాలను విచ్ఛిన్నం చేయడం చాలా శక్తితో కూడుకున్న పని. అందువల్ల డైమండ్ (వజ్రం) కఠినమైనది.

ప్రశ్న 43.
కింది వాటిని వేడి చేసినపుడు ఏమి జరుగుతుంది ?
a) CaCO₃
b) CaCO₃, SiO₂
c) CaCO₃ అధికంగా కోక్
జవాబు:
a) కాల్షియం కార్బొనేటు విఘటనం చెంది CO₂ విడుదలవుతుంది.
CaCO₃ (ఘ) → CaO (ఘ) + CO₂ (వా)

b) CaCO₃ మరియు SiO₂
CaCO₃ విఘటనం చెందినపుడు ఏర్పడిన CaO తో SiO₂ చర్యపొంది కాల్షియం సిలికేటు ఏర్పడుతుంది.
CaCO₃ → CaO + CO₂
CaO + SiO₂ → CaSiO₃

c) CaCO₃ విఘటనం వల్ల ఏర్పడిన CaO తో కోక్ చర్య పొందుతుంది. కాల్షియం కార్బైడ్ ఏర్పడుతుంది.
CaCO₃ → CaO + CO₂

ప్రశ్న 44.
Na₂CO₃ ద్రావణాన్ని CO₂ వాయువులో సంతృప్తం చేస్తే అవలంబనం అవుతుంది. ఎందువల్ల ?
జవాబు:
నీటిలో సోడియం బైకార్బొనేటు అల్పద్రావణీయత గలది. స్వల్పంగా కరుగుతుంది. దీనికి బై కార్బొనేటు అయాన్లు హైడ్రోజన్ బంధాల వల్ల పొలిమరీకరణం చెంది ఉంటుంది. Na₂CO₃ ద్రావణంలోని CO₂ ను పంపితే అల్ప ద్రావణీయత కల సోడియం బై కార్బొనేటు ఏర్పడుతుంది. అందువల్ల NaHCO₃ అవలంబనం చెందుతుంది.
Na₂CO₃ + H₂O + CO₂ → 2 NaHCO₃

ప్రశ్న 45.
ఈ క్రింది చర్యలలో ఏమి జరుగుతుంది ?
a) తడిసున్నం ద్వారా CO₂ను పంపడం
b) CaC₂ ను N₂ తో వేడిచేయడం
జవాబు:
a) తడిసున్నంలోనికి CO₂ ను పంపితే నీటిలో కరగని CaCO₃ ఏర్పడుతుంది. ద్రావణం పాలవలె మారుతుంది.
Ca(OH)₂ + CO₂ → CaCO₃ + H₂O + CO₂
CO₂ అధికంగా పంపితే కాల్షియం బైకార్బొనేటు ఏర్పడుతుంది. అందువల్ల CaCO₃ కరుగుతుంది.
CaCO₃ + H₂O + CO₂ → Ca(HCO₃)₂
Ca(HCO₃)₂ నీటిలో కరుగుతుంది.

b) వేడి చేసిన CaC₂ మీదికి నైట్రోజన్ వాయువును పంపితే కాల్షియం సైనమైడ్ మరియు గ్రాఫైట్ల మిశ్రమం ఏర్పడుతుంది.
CaC₂ + N₂ → Ca CN₂ + C
కాల్షియం సైనమైడ్, గ్రాఫైట్ల మిశ్రమాన్ని నైట్రోలిమ్ అంటారు.

ప్రశ్న 46.
గ్రూపు 14 లో కార్బన్ అసంగత స్వభావాన్ని గురించి వ్రాయండి.
జవాబు:
ఒక గ్రూపులోని మొదటి మూలకం మిగిలిన మూలకాల కంటే భిన్న ధర్మాలను చూపుతుంది. కార్బన్ కూడా గ్రూపులోని మిగిలిన మూలకాలతో పోలిస్తే భిన్నంగా ప్రవర్తిస్తుంది. దీనికి కారణం కార్బన్కు గల తక్కువ పరిమాణం, అధిక ఋణ విద్యుదాత్మకత, అధిక అయనీకరణ ఎంథాల్పీ, d – ఆర్బిటాళ్ళు లేకపోవటం.

1. కార్బన్ ప్రకృతిలో స్వేచ్ఛా స్థితిలో లభిస్తుంది. మిగతా మూలకాలు ప్రకృతిలో స్వేచ్ఛా స్థితిలో దాదాపుగా దొరకవు.
2. కార్బన్లో అందుబాటులో ఉండే d – ఆర్బిటాళ్ళు ఉండవు. మిగతా మూలకాలలో d – ఆర్బిటాళ్ళు అందుబాటులో ఉంటాయి.
3. కార్బన్ అలోహం. దీని పరమాణు సైజు చాలా చిన్నది. అందువలన ఇది అధిక కోవలంటే స్వభావం ఉన్న సమ్మేళనాలను ఇస్తుంది.
4. కార్బన్ కెటనేషన్ అనే విశిష్ట లక్షణం చూపిస్తుంది. ఈ లక్షణం కొంతవరకు సిలికాన్లో ఉంటుంది.
5. కార్బన్ తన పరమాణువుల మధ్య బహు బంధాలను ఏర్పరచగలదు. అలాగే ఇతర మూలకాలతో కూడా బహు బంధాలను ఏర్పరచగలదు.
6. కార్బన్ యొక్క హైడ్రైడ్లను హైడ్రోకార్బన్లు అంటారు. మిగిలిన మూలకాలు కూడా హైడ్రైడ్లను ఇస్తాయి. ఈ హైడ్రైడ్ స్థిరత్వం క్రమంగా తగ్గుతుంది.
7. కార్బన్ క్షయకరణ సామర్థ్యం చాలా ఎక్కువ. మిగిలిన మూలకాల క్షయకరణ సామర్థ్యం తక్కువ.
8. కార్బన్ – హాలోజన్ సమ్మేళనాలు జల విశ్లేషణం చెందవు. కాని మిగతా మూలకాలు టెట్రాహాలైడ్లు తేలిగ్గా జలవిశేషణం చెందుతాయి.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 47.
సిలికోన్లు అంటే ఏమిటి ? వాటిని ఏ విధంగా తయారుచేస్తారు ? ఉదాహరణ ఇవ్వండి.
జవాబు:
సిలికోన్లు ఆర్గానో సిలికాన్ సమ్మేళనాలు. వీటిలో సిలికాన్కు ఆక్సిజన్, కార్బన్లు బలంగా బంధింపబడి ఉంటాయి. వీటి నిర్మాణాత్మక ఫార్ములా క్రింది విధంగా ఉంటుంది.

573 K వద్ద కాపర్ ఉత్ప్రేరకం సమక్షంలో మిథైల్ క్లోరైడును సిలికాన్ పైకి పంపితే అనేక రకాలైన మిథైల్ ప్రతిక్షేపిత క్లోరోసిలేనులు, ఏర్పడతాయి.

డై మిథైల్ డైక్లోరోసిలేన్ (CH₃)₂ SiCl₂ జల విశ్లేషణ చెందగా ఏర్పడిన ఉత్పన్నాలు సంఘనన అణుపుంజీకరణం చెంది పొడవైన గొలుసుల అణుపుంజాలు ఇస్తాయి.

పొలిమర్ శృంఖలం పొడవును (CH₃)₃ SiCl ను కలిపి నియంత్రించవచ్చు.

ధర్మాలు :

అధ్రువ ఆల్కెల్ సమూహాలతో చుట్టుకొన్న సిలికోన్లు జలవికర్షణ స్వభావం ఉన్నవి.
వీటికి అధిక ఉష్ణ స్థిరత్వం కలదు. ఆక్సీకరణం, ఇతర రసాయన చర్యలను నిరోధిస్తాయి.

ఉపయోగాలు :

1. సిలికోన్ రబ్బర్లు తయారీలో వాడతారు.
2. వాటర్ ఫ్రూఫ్ బట్టలు, కాగితాలు తయారుచేయడానికి వాడతారు.
3. విమానాలలో కందెనలుగాను, గ్రీజు తయారీలోను వాడతారు.
4. వీటికి రసాయన జడత్వం ఉన్నది. అందువలన అధిక ఉష్ణోగ్రతలను తట్టుకొంటాయి. కనుక పెయింటులలోను, పింగాణీలలోను ఉపయోగిస్తారు.
5. సీలు వేసే పదార్థాలుగా
6. విద్యుత్ బంధకాలుగా ఉపయోగిస్తారు.
7. -40°C వద్ద కూడా గడ్డ కట్టవు. అందువలన విమానాలలో కందెనగా ఉపయోగిస్తారు.

ప్రశ్న 48.
సిలికా నిర్మాణాన్ని వివరించండి. అది
a) NaOH
b) HF తో ఏ విధంగా చర్య జరుపుతుంది ?
జవాబు:
సిలికాన్ డై ఆక్సైడ్ను సాధారణంగా సిలికా అంటారు. ఇది అనేక స్ఫాటిక రూపాలలో దొరుకుతుంది. క్వార్ట్జ్, క్రిస్టో బలైట్, ట్రిడిమైట్లు సిలికా యొక్క కొన్ని స్ఫటికాకారాలు. సిలికాన్ ఆక్సైడ్ సమయోజనీయ, త్రిమితీయ అల్లికగన ఘనం.

సిలికాన్ నిర్మాణం : సిలికాలో ప్రతి సిలికాన్ పరమాణువు నాలుగు ఆక్సిజన్ పరమాణువులతో ఏక సమయోజనీయ బంధంతో చతుర్ముఖీయంగా అమర్చబడి ఉంటుంది. ప్రతి ఆక్సిజన్ పరమాణువు రెండు సిలికాన్ పరమాణువుల మధ్య బంధింపబడి ఉంటుంది. ఈ విధంగా SiO₂ బలమైన త్రిజ్యామితీయ బృహదణు నిర్మాణం కలిగి ఉంటుంది. సాధారణ స్థితిలో సిలికా దాదాపు చర్యాశీలత లేనిది. ఎందుకంటే Si – O బంధ ఎంథాల్ఫీ చాలా ఎక్కువ.

a) NaOH తో చర్య జరిపి సోడియం సిలికేటును ఏర్పరుస్తుంది.
SiO₂ + 2 NaOH → Na₂ SiO₃ + H₂O

b) HF తో చర్య జరిపి SiF₄ ను ఏర్పరుస్తుంది.
SiO₂ + 4 HF → SiF₄ + 2H₂O

ప్రశ్న 49.
కార్బన్ రూపాంతరాలపై వివరణ వ్రాయండి.
జవాబు:
కార్బన్ భిన్న రూపాలలో లభిస్తుంది. అవి స్పటిక, అస్ఫాటిక రూపాలు.

స్ఫాటిక రూపాలు : డైమండ్, గ్రాఫైట్, ఫుల్లరీన్
అస్ఫాటిక రూపాలు : కోక్, కోల్ మొదలైనవి.

డైమండ్ మరియు గ్రాఫైట్లు కార్బన్ యొక్క స్ఫటిక రూపాంతరాలు. డైమండ్ త్రిజ్యామితీయ బృహదణు నిర్మాణం కలిగి ఉంటుంది.

వజ్రం (డైమండ్) నిర్మాణం : వజ్రంలో ప్రతికార్బన్ పరమాణువు sp³ సంకరీకరణాన్ని పొందుతుంది. దానివలన ప్రతి కార్బన్ పరమాణువు మీద నాలుగు sp³ సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి. ప్రతి కార్బన్ పరమాణువులోని నాలుగు sp³ సంకర ఆర్బిటాళ్ళు నాలుగు ఇతర కార్బన్ పరమాణువులతో బంధాలను ఏర్పరచుకుంటాయి. ప్రతి కార్బన్ పరమాణువు చతుర్ముఖీయ సౌష్ఠవాన్ని కలిగి ఉంటుంది. ఈ విధంగా కార్బన్ పరమాణువులు ఒకదానితో ఒకటి బంధింపబడి ఉండటం వలన పెద్ద అణువు ఏర్పడుతుంది.

దీనిలో C – C బంధదూరం 1.54 Ä, బంఢకోణం 190°28′

ఉపయోగాలు :

1. ఆభరణాలలో విలువైన రాళ్ళుగా ఉపయోగిస్తారు.
2. పాలరాయిని కోయడానికి ఉపయోగిస్తారు.
3. టంగ్స్టన్ వంటి లోహాల నుండి అతి సన్నని తీగను తీయుటకు వాడతారు.

గ్రాఫైట్ నిర్మాణము : గ్రాఫైట్ ద్విజ్యామితీయ పొరల నిర్మాణాన్ని కల్గి ఉంటుంది. ఈ నిర్మాణం కార్బన్ పరమాణువులతో కూడిన షడ్భుజాకార వలయాలను కల్గి ఉంటుంది. గ్రాఫైట్లో ప్రతి కార్బన్ పరమాణువు sp² సంకరీకరణాన్ని పొంది, మూడు ఇతర కార్బన్ పరమాణువులతో షడ్భుజాకార వలయాలుగా బంధించబడి ఉంటాయి. ఇటువంటి అనేక వలయాలు కలిసి ఒకే తలంలో ఉంటాయి. ఒంటరి ఎలక్ట్రాలు గల p ఆర్బిటాల్ ఈ తలానికి లంబంగా ఉంటుంది. ఈ p ఆర్బిటాళ్ళు ఒకదానితో ఒకటి కలిసిపోయి షడ్భుజాకార తలానికి పైన, క్రింద విస్తరించి ఉంటాయి. ఈ వలయాకారాలు ఒకదానిపై ఒకటి బలహీనమైన వాండర్వాల్ బలాలచే బంధించబడి ఉంటాయి. దీనిలో C – C బంధదూరం 1.42 రెండు వలయాల మధ్య దూరం 3.4 .

ఉపయోగాలు :

1. కందెనగా ఉపయోగిస్తారు.
2. లెడ్ పెన్సిళ్ళ తయారీలో ఉపయోగిస్తారు.
3. గ్రాఫైట్ ఉత్తమ విద్యుద్వాహకము. అందువల్ల ఎలక్ట్రోడ్ల తయారీలో ఉపయోగిస్తారు.

ఫుల్లరీన్ : ఫుల్లరీన్ కార్బన్ స్పాటిక రూపాంతరం

తయారుచేయుట : జడవాయువులైన హీలియం లేదా ఆర్గాన్ల సమక్షంలో గ్రాఫైట్ను విద్యుచ్ఛాపంతో వేడి చేసిన ఫుల్లరీన్ తయారవుతుంది.

బాష్పీభవనం చెందిన C_n చిన్న అణువులు ఘనీభవించడం వల్ల వచ్చిన మసిలాంటి పదార్థంలో ముఖ్యంగా C₆₀, తక్కువ పరిమాణంలో C₇₀ ఉంటాయి. కార్బన్ పరమాణువులు 350 ఆ పైన పుల్లరిన్లు లేశమాత్రం ఉంటాయి.
ఫుల్లరీన్లు పంజరాన్ని పోలిన అణువులు. C₆₀ అణువుకు సాకర్ బంతిని పోలిన నిర్మాణం ఉండటం వల్ల దీనిని బక్ మినిష్టర్ ఫుల్లరీన్ అంటారు. దీనిలో ఆరు కార్బన్లున్న వలయాలు ఇరవై, ఐదు కార్బన్లున్న వలయాలు పన్నెండు ఉంటాయి. .ఆరు కార్బన్ల వలయం ఆరు కార్బన్ల వలయం లేదా అయిదు కార్బన్ల వలయంతో సంలీనం చెందుతాయి. కానీ అయిదు కార్బన్ల వలయాలు ఆరు కార్బన్ల వలయాలతో మాత్రమే సంలీనం చెందుతాయి. అన్ని కార్బన్లు sp² సంకరీకరణం చెంది ఉంటాయి.

ప్రతి కార్బన్ ఆసన్న కార్బన్లతో మూడు సిగ్మా బంధాలను ఏర్పరుస్తుంది. మిగిలిన ఎలక్ట్రాన్ ఆర్బిటాల్లతో అస్థానీకృతమయి అణువుకు ఎరోమాటిక్ స్వభావం చేకూరుస్తుంది. ఈ బంతి ఆకృతి గల అణువుకు 60 శీర్షాలు ఉన్నాయి. ప్రతి శీర్షంను ఒక కార్బన్ పరమాణువు ఆక్రమించి ఉంటుంది. ఈ కార్బన్లకు ఏక, ద్విబంధాలు రెండు ఉండి C – C బంధ దూరాలు 143.5 pm, 138.3 pm లు ఉంటాయి.

అస్ఫాటిక రూపాంతరాలు :

కోల్ : భూమిలో కొన్ని శతాబ్దాల క్రితం మట్టితో కప్పబడిపోయిన వృక్ష సంబంధమైన పదార్థాలు ఆక్సిజన్ సమక్షంలో అధిక పీడనం, ఉష్ణోగ్రతల వద్ద కృశించిపోయినపుడు కోల్ ఏర్పడుతుంది. కోల్లో కార్బన్, హైడ్రోజన్, ఆక్సిజన్, నైట్రోజన్ ఉంటాయి. 60% కార్బన్ ఉన్న కోలన్ను పీట్ అని 70% కార్బన్ ఉన్న కోల్న లిగ్నైట్ అని, 78% బిట్యూ మినస్ అని, 83% సెమి బిట్యూమినస్ కోల్, 90% కార్బన్ ఉన్నదాన్ని ఆంధ్ర సైట్ అని అంటారు.

కోక్ : కోల్న ఆక్సిజన్ లేని వాతావరణంలో విధ్వంసక స్వేదనం చర్యకు గురి చేసినపుడు భాష్పశీలి పదార్థాలయిన కోల్స్, అమ్మోనియా, బెంజీన్ లు ఏర్పడతాయి. మిగిలిన అవశేషాన్నే కోక్ అంటారు.

ఉపయోగాలు :

1. కోల్ను ఇంధనంగా వాడతారు.
2. కృత్రిమ పెట్రోలు తయారీలో వాడతారు.
3. కోకను స్టీలు పరిశ్రమలో క్షయకారిణిగా వాడతారు.
4. గ్రాఫైట్ను, వాటర్ సన్ను తయారుచేయడానికి వాడతారు.

ప్రశ్న 50.
కిందివాటిపై వివరణ వ్రాయండి.
ఎ) సిలికేట్లు
బి) జియోలైట్లు
సి) పుల్లరీన్లు
జవాబు:
ఎ) సిలికేట్లు : సిలికేట్ల మూల నిర్మాణాత్మక యూనిట్ Si\(\mathrm{O}_4^{4-}\). ఇందులో సిలికాన్ పరమాణువు నాలుగు ఆక్సిజన్ పరమాణువులతో టెట్రాహెడ్రల్ రీతిలో బంధంలో కలిసి ఉంటాయి. సిలికేట్లలో ఆక్సిజన్ పరమాణువులను ఇతర యూనిట్లతో పంచుకోవడం ద్వారా శృంఖల, వలయ, షీట్ లేదా త్రిమితీయ నిర్మాణాలు ఏర్పడవచ్చు.

సిలికేట్ యూనిట్లలో రుణావేశం ధనావేశం గల లోహ అయానులతో తటస్థీకరించబడుతుంది. ఒకవేళ, యూనిట్ యొక్క నాలుగు మూలలు ఇతర టెట్రాహెడ్రల్ యూనిట్లతో పంచుకుంటే త్రిమితీయ అల్లిక నిర్మాణాన్ని పొందుతుంది.

బి) జియోలైట్లు : అల్యూమినియం సిలికేటులను జియొలైట్లు అంటారు. త్రిమితీయంగా అల్లిక గల సిలికాన్ డై ఆక్సైడ్ కొన్ని సిలికాన్ పరమాణువులను అల్యూమినియం పరమాణువులు స్థానభ్రంశం చేస్తే అల్యూమినియం సిలికేట్లు ఏర్పడతాయి. దీనికి రుణావేశం ఉంటుంది. Na⁺, K⁺ లేదా Ca⁺⁺ కేటయాన్లు రుణావేశాన్ని తుల్యం చేస్తాయి.
ఉదా : ఫెల్డ్ స్పార్ జియొలైటులు. పెట్రో కెమికల్ పరిశ్రమల్లో హైడ్రోకార్బన్లను భంజనం చేయడానికి, వాటి సాదృశీకరణ చర్యలకు జియొలైట్లను ఉత్ప్రేరకాలుగా విస్తృతంగా వాడతారు. ఉదా : ZSM – 5 ఆల్కహాల్లను నేరుగా గాసోలీన్ మార్చడానికి ఉపయోగిస్తారు. కఠినజలం కఠినత్వాన్ని తగ్గించడానికి ఆర్ద్ర జియొలైట్లను అయాన్ వినిమయాలుగా ఉపయోగిస్తారు.

సి) ఫుల్లరీన్లు : ఫుల్లరీన్ కార్బన్ స్పాటిక రూపాంతరం
తయారుచేయుట : జడవాయువులైన హీలియం లేదా ఆర్గాన్ల సమక్షంలో గ్రాఫైట్ను విద్యుచ్ఛాపంతో వేడి చేసిన ఫుల్లరీన్ తయారవుతుంది.

బాష్పీభవనం చెందిన C_n చిన్న అణువులు ఘనీభవించడం వల్ల వచ్చిన మసిలాంటి పదార్థంలో ముఖ్యంగా C₆₀. తక్కువ పరిమాణంలో C₇₀ ఉంటాయి. కార్బన్ పరమాణువులు 350 ఆ పైన పుల్లరిన్లు లేశమాత్రం ఉంటాయి.

ఫుల్లరీన్ లు పంజరాన్ని పోలిన అణువులు. C₆₀ అణువుకు సాకర్ బంతిని పోలిన నిర్మాణం ఉండటం వల్ల దీనిని బక్ మినిష్టర్ ఫుల్లరీన్ అంటారు. దీనిలో ఆరు కార్బన్లున్న వలయాలు ఇరవై, ఐదు కార్బన్లున్న వలయాలు పన్నెండు ఉంటాయి. ఆరు కార్బన్ల వలయం. ఆరు కార్బన్ల వలయం లేదా అయిదు కార్బన్ల వలయంతో సంలీనం చెందుతాయి. కానీ అయిదు కార్బన్ల వలయాలు ఆరు కార్బన్ల వలయాలతో మాత్రమే సంలీనం చెందుతాయి. అన్ని కార్బన్లు sp² సంకరీకరణం చెంది ఉంటాయి.

ప్రతి కార్బన్ ఆసన్న కార్బన్లతో మూడు సిగ్మా బంధాలను ఏర్పరుస్తుంది. మిగిలిన ఎలక్ట్రాన్ అణు ఆర్బిటాల్లతో అస్థానీకృతమయి అణువుకు ఎరోమాటిక్ స్వభావం చేకూరుస్తుంది. ఈ బంతి ఆకృతి గల అణువుకు 60 శీర్షాలు ఉన్నాయి. ప్రతి శీర్షంను ఒక కార్బన్ పరమాణువు ఆక్రమించి ఉంటుంది. ఈ కార్బన్లకు ఏక, ద్విబంధాలు రెండు ఉండి C – C బంధ దూరాలు 143.5 pm, 138.3 pm లు ఉంటాయి.

అదనపు పశ్నలు

ప్రశ్న 1.
14వ గ్రూపు మూలకాలలో
1) అధిక ఆమ్ల డై ఆక్సెడును ఏర్పరచేది
2) సాధారణంగా +2 ఆక్సీకరణ స్థితిలో ఏర్పడేది.
3) అర్థవాహక ఉపకరణాలలో ఉపయోగపడేది
జవాబు:
1) కార్బన్
2) లెడ్
3) సిలికాన్, జెర్మేనియం

ప్రశ్న 2.
డైమండ్ సమయోజనీయ స్వభావం కలది. అయినప్పటికి అధిక ద్రవీభవన ఉష్ణోగ్రత ఎందుకు ?
జవాబు:
ధృఢమైన C – C బంధాల అల్లికతో ఉన్న త్రిమితీయ నిర్మాణం డైమండ్కు ఉంటుంది. దృఢమైన C – C బంధాలను విచ్ఛిన్నం చేయడానికి చాలా శక్తి కావాలి. అందువల్ల దీని ద్రవీభవన ఉష్ణోగ్రత చాలా అధికం.

ప్రశ్న 3.
కార్బన్ మోనాక్సైడ్ నిర్మాణం వ్రాయండి.
జవాబు:
CO అణువులో ఒక సిగ్మా, రెండు π బంధాలు కార్బన్ ఆక్సిజన్ల మధ్య గలవు. :C ≡ O: కార్బన్ పై ఒంటరి ఎలక్ట్రాన్ ఉండుటవలన CO అణువు ఎలక్ట్రాన్ జంట దాతగా పనిచేస్తుంది.

ప్రశ్న 4.
IV A గ్రూపులో రూపాంతరతను చూపించని మూలకం ఏది ?
జవాబు:
లెడ్

ప్రశ్న 5.
కార్బన్ మోనాక్సైడ్ యొక్క అనువర్తనాలను రాయండి.
జవాబు:

1. వాటర్స్, ప్రొడ్యూసర్గాస్, కోల్గాస్ల వంటి వాయు ఇంధనాలలో CO ముఖ్యమైన అనుఘటకం.
2. అనేక లోహ ఆక్సైడ్లను క్షయకరణం చెందించి లోహాలుగా మారుస్తుంది.
3. మాండ్ పద్ధతిలో Ni నిష్కర్షణలో CO ని లైగాండ్గా వాడతారు.

ప్రశ్న 6.
కార్బన్ డై ఆక్సైడ్ యొక్క అనువర్తనాలను రాయండి.
జవాబు:

1. ఘనస్థితిలో ఉన్న CO₂ ను డ్రై ఐస్ అంటారు. దీనిని ప్రశీతకంగా వాడతారు.
2. ప్రయోగశాలలో శీతలీకరణిగా వాడతారు.
3. యూరియాను తయారుచేయడానికి, జడవాతావరణాన్ని ఏర్పరచడానికి, క్షారాలను తటస్థీకరించడానికి వాడతారు.
4. అగ్నిమాపక యంత్రాలలో వాడతారు.

ప్రశ్న 7.
CO₂, SiO₂ ధర్మాలలో భేదాలు వ్రాయండి.
జవాబు:

ప్రశ్న 8.
కార్బన్, సిలికాన్ల మధ్య గల పోలికలను రాయండి.
జవాబు:

ప్రశ్న 9.
పెన్సిళ్ళ తయారీలో కార్బన్ యొక్క ఏ రూపాంతరాన్ని వాడతారు ?
జవాబు:
గ్రాఫైట్ను పెన్సిళ్ళ తయారీలో వాడతారు.

ప్రశ్న 10.
లెడ్ యొక్క స్థిర ఆక్సీకరణ స్థితి ఏది ? కారణం ఏమిటి ?
జవాబు:
లెడ్ యొక్క స్థిర ఆక్సీకరణ స్థితి + 2 (జడ ఎలక్ట్రాన్ +4 ఆక్సీకరణ స్థితి అస్థిరమైనది. జంట ప్రభావం వల్ల చూపదు)

ప్రశ్న 11.
కార్బొరండం అనగా ఏమి ? ఇది ఎలా ఏర్పడుతుంది ?
జవాబు:
సిలికాన్ కార్బెడు కార్బొరండం అంటారు. విద్యుత్ కొలిమిలో సిలికాన్, కార్బన్లను కలిపి వేడి చేయడం ద్వారా దీనిని తయారుచేస్తారు.

ప్రశ్న 12.
గ్రాఫైట్లో రెండు పొరల మధ్య దూరం ఎంత ? కారణం ఏమిటి ?
జవాబు:
గ్రాఫైట్లో రెండు పొరల మధ్య దూరం 3.35. గ్రాఫైట్ పొరల మధ్య బలహీన వాన్ డర్ వాల్ బలాలు ఉండటం వల్ల పొరల మధ్య దూరం ఎక్కువగా ఉంటుంది.

ప్రశ్న 13.
CO₂మరియు SiO₂ లలో ఉండే సంకరీకరణాలు ఏమిటి ?
జవాబు:
CO₂ లో sp సంకరీకరణం ఉంటుంది. SiO₂ లో sp³ సంకరీకరణం ఉంటుంది.

ప్రశ్న 14.
డైమండ్ కఠినంగా ఉండగా గ్రాఫైట్ మృదువుగా ఉంటుంది. ఎందువలన ?
జవాబు:
డైమండ్కు బృహదణు నిర్మాణం ఉంటుంది. అందువలన అది కఠినంగా ఉంటుంది. గ్రాఫైట్లో పొరల నిర్మాణం ఉంటుంది. అందువలన అది మృదువుగా ఉంటుంది.

ప్రశ్న 15.
సిలికా ఫార్ములా SiO₂ గా ఎందుకు ఉంటుంది ?
జవాబు:
Si సిలికా నిర్మాణంలో ప్రతి టెట్రాహెడ్రన్ మూలమీద ఉన్న ఆక్సిజన్ను రెండు సిలికాన్ పరమాణువులు పంచుకుంటాయి. ప్రతి సిలికాన్ పరమాణువు శీర్షం వద్ద ఆక్సిజన్లో అర్ధ భాగాన్ని మాత్రమే ప్రదానం చేస్తుంది అన్నమాట. అందువలననే సిలికా ఫార్ములా SiO₂ అవుతుంది.

ప్రశ్న 16.
క్వార్ట్జ్ అంటే ఏమిటి ?
జవాబు:
పరిశుద్ధ సిలికాను క్వార్ట్జ్ అంటారు.

ప్రశ్న 17.
ఆర్థో సిలికేట్స్, పైరో సిలికేట్స్ మరియు చైన్ సిలికేట్స్లోలో గల యూనిట్లను తెలపండి.
జవాబు:
ఆర్థో సిలికేట్లు : Si\(\mathrm{O}_4^{-4}\) యూనిట్లు
పైరో సిలికేట్లు : SiO^-6 యూనిట్లు
చైన్ సిలికేట్లు : \(\mathrm{O}_3^{-4}\) యూనిట్లు

Telangana TSBIE TS Inter 1st Year Physics Study Material 12th Lesson పదార్ధ ఉష్ణ ధర్మాలు Textbook Questions and Answers.

TS Inter 1st Year Physics Study Material 12th Lesson పదార్ధ ఉష్ణ ధర్మాలు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఉష్ణం, ఉష్ణోగ్రతల మధ్య భేదాలను పేర్కొనండి.
జవాబు:
ఉష్ణము మరియు ఉష్ణోగ్రతల మధ్య భేదాలు :
ఉష్ణము

1. ఉష్ణము శక్తి స్వరూపము. దీనికి ప్రమాణాలు జౌల్ లేదా ఉష్ణోగ్రత
2. మనం వస్తువుకు నేరుగా ఉష్ణశక్తిని అందించగలము.
3. వస్తువు ఉష్ణోగ్రతను పెంచడానికి ఉష్ణశక్తిని మనం అందించాలి.
4. వస్తువుకు అందజేసిన ఉష్ణరాశి Q = mSt.

ఉష్ణోగ్రతల

1. ఉష్ణోగ్రత ఒక పదార్థము యొక్క వేడిమి లేదా చల్లదనాన్ని తెలిపే కొలమానము. ప్రమాణము °F లేదా °C.
2. వస్తువుకు ఉష్ణశక్తిని అందించడంవల్ల దాని ఉష్ణోగ్రత పెరుగుతుంది. మనం వస్తువుకు ఉష్ణోగ్రతను నేరుగా అందించలేము.
3. వస్తువుల మధ్య ఉష్ణోగ్రతాభేదం ఉంటేనే ఉష్ణరాశి ఒక వస్తువు నుండి మరొక వస్తువుకు ప్రవహిస్తుంది.
4. వస్తువు ఉష్ణోగ్రతలో మార్పు ∆t = \(\frac{\mathrm{Q}}{\mathrm{mS}}\)

ప్రశ్న 2.
సెల్సియస్, ఫారన్ హీట్ ఉష్ణోగ్రతా మానాలలో అధో, ఊర్ధ్వ స్థిర విలువలను తెలపండి. (మే 2014)
జవాబు:
సెల్సియస్ మానంలో నీటి త్రిక బిందు ఉష్ణోగ్రతను నిమ్న స్థిర బిందువు (°C అని వ్యవహరిస్తారు. సాధారణ వాతావరణ దగ్గర నీరు మరుగు స్థానాన్ని ఊర్ధ్వ స్థిర బిందువు 100°C అంటారు.
ఫారన్హీట్ మానంలో నీటి త్రిక బిందువును నిమ్న స్థిర బిందువు 32°F గా వ్యవహరిస్తారు. సాధారణ వాతావరణ పీడనం వద్ద నీరు మరుగు స్థానాన్ని ఊర్ధ్వ స్థిర బిందువు 212°F అంటారు.

ప్రశ్న 3.
ఉష్ణోగ్రతలను సెల్సియస్ లేదా ఫారస్వీట్ మానాలలో కొలిస్తే, వ్యాకోచ గుణకాల విలువలు మారతాయా ?
జవాబు:
వ్యాకోచ గుణకాలు ఉష్ణోగ్రతామానంపై ఆధారపడతాయి. ఉష్ణోగ్రతామానం మారితే ఉష్ణోగ్రతను కొలిచే ప్రమాణం విలువ మారుతుంది. α, β మరియు γ ను 1°C ఉష్ణోగ్రతా భేదానికి నిర్వచించటం వల్ల సెల్సియస్ మానంలో α, β, γ లు ఫారెన్హీట్ మానంలోని α, β మరియు γ విలువల కన్న 1.8 రెట్లు పెద్దవి.

ప్రశ్న 4
వేడిచేస్తే పదార్థాలు సంకోచిస్తాయా ? ఒక ఉదాహరణ ఇవ్వండి.
జవాబు:
కొన్ని రకాలైన పదార్థాలు వేడిచేస్తే సంకోచిస్తాయి.
ఉదా : రబ్బరు, తోలు, పోత ఇనుము మరియు టైపు మెటల్ వంటివి.

ప్రశ్న 5.
రైల్వే ట్రాక్పై రెండు వరస రైలు పట్టాల మధ్య ఖాళీ ప్రదేశం ఎందుకు వదులుతారు ?
జవాబు:
వేసవికాలంలో రైలు పట్టాలలోని వ్యాకోచ ప్రభావాన్ని తొలగించడానికి వీలుగా రైలు పట్టాల మధ్య ఖాళీని వదులుతారు. ఖాళీని వదలకపోతే రైలు పట్టాల వ్యాకోచం వల్ల రై. పటాలు వంకర చెంది ప్రమాదాలను కలగజేస్తాయి.

ప్రశ్న 6.
ద్రవాలకు దైర్ఘ్య, విస్తీర్ణ వ్యాకోచ గుణకాలు ఎందుకు లేవు ?
జవాబు:
ద్రవాలకు స్వతంత్ర ఆకారం లేదు. అందువల్ల వాటికి దైర్ఘ్య వ్యాకోచ గుణకము, విస్తీర్ణ వ్యాకోచ గుణకాలు ఉండవు. వీటిని పాత్రలలో తీసుకోవటం వల్ల కేవలం ఘనపరిమాణమును మాత్రమే లెక్కలోకి తీసుకుంటారు. అందుకని ద్రవాలకు ఘనపరిమాణ వ్యాకోచ గుణకం మాత్రమే చెపుతారు.

ప్రశ్న 7.
ద్రవీభవన గుప్తోష్ణం అంటే ఏమిటి ?
జవాబు:
ద్రవీభవన గుప్తోష్ణము : ప్రమాణ ద్రవ్యరాశి గల పదార్థము ఘనస్థితి నుండి ద్రవస్థితికి లేదా ద్రవస్థితి నుండి ఘనస్థితికి మార్పుచెందునపుడు గ్రహించిన లేక కోల్పోయిన ఉష్ణరాశిని ద్రవీభవన గుప్తోష్ణముగా నిర్వచించినారు.

ప్రశ్న 8.
బాష్పీభవన గుప్తోష్టం అంటే ఏమిటి ?
జవాబు:
బాష్పీభవన గుప్తోష్ణం : ప్రమాణ ద్రవ్యరాశి గల పదార్థము ద్రవస్థితి నుండి బాష్పస్థితికి లేదా బాష్పస్థితి నుండి ద్రవస్థితికి మారునపుడు అది గ్రహించిన లేక కోల్పోయిన ఉష్ణరాశిని బాష్పీభవన గుప్తోష్ఠముగా నిర్వచించినారు.

ప్రశ్న 9.
వంట పాత్రలకు నల్లటి రంగు ఎందుకు పూస్తారు ? వంట పాత్రల అడుగు భాగాన్ని రాగితో ఎందుకు తయారుచేస్తారు?
జవాబు:
వంట పాత్రల అడుగు భాగం నల్లని పూత వేయటానికి ముఖ్య కారణము నల్లని వస్తువులు ఉత్తమ శోషకాలు. కావున అవి ఎక్కువ మొత్తంలో ఉష్ణాన్ని శోషిస్తాయి. రాగి ఉత్తమ ఉష్ణవాహకం కావున వంట పాత్రల అడుగు భాగంలో రాగిని ఉపయోగిస్తారు.

ప్రశ్న 10.
వీన్ స్థానభ్రంశ నియమాన్ని తెలపండి.
జవాబు:
కృష్ణ వస్తువు గరిష్ట వికిరణం జరిగే తరంగదైర్ఘ్యం, ఆ కృష్ణ వస్తువు పరమ ఉష్ణోగ్రతకు విలోమానుపాతంలో ఉంటుంది.
అనగా λ_m = \(\frac{1}{T}\) లేదా λ_m = \(\frac{b}{T}\)
ఇచ్చట ‘b’ ను వీన్ స్థిరాంకం అని అందురు.

ప్రశ్న 11.
వెంటిలేటర్లను గదిలోని ఇంటిపై కప్పుకు కొద్దిగా కిందకి అమరుస్తారు. ఎందుకు ? (మార్చి 2014)
జవాబు:
వేడిగాలికి సాంద్రత తక్కువ. ఇది వాతావరణంలో పై పొరలను ఆక్రమిస్తుంది. గదిలో వేడిగాలి పైకప్పుకు దగ్గరగా చేరుతుంది. అందువల్ల వెంటిలేటర్లను కప్పుకు దగ్గరగా అమర్చితే వేడిగాలి తొందరగా బయటకు పోతుంది. ఫలితంగా గదిలోకి చల్లని గాలి ధారాళంగా క్రింది భాగాల గుండా రావటం జరుగుతుంది.

ప్రశ్న 12.
0 K వద్ద మానవ దేహం ఉష్ణాన్ని వికిరణం చేస్తుందా ? 0°C వద్ద కూడా అది వికిరణం చేస్తుందా ?
జవాబు:
ప్రివోస్ట్ సిద్ధాంత ప్రకారము ‘సున్న’ కెల్విన్ కన్న ఎక్కువ ఉష్ణోగ్రత వద్ద గల ప్రతి వస్తువు పరిసరాలలో ఉష్ణ వినిమయాన్ని కలిగి ఉంటుంది. కావున

1. ‘సున్న’ కెల్విన్ వద్ద గల వస్తువు నుండి ఏ విధమైన ఉష్ణవికిరణ శక్తి వెలువడదు. అనగా ఉష్ణ వికిరణం సాధ్యం కాదు.
2. 0 K అనగా 273 K కావున 0°C వద్ద గల వస్తువు ఉష్ణశక్తి వికిరణం వెలువడును. అనగా ఉష్ణ వికిరణం సాధ్యపడును.

ప్రశ్న 13.
ఉష్ణ బదిలీకి సంబంధించి వివిధ విధానాలను తెలపండి. వీటిలో ఏ విధానాలకు యానకం అవసరం ?
జవాబు:
ఉష్ణ ప్రసారము మూడు రకాలుగా జరుగుతుంది.

1. ఉష్ణ వహనము
2. ఉష్ణ సంవహనము
3. ఉష్ణ వికిరణము.

ఉష్ణ ప్రసారంలో ఉష్ణ వహనము మరియు ఉష్ణ సంవహనము అన్న పద్ధతుల ద్వారా ఉష్ణము ప్రసరించడానికి యానకం అవసరము.

ప్రశ్న 14.
ఉష్ణ వాహకత్వ గుణకం, ఉష్ణోగ్రత ప్రవణతలను నిర్వచించండి.
జవాబు:
పదార్థం ఏకాంక అడ్డుకోత వైశాల్యానికి లంబంగా, ఏకాంక ఉష్ణోగ్రతా ప్రవణత ఉన్నపుడు సెకనుకు జరిగిన ఉష్ణరాశి ప్రసారాన్నే ఉష్ణ వహన గుణకంగా నిర్వచించినారు.
ఉష్ణ వహన గుణకం K = \(\frac{\mathrm{Q} \cdot \mathrm{d}}{\mathrm{A}\left(\theta_2-\theta_1\right) \cdot \mathrm{t}}\)

ప్రశ్న 15.
ఉద్గార సామర్థ్యం, ఉద్గారతలను నిర్వచించండి.
జవాబు:
ఉద్గార సామర్థ్యము (E_λ) : ఏదైనా ఉష్ణోగ్రత వద్ద ఏకాంక వైశాల్యం గల వస్తువు నుండి తరంగదైర్ఘ్యము . మరియు λ + dλ. అవధులలో వస్తువు ప్రమాణ కాలంలో వికిరణం చెందించిన ఉష్ణరాశిని ఆ వస్తువు ఉద్గార సామర్థ్యంగా నిర్వచించినారు.
ఉద్గార సామర్థ్యము E_λ = \(\frac{\mathrm{dQ}}{\mathrm{d} \lambda}\); ప్రమాణము : వాట్ / మీ².
ఉద్గారత (e_λ) : ఒక వస్తువు ఉద్గార సామర్థ్యానికి అదే ఉష్ణోగ్రత వద్ద పరిపూర్ణ కృష్ణ వస్తువు ఉద్గార సామర్థ్యానికి గల నిష్పత్తినే ఆ వస్తువు ఉద్గారత e_λ గా నిర్వచించినారు.

ప్రశ్న 16.
హరితగృహ ప్రభావం అంటే ఏమిటి ? గ్లోబల్ వార్మింగ్ గురించి వివరించండి.
జవాబు:
హరితగృహ ప్రభావము : భూమి నుండి శూన్యంలోకి వికిరణం చెందే ఉష్ణశక్తి తరంగదైర్ఘ్యం ఎక్కువ. ఈ ఉష్ణశక్తిని కార్బన్ డై ఆక్సైడ్ (CO₂), మీథేన్ (CH₄), క్లోరోఫ్లోరో కార్బన్ (CF_x Cl_x) వంటి వాయువులు గ్రహించి భూమి వాతావరణాన్ని వేడెక్కిస్తాయి. ఈ ప్రక్రియను హరితగృహ ప్రభావము అంటారు.

గ్లోబల్ వార్మింగ్ :
మానవుల చర్యల వల్ల హరితగృహ వాయువుల (CO₂, CH₄, N₂O మొ॥) గాఢత అధికమై భూమి వేడిగా తయారవుతుంది. భూమి ఉష్ణోగ్రత పెరుగుదలను గ్లోబల్ వార్మింగ్ అందురు. దీనివల్ల మంచు పర్వతాలు త్వరగా ద్రవీభవించడం, సముద్రమట్టం పెరగడం, వాతావరణం విధానం మార్పు చెందడం జరుగుతుంది.

ప్రశ్న 17.
ఒక వస్తువు శోషణ సామర్థ్యాన్ని నిర్వచించండి. పరిపూర్ణ కృష్ణ వస్తువు శోషణ సామర్థ్యం ఎంత ?(మార్చి 2014)
జవాబు:
శోషణ సామర్థ్యము (a_λ) : ఏదైనా వస్తువు యొక్క నియమిత వైశాల్యం మీద నియమిత కాలంలో dλ) తరంగ వ్యవధిలో పతనమైన వికిరణ శక్తి తరంగ అభివాహం (dΦ_λ) మరియు అదే కాలవ్యవధిలో అదే వైశాల్యం గల తలం శోషణం చేసుకున్న అభివాహానికి (dΦ_λ) గల నిష్పత్తి నిశోషణ సామర్థ్యము (a_λ) గా నిర్వచించినారు.

ఉత్తమ కృష్ణ వస్తువు శోషణ సామర్థ్యం ఒకటి (1).

ప్రశ్న 18.
న్యూటన్ శీతలీకరణ నియమాన్ని తెలపండి.
జవాబు:
న్యూటన్ శీతలీకరణ నియమము : వస్తువుకు, పరిసరాలకు మధ్య ఉష్ణోగ్రతా భేదం స్వల్పంగా ఉన్నపుడు ఆ వస్తువు కోల్పోయే ఉష్ణ శక్తి రేటు వస్తువుకూ, పరిసరాలకు మధ్య గల ఉష్ణోగ్రతా భేదానికి అనులోమానుపాతంలో ఉంటుంది.
వస్తువు కోల్పోయే ఉష్ణశక్తి రేటు \(\frac{\mathrm{dE}}{\mathrm{dt}}\) ∝ (T – T_s) లేదా
శీతలీకరణ రేటు \(\frac{\mathrm{dT}}{\mathrm{dt}}\) = – \(\frac{\mathrm{b}}{\mathrm{mc}}\) (T – T_s) ఇందులో T_s పరిసరాల ఉష్ణోగ్రత, T వస్తువు ఉష్ణోగ్రత.

ప్రశ్న 19.
న్యూటన్ శీతలీకరణ నియమం అనువర్తించడానికి కావలసిన పరిస్థితులను తెలపండి.
జవాబు:
న్యూటన్ శీతలీకరణ నియమం అనువర్తింపచేయడానికి అనువైన పరిస్థితులు :

1. వహనం ద్వారా ఉష్ణ నష్టం విస్మరించ దగినంత తక్కువగా ఉండి కేవలం సంవహనం ద్వారానే ఉష్ణ నష్టం జరిగినపుడు,
2. లేదా బలాత్కృత సంవహనం వలన ఉష్ణ నష్టం జరిగినపుడు,
3. వస్తువుకు, పరిసరాలకు గల ఉష్ణోగ్రతా భేదం స్వల్పంగా ఉన్నపుడు అనగా సుమారు 30 K ఉన్నపుడు,
4. వస్తువుపై ఉష్ణోగ్రత ఏకరీతి వితరణలో ఉన్నపుడు.

ప్రశ్న 20.
వేసవి కాలంలో భవనాలపై పై కప్పుకు తరచుగా తెలుపు రంగును పూతగా పూస్తారు. ఎందుకు ?
జవాబు:
భవనాల పైభాగాన తెల్లని రంగు పూయటం వల్ల ఎండాకాలంలో భవనం లోపలి భాగం చల్లగా ఉంటుంది.
ఎందుకనగా తెల్లని వస్తువులకు శోషణ గుణకము తక్కువ. కావున తెల్లని భాగాలు వాటిపై పడిన ఉష్ణశక్తిలో తక్కువ భాగాన్ని శోషణం చేసుకొని ఎక్కువ ఉష్ణశక్తిని పరావర్తనం చెందిస్తాయి. ఫలితంగా ఆ వస్తువు తక్కువ వేడెక్కును. అనగా ఇంటి పైకప్పు ఇంటి లోపలికి తక్కువ ఉష్ణశక్తిని ప్రసారం చేస్తుంది.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
సెల్సియస్, ఫారన్హీట్ ఉష్ణోగ్రతా మానాలను వివరించండి. సెల్సియస్, ఫారన్హీట్ ఉష్ణోగ్రతా మానాల మధ్య సంబంధాన్ని రాబట్టండి.
జవాబు:
సెంటిగ్రేడ్ లేదా సెల్సియస్ ఉష్ణమానము : సెంటీగ్రేడ్ ఉష్ణమానంలో సాధారణ వాతావరణ పీడనం వద్ద నీరు ఘనీభవించు స్థానాన్ని అధోస్థిరస్థానంగా తీసుకున్నారు. దీనిని 0°C గా వ్యవహరిస్తారు.

సాధారణ వాతావరణ పీడనం వద్ద నీరు మరుగు స్థానాన్ని ఊర్ధ్వ స్థిరస్థానంగా తీసుకున్నారు. దీనిని 100°C గా వ్యవహరిస్తారు.

ఊర్ధ్వ, అధో స్థిరస్థానాల మధ్య భేదాన్ని (100 – 0 = 100) వంద సమాన భాగాలుగా చేసి ఒక్కొక్క భాగాన్ని 1°C గా పిలుస్తారు.

ఫారన్హీట్ ఉష్ణోగ్రతామానము : ఫారెన్హీట్ ఉష్ణోగ్రతామానంలో సాధారణ వాతావరణ పీడనం వద్ద నీరు ఘనీభవించు ఉష్ణోగ్రతను అధో స్థిరస్థానంగా తీసుకున్నారు. దీనిని 32°F గా నిర్వచించారు.

సాధారణ వాతావరణ పీడనం వద్ద నీరు మరుగుస్థానాన్ని ఊర్ధ్వ స్థిరస్థానంగా నిర్ణయించారు. దీనిని 212°F గా తీసుకున్నారు.

ఊర్ధ్వ, అధో స్థిరస్థానాల మధ్య భేదాన్ని (212 – 32 = 180) 180 సమాన భాగాలుగా చేసి ఒక్కొక్క భాగాన్ని 1°C గా పిలుస్తారు.

సెంటీగ్రేడ్ మరియు ఫారెన్హీట్ ఉష్ణోగ్రతల మధ్య సంబంధము : సెంటీగ్రేడ్ మరియు ఫారెన్హీట్ మానములలో ప్రామాణికంగా తీసుకున్న ఊర్ధ్వ స్థిరబిందువు మరియు అధో స్థిర బిందువులు ఒక్కటే.
కావున \(\frac{\mathrm{t}_{\mathrm{F}}-32}{180}=\frac{\mathrm{t}_{\mathrm{C}}}{100}\) (లేదా) \(\frac{9}{5}\) C = F – 32 (లేదా) 1.8 C = F – 32
C = సెల్సియస్ మానంలో ఉష్ణోగ్రత, F = ఫారెన్హీట్ మానంలో ఉష్ణోగ్రత.

ప్రశ్న 2.
రాగి, స్టీల్తో చేసిన రెండు సర్వసమాన లోహ పట్టీలను ఒకదానితో ఒకటి కలిపి సంయోగ పట్టీగా తయారుచేశారు. ఆ సంయోగ పట్టీని వేడిచేస్తే ఏమవుతుంది ?
జవాబు:
రెండు భిన్నజాతిలోహపు బద్దలను (రాగి మరియు ఇనుము అనుకోండి) రివిట్ల సహాయంతో అతికితే ఆ అమరికను ద్విలోహపు పట్టి అంటారు. ఇటువంటి ద్విలోహపు పట్టీని వేడిచేస్తే అది ఒక లోహపు ముక్కవలె సంకోచ వ్యాకోచాలను పొందుతుంది.

ద్విలోహాత్మక పట్టీని వేడిచేసినపుడు వృత్త చాపము వలె వంగుతుంది. ఈ చాపంపైభాగంలో ఎక్కువ వ్యాకోచ గుణకం గల పదార్థము, క్రింది భాగంలో తక్కువ వ్యాకోచ గుణకం గల పదార్థము ఉంటాయి.
ఈ స్థిరాంకమును స్థితిస్థాపక గుణకము అంటారు.

ప్రశ్న 3.
లోలక గడియారాలు సాధారణంగా శీతాకాలంలో అధిక కాలాన్ని చూపుతాయి. వేసవిలో తక్కువ కాలాన్ని చూపుతాయి. ఎందుకు ?
జవాబు:
సాధారణంగా లోలకంతో పనిచేసే గడియారాలను తయారుచేసేటప్పుడు అవి రోజుకు ఒక నిర్దిష్ట సంఖ్యలో (0 డోలనాలు చేసే విధంగా తయారుచేస్తారు).

ఎండాకాలంలో వాతావరణంలో ఉష్ణోగ్రత పెరగడం వల్ల ఘనపదార్థాలు వ్యాకోచిస్తాయి. అనగా లోలకం పొడవు పెరుగును. లోలకం పొడవు l₁ = l (l + α ∆t)

లోలకం ఆవర్తన కాలము T = 2π\(\sqrt{\frac{l}{g}}\) లేదా T ∝ \(\sqrt{l}\) అనగా లోలకం పొడవు పెరిగితే దాని ఆవర్తనకాలం పెరగడం వల్ల అది ఒకరోజులో చేసే డోలనాల సంఖ్య తగ్గుతుంది. అనగా గడియారం నెమ్మదిగా నడుస్తుంది.

చలికాలంలో వాతావరణ ఉష్ణోగ్రత తగ్గటం వల్ల లోలక పదార్థం సంకోచిస్తుంది. అనగా లోలకం పొడవు తగ్గుతుంది. ఫలితంగా డోలనావర్తన కాలం తగ్గుతుంది. అనగా లోలకం ఒకరోజులో చేసిన డోలనాల సంఖ్య పెరుగును. అంటే చలికాలంలో గడియారాలు వేగంగా చలిస్తాయి.

ప్రశ్న 4.
నీటి అసంగత వ్యాకోచం ఏ విధంగా జలచర సంబంధమైన జంతువులకు లాభం చేకూరుస్తుంది ? (March 2014 / May 2014)
జవాబు:
చలి దేశాలలో ముఖ్యంగా ధృవ ప్రాంతాలలో చలికాలంలో వాతావరణంలో ఉష్ణోగ్రతలు 0°C కన్న చాలా తక్కువకు పడిపోతాయి. ఫలితంగా నదులు, సరస్సులు మరియు సముద్రాల పైభాగాలు గడ్డ కడతాయి. కాని మంచు అధమ ఉష్ణవాహకం కావడం వల్ల మంచు పొరలలో లోతుకు పోయిన కొలది మనం నీరు 1°C, 2°C లేదా 3°C వంటి వివిధ పొరల రూపంలో ఉంటుంది. కాని సముద్రం అడుగు భాగం వద్ద నీరు 4°C వద్ద ఉంటుంది. దీనికి కారణము నీటికి 4°C వద్ద గరిష్ఠ సాంద్రత ఉండుట.

ప్రాముఖ్యత : సముద్ర జలాలు ఉపరితలం వద్ద గడ్డ కట్టినప్పటికి లోపలి భాగం 4°C వద్ద ఉండటం వల్ల జలచరాలు జీవించగలుగుతున్నాయి.

ప్రశ్న 5.
వహనం, సంవహనం, వికిరణాలను ఉదాహరణలతో వివరించండి.
జవాబు:
వహనం : వస్తువులోని కణాలు స్థానాంతరం చెందకుండా, వస్తువులో ఎక్కువ ఉష్ణోగ్రత గల ప్రదేశం నుండి తక్కువ ఉష్ణోగ్రత గల ప్రదేశానికి జరుగు ఉష్ణ ప్రసారాన్ని ఉష్ణ వహనం అంటారు.
ఉదా : ఒక పొడవైన లోహపు కడ్డీని ఒక చివర చేతితో పట్టుకొని రెండవ కొన మంటలో ఉంచితే, ఉష్ణం వాహనం ద్వారా కడ్డీ ఒక కొన నుండి మరొక కొనకు ప్రసరిస్తుంది.

సంవహనం : వస్తువులోని కణాలు స్థానాంతరం చెందుతూ, వస్తువులో ఎక్కువ ఉష్ణోగ్రత గల ప్రదేశం నుండి తక్కువ ఉష్ణోగ్రత గల ప్రదేశానికి ఉష్ణ ప్రసారాన్ని ఉష్ణ సంవహనం అంటారు.
ఉదా : సముద్రగాలి, భూగాలి

వికిరణం : యానకం నిమిత్తం లేకుండా ఒకచోట నుండి మరొక చోటుకు జరుగు ఉష్ణ ప్రసారాన్ని ఉష్ణ వికిరణం అంటారు.
ఉదా : సూర్యుని నుండి భూమికి ఉష్ణం వికిరణం ద్వారా చేరుతుంది..

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఉష్ణవాహకత్వం, ఉష్ణవాహకత్వ గుణకాన్ని వివరించండి. 0.10 m పొడవు, 1.0 × 10⁶ m^-2 మధ్యచ్ఛేద వైశాల్యం ఉన్న ఒక రాగి కడ్డీ ఉష్ణ వాహకత్వం 401 W/(mK). కడ్డీ ఒక కొన 104°C వద్ద, మరొక కొన 24° C వద్ద కలవు. కడ్డీ వెంబడి ఉష్ణ ప్రవాహ రేటు ఎంత ?
జవాబు:
ఉష్ణవహనము : ఈ పద్ధతిలో ఉష్ణము ఒకచోటు నుండి మరొక చోటికి యానకంలోని అణువులను స్థానభ్రంశము చెందించకుండా ప్రయాణం చేస్తుంది.

ఉష్ణవహనము ద్వారా ఉష్ణము ఘనపదార్థాలలో ప్రసరిస్తుంది.

పటంలో చూపిన విధంగా ఒక దీర్ఘ ఘనమును తీసుకొనుము. దీని ఎదురెదురు సమాంతర తలాలు ABCD మరియు EFGH అనుకొనుము. ఈ తలాలను θ₁ మరియు θ₂ ఉష్ణోగ్రతల మధ్య ఉంచినామనుకొనుము. దీని అడ్డుకోత వైశాల్యము A మరియు పొడవు l అనుకొనుము.

ఒక పదార్థం గుండా ప్రవహించు ఉష్ణరాశి (Q) ఈ క్రింది నియమాలను పాటిస్తుంది అని ప్రయోగపూర్వకంగా కనుగొన్నారు.

1. ఇచ్చిన వాహకం గుండా ప్రవహించు ఉష్ణరాశి వాహకం అడ్డుకోత వైశాల్యము (A) కి అనులోమానుపాతంలో ఉంటుంది.
   ∴ Q∝ A ……………. (1)
2. వాహకం గుండా ప్రవహించిన ఉష్ణరాశి (Q) వాహకపు కొనల మధ్య గల ఉష్ణోగ్రతా భేదానికి అనులోమానుపాతంలో
   ఉంటుంది.
   ∴ Q ∝ (θ₂ – θ₁) …………….. (2)
3. వాహకం గుండా ప్రవహించిన ఉష్ణరాశి (Q) ఉష్ణము ప్రవహించిన కాలము (t) నకు అనులోమానుపాతంలో ఉంటుంది.
   Q ∝ t …………. (3)
4. వాహకం గుండా ప్రవహించిన ఉష్ణరాశి (Q) వాహకము పొడవు (l) కు విలోమానుపాతంలో ఉంటుంది.
   Q ∝ \(\frac{1}{l}\) ……………….. (4)

పై నాలుగు నియమాల నుండి Q ∝ \(\frac{\mathrm{A}\left(\theta_2-\theta_1\right) \mathrm{t}}{l}\) (లేదా) Q = \(\frac{{KA}\left(\theta_2-\theta_1\right) \mathrm{t}}{l}\)
ఇందులో K స్థిరాంకము. దీనిని ఉష్ణవహన గుణకము అంటారు.

ఉష్ణవహన గుణకము (K) : ప్రమాణ అడ్డుకోత వైశాల్యం గల పదార్థపు ఎదురెదురు సమాంతర తలముల మధ్య ఏకాంక ఉష్ణోగ్రతా అతిక్రమం ఉన్నపుడు ప్రమాణ కాలంలో ఆ తలముల మధ్య ప్రవహించిన ఉష్ణరాశిని ఆ పదార్థం ఉష్ణవహన గుణకంగా నిర్వచించినారు.
ఉష్ణవహన గుణకము K = \(\frac{\mathrm{Q} . l}{\mathrm{~A}\left(\theta_2-\theta_1\right) \mathrm{t}}\)
ఉష్ణవహన గుణకానికి ప్రమాణాలు వాట్ మీటర్^-1 కెల్విన్^-1 లేదా జౌల్సకన్^-1 మీటర్^-1 కెల్విన్^-1
మితి ఫార్ములా = [ M¹L¹T^-3θ^-1]

సమస్య :
రాగి ఉష్ణవహన గుణకము K_c = 401 W/m-k
ఒక కొన వద్ద ఉష్ణోగ్రత θ₂ = 104°C
రెండవ కొన వద్ద ఉష్ణోగ్రత θ₁ = 24°C
రాగి దండం పొడవు l = 0.1m; వైశాల్యము = A = 1.0 × 10^-6 m²
ఉష్ణవహన రేటు \(\frac{\mathrm{Q}}{\mathrm{t}}=\frac{{KA}\left(\theta_2-\theta_1\right)}{l}=\frac{401 \times 1 \times 10^{-6}(104-24)}{0.1}\) = 401 × 80 × 10^-5 = 0.3208 J/S

ప్రశ్న 2.
న్యూటన్ శీతలీకరణ నియమాన్ని తెలిపి, వివరించండి. న్యూటన్ శీతలీకరణ నియమం అనువర్తించడానికి కావలసిన పరిస్థితులను తెలపండి.
ఒక వస్తువు 60°Cనుంచి 50°C కు చల్లబడటానికి 5 నిమిషాల కాలం పట్టింది. తరువాత 40°C కు చల్లబడటానికి మరొక 8 నిమిషాలు పట్టింది. పరిసరాల ఉష్ణోగ్రతను కనుక్కోండి.
జవాబు:
న్యూటన్ శీతలీకరణ నియమము : వస్తువుకు, పరిసరాలకు మధ్య ఉష్ణోగ్రతా భేదం స్వల్పంగా ఉన్నపుడు ఆ వస్తువు కోల్పోయే ఉష్ణ శక్తి రేటు వస్తువుకూ, పరిసరాలకు మధ్య గల ఉష్ణోగ్రతా భేదానికి అనులోమానుపాతంలో ఉంటుంది.

వస్తువు కోల్పోయే ఉష్ణశక్తి రేటు \(\frac{\mathrm{dE}}{\mathrm{dt}}\) ∝ (T – T_s) లేదా
శీతలీకరణ రేటు \(\frac{\mathrm{dT}}{\mathrm{dt}}\) = – \(\frac{\mathrm{b}}{\mathrm{mc}}\) (T – T_s). ఇందులో T_s పరిసరాల ఉష్ణోగ్రత, T వస్తువు ఉష్ణోగ్రత.
ఉష్ణోగ్రతా భేదం స్వల్పంగా ఉన్నప్పుడు మాత్రమే ఈ నియమం వర్తిస్తుంది. వికిరణం ద్వారా నష్టపోయే ఉష్ణం, వస్తువు ఉపరితల స్వభావం మీద, ప్రత్యక్షీకరణం అయ్యే ఉపరితల వైశాల్యంపై ఆధారపడి ఉంటుంది.
– \(\frac{\mathrm{dQ}}{\mathrm{dt}}\) = k (T₂ – T₁) (రుణ గుర్తు నష్టాన్ని సూచిస్తుంది) ………………. (1)
ఇక్కడ k ధనాత్మక స్థిరాంకం. దీని విలువ వస్తువు ఉపరితల స్వభావం, వైశాల్యంపై ఆధారపడి ఉంటుంది. s విశిష్టోష్ణ సామర్థ్యం, mద్రవ్యరాశి ఉన్న వస్తువు, T₂ ఉష్ణోగ్రత వద్ద ఉందనుకోండి. పరిసరాల ఉష్ణోగ్రత T₁ అనుకోండి. dtకాలంలో స్వల్ప పరిమాణంలో ఉష్ణోగ్రతలో తగ్గుదల dT₂ అనుకొంటే, నష్టపోయిన ఉష్ణ పరిమాణం
dQ = ms dT₂
∴ నష్టపోయిన ఉష్ణ రేటును కింది విధంగా ఇవ్వచ్చు.
\(\frac{\mathrm{dQ}}{\mathrm{dt}}\) = ms \(\frac{\mathrm{dT}_2}{\mathrm{dt}}\) ………….. (2)
సమీకరణాలు (1), (2) ల నుంచి
-ms \(\frac{\mathrm{dT}_2}{\mathrm{dt}}\) = k (T₂ – T₁)
\(\frac{\mathrm{dT}_2}{\mathrm{~T}_2-\mathrm{T}_1}\) = – \(\frac{\mathrm{k}}{\mathrm{ms}}\) dt = -Kdt …………….. (3)
ఇక్కడ K = k/ms
సమాకలనం చేయగా,
loge (T₂ – T₁) = – Kt + c …………….. (4)
(T₂ – T₂) = e^{-Kt + c}
లేదా T₂ = T₁ + C’ e^-Kt; ఇక్కడ C’ = e^c ……………. (5)
ప్రత్యేకమైన ఉష్ణోగ్రత అవధిలో ఒక వస్తువు శీతలీకరణానికి పట్టే కాలాన్ని సమీకరణం (5) ఉపయోగించి లెక్కించవచ్చు.

స్వల్ప ఉష్ణోగ్రతా భేదాలకు, ఉష్ణ వహనం, సంవహనం, వికిరణాల కలయిక వల్ల శీతలీకరణ రేటు ఉష్ణోగ్రతా భేదానికి అనులోమానుపాతంలో ఉంటుంది. ఒక వికిరణకం నుంచి గదిలోకి బదిలీ అయ్యే ఉష్ణం, గదిలోని గోడల ద్వారా నష్టపోయే ఉష్ణం లేదా టేబుల్పై అమర్చిన కప్పులోని వేడి టీ శీతలీకరణం చెందే సందర్భాలలో ఈ నియమం ఉజ్జాయింపుగా చెల్లుబాటు అవుతుంది.

న్యూటన్ శీతలీకరణ నియమం అనువర్తింపచేయడానికి అనువైన పరిస్థితులు :

1. వహనం ద్వారా ఉష్ణ నష్టం విస్మరించదగినంత తక్కువగా ఉండి కేవలం సంవహనం ద్వారానే ఉష్ణ నష్టం జరిగినపుడు,
2. లేదా బలాత్కృత సంవహనం వలన ఉష్ణ నష్టం జరిగినపుడు,
3. వస్తువుకు, పరిసరాలకు గల ఉష్ణోగ్రతా భేదం స్వల్పంగా ఉన్నపుడు అనగా సుమారు 30K ఉన్నపుడు,
4. వస్తువుపై ఉష్ణోగ్రత ఏకరీతి వితరణలో ఉన్నపుడు.

సమస్య :
తొలి ఉష్ణోత్ర θ₁ = 60 C;
తుది ఉష్ణోగ్రత θ₂ = 50°C
పట్టిన కాలము t = 5 ని॥ = 300 సె॥; గది ఉష్ణోగ్రత = θ₀ అనుకొనుము.
న్యూటన్ శీతలీకరణ నియమం నుండి \(\frac{\mathrm{d} \theta}{\mathrm{dt}}=K\left[\frac{\theta_1+\theta_2}{2}-\theta_0\right]\)
⇒ \(\frac{60-50}{300}\) = K \(\left[\frac{60+50}{2}-\theta_0\right]\) ⇒ \(\frac{10}{300}\) = K [55 – θ₀] (లేదా) ⇒ \(\frac{1}{30}\) = K[55 – θ₀] ….. (1)
రెండవ సందర్భంలో వస్తువు 50 C నుండి 40°C కు 8 నిమిషాలలో చల్లారింది.
న్యూటన్ నియమం నుండి \(\frac{50-40}{8 \times 60}\) = K \(\left[\frac{50+40}{2}-\theta_0\right]\)
⇒ \(\frac{10}{480}\) = K[45 – θ₀] ⇒ 1 = 48K (45 – θ₀)
1 మరియు 2 సమీకరణముల నుండి 30 K (55 – θ₀) = 48K (45 – θ₀)
275 – 5θ₀ = 360 – 8θ₀ ⇒ 3θ₀ = 360 – 275
∴ θ₀ = \(\frac{85}{3}\) = 28.33°C

లెక్కలు

ప్రశ్న 1.
ఏ ఉష్ణోగ్రత వద్ద కెల్విన్ మానంలోని రీడింగ్, ఫారన్హీట్ మానంలోని రీడింగ్లు సమానం అవుతాయి ?
సాధన:
కెల్విన్, ఫారన్ హీట్ మానాలలో \(\frac{\mathrm{K}-273.15}{100}\) = \(\frac{F-32}{180}\)
ఇక్కడ K = F కావున
\(\frac{\mathrm{F}-273.15}{100}=\frac{\mathrm{F}-32}{180}\)
⇒ F – 273.15 = \(\frac{5}{9}\) F – \(\frac{160}{9}\)
\(\frac{4}{9}\) F – 273.15 – 17.77
⇒ F = \(\frac{9}{4}\) (255.38) = 574.6
∴ 574.6K = 574.6°F.

ప్రశ్న 2.
ఒక అల్యూమినియం కడ్డీ పొడవును 1% పెంచాలంటే దాని ఉష్ణోగ్రతలో కలిగే పెరుగుదల కనుక్కోండి. (అల్యూమినియం విలువ = 25 × 10^-6 / °C)
సాధన:
అల్యూమినియం దైర్ఘ్య వ్యాకోచ గుణకము, α = 25 × 10^-6 / °C

ప్రశ్న 3.
20°C ఉష్ణోగ్రత, 100 g ద్రవ్యరాశి ఉన్న నీటి ఉష్ణోగ్రతను 5°C పెంచడానికి 100°C ఉష్ణోగ్రత వద్ద ఉన్న ఎంత ఆవిరిని ఆ నీటిలోకి పంపించాలి ? (నీటి ఆవిరి గుప్తోష్ణం 510 cal / g, నీటి విశిష్టోష్ణం 1 cal / g°C)
సాధన:
నీటి బాష్పీభవన గుప్తోష్ణం, L_s = 540 cal / g; నీటి విశిష్టోష్ణం, S_w = 1 cal / g°C
నీటి ద్రవ్యరాశి, m_w = 100g
మిశ్రమ పద్ధతి సూత్రం ప్రకారం
నీటి ఆవిరి కోల్పోయిన ఉష్ణరాశి = నీరు గ్రహించిన ఉష్ణరాశి
i.e., m_sL_s + m_sS_w (100 – t) = m_wS_w (t – 20)
⇒ m_s × 540 + m_s × 1(100 – 25) = 100 × 1 × (25 – 20)
⇒ 615m_s = 500 (or)m_s = \(\frac{500}{615}\) = 0.813 g

ప్రశ్న 4.
2 kg ల గాలిని స్థిర ఘనపరిమాణం వద్ద వేడిచేశారు. గాలి ఉష్ణోగ్రత 293 K నుంచి 313 K కు పెరిగింది. స్థిర ఘనపరిమాణం వద్ద గాలి విశిష్టోష్ణం 0.718kJ/kg K. అది శోషించుకొనే ఉష్ణ పరిమాణాన్ని kJ లలో, kcalలలో కనుక్కోండి. (J = 4.2 kJ/kcal.)
సాధన:
గాలి సాంద్రత m = 2 kg;
ఉష్ణోగ్రతలో మార్పు ∆T = 313 – 293 20K.
స్థిర ఘనపరిమాణ విశిష్టోష్ణము C_v = 0.718 k. J/kg – K.
ఉష్ణ యాంత్రిక తుల్యాంకము = J. = 4.2 kJ/k.cal.
C_v = \(\frac{1}{\mathrm{~m}} \frac{\mathrm{dQ}}{\mathrm{dT}}\) ⇒ dQ = mC_vdT (లేదా) dQ = \(\frac{\mathrm{mC}_{\mathrm{v}} \mathrm{dT}}{\mathrm{J}}\) cal.
∴ గాలి శోషించుకొనిన ఉష్ణరాశి Q = 2 × 0.718 × 10³ × 20 = 28.72 kJ = 6.838 k calories.

ప్రశ్న 5.
ఇత్తడి లోలకం కలిగిన ఒక గడియారం 20°C వద్ద సరియైన కాలాన్ని చూపుతుంది. ఉష్ణోగ్రత 30°C కు పెరిగినప్పుడు ఆ గడియారం రోజుకు 8.212 సెకనుల కాలం తక్కువ చూపుతుంది. ఇత్తడి దైర్ఘ్య వ్యాకోచ గుణకం కనుక్కోండి.
సాధన:
సరియైన కాలం వద్ద ఉష్ణోగ్రత t = 20°C;
ఒక రోజులో నష్టపోయిన లేక లాభపడిన కాలము = 8.212 sec.
తుది ఉష్ణోగ్రత t₂ = 30 C ∴ ∆t = 30 – 20 = 10;
లోలకం చేయబడిన పదార్థం α = ?
లోలకంలో ఒక రోజుకు నష్టపోయిన లేదా లాభపడిన సెకండ్ల సంఖ్య = 43,200. α ∆t
∴ α = \(\frac{8.212}{43.200 \times 10}\) = 19 × 10^-6 / C.

ప్రశ్న 6.
ఒక వస్తువు 7 నిమిషాలలో 60°C నుంచి 40°C కు చల్లబడుతుంది. పరిసరాల ఉష్ణోగ్రత 10°C అయితే, తదుపరి 7 నిమిషాల తరువాత అది ఎంత ఉష్ణోగ్రతకు చేరుకొంటుంది ?
సాధన:
మొదటి సందర్భము :
తొలి’ ఉష్ణోగ్రత, θ₁ = 60°C;
తుది ఉష్ణోగ్రత, θ₂ = 40°C
చల్లబడటానికి పట్టిన కాలము, t₁ = 7 నిమిషాలు = 7 × 60 = 420s ;
పరిసరాల ఉష్ణోగ్రత, θ₀ = 10°C
న్యూటన్ శీతలీకరణ నియమం ప్రకారం,
\(\frac{\mathrm{d} \theta}{\mathrm{dt}}\) = k \(\left[\frac{\theta_1+\theta_2}{2}-\theta_0\right]\) ⇒ \(\frac{60-40}{420}\) = k \(\left[\frac{60+40}{2}-10\right]\)
⇒ \(\frac{20}{420}\) = k × 40 …………….. (1)
రెండవ సందర్భము :
తొలి ఉష్ణోగ్రత, θ₁ = 40°C
చల్లబడటానికి పట్టిన కాలము, t₂ = 7 నిమిషాలు = 7 × 60 = 420s
న్యూటన్ శీతలీకరణ నియమం ప్రకారం,
\(\frac{50-\theta}{420}\) = k\(\left[\frac{50+\theta}{2}-10\right]\)
సమీకరణాలు (1) మరియు (2) లను సాధించగా, θ = 34°C

ప్రశ్న 7.
ఒక కృష్ణ వస్తువు గరిష్ఠ వికిరణ తీవ్రత 2.65 µ m వద్ద కనుక్కోవడమైంది. వికిరణాన్ని ఉద్గారం చేసే వస్తువు ఉష్ణోగ్రత ఎంత ? (వీన్ స్థిరాంకం = 2.9 × 10^-3 mK)
సాధన:
గరిష్ట తీవ్రత పద్ధతి తరంగదైర్ఘ్యం λ_max = 2.65 µm = 2.65 × 10^-6 m.
వస్తువు ఉష్ణోగ్రత T = ? వీన్ స్థిరాంకము b = 2.90 × 10^-3 mK.
వీస్ నియమం నుండి T = \(\frac{b}{\lambda_m}\) = \(\frac{2.90 \times 10^{-3}}{2.65 \times 10^{-6}}\) = 1094 K.

ముఖ్యమైన అదనపు లెక్కలు

ప్రశ్న 1.
నియాన్, కార్బన్-డై-ఆక్సైడ్ త్రిక బిందువులు వరుసగా 24.57 K, 216.55 K. ఈ ఉష్ణోగ్రతలను సెల్సియస్, ఫారన్హీట్ మానాలలో తెలియచేయండి.
సాధన:
కెల్విన్ మానము మరియు సెల్సియస్ మానముల మధ్య సంబంధము T_C = T_K – 273.15
ఇక్కడ T_C, T_K లు సెల్సియస్ మరియు కెల్విన్ మానాలలో ఉష్ణోగ్రతలు
నియాను, T_C = 24.57 – 273.15 = – 248.58°C
CO₂, T_C = 216.55 – 273.15 = – 56.60°C.
ఫారన్హీట్ మానము మరియు కెల్విన్ మానంల మధ్య గల సంబంధము = \(\frac{\mathrm{T}_{\mathrm{F}}-32}{180}=\frac{\mathrm{T}_{\mathrm{K}}-273.15}{100}\)
T_F = \(\frac{180}{100}\) (T_K – 273.15) + 12
నియాను, T_F = \(\frac{180}{100}\) (24.57 – 273.15) + 32 = -415.44°F
CO₂, T_F = \(\frac{180}{100}\) (216.55 – 273.15) + 32 = -69.88°F

ప్రశ్న 2.
A, B అనే రెండు పరమ ఉష్ణోగ్రతా మానాలు నీటి త్రిక బిందువును 200 A, 350 B గా నిర్వచించాయి. T_A, T_B మధ్య ఉన్న సంబంధం ఏమిటి ?
సాధన:
దత్తాంశం ప్రకారం, ఉష్ణోగ్రతా మానం A లో నీటి త్రిక బిందువు = 200A
ఉష్ణోగ్రతా మానం Bలో నీటి త్రిక బిందువు = 350 B.
మన ప్రశ్నను బట్టి, 200A = 350 B = 273.16 లేదా 1A = \(\frac{273.16}{200}\)K మరియు 1B = \(\frac{273.16}{350}\) K
T_A మరియు T_B అనునవి వరుసగా నీటి త్రిక బిందువులుగా మానము A మరియు మానము B లలో సూచిస్తే
\(\frac{273.16}{200}\) T_A = \(\frac{273.16}{350}\) T_B (లేదా) \(\frac{\mathrm{T}_{\mathrm{A}}}{\mathrm{T}_{\mathrm{B}}}\) = \(\frac{200}{350}\) = \(\frac{4}{7}\) (లేదా) T_A = \(\frac{4}{7}\) T_B

ప్రశ్న 3.
ఒక థర్మామీటర్ విద్యుత్ నిరోధం ఓమ్లలో ఉష్ణోగ్రతతో ఉజ్జాయింపు నియమం ప్రకారం క్రింది విధంగా మారుతుంది. R = R₀ [1 + α (T – T₀)]
నీటి త్రిక బిందువు 273.16 K వద్ద నిరోధం 101.6 Ω, సీసం ప్రమాణ ద్రవీభవన స్థానం 600.5 Ω వద్ద నిరోధం 165.5 Ω. ఏ ఉష్ణోగ్రత వద్ద నిరోధం 123.4 Ω అవుతుంది ?
సాధన:
దత్తాంశము నుండి R₀ = 101.6 Ω; T₀ = 273.16 K
సందర్భం (i) R₁ = 165.5 Ω; T₁ = 600.5 K
సందర్భం (ii) R₂ = 123.4 Ω; T₂ = ?
R = R₀ [1 + α (T – T₀)] నకు సందర్భము (i) ఉపయోగించిన
165.5 = 101.6 [1 + α (600.5 – 273.16)]
α = \(\frac{165.5-101.6}{101.6 \times(600.5-273.16)}=\frac{63.9}{101.6 \times 327.34}\)
సందర్భం (ii) నుండి 123.4 = 101.6 [1+ α(T₂ – 273.16)]
(లేదా) 123.4 = 101.6 [1 + \(\frac{63.9}{101.6 \times 327.34}\) (T₂ – 273.16)] = 101.6 + \(\frac{63.9}{327.34}\) (T₂ – 273.16)
(లేదా) T₂ = \(\frac{(123.4-101.6) \times 327.34}{63.9}\) + 273.16 = 111.67 + 273.16 = 384.83K

ప్రశ్న 4.
క్రింది వాటికి సమాధానాలు ఇవ్వండి :
(a) ఆధునిక ఉష్ణమితిలో నీటి త్రిక బిందువు ప్రమాణ స్థిర బిందువు. ఎందుకు ? మంచు ద్రవీభవన స్థానాన్ని, నీటి బాష్పీభవన స్థానాన్ని ప్రమాణ స్థిర బిందువులుగా తీసుకొంటే కలిగే తప్పు ఏమిటి ? (సెల్సియస్ మానంలో అదే విధంగా తీసుకోవడమైంది)
(b) సెల్సియస్ మానంలో పై ప్రశ్నలో తెలిపిన విధంగా రెండు స్థిర బిందువులు కలవు. వాటికి వరుసగా 0°C, 100°C సంఖ్యలను కేటాయించడమైంది. పరమమానంలో రెండు స్థిర బిందువుల్లో ఒకటి నీటి త్రిక బిందువుగా తీసుకొని కెల్విన్ మానంలో 273.16 K సంఖ్యను కేటాయించడమైంది. ఈ (కెల్విన్) మానంలో మరొక స్థిర బిందువు ఏమిటి ?
(c) పరమ ఉష్ణోగ్రత (కెల్విన్ మానం) T, సెల్సియస్ మానంపై ఉష్ణోగ్రత t_c కి మధ్య సంబంధం t_c = T – 273.15
ఈ సంబంధంలో 273.16 కాకుండా, 273.15 ను తీసుకోవడానికి కారణం ఏమిటి ?
(d) పరమ ఉష్ణోగ్రతా మానంలో యూనిట్ అంతరం ఫారన్హీట్ మానంలో యూనిట్ అంతరానికి సమానం అయితే పరమ ఉష్ణోగ్రత మానంపై నీటి త్రిక బిందువు ఉష్ణోగ్రత ఎంత ?
సాధన:
(a) నీటి త్రిక బిందువుకు ఒకే ఒక విలువ 273.16 K. ఒకే ఒక బిందువు వుండుట ఒక సత్యం. అక్కడ పీడనానికి మరియు ఘనపరిమాణానికి ఒకే ఒక విలువ కలిగి వుంటుంది. వేరే విధంగా తెలిపిన, పీడనము మరియు ఘనపరిమాణములో మార్పు వచ్చునప్పుడు, నీరు మరుగు స్థానము, బాష్పీభవన స్థానములకు ఒకే విలువ వుండక మార్పు చెందుతూ ఉంటాయి.

(b) కెల్విన్ మానం లేదా కెల్విన్ సంపూర్ణ మానం నందు నిర్దేశ బిందువే దాని సంపూర్ణ లేదా పరమ శూన్య బిందువు.

(c) సెల్సియస్ మానంలో ‘C అనునది సాధారణ పీడనం వద్ద మంచు మరుగు బిందువు. దానికి అనుగుణమైన పరమ ఉష్ణోగ్రత 273.15 K, 273.16 K అనే ఉష్ణోగ్రత నీటి త్రిక బిందువును సూచిస్తుంది. ఈ సంబంధంను బట్టి నీటి త్రిక బిందువు సెల్సియస్ మానం నందు = 273.16 – 273.15 = 0.01°C.

(d) ఫారన్ హీట్ మానం మరియు పరమ ఉష్ణోగ్రతల మధ్య సంబంధము

నీటి త్రిక బిందువు ఉష్ణోగ్రత 273.16 K అనునది కొత్త ఉష్ణోగ్రత మానంలో
= 273.16 × \(\frac{9}{5}\) = 491.69

ప్రశ్న 5.
A, B అనే ఆదర్శవాయు థర్మామీటర్లలో వరుసగా ఆక్సిజన్, హైడ్రోజన్ వాయువులను ఉపయోగించారు. కింది పరిశీలనలు చేయడమైంది.

(a) A, B థర్మామీటర్లు సూచించే సల్ఫర్ సాధారణ ద్రవీభవన స్థానం పరమ ఉష్ణోగ్రత ఎంత ?
(b) A, B థర్మామీటర్ల జవాబులో స్వల్పంగా తేడా ఉండటానికి గల కారణాన్ని మీరు ఏమని ఊహిస్తున్నారు ? (థర్మామీటర్లలో ఎలాంటి దోషం లేదు) రెండింటి రీడింగ్ల మధ్య ఉన్న తేడాను తగ్గించడానికి పై ప్రయోగంలో ఇంకా ఏ పద్ధతి అవసరం ?
సాధన:
సల్ఫర్ ద్రవీభవన స్థానంను “T” అనుకొనుము.
(a) థర్మామీటర్ A లో T = \(\frac{\mathrm{P}}{\mathrm{P}_{\mathrm{tr}}}\) × 273.16 = \(\frac{1.797 \times 10^5}{1.250 \times 10^5}\) × 273.16 = 392.69K
థర్మామీటర్ B లో T = \(\frac{\mathrm{P}}{\mathrm{P}_{\mathrm{tr}}}\) × 273.16 = \(\frac{0.287 \times 10^5}{0.200 \times 10^5}\) × 273.16 = 391.98 K

(b) థర్మామీటర్ A మరియు B ల సమాధానముల యందు స్వల్ప తేడా వచ్చుటకు కారణం ఆక్సిజన్ మరియు హైడ్రోజన్ వాయువులు కచ్చితమైన ఆదర్శవాయువులు కావు.

ఇలాంటి అసమానతను తగ్గించాలంటే, అతి తక్కువ పీడనం వద్ద పరిశీలనలను తీసుకోవాలి. ఇలాంటి సందర్భము నందు వాయువులు ఆదర్శ వాయు ప్రవర్తనకు దగ్గరగా వుండగలవు.

ప్రశ్న 6.
1m పొడవు ఉన్న ఉక్కు కొలబద్ద 27.0°C ఉష్ణోగ్రత వద్ద సరియైన కొలతను ఇచ్చే విధంగా క్రమాంకనం చేశారు. బాగా వేడిగా ఉన్న రోజు, అంటే 45.0°C ఉష్ణోగ్రత ఉన్నప్పుడు ఈ కొలబద్ద ఉక్కు కడ్డీ పొడవును 63.0 cm గా కొలిచింది. ఆ రోజున ఉక్కు కడ్డీ అసలు పొడవు ఎంత ? 27.0°C ఉష్ణోగ్రత ఉన్న రోజున అదే ఉక్కు కడ్డీ పొడవు ఎంత ? ఉక్కు దైర్ఘ్య వ్యాకోచ గుణకం = 1.20 × 10^-5°K^-1
సాధన:
27°C వద్ద ఉక్కు కొలబద్ద పొడవు 100 cm. i.e., L = 100 cm మరియు T = 27°C
45°C వద్ద ఉక్కు కొలబద్ద పొడవు L’ = L + ∆L = L + αL∆T
= 100 + (1.20 × 10^-5°) × 100 × (45° – 27°) = 100.0216 cm.
27°C వద్ద కొలబద్దపై 1 భాగము పొడవు 45°C = 100.0216/100 cm.
63 cm ల ఉక్కు కడ్డీని కొలచిన పొడవు 45°C = \(\frac{100.0216}{100}\) × 63 = 63.0136 cm
27°C ఉష్ణోగ్రత ఉన్న రోజున అదే ఉక్కు కడ్డీ పొడవు = 63 × 1 = 63 cm.

ప్రశ్న 7.
ఒక పెద్ద ఉక్కు చక్రాన్ని అదే పదార్థంతో చేసిన కమ్మీపై 27°C ఉష్ణోగ్రత వద్ద బిగించాలి. ఆ కమ్మీ వెలుపల వ్యాసం 8.70 cm, చక్రం మధ్య ఉన్న రంధ్రం వ్యాసం 8.69 cm. కమ్మీని పొడి మంచు ఉపయోగించి చల్లబరచారు. కమ్మీ ఏ ఉష్ణోగ్రత వద్ద చక్రాన్ని కమ్మీపై బిగించవచ్చు. మనకు కావలసిన ఉష్ణోగ్రత అవధిలో ఉక్కు దైర్ఘ్య వ్యాకోచ గుణకం స్థిరంగా ఉంటుంది అని అనుకోండి. α_{ఉక్కు} 1.20 × 10^-5 K^-1.
సాధన:
ఇచ్చట T₁ = 27°C = 27 + 273 = 300 K.
T₁K ఉష్ణోగ్రత వద్ద పొడవు = l_T1 = 8.70 cm;
T₂ K ఉష్ణోగ్రత వద్ద పొడవు = l_T2 = 8.69 cm
పొడవులో మార్పు = l_T2 – l_T1 = l_T1 α (T₂ – T₁) (లేదా) 8.69 – 8.70 = 8.70 × (1.20 × 10^-5) (T₂ – 300)
(లేదా) T₂ – 300 = – \(\frac{0.01}{8.70 \times 1.2 \times 10^{-5}}\) = -95.8 (లేదా) T₂ = 300 – 95.8 = 204.2 K = – 68.8°C.

ప్రశ్న 8.
ఒక రాగి పలకలో రంధ్రం చేశారు. 27°C వద్ద ఆ రంధ్రం వ్యాసం 4.24 cm. ఆ పలకను 227°C కు వేడిచేసినప్పుడు ఆ రంధ్రం వ్యాసంలో కలిగే మార్పు ఎంత ? రాగి దైర్ఘ్య వ్యాకోచ గుణకం = 1.70 × 10^-5 K^-1
సాధన:
ఈ లెక్కలో వేడిచేసినపుడు రాగి రేకు విస్తీర్ణ వ్యాకోచము ఇమిడి ఉంటుంది.
27°C వద్ద రంధ్రం వైశాల్యం, S₁ = \(\frac{\pi \mathrm{D}_1^2}{4}=\frac{\pi}{4}\) × (4.24)² cm²
227°C వద్ద రంధ్రం వ్యాసార్ధం, D₂ cm అయిన
227°C వద్ద రంధ్రం వైశాల్యం, S₂ = \(\frac{\pi \mathrm{D}_2^2}{4}\) cm².
రాగి విస్తీర్ణ వ్యాకోచ గుణకం β = 2 α = 2 × 1.70 × 10^-5 = 3.4 × 10^-5 °C^-1
వైశాల్యంలో పెరుగుదల = S₂ – S₁ = βS₁∆T (లేదా) S₂ = S₁ + βS₁∆T = S₁ (1 + β∆T)
\(\frac{\pi \mathrm{D}_2^2}{4}=\frac{\pi}{4}\) (4.24)² [1 + 3.4 × 10^-5 (228 – 27)] (లేదా) D₂² = (4.24)² × 1.0068
D₂ = 4.2544 cm
వ్యాసంలో మార్పు = D₂ – D₁ = 4.2544 – 4.24 = 0.0144 cm

ప్రశ్న 9.
1.8 m పొడవు, 20 mm వ్యాసం ఉన్న ఒక ఇత్తడి తీగను 27°C వద్ద రెండు దృఢమైన ఆధారాల మధ్య తీగలో స్వల్ప తన్యత ఉండేటట్లు బిగించారు. ఒకవేళ తీగను -39°C ఉష్ణోగ్రతకు చల్లబరిస్తే, తీగలో ఏర్పడే తన్యత ఎంత ? తీగ వ్యాసం 2.0 mm. ఇత్తడి దైర్ఘ్య వ్యాకోచ గుణకం 2.0 × 10^-5 K^-1; ఇత్తడి యంగ్ గుణకం = 0.91 × 10¹¹ Pa.
సాధన:
ఇచ్చట L = 1.8 m, T₁ = 27°C, T₂ = -39°C, F = ?, r = 1 mm = 10^-3 m,
α = 2 × 10^-5 °K^-1, Y = 0.91 × 10¹¹ N/m²
Y = \(\frac{F \cdot L}{a \Delta L}\) . ∆L = \(\frac{F L}{a Y}\) నుండి
ఇంకా ∆L = α L ∆T ∴ \(\frac{F L}{a Y}\) = α L ∆T (లేదా) F = α∆TaY = α(T₂ – T₁) πr²Y
= 2 × 10^-5 × (39 – 27) × \(\frac{22}{7}\) (10^-3)² × 0.91 × 10¹¹ = -3.77 × 10² N
తీగ సంకోచం చెందునపుడు బలం లోపలి వైపు పనిచేయును అని ఋణగుర్తు తెలుపుతున్నది.

ప్రశ్న 10.
50 cm పొడవు, 3.0 mm వ్యాసం ఉన్న ఒక ఇత్తడి కడ్డీని అంతే పొడవు, వ్యాసం ఉన్న మరొక ఉక్కు కడ్డీతో జతపరచారు. వాటి తొలి పొడవులు 40°C వద్ద ఉంటే, 250°C ఉష్ణోగ్రత వద్ద ఆ సంయోగ కడ్డీ పొడవులో కలిగే మార్పు ఎంత ? ఆ రెండు కడ్డీలు కలిసే సంధి వద్ద ఉష్ణప్రతిబలం ఏర్పడుతుందా ? కడ్డీ ఛివరి కొనలు స్వేచ్ఛగా వ్యాకోచించగలవు. (ఇత్తడి, ఉక్కు కడ్డీల దైర్ఘ్య వ్యాకోచ గుణకాలు వరుసగా 2.0 × 10^-5K^-1, 1.2 × 10^-5 K^-1).
సాధన:
∆L₁ =L₁α₁∆T= 50 × (2.10 × 10^-5 )(250 – 40) = 0.2205 cm
∆L₂ = L₂α₂∆T = 50(1.2 × 10^-5) (250 – 40) = 0.126 cm
∴ సంయోగ కడ్డీలో మార్పు = ∆L₁ + ∆L₂ = 0.220 + 0.126 = 0.346 cm

ప్రశ్న 11.
గ్లిసరిన్ ఘనపరిమాణ వ్యాకోచ గుణకం 49 × 10^-5K^-1. ఉష్ణోగ్రతను 30°C కు పెంచితే దాని సాంద్రతలో కలిగే అంశిక మార్పు ఎంత ?
సాధన:
ఇచ్చట γ = 49 × 10^-5K^-1,
∆T = 30°C
V’ = V + ∆V = V(1 + γ∆T)
∴ V’ =V(1 + 49 × 10^-5 × 30) = 1.0147 V
ρ = కనుక ρ’ = \(\frac{\mathrm{m}}{\mathrm{V}^{\prime}}=\frac{\mathrm{m}}{1.0147 \mathrm{~V}}\) = 0.9855p
సాంద్రతలో కలిగే అంశిక మార్పు = \(\frac{\rho-\rho^{\prime}}{\rho}=\frac{\rho-0.9855 \rho}{\rho}\) = 0.0145

ప్రశ్న 12.
8.0 kg ద్రవ్యరాశి ఉన్న ఒక చిన్న అల్యూమినియం దిమ్మెలో రంధ్రం వేయడానికి 10kW (రంధ్రాలు చేసే) యంత్రాన్ని ఉపయోగించారు. 50% యంత్రం సామర్థ్యం యంత్రం వేడెక్కడానికి లేదా పరిసరాలలోకి ఉష్ణ నష్టం జరగడానికి ఉపయోగపడింది అనుకొంటే 2.5 నిమిషాలలో దిమ్మె ఉష్ణోగ్రతలో కలిగే పెరుగుదల ఎంత ? అల్యూమినియం విశిష్ట గుప్తోష్ణం = 0.91 Jg^-1 °K^-1,
సాధన:
ఇచ్చట P = 10 k W = 10⁴W, ద్రవ్యరాశి,m = 8.0 kg = 8 × 10³ g
ఉష్ణోగ్రతలో తగ్గుదల AT = ?, కాలం t = 2.5 నిమిషాలు = 2.5 × 60 = 150s
రాగి విశిష్టోష్టం, C = 0.91 Jg^-1 K^-1
మొత్తం శక్తి Q = P × t = 10⁴ × 150 = 15 × 10⁵ J
50% శక్తి నష్టపోయిన ఉపయోగించుటకు వీలుగా వున్న శక్తి ∆Q = \(\frac{1}{2}\) × 15 × 10⁵ = 7.5 × 10⁵ J
As, ∆Q = m c ∆T
∴ ∆T = \(\frac{\Delta Q}{\mathrm{mc}}=\frac{7.5 \times 10^5}{8 \times 10^3 \times 0.91}\) = 103°C

ప్రశ్న 13.
2.5 kg ద్రవ్యరాశి ఉన్న ఒక రాగి దిమ్మెను కొలిమిలో 500°C ఉష్ణోగ్రతకు వేడిచేసి ఒక పెద్ద మంచు దిమ్మెపై ఉంచారు. అప్పుడు గరిష్ఠంగా కరిగే మంచు పరిమాణం ఎంత ? (రాగి విశిష్టోష్ణం = 0.39 Jg^-1 K^-1 నీటి ద్రవీభవన గుప్తోష్ణం = 335 Jg^-1 ).
సాధన:
రాగి దిమ్మె ద్రవ్యరాశి m = 2.5 kg = 2500 g ;
రాగి విశిష్టోష్ణం c = 0.39 J g^-1 K^-1;
ఉష్ణోగ్రతలో తగ్గుదల ∆T = 500 – 0 = 500°C
ద్రవీభవన గుప్తోష్ణం L = 335 J g^-1
కరుగుచున్న మంచు ద్రవ్యరాశిని m’ అని అనుకొనుము.
మంచు గ్రహించిన ఉష్ణరాశి = రాగి కోల్పోయిన ఉష్ణరాశి
∴ m’L = mc ∆T
m’ = \(\frac{\mathrm{mc} \Delta \mathrm{T}}{\mathrm{L}}=\frac{2500 \times 0.39 \times 500}{335}\) = 1500g = 1.5kg

ప్రశ్న 14.
ఒక పదార్థం విశిష్టోష్ణం కనుక్కొనే ప్రయోగంలో 150°C వద్ద ఉన్న 0.20 kg ల ఒక లోహపు దిమ్మెను 27°C వద్ద 150 cm3 నీరు ఉన్న కెలోరిమీటరు (జల తుల్యాంకం 0.025 kg) లోకి జారవిడిచారు. తుది ఉష్ణోగ్రత 40°C. లోహపు దిమ్మె విశిష్టోష్ణం గణన చేయండి. పరిసరాలలోకి నష్టపోయిన ఉష్ణం విస్మరించదగినంత కాకపోతే మీ సమాధానం ఆ పదార్థం విశిష్టోష్టం అసలు విలువ కంటే ఎక్కువగా ఉంటుందా లేదా తక్కువగా ఉంటుందా ?
సాధన:
లోహం ద్రవ్యరాశి m = 0.20 kg = 200 g
లోహం ఉష్ణోగ్రతలో తగ్గుదల ∆T = 150 – 40 = 110°C
‘C’ అనునది లోహం విశిష్టోష్టం అయిన లోహం కోల్పోయిన ఉష్ణరాశి
∆Q = mC∆T = 200 × c × 110 ………………. (i)
నీటి ఘనపరిమాణం = 150 c.c.
∴ నీటి ద్రవ్యరాశి m’. = 150 g
కైలోరి మీటరు నీటి తుల్యాంకం w = 0.025 kg = 25 g
నీటి మరియు కెలోరీ మీటరు ఉష్ణోగ్రతలో పెరుగుదల ∆T’ = 40 – 27 = 13°C
నీరు మరియు కెలోరీ మీటరు గ్రహించిన ఉష్ణరాశి
∆Q’ = (m’ + w)∆T’ = (150 + 25) × 13 = 175 × 13 …………….. (ii)
∆Q = ∆Q’ కావున
∴ (i) మరియు (ii) సమీకరణముల నుంచి 200 × c × 110 = 175 × 13 (లేదా) c = \(\frac{175 \times 13}{200 \times 110}\) ≈ 0.1.
పరిసరాలకు కొంత ఉష్ణం నష్టపోవడం వలన నిజ విలువ కన్నా సాధించిన c విలువ తక్కువగా ఉంటుంది.

ప్రశ్న 15.
గది ఉష్ణోగ్రత వద్ద కొన్ని సాధారణ వాయువుల మోలార్ విశిష్టోష్టాలపై చేసిన పరిశీలనలు కింద ఇవ్వడమైంది.

ఈ విధంగా కొలచిన వాయువుల మోలార్ విశిష్టోష్ట విలువలు ఏక పరమాణు వాయువుల విలువల కంటె విశేషంగా భిన్నమైనవి. ఉదాహరణకు, ఏక పరమాణుక వాయువు మోలార్ విశిష్టోష్ణం 2.92 cal/mol K. ఈ వ్యత్యాసం ఎందుకో వివరించండి. క్లోరిన్ విలువ కొంత వరకు అధికంగా (మిగతా వాటి కంటే) ఉండటాన్ని బట్టి ఏమి చెప్పవచ్చు ?
సాధన:
పైన పట్టికలో ఇవ్వబడిన వాయువుల ద్వి పరమాణు వాయువులు, ఏక పరమాణు వాయువులు కావు. ద్విపరమాణువు వాయువుల మోలార్ విశిష్టోష్ణం = \(\frac{1}{2}\)R = \(\frac{5}{2}\) × 1.98=4 .95 ఈ పట్టిక నందు ఇచ్చిన పరిశీలనల దృష్ట్యా క్లోరిన్ మినహాయించి మిగిలిన వాయువులు అన్నియూ నియమానుసారం ఉన్నట్లుగా ఆమోదించవచ్చును. ఏక పరమాణు వాయువులలో β అణువులకు స్థానాంతర చలనం మాత్రమే ఉంటుంది.

ద్వి పరమాణువు వాయువులో β అణువులు స్థానాంతర చలనంతో పాటు కంపన మరియు భ్రమణ చలనాలను కూడా కలిగి ఉంటాయి. అందువలన 1 మోల్ ద్విపరమాణు వాయువు ఉష్ణోగ్రతను 1°C పెంచుటకు, స్థానాంతర శక్తితో పాటుగా, భ్రమణ మరియు కంపన శక్తులను పెంచుటకు కావలసిన ఉష్ణరాశిని సరఫరా చేయవలెను. అందువల్ల మోలార్ విశిష్టోష్టం ఏక పరమాణు వాయువుల కన్నా ద్వి పరమాణు వాయువులకు ఎక్కువ.

గది ఉష్ణోగ్రత వద్ద క్లోరిన్ మోలార్ విశిష్టోష్ణం విలువ మిగిలిన ద్విపరమాణు వాయువులు హైడ్రోజన్, నైట్రోజన్, ఆక్సిజన్ మొ॥ కన్నా అధికముగా ఉండటాన్ని బట్టి క్లోరిన్క స్థానాంతర, భ్రమణ చలనాలతో పాటు కంపన చలనాలు కూడా ఉంటాయి. మిగిలిన వాయువులకు స్థానాంతర మరియు భ్రమణ చలనాలు మాత్రమే ఉంటాయి. ఈ కారణం వలన క్లోరిన్ వాయువు కొంత అధిక మోలార్ విశిష్టోష్ణం విలువను కలిగి ఉంటుంది.

ప్రశ్న 16.
కార్బన్ డై ఆక్సైడ్ P-T ప్రావస్థా పటం ఆధారంగా కింది ప్రశ్నలకు సమాధానాలను ఇవ్వండి.
(a) ఏ ఉష్ణోగ్రతా పీడనాల వద్ద సమతాస్థితిలో CO₂ ఘన, ద్రవ, బాష్ప స్థితులు కలిసి ఉంటాయి ?
(b) CO₂ ఘనీభవన, బాష్పీభవన స్థానాలపై పీడన తగ్గుదల ప్రభావమేమిటి ?
(c) CO₂ సందిగ్ధ ఉష్ణోగ్రత, పీడన విలువలు ఏమిటి ? వాటి ప్రాముఖ్యత ఏమిటి ?
(d) క్రింది వివిధ సందర్భాలలో CO₂ ఘనమా, ద్రవమా లేదా వాయువా తెలపండి. a) 1atm, – 70°C వద్ద b) 10atm, -60°C వద్ద c) 56 atm, 15°C వద్ద ?

సాధప:
(a) -56.6° C ఉష్ణోగ్రత, 5.11 వాతావరణ పీడనం (త్రిక బిందువు) ల వద్ద CO₂, ఘన, ద్రవ మరియు బాష్ప స్థితులు కలసి ఉంటాయి.

(b)పీడనాన్ని తగ్గిస్తూ ఉంటే, CO₂ యొక్క ఘనీభవన మరియు బాష్పీభవన స్థానాలు తగ్గుతాయి.

(c) CO₂ సందిగ్ధ ఉష్ణోగ్రత విలువ 31.1°C మరియు సందిగ్ధ పీడనము విలువ 73 వాతావరణ పీడనము. CO₂ ఉష్ణోగ్రత 31.1°C కన్నా పెంచినపుడు ఎంత ఎక్కువ పీడనాన్ని ప్రయోగించిన అది ద్రవంగా మారదు.

(d) (a) 1 atm, -70° C వద్ద CO₂ వాయువు వాయు స్థితిలో ఉంటుంది.
(b) 1 atm, -60°C వద్ద CO₂ ఘన స్థితిలో ఉంటుంది.
(c) 56 atm, 150°C వద్ద CO₂ ద్రవ స్థితిలో ఉంటుంది.

ప్రశ్న 17.
CO₂ P-T ప్రావస్థా పటం ఆధారంగా క్రింది ప్రశ్నలకు సమాధానాలు ఇవ్వండి.
(a) 1 atm పీడనం, -60°C ఉష్ణోగ్రత వద్ద CO₂ ను సమోష్ణోగ్రతా ప్రక్రియలో సంపీడనం చెందిస్తే దానిలో మార్పు ద్రవ ప్రావస్థ ద్వారా జరుగుతుందా ?
(b) 4 atm పీడనం వద్ద ఉన్న CO₂ను స్థిర పీడనం వద్ద గది ఉష్ణోగ్రత నుంచి చల్లబరిస్తే ఏమవుతుంది ?
(c) 10 atm పీడనం, -65°C ఉష్ణోగ్రత వద్ద నిర్దిష్ట ద్రవ్యరాశి ఉన్న ఘన CO₂ ను స్థిర పీడనం వద్ద గది ఉష్ణోగ్రతకు వేడిచేస్తే, దానిలో కలిగే మార్పులను గుణాత్మకంగా వివరించండి.
(d) CO₂ను 70°C ఉష్ణోగ్రతకు వేడిచేసి సమోష్ణోగ్రతా ప్రక్రియలో సంపీడనం చెందించారు. దాని ధర్మాలలో ఎలాంటి మార్పులు కలుగుతాయో మీరు ఊహించగలరా ?
సాధన:
(a) 60°C ఉష్ణోగ్రత వక్రంలో 56.6°C కు ఎడమవైపు ఉన్నది. అనగా ఇది ఘన మరియు బాష్ప ప్రదేశాలలో ఉంటుంది. కావున CO₂ ద్రవ ప్రావస్థను చేరకుండా బాష్ప ప్రావస్థ నుండి ఘన ప్రావస్థను చేరుతుంది.

(b) CO₂ పీడనం 4 atm విలువ 5.11 atm ల కన్నా తక్కువగా ఉన్నది కావున, అది ద్రవ ప్రావస్థను పొందకుండా నేరుగా ఘనీభవిస్తుంది.

(c) 10 atm పీడనం, -65°C ఉష్ణోగ్రత వద్ద నిర్దిష్ట ద్రవ్యరాశి ఉన్న ఘన CO₂ ను స్థిర పీడనం వద్ద వేడిచేస్తే ఘన స్థితి నుండి ద్రవ స్థితికి మారి ఆ తరువాత బాష్ప స్థితికి చేరుతుంది. P-T పటంలో క్షితిజ సమాంతర రేఖ 10 atm స్థిర పీడనం వద్ద ఘనీభవన, బాష్పీభవన వక్రాలను ఖండించే బిందువులు ఘనీభవన, బాష్పీభవన బిందువులను ఇస్తాయి.

(d) CO₂ ను 70°C ఉష్ణోగ్రతకే వేడిచేసి సమ ఉష్ణోగ్రతా ప్రక్రియలో సంపీడనం చెందించిన ద్రవస్థితికి పరివర్తనను విస్పష్టంగా ప్రదర్శించదు. ఎందుకనగా వాయువు ఉష్ణోగ్రత, సందిగ్ధ ఉష్ణోగ్రత కన్నా ఎక్కువ. కాని పీడనం అధికమయ్యే కొలదీ ఆదర్శ వాయు ప్రవర్తన నుంచి విచలనము పెరుగుతుంది.

ప్రశ్న 18.
ఒక బాలుడు 101°F ఉష్ణోగ్రత జ్వరంతో ఉన్నాడు. అతడు జ్వరాన్ని తగ్గించే ఆంటీసైరిన్ మాత్ర తీసుకొన్నప్పుడు ఆ మాత్ర కారణంగా అతని దేహం నుంచి వెలువడే చెమట ఆవిరయ్యే రేటు పెరుగుతుంది. 20 నిమిషాలలో బాలుడి జ్వరాన్ని 98°Fకు తగ్గిస్తే, ఆ మాత్ర వల్ల కలిగే ఆదనపు ఆవిరయ్యే రేటు ఎంత ? ఆవిరిగా మారే క్రియ వల్లనే ఉష్ణ నష్టం జరుగుతుంది అనుకోండి. బాలుడి ద్రవ్యరాశి 30 kg. మానవ దేహం విశిష్టోష్ణం ఉజ్జాయింపుగా నీటి విశిష్టోష్ణానికి సమానం. ఆ ఉష్ణోగ్రత వద్ద నీటి ఆవిరి గుప్తోష్టం సుమారుగా 580 cal g^-1,
సాధన:
ఉష్ణోగ్రతలో తగ్గుదల, ∆T = 101 – 98 = 3°F = 3 × \(\frac{5}{9}\)°C = 5/3°C
బాలుడు ద్రవ్యరాశి, m = 30 kg
మానవ శరీరం విశిష్టోష్ణం = నీటి విశిష్టోష్ణం c = 1000 cal. kg^-1 °C^-1
∴ బాలుడు నష్టపోయిన ఉష్ణరాశి, ∆Q = mc∆T = 30 × 1000 × \(\frac{5}{3}\) = 50000 cals
20 నిమిషాలలో ఆవిరి అయిన నీటి ద్రవ్యరాశి m’ అయిన m’L = ∆Q (లేదా) m’ = \(\frac{\Delta Q}{L}\) = \(\frac{50000}{580}\) = 86.2g
∴ అధికంగా ఆవిరి కాబడిన నీటి సగటు రేటు = \(\frac{86.2}{20}\) = 4.31 g min^-1

ప్రశ్న 19.
ప్రత్యేకంగా వేసవి కాలంలో తక్కువ పరిమాణంలో వండిన ఆహారాన్ని నిల్వ చేయడానికి చౌకయిన, సమర్థవంతమైన పద్ధతి థర్మోకోల్ మంచుపెట్టె. 30 cm పొడవు గల ఘన మంచు పెట్టె మందం 5.0 cm. ఆ పెట్టెలో 4.0 kg ల మంచును ఉంచారు. 6 గంటల తరువాత మిగిలి ఉండే మంచు పరిమాణాన్ని అంచనా వేయండి. వెలుపలి ఉష్ణోగ్రత 45°C, థర్మోకోల్ ఉష్ణ వాహకత్వ గుణకం 0.01 J s^-1 m^-1K^-1 [నీటి ద్రవీభవన ఉష్ణం = 335 × 10^-3 J kg^-1]
సాధన:
మంచు పెట్టె పొడవు, l = 30 cm = 0.3 m;
మందం, ∆x = 5 cm = 0.05 m
మొత్తం ఉపరితల వైశాల్యం, A = 6l² = 6 × 0.3 × 0.3 = 0.54 m²
ఉష్ణోగ్రతలో వ్యత్యాసము, ∆T = 45 – 0 = 45°C, K = 0.01 Js^-1 m^-1 K^-1
కాలం = ∆t = 6hrs = 6 × 60 × 60s
ద్రవీభవన గుప్తోష్టం, L = 335 × 10³ J / kg
ఈ కాలంలో కరిగిన మంచు ద్రవ్యరాశిని ‘m’ అనుకొనిన ∆Q = mL = KA\(\left(\frac{\Delta \mathrm{T}}{\Delta \mathrm{x}}\right)\)ΔΤ
m = KA \(\left(\frac{\Delta \mathrm{T}}{\Delta \mathrm{x}}\right) \frac{\Delta \mathrm{t}}{\mathrm{L}}\) = 0.01 × 0.54 × \(\frac{45}{0.05}\) × \(\frac{6 \times 60 \times 60}{335 \times 10^3}\) = 0.313kg
∴ మిగిలిన మంచు ద్రవ్యరాశి = 4 – 0.313 = 3.687 kg.

ప్రశ్న 20.
ఒక ఇత్తడి బాయిలర్ అడుగు భాగం వైశాల్యం 0.15 m², మందం 1.0 cm. దీనిని ఒక గ్యాస్ స్టవ్ పై పెట్టినప్పుడు 6.0 kg/min రేటున నీటిని మరిగిస్తుంది. బాయిలర్తో స్పర్శలో ఉన్న మంటలోని కొంత భాగం ఉష్ణోగ్రతను అంచనా వేయండి. ఇత్తడి-ఉష్ణవాహకత్వం = 109 J s^-1 m^-1 K^-1; నీటి బాష్పీభవన ఉష్ణం = 2256 × 10³ J kg^-1.
సాధన:
ఇచ్చట A = 0.15 m², ∆x = 1.0 cm = 10^-2 m.
\(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{t}}=\frac{6 \times 10^3 \times 2256}{60}\) Js^-1 = 2256 × 10² Js^-1
K = 609 J s^-1 m^-1 °C^-1, ∆T = (t-100)
\(\frac{\Delta Q}{\Delta t}\) = KA \(\left(\frac{\Delta T}{\Delta \mathrm{x}}\right)\) నుండి 2256 × 10² = 609 × 0.15\(\frac{(\mathrm{t}-100)}{10^{-2}}\)
t – 100 = \(\frac{2256}{609 \times 0.15}\) = 24.70
⇒ t = 124.70°C

ప్రశ్న 21.
ఎందుకో వివరించండి :
(a) అధిక పరావర్తకత ఉన్న వస్తువు అధమ ఉద్గారకం.
(b) అతి శీతలంగా ఉన్న రోజు చెక్క పళ్ళెం కంటే ఇత్తడి పాత్ర చాలా చల్లగా ఉంటుంది.
(c) పరిపూర్ణ కృష్ణ వస్తువు వికిరణానికి క్రమాంకనం చేసిన దృశా పైరామీటరు (అధిక ఉష్ణోగ్రత కొలవడానికి) బాహ్య ప్రదేశంలో ఉన్న బాగా ఎర్రగా వేడెక్కిన ఇనుప కడ్డీ ఉష్ణోగ్రతను చాలా తక్కువ విలువగా చూపుతుంది. కాని, అదే కడ్డీని కొలిమిలో అమర్చినప్పుడు ఆ ఉష్ణోగ్రత వద్ద సరైన విలువను చూపుతుంది.
(d) భూమిపై భూ వాతావరణం లేకుంటే జీవకోటి ఉండటానికి వీలులేనంత చల్లగా ఉండేది.
(e) వేడి నీటిని ప్రవహింపచేయడంపై ఆధారపడ్డ తాపన వ్యవస్థ కంటే ఆవిరిని ప్రవహింప చేయడంపై ఆధారపడ్డ తాపన వ్యవస్థ చాలా సమర్థవంతంగా భవంతిని వేడి చేయగలదు.
సాధన:
(a) అధిక పరావర్తకత కలిగిన వస్తువు ఉష్ణాన్ని అధమంగా శోషించుకుంటుంది. ప్రివోస్ట్ సిద్ధాంతము ప్రకారము అధమ శోషకాలు, అధమ ఉద్గారకాలు.

(b) అతిశీతలంగా ఉన్న రోజున ఇత్తడి పాత్రను తాకిన, ఉష్ణం మనిషి శరీరం నుండి ఇత్తడి పాత్రకు ప్రవర్తిస్తుంది. అందువల్ల ఇత్తడి పలక చల్లగా ఉంటుంది. చెక్క పళ్ళెంను తాకిన, ఉష్ణం మనిషి శరీరం నుండి పళ్ళెంనకు ప్రసరించదు.

(c) కొలమిలో అమర్చి బాగా ఎర్రగా వేడిచేసిన ఇనుపకడ్డీ ఉష్ణోగ్రత TK ను E = σT^-1 అను సంబంధము ద్వారా రాబట్టవచ్చు. T_o ఉష్ణోగ్రత కలిగిన బాహ్య ప్రదేశంలో ఉంచిన బాగా ఎర్రగా వేడెక్కిన ఇనుప కడ్డీ విడుదల చేసే శక్తిని, E = σ(T⁴ – T_o^4-) అను సంబంధము ద్వారా కనుగొనవచ్చు.

దృశ్యా పైరోమీటరు అను పరికరము వస్తువు యొక్క ప్రకాశం, దాని ఉష్ణోగ్రతపై ఆధారపడి ఉంటుందనే సూత్రముపై పనిచేస్తుంది. అందువల్ల బాహ్య ప్రదేశంలో ఉంచిన ఇనుప కడ్డీ ఉష్ణోగ్రతను చాలా తక్కువగా చూపుతుంది.

(d) సూర్యుని నుంచి భూమికి వచ్చే ఉష్ణ వికిరణాలలో పరారుణ వికిరణాలను భూవాతావరణంలోని పొరలు పరావర్తనం చెందించి భూఉపరితలానికి చేరుస్తాయి. దీని ఫలితంగా భూవాతావరణం వెచ్చగా ఉంటుంది. భూమిపై భూవాతావరణం లేకుంటే, పరారుణ వికిరణాలు పరావర్తనం జరగక జీవకోటి ఉండటానికి వీలు లేనంత చల్లగా ఉంటుంది.

(e) 100°C ఉష్ణోగ్రత వద్ద ఉన్న బాష్పం, 100°C ఉష్ణోగ్రత వద్ద ఉన్న అంతే ద్రవ్యరాశి కలిగిన వేడి నీటికన్నా ఎక్కువ ఉష్ణరాశిని కలిగియుంటుంది. 100°C వద్ద ఉన్న 1 గ్రామ్ నీటి ఉష్ణం కన్నా, 100°C వద్ద ఉన్న 1 గ్రామ్ బాష్పం 540 కెలరీల ఎక్కువ ఉష్ణరాశిని కలిగియుంటుంది. కావున వేడినీటిని ప్రవహింపచేయడంపై ఆధారపడ్డ తాపన వ్యవస్థ కంటే ఆవిరిని ప్రవహింపచేయటంపై ఆధారపడ్డ తాపన వ్యవస్థ చాలా సమర్థవంతంగా భవంతిని వేడి చేయగలదు.

ప్రశ్న 22.
ఒక వస్తువు 5 నిమిషాలలో 80°C నుంచి 50°C కు చల్లబడుతుంది. 60°C నుంచి 30°C కు చల్లబడటానికి పట్టే కాలం కనుక్కోండి. పరిసరాల ఉష్ణోగ్రత 20°C.
సాధన:
వస్తువు ఉష్ణోగ్రత మరియు పరిసరాల ఉష్ణోగ్రతలు వరుసగా T మరియు T_o అయిన న్యూటన్ శీతలీకరణ సిద్ధాంతము ప్రకారము
\(\frac{\mathrm{dT}}{\mathrm{dt}}\) = -K(T – T_o) (లేదా) \(\frac{\mathrm{dT}}{\mathrm{T}-\mathrm{T}_0}\) = -K dt
వస్తువు ఉష్ణోగ్రత T₁ నుంచి T₂ వరకు t అనే కాలంలో తగ్గిన పై సంబంధాన్ని సమాకలనం చేయగా

ప్రశ్నలోని మొదటి సందర్భమునకు,
T₁ = 80°C,
T₂ = 50°C,
T₀ = 20°C,
t = 5 min. = 5 × 60s

(లేదా) t = 5 × 60 × 2 = 10 × 60s = 10 min.

Students must practice these TS Intermediate Maths 1A Solutions Chapter 5 Products of Vectors Ex 5(b) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Products of Vectors Solutions Exercise 5(b)

I.
Question 1.
If |p̅| = 2, |q̅| = 3 and (p, q) = \(\frac{\pi}{6}\), then find |p̅ × q̅|².
Answer:
p̅ × q̅ = |p̅| |q̅| sinθn̂
Given p̅ = 2, q̅ = 3 and (p̅. q̅) = \(\frac{\pi}{6}\)
|p̅ × q̅| = (2) (3)sin\(\frac{\pi}{6}\) = 3
∴ |p̅ × q̅|² = 9

Question 2.
If a̅ = 2i̅ – j̅ + k̅ and b̅ = i̅ – 3j̅ – 5k̅, then find |a̅ × b̅|. (March 2013)
Answer:
a̅ = 2 i̅ – j̅ + k̅ and b̅ = i̅ – 3 j̅ – 5k̅

Question 3.
If a̅ = 2i̅ – 3j̅ + k̅ and b̅ = i̅ + 4j̅ – 2k̅, then find (a̅ + b̅) × (a̅ – b̅).
Answer:
Given a̅ = 2i̅ – 3j̅ + k̅ and b̅ = i̅ + 4j̅ – 2k̅
Then a̅ + b̅ = 3 i̅ + j̅ – k̅ and a̅ – b̅ = i̅ – 7j̅ + 3k̅
(a + b) × (a – b) = \(\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
3 & 1 & -1 \\
1 & -7 & 3
\end{array}\right|\)
= i̅(3 – 7) – j̅(9 + l) + k̅ (- 21 – 1)
= -4i̅ – 10j̅ – 22k̅
= -2 (2i̅ + 5j̅ + 11k̅)

Question 4.
If 4i̅ + \(\frac{2 p}{3}\) j̅ + pk̅ is parallel to the vector 3 i̅ + 2j̅ + 3k̅, find p.
Answer:
Given 4i̅ + \(\frac{2 p}{3}\) j̅ + pk̅ is parallel to
i̅ + 2j̅ + 3k̅
∴ \(\frac{4}{1}=\frac{\frac{2 p}{3}}{2}=\frac{p}{3}\)
⇒ \(\frac{2 p}{3}\) = -4 ⇒ p = 12

Question 5.
Compute
a̅ × (b̅ + c̅) + b̅ × (c̅ + a̅) + c̅ × (a̅ + b̅)
Sol.
a̅ × (b̅ + c̅) + b̅ × (c̅ + a̅) + c̅ × (a̅ + b̅)
= (a̅ × b̅) + (a̅ × c̅) + (b̅ × c̅) + (b̅ × a̅) + (c̅ × a̅) + (c̅ × b̅)
= (a̅ × b̅) + (a̅ × c̅) + (b̅ × c̅) – (a̅ × b̅) – (a̅ × c̅) – (b̅ × c̅)
= 0

Question 6.
If p̅ = xi̅ + yj̅ + zk̅, then find |p̅ × k̅|².
Answer:
p̅ × k̅ = (xi̅ + yj̅ + zk̅) × k̅
= x(i̅ × k̅) + y(j̅ × k̅) + z(k̅ × k̅)
= -xj̅ + yi̅ + z(0)
= yi̅ – xj̅
|p̅ × k̅|² = x² + y²

Question 7.
Compute 2j̅ × (3i̅ – 4k̅) + (i̅ + 2j̅) × k̅
Sol.
2j̅ × (3i̅ – 4k̅) + (i̅ + 2j̅) × k̅
= 6(j̅ × i̅) – 8(j̅ × k̅) + (i̅ × k̅) + 2(j̅ × k̅)
= -6k̅ – 8i̅ – j̅ + 2i̅
= -6i̅ – j̅ – 6k̅

Question 8.
Find unit vector perpendicular to both i̅ + j̅ + k̅ and 2i̅ + j̅ + 3k̅.
Answer:
Given a̅ = i̅ + j̅ + k̅ and b̅ = 2i̅ + j̅ + 3k̅
then a̅ × b̅ = \(\left|\begin{array}{lll}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & 1 \\
2 & 1 & 3
\end{array}\right|\)
= i̅(3 – 1) – j̅(3 – 2) + k̅(1 – 2)
= 2i̅ – j̅ – k̅
|a̅ × b̅| = \(\sqrt{4+1+1}=\sqrt{6}\)
Unit vector perpendicular to both a̅ and b̅
= ±\(\frac{\overline{\mathrm{a}} \times \overline{\mathrm{b}}}{|\overline{\mathrm{a}} \times \overline{\mathrm{b}}|}=\pm\left(\frac{2 \overline{\mathrm{i}}-\overline{\mathrm{j}}-\overline{\mathrm{k}}}{\sqrt{6}}\right)\)

Question 9.
If θ is the angle between the vectors i̅ + j̅ and j̅ + k̅, then find sin θ.
Answer:
Let a̅ = i̅ + j̅ and b̅ = j̅ + k̅

Question 10.
Find the area of the parallelogram having a̅ = 2j̅ – k̅ and b̅ = – i̅ + k̅ as adjacent sides.
Answer:
Vector area of the parallelogram having
a̅ = 2j̅ – k̅ and b̅ = -i̅ + k̅ as adjacent sides = a̅ × b̅
= \(\left|\begin{array}{rrr}
\bar{i} & \bar{j} & \bar{k} \\
0 & 2 & -1 \\
-1 & 0 & 1
\end{array}\right|\) = 2 i̅ + j̅ + 2k̅
Area of the parallelogram
= |a̅ × b̅| = \(\sqrt{4+1+4}\) = 3 sq. units.

Question 11.
Find the area of the parallelogram whose diagonals are 3i̅ + j̅ – 2k̅ and i̅ – 3j̅ + 4k̅.
Answer:
Let a̅ = 3i̅ + j̅ – 2k̅ and b̅ = i̅ – 3j̅ + 4k̅ be the diagonals of a parallelogram then its vector area = \(\frac{1}{2}\)(a̅ × b̅) and area |\(\frac{1}{2}\)(a̅ × b̅)|
a̅ × b̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
3 & 1 & -2 \\
1 & -3 & 4
\end{array}\right|\)
= i̅ [4 – 6] – j̅ [12 + 2] + k̅ [-9 – 1]
= -2i̅ – 14j̅ – 10k̅
= 2(-i̅ – 7j̅ – 5k̅)
Vector area of parallelogram = |\(\frac{1}{2}\)(a̅ × b̅)|
= |[2(-i̅ – 7j̅ – 5k̅)]
= (-i̅ – 7j̅ – 5k̅)
Area of the parallelogram = |- i̅ – 7 j̅ – 5k̅|
= \(\sqrt{1+49+25}=\sqrt{75}\) = 5√3 sq. units.

Question 12.
Find the area of the triangle having 3 i̅ + 4j̅ and – 5 i̅ + 7j̅ as two of its sides.
Answer:
Area of the triangle = \(\frac{1}{2}\) \(|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|\)
\(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}\) = (3i̅ + 4j̅) × (-5i̅ + 7j̅)
= -15(i̅ × i̅) – 20(j̅ × i̅) + 21(i̅ × j̅) + 28 (j̅ × j̅)
= 20k̅ + 21k̅ = 41k̅
Area of the ΔABC = \(\frac{1}{2}\) \((41) = 20.5 sq. units

Question 13.
Find unit vector perpendicular to the plane determined by the vectors a̅ = 4i + 3j – k and b̅ = 2 i – 6 j 3k .
Answer:
Here a̅ = 4 i̅ + 3 j̅ – k̅ and b̅ = 2 i̅ – 6 j̅ – 3k̅
then a̅ × b̅

= i̅(-15) – j̅(-10) + k̅(-30)
= -15i̅ +10j̅ – 30k̅
= -5(3i̅ – 2j̅ + 6k̅)
|a̅ × b̅| = 5[latex]\sqrt{9+4+36}\) = 5(7) = 35
∴ Unit vector perpendicular to the plane
= \(\pm \frac{5(3 \bar{i}-2 \bar{j}+6 \bar{k})}{35}\)
= \(\frac{\pm(3 \bar{i}-2 \bar{j}+6 \bar{k})}{7}\)

Question 14.
Find the area of the triangle whose vertices are A (1, 2, 3), B (2, 3, 1) and C (3, 1, 2). (Mar. ’14, ’06)
Answer:
Suppose i̅, j̅, k̅ are unit vectors along the coordinate axes.
Position vectors of A, B, C are i̅ + 2j̅ + 3k̅, 2i̅ + 3j̅ + k̅, 3i̅ + j̅ + 2k̅
\(\overline{\mathrm{AB}}\) = (2i̅ + 3j̅ + k̅) – (i̅ + 2j̅ + 3k̅)
= i̅ + j̅ – 2k̅
\(\overline{\mathrm{AC}}\) = (3 i̅ + j̅ + 2k̅) – (i̅ + 2 j̅ + 3k̅)
= 2i̅ – j̅ + k̅

\(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}=\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & -2 \\
2 & -1 & -1
\end{array}\right|\)
= i̅(-1 – 2) – j̅(-1 + 4) + k̅(-1 – 2)
= -3i̅ – 3 j̅ – 3k̅ = -3(i̅ + j̅ + k̅)
Area of the ΔABC = \(\frac{1}{2}|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|\)
= \(\frac{3}{2} \sqrt{1+1+1}=\frac{3 \sqrt{3}}{2}\)sq.units

II.
Question 1.
If a̅ + b̅ + c̅ = 0, then prove that a̅ × b̅ = b̅ × c̅ = c̅ × a̅.
Answer:
Given a̅ + b̅ + c̅ = 0
⇒ a̅ = -b̅ – c̅
∴ a̅ × b̅ = -(b̅ × b̅) – (c̅ × b̅)
= 0 + (b̅ × c̅) = (b̅ × c̅) …………(1)
Again a̅ + b̅ + c̅ = 0
⇒ c = -a̅ – b̅
⇒ c̅ × a̅ = (-a̅ – b̅) × a̅
= -(a̅ × a̅) – (b̅ × a̅)
= 0 + (a̅ × b̅)
∴ (c̅ × a̅) = (a̅ × b̅) …………..(2)
From (1) and (2), a̅ × b̅ = b̅ × c̅ – c̅ × a̅

Question 2.
If a̅ = 2i̅ + j̅ – k̅, b̅ = -i̅ + 2j̅ – 4k̅ and c̅ = i̅ + j̅ + k̅, then find (a̅ × b̅) – (b̅ × c̅). (March 2015-A.P)
Answer:
Given a̅ = 2i̅ + j̅ – k̅, b̅ = – i̅ + 2 j̅ – 4k̅ and c̅ = i̅ + j̅ + k̅
Then a̅ × b̅ = \(\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
2 & 1 & -1 \\
-1 & 2 & -4
\end{array}\right|\)
= i̅ (-4 + 2) – j̅ (-8 – 1) + k̅(4 + 1)
= -2i̅ + 9 j̅ + 5k̅
b̅ × c̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
-1 & 2 & -4 \\
1 & 1 & 1
\end{array}\right|\)
= i̅ (2 + 4) – j̅ (-1 + 4) + k̅(-1 – 2)
= 6i̅ – 3j̅ – 3k̅
(a̅ × b̅) – (b̅ × c̅) = (-2i̅ + 9j̅ + 5k̅) – (6i̅ – 3j̅ – 3k̅)
= -12 – 27 – 15
= -54

Question 3.
Find the vector area and the area of the parallelogram having a̅ = i̅ + 2j̅ – k̅ and b̅ = 2i̅ – j̅ + 2k̅ as adjacent sides.
Answer:
Given a̅ = i̅ + 2j̅ – k̅ and b̅ = 2i̅ – j̅ + 2k̅
Then the vector area of parallelogram = a̅ × b̅
∴ (a̅ x b̅) = \(\left|\begin{array}{rrr}
\bar{i} & \bar{j} & \bar{k} \\
1 & 2 & -1 \\
2 & -1 & 2
\end{array}\right|\)
= i̅ (4 – 1)- j̅ (2 + 2) + k̅(-1 – 4)
= 3i̅ – 4j̅ – 5k̅

Magnitude of the area = \(\sqrt{9+16+25}\)
= \(\sqrt{50}\) = 5√2 sq. units

Question 4.
If a̅ × b̅ = b̅ × c̅ ≠ 0, then show that a̅ + c̅ = pb̅, where p is some scalar.
Answer:
Consider (a̅ + c̅ – pb̅) × b̅
= (a̅ × b̅) + (c̅ × b̅) – p(b̅ × b̅)
= (b̅ × c̅) – (b̅ × c̅) – p(0) = 0
∴ a̅ + c̅ – pb̅ = 0 ⇒ a̅ + c̅ = pb̅

Question 5.
Let a and b be vectors, satisfying |a̅| = |b̅| = 5 and (a̅, b̅) = 45°. Find the area of the triangle having a̅ – 2b̅ and 3a̅ + 2b̅ as two of its sides. [March 2007]
Answer:
Area of the triangle = \(\frac{1}{2}\) |(a̅ – 2b̅) × (3a̅ + 2b̅)|
Now |(a̅ – 2b̅) × (3a̅ + 2b̅)|
= 13(a̅ × a̅) – 2(b̅ × a̅) – 6(b̅ × a̅) – 4(b̅ × b̅)|
= 12(a̅ × b̅) + 6(a̅ × b̅)| = 18(a̅ × b̅)|
= 8|a̅| |b̅| sin45°
= 8(5)(5)\(\frac{1}{\sqrt{2}}\)n̂
= 100√2n̂
From (1)
Area of the triangle = \(\frac{1}{2}\)(100)√2
= 50√2 sq. units

Question 6.
Find die vector having magnitude √6 units and perpendicular to both 2j̅ – k̅ and 3j̅ – i̅ – k̅.
Answer:
Let a̅ = 2 i̅ – k̅ and b̅ = 3i̅ – j̅ – k̅
Then a̅ × b̅ = \(\left|\begin{array}{ccc}
\bar{j} & \bar{i} & \bar{k} \\
2 & 0 & -1 \\
3 & -1 & -1
\end{array}\right|\)
= i̅(-1) – j̅(-2 + 3) + k̅(-2)
= – i̅ – j̅ – 2k̅
= -(i̅ + j̅ + 2k̅)
|a̅ × b̅| = \(\sqrt{1+1+4}=\sqrt{6}\)
Vector perpendicular to a̅ and b̅ and having magnitude √6 units is = -(i̅ + j̅ + 2k̅)
Unit vector perpendicular to a and b and having magnitude √6 units is ±\(\left(\frac{\bar{a} \times \bar{b}}{|\bar{a} \times \bar{b}|}\right)\)

Question 7.
Find unit vector perpendicular to the plane determined by the points P (1, – 1, 2), Q (2, 0, – 1) and R (0, 2, 1).
Answer:
Let O be the origin.
\(\overline{\mathrm{OP}}\) = i̅ – j̅ + 2k̅
\(\overline{\mathrm{OQ}}\) = 2i̅ – k̅
\(\overline{\mathrm{OR}}\) = 2j̅ + k̅
\(\overline{\mathrm{PQ}}=\overline{\mathrm{OQ}}-\overline{\mathrm{OP}}\) = (2i̅ – k̅) – (i̅ – j̅ + 2k̅)
= i̅ + j̅ – 3k̅
\(\overline{\mathrm{PR}}=\overline{\mathrm{OR}}-\overline{\mathrm{OP}}\) = (2j̅ + k̅) – (i̅ – j̅ + 2k̅)
= – i̅ + 3 j̅ – k̅

Now \(\overline{\mathrm{PQ}} \times \overline{\mathrm{PR}}=\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & -3 \\
-1 & 3 & -1
\end{array}\right|\)
= i̅ (-1 + 9) – j̅ (-1 – 3) + k̅(3 + 1)
= 8i̅ + 4j̅ + 4k̅
= 4(2i̅ + j̅ + k̅)
\(|\overline{\mathrm{PQ}} \times \overline{\mathrm{PR}}|=4 \sqrt{4+1+1}=4 \sqrt{6}\)

∴ Unit vector perpendicular to the plane determined by the points P, Q and R is

Question 8.
If a̅. b̅ = a̅. c̅ and a̅ × b̅ = a̅ × c̅, a ≠ 0, then show that b̅ = c̅.
Answer:
a̅ . b̅ = a̅. c̅
⇒ a̅.b̅ – a̅.c̅ = 0
⇒ a̅ . (b̅ – c̅) = 0
⇒ b̅ – c̅ = 0 (or) a̅ is perpendicular to
b̅ – c̅ ……… (1) (∵ a̅ ≠ 0)
Again a̅ × b̅ = a̅ × c̅ = 0
⇒ a̅ × b̅ – a̅ × c̅
⇒ a̅ × (b̅ – c̅) = 0 (∵ a ≠ 0)
⇒ b̅ – c̅ = 0 (or) a is parallel to
b̅ – c̅ ………(2)
From (1) and (2);
b̅ – c̅ = 0 ⇒ b̅ = c

Question 9.
Find a vector of magnitude 3 and perpendicular to both the vectors b̅ = 2 i̅ – 2j̅ + k̅ and c̅ = 2i̅ + 2j̅ + 3k̅.
Answer:
b̅ × c̅ = \(\left|\begin{array}{ccc}
\bar{i} & \vec{j} & \bar{k} \\
2 & -2 & 1 \\
2 & 2 & 3
\end{array}\right|\)
= i̅ [-6 – 2] – j̅ [6 – 2] + k̅ [4 + 4]
= -8i̅ – 4j̅ + 8k̅ = -4(2i̅ + j̅ – 2k̅)
∴ A vector of magnitude 3 and perpendicular to both the vectors b̅ and c̅ is = ± 3\(\frac{\bar{b} \times \bar{c}}{|\bar{b} \times \bar{c}|}\)
= 3\(\left[\frac{-4(2 \bar{i}+\bar{j}-2 \bar{k})}{12}\right]\)
= ± (2i̅ + j̅ – 2k̅)

Question 10.
If |a̅|=13, |b̅| = 5 and a̅. b̅ = 60, then find |a̅ × b̅|.
Answer:
We have |a̅ × b̅| = |a̅|² |b̅|² – (a̅. b̅)²
= (13)² (5)² – (60)²
= (169) 25 – 3600
= 4224 – 3600 = 625
|a̅ × b̅| = \(\sqrt{625}\) = 25

Question 11.
Find unit vector perpendicular to the plane passing through the points (1, 2, 3), (2,-1, 1) and (1,2,- 4). (March 2005)
Answer:
Let O’ be the origin and let A (1, 2, 3), B (2, – 1, 1) and C (1, 2,-4) be the given points.
Then \(\overline{\mathrm{OA}}\) = i̅ + 2 j̅ + 3k̅
\(\overline{\mathrm{OB}}\) = 2 i̅ – j̅ + k̅
\(\overline{\mathrm{OC}}\) = i̅ + 2j̅ – 4k̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\)
= (2i̅ – j̅ + k̅) – (i̅ + 2j̅ + 3k̅)
= i̅ – 3 j̅ – 2k̅
\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\)
= (i̅ + 2j̅ – 4k̅) – (i̅ + 2j̅ + 3k̅)
= -7k̅
\(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}=\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & -3 & -2 \\
0 & 0 & -7
\end{array}\right|\)
= i̅(21) – j̅(-7) + k̅(0)
= 7(3i̅ + j̅)
\(|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|=7 \sqrt{9+1}=7 \sqrt{10}\)

Unit vector perpendicular to the plane

III.
Question 1.
If a̅, b̅ and c̅ represent the vertices A, B and C respectively of ΔABC, then prove that |(a̅ × b̅) + (b̅ × c̅) + (c̅ × a̅)| is twice the area of ΔABC.
Answer:
Let ‘O’ be the origin and
\(\overline{\mathrm{OA}}\) = a̅, \(\overline{\mathrm{OB}}\) = b̅, \(\overline{\mathrm{OC}}\) = c̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = b – a
and \(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\) = c – a
∴ Area of ΔABC = \(\frac{1}{2}|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|\) ………(1)
Here \(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}\) = (b̅ – a̅) × (c̅ – a̅)
= (b̅ × c̅) – (a̅ × c̅) – (b̅ × a̅) + (a̅ × a̅)
= (b̅ × c̅) + (c̅ × a̅) + (a̅ × b̅) (v a̅ × a̅ = 0)
∴ Area of ΔABC = \(\frac{1}{2}\)|b̅ × c̅ + c̅ × a̅ + a̅ × b̅|
⇒ |b̅ × c̅ + c̅ × a̅ + a̅ × b̅| = 2 (area of ΔABC)
⇒ |(a̅ × b̅) + (b̅ × c̅) + (c̅ × a̅)|
= 2 (area of ΔABC)

Question 2.
If a̅ = 2i̅ + 3j̅ + 4k̅, b̅ = i̅ + j̅ – k̅ and c̅ = i̅ – j̅ + k̅, then compute a̅ × (b̅ × c̅) and verify that it is perpendicular to a̅.
Answer:
b̅ × c̅ = \(\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & -1 \\
1 & -1 & 1
\end{array}\right|\)
= i̅(1 – 1) – j̅(1 + 1) + k̅(-1 – 1)
= -2j̅ – 2k̅

a̅ × (b̅ × c̅) = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
2 & 3 & 4 \\
0 & -2 & -2
\end{array}\right|\)
= i̅(-6 + 8)- j̅(-4) + k̅(-4)
= 2i̅ + 4j̅ – 4k̅
Now [a̅ × (b̅ × c̅)].a̅
= (2i̅ + 4j̅ – 4k̅)(2i̅ + 3j̅ + 4k̅)
= 4 + 12 – 16 = 0
a̅ × (b̅ × c̅) is perpendicular to a̅.

Question 3.
If a̅ = 7i̅ – 2j̅ + 3k̅, b̅ = 2i̅ + 8k̅ and c̅ = i̅ + j̅ + k̅, then compute a̅ × b̅, a̅ × c̅ and a̅ × (b̅ + c̅), Verify whether the cross product is distributive over vector addition.
Answer:
a̅ × b̅ = \(\left|\begin{array}{rrr}
\bar{i} & \bar{j} & \bar{k} \\
7 & -2 & 3 \\
2 & 0 & 8
\end{array}\right|\)
= i̅ (-16 – 0) – j̅ (56 – 6) + k̅(4)
= -16 i̅ – 50 j̅ + 4k̅

a̅ × c̅ = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
7 & -2 & 3 \\
1 & 1 & 1
\end{array}\right|\)
= i̅ (-2 – 3) – j̅ (7 – 3) + k̅(7 + 2)
= -5i̅ – 4 j̅ + 9k̅

b̅ + c̅ = 2i̅ + 8k̅ + i̅ + j̅ + k̅
= 3 i̅ + j̅ + 9k̅

a̅ × (b̅ + c̅) = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
7 & -2 & 3 \\
3 & 1 & 9
\end{array}\right|\)
= i̅ (-18 – 3) – j̅ (63 – 9) + k̅(7 + 6)
= -21i̅ – 54j̅+ 13k̅ …………..(1)
Now (a̅ × b̅) + (a̅ × c̅)
= -16i̅ – 50j̅ + 4k̅ – 5i̅ – 4j̅ + 9k̅
= -21i̅ – 54j̅ + 13k̅ …………(2)
From (1) and (2);
a̅ × (b̅ + c̅) = (a̅ × b̅) + (a̅ × c̅)
∴ Vector product is distributive over vector addition.

Question 4.
If a̅ = i̅ + j̅ + k̅, c = j̅ – k̅, then find vector b such that a̅ × b̅ = c̅ and a̅. b̅ = 3
Answer:
Let b̅ = b₁i̅ + b₂j̅ + b₃k̅
Given a̅. b̅ = 3
⇒ b₁ + b₂ + b₃ = 3 ………..(1)
and a̅ × b̅ = c̅
\(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & 1 \\
\mathrm{~b}_1 & \mathrm{~b}_2 & \mathrm{~b}_3
\end{array}\right|\) = j̅ – k̅
⇒ i̅(b₃ – b₂) – j̅(b₃ – b₁) + k̅(b₂ -b₁) = j̅ – k̅
∴ b₃ – b₁ = – 1 ……………(2)
and b₂ – b₁ = – 1 ……………(3)

∴ b₃ – b₂ = 0 ⇒ b₃ = b₂
∴ From (1), b₁ + 2b₂ = 3 ………(4)
∴ From (3), – b₁ + b₂ = – 1
∴ 3b₂ = 2 ⇒ b₂ = \(\frac{2}{3}\) ……..(5)
∴ b₂ = b₃ = \(\frac{2}{3}\)
b₁ = 3 – 2b₂ = 3 – \(\frac{4}{3}=\frac{5}{3}\) ………(6)

b = b₁ i̅ + b₂ j̅ + b₃k̅
= \(\frac{5}{2}\)i̅ + \(\frac{2}{3}\) j̅ + \(\frac{2}{3}\)k̅
= \(\frac{1}{3}\) (5i̅ + 2 j̅ + 2k̅)

Question 5.
a̅, b̅, c̅ are three vectors of equal magnitudes and each of them is inclined at an angle of 60° to the others. If |a̅ + b̅ + c̅| = √6(5 then find |a̅|.
Answer:
Given |a̅| = |b̅| = |c̅| = k(suppose)
and (a̅,b̅) = (b̅, c̅) = (c̅, a̅) = 60°
Also
(a̅ + b̅ + c̅) = |a̅|² + |b̅|² + |c̅|² + 2(a̅.b̅ + b̅.c̅ + c̅.a̅)
= k² + k² + k² + 2 [|a̅| |b̅| cos60° + |b̅| |c̅| cos60° + |c̅||a̅|cos60°]
= 3k² + \(\frac{2}{2}\)[k² + k² + k²] = 6k²
∴ 6 = 6k² (∵ |a̅ + b̅ + c̅| = √6)
⇒ k = 1
∴ |a̅| = 1

Question 6.
For any two vectors a and b, show that (1 + |a̅|²)(1 + |b̅|²) = |1 – a̅.b̅|² + |a̅ + b̅ + a̅ × b̅|²
Answer:

Question 7.
If a̅, b̅, c̅ are unit vectors such that a is perpendicular to the plane of b̅, c̅ and the angle between b̅ and c̅ is \(\frac{\pi}{3}\), then find |a̅ + b̅ + c̅|.
Answer:
Given that |a̅| = |b̅| = |c̅| = 1
Since a is perpendicular to the plane of b̅, c̅
⇒ We have a̅ . b̅ = 0 and a̅ . c̅ = 0
and given (b̅, c̅) = \(\frac{\pi}{3}\)
Now (a̅ + b̅ + c̅)² = |a̅|² + |b̅|² + |c̅|² + 2[(a̅. b̅) + (b̅. c̅) + (c̅. a̅)]
= 1 + 1 + 1 + 2|b̅||c̅|cos \(\frac{\pi}{3}\)
= 3 + 2\(\left(\frac{1}{2}\right)\) = 4
∴ |a + b + c| = 2

Question 8.
If a̅ = 3i̅ – j̅ + 2k̅, b̅ = – i̅ + 3j̅ + 2k̅, c̅ = 4i̅ + 5j̅ – 2k̅ and d̅ = i̅ + 3j̅ + 5k̅. then compute the following
i) (a̅ × b̅) × (c̅ × d̅)
Answer:
a̅ × b̅ = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
3 & -1 & 2 \\
-1 & 3 & 2
\end{array}\right|\)
= i̅ (-2 – 6) – j̅ (6 + 2) + k̅(9 – 1)
= -8i̅ – 8j̅ + 8k̅ = 8(-i̅ – j̅ + k̅)

c̅ × d̅ = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
4 & 5 & -2 \\
1 & 3 & 5
\end{array}\right|\)
= i̅(25 + 6) – j̅(20 + 2) + k̅(12 – 5)
= 31i̅ – 22j̅ + 7k̅

(a̅ × b̅) × (c̅ × d̅) = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
-8 & -8 & 8 \\
31 & -22 & 7
\end{array}\right|\)
= i̅ (-56 +176) – j̅ (-56 – 248) + k̅(176 + 248)
= i̅(120) + j̅(304) + 424 k̅
= 8[15i̅ + 38j̅ + 53k̅]

ii) (a̅ × b̅) . c̅ – (a̅ × d̅), b̅
Answer:
a̅ × b̅ = -8i̅ – 8j̅ + 8k̅
c̅ = 4 i̅ + 5 j̅ – 2k̅
∴ (a̅ × b̅). c̅ = -32 – 40 – 16 = -88 ………(1)
a̅ × d̅ = \(\left|\begin{array}{rrr}
\overline{\mathbf{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
3 & -1 & 2 \\
1 & 3 & 5
\end{array}\right|\)
= i̅ (-5 – 6) – j̅ (15 – 2) + k̅(9 + 1)
= -11i̅ – 13j̅ + 10k̅
(a̅ × d̅) . b̅ = (-11i̅ – 13 j̅ + 10k̅) – (-i̅ + 3j̅ + 2k̅)
= 11 – 39 + 20 = -8 ……….(2)
(a̅ × b̅).c̅ – (a̅ × d̅).b̅ = – 88 + 8 = – 80

Students must practice these TS Intermediate Maths 1A Solutions Chapter 5 Products of Vectors Ex 5(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Products of Vectors Solutions Exercise 5(a)

Question 1.
Find the angle between the vectors i̅ + 2j̅ + 3k̅ and 3i̅ – j̅ + 2k̅. (Mar. ’14)
Answer:
Let a̅ = i̅ + 2j̅ + 3k̅ and b̅ = 3i̅ – j̅ + 2k̅ and θ be the angle between them. Then

Question 2.
If the vectors 2i̅ + λ j̅ – k̅ and 4i̅ – 2j̅+ 2k̅ are perpendicular to each other then find λ. [March, May 2005]
Answer:
Let a̅ = 2i̅ + λ j̅ – k̅ and b̅ = 4i̅ – 2j̅+ 2k̅ and If a̅ is perpendicular to b̅ then a̅.b̅ = o
⇒ (2i̅ + λ j̅ – k̅).(4i̅ – 2j̅+ 2k̅) = o
⇒ 8 – 2λ – 2 = 0 ⇒ 6 – 2λ = 0 ⇒ λ = 3

Question 3.
For what values of , the vectors i̅ – j̅ + 2k̅ and 8i̅ + 6j̅ – k̅ are at right angles?
Answer:
Let a̅ = i̅ – j̅ + 2k̅ and b̅ = 8i̅ + 6j̅ – k̅
If a̅, b̅ are right angles then a̅.b̅ = o
⇒ 8 – 6λ – 2 = 0
⇒ -6λ + 6 = 0
⇒ λ = 1

Question 4.
a̅ = 2i̅ – j̅ + k̅, b̅ = i̅ – 3j̅ – 5k̅. Find the vector c such that a, b and c form the sides of a triangle.
Answer:
a̅ = 2i̅ – j̅ + k̅, b̅ = i̅ – 3j̅ – 5k̅
∵ a̅, b̅, c̅ form the sides of a triangle a̅ + b̅ + c̅ = 0

∴ c̅ = -a̅ – b̅
= -(2i̅ – j̅ + k̅) – (i̅ – 3 j̅ – 5k̅)
= -3i̅ + 4j̅ + 4k̅

Question 5.
Find the angle between the planes r̅ . (2i̅ – j̅ + 2k̅) = 3 and r̅ .(3i̅ + 6j̅ + k̅) =4 (March 2015-T.S)
Answer:
If the angle between planes

Question 6.
Let \(\overline{\mathrm{e}}_1\) and \(\overline{\mathrm{e}}_{\mathbf{2}}\) be unit vectors making angle θ. If \(\frac{1}{2}\left|\overline{\mathrm{e}}_1-\overline{\mathrm{e}}_2\right|\) = sin λθ, then find λ.
Answer:

Question 7.
Let a̅ = i̅ + j̅ + k̅ and b̅ = 2 i̅ + 3j̅ + k̅. Find
(i) the projection vector of bona and its magnitude
(ii) The vector components of b̅ in the direction of a̅ and perpendicular to a̅. [May 2006]
Answer:
Orthogonal projection of a vector b̅ on a̅ is

(ii) The component vector b in the direction of –

Question 8.
Find the equation of the plane through the point (3, – 2, 1) and perpendicular to the vector (4, 7, – 4).
Answer:
The equation of the plane passing through a̅ and perpendicular to the vector n̅ is r̅. n̅ = a̅. n̅
Given n̅ = 4i̅ + 7j̅ – 4k̅ and a̅ = 3i̅ – 2j̅ + k̅
r̅ . (4i̅ + 7j̅ – 4k̅) – (3i̅ – 2j̅ + k̅) . (4i̅ + 7j̅ – 4k̅)
r . (4i̅ + 7j̅ – 4k̅) = 12 – 14 – 4 = – 6
⇒ r̅ . (-4i̅ – 7j̅ + 4k̅) = 6

Question 9.
If a̅ = 2i̅ + 2j̅ – 3k̅, b = 3i̅ – j̅ + 2k̅, then find the euigle between 2a̅ + b̅ and a̅ + 2b̅.
Answer:
Given a̅ = 2i̅ + 2j̅ – 3k̅ and b̅ = 3i̅ – j̅ + 2k̅
We have
2a̅ + b = 4i + 4j̅ – 6k̅ + 3i̅ – j̅ + 2k̅ = 7i̅ + 3j̅ – 4k̅
and a̅ + 2b̅ = (2i̅ + 2 j̅ – 3k̅) + 2(31-7 + 2k) = 8i̅ + k̅
Let ‘θ’ be the angle between the vectors 2a̅ + b̅ and a̅ + 2b̅

II.
Question 1.
Find the unit vector parallel to the XOY plane and perpendicular to the vector 4i̅ – 3j̅ + k̅.
Answer:
Any vector parallel to XOY plane will be of the form xi̅ + yj̅.
The vector parallel to the XOY plane and perpendicular to the vector 4i̅ – 3j̅ + k̅ is 3i̅ + 4j̅
Its magnitudes |3i̅ + 4j̅| = \(\sqrt{9+16}\) = 5
Unit vector parallel to XOY plane and perpendicular to the vector 4i̅ – 3j̅ + k̅ is
\(\pm\left(\frac{3 \overline{\mathrm{i}}+4 \overline{\mathrm{j}}}{\sqrt{9+16}}\right)=\pm\left(\frac{3 \overline{\mathrm{i}}+4 \overline{\mathrm{j}}}{5}\right)\)

Question 2.
If a̅ + b̅ + c̅ = 0, |a̅I|= 3, |b̅| = 5 and |c̅| = 5 then find the angle between a̅ and b̅.
Answer:
Given a̅ + b̅ + c̅ = 0
c̅ = -(a̅ + b̅)
⇒ |c̅|² = (a̅ + b̅)² = a̅² + b̅² + 2(a̅. b̅)
⇒ 49 = 9 + 25 + 2( .6)

Question 3.
If |a̅| = 2, |b̅| = 3 and |c̅| = 4 juid each of a̅, b̅, c̅ is perpendicular to the sum of the other two vectors, then find the magnitude of a̅ + b̅ + c̅.
Answer:
Given |a̅| = 2, |b̅| = 3 and |c̅| = 4
Since each of a̅, b̅, c̅ is perpendicular to the sum of other two vectors i.e., a̅ is perpendicular to b̅ + c̅
a̅ . (b̅ + c̅) = 0 ⇒ a̅ . b̅ + a̅ . c̅ = 0
Similarly
b̅.(c̅ + a̅) = 0 ⇒ b̅.c̅ + b̅.a̅ = 0
and c-(a + b) = 0 ⇒ c̅. a̅ + c̅. b̅ = 0 Adding we get
2 [(a̅ . b̅) + (b̅ . c̅) + (c̅ . a̅)] = 0 …….(1)
Also (a̅ + b̅ + c̅)
= |a̅|² + |b̅|² + |c̅|² + 2(a̅.b̅ + b̅.c̅ + c̅.a̅)
= 4 + 9 + 16 + 2(a̅.b̅ + b̅. c̅ + c̅.a̅)
= 4 + 9 + 16 + 2 (0) = 29
∴ |a̅ + b̅ + c̅| = \(\sqrt{29}\)

Question 4.
Find the equation of the plane passing through the point a̅ = 2i̅ + 3j̅ – k̅ and perpendicular to the vector 3i̅ – 2j̅ – 2k̅ and the distance of this plane from the origin.
Answer:
Equation of the plane passing through the point a, and perpendicular to the vector n̅ is (r̅ – a̅) . n̅ = 0
⇒ 7 . n̅ = a̅ . n̅
(liven a̅ = 2i̅ + 3 j̅ – k̅ and n̅ = 3i̅ – 2j̅ – 2k̅
We have r̅ . (3 i̅ – 2 j̅ – 2k̅)
= (2i̅ + 3j̅ – k̅) . (3i̅ – 2j̅ – 2k̅)
= 6 – 6 + 2 = 2
⇒ r̅ . (3i̅ – 2j̅ – 2k̅) = 2
The distance from origin to this plane is

Question 5.
a̅, b̅, c̅ and d̅ are the position vectors of four coplanar points such that (a̅ – d̅) . (b̅ – c̅) = (b̅ – d̅) . (c̅ – a̅) = 0. Show that the point d represents the orthocentre of the triangle with a̅, b̅ and c̅ as its vertices.
Answer:

Position vectors of A, B, C, D are a̅, b̅, c̅, d̅ respectively.
\(\overline{\mathrm{DA}}=\overline{\mathrm{OA}}-\overline{\mathrm{OD}}\) = a̅ – d̅
\(\overline{\mathrm{CB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OC}}\) = b̅ – c̅
\(\overline{\mathrm{DB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OD}}\) = b̅ – d̅
\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\) = c̅ – a̅
Given (a̅ – d̅) . (b̅ – c̅) = 0
⇒ \(\overline{\mathrm{DA}} \cdot \overline{\mathrm{CB}}\) = 0
⇒ \(\overline{\mathrm{DA}}\) is perpendicular to \(\overline{\mathrm{BC}}\)
∴ \(\overline{\mathrm{AD}}\) is an altitude of ΔABC
and (b̅ – d̅) . (c̅ – a̅) = 0
⇒ \(\overline{\mathrm{DB}} \cdot \overline{\mathrm{AC}}\) = 0
⇒ \(\overline{\mathrm{DB}}\) is perpendicular to \(\overline{\mathrm{AC}}\)
\(\overline{\mathrm{DB}}\) another altitude ΔABC
Altitudes AD and BD intersect at D
D(d) is the orthocentre of ΔABC.

III.
Question 1.
Show that the points (5, – 1, 1), (7, – 4, 7), (1,-6, 10) and (- 1, – 3, 4) are the vertices of a rhombus. (March 2013)
Answer:
Let A (5,-1, 1), B (7,-4, 7), C (1,-6, 10) and D (- 1, – 3, 4) are the given points.

∴ AB = BC = CD = DA = 7 units and AC ≠ BD
∴ A, B, C, D are the points which are the vertices of a rhombus.

Question 2.
Let a̅ = 4i̅ + 5j̅ – k̅, b̅ = i̅ – 4j̅ + 5k̅ and c̅ = 3i̅ + j̅ – k̅. Find the vector which is perpendicular to both a and b and whose magnitude is twenty one times the magnitude of c̅.
Answer:
Given a̅ = 4 i̅ + 5 j̅ – k̅
b̅ = i̅ – 4 j̅ + 5k̅
and c̅ = 3 i̅ + j̅ – k̅
Let r̅ = xi̅ + yj̅ + zk̅ be the vector which is perpendicular to both a and b.
Then r̅. a̅ = 0 and r̅.b̅ = 0
⇒ 4x + 5y – z = 0 …………..(1)
and x – 4y + 5z = 0 ……….(2)

⇒ x = λ, y = -λ, z = -λ
∴ The vector which is perpendicular to both a̅ and b̅ is r̅ = λ(i̅ – j̅ – k̅)
Magnitude of c = \(\sqrt{9+1+1}=\sqrt{11}\)
∴ The vector which is perpendicular to both a̅ and b̅ whose magnitude is 21 times the
magnitude of c̅ is = ± \(\frac{21 \sqrt{11}(\bar{i}-\bar{j}-\bar{k})}{|\bar{i}-\bar{j}-\bar{k}|}\)
= ± 7\(\sqrt{33}\) (i̅ – j̅ – k̅)

Question 3.
G is the centroid of ΔABC and a̅, b̅, c̅ are the lengths of the sides \(\overline{\mathrm{B C}}, \overline{\mathrm{C A}}\) and \(\overline{\mathrm{AB}}\) respectively. Prove that \(\bar{a}^2+\bar{b}^2+\bar{c}^2=3\left(\overline{\mathrm{OA}}^2+\overline{\mathrm{OB}}^2+\overline{\mathrm{OC}}^2\right)-9(\overline{\mathrm{OG}})^2\). where ‘O’ is any point.

Answer:
Given that \(\overline{\mathrm{BC}}=\overline{\mathrm{a}}, \overline{\mathrm{CA}}=\overline{\mathrm{b}}\) and \(\overline{\mathrm{AB}}=\overline{\mathrm{c}}\).
Let O’ be the origin and let p.q.r be the position vectors of A, B, C then \(\overline{\mathrm{OA}}=\overline{\mathrm{p}}\), \(\overline{\mathrm{OB}}=\overline{\mathrm{q}}, \quad \overline{\mathrm{OC}}=\overline{\mathrm{r}}\) respectively.
Then the position vector of centroid

Question 4.
A line makes angles θ₁, θ₂, θ₃, and θ₄ with the diagonals of a cube. Show that cos²θ₁ + cos²θ₂ + cos²θ₃ + cos²θ₄ = \(\frac{4}{3}\).
Answer:

Let ‘O’ be the origin and ‘a’ be the length of the side of a cube.
i̅, j̅, k̅ are unit vectors along X, Y and Z axes respectively.

Let r̅ = xi̅ + yj̅ + zk̅ be the line makes angles θ₁, θ₂, θ₃, θ₄ with diagonals of a cube

Telangana TSBIE TS Inter 1st Year Chemistry Study Material 10th Lesson P బ్లాక్ మూలకాలు – 13వ గ్రూప్ Textbook Questions and Answers.

TS Inter 1st Year Chemistry Study Material 10th Lesson P బ్లాక్ మూలకాలు – 13వ గ్రూప్

అత్యంత లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 1.
బోరాన్, థాలియం ఆక్సిడేషన్ స్థితుల మార్పు విధానాన్ని చర్చించండి.
జవాబు:
IIIA గ్రూపు మూలకాల బాహ్య ఎలక్ట్రాన్ విన్యాసం ns² np¹. ఈ విన్యాసం వలన ఈ మూలకాలన్ని +3 ఆక్సిడేషన్ స్థితిని కనపరుస్తాయి. B, Al మినహా మిగిలిన అన్ని మూలకాలు +1 ఆక్సిడేషన్ స్థితిని చూపిస్తాయి. +3 ఆక్సీకరణ స్థితి యొక్క స్థిరత్వం B నుంచి Tl కు తగ్గుతుంది. +1 ఆక్సీకరణ స్థితి యొక్క స్థిరత్వం జడ ఎలక్ట్రాన్ జంట ప్రభావం వలన పై నుంచి క్రిందకు పెరుగుతుంది.

ప్రశ్న 2.
Tl Cl₃ అధిక స్థిరత్వాన్ని ఎట్లా వివరిస్తారు ?
జవాబు:
TlCl₃ అస్థిరమైనది జడ ఎలక్ట్రాన్ జంట ప్రభావం వలన Tl⁺³ అయాన్ అస్థిరమైనది. థాలియం +1 ఆక్సీకరణ స్థితిలో స్థిరంగా ఉంటుంది. కావున TlCl స్థిరమైనది.

ప్రశ్న 3.
BF₃ లూయీ ఆమ్లంగా ఎందుకు ప్రవర్తిస్తుంది ?
జవాబు:

• BF₃ ఎలక్ట్రాన్ కొరత గల సమ్మేళనం.
• అష్టక విన్యాసం పొందటం కోసం ఇది ఎలక్ట్రాన్ జంటను స్వీకరిస్తుంది.
• ఎలక్ట్రాన్ జంటల స్వీకర్తలను లూయీ ఆమ్లాలు అంటారు.
• కావున BF₃ లూయీ ఆమ్లంగా ప్రవర్తిస్తుంది.

ప్రశ్న 4.
బోరిక్ ఆమ్లం ప్రోటాన్ ఇచ్చే ఆమ్లమా ? వివరించండి.
జవాబు:

• బోరిక్ ఆమ్లం ప్రోటాన్ ఇచ్చే ఆమ్లము కాదు. కాని ఇది లూయీ ఆమ్లంగా ప్రవర్తిస్తుంది.
• ఇది ఎలక్ట్రాన్ జంటను హైడ్రాక్సిల్ అయాన్ నుంచి స్వీకరించి లూయీ ఆమ్లంగా పనిచేస్తుంది.
  B(OH)₃ + 2HOH → [B(OH)₄]^– + H₃\(\mathrm{O}^{+}\)

ప్రశ్న 5.
బోరిక్ ఆమ్లాన్ని వేడిచేస్తే ఏమవుతుంది ?
జవాబు:
బోరిక్ ఆమ్లాన్ని 370K కంటే ఎక్కువ ఉష్ణోగ్రతకు వేడిచేస్తే మెటాబోరికామ్లం (HBO₂) ఏర్పడుతుంది. దీనిని ఇంకా వేడిచేస్తే బోరిక్ ఆక్సైడ్ (B₂O₃) ఏర్పడుతుంది.

ప్రశ్న 6.
BF₃, B\(H_4^{-}\) ల ఆకారాలను వర్ణించండి. ఈ కణాలలో బోరాన్ సంకరకరణం రాయండి.
జవాబు:

• BF₃ అణువు ఆకారం సమతల త్రిభుజాకారం. దీనిలో బోరాన్ sp² సంకరీకరణం జరుపుకుంటుంది.
• B\(\mathrm{H}_4^{-}\) అణువు ఆకారం టెట్రాహెడ్రల్. దీనిలో బోరాన్ sp³ సంకరీకరణం జరుపుకుంటుంది.

ప్రశ్న 7.
Ga పరమాణు వ్యాసార్ధం Al కంటే ఎందుకు తక్కువ ఉంటుంది ? వివరించండి.
జవాబు:

• గాలియంలో ఉపాంత్యకర్పరంలో పది 3d – ఎలక్ట్రాన్లు ఉంటాయి.
• ఈ ఎలక్ట్రాన్ల వలన పరిరక్షక ప్రభావం తక్కువగా ఉంటుంది. కావున ‘Ga’ లో కేంద్రక ఆవేశం పెరుగును.
• కావున Ga యొక్క పరమాణు వ్యాసార్ధం Al కంటే తక్కువగా ఉంటుంది.

ప్రశ్న 8.
జడజంట ప్రభావాన్ని వివరించండి.
జవాబు:
బాహ్యస్థాయి (ns) లోని ఎలక్ట్రాన్లను విడగొట్టి బంధంలో పాల్గొనకుండా చేసే ప్రభావాన్ని జడ ఎలక్ట్రాన్ జంట ప్రభావం అంటారు.

ప్రశ్న 9.
ఈ క్రింది సమీకరణాలను తుల్యంచేసి రాయండి.
a) BF₃ + LiH →
b) B₂H₆ + H₂O →
c) NaH + B₂H₆
d)

e)

జవాబు:
a) 2BF₃ + 6LiH → B₂H₆ + 6LiF
b) B₂H₆ + 6H₂O → 2 H₃BO₃ + 6H₂
c) 2NaH + B₂H₆ → 2 NaBH₄
d)

e)

ప్రశ్న 10.
బోరిక్ ఆమ్లం బహ్వణుకగా ఎందుకు ఉంటుంది ?
జవాబు:
బోరిక్ ఆమ్లం పొరలవంటి జాలక నిర్మాణాన్ని కలిగి ఉంటుంది. ఈ నిర్మాణంలో BO₃ యూనిట్లు హైడ్రోజన్ బంధాలతో కలుపబడి బహ్వణుక (పాలిమర్) అణువుగా ఏర్పడుతుంది.

ప్రశ్న 11.
డైబోరేన్, బోరజీన్లలో బోరాన్ సంకరకరణం ఏమిటి ?
జవాబు:

• డై బోరేన్లో బోరాన్ sp³ సంకరీకరణం జరుపుకుంటుంది.
• బోరజీన్లో బోరాన్ sp² సంకరీకరణం జరుపుకుంటుంది.

ప్రశ్న 12.
13 గ్రూప్ మూలకాల ఎలక్ట్రాన్ విన్యాసాన్ని రాయండి.
జవాబు:
13 గ్రూపు మూలకాల ఎలక్ట్రాన్ విన్యాసం

ప్రశ్న 13.
బోరజీన్ సాంకేతికాన్ని రాయండి. దాని సాధారణ నామం ఏమిటి?
జవాబు:

• బోరజీనన్ను B₃N₃H₆ అనే ఫార్ములాతో సూచిస్తారు.
• దీని నిర్మాణం బెంజీన్ నిర్మాణాన్ని పోలి ఉండటం వలన దీనిని ఇనార్గానిక్ బెంజీన్ అని అంటారు.

ప్రశ్న 14.
(a) బోరాక్స్
(b) కోలిమనైట్ సాంకేతికాలు ఇవ్వండి.
జవాబు:
a) బోరాక్స్ ఫార్ములా Na₂B₄O₇. 10H₂O
b) కోలిమనైట్ ఫార్ములా Ca₂B₆O₁₁ . 5H₂O

ప్రశ్న 15.
అల్యూమినియం ఉపయోగాలు రెండు రాయండి.
జవాబు:

• అల్యూమినియమ్న మిశ్రమ లోహాల తయారీలో ఉపయోగిస్తారు.
• విమాన విడిభాగాల తయారీలో ఉపయోగిస్తారు.
• పైపులు, ట్యూబులు, రాడ్లు, తీగలు వంటి వాటి తయారీలో ఉపయోగిస్తారు.
• నిర్మాణాలలో, రవాణా పరిశ్రమల్లో కూడా దీనిని ఉపయోగిస్తారు.

ప్రశ్న 16.
కింది చర్యల్లో ఏమి జరుగుతుంది ?
(a) LiAlH₄, BCl₃ మిశ్రమాన్ని అనార్ద్ర ఈథర్లో వెచ్చబెట్టినప్పుడు
b) బోరాక్స్న H₂SO₄ తో వేడిచేసినప్పుడు
జవాబు:
a) LiAlH₄, BCl₃ మిశ్రమాన్ని అనార్ద్ర ఈథర్ వెచ్చబెట్టినపుడు డైబోరేన్ ఏర్పడుతుంది.

b) బోరాక్స్ను H₂SO₄ తో వేడిచేసినపుడు బోరిక్ ఆమ్లం ఏర్పడును.
Na₂B₄O₇ + H₂SO₄ + 5H₂O → Na₂SO₄ + 4H₃BO₃

ప్రశ్న 17.
ఆర్థోబోరిక్ ఆమ్ల నిర్మాణాన్ని గీయండి.
జవాబు:
ఆర్థోబోరిక్ ఆమ్లం నిర్మాణం :

ప్రశ్న 18.
AlCl₃ ద్విఅణుక నిర్మాణాన్ని రాయండి.
జవాబు:
AlCl₃ ద్విఅణుక నిర్మాణం :

ప్రశ్న 19.
లోహ బోరైడ్లను (¹⁰B) రక్షణ కవచాలుగా వాడతారు. ఎందుకు ?
జవాబు:
లోహ బోరైడ్లకు (¹⁰B) న్యూట్రాన్లను శోషించుకొనే సామర్థ్యం కలదు. కావున వీనిని న్యూక్లియర్ పరిశ్రమలలో రక్షణ కవచాలుగా వాడతారు.

లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 20.
అల్యూమినియంకు ద్విస్వభావికం ఉన్నదని రుజువు చేసే చర్యలు రాయండి.
జవాబు:
అల్యూమినియం ఆమ్ల మరియు క్షారద్రావణాలలో కరుగుతుంది. కావున దీనికి ద్విస్వభావికం కలదు.

• విలీన ఆమ్లాలలో Al కరిగి H₂ వాయువును విడుదల చేస్తుంది.
  2 Al + 6 HCl → 2 AlCl₃ + 3H₂↑
• క్షారాలలో Al కరిగి H2 వాయువును విడుదలచేస్తుంది.
  2 Al + 2NaOH + 6H₂O → 2 Na⁺ [Al (OH)₄]^– + 3H₂

ప్రశ్న 21.
ఎలక్ట్రాన్ కొరత గల సమ్మేళనాలంటే ఏమిటి ? BCl₃ ఎలక్ట్రాన్ కొరత గల సమ్మేళనమా ? వివరించండి.
జవాబు:

• అష్టక విన్యాసాన్ని పొందని కేంద్రక పరమాణువులు కలిగి ఉన్న అణువులను ఎలక్ట్రాన్ కొరత గల అణువులు అంటారు.
• BCl₃ ఎలక్ట్రాన్ కొరత గల సమ్మేళనం. దీనిలో కేంద్రకం B చుట్టూ 6 ఎలక్ట్రాన్లు మాత్రమే ఉంటాయి.
• BCl₃ అణువులోని కేంద్రక బోరాన్ పరమాణువు అష్టక విన్యాసాన్ని పొందలేదు.

ప్రశ్న 22.
BF₃, B\(F_4^{-}\) లో B – F బంధ దూరాలు వరసగా 130 pm, 143 pm ఎందుకు వేరువేరుగా ఉన్నాయో కారణాలు సూచించండి.
జవాబు:
BF₃ లో B పరమాణువు sp² సంకరీకరణం జరుపుకుంటుంది. ఇది సమతల త్రిభుజాకృతిని కలిగి ఉంటుంది. BF₃ లో బోరాన్ పరమాణువు ఫ్లోరిన్ నుంచి ఒక ఎలక్ట్రాన్ జంటను స్వీకరించి దానితో బాక్ బంధంలో పాల్గొంటుంది. కావున B – F బంధము కొంత ద్విబంధ స్వభావాన్ని కలిగి ఉంటుంది.

కాని B\(F_4^{-}\) లో B పరమాణువు sp³ సంకరీకరణం జరుపుకుంటుంది. ఇది టెట్రెహెడ్రల్ ఆకృతిని కలిగి ఉంటుంది. బోరాన్కు ఫ్లోరిన్కు మధ్య బాక్ బంధం ఉండదు.
కావున BF₃ లో బంధ దూరం 130PPM ఉంటే B\(F_4^{-}\) లో 143 PPM ఉంటుంది.

ప్రశ్న 23.
B – Cl బంధానికి బంధ భ్రామకం ఉంది కాని BCl₃ అణువుకు ద్విధ్రువ భ్రామకం సున్నా ఉంటుంది. వివరించండి.
జవాబు:
B – Cl బంధం దృవణ బంధం కావున బంధ భ్రామకం ఉంటుంది. కాని BCl₃ అణువు సౌష్టవ నిర్మాణాన్ని కలిగి ఉంటుంది. మూడు B – Cl బంధ బ్రామకాలు వ్యతిరేక దిశలలో పనిచేయటం వలన మొత్తం ద్విద్రువ భ్రామకం సున్నాగా ఉంటుంది.

ప్రశ్న 24.
బోరిక్ ఆమ్లం నిర్మాణాన్ని వివరించండి.
జవాబు:

• బోరిక్ ఆమ్లం పొరలవంటి జాలక నిర్మాణాన్ని కలిగి ఉంటుంది.
• ఈ నిర్మాణంలో BO₃ యూనిట్లు హైడ్రోజన్ బంధాలతో కలపబడి ఉంటాయి.
• కావున బోరిక్ ఆమ్లం బాహ్వణుక అణువుగా ఉంటుంది.

ఆర్థోబోరిక్ ఆమ్లం నిర్మాణం :

ప్రశ్న 25.
ఏమి జరుగుతుంది :
a) బోరాక్స్న ప్రబలంగా వేడిచేస్తే,
b) బోరిక్ ఆమ్లాన్ని నీటికి కలిపితే,
c) అల్యూమినియాన్ని సజల NaOH తో వేడిచేస్తే
d) అమ్మోనియాతో BF₃ చర్య జరిపినప్పుడు
e) అర్థ అల్యూమినాను సజల NaOH ద్రావణంతో చర్య జరిపినప్పుడు
జవాబు:
a) బోరాక్స్న ప్రబలంగా వేడిచేస్తే చివరగా గాజువంటి పదార్థం ఏర్పడుతుంది.

b) బోరిక్ ఆమ్లంనకు నీటిని కలిపితే బోరిక్ ఆమ్లం నీటి నుంచి OH అయాన్లను స్వీకరిస్తుంది.
B(OH)₃ + 2H₂O → [B(OH)₄]^– + H₃O⁺

c) Al ను సజల NaOH తో వేడిచేస్తే సోడియం మెటా అల్యూమినేట్తో పాటు H₂ వాయువు విడుదలవుతుంది.

d) BF₃, ని NH₃ లో చర్య జరిపినపుడు NH₃ ఎలక్ట్రాన్ జంటను BF₃ కి దానం చేస్తుంది. రెండింటి మధ్య సమన్వయ సమయోజనీయ బంధం ఏర్పడుతుంది.
BF₃ + NH₃ → [BF₃ ← NH₃] లేదా [BF₃ . NH₃]

e) ఆర్ద్ర అల్యూమినాను సజల NaOH ద్రావణంతో చర్య జరిపితే సోడియం మెటా అల్యూమినేట్ ఏర్పడుతుంది.

ప్రశ్న 26.
కారణాలు తెలపండి :
సోడియమ్ మెటా అల్యుమినేట్
a) అల్యూమినియం పాత్రలలో గాఢ HNO₃ రవాణా చేయవచ్చు.
b) సజల NaOH, అల్యూమినియం ముక్కల మిశ్రమాన్ని మురుగు కాలువను తెరవడానికి వాడతారు.
c) అల్యూమినియం మిశ్రమలోహాన్ని విమానాలను తయారుచేయడానికి వాడతారు.
d) అల్యూమినియం పాత్రలను రాత్రంతా నీళ్ళలో పెట్టకూడదు.
e) అల్యూమినియం తీగలను ప్రసార కేబుల్ తయారీకి వాడతారు.
జవాబు:
a) Al మరియు గాఢ HNO₃ కి మధ్య చర్యారాహిత్యం కలదు. అందువలన అల్యూమినియం పాత్రలలో గాఢ HNO₃ని రవాణా చేయవచ్చు.

b) సజల NaOH అల్యూమినియమ్ చర్య జరిపి H₂ వాయువును విడుదలచేస్తుంది. ఈ వాయు పీడనం వలన మురుగు కాలువలు తెరచుకుంటాయి. కావున సజల NaOH, Al మిశ్రమాన్ని మురుగు కాలువను తెరవటానికి వాడతారు.

c) Al తేలికయిన, బలమైన లోహం. గాలిలో క్షయం చెందదు. కావున దీనిని విమాన విడిభాగాలను తయారుచేయటానికి వాడతారు.

d) అల్యూమినియమ్ పాత్రలను రాత్రంతా నీటిలో పెట్టకూడదు. నీటిలోని లవణాలు పాత్ర ఉపరితలంపై ఉన్న ఆక్సైడ్ పొరతో చర్య జరిపి అల్యూమినియమ్ యొక్క చర్యాశీలతను పెంచుతాయి. దీనివలన Al నీటితో చర్య జరుపుతుంది.

e) అల్యూమినియమ్ తీగలను ప్రసార కేబుల్ తయారీకి వాడతారు. దీనికి కారణం దాని యొక్క మంచి విద్యుద్వాహకత.

ప్రశ్న 27.
Ga, ln, Tl లలో రుణవిద్యుదాత్మకత భేదం ఎందుకు ఎక్కువగా మారదో వివరించండి.
జవాబు:
Ga మరియు ln లలో d ఎలక్ట్రాన్ల వలన పరిరక్షక ప్రభావం తక్కువగా ఉంటుంది. అలాగే Tl లో ‘d’ మరియు ‘f’ ఎలక్ట్రాన్ల వలన పరిరక్షక ప్రభావం తక్కువగా ఉంటుంది. కావున Ga, ln, Tl ల యొక్క పరమాణు పరిమాణంలో పెద్దగా మార్పు ఉండదు. కాని కేంద్రక ఆవేశం మాత్రము పెరుగుతుంది. కావున ఈ మూడు మూలకాల ఋణవిద్యుదాత్మకత విలువలలో భేదం ఎక్కువగా మారదు.

ప్రశ్న 28.
సరైన ఉదాహరణతో బోరాక్స్ పూస పరీక్షను వివరించండి. (March 2013)
జవాబు:
బోరాక్సిని వేడిచేస్తే మొదట నీటి అణువులను కోల్పోయి ఉబ్బి పరిమాణంలో పెద్దదవుతుంది. ఇంకా వేడిచేస్తే అది పారదర్శక ద్రవంగా మారి ఘనీభవనం చెంది గాజులాంటి పదార్థంగా మారుతుంది. దీనిలో సోడియం బొరేట్ మరియు B₂O₃ ఉంటాయి. ఈ B₂O₃ను లోహ ఆక్సైడ్ తో కలిపి వేడి చేస్తే లోహ మెటాబొరేట్లు ఏర్పడతాయి. ఈ మెటాబొరేట్లు ప్రత్యేకమైన రంగును కలిగి ఉంటాయి. వచ్చిన రంగును బట్టి లవణంలోని కేటయాను గుర్తించవచ్చును.

Na₂B₄O₇ + CoO → 2NaBO₂ + Co (BO₂)

ఆక్సీకరణ, క్షయకరణ జ్వాలలో వేడి చేసినపుడు ఒక్కొక్క లోహం ఒక్కొక్క రంగుగల మెటాబోరేట్లను ఏర్పరుస్తుంది. దీనిని బోరాన్ పూస పరీక్ష అంటారు.

ప్రశ్న 29.
డైబోరేన్ నిర్మాణాన్ని వివరించండి.
జవాబు:
డైబోరేన్ నిర్మాణము :

• డైబోరేన్లో రెండు సమతల BH₂ గ్రూపులు ఉంటాయి. ఈ రెండు BH₂ గ్రూపులను కలుపుతూ రెండు H పరమాణువులు ఉంటాయి. రెండు బోరాన్ పరమాణువులకు అతకబడి ఉన్న నాలుగు H లను అంత్య హైడ్రోజన్లు అని, BH₂ గ్రూపులను కలిపే రెండు H పరమాణువులను వారధి (బ్రిడ్జ్) H పరమాణువులని అంటారు.
• B₂H₆ లో రెండు బోరాన్ పరమాణువులు sp³ సంకరీకరణం జరుపుకొని నాలుగు sp³ సంకర ఆర్బిటాళ్ళను ఏర్పరుస్తాయి. నాలుగు sp³ సంకర ఆర్బిటాళ్లలో ఒక ఆర్బిటాల్లో ఎలక్ట్రాన్ ఉండదు.
• ప్రతి బోరాన్లోని రెండు బంధ ఎలక్ట్రాన్లు గల sp³ సంకర ఆర్బిటాల్స్లో రెండు హైడ్రోజన్ల యొక్క s ఆర్బిటాల్స్తో అతిపాతం చెంది సహజమైన B-H బంధాలు (2 – కేంద్రక 2 – ఎలక్ట్రాన్లు) ఏర్పడతాయి.
• ఒక బోరాన్లోని బంధ ఎలక్ట్రాన్ గల sp³ సంకర ఆర్బిటాల్, వేరొక బోరాన్లోని ఖాళీ sp³ సంకర ఆర్బిటాల్ మరియు H యొక్క 1s ఆర్బిటాల్తో అతిపాతం చెంది B-H-B (బిడ్జ్ బంధాన్ని ఏర్పరుస్తాయి. ఈ విధంగా B₂H₆ లో రెండు B-H-B బ్రిడ్జ్ బంధాలు ఏర్పడతాయి. ఈ బంధాలనే బనానా బంధాలు అని లేదా 3-కేంద్రక-2-ఎలక్ట్రాన్ బంధాలని అంటారు.
  

ప్రశ్న 30.
ఆమ్లాలతో అల్యూమినియం చర్యలను వివరించండి.
జవాబు:

1. అల్యూమినియమ్ విలీన లేదా గాఢ HCl లో కరిగి H₂ వాయువును విడుదలచేస్తుంది.
   2Al + 6HCl → 2AlCl₃ + 3H₂ ↑
2. అల్యూమినియమ్ విలీన H₂SO₄ లో H₂ ను విడుదలచేస్తుంది.
   2Al + 3H₂SO₄ → Al₂ (SO₄)₃ + 3H₂ ↑
3. అల్యూమినియమ్ గాఢ H₂SO₄ లో కరిగి SO₄ ను ఇస్తుంది.
   2Al + 6H₂SO₄ → Al₂(SO₄)₃ + 3SO₂ + 6H₂O
4. అతి విలీన HNO₃ని అల్యూమినియమ్ NH₄NO₃ గా క్షయకరణం చేస్తుంది.
   8Al + 30HNO₃ → 8Al (NO₃)₃ + 3NH₄NO₃ + 9H₂O
5. గాఢ HNO₃ తో Al క్రియారహితం అవుతుంది. లోహపు ఉపరితలంపై పలుచని ఆక్సైడ్ పొర ఏర్పడటం వలన క్రియారాహిత్యం వస్తుంది.

ప్రశ్న 31.
గ్రూపు 13లో బోరాన్ అసంగత ప్రవర్తనను సంక్షిప్తంగా రాయండి.
జవాబు:
బోరాన్ పరమాణు సైజు చిన్నది కావటం, అయొనైజేషన్ పొటెన్షియల్ ఎక్కువగా ఉండటం వలన మిగిలిన మూలకాలతో అసంగత ప్రవర్తనను చూపిస్తుంది. ఉదా :

• బోరాన్ అలోహం, Al ద్వంద్వ స్వభావం గల లోహం Ga, ln, Tl లు లోహాలు.
• బోరాన్ ఎల్లప్పుడు కోవలంట్ సమ్మేళనాలను ఇస్తుంది. కాని మిగిలిన మూలకాలు అయానిక సమ్మేళనాలను ఇస్తాయి.
• బోరాన్కు సిలికాన్తో కర్ణ సంబంధం ఉంటుంది. మిగిలిన మూలకాలు ఈ కర్ణ సంబంధాన్ని చూపవు.
• ఆమ్లాల నుండి బోరాన్ H₂ ను స్థానభ్రంశం చేయదు. కాని మిగిలిన మూలకాలు H₂ స్థానభ్రంశం చెందిస్తాయి. బోరాన్ ఆక్సైడ్ ఆమ్ల ఆక్సెడ్. కాని మిగిలిన మూలకాల ఆక్సైడ్లు ద్విస్వభావ ఆక్సైడ్లుగా గాని క్షార ఆక్సైడ్లుగా గాని ఉంటాయి.
• సరళ బోరేట్లు, సిలికేటులు తేలికగా పాలిమరీకరణం చెంది పాలీ ఆమ్లాలను ఇస్తాయి. మిగిలిన మూలకాలు పాలిమర్ ఆమ్లాలను ఇవ్వవు.
• బోరాన్ అత్యధిక కో వేలన్సీ 4. ఇతర మూలకాల అత్యధిక కోవలన్సీ 6.
• స్థిరమైన కోవలంట్ హైడ్రేడ్లను ఇస్తుంది. మిగిలిన మూలకాలు స్థిరమైన హైడ్రైడ్లను ఇవ్వవు.

ప్రశ్న 32.
అల్యూమినియం సజల HNO₃ తో చర్య జరుపుతుంది కాని గాఢ HNO₃ తో చర్య జరపదు. వివరించండి.
జవాబు:
విలీన HNO₃ తో అల్యూమినియమ్ చర్యజరిపి HNO₃ ని NH₄ NO₃ గా క్షయకరణం చేస్తుంది.
8Al + 3OHNO₃ → 8Al(NO₃)₃ + 3NH₄NO₃ + 9H₂O

కాని గాఢ HNO₃ కి అల్యూమినియమ్ను కలిపినపుడు లోహపు తలంపై పలుచని ఆక్సైడ్పొర ఏర్పడుతుంది.. ఈ. ఆక్సైడ్ పొర రక్షిత పొరగా పనిచేసి Al ని HNO₃ తో చర్య జరగకుండా అడ్డుకుంటుంది. కావున గాఢ HNO₃ తో Al క్రియారహితం అవుతుంది.

ప్రశ్న 33.
డైబోరేన్ ను తయారుచేసే రెండు పద్ధతులు రాయండి.
జవాబు:
డైబోరేన్ [B₂H₆] ను తయారుచేయు పద్ధతులు :
బోరాన్ ట్రై ఫ్లోరైడు లిథియమ్ అల్యూమినియమ్ హైడ్రైడ్తో డైఈథైల్ ఈథర్లో చర్య జరిపి డైబోరేన్ను తయారుచేస్తారు.
4BF₃ + 3LiAlH₄ → 2B₂H₆ + 3LiF + 3AlF₃

• ప్రయోగశాలలో సోడియం బోరోహైడ్రైడు, అయోడిన్ ఆక్సీకరణం చేసి డైబోరేన న్ను తయారుచేస్తారు.
  2NaBH₄ + I₂ → B₂H₆ + 2Nal + H₂
• పారిశ్రామికంగా డైబోరేన్ న్ను ఉత్పత్తి చేయడానికి BF₃ ని సోడియం హైడ్రైడ్తో చర్య జరిపిస్తారు.
  

ప్రశ్న 34.
డైబోరేన్ ఈ కింది వాటితో ఏ విధంగా చర్య జరుపుతుంది ?
a) H₂O
b) CO
c) N(CH₃)₃
జవాబు:
a) డైబోరేన్ నీటితో చర్య : డైబోరేన్ నీటిలో జలవిశ్లేషణ చెంది బోరిక్ ఆమ్లాన్ని ఇస్తుంది.

b) డైబోరేన్ CO తో చర్య : డైబోరేన్ 1000°C ఉష్ణోగ్రత మరియు 2 atm పీడనం వద్ద CO తో చర్య జరిపి బోరేన్ కార్బోనైల్ను ఏర్పరుస్తుంది.

c) డైబోరేన్ N(CH₃)₃ తో చర్య : డైబోరేన్ N(CH₃)₃ తో చర్య జరిపి బోరాన్ సంకలితాన్ని ఏర్పరుస్తుంది.

ప్రశ్న 35.
Al₂O₃ ద్విస్వభావం కలదని సరైన చర్యలతో వివరించండి.
బోరాన్ సంకలితం
జవాబు:
Al₂O₃ కు ద్విస్వభావం కలదు. ఇది ఆమ్లాలతో మరియు క్షారాలతో చర్య జరిపి లవణాలను ఏర్పరుస్తుంది.
ఆమ్లాలతో చర్య : ‘Al₂O₃ ఆమ్లాలతో ఈ క్రింది విధంగా చర్య జరుపుతుంది.
Al₂O₃ +6HCl → 2AlCl₃ + H₂O
క్షారాలతో చర్య : Al₂O₃ క్షారాలతో ఈ క్రింది విధంగా చర్య జరుపుతుంది.
Al₂O₃ + 2NaOH → NaAlO₂ + H₂O

ప్రశ్న 36.

జవాబు:

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 37.
బోరాక్స్న, బోరిక్ ఆమ్లాన్ని ఎలా తయారుచేస్తారు ? వాటిమీద ఉష్ణం చర్యను వివరించండి.
జవాబు:
బోరాక్స్ తయారీ : బోరిక్ ఆమ్లంను వేడిచేయగా టెట్రాబోరిక్ ఆమ్లం ఏర్పడుతుంది. దీనిని NaOH తో చర్య జరపగా బోరాక్స్ ఏర్పడును.

బోరాకున్ను అధికంగా వేడిచేస్తే గాజులాంటి పదార్థంగా మారుతుంది. దీనినే బోరాక్స్ పూస అంటారు.

బోరిక్ ఆమ్లం తయారీ : బోరాక్స్ను గాఢ H₂SO₄ తో చర్య జరిపినపుడు బోరిక్ ఆమ్లం ఏర్పడుతుంది.

బోరిక్ ఆమ్లంను వేడిచేయగా మెటాబోరికామ్లం ఏర్పడుతుంది. దీనిని ఇంకా వేడిచేస్తే బోరిక్ ఆక్సైడ్ ఏర్పడుతుంది.

ప్రశ్న 38.
డైబోరేన్ ను ఎలా తయారుచేస్తారు ? దాని నిర్మాణాన్ని వివరించండి.
జవాబు:
డైబోరేన్ [B₂H₆] ను తయారుచేయు పద్ధతులు :

• బోరాన్ ట్రై ఫ్లోరైడ్ను లిథియమ్ అల్యూమినియమ్ హైడ్రైడ్తో డైఈథైల్ ఈథర్లో చర్య జరిపి డైబోరేన్ ను తయారుచేస్తారు.
  4BF₃ + 3LiAlH₄ → 2B₂H₆ + 3LiF + 3AlF₃
• ప్రయోగశాలలో సోడియం బోరోహైడ్రైడ్న, అయోడిన్తో ఆక్సీకరణం చేసి డైబోరేన్ తయారుచేస్తారు.
  2NaBH₄ + I₂ → B₂H₆ + 2Nal + H₂
  పారిశ్రామికంగా డైబోరేన్ ను ఉత్పత్తి చేయడానికి BF₃ ని సోడియం హైడ్రైడ్తో చర్య జరిపిస్తారు.
  

డైబోరేన్ నిర్మాణము :

• డైబోరేన్లో రెండు సమతల BH₂ గ్రూపులు ఉంటాయి. ఈ రెండు BH₂ గ్రూపులను కలుపుతూ రెండు H పరమాణువులు ఉంటాయి. రెండు బోరాన్ పరమాణువులకు అతకబడి ఉన్న నాలుగు H లను అంత్య హైడ్రోజన్లు అని, BH₂ గ్రూపులను కలిపే రెండు H పరమాణువులను వారధి (బ్రిడ్జ్) H పరమాణువులని అంటారు.
• B₂H₆ లో రెండు బోరాన్ పరమాణువులు sp³ సంకరీకరణం జరుపుకొని నాలుగు sp³ సంకర ఆర్బిటాళ్ళను ఏర్పరుస్తాయి. నాలుగు sp³ సంకర ఆర్బిటాళ్లలో ఒక ఆర్బిటాల్లో ఎలక్ట్రాన్ ఉండదు.
• ప్రతి బోరాన్లోని రెండు బంధ. ఎలక్ట్రాన్లు గల sp³ సంకర ఆర్బిటాల్స్తో రెండు హైడ్రోజన్ల యొక్క s – ఆర్బిటాల్స్తో అతిపాతం చెంది సహజమైన B – H బంధాలు (2 – కేంద్రక 2 – ఎలక్ట్రాన్లు) ఏర్పడతాయి.
• ఒక బోరాన్లోని బంధ ఎలక్ట్రాన్ గల sp³ సంకర ఆర్బిటాల్, వేరొక బోరాన్లోని ఖాళీ sp³ సంకర ఆర్బిటాల్ మరియు H యొక్క 1s ఆర్బిటాల్తో అతిపాతం చెంది B-H-B బ్రిడ్జ్ బంధాన్ని ఏర్పరుస్తాయి. ఈ విధంగా B₂H₆ లో రెండు B-H-B బ్రిడ్జ్ బంధాలు ఏర్పడతాయి. ఈ బంధాలనే బనానా బంధాలు అని లేదా 3-కేంద్రక-2-ఎలక్ట్రాన్ బంధాలని అంటారు.
  

ప్రశ్న 39.
డైబోరేన్ను తయారుచేసే ఏవైనా రెండు పద్ధతులు రాయండి. అది ఈ కింది వాటితో ఏ విధంగా చర్య జరుపుతుంది?
a) కార్బన్ మోనాక్సైడ్
b) అమ్మోనియా
జవాబు:
డైబోరేన్ [B₂H₆] ను తయారుచేయు పద్ధతులు :

• బోరాన్ ట్రై ఫ్లోరైడ్ను లిథియమ్ అల్యూమినియమ్ హైడ్రైడ్ డైఈథైల్ ఈథర్లో చర్య జరిపి డైబోరేన్ను తయారుచేస్తారు.
  4BF₃ + 3LiAlH₄ → 2B₂H₆ + 3LiF + 3AlF₃
• ప్రయోగశాలలో సోడియం బోరోహైడ్రైడ్న, అయోడిన్తో ఆక్సీకరణం చేసి డైబోరేన్ ను తయారుచేస్తారు.
  2NaBH₄ + I₂ → B₂HË₆ + 2Nal + H₂
• పారిశ్రామికంగా డైబోరేన్ను ఉత్పత్తి చేయడానికి BF₃ ని సోడియం హైడ్రైడ్తో చర్య జరిపిస్తారు.
  

a) డైబోరేన్ కార్బన్ మోనాక్సైడ్తో చర్య : డైబోరేన్ 1000°C ఉష్ణోగ్రత మరియు 22atm పీడనం వద్ద CO తో చర్య జరిపి బోరేన్ కార్బనైల్ అనే బోరాన్ సంకలితాన్ని ఏర్పరుస్తుంది.

b) డైబోరేన్ అమ్మోనియాతో చర్య డైబోరేన్ అమ్మోనియాతో చర్యనొంది మొదట B₆H₆. 2NH₃ ని ఇస్తుంది. దీనినే
(BH₂(NH₃)₂)⁺ B\(\mathrm{H}_4^{-}\) గా కూడా వ్రాయవచ్చు. దీనిని ఇంకా వేడిచేస్తే బోరజీన్ ఏర్పడుతుంది. బోరజీన్కు బెంజీన్ వంటి వలయ నిర్మాణం ఉంటుంది. కావున దీనిని ఇనార్గానిక్ బెంజీన్ అని కూడా అంటారు.

Here students can locate TS Inter 1st Year Political Science Notes Chapter 12 Forms of Governments to prepare for their exam.

TS Inter 1st Year Political Science Notes Chapter 12 Forms of Governments

→ Government formulates, expresses and realizes the will of the State.

→ Government is described as the executive organ of the State.

→ Government consists of three organs i.e. Legislature, Executive and Judiciary.

→ Legislature Makes laws, the Executive executes laws and Judiciary interprets laws.

→ Aristotle classified Governments into normal and perverted forms.

→ Aristotle says that monarchy, aristocracy and polity are the normal forms of Government. Tyranny, oligarchy and democracy are the perverted forms of Government.

→ “Unitary Government is one in which one central power habitually exercises the supreme legislative authority.” -A.V. Dicey

→ The term ‘Federation’ is derived from the Latin word ‘Foedus’ which means ‘treaty’ or ‘agreement’.

→ “Federation is an association of states that forms a new one.” – Hamilton

→ Collective responsibility is the salient feature of the Parliamentary form of Government.

→ Presidential form of Government is known as single Executive Government.

→ Montesque advocated ‘the theory of separation of powers’, that is based on ‘checks and balance.’

TS Inter 1st Year Political Science Notes Chapter 12 ప్రభుత్వం – రకాలు

→ రాజ్యానికి ముఖ్యసాధనం ప్రభుత్వం.

→ రాజ్యము యొక్క లక్ష్యాలను, ఆశయాలను రూపొందించి, అమలుపరిచేందుకు తోడ్పడే సాధనమే ప్రభుత్వం.

→ ప్రభుత్వం మూడు అంగాలను కలిగి ఉంటుంది. అవి 1) శాసననిర్మాణశాఖ 2) కార్యనిర్వాహకశాఖ 3) న్యాయశాఖ,

→ శాసననిర్మాణశాఖ శాసనాలను రూపొందిస్తుంది. కార్యనిర్వాహకశాఖ శాసనాలను అమలు చేస్తుంది. న్యాయశాఖ శాసనాలకు అర్థవివరణ ఇస్తుంది. మరియు నిష్పక్షపోతంగా న్యాయాన్ని ప్రసాదిస్తుంది.

→ ఏ వ్యవస్థలో రాజ్యము యొక్క సర్వాధికారాలను ఒకే కేంద్రీయ అధికార వ్యవస్థ వాడుకగా వినియోగిస్తుందో ఆ వ్యవస్థనే “ఏకకేంద్ర ప్రభుత్వము” అని ఎ.వి.డైసీ మహాశయుడు పేర్కొన్నాడు.

→ సమాఖ్య ప్రభుత్వాన్ని ఆంగ్లంలో ‘ఫెడరేషన్’ అని అంటారు. ఈ పదం ‘ఫోడస్’ అనే లాటిన్ పదము నుండి గ్రహించబడింది. ఫోడస్ అనగా ‘ఒప్పందము’ లేదా ‘ఒడంబడిక’ అని అర్థం.

→ సమాఖ్య ప్రభుత్వము యొక్క లక్షణం ‘లిఖిత, దృఢ, ఉన్నత రాజ్యాంగం మరియు కేంద్ర – రాష్ట్ర ప్రభుత్వాల మధ్య స్పష్టమైన, నిర్దిష్టమైన అధికారాల పంపిణి.

→ పార్లమెంటరీ ప్రభుత్వ వ్యవస్థలో కార్యనిర్వాహక వర్గం శాసనసభ నుండి ఎన్నుకోబడి, శాసనసభ యొక్క విశ్వాసాన్ని కలిగి ఉన్నంత కాలం అధికారంలో కొనసాగుతుంది.
ఉదా : ఇంగ్లాండ్ మరియు ఇండియా.

→ అధ్యక్షతరహా ప్రభుత్వ వ్యవస్థలో కార్యనిర్వాహక వర్గం తన చర్యలకు శాసననిర్మాణ శాఖకు ఎటువంటి బాధ్యత వహించదు. ఉదా : అమెరికా.