TS Inter 1st Year Maths 1A Solutions Chapter 5 Products of Vectors Ex 5(b)

Students must practice these TS Intermediate Maths 1A Solutions Chapter 5 Products of Vectors Ex 5(b) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Products of Vectors Solutions Exercise 5(b)

I.
Question 1.
If |p̅| = 2, |q̅| = 3 and (p, q) = \(\frac{\pi}{6}\), then find |p̅ × q̅|².
Answer:
p̅ × q̅ = |p̅| |q̅| sinθn̂
Given p̅ = 2, q̅ = 3 and (p̅. q̅) = \(\frac{\pi}{6}\)
|p̅ × q̅| = (2) (3)sin\(\frac{\pi}{6}\) = 3
∴ |p̅ × q̅|² = 9

Question 2.
If a̅ = 2i̅ – j̅ + k̅ and b̅ = i̅ – 3j̅ – 5k̅, then find |a̅ × b̅|. (March 2013)
Answer:
a̅ = 2 i̅ – j̅ + k̅ and b̅ = i̅ – 3 j̅ – 5k̅

Question 3.
If a̅ = 2i̅ – 3j̅ + k̅ and b̅ = i̅ + 4j̅ – 2k̅, then find (a̅ + b̅) × (a̅ – b̅).
Answer:
Given a̅ = 2i̅ – 3j̅ + k̅ and b̅ = i̅ + 4j̅ – 2k̅
Then a̅ + b̅ = 3 i̅ + j̅ – k̅ and a̅ – b̅ = i̅ – 7j̅ + 3k̅
(a + b) × (a – b) = \(\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
3 & 1 & -1 \\
1 & -7 & 3
\end{array}\right|\)
= i̅(3 – 7) – j̅(9 + l) + k̅ (- 21 – 1)
= -4i̅ – 10j̅ – 22k̅
= -2 (2i̅ + 5j̅ + 11k̅)

Question 4.
If 4i̅ + \(\frac{2 p}{3}\) j̅ + pk̅ is parallel to the vector 3 i̅ + 2j̅ + 3k̅, find p.
Answer:
Given 4i̅ + \(\frac{2 p}{3}\) j̅ + pk̅ is parallel to
i̅ + 2j̅ + 3k̅
∴ \(\frac{4}{1}=\frac{\frac{2 p}{3}}{2}=\frac{p}{3}\)
⇒ \(\frac{2 p}{3}\) = -4 ⇒ p = 12

Question 5.
Compute
a̅ × (b̅ + c̅) + b̅ × (c̅ + a̅) + c̅ × (a̅ + b̅)
Sol.
a̅ × (b̅ + c̅) + b̅ × (c̅ + a̅) + c̅ × (a̅ + b̅)
= (a̅ × b̅) + (a̅ × c̅) + (b̅ × c̅) + (b̅ × a̅) + (c̅ × a̅) + (c̅ × b̅)
= (a̅ × b̅) + (a̅ × c̅) + (b̅ × c̅) – (a̅ × b̅) – (a̅ × c̅) – (b̅ × c̅)
= 0

Question 6.
If p̅ = xi̅ + yj̅ + zk̅, then find |p̅ × k̅|².
Answer:
p̅ × k̅ = (xi̅ + yj̅ + zk̅) × k̅
= x(i̅ × k̅) + y(j̅ × k̅) + z(k̅ × k̅)
= -xj̅ + yi̅ + z(0)
= yi̅ – xj̅
|p̅ × k̅|² = x² + y²

Question 7.
Compute 2j̅ × (3i̅ – 4k̅) + (i̅ + 2j̅) × k̅
Sol.
2j̅ × (3i̅ – 4k̅) + (i̅ + 2j̅) × k̅
= 6(j̅ × i̅) – 8(j̅ × k̅) + (i̅ × k̅) + 2(j̅ × k̅)
= -6k̅ – 8i̅ – j̅ + 2i̅
= -6i̅ – j̅ – 6k̅

Question 8.
Find unit vector perpendicular to both i̅ + j̅ + k̅ and 2i̅ + j̅ + 3k̅.
Answer:
Given a̅ = i̅ + j̅ + k̅ and b̅ = 2i̅ + j̅ + 3k̅
then a̅ × b̅ = \(\left|\begin{array}{lll}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & 1 \\
2 & 1 & 3
\end{array}\right|\)
= i̅(3 – 1) – j̅(3 – 2) + k̅(1 – 2)
= 2i̅ – j̅ – k̅
|a̅ × b̅| = \(\sqrt{4+1+1}=\sqrt{6}\)
Unit vector perpendicular to both a̅ and b̅
= ±\(\frac{\overline{\mathrm{a}} \times \overline{\mathrm{b}}}{|\overline{\mathrm{a}} \times \overline{\mathrm{b}}|}=\pm\left(\frac{2 \overline{\mathrm{i}}-\overline{\mathrm{j}}-\overline{\mathrm{k}}}{\sqrt{6}}\right)\)

Question 9.
If θ is the angle between the vectors i̅ + j̅ and j̅ + k̅, then find sin θ.
Answer:
Let a̅ = i̅ + j̅ and b̅ = j̅ + k̅

Question 10.
Find the area of the parallelogram having a̅ = 2j̅ – k̅ and b̅ = – i̅ + k̅ as adjacent sides.
Answer:
Vector area of the parallelogram having
a̅ = 2j̅ – k̅ and b̅ = -i̅ + k̅ as adjacent sides = a̅ × b̅
= \(\left|\begin{array}{rrr}
\bar{i} & \bar{j} & \bar{k} \\
0 & 2 & -1 \\
-1 & 0 & 1
\end{array}\right|\) = 2 i̅ + j̅ + 2k̅
Area of the parallelogram
= |a̅ × b̅| = \(\sqrt{4+1+4}\) = 3 sq. units.

Question 11.
Find the area of the parallelogram whose diagonals are 3i̅ + j̅ – 2k̅ and i̅ – 3j̅ + 4k̅.
Answer:
Let a̅ = 3i̅ + j̅ – 2k̅ and b̅ = i̅ – 3j̅ + 4k̅ be the diagonals of a parallelogram then its vector area = \(\frac{1}{2}\)(a̅ × b̅) and area |\(\frac{1}{2}\)(a̅ × b̅)|
a̅ × b̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
3 & 1 & -2 \\
1 & -3 & 4
\end{array}\right|\)
= i̅ [4 – 6] – j̅ [12 + 2] + k̅ [-9 – 1]
= -2i̅ – 14j̅ – 10k̅
= 2(-i̅ – 7j̅ – 5k̅)
Vector area of parallelogram = |\(\frac{1}{2}\)(a̅ × b̅)|
= |[2(-i̅ – 7j̅ – 5k̅)]
= (-i̅ – 7j̅ – 5k̅)
Area of the parallelogram = |- i̅ – 7 j̅ – 5k̅|
= \(\sqrt{1+49+25}=\sqrt{75}\) = 5√3 sq. units.

Question 12.
Find the area of the triangle having 3 i̅ + 4j̅ and – 5 i̅ + 7j̅ as two of its sides.
Answer:
Area of the triangle = \(\frac{1}{2}\) \(|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|\)
\(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}\) = (3i̅ + 4j̅) × (-5i̅ + 7j̅)
= -15(i̅ × i̅) – 20(j̅ × i̅) + 21(i̅ × j̅) + 28 (j̅ × j̅)
= 20k̅ + 21k̅ = 41k̅
Area of the ΔABC = \(\frac{1}{2}\) \((41) = 20.5 sq. units

Question 13.
Find unit vector perpendicular to the plane determined by the vectors a̅ = 4i + 3j – k and b̅ = 2 i – 6 j 3k .
Answer:
Here a̅ = 4 i̅ + 3 j̅ – k̅ and b̅ = 2 i̅ – 6 j̅ – 3k̅
then a̅ × b̅

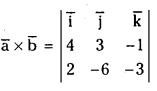
= i̅(-15) – j̅(-10) + k̅(-30)
= -15i̅ +10j̅ – 30k̅
= -5(3i̅ – 2j̅ + 6k̅)
|a̅ × b̅| = 5[latex]\sqrt{9+4+36}\) = 5(7) = 35
∴ Unit vector perpendicular to the plane
= \(\pm \frac{5(3 \bar{i}-2 \bar{j}+6 \bar{k})}{35}\)
= \(\frac{\pm(3 \bar{i}-2 \bar{j}+6 \bar{k})}{7}\)

Question 14.
Find the area of the triangle whose vertices are A (1, 2, 3), B (2, 3, 1) and C (3, 1, 2). (Mar. ’14, ’06)
Answer:
Suppose i̅, j̅, k̅ are unit vectors along the coordinate axes.
Position vectors of A, B, C are i̅ + 2j̅ + 3k̅, 2i̅ + 3j̅ + k̅, 3i̅ + j̅ + 2k̅
\(\overline{\mathrm{AB}}\) = (2i̅ + 3j̅ + k̅) – (i̅ + 2j̅ + 3k̅)
= i̅ + j̅ – 2k̅
\(\overline{\mathrm{AC}}\) = (3 i̅ + j̅ + 2k̅) – (i̅ + 2 j̅ + 3k̅)
= 2i̅ – j̅ + k̅

\(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}=\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & -2 \\
2 & -1 & -1
\end{array}\right|\)
= i̅(-1 – 2) – j̅(-1 + 4) + k̅(-1 – 2)
= -3i̅ – 3 j̅ – 3k̅ = -3(i̅ + j̅ + k̅)
Area of the ΔABC = \(\frac{1}{2}|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|\)
= \(\frac{3}{2} \sqrt{1+1+1}=\frac{3 \sqrt{3}}{2}\)sq.units

II.
Question 1.
If a̅ + b̅ + c̅ = 0, then prove that a̅ × b̅ = b̅ × c̅ = c̅ × a̅.
Answer:
Given a̅ + b̅ + c̅ = 0
⇒ a̅ = -b̅ – c̅
∴ a̅ × b̅ = -(b̅ × b̅) – (c̅ × b̅)
= 0 + (b̅ × c̅) = (b̅ × c̅) …………(1)
Again a̅ + b̅ + c̅ = 0
⇒ c = -a̅ – b̅
⇒ c̅ × a̅ = (-a̅ – b̅) × a̅
= -(a̅ × a̅) – (b̅ × a̅)
= 0 + (a̅ × b̅)
∴ (c̅ × a̅) = (a̅ × b̅) …………..(2)
From (1) and (2), a̅ × b̅ = b̅ × c̅ – c̅ × a̅

Question 2.
If a̅ = 2i̅ + j̅ – k̅, b̅ = -i̅ + 2j̅ – 4k̅ and c̅ = i̅ + j̅ + k̅, then find (a̅ × b̅) – (b̅ × c̅). (March 2015-A.P)
Answer:
Given a̅ = 2i̅ + j̅ – k̅, b̅ = – i̅ + 2 j̅ – 4k̅ and c̅ = i̅ + j̅ + k̅
Then a̅ × b̅ = \(\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
2 & 1 & -1 \\
-1 & 2 & -4
\end{array}\right|\)
= i̅ (-4 + 2) – j̅ (-8 – 1) + k̅(4 + 1)
= -2i̅ + 9 j̅ + 5k̅
b̅ × c̅ = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
-1 & 2 & -4 \\
1 & 1 & 1
\end{array}\right|\)
= i̅ (2 + 4) – j̅ (-1 + 4) + k̅(-1 – 2)
= 6i̅ – 3j̅ – 3k̅
(a̅ × b̅) – (b̅ × c̅) = (-2i̅ + 9j̅ + 5k̅) – (6i̅ – 3j̅ – 3k̅)
= -12 – 27 – 15
= -54

Question 3.
Find the vector area and the area of the parallelogram having a̅ = i̅ + 2j̅ – k̅ and b̅ = 2i̅ – j̅ + 2k̅ as adjacent sides.
Answer:
Given a̅ = i̅ + 2j̅ – k̅ and b̅ = 2i̅ – j̅ + 2k̅
Then the vector area of parallelogram = a̅ × b̅
∴ (a̅ x b̅) = \(\left|\begin{array}{rrr}
\bar{i} & \bar{j} & \bar{k} \\
1 & 2 & -1 \\
2 & -1 & 2
\end{array}\right|\)
= i̅ (4 – 1)- j̅ (2 + 2) + k̅(-1 – 4)
= 3i̅ – 4j̅ – 5k̅

Magnitude of the area = \(\sqrt{9+16+25}\)
= \(\sqrt{50}\) = 5√2 sq. units

Question 4.
If a̅ × b̅ = b̅ × c̅ ≠ 0, then show that a̅ + c̅ = pb̅, where p is some scalar.
Answer:
Consider (a̅ + c̅ – pb̅) × b̅
= (a̅ × b̅) + (c̅ × b̅) – p(b̅ × b̅)
= (b̅ × c̅) – (b̅ × c̅) – p(0) = 0
∴ a̅ + c̅ – pb̅ = 0 ⇒ a̅ + c̅ = pb̅

Question 5.
Let a and b be vectors, satisfying |a̅| = |b̅| = 5 and (a̅, b̅) = 45°. Find the area of the triangle having a̅ – 2b̅ and 3a̅ + 2b̅ as two of its sides. [March 2007]
Answer:
Area of the triangle = \(\frac{1}{2}\) |(a̅ – 2b̅) × (3a̅ + 2b̅)|
Now |(a̅ – 2b̅) × (3a̅ + 2b̅)|
= 13(a̅ × a̅) – 2(b̅ × a̅) – 6(b̅ × a̅) – 4(b̅ × b̅)|
= 12(a̅ × b̅) + 6(a̅ × b̅)| = 18(a̅ × b̅)|
= 8|a̅| |b̅| sin45°
= 8(5)(5)\(\frac{1}{\sqrt{2}}\)n̂
= 100√2n̂
From (1)
Area of the triangle = \(\frac{1}{2}\)(100)√2
= 50√2 sq. units

Question 6.
Find die vector having magnitude √6 units and perpendicular to both 2j̅ – k̅ and 3j̅ – i̅ – k̅.
Answer:
Let a̅ = 2 i̅ – k̅ and b̅ = 3i̅ – j̅ – k̅
Then a̅ × b̅ = \(\left|\begin{array}{ccc}
\bar{j} & \bar{i} & \bar{k} \\
2 & 0 & -1 \\
3 & -1 & -1
\end{array}\right|\)
= i̅(-1) – j̅(-2 + 3) + k̅(-2)
= – i̅ – j̅ – 2k̅
= -(i̅ + j̅ + 2k̅)
|a̅ × b̅| = \(\sqrt{1+1+4}=\sqrt{6}\)
Vector perpendicular to a̅ and b̅ and having magnitude √6 units is = -(i̅ + j̅ + 2k̅)
Unit vector perpendicular to a and b and having magnitude √6 units is ±\(\left(\frac{\bar{a} \times \bar{b}}{|\bar{a} \times \bar{b}|}\right)\)

Question 7.
Find unit vector perpendicular to the plane determined by the points P (1, – 1, 2), Q (2, 0, – 1) and R (0, 2, 1).
Answer:
Let O be the origin.
\(\overline{\mathrm{OP}}\) = i̅ – j̅ + 2k̅
\(\overline{\mathrm{OQ}}\) = 2i̅ – k̅
\(\overline{\mathrm{OR}}\) = 2j̅ + k̅
\(\overline{\mathrm{PQ}}=\overline{\mathrm{OQ}}-\overline{\mathrm{OP}}\) = (2i̅ – k̅) – (i̅ – j̅ + 2k̅)
= i̅ + j̅ – 3k̅
\(\overline{\mathrm{PR}}=\overline{\mathrm{OR}}-\overline{\mathrm{OP}}\) = (2j̅ + k̅) – (i̅ – j̅ + 2k̅)
= – i̅ + 3 j̅ – k̅

Now \(\overline{\mathrm{PQ}} \times \overline{\mathrm{PR}}=\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & -3 \\
-1 & 3 & -1
\end{array}\right|\)
= i̅ (-1 + 9) – j̅ (-1 – 3) + k̅(3 + 1)
= 8i̅ + 4j̅ + 4k̅
= 4(2i̅ + j̅ + k̅)
\(|\overline{\mathrm{PQ}} \times \overline{\mathrm{PR}}|=4 \sqrt{4+1+1}=4 \sqrt{6}\)

∴ Unit vector perpendicular to the plane determined by the points P, Q and R is

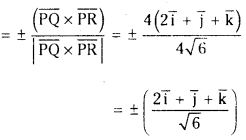
Question 8.
If a̅. b̅ = a̅. c̅ and a̅ × b̅ = a̅ × c̅, a ≠ 0, then show that b̅ = c̅.
Answer:
a̅ . b̅ = a̅. c̅
⇒ a̅.b̅ – a̅.c̅ = 0
⇒ a̅ . (b̅ – c̅) = 0
⇒ b̅ – c̅ = 0 (or) a̅ is perpendicular to
b̅ – c̅ ……… (1) (∵ a̅ ≠ 0)
Again a̅ × b̅ = a̅ × c̅ = 0
⇒ a̅ × b̅ – a̅ × c̅
⇒ a̅ × (b̅ – c̅) = 0 (∵ a ≠ 0)
⇒ b̅ – c̅ = 0 (or) a is parallel to
b̅ – c̅ ………(2)
From (1) and (2);
b̅ – c̅ = 0 ⇒ b̅ = c

Question 9.
Find a vector of magnitude 3 and perpendicular to both the vectors b̅ = 2 i̅ – 2j̅ + k̅ and c̅ = 2i̅ + 2j̅ + 3k̅.
Answer:
b̅ × c̅ = \(\left|\begin{array}{ccc}
\bar{i} & \vec{j} & \bar{k} \\
2 & -2 & 1 \\
2 & 2 & 3
\end{array}\right|\)
= i̅ [-6 – 2] – j̅ [6 – 2] + k̅ [4 + 4]
= -8i̅ – 4j̅ + 8k̅ = -4(2i̅ + j̅ – 2k̅)
∴ A vector of magnitude 3 and perpendicular to both the vectors b̅ and c̅ is = ± 3\(\frac{\bar{b} \times \bar{c}}{|\bar{b} \times \bar{c}|}\)
= 3\(\left[\frac{-4(2 \bar{i}+\bar{j}-2 \bar{k})}{12}\right]\)
= ± (2i̅ + j̅ – 2k̅)

Question 10.
If |a̅|=13, |b̅| = 5 and a̅. b̅ = 60, then find |a̅ × b̅|.
Answer:
We have |a̅ × b̅| = |a̅|² |b̅|² – (a̅. b̅)²
= (13)² (5)² – (60)²
= (169) 25 – 3600
= 4224 – 3600 = 625
|a̅ × b̅| = \(\sqrt{625}\) = 25

Question 11.
Find unit vector perpendicular to the plane passing through the points (1, 2, 3), (2,-1, 1) and (1,2,- 4). (March 2005)
Answer:
Let O’ be the origin and let A (1, 2, 3), B (2, – 1, 1) and C (1, 2,-4) be the given points.
Then \(\overline{\mathrm{OA}}\) = i̅ + 2 j̅ + 3k̅
\(\overline{\mathrm{OB}}\) = 2 i̅ – j̅ + k̅
\(\overline{\mathrm{OC}}\) = i̅ + 2j̅ – 4k̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\)
= (2i̅ – j̅ + k̅) – (i̅ + 2j̅ + 3k̅)
= i̅ – 3 j̅ – 2k̅
\(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\)
= (i̅ + 2j̅ – 4k̅) – (i̅ + 2j̅ + 3k̅)
= -7k̅
\(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}=\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & -3 & -2 \\
0 & 0 & -7
\end{array}\right|\)
= i̅(21) – j̅(-7) + k̅(0)
= 7(3i̅ + j̅)
\(|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|=7 \sqrt{9+1}=7 \sqrt{10}\)

Unit vector perpendicular to the plane

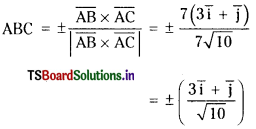
III.
Question 1.
If a̅, b̅ and c̅ represent the vertices A, B and C respectively of ΔABC, then prove that |(a̅ × b̅) + (b̅ × c̅) + (c̅ × a̅)| is twice the area of ΔABC.
Answer:
Let ‘O’ be the origin and
\(\overline{\mathrm{OA}}\) = a̅, \(\overline{\mathrm{OB}}\) = b̅, \(\overline{\mathrm{OC}}\) = c̅
\(\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}\) = b – a
and \(\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}\) = c – a
∴ Area of ΔABC = \(\frac{1}{2}|\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}|\) ………(1)
Here \(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}}\) = (b̅ – a̅) × (c̅ – a̅)
= (b̅ × c̅) – (a̅ × c̅) – (b̅ × a̅) + (a̅ × a̅)
= (b̅ × c̅) + (c̅ × a̅) + (a̅ × b̅) (v a̅ × a̅ = 0)
∴ Area of ΔABC = \(\frac{1}{2}\)|b̅ × c̅ + c̅ × a̅ + a̅ × b̅|
⇒ |b̅ × c̅ + c̅ × a̅ + a̅ × b̅| = 2 (area of ΔABC)
⇒ |(a̅ × b̅) + (b̅ × c̅) + (c̅ × a̅)|
= 2 (area of ΔABC)

Question 2.
If a̅ = 2i̅ + 3j̅ + 4k̅, b̅ = i̅ + j̅ – k̅ and c̅ = i̅ – j̅ + k̅, then compute a̅ × (b̅ × c̅) and verify that it is perpendicular to a̅.
Answer:
b̅ × c̅ = \(\left|\begin{array}{rrr}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & -1 \\
1 & -1 & 1
\end{array}\right|\)
= i̅(1 – 1) – j̅(1 + 1) + k̅(-1 – 1)
= -2j̅ – 2k̅

a̅ × (b̅ × c̅) = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
2 & 3 & 4 \\
0 & -2 & -2
\end{array}\right|\)
= i̅(-6 + 8)- j̅(-4) + k̅(-4)
= 2i̅ + 4j̅ – 4k̅
Now [a̅ × (b̅ × c̅)].a̅
= (2i̅ + 4j̅ – 4k̅)(2i̅ + 3j̅ + 4k̅)
= 4 + 12 – 16 = 0
a̅ × (b̅ × c̅) is perpendicular to a̅.

Question 3.
If a̅ = 7i̅ – 2j̅ + 3k̅, b̅ = 2i̅ + 8k̅ and c̅ = i̅ + j̅ + k̅, then compute a̅ × b̅, a̅ × c̅ and a̅ × (b̅ + c̅), Verify whether the cross product is distributive over vector addition.
Answer:
a̅ × b̅ = \(\left|\begin{array}{rrr}
\bar{i} & \bar{j} & \bar{k} \\
7 & -2 & 3 \\
2 & 0 & 8
\end{array}\right|\)
= i̅ (-16 – 0) – j̅ (56 – 6) + k̅(4)
= -16 i̅ – 50 j̅ + 4k̅

a̅ × c̅ = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
7 & -2 & 3 \\
1 & 1 & 1
\end{array}\right|\)
= i̅ (-2 – 3) – j̅ (7 – 3) + k̅(7 + 2)
= -5i̅ – 4 j̅ + 9k̅

b̅ + c̅ = 2i̅ + 8k̅ + i̅ + j̅ + k̅
= 3 i̅ + j̅ + 9k̅

a̅ × (b̅ + c̅) = \(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
7 & -2 & 3 \\
3 & 1 & 9
\end{array}\right|\)
= i̅ (-18 – 3) – j̅ (63 – 9) + k̅(7 + 6)
= -21i̅ – 54j̅+ 13k̅ …………..(1)
Now (a̅ × b̅) + (a̅ × c̅)
= -16i̅ – 50j̅ + 4k̅ – 5i̅ – 4j̅ + 9k̅
= -21i̅ – 54j̅ + 13k̅ …………(2)
From (1) and (2);
a̅ × (b̅ + c̅) = (a̅ × b̅) + (a̅ × c̅)
∴ Vector product is distributive over vector addition.

Question 4.
If a̅ = i̅ + j̅ + k̅, c = j̅ – k̅, then find vector b such that a̅ × b̅ = c̅ and a̅. b̅ = 3
Answer:
Let b̅ = b₁i̅ + b₂j̅ + b₃k̅
Given a̅. b̅ = 3
⇒ b₁ + b₂ + b₃ = 3 ………..(1)
and a̅ × b̅ = c̅
\(\left|\begin{array}{ccc}
\overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
1 & 1 & 1 \\
\mathrm{~b}_1 & \mathrm{~b}_2 & \mathrm{~b}_3
\end{array}\right|\) = j̅ – k̅
⇒ i̅(b₃ – b₂) – j̅(b₃ – b₁) + k̅(b₂ -b₁) = j̅ – k̅
∴ b₃ – b₁ = – 1 ……………(2)
and b₂ – b₁ = – 1 ……………(3)

∴ b₃ – b₂ = 0 ⇒ b₃ = b₂
∴ From (1), b₁ + 2b₂ = 3 ………(4)
∴ From (3), – b₁ + b₂ = – 1
∴ 3b₂ = 2 ⇒ b₂ = \(\frac{2}{3}\) ……..(5)
∴ b₂ = b₃ = \(\frac{2}{3}\)
b₁ = 3 – 2b₂ = 3 – \(\frac{4}{3}=\frac{5}{3}\) ………(6)

b = b₁ i̅ + b₂ j̅ + b₃k̅
= \(\frac{5}{2}\)i̅ + \(\frac{2}{3}\) j̅ + \(\frac{2}{3}\)k̅
= \(\frac{1}{3}\) (5i̅ + 2 j̅ + 2k̅)

Question 5.
a̅, b̅, c̅ are three vectors of equal magnitudes and each of them is inclined at an angle of 60° to the others. If |a̅ + b̅ + c̅| = √6(5 then find |a̅|.
Answer:
Given |a̅| = |b̅| = |c̅| = k(suppose)
and (a̅,b̅) = (b̅, c̅) = (c̅, a̅) = 60°
Also
(a̅ + b̅ + c̅) = |a̅|² + |b̅|² + |c̅|² + 2(a̅.b̅ + b̅.c̅ + c̅.a̅)
= k² + k² + k² + 2 [|a̅| |b̅| cos60° + |b̅| |c̅| cos60° + |c̅||a̅|cos60°]
= 3k² + \(\frac{2}{2}\)[k² + k² + k²] = 6k²
∴ 6 = 6k² (∵ |a̅ + b̅ + c̅| = √6)
⇒ k = 1
∴ |a̅| = 1

Question 6.
For any two vectors a and b, show that (1 + |a̅|²)(1 + |b̅|²) = |1 – a̅.b̅|² + |a̅ + b̅ + a̅ × b̅|²
Answer:

Question 7.
If a̅, b̅, c̅ are unit vectors such that a is perpendicular to the plane of b̅, c̅ and the angle between b̅ and c̅ is \(\frac{\pi}{3}\), then find |a̅ + b̅ + c̅|.
Answer:
Given that |a̅| = |b̅| = |c̅| = 1
Since a is perpendicular to the plane of b̅, c̅
⇒ We have a̅ . b̅ = 0 and a̅ . c̅ = 0
and given (b̅, c̅) = \(\frac{\pi}{3}\)
Now (a̅ + b̅ + c̅)² = |a̅|² + |b̅|² + |c̅|² + 2[(a̅. b̅) + (b̅. c̅) + (c̅. a̅)]
= 1 + 1 + 1 + 2|b̅||c̅|cos \(\frac{\pi}{3}\)
= 3 + 2\(\left(\frac{1}{2}\right)\) = 4
∴ |a + b + c| = 2

Question 8.
If a̅ = 3i̅ – j̅ + 2k̅, b̅ = – i̅ + 3j̅ + 2k̅, c̅ = 4i̅ + 5j̅ – 2k̅ and d̅ = i̅ + 3j̅ + 5k̅. then compute the following
i) (a̅ × b̅) × (c̅ × d̅)
Answer:
a̅ × b̅ = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
3 & -1 & 2 \\
-1 & 3 & 2
\end{array}\right|\)
= i̅ (-2 – 6) – j̅ (6 + 2) + k̅(9 – 1)
= -8i̅ – 8j̅ + 8k̅ = 8(-i̅ – j̅ + k̅)

c̅ × d̅ = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
4 & 5 & -2 \\
1 & 3 & 5
\end{array}\right|\)
= i̅(25 + 6) – j̅(20 + 2) + k̅(12 – 5)
= 31i̅ – 22j̅ + 7k̅

(a̅ × b̅) × (c̅ × d̅) = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
-8 & -8 & 8 \\
31 & -22 & 7
\end{array}\right|\)
= i̅ (-56 +176) – j̅ (-56 – 248) + k̅(176 + 248)
= i̅(120) + j̅(304) + 424 k̅
= 8[15i̅ + 38j̅ + 53k̅]

ii) (a̅ × b̅) . c̅ – (a̅ × d̅), b̅
Answer:
a̅ × b̅ = -8i̅ – 8j̅ + 8k̅
c̅ = 4 i̅ + 5 j̅ – 2k̅
∴ (a̅ × b̅). c̅ = -32 – 40 – 16 = -88 ………(1)
a̅ × d̅ = \(\left|\begin{array}{rrr}
\overline{\mathbf{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\
3 & -1 & 2 \\
1 & 3 & 5
\end{array}\right|\)
= i̅ (-5 – 6) – j̅ (15 – 2) + k̅(9 + 1)
= -11i̅ – 13j̅ + 10k̅
(a̅ × d̅) . b̅ = (-11i̅ – 13 j̅ + 10k̅) – (-i̅ + 3j̅ + 2k̅)
= 11 – 39 + 20 = -8 ……….(2)
(a̅ × b̅).c̅ – (a̅ × d̅).b̅ = – 88 + 8 = – 80