TS Inter 1st Year

Here students can locate TS Inter 1st Year Commerce Notes Chapter 5 Joint Stock Company to prepare for their exam.

TS Inter 1st Year Commerce Notes Chapter 5 Joint Stock Company

→ The Company form of organisation has emerged due to the limitations of sole trading and partnership business.

→ Company form of organisation is chosen whenever large-scale production or trading activity is taken up.

→ In India, the formation and management of Joint Stock Companies are Governed by the Companies Act, of 2013.

→ Limited liability, perpetual existence, transfer of shares, and separate legal entity are some of the characteristics of companies.

→ Large financial resources, limited liability, transfer of shares, and perpetual succession are some of the merits of the company.

→ Difficulty in formation, fraudulent management, control by few, and excess government control are some of the limitations of a company.

→ Chartered Companies, Statutory Companies, Government Companies, and Private and Public Companies are some types of companies.

Telangana TSBIE TS Inter 1st Year Hindi Study Material 1st Poem कबीर के दोहे Textbook Questions and Answers.

TS Inter 1st Year Hindi Study Material 1st Poem कबीर के दोहे

दीर्घ समाधान प्रश्न

प्रश्न 1.
सत्गुरु के विषय में कबीर के क्या विचार है ?
उत्तर:
कबीरदास गुरु का बड़ा मान रखते थे । उनकी दृष्टि में गुरु का स्थान भगवान से भी बढकर है । गुरु की महिमा अपार और अनंत है, जो शब्दों से बयान नही होती । गुरु ही अपने अज्ञान रूपी अंधकार को दूर करके ज्ञान रूपी दीप (ज्योती) जलाते है ! सत्गुरु ही भगवान के बारे में हमें बताते है । भगवान तक पहुँचने के मार्ग हमें दिखाते हैं ।

प्रश्न 2.
कबीरदास का संक्षिप्त परिचय लिखिए ।
उत्तर:
कबीरदास का स्थान भक्तिकाल के ज्ञानाश्रयी शाखा में सर्वोन्नत है । वे ज्ञानाश्रयी शाखाः के प्रवर्तक माने जाते हैं। कबीरदास के जन्म और मृत्यु को लेकर विभिन्न मत प्रचलित हैं । किंतु अधिकार विद्वानों के मतानुसार कबीर का जन्म काशी में संवत् 1455 (सन् 1398) में हुआ। कबीर का देहातं संवत् 1575 (सन् 1518 ) में मगहर में हुआ । कबीर अनपढ़ और निरक्षर थे । उनके गुरु रामानंद थे । कबीर समाज सुधारक महान कवि और दार्शनिक माने जाते हैं। उनकी वाणी ‘बीजक’ नाम से संग्रहित की गयी है । इसके तीन भाग हैं – 1. साखी 2 सबद 3. रमैनी

कबीर का विवाह लोई नामक स्त्री से हुआ। उनके दो बच्चे भी हुए जिनेक नाम हैं कमाल और कमाली ।

एक शब्द में उत्तर दीजिए

प्रश्न 1.
कबीर के गुरु कौन थे ?
उत्तर:
रामानन्द ।

प्रश्न 2.
कबीर की एक मात्र प्रामाणिक रचना का नाम क्या है ?
उत्तर:
‘बीजक’ ।

प्रश्न 3.
कबीर ने दुर्जन की तुलना किससे की है ?
उत्तर:
मिट्टी का घड़ा से की है ।

प्रश्न 4.
कबीर के अनुसार जहाँ दया होती है, वहाँ क्या होता है ?
उत्तर:
धर्म होता है ।

प्रश्न 5.
कबीरदास किस शाखा के प्रमुख कवि थे ?
उत्तर:
निर्गुण भक्ति शाखा ।

प्रश्न 6.
आचार्य हजारी प्रसाद द्विवेदी के अनुसार कबीर को क्या कहते थे ?
उत्तर:
वाणी के डिक्टेर ।

प्रश्न 7.
कबीरदास किस काल के कवि हैं ?
उत्तर:
भक्तिकाल के ।

प्रश्न 8.
कबीरदास के अनुसार सज्जन किसके समान है ?
उत्तर:
सोना ।

प्रश्न 9.
“काल” शब्द का अर्थ क्या है ?
उत्तर:
मृत्यु, समय, वक्त ।

प्रश्न 10.
कबीरदास समय की तुलना किससे की है ?
उत्तर:
अमोल हीरा से की है ।

संदर्भ सहित व्याख्याएँ

प्रश्न 1.
सतगुरु की महिमा अनंत, अनंत किया उपकार ।
लोचन अनंत उघारिया, अनंत दिखावनहार ॥
उत्तर:
संदर्भ: प्रस्तुत दोहा कबीरदास के दोहे नामक पाठ से संकलित है। कबीरदास हिन्दी साहित्य के भक्तिकालं की निर्गुण भक्तिधारा में ज्ञानाश्रयी शाखा के प्रतिनिधि कवि हैं । ‘बीजक’ आपकी रचनाओं का संकलन है। इसके तीन भाग हैं- ‘साखी’, ‘सबद’ और ‘रमैनी’ । कबीर की भाषा को सधुक्कड़ी कहा जाता है । ज्ञानी, भक्त एवं समाज सुधारक के रूप में कबीरदास हिन्दी साहित्य में अमर हैं ।

व्याख्या : कबीरदास इस दोहे में “सतगुरु की महिमा” अनन्त है और उनके उपकार भी अनन्त हैं । उन्होंने मेरी अनन्त दृष्टि खोल दी जिससे मुझे उस अनन्त प्रभु का दर्शन प्राप्त हो गया । सतगुरु ही भगवान के बारे में हमें बताते हैं । भगवान तक पहुँचने के मार्ग वही हमें दिखाता है ।

विशेषताएँ: इस दोहे में कबीरदास गुरु की महिमा का वर्णन करते है । उनके अनुसार गुरु भगवान से भी महान है । गुरु महिमा का वर्णन संत काव्यधारा की एक प्रमुख विशेषता है ।

प्रश्न 2.
साच बराबर तप नही, झूठ बराबर पाप ।
जाके हिरदे साच है, ता हिरदे गुरु आप ॥
उत्तर:
संदर्भ: प्रस्तुत दोहा कबीरदास के दोहे नामक पाठ से संकलित है । कबीरदास हिन्दी साहित्य के भक्तिकाल की निर्गुण भक्तिधारा में ज्ञानाश्रयी शाखा के प्रतिनिधि कवि हैं । ‘बीजक’ आपकी रचनाओं का संकलन है। इसके तीन भाग हैं- ‘साखी’, ‘सबद’ और ‘रमैनी’ । कबीर की भाषा को सधुक्कड़ी कहा जाता है । ज्ञानी, भक्त एवं समाज सुधारक के रूप में कबीरदास हिन्दी साहित्य में अमर हैं ।

व्याख्या : कबीरदास इस दोहे में “सत्य का महत्व” के बारे में बताया । कबीरदास जी कहते है कि इस जगत् में सत्य के मार्ग पर चलते से बडी कोई तपस्या नही है और ना ही झूठ बोलने सं बडा कोई पाप है । क्यों कि जिसके हृदय में सत्य का निवास होता है उसके हृदय में साक्षात परमेश्वर का वास होता है । सत्य मार्ग में चलनेवालों पर हमेशा भगवान की कृपा होती है ।

विशेषताएँ : कबीरदास इस दोहे में सत्य की महानता के बारें पर जोर देते है । सत्य मार्ग पर चलनेवालों पर ही भगवान की कृपा होती है। झूठ बोलता बड़ा पाप है। सत्य बतानेवाले के हृदय में भगवान रहता है ।

प्रश्न 3.
सोना सज्जन साधुजन, टूटि जुटै सौ बार ।
दुर्जन कुंभ कुम्हार का, एकै धका दरार ।।
उत्तर:
संदर्भ: प्रस्तुत दोहा कबीरदास के दोहे नामक पाठ से संकलित है। कबीरदास हिन्दी साहित्य के भक्तिकाल की निर्गुण भक्तिधारा में ज्ञानाश्रयी शाखा के प्रतिनिधि कवि हैं । ‘बीजक’ आपकी रचनाओं का संकलन है। इसके तीन भाग हैं – ‘साखी’, ‘सबद’ और ‘रमैनी’ । कबीर की भाषा को सधुक्कड़ी कहा जाता है । ज्ञानी, भक्त एवं समाज सुधारक के रूप में कबीरदास हिन्दी साहित्य में अमर हैं ।

व्याख्या : कबीरदास इस दोहे में “सज्जन के गुण” कैसे होना है इसके बारे में हमें बता रहे है। सोने को अगर सौ बार भी तोडा जाए, तो भी उसे फिर जोड़ा जा सकता है। इसी तरह भले मनुष्य हर अवस्था में भले की रहते हैं । इसके विपरीत बुरे या दृष्ट लोग कुम्हार के घड़े की तरह होते हैं जो एक बार टूटने पर दुबारा नही जुड़ता । बुरे आदमी के स्वभाव हमेशा दूसरों की प्रती बुरा ही होता है ।

विशेषताएँ : इस दोहे में सज्जन महानता के बारे में बताया । सज्जन सोने के समान और दुर्जन कुम्हार के घड़े की तरह होते है ।

प्रश्न 4.
जग में बैरी कोइ नहीं, जो मन सीतल होय ।
यह आपा तू डरि दे, दया करै सब कोय ।
उत्तर:
संदर्भ: प्रस्तुत दोहा कबीरदास के दोहे नामक पाठ से संकलित है। कबीरदास हिन्दी साहित्य के भक्तिकाल की निर्गुण भक्तिधारा में ज्ञानाश्रयी शाखा के प्रतिनिधि कवि हैं । ‘बीजक’ आपकी रचनाओं का संकलन है। इसके तीन भाग हैं- ‘साखी’, ‘सबद’ और ‘रमैनी’ । कबीर की भाषा को सधुक्कड़ी कहा जाता है । ज्ञानी, भक्त एवं समाज सुधारक के रूप में कबीरदास हिन्दी साहित्य में अमर हैं ।

व्याख्या : कबीरदास इस दोहे में “अहंकार को त्याग” करने के लिए कहते है । आपके मन में यदि शीतलता है अभति दया और सहानुभूति है, तो संसार में आपकी किसी से शत्रुता नही हो सकती। इसलिए अपने अहंकार को निकाल बाहर करे और आप अपने प्रति दूसरों में भी संवेदना पायेंगे ।

विशेषताएँ: इस दोहे में कबीरदास मन में हुए “अहंकार” को त्याग करने लिए कहते है । दया और सहानुभूति हमारे मन में हो तो संसार के सभी अपने मित्र होते है ।

प्रश्न 5.
बोली तो अनमोल है, जो कोइ जानै बोल ।
हिये तराजू तोलि के, तब मुख बाहर खोल ।।
उत्तर:
संदर्भ: प्रस्तुत दोहा कबीरदास के दोहे नामक पाठ से संकलित है । कबीरदास हिन्दी साहित्य के भक्तिकाल की निर्गुण भक्तिधारा में ज्ञानाश्रयी शाखा के प्रतिनिधि कवि हैं । ‘बीजक’ आपकी रचनाओं का संकलन है। इसके तीन भाग हैं – ‘साखी’, ‘सबद’ और ‘रमैनी’ । कबीर की भाषा को सधुक्कड़ी कहा जाता है । ज्ञानी, भक्त एवं समाज सुधारक के रूप में कबीरदास हिन्दी साहित्य में अमर हैं !

व्याख्या : कबीरदास इस दोहे में “मधुर वाणी” की महानता के बारे हमें बता रहे हैं। यदि कोई सही तरीके से बोलना जानता है। तो उसे पता है कि वाणी एक अमूल्य रत्न है । इसलिए वह हृदय के तराजू में तोलकर ही उसे मुँह से बाहर आने देता है ।

विशेषताएँ : इस दोहे में कबीर ‘वाणी’ की महिमा का वर्णन करते हैं । दूसरों को अपने वश करने के लिए हमेशा मधुर वाणी में बोलने की सलाह दे रहे हैं।

प्रश्न 6.
जहाँ दया तहँ धर्म है, जहाँ लोभ तहँ पाप ।
जहाँ क्रोध तहँ काल है, जहाँ छिमा तहँ आप ॥
उत्तर:
संदर्भ: प्रस्तुत दोहा कबीरदास के दोहे नामक पाठ से संकलित है। कबीरदास हिन्दी साहित्य के भक्तिकाल की निर्गुण भक्तिधारा में ज्ञानाश्रयी शाखा के प्रतिनिधि कवि हैं । ‘बीजक’ आपकी रचनाओं का संकलन है। इसके तीन भाग हैं- ‘साखी’, ‘सबद’ और ‘रमैनी’ । कबीर की भाषा को सधुक्कड़ी कहा जाता है । ज्ञानी, भक्त एवं समाज सुधारक के रूप में कबीरदास हिन्दी साहित्य में अमर हैं ।

व्याख्या : कबीरदास इस दोहे में “दया और क्षमा’ जैसे गुणों का महत्व के बारे में बता रहे हैं । जहाँ दया भाव है वहाँ धर्म व्यवहार होता है। जहाँ क्षमा और सहानुभूति होती है वहाँ भगवान रहते है । दया और क्षमा दोनों इस दुनिया में सबसे महान गुण है ।

विशेषताएँ: इस दोहे में कबीरदास दया और क्षमा पर जोर देते हैं। जिसके हृदय में दया भाव है उसके हृदय में भगवान रहते हैं । उपकार के बदले उपकार करना ही क्षमा गुण है ।

दोहों के भाव

प्रश्न 1.
सतगुरु की महिमा अनंत, अनंत किया उपकार ।
लोचन अनंत उघारिया, अनंत दिखावनहार ॥
उत्तर:
भावार्थ : कबीरदास इस दोहे में “सतगुरु की महिमा” के बारे में बताया । सतगुरु की महिमा अनन्त है और अनेक उपकार भी अनन्त हैं। उन्होंने मेरी अनन्त दृष्टि खोल दी जिससे मुझे उस अनन्त प्रभु का दर्शन प्राप्त हो गया। सतगुरु ही भगवान के बारे में हमें बताते हैं । भगवान तक पहुँचने के मार्ग वही हमें दिखाता हैं ।

భావం : కబీర్దాసు ఈ దోహాలో గురువు యొక్క మహిమను వివరించు చున్నారు. సద్గురువు యొక్క మహిమ మరియు గురువు యొక్క ఉపకారం అనంతమైనది. గురువు నా యొక్క జ్ఞానదృష్టిని తెరిపించిరి. ఆ జ్ఞానదృష్టి సహాయంతోనే నేను భగవంతుని సాక్షాత్కారం పొందగలిగాను అని కబీర్ అంటున్నారు. భగవంతుని వద్దకు వెళ్ళుటకు సరియైన మార్గమును చూపించ గలిగే వ్యక్తి సద్గురువు.

प्रश्न 2.
साच बराबर तप नही, झूठ बराबर पाप ।
जाके हिरदे साच है, ता हिरदे गुरु आप ।
उत्तर:
भावार्थ : कबीरदास इस दोहे में “सत्य का महत्व” के बारे में बताया । कबीरदास जी कहते है कि इस जगत् में सत्य के मार्ग पर चलने से बड़ी कोई तपस्या नही है और ना ही झूठ बोलने से बड़ा कोई पाप है । क्यों कि जिसके हृदय में सत्य का निवास होता है उसके हृदय में साक्षात् परमेश्वर का वास होता है । सत्य मार्ग में चलनेवालों पर हमेशा भगवान की कृपा होती है ।

భావం : కబీర్దాసు ఈ దోహాలో సత్యము యొక్క గొప్పతనాన్ని వివరించిరి. సత్యమార్గమునందు పయనించువారు ఒక మహాతపస్వి కంటే గొప్పవారు. అసత్యము మాట్లాడేవారి కంటే పాపాత్ములు ఈ భూమినందు లేరు. ఎవరైతే ఎల్లప్పుడు సత్యమునే మాట్లాడతారో వారి హృదయంనందు సాక్షాత్తు భగవంతుడు ఉంటాడు. సత్యమార్గమునందు ప్రయాణంచేయు వారిపై ఎల్లప్పుడు భగవంతుని కృప ఉంటుంది.

प्रश्न 3.
सोना सज्जन साधुजन, टूटि जुटै सौ बार ।
दुर्जन कुंभ कुम्हार का, एकै धका दरार ॥
उत्तर:
भावार्थ : कबीरदास इस दोहे में “सज्जन के गुण” कैसे होते है इसके बारे में हमें बता रहे है। सोने को अगर सौ बार भी तोड़ा जाए, तो भी उसे फिर जोड़ा जा सकता है। इसी तरह भले मनुष्य अवस्था में भले ही रहते हैं। इसके विपरीत बुरे या दुष्ट लोग कुम्हार के घड़े की तरह होते हैं जो एक बार टूटने पर दुबारा नही जुड़ता । बुरे आदमी के स्वभाव हमेशा दूसरों की प्रती बुरा ही होता है ।

భావం :- కబీర్ దాసు ఈ దోహాలో మంచి వ్యక్తి యొక్క గుణం ఏవిధంగా ఉండునో మనకు వివరించుచున్నారు. బంగారం మనం ఎన్నిసార్లు ముక్కలు చేసినను మరల అతుకవచ్చునో అదేవిధంగా మంచి వ్యక్తి ఎటువంటి పరిస్థితులలోనైనా మంచితనంగానే ఉండును. కాని చెడ్డ వ్యక్తి. కుమ్మరివాని యొక్క కుండతో సమానం. ఒక్కసారి కుండను విరగగొట్టిన మరల ఎప్పటికి అతుకదు. చెడ్డవారి మనస్థితి ఎల్లప్పుడు చెడుగానే ఉండును.

प्रश्न 4.
जग में बैरी कोइ नहीं, जो मन सीतल होय ।
यह आपा तू डरि दे, दया करै सब कोय ॥
उत्तर:
भावार्थ : कबीरदास इस दोहे में “अहंकार को त्याग” करने के लिए कहते है । आपके मन में यदि शीतलता है अर्थात दया और सहानुभूति है, तो संसार में आपकी किसी से शत्रुता नही हो सकती। इसलिए अपने अहंकार को निकाल बाहर करे और आप अपने प्रति दूसरों में भी समवेदना पायेगें ।

భావం : కబీర్దాసు ఈ దోహాలో మనిషి తనలోని అహంకారమును త్యాగం చేయవలనని చెబుతున్నారు. మన మనస్సునందు సానుభూతి మరియు దయాగుణము ఉన్నట్లయితే ఈ ప్రపంచంతో శతృత్వం అనేది ఉండదు. అందువలన మనయందు ఉండు అహంకారాన్ని బయటకు త్రోయవలెను. ఇతరుల నుండి మనము సమవేదన పొందుతాము.

प्रश्न 5.
बोली तो अनमोल है, जो कोइ जानै बोल ।
हिये तराजू तोलि के, तब मुख बाहर खोल ।।
उत्तर:
भावार्थ : कबीरदास इस दोहे में “मधुरवाणी’ की महानता के बारे हमें बता रहे हैं। यदि कोई सही तरीके से बोलना जानता है तो उसे पता है कि वाणी एक अमूल्य रत्न है । इसलिए वह हृदय के तराजू में तोलकर ही उसे मुँह से बाहर आने देता है।

భావం : కబీర్దాసు ఈ దోహానందు “మధురవాణి” అనగా మంచి మాటల యొక్క గొప్పతనము వర్ణించుచున్నారు. ఇతరులతో మంచి మాటలు మాట్లాడటం తెలిసినట్లయితే బహుశా వానికి మంచిమాట అనేది అమూల్యమైన రత్నం అని తెలియును. అందువలన హృదయం అనే తరాజు (కాటా)లో కొలచి నోటి నుండి బయటకు పంపును.

प्रश्न 6.
कबीर गर्व न कीजिये, काल गहे कर केस ।
ना जानौ कित मारि है, क्या घर क्या परदेस ॥
उत्तर:
भावार्थ : कबीरदास इस दोहे में “जीवन की अनिश्चितता” के बारे में बता रहे है। अपनी शक्ति और संपत्ति देखकर घमंडी मत बनिए । इस शरीर से आत्मा कब निकल जाती है किसी को पता नही । मृत्यु किस रूप मे आती है हमें पता नही । किसी भी क्षण हमें अपने साथ ले जाती है । बाल (या) अपना हाथ पकडकर अपने साथ काल ले जाता है । तब इस दुनिया में तुम्हारा घर (ठिकाना) नही होता । मृत्यु कही भी हो (या) किधर भी हो, चाहे घर में हो या परदेश में भी तुमको आने साथ ले जाती है ।

భావం : కబీర్దాసు ఈ దోహానందు జీవితం యొక్క అనిశ్చితత గురించి వివరించుచున్నారు. మన యొక్క శక్తి మరియు సంపదను చూసి ఎప్పుడు గర్వపడకూడదు. ఈ శరీరం నుండి ఆత్మ ఎప్పుడు బయటకు వెళుతుందో ఎవ్వరికి తెలియదు. మృత్యువు ఏ రూపములో వచ్చునో మనము ఊహించ లేము. ఏ క్షణములోనైనా మనలని తనతో మృత్యువు తీసుకువెళ్ళును. మన శిరస్సులోని వెంట్రుకలను (లేక) మన చేతులు పట్టుకొని యముడు ప్రాణాలు హరించును. అప్పుడు ఈ ప్రపంచంనందు నీకు ఉండుటకు ಇಲ್ಲು ఉండదు. మృత్యువు నిన్ను ఎక్కడ దాగి ఉన్న తనతోపాటు తీసుకుపోవును.

प्रश्न 7.
जहाँ दया तहाँ धर्म है, जहाँ लोभ तहाँ पाप ।
जहाँ क्रोध तहँ काल है, जहाँ छिमा तहँ आप ॥
उत्तर:
भावार्थ : कबीरदास इस दोहे में “दया और क्षमा” जैसे गुणों का महत्व के बारे में बता रहे हैं । जहाँ तया भाव है वहाँ धर्म व्यवहार होता है । जहाँ क्षमा और सहानुभूति होती है वहाँ भगवान रहते है । दया और क्षमा दोनों इस दुनिया में सबसे महान गुण हैं ।

భావం : కబీర్దాసు ఈ దోహానందు “దయ మరియు క్షమాగుణం” యొక్క గొప్పతనమును చెప్పుచున్నారు. ఎక్కడైతే దయా భావం ఉండునో అక్కడ ధర్మ వ్యవహారం ఉండును. ఎక్కడైతే దురాశ మరియు కోపం ఉండునో అక్కడ పాపం ఉండును. ఎక్కడైతే క్షమ మరియు సహానుభూతి ఉండునో అక్కడ దేవుడు ఉండును. దయ మరియు క్షమాపణ ఈ రెండు ప్రపంచం నందు మహాగుణములుగా చెప్పుదురు.

प्रश्न 8.
रात गाँवाई सोय करि, दिवस गाँवाये खाय ।
हीरा जनम अमोल था, कौडी बदले जाय ॥
उत्तर:
भावार्थ : कबीरदास इस दोहे में “समय का महत्व” के बारे में बता रहे हैं । जो व्यक्ति इस संसार में बिना कोई कर्म किए पूरी रात को सोते हुए और सारे दिन को खाते हुए ही व्यतीत कर देता है, वह अपने हीरे तुल्य अमूल्य जीवन को कौड़ियों के भाव व्यर्थ ही गवा देता है । समय एक बार ने हाथ से छूट जाए तो फिर वापस कभी नही आता । इसलिए इस जीवन में समय को व्यर्थ न कीजिए ।

భావం : కబీర్ దాసు ఈ దోహానందు సమయం యొక్క గొప్పతనాన్ని వివరించుచున్నారు. ఏ వ్యక్తి అయితే ఈ ప్రపంచంనందు ఎటువంటి పని చేయకుండా రాత్రి అంతా నిద్రిస్తూ, పగలంతా ఆహారం తింటూ గడుపుతాడో ఆ వ్యక్తి తస వజ్రం వంటి విలువైన జీవితమును ఎందుకు పనికి రాకుండా వ్యర్థం చేసుకొనును. సమయం ఒక్కసారి మన చేతినుండి జారిపోతే తిరిగి ఎప్పటికిరాదు, అందువలన ఈ జీవితంలో సమయమును వ్యర్థం చేసుకోరాదు.

कवि परिचय

सन्त कबीरदास का हिंदी साहित्य के भक्तिकाल में एक विशिष्ट स्थान है । आप भक्तिकाल की निर्गुण भक्तिधारा में ज्ञानश्रयी शाखा अथवा ‘संत काव्यधारा’ के प्रतिनिधि कवि थे। कहा जाता है कि आपका जन्म एक विधवा ब्राह्मणी के गर्भ से हुआ था । लोकलाज के भय से उसने शिशु को लहरतारा नामक तालाब के पास छोड़ दिया। तब नीरू और नीमा नामक मुसलमान दम्पति ने कबीर को पाल-पोसकर बड़ा किया ।

कबीरदास ‘अनपढ़’ थे । आप पेशेवर जुलाहा थे । एक ओर अपना काम करते हुए भी आपने देशाटन, सज्जन – सांगत्य तथा अनुभव से ज्ञान समुपार्जन किया । रामानन्द आपके गुरु थे । कबीरदास की ‘रचनाओं को शिष्यों ने ‘बीजक’ नाम से संकलित किया जो ‘साखी’, ‘सबद’ और ‘रमैनी’ नामक तीन भागों में है । नीति, मिथ्या, विश्वास एवं मूढ परंपराओ का खण्डन तीखी भाषा आपकी कविता की विशेषताएँ हैं । सर्वधर्म – समानता का संदेश देकर हिन्दू-मुसलमान की एकता के लिए कबीरदास ने विशेष प्रयास किया। कबीर की भाषा सधुक्कडी अर्थात् “साधुओं की भाषा’ थी । इसमें कई भाषाओं के शब्द पाये जाते हैं । ज्ञानी, भक्त एवं समाज सुधारक के रूप में कबीरदास हिन्दी साहित्य में अमर हैं ।

कठिन शब्दों के अर्थ

1.
सत्गुरु = सत्य के मार्ग दर्शक – गुरु, सच्चा गुरु, Master, true teacher, గురువు (సత్యమార్గం చూపించు)
महिमा = गुण- गान, महत्व, Greatness, స్తుతించు
अनंत = जिसका कोई अंत न हो, Infinite, endless, అనంతం
उपकार = भलाई, Help, favour, ఉపకారం
लोचन अनंत = ज्ञान की दृष्टि, Vision of knowledge, జ్ఞానదృష్టి
उघारिया = खोलना, खोलदिया, Opend, తెరచుట
दिखावनहार = दर्शन कराने वाला , To be shown the correct, మంచిమార్గం- చూపించువాడు.

2.
साच = सच्चाई, सत्य, Truth, నిజము, సత్యము.
तप = कठिन परिश्रम, तपस्या, Hardwork, penance, కఠిన పరిశ్రమ, తపస్సు.
झूठ = असत्य, Falsehood, అబద్దం
पाप = बुरा कार्य, Sin, evil, పాపం
जाके = जिसके, In whom, ఎవనికైతే
हिरदे = मन, दिल, Heart, మనస్సు
ता = उसके, Belongs to, అతనియొక్క

3.
सोना = स्वर्ण, Gold, బంగారం
सज्जन = सच्चे मनुष्य, Good person, మంచివ్యక్తి
जुटै = जुड़ना, मिलना, To be joined, కలుపుట,
दुर्जन = बुरे मनुष्य, Bad person, చెడ్డ వ్యక్తి.
कुंभ = मिट्टी का घड़ा, Pot, మట్టికుండ
एकै = इसको, He (possesed), ఇతనికి
धका = धक्का, ठोकर, मारना, Push, jerk, నెట్టుట
दशार = तड़कना, Crack, పగులు, బీటిక,

4.
जग = संसार, जगत, दुनिया, World, ప్రపంచం
बैरी = दुश्मन, शत्रु, Enemy, శత్రువు
शीतल = ठंडा (शांत अथवा क्रोधरहित, Cold, చల్లని
होय = होना, Completed, పూర్తియగు
आपा = अहंकार, घमंड, Proud, గర్వం
डारि = छोड़कर, Except, తప్ప
कोय = हर कोई (प्रति व्यक्ति, Every person, ప్రతి మనిషి,

5.
बोली = बोलना, वाणी, Speech, ఉపన్యాసం, పలుకుట,, మాట్లాడుట.
अनमोल = अमूल्य (जिसका कोई मोल न हो), Priceless, వెలకట్టలేనటువంటి.
जानै = जानकर, Understand, అర్థం చేసుకొనుట.
हिये = हृदय, मन, Heart, హృదయం
तराजू = काँटा, Weighing balance, బరువు కొలుచు యంత్రం
तौलि = तोलकर, तोलना, To weight, బరువు కొలుచుట.
के = करना, To do, చేయుట
मुख = मुँह, Mouth, నోరు
आनि = आने देना, To come, రావడం

6.
गर्व = घमडं करना, To feel proud, గర్వపడుట
काल = मृत्यु, समय, वक्त, death, (కాలుడు) యముడు
गहे = पकड़े, a hold, పట్టుకొనుట
कर = हाथ, Hand, చేయి
केस = केश, बाल, Hair, జుట్టు
ना जानी = मालूम नही, Don’t know, తెలియదు.
कित = कहाँ, Where, ఎక్కడ.
मारि = मारना, To kill, చంపుట.
क्या = किसी भी, किधर भी, कही भी, What, any, ఏమిటి, ఏదైన

7.
दया = कृपा, रहम, Kindness, దయ
तहाँ = वहाँ, There, అక్కడ
लोभ = लालच, Greed, దురాశ
पाप = बुरा कार्य, Sin evil, పాపం
छिमा = क्षमा, दया, रहम, Pity, kind hearted, దయార్ధహృదయం.
काल = मृत्यु, मौत, समय, death, చావు
आप = स्वयं / परमात्मा, God, దేవుడు

8.
गवाई = नष्ट किया, खोया, व्यर्थकिया, lost, పోగొట్టుకొనుట
सोय कर = सोते रहना, नींद, निद्रा, सोकर To sleep, నిద్రించుట
दिवस = दिन, Day, రోజు
खाया = खाना-पीना ( आराम करना), To eat & drink, To take rest, తినుట-త్రాగుట.
हीरा = मूल्यवान वस्तु, Diamond, వజ్రం
जनम = जन्म, जीवन, Birth, జన్మ
अमोल = अमूल्य, Precious, priceless, మూల్యమైన, విలువైన
कौडी = = कम से कम मूल्य, Very less, price, తక్కువ వెల.
बदले जाय = = अदल बदल किया जाय, विनिमय, Exchange, మార్పులు చేర్పులు.

Here students can locate TS Inter 1st Year Physics Notes 13th Lesson ఉష్ణోగతిక శాస్త్రం to prepare for their exam.

TS Inter 1st Year Physics Notes 13th Lesson ఉష్ణోగతిక శాస్త్రం

→ ఉష్ణగతిక శాస్త్రము ఉష్ణశక్తి మరియు యాంత్రిక శక్తుల మధ్యగల సంబంధాలను వివరిస్తుంది.

→ ఉష్ణ సమతాస్థితి : ఒక వ్యవస్థలో స్థూల చలరాశులైన పీడనం, ఘనపరిమాణం, ఉష్ణోగ్రత, ద్రవ్యరాశి వాటి సంఘటన కాలంతోపాటు మారకుండా ఉంటే ఆ వ్యవస్థ ఉష్ణ సమతాస్థితిలో ఉంది అంటారు.
రెండు వ్యవస్థలు ఉష్ణ సమతాస్థితిలో ఉండాలంటే ఆ రెండు వ్యవస్థల ఉష్ణోగ్రతలు సమానంగా ఉండాలి.

→ ఉష్ణగతికశాస్త్ర శూన్యాంక నియమం : రెండు వ్యవస్థలు (A, B) విడివిడిగా మూడవ వ్యవస్థ ‘C’ తో ఉష్ణ సమతా స్థితిలో ఉంటే ఆ వ్యవస్థలు A, B లు కూడా ఒక దానితో ఒకటి ఉష్ణసమతాస్థితిలో ఉంటాయి.

→ అంతరికశక్తి (U) : ప్రతివ్యవస్థ అసంఖ్యాకమైన అణువుల సముదాయము. వ్యవస్థలో గల మొత్తం అణువుల స్థితిశక్తి మరియు గతిశక్తుల మొత్తాన్ని అంతరికశక్తి అంటారు.
లేదా
వ్యవస్థలో ఉన్న అణువుల క్రమరహితచలనం వల్ల వస్తువు కలిగి ఉండే స్థితిశక్తి, గతిశక్తుల మొత్తాన్ని అంతరికశక్తి అంటారు.

→ ఉష్ణగతికశాస్త్ర మొదటి నియమం : ఏదైనా వ్యవస్థకు అందించిన మొత్తం ఉష్ణరాశి ΔQ, ఆ వ్యవస్థ జరిపిన పని ΔW మరియు వ్యవస్థ అంతరికశక్తిలోని మార్పుల ΔU ల మొత్తానికి సమానము.
ΔQ = ΔU + ΔW లేదా ΔQ = ΔU + PΔV

→ విశిష్టోష్ణ సామర్ధ్యం (S) : ప్రమాణ ద్రవ్యరాశిగల పదార్థంలో ఏకాంక ఉష్ణోగ్రతా మార్పు కోసం అందజేసిన ఉష్ణరాశిని లేదా కోల్పోయిన ఉష్ణరాశిని విశిష్టోష్ణ సామర్థ్యము అంటారు.
విశిష్టోష్ట సామర్థ్యం S = \(\frac{1}{m} \frac{\Delta Q}{\Delta T}\) ప్రమాణము J/kg-k

→ స్థిరఘనపరిమాణ మోలార్ విశిష్టోష్ణ సామర్ధ్యము (C) : స్థిరఘనపరిమాణము వద్ద ఒక గ్రామ్ మోల్ ద్రవ్యరాశి గల వాయువు ఉష్ణోగ్రతను 1°C లేదా 1 కెల్విన్ పెంచడానికి కావలసిన ఉష్ణరాశిని స్థిరఘనపరిమాణ మోలార్ విశిష్టోష్ణ సామర్థ్యము Cగా నిర్వచించినారు.
C_v = \(\frac{1 \mathrm{dQ}}{\mu \mathrm{dT}}\) μ = వాయువులోని మోల్ల సంఖ్య

→ స్థిరపీడన మోలార్ విశిష్టోష్ణ సామర్ధ్యము (C): స్థిరపీడనము వద్ద ఒక గ్రామ్ మోల్ ద్రవ్యరాశి గల వాయువు ఉష్ణోగ్రతను 1°C లేదా 1 కెల్విన్ మేరకు పెంచడానికి కావలసిన ఉష్ణరాశిని స్థిరపీడన మోలార్ విశిష్టోష్ట సామర్థ్యము C_p గా నిర్వచించినారు.
C_p = \(\frac{1}{\mu} \frac{d Q}{d T}\) μ = వాయువులోని గ్రామ్ మోల్ల సంఖ్య
గమనిక : విశిష్టోష్ణము మరియు విశిష్టోష్ణ సామర్ధ్యములను ఒకే అర్థంలో వాడతారు.

→ సమ ఉష్ణోగ్రతా ప్రక్రియ : ఉష్ణ యాంత్రిక మార్పులు జరుగుతున్నంతసేపు ఒక వ్యవస్థ ఉష్ణోగ్రత T ని స్థిరంగా ఉంచితే ఆ ప్రక్రియను సమఉష్ణోగ్రతా ప్రక్రియ అంటారు.

→ సమ పీడన ప్రక్రియ : ఈ విధమైన ప్రక్రియలో ఉష్ణ యాంత్రిక మార్పులు జరుగుతున్నంత సేపు వ్యవస్థ పీడనం (P) స్థిరము.

→ సమ ఘనపరిమాణ ప్రక్రియ : ఇటువంటి ప్రక్రియలో ఉష్ణ యాంత్రిక మార్పులు జరుగుతున్నంతసేపు వ్యవస్థ ఘనపరిమాణం (V) స్థిరంగా ఉండాలి.

→ స్థిరోష్ణక ప్రక్రియ : ఇటువంటి ప్రక్రియలో ఉష్ణ యాంత్రిక మార్పులు జరుగుతున్నంతసేపు వ్యవస్థ మొత్తం శక్తి (Q) స్థిరంగా ఉండాలి.

→ చక్రీయ ప్రక్రియ : చక్రీయ ప్రక్రియలో ఉష్ణ యాంత్రిక వ్యవస్థపై అన్ని ప్రక్రియలు జరిపిన తరువాత చివరికి అది తొలి ఉష్ణోగ్రతా పీడనాలను పొందుతుంది. చక్రీయ ప్రక్రియలో ΔU = 0 కావున వ్యవస్థ శోషించుకున్న ఉష్ణరాశి చక్రీయ ప్రక్రియలో జరిగినపని. (చక్రీయ ప్రక్రియలో dW – dQ)

→ ఉష్ణగతిక శాస్త్ర రెండవ నియమము :
a) కెల్విన్ – ప్లాంక్ ప్రవచనము : ఒక ఉష్ణాశయం నుంచి ఉష్ణశక్తిని గ్రహించి ఏ ఇతర ఫలితాలు కలుగజేయకుండా మొత్తం శక్తిని పనిగా మార్చే చక్రీయ ప్రక్రియ సాధ్యం కాదు.
b) క్లాసియస్ ప్రవచనము : తక్కువ ఉష్ణోగ్రత గల ఒక వస్తువు నుంచి ఎక్కువ ఉష్ణోగ్రత గల మరొక వస్తువుకు తనంతట తాను ఉష్ణరూపంలో శక్తిని బదిలీ చేసే ఏ ప్రక్రియ సాధ్యం కాదు.

→ ఉష్ణగతిక శాస్త్ర రెండవ నియమం ఉష్ణ ప్రసార దిశను తెలుపుతుంది.

→ ఉష్ణగతిక శాస్త్ర రెండవ నియమం ప్రకారము ఏ ఉష్ణ యంత్రం దక్షత η విలువ 1 కి సమానం కాదని మరియు శీతలీకరణ యంత్రం క్రియాశీలతా గుణకం (∝) విలువ అనంతం కాదని చెపుతుంది.

→ ద్విగత ప్రక్రియలు లేదా ఉత్రమణీయ ప్రక్రియలు : ఉష్ణగతిక ప్రక్రియలు తొలిస్థితి (i) నుండి తుదిస్థితి (f) కి చేరేలోపు ఉష్ణరాశి (Q) ని గ్రహించి పని (W) ని జరుపుతాయి. వేరే ఏ ఇతర ఫలితాలు లేకుండా వ్యవస్థను తుదిస్థితి నుండి తొలిస్థితికి తీసుకొనిపోగలిగితే అటువంటి ప్రక్రియలను ద్విగత ప్రక్రియలు లేదా ఉత్రమణీయ ప్రక్రియలు అంటారు.

→ అనుత్రమణీయ ప్రక్రియ లేదా ఏకగతప్రక్రియ : ఈ విధమైన ప్రక్రియలను తొలిస్థితి (i) నుండి తుదిస్థితి (f) కి మారునపుడు ఉష్ణరాశి గ్రహించి పనిని చేయడం జరుగుతుంది. కాని ఏ ఇతర ఫలితాలు లేకుండా వ్యవస్థను తుదిస్థితి (f) నుండి తొలిస్థితి (1) కి తేవడం సాధ్యం కాదు.
ప్రకృతిలో తమంతట తాముగా జరిగే అన్ని ప్రక్రియలు ఏకగత లేక అనుమణీయ ప్రక్రియలే.

→ కార్నో యంత్రము రెండు ఉష్ణోగ్రతల మధ్య ఆదర్శవాయువుతో పనిచేసే ఉత్రమణీయ ఉష్ణయంత్రము.
దీని దక్షత η = \(\frac{w}{Q_l}\) = 1 – \(\frac{\mathrm{Q}_2}{\mathrm{Q}_1}\) లేదా η = 1 – \(\frac{\mathrm{T}_2}{\mathrm{~T}_1}\)
(T₁ = జనకం ఉష్ణోగ్రత, T₂ = ఉష్ణాశయం ఉష్ణోగ్రత, W = జరిగిన పని)

→ వస్తువు స్థితి ‘మార్పు లేకుండా వేడిచేయడానికి అందించిన ఉష్ణరాశి Q = mct.

→ స్థితి మార్పు పొందటానికి వస్తువుకు అందజేసిన ఉష్ణరాశి Q = mL.

→ జౌల్ నియమం నుండి పని W ∝ Q లేదా W = JQ.
J = ఉష్ణయాంత్రిక తుల్యాంకము

→ స్థితి శక్తి ఉష్ణంగా మారినపుడు
(a) జరిగిన పని మొత్తం వస్తువును వేడిచేయటానికి ఉపయోగిస్తే mgh = mct లేదా Δt = \(\frac{\mathrm{Mgh}}{\mathrm{mL}}\)
(b) జరిగిన పని వస్తువు స్థితి మార్పుకు ఉపయోగపడితే mgh = mL లేదా ద్రవీభవించిన వస్తువు ద్రవ్యరాశి m = \(\frac{\mathrm{Mgh}}{\mathrm{L}}\)

→ గతిశక్తి ఉష్ణంగా మారిన సందర్భంలో
(a) గతిశక్తి వస్తువును వేడిచేయటానికి మాత్రమే ఉపయోగపడితే
\(\frac{1}{2}\)mv2 = mct ⇒ Δt = \(\frac{\mathrm{mv}^2}{2 \mathrm{mc}}\)
(b) గతిశక్తి వస్తువు స్థితి మార్పు వరకు మాత్రమే ఉపయోగపడితే \(\frac{\mathrm{mv}^2}{2 \mathrm{mc}}\)mv² = ML
ద్రవీభవించిన వస్తువు ద్రవ్యరాశి M = \(\frac{\mathrm{mv}^2}{2 \mathrm{mc}}\)

→ ఉష్ణగతిక శాస్త్ర మొదటి నియమం నుండి dQ = dU + dW

→ వస్తువు ఉష్ణధారణ సామర్థ్యము \(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{t}}\) = mc (i.e., ద్రవ్యరాశి × విశిష్టోష్ణము)

→ విశిష్టోష్టము S లేదా C

→ మిశ్రమ పద్ధతి నియమం నుండి వేడిగా ఉన్న వస్తువు కోల్పోయిన ఉష్ణరాశి = చల్లగా ఉన్న వస్తువు గ్రహించిన ఉష్ణరాశి
a) మిశ్రమ పద్దతి నియమంలో ఘపపదార్థపు విశిష్టోష్ఠము S = \(\frac{\mathrm{m}_1 \mathrm{~S}_1+\left(\mathrm{m}_2 \mathrm{~m}_1\right) \mathrm{S}_2\left(\mathrm{t}_2-\mathrm{t}_1\right)}{\left(\mathrm{m}_3-\mathrm{m}_2\right)\left(\mathrm{t}_2-\mathrm{t}_1\right)}\)J/kg-k
b) ద్రవాల విశిష్టోష్టము S = \(\frac{\left(m_3-m_2\right) S_1\left(t_2-t_1\right)}{\left(m_2-m_1\right)\left(t_3-t_1\right)}-\frac{m_1 S_2}{m_2-m_1}\)

→ రెండు గోళాల వ్యాసార్థాల నిష్పత్తి r₁: r₂ విశిష్టోష్ణముల నిష్పత్తి S₁ : S₂ మరియు సాంద్రతల నిష్పత్తి ρ₁ : ρ₂ అయితే
వాటి ఉష్ణధారణ సామర్థ్యాల నిష్పత్తి = \(\frac{m_1 S_1}{m_2 S_2}=\left(\frac{r_1}{r_2}\right)^3\left(\frac{\rho_1}{\rho_2}\right)\left(\frac{s_1}{S_2}\right)\)
a) వాయువుల విశిష్టోష్టము C_p = ΔQ / mΔT
b) మోలార్ విశిష్టోష్ఠముల నిష్పత్తి C_p = \(\frac{\Delta Q}{\mu \Delta t}\) (μ = మోల్ల సంఖ్య)
c) విశిష్టోష్ఠముల నిష్పత్తి γ = C_p/ C_v; C_v = \(\frac{\gamma \mathrm{R}}{\gamma-1}\). C_p = \(\frac{\gamma \mathrm{R}}{\gamma-1}\)

→ స్థిర పీడనానికి వ్యతిరేకంగా వాయువు వ్యాకోచించుటలో జరిగిన పని dW = P dV.

→ ఆదర్శవాయువు వ్యాకోచించుటలో జరిగిన పని
a) W = P (V₂ – V₁) లేదా W = R (T₂ – T₁)
μ = వాయువులోని మోత్ల సంఖ్య; R = సార్వత్రిక వాయు స్థిరాంకము

→ Cp మరియు Cv ల మధ్య సంబంధము C_p – C_v = R.

→ సమోష్ణోగ్రతా ప్రక్రియలో P, V మరియు T ల మధ్య సంబంధము PV = RT లేదా PV = μRT.

→ సమ ఉష్ణప్రక్రియ (adiabatic process) లో P, V మరియు T ల మధ్య సంబంధాలు

• PV^γ = స్థిరరాశి
• TV^γ-1 = స్థిరరాశి
• PV^1-γ T^γ = స్థిరరాశి.

→ సమోష్ణోగ్రతా ప్రక్రియలో జరిగిన పని
a) W = RT log_e\(\frac{v_2}{v_1}\)
b) W = 2.303 RT log₁₀\(\frac{v_2}{v_1}\)

→ సమోష్ణ ప్రక్రియలో జరిగిన పని
a) W = \(\frac{1}{\gamma-1}\)(P₁V₁ – P₂V₂) మోల్^-1 (లేదా)
b) W = \(\frac{\mu \mathrm{R}}{\gamma-1}\)(T₁ – T₂); μ = మోల్ల సంఖ్య

→ ఉష్ణయంత్రపు దక్షత η = 1 – \(\frac{\mathrm{Q}_2}{\mathrm{Q}_1}\) లేదా η = 1 − \(\frac{\mathrm{T}_2}{\mathrm{~T}_1}\)
T₁ = జనకం ఉష్ణోగ్రత, T₂ = ఉష్ణాశయం ఉష్ణోగ్రత.

→ వస్తువు స్థితి మార్పు లేకుండా వేడిచేయడానికి అందించిన ఉష్ణరాశి Q = mct.

→ స్థితి మార్పు పొందటానికి వస్తువుకు అందజేసిన ఉష్ణరాశి Q = mL.

→ ప్రయోగశాలలో నీటి బాష్పీభవన గుప్తోష్ణము కనుగొనుటలో
L = \(\frac{\left[\mathrm{m}_1 \mathrm{~S}_{\mathrm{c}}+\left(\mathrm{m}_2-\mathrm{m}_1\right) \mathrm{S}_{\mathrm{w}}\right]\left(\mathrm{t}_1-\mathrm{t}_2\right)}{\mathrm{m}_1-\mathrm{m}_2}\) – (t – t₂)S_w
S_w = నీటి విశిష్టోష్టము ; S_c = కెలోరీ మీటరు విశిష్టోష్టము

Here students can locate TS Inter 1st Year Commerce Notes Chapter 4 Partnership Firm to prepare for their exam.

TS Inter 1st Year Commerce Notes Chapter 4 Partnership Firm

→ Partnership is a form of business where two or more persons join together, enter into an agreement to share profits and losses by organizing business.

→ The partner’s liability is unlimited.

→ The written agreement among the partners is called Partnership Deed.

→ All the rights, duties and liabilities of the partners are mentioned in the deed.

→ The partnership firm may or may not be registered.

→ Types of partners are : Active partner-Sleeping partners-Nominal partner-Partners in profits-Limited partner-General partner-partner by Estoppel-partner by Holding out-Minor as partner.

→ Dissolution of partnership firm-By agreement-By giving notice-By Compulsory dissolution- contingent dissolution-Dissolution through court.

TS Inter 1st Year Commerce Notes Chapter 4 భాగస్వామ్య సంస్థ

→ సొంత వ్యాపారములోని లోపాలు, పరిమితుల వలన భాగస్వామ్యము ఉద్భవించినది.

→ కనీసము ఇద్దరు లేక ఎక్కువమంది కలసి ఒప్పందము కుదుర్చుకొని భాగస్వామ్యము ప్రారంభించవచ్చు.

→ భాగస్తుల ఋణబాధ్యత అపరిమితము.

→ భాగస్వామ్య వ్యాపారము భాగస్వాముల మధ్య కుదిరిన ఒప్పందము ద్వారా ఏర్పడుతుంది.

→ వ్యాపారం నిర్వహించడానికి లాభాలు పంచుకోవడానికి, పెట్టుబడికి, సొంతవాడకాలకు సంబంధించి భాగస్తుల మధ్య కుదిరిన ఒడంబడికను భాగస్వామ్య ఒప్పందము అంటారు.

→ భాగస్వామ్య సంస్థను నమోదు చేయుట తప్పనిసరి కాదు. కాని నమోదు చేయటం వలన కొన్ని ప్రయోజనాలుంటాయి.

→ భాగస్తుల గరిష్ట సంఖ్య బ్యాంకింగ్ వ్యాపారాలలో 10 ఇతర వ్యాపారాలలో 20.

→ భాగస్తులలో రకాలు 1. సక్రియ భాగస్తుడు, 2. నిష్క్రియ భాగస్తుడు, 3. నామమాత్రపు భాగస్తుడు, 4. లాభాలలో భాగస్తుడు, 5. భావిత భాగస్తుడు, 6. మౌన నిర్ణీత భాగస్తుడు, 7. పరిమిత భాగస్తుడు, 8. సాధారణ భాగస్తుడు.

→ భాగస్తులకు కొన్ని హక్కులు, విధులు ఉంటాయి.

→ భారత ప్రభుత్వం పరిమిత ఋణబాధ్యత భాగస్వామ్య చట్టం 2008లో రూపొందించింది. దీనిని 31, మార్చి 2009లో ప్రకటించడం జరిగింది. ఈ చట్టం ప్రకారం పరిమిత ఋణ బాధ్యత భాగస్వామ్యం ఒక కార్పొరేట్ సంస్థ మాదిరిగా ప్రత్యేక న్యాయసత్వాన్ని కలిగి ఉంటుంది.

→ భాగస్వామ్య ఒప్పందము ఏ కారణముచేతనైనా రద్దయితే భాగస్వామ్యము రద్దవుతుంది.

→ భాగస్వామ సంస్థను దిగున పద్ధతులలో రద్దు చేయవచ్చును:

• ఒప్పందము ద్వారా
• నోటీసు ద్వారా
• ఆగంతుక రద్దు
• అనివార్య రద్దు
• కోర్టు ద్వారా రద్దు.

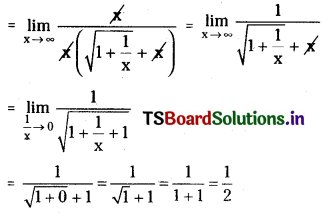
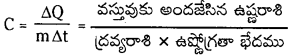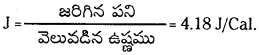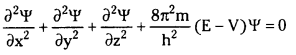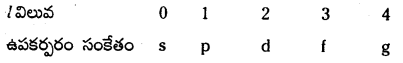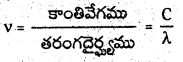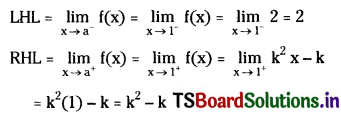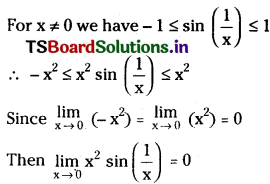Telangana TSBIE TS Inter 1st Year Chemistry Study Material 1st Lesson పరమాణు నిర్మాణం Textbook Questions and Answers.

TS Inter 1st Year Chemistry Study Material 1st Lesson పరమాణు నిర్మాణం

అత్యంత లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఎలక్ట్రాన్ ఆవేశం, ద్రవ్యరాశి ఎంత ఉంటాయి ? ఎలక్ట్రాన్ ఆవేశానికి, ద్రవ్యరాశికి గల నిష్పత్తి ఎంత ?
జవాబు:
ఎలక్ట్రాన్ ఆవేశం = 1.602 × 10^-19
ఎలక్ట్రాన్ ద్రవ్యరాశి = 9.109 × 10^-31 కేజి
\(\frac{\mathrm{e}}{\mathrm{m}}\) విలువ = 1.7588 × 10¹¹ కు. కేజి^-1

ప్రశ్న 2.
ఒక మోల్ ఎలక్ట్రాన్ల ఆవేశాన్ని గణించండి.
జవాబు:
ఒక మోల్ ఎలక్ట్రాన్లపై గల ఆవేశం = 1.602 × 10^-19 × 6.023 × 10²³ కులూంబ్లు
= 96,500 కులూంబ్లు

ప్రశ్న 3.
ఒక మోల్ ఎలక్ట్రాన్ల ద్రవ్యరాశిని గణించండి.
జవాబు:
ఒక మోల్ ఎలక్ట్రాన్ల ద్రవ్యరాశి = 9.1 × 10^-31 × 6.023 × 10²³ కేజి
= 5.48 × 10^-7 కేజి

ప్రశ్న 4.
ఒక మోల్ ప్రోటాన్ల ద్రవ్యరాశిని గణించండి.
జవాబు:
ఒక మోల్ ప్రోటాన్ల ద్రవ్యరాశి = 1.672 × 10^-27 × 6.023 × 10²³ కేజి
= 1.007 × 10^-3 కేజి

ప్రశ్న 5.
ఒక మోల్ న్యూట్రాన్ల ద్రవ్యరాశిని గణించండి.
జవాబు:
ఒక మోల్ న్యూట్రాన్ల ద్రవ్యరాశి = 1.675 × 10^-27 × 6.023 × 10²³ కేజి
= 1.00885 × 10^-3 కేజి

ప్రశ్న 6.
\({ }_6^{13} \mathrm{C}\), \({ }_8^{16} \mathrm{O}\), \({ }_{12}^{24} \mathrm{Mg}\), \({ }_{26}^{56} \mathrm{Fe}\), \({ }_{38}^{88} \mathrm{Sr}\) కేంద్రకాలలో ఉండే న్యూట్రాన్ల, ఎలక్ట్రాన్ల సంఖ్య ఎంత ?
జవాబు:
ఎలక్ట్రాన్ల సంఖ్య పరమాణు సంఖ్య “Z” కు సమానం.
న్యూట్రాన్ల సంఖ్య = ద్రవ్యరాశి సంఖ్య – పరమాణు సంఖ్య
\({ }_6^{13} \mathrm{C}\) లో ఎలక్ట్రాన్ల సంఖ్య = 6
న్యూట్రాన్ల సంఖ్య = 13
\({ }_8^{16} \mathrm{O}\) లో ఎలక్ట్రాన్ల సంఖ్య = 8
న్యూట్రాన్ల సంఖ్య = 16 – 8 = 8
\({ }_{12}^{24} \mathrm{Mg}\) లో ఎలక్ట్రాన్ల సంఖ్య = 12
న్యూట్రాన్ల సంఖ్య = 24 – 12 = 12
\({ }_{26}^{56} \mathrm{Fe}\) లో ఎలక్ట్రాన్ల సంఖ్య = 26
న్యూట్రాన్ల సంఖ్య = 56 – 26 = 30
\({ }_{38}^{88} \mathrm{Sr}\) లో ఎలక్ట్రాన్ల సంఖ్య = 38
న్యూట్రాన్ల సంఖ్య = 88 – 38 = 50

ప్రశ్న 7.
కృష్ణ పదార్థం అంటే ఏమిటి ?
జవాబు:
అన్ని రకాల పౌనఃపున్యాలు గల వికిరణాలను ఉద్గారించే మరియు శోషించుకొనే వస్తువును కృష్ణ పదార్థం అంటారు.

ప్రశ్న 8.
బామర్ శ్రేణి విద్యుదయస్కాంత వర్ణపటంలో ఏ ప్రాంతానికి చెందినది ?
జవాబు:
హైడ్రోజన్ పరమాణువులోని ఎలక్ట్రాన్ పై శక్తి స్థాయిల నుండి, రెండవ శక్తి స్థాయికి పరివర్తన చెందినపుడు బామర్ శ్రేణి రేఖలు ఏర్పడతాయి. బామర్ శ్రేణిలోని రేఖల తరంగదైర్ఘ్యము దృశా ప్రాంతంలో ఉంటుంది.

ప్రశ్న 9.
పరమాణు ఆర్బిటాల్ అంటే ఏమిటి ?
జవాబు:
పరమాణువులో కేంద్రకం చుట్టూ ఉన్న త్రిజ్యామితీయ ప్రదేశంలో ఎలక్ట్రాన్ను కనుగొనే సంభావ్యత గరిష్ఠంగా గల ప్రదేశాన్ని ఆర్బిటాల్ అంటారు.
పరమాణువులో ఒక నిర్దిష్టమైన బిందువు వద్ద ఎలక్ట్రాను కనుగొనే సంభావ్యత ఆ బిందువు వద్ద 1412 కి అనులోమానుపాతంలో ఉంటుంది. ఆర్బిటాల్కు 1412 విలువ గరిష్ఠంగా ఉంటుంది.

ప్రశ్న 10.
హైడ్రోజన్ పరమాణువులో ఎలక్ట్రాన్ n = 4 కక్ష్య నుంచి n = 5 కక్ష్యకు మార్పు చెందినపుడు గ్రహించిన కాంతిరేఖ వర్ణపట శ్రేణిలో దేనికి చెందుతుంది ?
జవాబు:
బ్రాకెట్ శ్రేణికి చెంది ఉంటుంది. ఇది పరారుణ ప్రాంతంలో ఉంటుంది.

ప్రశ్న 11.
సల్ఫర్ పరమాణువులో ఎన్ని p ఎలక్ట్రాన్లు ఉన్నాయి ?
జవాబు:
సల్ఫర్ ఎలక్ట్రాన్ విన్యాసం (Z = 16) 1s² 2s²2p⁶3s²3p⁴
p ఎలక్ట్రానుల మొత్తం సంఖ్య 6 + 4 = 10

ప్రశ్న 12.
3d ఎలక్ట్రాన్ ప్రధాన క్వాంటం సంఖ్య (n), ఎజిముతల్ క్వాంటం సంఖ్య (l) విలువలు ఎంత ?
జవాబు:
3d ఎలక్ట్రాన్కు ప్రధాన క్వాంటం సంఖ్య = 3
ఎజిముతల్ క్వాంటం సంఖ్య = 2

ప్రశ్న 13.
ఇచ్చిన పరమాణు సంఖ్య (z), పరమాణు ద్రవ్యరాశి (A) గల పరమాణు పూర్తి గుర్తు ఏమిటి ?
(I) Z = 4, A = 9;
(II) Z = 17, A = 35
(III) Z = 92, A = 233
జవాబు:
(I) \({ }_4^9 \mathrm{Be}\) బెరిలియం
(II) \({ }_{17}^{35} \mathrm{Cl}\) క్లోరిన్
(III) \({ }_{92}^{233} \mathrm{U}\) యురేనియం

ప్రశ్న 14.
\(d_z 2\) ఆర్బిటాల్ ఆకారాన్ని గీయండి.
జవాబు:

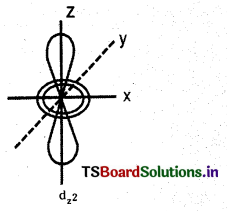
ప్రశ్న 15.
\(d_{x^2-y^2}\) ఆర్బిటాల్ ఆకారాన్ని గీయండి.
జవాబు:

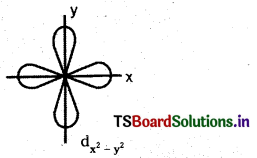
ప్రశ్న 16.
600 nm తరంగదైర్ఘ్యం గల వికిరణాల పౌనఃపున్యం ఎంత ?
జవాబు:
λ = 600 nm
పౌనఃపున్యం v = \(\frac{c}{\lambda}\) = \(\frac{3 \times 10^8 \mathrm{~ms}^{-1}}{600 \times 10^{-9} \mathrm{~m}}\) = 5 × 10¹⁴ s^-1
‘C’ అంటే కాంతి వేగం;
‘λ’ అంటే తరంగదైర్ఘ్యం;
‘v’ అంటే పౌనఃపున్యం

ప్రశ్న 17.
జీమన్ ప్రభావం అంటే ఏమిటి ?
జవాబు:
అయస్కాంతక్షేత్రంలో వర్ణపట రేఖల సూక్ష్మ విభజనను జీమన్ ఫలితము అంటారు.

ప్రశ్న 18.
స్టార్క్ ప్రభావం అంటే ఏమిటి ?
జవాబు:
విద్యుత్ క్షేత్రంలో వర్ణపట రేఖల సూక్ష్మ విభజనను స్టార్క్ ప్రభావం అంటారు.

ప్రశ్న 19.
ఈ క్రింది ఎలక్ట్రాన్ విన్యాసాలు ఏ మూలకానికి చెందినవి ?
i) 1s² 2s² 2p⁶ 3s² 3p¹
ii) 1s² 2s² 2p⁶ 3s² 3p⁶
iii) 1s² 2s² 2p⁵
iv) 1s² 2s² 2p²
జవాబు:
i) 1s² 2s² 2p⁶ 3s² 3p¹ – అల్యూమినియం (Al)
ii) 1s² 2s² 2p⁶ 3s² 3p⁶ – ఆర్గాన్ (Ar)
iii) 1s² 2s² 2p⁵ – ఫ్లోరిన్ (F)
iv) 1s² 2s² 2p² – కార్బన్ (C)

ప్రశ్న 20.
4000 తరంగదైర్ఘ్య వికిరణాలను లోహతలంపై పడేటట్లు చేస్తే శూన్యం వేగం గల ఎలక్ట్రాన్లు ఉద్గారమయ్యాయి. ఆరంభ పౌనఃపున్యం ‘v₀‘ ఎంత ?
జవాబు:
ఫోటాన్ శక్తి = \(\frac{\mathrm{hc}}{\lambda}\) = \(\frac{6.63 \times 10^{-34} \mathrm{Js} \times 3 \times 10^8 \mathrm{~ms}^{-1}}{4000 \times 10^{-10} \mathrm{~m}}\) = 4.9725 × 10^-19 J
ఫోటాన్ శక్తి = ఎలక్ట్రాన్ గతిజశక్తి + పని ప్రమేయం
4.9725 × 10^-19 = 0 + hv₀
v₀ = \(\frac{4.9725 \times 10^{-19} \mathrm{~J}}{6.625 \times 10^{-34} \mathrm{~J} \mathrm{~s}}\)
v₀ = 7.51 × 10¹⁴s^-1

ప్రశ్న 21.
పౌలి వర్ణన సూత్రాన్ని వివరించండి.
జవాబు:
“ఒకే పరమాణువులో ఏ రెండు ఎలక్ట్రాన్లకైనా ఒకే సమితి గల నాలుగు క్వాంటం సంఖ్యలు ఉండకూడదు.” దీనినే పౌలి వర్ణన సూత్రం అంటారు.

ప్రశ్న 22.
ఆఫ్గ నియమం అంటే ఏమిటి ?
జవాబు:
“భూస్థాయిలో ఉన్న పరమాణువులోని ఆర్బిటాల్లను వాటి శక్తులు పెరిగే క్రమంలో ఎలక్ట్రాన్లతో భర్తీ చేయాలి.” ఇంకొక రకంగా చెప్పాలంటే ఎలక్ట్రానులు అందుబాటులో ఉన్న కనిష్ఠ శక్తి ఆర్బిటాల్లలోకి మొదట ప్రవేశిస్తాయి.

ప్రశ్న 23.
హుండ్ నియమం అంటే ఏమిటి ?
జవాబు:
ఉపకర్పరంలో గల ప్రతి సమశక్తి (డీజనరేట్) ఆర్బిటాల్లోకి ఒక్కొక్క ఎలక్ట్రాన్ చేరేంత వరకూ అదే ఉపకర్పరం (p, d, f) లోని ఆర్బిటాల్లో ఎలక్ట్రాన్ జతగూడటం జరగదు. అంటే ముందు ఒక్కొక్కటీ చేరాలి. దీనినే హుండ్ నియమం అంటారు.

ప్రశ్న 24.
హైసెన్బర్గ్ అనిశ్చితత్వ నియమం వివరించండి.
జవాబు:
“పరమాణువులో ఎలక్ట్రాన్ వంటి సూక్ష్మ కణాల ఖచ్చితమైన స్థానం, ఖచ్చితమైన ద్రవ్యవేగం (లేక వేగం) ఏకకాలంలో నిర్ణయించటం అసాధ్యం.”
గణితాత్మకంగా సమీకరణ రూపంలో
Δx × Δp ≥ \(\frac{\mathrm{h}}{4 \pi}\)
లేదా Δx × Δ(mv) ≥ \(\frac{h}{4 \pi}\)
లేదా Δx × Δv ≥ \(\frac{h}{4 \pi}\)
Δx స్థానంలో అనిశ్చితత్వం, Δp ద్రవ్యవేగంలో అనిశ్చితత్వం, Δv వేగంలో అనిశ్చితత్వం.

ప్రశ్న 25.
2.0 × 10⁷ ms^-1 వేగంతో ప్రయాణించే ఎలక్ట్రాన్ తరంగదైర్ఘ్యం ఎంత ?
జవాబు:
డీబ్రోలి తరంగదైర్ఘ్యం λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\)
λ = \(\frac{6.625 \times 10^{-34} \mathrm{Js}}{9.1 \times 10^{-31} \mathrm{~kg} \times 2 \times 10^7 \mathrm{~ms}^{-1}}\)
= \(\frac{6.625 \times 10^{-34} \times 10^{31} \times 10^{-7}}{9.1 \times 2}\) = \(\frac{6.625}{18.2}\) × 10^-10 = 3.55 × 10^-11m = 0.355 × 10^-10m = 0.355A

ప్రశ్న 26.
పరమాణు ఆర్బిటాల్క n విలువ 2 అయిన l, m_l లకు సాధ్యమైన విలువలేమి ?
జవాబు:
n = 2 అయితే l = 0, 1
l = 0 m = 0
l = 1 m = – 1, 0, +1

ప్రశ్న 27.
ఇక్కడ ఇచ్చిన ఆర్బిటాల్లో ఏవి సాధ్యం ? 2s, 1p, 3f, 2p.
జవాబు:
2s, 2p లు సాధ్యం. 1p సాధ్యం కాదు. ప్రథమశక్తి స్థాయిలో S ఆర్బిటాల్ మాత్రమే ఉంటుంది. p ఆర్బిటాల్ ఉండదు. 3f సాధ్యం కాదు. తృతీయ శక్తిస్థాయిలో 3s, 3p మరియు 3d ఉంటాయి. 3f ఉండదు.

ప్రశ్న 28.
నూనె చుక్క మీద ఉన్న స్థిర విద్యుత్ ఆవేశం -3.2044 × 10^-19 C. దాని మీద ఎన్ని ఎలక్ట్రానులు ఉన్నాయి ?
జవాబు:

ప్రశ్న 29.
కింద ఇచ్చిన వికిరణాలను పౌనఃపున్యాలు పెరిగే క్రమంలో ఏర్పరచండి.
a) X – కిరణాలు
b) దృగ్గోచర వికిరణాలు
c) సూక్ష్మతరంగ వికిరణాలు
d) రేడియోతరంగ వికిరణాలు
జవాబు:
రేడియో తరంగాలు – సూక్ష్మ తరంగ వికిరణాలు < దృగ్గోచర వికిరణాలు < X – కిరణాలు

ప్రశ్న 30.
n = 4 ms = +1/2 తో పరమాణువులో ఉండే ఎలక్ట్రానుల సంఖ్య ఎంత ?
జవాబు:
n = 4 అయినపుడు ‘l’ కు విలువలు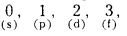
∴ మొత్తం ఆర్బిటాళ్ళ సంఖ్య 1 + 3 + 5 + 7 = 16
ప్రతి ఒక్క ఆర్బిటాల్లో m_s = + 1/2 గల ఎలక్ట్రాన్ 1, m = -1/2 గల ఎలక్ట్రాన్ 1కి ఉంటాయి.
∴ n = 4 లో m_s = +1/2 గల ఎలక్ట్రాన్ల సంఖ్య = 16.

ప్రశ్న 31.
n = 5 లో ఉండే ఉపకర్పరాల సంఖ్య ఎంత ?
జవాబు:
n = 5 లో ఐదు ఉపకర్పరాలు ఉంటాయి. అవి s, p, d, f మరియు g. వీటి l విలువలు వరుసగా 0, 1, 2, 3, 4.

ప్రశ్న 32.
విద్యుదయస్కాంత వికిరణాల కణ స్వభావాన్ని వివరించండి.
జవాబు:
ప్లాంక్ క్వాంటం సిద్ధాంతం ప్రకారం, శక్తి ఉద్గారం మరియు శోషణాలు చిన్న చిన్న పాకెట్ల రూపంలో జరుగుతాయి. వీటినే శక్తి పాకెట్లు లేక క్వాంటంలు అంటారు. ప్రతి ఒక్క క్వాంటంలో ఇమిడి ఉన్న శక్తినిని E = hv ద్వారా తెలియచేస్తారు. కాంతి కణస్వభావం కృష్ణ వస్తువుల వికిరణాలను మరియు కాంతి విద్యుత్ ఫలితాన్ని వివరించింది.
ఐన్స్టీన్ భావన ప్రకారం శక్తి ఉద్గారం మరియు శోషణాలు ఫోటాన్ల రూపంలో జరుగుతాయి. ఫోటాన్ అనేది ఒక తరంగ కణం. దానికి ద్రవ్యరాశి ఉండదు. శక్తి ఉంటుంది. ఫోటాన్ శక్తి కూడా E = hv ద్వారా తెలియచేస్తారు. ఈ ఫోటాన్ యానకంలో తరంగ రూపంలో వ్యాప్తి చెందుతుంది.

ప్రశ్న 33.
హైసెన్ బర్గ్ అనిశ్చితత్వ నియమం ప్రాముఖ్యాన్ని వివరించండి.
జవాబు:
హైసెన్ బర్గ్ అనిశ్చితత్వ నియమంలో ముఖ్యమైన సారాంశం :

1. ఎలక్ట్రాన్కు గాని, ఎలక్ట్రాన్ లాంటి ఇతర కణాలకు గాని, స్థిరమైన కక్ష్య లేక ప్రక్షేప్యమార్గం ఉండే అవకాశం లేదు. వస్తువు స్థానం, దాని వేగం ప్రక్షేప్య మార్గాన్ని నిర్ణయిస్తాయి. ఉపపరమాణు కణాలైన ఎలక్ట్రాన్ లాంటి వాటికి ఒకే కాలంలో స్థానాన్ని వేగాన్ని కచ్చితంగా తెలుసుకోవటం సాధ్యంకాదు కాబట్టి దాని ప్రక్షేప్య మార్గాన్ని గురించి మాట్లాడే అవకాశం లేదు.
2. హైసెన్బర్గ్ అనిశ్చితత్వ నియమం సూక్ష్మాతి సూక్ష్మ కణాలకు మాత్రమే ప్రాముఖ్యం ఇస్తుంది. స్థూలకణాలకు దీని ప్రభావం కొద్దిగా మాత్రమే ఉంటుంది.
3. ఈ నియమం ప్రకారం బోర్ కక్ష్యలలో ఎలక్ట్రాన్లు చలించడమనేది సరైంది కాదు. కేవలం ఎలక్ట్రాన్ కనుగొనే సంభావ్యతను మాత్రమే చెప్పవచ్చు.

ప్రశ్న 34.
హైడ్రోజన్ వర్ణపటంలో పరిశీలించిన రేఖ శ్రేణులు ఏమిటి ?
జవాబు:

1. లైమన్ శ్రేణి
2. బామర్ శ్రేణి
3. పాషన్ శ్రేణి
4. బ్రాకెట్ శ్రేణి
5. ఫండ్ శ్రేణి

లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 35.
హైడ్రోజన్ పరమాణువులో ఎలక్ట్రాన్ n = 5 శక్తిస్థాయి నుంచి n = 3 శక్తి స్థాయికి పరివర్తనం చెందినపుడు ఉద్గారమయ్యే కాంతి తరంగదైర్ఘ్యం ఎంత ?
జవాబు:

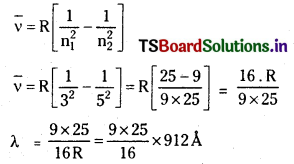
= 12825A
= 12825 × 10^-10m
= 1282.5 × 10^-9 m (లేక) 12,821 A
[Note: Take \(\frac{1}{R}\) = 912A]

ప్రశ్న 36.
ఒక మూలకపు పరమాణువులో 29 ఎలక్ట్రానులు, 35 న్యూట్రానులు ఉన్నాయి.

1. ప్రోటానుల సంఖ్యను,
2. మూలకం ఎలక్ట్రాన్ విన్యాసాన్ని రాబట్టండి.

జవాబు:

1. ప్రోటాన్ల సంఖ్య = ఎలక్ట్రాన్ల సంఖ్య = 29
2. ఎలక్ట్రాన్ విన్యాసం 1s² 2s² 2p⁶ 3s² 3p⁶ 4s¹ 3d¹⁰. మూలకం కాపర్.

ప్రశ్న 37.
ఈ క్రింది క్వాంటం సంఖ్యల సమితులలో అసాధ్యమైనవేవి ? కారణాలతో వివరించండి.
a) n = 0, l = 0, m_l = 0, m_s = +1/2
b) n = 1, l = 0, m_l = 0, m_s = -1/2
c) n = 1, l = 1, m_l = 0, m_s = +1/2
d) n = 2, l = 1, m_l = 0, m_s = +1/2
e) n = 3, l = 3, m_l = -3, m_s = +1/2
f) n = 3, l = 1, m_l = 0, m_s = +1/2
జవాబు:
సమితి (a) సాధ్యం కాదు.
కారణం : n విలువ 1 నుంచి మొదలు. అందువల్ల n = 0 సాధ్యంకాదు.
సమితి (c) సాధ్యం కాదు.
కారణం : n = 1కి l = 0 మాత్రమే సాధ్యం. s ఉపస్థాయి మాత్రమే సాధ్యం. l = 1 అనగా (p ఉపస్థాయి) సాధ్యంకాదు.
సమితి (e) సాధ్యంకాదు.
కారణం : n = 3కి 1 = 0, 1, 2 (s, p, d) మాత్రమే సాధ్యం. n = 3కి 1 = 3. (f ఆర్బిటాల్) సాధ్యం కాదు.

ప్రశ్న 38.
హైడ్రోజన్ పరమాణువు బోర్ కక్ష్యలో తిరుగుతున్న ఎలక్ట్రాన్ కక్ష్య చుట్టుకొలత డీబ్రోలి తరంగదైర్ఘ్యానికి పూర్ణాంక గుణిజంగా ఉంటుందని చూపించండి.
జవాబు:
బోర్ సిద్ధాంతం ప్రకారం
mvr = n\(\frac{\mathbf{h}}{2 \pi}\) 2лr = n\(\frac{\mathrm{h}}{\mathrm{mv}}\)
కాని \(\frac{\mathrm{h}}{\mathrm{mv}}\) = λ(డీబ్రోలి సిద్ధాంతం)
2лr = λ
కనుక బోర్ కక్ష్యలో తిరుగుచున్న ఎలక్ట్రాన్ కక్ష్య చుట్టుకొలత డీబ్రోలి తరంగదైర్ఘ్యానికి పూర్ణాంక గుణిజంగా ఉంటుంది.

ప్రశ్న 39.
589.0, 589.6 mm లు గరిష్ట ద్వంద్వ శోషణ పరివర్తన తరంగదైర్ఘ్యాలుగా పరిశీలించబడ్డాయి. పరివర్తన పౌనఃపున్యాలను, రెండు ఉత్తేజస్థితుల మధ్య శక్తి తేడాలను లెక్కించండి.
జవాబు:
పౌనఃపున్యం v = \(\frac{\mathrm{c}}{\lambda}\)
589 nm తరంగదైర్ఘ్యానికి v = \(\frac{3 \times 10^8 \mathrm{~ms}^{-1}}{589 \times 10^{-9} \mathrm{~m}}\)
= 5.09 × 10¹⁴ Hz
589.6 nm తరంగదైర్ఘ్యానికి v = \(\frac{3 \times 10^8 \mathrm{~ms}^{-1}}{589.6 \times 10^{-9} \mathrm{~m}}\)
= 5.088 × 10¹⁴ Hz
589 nm కు గల శక్తి E = hv
E = 6.625 × 10^-34 Js × 5.088 × 10¹⁴ Hz
= 33.73 × 10^-20J
రెండు ఉత్తేజిత స్థితుల మధ్య శక్తి తేడా
ΔE = 33.73 × 10^-20 – 33.71 × 10^-20
= 0.02 × 10^-20 = 2 × 10^-22 J

ప్రశ్న 40.
పరమాణువు క్వాంటమ్ యాంత్రిక నమూనా ముఖ్య లక్షణాలు ఏమిటి ?
జవాబు:
క్వాంటమ్ యాంత్రికశాస్త్రం సూక్ష్మాతి సూక్ష్మమైన తరంగ, కణ స్వభావాలు గల కణాల చలనాలను వివరిస్తుంది. ఇటువంటి వాటికి వర్తించేదే ప్రోడింగర్ సమీకరణం.

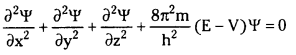
క్వాంటమ్ యాంత్రిక నమూనా ముఖ్యలక్షణాలు :

1. పరమాణువులోని ఎలక్ట్రాన్ల శక్తి క్వాంటీకృతమై ఉంటుంది.
2. ఎలక్ట్రాన్కు క్వాంటీకృత శక్తి స్థాయిలు ఉండడానికి కారణం ఎలక్ట్రాన్కు తరంగ స్వభావం ఉండటంతో బాటు ప్రోడింగర్ తరంగ సమీకరణానికి ఆమోదయోగ్యమైన ఫలితాలు కూడా ఉండటం.
3. పరమాణువులో ఎలక్ట్రాన్ యొక్క కచ్చితమైన వేగాన్ని ఒకే కాలంలో తెలుసుకోవడం అసాధ్యం.
4. పరమాణువు ఆర్బిటాల్ తరంగ ప్రమేయం \(\Psi\). తరంగ ప్రమేయాలు ఎలక్ట్రాన్కు చాలా ఉండే అవకాశం ఉంది కనుక పరమాణువులో చాలా శక్తి స్థాయిలు ఉంటాయి.
5. పరమాణువులో ఏదైనా బిందువు వద్ద ఎలక్ట్రాన్ను కనుగొనే సంభావ్యత, ఆ బిందువు వద్ద ఆర్బిటాల్ తరంగ ప్రమేయ వర్గానికి \(|\Psi|^2\) అనుపాతంలో ఉంటుంది. పరమాణువులో వేరు వేరు బిందువుల వద్ద సంభావ్యతా సాంద్రత \(|\Psi|^2\) విలువలు తెలిస్తే కేంద్రకం చుట్టూ ఎలక్ట్రాన్ ఉండే గరిష్ఠ సంభావ్యత గల ప్రదేశాన్ని గుర్తించవచ్చు. దీనినే ఆర్బిటాల్ అంటారు.

ప్రశ్న 41.
నోడల్ తలం అంటే ఏమిటి ? 2p, 3d ఆర్బిటాల్లలో ఎన్ని నోడల్ తలాలు ఉంటాయి ?
జవాబు:
ఏ ప్రదేశాలలోనైతే ఎలక్ట్రాన్ సంభావ్యతా సాంద్రత ప్రమేయం విలువ (ψ²) సున్నాకు తగ్గుతుందో వాటిని నోడల్ తలాలు లేదా నోడ్లు అంటారు.

ఒక ఆర్బిటాల్కు నోడల్ తలాలు సంఖ్య ఎజిముతల్ క్వాంటం సంఖ్య ‘l’ కు సమానం.
p – ఆర్బిటాల్క నోడల్ తలాల సంఖ్య = 1
d – ఆర్బిటాల్కు నోడల్ తలాల సంఖ్య = 2
2p ఆర్బిటాల్ నోడల్ తలాలు = 1
3d ఆర్బిటాల్ నోడల్ తలాలు = 2

ప్రశ్న 42.
91.2 nm నుండి 121.6 nm ల మధ్య లైమన్ శ్రేణి, 364.7 mm నుంచి 656.5 nm ల మధ్య బామర్ శ్రేణి, 820.6 nm నుంచి 1876 nm ల మధ్య పాశ్చన్ శ్రేణి కనబడతాయి. ఈ తరంగదైర్ఘ్యాలు వర్ణపటంలో ఏ ప్రాంతానికి చెందినవో కనుక్కోండి.
జవాబు:

1. లైమన్ శ్రేణి – అతినీలలోహిత
2. బామర్ శ్రేణి – దృశా ప్రాంతం
3. పాశ్చన్ శ్రేణి – సమీప పరారుణ

ప్రశ్న 43.
హైడ్రోజన్ పరమాణువులో n, I, m, క్వాంటం సంఖ్యలు ఎలా వస్తాయి ?
జవాబు:
హైడ్రోజన్ పరమాణు సంఖ్య (Z) = 1
∴ ఎలక్ట్రాన్ విన్యాసం = 1s¹
ఈ విన్యాసం ప్రకారం, హైడ్రోజన్ పరమాణువుకు
n = 1; l = 0 (s – ఉపస్థాయి); m_l = 0 (s – ఆర్బిటాల్); m_s = +1/2

ప్రశ్న 44.
హైడ్రోజన్ పరమాణువులో లైమన్ శ్రేణిలో ఒక రేఖ తరంగదైర్ఘ్యం 1.03 × 10^-7 m అయితే ఎలక్ట్రాన్ తొలి శక్తిస్థాయి ఏది ?
జవాబు:

ప్రశ్న 45.
ఎలక్ట్రాన్ స్థితిని ± 0.002 nm లోపు కచ్చితంగా కొలవగలిగినట్లైతే ఎలక్ట్రాన్ ద్రవ్యవేగంలో అనిశ్చితత్వం గణించండి.
జవాబు:
హైసెన్ బర్గ్ అనిశ్చితత్వ నియమం ప్రకారం
Δx. Δp = \(\frac{\mathrm{h}}{4 \pi}\)
Δp = ద్రవ్యవేగంలో అనిశ్చితత్వం = ?
Δx = స్థానంలో అనిశ్చితత్వం = 0.002 nm
Δp = \(\frac{\mathrm{h}}{4 \pi \cdot \Delta \mathrm{x}}\) = \(\frac{6.626 \times 10^{-34}}{4 \times 3.14 \times 0.002 \times 10^{-10} \mathrm{~m}}\)
= 5.275 × 10^-22 m

ప్రశ్న 46.
1.6 × 10⁶ ms^-1 ఎలక్ట్రాన్ వేగం ఉన్నట్లయితే దానితో ఉన్న డీబ్రోలీ తరంగదైర్ఘ్యాన్ని గణించండి.
జవాబు:
λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\)
h = ప్లాంక్ స్థిరాంకం = 6.626 × 10^-34 Js
m = ఎలక్ట్రాన్ ద్రవ్యరాశి = 9.1 × 10^-31 kg
v = ఎలక్ట్రాన్ వేగం = 1.6 × 10⁶ ms^-1
λ = \(\frac{6.626 \times 10^{-34} \mathrm{Js}}{9.1 \times 10^{-31} \mathrm{~kg} \times 1.6 \times 10^6 \mathrm{~ms}^{-1}}\)
= 4.55 × 10^-10 m

ప్రశ్న 47.
శోషణ, ఉద్గార వర్ణపటాల మధ్య తేడాలను వివరించండి.
జవాబు:

ప్రశ్న 48.
ఎలక్ట్రానుల క్వాంటం సంఖ్యలు కింద ఇవ్వడమైనది. వాటిని శక్తిపరంగా ఆరోహణక్రమంలో వ్రాయండి.
a) n = 4, l = 2, m_l = – 2, m_s = + 1/2
b) n = 3, l = 2, m_l = -1, m_s = -1/2
c) n = 4, l = 1, m_l = 0, m_s = +1/2
d) n = 3, l = 1, m = -1, m_s = – 1/2
జవాబు:
1. ఆర్బిటాల్లోని ఎలక్ట్రాన్ శక్తి (n + l) విలువకు సమానం. m మరియు s విలువల ప్రాధాన్యం తక్కువ.
2. రెండు ఎలక్ట్రానుల (n + l) విలువలు సమానమైతే, తక్కువ n విలువ గల ఎలక్ట్రానుకు తక్కువ శక్తి.
a) n = 4 l = 2 ; 4d (n + l) విలువ 6
b) n = 3 l = 2 ; 3d (n + 1) విలువ 5
c) n = 4 l = 1; 4p (4 + 1) విలువ 5
d) n = 3 l = 1; 3p (3 + 1) విలువ 4
ఆరోహణ క్రమం : 3p < 3d < 4p < 4d (లేక) d < b < c < a

ప్రశ్న 49.
సీజియం పరమాణువు పని ప్రమేయం 1.9eV. ఆరంభ వికిరణాల పౌనఃపున్యాన్ని గణించండి. సీజియం మూలకాన్ని 500 nm ల తరంగదైర్ఘ్యం కల వికిరణాలతో ఉద్యోతనం చేస్తే వెలువడే ఫోటో ఎలక్ట్రాన్ గతిజశక్తి గణించండి.
జవాబు:
ఆరంభశక్తి = 1.9 eV × 1.602 × 10^-19 J
= 3.044 × 10^-19 J
ఆరంభ పౌనఃపున్యం v_o = \(\frac{3.044 \times 10^{-19}}{6.626 \times 10^{-34}}\)
v₀ = 0.459 × 10¹⁵ = 4.59 × 10¹⁴ s^-1
500 nm వికిరణ శక్తి
E = \(\frac{\mathrm{hc}}{\dot{\lambda}}\) = \(\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{500 \times 10^{-9}}\) = 3.97 × 10^-19 J
ఎలక్ట్రాన్ గతిజశక్తి = ఫోటాన్ శక్తి – ఆరంభ శక్తి
= 3.976 × 10^-19 J – 3.044 × 10^-19 J
= 0.932 × 10^-19 J = 9.32 × 10^-20 J

ప్రశ్న 50.
1.3225 nm వ్యాసార్ధం గల కక్ష్యలో మొదలై 211.6 pm వ్యాసార్ధం గల కక్ష్యలో చేరినట్లయితే ఉద్గార పరివర్తన తరంగదైర్ఘ్యాన్ని గణించండి. ఈ పరివర్తన ఏ శ్రేణికి చెందుతుంది ? అది వర్ణపటంలో ఏ ప్రాంతానికి చెందుతుంది ?
జవాబు:
కక్ష్య వ్యాసార్ధం = 1.3225 nm = 1.3225 × 10^-7 cm = 13.225 × 10^-8 cm
కక్ష్య వ్యాసార్ధం = 0.529 × n² = 13.225
n = \(\sqrt{\frac{13.225}{0.529}}\) = 5
మరొక కక్ష్య వ్యాసార్ధం = 211.6 pm = 2.116 × 10^-8 cm
0.529 n² = 2.116
n = \(\sqrt{\frac{2.116}{0.529}}\) = 2
∴ ఎలక్ట్రాన్ పరివర్తన 5వ కక్ష్య నుండి 2వ కక్ష్యకు జరుగుతుంది. పరివర్తన బామర్ శ్రేణికి చెందుతుంది. అది దృశా ప్రాంతంలో ఉంటుంది.
\(\bar{v}\) = R[\(\frac{1}{2^2}\) – \(\frac{1}{5^2}\)] ; \(\bar{v}\) = R[latex]\frac{21}{100}[/latex]
λ = \(\frac{100}{21}\) R = \(\frac{100 \times 912}{21}\) = 4328Å
వెలువడే వికిరణ తరంగదైర్ఘ్యం = 4328À

ప్రశ్న 51.
కక్ష్య (ఆర్బిట్)కు, ఆర్బిటాల్కు గల భేదాన్ని తెలపండి.
జవాబు:

1. కక్ష్య (ఆర్బిట్) అనేది కేంద్రకం చుట్టూ గల ద్విజ్యామితీయ వృత్తాకార మార్గం. దీనిలో ఎలక్ట్రాన్లు తిరుగుతూ ఉంటాయి. కేంద్రకం చుట్టూ ఉండే ఏ త్రిజ్యామితీయ ప్రదేశంలో ఎలక్ట్రాన్ ను కనుగొనే సంభావ్యత గరిష్ఠంగా ఉంటుందో ఆ ప్రదేశాన్ని ఆర్బిటాల్ అంటారు.
2. ఆర్బిట్లో ఉండగల ఎలక్ట్రాన్ సంఖ్య గరిష్ఠంగా 2n². ఆర్బిటాల్లో 2 ఎలక్ట్రాన్లు మాత్రమే ఉండగలవు.

ప్రశ్న 52.
కాంతి విద్యుత్ ప్రభావాన్ని వివరించండి.
జవాబు:
కాంతి విద్యుత్ ప్రభావం : “అనుకూలమైన తరంగదైర్ఘ్యం గల కాంతి, ఒక లోహ ఉపరితలాన్ని తాకినపుడు, ఆ లోహ ఉపరితలం నుండి ఎలక్ట్రాన్లు విడుదలవుతాయి” అని J.J. థామ్సన్ మరియు P. లెనార్డ్ అనే శాస్త్రవేత్తలు నిరూపించినారు.

కాంతి విద్యుత్ ప్రభావానికి ఐన్స్టీన్ వివరణ :

i) లోహం నుంచి ఎలక్ట్రానును తొలగించడానికి అవసరమైన శక్తి ఫోటాన్ కు ఉన్నపుడు, ఆ లోహంతో ఈ ఫోటాన్ ఢీకొన్నపుడు లోహం నుండి ఎలక్ట్రాన్ వెలువడుతుందని ఐన్స్టీన్ భావించినాడు.

ii) ఫోటాన్ కు అధికశక్తి ఉంటే అందులోని కొంతశక్తిని ఎలక్ట్రాన్ గ్రహించి, బయటకు వచ్చే ఆ ఎలక్ట్రాన్కు అది గతిజశక్తిగా మారుతుంది. ఫోటాన్ శక్తి అవసరమైన దానికన్నా తక్కువైతే, లోహం నుంచి ఎలక్ట్రాన్ విడుదల కాదు.

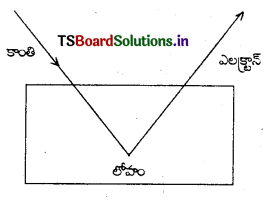
iii) ఒక ఫోటాన్ లోహపు ఉపరితలాన్ని ఢీకొన్నపుడు, ఫోటాన్ శక్తి (hν) ని ఎలక్ట్రాన్ గ్రహిస్తుంది. ఈ గ్రహించిన శక్తిలోని కొంతభాగం ఎలక్ట్రాను లోహం యొక్క ఆకర్షణ శక్తి నుంచి విడుదల చేస్తుంది (W). ఫోటాన్ శక్తిలోని మిగతా భాగం, విడుదలైన ఎలక్ట్రాన్ యొక్క గతిజశక్తి (K.E) గా మారుతుంది.
కాబట్టి hν = W + K.E.
hν = ఫోటాన్ శక్తి, W = లోహం నుండి ఎలక్ట్రాన్ను విడుదల చేయడానికి ఉపయోగింపబడ్డ శక్తి, K.E. = విడుదలైన ఎలక్ట్రాన్ గతిజశక్తి.
∴ hν = hυ_o + \(\frac{1}{2}\)m_ev²
m_e = ఎలక్ట్రాన్ ద్రవ్యరాశి; v = విడుదలైన ఎలక్ట్రాన్ వేగం, υ_o = ఆరంభ పౌనఃపున్యం
ఈ విధంగా కాంతి విద్యుత్ ప్రభావానికి ఐన్స్టీన్ వివరణను అందించినాడు.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 53.
రూథర్ ఫర్డ్ పరమాణువు కేంద్రక నమూనాను వివరించండి. దానిలోని లోపాలు ఏమిటి ?
జవాబు:
α – పరిక్షేపణ ప్రయోగ ఫలితాలను వివరించడానికి, 1910 సం॥లో రూథర్ ఫర్డ్ ఒక పరమాణు నమూనాను ప్రతిపాదించినాడు. దాన్ని ‘గ్రహమండల నమూనా’ లేదా ‘కేంద్రక నమూనా’ అంటారు. ఈ సిద్ధాంతంలోని ముఖ్య

అంశాలు :

1. పరమాణువు గోళాకారంలో ఉంటుంది. అందులో అత్యధికంగా శూన్య ప్రదేశం ఉంటుంది.
2. పరమాణువులోని ధనావేశం మరియు పరమాణు ద్రవ్యరాశి మొత్తం కూడా కొద్ది ప్రాంతంలో సాంద్రీకృతమై ఉంటుంది. దాన్ని కేంద్రకం అంటారు.
3. కేంద్రకం బయట ఉండే ఎలక్ట్రాన్ల సంఖ్య, కేంద్రకంలో గల ప్రోటాన్ల సంఖ్యకు సమానంగా ఉంటుంది.
4. సూర్యుని చుట్టూ గ్రహాలు తిరుగుతున్నట్లుగానే కేంద్రకం చుట్టూ ఎలక్ట్రాన్లు గుండ్రంగా తిరుగుతుంటాయి. ఈ విధంగా ఎలక్ట్రాన్లు తిరిగే మార్గాల్ని కక్ష్యలు అంటారు.
5. కేంద్రకం చుట్టూ తిరిగే ఎలక్ట్రాన్ పైన రెండు రకాల బలాలు పనిచేస్తుంటాయి. అవి
   1. కేంద్రక ఆకర్షణ బలాలు
   2. అపకేంద్రక బలాలు. మొదటి రకపు బలాలను రెండవ రకపు బలాలు సంతులనం చేస్తుంటాయి. అందువల్ల ఎలక్ట్రాను కేంద్రకం వైపు త్వరణం చెందక, తన కక్ష్యలోనే తిరుగుతూ ఉంటుంది.

రూథర్ ఫర్డ్ నమూనాలోని లోపాలు :

1) రూథర్ ఫర్డ్ పరమాణు నమూనా ప్రకారం, దానిలోని ఎలక్ట్రాన్లు నిర్దిష్టమైన కక్ష్యల్లో కేంద్రకం చుట్టూ తిరుగుతుంటాయి. కాని విద్యుత్ గతికశాస్త్ర (electro- dynamics) నియమం ప్రకారం, ఆవేశిత కణాలు త్వరణం చెందినపుడు శక్తిని ప్రసరణ చేస్తాయి. అందువల్ల కక్ష్యలోని ఎలక్ట్రాన్ శక్తిని ప్రసరిస్తూ ఉండాలి. ఆ విధంగా వృత్తాకార కక్ష్యలో ఎలక్ట్రాన్ శక్తిని కోల్పోవడం వల్ల కక్ష్య కుంచించుకుపోయి, ఎలక్ట్రాన్ సర్పిలాకారంలో తిరుగుతూ కేంద్రకాన్ని సమీపించి దానితో కలిసిపోతుంది. అప్పుడు పరమాణువు క్షీణిస్తుంది. కాని పరమాణువు స్థిరంగా ఉంటుంది.

2) ఎలక్ట్రాను, నిరంతరంగా శక్తిని కోల్పోతుంటే, పరమాణు వర్ణపటంలో పట్టీలు (bands) ఉండాలి. కాని విడివిడి రేఖలు (discrete lines) ఉన్నాయి. ఈ పరిస్థితిని రూథర్ఫర్డ్ పరమాణు నమూనా వివరింపలేకపోయింది.

3) రూథర్ ఫర్డ్ నమూనా, పరమాణువులో ఎలక్ట్రాన్ల వితరణను (distribution of electrons in an atom) వివరించలేదు.

ప్రశ్న 54.
ప్లాంక్ క్వాంటం సిద్ధాంతాన్ని క్లుప్తంగా వివరించండి.
జవాబు:
విద్యుదయస్కాంత సిద్ధాంత సహాయంతో వివరించలేని కొన్ని పరిశీలనలను, 1900 సం॥లో మాక్స్ ప్లాంక్ తన క్వాంటం సిద్ధాంతంతో వివరించగల్గినాడు.
ప్లాంక్ సిద్ధాంతము, కృష్ణ పదార్థం ఉద్గారించే వికిరణాలను విజయవంతంగా వివరించింది.

ప్లాంక్ క్వాంటం సిద్ధాంతంలోని ముఖ్యాంశాలు :

1. కృష్ణ పదార్థంలోని డోలనం (కంపనం) చేసే కణం, (ఎలక్ట్రాన్) శక్తిని అవిచ్ఛిన్నంగా ఉద్గారిస్తుంది.
2. వికిరణం ‘క్వాంటా’ అనే కొన్ని చిన్న శక్తి పాకెట్లుగా ఉద్గారం చెందుతుంది.
3. నిర్ణీత శక్తి పాకెట్ను ‘క్వాంటమ్’ అంటారు.
4. డోలనం చెందే కణం పౌనఃపున్యం అయితే దానికి సంబంధించిన శక్తి క్వాంటమ్ E ను E = hν సమీకరణం తెలుపుతుంది.
5. శక్తి ఉద్గారం, శోషణం సరళ పూర్ణాంక క్వాంటంలలో మాత్రమే ఉంటుంది. భిన్నాంక విలువలలో ఉండదు. దీనినే శక్తి క్వాంటీకరణం అంటారు.
   E = n(hν); n = పూర్ణాంకము.
   E ∝ ν ; E = hν. h = ప్లాంక్ స్థిరాంకం
   దీని విలువ h = 6.6256 × 10^-37 జౌ. సె (Js) = 6.6256 × 10^-27 ఎర్గ్. సె (erg.s)
6. ఉద్గారితమైన శక్తి తరంగాలుగా వ్యాపిస్తుంది.

ప్రశ్న 55.
హైడ్రోజన్ పరమాణువు బోర్ నమూనా ప్రతిపాదనలు ఏమిటి ? (March 2013)
జవాబు:

1. కేంద్రకం నుంచి స్థిర వ్యాసార్థాలు గల వృత్తాకార మార్గాలలో నిర్ణీత శక్తులతో ఎలక్ట్రానులు తిరుగుతూ ఉంటాయి. ఈ వృత్తాకార మార్గాలనే కక్ష్యలు అంటారు.
2. కక్ష్యలో తిరిగే ఎలక్ట్రాన్ శక్తి స్థిరంగా వుంటుంది. కాలంతో మారదు. ఎలక్ట్రాన్ తగిన శక్తిని శోషించుకున్నపుడు దిగువ స్థిరస్థితి నుంచి ఎగువ స్థిర స్థితికి పోతుంది. లేదా శక్తి ఉద్గారమైనపుడు ఎగువ శక్తి స్థాయి నుంచి దిగువ శక్తి స్థాయికి మారుతుంది. శక్తి మాత్రం అవిరళంగా మార్పు చెందదు.
3. ΔE శక్తి తేడా ఉన్న ఇచ్చిన రెండు స్థిరస్థాయిలలో ఎలక్ట్రాన్ పరివర్తనం జరగడానికి శోషించుకునే లేదా ఉద్గారమయ్యే వికిరణ పౌనఃపున్యంను కింది సమీకరణం ద్వారా గణిస్తారు.
   v = \(\frac{\Delta \mathrm{E}}{\mathrm{h}}\) = \(\frac{E_2-E_1}{h}\)
   E₁, E₂ లు వరుసగా దిగువ, ఎగువ అనుమతించదగిన శక్తి స్థాయిలు. ఈ సమీకరణాన్ని బోర్ పౌనఃపున్య నియమం అంటారు.
4. ఏదైనా ఇచ్చిన స్థిరస్థాయిలోని ఎలక్ట్రాన్ కోణీయ ద్రవ్యవేగం కింది సమీకరణం ద్వారా సూచిస్తారు.
   m_e vr = n . \(\frac{\mathrm{h}}{2 \pi}\) ఇచ్చట n = 1, 2, 3, ……
   ఎలక్ట్రాన్ కోణీయ ద్రవ్యవేగం \(\frac{\mathrm{h}}{2 \pi}\) విలువకు పూర్ణాంక గుణిజంగా ఉండే కక్ష్యలలో మాత్రమే తిరుగుతుంది.
5. బోర్ స్థిర కక్ష్యల వ్యాసార్ధం r_n = 0.529 × n² Å
   లేదా r_n = 52.9 × n² pm
6. స్థిరస్థాయిల శక్తి
   E_n = -A_H(\(\frac{1}{n^2}\)) n = 1, 2, 3, ……
   A_H = 2.18 × 10^-18 J దీనినే భూస్థాయి అంటారు.

ప్రశ్న 56.
హైడ్రోజన్ పరమాణువుకు బోర్ సిద్ధాంత విజయాలను వివరించండి.
జవాబు:
బోర్ సిద్ధాంత విజయాలు :

1. పరమాణువు స్థిరత్వాన్ని వివరించగలిగింది : బోర్ సిద్ధాంతం ప్రకారం స్థిర కక్ష్యలలోని ఎలక్ట్రాన్ శక్తి స్థిరంగా ఉంటుంది. అది శక్తిని కోల్పోదు. ఈ ప్రతిపాదన రూథర్ఫర్డ్ నమూనా లోపాన్ని సరిదిద్దినది.
2. ఒక కక్ష్యలోని ఎలక్ట్రాన్ శక్తిని లెక్కించవచ్చు: బోర్ సిద్ధాంత ప్రతిపాదనల ఆధారంగా కక్ష్యలోని ఎలక్ట్రాన్ శక్తిని గణించవచ్చు.
E_n = \(\frac{-2 \pi^2 m e^4}{n^2 h^2}\)
ఇక్కడ m = ఎలక్ట్రాన్ ద్రవ్యరాశి
e = ఎలక్ట్రాన్ పై ఆవేశం
h = ప్లాంక్ స్థిరాంకం
3. హైడ్రోజన్ వర్ణపటాన్ని వివరించగలిగినది :
బోర్ వివరణ ప్రకారం ఎలక్ట్రాన్ శక్తిని గ్రహించినపుడు పై శక్తి స్థాయిలలోనికి ఉత్తేజితం చెందుతుంది. పై శక్తి స్థాయిలోని ఎలక్ట్రాన్ భూస్థితికి చేరినపుడు రెండు శక్తిస్థాయిల భేదానికి సమానమైన శక్తి కాంతి రూపంలో విడుదల చేస్తుంది. అందువల్లనే వర్ణపటంలోని రేఖలు ఏర్పడుతున్నాయి.
4. బోర్ సిద్ధాంతం ప్రధాన క్వాంటం సంఖ్య గురించి వివరణ ఇచ్చింది.
5. కక్ష్య వ్యాసార్ధం గురించి వివరణ ఇచ్చింది.

ప్రశ్న 57.
పరమాణువు క్వాంటమ్ యాంత్రిక నమూనా సిద్ధాంతానికి దారితీసిన కారణాలను వివరించండి.
జవాబు:
బోర్ నమూనాలో ఎలక్ట్రాన్ను ఒక ఆవేశకణంగా భావించి అది కేంద్రకం చుట్టూ కచ్చితమైన వృత్తాకార కక్ష్యలలో తిరుగుతుందని ప్రతిపాదించడం జరిగింది.

కాంతి వికిరణాల మాదిరిగానే పదార్థానికి కూడా ద్వంద్వ స్వభావం ఉంటుంది. అంటే కణస్వభావం తరంగ స్వభావం ఉంటాయి. పదార్థ కణాల ద్రవ్యవేగానికి (p) తరంగదైర్ఘ్యానికి సంబంధాన్ని డీబ్రోలీ సూచించాడు. డీబ్రోలీ ప్రకారం,
λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) = \(\frac{h}{p}\)
m కణం ద్రవ్యరాశి, V కణవేగం, P ద్రవ్యవేగం, ఎలక్ట్రానులు, ఇతర ఉపపరమాణు కణాల తరంగదైర్ఘ్యాలను ప్రయోగం ద్వారా గుర్తించవచ్చు.

హైసెన్బర్గ్ నియమం ప్రకారం ఎలక్ట్రాన్కు కచ్చితమైన స్థానం, కచ్చితమైన ద్రవ్యవేగం ఏకకాలంలో నిర్ణయించడం అసాధ్యం.
Δx. Δp ≥ \(\frac{h}{4 \pi}\)

Δx స్థానంలో అనిశ్చితత్వం, Δp ద్రవ్యవేగంలో కణం యొక్క అనిశ్చితత్వం. ఎలక్ట్రాన్ తరంగ స్వభావాన్ని బోర్ నమూనా పరిగణనలోకి తీసుకోలేదు. ఇంకా కక్ష్య అనేది ఖచ్చితంగా నిర్వచించిన మార్గం. ఈ మార్గాన్ని పూర్తిగా నిర్వచించడానికి ఒకే సమయంలో ఎలక్ట్రాన్ స్థానం, వేగం ఖచ్చితంగా తెలియాలి. హైసెన్బర్గ్ అనిశ్చితత్వ నియమం ప్రకారం ఇది సాధ్యంకాదు. హైడ్రోజన్ పరమాణువు బోర్ నమూనా పదార్థం ద్వంద్వ స్వభావాన్ని వదిలివేయడమేగాక హైసెన్బర్గ్ నియమాన్ని వ్యతిరేకిస్తుంది. ఇలాంటి స్వాభావికమైన బలహీనతల వల్ల బోర్ నమూనాను వేరే పరమాణువులకు విస్తరించే అవకాశం లేదు. ఏ నమూనా అయినా, పదార్థ తరంగ ‘కణ స్వభావాన్ని వర్ణించడమే కాక హైసెన్బర్గ్ అనిశ్చితత్వ నియమంతో సత్సంబంధం కలిగి ఉండాలి. ఈ కారణంగానే క్వాంటం యాంత్రిక నమూనా ఆవిష్కరించబడింది.

సూక్ష్మాతి సూక్ష్మమైన కణాలైన ఎలక్ట్రానులు, పరమాణువుల, అణువులకు సంప్రదాయ యాంత్రికశాస్త్రం వర్తించదు. ఉపపరమాణు కణాల ద్వంద్వ స్వభావం, అనిశ్చితత్వ స్వభావాన్ని సంప్రదాయ యాంత్రికశాస్త్రం పరిగణనలోకి తీసుకోక పోవడమే ఇందుకు కారణం.
క్వాంటం యాంత్రికశాస్త్రం అనేది సిద్ధాంత విజ్ఞానశాస్త్రం. ఇది సూక్ష్మాతి సూక్ష్మమైన తరంగ, కణ స్వభావాలు గల కణాల చలనాలను వివరిస్తుంది. ప్రోడింగర్ క్వాంటమ్ యాంత్రికశాస్త్రానికి మూల సమీకరణాన్ని అభివృద్ధి చేశాడు.
\(\frac{\partial^2 \Psi}{\partial x^2}\) + \(\frac{\partial^2 \psi}{\partial \mathrm{y}^2}\) + \(\frac{\partial^2 \psi}{\partial z^2}\) + \(\frac{8 \pi^2 \mathrm{~m}}{\mathrm{~h}^2}\)(E – V)ψ = 0
ψ = తరంగ ప్రమేయం
E = మొత్తం శక్తి
V = స్థితిశక్తి
m = కణ ద్రవ్యరాశి

ప్రశ్న 58.
పరమాణు క్వాంటం యాంత్రిక నమూనా ముఖ్యలక్షణాలను వివరించండి.
జవాబు:
క్వాంటం యాంత్రికశాస్త్రం అనేది సిద్ధాంత విజ్ఞానశాస్త్రం. ఇది సూక్ష్మాతి సూక్ష్మమైన తరంగ, కణ స్వభావాలు గల కణాల చలనాలను వివరిస్తుంది.
ఒక వ్యవస్థకు ప్రోడింగర్ సమీకరణం కింది విధంగా రాస్తారు.
\(\frac{\partial^2 \Psi}{\partial x^2}\) + \(\frac{\partial^2 \Psi}{\partial \mathbf{y}^2}\) + \(\frac{\partial^2 \Psi}{\partial z^2}\) + \(\frac{8 \pi^2 \mathrm{~m}}{\mathbf{h}^2}\)(E – V)ψ = 0
ψ = తరంగ ప్రమేయం
E = మొత్తం శక్తి
V = స్థితిశక్తి
m = కణ ద్రవ్యరాశి

పరమాణువు క్వాంటం యాంత్రిక నమూనా ప్రోడింగర్ సమీకరణాన్ని పరమాణువుకు ఉపయోగించడం ద్వారా వచ్చిన పరమాణువు నిర్మాణం.

1. పరమాణువులోని ఎలక్ట్రానుల శక్తి క్వాంటీకృతమై ఉంటుంది. ఎలక్ట్రాన్కు కొన్ని నిర్దిష్టమైన విశిష్ఠ విలువలు ఉంటాయి.
2. ఎలక్ట్రాన్కు క్వాంటీకృత శక్తి స్థాయిలు ఉండటానికి కారణం ఎలక్ట్రాన్కు తరంగ స్వభావంతో పాటు ప్రోడింగర్ తరంగ సమీకరణానికి ఆమోదయోగ్యమైన ఫలితాలు కూడా ఉండటం.
3. పరమాణువులో ఎలక్ట్రాన్ యొక్క ఖచ్చితమైన స్థానాన్ని, ఖచ్చితమైన వేగాన్ని ఒకే కాలంలో తెలుసుకోవడం అసాధ్యం. కాబట్టి పరమాణువులో ఎలక్ట్రాన్ మార్గం ఖచ్చితంగా నిర్ధారించడంగాని, తెలుసుకోవడంగాని సాధ్యపడదు.
4. పరమాణువు ఆర్బిటాల్ తరంగ ప్రమేయం పరమాణువులోని ఎలక్ట్రాన్ల స్థితికి ప్రాతినిధ్యం వహిస్తుంది. అలాంటి తరంగ ప్రమేయాలు ఎలక్ట్రాన్కు చాలా ఉండే అవకాశం ఉంది. కనుక, పరమాణువులో కూడా చాలా శక్తి స్థాయిలు ఉంటాయి.
5. పరమాణువులో ఏదైనా ఒక బిందువు వద్ద ఎలక్ట్రానును కనుక్కొనే సంభావ్యత, ఆ బిందువు వద్ద ఆర్బిటాల్ తరంగ ప్రమేయ వర్గానికి |ψ|² అనులోమానుపాతంలో ఉంటుంది.
   పరమాణువులో వేరువేరు బిందువుల వద్ద సంభావ్యతా సాంద్రత |ψ|² విలువలు తెలిసినట్లయితే కేంద్రకం చుట్టూ ఎలక్ట్రాన్ ఉండే గరిష్ఠ సంభావ్యత గల ప్రదేశాన్ని గుర్తించవచ్చు. దీనినే ఆర్బిటాల్ అంటారు.

ప్రశ్న 59.
బోర్ పరమాణు నమూనాలోని లోపాలను విశదీకరించండి. (March 2013)
జవాబు:
ఒంటరి ఎలక్ట్రాన్ గల హైడ్రోజన్ పరమాణువు వర్ణపటాన్ని, ఇతర అయానులైన He⁺, Li²⁺, Be³⁺ కణాల వర్ణ పటాలను, స్థిరత్వాన్ని బోర్ పరమాణు నమూనా వివరించగలిగినది. కాని క్రింది అంశాలను అది వివరించలేకపోయింది.

1. హైడ్రోజన్ వర్ణపటాన్ని అధిక పృథఃకరణం గల వర్ణపటమాపకంతో గ్రహించినపుడు, ఇదివరలో ఒక ‘గీత’గా కనబడే గీత నిజానికి అతి సన్నిహిత గీతల సముదాయమని తెల్సింది. దీన్ని హైడ్రోజన్ యొక్క సూక్ష్మ వర్ణపటం అంటారు. ఈ సూక్ష్మ వర్ణపటాన్ని బోర్ నమూనా వివరించలేకపోయింది.
2. హైడ్రోజన్ వాయువును బాహ్య అయస్కాంత క్షేత్ర ప్రభావానికి గురిచేసి, హైడ్రోజన్ వర్ణపటాన్ని గ్రహించినపుడు, వర్ణపటంలోని ప్రతి గీతా సూక్ష్మ గీతల సముదాయంగా చీలి ఉండటం కన్పించింది. దీనిని ‘జీమన్ ఫలిత’ మంటారు. ఈ జీమన్ ఫలితాన్ని బోర్ నమూనా వివరించలేకపోయింది.
3. ఇదేవిధంగా విద్యుత్ క్షేత్ర ప్రభావంతో హైడ్రోజన్ వాయువు వర్ణపటం గ్రహించినపుడు ప్రతి గీత, సూక్ష్మ గీతల సముదాయంగా చీలి ఉండటం కన్పించింది. దీనిని ‘స్టార్క్ ప్రభావ’ మంటారు. బోర్ నమూనా ఈ ప్రభావాన్ని వివరించలేదు.
4. రసాయన బంధాల ద్వారా అణువులను ఏర్పరచే పరమాణువుల సామర్థ్యాన్ని కూడా బోర్ నమూనా వివరించలేదు.
5. హైసెన్ బర్గ్ నియమం ప్రకారం స్థిరకక్ష్యల భావన సరికాదు.
6. ఎలక్ట్రాన్ తరంగ స్వభావాన్ని బోర్ నమూనా పరిగణనలోకి తీసుకోలేదు.

ప్రశ్న 60.
ఎలక్ట్రాన్ ద్వంద్వ స్వభావానికి ఋజువులు ఏమిటి ?
జవాబు:
కాంతి వికిరణాల మాదిరిగానే పదార్థానికి కూడా ద్వంద్వ స్వభావం ఉంటుంది. అంటే కణస్వభావం, తరంగ స్వభావం ఉంటాయని డీబ్రోలీ ప్రతిపాదించాడు. పదార్థ కణాల ద్రవ్యవేగానికి, తరంగదైర్ఘ్యానికి కింది సంబంధాన్ని సూచించాడు. డీబ్రోలీ ప్రకారం
λ = \(\frac{h}{m v}\) = \(\frac{h}{p}\)
m కణం ద్రవ్యరాశి, V కణవేగం, ద్రవ్యవేగం, కాంతి తరంగస్వభావానికి లక్షణమైన ఎలక్ట్రాన్ పుంజం వివర్తనకు లోనయ్యే ప్రయోగం (Davission and Germer diffraction experiment with a beam of fast moving electrons) ద్వారా డీబ్రోలీ ఊహ నిర్ధారించబడింది. ఈ వాస్తవాన్ని ఆధారంగా ఎలక్ట్రాన్ మైక్రోస్కోపు నిర్మాణం జరిగింది. అది ఎలక్ట్రాన్ తరంగ స్వభావంపై ఆధారపడినది. శాస్త్ర పరిశోధనలలో ఎలక్ట్రాన్ మైక్రోస్కోపు అతిశక్తివంతమైన పరికరంగా 15 మిలియన్ల రెట్లు పెద్దగా చేయడానికి ఉపకరిస్తుంది.

నిర్దిష్ఠమైన లోహాలపై కాంతిపుంజం పడినపుడు ఎలక్ట్రానులు బయటకు వెలువడ్డాయి. విద్యుత్ అయస్కాంత వికిరణాల ప్లాంక్ క్వాంటం సిద్ధాంతాన్ని ఆధారంగా తీసుకొని ఐన్స్టీన్ కాంతి విద్యుత్ ప్రభావాన్ని వివరించాడు. లోహ తలంపై కాంతిపుంజాన్ని ప్రకాశింపచేయడాన్ని కాంతికణ పుంజంతో తాడించిన దృశ్యంగా పరిగణించాలి. ఆ కణపుంజమే ఫోటానులు. కాంతి కణ స్వభావ భావన కృష్ణపదార్థం నుంచి ఉద్గారమయ్యే వికిరణాలను, కాంతి విద్యుత్ ప్రభావాన్ని వివరించగలిగింది. వెలువడే ఎలక్ట్రాన్ల గతిజశక్తి కాంతిపుంజం పౌనఃపున్యానికి అనులోమానుపాతంలో ఉంటుంది. ఎలక్ట్రాన్ల గతిజశక్తి కాంతి తీక్షణతపై ఆధారపడదు. కాంతి తీక్షణత వల్ల ఫోటానుల సంఖ్య పెరుగుతుంది. అందువల్ల ఫోటో ఎలక్ట్రానుల సంఖ్య పెరుగుతుంది. ఈ దృగ్విషయం కాంతి కణ స్వభావాన్ని ఋజువు చేస్తుంది.

ప్రశ్న 61.
n, l, m_l క్వాంటం సంఖ్యలు ఎలా వచ్చాయి ? వాటి ప్రాముఖ్యాన్ని వివరించండి.
జవాబు:
క్వాంటం సంఖ్యలు పరమాణు ఆర్బిటాళ్ల ఖచ్చితమైన తారతమ్యాలను తెలుపుతాయి. ప్రతి ఆర్బిటాల్ మూడు క్వాంటం సంఖ్యల చేత గుర్తించబడుతుంది. అవి n, l, m_l.

ప్రధాన క్వాంటం సంఖ్య ‘n’ :

1. ఈ క్వాంటం సంఖ్యను బోర్ ప్రతిపాదించాడు. దీనిని ‘n’ తో సూచిస్తారు.
2. ఇది కేంద్రకం చుట్టూ ఉండే వృత్తాకార కర్పరాలను సూచిస్తుంది.
3. n కు సరళ పూర్ణాంక విలువలు ఉంటాయి. n = 1, 2, 3, …… విలువలు ఉంటాయి.
4. ప్రధాన క్వాంటం సంఖ్య ఆర్బిటాల్ పరిమాణాన్ని, దాదాపుగా దాని శక్తిని తెలుపుతుంది.
5. ప్రధాన క్వాంటం సంఖ్య విలువ పెరిగే కొద్దీ, దానిలో పరిమితమయ్యే ఆర్బిటాల్ల సంఖ్య కూడా పెరుగుతుంది. ఆర్బిటాల్లల సంఖ్య n² ఇస్తుంది.
6. ప్రధాన క్వాంటం సంఖ్య ‘n’ పెరిగేకొద్దీ, దానిలోని ఆర్బిటాల్ల పరిమాణం కూడా పెరగటమే కాకుండా ఆర్బిటాల్ కూడా పెరుగుతుంది.
7. ప్రాధాన్యత కర్పరం యొక్క పరిమాణాన్ని ఎలక్ట్రాన్ యొక్క శక్తిని తెలియచేస్తుంది.

ఎజిముతల్ క్వాంటం సంఖ్య ‘l’ :

1. ఈ క్వాంటం సంఖ్యను సోమర్ఫెల్డ్ ప్రవేశపెట్టాడు. దీనిని ‘l’ తో సూచిస్తారు. దీనిని ఆర్బిటాల్ కోణీయ ద్రవ్యవేగం క్వాంటం సంఖ్య అని కూడా అంటారు.
2. l విలువలు …… 0 నుంచి (n – 1) వరకు ఉంటాయి. అంటే ఏదైన ఇచ్చిన ‘n’ విలువకు lకు సాధ్యమయ్యే విలువలు l = 0, 1, 2 …… (n – 1).
3. ప్రధాన కర్పరంలో ఉండే ఉపకర్పరాల సంఖ్య ‘n’ కి సమానం. ప్రతి ఉపకర్పరానికి ఒక ఎజిముతల్ క్వాంటం
   విలువ (l) సంఖ్య నిర్దేశించబడుతుంది.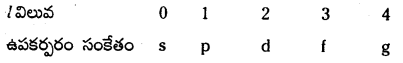
4. 
5. ప్రాధాన్యత : ఆర్బిటాల్ ఆకృతిని తెలియచేస్తుంది.
   s – ఆర్బిటాల్ ఆకృతి – గోళాకారం
   p – ఆర్బిటాల్ ఆకృతి – డంబెల్
   d – ఆర్బిటాల్ ఆకృతి – డబుల్ డంబెల్
   f – ఆర్బిటాల్ ఆకృతి – క్లిష్టమైనది

అయస్కాంత ఆర్బిటాల్ క్వాంటం సంఖ్య ‘m’:

1. ఈ క్వాంటం సంఖ్యను లాండే ప్రవేశపెట్టాడు. దీనిని m_l తో సూచిస్తారు.
2. నిర్దిష్ట ఉపకర్పరంకు సాధ్యపడే m_l విలువలు – l నుండి + l వరకు (2l + 1) విలువలు ఉంటాయి.
3. ఈ క్వాంటం సంఖ్య ఉపకర్పరాలలోని ఉప ఉపకర్పరాలను లేక ఆర్బిటాళ్ళను తెలియచేస్తుంది.
4. ఉపకర్పరాలకు దానిలోని ఆర్బిటాళ్ళ సంఖ్య మధ్య సంబంధం క్రింది పట్టికలో ఇవ్వబడింది.
   
5. ఒక ఉపస్థాయిలోని ఆర్బిటాళ్లన్నీ ఒకే శక్తిని కలిగి ఉంటాయి. వీటన్నింటికి ఒకే n, l విలువలు ఉండుటయే దీనికి కారణం.
6. ప్రాధాన్యత : ఆర్బిటాళ్ల ప్రాదేశిక అమరికను తెలియచేస్తుంది.

ప్రశ్న 62.
పదార్థం ద్వంద్వ స్వభావాన్ని వివరించండి. ఎలక్ట్రాన్ లాంటి సూక్ష్మ కణాలకు దీని ప్రాముఖ్యాన్ని చర్చించండి.
జవాబు:
డీబ్రోలీ ఎలక్ట్రాన్కు ద్వంద్వ స్వభావాన్ని ప్రతిపాదించాడు. అనగా ఎలక్ట్రాన్కు కణ స్వభావం మరియు తరంగ స్వభావం రెండూ ఉంటాయి. డీబ్రోలీ తిరుగుతూ ఉన్న ఎలక్ట్రాన్ యొక్క తరంగదైర్ఘ్యానికి సమీకరణం ఉత్పాదించాడు. ఈ సమీకరణం ప్రకారం λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) ఇచ్చట λ తరంగదైర్ఘ్యం, m = ఎలక్ట్రాన్ యొక్క ద్రవ్యరాశి, v = ఎలక్ట్రాన్ యొక్క వేగం, h = ప్లాంక్ స్థిరాంకం.
డీబ్రోలీ ప్రకారం, ఎలక్ట్రాన్ పదార్థ తరంగం వలె ప్రవర్తిస్తుంది. ఈ ఎలక్ట్రాన్ తరంగం యొక్క తరంగదైర్ఘ్యం λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) పరమాణు ఆర్బిటాళ్ళలో ఈ ఎలక్ట్రాన్ తరంగం స్థిర తరంగం వలె ఉంటుంది.

λ = \(\frac{\mathbf{h}}{\mathbf{m v}}\) సమీకరణం ఉత్పాదన : డీబ్రోలీ సమీకరణాన్ని ప్లాంక్ సిద్ధాంతం మరియు ఐన్స్టీన్ సిద్ధాంతాల నుండి
ఉత్పాదన చేస్తారు.
ప్లాంక్ సిద్ధాంతం ప్రకారం, E = hν ……. (1)
ఇచ్చట E = శక్తి,
h = ప్లాంక్ స్థిరాంకం,
ν = పౌనఃపున్యం
ఐనస్టీన్ సమీకరణం ప్రకారం, E = mc² ……. (2)
ఇచ్చట m = ఎలక్ట్రాన్ ద్రవ్యరాశి,
E = శక్తి,
C = కాంతివేగం

(1), (2) ల నుండి hv = mc² కాని ν = \(\frac{c}{\lambda}\)
∴ h × \(\frac{\mathrm{c}}{\lambda}\) = mc² (లేక) \(\frac{\mathrm{h}}{\lambda}\) = mc (లేక) λ = \(\frac{\mathrm{h}}{\mathrm{mc}}\)
ఎలక్ట్రాన్ వంటి కణాలకు వేగాన్ని ‘v’ గా తీసికొంటారు.
అపుడు λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) అవుతుంది. కాని mv = p (ద్రవ్యవేగం)
∴ λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) = \(\frac{\mathrm{h}}{\mathrm{p}}\)
డీబ్రోలీ భావన యొక్క సార్థకత :
డీబ్రోలీ ప్రకారం, న్యూక్లియస్ చుట్టూ వృత్తాకార మార్గంలో తిరుగుతున్న ఎలక్ట్రాన్ స్థిర తరంగంవలె ప్రవర్తిస్తుంది. అలా ప్రవర్తించాలంటే బోర్ ప్రతిపాదించిన కర్పరం యొక్క వ్యాసం ఎలక్ట్రాన్ తరంగం యొక్క తరంగదైర్ఘ్యానికి పూర్ణ సంఖ్య గుణిజంగా ఉండాలి.
అనగా 2πr = nλ
∴ λ = \(\frac{2 \pi r}{n}\) ….. (3) ఇచ్చట n = పూర్ణసంఖ్య
కాని డీబ్రోలీ ప్రకారం, λ = \(\frac{h}{m v}\) ……. (4)
(3) (4) ల నుండి, \(\frac{\mathrm{h}}{\mathrm{mv}}\) = \(\frac{2 \pi r}{n}\) (లేక) mvr = n × \(\frac{\mathbf{h}}{2 \pi}\)
కాబట్టి డీబ్రోలీ భావన బోర్ సిద్ధాంతానికి అనుగుణంగా ఉన్నదని తెలుస్తుంది.

డీబ్రోలీ ప్రకారం చలించే ప్రతి వస్తువుకు తరంగ స్వభావం ఉంటుందనేది గుర్తు పెట్టుకోవలసిన అవసరం ఉంది. మామూలు వస్తువులతో ఉన్న తరంగదైర్ఘ్యం చాలా తక్కువ (వాటి ద్రవ్యరాశి ఎక్కువగా ఉంటుంది కాబట్టి). కనుక వాటి తరంగ స్వభావం గుర్తించలేం. ఎలక్ట్రాన్లు, ఇతర ఉపపరమాణు కణాల (ద్రవ్యరాశి చాలా తక్కువ) తరంగదైర్ఘ్యాలను ప్రయోగం ద్వారా గుర్తించవచ్చు.

ప్రశ్న 63.
విద్యుదయస్కాంత వికిరణాలలో వేర్వేరు అవధులు ఏమిటి ? విద్యుదయస్కాంత వికిరణాల లక్షణాలను వివరించండి.
జవాబు:
విద్యుదయస్కాంత వికిరణము (కాంతి) : మాక్స్వెలె ననుసరించి, విద్యుదయస్కాంత వికిరణము, విద్యుదయస్కాంత తరంగాల సమూహము. డోలాయమానం చెందుతున్న ఆవేశపూరిత కణాలు ఉత్పత్తి చేసే విద్యుత్ మరియు అయస్కాంత క్షేత్రాలు ఒకదానికొకటి లంబంగా ఉండి, తరంగ వ్యాపన దిశకు కూడా లంబంగా ఉంటాయి.

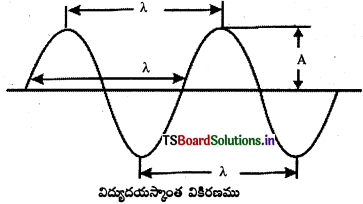
విద్యుదయస్కాంత వికిరణాల అభిలాక్షణిక ధర్మాలు :

1. పదార్ధంలో డోలాయమానం చెందే ఆవేశిత కణాలు విద్యుదయస్కాంత వికిరణాలను ఉత్పత్తి చేస్తాయి.
2. ఈ తరంగాల వ్యాపనానికి యానకం అవసరం లేదు. అవి శూన్యంలో కూడా ప్రయాణిస్తాయి.
3. పటంలో A అనునది డోలన పరిమితి (లేదా తరంగ కంపనపరిమితి). ఇది ఒక బిందువు వద్ద గల విద్యుత్ క్షేత్ర బలాన్ని చూపుతుంది. తరంగంలోని రెండు శృంగాలకు (crests) లేదా తొట్టెలకు (troughs) గల మధ్య దూరాన్ని తరంగదైర్ఘ్యం (λ) అంటారు. ఓకు ప్రమాణము సెం.మీ.; మీ; నా.మీ; ఆంగ్హామ్. S.I. ప్రమాణము, మీటరు.
4. ఒక సెకనులో ఒక బిందువు నుంచి దాటి వెళ్ళే తరంగాల సంఖ్యను తరంగ పౌనఃపున్యం (frequency) అంటారు. దీన్ని న్యూ (ν) తో సూచిస్తారు.
   
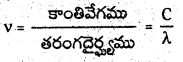
   పౌనఃపున్యానికి S.I. ప్రమాణం హెర్ట్జ్ (Hz)
5. ఒక సెకనులో కాంతి తరంగం ప్రయాణించే దూరాన్ని కాంతివేగం (C) అంటారు.
   కాంతివేగం = తరచుదనం × తరంగదైర్ఘ్యం
   C = ν × λ
   తరంగదైర్ఘ్యానికి సంబంధం లేకుండా అన్ని రకాలైన విద్యుదయస్కాంత వికిరణాలు శూన్యంలో 3.0 × 10⁸ మీ. సె^-1 వేగంతో ప్రయాణిస్తాయి.
6. ఒక సెం.మీ. పొడవులో ఇమిడివున్న తరంగాల సంఖ్యను తరంగసంఖ్య (\(\bar{v}\)) అంటారు. ఇది తరంగ దైర్ఘ్యానికి వ్యుతమము. \(\bar{v}\) ప్రమాణము సెం.మీ
7. డోలన పరిమితి (A) అంటే, శృంగపు ఎత్తు లేదా తొట్టె యొక్క లోతు. ఇది కాంతి తీవ్రతను లేదా ప్రకాశాన్ని తెలియజేస్తుంది.
8. విద్యుదయస్కాంత వికిరణాల తరంగదైర్ఘ్యాలు లేదా పౌనఃపున్యాలు గుర్తింపబడ్డ పటాన్ని విద్యుదయస్కాంత వర్ణపటం అంటారు.
   

ప్రశ్న 64.
పరమాణు ఆర్బిటాల్ను నిర్వచించండి. a, p, d, f ఆర్బిటాళ్ళ ఆకారాలను పటాల ద్వారా వివరించండి.
జవాబు:
పరమాణు ఆర్బిటాల్ : పరమాణువులో కేంద్రకం చుట్టూ ఉండే త్రిమితీయ ప్రదేశంలో ఎలక్ట్రాన్ను కనుగొనే సంభావ్యత గరిష్ఠంగా గల ప్రదేశాన్ని ఎలక్ట్రాన్ పరమాణు ఆర్బిటాల్ అంటారు.
ప్రోడింగర్ సమీకరణం నుండి ఆర్బిటాళ్ళ ఆకృతులను సాధించవచ్చు. ఈ ఆర్బిటాళ్ళు, కోణీయ వితరణ వక్రరేఖలు.

S – ఆర్బిటాల్ ఆకృతి :

1) S-ఆర్బిటాళ్ళు గోళాకారంలో ఉంటాయి. ప్రధాన క్వాంటం సంఖ్య n విలువ పెరిగేకొద్దీ S – ఆర్బిటాల్ పరిమాణం కూడా పెరుగుతుంది. 1s < 2s < 3s

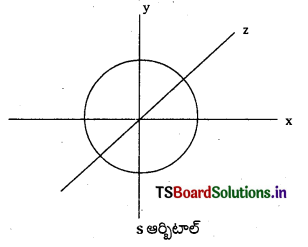
2) వీటికి ఎలక్ట్రాన్ను కనుగొనే సంభావ్యత త్రిమితీయ ప్రదేశంలో అన్ని దిక్కులలోను సమానంగా ఉంటుంది. అనగా ఈ ఆర్బిటాళ్లకు దిశానిర్దేశకత (directional property) లేదు.

p-ఆర్బిటాల్ ఆకృతి :

p – ఆర్బిటాల్ ‘డంబెల్’ ఆకారంలో ఉంటుంది. మొత్తం మూడు p ఆర్బిటాళ్ళుంటాయి. అవి p_x, p_y, మరియు p_z ఆర్బిటాళ్లు. ఒక p – ఆర్బిటాల్లో రెండు లోన్లు ఉంటాయి. ఈ లోన్లు ఆయా అక్షాల వెంబడి విస్తరించి ఉంటాయి. ప్రతి p ఆర్బిటాల్క ఒక నోడల్ తలం (p_xకు YZ; p_yకు XZ; p_zకు XY) ఉంటుంది.

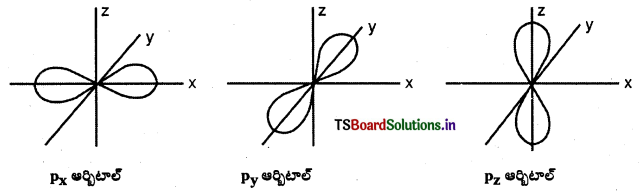
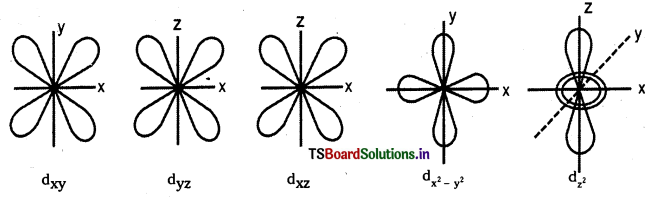
d- ఆర్బిటాల్ ఆకృతి :

d – ఆర్బిటాల్. డబుల్ డంబెల్ ఆకారంలో ఉంటుంది.
ఇవి మొత్తం ఐదు ఆర్బిటాళ్లు. అవి వరుసగా d_xy, d_yz, d_zx, \(d_{x^2-y^2}\) మరియు \(\mathrm{d}_{\mathrm{z}^2}\). మొదటి నాలుగు డబుల్ డంబెల్ ఆకారాల్లో ఉంటాయి. ప్రతి దానికి 4 లోన్లు ఉంటాయి.
\(\mathrm{d}_{\mathrm{z}^2}\) ఆర్బిటాల్ Z అక్షం చుట్టూ డంబెల్ ఆకారంలో వ్యాప్తి చెంది ఉంటుంది. దీనికి ఉంగరం (లేదా టోరస్ లేదా కాలర్ లేదా టైర్) ఆకారంలో XY తలంలో ఎలక్ట్రాన్ సాంద్రత ఉంటుంది. ప్రతి d ఆర్బిటాల్కు రెండు నోడ్లు మిగిలిన అక్షాలపరంగా ఉంటాయి.

ప్రశ్న 65.
మూడు p- ఆర్బిటాల్ల, అయిదు d – ఆర్బిటాల్ల సమతలాలను రేఖాపటాల ద్వారా వివరించండి..
జవాబు:
వేరువేరు ఆర్బిటాళ్ళకు స్థిర సంభావ్యతా సాంద్రతను సూచించే సమతల పటాలు ఆ ఆర్బిటాళ్ళ ఆకారాలకు ప్రాతినిధ్యం వహిస్తాయి. సంభావ్యతా సాంద్రత || 2 స్థిరంగా ఉన్న ప్రదేశంపై సమతల లేదా తీరరేఖను గీస్తే ఆర్బిటాళ్ల ఆకారం వస్తుంది. అలాంటి సమతలాలు చాలా ఉండే అవకాశం ఉన్నప్పటికీ 90 శాతం కంటే ఎక్కువ ఎలక్ట్రాన్ను కనుక్కొనే సంభావ్యత గల ప్రదేశం లేదా ఘనపరిమాణం స్థిర సంభావ్యతా సాంద్రతను చుట్టేటట్లు గీసిన సమతలం ఆర్బిటాళ్ల ఆకారాన్ని సూచిస్తుంది.
p-ఆర్బిటాల్

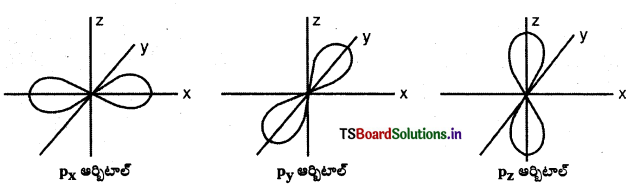
ఈ పటాలలో కేంద్రకం మూలస్థానంలో ఉంటుంది. p – ఆర్బిటాలు 2 భాగాలు కలిగి ఉంటుంది. వీటినే “లోబ్లు” అంటారు. కేంద్రకం నుంచి పోయే తలానికి రెండు వైపులా ఈ గోళాకార లోన్లు ఉంటాయి. ఈ రెండు లోన్లు కలిసే సమతలం దగ్గర సంభావ్యతా సాంద్రత ప్రమేయం సున్నాగా ఉంటుంది. మూడు p- ఆర్బిటాల్ల పరిమాణం, ఆకారం, శక్తి సమానంగా ఉంటుంది. మూడు p- ఆర్బిటాల్లలో ఉన్న ‘లోబ్’ల దిగ్విన్యాసం వేరుగా ఉంటుంది. వీటిలో ఉన్న లోబ్లు X, Y, Z అక్షాలవైపు ఉండటంవల్ల వాటిని p_x, p_y, p_z ఆర్బిటాల్లు అంటారు. m, (-1, 0, +1) విలువలకు XYZ అక్షాల దిశలకు అంత సులభమైన సంబంధం లేదు. అయినప్పటికి m, కి మూడు విలువలున్నాయి. కాబట్టి పరస్పరం లంబంగా ఉండే మూడు ఆర్బిటాల్లు ఉంటాయి. p- ఆర్బిటాల్ల శక్తి పరమాణు క్రమం 4p > 3p > 2p.

l = 2 అయినపుడు ఆ ఆర్బిటాల్ను ‘d’ ఆర్బిటాల్లు అంటారు.

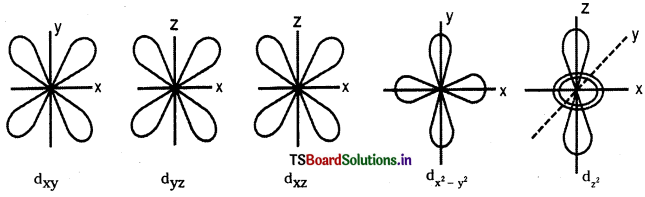
ఈ ‘d’ ఆర్బిటాలు కనిష్ఠ ప్రధాన క్వాంటం సంఖ్య (n) = 3. ఎందుకంటే / విలువ (n – 1) కంటే ఎక్కువ ఉండదు. l = 2 అయినప్పుడు mకి అయిదు విలువలు ఉంటాయి. అవి (-2, -1, 0, +1, +2) అందుకని అయిదు d – ఆర్బిటాల్లు ఉంటాయి.

అయిదు d – ఆర్బిటాల్ ను d_xy, d_yz, d_xz, \(\mathrm{d}_{\mathrm{x}^2-\mathrm{y}^2}\), \(\mathrm{d}_{\mathrm{z}^2}\) సంకేతాలతో చూపిస్తారు. మొదటి నాలుగు d- ఆర్బిటాల్ల ఆకృతులు ఒకే విధంగా ఉంటాయి. అయిదోది మాత్రం మిగతా వాటి కంటే వేరుగా ఉంటుంది. అయిన అన్ని d – ఆర్బిటాల్ల శక్తి సమానంగా ఉంటుంది. , ఆర్బిటాల్క రెండు నోడల్ సమతలాలు ఉత్పత్తి స్థానం నుంచి పోతూ z – అక్షం గల XY సమతలాన్ని సమద్విఖండన చేస్తాయి. వీటినే కోణీయ నోడ్లు అంటారు. ఒక ఆర్బిటాల్కు కోణీయ- నోడ్లు ఎజిముతల్ క్వాంటం సంఖ్య lకు సమానం.

ప్రశ్న 66.
పూర్తిగా నిండిన, సగం నిండిన ఉపకర్పరాల స్థిరత్వానికి కారణాలను తెలపండి.
జవాబు:
క్రోమియం ఎలక్ట్రాన్ విన్యాసం 1s² 2s² 2p⁶ 3s² 3p⁶ 4s¹ 3d⁵
కాపర్ ఎలక్ట్రాన్ విన్యాసం 1s² 2s² 2p⁶ 3s² 3p⁶ 4s¹ 3d¹⁰
క్రోమియంకు d – ఆర్బిటాల్లో 5 ఎలక్ట్రాన్లు ఉన్నాయి. అనగా d – ఆర్బిటాలు సగం నిండినది. అదే విధంగా కాపర్లో d – ఆర్బిటాలు పూర్తిగా నిండినది. పూర్తిగా నిండిన, సగం నిండిన ఉపకర్పరాలు కింది కారణాల వల్ల స్థిరంగా ఉంటాయి.

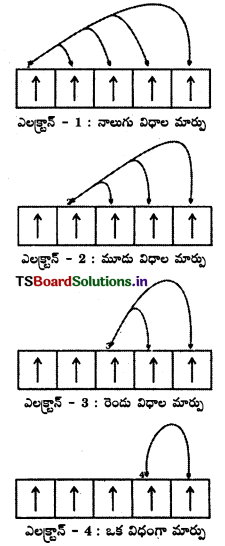
1. ఎలక్ట్రాన్ల సౌష్టవ పంపిణీ : పూర్తిగా గాని, సగంగాని నిండిన ఉపకర్పరాలలో ఎలక్ట్రాన్లు సౌష్ఠవంగా పంపిణీ జరగడం వల్ల అధిక స్థిరత్వం ఉంటుంది.

2. మార్చుకొనే శక్తి : సమానశక్తి గల ఆర్బిటాళ్ళలో రెండుగాని అంతకంటే ఎక్కువ సమాంతర స్పిన్లు గల ఎలక్ట్రాన్లు ఉన్నట్లయితే స్థిరత్వ ప్రభావం సంభవిస్తుంది. ఈ ఎలక్ట్రానులు ఒకదాని స్థానాన్ని మరొక దానితో మార్చుకొంటాయి. ఈ మార్పు వల్ల ఎలక్ట్రాన్ శక్తి తగ్గుతుంది. దీనినే మార్చుకొనే శక్తి అంటారు. పూర్తిగా లేదా సగం నిండిన ఉపకర్పరాలలో మార్చుకొనే ఎలక్ట్రాన్ సంఖ్య గరిష్ఠంగా ఉంటుంది.

ఇంకొక విధంగా చెప్పాలంటే సగం నిండిన లేదా పూర్తిగా నిండిన ఉపకర్పరాలకు అధిక స్థిరత్వం ఎందుకంటే

1. సాపేక్షంగా తక్కువ కవచం ఉండడం,
2. కూలంబిక్ వికర్షణ శక్తి స్వల్పంగా ఉండడం,
3. మార్చుకొనే శక్తి అధికంగా ఉండడం.

ప్రశ్న 67.
శోషణ, ఉద్గార వర్ణపటాలను వివరించండి. హైడ్రోజన్ పరమాణువులో రేఖా వర్ణపటాల సాధారణ వర్ణనపై చర్చించండి.
జవాబు:
పదార్థం శోషించుకొన్న శక్తిని ఉద్గారించే వికిరణాల వర్ణపటాన్ని ఉద్గారవర్ణపటం అంటారు. ఒక పదార్ధం ద్వారా అవిచ్ఛిన్న వికిరణ కాంతిని పంపించిన వర్ణ పటాన్ని నమోదు చేసినట్లయితే కొన్ని తరంగ దైర్ఘ్యాలు కనపడవు. అవి పదార్థం శోషించుకోవడంవల్ల వాటికి సంబంధించి అవిచ్ఛిన్న వర్ణపటంలో నల్లని గీతలు ఏర్పడతాయి.

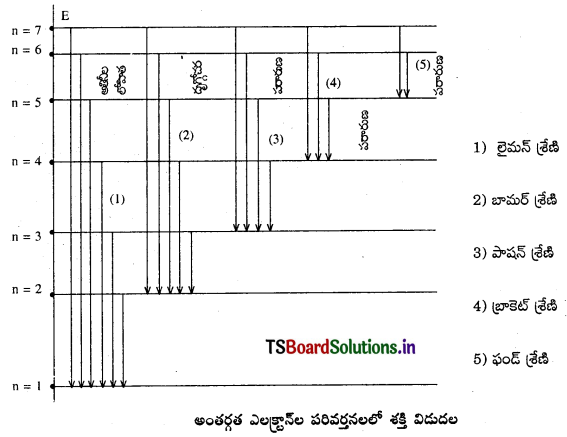
హైడ్రోజన్ పరమాణు వర్ణ పటంలో వివిధ శ్రేణులలో ఏర్పడే వివిధ రేఖలను వివరించుట :
హైడ్రోజన్ పరమాణువులో ఒకే ఒక ఎలక్ట్రాన్ ఉన్నది. అది 1వ కర్పరంలో తిరుగుతుంది. అసంఖ్యాక ఎలక్ట్రాన్లు కలిగి ఉన్న కొంత ద్రవ్యరాశి గల హైడ్రోజన్ వాయువును వేడి చేసినా (లేక) కాంతి శక్తికి గురి చేసినా (లేక) విద్యుత్ ఉత్సర్గానికి గురి చేసినా, విభిన్న ఎలక్ట్రాన్లు విభిన్న మొత్తాలలో శక్తిని శోషణం చేసుకొని విభిన్న పై కర్పరాలలోకి చేరుకుంటాయి. దీనిని excitation అంటారు. కాని ఆ పై కర్పరాలలో అవి ఎక్కువ కాలం ఉండలేవు. అందువలన అవి తిరిగి క్రింది కర్పరాలలోకి రావటానికి ప్రయత్నిస్తాయి. దీనిని De-excitation అంటారు.

ఈ Deexcitation అన్ని ఎలక్ట్రాన్లకు సమానంగా ఉండాలనేమీ లేదు. కొన్ని ఉత్తేజిత, ఎలక్ట్రాన్లు, పై స్థాయిల నుండి ఒకటవ స్థాయిలోనికి దూకవచ్చు. అపుడు వర్ణ పటరేఖలు U.V. ప్రాంతంలో ఏర్పడతాయి. వాటిని లైమన్ శ్రేణి అంటారు. కొన్ని ఉత్తేజిత ఎలక్ట్రాన్లు, పై స్థాయిల నుండి రెండవ స్థాయిలోకి దూకవచ్చు. అపుడు వర్ణ పటరేఖలు దృగ్గోచర కాంతి ప్రాంతంలో ఏర్పడతాయి. వాటిని బామర్ శ్రేణి అంటారు. అదే విధంగా, ఉత్తేజిత ఎలక్ట్రాన్లు ఏ పై శక్తి స్థాయిల నుండైనా 3, 4, 5 క్రింది స్థాయిలోకి దూకినపుడు ఏర్పడే వర్ణపటరేఖలను పాషన్, బ్రాకెట్, ఫండ్ శ్రేణులు అంటారు.

పై స్థాయి నుండి క్రింది స్థాయిలోకి De–excitation విధానం ఏక దశలో గాని (లేక) అనేక దశలలో గాని జరగవచ్చు. ఉదాహరణకు నాల్గవ స్థాయి నుండి ఒకటవ స్థాయికి జరిగే De-excitation విధానం ఈ క్రింది విధానంగా ఉంటుంది.
ఏకదశ : నాల్గవ స్థాయి నుండి ఒకటవ స్థాయిలోకి (i.e.) 4 → 1
అనేక దశలు : 4 → 3 → 2 → 1 ; 4 → 3 → 1 ; 4 → 2 → 1.
ఎలక్ట్రాన్లు ఒక కర్పరం నుండి వేరొక కర్పరంలోకి దూకినప్పుడు వర్ణపటంలో ఒక రేఖ ఏర్పడుతుంది. ఆ విధంగా ఎలక్ట్రాన్లు ఎన్ని దూకుళ్ళు జరిపితే అన్ని రేఖలు ఏర్పడతాయి. అందువలననే ఒకే శ్రేణిలో అసంఖ్యాక రేఖలు ఏర్పడతాయి.

అదనపు ప్రశ్నలు

ప్రశ్న 1.
\({ }_{35}^{80} \mathrm{Br}\) లోని ప్రోటాన్లు, న్యూట్రానుల సంఖ్యను లెక్కించండి.
జవాబు:
\({ }_{35}^{80} \mathrm{Br}\) లో Z = 35 ; A = 80 ఇది తటస్థ పరమాణువు.
ప్రోటానుల సంఖ్య Z = 35
న్యూట్రానుల సంఖ్య = 80 – 35 = 45

ప్రశ్న 2.
ఒక కణంలో ఎలక్ట్రానులు, ప్రోటానులు, న్యూట్రానుల సంఖ్య 18, 16, 16 వరుసగా కలవు. ఆ కణానికి సరైన గుర్తును ఇవ్వండి.
జవాబు:
పరమాణు సంఖ్య ప్రోటానుల సంఖ్యకు సమానం = 16
మూలకం సల్ఫర్ S.
ద్రవ్యరాశి సంఖ్య = ప్రోటానుల సంఖ్య + న్యూట్రానుల సంఖ్య
= 16 + 16 = 32
ప్రోటాన్ల సంఖ్య ఎలక్ట్రానుల సంఖ్యకు సమానం కాదు. అది తటస్థమైనది కాదు. అది ఆనయాన్. ఋణావేశం కలది. దాని మీద ఆవేశం ఎలక్ట్రాన్లు ఎన్ని ఎక్కువ ఉన్నవో అంత ఎక్కువగా వున్న ఎలక్ట్రానులు = 18 – 16 = 2
గుర్తు \({ }_{16}^{32} \mathrm{~s}^{2-}\)

ప్రశ్న 3.
ఆకాశవాణి ఢిల్లీ, వివిధ భారతి స్టేషన్ నుండి 1,368 KHz పౌనఃపున్యంపై ప్రసారాలు చేస్తుంది. ప్రసారిణి ఉద్గారించే విద్యుదయస్కాంత వికిరణాల తరంగదైర్ఘ్యం ఎంత ? ఇది విద్యుదయస్కాంత వర్ణపటంలో ఏ ప్రాంతానికి చెందుతుంది ?
జవాబు:
C = νλ
λ = \(\frac{c}{v}\) = \(\frac{3 \times 10^8 \mathrm{~ms}^{-1}}{1368 \times 10^3 \mathrm{~s}^{-1}}\)
λ = 219.3 m
ఈ తరంగదైర్ఘ్యం రేడియో తరంగాల కోవలోకి వస్తుంది.

ప్రశ్న 4.
దృగ్గోచర వర్ణపటం ఊదా (400 nm) నుంచి ఎరుపు (750 nm) వరకు ఉంటుంది. ఈ తరంగదైర్ఘ్యాలను పౌనఃపున్యాలలో తెలపండి.
జవాబు:
ఊదా రంగు :
ν = \(\frac{\mathrm{c}}{\lambda}\) = \(\frac{3 \times 10^8 \mathrm{~ms}^{-1}}{400 \times 10^{-9} \mathrm{~m}}\) = 7.5 × 10¹⁴Hz
ఎరుపు రంగు :
ν = \(\frac{c}{\lambda}\) = \(\frac{3 \times 10^8 \mathrm{~ms}^{-1}}{750 \times 10^{-9} \mathrm{~m}}\) = 4.00 × 10¹⁴ Hz
దృగ్గోచర వర్ణపటం 4.0 × 10¹⁴ Hz నుండి 7.5 × 10¹⁴ Hz పౌనఃపున్యం ప్రమాణాలలో ఉంటుంది.

ప్రశ్న 5.
5800 À తరంగదైర్ఘ్యం గల పసుపు వికిరణాల తరంగ సంఖ్యను, పౌనఃపున్యాన్ని గణించండి.
జవాబు:
తరంగ సంఖ్య \(\bar{v}\) = \(\frac{1}{\lambda}\) = \(\frac{1}{5800 \times 10^{-10} \mathrm{~m}}\) = 1.724 × 10⁶ m^-1
\(\bar{v}\) = 1.724 × 10⁶ m^-1
పౌనఃపున్యం v = \(\frac{\mathrm{c}}{\lambda}\) = \(\frac{3 \times 10^8 \mathrm{~ms}^{-1}}{5800 \times 10^{-10} \mathrm{~m}}\) = 5.172 × 10¹⁴s^-1

ప్రశ్న 6.
ఒక 100 వాట్ల బల్బు 400 nm ల ఏకవర్ణ కాంతిని ఉద్గారం చేస్తుంది. ఒక సెకనుకు ఆ బల్బు ఎన్ని ఫోటానులను ఉద్గారం చేస్తుందో లెక్కించండి.
జవాబు:
బల్బు సామర్థ్యం = 100 watt = 100 Js^-1
ఒక ఫోటాన్ శక్తి E = hν = \(\frac{\mathrm{hc}}{\lambda}\)
= \(\frac{\mathrm{hc}}{\lambda}\) = 4.969 × 10^-19J
ఉదార్గమైన ఫోటానుల సంఖ్య = \(\frac{100 \mathrm{Js}^{-1}}{4.969 \times 10^{-19} \mathrm{~J}}\) = 2.012 × 10²⁰ s^-1

ప్రశ్న 7.
లోహం ఆరంభ పౌనఃపున్యం (v₀) 7.0 × 10¹⁴ s^-1, v = 1.0 × 10¹⁵ s^-1 పౌనఃపున్యం గల వికిరణాలు లోహంపై పతనమైనప్పుడు బయటకు వెలువడే ఎలక్ట్రానుల గతిజశక్తి గణించండి.
జవాబు:
ఐన్స్టీన్ సమీకరణం ప్రకారం
గతిజశక్తి \(\frac{1}{2}\)m_e v² = h(ν – ν₀)
= h (1.0 × 10¹⁵ – 7 × 10¹⁴)
= (6.626 × 10^-34 Js × 3 × 10¹⁴ s^-1)
= 1.988 × 10^-19 J

ప్రశ్న 8.
హైడ్రోజన్ పరమాణువులో ఎలక్ట్రాన్కు ఋణశక్తి అంటే ఏమిటి ?
జవాబు:
విరామంలో ఉన్న స్వేచ్ఛా ఎలక్ట్రాన్ శక్తి కంటే పరమాణువులో ఉన్న ఎలక్ట్రాన్ శక్తి తక్కువ అని ఋణ గుర్తు తెలియచేస్తుంది. కేంద్రకం నుంచి ఎలక్ట్రాన్ అనంత దూరంలో ఉంటే దానిని విరామంలో ఉంది అంటారు. అలాంటి ఎలక్ట్రాన్కు శక్తి విలువ శూన్యంగా తీసుకుంటారు.
E_∞ = 0 ఎలక్ట్రాన్ కేంద్రకానికి దగ్గర అవుతున్న కొద్దీ n విలువ తగ్గుతుంది. కనుక ఋణ విలువ ఎక్కువ అవుతుంది. అత్యధిక ఋణ విలువ n = 1కి వస్తుంది. అది అధిక స్థిరత్వం కలది.

ప్రశ్న 9.
రిడ్బర్గ్ సమీకరణం వ్రాయండి.
జవాబు:
హైడ్రోజన్ వర్ణపటంలోని రేఖల తరంగ సంఖ్యను రిడ్బర్గ్ సమీకరణం ద్వారా లెక్కించవచ్చు.
\(\bar{v}\) = R\(\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\)
= 1.09677 × 10⁷\(\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\)m^-1

ప్రశ్న 10.
హైడ్రోజన్ పరమాణువులో n = 5 స్థాయి నుంచి n = 2 స్థాయికి ఎలక్ట్రాన్ పరివర్తనం చెందినప్పుడు ఉద్గారమయ్యే ఫోటాన్ పౌనఃపున్యం, తరంగదైర్ఘ్యం ఎంత ?
జవాబు:
n = 5, n = 2 కి పరివర్తనం చెందినపుడు వర్ణపటం రేఖ దృగ్గోచర ప్రాంతంలో ఉండే బామర్ శ్రేణికి చెందుతుంది.
ΔE = 2.18 × 10⁻¹⁸ J \(\left[\frac{1}{5^2}-\frac{1}{2^2}\right]\)
= 4.58 × 10^-19J
ఇది ఉద్గారశక్తి.
ఫోటాన్ పౌనఃపున్యం
ν = \(\frac{\Delta \mathrm{E}}{\mathrm{h}}\) = \(\frac{4.58 \times 10^{-19} \mathrm{~J}}{6.626 \times 10^{-34} \mathrm{Js}}\)
పౌనఃపున్యం = 6.91 × 10¹⁴ Hz
తరంగదైర్ఘ్యం λ = \(\frac{\mathrm{c}}{\mathrm{v}}\) = \(\frac{3.0 \times 10^8 \mathrm{~ms}^{-1}}{6.91 \times 10^{14} \mathrm{~Hz}}\) = 434 nm

ప్రశ్న 11.
He⁺ మొదటి కక్ష్యలో శక్తిని గణించండి. ఆ కక్ష్య వ్యాసార్ధం ఎంత ?
జవాబు:

ప్రశ్న 12.
10ms^-1 వేగంతో చలించే 0.1 kg బంతి తరంగదైర్ఘ్యం ఎంత ?
జవాబు:
డీబ్రోలీ సమీకరణం ప్రకారం
λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) = \(\frac{\left(6.626 \times 10^{-34} \mathrm{Js}\right)}{(0.1 \mathrm{~kg})\left(10 \mathrm{~ms}^{-1}\right)}\) = 6.626 × 10^-34 m (J = kg m² s^-2)

ప్రశ్న 13.
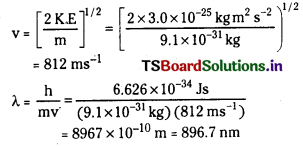
ఎలక్ట్రాన్ ద్రవ్యరాశి 9.1 × 10^-3 kg దాని గతిజశక్తి 3.0 × 10^-25 J. దాని తరంగదైర్ఘ్యాన్ని లెక్కించండి.
జవాబు:

ప్రశ్న 14.
3.6 À తరంగదైర్ఘ్యం గల ఫోటాన్ ద్రవ్యరాశిని గణించండి.
జవాబు:
λ = 3.6 Å = 3.6 × 10^-10 m
ఫోటాన్ వేగం = కాంతి వేగం
m = \(\frac{\mathrm{h}}{\mathrm{mv}}\) = \(\frac{6.626 \times 10^{-34} \mathrm{Js}}{\left(3.6 \times 10^{-10} \mathrm{~m}\right)\left(3 \times 10^8 \mathrm{~ms}^{-1}\right)}\) = 6.135 × 10^-29 kg

ప్రశ్న 15.
సరియైన ఫోటాన్లను ఉపయోగించి మైక్రోస్కోప్ ద్వారా పరమాణువులో ఉన్న ఎలక్ట్రాన్ను 0.1 A దూరం లోపల చూడగలిగారు. దాని వేగం కొలతలో ఉన్న అనిశ్చితత్వం ఎంత ?
జవాబు:
Δx. Δp = \(\frac{\mathrm{h}}{4 \pi}\) లేదా Δx mΔv = \(\frac{\mathrm{h}}{4 \pi}\)
Δv = \(\frac{h}{4 \pi \Delta x m}\)
Δv = \(\frac{6.626 \times 10^{-34} \mathrm{Js}}{4 \times 3.14 \times 0.1 \times 10^{-10} \mathrm{~m} \times 9.11 \times 10^{-31} \mathrm{~kg}}\)
= 0.579 × 10⁷ ms^-1 (1 J = 1 kg m² s^-2)
= 5.79 × 10⁶ ms^-1

ప్రశ్న 16.
గల్ఫ్ బంతి ద్రవ్యరాశి 40 g. దాని వేగం 45 m/s. దాని వేగాన్ని 2% లోపల కొలవగలిగినట్లయితే దాని స్థానంలో అనిశ్చితత్వం ఎంత ?
జవాబు:
వేగంతో అనిశ్చితత్వం 2% అంటే

ఈ విలువ పరమాణు కేంద్రకం వ్యాసం కంటే -1018 రెట్లు చిన్నది. ఇంతకు ముందు చెప్పినట్లు పెద్ద కణాలకు అనిశ్చితత్వ నియమం కచ్చితమైన కొలతలకు అర్థవంతమైన అవధులు పెట్టలేదు.

ప్రశ్న 17.
ప్రధాన క్వాంటం సంఖ్య n = 3 తో ఉన్న మొత్తం ఆర్బిటాళ్ళ సంఖ్య ఎంత ?
జవాబు:
n = 3.కు సాధ్యమైన l విలువలు 0, 1, 2. ఆ విధంగా ఒక 3s ఆర్బిటాల్ (n = 3, l = 0, m_l = 0); మూడు 3p ఆర్బిటాల్ (n = 3, l = 1, m_l = – 1, 0, + 1); అయిదు 3d ఆర్బిటాల్లు (n = 3, l = 2, m_l = -2, -1, 0, +1, +2)
∴ మొత్తం ఆర్బిటాల్ల సంఖ్య = 1 + 3 + 5 = 9
ఇదే విలువను వేరే విధంగా పొందవచ్చు.
ఆర్బిటాల్ల సంఖ్య = n² = 3² = 9.

ప్రశ్న 18.
s, p, d, f సంకేతాలను ఉపయోగించి కింది క్వాంటం సంఖ్యలతో ఆర్బిటాల్లను వర్ణించండి.
a) n = 2, l = 1
b) n = 4, l = 0
c) n = 5, l = 3
d) n = 3, l = 2
జవాబు:

ప్రశ్న 19.
హైసెస్బర్గ్ అనిశ్చితత్వ నియమాన్ని రాసి వివరించండి.
జవాబు:
హైస్బెర్గ్ అనిశ్చితత్వ నియమం : “అతి వేగంగా ప్రయాణించే ఎలక్ట్రాన్ వంటి సూక్ష్మ పరమాణు కణాల స్థానం, ద్రవ్యవేగం రెండింటినీ ఏక కాలములో ఖచ్చితంగా నిర్ణయించలేము.
వివరణ : తరంగ యాంత్రికశాస్త్రం యొక్క ప్రధాన సూత్రాలలో హైసెన్బర్గ్ అనిశ్చితత్వ నియమం ఒకటి.
సూక్ష్మకణం యొక్క స్థానం నిర్ణయంలో అనిశ్చితత్వం Δx, ద్రవ్యవేగంలో అనిశ్చితత్వం Δp అయితే,
(Δx) (Δp) ≥ \(\frac{h}{n \pi}\) (ఇక్కడ n = 1, 2, 3, 4, ……)
పరమాణు కేంద్రకం చుట్టూ తిరిగే ఎలక్ట్రాన్ విషయంలో n విలువ దాదాపు 4. కాబట్టి
(Δx) (Δp) ≥ \(\frac{\mathrm{h}}{4 \pi}\)
లేదా (Δx) Δ (mV_x) ≥ \(\frac{\mathrm{h}}{4 \pi}\)
లేదా Δx. Δv_x ≥ \(\frac{\mathrm{h}}{4 \pi \mathrm{m}}\)
దీన్ని బట్టి, Δx = 0 అయితే, అనగా ఎలక్ట్రాన్ స్థానాన్ని కచ్చితంగా కనుగొంటే, Δv_x = అనగా ఎలక్ట్రాన్ వేగాన్ని కచ్చితంగా అసలు కనుగొనలేము.
Δv_x = 0 అయితే, Δx = ∞ అవుతుంది.
అనగా ఎలక్ట్రాన్ వేగాన్ని కచ్చితంగా కనుగొంటే ఎలక్ట్రాన్ స్థానాన్ని కచ్చితంగా అసలు కనుగొనలేము.

అనిశ్చిత నియమం ప్రాముఖ్యత :

1. ఈ నియమం ప్రకారం, ఎలక్ట్రాన్కు గాని, ఎలక్ట్రాన్ లాంటి ఇతర కణాలకు గాని స్థిరమైన కక్ష్య లేదా ప్రక్షేప మార్గం ఉండే అవకాశం లేదు.
2. ఈ నియమం సూక్ష్మాతి సూక్ష్మ కణాలకు మాత్రమే వర్తిస్తుంది. స్థూల కణాలకు వర్తించదు.
3. మిల్లీ గ్రాము లేదా అంతకుమించి బరువు గల పదార్థాలలో గల అనిశ్చితత్వానికి ప్రాముఖ్యత ఏమీ ఉండదు.

ప్రశ్న 20.
ప్రోడింగర్ సమీకరణం రాసి దానిలోని పదాలను వివరించండి.
జవాబు:
ప్రోడింగర్ తరంగ సమీకరణం :
\(\frac{\partial^2 \Psi}{\partial x^2}\) + \(\frac{\partial^2 \Psi}{\partial y^2}\) + \(\frac{\partial^2 \Psi}{\partial z^2}\) + \(\frac{8 \pi^2 \mathrm{~m}}{\mathrm{~h}^2}\)(E – V)ψ = 0
పై సమీకరణంలో,
m = ఎలక్ట్రాన్ ద్రవ్యరాశి; E = ఎలక్ట్రాన్ మొత్తం శక్తి (P.E + K.E);
V = ఎలక్ట్రాన్ స్థితిజశక్తి (P.E.);
(E – V) = ఎలక్ట్రాన్ గతిజశక్తి;
ψ = తరంగ ప్రమేయము.
x, y, z లు త్రిమితీయ ప్రదేశంలో కార్టీజియన్ అక్షాలు.

ψ అర్థం, దాని ప్రాముఖ్యం :

1. ψ అనేది, ఆమోదయోగ్యమైన తరంగ ప్రమేయాన్ని సూచిస్తుంది. దీనినే ఐగన్ తరంగ ప్రమేయమంటారు.
2. అది ఎలక్ట్రాన్ తరంగం యొక్క డోలన పరిమితిని తెలియజేస్తుంది.
3. అక్షానికి పైన ψ కి ధన విలువ, అక్షానికి క్రింద ఋణ విలువ మరియు అక్షాన్ని దాటిపోవునపుడు శూన్య విలువలు ఉంటాయి.
   
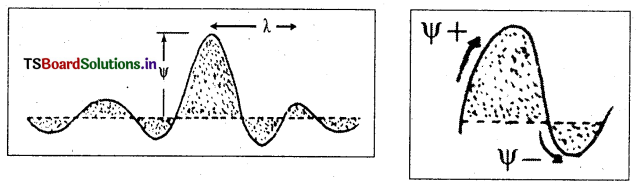
4. ψ విలువ అవిచ్ఛిన్నంగా ఉండాలి.
5. ψ విలువ నిశ్చితంగా ఉండాలి.
6. ψ కి ఏ బిందువు వద్దనైనా ఒకే విలువ ఉండాలి.
7. + ∞ నుంచి -∞ వరకు ఉండే త్రిమితీయ ప్రదేశంలో ఎలక్ట్రాన్ సంభావ్యత ఒకటి అయి ఉండాలి.

ψ² ప్రాముఖ్యత :

1. ఇది సంభావ్యతా ప్రమేయము.
2. ψ విలువ ధనాత్మకం లేదా ఋణాత్మకం కావచ్చు. కాని ఆ విలువ ఎప్పుడూ ధనాత్మకమే.
3. పరమాణువులోని కేంద్రకం చుట్టూ, ఎలక్ట్రాన్ ను కనుగొనే సంభావ్యత గరిష్ఠంగా ఉన్న ప్రదేశాన్ని ఆర్బిటాల్ అంటారు. అక్కడ ψ² విలువ గరిష్ఠము.

ప్రశ్న 21.
ఆఫ్ నియమం అంటే ఏమిటి ? ఆర్బిటాల్లో ఎలక్ట్రానులు నింపే క్రమాన్ని వివరించండి.
జవాబు:
ఆఫ్ నియమం ప్రకారం “ఎలక్ట్రాన్లు భూస్థాయిలో అందుబాటులో ఉండే కనిష్ఠశక్తి ఆర్బిటాళ్ళలోనికి ప్రవేశించడానికి ప్రయత్నిస్తాయి. శక్తి పెరిగే క్రమంలో ఈ ఆర్బిటాల్లు వరుసగా ఎలక్ట్రాన్లతో భర్తీ అవుతాయి”. పరమాణువులలోని ఆర్బిట్లో ఎలక్ట్రాన్లు వాటి శక్తి విలువల ఆరోహణ క్రమంలో ప్రవేశిస్తాయి. పరమాణువులలోని ఆర్బిటాళ్ళ శక్తి క్రమాన్ని మాయిలర్ రేఖా చిత్రం సహాయంతో కనుగొనవచ్చు. లేక (n + l) విలువలు సహాయంతో కూడ కనుగొనవచ్చును. 2 లేక అంతకన్న ఎక్కువ ఆర్బిటాళ్ళకు (n + l) విలువలు సమానంగా ఉన్నట్లైతే, వాటిలోనికి ఎలక్ట్రాన్లను పంపించేటప్పుడు వాటి n విలువల ఆరోహణ క్రమాన్ని పాటించాలి.

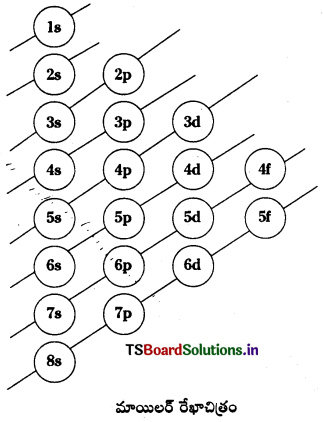
మాయిలర్ రేఖాచిత్రం ప్రకారం ఆర్బిటాళ్ళ శక్తి విలువల ఆరోహణ క్రమం ఈ క్రింది విధంగా ఉంటుంది.
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d <5p < 6s < 4f <5d < 6p < 7s < 5f < 6d < 7p < 8s

ప్రశ్న 22.
పౌలి వర్ణన నియమాన్ని రాసి వివరించండి.
జవాబు:
పౌలి వర్ణన సూత్రం : “ఒకే పరమాణువులో ఉండే ఏ రెండు ఎలక్ట్రాన్లకైనా ఒకే విలువలు గల నాల్గు క్వాంటం సంఖ్యలు ఉండటానికి వీల్లేదు”. దీన్ని ఇంకొక విధంగా కూడా నిర్వచిస్తారు. “ఒక ఆర్బిటాల్ రెండు ఎలక్ట్రాన్లను మాత్రమే అత్యధికంగా తీసుకోగల్గుతుంది”.
వివరణ : ఒక ఆర్బిటాల్లో గల రెండు ఎలక్ట్రానులు ఒకే n, l, m విలువలు కల్గి ఉన్నప్పటికి ఈ నియమం ప్రకారం కనీసం అవి s విలువలలో అయినా భేదిస్తాయి. అనగా ఆ రెండు ఎలక్ట్రానులకు వ్యతిరేక స్పిన్లు ఉంటాయి.

ఉపయోగాలు :

1. భూస్థాయిలో పరమాణు ఎలక్ట్రాన్ విన్యాసం వ్రాయడానికి ఈ సూత్రం సహకరిస్తుంది.
2. ఒక ప్రధాన కర్పరం లేదా ఒక ఉపకర్పరం లేదా ఒక ఆర్బిటాల్లో ఉండగల ఎలక్ట్రాన్ల గరిష్ఠసంఖ్యను తెల్సుకోడానికి పౌలివర్జన సూత్రం సహాయపడుతుంది.
   ఉదా : n = 2 లో 4 ఆర్బిటాళ్లుంటాయి. కాబట్టి వానిలోని ఎలక్ట్రాన్ల గరిష్ఠసంఖ్య = 4 × 2 = 8.

ప్రశ్న 23.
హుండ్ గరిష్ఠ బాహుళ్యతా నియమం రాసి వివరించండి.
జవాబు:
హుండ్ గరిష్ఠ బాహుళ్యతా నియమం: సమాన శక్తి గల ఆర్బిటాళ్ళలో ఎలక్ట్రాన్ విన్యాసాలను వివరించడానికి ఈ నియమము వర్తిస్తుంది.
“సమాన n, l విలువలు గల సమశక్తి (డీ జనరేట్) ఆర్బిటాళ్ళ సమితిలో అందుబాటులో ఉండే ఆర్బిటాళ్ళలో మొదటగా సమాంతర స్పిన్ల ఒక్కొక్క ఎలక్ట్రాన్ చేరిన తర్వాత మాత్రమే ఎలక్ట్రాన్లు జతకూడతాయి”.
వివరణ : ఈ నియమాన్ని క్రింది ఉదాహరణలతో వివరించవచ్చు.

ప్రశ్న 24.
3d¹ ఎలక్ట్రాన్ నాల్గు క్వాంటం సంఖ్యలు వ్రాయండి.
జవాబు:
n = 3,
l = 2;
m = -2;
s = +\(\frac{1}{2}\)

ప్రశ్న 25.
ఎలక్ట్రాన్ విన్యాసం అంటే ఏమిటి ? సోడియం పరమాణువు ఎలక్ట్రాన్ విన్యాసం వ్రాయండి.
జవాబు:
ఒక పరమాణువు భూస్థాయిలో దాని ప్రధాన కర్పరాలు, ఉపకర్పరాలు, ఉప-ఉపకర్పరాల (ఆర్బిటాల్ల)లో ఎలక్ట్రాన్ల పంపిణీ, అమరికను, ఆ మూలక పరమాణువు ఎలక్ట్రాన్ విన్యాసం అంటారు.
ఎలక్ట్రాన్ విన్యాసాన్ని nl^X పద్ధతిలో వ్రాస్తారు.
Na (Z = 11) 1s²2s²2p⁶3s¹.

ప్రశ్న 26.
క్రోమియం, కాపర్ ఎలక్ట్రాన్ల విన్యాసంలో ప్రత్యేక లక్షణాలు ఎందుకు ఉన్నాయి ?
జవాబు:
శక్తి స్థాయిల క్రమం ఆధారంగా క్రోమియం ఎలక్ట్రాన్ విన్యాసం :
Cr (Z = 24) 1s²2s²2p⁶3s²3p⁶3d⁴4s² గా రాయాలి. కాని ప్రయోగ ఫలితాల ఆధారంగా ఇట్లా వ్రాస్తారు.
కారణం : డీజనరేట్ ఆర్బిటాళ్లు అయిదు కూడా సమాంతర స్పిన్లు గల ఒక్కొక్క ఎలక్ట్రాన్తో సగం నిండితే దీనికి స్థిరత్వం వస్తుంది. అందువలన ఒక ఎలక్ట్రాను 4s నుంచి 3d కి బదిలీ అవుతుంది.

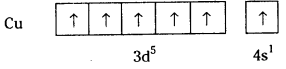
ఇదే విధంగా కాపర్ యొక్క ఎలక్ట్రాన్ విన్యాసం Cu (Z = 29) 1s²2s²2p⁶3s²3p⁶3d⁹4s² కు బదులుగా 1s²2s²2p⁶3s²3p⁶3d¹⁰4s¹ గా ఉంటుంది. అనగా అందుబాటులో గల అన్ని d ఆర్బిటాళ్ళు పూర్తిగా రెండేసి ఎలక్ట్రాన్లతో నిండి అధిక స్థిరత్వాన్ని పొందుతుంది. అందువలన 4s నుంచి 3d కి ఒక ఎలక్ట్రాన్ బదిలీ అవుతుంది.

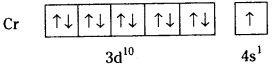
పూర్తిగా లేదా సగం నిండిన ఉపకర్పరాల స్థిరత్వానికి కారణం :

1. స్థిరత్వానికి మూలకారణం, సౌష్ఠవము (Symmetry). సగం లేదా పూర్తిగా ఎలక్ట్రాన్లతో నిండిన ఉపకర్పరాలలో ఎలక్ట్రాన్లు సౌష్ఠవంగా పంచబడి ఉంటాయి. అందువల్ల పరమాణువుకు స్థిరత్వం వస్తుంది.
2. డీజనరేట్ ఆర్బిటాళ్లలో సమాంతర స్పిన్లు గల ఎలక్ట్రాన్లు ఉన్నపుడు, అవి పరస్పరం వాటి స్థానాలను మార్చుకుంటాయి. ఈ మార్పు వల్ల ఎలక్ట్రాన్ శక్తి తగ్గుతుంది. సమాంతర స్పిన్లు గల ఎలక్ట్రాన్లు అధికంగా ఉన్నపుడు, ఈ మార్చుకొనే అవకాశం అధికంగా ఉంటుంది. అందువల్ల ఉపకర్పరాలలో ఎలక్ట్రానులకు స్థిరత్వం అధికంగా ఉంటుంది.

ప్రశ్న 27.
డీబ్రోలీ సిద్ధాంత ప్రాముఖ్యాన్ని విపులీకరించండి.
జవాబు:
“అధిక వేగంతో ప్రయాణించే ఎలక్ట్రాన్తో సహా అన్ని సూక్ష్మ కణాలకూ తరంగ స్వభావం ఉంటుందని” 1924 లో డీబ్రోలీ ప్రతిపాదించాడు.

వివరణ : అతి వేగంతో ప్రయాణించే ఎలక్ట్రాన్లు, ప్రోటాన్లు, పరమాణువుల వంటి సూక్ష్మ కణాలకూ అణువులకూ సైతం కణ స్వభావం, తరంగ స్వభావం రెండూ (ద్వంద్వ) ఉంటాయి.
డీబ్రోలీ తరంగ సమీకరణం, λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\)
ఇందులో, h = ప్లాంక్ స్థిరాంకం; λ = డీబ్రోలీ తరంగదైర్ఘ్యం.
బోర్ పరమాణు నమూనా ప్రకారం, పరమాణువులోని ఎలక్ట్రాన్ యొక్క కోణీయ ద్రవ్యవేగం క్వాంటీకరణం చెందుతుంది.
అనగా
mνr = \(\frac{\mathrm{nh}}{2 \pi}\) (బోర్ సమీకరణం)

ఈ సమీకరణాన్ని, డీబ్రోలీ ప్రతిపాదించిన ఎలక్ట్రాన్ యొక్క తరంగ స్వభావ భావన నుండి రాబట్టవచ్చు.
డీబ్రోలీ ప్రకారం, ఎలక్ట్రాన్ ఒక స్థిర తరంగాన్ని ఏర్పరుస్తుంది. అప్పుడు, బోర్కక్ష్య యొక్క చుట్టుకొలత (2πr), ఎలక్ట్రాన్ తరంగం యొక్క తరంగదైర్ఘ్యం యొక్క పూర్ణాంక గుణకానికి సమానమవ్వాలి.
అనగా, 2πr = nλ లేదా λ = \(\frac{2 \pi \mathrm{r}}{\mathrm{n}}\) కాని λ = \(\frac{\mathrm{h}}{\mathrm{mv}}\) (డీబ్రోలీ సమీకరణం)
∴ \(\frac{2 \pi r}{n}\) = \(\frac{\mathrm{h}}{\mathrm{mv}}\) లేదా mvr = \(\frac{\mathrm{nh}}{2 \pi}\) (బోర్ సమీకరణం)

ప్రశ్న 28.
నోడల్ తలం అంటే ఏమిటి ? p, d ఆర్బిటాళ్ళలో ఎన్ని నోడల్ తలాలు ఉంటాయి ?
జవాబు:
ఒక పరమాణువులోని కేంద్రకం వద్ద ఎలక్ట్రాన్ను కనుగొనే సంభావ్యత అత్యంత అల్పము లేదా దాదాపు శూన్యము. ఈ బిందువును నోడల్ బిందువు అంటారు. నోడల్ బిందువు గుండాపోయే తలాన్ని నోడల్ తలం అంటారు. దీనినే కోణీయ నోడ్ అంటారు. అనగా ఎలక్ట్రాన్ సాంద్రత శూన్యంగా గల తలాన్ని నోడల్ తలమంటారు.
ఒక ఆర్బిటాలు, దాని ఎజిముతల్ క్వాంటం విలువతో సమానమైన సంఖ్యలో నోడల్ తలాలుంటాయి.

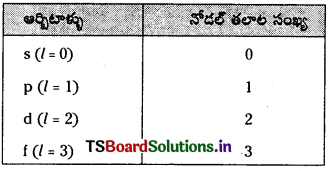
ప్రశ్న 29.
పరమాణు ఎలక్ట్రాన్ నిర్మాణంలో స్పిన్ క్వాంటం సంఖ్య ప్రాముఖ్యం ఏమిటి ?
జవాబు:

1. మూలకాల వర్ణపటాలలోని జంటరేఖలను (doublets) మరియు మూడు రేఖల సముదాయాలను (triplets) వివరించడానికి గౌడ్స్మిత్ మరియు ఉలెన్బెక్ అనే శాస్త్రవేత్తలు స్పిన్ క్వాంటం సంఖ్యను ప్రవేశపెట్టినారు.
2. ప్రోడింగర్ తరంగ సమీకరణం సాధన నుండి స్పిన్ క్వాంటం సంఖ్యను పొందలేము.
   
3. ఎలక్ట్రాన్ తన అక్షం చుట్టూ తాను ఆత్మభ్రమణం చేస్తూ కేంద్రకం చుట్టూ కక్ష్యలో తిరుగుతుంటుంది.
4. దీని ఫలితంగా ఎలక్ట్రాన్ యొక్క స్పిన్ క్వాంటీకరణం చెందుతుంది. అనగా స్పిన్కు నిర్దిష్ట కోణీయ ద్రవ్యవేగం విలువలు మాత్రమే ఉంటాయి.
5. స్పిన్ యొక్క కోణీయ ద్రవ్యవేగం విలువలు సవ్యదిశలో + \(\frac{1}{2}\left(\frac{\mathrm{h}}{2 \pi}\right)\) మరియు అపసవ్య దిశలో
   –\(\frac{1}{2}\left(\frac{\mathrm{h}}{2 \pi}\right)\)లు.
6. మిగతా మూడు క్వాంటం సంఖ్యల మాదిరిగానే, రెండు వరుస స్పిన్ క్వాంటం సంఖ్యల తేడా 1 అనగా
   + \(\frac{1}{2}\) – (-\(\frac{1}{2}\)) = 1
7. ఒక ఆర్బిటాల్లో, పరస్పరం వ్యతిరేక దిశల్లో ఆత్మభ్రమణం చేసే రెండు ఎలక్ట్రాన్లు మాత్రమే ఉండగలవు (పౌలి వర్జన సూత్రము).

Here students can locate TS Inter 1st Year Chemistry Notes 1st Lesson పరమాణు నిర్మాణం to prepare for their exam.

TS Inter 1st Year Chemistry Notes 1st Lesson పరమాణు నిర్మాణం

→ ఉత్సర్గనాళ ప్రయోగం ద్వారా విడుదలైన కాథోడ్ కిరణాలను విద్యుత్, అయస్కాంత క్షేత్రాలలో ఉంచినపుడు వాటి ప్రవర్తన రుణ విద్యుదాత్మక కణాల ప్రవర్తనను పోలి ఉంది. వీటినే ఎలక్ట్రానులు అంటారు.

→ అన్ని పరమాణువులకు, ఎలక్ట్రానులు, ప్రోటానులు, న్యూట్రానులు ప్రాథమిక కణాలు. * ఎలక్ట్రాన్ ద్రవ్యరాశి 9.10939 x 10^-31 kg .

→ ఎలక్ట్రాన్ ఆవేశం –1.6022 × 10^-19 coulomb

→ ప్రోటాన్ ద్రవ్యరాశి 1.67262 × 10^-27 kg
ప్రోటాన్ ఆవేశం +1.6022 × 10^-19 coulomb

→ న్యూట్రాన్ ద్రవ్యరాశి 1.67493 × 10^-27 kg న్యూట్రాన్ ఆవేశం 0

→ ఎలక్ట్రాన్ \(\frac{e}{m}\) విలువ 1.758820 × 10¹¹ c.kg^-1

→ ఒకే ద్రవ్యరాశి సంఖ్య ఉండి పరమాణు సంఖ్య వేరుగా ఉన్న పరమాణువులను ఐసోబార్లు అంటారు. ఉదా : ¹⁴₆C, ¹⁴₇N

→ ఒకే పరమాణు సంఖ్య కలిగి వేర్వేరు ద్రవ్యరాశి సంఖ్యలు గల పరమాణువులను ఐసోటోపులు అంటారు.

→ రూథర్ ఫర్డ్ పరమాణు నమూనా ప్రకారం పరమాణువులోని ధనావేశం, ద్రవ్యరాశి అంతా కొద్ది ప్రాంతంలో కేంద్రీకృతమై ఉంటుంది. దీనినే కేంద్రకం అంటారు.

→ కేంద్రకం చుట్టూ ఎలక్ట్రానులు వృత్తాకార కక్ష్యలలో తిరుగుతూ ఉంటాయి.

→ న్యూట్రానుల సంఖ్య = ద్రవ్యరాశి సంఖ్య – పరమాణు సంఖ్య

→ ఆవేశిత కణాలు త్వరణం చెందుట వలన ఏకాంతర విద్యుత్, అయస్కాంతక్షేత్రాలు ఉత్పత్తి అయి ప్రసారం అవుతాయి.

→ Maxwell కాంతి తరంగాలు విద్యుత్ అయస్కాంత లక్షణాల డోలనంతో కూడి ఉంటాయని తెలిపేను.

→ కాంతి విద్యుత్ ప్రభావం ఎలక్ట్రానుల కణ స్వభావాన్ని సూచిస్తుంది.

→ కాంతికి తరంగ స్వభావం అనువర్తిస్తే- వివర్తనం, వ్యతికరణం ‘దృగ్విషయాలను వివరించవచ్చు. అంటే కాంతికి ద్వంద్వ స్వభావం ఉంటుంది.

→ పదార్థం శోషించుకొన్న శక్తిని ఉద్గారించే వికిరణాల వర్ణపటాలను ఉద్గార వర్ణపటం అంటారు.

→ హైడ్రోజన్ వర్ణపటంలో లైమన్, చామర్, పాషన్, బ్రాకెట్, ఫండ్ శ్రేణులు తరంగ సంఖ్యలను రిబ్బర్గ్ సమీకరణం ద్వారా గణించవచ్చు.
υ = 1.09677 × 10⁷\(\left(\frac{1}{n_1^2} \frac{-1}{n_2^2}\right)\)m^-1

→ బోర్ నమూనా ప్రకారం స్థిర వ్యాసార్థాలు గల వృత్తాకార కక్ష్యలలో నిర్ణీత శక్తులతో ఎలక్ట్రాన్లు తిరుగుతూ ఉంటాయి.

→ హైడ్రోజన్ వర్ణపట సూక్ష్మ నిర్మాణాన్ని బోర్ నమూనా వివరించలేకపోయింది.

→ కాంతి వలెనే పదార్థానికి కూడా ద్వంద్వ స్వభావం వర్తిస్తుందని డీబ్రోలి ప్రతిపాదించెను. పదార్థ కణాల ద్రవ్యవేగానికి, తరంగదైర్ఘ్యానికి సంబంధం
λ = \(\frac{h}{m v}=\frac{h}{p}\)
m = కణ ద్రవ్యరాశి v = కణవేగం P = ద్రవ్యవేగం

→ ఎలక్ట్రాన్ వివర్తన ప్రయోగం ద్వారా ఎలక్ట్రాన్ తరంగ స్వభావం నిర్ధారించబడింది. ఎలక్ట్రాన్ తరంగ స్వభావంపై ఆధారపడి ఎలక్ట్రాన్ మైక్రోస్కోపు నిర్మించబడింది.

→ ఎలక్ట్రాన్ వంటి సూక్ష్మకణం స్థానాన్ని, ద్రవ్యవేగాన్ని ఒకేసారి ఖచ్చితంగా ఏకకాలంలో నిర్ణయించడం అసాధ్యం.
ΔX. Δp ≥ \(\frac{\mathrm{h}}{4 \pi}\)

→ హైసెన్ బర్గ్ నియమం ప్రకారం బోర్ స్థిరకక్ష్యల భావన సరైనది కాదు.

→ క్వాంటం యాంత్రికశాస్త్రం సూక్ష్మాతిసూక్ష్మమైన తరంగ, కణస్వభావాలు గల కణాల చలనాలను వివరిస్తుంది.

→ ఒక వ్యవస్థకు ప్రోడింగర్ సమీకరణం
\(\frac{\partial^2 \Psi}{\partial \mathrm{x}^2}+\frac{\partial^2 \Psi}{\partial \mathrm{y}^2}+\frac{\partial^2 \psi}{\partial \mathrm{z}^2}+\frac{8 \pi^2 \mathrm{~m}}{\mathrm{~h}^2}\)(E – V)Ψ = 0
Ψ అనునది తరంగ ప్రమేయం. ప్రతి శక్తి స్థాయికి సహచరితమైన తరంగ ప్రమేయం ఉంటుంది.

→ పరమాణువులో ఒక నిర్దిష్టమైన బిందువు వద్ద ఎలక్ట్రానును కనుక్కొనే సంభావ్యత ఆ బిందువు వద్ద |Ψ|² కి అనులోమానుపాతంలో ఉంటుంది.

→ హైడ్రోజన్ గాని, హైడ్రోజన్ లాంటి ఒక ఎలక్ట్రాన్ గల కణాల యొక్క తరంగ ప్రమేయ వర్గాన్ని పరమాణు ఆర్బిటాల్ అంటారు.

→ క్వాంటం సంఖ్యలు పరమాణు ఆర్బిటాలుల తారతమ్యాలను తెలుపును.

→ ప్రధాన క్వాంటం సంఖ్య n కు సరళ పూర్ణాంక విలువలు ఉంటాయి. n = 1, 2, 3,…………. ఇది ఆర్బిటాల్ పరిమాణాన్ని, దాదాపుగా దాని శక్తినీ తెలుపుతుంది.

→ ప్రతీ శక్తి స్థాయికీ ఉపశక్తి స్థాయిలుంటాయి. వీటిని ఎజిమూతల్ క్వాంటం సంఖ్య l చే సూచిస్తారు. lకి n విలువలు ఉంటాయి. అవి 0 నుండి (n – 1) వరకు ఉంటాయి. అయస్కాంతక్షేత్రంలో వర్ణపటరేఖల సూక్ష్మవిభజనను జీమన్ ఫలితం అంటారు. ఈ విషయాన్ని అయస్కాంత క్వాంటం సంఖ్య వివరిస్తుంది. దీనిని ‘m’ చే సూచిస్తారు. ml కు సాధ్యపడే విలువలు 2l + 1.
m₁ = -l, – (l – 1), – (l – 2),…………..0, l ………….(l – 2)(l – 1), l

→ ఈ మూడు క్వాంటం సంఖ్యలు బహు ఎలక్ట్రాన్ల పరమాణువుల వర్ణపట రేఖలను వివరించడానికి చాలవు. అందువల్ల 4వ క్వాంటం సంఖ్య అవసరం. దానినే ఎలక్ట్రాన్ స్పిన్ క్వాంటం సంఖ్య m_s య అంటారు. ఎలక్ట్రాన్ ఆత్మ ప్రదక్షిణ దిశ సవ్యదిశ స్పిన్ క్వాంటం సంఖ్య S = +\(\frac{1}{2}\) అపసవ్యదిశ అయితే S = –\(\frac{1}{2}\)

→ ఏ ప్రదేశాలలోనైతే ఎలక్ట్రాన్ సంభావ్యతా సాంద్రత ప్రమేయం విలువ సున్నాకు తగ్గుతుందో వాటిని నోడల్ తలాలు లేదా నోడ్లు అంటారు.

→ ఆఫ్గ నియమం : భూస్థాయిలో ఉన్న పరమాణువులోని ఆర్బిటాల్లను వాటి శక్తులు పెరిగే క్రమంలో ఎలక్ట్రాన్లతో భర్తీ చేయాలి.

→ పౌలివర్ణన సూత్రం : ఒకే పరమాణువులో ఏ రెండు ఎలక్ట్రాన్లకైనా ఒకే సమితి గల నాలుగు క్వాంటం సంఖ్యలు ఉండకూడదు.

→ హుండ్ గరిష్ట బాహుళ్యతా నియమం : ఉపకర్పరంలో గల ప్రతి సమశక్తి (డీజనరేటి) ఆర్బిటాల్లోకి ఒక్కొక్క ఎలక్ట్రాన్ చేరేంతవరకు అదే ఉపకర్పరం (p, d, f) లోని ఆర్బిటాల్లో ఎలక్ట్రాన్ జతగూడటం జరగదు. అంటే ముందు ఒక్కొక్కటి చేరాలి.

→ సగం నిండిన లేదా పూర్తిగా నిండిన ఉపకర్పరాలకు అధిక స్థిరత్వానికి కారణం సౌష్ఠవంగా ఉండడంవల్ల

• సాపేక్షంగా తక్కువ కవచం ఉండడం,
• కులంబిక్ వికర్షణ శక్తి స్వల్పంగా ఉండడం
• మార్చుకొనే శక్తి అధికంగా ఉండటం.

→ s – ఆర్బిటాల్ గోళాకారంలో ఉంటుంది. p – ఆర్బిటాల్ డంబెల్ ఆకారంలో ఉంటుంది. d- ఆర్బిటాల్ డబుల్ డంబెల్ ఆకారంలో ఉంటుంది.

→ సమాన శక్తిగల ఆర్బిటాళ్లను డీజనరేట్ ఆర్బిటాళ్లు అంటారు.

→ బలమైన విద్యుత్ క్షేత్రంలో వర్ణపట రేఖల సూక్ష్మ విభజనను స్టార్క్ ఫలితం అంటారు.

→ క్రోమియం ఎలక్ట్రాన్ విన్యాసం 1s² 2s² 2p⁶ 3s² 3p⁶ 3d⁵ 4s¹
కాపర్ ఎలక్ట్రాన్ విన్యాసం 1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰ 4s¹

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Limits and Continuity Important Questions Short Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Limits and Continuity Important Questions Short Answer Type

Question 1.
Is the function f, defined by f(x) = \(\left\{\begin{array}{l}
x^2 \text { if } x \leq 1 \\
x \text { if } x>1
\end{array}\right.\), continuous on R. [May ’15 (AP), ’11]
Solution:
We find the limit at a = 1

∴ f is continuous at x = 1
Hence f is continuous on R.

Question 2.
Is f defined by f(x) = \(\begin{cases}\frac{\sin 2 x}{x} & \text { if } x \neq 0 \\ 1, & \text { if } x=0\end{cases}\), continuous on ‘0’? [May ’12, ’10, ’04; Mar. ’05]
Solution:
Given, f(x) = \(\begin{cases}\frac{\sin 2 x}{x} & \text { if } x \neq 0 \\ 1, & \text { if } x=0\end{cases}\)
Take a = 0

∴ f is discontinuous at x = 0.

Question 3.
Check the continuity of the following function at 2.
f(x) = \(\begin{cases}\frac{1}{2}\left(x^2-4\right) & \text { if } 0<x<2 \\ 0, & \text { if } x=2 \\ 2-8 x^{-3}, & \text { if } x>2\end{cases}\). [Mar. ’19 (TS): Mar. ’17 (AP): May ’15 (TS), ’08]
Solution:

Question 4.
Check the continuity of f given by f(x) = \(f(x)= \begin{cases}\frac{x^2-9}{x^2-2 x-3} & \text { if } 0<x<5 \text { and } x \neq 3 \\ 1.5 & \text { if } x=3\end{cases}\) at the point 3. [Mar. ’15 (AP), ’14, ’13, ’02; May ’04]
Solution:

Question 5.
Prove that the functions sin x and cos x are continuous on R. [May ’08]
Solution:
(i) Let f(x) = sin x and a ∈ R
\(\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} \sin x\) = sin a = f(a)
∴ \(\lim _{x \rightarrow a} f(x)\) = f(a)
∴ f is continuous at x = a
∴ Since a is arbitrary, f is continuous on R.
(ii) Let g(x) = cos x and a ∈ R
\(\lim _{x \rightarrow a} g(x)=\lim _{x \rightarrow a} \cos x\) = cos a = g(a)
∴ \(\lim _{x \rightarrow a} g(x)\) = g(a)
∴ g is continuous at x = a
∴ since a is arbitrary, g is continuous on R.

Question 6.
Find real constants a, b so that the function f is given by f(x) = \(\begin{cases}\sin x & \text { if } x \leq 0 \\ x^2+\mathbf{a} & \text { if } 0<x<1 \\ \mathbf{b x}+3 & \text { if } 1 \leq x \leq 3 \\ -3 & \text { if } x>3\end{cases}\) is continuous on R. [Mar. ’18 (AP & TS); May ’13]
Solution:
Given, f(x) = \(\begin{cases}\sin x & \text { if } x \leq 0 \\ x^2+\mathbf{a} & \text { if } 0<x<1 \\ \mathbf{b x}+3 & \text { if } 1 \leq x \leq 3 \\ -3 & \text { if } x>3\end{cases}\)
Since f is continuous on R.
f is continuous at 0, 3.

Since f is continuous at x = 3 then
LHL = RHL
3b + 3 = -3
3b = -3 – 3
b = -2
∴ a = 0, b = -2

Question 7.
Show that f(x) = \(\left\{\begin{array}{cl}
\frac{\cos a x-\cos b x}{x^2} & \text { if } x \neq 0 \\
\frac{1}{2}\left(b^2-a^2\right) & \text { if } x=0
\end{array}\right.\) where a and b are real constants, is continuous at ‘0’. [Mar. ’17 (TS), ’13(old), ’09; May ’14; B.P.]
Solution:

Some More Maths 1B Limits and Continuity Important Questions Short Answer Type

Question 8.
Find \(\lim _{x \rightarrow 3} \frac{x^3-6 x^2+x}{x^2-9}\)
Solution:

Question 9.
Find \(\lim _{x \rightarrow 3} \frac{x^3-3 x^2}{x^2-5 x+6}\)
Solution:

Question 10.
Compute \(\lim _{x \rightarrow 3} \frac{x^4-81}{2 x^2-5 x-3}\)
Solution:
Given, \(\lim _{x \rightarrow 3} \frac{x^4-81}{2 x^2-5 x-3}\)

Question 11.
Compute \(\lim _{x \rightarrow 3} \frac{x^2-8 x+15}{x^2-9}\). [Mar. ’16 (AP & TS)]
Solution:

Question 12.
If f(x) = \(-\sqrt{25-x^2}\) then find \(\lim _{x \rightarrow 1} \frac{f(x)-f(1)}{x-1}\)
Solution:

Question 13.
Compute \(\lim _{x \rightarrow 0} \frac{\sin a x}{\sin b x}\), b ≠ 0, a ≠ b. [Mar. ’18 (TS)]
Solution:
Given, \(\lim _{x \rightarrow 0} \frac{\sin a x}{\sin b x}\)
Now dividing the numerator and denominator by x, we get

Question 14.
Compute \(\lim _{x \rightarrow 0} \frac{e^{3 x}-1}{x}\). [Mar. ’18 (AP); May ’15 (TS)]
Solution:

Question 15.
Evaluate \(\lim _{x \rightarrow 1} \frac{\log _e x}{x-1}\).
Solution:

Question 16.
Compute \(\lim _{x \rightarrow 3} \frac{e^x-e^3}{x-3}\)
Solution:

Question 17.
Compute \(\lim _{x \rightarrow 0} \frac{e^{\sin x}-1}{x}\)
Solution:

Question 18.
Compute \(\lim _{x \rightarrow 1} \frac{(2 x-1)(\sqrt{x}-1)}{2 x^2+x-3}\)
Solution:

Question 19.
Compute \(\lim _{x \rightarrow 0} \frac{\log _e(1+5 x)}{x}\)
Solution:

Question 20.
Compute \(\lim _{x \rightarrow 0} \frac{(1+x)^{\frac{1}{8}}-(1-x)^{\frac{1}{8}}}{x}\)
Solution:

Question 21.
Compute \(\lim _{x \rightarrow 0} \frac{1-\cos x}{x}\)
Solution:

Question 22.
Compute \(\lim _{x \rightarrow 0} \frac{\sec x-1}{x^2}\)
Solution:

Question 23.
Compute \(\lim _{x \rightarrow 0} \frac{1-\cos m x}{1-\cos n x}\), n ≠ 0.
Solution:

Question 24.
Compute \(\lim _{x \rightarrow 0} \frac{x\left(e^x-1\right)}{1-\cos x}\). [May ’14]
Solution:
Given, \(\lim _{x \rightarrow 0} \frac{x\left(e^x-1\right)}{1-\cos x}\)

Question 25.
Compute \(\lim _{x \rightarrow 0} \frac{\log \left(1+x^3\right)}{\sin ^3 x}\)
Solution:

Question 26.
Compute \(\lim _{x \rightarrow 0} \frac{x \tan 2 x-2 x \tan x}{(1-\cos 2 x)^2}\)
Solution:
Given, \(\lim _{x \rightarrow 0} \frac{x \tan 2 x-2 x \tan x}{(1-\cos 2 x)^2}\)

Question 27.
Compute \(\lim _{x \rightarrow \infty} \frac{x^2-\sin x}{x^2-2}\). [May ’16 (AP)]
Solution:

Question 28.
Compute \(\lim _{x \rightarrow 3} \frac{x^2+3 x+2}{x^2-6 x+9}\). [Mar. ’19 (AP)]
Solution:

Question 29.
Compute \(\lim _{x \rightarrow \infty} \frac{3 x^2+4 x+5}{2 x^3+3 x-7}\). [May ’15 (AP)]
Solution:

Question 30.
Compute \(\lim _{x \rightarrow \infty} \frac{6 x^2-x+7}{x+3}\).
Solution:

Question 31.
Compute \(\lim _{x \rightarrow \infty} \frac{x^2+5 x+2}{2 x^2-5 x+1}\). [May ’14; Mar. ’17 (AP)]
Solution:

Question 32.
Compute \(\lim _{x \rightarrow 2}\left[\frac{1}{x-2}-\frac{4}{x^2-4}\right]\)
Solution:

Question 33.
Compute \(\lim _{x \rightarrow-\infty} \frac{5 x^3+4}{\sqrt{2 x^4+1}}\)
Solution:

Question 34.
Compute \(\lim _{x \rightarrow \infty} \frac{2+\cos ^2 x}{x+2007}\)
Solution:
Given, \(\lim _{x \rightarrow \infty} \frac{2+\cos ^2 x}{x+2007}\)
We know that
-1 ≤ cos x ≤ 1
0 ≤ cos²x ≤ 1
2 + 0 ≤ 2 + cos²x ≤ 2 + 1
2 ≤ 2 + cos²x ≤ 3
\(\frac{2}{x+2007} \leq \frac{2+\cos ^2 x}{x+2007} \leq \frac{3}{x+2007}\)

Question 35.
Compute \(\lim _{x \rightarrow-\infty} \frac{6 x^2-\cos 3 x}{x^2+5}\)
Solution:
We know that
-1 ≤ cos x ≤ 1
-1 ≥ cos 3x ≥ 1
1 ≥ -cos 3x ≥ -1
-1 ≤ -cos 3x ≤ 1

Question 36.
Show that f, given by f(x) = \(\frac{\mathbf{x}-|\mathbf{x}|}{\mathbf{x}}\) (x ≠ 0), is continuous on R – {0}.
Solution:

∴ f is discontinuous at x = 0.
∴ Hence f is continuous on R – {0}.

Question 37.
If f is a function defined by f(x) = \(\begin{cases}\frac{x-1}{\sqrt{x}-1} & \text { if } x>1 \\ 5-3 x & \text { if }-2 \leq x \leq 1 \\ \frac{6}{x-10} & \text { if } x<-2\end{cases}\) then discuss the continuity of ‘f’.
Solution:

Question 38.
If f, given by f(x) = \(\begin{cases}\mathbf{k}^2 x-k & \text { if } \mathbf{k} \geq 1 \\ 2 & \text { if } x<1\end{cases}\) is a continuous function on R, then find the values of k. [Mar. ’15 (TS)]
Solution:
Given, \(\begin{cases}\mathbf{k}^2 x-k & \text { if } \mathbf{k} \geq 1 \\ 2 & \text { if } x<1\end{cases}\)
∴ f is continuous on R
∴ f is continuous at x = 1
at x = 1, LHL = RHL = f(1) ………(1)

From (1), LHL = RHL
⇒ 2 = k² – k
⇒ k² – k – 2 = 0
⇒ k² – 2k + k – 2 = 0
⇒ k(k – 2) + 1(k – 2) = 0
⇒ (k – 2)(k + 1) = 0
⇒ k – 2 = 0 (or) k + 1 = 0
⇒ k = 2 (or) k = -1

Question 39.
Check the continuity of ‘f’ given by f(x) = \(\left\{\begin{array}{rlr}
4-x^2, & \text { if } & x \leq 0 \\
\mathbf{x}-5, & \text { if } & 0 4 x^2-9, & \text { if } & 1<x<2 \\
3 x+4, & \text { if } & x \geq 2
\end{array}\right.\) at points x = 0, 1, 2. [Mar. ’16 (TS)]
Solution:

Here students can locate TS Inter 1st Year Chemistry Notes 8th Lesson హైడ్రోజన్ – దాని సమ్మేళనాలు to prepare for their exam.

TS Inter 1st Year Chemistry Notes 8th Lesson హైడ్రోజన్ – దాని సమ్మేళనాలు

→ జగత్తులో అత్యధిక సమృద్ధిగా దొరికేది హైడ్రోజన్. దీనిని శక్తికి మూలస్థానంలో వాడుకోవచ్చు. దీనినే డై హైడ్రోజన్ అని కూడా అంటారు.

→ ఆవర్తన పట్టికలో హైడ్రోజన్ యొక్క స్థానం చర్చనీయాంశం.

→ హైడ్రోజన్ IA గ్రూపులోని క్షార లోహలతోను, VII A గ్రూపులోని హాలోజన్లతోను పోలికలు కలిగి ఉంటుంది.

→ హైడ్రోజన్ కు మూడు సమస్థానీయాలున్నాయి. అవి ప్రోటియమ్, డ్యూటీరియమ్, ట్రైటియమ్.

→ ట్రెటియమ్ మాత్రమే రేడియోధార్మిక పదార్ధం. ఇది అల్పశక్తి కల B-కణాలను ఉద్గారం చేస్తుంది.

→ డై హైడ్రోజన్ను వివిధ పద్ధతులలో తయారుచేస్తారు.

→ హైడ్రోజన్ హాలోజన్లతో హాలైడ్లను, ఆక్సిజన్లో నీటిని, నైట్రోజన్తో అమ్మోనియాను, లోహలతో హైడ్రైడ్లను ఏర్పరుస్తుంది.

→ హైడ్రోజను అమ్మోనియా సంశ్లేషణలో, నూనెల హైడ్రోజనీకరణంలో, కర్బన రసాయనాల తయారీలో, వెల్డింగ్ మరియు కటింగ్ చేయటానికి, రాకెట్లలో ఇంధనంగా మరియు విద్యుత్ శక్తిని ఉత్పత్తి చేయటంలో వాడతారు.

→ మిగిలిన మూలకాలతో హైడ్రోజన్ ఏర్పరచే ద్విగుణాత్మక సమ్మేళనాలను హైడ్రేడ్లు అంటారు. వీటిని మూడు రకాలుగా వర్గీకరించారు. అయానిక హైడ్రైడ్లు, కోవలెంట్ హైడ్రైడ్లు, నాన్-స్టాయికియోమెట్రిక్ హైడ్రైడ్లు.

→ అన్ని జీవరాశులలోను ఎక్కువ భాగం నీరు ఉంటుంది. ఇది రంగు, రుచిలేని ద్రవం. జలాణువుల మధ్య విస్తృతమైన హైడ్రోజన్ బంధాలు ఉంటాయి. ఇది ద్విస్వభావ ప్రవృత్తిని కలిగి ఉంటుంది.

→ సబ్బుతో నురగను ఇవ్వని నీటిని కఠినజలం అంటారు. నీటిలో కరిగి ఉన్న Ca⁺² మరియు Mg⁺² లవణాలు నీటి కాఠిన్యానికి కారణాలు.

→ మరిగించటం ద్వారాగాని, క్లార్క్ పద్ధతి, కాల్గన్ పద్ధతి, అయాన్ వినిమయ పద్ధతి, సంశ్లేషిత రెజిన్ల పద్ధతి ద్వారా గాని నీటి కాఠిన్యాన్ని తొలగించవచ్చు.

→ D₂O ను భారజలం అంటారు. న్యూక్లియర్ రియాక్టర్లలో మోడరేటు చర్యా విధానాల అధ్యయనంలో వినిమయ కారకంగా D₂O ను ఉపయోగిస్తారు.

→ 50% H₂SO ను విద్యుద్విశ్లేషణం చేయటం ద్వారా H₂O₂ తయారు చేస్తారు. H₂O₂, తెరిచిన పుస్తకాకృతిని కలిగి ఉంటుంది. 30% \(\left(\frac{w}{v}\right)\)H₂O ను పెరై డ్రోల్ అంటారు.

Here students can locate TS Inter 1st Year Chemistry Notes 6th Lesson ఉష్ణగతిక శాస్త్రం to prepare for their exam.

TS Inter 1st Year Chemistry Notes 6th Lesson ఉష్ణగతిక శాస్త్రం

→ ఉష్ణగతికశాస్త్ర అధ్యయనంలో మనం విశ్వం అంతటినీ ఊహాత్మకంగా రెండు ఖండాలుగా విభజిస్తాం. దాన్ని వ్యవస్థ అంటారు. మిగిలిన ఖండాన్ని అనియతంగా భావించి, పరిసరాలు అంటారు.

→ వ్యవస్థలను మూడు రకాలుగా వివృత (తెరిచిన) సంవృత (మూసి వుంచిన) వివక్త వ్యవస్థలు అంటాం.

→ వ్యవస్థ ధర్మాలను సౌలభ్యం కోసం గహన (ద్రవ్యం పరిమాణం మీద ఆధారపడినవి) విస్తార (ద్రవ్యం పరిమాణంపై ఆధారపడనివి)లను ఉష్ణగతిక శాస్త్రం ధర్మాలు అని వర్గీకరిస్తాం.

→ ఉష్ణగతికశాస్త్ర ధర్మాలు అంతరిక శక్తి (E), ఎంథాల్పి (H), గిబ్స్ శక్తి (G), ఎంట్రోపి (S), పని (w) మొ॥

→ శూన్య నియమం, రెండు వస్తువుల మధ్య ఉష్ణ సమతాస్థితికి సంబంధించింది. మొదటి నియమం శక్తి నిత్యత్వానికి సంబంధించింది. రెండవ నియమం ప్రక్రియ అయత్నీకృత స్వభావానికి సంబంధించింది. మూడవ నియమం పరమ శూన్య ఉష్ణోగ్రత వద్ద ఉష్ణ మార్పుకు సంబంధించింది.

→ రసాయన చర్యలకు ఉష్ణగతికశాస్త్ర మొదటి నియమ అనువర్తనమే ఉష్ణరసాయనశాస్త్రం,

→ ఈ విభాగంలో భిన్న చరరాశుల పరంగా ఉష్ణశక్తి మార్పులను పరిమాణాత్మకంగా పరిశీలిస్తాం.

→ ఇవి సంశ్లేషణ, బంధ వియోజన, దహనం, తటస్థీకరణ, పరమాణీకరణ ఉత్పతన, ప్రావస్థ మార్పు అయనీకరణ విలీన ఉష్ణాలు.

→ ఉష్ణం మార్పులను కాలరీ మీటర్ల ద్వారా నిర్ణయిస్తారు.

→ ΔG = ΔH – TDS అయత్నీకృత చర్యలను ΔG ఋణ విలువలో వుంటుంది. అయత్నీకృత చర్యలకు ఇదే ధనవిలువలో వుంటుంది. సమతాస్థితి చర్యలకు ఇది సున్నగా వుంటుంది.

→ ఎంట్రోపి (S) ఉష్ణగతికశాస్త్ర ధర్మాన్ని, ఒక వ్యవస్థ క్రమ రాహిత్యాన్ని తెలపడానికి ప్రవేశపెట్టారు.

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Limits and Continuity Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Limits and Continuity Important Questions Very Short Answer Type

Question 1.
Find \(\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-1}{x}\). [Mar. ’14, ’07, ’04; May ’10]
Solution:

Question 2.
Compute \(\lim _{x \rightarrow 0}\left[\frac{e^x-1}{\sqrt{1+x}-1}\right]\). [Mar. ’15 (TS), ’13 (0ld), ’09]
Solution:

Question 3.
Compute \(\lim _{x \rightarrow 0} \frac{\mathbf{a}^x-1}{\mathbf{b}^x-1}\), (a > 0), (b > 0), (b ≠ 1). [Mar. ’19 (TS); Mar. ’15 (AP), ’13, ’08, ’02; May ’02]
Solution:
Given \(\lim _{x \rightarrow 0} \frac{\mathbf{a}^x-1}{\mathbf{b}^x-1}\)
Now dividing Numerator and Denominator by x, we get

Question 4.
Compute \(\lim _{x \rightarrow 0} \frac{e^x-\sin x-1}{x}\). [Mar. ’16 (TS), ’13]
Solution:

Question 5.
Compute \(\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cos x}{\left(x-\frac{\pi}{2}\right)}\). [Mar. ’18 (TS); May ’13 (old), ’05; Mar. ’08]
Solution:

Question 6.
Compute \(\lim _{x \rightarrow 0} \frac{\sin a x}{x \cos x}\). [Mar. ’03, ’02]
Solution:

Question 7.
Compute \(\lim _{x \rightarrow 1} \frac{\sin (x-1)}{x^2-1}\). [May ’06, ’02]
Solution:

Question 8.
Compute \(\lim _{x \rightarrow 0} \frac{\sin (a+b x)-\sin (a-b x)}{x}\). [Mar. ’12, ’08, ’05; May ’09]
Solution:

Question 9.
Compute \(\lim _{x \rightarrow a} \frac{\tan (x-a)}{x^2-a^2}\) (a ≠ 0) [May ’04, Mar. ’15 (TS)]
Solution:

Question 10.
Compute \(\lim _{x \rightarrow 0} \frac{e^{7 x}-1}{x}\). [Mar. ’17 (AP); May ’13]
Solution:

Question 11.
Compute \(\lim _{x \rightarrow 0} \frac{e^{3+x}-e^3}{x}\). [Mar. ’19 (AP); B.P.]
Solution:

Question 12.
Compute \(\lim _{x \rightarrow a} \frac{x \sin a-a \sin x}{x-a}\). [Mar. ’11; Mar. ’19 (AP); Mar. ’16 (AP)]
Solution:
Given \(\lim _{x \rightarrow a} \frac{x \sin a-a \sin x}{x-a}\)
Adding and subtracting, a sin a, in the numerator, We get

Question 13.
Compute \(\lim _{x \rightarrow 0} \frac{\cos a x-\cos b x}{x^2}\). [May ’11; Mar. ’07, ’04]
Solution:

Question 14.
Compute \(\lim _{x \rightarrow 2} \frac{2 x^2-7 x-4}{(2 x-1)(\sqrt{x}-2)}\). [May ’12, ’07]
Solution:

Question 15.
Compute \(\lim _{x \rightarrow 0} \frac{3^x-1}{\sqrt{1+x}-1}\). [Mar. ’05]
Solution:

Question 16.
Compute \(\lim _{x \rightarrow 0} \frac{\sqrt[3]{1+x}-\sqrt[3]{1-x}}{x}\). [May ’15 (AP), ’06, ’97, ’02; Mar. ’93]
Solution:

Question 17.
Compute \(\lim _{x \rightarrow a} \frac{\sin (x-a) \tan ^2(x-a)}{\left(x^2-a^2\right)^2}\). [Mar. ’06]
Solution:

Question 18.
Compute \(\lim _{x \rightarrow 0} \frac{1-\cos 2 m x}{\sin ^2 n x}\). [Mar. ’10; May ’15 (TS)]
Solution:

Question 19.
Show that \(\lim _{\mathbf{x} \rightarrow 0^{-1}} \frac{|\mathbf{x}|}{\mathbf{x}}=1\) and \(\lim _{\mathbf{x} \rightarrow 0^{+1}} \frac{|\mathbf{x}|}{\mathbf{x}}=-1\). [Mar. ’93, ’85; May ’86, ’83]
Solution:

Question 20.
Show that \(\lim _{x \rightarrow 2^{-}} \frac{|x-2|}{x-2}=-1\). [May ’04]
Solution:

Question 21.
Show that \(\lim _{x \rightarrow 0^{+}} \frac{2|x|}{x}\) + x + 1 = 3. [Mar. ’15 (AP); May ’08; B.P.]
Solution:

Question 22.
Compute \(\lim _{x \rightarrow \infty} \frac{8|x|+3 x}{3|x|-2 x}\). [Mar. ’17 (TS), ’12; May ’10, ’09]
Solution:

Question 23.
Compute \(\lim _{x \rightarrow \infty} \frac{11 x^3-3 x+4}{13 x^3-5 x^2-7}\). [Mar. ’18 (AP); Mar. ’14; May ’07]
Solution:
Given \(\lim _{x \rightarrow \infty} \frac{11 x^3-3 x+4}{13 x^3-5 x^2-7}\)

Question 24.
Compute \(\lim _{x \rightarrow \infty}(\sqrt{x+1}-\sqrt{x})\). [May ’13]
Solution:

Question 25.
Compute \(\lim _{x \rightarrow \infty}\left(\sqrt{x^2+x}-x\right)\). [Mar. ’11, ’10, ’09, ’08]
Solution:

Question 26.
Compute \(\lim _{x \rightarrow 0} x \sin \left(\frac{1}{x}\right)\). [Mar. ’17 (TS)]
Solution:

Here students can locate TS Inter 1st Year Commerce Notes Chapter 1 Introduction to Business to prepare for their exam.

TS Inter 1st Year Commerce Notes Chapter 1 Introduction to Business

→ Human activities are divided into economic and non-economic activities.

→ Economic activities related to the production and distribution of goods and services.

→ Non-economic activities are those which are undertaken without economic consideration.

→ The activities which involve the production of goods and services with the object of selling them for a profit is called business.

→ Professions are those occupations that involve rendering a personal service of a specialized and expert nature.

→ If a person undertake to work for another under a contract is called employment.

→ Objects of business can be classified as :
a) Economic objectives b) Social objectives c) Human objectives d) National objectives

→ Obligations to owners, employees, suppliers, consumers, government and to society are the social responsibilities of the business.

→ Profit is essential for the survival, growth, expansion and diversification of the business.

TS Inter 1st Year Commerce Notes Chapter 1 వ్యాపార భావన – పరిచయం

→ ప్రతి వ్యక్తి తన కోర్కెలను సంతృప్తిపరుచుకొనడానికి నిరంతరము శ్రమిస్తాడు. ఫలితముగా మానవ కార్యకలాపాలు ఏర్పడతాయి. వీటిని ఆర్థిక కార్యకలాపాలు అని, ఆర్థికేతర కార్యకలాపాలు అని విభజించవచ్చు.

→ ఆర్థిక కార్యకలాపాలు వృత్తి, ఉద్యోగము, వ్యాపారము. సమర్థవంతమైన వ్యక్తిగత సేవలను అందించే పనులను వృత్తులు అంటారు. ఒప్పందము ప్రకారము యజమాని చెప్పిన పనులను నిర్వహించడాన్ని ఉద్యోగము అంటారు. లాభాన్ని సంపాదించే ఉద్దేశముతో వస్తుసేవల ఉత్పత్తి, వినిమయము, పంపిణీలతో ఉండే వ్యాపకాన్ని వ్యాపారము అంటారు.

→ వ్యాపార లక్షణాలలో ప్రయోజనాల కల్పన, వస్తుసేవలతో సంబంధము, పునరావృతము కాకపోవడం, లాభార్జన, నష్టభయం, అనిశ్చిత పరిస్థితి, కళ అనేవి ఉంటాయి.

→ ప్రతి వ్యాపారానికి ఆర్థిక, సామాజిక, మానవ సంబంధిత, జాతీయ ఉంటాయి.

→ ఆర్థిక లక్ష్యాలలో లాభాల సంపాదన, ఖాతాదారుల సృష్టి, నవకల్పన ఉన్నాయి.

→ సామాజిక లక్ష్యాలలో సరైన వస్తువులను సరైన ధరలకు సప్లయి చేయడము, ఉద్యోగులకు చాలినంత ప్రతిఫలం అందజేయడము, సాంఘిక సంక్షేమము, ప్రభుత్వానికి సహకారము, సహజ వనరుల సక్రమ వినియోగము ఉన్నవి.

→ మానవ సంబంధిత లక్ష్యాలలో మానవ వనరుల అభివృద్ధి, ప్రజాస్వామ్య నిర్వహణ, శ్రామిక యజమానుల సహకారము ఉన్నాయి.

→ జాతీయ లక్ష్యాలలో వనరుల గరిష్ఠ వినియోగము, జాతీయ గౌరవం, చిన్నతరహా పరిశ్రమల వృద్ధి వెనుకబడిన ప్రాంతాల అభివృద్ధి అనేది ఉంటాయి.

→ వ్యాపారము సమాజములో అంతర్భాగము అయినందున లాభార్జనతో పాటు సామాజిక సంక్షేమాన్ని గురించి కూడా వ్యాపార సంస్థలు ఆలోచించాలి. దీనినే సామాజిక బాధ్యత అంటారు. యజమానులకు, ఉద్యోగులకు, సప్లయిదారులకు, ప్రభుత్వానికి, సమాజానికి సంబంధించి వ్యాపార సంస్థలకు వేర్వేరు బాధ్యతలు ఉంటాయి.