TS Inter 1st Year Physics Notes Chapter 13 ఉష్ణోగతిక శాస్త్రం

Here students can locate TS Inter 1st Year Physics Notes 13th Lesson ఉష్ణోగతిక శాస్త్రం to prepare for their exam.

TS Inter 1st Year Physics Notes 13th Lesson ఉష్ణోగతిక శాస్త్రం

→ ఉష్ణగతిక శాస్త్రము ఉష్ణశక్తి మరియు యాంత్రిక శక్తుల మధ్యగల సంబంధాలను వివరిస్తుంది.

→ ఉష్ణ సమతాస్థితి : ఒక వ్యవస్థలో స్థూల చలరాశులైన పీడనం, ఘనపరిమాణం, ఉష్ణోగ్రత, ద్రవ్యరాశి వాటి సంఘటన కాలంతోపాటు మారకుండా ఉంటే ఆ వ్యవస్థ ఉష్ణ సమతాస్థితిలో ఉంది అంటారు.
రెండు వ్యవస్థలు ఉష్ణ సమతాస్థితిలో ఉండాలంటే ఆ రెండు వ్యవస్థల ఉష్ణోగ్రతలు సమానంగా ఉండాలి.

→ ఉష్ణగతికశాస్త్ర శూన్యాంక నియమం : రెండు వ్యవస్థలు (A, B) విడివిడిగా మూడవ వ్యవస్థ ‘C’ తో ఉష్ణ సమతా స్థితిలో ఉంటే ఆ వ్యవస్థలు A, B లు కూడా ఒక దానితో ఒకటి ఉష్ణసమతాస్థితిలో ఉంటాయి.

→ అంతరికశక్తి (U) : ప్రతివ్యవస్థ అసంఖ్యాకమైన అణువుల సముదాయము. వ్యవస్థలో గల మొత్తం అణువుల స్థితిశక్తి మరియు గతిశక్తుల మొత్తాన్ని అంతరికశక్తి అంటారు.
లేదా
వ్యవస్థలో ఉన్న అణువుల క్రమరహితచలనం వల్ల వస్తువు కలిగి ఉండే స్థితిశక్తి, గతిశక్తుల మొత్తాన్ని అంతరికశక్తి అంటారు.

→ ఉష్ణగతికశాస్త్ర మొదటి నియమం : ఏదైనా వ్యవస్థకు అందించిన మొత్తం ఉష్ణరాశి ΔQ, ఆ వ్యవస్థ జరిపిన పని ΔW మరియు వ్యవస్థ అంతరికశక్తిలోని మార్పుల ΔU ల మొత్తానికి సమానము.
ΔQ = ΔU + ΔW లేదా ΔQ = ΔU + PΔV

→ విశిష్టోష్ణ సామర్ధ్యం (S) : ప్రమాణ ద్రవ్యరాశిగల పదార్థంలో ఏకాంక ఉష్ణోగ్రతా మార్పు కోసం అందజేసిన ఉష్ణరాశిని లేదా కోల్పోయిన ఉష్ణరాశిని విశిష్టోష్ణ సామర్థ్యము అంటారు.
విశిష్టోష్ట సామర్థ్యం S = \(\frac{1}{m} \frac{\Delta Q}{\Delta T}\) ప్రమాణము J/kg-k

→ స్థిరఘనపరిమాణ మోలార్ విశిష్టోష్ణ సామర్ధ్యము (C) : స్థిరఘనపరిమాణము వద్ద ఒక గ్రామ్ మోల్ ద్రవ్యరాశి గల వాయువు ఉష్ణోగ్రతను 1°C లేదా 1 కెల్విన్ పెంచడానికి కావలసిన ఉష్ణరాశిని స్థిరఘనపరిమాణ మోలార్ విశిష్టోష్ణ సామర్థ్యము Cగా నిర్వచించినారు.
C_v = \(\frac{1 \mathrm{dQ}}{\mu \mathrm{dT}}\) μ = వాయువులోని మోల్ల సంఖ్య

→ స్థిరపీడన మోలార్ విశిష్టోష్ణ సామర్ధ్యము (C): స్థిరపీడనము వద్ద ఒక గ్రామ్ మోల్ ద్రవ్యరాశి గల వాయువు ఉష్ణోగ్రతను 1°C లేదా 1 కెల్విన్ మేరకు పెంచడానికి కావలసిన ఉష్ణరాశిని స్థిరపీడన మోలార్ విశిష్టోష్ట సామర్థ్యము C_p గా నిర్వచించినారు.
C_p = \(\frac{1}{\mu} \frac{d Q}{d T}\) μ = వాయువులోని గ్రామ్ మోల్ల సంఖ్య
గమనిక : విశిష్టోష్ణము మరియు విశిష్టోష్ణ సామర్ధ్యములను ఒకే అర్థంలో వాడతారు.

→ సమ ఉష్ణోగ్రతా ప్రక్రియ : ఉష్ణ యాంత్రిక మార్పులు జరుగుతున్నంతసేపు ఒక వ్యవస్థ ఉష్ణోగ్రత T ని స్థిరంగా ఉంచితే ఆ ప్రక్రియను సమఉష్ణోగ్రతా ప్రక్రియ అంటారు.

→ సమ పీడన ప్రక్రియ : ఈ విధమైన ప్రక్రియలో ఉష్ణ యాంత్రిక మార్పులు జరుగుతున్నంత సేపు వ్యవస్థ పీడనం (P) స్థిరము.

→ సమ ఘనపరిమాణ ప్రక్రియ : ఇటువంటి ప్రక్రియలో ఉష్ణ యాంత్రిక మార్పులు జరుగుతున్నంతసేపు వ్యవస్థ ఘనపరిమాణం (V) స్థిరంగా ఉండాలి.

→ స్థిరోష్ణక ప్రక్రియ : ఇటువంటి ప్రక్రియలో ఉష్ణ యాంత్రిక మార్పులు జరుగుతున్నంతసేపు వ్యవస్థ మొత్తం శక్తి (Q) స్థిరంగా ఉండాలి.

→ చక్రీయ ప్రక్రియ : చక్రీయ ప్రక్రియలో ఉష్ణ యాంత్రిక వ్యవస్థపై అన్ని ప్రక్రియలు జరిపిన తరువాత చివరికి అది తొలి ఉష్ణోగ్రతా పీడనాలను పొందుతుంది. చక్రీయ ప్రక్రియలో ΔU = 0 కావున వ్యవస్థ శోషించుకున్న ఉష్ణరాశి చక్రీయ ప్రక్రియలో జరిగినపని. (చక్రీయ ప్రక్రియలో dW – dQ)

→ ఉష్ణగతిక శాస్త్ర రెండవ నియమము :
a) కెల్విన్ – ప్లాంక్ ప్రవచనము : ఒక ఉష్ణాశయం నుంచి ఉష్ణశక్తిని గ్రహించి ఏ ఇతర ఫలితాలు కలుగజేయకుండా మొత్తం శక్తిని పనిగా మార్చే చక్రీయ ప్రక్రియ సాధ్యం కాదు.
b) క్లాసియస్ ప్రవచనము : తక్కువ ఉష్ణోగ్రత గల ఒక వస్తువు నుంచి ఎక్కువ ఉష్ణోగ్రత గల మరొక వస్తువుకు తనంతట తాను ఉష్ణరూపంలో శక్తిని బదిలీ చేసే ఏ ప్రక్రియ సాధ్యం కాదు.

→ ఉష్ణగతిక శాస్త్ర రెండవ నియమం ఉష్ణ ప్రసార దిశను తెలుపుతుంది.

→ ఉష్ణగతిక శాస్త్ర రెండవ నియమం ప్రకారము ఏ ఉష్ణ యంత్రం దక్షత η విలువ 1 కి సమానం కాదని మరియు శీతలీకరణ యంత్రం క్రియాశీలతా గుణకం (∝) విలువ అనంతం కాదని చెపుతుంది.

→ ద్విగత ప్రక్రియలు లేదా ఉత్రమణీయ ప్రక్రియలు : ఉష్ణగతిక ప్రక్రియలు తొలిస్థితి (i) నుండి తుదిస్థితి (f) కి చేరేలోపు ఉష్ణరాశి (Q) ని గ్రహించి పని (W) ని జరుపుతాయి. వేరే ఏ ఇతర ఫలితాలు లేకుండా వ్యవస్థను తుదిస్థితి నుండి తొలిస్థితికి తీసుకొనిపోగలిగితే అటువంటి ప్రక్రియలను ద్విగత ప్రక్రియలు లేదా ఉత్రమణీయ ప్రక్రియలు అంటారు.

→ అనుత్రమణీయ ప్రక్రియ లేదా ఏకగతప్రక్రియ : ఈ విధమైన ప్రక్రియలను తొలిస్థితి (i) నుండి తుదిస్థితి (f) కి మారునపుడు ఉష్ణరాశి గ్రహించి పనిని చేయడం జరుగుతుంది. కాని ఏ ఇతర ఫలితాలు లేకుండా వ్యవస్థను తుదిస్థితి (f) నుండి తొలిస్థితి (1) కి తేవడం సాధ్యం కాదు.
ప్రకృతిలో తమంతట తాముగా జరిగే అన్ని ప్రక్రియలు ఏకగత లేక అనుమణీయ ప్రక్రియలే.

→ కార్నో యంత్రము రెండు ఉష్ణోగ్రతల మధ్య ఆదర్శవాయువుతో పనిచేసే ఉత్రమణీయ ఉష్ణయంత్రము.
దీని దక్షత η = \(\frac{w}{Q_l}\) = 1 – \(\frac{\mathrm{Q}_2}{\mathrm{Q}_1}\) లేదా η = 1 – \(\frac{\mathrm{T}_2}{\mathrm{~T}_1}\)
(T₁ = జనకం ఉష్ణోగ్రత, T₂ = ఉష్ణాశయం ఉష్ణోగ్రత, W = జరిగిన పని)

→ వస్తువు స్థితి ‘మార్పు లేకుండా వేడిచేయడానికి అందించిన ఉష్ణరాశి Q = mct.

→ స్థితి మార్పు పొందటానికి వస్తువుకు అందజేసిన ఉష్ణరాశి Q = mL.

→ జౌల్ నియమం నుండి పని W ∝ Q లేదా W = JQ.
J = ఉష్ణయాంత్రిక తుల్యాంకము

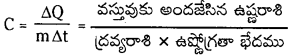
→ స్థితి శక్తి ఉష్ణంగా మారినపుడు
(a) జరిగిన పని మొత్తం వస్తువును వేడిచేయటానికి ఉపయోగిస్తే mgh = mct లేదా Δt = \(\frac{\mathrm{Mgh}}{\mathrm{mL}}\)
(b) జరిగిన పని వస్తువు స్థితి మార్పుకు ఉపయోగపడితే mgh = mL లేదా ద్రవీభవించిన వస్తువు ద్రవ్యరాశి m = \(\frac{\mathrm{Mgh}}{\mathrm{L}}\)

→ గతిశక్తి ఉష్ణంగా మారిన సందర్భంలో
(a) గతిశక్తి వస్తువును వేడిచేయటానికి మాత్రమే ఉపయోగపడితే
\(\frac{1}{2}\)mv2 = mct ⇒ Δt = \(\frac{\mathrm{mv}^2}{2 \mathrm{mc}}\)
(b) గతిశక్తి వస్తువు స్థితి మార్పు వరకు మాత్రమే ఉపయోగపడితే \(\frac{\mathrm{mv}^2}{2 \mathrm{mc}}\)mv² = ML
ద్రవీభవించిన వస్తువు ద్రవ్యరాశి M = \(\frac{\mathrm{mv}^2}{2 \mathrm{mc}}\)

→ ఉష్ణగతిక శాస్త్ర మొదటి నియమం నుండి dQ = dU + dW

→ వస్తువు ఉష్ణధారణ సామర్థ్యము \(\frac{\Delta \mathrm{Q}}{\Delta \mathrm{t}}\) = mc (i.e., ద్రవ్యరాశి × విశిష్టోష్ణము)

→ విశిష్టోష్టము S లేదా C

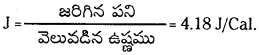
→ మిశ్రమ పద్ధతి నియమం నుండి వేడిగా ఉన్న వస్తువు కోల్పోయిన ఉష్ణరాశి = చల్లగా ఉన్న వస్తువు గ్రహించిన ఉష్ణరాశి
a) మిశ్రమ పద్దతి నియమంలో ఘపపదార్థపు విశిష్టోష్ఠము S = \(\frac{\mathrm{m}_1 \mathrm{~S}_1+\left(\mathrm{m}_2 \mathrm{~m}_1\right) \mathrm{S}_2\left(\mathrm{t}_2-\mathrm{t}_1\right)}{\left(\mathrm{m}_3-\mathrm{m}_2\right)\left(\mathrm{t}_2-\mathrm{t}_1\right)}\)J/kg-k
b) ద్రవాల విశిష్టోష్టము S = \(\frac{\left(m_3-m_2\right) S_1\left(t_2-t_1\right)}{\left(m_2-m_1\right)\left(t_3-t_1\right)}-\frac{m_1 S_2}{m_2-m_1}\)

→ రెండు గోళాల వ్యాసార్థాల నిష్పత్తి r₁: r₂ విశిష్టోష్ణముల నిష్పత్తి S₁ : S₂ మరియు సాంద్రతల నిష్పత్తి ρ₁ : ρ₂ అయితే
వాటి ఉష్ణధారణ సామర్థ్యాల నిష్పత్తి = \(\frac{m_1 S_1}{m_2 S_2}=\left(\frac{r_1}{r_2}\right)^3\left(\frac{\rho_1}{\rho_2}\right)\left(\frac{s_1}{S_2}\right)\)
a) వాయువుల విశిష్టోష్టము C_p = ΔQ / mΔT
b) మోలార్ విశిష్టోష్ఠముల నిష్పత్తి C_p = \(\frac{\Delta Q}{\mu \Delta t}\) (μ = మోల్ల సంఖ్య)
c) విశిష్టోష్ఠముల నిష్పత్తి γ = C_p/ C_v; C_v = \(\frac{\gamma \mathrm{R}}{\gamma-1}\). C_p = \(\frac{\gamma \mathrm{R}}{\gamma-1}\)

→ స్థిర పీడనానికి వ్యతిరేకంగా వాయువు వ్యాకోచించుటలో జరిగిన పని dW = P dV.

→ ఆదర్శవాయువు వ్యాకోచించుటలో జరిగిన పని
a) W = P (V₂ – V₁) లేదా W = R (T₂ – T₁)
μ = వాయువులోని మోత్ల సంఖ్య; R = సార్వత్రిక వాయు స్థిరాంకము

→ Cp మరియు Cv ల మధ్య సంబంధము C_p – C_v = R.

→ సమోష్ణోగ్రతా ప్రక్రియలో P, V మరియు T ల మధ్య సంబంధము PV = RT లేదా PV = μRT.

→ సమ ఉష్ణప్రక్రియ (adiabatic process) లో P, V మరియు T ల మధ్య సంబంధాలు

• PV^γ = స్థిరరాశి
• TV^γ-1 = స్థిరరాశి
• PV^1-γ T^γ = స్థిరరాశి.

→ సమోష్ణోగ్రతా ప్రక్రియలో జరిగిన పని
a) W = RT log_e\(\frac{v_2}{v_1}\)
b) W = 2.303 RT log₁₀\(\frac{v_2}{v_1}\)

→ సమోష్ణ ప్రక్రియలో జరిగిన పని
a) W = \(\frac{1}{\gamma-1}\)(P₁V₁ – P₂V₂) మోల్^-1 (లేదా)
b) W = \(\frac{\mu \mathrm{R}}{\gamma-1}\)(T₁ – T₂); μ = మోల్ల సంఖ్య

→ ఉష్ణయంత్రపు దక్షత η = 1 – \(\frac{\mathrm{Q}_2}{\mathrm{Q}_1}\) లేదా η = 1 − \(\frac{\mathrm{T}_2}{\mathrm{~T}_1}\)
T₁ = జనకం ఉష్ణోగ్రత, T₂ = ఉష్ణాశయం ఉష్ణోగ్రత.

→ వస్తువు స్థితి మార్పు లేకుండా వేడిచేయడానికి అందించిన ఉష్ణరాశి Q = mct.

→ స్థితి మార్పు పొందటానికి వస్తువుకు అందజేసిన ఉష్ణరాశి Q = mL.

→ ప్రయోగశాలలో నీటి బాష్పీభవన గుప్తోష్ణము కనుగొనుటలో
L = \(\frac{\left[\mathrm{m}_1 \mathrm{~S}_{\mathrm{c}}+\left(\mathrm{m}_2-\mathrm{m}_1\right) \mathrm{S}_{\mathrm{w}}\right]\left(\mathrm{t}_1-\mathrm{t}_2\right)}{\mathrm{m}_1-\mathrm{m}_2}\) – (t – t₂)S_w
S_w = నీటి విశిష్టోష్టము ; S_c = కెలోరీ మీటరు విశిష్టోష్టము