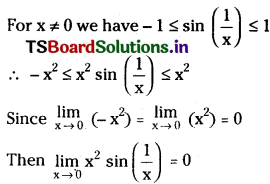TS Inter 1st Year Maths 1B Limits and Continuity Important Questions Very Short Answer Type

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Limits and Continuity Important Questions Very Short Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Limits and Continuity Important Questions Very Short Answer Type

Question 1.
Find \(\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-1}{x}\). [Mar. ’14, ’07, ’04; May ’10]
Solution:

Question 2.
Compute \(\lim _{x \rightarrow 0}\left[\frac{e^x-1}{\sqrt{1+x}-1}\right]\). [Mar. ’15 (TS), ’13 (0ld), ’09]
Solution:

Question 3.
Compute \(\lim _{x \rightarrow 0} \frac{\mathbf{a}^x-1}{\mathbf{b}^x-1}\), (a > 0), (b > 0), (b ≠ 1). [Mar. ’19 (TS); Mar. ’15 (AP), ’13, ’08, ’02; May ’02]
Solution:
Given \(\lim _{x \rightarrow 0} \frac{\mathbf{a}^x-1}{\mathbf{b}^x-1}\)
Now dividing Numerator and Denominator by x, we get

Question 4.
Compute \(\lim _{x \rightarrow 0} \frac{e^x-\sin x-1}{x}\). [Mar. ’16 (TS), ’13]
Solution:

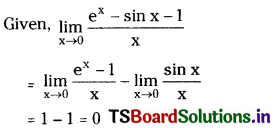
Question 5.
Compute \(\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cos x}{\left(x-\frac{\pi}{2}\right)}\). [Mar. ’18 (TS); May ’13 (old), ’05; Mar. ’08]
Solution:

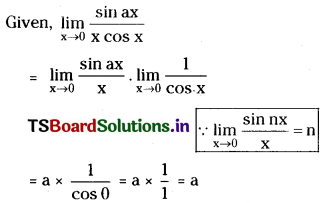
Question 6.
Compute \(\lim _{x \rightarrow 0} \frac{\sin a x}{x \cos x}\). [Mar. ’03, ’02]
Solution:

Question 7.
Compute \(\lim _{x \rightarrow 1} \frac{\sin (x-1)}{x^2-1}\). [May ’06, ’02]
Solution:

Question 8.
Compute \(\lim _{x \rightarrow 0} \frac{\sin (a+b x)-\sin (a-b x)}{x}\). [Mar. ’12, ’08, ’05; May ’09]
Solution:

Question 9.
Compute \(\lim _{x \rightarrow a} \frac{\tan (x-a)}{x^2-a^2}\) (a ≠ 0) [May ’04, Mar. ’15 (TS)]
Solution:

Question 10.
Compute \(\lim _{x \rightarrow 0} \frac{e^{7 x}-1}{x}\). [Mar. ’17 (AP); May ’13]
Solution:

Question 11.
Compute \(\lim _{x \rightarrow 0} \frac{e^{3+x}-e^3}{x}\). [Mar. ’19 (AP); B.P.]
Solution:

Question 12.
Compute \(\lim _{x \rightarrow a} \frac{x \sin a-a \sin x}{x-a}\). [Mar. ’11; Mar. ’19 (AP); Mar. ’16 (AP)]
Solution:
Given \(\lim _{x \rightarrow a} \frac{x \sin a-a \sin x}{x-a}\)
Adding and subtracting, a sin a, in the numerator, We get

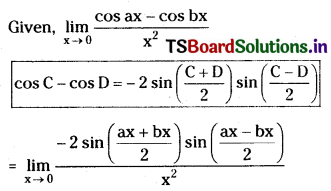
Question 13.
Compute \(\lim _{x \rightarrow 0} \frac{\cos a x-\cos b x}{x^2}\). [May ’11; Mar. ’07, ’04]
Solution:

Question 14.
Compute \(\lim _{x \rightarrow 2} \frac{2 x^2-7 x-4}{(2 x-1)(\sqrt{x}-2)}\). [May ’12, ’07]
Solution:

Question 15.
Compute \(\lim _{x \rightarrow 0} \frac{3^x-1}{\sqrt{1+x}-1}\). [Mar. ’05]
Solution:

Question 16.
Compute \(\lim _{x \rightarrow 0} \frac{\sqrt[3]{1+x}-\sqrt[3]{1-x}}{x}\). [May ’15 (AP), ’06, ’97, ’02; Mar. ’93]
Solution:

Question 17.
Compute \(\lim _{x \rightarrow a} \frac{\sin (x-a) \tan ^2(x-a)}{\left(x^2-a^2\right)^2}\). [Mar. ’06]
Solution:

Question 18.
Compute \(\lim _{x \rightarrow 0} \frac{1-\cos 2 m x}{\sin ^2 n x}\). [Mar. ’10; May ’15 (TS)]
Solution:

Question 19.
Show that \(\lim _{\mathbf{x} \rightarrow 0^{-1}} \frac{|\mathbf{x}|}{\mathbf{x}}=1\) and \(\lim _{\mathbf{x} \rightarrow 0^{+1}} \frac{|\mathbf{x}|}{\mathbf{x}}=-1\). [Mar. ’93, ’85; May ’86, ’83]
Solution:

Question 20.
Show that \(\lim _{x \rightarrow 2^{-}} \frac{|x-2|}{x-2}=-1\). [May ’04]
Solution:

Question 21.
Show that \(\lim _{x \rightarrow 0^{+}} \frac{2|x|}{x}\) + x + 1 = 3. [Mar. ’15 (AP); May ’08; B.P.]
Solution:

Question 22.
Compute \(\lim _{x \rightarrow \infty} \frac{8|x|+3 x}{3|x|-2 x}\). [Mar. ’17 (TS), ’12; May ’10, ’09]
Solution:

Question 23.
Compute \(\lim _{x \rightarrow \infty} \frac{11 x^3-3 x+4}{13 x^3-5 x^2-7}\). [Mar. ’18 (AP); Mar. ’14; May ’07]
Solution:
Given \(\lim _{x \rightarrow \infty} \frac{11 x^3-3 x+4}{13 x^3-5 x^2-7}\)

Question 24.
Compute \(\lim _{x \rightarrow \infty}(\sqrt{x+1}-\sqrt{x})\). [May ’13]
Solution:

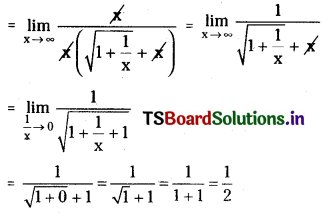
Question 25.
Compute \(\lim _{x \rightarrow \infty}\left(\sqrt{x^2+x}-x\right)\). [Mar. ’11, ’10, ’09, ’08]
Solution:

Question 26.
Compute \(\lim _{x \rightarrow 0} x \sin \left(\frac{1}{x}\right)\). [Mar. ’17 (TS)]
Solution: