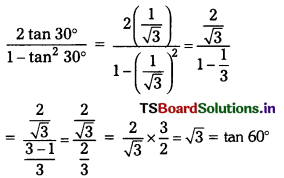
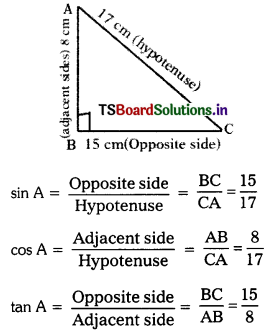
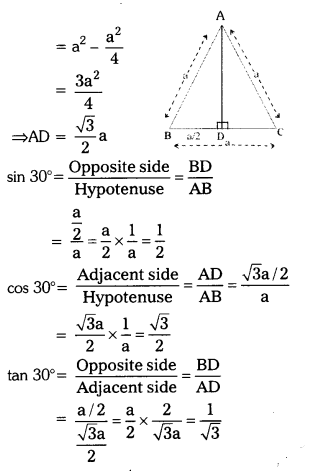
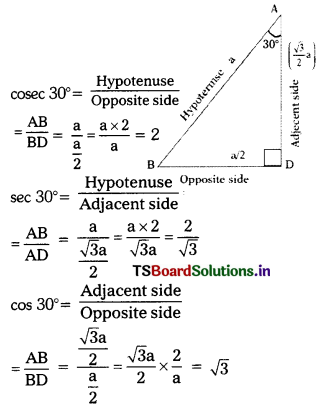
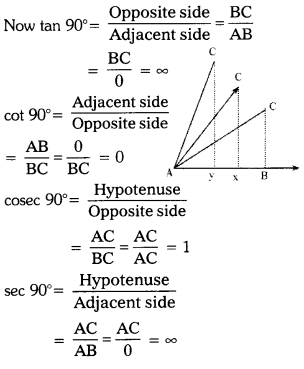
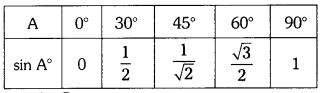
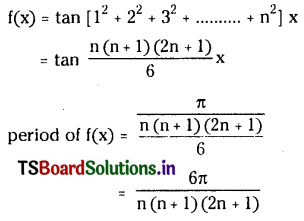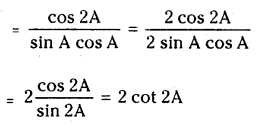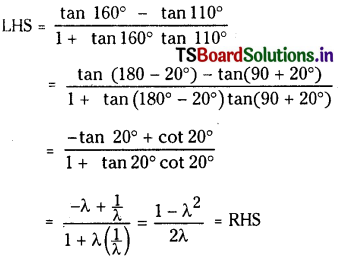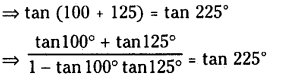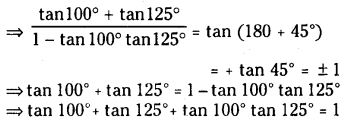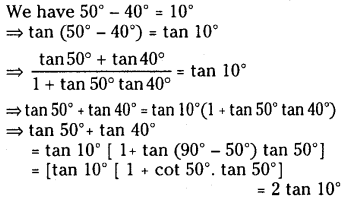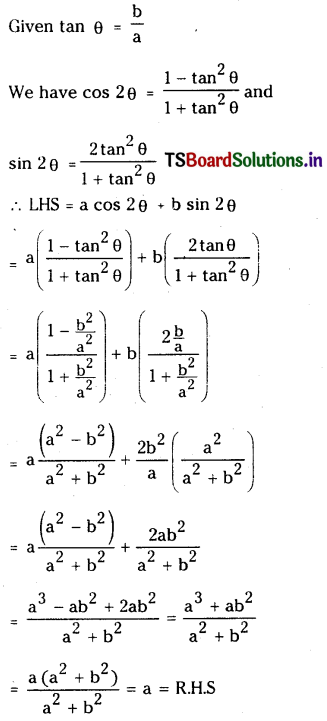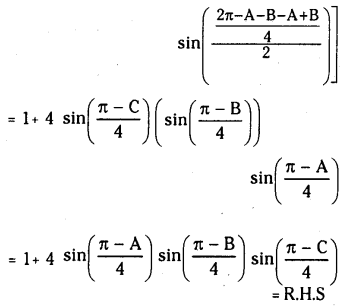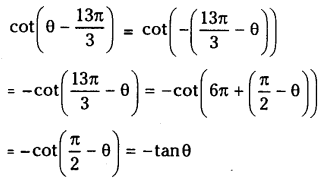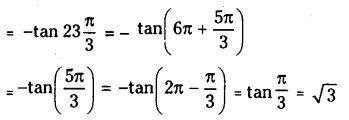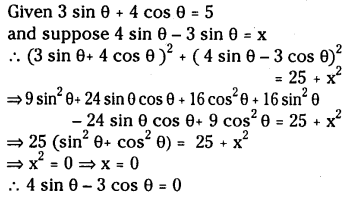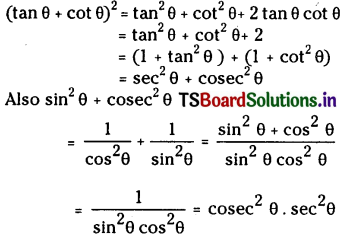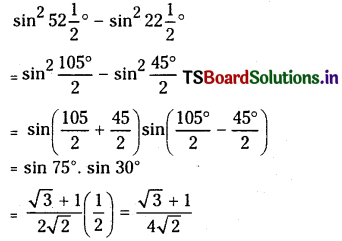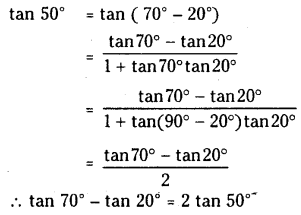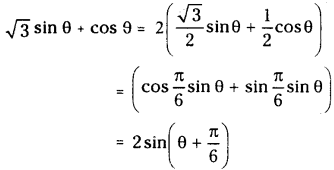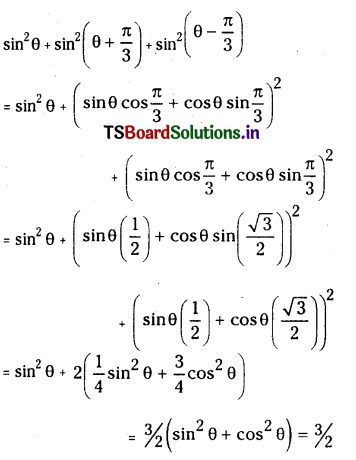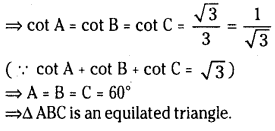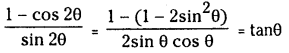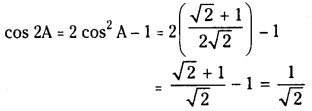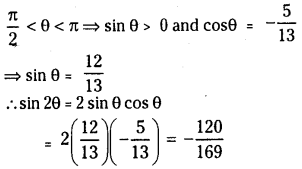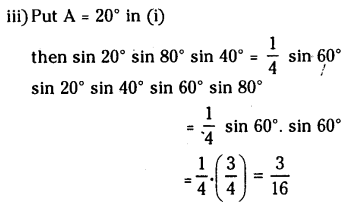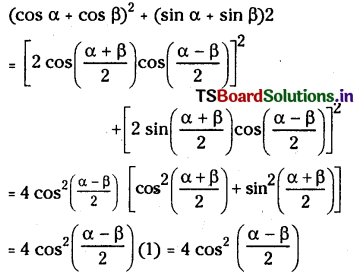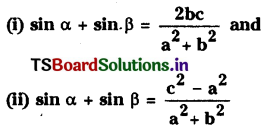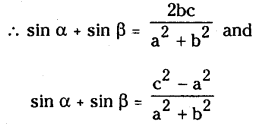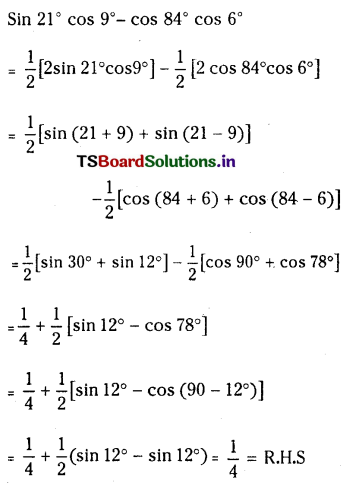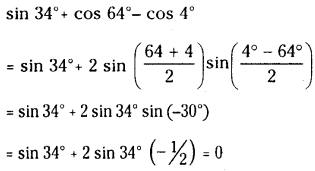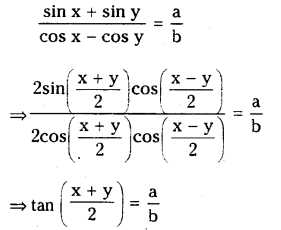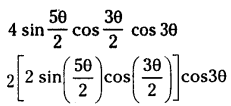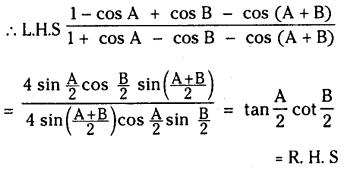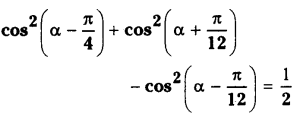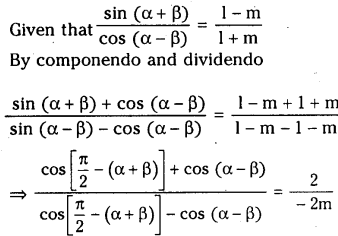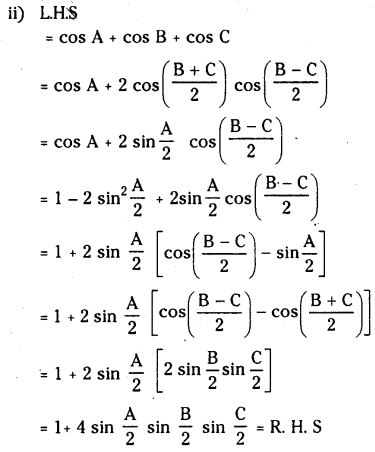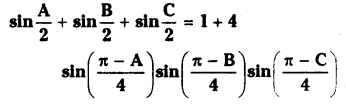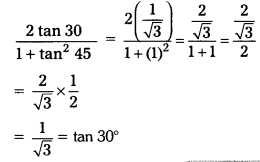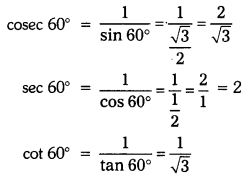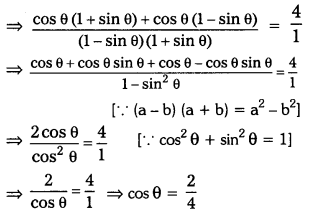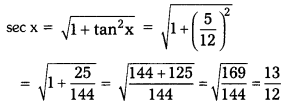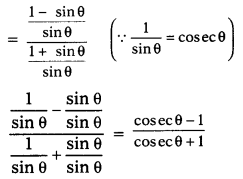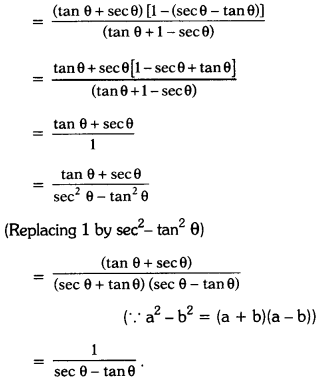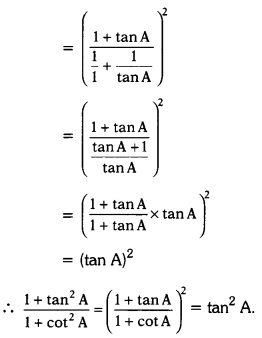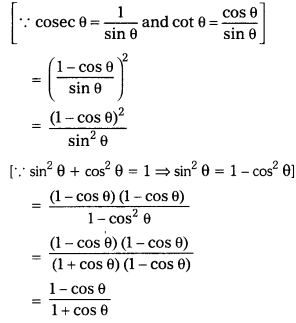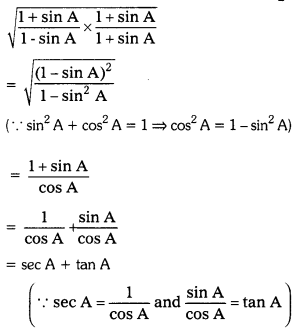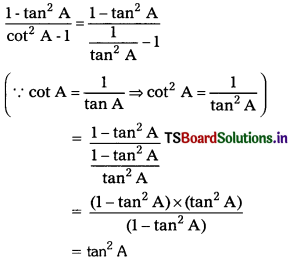Students must practice these TS Inter 1st Year Maths 1A Important Questions Chapter 6 Trigonometric Ratios up to Transformations to help strengthen their preparations for exams.
TS Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Important Questions
Question 1.
Prove that \(\frac{\cos 9^{\circ}+\sin 9^{\circ}}{\cos 9^{\circ}-\sin 9^{\circ}}=\cot 36^{\circ}\)
Solution:

Question 2.
Find the period of the function defined by f (x) = tan (x+ 4x + 9x+…………+ n2x)
Solution:
The given function is
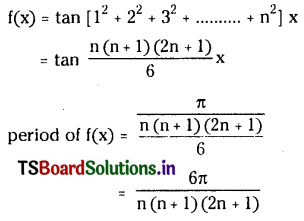

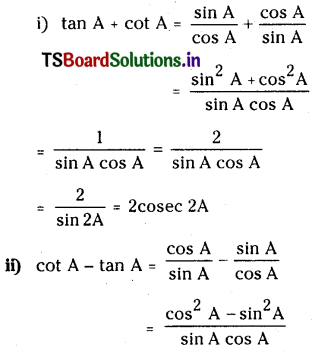
Question 3.
If A is not an integral multiple of \(\frac{\pi}{2}\), prove that
(i) tan A + cot A = 2 cosec 2A
(ii) cot A – tan A = 2 cot 2A
Solution:
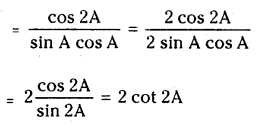
Question 4.
If ABC are angle of a triangle then prove that
\(\begin{aligned} \sin ^2 \frac{A}{2} & +\sin ^2 \frac{B}{2}-\sin ^2 \frac{C}{2} \\
& =1-2 \cos \frac{A}{2} \cos \frac{B}{2}-\sin ^2 \frac{C}{2} \end{aligned}\)
Solution:


Question 5.
If tan 20° = λ then show that
\(\frac{\tan 160^{\circ}-\tan 110^{\circ}}{1+\tan 160^{\circ} \tan 110^{\circ}}=\frac{1-\lambda^2}{2 \lambda}\)
Solution:
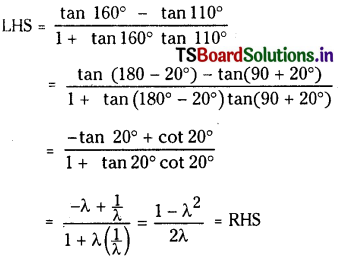
Question 6.
If \(\cos \theta+\sin \theta=\sqrt{2} \cos \theta\) then show that \(\cos \theta-\sin \theta=\sqrt{2} \sin \theta\)
Solution:

Question 7.
Show that cos 340° cos 40° + sin 200° sin 140°=\(\frac{1}{2}\)
Solution:
LH.S = cos 3400 cos 40° + sin 2000 sin 140°
= cos (360 – 20°) cos 40° + sin (180 + 20°) sin (180 – 40°)
= cos 20° cos 40° – sin 20° sin 40°
= cos (20° + 40°) = cos 60° = R.H.S
Question 8.
Find the value of tan 100° + tan 125° + tan 100° + tan 125°
Solution:
We have tan 100° + tan 125° = 225
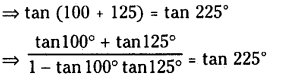
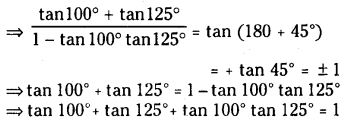
Question 9.
Prove that tan 500° – tan 400° = 2 tan 10°
Solution:
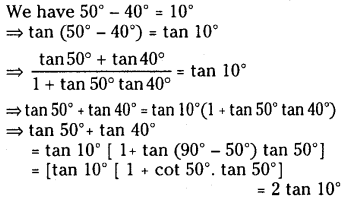
Question 10.
Show that cos 42° + cos 78° + cos 162° = 0
Solution:

Question 11.
Find the value of \(\cos ^2 52 \frac{1}{2}^{\circ}-\sin ^2 22 \frac{1}{2}^{\circ}\)
Solution:


Question 12.
If A+B+C= \(\frac{\pi}{2}\) then show that cos A + cos B + cos C
Solution:

Question 13.
If tanθ=\(\frac{b}{a}\) then prove that a cos bθ + b sinθ = a
Solution:
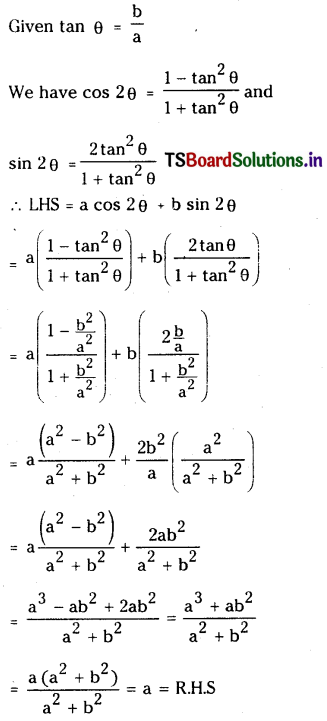
Question 14.
If A + B + C = 1800 than show that sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C
Solution:
A+B+C=180°
⇒ sin (A + B) = sin C
L.H.S = sin 2A sin 2B + sin 2C
\(=2 \sin \left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right) \cos \left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)+\sin 2 \mathrm{C}\)
= 2 sin (A+B) cos (A – b) + 2 sin C cos C
= 2 sin C cos(A-B) + 2 sinC cosC
= 2 sin C [ cos (A – B) + cos C]
= 2 sinC [cos(A – B) – cos(A+B)
= 2 sinC (2 sin A sin B)= 4 sin A sin B sin C
= R.H.S
Question 15.
If A, B, C and angles in a triangle then prove that cos A + cos B + cos C
\(=1+4 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}\)
Solution:


Question 16.
If ABC are the angles in a triangle then prove that \(\sin \frac{A}{2}+\sin \frac{B}{2}+\sin \frac{C}{2}=1+4 \sin \left(\frac{\pi-A}{4}\right) \sin \left(\frac{\pi-B}{4}\right) \sin \left(\frac{\pi-C}{4}\right)\)
Solution:

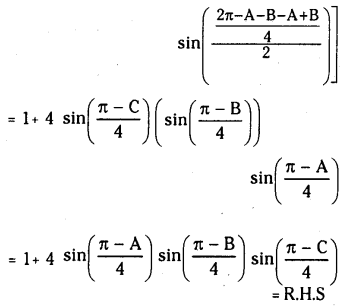
Question 17.
Find the values of
i) sin \(\frac{5 \pi}{3}\)
ii) tan (885)°
iii) sec \(\left(\frac{13 \pi}{3}\right)\)
Solution:

Question 18.
Simplify
(i) \(\cot \left(\theta-\frac{13 \pi}{3}\right)\)
(ii) \(\tan \left(-23 \frac{\pi}{3}\right)\)
Solution:
(i) \(\cot \left(\theta-\frac{13 \pi}{3}\right)\)
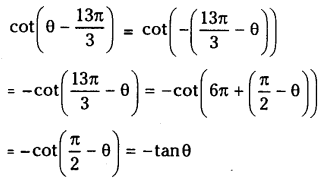
(ii) \(\tan \left(-23 \frac{\pi}{3}\right)\)
Solution:
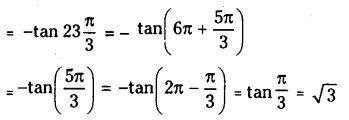

Question 19.
Find the value of \(\begin{aligned} \sin ^2 \frac{\pi}{10} & +\sin ^2 \frac{4 \pi}{10}+ \sin ^2 \frac{6 \pi}{10}+\sin ^2 \frac{9 \pi}{10} \end{aligned}\)
Solution:

Question 20.
If sinθ= \(\frac{4}{5}\) and θ is not in the first quadrant, find the value of cos θ
Solution:
Since θ is not in the first quadrant and sin θ >0 we have 90°< θ < 180°
∴ \(\cos \theta=\sqrt{1-\sin ^2 \theta}=\sqrt{1-\frac{16}{25}}=-3 / 5\)
Question 21.
If sec θ+tan θ=\(\frac{2}{3}\) find the value of sin θ and determine the quadrant in which θ lies.
Solution:

Since tan θ is negative, sec θ is positive
∴ θ lies in fourth quadrant.
Question 22.
Prove that \(\begin{array}{r} \cot \frac{\pi}{16} \cdot \cot \frac{2 \pi}{16} \cdot \cot \frac{3 \pi}{16} \cdots \\ \cot \frac{7 \pi}{16}=1 \end{array}\)
Solution:
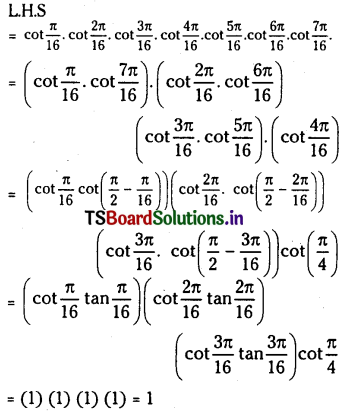
Question 23.
If 3 sin θ + 4 cos θ = 5 then find the value of 4 sinθ – 3 cos θ.
Solution:
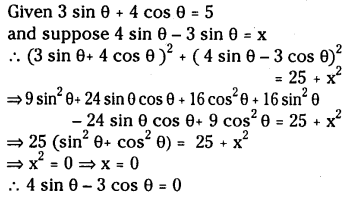
Question 25.
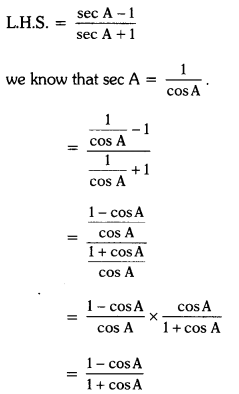
Prove that (tanθ + cot θ)2 = sec2θ + cosec2θ = sec2 θ cosec2θ
Solution:
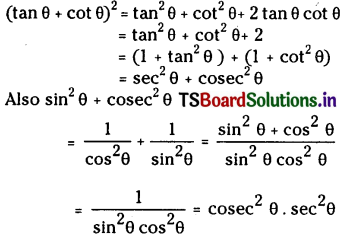
Question 26.
If cos θ > θ , tan θ+ sin θ = m and tan θ – sin θ = n then show that m2 – n2 = \(4 \sqrt{m n}\)
Solution:
Given that m = tan θ + sin θ
n tan θ – sin θ
∴ m+ n = 2tanθ,m – n= 2 sinθ
and (m + n)(m – n) = 4 tanθ sinθ

Question 27.
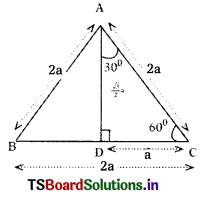
Find the rules of sin 75°, cos 75°, tan 75° and cot 75°
Solution:


Question 28.
Prove that \(\sin ^2 52 \frac{1}{2}^{\circ}-\sin ^2 22 \frac{1}{2}^{\circ}=\frac{\sqrt{3}+1}{4 \sqrt{2}}\)
Solution:
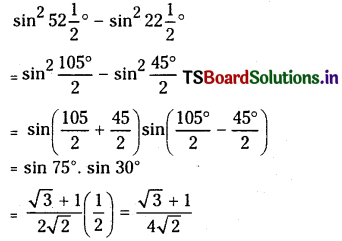
Question 29.
Prove that tan 700 tan 200 = 2 tan 50°
Solution:
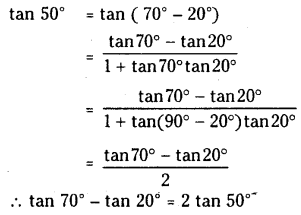
Question 30.
Express \(\sqrt{3} \sin \theta\) sinθ + cosθ as a sine of an angle
Solution:
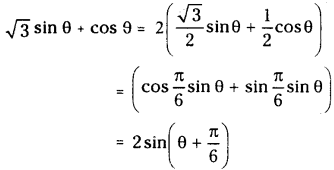
Question 31.
Prove that \(\sin ^2 \theta+\sin ^2\left(\theta+\frac{\pi}{3}\right)+\sin ^2\left(\theta-\frac{\pi}{3}\right)=\frac{3}{2}\)
Solution:
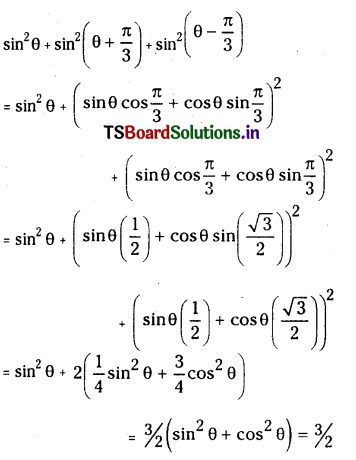
Question 32.
Let ABC be a triangle such that \(\cot A+\cot B+\cot C=\sqrt{3}\) then prove that ABC is an equilateral triangle.
Solution:
Given that \(\mathrm{A}+\mathrm{B}+\mathrm{C}=180^{\circ}\)

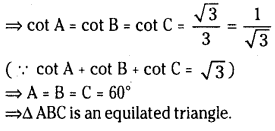

Question 33.
Suppose x= tan A, y = tan B, z = tan C Suppose none of A,B,C,A-B,B-C, is an odd multiple of \(\frac{\pi}{2}\) then prove that \(\Sigma\left(\frac{x-y}{1+x y}\right)=\Pi\left(\frac{x-y}{1+x y}\right)\)
Solution:
\(\frac{1}{2}^{\circ}\) lies in first quadrant and hence all ratios are position.
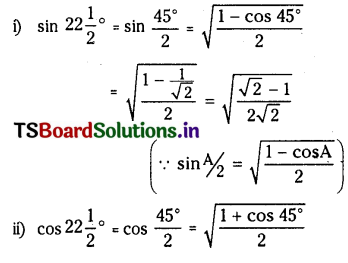

Question 35.
Find the rules of
(i) \(\sin 67 \frac{1}{2}^{\circ}\)
(ii) \(\cos 67 \frac{1}{2}^{\circ}\)
(iii) \(\tan 67 \frac{1}{2}^{\circ}\)
(iv) \(\cot 67 \frac{1}{2}^{\circ}\)
Solution:
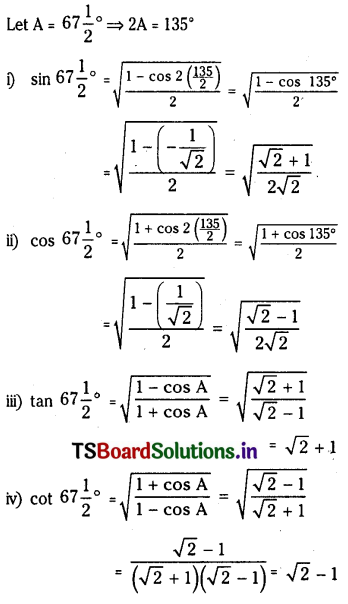
Question 36.
Simplify \(\frac{1-\cos 2 \theta}{\sin 2 \theta}\)
Solution:
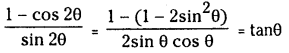
Question 37.
If \(\cos A=\sqrt{\frac{\sqrt{2}+1}{2 \sqrt{2}}}\) find the value of cos 2A
Solution:
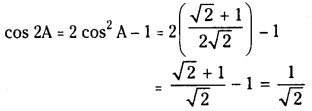
Question 38.
If \(\cos \theta=-\frac{5}{13}\) and \(\frac{\pi}{2}<\theta<\pi\) find the value of sin 2θ
Solution:
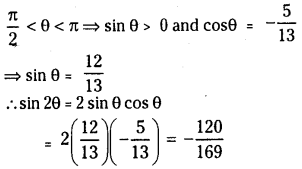

Question 39.
For what values of x in the first quadrant \(\frac{2 \tan x}{1-\tan ^2 x}\) is positive?
Solution:

Question 40.
If \(\cos \theta=-3 / 5\) and \(\pi<\theta<\frac{3 \pi}{2}\) find the value of \(\tan \frac{\theta}{2}\)
Solution:

Question 41.
If θ is not an integral multiple of \(\frac{\pi}{2}\) prove that tanθ + 2 tan 2θ + 4 tan 4θ + 8 cot 8θ = cot θ.
Solution:
We have cotA – tan A = 2 cot 2A
tan A = cot A – 2 cot 2A
tanθ+ 2tan2θ+4tan4θ+8cot8θ
= (cotθ – 2 cot 2θ) +2 (cot 2θ – 2 cot 4θ) + 4 (cot 4θ – 2 cot 8θ) + 8 cot 8θ= cot θ
Question 42.
For A∈R prove that
(i) sin A sin \(\left(\frac{\pi}{3}+A\right) \sin \left(\frac{\pi}{3}-A\right)=\frac{1}{4}\) sin 3A
(ii) cos A cos \(\left(\frac{\pi}{3}+A\right) \cos \left(\frac{\pi}{3}-A\right)=\frac{1}{4}\) cos 3A
iii) sin 20° sin 40° sin 60° sin 80° = \(\frac{3}{16}\)
iv) \(\cos \frac{\pi}{9} \cos \frac{2 \pi}{9} \cos \frac{3 \pi}{9} \cos \frac{4 \pi}{9}=\frac{1}{16}\)
Solution:

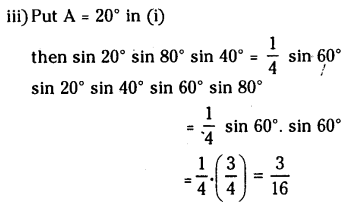


Question 43.
If 3A is not an odd multiple of \(\frac{\pi}{2}\), prove that tan A tan(60+A) tan(60-A) = tan 3A and hence find the value of \(\tan 6^{\circ} \tan 42^{\circ} \tan 66^{\circ} \tan 78^{\circ}\)
Solution:

Question 44.
For α,β∈R prove that (cosα + cosβ)2 + (sinα +sinβ)2 = 4 cos2 \(\left(\frac{\alpha-\beta}{2}\right)\)
Solution:
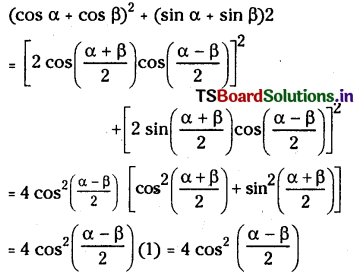
Question 45.
If a, b, c are non-zero real numbers and a, are solutions of the equation a cosθ + b sinθ=c then show that
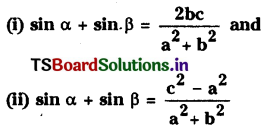
Solution:
Given acosθ + bsinθ = c
a cos θ = c b sin e
= a2 cos2θ = C2 – 2bc sin θ + b2 sin2 θ
⇒ a2 (1 – sin2 θ) = c2 – 2bc sin θ + b2 sin2 θ
⇒ (b+a) sin2 θ- 2bc sinθ + (C2 – a2) = θ
This is a quadrant equation in sin θ and suppose sin α, sin β are roots of the equation
∴ given α, β are solutions of the equation
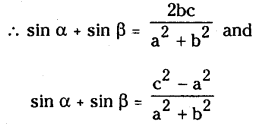
Question 46.
If θ is not an odd multiple of \(\frac{\pi}{2}\) and \(\cos \theta=-\frac{1}{2}\) prove that \(\frac{\sin \theta+\sin 2 \theta}{1-\cos \theta+\cos 2 \theta}=\tan \theta\)
Solution:

Question 47.
Prove that
\(\sin ^4 \frac{\pi}{8}+\sin ^4 \frac{3 \pi}{8}+\sin ^4 \frac{5 \pi}{8}+\sin ^4 \frac{7 \pi}{8}=\frac{3}{2}\)
Solution:


Question 48.
If none of 2A and 3A is an odd multiple of \(\frac{\pi}{2}\) then prove that
tan 3A tan 2A tanA = tan 3A – tan 2A – tan A
Solution:
We have 3A = 2A+A
∴ tan 3A = tan (2A+A)
\(=\frac{\tan 2 A+\tan A}{1-\tan 2 A \tan A}\)
⇒ tan 2A + tan A tan 3A (1 – tan 2A tanA)
⇒ tan A tan2A tan 3A = tan 3A – tan 2A – tan A
Question 49.
Prove tant sin 78° + cos 132° = \(\frac{\sqrt{5}-1}{4}\)
Solution:

Question 50.
Prove tant sin 21° cos 9° – cos 84° cos 6° = \(\frac{1}{4}\)
Solution:
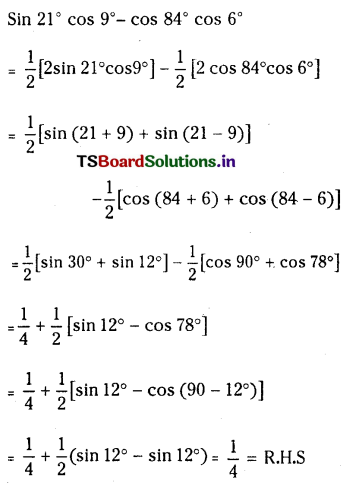
Question 51.
Find the value of sin 34° + cos 64°- cos 4°
Solution:
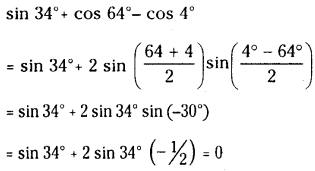
Question 52.
Prove that cos2 76°+cos2 16°- cos 76° cos 16° \(=\frac{3}{4}\)
Solution:


Question 53.
If a, b ≠ 0 and sin x+sin y=a and cos x+cos y=b find two values of
(i) \(\tan \left(\frac{x+y}{2}\right)\)
ii) \( \sin \left(\frac{x-y}{2}\right)\) is terms of a and b
Sol.
i) Given sin x+sin y=a and cos x+cos y=b we have
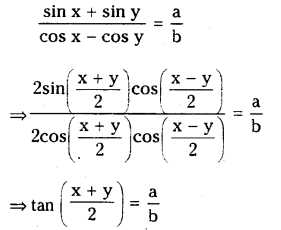
ii) consider
a2. b2 = (sin x + sin y)2 + (cos x + cos y)2
= sin2x + cos2 x + sin2 y cos2 y
+ 2 (sin x sin y + cos x cos y)
= 2. 2 cos (x – y)
= 2[1 .cos (x-y)]

Question 54.
Prove that cos 12°+ cos 84°+cos 132°+cos 156°
Solution:

Question 55.
Show that for any 0∈ R \(4 \sin \frac{5 \theta}{2} \cos \frac{3 \theta}{2} \cos 3 \theta \) sinθ – sin 2θ+ sin 4θ +sinθ
Solution:
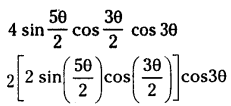
⇒ 2 cos 3θ [ sin 4θ + sin θ]
⇒ 2 cos 3θ sin 4θ + 2 cos 3θ sin θ
⇒ sin (4θ + 3θ) sin (4θ – 3θ) + sin 4θ + sin (-2θ)
⇒ sin7θ+ sinθ + sin4θ – sin2θ
⇒ sin θ – sin 2θ+ sin 4θ – sin 7θ = R. H. S.

Question 56.
If none of A, B, A + B is an integral multiple of π, then prove that
\(\begin{aligned} \frac{1-\cos A+\cos B-\cos (A+B)}{1+\cos A-\cos B-} & \cos (A+B) \\ =\tan \frac{A}{2} \cot \frac{B}{2} \end{aligned}\)
Solution:

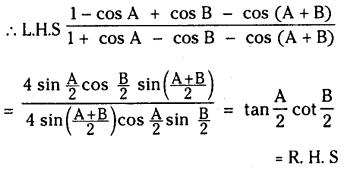
Question 57.
For any α∈R prove that cos2
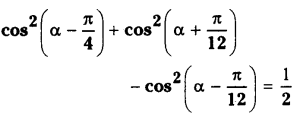
Solution:
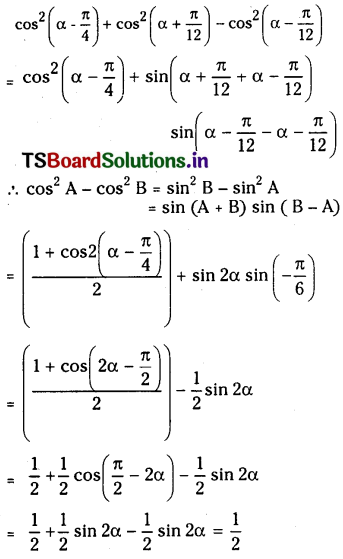

Question 58.
Suppose (α-β) is not an odd multiple of \(\frac{\pi}{2}\), m is a non zero number such that m ≠ – 1 and \(\frac{\sin (\alpha+\beta)}{\cos (\alpha-\beta)}=\frac{1-m}{1+m} \quad\) then prove that \(\tan \left(\frac{\pi}{4}-\alpha\right)=m \cdot \tan \left(\frac{\pi}{4}+\beta\right)\)
Solution:
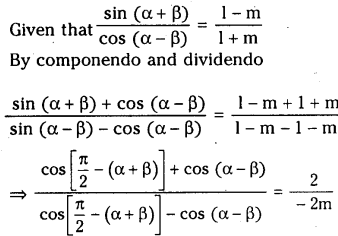
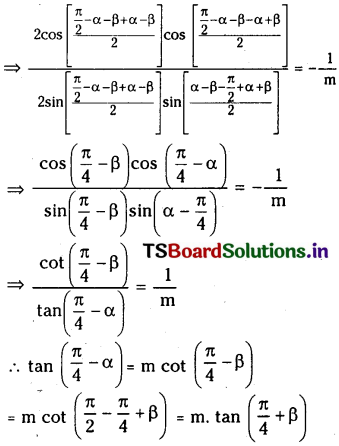
Question 59.
If A,B, C are the angles of a triangle prove that sin 2A + sin 2B – sin 2C 4 cos A cos B sin C
Solution:
Given A, B, C are the angles of a triangle
A+B+C= π
∴ sin 2A + sin 2B – sin 2C
= sin 2A + 2cos (B + C) sin (B-C)
= sin 2A-2cosAsin (B-C)
=2 sinA cosA-2cosA sin(B – C)
= 2 cosA [sinA-sin(B – C)]
= 2 cosA [sin(B+C)-sin(B-C)]
= 2 cos A (2 cos B sin C)
= 4 cos A cos B sin C
Question 60.
If A, B, C are angles of a triangle prove that cos 2A + cos 2B – cos 2C = 1 – 4 sin A sin B cos C
Solution:
Given A + B + C = it, we have
cos 2A + cos 2B – cos 2C
=cos2A – 2sin (B+C) sin(B-C)
cos2A – 2sinA sin(B-C)
=1 – 2 sin2A – 2sinA sin(B – C)
= 1 – 2 sinA [sin A + sin (B-C)]
= 1 – 2 sinA [sin (B+C) + sin (B-C)]
= 1 – 2 sinA (2 sin B cos C)
= 1 – 4 sin A sin B cos

Question 61.
If A, B, C are angles in a triangle then prove that
(i) sin A + sin B + sin C = 4 \(\cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}\)
(ii) cos A + cos B + cos C = \(1+4 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}\)
Solution:

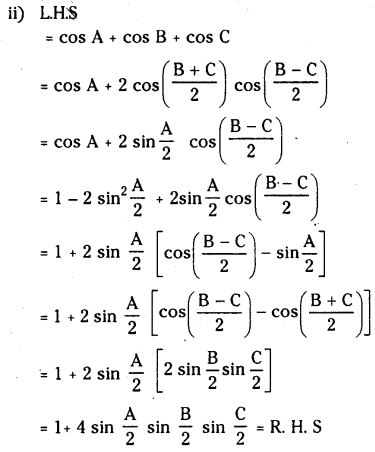

Question 62.
If A+B+C = \(\frac{\pi}{2}\) than show that
sin2 A+ sin2 B+ sin2 C = 1-2 sin A sin B sin C
Solution:
Given A+B + C = \(\frac{\pi}{2}\)
L.H.S = sin2 A + sin2 B + sin2 C
= sin2 A. sin2 B + 1- cos2 C
= 1 + sin2 A – (cos2 C – sin2 B)
= 1 + sin2 A-cos (C-B) cos (C-B)
=1 +sin2A-sinAcos(C-B)
= 1 +sinA [sinA – cos(B-C)]
= 1sinA [cos(B+C) – cos(B-C)]
= 1-sin A [ 2 sin B sin C]
1-2 sin A sin B sin C = R. H. S
Question 63.
If A+B+C=\(\frac{3 \pi}{2}\),prove that
cos2A+cos 2B+cos 2C = 1-4sinA sinB sinC
Solution:
LH.S. = cos2A + cos2B + cos2C
= 2cos(A+B)cos(A-B) +cos2
=-2smCcos(A-B)+ 1-2sm C
[A+B= \(\frac{3 \pi}{2}\) – C=cos(A+B)=-sinC]
=1-2 sin C[cos(A-B).sinC]
= 1-2 sin C[cos(A-B)-cos(A+B)]
= 1-2 sinC[2sinA sinB]
= 1-4 sin A sinB sinC=RH.S
Question 64.
If A,B,C are angles of a triangle then prove that
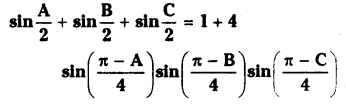
Solution:

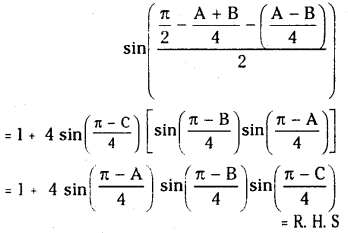

Question 65.
IfA+B+C = 0 then prove that
cos2A +cos2 B + cos2C = 1+2 cosA cosB cosC
Solution:
L.H.S = cos A. cos2 B + cos2 C
= cos2 A . cos2 B. + 1 – sin.2 C
= 1 + cos2 A + cos (B + C) cos (B – C)
( ∵ A+B+C = 0 cos(B+C) = cosA)
= 1 + cos2 A + cos A cos (B – C)
= 1+ cosA [cosA+cos(B-C)]
1 – cos A [cos(B+ C) +cos(B-C)]
= 1 +cosA [2 cosB cosC]
= 1 .2 cosA cosB cosC = R.H.S
Question 66.
If A+B+C=2S then prove that
cos (S – A) + cos (S – B) + cos (S – C) + cos S = \(4 \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}\)
Solution:

![]()
![]()

![]()
![]()