TS 10th Class Maths Solutions Chapter 11 Trigonometry Ex 11.1

Students can practice 10th Class Maths Study Material Telangana Chapter 11 Trigonometry Ex 11.1 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 11 Trigonometry Exercise 11.1

Question 1.
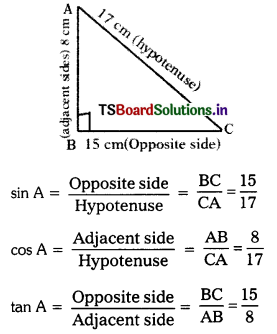
In a right angle triangle ABC, 8 cm, 15 cm and 17 cm are the lengths of AB, BC and CA respectively. Then, find out sin A, cos A and tan A. (AS₁)
Solution:
Given that ∆ABC, AB = 8 cm; BC = 15 cm; CA = 17 cm

Question 2.
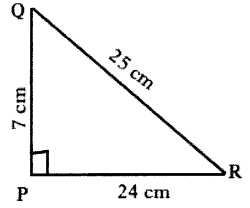
The sides of a right angle triangle PQR are PQ = 7 cm, QR = 25 cm and ∠Q = 90° respectively. Then find tan Q – tan R.
(AS₁)
Solution:
Given that in ∆PQR, PQ = 7 cm
QR = 25 cm and RP = 24 cm
PR = \(\sqrt{\mathrm{QR}^2-\mathrm{PQ}^2}\) = \(\sqrt{25^2-7^2}\)
= \(\sqrt{625-49}\) = \(\sqrt{576}\) – 24
In the text given problem is wrong. We take
∠P = 90° instead of ∠Q = 90°
tan P = \(\frac{\text { Side opposite to } \angle \mathrm{P}}{\text { Side adjacent to } \angle \mathrm{P}}\)
= \(\frac{\mathrm{PR}}{\mathrm{PQ}}\) = \(\frac{24}{7}\)
tan R = \(\frac{\text { Side opposite to } \angle \mathrm{R}}{\text { Side adjacent to } \angle \mathrm{R}}\)
= \(\frac{\mathrm{PQ}}{\mathrm{PR}}\) = \(\frac{7}{24}\)

∴ tan P – tan R = \(\frac{24}{7}\) – \(\frac{7}{24}\)
= \(\frac{576-49}{168}\) = \(\frac{27}{168/}\)

Question 3.
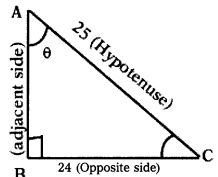
In a right tingle triangle ABC with right angle at B, in which a = 24 units, b = 25 units and ∠BAC = θ. Then, find cos θ and tan θ.
Solution:
In ∆ABC, ∠B = 90°
a = BC = 24 units
b = AC = 25 units
In ∆ABC,
∴ AC² = AB² + BC²
∠B = 90° (Pythagoras theorem)

25² = AB² + 24²
⇒ AB² = 25² – 24²
= 625 – 576 = 49
⇒ AB = \(\sqrt{49}\) = 7
c = AB = 7 units
cos θ = \(\frac{\text { Side adjacent to } \theta}{\text { Hypotenuse }}\)
= \(\frac{\mathrm{AB}}{\mathrm{AC}}\) = \(\frac{7}{25}\)
sin θ = \(\frac{\text { Side opposite to } \theta}{\text { Hypotenuse }}\)
= \(\frac{\mathrm{BC}}{\mathrm{AC}}\) = \(\frac{24}{25}\)
∴ tan θ
= \(\frac{\sin \theta}{\cos \theta}=\frac{\mathrm{BC}}{\mathrm{AC}} \times \frac{\mathrm{AC}}{\mathrm{AB}}=\frac{24}{25} \times \frac{25}{7}=\frac{24}{7}\)

Question 4.
If cos A = \(\frac{12}{13}\), then find sin A and tan A. (AS₁) (A.P. Mar. ’16)
Solution:
Given that, cos A = \(\frac{12}{13}\)
and cos A = \(\frac{\text { Adjacent side }}{\text { Hypotenuse }}\)
For angle A, adjacent side = AB = 12 k Hypotenuse = AC = 13 k (Where k is a positive number)

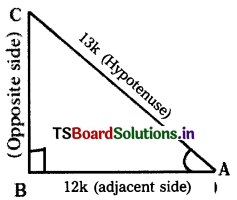
Now, we have in ∆ABC
AC² = AB² + BC² (Pythagoras theorem)
⇒ (13k)² = (12k)² + BC²
⇒ BC² = (13k)² – (12k)²
= 169 k² – 144 k²
= 25 k²
∴ BC = \(\sqrt{25 \mathrm{k}^2}\) = 5 k
BC = 5 k = Opposite side

Question 5.
If 3 tan A = 4, then find sin A and cos A. (AS₁)
Solution:
Given that, 3 tan A = 4

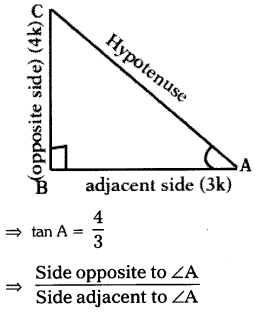
Opposite side to ∠A = BC = 4k
Adjacent side to ∠A = AB = 3k
Now we have in ∆ABC, ∠B = 90°
∴ AC² = AB² + BC² (By Pythagoras theorem)
= (3k)² + (4k)²
= 9k² + 16k²
= 25k²
∴ AC = \(\sqrt{25 \mathrm{k}^2}\) = 5k
AC = 5k = Hypotenuse
sin A = \(\frac{\text { Opposite side }}{\text { Hypotenuse }}\)
= \(\frac{4 \mathrm{k}}{5 \mathrm{k}}\) = \(\frac{4}{5}\)
cos A = \(\frac{\text { Adjacent side }}{\text { Hypotenuse }}\)
= \(\frac{3 \mathrm{k}}{5 \mathrm{k}}\) = \(\frac{4}{5}\)

Question 6.
If ∠A and ∠X are acute angles such that cos A = cos X, then show that ∠A = ∠X. (AS₂)
Solution:
In the given triangle,

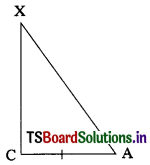
⇒ \(\frac{\mathrm{AC}}{\mathrm{AX}}\) = \(\frac{\mathrm{XC}}{\mathrm{AX}}\)
⇒ AC = XC
⇒ ∠A = ∠X
(∴ Angles opposite to equal sides are also equal)

Question 7.
Given cot θ = \(\frac{7}{8}\), then evaluate
i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
ii) \(\frac{(1+\sin \theta)}{\cos \theta}\) (AS₁)
Solution:
Given,

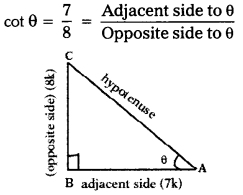
Let AB = 7k and BC = 8k
In a right angled triangle,
AC² = AB² + BC² (By Pythagoras theorem)
= (7k)² + (8k)²
= 49 k² + 64 k²
AC² = 113 k²
AC = \(\sqrt{113}\) k
Now,

Question 8.
In a right angle triangle ABC, right angle Is at B, If tan A = \(\sqrt{3}\), then find the value of
i) sin A cos C + cos A sin C
ii) cos A cos C – sin A sin C (AS₁)
Solution:
Given, tan A = \(\frac{\sqrt{3}}{1}\)

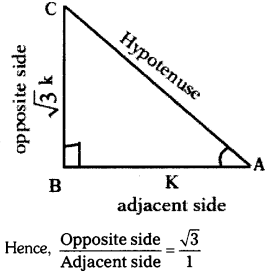
Let opposite side = \(\sqrt{3}\)k and adjacent side = 1 k
In right angled ∆ABC
AC² = AB² + BC² (By Pythagoras theorem)
⇒ AC² = (1k)² + (\(\sqrt{3}\)k)²
⇒ AC² = 1k² + 3k²
⇒ AC² = 4k² ⇒ AC = \(\sqrt{4 \mathrm{k}^2}\)
AC = 2k
Now,
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\sqrt{3} \mathrm{k}}{2 \mathrm{k}}=\frac{\sqrt{3}}{2}\)
cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{1 \mathrm{k}}{2 \mathrm{k}}=\frac{1}{2}\)

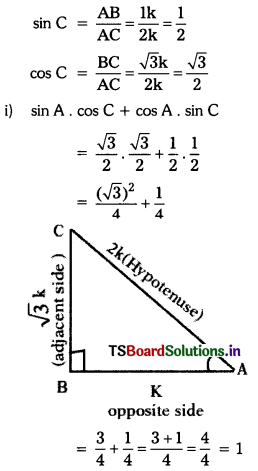
ii) cos A . cos C – sin A . sin C
= \(\frac{1}{2}\) . \(\frac{\sqrt{3}}{2}\) – \(\frac{\sqrt{3}}{2}\) . \(\frac{1}{2}\)
= \(\frac{\sqrt{3}}{4}\) – \(\frac{\sqrt{3}}{4}\) = 0