TS 10th Class Maths Solutions Chapter 10 Mensuration Ex 10.2

Students can practice 10th Class Maths Study Material Telangana Chapter 10 Mensuration Ex 10.2 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 10 Mensuration Exercise 10.2

Question 1.
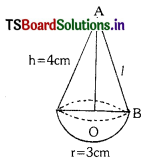
A toy is in the form of a cone mounted on a hemisphere. The diameter of the base and the height of the cone are 6 cm and 4 cm respectively. Determine the surface area of the toy. [use π = 3.14] (AS4)
Solution:
Diameter of the base of the cone (d)= 6 cm
∴ Radius of the base (r) = d/2 = 3 cm
Radius of the hemisphere = 3 cm
Let the slant height of the cone be ‘l’
l² = h² + r²
= 4² + 3²
= 16 + 9 = 25
∴ l = \(\sqrt{25}=\) = 5 cm.

Surface area of the toy = curved surface area of the cone + curved surface area of the hemisphere
= πrl + 2πr²
= \(\frac{22}{7}\) × 3 × 5 + 2 × \(\frac{22}{7}\) × 3 × 3
= \(\frac{22}{7}\) [3 × 5 + 2 × 3 × 3]
= \(\frac{22}{7}\) [15 + 18] = \(\frac{22}{7}\) × 33 = \(\frac{726}{7}\)
= 103.71 cm²

Question 2.
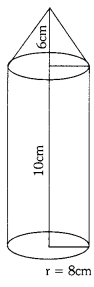
A Solid is in the form of a right circular cylinder with a hemisphere at one end and a cone at the other end. The radius of the common base is 8 cm. and heights of the cylindrical and conical portions are 10 cm and 6cm respectively. Find the total surface area of the solid. [use π = 3.14](AS4)
Solution:
Total surface area = C.S.A of the cone + C.S.A of cylinder + C.S.A of the hemisphere
Cone : Radius (r) = 8 cm
Height (h) = 6 cm
Slant height
l = \(\sqrt{\mathrm{r}^2+\mathrm{h}^2}\)
= \(\sqrt{8^2+6^2}\)
= \(\sqrt{64+36}\)
= \(\sqrt{100}\)
= 10 cm

C.S.A = πrl
= \(\frac{22}{7}\) × 8 × 10 = \(\frac{1760}{7}\) cm²
Cylinder : Radius (r) = 8 cm
Height(h) = 10 cm
C.S.A = 2πrh = 2 × \(\frac{22}{7}\) × 8 × 10
= \(\frac{3520}{7}\) cm
Hemisphere : Radius (r) = 8 cm
C.S.A = 2πr² = 2 × \(\frac{22}{7}\) × 8 × 8
= \(\frac{2816}{7}\) cm²
∴ Total surface area of the given solid
= \(\frac{1760}{7}\) + \(\frac{3520}{7}\) + \(\frac{2816}{7}\)
T.S.A = \(\frac{8096}{7}\) = 1156.57 cm²

Question 3.
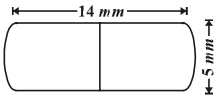
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends. The length of the capsule is 14 mm. and the width is 5mm. Find its surface area. (AS4)

Solution:
Surface area of the capsule = C.S.A of 2 hemispheres + C.S.A of the cylinder
Hemisphere : Radius (r) = \(\frac{\mathrm{d}}{2}\) = \(\frac{5}{2}\)
= 2.5 mm
C.S.A of two hemispheres = 2 × 2πr²
= 4 × \(\frac{22}{7}\) × 2.5 × 2.5 7
= \(\frac{550}{7}\) mm² = 78.57 mm²
Cylinder : Radius (r) = \(\frac{\mathrm{d}}{2}\) = \(\frac{5}{2}\) = 2.5 mm
Height (h) = 14 mm
C.S.A = 2πrh
= 2 × \(\frac{22}{7}\) × 2.5 × 14 = 220 mm²
∴ Surface area of the capsule = 78.57 + 220 = 298.57mm²

Question 4.
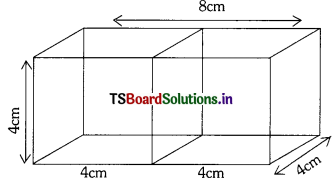
Two cubes each of volume 64 cm3 are joined end to end together. Find the surface area of the resulting cuboid. (AS1) (Mar ’15 (A.P.))
Solution:
Given, volume of the cube, V = a³ = 64 cm³
∴ a³ = 4 × 4 × 4 = 4³
Hence a = 4 cm
When two cubes are added, the length of cuboid = 2a
= 2 × 4 = 8 cm
breadth = a = 4 cm
height = a = 4 cm is formed

∴ T.S.A. of the cuboid
= 2 (lb + bh + lh)
= 2(8 × 4 + 4 × 4 + 8 × 4)
= 2(32 + 16 + 32)
= 2(80) = 160 cm².
∴ The surface area of resulting cuboid is 160 cm².

Question 5.
A storage tank consists of a circular cylinder with a hemisphere stuck on either end. If the external diameter of the cylinder be 1.4 in and its length be 8 m. Find the cost of pointing it on the outside at rate of ₹ 20 per m². (AS4)
Solution:
Total surface area of the tank = 2 × C.S.A of hemisphere + C.S.A of cylinder

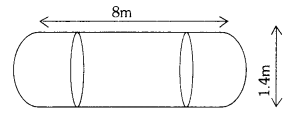
Hemisphere :
Radius (r) = \(\frac{\text { diameter }}{2}\)
= \(\frac{1.4}{2}\)
= 0.7m
C.S.A of hemisphere = 2πr²
= 2 × \(\frac{22}{7}\) × 0.7 × 0.7 7
= 3.08 m²
2 × C.S.A = 2 × 3.08 m² = 6.16 m²
Cylinder : Radius (r) = \(\frac{\text { diameter }}{2}\)
= \(\frac{1.4}{2}\)
= 0.7 m
Height (h) = 8 m
C.S.A of the cylinder = 2πrh
= 2 × \(\frac{22}{7}\) × 0.7 × 8 = 35.2 m²
∴ Total surface area of the storage tank
= 35.2 + 6.16 = 41.36 m²
Cost of painting is surface area ₹ 20 per sq.m = 41.36 × 20 = ₹ 827.2

Question 6.
A sphere, a cylinder and a cone have the same radius and same height. Find the ratio of their volumes. (AS4)
[Hint: Diameter of the sphere is equal to heights of the cylinder and the cone].
Solution:
It is given that the three solids namely a sphere, a cylinder and a cone have the same radius. It is persumed that the three solids are of equal heights.

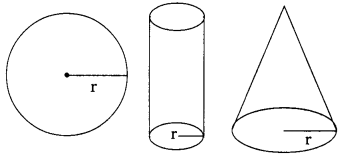
Sphere :
Radius of sphere = r
∴ volume of the sphere = \(\frac{4}{3}\) πr³.

Cylinder :
Radius of cylinder = r
Height of cylinder h = 2r (diameter of sphere)
∴ volume of cylinder = πr²h
= πr² × 2r
= 2πr × 2r
= 2πr³

Cone :
Radius of cone = r
Height of cone h = 2r
∴ Volume of cone = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) πr² × 2r
= \(\frac{2}{3}\) πr³
∴ The ratios of the volumes
= sphere : cylinder : cone
= \(\frac{4}{3}\) πr³ : 2πr³ : \(\frac{2}{3}\) πr³
= 4 πr³ : 6πr³ : 2πr³
= 4 : 6 : 2
= 2 : 3 : 1.

Question 7.
A hemisphere is cut out from one face of a cubical wooden block such that the diameter of the hemisphere is equal to the length of the cube. Determine the surface area of the remaining solid. (AS4)
Solution:
T.S.A. of the remaining solid = area of each surface of cube + Area of hemisphere – Area of cutting part of hemisphere.

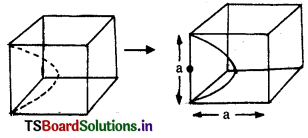
Square surface : Side = a units.
Area a = a × a = a² sq. units.
6 × square surface area = 6a² sq. units.
Hemisphere : Diameter = a, Radius = \(\frac{\mathrm{a}}{2}\)
Area of hemisphere = 2πr²
= 2 × π × \(\left(\frac{\mathrm{a}}{2}\right)^2\)
= 2 × π × \(\frac{\mathrm{a}}{4}\) = \(\frac{\pi \mathrm{a}^2}{2}\)
Area of cutting part of hemisphere
= 2πr² = πr²
= \(\frac{\pi \mathrm{a}^2}{2}\) – π\(\left(\frac{a}{2}\right)^2\)
= \(\frac{\pi \mathrm{a}^2}{2}\) – \(\frac{\pi \mathrm{a}^2}{4}\) = \(\frac{\pi \mathrm{a}^2}{4}\)

Question 8.
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm and its radius is of 3.5 cm, find the total surface are of the article. (AS4)
Solution:
Surface area of the given solid.
= C.S.A. of the cylinder + 2 × C.S.A. of hemisphre.

= 2πrh + 2 × 2πr²
= 2πrh + 4πr²
= 2 × \(\frac{22}{7}\) × 3.5 × 10 + 4 × \(\frac{22}{7}\) × 3.5 × 3.5
= 220 + 2(77)
= 220 + 154 = 374 cm²