TS 10th Class Maths Solutions Chapter 11 Trigonometry Ex 11.4

Students can practice 10th Class Maths Study Material Telangana Chapter 11 Trigonometry Ex 11.4 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 11 Trigonometry Exercise 11.4

Question 1.
Evaluate the following :
i) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
ii) (sin θ + cos θ)² + (sin θ – cos θ)²
iii) (sec² θ – 1) (cosec² θ – 1) (AS₁)
Solution:
i) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
= (1 + tan θ + sec θ)

ii) (sin θ + cos θ)² + (sin θ – cos θ)²
(sin θ + cos θ)² = sin² θ + cos² θ + 2 sin θ cos θ …………. (1)
(sin θ – cos θ)² = sin² θ + cos² θ – 2 sin θ cos θ ……………. (2)
Adding (1) & (2)
sin² θ + cos² θ + 2 sin θ (cos θ) + sin² θ + cos² θ – 2 sin θ (cos θ)
= 2 (sin² θ + cos² θ)
= 2(1) = 2

iii) (sec² θ – 1) (cosec² θ – 1)
sec² θ – 1 = tan² θ …………… (1)
[∵ 1 + tan² θ = sec² θ ⇒ tan² θ = sec² θ – 1]
cosec² θ – 1 = cot² θ …………… (2)
[∵ 1 + cot² θ = cosec² θ ⇒ cot² θ = cosec² θ – 1]
⇒ tan² θ cot² θ
⇒ (tan θ cot θ)² [∵ (tan θ) (cot θ) = 1]
⇒ (1)² = 1

Question 2.
Show that   (A.P. June ’15)
(cosec θ – cot θ)² = \(\frac{1-\cos \theta}{1+\cos \theta}\) (AS₂)
Solution:
(cosec θ – cot θ)² = \(\left(\frac{1}{\sin \theta}-\frac{\cos \theta}{\sin \theta}\right)^2\)

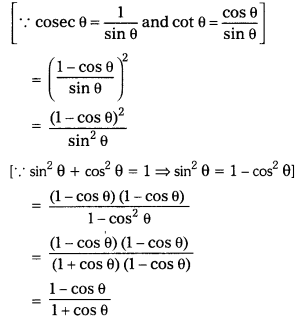
Question 3.
Show that \(\sqrt{\frac{1+\sin A}{1-\sin A}}\) = sec A + tan A. (AS₂)
Solution:

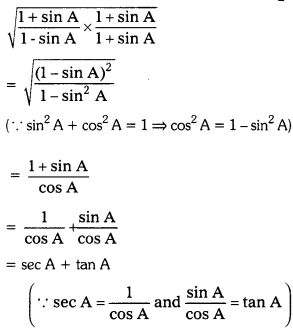
Question 4.
Show that \(\frac{1-\tan ^2 A}{\cot ^2 A-1}\) = tan² A. (AS₂)
Solution:

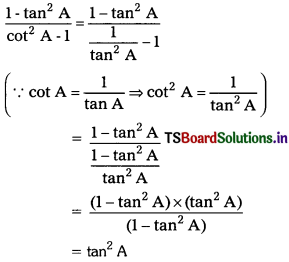
Question 5.
Show that \(\frac{1}{\cos \theta}\) – cos θ = tan θ . sin θ (AS₂)
Solution:
L.H.S. = \(\frac{1}{\cos \theta}\) = cos θ = \(\frac{1-\cos ^2 \theta}{\cos \theta}\)
= \(\frac{\sin ^2 \theta}{\cos \theta}\)
[∵ sin²θ + cos²θ = 1 ⇒ sin²θ = 1 – cos²θ]
= \(\frac{\sin \theta}{\cos \theta}\) . sin θ
= tan θ . sin θ (∵ tan θ = \(\frac{\sin \theta}{\cos \theta}\))

Question 6.
Simplify: sec A (1 – sin A). (sec A + tan A). (AS₃)
Solution:
sec A (1 – sin A) = (sec A – sec A . sin A)
= (sec A – \(\frac{\sin A}{\cos A}\))
= (sec A – tan A)
∴ sec A (1 – sin A) = (sec A + tan A)
= (sec A + tan A) (sec A – tan A)
= sec² A – tan² A
= 1
[∵ 1 + tan² A = sec² A ⇒ sec² A – tan² A = 1]

Question 7.
Prove that (sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot² A) (AS₁, AS₂)
Solution:
L.H.S. = (sin A + cosec A)² + (cos A + sec A)²
= sin² A + cosec² A + 2 sin A. cosec A + cos² A + sec² A + 2 cos A . sec A
= (sin² A + cos² A) + cosec² A+ 2 + sec² A + 2
= 1 + cosec² A + 2 + sec² A + 2
[∵ sin² A + cos² A = 1]
= 5 + cosec² A + sec² A
= 5 + 1 + cot² A + 1 + tan² A
(∵ 1 + cot² A = cosec² A and 1 + tan² A = sec² A)
= 7 + tan² A + cot² A

Question 8.
Simplify : (T.S. Mar.’15) (AS₁, AS₃)
(1 – cos θ) (1 + cos θ) (1 + cot² θ)
Solution:
(1 – cos θ) (1 + cos θ) (1 + cot² θ)
= (1 – cos² θ) (1 + cot² θ)
[∵ (a – b) (a + b) = a² – b²]
= sin² θ (1 + cot² θ)
(∵ sin² θ + cos² θ = 1 ⇒ sin² θ = 1- cos² θ)
= sin² θ + sin² θ . cot² θ
= sin² θ + sin² θ . \(\frac{\cos ^2 \theta}{\sin ^2 \theta}\)
(∵ cot θ = \(\frac{\cos \theta}{\sin \theta}\) cot²θ = \(\frac{\cos ^2 \theta}{\sin ^2 \theta}\))
= sin² θ + cos² θ
= 1

Question 9.
If sec θ + tan θ = p, then what is the value of sec θ – tan θ ? (AS₁)
Solution:
We know that 1 + tan² θ = sec2 θ
⇒ sec² θ – tan² θ = 1
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1
[∵ a² – b² = (a + b) (a – b)]
⇒ p(sec θ – tan θ) = 1
⇒ sec θ – tan θ = \(\frac{1}{\mathrm{p}}\).
∴ The value of sec θ – tan θ = \(\frac{1}{\mathrm{p}}\)

Question 10.
If cosec θ + cot θ = k, then prove that cos θ = \(\frac{\mathrm{k}^2-1}{\mathrm{k}^2+1}\). (A.P. Mar.’16) (AS₁)
Solution:
Given that cosec θ – cot θ = k