TS 10th Class Maths Solutions Chapter 11 Trigonometry InText Questions

Students can practice 10th Class Maths Study Material Telangana Chapter 11 Trigonometry InText Questions to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 11 Trigonometry InText Questions

Do This

Identify “Hypotenuse”, “Opposite side” and “Adjacent side” for the given angles in the given triangles. (AS₃) (Page No. 271)

Question 1.
For angle R
Solution:

In the ∆PQR
Opposite side = PQ
Adjacent side = QR
Hypotenuse side = PR

Question 2.
i) For angle X
ii) For angle Y

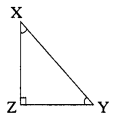
Solution:
i) In the ∆XYZ
For angle X
Opposite side = YZ
Adjacent side = XZ
Hypotenuse = XY

ii) For angle Y
Opposite side = XZ
Adjacent side = YZ
Hypotenuse = XY

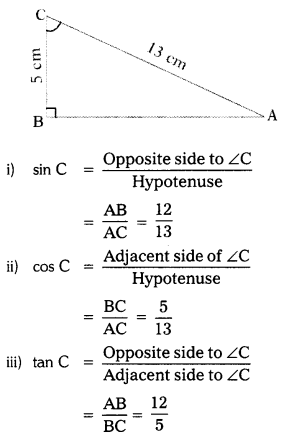
Question 3.
Find (i) sin C (ii) cos C (iii) tan C in the given triangle.
Solution:
By Pythagoras theorem
AC² = AB² + BC²
(13)² = AB² + (5)²
AB² = 169 – 25
AB² = 144
∴ AB = \(\sqrt{144}\) = 12

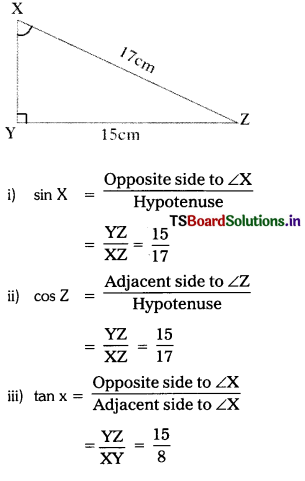
Question 4.
In a triangle XYZ, ZY is right angle. XZ = 17 cm and YZ = 15 cm, then find
(i) sin X (ii) cos Z (iii) tan X. (AS₁) (Page No. 274)
Solution:
Given ∆XYZ, ∠Y is right angle.
By Pythagoras theorem
XZ² = YZ² + XY²
17² = 15² + XY²
XY² = 17² – 15² = 289 – 225 = 64
XY = \(\sqrt{64}\) = 8

Question 5.
In a triangle PQR with right angle at Q, the value of ∠P is x, PQ = 7 cm and QR = 24 cm then find sin x and cos x. (AS₁) (Page No. 274)
Solution:
Given right angled triangle is PQR with right angle at Q. The value of ∠P is x.
By Pythagoras theorem
PR² = PQ² + QR²
= 7² + 24²

PR² = 49 + 576
PR² = 625
PR = \(\sqrt{625}\) = 25
sin x = \(\frac{\mathrm{QR}}{\mathrm{PR}}\) = \(\frac{24}{25}\)
cos x = \(\frac{\mathrm{PQ}}{\mathrm{PR}}\) = \(\frac{7}{25}\)

Try This

Question 1.
Write lengths of “Hypotenuse”, “Opposite side” and “Adjacent side” for the given angles in the given triangles. (AS₁) (Page No. 271)
i) For angle C
ii) For angle A
Solution:

In ∆ ABC, ∠B = 90°
∴ AC² = AB² + BC² (By Pythagoras theorem)
⇒ AB² = AC² – BC²
Substitute BC = 4 cm and AC = 5 cm in eq. (1), we get
AB² = 5² – 4² = 25 – 16 = 9
∴ AB = \(\sqrt{9}\) = 3
i) For angle C :
Length of hypotenuse = AC = 5 cm
Length of opposite side = AB = 3 cm
Length of adjacent side = BC = 4 cm

ii) For angle A :
Length of hypotenuse AC = 5 cm
Length of opposite side = BC = 4 cm
Length of adjacent side = AB = 3 cm

Question 2.
In a right angle triangle ABC, right angle is at C, BC + CA = 23 cm and BC – CA = 7 cm, then find sin A and tan B. (AS₁) (Page No. 274)
Solution:
∆ABC, ∠C = 90°
Given that,

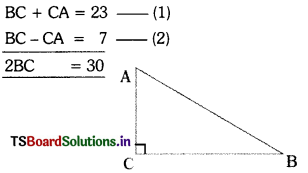
⇒ BC = \(\frac{30}{2}\) = 15
BC + CA = 23
15 + CA = 23
CA = 23 – 15 = 8
AB² = BC² + CA² (By Pythagoras theorem)
= 15² + 8² = 225 + 64 = 289
∴ AB = \(\sqrt{289}\) = 17
sin A = \(\frac{\mathrm{BC}}{\mathrm{AB}}\) = \(\frac{15}{17}\) ; tan B = \(\frac{\mathrm{AC}}{\mathrm{BC}}\) = \(\frac{8}{15}\)

Question 3.
What will be the ratio of sides for sec A and cot A ? (AS₃) (Page No. 275)
Solution:
sec A = \(\frac{1}{\cos A}\) = \(\frac{\text { Hypotenuse } }{\text { Side opposite to angle A }}\)
cot A = \(\frac{1}{\tan A}\) = \(\frac{\text { Side adjacent to angle A} }{\text { Side opposite to angle A }}\)

Think – Discuss

Question 1.
Discuss between your friends that
i) sin x = \(\frac{4}{3}\) does exist for some value of angle x ?
ii) The value of sin A and cos A is always less than 1. Why ?
iii) tan A is product of tan and A.   (AS₂) (Page No. 274)
Solution:
i) The value of sin0 always lies between 0 and 1. Here, sin x = \(\frac{4}{3}\) which is greater than 1. So, it does not exist.

ii) Draw a circle of radius 1 unit with centre at the origin. Let P(a, b) be any point on the circle with angle AOP = θ
sin θ = \(\frac{\mathrm{AP}}{\mathrm{OP}}=\frac{\mathrm{b}}{1}\) = y – co-ordinate
cos θ = \(\frac{\mathrm{OA}}{\mathrm{OP}}=\frac{\mathrm{a}}{1}\) = x – co-ordinate
One complete rotation of point ‘P’ in a circular an angle 360° at the centre.

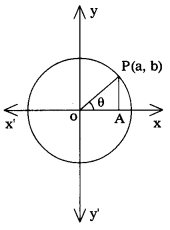
Quarter rotation substends an angle of AOB equals to 90°.
Half rotation substends an angle of AOC equal to 180°.
Three quarter substends an angle of AOD equals to 270°.
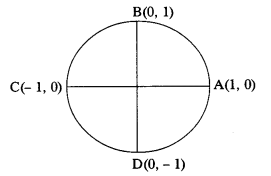
The co-ordinates of the points A, B, C and D respectively (1, 0), (0, 1) (-1, 0) and (0, -1).
According to the co-ordinates
cos 0° = 1 sin 0° = 0
cos 90° = 0 sin 90° = 1
cos 180° = – 1 sin 180° = 0
cos 270° = 0 sin 270° = -1
cos 360° = 1 sin 360° = 0

Hence, the value of “sine” and “cosine” is always less than 1.

iii) The symbol tan A is used as an abbreviation for “the tan of the angle A”, tan A is not the product of “tan” and A “tan” separated from “A” has no meaning.

Question 2.
Is \(\frac{\sin \mathrm{A}}{\cos \mathrm{A}}\) equal to tan A ? (Page No. 275)
Solution:

Question 3.
Is \(\frac{\cos \mathrm{A}}{\sin \mathrm{A}}\) equal to cot A ? (Page No. 275)
Solution:

Do This

Question 1.
Find cosec 60°, sec 60° and cot 60°. (AS₁) (Page No. 279)
Solution:
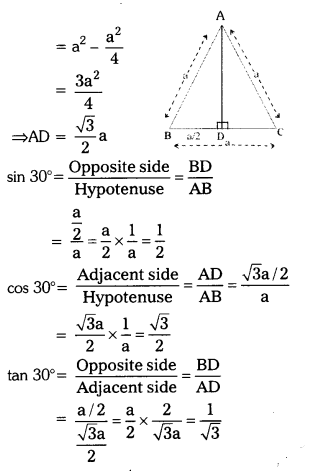
Consider an equilateral triangle ABC. Since each angle is 60° in an equilateral triangle, we have ∠A = ∠B = ∠C = 60° and the sides of equilateral triangle is AB = BC = CA = 2a units

Draw the perpendicular line AD from vertex A to BC as shown in the given figure.

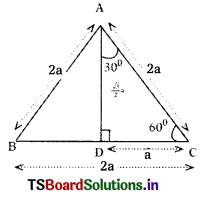
Perpendicular AD acts as “angle bisector of angle A” and “bisector of the side BC” in the equilateral triangle ABC.
Therefore, ∠BAD = ∠CAD = 30°.
Since point D divides the side BC into equal halves.
BD = \(\frac{1}{2}\) BC = \(\frac{2 \mathrm{a}}{2}\) = a units
Consider right angle triangle ABD in the above given figure.
We have AB = 2a, and BD = a
Then AD² = AB² – BD² (By Pythagoras theorem)
= (2a)² – (a)² = 3a²
Therefore, AD = a\(\sqrt{3}\)
From, definitions of trigonometric ratios.
sin 60° = \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{a} \sqrt{3}}{2 \mathrm{a}}=\frac{\sqrt{3}}{2}\)
cos 60° = \(\frac{\mathrm{BD}}{\mathrm{AB}}=\frac{\mathrm{a}}{2 \mathrm{a}}=\frac{1}{2}\)
So, similarly tan 60° = \(\sqrt{3}\)

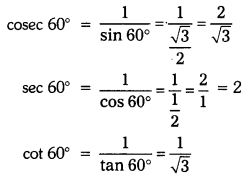
Try This

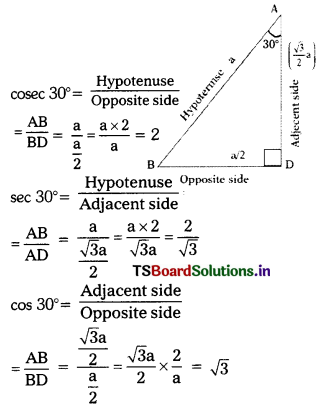
Question 1.
Find sin 30°, cos 30°, tan 30°, cosec 30°, sec 30° and cot 30° by using the ratio concepts. (AS₁) (Page No. 279)
Solution:
Let ABC be an equilateral triangle.
∴ ∠A = ∠B = ∠C = 60°
Let AB BC = CA ‘a’ units
Draw AD ⊥ BC, AD bisects BC.
∴ BD = a/2
In ∆ABD, ∠ADB = 90°; ∠B = 60°
∴ ∠BAD = 180° – (90° + 60°)
= 180° – 150° = 30°
By Pythagoras theorem,
AB² = AD² + BD²
⇒ AD² = AB² – BD²

Question 2.
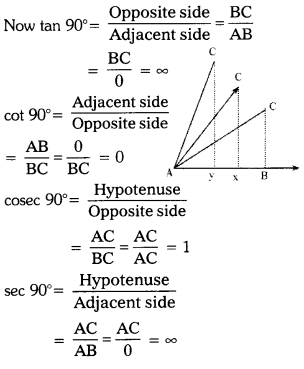
Find the values for tan 90°, cosec 90°, sec 90° and cot 90°. (AS₁) (Page No. 281)
Solution:
Let us see what happens when angle made by AC with ray AB increases. When angle A is increased, height of point C increases and the foot of the perpendicular shifts from B to X and then to Y and so on. So, when the angle becomes 90°, base (adjacent side of the angle) would become zero; the height of C from AB ray increases and it would be equal to AC.
AB = 0 and BC = AC

Think – Discuss

Question 1.
Discuss between your friend about the following conditions :
What can you say about cosec 0° = \(\frac{1}{\sin 0}\) ? Is it not defined ? Why ? (AS₂) (Page No. 280)
Solution:
sin 0° = 0
cosec 0° = \(\frac{1}{\sin 0}\) = \(\frac{1}{0}\) = not defined
Reason : Division by ‘0’ is not allowed, hence \(\frac{1}{0}\) is indeterminate.

Question 2.
Is it defined cot 0° = \(\frac{1}{\tan 0}\) ? Why ? (Page No. 281)
Solution:
tan 0° = 0
cot 0° = \(\frac{1}{\tan 0}\) = \(\frac{1}{0}\) undefined
Reason : Division by ‘0’ is not allowed, hence \(\frac{1}{\tan 0}\) is indeterminate.

Question 3.
sec 0° = 1. Why ? (Page No. 281)
Solution:
sec 0° = \(\frac{1}{\cos 0^{\circ}}\) [∵ cos 0° = 1]
= \(\frac{1}{1}\) = 1

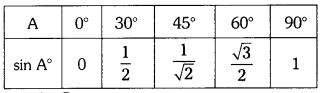
Question 4.
What can you say about the values of sin A and cos A, as the value of angle A increases from 0° to 90° ? (AS₃) (Page No. 282)
i) If A > B, then sin A > sin B. Is it true ?
ii) If A > B, then cos A > cos B. Is it true ? Discuss.
Solution:
i) Given statement
“If A > B, then sin A > sin B”.
Yes, this statement is true.
Because, it is clear from the table below that the sin A increases as A increases.

ii) Given statement
“If A > B, then cos A > cos B”.
No, this statement is not true.
Because it is clear from the table below that cos A decreases as A increases.

Think – Discuss

Question 1.
For which value of acute angle
i) \(\frac{\cos \theta}{1-\sin \theta}+\frac{\cos \theta}{1+\sin \theta}\) = 4 is true ? For which value of 0° ≤ θ ≤ 90°, above equa-tion is not defined ? (AS₁, AS₂) (Page No. 285)
Solution:
Given \(\frac{\cos \theta}{1-\sin \theta}+\frac{\cos \theta}{1+\sin \theta}\) = 4

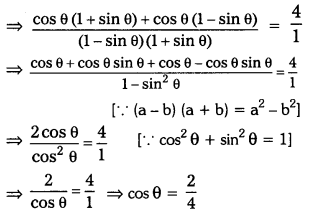
cos θ = \(\frac{1}{2}\)
cos θ = cos 60°
∴ θ = 60°
Given statement is true for the acute angle i.e., θ = 60°

Question 2.
Check and discuss the above relations AB
[sin (90° – x) = \(\frac{\mathrm{A B}}{\mathrm{A C}}\) = cos x and BC
cos (90° – x) = \(\frac{\mathrm{B C}}{\mathrm{A C}}\) = sin x,
tan (90° – x) = \(\frac{\mathrm{A B}}{\mathrm{A C}}\) = cot x and
cot (90° – x) = \(\frac{\mathrm{B C}}{\mathrm{A B}}\) = tan x,
cosec (90° – x) = \(\frac{\mathrm{A C}}{\mathrm{A B}}\) = sec x and
sec (90° – x) = \(\frac{\mathrm{A C}}{\mathrm{B C}}\) = cosec x] in the case of angles between 0° and 90°, whether they hold for these angles or not ? So,
(i) sin (90° – A) = cos A
(ii) cos (90° – A) = sin A
(iii) tan (90° – A) = cot A and
(iv) cot (90° – A) = tan A
(vi) cosec (90° – A) = cosec A
(v) sec (90° – A) = cosec A (AS₂) (Page No. 286)
Solution:
Let A = 30°
i) sin (90° – A ) = cos A
⇒ sin (90° – 30°) = cos 30°
⇒ sin 60° = cos 30° = \(\frac{\sqrt{3}}{2}\)

ii) cos (90° – A ) = sin A
⇒ cos (90° – 30°) = sin 30°
⇒ cos 60° – sin 30° = \(\frac{1}{2}\)

iii) tan (90° – A ) = cot A
⇒ tan (90° – 30°) = cot 30°
⇒ tan 60° = cot 30° = \(\sqrt{3}\)

iv) cot (90° – A ) = tan A
⇒ cot (90° – 30°) = tan 30°
⇒ cot 60° = tan 30° = \(\frac{1}{\sqrt{3}}\)

v) sec (90° – A ) = cosec A
⇒ sec (90° – 30°) = cosec 30°
⇒ sec 60° = cosec 30° = 2

vi) cosec (90° – A ) = sec A
⇒ cosec (90° – 30°) = sec 30°
⇒ cosec 60° = sec 30° = \(\frac{2}{\sqrt{3}}\)
So, the above relations hold for all the angles between 0° and 90°.

Do This

i) If sin C = \(\frac{15}{17}\), then find cos C. (AS₁) (Page No. 290)
Solution:
Given sin C = \(\frac{15}{17}\)
cos C = \(\sqrt{1-\sin ^2 \mathrm{C}}\) (from identity – 1)
= \(\sqrt{1-\left(\frac{15}{17}\right)^2}\) = \(\sqrt{\frac{289-225}{289}}\) = \(\sqrt{\frac{64}{289}}\) = \(\frac{8}{17}\)

ii) If tan x = \(\frac{5}{12}\), then find sec x. (AS₁) (Page No. 290)
Solution:
Given tan x = \(\frac{5}{12}\)
We know that sec²x – tan²x = 1
sec²x = 1 + tan²x

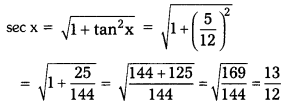
iii) If cosec θ = \(\frac{25}{7}\), then find cot θ. (AS₁) (Page No. 290)
Solution:
Given cosec θ = \(\frac{25}{7}\)
We know that cosec²θ – cot²θ = 1
cot²θ = cosec²θ – 1

Try This

Question 1.
Evaluate the following and justify your answer. (AS₄) (Page No. 290)
i) \(\frac{\sin ^2 15+\sin ^2 75}{\cos ^2 36+\cos ^2 54}\)
ii) sin 5° cos 85° + cos 5° sin 85°
iii) sec 16° cosec 74° – cot 74° tan 16°
Solution:
i) \(\frac{\sin ^2 15+\sin ^2 75}{\cos ^2 36+\cos ^2 54}\)
We can write sin 15°= sin (90° – 75°)
= cos 75°
∴ sin² 15° = cos² 75°
Similarly, cos 36°= cos (90° – 54°) = sin 54°
∴ cos² 36° = sin² 54°
sin² 15° + sin² 75°= cos² 75° + sin² 75°
(∵ sin² 15° = cos² 75°)
= 1 ———– (1) (∵ cos²θ + sin²θ = 1)
(Here θ = 75°)
cos² 36° + cos² 54°= sin² 54° + cos² 54°
(∵ cos² 36° = sin² 54°)
= 1 ———– (2) (∵ sin²θ + cos²θ = 1)
(Here θ = 54°)
From (1) & (2), we get
\(\frac{\sin ^2 15+\sin ^2 75}{\cos ^2 36+\cos ^2 54}\) = \(\frac{1}{1}\) = 1

ii) sin 5° cos 85° + cos 5° sin 85° …………….. (1)
sin 5°= sin (90° – 85°) = cos 85°
cos 5° = cos (90° – 85°) = sin 85°
Substitute these values of sin 5° and cos 5° in (1).
We get
sin 5° cos 85° + cos 5° sin 85°
= cos 85°. cos 85° + sin 85°. sin 85°
= cos² 85° + sin² 85°
= 1 (∵ cos² θ + sin² θ = 1, Here θ = 85°)

iii) sec 16° cosec 74° – cot 74° tan 16° …………….. (1)
cosec 74° = cosec (90° – 16°) = sec 16°
[(∵ cosec (90° – θ) = sec θ) and cot(90° – θ) = tan θ]
cot 74° = cot (90° – 16°) = tan 16°
Substitute the equivalents of cosec 74° and cot 74° in (1), we get
sec 16° . cosec 74° – cot 74° . tan 16°
= sec 16° . sec 16° – tari 16° . tan 16°
= sec² 16° – tan² 16° = 1
(∵ sec² θ – tan²θ = 1) Here θ = 16°

Think – Discuss

Question 1.
Are these identities true for 0° ≤ A ≤ 90° ? If not, for which values of A they are true ?
i) sec² A – tan² A = 1
ii) cosec² A – cot² A = 1 (AS₂) (Page No. 290)
Solution:
i) Given identity is sec² A – tan² A = 1
Let A = 0°
LHS = sec² 0° – tan² 0°
= 1 – 0 = 1 = R.H.S.
Let A =90°
tan A and sec A are not defined.
So it is true.
∴ For all given values of ‘A’ such that 0° ≤ A ≤ 90° this trigonometric identity is true.

ii) Given identity is cosec² A – cot² A = 1
Let A = 0°
cosec A and cot A are not defined for A = 0°.
Therefore identity is true for A = 0°
Let A = 90°
cosec A = cosec 90° = 1
cot A = cot 90° = 0
∴ L.H.S. = 1² – 0² = 1 – 0 = 1 = R.H.S.
∴ This identity is true for all values of A, such that 0° ≤ A ≤ 90°