TS 10th Class Maths Solutions Chapter 11 Trigonometry Ex 11.2

Students can practice 10th Class Maths Study Material Telangana Chapter 11 Trigonometry Ex 11.2 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 11 Trigonometry Exercise 11.2

Question 1.
Evaluate the following. (AS₁)
i) sin 45° + cos 45°
Solution:
sin 45° + cos 45°
= \(\frac{1}{\sqrt{2}}\) + \(\frac{1}{\sqrt{2}}\)
= \(\frac{1+1}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\frac{2}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2}=\sqrt{2}\)

ii) \(\frac{\cos 45}{\sec 30 + cosec 60}\)
Solution:

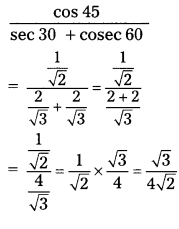
iii) \(\frac{\sin 30+\tan 45-\ cosec 60}{\cot 45+\cos 60-\sec 30}\)
Solution:

iv) 2 tan² 45° + cos² 30° – sin² 60°
Solution:
2 tan² 45° + cos² 30° – sin² 60°
= 2(1)² + \(\left(\frac{\sqrt{3}}{2}\right)^2\) – \(\left(\frac{\sqrt{3}}{2}\right)^2\)
= \(\frac{2}{1}\) + \(\frac{3}{4}\) – \(\frac{3}{4}\)
= \(\frac{8+3-3}{4}\) = \(\frac{8}{4}\) = 2

v) \(\frac{\sec ^2 60-\tan ^2 60}{\sin ^2 30+\cos ^2 30}\)
Solution:

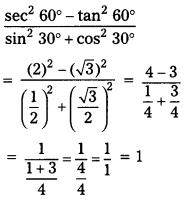
Question 2.
Choose the right option and justify your choice.
i) \(\frac{2 \tan 30}{1+\tan ^2 45}\)
(a) sin 60°
(b) cos 60°
(c) tan 30°
(d) sin 30°
Solution:
(c)

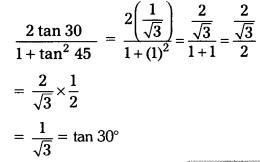
ii) \(\frac{1-\tan ^2 45}{1+\tan ^2 45}\)
(a) tan 90°
(b) 1
(c) sin 45°
(d) 0
Solution:
(d)
\(\frac{1-\tan ^2 45^{\circ}}{1+\tan ^2 45^{\circ}}=\frac{1-(1)^2}{1+(1)^2}=\frac{0}{1+1}=\frac{0}{2}\) = 0

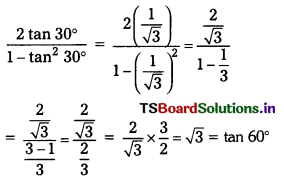
iii) \(\frac{2 \tan 30}{1-\tan ^2 30}\)
(a) cos 60°
(b) sin 60°
(c) tan 60°
(d) sin 30°
Solution:
(c)

Question 3.
Evaluate sin 60° cos 30° + sin 30° cos 60°. What is the value of sin (60° + 30°) ? What can you conclude ? (AS₁, AS₃)
Solution:
Take sin 60°. cos 30° + sin 30°. cos 60°
= \(\frac{\sqrt{3}}{2}\) . \(\frac{\sqrt{3}}{2}\) + \(\frac{1}{2}\) . \(\frac{1}{2}\)
= \(\frac{(\sqrt{3})^2}{4}\) + \(\frac{1}{4}\) = \(\frac{3}{4}\) + \(\frac{1}{4}\)
= \(\frac{3+1}{4}\) = \(\frac{4}{4}\) = 1 …………….. (1)
Now take sin (60° + 30°) = sin 90° = 1 ………….. (2)
From equations (1) and (2), I conclude that sin (60° + 30°) = sin 60°. cos 30° + sin 30° . cos 60°
i.e., sin (A + B) = sin A . cos B + cos A . sin B

Question 4.
Is it right to say cos (60° + 30°) = cos 60°. cos 30° – sin 60°. sin 30° ? (AS₂, AS₃)
Solution:
L.H.S. = cos (60° + 30°)
= cos 90° = 0
R.H.S. = cos 60° . cos 30° – sin 60° . sin 30°
= \(\frac{1}{2}\) . \(\frac{\sqrt{3}}{2}\) – \(\frac{\sqrt{3}}{2}\) . \(\frac{1}{2}\)
= \(\frac{\sqrt{3}}{4}\) – \(\frac{\sqrt{3}}{4}\) = 0
∴ L.H.S. = R.H.S.
Yes, it is right to say
cos (60° + 30°) = cos 60°. cos 30° – sin 60°. sin 30°
i.e., cos (A + B) = cos A . cos B – sin A . sin B

Question 5.
In right angled triangle ∆PQR, right angle is at Q and PQ = 6 cm, ∠RPQ = 60°. Determine the lengths of QR and PR. (AS₄)
Solution:
In ∆PQR, ∠Q = 90°
∠RPQ = 60°

Question 6.
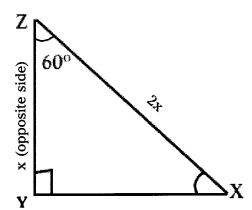
In ∆XYZ, right angle is at Y, YZ = x and XY = 2x, then determine ∠YXZ and ∠YZX. (AS₄)
Solution:
In ∆XYZ, ∠YXZ = ?
Given that ∠XYZ = 90°
sin x = \(\frac{Y Z}{X Y}=\frac{X}{2 x}=\frac{1}{2}\)
We know that sin 30° = \(\frac{1}{2}\)
∴ x = 30°
In ∆XYZ, ∠Y = 90°, ∠X = 30°
∠YZX = 180° – (∠Y + ∠X)

= 180° – (90° + 30°)
= 180° – 120°
= 60°

Question 7.
Is it right to say that sin (A + B) = sin A + sin B ? Justify your answer. (AS₂)
Solution:
Take A = 60°, B = 30°
Then sin (A + B) = sin (60° + 30°)
= sin 90° = 1
sin A + sin B = sin 60° + sin 30°
= \(\frac{\sqrt{3}}{2}\) + \(\frac{1}{2}\)
= \(\frac{\sqrt{3}+1}{2}\)
∴ sin (A + B) ≠ sin A + sin B
It is not right to say that sin (A + B) = sin A + sin B