Mahesh

Students must practice these TS Intermediate Maths 1B Solutions Chapter 6 Direction Cosines and Direction Ratios Ex 6(b) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Direction Cosines and Direction Ratios 6(b)

Question 1.
Find the direction ratios of the line joining the points (3, 4, 0) and (4, 4, 4). (V.S.A.Q.)
Answer:
Let A = (3, 4, 0) and B = (4, 4, 4) be the given points.
Then d.r.’s of AB = ( 4 – 3, 4 – 4, 4 – 0) = (1, 0, 4)

Question 2.
The direction ratios of a line are (-6, 2, 3). Find its direction cosines. (V.S.A.Q.)
Answer:
d.r’s of the line are -6, 2, 3.
∴ \(\sqrt{a^2+b^2+c^2}\) = \(\sqrt{36+4+9}\) = √49 = 7
d.c.’s of the line are \(\frac{-6}{7}, \frac{2}{7}, \frac{3}{7}\).

Question 3.
Find the cosine of the angle between the lines whose direction cosines are
\(\left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right)\) and \(\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0\right)\).
Answer:
cos θ = l₁ l₂ + m₁ m₂ + n₁n₂

Question 4.
Find the angle between the lines whose d.r.’s are (1, 1, 2), (√3 , – √3, 0). (V.S.A.Q.)
Answer:
We have

Question 5.
Show that the lines with direction cosines \(\left(\frac{12}{13}, \frac{-3}{13}, \frac{-4}{13}\right)\) and \(\left(\frac{4}{13}, \frac{12}{13}, \frac{3}{13}\right)\) are Perpendicular to each other. (V.S.A.Q.)
Answer:
We have the condition for two lines with d.c.’s (l₁, m₁, n₁) and (l₂, m₂, n₂) to be perpendicular is l₁l₂ + m₁m₂ + n₁n₂ = 0
∴ l₁l₂ + m₁m₂ + n₁n₂

∴ The given lines are perpendicular.

Question 6.
O is the origin, P(2, 3, 4) and Q (1, k, 1) are points such that OP ⊥ OQ . Find k.
Answer:
d.r.’s of OP = 2, 3, 4
d.r.’s of OQ = 1, k, 1
OP and OQ are perpendicular.
⇒ a₁a₂ + b₁b₂ + c₁c₂ = 0
⇒ 2 + 3k + 4 = 0 ⇒ 3k + 6 = 0 ⇒ k = – 2

II.
Question 1.
If the direction ratios of a line are (3, 4, 0) find its direction cosines and also the angles made with the coordinate axes. (S.A.Q.)
Answer:
d.c.’s of the line are (3, 4, 0).
\(\sqrt{a^2+b^2+c^2}\) = \(\sqrt{9+16}\) = 5
∴ d.c.’s of the line are
If α, β, γ are angles made by the line with the
coordinate axes then cos α = \(\frac{3}{5}\), cos β = \(\frac{4}{5}\), cos γ = 0
∴ α = cos^-1 (3/5), β = cos^-1 (4/5), γ = \(\frac{\pi}{2}\)
∴ Angles made with coordinate axes are
cos^-1 (3/5), cos^-1 (4/5) and \(\frac{\pi}{2}\).

Question 2.
Show that the line through the points (1, -1, 2), (3, 4, -2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6). (S.A.Q.)
Answer:
Let A = (1, -1, 2), B = (3, 4, -2), C = (0, 3, 2) and D = (3, 5, 6) be the given points.
d.r.’s of AB = (3 – 1, 4 + 1, -2 – 2) = (2, 5,4)
d.r.’s of CD = (3 – 0, 5 – 3, 6 – 2) = (3, 2, 4)
∴ a₁ a₂ + b₁ b₂ + c₁ c₂ = 2(3) + 5(2) + (-4) (4) = 0
∴ AB and CD are perpendicular.

Question 3.
Find the angle between DC and AB where A = (3, 4, 5), B = (4, 6, 3), C = (-1, 2, 4) and D = (1, 0, 5). (S.A.Q.)
Answer:
d.r.’s of AB are (4 – 3, 6 – 4, 3 – 5) = (1, 2, -2)
d.r.’s of CD are (1 + 1, 0 – 2, 5 – 4) = (2, -2, 1)

Question 4.
Find the direction cosines of a line which is perpendicular to the lines, whose direction ratios are (1, -1, 2) and (2, 1, -1). (S.A.Q.)
Answer:
Let the d.c.’s of the required line be a, b, c. This is perpendicular to the line whose d.r.’s are (1,-1, 2) and (2, 1, -1).
Then a – b + 2c = 0
and 2a + b – c = 0

Question 5.
Show that the points (2, 3, -4), (1, -2 ,3) and (3, 8, -11) are collinear. (S.A.Q.)
Answer:
Let A = (2, 3, -4), B = (1, -2, 3) and C = (3, 8, -11) be the three given points.

∵ AB + AC = 5√3 + 5√3 = 10√3 = BC
We have A, B, C are collinear.

Question 6.
Show that the points (4, 7, 8), (2, 3, 4), (-1, -2, 1), (1, 2, 5) are the vertices of a parallelogram. (S.A.Q.)
Answer:
Let A = (4, 7, 8), B = (2, 3, 4), C = (-1, -2, 1) and D = (1, 2, 5) be the four given points.

d.r.’s of \(\overline{\mathrm{AB}}\) = (2 – 4, 3 – 7, 4 – 8)
= (-2, -4, -4) ………………. (1)
d.r.’s of \(\overline{\mathrm{DC}}\) = (- 1 – 1, – 2 – 2, 1 – 5)
= (-2, -4, -4) ………………… (2)
d.r.’s of \(\overline{\mathrm{AB}}\) = DR’s of \(\overline{\mathrm{DC}}\) we have \(\overline{\mathrm{AB}}\) is parallel to \(\overline{\mathrm{DC}}\).
d.r.’s of \(\overline{\mathrm{AD}}\) = (1 – 4, 2 – 7, 5 – 8)
= (-3, -5, -3) ……………………. (3)
d.r.’s of \(\overline{\mathrm{BC}}\) = (-1 – 2, -2 – 3, 1 – 4)
= (-3, -5, -3) …………………….. (4)
∵ d.r.’s of \(\overline{\mathrm{AD}}\) = d.r.’s of \(\overline{\mathrm{BC}}\), we have \(\overline{\mathrm{AD}}\) is parallel to \(\overline{\mathrm{BC}}\).
From (1) and (3),
(-2) (-3) + (-4) (-5) + (-4) (-3) ≠ 0
From (2) and (4),
(-2) (-3) + (-4) (-5) + (-4) (-3) ≠ 0
We have \(\overline{\mathrm{AD}}\) is not perpendicular to \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{DC}}\) is not perpendicular to \(\overline{\mathrm{BC}}\).
Also d.r.’s of \(\overline{\mathrm{AC}}\) = (-1 – 4, -2 -7, 1 – 8)
= (-5, -9, -7) ………………….. (5)
d.r.’s of B\(\overline{\mathrm{BD}}\) = (1 – 2, 2 – 3, 5 – 4)
= (-1, -1, 1) ………………….. (6)
From (5) and (6)
(- 5) (- 1) + (- 9) (- 1) + (1) (-7) ≠ 0
Hence diagonals \(\overline{\mathrm{AC}}\) and \(\overline{\mathrm{BD}}\) are not perpendicular. Hence ABCD is a parallelogram.

III.
Question 1.
Show that the lines whose direction cosines are given by l + m + n = 0, 2mn + 3nl – 5lm= 0 are perpendicular to each other.(E.Q.) (March ’12)
Answer:
Given l + m + n = 0 ………………… (1)
and 2mn + 3nl – 5lm = 0 …………………….. (2)
From (1), l = – (m + n)
∴ From (2), 2mn – 3n(m + n) + 5m(m + n) = 0
⇒ 2mn – 3mn – 3n² + 5m² + 5mn = 0
⇒ 5m² + 4mn – 3n² = 0
⇒ 5\(\left(\frac{m}{n}\right)^2\) + 4\(\left(\frac{m}{n}\right)\) – 3 = 0
This is a quadratic equation in \(\left(\frac{m}{n}\right)\) and let \(\frac{m_1}{n_1}\) and \(\frac{m_2}{n_2}\) be the roots of the quadratic equation.
Then product of roots \(\frac{m_1}{n_1} \cdot \frac{m_2}{n_2}=\frac{-3}{5}\)
⇒ \(\frac{m_1 m_2}{3}=\frac{n_1 n_2}{-5}\) = k (suppose) …………… (3)
From (1), m = – (l + n)
– 2n (l + n) + 3nl + 5l (l + n) = 0
⇒ 5l² + 6nl – 2n² = 0

∴ l₁l₂ = 2k, m₁m₂ = 3k, n₁n₂ = – 5k
∴ l₁l₂ + m₁m₂ + n₁n₂ = 0
∴ The two lines are perpendicular.

Question 2.
Find the angle between the lines whose direction cosines satisfy the equations l + m + n = 0, l² + m² – n² = 0. (E.Q.) (May 2014, ‘11,2007, Mar. ’13, ’07, June 2004)
Answer:
Given equations are
l + m + n = 0 ………………….. (1) and
l² + m² – n² = 0 …………………… (2)
From (1), l = – (m + n)
From (2), [-(m + n)]² + m² – n² = 0
⇒ m² + n² + 2mn + m² – n² = 0
⇒ 2m² + 2mn = 0
⇒ 2m (m + n) = 0
⇒ m = 0 or m = -n

Case (i): If m = 0 then
l(0) + m (1) + n(0) = 0
and l + m + n = 0 ……………… (1)
Solving

∴ d.c.’s of one pair of lines
(l₁, m₁, n₁) = \(\left(\frac{1}{\sqrt{2}}, \frac{0}{\sqrt{2}}, \frac{-1}{\sqrt{2}}\right)\)

Case (ii): If m + n = 0 then
l(0) + m(1) + n(1) = 0
and l + m + n = 0
Solving

Question 3.
If a ray makes angles α, β, γ and δ with the four diagonals of a cube find a cube find cos² α + cos² β + cos² γ + cos² δ (E.Q.) (March 2005, May 2005)
Answer:

Let the side of the cube be of length ‘a’. Let one of the vertices of the cube through the origin ‘O’ and axes be along the three edges \(\overline{\mathrm{OA}}\), \(\overline{\mathrm{OB}}\) and \(\overline{\mathrm{OC}}\). The diagonals of the cube are OP, CD, AE and BF d.r.’s of the diagonals are (a, a, a), (a, a, -a), (-a, a, a) and (a, -a, a) respectively.
Let the d.c.’s of the given ray be l, m, n. If this make angles α, β, γ and δ with the four diagonals of the cube then

Question 4.
If (l₁, two intersecting lines. Show that the d.c’s of two lines bisecting the angles between them are proportioned to l₁ ± l₂, m₁ ± m₂, n₁ ± n₂ (E.Q.)
Answer:
Let OA, OB be the given lines and A, B be the points at which distances from 0.
⇒ Coordinates of A = (l₁, m₁, n₁) and B = (l₂, m₂, n₂)
Mid point of AB, is:
P = \(\left(\frac{l_1+l_2}{2}, \frac{m_1+m_2}{2}, \frac{n_1+n_2}{2}\right)\)
∴ OP is the bisector of ∠AOB ⇒ d.r,’s of OP are l₁ + l₂, m₁ + m₂, n₁ + n₂
Now coordinates of B = (-l₂, -m₂, -n₂) and mid point of AB’ is
Q = \(\left(\frac{l_1-l_2}{2}, \frac{m_1-m_2}{2}, \frac{n_1-n_2}{2}\right)\)
∴ OQ is a bisector of ∠AOB ⇒ d.r.’s of OQ are l₁ – l₂, m₁ – m₂, n₁ – n₂

Question 5.
A (-1, 2, -3), B (5, 0, -6), C (0, 4, -1) are three points. Show that the direction cosines of the bisector of ∠BAC are proportional to (25, 8, 5) and (-11, 20, 23). (E.Q.)
Answer:
Given A (-1, 2, -3), B (5, 0, -6) and C (0,4, -1) are three points.
d.r.’s of AB are = (5 + 1, 0 – 2, – 6 + 3) = (6, – 2, – 3)

Hence d.r.’s of other bisector are (-11, 20, 23) Hence direction cosines of the bisectors of ∠BAC are proportional to (25, 8, 5) and (-11, 20, 23).

Question 6.
If (6, 10, 10), (1, 0, -5), (6, – 10, 0) are vertices of a triangle. Find the direction ratios of its sides. Determine whether it is fight angled or isoceles. (S.A.)
Answer:
Let A (6,10,10), B (1, 0, -5) and C (6, -10, 0) are the vertices of ∆ABC
d.r.’s of AB = (-5, -10, -15) ⇒ (1,2, 3)
d.r.’s of BC = (5, -10, -5) ⇒ (1, -2, 1)
d.r.’s of AC = (0, 20, 10) ⇒ (0, 2, 1)

∴ The given triangle is a right angled triangle.

Question 7.
The vertices of a triangle are A (1, 4, 2), B (-2, 1, 2), C (2, 3, -4). Find ∠A, ∠B, ∠C. (S.A.Q.)
Answer:
Given A (1, 4, 2), B (-2, 1, 2) and C (2, 3, -4) are the vertices of ABC.
d.r.’s of AB are = 3, 3, 0 i.e., 1, 1, 0
d.r.’s of BC are = -4, -2, 6 i.e., 2, 1,- 3
d.r.’s of AC are – 1, 1, 6

Question 8.
Find the angle between the lines whose direction cosines are given by the equation 3l + m + 5n = 0 and 6mn – 2nl + 5lm = 0 (E.Q.) ( May’06, ’12))
Answer:
Given 3l + m + 5n = 0 ……………………. (1)
and 6mn – 2nl + 5lm = 0 ……………………. (2)
From (1), m = – (3l + 5n)
From (2)
– 6n (31 + 5n) – 2n/ – 5/ (31 + 5n) = 0
⇒ – 18nl – 30n² – 2nl – 15l² – 25ln = 0
⇒ – 15l² – 45ln – 30n² = 0
⇒ l² + 3ln + 2n² = 0
⇒ (l + 2n) (l + n) = 0
⇒ l + 2n = 0 or l + n = 0
⇒ l = – n or l = – 2n
If l = -n then m = 3n – 5n = – 2n
⇒ l : m : n = -n : -2n : n
= 1 : 2 : – 1
If l = -2n then m = 6n – 5n = n
⇒ l : m : n = -2n : n : n = 2 : -1 : -1
Hence d.r.’s of two lines are (1, 2, -1) and (2, -1,-1).
If θ is the angle between the two lines then

Question 9.
If a variable line in two adjacent positions has direction cosines (l, m, n) and (l + δl, m + δm, n + δn), show that the small angle δθ between two positions is given by (δθ)² = (δl)² + (δm)² + (δn)². (E.Q.)
Answer:
Given direction cosines of a variable line in two adjacent positions are (l, m, n) and (l + δl, m + δm, n + δn)
We have l² + m² + n² = 1 …………………… (1)
and (l + δl)² + (m + δm)² + (n + δn)² = 1 ………………… (2)
From (2) – (1) we have
(l + δl)² + (m + δm)² +(n + δn)² – l² – m² – n² = 0
⇒ 2 (l. δl + m . δm + n . δn) = – [(δl)² + (δm)² +(δn)²]
⇒ (δl)² + (δm)² + (δn)² = – 2 (lδl + mδm + nδn) …………………… (3)
Now angle between two adjacent sides
cos δθ = l (l + δl) + m (m + δm) + n (n + δn)
= (l² + m² + n²) + l.δl + m.δm + n.δn
= 1 + l.δl + m.δm + n.δn
= 1 – \(\frac{1}{2}\) [(δl)² + (δm)² +(δn)²]
∴ (δl)² + (δm)² + (δn)² = (1 – cos δθ)
Since δθ is very small, sin\(\left(\frac{\delta \theta}{2}\right)\) = \(\frac{\delta \theta}{2}\)
∴ (δl)² + (δm)² + (δn)² = 4\(\frac{(\delta \theta)^2}{4}\) = (δθ)²
[∵ 1 – cosθ = 2 sin²\(\frac{\theta}{2}\)]
∴ (δθ)² = (δl)² + (δm)² + (δn)²

Students must practice these TS Intermediate Maths 1B Solutions Chapter 6 Direction Cosines and Direction Ratios Ex 6(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Direction Cosines and Direction Ratios 6(a)

I.
Question 1.
A line makes angles 90°, 60° and 30° with positive directions of X, Y, Z axes respectively. Find the direction cosines. (V.S.A.Q.)
Answer:
If l, m, n are the d.c.’s of the line
l = cos l = cos 90° = 0, m = cos β = cos 60° = \(\frac{1}{2}\)
n = cos γ = cos 30° = \(\frac{\sqrt{3}}{2}\)
d.c.’s of the line are \(\left(0, \frac{1}{2}, \frac{\sqrt{3}}{2}\right)\)

Question 2.
If a line makes angles α, β, γ with the positive directions of X, Y, Z axes, what is the value of sin²α + sin²β + sin²γ ? (V.S.A.Q.)
Answer:
sin²α + sin²β + sin²γ
= 1 – cos²α + 1 – cos²β + 1 – cos²γ
= 3 – l² – m² – n²
= 3 – (l² + m² + n²) = 3 – 1 = 2
(cos α = l, cos β = m, cos γ = n are d.c.’s of a line)

Question 3.
If P (√3 , 1, 2√3) is a point in space, find the direction cosines of OP (V.S.A.Q.)
Answer:
Direction ratios of
\(\overrightarrow{\mathrm{OP}}\) = (√3 – 0, 1 – 0, 2√3 – 0) = (√3, 1, 2√3)
∴ a2+ b2 + c2 = 3 + 1+ 12 = 16
⇒ \(\sqrt{a^2+b^2+c^2}\) = 4
∴ Direction cosines of \(\overrightarrow{\mathrm{OP}}\)

Question 4.
Find the direction cosines of the line joining the points (-4, 1, 7) and (2, -3, 2). (V.S.A.Q.)
Answer:
Let A = (-4, 1, 7) and B = (2, -3, 2)
d.r.’s of AB = (2 + 4, -3 -1, 2 – 7) = (6, -4, -5)

II.
Question 1.
Find the direction cosines of the sides of the triangle whose vertices are (3, 5, -4), (-1, 1, 2) and (-5, -5, -2). (S.A.Q.)
Answer:
Let A (3, 5, -4), B (-1, 1, 2) and C (-5, -5, -2) be the vertices of ∆ABC.
d.r.’s of AB = (-1 – 3, 1 – 5, 2 + 4) = (-4, -4, 6)

Question 2.
Show that the lines \(\overleftrightarrow{\mathrm{PQ}}\) and \(\overleftrightarrow{\mathrm{RS}}\) are parallel where P, Q, R, S erne the points (2, 3, 4), (4, 7, 8), (-1, -2, 1) and (1, 2, 5) respectively. (V.S.A.Q.)
Answer:
P (2, 3, 4), Q ( 4, 7, 8), R (-1, -2, 1) and S (1, 2, 5) are the given points.
d.r.’s of \(\overleftrightarrow{\mathrm{PQ}}\) = (4 — 2,7 — 3, 8 – 4) = (2, 4, 4)
d.r.’s of \(\overleftrightarrow{\mathrm{RS}}\) = (1 + 1 , 2 + 2, 5 – 1) = (2, 4, 4)
d.r.’s of \(\overleftrightarrow{\mathrm{PQ}}\) and \(\overleftrightarrow{\mathrm{RS}}\) are proportional. Hence \(\overleftrightarrow{\mathrm{PQ}}\) and \(\overleftrightarrow{\mathrm{RS}}\) are parallel.

III.
Question 1.
Find the direction cosines of two lines which are connected by the relations l – 5m + 3n = 0 and 7l² + 5m² – 3n² = 0 (E.Q.) (June 2009)
Answer:
The given relations are
l – 5m + 3n = 0 …………………….. (1)
7l² + 5m² – 3n² = 0 ………………….. (2)
From (1), l = 5m – 3n ………………….. (3)
∴ From (2),
7(5m – 3n)² + 5m² – 3n² = 0
⇒ 7(25m² – 30mn + 9n²) + 5m² – 3n² = 0
⇒ 175m² + 63n² – 210mn + 5m² – 3n² = 0
⇒ 180m² – 210mn + 60n² = 0
⇒ 6m² – 7mn + 2n² = 0
⇒ (3m – 2n) (2m – n) = 0
⇒ 3m = 2n ⇒ m = \(\frac{2 n}{3}\) (or) 2m = n ⇒ m = \(\frac{n}{2}\)

Case (i):

Case (ii):

Students must practice these TS Intermediate Maths 1B Solutions Chapter 4 Pair of Straight Lines Ex 4(b) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(b)

I.
Question 1.
Find the angle between the lines represented by 2x²
2x² + xy – 6y² + 7y – 2 = 0. (V.S.A.Q.)
Answer:
Comparing with the general equation
ax² + 2hxy + by² + 2gx + 2fy + c = 0 …………………….. (1)
We have a = 2, h = \(\frac{1}{2}\), b = – 6, g = 0, f = \(\frac{7}{2}\), c = – 2.
Also if θ is the angle between pair of lines (1)

Question 2.
Prove that the equation 2x² + 3xy – 2y² + 3x + y + 1 = 0 represents a pair of perpendicular lines. (V.S.A.Q.)
Answer:
We have coefficient of x² = 2 ⇒ a = 2
and coefficient of y² = – 2 ⇒ b = – 2
Since a + b = 0; the lines are perpendicular.

II.
Question 1.
Prove that the equation 3x² + 7xy + 2y² + 5x + 5y + 2 = 0 represents a pair of straight lines and find the coordinates of the point of intersection. (S.A.Q.)
Answer:
Comparing the given equation
3x² + 7xy + 2y² + 5x + 5y + 2 = 0 with the general equation ax² + 2hxy + by² + 2gx + 2fy + c = 0, we get a = 3, h = \(\frac{7}{2}\), b = 2, g = \(\frac{5}{2}\), f = \(\frac{5}{2}\) and c = 2.
∆ = abc + 2fgh – af² – bg² – ch²

∴ The given equation represents a pair of lines and point of intersection is

Question 2.
Find the value of k, if the equation 2x² + kxy – 6y² + 3x + y + 1 = 0 represents a pair of straight lines. Find the point of intersection of the lines and the angle between the straight lines for this value of k. (E.Q.)
Answer:
Comparing
2x² + kxy – 6y² + 3x + y + 1 = 0 with the general equation, we get
a = 2, h = \(\frac{\mathrm{k}}{2}\), b = -6, g = \(\frac{3}{2}\), f = \(\frac{1}{2}\), c = 1
The given equation represents a pair of straight lines if abc + 2fgh – af² – bg² – ch² = 0 (necessary condition)
⇒ – 12 + 2\(\left(\frac{1}{2}\right)\left(\frac{3}{2}\right)\left(\frac{k}{2}\right)\) – 2\(\left(\frac{1}{4}\right)\) + 6\(\left(\frac{9}{4}\right)-\frac{k^2}{4}\) = 0
⇒ – 48 + 3k – 2 + 54 – k² = 0
⇒ – k² + 3k + 4 = 0 ⇒ k² – 3k – 4 = 0
⇒ (k – 4) (k + 1) = 0 ⇒ k = 4 or – 1

Case (i):

Case (ii):
When k = 4, then h = 2

Question 3.
Show that the equation x² – y² – x + 3y – 2 = 0 represents a pair of perpendicular lines and find their equations. (S.A.Q.)
Answer:
First we show that the given equation x² – y² – x + 3y – 2 = 0 represents a pair of lines comparing with the general equation
we get a = 1, b = -1, g = \(\frac{-1}{2}\), f = \(\frac{3}{2}\), h = 0, c = -2
∴ abc + 2fgh – af² – bg² – ch²

Hence the given equation represents a pair of lines. Coefficient of x² + coefficient of y² = 1 – 1 = 0
∴ The given equation represents a pair of perpendicular lines.
Let x² – y² – x + 3y – 2
= (x + y + c₁) (x – y + c₂)
Equating coefficients of x and y both sides
we get c₁ + c₂ = – 1 and – c₁ + c₂ = 3
Solving 2c₂ = 2 ⇒ c₂ = 1
and c₁ + c₂ = -1 ⇒ c₁ = -2
∴ Equations of lines are x + y – 2 = 0 and x – y + 1 = 0.

Question 4.
Show that the lines x² + 2xy – 35y² – 4x + 44y – 12 = 0 and 5x + 2y – 8 = 0 are concurrent. (S.A.Q.)
Answer:
Given x² + 2xy – 35y² – 4x + 44y – 12 = 0 and comparing this with general equation we get a = 1, h = 1, b = – 35, g = -2, f = 22, c = – 12
Point of intersection

∴ The point of intersection lies on the line 5x + 2y – 8 = 0.
Hence the given lines are concurrent.

Question 5.
Find the distance between the following pairs of parallel straight lines. (V.S.A.Q.)
(i) 9x² – 6xy + y² + 18x – 6y + 8 = 0
(ii) x²+ 2√3 xy + 3y² – 3x – 3√3 y – 4 = 0
Answer:
(i) The formula for distance between parallel lines = \(\sqrt{\frac{g^2-a c}{a(a+b)}}\)

(ii) Distance between given parallel lines

Question 6.
Show that the two pairs of lines 3x² + 8xy – 3y² = 0 and 3x² + 8xy – 3y² + 2x – 4v – 1 = 0 form a square. (S.A.Q.)
Answer:

Given equations of lines represented by OA and OB is 3x² + 8xy – 3y² = 0
⇒ (x + 3y) (3x – y) = 0
⇒ x + 3y = 0, 3x – y = 0
∴ Equation of OA is 3x – y = 0 ………………… (1)
Equation of OB is x + 3y = 0 ……………… (2)
The combined equation of CA and CB is
3x² + 8xy – 3y² + 2x – 4y – 1 = 0 …………….. (3)
Let 3x² + 8xy – 3y² + 2x – 4y – 1
= (3x – y + c₁) (x + 3y + c₂)
Equating the coefficients of x and y on both sides,
and c₁ + 3C₂ = 2
3c₁ – c₂ = – 4
Solving

⇒ c₁ = – 1, c₂ = 1
Equation of BC is 3x – y – 1 = 0 ……………………. (4)
Equation of AC is x + 3y + 1 = 0 …………………… (5)
Equations OA and BC differ by a constant.
⇒ OA is parallel to BC.
Equations OB and CA differ by a constant
⇒ OB is parallel to AC.
Also from equation (3), OACB is a rectangle and a + b = 3 – 3 = 0
OA = Length of the perpendicular from O to
AC = \(\frac{|0+0+1|}{\sqrt{1+9}}=\frac{1}{\sqrt{10}}\)
OB = Length of the perpendicular from O to
BC = \(\frac{|0+0-1|}{\sqrt{9+1}}=\frac{1}{\sqrt{10}}\)
∴ OA = OB and OACB is a rectangle
⇒ OACB is a square.

III.
Question 1.
Find the product of the length of the perpendiculars drawn from (2, 1) upon the lines (E.Q.)
12x² + 25xy + 12y² + 10x + 11y + 2 = 0
Answer:
Given equation
12x² + 25xy + 12y² + 10x + 11y + 2 = 0
represents the combined equation of AB & AC.
12x² + 25xy + 12y²
= 12x² + 16xy + 9xy + 12y²
= 4x (3x + 4y) + 3y (3x + 4y)
= (3x + 4y) (4x + 3y)
Let 12x² + 25xy + 12y² + 10x + 11y + 2 = (3x + 4y + c₁) (4x + 3y’ + C₂)
Equating the coefficients of x and y
4c₁ + 3C₂ = 10 ………………. (1)
and 3c₁ + 4c₂ = 11 ………………. (2)
Solving (1) and (2)

⇒ c₁ = 1, c₂ = 2
∴ Equation of AB is 3x + 4y + 1 = 0
and equation of AC is 4x + 3y + 2 = 0
PL = Length of the perpendicular from
P(2, 1) on AB = \(\left|\frac{6+4+1}{\sqrt{9+16}}\right|=\frac{11}{5}\)
PM = Length of the perpendicular from
P(2, 1) on AC = \(\left|\frac{8+3+2}{\sqrt{16+9}}\right|=\frac{13}{5}\)
∴ Product of lengths of perpendiculars
= PL × PM = \(\frac{11}{5} \times \frac{13}{5}=\frac{143}{25}\)

Question 2.
Show that the straight lines y² – 4y + 3 = 0 and x² + 4xy + 4y² + 5x + 10y + 4 = 0 form a parallelogram and find the lengths of its sides. (E.Q.)
Answer:

The equation of first pair of lines is y² – 4y + 3 = 0
⇒ (y – 1) (y – 3) = 0 ⇒ y = 1 ………………….. (1)
and y = 3 ………………….. (2)
∴ AB, CD are parallel.
The equation of second pair of lines is
x² + 4xy + 4y² + 5x + 10y + 4 = 0
⇒ (x + 2y)² + 5 (x + 2y) + 4 = 0
⇒ (x + 2y)² + 4 (x + 2y) + (x + 2y) + 4 = 0
⇒ (x + 2y) [x + 2y + 4] + 1 [(x + 2y) + 4] = 0
⇒ (x + 2y + 1) (x + 2y + 4) = 0
⇒ x + 2y + 1 = 0, x + 2y + 4 = 0
Equation of AD is x + 2y + 1 = 0 ……………………. (3)
Equation of BC is x + 2y + 4 = 0 ……………………. (4)
∴ AD and BC are parallel.
Solving (1) and (3), x + 2 + 1 = 0
⇒ x = – 3
∴ Co-ordinates of A = (-3, 1)
Solving (2) and (3), x + 6 + 1 = 0 ⇒ x = -7
and coordinates of D = (-7, 3)
Solving (2) and (4) x + 6 + 4 = 0 ⇒ x = -10
∴ Coordinates of C = (-10, 3)
Solving (1) and (4), we get x + 2 + 4 = 0
⇒ x = -6
∴ Coordinates of B = (- 6, 1)
Hence A = (-3, 1), B = (-6, 1), C = (-10, 3), D = (-7, 3)

∴ AC ≠ BD
Hence a parallelogram is formed with the
lines y² – 4y + 3 = 0 and x² + 4xy + 4y² + 5x + 10y + 4 = 0.

Question 3.
Show that the product of the perpendicular distances from the origin to the pair of straight lines represented by ax² + 2hxy +
by² + 2gx + 2fy + c = 0 is \(\frac{|c|}{\sqrt{(a-b)^2+4 h^2}}\) (E.Q.)
Answer:
Let ax² + 2hxy + by² + 2gx + 2fy + c = 0 represent the lines
l₁x + m₁y + n₁ = 0 ……………. (1)
and l₂x + m₂y + n₂ = 0 ……………. (2)
∴ ax² + 2hxy + by² + 2gx + 2fy + c
= (l₁x + m₁y + n₁) (l₂x + m₂y + n₂)
∴ l₁l₂ = a, m₁m₂ = b, l₁m₂ + l₂m₁ = 2h,
l₁n₂ +l₂n₁ = 2g, m₁n₂ + m₂n₁ = 2f, n₁n₂ = c
∴ Perpendicular distance from origin to (1) is
= \(\frac{\left|\mathrm{n}_1\right|}{\sqrt{l_1^2+\mathrm{m}_1^2}}\)
Perpendicular distance from origin to (2) is
= \(\frac{\mathrm{n}_2}{\sqrt{l_2^2+\mathrm{m}_2^2}}\)
Product of perpendiculars

Question 4.
If the equation ax² + 2hxy + by2 + 2gx + 2fy + c = 0 represent a pair of intersecting lines, then show that the square of the distance of their point of intersection from the origin is \(\). Also show that the square of this distance is \(\frac{f^2+g^2}{h^2+b^2}\) if the given lines are perpendicular. (E.Q.)
Answer:
Let the equation
ax² + 2hxy + by² + 2gx + 2fy + c = 0 represent the lines
l₁x + m₁y + n₁ = 0 ………………. (1)
and l₂x + m₂y + n₂ = 0 ……………….. (2)
∴ (l₁x + m₁y + n₁) (l₂x + m₂y + n₂)
= ax² + 2hxy + by² + 2gx + 2fy + c
Comparing coefficients
l₁l₂ = a, m₁ m₂ = b, n₁n₂ = c
l₁m₂ + l₂m₁ = 2h, l₁n₂ + l₂n₁ = 2g and
m₁n₂ + m₂n₁ = 2f
From (1) and (2) on solving

Telangana TSBIE TS Inter 1st Year Chemistry Study Material 3rd Lesson రసాయన బంధం – అణు నిర్మాణం Textbook Questions and Answers.

TS Inter 1st Year Chemistry Study Material 3rd Lesson రసాయన బంధం – అణు నిర్మాణం

అత్యంత లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 1.
అష్టక నియమం అంటే ఏమిటి?
జవాబు:
పరమాణువులు ఎలక్ట్రాన్లను కోల్పోవడం, స్వీకరించడం లేదా పంచుకోవడం ద్వారా వాటి వేలన్స్ కర్పరంలో ఎనిమిది ఎలక్ట్రాన్లు పొందటానికి ప్రయత్నిస్తాయి. దీనినే అష్టక నియమం అంటారు. కొస్సెల్, లూయీలు ఈ సిద్ధాంతాన్ని ప్రవేశపెట్టారు.

ప్రశ్న 2.
S, S^2- లకు లూయీ ఎలక్ట్రాన్ చుక్కల సంకేతాలు రాయండి.
జవాబు:

ప్రశ్న 3.
SO₃ కి వీలయినన్ని రెజోనెన్స్ నిర్మాణాలు రాయండి.
జవాబు:

ప్రశ్న 4.
AlCl₃ + Cl^– →AlC\(l_4^{-}\) చర్యలో Al పరమాణువు సంకరీకరణంలో మార్పు ఏమైనా ఉంటే ఊహించి రాయండి.
జవాబు:
AlCl_౩ అణువు ఏర్పడేటప్పుడు కేంద్రక ‘Al’ పరమాణువు దాని 1వ ఉత్తేజిత’.
స్థితిలో (1s² 2s² 2p⁶ 3s¹ 3p²sp²) సంకరీకరణం పొందుతుంది. అపుడు దానిపై మూడు sp² సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి. వాటన్నింటిలో బంధ ఎలక్ట్రాన్లు ఉంటాయి. మూడు సంకర sp² ఆర్బిటాళ్ళు మూడు Cl పరమాణువుల 3p_z ఆర్బిటాళ్ళతో అభిముఖ ఆవరింపు చేసికొని మూడు సిగ్మా బంధాలను ఇస్తాయి. కేంద్రక ‘Al’ పరమాణువు sp² సంకరీకరణం పొందడం వల్ల AlCl₃ అణువు సమతల త్రిభుజాకృతిని కలిగి ఉంటుంది.

AlCl₃ లో కేంద్రక ‘Al’ పరమాణువు మీద ఖాళీగా P_z ఆర్బిటాల్ ఉంటుంది.
Cl^– అయాన్ విన్యాసం = 1s²2s²2p⁶3s²3p⁶

AlCl₃ అణువు Cl^– అయాన్ తో చర్య జరిపేటపుడు “Al” పరమాణువు తన sp² సంకరీకరణాన్ని sp³ సంకరీకరణంగా మార్చుకుంటుంది. అట్లేర్పడ్డ నాలుగు sp³ సంకర ఆర్బిటాళ్లలో మూడింటిలో బంధ జంటలు ఉండగా ఒక sp³ ఆర్బిటాల్ మాత్రం ఖాళీగా ఉంటుంది. బంధ జంటలు గల మూడు sp³ సంకర ఆర్బిటాళ్ళు మూడు ‘C’ పరమాణువుల 3p_z, ఆర్బిటాళ్ళతో అభిముఖ ఆవరింపు చేసుకొని మూడు సిగ్మా బంధాలను ఇస్తాయి. ఇపుడు కేంద్రక ‘Al’ పరమాణువులోని ఖాళీగా ఉన్న నాల్గవ sp³ సంకర ఆర్బిటాల్ Cl^– అయాన్ నుండి ఒక జత ఎలక్ట్రాన్ను స్వీకరించి సమన్వయ సమయోజనీయ బంధం ఏర్పరచుకుంటుంది. ఈ విధంగా AlC\(l_4^{-}\) లో కేంద్రక ‘Al’ పరమాణువు sp³ సంకరీకరణం పొందడం వల్ల AlC\(l_4^{-}\), టెట్రాహెడ్రల్ ఆకృతి ఏర్పడుతుంది.
AlCl₃ నుండి AlC\(l_4^{-}\) మారినపుడు అల్యూమినియంలో సంకరీకరణం sp² నుండి sp³ కి మారుతుంది.

ప్రశ్న 5.
Ca²⁺, Zn²⁺ లలో ఏది స్థిరమైనది ? ఎందువల్ల ?
జవాబు:
1) Ca²⁺ అయాను Zn²⁺ అయాను కంటె అధిక స్థిరమైనది.
కారణం : మిధ్యా జడవాయు ఎలక్ట్రాన్ విన్యాసం వల్ల ఉన్న అయాను కన్న జడవాయు ఎలక్ట్రాన్ విన్యాసం ఉన అయాను స్థిరమైనది.
Ca²⁺ (2, 8, 8) కు జడవాయు ఎలక్ట్రాన్ విన్యాసం ఉంది. అనగా బాహ్య కర్పరంలో ఎనిమిది ఎలక్ట్రాన్లు ఉన్నాయి అందువల్ల స్థిరమైనది.
Zn²⁺ (2, 8, 18) బాహ్య కర్పరంలో 18 ఎలక్ట్రాన్లు ఉన్నాయి. ఇది మిధ్యా జడవాయు ఎలక్ట్రాన్ విన్యాసం.

ప్రశ్న 6.
CI అయాను CI పరమాణువు కంటే స్థిరమైనది. ఎందువల్ల ?
జవాబు:
ns² np⁶ ఎలక్ట్రాన్ విన్యాసం గల పరమాణువు లేదా అయాను స్థిరమైనది. Cl^– కు స్థిర ఎలక్ట్రాన్ విన్యాసం కలదు.
Cl (Z) = 17 ఎలక్ట్రాన్ విన్యాసం 1s² 2s² 2p⁶ 3s² 3p⁵
Cl^– ఎలక్ట్రాన్ విన్యాసం 1s² 2s² 2p⁶ 3s² 3p⁶
అందువల్ల Cl కన్నా Cl^– అయాను స్థిరమైనది.

ప్రశ్న 7.
ఆర్గానన్ను Ar, గా ఎందుకు రాయకూడదు ?
జవాబు:
Ar ఎలక్ట్రాన్ విన్యాసం 1s² 2s² 2p⁶ 3s² 3p⁶.
Ar పరమాణువుకు స్థిరమైన ఎలక్ట్రాన్ విన్యాసం ఉండుట వలన అది బంధంలో పాల్గొనదు. Ar₂ ఏర్పడదు.

ప్రశ్న 8.
హైడ్రోజన్ సల్ఫైడ్ కంటే నీటి బాష్పీభవన స్థానం ఎక్కువ. ఎందువల్ల ?
జవాబు:
నీటియందు హైడ్రోజన్ బంధాల వల్ల అది సహచరిత ద్రవం. నీటి అణువుల మధ్య గల అనేక అంతర అణు హైడ్రోజన్ బంధాలను ఛేదించుటకు అధిక శక్తి అవసరం. అందువల్ల నీరు ద్రవస్థితి నుంచి బాష్పస్థితికి మారడానికి అధిక ఉష్ణోగ్రత అవసరం.
హైడ్రోజన్ సల్ఫైడ్ అణువుల మధ్య హైడ్రోజన్ బంధాలు లేవు. వాటి మధ్య బలహీన వాండర్ వాల్ బలాలు మాత్రమే ఉంటాయి. అందువల్ల H₂S బాష్పీభవన స్థానం తక్కువ.

ప్రశ్న 9.
నీటి బాష్పీభవన స్థానం హైడ్రోజన్ ఫ్లోరైడ్ బాష్పీభవన స్థానం కంటే ఎక్కువ. ఎందువల్ల ?
జవాబు:
నీటి అణువుల మధ్య ఉన్న హైడ్రోజన్ బంధాలు హైడ్రోజన్ ఫ్లోరైడ్ అణువుల మధ్య ఉన్న హైడ్రోజన్ బంధాల కన్న రెట్టింపు. అందువల్ల బాష్పీభవన స్థానం ఎక్కువ. HF లోని హైడ్రోజన్ బంధాలు నీటిలోని హైడ్రోజన్ బంధాల కన్నా . బలమైనవి. అందువల్ల వాయు స్థితిలో కూడా HF అణువుల మధ్య హైడ్రోజన్ బంధాలుంటాయి. అందువల్ల HF ద్రవ స్థితినుంచి వాయు స్థితిలోకి మార్చడానికి అన్ని హైడ్రోజన్ బంధాలను ఛేదించనక్కరలేదు. ఈ కారణంగా HF బాష్పీభవన స్థానం తక్కువ. HF బాష్పీభవన స్థానం 19.4°C. నీరు బాష్పీభవన స్థానం 100°C.

ప్రశ్న 10.
ఒక పరమాణువు చుట్టూ నాలుగు బంధజంటల ఎలక్ట్రాన్లు ఉంటే వాటి మధ్య కనిష్ఠ వికర్షణలు ఉండేటట్లు ఎట్లా అమర్చాలి?
జవాబు:
నాలుగు బంధ ఎలక్ట్రాన్ జంటలు చతుర్ముఖి యొక్క నాలుగు శీర్షాలయందు అమరి ఉంటే వికర్షణలు అతి తక్కువగా ఉంటాయి. ఎలక్ట్రాన్ జంటలు గరిష్ఠ దూరంలో ఉండి వాటి మధ్య కోణం 109°28′ ఉంటుంది.

ప్రశ్న 11.
A, B లు రెండు వేర్వేరు పరమాణువులైతే అవి AB అణువును ఇస్తే ఆ అణువులో సమయోజనీయ బంధం ఎప్పుడు ఏర్పడుతుంది.
జవాబు:
AB పరమాణువుల ఋణ విద్యుదాత్మకతలలో తేడా తక్కువగా ఉన్నపుడు లేదా దాదాపు సమానంగా ఉన్నపుడు వాటి మధ్య సమయోజనీయ బంధం ఏర్పడుతుంది. ఋణ విద్యుదాత్మకతలలో తేడా 1.7 కన్నా తక్కువ ఉంటే సమయోజనీయ బంధం ఏర్పడుతుంది.

ప్రశ్న 12.
స్థానీకృత ఆర్బిటాళ్ళు అంటే ఏమిటి ?
జవాబు:
రెండు పరమాణువుల మధ్య సమయోజనీయ బంధం ఏర్పడినపుడు ఎలక్ట్రాన్ జంట మేఘ విస్తరణ రెండు పరమాణువుల మధ్య సాంద్రీకృతమై ఉంటుంది. దీనినే స్థానీకృత ఆర్బిటాలు అంటారు.
ఉదా : మీథేన్ అణువులో °C – H బంధం స్థానీకృత ఆర్బిటాల్. ఆ బంధంలోని ఎలక్ట్రాన్లను స్థానీకృత ఎలక్ట్రానులు అంటారు.

ప్రశ్న 13.
(a) C₂H₂;
(b) C₂H₄ ఈ రెండు అణువుల్లో వరుసగా దేనిలో ఎన్ని సిగ్మా పై బంధాలున్నాయో తెల్పండి.
జవాబు:

ప్రశ్న 14.
BF₃ + NH₃ → F₃BNH₃ ఈ చర్యలో బోరాన్, నైట్రోజన్ పరమాణువుల సంకరకరణంలో మార్పు ఉంటుందా ? ఉంటే ఏమిటి ?
జవాబు:

బోరాన్ [Z = 5 = 1s²2s²2p¹] ట్రైఫ్లోరైడ్ అణువు ఏర్పడేటప్పుడు కేంద్రక ‘B’ పరమాణువు దాని ఒకటవ ఉత్తేజిత స్థితి (1s² 2s¹ \(2 \mathrm{p}_{\mathrm{x}}^1 2 \mathrm{p}_{\mathrm{y}}^1 2 \mathrm{p}_{\mathrm{z}}^0\)) లో sp² సంకరీకరణం పొందుతుంది. అపుడు దానిపై మూడు sp² సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి. వాటన్నింటిలో బంధ ఎలక్ట్రాన్ జంటలు ఉంటాయి. ఆ మూడు బంధ ఎలక్ట్రాన్ జంటలు గల sp² సంకర ఆర్బిటాళ్ళు మూడు F పరమాణువుల (1s²2s²2p⁵) 2p_z ఆర్బిటాళ్లతో అభిముఖ ఆవరింపు చేసికొని మూడు సిగ్మా బంధాలను ఇస్తాయి. అంతేకాకుండా BF₃ లో కేంద్రక బోరాన్ పరమాణువు మీద ఖాళీ ‘p_z‘ ఆర్బిటాల్ కూడా ఉంటుంది.

అమ్మోనియా అణువు ఏర్పడేటపుడు కేంద్రక ‘N’ పరమాణువు (1s² 2s² 2p³) దాని భూస్థితిలో sp³ సంకరీకరణం పొందుతుంది. అపుడు దానిపై నాలుగు sp³ సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి. వాటిలో మూడు సంకర ఆర్బిటాళ్ళలో, బంధ జంటలు, నాల్గవ దానిలో ఒంటరి జంట ఉంటాయి. బంధ జంటలు గల మూడు సంకర ఆర్బిటాళ్ళు మూడు H పరమాణువుల 1s³ ఆర్బిటాళ్ళతో అభిముఖ ఆవరింపు చేసికొని మూడు సిగ్మా బంధాలను ఇస్తాయి. sp³ సంకరీకరణం వల్ల NH₃ అణువుకు టెట్రాహెడ్రల్ ఆకృతి ఏర్పడుతుంది.

అమ్మోనియా, బోరాన్ ట్రైఫ్లోరైడ్తో చర్య జరిపేటపుడు తన ఒంటరి జంట ఎలక్ట్రాన్లను BF₃ లో ఉన్న ఖాళీ ‘p’ ఆర్బిటాల్క అందచేస్తుంది. అపుడు ఆ రెండింటి మధ్య సమన్వయ సమయోజనీయ బంధం ఏర్పడుతుంది. ఈ ప్రక్రియలో బోరాన్ తన sp² సంకరీకరణాన్ని sp³ సంకరీకరణంగా మార్చుకుంటుంది. అందువల్ల NH₃, BF₃ అణువులు రెండూ అణువులో టెట్రాహెడ్రల్ ఆకృతిని కలిగి ఉంటాయి. ఇట్లేర్పడ్డ [NH₃ → BF₃] అణువులో N, B ల కోవేలన్సీ విలువ 4 ఉంటుంది.

లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 15.
రసాయన బంధాన్ని కొస్సెల్, లూయీలు ఎట్లా వివరించారు ?
జవాబు:
కోసెల్, లూయీలు రసాయనిక బంధాలు ఎలక్ట్రానిక్ సిద్ధాంతం ప్రతిపాదించారు. దీని ప్రకారం పరమాణువులు ఎలక్ట్రానులను కోల్పోవడం, స్వీకరించడం లేదా పంచుకోవడం ద్వారా వాటి వేలన్స్ కర్పరంలో ఎనిమిది ఎలక్ట్రానులు పొందడానికి ప్రయత్నిస్తాయి. దీనినే అష్టక నియమం అంటారు.

లూయీ, పరమాణువును ధన విద్యుదావేశం గల కెర్నెల్ గాను, బాహ్య కర్పరంగాను రెండు భాగాలుగా భావించాడు. కెర్నెల్ అంటే బాహ్య కర్పరం కాక మిగిలిన భాగం, అంటే కేంద్రకం, లోపలి కర్పరాల్లోని ఎలక్ట్రాన్లు కలిసి కెర్నెల్ అవుతుంది. వేలన్స్ కర్పరంలో అత్యధికంగా ఎనిమిది ఎలక్ట్రాన్లతో మాత్రమే ఉంటుంది. ఉత్కృష్ట వాయు పరమాణువులోని ఎలక్ట్రానులు ఘనం ఎనిమిది మూలలను ఆక్రమించి ఉంటాయి. ఈ ఎనిమిది ఎలక్ట్రానుల అమరిక ఒక స్థిరమైన ప్రత్యేక అమరిక. మూలక పరమాణువులు అష్టకం రావడం కోసమే రసాయన బంధంలో పాల్గొంటాయి.

అణువు ఏర్పడటానికి సాధారణంగా పరమాణువుల్లోని బాహ్య కర్పరాల్లోని ఎలక్ట్రానులు రసాయన సంకలన చర్యల్లో పాల్గొంటాయి. వీటిని వేలన్స్ ఎలక్ట్రానులు అంటారు.
కొస్సెల్ ప్రతిపాదనలు : 1. హాలోజన్లు ఋణ అయానులను ఏర్పరచడానికి వాటి పరమాణువులు ఎలక్ట్రానులు స్వీకరించగా, క్షార లోహాలు వాటి పరమాణువులు ధన అయానులుగా మారడానికి ఎలక్ట్రానులను కోల్పోతాయి. ధన, ఋణ అయానులు ఏర్పడినపుడు అవి స్థిరమైన ఉత్కృష్టవాయు పరమాణువుల ఎలక్ట్రాన్ విన్యాసాల్ని పొందుతాయి.

ధన, ఋణ అయానులు స్థిర విద్యుత్ బలాల చేత ఆకర్షితమై అయానిక స్ఫటికాల నేర్పరుస్తాయి.
ఈ విధంగా ఎలక్ట్రానులను పంచుకోవడం ద్వారా సమయోజనీయ బంధం, ఎలక్ట్రాన్ బదిలీ ద్వారా అయానిక బంధం ఏర్పడతాయి.

ప్రశ్న 16.
అయానిక సంయోగ పదార్థాల సాధారణ ధర్మాలు వ్రాయండి.
జవాబు:

1. అయానిక పదార్థాలు ఘన స్థితిలో చాలా గట్టిగా అధిక బాష్పీభవన స్థానం, ద్రవీభవన స్థానాలతో ఉంటాయి.
2. అయానిక పదార్థాలు ధ్రువ ద్రావణులైన నీటి వంటి ద్రావణులలో అధికంగా కరుగుతాయి.
3. జల ద్రావణాల్లోను, గలన స్థితిలోను, ఇవి విద్యుత్, ఉష్ణవాహకాలు.
4. అయానిక సంయోగ పదార్థాలు దిశలేని బంధాల నేర్పరచి ఐసోమెరిజం చూపవు.
5. అయానిక పదార్థాల మధ్య చర్యలు వేగంగా జరుగుతాయి.

ప్రశ్న 17.
ఫాజన్స్ నియమాలు వ్రాసి, సరియైన ఉదాహరణలు ఇవ్వండి.
జవాబు:
సమయోజనీయ బంధాలకు పాక్షిక అయానిక బంధ లక్షణం ఉన్నట్లే, అయానిక బంధాలకు కూడా పాక్షిక సమయోజనీయ బంధ లక్షణాలుంటాయి. అయానిక బంధాల పాక్షిక సమయోజనీయ బంధ లక్షణాలను అర్థం చేసుకోవడానికి ఫాజన్స్ నియమాలను ప్రతిపాదించెను.

1. ఏనయాన్ పరిమాణం పెరిగిన కొలదీ ఆ సంయోగ పదార్థం సమయోజనీయ బంధ లక్షణం పెరుగుతుంది. ఉదా : KF, KI అయానిక పదార్థాల్లో కేటయాన్ K⁺ స్థిరం. F^– కంటే I^– పెద్దది. అందుచేత KI కి KF కంటె సమయోజనీయ బంధలక్షణాలు ఎక్కువ.
2. కేటయాన్ పరిమాణం తగ్గిన కొద్దీ సమయోజ బంధ లక్షణం పెరుగుతుంది.
   ఉదా : LiF కు KF కంటే సమయోజనీయ బంధ లక్షణాలు ఎక్కువ.
3. కేటయాన్ల, ఏనయాన్ల విద్యుదావేశ పరిమాణాలు పెరిగిన కొలదీ వాటి మధ్య ఏర్పడే బంధాల సమయోజనీయ లక్షణం పెరుగుతుంది.
   ఉదా : Sn⁺² Cl₂ కంటే Sn⁺⁴Cl₄ కు సమయోజనీయ బంధ లక్షణాలు ఎక్కువ.
4. ఒకే విద్యుదావేశం, ఒకే పరిమాణం ఉన్న రెండు కేటయాన్లలో మిధ్యా ఉత్కృష్ట వాయు ఎలక్ట్రాన్ విన్యాసం ఉన్న కేటయాన్ ఉత్కృష్ట వాయు ఎలక్ట్రాన్ విన్యాసం ఉన్న కేటయాన్ల కంటె ధ్రువణ సామర్థ్యం ఎక్కువ. ఉదా : NaCl కంటే CuCl ఎక్కువ సమయోజనీయ బంధ లక్షణాలతో ఉంటుంది.
   కారణం · Cu⁺, Cl^– ను Na⁺ కంటే ఎక్కువ ధ్రువణం చెందిస్తుంది.

ప్రశ్న 18.
అష్టక నియమం అంటే ఏమిటి ? దీనిని సంక్షిప్తంగా వివరించి దాని లోపాలు తెలపండి.
జవాబు:
పరమాణువులు ఎలక్ట్రానులను కోల్పోవడం, స్వీకరించడం లేదా పంచుకోవడం ద్వారా వేలన్స్ కర్పరంలో ఎనిమిది ఎలక్ట్రాన్లు పొందడానికి ప్రయత్నిస్తాయి. దీనినే నియమం అంటారు.

“స్థిరత్వం పొందటానికై ప్రతి పరమాణువు తన బాహ్య కర్పరంలో 8 ఎలక్ట్రాన్లను కలిగి ఉండాలి” అనే నియమాన్ని అష్టక నియమం అనవచ్చు. బాహ్య కర్పరంలో 8 ఎలక్ట్రాన్లు కలిగి ఉన్న పరమాణువులు రసాయనికంగా స్థిరత్వం కలిగి ఉంటాయి. అందువల్ల అవి రసాయన చర్యలలో పాల్గొనవు. బాహ్య కర్పరంలో 8 కన్నా తక్కువ ఎలక్ట్రాన్లు గల పరమాణువులు స్థిరత్వం పొందడానికై అంటే ఎలక్ట్రాన్ అష్టకాన్ని పొందడానికై ఇతర పరమాణువులతో కలుస్తాయి.

పరమాణువులు తమ బాహ్య కర్పరంలో అష్టకాన్ని పొందడానికై రెండు విధాలుగా కలుస్తాయి. ఒక పద్దతిలో ఒక పరమాణువు నుండి వేరొక పరమాణువుకు ఎలక్ట్రాన్లు బదిలీ అయి వెళ్ళిపోవడం. రెండవ పద్ధతిలో సంయోగం చెందే రెండు పరమాణువులు ఎలక్ట్రాన్లను సమానంగా సమిష్టిగా పంచుకోవడం.
సార్ధకత : బాహ్య కర్పరంలో అష్టక విన్యాసం కలిగిఉన్న అణువులు అధిక స్థిరత్వం కలిగి ఉంటాయి.
ఉదా : NH₃, H₂O అణువులు. ఈ అణువులలో కేంద్రక ‘N’ పరమాణువు మరియు కేంద్రక ‘0’ పరమాణువులు ఎలక్ట్రాన్ అష్టకాన్ని కలిగి ఉంటాయి. అందువల్ల అవి అధిక స్థిరత్వం కలిగి ఉంటాయి.

పరమాణువులే కాకుండా అష్టక విన్యాసం కలిగి ఉన్న అయాన్లు కూడా స్థిరంగా ఉంటాయి. ఆ కారణంగా పరమాణువుల నుండి కొన్ని అయాన్లు మాత్రమే పొందగలం. కొన్నింటిని పొందలేం. ఉదా : Na పరమాణువు నుండి Na⁺ సులువుగా పొందవచ్చును. Na⁺² ను పొందజాలము. ఎందుకనగా Na⁺ కు స్థిర ‘Ne’ విన్యాసం ఉంటుంది. దీని నుండి మరొక ఎలక్ట్రానన్ను తీసివేసి Na⁺² ను పొందడం చాలా కష్టం.

లోపాలు :

1. కొన్ని సంయోగ పదార్థాలలో కేంద్ర పరమాణువు చుట్టూ ఎనిమిది కంటే తక్కువ ఎలక్ట్రానులు ఉంటున్నాయి.
   ఉదా : BCl₃, LiCl, BeH₂
2. కొన్ని సందర్భాలలో అష్టక విస్తృతి జరిగి కేంద్ర పరమాణువు చుట్టూ 8 కంటే ఎక్కువ ఎలక్ట్రానులు పరివేష్టించి ఉండవచ్చు. ఉదా : PF₅, SF₆
3. అష్టక నియమం ఉత్కృష్ట వాయువుల జడస్వభావం ఆధారంగా ప్రతిపాదించబడింది. అయితే కొన్ని ఉత్కృష్ట వాయువులు Kr, Xe ఆక్సిజన్, ఫ్లోరీన్లతో కలిసి అనేక సమ్మేళనాలనిస్తున్నాయి.
   ఉదా : XeF₂, XeF₄, KrF₂, XeO₂, XeO₃, XeO₄.
4. అణువుల ఆకృతిని అష్టక సిద్ధాంతం వివరించదు.
5. ఈ సిద్ధాంతం అణువుల సాపేక్ష స్థిరత్వాలను కాని అణువు శక్తిని గాని వివరించదు.

ప్రశ్న 19.
NO₂, N\(\mathbf{O}_3^{-}\) ల రెజోనెన్సు నిర్మాణాలు రాయండి.
జవాబు:
NO₂ రెజోనెన్సు రూపాలు :

N\(\mathrm{O}_3^{-}\) రెజోనెన్సు నిర్మాణాలు :

ప్రశ్న 20.
కింది పరమాణు జంటల్లో అవి కాటియాన్లు, ఏనయాన్లు ఏర్పరచేటప్పుడు జరిపే ఎలక్ట్రానుల మార్పులను లూయీ చుక్కల పద్ధతిలో ఇవ్వండి.
(a) K, S
(b) Ca, O
(c) Al, N.
జవాబు:
(a) ₁₉K ఎలక్ట్రాన్ విన్యాసం = 1s² 2s² 2p⁶ 3s² 3p⁶ 4s¹
₁₆S ఎలక్ట్రాన్ విన్యాసం = 1s² 2s² 2p⁶ 3s² 3p⁴

b) ₂₀Ca ఎలక్ట్రాన్ విన్యాసం = 1s² 2s² 2p⁶ 3s² 3p⁶ 4s²
₈O ఎలక్ట్రాన్ విన్యాసం = 1s² 2s² 2p⁴

c) ₁₃Al = 1s² 2s² 2p⁶ 3s² 3p¹
₇N = 1s² 2s² 2p³

ప్రశ్న 21.
H₂O కు ద్విధ్రువ భ్రామకం ఉంది. కాని CO₂ కు లేదు ఎందువల్ల ?
జవాబు:
బహుపరమాణుక అణువుల్లో అణువుల ద్విధ్రువ భ్రామకాలు అణువుల్లోని ప్రతిబంధం ద్విధ్రువభ్రామకం విలువల మీదనే కాక కేంద్రక పరమాణువు చుట్టూ ఆ బంధాలు ప్రాదేశికంగా ఎలా అమర్చబడ్డాయి అన్న అంశంపై కూడా ఆధారపడి ఉంటాయి. అలాంటప్పుడు అణువు ద్విధ్రువ భ్రామకం అందులోని బంధాల బంధ భ్రామకాల సదిశ మొత్తం విలువ అవుతుంది.

నీటి అణువుకు కోణీయ నిర్మాణం ఉంటుంది. H₂O లో బంధకోణం 104.5° నీటి అణువు ఫలిత ద్విధ్రువ భ్రామకం
µ = 1.85-డిబై.

CO₂ అణువు ద్విధ్రువ భ్రామకం సున్న. దీనికి కారణం రెండు C = O బంధాలు 180° కోణంలో ఒకదానికి ఇంకొకటి.వ్యతిరేక దిశలో సమాన బంధ భ్రామకాలతో ఉండి రెండు C = 0 బంధాల బంధ ద్విధ్రువ విలువల మొత్తం సున్నా అవుతుంది.

ప్రశ్న 22.
ద్విధ్రువ భ్రామకాన్ని నిర్వచించండి. దీని అనువర్తనాలేమిటి?
జవాబు:
రెండు వేర్వేరు మూలకాల పరమాణువుల మధ్య సమయోజనీయబంధం ఏర్పడినపుడు బంధ ఎలక్ట్రాన్ జంట అధిక ఋణ విద్యుదాత్మక పరమాణువుకు దగ్గరగా ఉంటుంది. అందువల్ల అధిక ఋణ విద్యుదాత్మక పరమాణువుకు పాక్షిక రుణావేశం, అల్ప ఋణ విద్యుదాత్మక పరమాణువుకు పాక్షిక ధనావేశం కలుగుతాయి. ఇటువంటి అణువును ధృవాణువు అంటారు.

ద్విధ్రువ భ్రామకం : ఒక ద్విపరమాణుక ధ్రువ అణువు ద్విధ్రువ భ్రామకం ఆ అణువులోని ఒకదాని మీది విద్యుదావేశ పరిమాణం, ధన, ఋణ ఆవేశాల మధ్య దూరం లబ్ధంగా నిర్వచించవచ్చు.
ద్విధ్రువ భ్రామకం µ = విద్యుదావేశం (δ) × విద్యుదావేశాల మధ్య దూరం.
µ = δ × l
ద్విధ్రువభ్రామకాన్ని డిబై ప్రమాణాలలో తెలుపుతారు.
1 D = 3.33564 × 10^-30c.m.
C = కులూంబ్; m = మీటర్

అనువర్తనాలు :

1. సమయోజనీయ బంధ అయానిక స్వభావ శాతాన్ని లెక్కించవచ్చు.
   అయానిక స్వభావ శాతం = \(\frac{\mu_{\text {obs }}}{\mu_{\text {ionic }}}\) × 100
2. అణువుల ఆకృతులను ఊహించవచ్చు.
   1. AX₂ రకం అణువులు రేఖీయ నిర్మాణాన్ని కల్గిఉంటే µ = 0
      రేఖీయ నిర్మాణాన్ని కలిగి ఉంటే µ కు కొంత విలువ ఉంటుంది.
      CO₂ అణువు µ = 0
      H₂O అణువు µ = 1.85 D
   2. AX₃ రకపు అణువులు సమతల త్రిభుజాకారంలో ఉంటే µ = 0. పిరమిడల్ ఆకృతి కలిగి ఉంటే కొంత µ విలువను కలిగి ఉంటాయి.
      BF₃, µ = 1.47
   3. AX₄ రకపు అణువు చతుర్ముఖీయంగా ఉంటే µ = 0; విరూపణ చెందితే µ > 0.

ప్రశ్న 23.
BeF₂, బంధాలకు ధృవత్వమున్నా BeF₂ అణువుకు ద్విధ్రువ భ్రామకం సున్నా. వివరించండి.
జవాబు:
ఒక అణువు ద్విధ్రువ భ్రామకం అందులోని బంధాల బంధభ్రామకాల సదిశ మొత్తం విలువ అవుతుంది. Be-F బంధం ధ్రువశీలత గలది. BeF₂ రేఖీయ నిర్మాణం గలది. రెండు Be-F బంధాలు 180° కోణంలో ఒకదానికి ఇంకొకటి వ్యతిరేక దిశలో ఉంటాయి. బంధ భ్రామకం సదిశరాశి కావటం వల్ల వ్యతిరేక దిశలలో ఉన్న సదిశల మొత్తం సున్న. అందువల్ల రెండు Be-F బంధాల బంధ భ్రామకాల మొత్తం విలువ సున్న.

BeF₂ లో బంధ భ్రామకాలు.

ప్రశ్న 24.
CH₄ అణువు నిర్మాణాన్ని వివరించండి.
జవాబు:
CH₄ అణువును ఏర్పరచే కార్బన్ పరమాణువు భూస్థితి ఎలక్ట్రాన్ విన్యాసం 1s² 2s² 2p² ఉద్రిక్తస్థితిలో ఒక 2s ఎలక్ట్రాన్ ఖాళీ 2p ఆర్బిటాల్క మారుతుంది. ఉద్రిక్త స్థితి విన్యాసం కార్బన్ పరమాణువుకు 1s² 2s¹ 2p³. ఒక్కొక్క ఎలక్ట్రాన్ మాత్రమే ఉన్న వేలన్స్ కర్పరంలలోని 2s ఆర్బిటాల్, మూడు 2p ఆర్బిటాళ్ళు సంకరకరణం చెంది నాలుగు సర్వ సమానమైన sp³ ఆర్బిటాళ్ళనిస్తాయి.

ఒక్కొక్క sp³ ఆర్బిటాల్కు 25% s లక్షణం 75% p లక్షణం ఉంటుంది. నాలుగు సంకర sp³ ఆర్బిటాళ్ళు ఒకదానికొకటి దూరంగా త్రిమితీయ ప్రదేశంలో దిగ్విన్యాసం చెందుతాయి. కేంద్ర పరమాణువు కార్బన్ కనుక చతుర్ముఖి కేంద్రంలో ఉందనుకుంటే నాలుగు సంకర sp³ ఆర్బిటాళ్ళు చతుర్ముఖి నాలుగుమూలలకు దిగ్విన్యాసం చెందుతాయనుకోవచ్చు.’ ఈ నాలుగు సంకర sp³ ఆర్బిటాళ్ళు నాలుగు హైడ్రోజన్ పరమాణువుల 1s ఆర్బిటాళ్ళతో అతిపాతం చెందిస్తాయి. sp³ ఆర్బిటాళ్ళ మధ్యకోణం 109.5° అంటే CH₄ అణువులో HCH = 109.5° అణువు ఆకృతి చతుర్ముఖీయం.

ప్రశ్న 25.
ధ్రువ సమయోజనీయ బంధాన్ని సరియైన ఉదాహరణలతో వివరించండి.
జవాబు:
రెండు ఒకే మూలకపు పరమాణువుల మధ్య సమయోజనీయబంధం ఏర్పడితే, పంచుకోబడిన ఎలక్ట్రాన్ జంట రెండు కేంద్రకాలకు మధ్య సమానంగా పంచుకోబడుతుంది. రెండు కేంద్రకాలకు సమాన దూరంలో ఉంటుంది. ఈ విధంగా ఏర్పడిన బంధాన్ని అధ్రువ సమయోజనీయ బంధం అంటారు.

వేర్వేరు మూలకాల రెండు పరమాణువుల మధ్య బంధం వల్ల ఏర్పడే HF లాంటి విజాతీయ కేంద్రకాల అణువులో పంచుకోబడ్డ ఎలక్ట్రాన్ జంట రెండు కేంద్రకాలకు సమాన దూరంలో ఉండదు. ఎక్కువ రుణ విద్యుదాత్మకత ఉన్న ఫ్లోరీన్ ‘వైపు ఎక్కువగా జరుగుతుంది. అంటే హైడ్రోజన్ పరమాణు కేంద్రానికి దూరంలో స్థానభ్రంశం చెందుతాయి. దీని ఫలితంగా ఆ రెండు (H, F) పరమాణువుల మధ్య ఏర్పడిన బంధం ధ్రువ సమయోజనీయ బంధం.

ప్రశ్న 26.
BCl₃ అణువులోని బంధకోణం, అణువు నిర్మాణాలను వేలన్స్ బంధ సిద్ధాంతం ఉపయోగించి వివరించండి.
జవాబు:

1. ఈ సంకరణంలో ఒక s ఆర్బిటాల్, రెండు p- ఆర్బిటాళ్ళు పాల్గొని మూడు సమానమైన sp² సంకర ఆర్బిటాళ్ళనిస్తాయి. ఉదాహరణకు BCl₃ ని తీసికొన్నచో అణువులోని కేంద్ర ‘B’ పరమాణువుకు భూస్థితిలోని ఎలక్ట్రాన్ విన్యాసం 1s² 2s² 2p¹ ఉద్రిక్తస్థితిలో ఒక 25 ఎలక్ట్రాన్ ఖాళీగా ఉన్న ఒక 2p ఆర్బిటాల్క మారుతుంది. దీని కారణంగా ‘B’ పరమాణువుకు మూడు జతకూడని ఒంటరి ఎలక్ట్రాన్లు ఉంటాయి.
2. ఒక్కొక్క ఎలక్ట్రాన్ మాత్రమే ఉన్న మూడు ఆర్బిటాళ్ళు (ఒక 2s, రెండు 2p) సంకరీకరణం చెంది మూడు sp సంకర ఆర్బిటాళ్ళనిస్తాయి.
3. ఈ మూడు సంకర ఆర్బిటాళ్ళు త్రికోణీయ సమతలంలో దిగ్విన్యాసం చెంది మూడు క్లోరీన్ పరమాణువులు ఒంటరి ఎలక్ట్రాన్లున్న 3p ఆర్బిటాళ్ళతో అతిపాతం చెంది మూడు B – C1 బంధాలనిస్తాయి.
4. BCl₃ అణువులో బంధకోణం ∠CIBCI 120° గాను అణువు ఆకృతి త్రికోణీయ సమతలంగాను ఉంటుంది.

ప్రశ్న 27.
σ, π బంధాలంటే ఏమిటి ? వాటి మధ్య భేదాలను తెలపండి.
జవాబు:
సమయోజనీయ బంధాన్ని ఆర్బిటాళ్ళ అతిపాతం చెందే విధానాన్ని బట్టి రెండు రకాలుగా విభజించవచ్చు.

1) సిగ్మా (σ) బంధం
2) π (పై) బంధం.

1) సిగ్మా (σ) బంధం : ఈ బంధం బంధక ఆర్బిటాళ్ళు అంతర్ కేంద్రక అక్షం దిశలో అతిపాతం చెందటం వల్ల ఏర్పడుతుంది. బంధమేర్పరచే రెండు పరమాణువుల కేంద్రకాల మధ్య ఆర్బిటాళ్ళు అతిపాతం చెందడాన్ని ఎండ్ – ఎండ్ (end – end) లేదా హెడ్ఆన్ (Head on) అతిపాతం అంటారు. దీనినే ఏక్సియల్ అతిపాతం అని కూడా అంటారు. అలాంటి అతిపాతం వల్ల వచ్చిన బంధాన్ని ‘σ’ బంధం అంటారు. ఇలాంటి అతిపాతం ఆర్బిటాళ్ళ స్వభావాన్ని బట్టి అనేక రకాలుగా ఉండవచ్చు.

s – s అతిపాతం : దీనిలో ఒకే ఎలక్ట్రాన్ ఉన్న ఒక పరమాణువు s ఆర్బిటాల్. ఒకే ఎలక్ట్రాన్ ఉన్న రెండో పరమాణువు ‘s’ ఆర్బిటాల్ అంతర్ కేంద్రక అక్షం దిశలో అతిపాతం చెంది σ_s-s బంధం ఇస్తాయి.

π బంధం : π బంధం ఏర్పరచే పరమాణు ఆర్బిటాళ్ళు ఒక్కొక్క ఎలక్ట్రాన్తో అంతర్ కేంద్రక అక్షానికి లంబదిశ అక్షంలో ఉంటాయి. అంటే ఈ ఆర్బిటాళ్ళ అక్ష దిశలు అంతర్ కేంద్రక అక్షానికి లంబంగా ఉంటాయి. ఈ ఆర్బిటాళ్ళు ఏటవాలుగా అతిపాతం చెందడంవల్ల ఏర్పడే విద్యుదావేశ మేఘాలు పరమాణు కేంద్రకాల తలానికి పైనా కిందా విస్తరించి ఉంటాయి.

సిగ్మా, పై బంధాల మధ్య గల తేడా:

ప్రశ్న 28.
NH₃ అణువులో నైట్రోజన్ పరమాణువు sp³ సంకరకరణ స్థితిలో ఉన్నా HNH బంధకోణం 109°28′ కాకుండా వేరేగా ఉంది. వివరించండి.
జవాబు:
అమ్మోనియా ఆణువు ఆకృతి : అమ్మోనియా అణువు ఏర్పడేటప్పుడు కేంద్రక నైట్రోజన్ పరమాణువు దాని ఉత్తేజిత స్థితిలో (1s²2s² \(2 p_x^1 2 p_y^1 2 p_z^1\) sp³) సంకరీకరణం పొందుతుంది. తత్ఫలితంగా దానిపై నాలుగు sp³ సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి. వాటిలో మూడు సంకర ఆర్బిటాళ్ళలో బంధ జంటలు, నాల్గవ దానిలో ఒంటరి జంట ఉంటాయి. కేంద్రక పరమాణువు sp³ సంకరీకరణం పొందడం వల్ల అణువుకు టెట్రాహెడ్రల్ ఆకృతి ఏర్పడాలి. కాని ఒంటరి ఎలక్ట్రాన్ జంట ఉండటం వల్ల VSEPR సిద్ధాంతం ప్రకారం అణువు యొక్క ఆకృతిలో విరూపణ వచ్చి, అణువు పిరమిడల్ ఆకృతిని పొందుతుంది. బంధకోణం 109°28′ లకు బదులుగా 107° లకు తగ్గుతుంది.

ప్రశ్న 29.
(a) C₂H₄,
(b) C₂ H₂ లలో వరుసగా కార్బన్ పరమాణువుల మధ్య ద్విబంధం, త్రికబంధం ఎలా ఏర్పడతాయో వివరించండి.
జవాబు:
C₂H₄ అణువు ఏర్పడుట :
C₂H₄ అణువు ఏర్పడేటపుడు రెండు కార్బన్ పరమాణువులు వాటి ఉత్తేజిత స్థితిలో sp² సంకరీకరణం పొందుతాయి. తత్ఫలితంగా వాటిపై ఆరు sp² సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి. వాటన్నింటిలో బంధ ఎలక్ట్రాన్ జంటలు ఉంటాయి. మొదటిగా ఒక కార్బన్ పరమాణువులోని ఒక sp² సంకర ఆర్బిటాల్ మరియు రెండవ కార్బన్ పరమాణువులోని ఒక sp² సంకర అర్బిటాల్ పరస్పరం అభిముఖ ఆవరింపు చేసుకొని రెండు కార్బన్ పరమాణువుల మధ్య సిగ్మా బంధాన్ని ఏర్పరచుకుంటాయి.

మిగిలిన నాలుగు sp² సంకర ఆర్బిటాళ్ళు నాలుగు H పరమాణువులు 1s ఆర్బిటాళ్ళతో అభిముఖ ఆవరింపు చేసుకొని కార్బన్ – హైడ్రోజన్ల మధ్య నాలుగు సిగ్మా బంధాలను యిస్తాయి. ఇప్పుడు రెండు కార్బన్ల మీద సంకరీకరణంలో పాల్గొనకుండా మిగిలిపోయిన పరిశుద్ధ 2p_z ఆర్బిటాళ్ళు ప్రక్కవాటుగా ఆవరింపు చేసుకుని రెండు కార్బన్ల మధ్య పై బంధాన్ని ఏర్పరుస్తాయి. ఈ విధంగా C₂H₄ (ఇథిలీన్) అణువులో అయిదు సిగ్మా బంధాలు ఒక పై బంధం ఉంటాయి. ఇథిలీన్ అణువు సమతల త్రిభుజాకృతిని కలిగి ఉంటుంది. బంధకోణం 120° ఉంటుంది.

C₂H₂ (ఎసిటిలీన్) అణువు ఏర్పడుట :
C₂H₂ అణువు ఏర్పడేటపుడు రెండు కార్బన్ పరమాణువులు sp సంకరీకరణము పొందుతాయి. తత్ఫలితంగా వాటిపై నాలుగు Sp సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి. వాటన్నింటిలోనూ బంధ జంటలు ఉంటాయి. మొదటిగా ఒక కార్బన్ పరమాణువులోని ఒక sp సంకర ఆర్బిటాల్, రెండవ కార్బన్ పరమాణువులోని ఒక sp సంకర ఆర్బిటాల్ అభిముఖ ఆవరింపు చేసుకొని రెండు కార్బన్ల మధ్య సిగ్మా బంధాన్ని ఏర్పరుస్తాయి.

మిగిలిన రెండు sp సంకర ఆర్బిటాళ్ళు రెండు H పరమాణువులు 1s ఆర్బిటాళ్ళతో అభిముఖ ఆవరింపు చేసుకొని C, Hల మధ్య సిగ్మా బంధాలను ఏర్పరచుకుంటాయి. ఇపుడు రెండు కార్బన్లలో సంకరీకరణంలో పాల్గొనకుండా మిగిలి ఉన్న 2p_y, 2p_z పరిశుద్ధ ఆర్బిటాళ్ళు పరస్పరం ప్రక్కవాటుగా ఆవరింపు చేసుకొని వాటి మధ్య రెండు పై బంధాలను యిస్తాయి. ఈ విధంగా ఎసిటలీన్ అణువులో మూడు సిగ్మా బంధాలు రెండు పై బంధాలు ఉన్నాయి. కేంద్రక కార్బన్ పరమాణువులు sp సంకరీకరణం పొందడం వల్ల C₂H₂ అణువు రేఖీయంగా ఉంటుంది. బంధకోణం 180° ఉంటుంది.

ప్రశ్న 30.
PCl₅ అణువు ఏర్పడటంలో p సంకరకరణం వివరించండి.
జవాబు:
ఫాస్పరస్ పరమాణు సంఖ్య = 15
భూస్థాయి విన్యాసం = 1s²2s²2p⁶3s²3p³
ఉత్తేజిత ఎలక్ట్రాన్ విన్యాసం = 1s²2s²2p⁶\(3 p_x^1 3 p_y^1 3 p_z^1 3 d_{x y}^1\) PCl₅ అణువు ఏర్పడేటప్పుడు కేంద్రక ‘P’ పరమాణువు దాని ఉత్తేజిత స్థితిలో sp³d సంకరీకరణం పొందుతాయి. తత్ఫలితంగా దానిపై అయిదు సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి. వాటన్నింటిలో బంధ ఎలక్ట్రాన్ జంటలు ఉంటాయి. ఇపుడు ఈ అయిదు సంకర ఆర్బిటాళ్ళు ఐదు క్లోరిన్ పరమాణువుల 3p_z ఆర్బిటాళ్ళతో అభిముఖ ఆవరింపు చేసుకుని ఐదు సిగ్మా బంధాలను యిస్తాయి. PCl₅ అణువు ట్రైగొనల్ బై పిరమిడల్ ఆకృతి కలిగి ఉంటుంది. బంధకోణం 90° మరియు 120° ఉంటుంది.

మూడు P – CI బంధాలు ఒక తలంలో ఉండి CI – P – CI బంధకోణం 120° గా ఉంటుంది. ఈ మూడు P – CI బంధాల్ని ఈక్వటోరియల్ బంధాలు అంటారు. మిగిలిన రెండు P-CI బంధాలు ఒకటి ఈక్వటోరియల్ తలానికి పైకి రెండోది కిందికి లంబంగా అంటే తలానికి 90° లో ఉంటాయి. ఈ బంధాల్ని ఏక్సియల్ (అక్షీయ) బంధాలంటారు. రెండు ఈక్విటోరియల్ బంధాల మధ్య 120° తో దూరం ఉంటే ఒక ఏక్సియల్ ఒక ఈక్వటోరియల్ బంధాల మధ్య కేవలం 90° ఉండటం వల్ల ఏక్సియల్ బంధాలు ఎక్కువ వికర్షణ నెదుర్కొంటాయి. దీనివల్ల ఇవి కొంత ఈక్వటోరియల్ బంధాల కంటె బలహీనమై సాగి ఉంటాయి. దీనివల్లనే PCl₅ అణువు చాలా చురుకుగా చర్యలో పాల్గొంటుంది.

ప్రశ్న 31.
SF₆ ఏర్పడటంలో సంకరకరణం వివరించండి.
జవాబు:
ఒక ‘S’ ఆర్బిటాల్, మూడు ‘p’ ఆర్బిటాళ్ళు, రెండు ‘d’ ఆర్బిటాళ్ళు కలిసిపోయి ఆరు సర్వసమానాలైన sp³d² సంకర ఆర్బిటాళ్ళను ఏర్పరిచే ప్రక్రియను sp³d² సంకరీకరణం అంటారు.
ఉదా : సల్ఫర్ హెక్సా ఫ్లోరైడ్ (SF6) అణువు ఏర్పడుట :
∴ సల్ఫర్ భూస్థాయి విన్యాసం = 1s²2s²2p⁶3s²3p⁴
1వ ఉత్తేజిత స్థితి విన్యాసం = 1s²2s²2p⁶3s²\(3 p_x^1 3 p_y^1 3 p_z^1 3 d_{x y}^1\)
2వ ఉత్తేజిత స్థితి విన్యాసం = 1s²2s²2p⁶3s¹\(3 p_x^1 3 p_y^1 3 p_z^1 3 d_{x y}^1 3 d_{y z}^1\)

SF₆ అణువు ఏర్పడేటప్పుడు కేంద్రక ‘S’ పరమాణువు sp³d² సంకరీకరణం పొందుతుంది. తత్ఫలితంగా దానిపై ఆరు sp³d² సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి. వాటన్నింటిలో బంధ ఎలక్ట్రాన్ జంటలు ఉంటాయి. ఇపుడు ఈ ఆరు సంకర ఆర్బిటాళ్ళు ఆరు F పరమాణువులు 2p_z ఆర్బిటాళ్ళతో అభిముఖ ఆవరింపు చేసుకుని ఆరు సిగ్మా బంధాలను యిస్తాయి.’ SF₆ అణువు ఆక్టాహెడ్రల్ ఆకృతి కలిగి ఉంటుంది. బంధకోణాలు 90° మరియు 180° ఉంటాయి.

ప్రశ్న 32.
సమన్వయ సమయోజనీయ బంధం ఏర్పడే విధానాన్ని ఉదాహరణతో వివరించండి.
జవాబు:
సమన్వయ సమయోజనీయ బంధం, సమయోజనీయ బంధంలో ఒక ప్రత్యేక రకం. ఈ బంధం కూడా రెండు పరమాణువుల మధ్య ఎలక్ట్రాన్లు పంచుకోవడం వల్ల ఏర్పడుతుంది. కాని పంచుకోబడ్డ జంటను ఒక పరమాణువు రెండవ పరమాణువుకు అందజేస్తుంది. దీనిని బాణం గుర్తు (‘→”) తో సూచిస్తారు. ఈ బాణం గుర్తు దాత నుండి స్వీకర్త వైపుకు ఉండాలి. పంచుకోబడ్డ ఎలక్ట్రాన్ జంటను ఏ పరమాణువైతే అందజేస్తుందో దానిని దాత అని, పంచుకోబడ్డ ఎలక్ట్రాన్ జంటను ఏ పరమాణువైతే స్వీకరిస్తుందో దానిని స్వీకర్త అని అంటారు. రెండు పరమాణువుల మధ్య సమన్వయ సమయోజనీయ బంధం ఏర్పడాలంటే, ఒక పరమాణువుకు ఒంటరి ఎలక్ట్రాన్ జంట ఉండాలి. రెండవ పరమాణువుకు ఖాళీ ఆర్బిటాల్ ఉండాలి.
ఉదా : 1) అమ్మోనియం అయాన్. (\(\mathrm{NH}_4^{+}\)) ఏర్పడుట :
NH₃ అణువు H⁺అయాన్ తో చర్య జరపడం వల్ల \(\mathrm{NH}_4^{+}\) అయాన్ ఏర్పడుతుంది. NH₃ అణువులోని కేంద్రక N- పరమాణువు ఒంటరి ఎలక్ట్రాన్ జంటను కలిగి ఉంటుంది. H⁺ అయాన్కు ఖాళీ ఆర్బిటాల్ ఉంటుంది. కాబట్టి NH₃ లోని కేంద్రక N – పరమాణువు తన ఒంటరి ఎలక్ట్రాన్ జంటను H⁺ అయాను దానం చేస్తుంది. అపుడు వాటి మధ్య సమన్వయ సమయోజనీయ బంధం ఏర్పడుతుంది.

2) హైడ్రోనియం అయాన్ ఏర్పడుట (\(\mathrm{H}_3 \mathrm{O}^{+}\)) :
H₂O అణువు H⁺అయాన్ తో చర్య జరపడం వల్ల H₃O⁺ అయాన్ ఏర్పడుతుంది. H₂O అణువులో కేంద్రక ‘O’- ఆక్సిజన్ పరమాణువుపై రెండు ఒంటరి ఎలక్ట్రాన్ జంటలు ఉంటాయి. H⁺ అయాన్కు ఖాళీ ఆర్బిటాల్ ఉంటుంది. కాబట్టి H₂O లోని కేంద్రక ‘O’- పరమాణువు ఒక ఒంటరి ఎలక్ట్రాన్ జంటను H⁺ అయాను దానం చేస్తుంది. అపుడు వాటి మధ్య సమన్వయ సమయోజనీయ బంధం ఏర్పడుతుంది.

సమన్వయ సమయోజనీయ సమ్మేళనాల ధర్మాలు :

1. ఈ సమ్మేళనాలు విద్యుద్వాహకాలు కాదు. ఎందులకనగా ఇవి నీటిలో అయనీకరణం చెందవు.
2. బెంజీన్, కార్బన్ టెట్రాక్లోరైడ్ వంటి అధృవ ద్రావణులలో కరుగుతాయి. నీరు వంటి ధృవ ద్రావణులలో పాక్షికంగా కరుగుతాయి.
3. ఈ సమ్మేళనాలు అణు సాదృశ్యాన్ని ప్రదర్శిస్తాయి. ఎందులకనగా ఈ బంధం దిశను కలిగి ఉంటుంది.
4. ఈ బంధానికి ధృవశీలత పాక్షికంగా ఉంటుంది. అందువలన ఈ సమ్మేళనాల బాష్పశీలత, అయానిక మరియు సమయోజనీయ సమ్మేళనాల బాష్పశీలతలకు మధ్యస్థంగా ఉంటుంది.

ప్రశ్న 33.
కింది అణువులు ఏర్పడటంలో కార్బన్ పరమాణువులు ఏ సంకర ఆర్బిటాళ్ళనుపయోగించాయి ?
(a) CH₃ – CH₃
(b) CH₃ – CH = CH₂
(c) CH₃ – CH₂ – OH
(d) CH₃ – CHO
జవాబు:
(a)

CH₃ – CH₃ లోని రెండు కార్బన్ పరమాణువులు sp³ సంకరీకరణంలో ఉంటాయి.

b) CH₃ – CH = CH₂
లో 1, 2 కార్బన్లు sp² సంకరీకరణం మరియు C₃ కార్బన్ sp³ సంకరీకరణం చెందును.

c) CH₃ – CH₂ – OH
లో C₁ కార్బన్ sp² సంకరీకరణాన్ని C₂ కార్బన్ sp³ సంకరీకరణం చెంది ఉన్నాయి.

d) CH₃ – CHO
లో CHO కార్బన్ sp² సంకరీకరణం, CH₃ కార్బన్ sp³ సంకరీకరణాన్ని పొంది ఉన్నాయి.

ప్రశ్న 34.
హైడ్రోజన్ బంధం అంటే ఏమిటి ? విభిన్న హైడ్రోజన్ బంధాలను ఉదాహరణలతో వివరించండి.
జవాబు:
నైట్రోజన్, ఫ్లోరీన్, ఆక్సిజన్ మూలకాలు అత్యధిక ఋణ విద్యుదాత్మకత గలవి. ఈ పరమాణువులు హైడ్రోజన్తో సమయోజనీయ బంధం ఏర్పరచినపుడు బంధ ఎలక్ట్రాన్ జంట ఈ పరమాణువుల వైపు ఎక్కువగా జరిగి ఉంటుంది. అందువల్ల ఈ పరమాణువుల మీద పాక్షిక ఋణావేశం హైడ్రోజన్ పరమాణువు మీద పాక్షిక ధనావేశం ఉత్పన్నమవుతుంది. ఈ ధృవ అణువు ప్రక్కన అదే పదార్థపు వేరొక అణువు ఉంటే ఒక అణువులోని పాక్షిక ధన విద్యుదావేశంగల H పరమాణువు ప్రక్క అణువులోని పాక్షిక ఋణ విద్యుదావేశం ఉన్న పరమాణువుతో బలహీనమైన స్థిరవిద్యుత్ బంధం ఏర్పరుస్తుంది. దీనినే హైడ్రోజన్ బంధం అంటారు.
ఉదా : H^{δ +} _ F^{δ –}…………..H^{δ +} _ F^{δ –}…………..H^{δ +} _ F^{δ –}

నిర్వచనం :
హైడ్రోజన్ పరమాణువు అత్యధిక ఋణ విద్యుదాత్మకత గల మూలకం లేదా మూలకాల రెండు పరమాణువుల మధ్య ఉన్నప్పుడు అది ఒక పరమాణువుతో ధ్రువ బంధాన్ని రెండో పరమాణువుతో ఒక బలహీనమైన స్థిరవిద్యుత్ బంధాన్ని ఏర్పరుస్తుంది. ఈ స్థిర విద్యుత్ బంధమే హైడ్రోజన్ బంధం.
హైడ్రోజన్ బంధాలు రెండు రకాలు : అవి
(i) అంతరణుక హైడ్రోజన్ బంధాలు
(ii) అణు అంతర హైడ్రోజన్ బంధాలు.

(i) ఒకే పదార్థ అణువుల మధ్య లేక వేరు వేరు పదార్థాల అణువుల మధ్య ఏర్పడే హైడ్రోజన్ బంధాన్ని అంతరణుక హైడ్రోజన్ బంధం అంటారు.

(ii) ఒకే అణువులోని రెండు సమూహాల్లోని రెండు అత్యధిక ఋణ విద్యుదాత్మకత గల ఒకే మూలకపు లేదా వేర్వేరు మూలకాల పరమాణువుల మధ్య హైడ్రోజన్ వారధిగా ఉండే బంధం. అణు అంతర హైడ్రోజన్ బంధాలు.

ఉదా : ఆర్థోనైట్రోఫినాల్

ప్రశ్న 35.
వేలన్స్ బంధ సిద్ధాంతంతో H₂ అణువు ఏర్పడడాన్ని వివరించండి.
జవాబు:
వేలన్స్ బంధ సిద్ధాంతం లోని అంశాలు :

1. సగం నిండిన పరమాణు ఆర్బిటాళ్ళు పరస్పరం ఆవరింపు చేసుకోవడం వల్ల సమయోజనీయ బందం ఏర్పడుతుంది.
2. ఆవరింపులో పాల్గొనే సగం నిండిన పరమాణు ఆర్బిటాళ్ళలోని ఎలక్ట్రాన్లు వ్యతిరేక స్పిన్లు కలిగి ఉండాలి. బంధంలో పాల్గొనే పరమాణువు తన ఆర్బిటాళ్ళ ఉనికిని పోగొట్టుకోలేదు. కాని అతిపాతం చెందే ఆర్బిటాల్లలోని ఎలక్ట్రాన్ జంటలను మాత్రం రెండు పరమాణువులు పంచుకుంటాయి.
3. ఆర్బిటాళ్ళ ఆవరింపు పరిమితి మీద బంధ బలం ఆధారపడి ఉంటుంది. ఆవరింపు ఎక్కువగా ఉంటే బంధ బలం ఎక్కువగా ఉంటుంది. ఆవరింపు తక్కువగా ఉంటే బంధబలం తక్కువగా ఉంటుంది.
4. ఆవరింపులో పాల్గొనే పరమాణు ఆర్బిటాళ్ళు ఎక్కువగా ఏ దిశలో కేంద్రీకృతం అవుతాయో ఆ దిశ ఏర్పడ్డ బంధం యొక్క దిశను సూచిస్తుంది.
5. సంయోగం చెందే రెండు పరమాణువుల ఆర్బిటాళ్ళు అతిపాతం చెందడం వల్ల అంతర్ కేంద్ర అక్షంపై ఎలక్ట్రాన్ సాంద్రత పెరుగుతుంది. దీనివల్ల రెండు పరమాణువులు ఒకదానివైపు మరొకటి ఆకర్షితం అవుతాయి. దీని ఫలితంగా అణువు స్థిరీకరణం చెందుతుంది.
6. ‘s’ ఆర్బిటాల్ తప్ప మిగిలిన అన్ని పరమాణు ఆర్బిటాళ్ళు దిశను కలిగి ఉంటాయి. అందువలన అవి ఆవరింపు చేసుకోవడం వల్ల ఏర్పడే బంధానికి కూడా దిశ ఉంటుంది. ఇది అణువు యొక్క ఆకృతిని నిర్ణయిస్తుంది.

ఉదా : హైడ్రోజన్ అణువు ఏర్పడుట ( s – s ఆవరింపు) : H పరమాణు సంఖ్య 1. కాబట్టి దాని ఎలక్ట్రాన్ విన్యాసం 1s¹. దీనిలో సగం నిండిన ” ఆర్బిటాల్ ఉన్నది. రెండు H పరమాణువుల 1s ఆర్బిటాళ్ళు పరస్పరం అభిముఖం ఆవరింపు చేసుకోవడం వల్ల H₂ అణువు ఏర్పడుతుంది. రెండు H పరమాణువుల మధ్య ఏర్పడే ఈ బంధాన్ని సిగ్మా సమయోజనీయ బంధం అంటారు. ఇది s-s ఆవరింపుకు ఉదాహరణ.

ప్రశ్న 36.
B₂ అణువు పరాయస్కాంత ధర్మం గలది ఉంది. అణు ఆర్బిటాల్ సిద్ధాంతంతో దానిని వివరించండి.
జవాబు:
బోరాన్ పరమాణువు ఎలక్ట్రాన్ విన్యాసం 1s² 2s² 2p¹. రెండు బోరాన్ పరమాణువులు వాటి పరమాణు ఆర్బిటాళ్ల రేఖీయ కలయికతో B₂ అణువు ఏర్పడుతుంది. B₂ అణువులో మొత్తం పది ఎలక్ట్రాన్లుంటాయి.
B₂ అణు ఎలక్ట్రాన్ విన్యాసం (σ 1s)₂ (σ* 1s)₂ (σ 2s)₂ (σ*2s)₂ (π2p¹ = x2p¹)
బంధ క్రమం B₂ అణువుకు \(\frac{\mathrm{N}_{\mathrm{b}}-\mathrm{N}_{\mathrm{a}}}{2}\) = \(\frac{6-4}{2}\) = 1
π అణు ఆర్బిటాల్లలో జతలేని ఎలక్ట్రానులు రెండు ఉన్నాయి. అందువల్ల B₂ పరాయస్కాంత ధర్మాన్ని కలిగి ఉంది.

ప్రశ్న 37.
పరమాణు ఆర్బిటాళ్ల రేఖీయ కలయికకు నియమాలేమిటి ? వివరించండి.
జవాబు:
రెండు హైడ్రోజన్ పరమాణువుల పరమాణు ఆర్బిటాళ్ళ తరంగ ప్రమేయాలు ψ_A, ψ_B అనుకుంటే, పరమాణు ఆర్బిటాళ్లు కలిసి అణు ఆర్బిటాళ్ళను ఏర్పరుస్తాయి.
అణుఆర్బిటాల్ = ψ_A ± ψ_B

ఆర్బిటాళ్లు రేఖీయంగా కలవడానికి కావలసిన పరిస్థితులు :

1. రేఖీయ కలయిక చెందే పరమాణు ఆర్బిటాళ్ల శక్తి ఒకే విలువతో కాని లేదా దాదాపు ఒకే విలువతోగాని ఉండాలి. ఒక పరమాణువు 1s ఆర్బిటాల్తో రెండో పరమాణువు 1s ఆర్బిటాల్ కలుస్తుంది. కాని ‘2s’ ఆర్బిటాల్తో కాదు. కారణం 2s ఆర్బిటాల్క 1s కంటే ఎక్కువ శక్తి ఉండటమే. ఇది ముఖ్యంగా ఒకే రకమైన కేంద్రకాల ద్విపరమాణుక అణువులకు వర్తిస్తుంది.
2. అణు అక్షం పరంగా కలయికలో పాల్గొనే పరమాణు ఆర్బిటాళ్ళకు ఒకే సౌష్ఠవం ఉండాలి. ఒక పరమాణువు 2p_z ఆర్బిటాల్ వేరే పరమాణువు 2p_z తో కలుస్తుంది. కాని 2p_x లేదా 2p_x లతో కలవదు.
3. రేఖీయ కలయిక చెందే ఆర్బిటాళ్లు గరిష్ఠంగా అతిపాతం చెందాలి.

ప్రశ్న 38.
బంధ క్రమం అంటే ఏమిటి ? క్రింది అణువుల్లో బంధ క్రమమెంత ?
(a) N₂
(b) O₂
(c) \(\mathrm{O}_2^{2+}\)
(d) \(\mathbf{O}_2^{-}\)
జవాబు:
బంధక్రమం’ బంధక ఆర్బిటాళ్లలోని మొత్తం ఎలక్ట్రాన్ల సంఖ్యకు (N_b) అపబంధక ఆర్బిటాళ్లలోని మొత్తం ఎలక్ట్రానులు సంఖ్య (N_a) భేదం గణించి దానిని సగం చేస్తే వచ్చే విలువ.
బంధక్రమం = \(\frac{1}{2}\)[N_b – N_a]
a) N₂ అణు ఆర్బిటాల్ విన్యాసం :

బంధక్రమం = \(\frac{6-2}{2}\) = 2

b) O₂ అణు విన్యాసం :

బంధక్రమం = \(\frac{6-2}{2}\) = 2

c) \(\mathbf{O}_2^{2+}\) అణు విన్యాసం :

బంధక్రమం = \(\frac{10-5}{2}\) = \(\frac{5}{2}\) = 2.5

d) \(\mathrm{O}_2^{-}\) అణు విన్యాసం :

బంధక్రమం = \(\frac{10-7}{2}\) = \(\frac{3}{2}\) = 1.5

ప్రశ్న 39.
BF₃, NF₃ అణువుల్లో NF₃ కి ద్విధ్రువ భ్రామకం ఉన్నది. BF₃ కి లేదు. ఎందువల్ల ?
జవాబు:
BF₃ అణువు నికర ద్విధ్రువభ్రామకం సున్నా. ఇక్కడ మూడు B – F బంధాలు అణువులో ఉన్నాయి. రెండు B – F బంధాల బంధ ద్విధ్రువాల సదిశ మొత్తం మూడో B – F బంధం బంధ ద్విధ్రువానికి సమంగాను పూర్తి వ్యతిరేక దిశలో ఉంటుంది. అందుకే మొత్తం అణువు ద్విధ్రువభ్రామకం విలువ సున్నా.

BF₃ అణువు సమతల త్రిభుజాకార ఆకృతిలో సౌష్ఠవంగా వుంటుంది. అందువల్లనే రెండు బంధాల బంధ ద్విధ్రువాల సదిశ మొత్తం మూడో B -F బంధం యొక్క బంధ ద్విధ్రువానికి సమంగాను, పూర్తి వ్యతిరేక దిశలోను ఉండి రద్దు కావడం వల్ల ఫలితభ్రామకం మొత్తం సున్నా అవుతుంది.

NF₃ లో మూడు N – F బంధాలు బంధ భ్రామకాన్ని కలిగి ఉన్నాయి. అణువు సూచ్యాకార (Pyramid) ఆకృతిలో ఉంటుంది. నైట్రోజన్పై గల ఒంటరి జంట బంధ భ్రామకం NF బంధాల ఫలిత భ్రామకానికి వ్యతిరేక దిశలో ఉంటుంది. కాని ఒకదానికి ఒకటి రద్దు కావు. కొంత ఫలితభ్రామకం మిగిలి ఉంటుంది. అందువల్ల NF₃ కు ద్విధ్రువభ్రామకం కలదు.

ప్రశ్న 40.
NH₃, NF₃ రెండు అణువులు సూచ్యాకృతిలో ఉంటాయి. అయినా NH₃ కి NF₃ కంటె ద్విధ్రువ భ్రామకం ఎక్కువ. ఎందువల్ల ?
జవాబు:
NH₃, NF₃, లు సూచ్యాకార అణువులే. రెండింటి లోను నైట్రోజన్ పరమాణువుపై ఒంటరి జత ఎలక్ట్రాన్లుంటాయి.
NH₃ కు ద్విధ్రువభ్రామకం 4.9 × 10^-30 cm
NF₃ కు ద్విధ్రువభ్రామకం 0.8 × 10^-30 cm
NH₃ అణువుకు ఎక్కువ ద్విధ్రువభ్రామకం ఉండటానికి కారణం NH₃ లోని మూడు N – H బంధాల ఫలిత ద్విధ్రువ భ్రామకం ఏ దిశలో ఉంటుందో ఒంటరి జంట ఎలక్ట్రాన్ల ఆర్బిటాల్ ద్విధ్రువం కూడా అదే దిశలో ఉంటుంది.
NF₃ అణువులో ఒంటరి జంట ఎలక్ట్రాన్ ఆర్బిటాల్ ద్విధ్రువం మూడు N – F బంధాల ద్విధ్రువాల ఫలిత ద్విధ్రువభ్రామకానికి వ్యతిరేక దిశలో ఉంటుంది. అందుకే మొత్తం మీద NH₃ కి NF₃ కంటే ద్విధ్రువ భ్రామకం ఎక్కువ విలువలో ఉంటుంది.

NH₃ లో నికర ద్విధ్రువభ్రామకం = 4.9 × 10^-30 cm NF_౩ లో నికర ద్విధ్రువభ్రామకం = 0.8 × 10^-30 cm

ప్రశ్న 41.
వేలన్స్ కర్పర ఎలక్ట్రాన్ జంటల వికర్షణ (VSEPR) సిద్ధాంతం ఉపయోగించి కింది అణువుల ఆకృతులను తెలపండి.
(a) XeF₄
(b) BrF₅
(c) CIF₃
(d) IC\(l_4^{-}\)
జవాబు:
a) Xe బాహ్యకర్పరంలో 8 ఎలక్ట్రానులు ఉన్నాయి. నాలుగు Xe పరమాణువులు 4 ఫ్లోరిన్లతో నాలుగు బంధాలను ఏర్పరుస్తుంది. మిగిలిన 4 ఎలక్ట్రానులు రెండు ఒంటరి ఎలక్ట్రాన్ జంటలుగా వుంటాయి. కనుక XeF₄ లో Xe పరమాణువు బాహ్య కర్పరంలో 4 బంధ ఎలక్ట్రాన్ జంటలు, 2 ఒంటరి ఎలక్ట్రాన్ జంటలు కలిసి మొత్తం 6 ఎలక్ట్రాన్ జంటలుంటాయి. ఈ ఆరు జంటలు అష్టముఖి ఆకృతిలో అమరి ఉంటాయి. వికర్షణలు కనిష్ఠంగా ఉండేటట్లు ఒంటరి జంటలు అష్టముఖి అభిముఖ శీర్షాలను ఆక్రమిస్తాయి. అందువల్ల XeF₄ సమతల చతురస్రాకార ఆకృతిలో ఉంటుంది.

b) Br బాహ్యకర్పరంలో 7 + 5 = 12 ఎలక్ట్రానులు ఉంటాయి. BrF₅ లో మొత్తం 5 బంధ జంటలు, ఒక ఒంటరి జంట ఉన్నాయి. మొత్తం ఆరు ఎలక్ట్రాన్ జంటలున్నాయి. ఒంటరి ఎలక్ట్రాన్ జంట ఉండుట వలన చతురస్రాకార పిరమిడ్ ఆకృతిలో ఉంటుంది.

c) ClF₃ లో Cl బాహ్యకర్పరంలో 7 ఎలక్ట్రానులు, ఫ్లోరిన్ నుంచి 3 ఎలక్ట్రానులు మొత్తం 10 ఎలక్ట్రానులు ఉన్నాయి. అవి 3 బంధ జంటలు, రెండు ఒంటరి ఎలక్ట్రాన్ జంటలుగా ఉంటాయి. 5 ఎలక్ట్రాను జంటలు ట్రిగొనాల్ బై పిరమిడల్ ఆకృతిలో అమరుతాయి. రెండు ఒంటరి జంటలు ఉండుట వలన ClF₃ కు ‘T’ ఆకృతి వస్తుంది.

d) \(\mathrm{lCl}_4^{-}\) లోని I బాహ్య కర్పరంలో మొత్తం ఎలక్ట్రానులు 7 + 4 + 1 = 12. వీటిలో 4 బంధ ఎలక్ట్రాన్ జంటలు. మిగిలినవి రెండు ఒంటరి జంట ఎలక్ట్రాన్లు. అవి అష్టముఖి అభిముఖ శీర్షాలను ఆక్రమిస్తాయి. \(\mathrm{lCl}_4^{-}\) కు సమతల చతురస్రాకృతి వస్తుంది.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 42.
అయానిక బంధం ఏర్పడటాన్ని సోదాహరణంగా వివరించండి.
జవాబు:
అల్ప అయొనైజేషన్ పొటెన్షియల్ విలువగల పరమాణువు నుండి అధిక ఋణ విద్యుదాత్మకత గల పరమాణువుకు ఎలక్ట్రానులు బదిలీ కావటం వల్ల ఏర్పడ్డ విరుద్ద ఆవేశాలు గల అయాన్ల మధ్య గల స్థిర విద్యుదాకర్షణ బలాలను అయానిక బంధం అంటారు.
ఉదా : సోడియం క్లోరైడ్ ఏర్పడుట.
సోడియం పరమాణువు పరమాణు సంఖ్య (Z = 11)
ఎలక్ట్రాన్ విన్యాసం 1s²2s²2p⁶3s¹ ఈ విన్యాసాన్ని ఆర్బిటాళ్ళ పరంగా కింది విధంగా చూపుతారు.

క్లోరిన్ పరమాణు సంఖ్య (Z = 17). ఎలక్ట్రాన్ విన్యాసం 1s² 2s² 2p⁶3s² 3p⁵. ఈ విన్యాసాన్ని ఆర్బిటాళ్ళ పరంగా కింది విధంగా చూపుతారు.

స్థిరత్వం పొందడం కోసం సోడియం పరమాణువు ఒక ఎలక్ట్రాన్ ను పోగొట్టుకొని Ne విన్యాసం పొంది Na⁺ ను ఇస్తుంది.
Na – e → Na⁺
Na⁺ అయాన్ ఆర్బిటాల్ విన్యాసం కింది విధంగా వుంటుంది.

అదే విధంగా స్థిరత్వం పొందడానికి Cl పరమాణువు ఒక ఎలక్ట్రాను గ్రహించుకొని Ar విన్యాసం పొంది Cl^– ను ఇస్తుంది.
Cl + e → Cl^–
Cl^– అయాన్ ఆర్బిటాల్ విన్యాసం కింది విధంగా ఉంటుంది.

ఈ విధంగా ఏర్పడ్డ అయాన్ల మధ్య స్థిర విద్యుదాత్మక ఆకర్షణబలాలు ఏర్పడి రెండు అయాన్లను బంధిస్తాయి.

ప్రశ్న 43.
అయానిక సంయోగ పదార్థాలు ఏర్పడటానికి అనువైన పరిస్థితులు వివరించండి.
జవాబు:
a) కేటయాన్ ఏర్పడటానికి అనుకూలించే అంశాలు :

1. అల్ప అయొనైజేషన్ పొటెన్షియల్ : అల్ప అయొనైజేషన్ పొటెన్షియల్ గల పరమాణువు ఎలక్ట్రాన్ను సులభంగా కోల్పోయి కేటయాన్ను ఏర్పరుస్తుంది.
   K⁺ (IP 496 kJ mol^-1) అయాన్ Na⁺ (IP 520 KJ mol^-1) కన్నా సులభంగా ఏర్పడుతుంది.
2. అల్ప ఆవేశం : తక్కువ ఆవేశం గల కేటయాన్ సులభంగా ఏర్పడుతుంది. Na⁺, Mg⁺⁺, Al⁺⁺⁺ అయాన్లలో సులభంగా ఏర్పడే క్రమం Na⁺ > Mg⁺⁺ > Al⁺⁺⁺.
3. అధిక పరమాణు పరిమాణం : అధిక పరమాణం గల పరమాణువులు ఎలక్ట్రాన్లను సులభంగా కోల్పోతాయి. వేలన్స్ ఎలక్ట్రాన్లపై కేంద్రక ఆకర్షణ స్వల్పంగా ఉంటుంది.
   ఉదా : ఆల్కలీ లోహాలలో Cs⁺ అయాను సులభంగా ఏర్పడుతుంది.
4. జడవాయు ఎలక్ట్రాన్ విన్యాసం : జడవాయు ఎలక్ట్రాన్ విన్యాసం గల కేటయాన్ సులభంగా ఏర్పడుతుంది. ఉదా : Ca⁺⁺, Zn⁺⁺ అయాన్లలో Ca⁺⁺ (2, 8, 8) అయాన్ Zn⁺⁺ (2, 8, 18) కన్నా సులభంగా ఏర్పడుతుంది.

b) ఆనయాన్ ఏర్పడుటకు అనుకూలించే అంశాలు :

1. అధిక ఋణ విద్యాదాత్మకత మరియు అధిక ఎలక్ట్రాన్ ఎఫినిటీ : అధిక EN మరియు EA గల మూలక పరమాణువులు సులభంగా ఎలక్ట్రాన్లను గ్రహించి ఆనయాన్ ను ఏర్పరుస్తాయి.
   ఉదా : F^– అయాను CI^– కన్నా సులభంగా ఏర్పడుతుంది.
2. స్వల్పపరిమాణం : చిన్న పరమాణువులు గ్రహించిన ఎలక్ట్రానులను బలంగా పట్టి ఉంచగలవు. అందువల్ల
   F^– > Cl^– > Br^– > I^– అయాన్లు ఏర్పడే క్రమం ఉంటుంది.
3. అల్ప ఆవేశం : అల్ప ఆవేశం గల అయాన్లు సులభంగా ఏర్పడతాయి.
   F^–, O^2- కన్నా సులభంగా ఏర్పడుతుంది.

ప్రశ్న 44.
కింది అణువులకు లూయీ నిర్మాణాలు వ్రాయండి.
(a) H₂S
(b) SiCl₄
(c) BeF₂
(d) HCOOH
జవాబు:

ప్రశ్న 45.
క్రింది వాటిని వివరించండి.
(a) బంధకోణం
(b) బంధ ఎంథాల్పీ
(c) బంధదైర్ఘ్యం
(d) బంధక్రమం.
జవాబు:
a) బంధకోణం :
ఒక అణువు లేదా సంక్లిష్ఠ అయాన్లోని కేంద్ర పరమాణువుపై ఉన్న రెండు బంధక ఆర్బిటాళ్ళ మధ్య కోణాన్ని బంధకోణం అని నిర్వచించవచ్చు. దీనిని వర్ణపట లేఖినినుపయోగించి తెలుసుకొంటారు. అణువు లేదా అణువు ఆకృతి తెలుస్తుంది.
ఉదా :

b) బంధ ఎంథాల్పీ :
ఒక మోల్ అణువుల్లోని పరమాణువుల మధ్య ఉన్న ఒక మోల్ బంధాలను విచ్ఛిత్తి చేయడానికి కావలసిన శక్తిగా బంధ ఎంథాల్పీని నిర్వచించవచ్చు. దీనిని kJ mol^-1 ప్రమాణాలలో చెబుతారు.
ఉదా : H-H బంధ ఎంథాల్పీ హైడ్రోజన్లో 435.8 kJ mol^-1

c) బంధ దూరం :
బంధ దైర్ఘ్యాన్ని అణువులో బంధాలు ఏర్పరచుకొన్న రెండు పరమాణువుల కేంద్రకాల మధ్య సమతాస్థితి దూరంగా నిర్వచించవచ్చు.
బంధ దైర్ఘ్యాల్ని వర్ణపట దర్శినితో గాని, X- కిరణ వివర్తన పద్ధతిలో గాని, ఎలక్ట్రాన్ – వివర్తన పద్ధతిలో కాని కొలిచి నిర్ణయిస్తారు.
రెండు ఒకే మూలకపు పరమాణువుల మధ్య సమయోజనీయ బంధం ఏర్పడితే అపుడు ఆ రెండు పరమాణు కేంద్రకాల మధ్య దూరంలో సగాన్ని పరమాణువు సమయోజనీయ వ్యాసార్ధం అంటారు.
సమయోజనీయ వ్యాసార్ధం = \(\frac{\mathrm{d}_{\mathrm{A}-\mathrm{A}}}{2}\)

d_{A – A} ను బంధ దైర్ఘ్యమని అంటారు. ఋణ విద్యుదాత్మక భేదం ఎక్కువగా ఉన్న AB లాంటి అణువులలో భిన్న కేంద్రకాల మధ్య దూరం
d_AB = r_A + r_B + C (X_A – X_B)
X_A, X_b లు A, B ల ఋణ విద్యుదాత్మకతలు. C విలువ A, B పరమాణువులపై ఆధారపడి ఉంటుంది. రెండు పీరియడ్ మూలకాల పరమాణువులు బంధంలో పాల్గొంటే C విలువ 0.08

d) బంధ క్రమాంకం :
లూయీ వివరణ ప్రకారం ఒక ద్విపరమాణుక అణువు బంధ క్రమాంకం ఆ అణువులోని రెండు పరమాణువుల మధ్య ఉన్న సమయోజనీయ బంధాలకు సమానం. H₂ లో H – H బంధానికి బంధక్రమాంకం ఒకటి. O₂ లో O = O అణువులో రెండు ఎలక్ట్రాన్ జంటలు రెండు పరమాణువుల మధ్య పంచుకోవటం వల్ల రెండు సమయోజనీయ బంధాలు ఏర్పడతాయి. బంధక్రమాంకం రెండు అణుఆర్బిటాల్ సిద్ధాంతం ప్రకారం బంధక్రమాంకం = \(\frac{1}{2}\) (బంధక ఆర్బిటాల్లలోని ఎలక్ట్రానుల మొత్తం – అపబంధక ఆర్బిటాల్లని ఎలక్ట్రానుల మొత్తం)
B. O = \(\frac{1}{2}\) (N_b – N_a)
బంధక్రమాంకం పెరిగిన కొద్దీ బంధ ఎంథాల్పీ పెరుగుతుంది. బంధ దైర్ఘ్యం తగ్గుతుంది. స్థిరత్వం పెరుగుతుంది.

ప్రశ్న 46.
వేలన్స్ కర్పర ఎలక్ట్రాన్ జంటల వికర్షణ సిద్ధాంతాన్ని వివరించండి. దీని అనువర్తనాలు ఏమిటి ?
జవాబు:
సమయోజనీయ బంధ అణువుల ఆకృతులను వివరించడానికి, బాహ్య కర్పరంలోని ఎలక్ట్రాన్ జంటల మధ్య అన్యోన్య వికర్షణ చర్యలుంటాయనే భావన ప్రాతిపదికగా కొన్ని ప్రతిపాదనలు చేశారు.
ప్రతిపాదనలు :
ఒక అణువు ఆకృతి ఆ అణువు కేంద్ర పరమాణువు వేలన్స్ కర్పరంలోని బంధ, బంధరహిత ఎలక్ట్రాన్ జంటలపై
ఆధారపడి ఉంటుంది.

VSEPR సిద్ధాంతంలోని అంశాలు :

1. అణువుల ఆకృతులు కేంద్రక పరమాణువు బాహ్య కర్పరంలో ఉన్న బంధ ఎలక్ట్రాన్ జంటల సంఖ్య మీద ఆధారపడి ఉంటాయి. కేంద్రక పరమాణువు మీద కేవలం బంధ జంటలు మాత్రమే ఉండి ఒంటరి జంటలు లేకపోయినట్లైతే అణువుకు స్థిరత్వం ఉండి క్రమ ఆకృతి ఏర్పడుతుంది.
   
2. కేంద్రక పరమాణువు బాహ్య కర్పరంలో ఒంటరి ఎలక్ట్రాన్ జంటలు ఉంటే అణువు యొక్క ఆకృతిలో విరూపణ ఏర్పడటమే కాకుండా బంధ కోణంలో తగ్గుదల వస్తుంది.
3. ఎలక్ట్రాన్ జంట మేఘాలు వాటి మధ్య వికర్షణ బలాలు కనిష్ఠంగా ఉండేటట్లుగా కేంద్రక పరమాణువు చుట్టూ వాటంతట అవి విస్తరించి ఉంటాయి.
4. ఎలక్ట్రాన్ జంటల మధ్య గల వికర్షణ బలాల క్రమం ఈ క్రింది విధంగా ఉంటుంది. ఒంటరి జంట – ఒంటరి జంట > ఒంటరి జంట బంధ జంట > బంధ జంట – బంధ జంట
5. బంధ ఎలక్ట్రాన్ జంటల మధ్య గల వికర్షణ బలాల పరిమాణాలు కేంద్రక పరమాణువుకు, దానితో బంధించబడిన ఇతర పరమాణువులకు మధ్య గల ఋణవిద్యుదాత్మకతల తేడా మీద ఆధారపడి ఉంటుంది.
6. విభిన్న బంధాల మధ్య గల వికర్షణ క్రమం : ఈ క్రింది విధంగా ఉంటుంది.
   త్రిబంధం > ద్విబంధం > ఏకబంధం.
7. కేంద్రక పరమాణువు చుట్టూ ఒంటరి ఎలక్ట్రాన్ జంట, బంధ ఎలక్ట్రాన్ జంట కన్నా ఎక్కువ ప్రదేశాన్ని ఆక్రమించి ఉంటుంది. కారణం ఏమనగా ఒంటరి ఎలక్ట్రాన్ జంట ఒకే ఒక్క కేంద్రక ఆకర్షణకు లోబడి ఉంటుంది. బంధ జంట రెండు కేంద్రకాల ఆకర్షణకు లోబడి ఉంటుంది.

ప్రశ్న 47.
వేలన్స్ బంధ సిద్ధాంతాన్ని ఉపయోగించి అణువుల జ్యామితిని ఎలా వివరిస్తారు ?
జవాబు:
వేలన్స్ బంధ సిద్ధాంతంలోని అంశాలు :

1. సగం నిండిన పరమాణు ఆర్బిటాళ్ళు పరస్పరం ఆవరింపు చేసుకోవడం వల్ల సమయోజనీయ బంధం ఏర్పడుతుంది.
2. ఆవరింపులో పాల్గొనే సగం నిండిన పరమాణు ఆర్బిటాళ్ళలో ఎలక్ట్రాన్లు వ్యతిరేక స్పిన్లు కలిగి ఉండాలి. బంధంలో పాల్గొనే పరమాణువు తన ఆర్బిటాళ్ళ ఉనికిని పోగొట్టుకోలేదు. కాని అతిపాతం చెందే ఆర్బిటాల్లలోని ఎలక్ట్రాన్ జంటలను మాత్రం రెండు పరమాణువులు పంచుకుంటాయి.
3. ఆర్బిటాళ్ళ ఆవరింపు పరిమితి మీద బంధ బలం ఆధారపడి ఉంటుంది. ఆవరింపు ఎక్కువగా ఉంటే బంధ బలం ఎక్కువగా ఉంటుంది. ఆవరింపు తక్కువగా ఉంటే బంధబలం తక్కువగా ఉంటుంది.
4. ఆవరింపులో పాల్గొనే పరమాణు ఆర్బిటాళ్ళు ఎక్కువగా ఏ దిశలో కేంద్రీకృతం అవుతాయో ఆ దిశ ఏర్పడ్డ బంధం యొక్క దిశను సూచిస్తుంది.
5. సంయోగం చెందే రెండు పరమాణువుల ఆర్బిటాళ్ళు అతిపాతం చెందడం వల్ల అంతర్ కేంద్ర అక్షంపై ఎలక్ట్రాన్ సాంద్రత పెరుగుతుంది. దీనివల్ల రెండు పరమాణువులు ఒకదానివైపు మరొకటి ఆకర్షితం అవుతాయి. దీని ఫలితంగా అణువు, స్థిరీకరణం చెందుతుంది.
6. ‘s’ ఆర్బిటాల్ తప్ప మిగిలిన అన్ని పరమాణు ఆర్బిటాళ్ళు దిశను కలిగి ఉంటాయి. అందువలన అవి ఆవరింపు చేసుకోవడం వల్ల ఏర్పడే బంధానికి కూడా దిశ ఉంటుంది. ఇది అణువు యొక్క ఆకృతిని నిర్ణయిస్తుంది.

ఉదా : హైడ్రోజన్ అణువు ఏర్పడుట (s – s ఆవరింపు) : H పరమాణు సంఖ్య 1. కాబట్టి దాని ఎలక్ట్రాన్ విన్యాసం 1s¹. దీనిలో సగం నిండిన ” ఆర్బిటాల్ ఉన్నది. రెండు H పరమాణువులు 1s ఆర్బిటాళ్ళు పరస్పరం అభిముఖం ఆవరింపు చేసుకోవడం వల్ల H₂ అణువు ఏర్పడుతుంది. రెండు H పరమాణువుల మధ్య ఏర్పడే ఈ బంధాన్ని సిగ్మా సమయోజనీయ బంధం అంటారు. ఇది s – s ఆవరింపుకు ఉదాహరణ.

అణుజ్యామితులను వివరించుట :
ఉదా : మీథేన్.

1. కార్బన్ పరమాణువుకు భూస్థితిలో ఎలక్ట్రాన్ విన్యాసం 1s²2s²2p².
2. ఉద్రిక్త స్థితిలో 1s²2s¹\(2 p_x^1 2 p_y^1 2 p_z^1\)
3. కార్బన్ పరమాణువులో నాలుగు ఆర్బిటాళ్ళు ఒక్కొక్కటి ఒక జత కూడని ఎలక్ట్రాన్తో ఉన్నాయి.
4. ఇవి నాలుగు హైడ్రోజన్ పరమాణువులలోని ఒక్కొక్క ఎలక్ట్రాన్లో ఉన్న 1s ఆర్బిటాల్పై అతిపాతం చెందుతుంది. దీనివల్ల నాలుగు C – H బంధాలు ఏర్పడతాయి.
5. నాలుగో C – H బంధం s – s అతిపాతం వల్ల ఏర్పడుతుంది. ఈ బంధం ప్రత్యేకమైన దిశ కలిగినది కాదు. అందువల్ల బంధకోణాన్ని చెప్పలేము.
6. ప్రయోగ ఫలితాలు మాత్రం ∠H C – H లు 109.5° గా చూపాయి.
7. అంటే కేవలం పరమాణు ఆర్బిటాళ్ళ అతిపాతం ఆధారంగా బంధ కోణాలను వివరించలేం.

ప్రశ్న 48.
సంకరీకరణం అంటే ఏమిటి ? s, p ఆర్బిటాళ్ళతో జరిగే విభిన్న రకాల సంకరీకరణాలను వివరించండి.
జవాబు:
పరమాణువు బాహ్య కర్పరాలలోని దాదాపు సమానశక్తి గల ఆర్బిటాళ్ళు పూర్తిగా కలిసిపోయి కొత్తగా అదే సంఖ్యలో సమానశక్తి, ఆకృతిగల ఆర్బిటాళ్ళ సంఖ్యను ఏర్పరిచే పద్ధతినే సంకరీకరణం అంటారు.

సంకరీకరణ లక్షణాలు :

1. సంకరీకరణంలో పాల్గొనేవి ఆర్బిటాళ్ళు. ఎలక్ట్రాన్లు కాదు.
2. ఎన్ని పరమాణు ఆర్బిటాళ్ళు సంకరీకరణంలో పాల్గొంటాయో అదే సంఖ్యలో సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి.
3. దాదాపు సమానశక్తి, స్థాయిల గల ఆర్బిటాళ్ళు కలిసి సంకర ఆర్బిటాళ్ళనిస్తాయి.
4. ఏర్పడిన సంకర ఆర్బిటాళ్ళకు ఆకృతి, శక్తి సమానంగా ఉంటాయి.
5. సంకర ఆర్బిటాళ్ళు పరమాణు ఆర్బిటాళ్ళ కంటే బలమైన బంధాల నేర్పరుస్తాయి. ఇది ఎక్కువ స్థిరమైన అణువులు ఏర్పడటానికి వీలుగా ఉంటుంది.
6. సంకర ఆర్బిటాళ్ళు వాటి ఎలక్ట్రాన్ల మధ్య కనిష్ఠ వికర్షణ ఉండేటట్లుగా కేంద్రకం చుట్టూ ఉన్న ప్రదేశంలో దిశాత్మకంగా వ్యాప్తి చెంది ఉంటాయి.

1) sp³ సంకరీకరణం : ఒక ‘s’ ఆర్బిటాల్, మూడు ‘p’ ఆర్బిటాళ్ళు కలిసిపోయి నాలుగు sp³ సంకర ఆర్బిటాళ్ళను ఏర్పరిచే ప్రక్రియను sp³ సంకరీకరణం అంటారు.
ఒక్కొక్క sp³ సంకర ఆర్బిటాల్క \(\frac{1}{4}\)-s స్వభావం \(\frac{3}{4}\)-P స్వభావం ఉంటుంది. ఏ రెండు sp³ సంకర ఆర్బిటాళ్ళ మధ్య కోణమైన 109°28′ ఉంటుంది. కేంద్రక పరమాణువు sp³ సంకరీకరనం పొందే అణువులకు టెట్రాహెడ్రల్’.ఆకృతి ఉంటుంది.

ఉదా : మీథేన్ (CH₄) అణువు ఏర్పడుట : మీథేన్ అణువు ఏర్పడేటప్పుడు కేంద్రక కార్బన్ పరమాణువు దాని ఉత్తేజిత స్థితిలో sp³ సంకరీకరణం పొందుతుంది. తత్ఫలితంగా దానిపై నాలుగు sp³ సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి. అట్లేర్పడ్డ నాలుగు సంకర ఆర్బిటాళ్ళలో బంధ ఎలక్ట్రాన్ జంటలు ఉంటాయి. ఈ నాలుగు sp³ సంకర ఆర్బిటాళ్ళు నాలుగు H పరమాణువుల ‘1s’ ఆర్బిటాళ్ళతో అభిముఖ ఆవరింపు చేసుకుని CH₄ అణువును ఏర్పరుస్తాయి. CH₄ అణువు టెట్రాహెడ్రల్ ఆకృతిని కలిగి ఉంటుంది. బంధకోణం 109°28′ ఉంటుంది.

2) sp² సంకరీకరణం : ఒక ‘S’ ఆర్బిటాల్, రెండు ‘p’ ఆర్బిటాళ్ళు కలిసిపోయి మూడు sp² సంకర ఆర్బిటాళ్ళను ఏర్పరిచే ప్రక్రియను sp² సంకరీకరణం అంటారు. ఒక్కొక్క sp² సంకర ఆర్బిటాల్క \(\frac{1}{3}\)s – స్వభావం మరియు \(\frac{2}{3}\)p- స్వభావం ఉంటాయి. ఏ రెండు sp² సంకర ఆర్బిటాళ్ళ మధ్య కోణమైనా 120° ఉంటుంది. కేంద్రక పరమాణువు sp² సంకరీకరణాన్ని పొందే అణువులకు సమతల త్రిభుజాకృతి ఉంటుంది.

ఉదా : బోరాన్ ట్రై క్లోరైడ్ (BCl₃) అణువు ఏర్పడుట :

BCl₃ అణువు ఏర్పడేటప్పుడు కేంద్రక బోరాన్ పరమాణువు దాని ఉత్తేజిత స్థితిలో (1s²2s¹\(2 p_x^1 2 p_y^1 2 p_z^0\)) sp² సంకరీకరణం పొందుతుంది. తత్ఫలితంగా దానిపై మూడు sp సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి. అట్లేర్పడ్డ మూడు సంకర ఆర్బిటాళ్ళలోనూ బంధ ఎలక్ట్రాన్ జంటలు ఉంటాయి. ఈ మూడు sp² సంకర ఆర్బిటాళ్ళు మూడు క్లోరిన్ పరమాణువుల ‘3p_z‘ ఆర్బిటాళ్ళతో అభిముఖ ఆవరింపు చేసుకొని BCl₃ అణువును యిస్తాయి. BCl₃ అణువు సమతల త్రిభుజాకృతిని కలిగి ఉంటుంది. బంధకోణం 120°.

3) sp సంకరీకరణం : ఒక ‘s’ – ఆర్బిటాల్, ఒక ‘p’ – ఆర్బిటాల్ కలిసిపోయి రెండు sp సంకర ఆర్బిటాళ్ళను ఏర్పరిచే ప్రక్రియను ‘sp’ సంకరీకరణం అంటారు.
ఒక్కొక్క ‘sp’ సంకర ఆర్బిటాల్కు \(\frac{1}{2}\) s – స్వభావం మరియు \(\frac{1}{2}\) p – స్వభావం ఉంటాయి. ఏ రెండు sp సంకర ‘ఆర్బిటాళ్ళ మధ్య కోణమైన 180° ఉంటుంది. కేంద్రక పరమాణువు sp సంకరీకరణం పొందిన అణువులకు రేఖీయ ఆకృతి ఉంటుంది.

ఉదా : బెరీలియం క్లోరైడ్ (BeCl₂) అణువు ఏర్పడుట:

బెరీలియం క్లోరైడ్ అణువు ఏర్పడేటప్పుడు కేంద్రక ‘Be’ పరమాణువు దాని ఉత్తేజిత స్థితిలో (1s²2s¹\(2 p_x^1 2 p_y^0 2 p_z^0\)). sp సంకరీకరణం పొందుతుంది. తత్ఫలితంగా రెండు sp సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి. ఆ రెండింటిలోనూ బంధ ఎలక్ట్రాన్ జంటలు ఉంటాయి. ఇపుడు, రెండు sp సంకర ఆర్బిటాళ్ళు రెండు H పరమాణువుల 1s ఆర్బిటాళ్ళతో అభిముఖ ఆవరింపు చేసుకొని BeCl₂ అణువును ఏర్పరుస్తాయి. BeCl₂ అణువు రేఖీయ ఆకృతిని కలిగి ఉంటుంది. బంధకోణం 180° ఉంటుంది.

ప్రశ్న 49.
అణు ఆర్బిటాల్ సిద్ధాంతం ముఖ్య లక్షణాలను వ్రాయండి.
జవాబు:
అణు ఆర్బిటాల్ సిద్ధాంతం :

1. పరమాణు ఎలక్ట్రానులు పరమాణు ఆర్బిటాళ్ళలో ఉన్నట్లు అణువు ఎలక్ట్రానులు అణు ఆర్బిటాళ్ళలో ఉంటాయి.
2. సరియైన సౌష్ఠత, దాదాపు సమాన శక్తులు గల పరమాణు ఆర్బిటాళ్ళు కలిసిపోయి అణు ఆర్బిటాళ్ళనిస్తాయి.
3. పరమాణు ఆర్బిటాల్క ఒకే కేంద్రకం ఉంటే అణు ఆర్బిటాల్క బహుకేంద్రకాలుంటాయి. అణు ఆర్బిటాల్లోని ఎలక్ట్రాన్ ఆ అణు ఆర్బిటాల్ ఏర్పరచిన పరమాణు కేంద్రకాలన్నింటివల్ల ప్రభావితమవుతుంది.
4. ఎన్ని పరమాణు ఆర్బిటాళ్ళు కలుస్తాయో అదే సంఖ్యలో అణు ఆర్బిటాళ్ళు ఏర్పడతాయి. రెండు పరమాణు ఆర్బిటాల్లు కలిసి రెండు అణు ఆర్బిటాల్ల లనిస్తాయి. ఇందులో ఒకదాన్ని బంధక ఆర్బిటాల్ అని, రెండోదాన్ని అపబంధక ఆర్బిటాల్ అని అంటారు.
5. బంధక ఆర్బిటాల్క్కు తక్కువ శక్తి, ఎక్కువ స్థిరత్వం ఉంటాయి. అపబంధక ఆర్బిటాల్క ఎక్కువ శక్తి, తక్కువ స్థిరత్వం ఉంటాయి.
6. పరమాణు ఆర్బిటాల్ పరమాణు కేంద్రకం చుట్టూ ఎలక్ట్రాన్ సాంద్రత వితరణ సంభావ్యతను ఇస్తుంది. అణు ఆర్బిటాల్ అణుకేంద్రకాలన్నింటి చుట్టూ దానికి సంబంధించిన ఎలక్ట్రాన్ వితరణ సంభావ్యతనిస్తుంది.
7. పరమాణు ఆర్బిటాళ్ళు ఆఫ్ బౌ, పౌలివర్జన లేదా మినహాయింపు సూత్రం, హుండ్ గరిష్ఠ బాహుళ్యతా నియమాలనను- సరించి, ఎలక్ట్రాన్లను నింపినట్లే అణు ఆర్బిటాళ్ళు కూడా ఈ నియమాల్ని పాటించి ఎలక్ట్రాన్లను నింపుతాయి.
8. పరమాణు ఆర్బిటాళ్ళ రేఖీయ సంకలన పద్ధతిని ఒకే విధమైన కేంద్రకాలున్న రెండు పరమాణువుల (హైడ్రోజన్) అణువుకు వర్తింపచేస్తే
   ψ అణు ఆర్బిటాల్ = ψ_A ± ψ_B
   బంధక ఆర్బిటాల్ σ = ψ_A + ψ_B
   అపబంధక ఆర్బిటాల్ σ* = ψ_A – ψ_B
   
9. అణు ఆర్బిటాళ్ళ సాపేక్ష శక్తులు : O₂, F₂ అణువుల ఆర్బిటాళ్ళ శక్తి స్థాయిల క్రమం
   
10. బంధక్రమం : బంధక ఆర్బిటాల్లోని ఎలక్ట్రాన్ల సంఖ్య N_a, అపబంధక అణు ఆర్బిటాల్లోని ఎలక్ట్రానుల సంఖ్య N_b, అయితే బంధక్రమం = \(\frac{1}{2}\)(N_b – N_a) బంధక్రమం ధనాత్మకమైతే అణువు స్థిరం. అంటే (Nb – Na) లో Na < Nb. అలాగే బంధక్రమాంకం ఋణాత్మకం అయితే అప్పుడు Na > Nb ఈ సందర్భాలలోను అణువు స్థిరంగా వుండదు.
11. అణువుల అయస్కాంత ధర్మాలను ఈ సిద్ధాంతం చక్కగా వివరించింది. ఆక్సిజన్ అణువు పరాయస్కాంత ధర్మాన్ని వివరించింది.

ప్రశ్న 50.
(a) N₂, (b) O₂ అణువులకు అణు ఆర్బిటాల్ శక్తి పటాలు వ్రాయండి. ఈ రెండు అణువుల అయస్కాంత లక్షణాలేమిటి ? వాటి బంధక్రమాలు గణించండి.
జవాబు:
నైట్రోజన్ పరమాణువు ఎలక్ట్రాన్ విన్యాసం 1s² 2s²2p³. రెండు నైట్రోజన్ పరమాణువులు, వాటి పరమాణు ఆర్బిటాళ్ళ ఏకీయ కలయికతో అణు ఆర్బిటాళ్ళను ఏర్పరుస్తాయి.
N² : అణు ఎలక్ట్రాన్ విన్యాసం.

బంధక్రమం \(\frac{10-4}{2}\) = 3, N₂ అణువు డయా అయస్కాంత ధర్మం కలది.

(b) O₂ అణువులు ఏర్పడుట : ఆక్సిజన్ పరమాణు ఎలక్ట్రాన్ విన్యాసం 1s²2s²2p⁴. ఒక్కొక్క ఆక్సిజన్ పరమాణువుకు ఎనిమిది ఎలక్ట్రాన్లు పరమాణు ఆర్బిటాళ్ళలో ఉన్నాయి. రెండు ఆక్సిజన్ పరమాణువులు కలిసినపుడు ఆ రెండింటి పరమాణు ఆర్బిటాళ్ళ రేఖీయ కలయికతో అణు ఆర్బిటాళ్ళనిస్తాయి.

అణు ఎలక్ట్రాన్ విన్యాసంలో రెండు జతకూడని ఎలక్ట్రానులున్నాయి. అందువల్ల ఆక్సిజన్ అణువుకు పరాయస్కాంత ధర్మాలు ఉంటాయి.
బంధక్రమం : \(\frac{10-6}{2}\) = 2 (0 = 0)

అదనపు ప్రశ్నలు

ప్రశ్న 1.
నీరు అణువు ఆకృతిని వివరించండి.
జవాబు:
నీరు అణువు ఆకృతి : నీరు అణువు ఏర్పడేటప్పుడు కేంద్రక ఆక్సిజన్ పరమాణువు దాని ఉత్తేజిత స్థితిలో (1s²2s²\(2 p_x^2 2 p_y^1 2 p_z^1\)) sp³ సంకరీకరణం పొందుతుంది. తత్ఫలితంగా దానిపై నాలుగు sp³ సంకర ఆర్బిటాళ్ళు ఏర్పడతాయి. వాటిలో రెండింటిలో బంధ జంటలు మిగిలిన రెండింటిలో ఒంటరి జంటలు ఉంటాయి. కేంద్రక పరమాణువు sp³ సంకరీకరణం పొందడం వల్ల అణువుకు టెట్రాహెడ్రల్ ఆకృతి ఏర్పడాలి. కాని ఒంటరి ఎలక్ట్రాన్ జంటలు ఉండటం వల్ల VSEPR సిద్ధాంతం ప్రకారం అణువు యొక్క ఆకృతిలో విరూపణ వచ్చి అణువు పిరమిడల్ ఆకృతిని పొందుతుంది. బంధకోణం 109°28′ లకు బదులుగా 104°5 లకు తగ్గుతుంది.

ప్రశ్న 2.
పరమాణు ఆర్బిటాళ్ళు, అణు ఆర్బిటాళ్ళు మధ్యగల తేడాలను రాయండి.
జవాబు:

ప్రశ్న 3.
బంధక ఆర్బిటాల్, అపబంధక ఆర్బిటాల్లు అంటే ఏమిటి ?
జవాబు:
పరమాణు ఆర్బిటాళ్ళ శక్తి కంటే తక్కువ శక్తి స్థాయిలో ఉన్న అణు ఆర్బిటాళ్ళను బంధక ఆర్బిటాళ్ళు అంటారు. పరమాణు ఆర్బిటాళ్ళ శక్తి కంటే ఎక్కువ శక్తి స్థాయిలో ఉన్న అణు ఆర్బిటాళ్ళను అపబంధక ఆర్బిటాళ్ళు అంటారు.

ప్రశ్న 4.
H₂ అణువు యొక్క MOED గీయండి.
జవాబు:

ప్రశ్న 5.
N, Cl ల ఋణవిద్యుదాత్మకతలు దాదాపుగా సమానంగా ఉన్నా NH₃ బాష్పీభవన స్థానం HCl కంటె అధికంగా ఉంటుంది. ఎందుకు ?
జవాబు:
NH₃లో హైడ్రోజన్ బంధాలు ఉంటాయి. HCl లో H – బంధాలు ఉండవు. అందువలన NH₃ బాష్పీభవన స్థానం HCl కంటే అధికంగా ఉంటుంది.

ప్రశ్న 6.
NH₃, H – బంధాలను ఇస్తుంది కాని HCl, H – బంధాలు ఇవ్వదు. ఎందుకు ?
జవాబు:
H-బంధాలను ఇవ్వాలంటే అధిక ఋణ విద్యుదాత్మకత విలువ గల మూలకం సైజు తక్కువగా ఉండాలి. క్లోరిన్ కంటె నైట్రోజన్ పరమాణువు సైజు చిన్నది. అందువల్ల NH₃, H – బంధాలను ఇస్తుంది. HCl, H – బంధాలను ఇవ్వదు.

ప్రశ్న 7.
s, p – ఆర్బిటాల్లు ఏర్పరిచే వివిధ బంధాల బలాలను క్రమంలో రాయండి. అవి ఎపుడు సంకరీకరణం చెందుతాయి?
జవాబు:
వేలన్స్ బంధ సిద్ధాంతం ప్రకారం ఆవరింపు అవధి ఎంత ఎక్కువగా ఉంటే బంధం యొక్క బంధ బలం అంత ఎక్కువగా ఉంటుంది. ఇతర ఆర్బిటాళ్ళ కన్నా ‘p’ ఆర్బిటాళ్ళకు గల డంబెల్ ఆకృతి వలన వాటి ఆవరింపు అవధి ఎక్కువగా ఉంటుంది. ‘s’ ఆర్బిటాల్ గోళాకారంగా ఉండటం వలన వాటి ఆవరింపు అవధి తక్కువగా ఉంటుంది. కాబట్టి ఆవరింపు
క్రమం : p – p > s – p > s – s
సంకర ఆర్బిటాళ్ళ బంధశక్తి క్రమం: sp < sp² < sp³.

VBT సిద్ధాంతం ప్రకారం అణువుల ఆకృతులను మరియు బంధకోణాలను వివరించలేము. అంతేకాకుండా VBT ప్రకారం అణువులో ఉండే అన్ని బంధాలకు శక్తి సమానంగా ఉండదు. అందువలన పరమాణు ఆర్బిటాళ్ళ సంకరీకరణ విధానాన్ని ప్రవేశపెట్టారు. ఈ ప్రక్రియలో ఒకే పరమాణువులోని ఆర్బిటాళ్ళు మాత్రమే పాల్గొంటాయి. అట్లేర్పడ్డ అన్ని సంకర ఆర్బిటాళ్ళు ఆకృతిలోనూ, శక్తిలోనూ మరియు దిగ్విన్యాసంలోనూ అన్ని విధాలా సమానంగా ఉంటాయి.

ప్రశ్న 8.
HF, NH₃ ల బాష్పీభవన స్థానాలకంటే H₂O బాష్పీభవన స్థానం ఎక్కువ. దానికి కారణాలు చెప్పండి.
జవాబు:
H₂O మరుగు ఉష్ణోగ్రత HF కన్నా ఎక్కువకు కారణాలు :

1. HF లో ఉన్న హైడ్రోజన్ బంధాల సంఖ్య కన్నా H₂O లో ఉన్న హైడ్రోజన్ బంధాల సంఖ్య దాదాపు రెట్టింపు ఉంటుంది.
2. బాష్ప స్థితిలో కూడా HF సహచరితంగా ఉంటుంది. (H₆F₆). కాని బాష్పస్థితిలో నీరు అణువులు విడివిడిగా ఉంటాయి.

NH₃ కన్నా H₂O మరుగు ఉష్ణోగ్రత ఎక్కువగుటకు కారణాలు :

1. NH₂ లో ఉన్న H బంధాల సంఖ్యకన్నా H₂O లో ఉన్న H బంధాల సంఖ్య రెట్టింపు ఉంటుంది.
2. నైట్రోజన్ యొక్క ఋణ విద్యుదాత్మకత తక్కువగా ఉండటం వల్ల NH₃ అణువులలో H – బంధం శక్తి తక్కువగా ఉంటుంది.

ప్రశ్న 9.
HF > HBr > HCl బాష్పీభవన స్థానాల క్రమానికి కారణాలు ఊహించండి.
జవాబు:

1. ద్రవస్థితిలో HF, H – బంధాల వలన (HF)₂ గా ఉంటుంది. అందువలన HF యొక్క మరుగు ఉష్ణోగ్రత HCl మరియు HBr ల కన్నా ఎక్కువ.
2. HBr మరియు HCl లు వాయువులు. HBr అణుభారం HCl అణుభారం కన్నా ఎక్కువ కాబట్టి, HBr యొక్క మరుగు ఉష్ణోగ్రత HCl కన్నా ఎక్కువ.
3. HCl అత్యంత బాష్పశీల సమ్మేళనం. అందువలన మరుగు ఉష్ణోగ్రతల క్రమం HF > HBr > HCl గా ఉంటుంది.

ప్రశ్న 10.
ఇథిలీన్ అణువులో ఎన్ని సిగ్మా మరియు పై బంధాలు ఉన్నాయి ?
జవాబు:
ఇథిలీన్ అణువులో 5 సిగ్మా బంధాలు, ఒక పై బంధం ఉన్నాయి.

ప్రశ్న 11.
H₂S కన్నా H₂O మరుగు ఉష్ణోగ్రత ఎక్కువ. ఎందుకు ?
జవాబు:
H₂O అణువులు ఒక దానితో ఒకటి H – బంధాల ద్వారా సహచరితం చెందుతాయి. కాని అట్టి అణువుల కలయిక (H– బంధాల ద్వారా) H₂S లో ఉండదు. అందువలన H₂O మరుగు ఉష్ణోగ్రత H₂S కన్నా ఎక్కువగా ఉంటుంది.

ప్రశ్న 12.
KCl జల ద్రావణం విద్యుద్వాహకం కాగా BeCl₂ జల ద్రావణం అవిద్యుద్వాహకం. ఎందువల్ల ?
జవాబు:
KClఅయానిక సమ్మేళనం కనుక అది జలద్రావణంలో K⁺, Cl^– అయాన్లను యిస్తుంది. అందువల్ల అది విద్యుద్వాహకంగా పని చేస్తుంది. కాని BeCl₂ సమయోజనీయ సమ్మేళనం. అది జల ద్రావణంలో అయాన్లను యివ్వదు. కనుక అది విద్యుద్వాహకం.

ప్రశ్న 13.
ఘన NaCl అవిద్యుద్వాహకం. కాని ద్రవ NaCl మంచి విద్యుద్వాహకం. ఎందువల్ల ?
జవాబు:
ఘన NaCl లో Na⁺ మరియు Cl^– అయాన్లు బలమైన విద్యుదాకర్షణ బలాలచే స్ఫటిక జాలకంలో బంధింపబడి ఉంటాయి. ఇవి స్వేచ్ఛగా కదలలేవు. కనుక ఘన NaCl అవిద్యుద్వాహకం. కాని ద్రవ NaCl లో Na⁺, Cl^– అయాన్లు స్వేచ్ఛగా చలిస్తూ ఉంటాయి. అందువలన ద్రవ NaCl విద్యుద్వాహకంగా పనిచేస్తుంది.

ప్రశ్న 14.
గది ఉష్ణోగ్రత వద్ద H₂O ద్రవం కాగా H₂ వాయువు. ఎందువల్ల ?
జవాబు:
H₂O లో అణువుల మధ్య అంతరణుక H – బంధాలు ఉంటాయి. అందువల్ల నీరు అణువులు సహచరితంగా ఉంటాయి. కనుక H₂O ద్రవస్థితిలో ఉంటుంది. కాని H₂S లో అణువుల మధ్య H – బంధం ఉండదు. కనుక అది వాయు స్థితిలో ఉంటుంది.

ప్రశ్న 15.
బెరీలియంలో ఒంటరి ఎలక్ట్రాన్లు లేనప్పటికీ అది రెండు సమయోజనీయ బంధాలను ఎలా ఏర్పరచగలుగుతుందో తెలుపండి ?
జవాబు:
బెరీలియం పరమాణు సంఖ్య 4. కాబట్టి దాని ఎలక్ట్రాన్ విన్యాసం 1s²2s². దీనిని భూస్థితి విన్యాసం అంటారు. ఈ స్థితిలో ఒంటరి ఎలక్ట్రాన్లు లేవు. కాని బెరీలియం ఉత్తేజిత ఎలక్ట్రాన్ విన్యాసం 1s²2s¹2p¹. ఈ స్థితిలో రెండు ఒంటరి ఎలక్ట్రాన్లు ఉన్నాయి. కాబట్టి బెరీలియం రెండు సమయోజనీయ బంధాలను యిస్తుంది.

ప్రశ్న 16.
కార్బన్ట్రాక్లోరైడ్ సిల్వర్ నైట్రేట్ అవక్షేపాన్ని యివ్వదు. ఎందువల్ల ?
జవాబు:
కార్బన్ట్రాక్లోరైడ్ అధృవ సమయోజనీయ అణువు. అందువలన అది స్వేచ్ఛా క్లోరైడ్ (Cl^–) అయాన్లను యివ్వలేదు. సిల్వర్ నైట్రేట్ అయానిక సమ్మేళనం. అది అయనీకరణం చెంది Ag⁺ అయాన్లను యిస్తుంది. కాని CCl₄ నుండి Cl^– అయాన్లు లభించకపోవడం వల్ల AgCl అవక్షేపం ఏర్పడదు.

ప్రశ్న 17.
అయానిక సమ్మేళనాలు అధిక కాఠిన్యతను కలిగి ఉండుటకు మరియు అధిక ద్రవీభవన, ఉష్ణోగ్రతలను కలిగి ఉండుటకు కారణం ఏమిటి ?
జవాబు:
అయానిక సమ్మేళనాలలో వ్యతిరేక విద్యుదావేశిత అయాన్లు బలమైన విద్యుదాకర్షణ బలాలతో స్పటిక జాలకంలో బంధింపబడి ఉంటాయి. అందువలన అవి అధిక కాఠిన్యతను మరియు అధిక ద్రవీభవన ఉష్ణోగ్రతను కలిగి ఉంటాయి.

ప్రశ్న 18.
అయానిక సమ్మేళనాలు దిశారహితంగా ఉంటాయి. కాని సమయోజనీయ సమ్మేళనాలు దిశాత్మకంగా ఉంటాయి. ఎందువలన ?
జవాబు:
వ్యతిరేక విద్యుదావేశిత అయాన్ల మధ్య ఆకర్షణ వల్ల అయానిక బంధం ఏర్పడుతుంది. వ్యతిరేక విద్యుదావేశిత అయాన్లు ఏ దిశలో ఒకదానికొకటి సమీపించినా వాటి మధ్య అయానిక బంధం ఏర్పడుతుంది. అందువల్ల అయానిక సమ్మేళనాలకు దిశ ఉండదు. బంధ ఎలక్ట్రాన్లు గల ఆర్బిటాళ్ళు అతిపాతం చేసుకోవడం వల్ల సమయోజనీయ బంధం ఏర్పడుతుంది. ఈ ఆర్బిటాళ్ళు ఒక నిర్దిష్ట దిశలో ఒకదానిని ఒకటి సమీపించినపుడే వాటి మధ్య సమయోజనీయ బంధం ఏర్పడుతుంది. అందువల్ల సమయోజనీయ బంధం దిశాత్మకంగా ఉంటుంది.

ప్రశ్న 19.
అయానిక సమ్మేళనాల మధ్య చర్యలు వేగంగా జరుగుతాయి. ఎందుకు ?
జవాబు:
అయానిక సమ్మేళనాలు వాటి జలద్రావణాలలో వ్యతిరేక విద్యుదావేశిత అయాన్లను యిస్తాయి. ఈ అయాన్లు అతి వేగంతో ప్రయాణిస్తూ ఉంటాయి. అందువల్ల అయానిక సమ్మేళనాల మధ్య చర్యలు వేగంగా జరుగుతాయి.

ప్రశ్న 20.
ఆల్కహాల్లో KCl కరగదు కాని అనార్ద్ర AlCl₃ కరుగుతుంది. ఎందువల్ల ?
జవాబు:
అధృవ ద్రావణులలో అయానిక సమ్మేళనాలు కరగవు. కాని సమయోజనీయ సమ్మేళనాలు కరుగుతాయి. ఆల్కహాల్ అధృవ ద్రావణి KCl అయానిక పదార్థం. అందువల్ల KCl ఆల్కహాల్లో కరగదు. AlCl₃ సమయోజనీయ సమ్మేళనం. కనుక అది ఆల్కహాల్లో కరుగుతుంది.

ప్రశ్న 21.
కర్పూరం కిరోసిన్లో కరుగుతుంది. కాని నీటిలో కరగదు. ఎందువల్ల ?
జవాబు:
సమయోజనీయ సమ్మేళనాలు అధృవ ద్రావణులలో కరుగుతాయి. కాని ధృవద్రావణులలో కరగవు. కర్పూరం సమయోజనీయ సమ్మేళనం. కనుక యిది అధృవ ద్రావణి అయిన కిరోసిన్లో కరుగుతుంది. కాని ధృవ ద్రావణి అయిన నీటిలో కరగదు.

ప్రశ్న 22.
a) BeCl₂
b) BF₃ అణువులలో కేంద్రక పరమాణువులు ఏ సంకరీకరణం పొందుతాయో తెలపండి.
జవాబు:
a) BeCl₂ అణువులో కేంద్రక Be పరమాణువు sp సంకరీకరణం పొందుతుంది. అది రేఖీయ ఆకృతి కలిగి ఉంటుంది.
b) BF₃ అణువులో కేంద్రక B పరమాణువు sp² సంకరీకరణం పొందుతుంది. అది సమతల త్రిభుజాకృతి కలిగి ఉంటుంది.

ప్రశ్న 23.
ఆల్కహాల్ లేదా ఈథర్ మొదలయిన కర్బన ద్రావణాలలో LiCl కరుగుతుందా ? ఎందుకు ? ఎందుకు కాదు ?
జవాబు:
LiCl కోవేలంట్ స్వభావం గల పదార్థం. అందువలన అది అధృవ ద్రావణులైన ఆల్కహాల్, ఈథర్ లో కరుగుతుంది.

ప్రశ్న 24.
KCl ను అయానిక ఘనపదార్థంగా ఎందుకు భావిస్తారు ?
జవాబు:
K, Cl పరమాణువుల ఋణవిద్యుదాత్మక విలువల తేడా 2.2. ఇది 1.7 కన్నా ఎక్కువ. అందువలన KCl ను అయానిక ఘనపదార్థంగా భావిస్తాము.

ప్రశ్న 25.
బేసి సంఖ్య ఎలక్ట్రాన్ అణువులకు ఉదాహరణ నివ్వండి.
జవాబు:
నైట్రిక్ ఆక్సైడ్ NO, నైట్రోజన్ డయాక్సైడ్ NO₂ లాంటి అణువుల్లో కొన్ని పరమాణువుల చుట్టూ బేసి సంఖ్య ఎలక్ట్రాన్లుంటాయి. అష్టకనియమాన్ని పాటించవు.

ప్రశ్న 26.
ఫార్మల్ ఛార్జి లేదా ఫార్మల్ ఆవేశం :
జవాబు:
ఫార్మల్ ఛార్జి : స్వేచ్ఛా స్థితిలో పరమాణువు వేలన్స్ కర్పరంలో ఎలక్ట్రాన్ సంఖ్యకు, అయాను లేదా అణువు లూయీ నిర్మాణంలో ఆ పరమాణువుకు చూపించిన ఎలక్ట్రాన్ల సంఖ్యకు ఉన్న భేదమే.

ఒక లూయీ నిర్మాణంలో పరమాణువు ఫార్మల్ ఛార్జి = (స్వేచ్ఛా స్థితిలో పరమాణువులో ఉన్న వేలన్స్ ఎలక్ట్రాన్ల సంఖ్య) – (పరమాణువు మీద ఉన్న పంచుకోబడని ఎలక్ట్రాన్లు) – (పరమాణువు చుట్టూ ఉన్న బంధాల సంఖ్య)
1గా గుర్తింపబడిన కేంద్ర ఆక్సిజన్ పరమాణువుకు = 6 (పరమాణువు వేలన్స్ ఎలక్ట్రాన్లు ) – 2 (ఒక ఒంటరి జత ఎలక్ట్రానులు) – 3 (ఒక సమయోజనీయ బంధానికి 1)
= 6 – 2 – 3 = +1

‘2’ గా గుర్తించిన ఒక చివరి ఆక్సిజన్ పరమాణువు ఫార్మల్ ఛార్జి = 6 – 4 – 2 = 0
‘3’ గా గుర్తించిన రెండో చివరి ఆక్సిజన్ పరమాణువు ఫార్మల్ ఛార్జి = 6 – 6 – 1 = -1
అందువల్ల O₃ అణువును ఫార్మల్ ఛార్జితో బాటు చూపవలెను.

ప్రశ్న 27.
ఓజోన్ రెజోనెన్సు నిర్మాణాలు వ్రాయండి.
జవాబు:

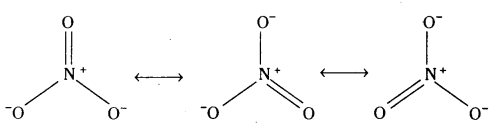
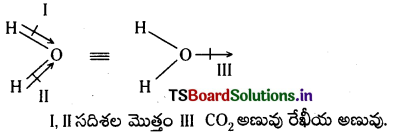
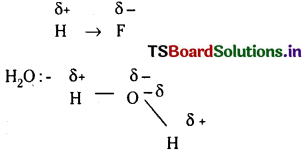
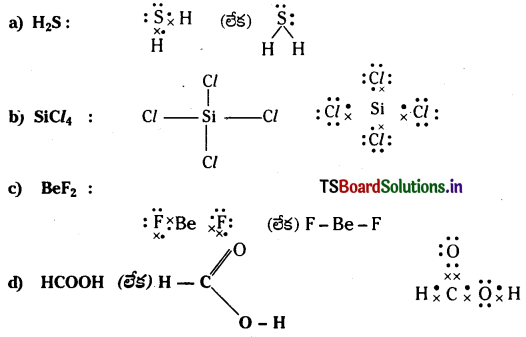
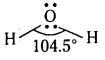
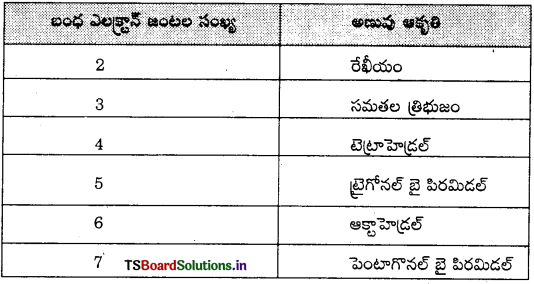
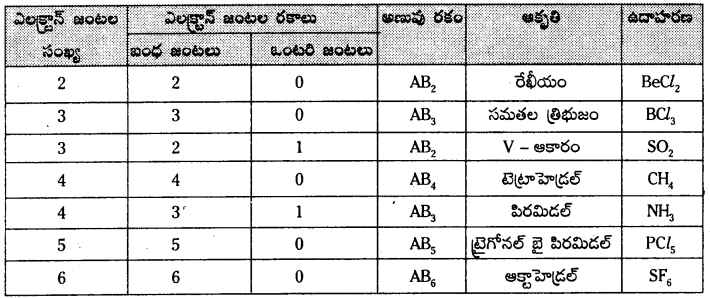
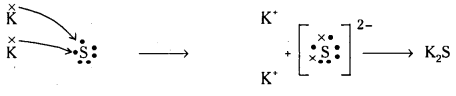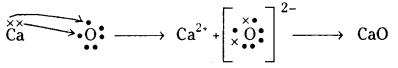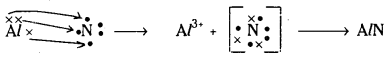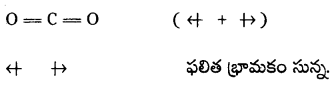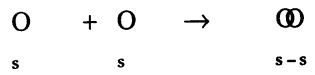Telangana TSBIE TS Inter 1st Year Chemistry Study Material 4th Lesson పదార్ధం స్థితులు : వాయువులు, ద్రవాలు Textbook Questions and Answers.

TS Inter 1st Year Chemistry Study Material 4th Lesson పదార్ధం స్థితులు : వాయువులు, ద్రవాలు

అత్యంత లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 1.
వాయు అణువుల మధ్య ఉండే వివిధ రకాల అంతర అణుబలాలను పేర్కొనండి.
జవాబు:
ఒక పదార్థంలోని కణాలైన పరమాణువులు లేదా అణువుల మధ్య ఉండే ఆకర్షణ, వికర్షణ బలాలను అంతర అణు బలాలు అంటారు. అంతర అణు ఆకర్షణ బలాలను వాండర్ వాల్స్ బలాలు అంటారు.

1. విక్షేపణ బలాలు లేదా లండన్ బలాలు : రెండు తాత్కాలిక ద్విధ్రువాల మధ్య ఉండే ఆకర్షణ బలాలను లండన్ బలాలు లేదా విక్షేపణ బలాలు అంటారు.
2. ద్విధ్రువ ద్విధ్రువ ఆకర్షణ బలాలు : శాశ్వత ద్విధ్రువాల మధ్య ఉండే బలాలను ద్విధ్రువ-ద్విధ్రువ బలాలు అంటారు.
3. ద్విధ్రువ – ప్రేరిత ద్విధ్రువ బలాలు : ఈ బలాలు శాశ్వత ద్విధ్రువ భ్రామకం ఉన్న అణువుకు శాశ్వత ద్విధ్రువ భ్రామకంలేని అణువులకు మధ్య ఉత్పన్నమవుతాయి.
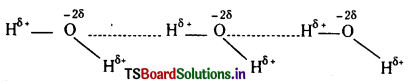
4. హైడ్రోజన్ బంధం : ఒక ప్రత్యేకమైన ద్విధృవ-ద్విధృవ ఆకర్షణ బలం.

ప్రశ్న 2.
బాయిల్ నియమాన్ని తెలిపి, దాని గణితాత్మక రూపం తెలపండి.
జవాబు:
బాయిల్ సూత్రం : స్థిర ఉష్ణోగ్రత వద్ద నియమిత ద్రవ్యరాశిగల వాయువు యొక్క ఘనపరిమాణం దాని పీడనానికి విలోమానుపాతంలో ఉంటుంది. దీనిని గణితాత్మకంగా ఈ క్రింది విధంగా రాస్తారు.
V ∝ \(\frac{1}{P}\) = (స్థిర ఉష్ణోగ్రత) లేక V = \(\frac{K}{P}\) (స్థిర ఉష్ణోగ్రత) లేక PV = K (స్థిరం)

ప్రశ్న 3.
ఛార్లెస్ నియమాన్ని తెలిపి, దాని గణితాత్మక రూపం తెలపండి.
జవాబు:
ఛార్లెస్ సూత్రం : స్థిర పీడనం వద్ద నియమిత ద్రవ్యరాశి గల వాయువు యొక్క ఘనపరిమాణం దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది. దీనిని గణితాత్మకంగా ఈ క్రింది విధంగా రాస్తారు.
V ∝ T (స్థిరపీడనం) లేక V = K × T (స్థిరపీడనం) లేక = \(\frac{\mathrm{V}}{\mathrm{T}}\) = K (స్థిరం)

ప్రశ్న 4.
సమోష్ణోగ్రతరేఖలు అంటే ఏమిటి ?
జవాబు:
స్థిర ఉష్ణోగ్రత వద్ద పీడనానికి, ఘనపరిమాణానికి మధ్యగల సంబంధాన్ని తెలియజేసే వక్రాలను సమోష్ణోగ్రతరేఖలు అంటారు.

ప్రశ్న 5.
పరమ ఉష్ణోగ్రత అంటే ఏమిటి ?
జవాబు:
-273.15°C ఉష్ణోగ్రతను 0° గా తీసికొని ఏర్పరచిన ఉష్ణోగ్రతమాలను పరమ ఉష్ణోగ్రత అందురు. (కెల్విన్ ఉష్ణోగ్రత అందురు). సెంటీగ్రేడ్ ఉష్ణోగ్రత + 273.15 = కెల్విన్ ఉష్ణోగ్రత. కెల్విన్ ఉష్ణోగ్రత – 273.15 = సెంటీ గ్రేడ్ ఉష్ణోగ్రత. -273.15°C ను పరమశూన్య ఉష్ణోగ్రత అందురు. దీనిని oK గా సూచిస్తారు.

ప్రశ్న 6.
సమపీడన రేఖలు అంటే ఏమిటి ?
జవాబు:
స్థిర పీడనం వద్ద వాయువు ఘనపరిమాణానికి, ఉష్ణోగ్రతకు మధ్యగల సంబంధాన్ని తెలియజేసే వక్రాలను సమపీడన రేఖలు అంటారు.

ప్రశ్న 7.
పరమశూన్య ఉష్ణోగ్రత అంటే ఏమిటి ?
జవాబు:
-273.15°C ఉష్ణోగ్రతను పరమశూన్య ఉష్ణోగ్రత అంటారు. దీనిని కెల్విన్మానంలో 0K గా సూచిస్తారు. పరమశూన్య ఉష్ణోగ్రత వద్ద వాయు అణువుల కదలిక ఆగిపోయి వాయువు యొక్క గతిజశక్తి శూన్యం అవుతుంది.

ప్రశ్న 8.
అవొగాడ్రో నియమాన్ని తెలపండి.
జవాబు:
అవొగాడ్రోనియమం: ఒకే ఉష్ణోగ్రత పీడన పరిస్థితులవద్ద సమాన ఘనపరిమాణములున్న విభిన్న వాయువులు సమాన సంఖ్యలో అణువులను కలిగి ఉంటాయి. V ∝ n (P, T లు స్థిరం) లేక V = K × n (P, T లు స్థిరం) లేక \(\frac{\mathrm{V}}{\mathrm{n}}\) = K స్థిరం

ప్రశ్న 9.
స్థిర ఘనపరిమాణ రేఖలు అంటే ఏమిటి ?
జవాబు:
స్థిర మోలార్ ఘనపరిమాణంగల వాయువు పీడన – ఉష్ణోగ్రతా రేఖలను స్థిర ఘనపరిమాణ రేఖలు అంటారు లేదా ‘ఐసోకోర్లు’ అంటారు.

ప్రశ్న 10.
STP పరిస్థితులను తెలపండి.
జవాబు:
273.15K ఉష్ణోగ్రత, 1 bar (10⁵ పాస్కల్) పీడనంలను ప్రమాణ ఉష్ణోగ్రత, పీడనాలు అంటారు.

ప్రశ్న 11.
గ్రామ్ మోలార్ ఘనపరిమాణం అంటే ఏమిటి ?
జవాబు:
ఒక మోల్ వాయువు STP వద్ద 22.71098 లీటర్ల ఘనపరిమాణమును ఆక్రమిస్తుంది. దీనినే గ్రామ్ మోలార్ ఘన పరిమాణం అంటారు.

ప్రశ్న 12.
ఆదర్శవాయువు అంటే ఏమిటి ?
జవాబు:
అన్ని ఉష్ణోగ్రతలు మరియు పీడనాల వద్ద వాయు నియమాలను పాటించే వాయువులను ఆదర్శవాయువులు అంటారు.
ఆదర్శవాయువులకు PV = nRT.

ప్రశ్న 13.
వాయు స్థిరాంకం ‘R’ ను విశ్వవాయు స్థిరాంకం అని ఎందుకు పిలుస్తారు ?
జవాబు:
‘R’ విలువ అన్ని వాయువులకు వర్తిస్తుంది. అన్ని వాయువులకు ‘R’ విలువ సమానం. అందువల్ల R ను విశ్వవాయు స్థిరాంకం అంటారు.

ప్రశ్న 14.
ఆదర్శవాయు సమీకరణాన్ని స్థితి సమీకరణం అని ఎందుకు అంటారు ?
జవాబు:
వాయువు యొక్క కొలవదగిన ధర్మాలైన P, V, T మరియు n ల మధ్య సంబంధాన్ని ఆదర్శవాయు సమీకరణం తెలియజేస్తుంది. అది వాయువు యొక్క స్థితిని వర్ణిస్తుంది. కనుక దానిని స్థితి సమీకరణం అంటారు.

ప్రశ్న 15.
వాయు స్థిరాంకం ‘R’ విలువను వివిధ ప్రమాణాల్లో తెలపండి.
జవాబు:
R = 8.20578 × 10^-2 L. atm K^-1 mol^-1
R = 8.314 JK^-1 mol^-1

ప్రశ్న 16.
ఒక వాయువు యొక్క సాంద్రత, మోలార్ ద్రవ్యరాశుల మధ్య సంబంధాన్ని తెలపండి.
జవాబు:
మోలార్ ద్రవ్యరాశి M = \(\frac{\mathrm{dRT}}{\mathrm{P}}\)
M = మోలార్ ద్రవ్యరాశి,
R = వాయు స్థిరాంకం,
P = పీడనం,
d = వాయు సాంద్రత,
T = పరమ ఉష్ణోగ్రత

ప్రశ్న 17.
గ్రాహం వాయు వ్యాపన నియమాన్ని తెలపండి.
జవాబు:
స్థిర ఉష్ణోగ్రత, పీడనాల వద్ద ఒక వాయువు యొక్క వ్యాపన రేటు దాని సాంద్రత లేక బాష్ప సాంద్రత లేక అణుభారాల వర్గమూలానికి విలోమానుపాతంలో ఉంటుంది.
వాయు వ్యాపన రేటు r ∝ \(\frac{1}{\sqrt{\mathrm{d}}}\)
r ∝ \(\frac{1}{\sqrt{m}}\)

ప్రశ్న 18.
N₂, O₂, CH₄ వాయువులలో ఏది త్వరితంగా వ్యాపనం చెందుతుంది. ఎందువల్ల ?
జవాబు:
CH₄ (మీథేన్) త్వరితంగా వ్యాపనం చెందుతుంది. ఎందువలన అంటే N₂, O₂ కంటే అది తేలికైనది.

ప్రశ్న 19.
సల్ఫర్ డయాక్సైడ్ కంటే మీథేన్ ఎన్ని రెట్లు త్వరితంగా వ్యాపనం చెందుతుంది ?
జవాబు:

సల్ఫర్ డయాక్సైడ్ కంటే మీథేన్ రెండు రెట్లు త్వరితంగా వ్యాపనం చెందుతుంది.

ప్రశ్న 20.
డాల్టన్ పాక్షిక పీడనాల నియమాన్ని తెలపండి.
జవాబు:
డాల్టన్ పాక్షిక పీడనాల నియమం : స్థిర ఉష్ణోగ్రత వద్ద రసాయనికంగా చర్య జరపని వాయు మిశ్రమం కలుగజేసే మొత్తం పీడనం, అందులోని అనుఘటక వాయువుల పాక్షిక పీడనాల మొత్తానికి సమానము. P = P₁ + P₂ + P₃

ప్రశ్న 21.
ఒక వాయువు పాక్షిక పీడనానికి, దాని మోల్ భాగానికి గల సంబంధాన్ని తెలపండి.
జవాబు:
పాక్షిక పీడనం = వాయు మిశ్రమం మొత్తం పీడనం × మోల్ భాగం
P₁ = P × x₁
P₂ = P × x₂

ప్రశ్న 22.
నీటి ఆవిరి సంతృప్త బాష్పపీడనం అంటే ఏమిటి ?
జవాబు:
నియమిత ఉష్ణోగ్రత వద్ద, నీటి ఆవిరి అణువులు ద్రవ నీటితో సమతాస్థితిలో ఉన్నప్పుడు, ద్రవనీటి ఉపరితలంపై నీటి ఆవిరి అణువులు కలుగజేసే పీడనాన్ని నీటి ఆవిరి సంతృప్త బాష్పపీడనం అంటారు.

ప్రశ్న 23.
వాయువుల అణుచలన సిద్ధాంతంలోని ఏ రెండు అంశాలు ఆదర్శ ప్రవర్తన నుంచి నిజవాయువుల విచలనాన్ని వివరించలేవు?
జవాబు:

1. వాయువు ఆక్రమించే మొత్తం ఘనపరిమాణంతో పోలిస్తే వాయు అణువులు తమంతట తాము ఆక్రమించే ఘనపరిమాణంను నిర్లక్ష్యం చేయవచ్చు.
2. వాయు అణువుల మధ్య ఆకర్షణ వికర్షణ బలాలు లేవు.

ప్రశ్న 24.
చలద్వాయు సమీకరణాన్ని వ్రాసి, దానిలోని పదాలను తెలపండి.
జవాబు:
pV = \(\frac{1}{3} \mathrm{mn} \mathrm{u}_{\mathrm{rms}}^2\)
p = పీడనం,
V = ఘనపరిమాణం,
m = వాయు అణువు ద్రవ్యరాశి,
n = వాయు అణువుల సంఖ్య,
u_rms = వాయు అణువుల RMS వేగం.

ప్రశ్న 25.
వాయు అణువుల గతిజశక్తిని లెక్కకట్టుటకు సమీకరణాన్ని తెలపండి.
జవాబు:
వాయు అణువుల సగటు గతిజశక్తి
E_k = \(\frac{3}{2}\)nRT
n = మోల్ల సంఖ్య
R = వాయు స్థిరాంకం
T = పరమ ఉష్ణోగ్రత
ఒక అణువు గతిజశక్తి E_k = \(\frac{3}{2}\)kT
k = బోల్ట్స్మన్ స్థిరాంకం
k = \(\frac{R}{N}\); N = అవగాడ్రో సంఖ్య

ప్రశ్న 26.
బోల్ట్స్మన్ స్థిరాంకం అంటే ఏమిటి ? దాని విలువను తెలపండి.
జవాబు:
ఒక వాయు అణువు యొక్క స్థిరాంకాన్ని బోల్ట్స్మన్ స్థిరాంకం అంటారు.
k = \(\frac{\mathrm{R}}{\mathrm{N}}\)
k = 1.38 × 10^-23 JK^-1 molecule^-1 (or) 1.38 × 10^-16 erg K^-1 molecule^-1

ప్రశ్న 27.
RMS వేగం అంటే ఏమిటి ?
జవాబు:
వాయు అణువుల వేగ వర్గాల సగటు యొక్క వర్గ మూలం, వాయు అణువుల వేగాలు u₁, u₂, u₃ ……. అయితే

n = వాయు అణువుల సంఖ్య, U_rms = \(\sqrt{\frac{3 R T}{M}}\)

ప్రశ్న 28.
సగటు వేగం అంటే ఏమిటి ?
జవాబు:
n వాయు అణువుల వేగాలు u₁, u₂, u₃ అయితే సరాసరి వేగం

ప్రశ్న 29.
గరిష్ఠ సంభావ్యత వేగం అంటే ఏమిటి ?
జవాబు:
గరిష్ఠ సంఖ్య అణువులకు గల వేగాన్ని గరిష్ఠ సంభావ్యత వేగం అంటారు.
U_mp = \(\sqrt{\frac{2 \mathrm{RT}}{\mathrm{M}}}\)
M = అణుభారం,
T = పరమ ఉష్ణోగ్రత

ప్రశ్న 30.
వాయు అణువుల వేగాలపై ఉష్ణోగ్రత ప్రభావమేమిటి ?
జవాబు:
వాయు అణువుల వేగం పెరుగుతుంది. అణువుల వేగాల పంపిణీ ప్రకారం, తక్కువ వేగాలు గల అణుభాగం ఉష్ణోగ్రత పెరిగితే తగ్గుతుంది. అదే విధంగా ఎక్కువ వేగాలు గల అణువుల భాగం పెరుగుతుంది.

ప్రశ్న 31.
వాయు అణువుల గతిజశక్తిపై ఉష్ణోగ్రత ప్రభావమేమిటి ?
జవాబు:
వాయు అణువుల గతిజశక్తి E_k = \(\frac{3}{2}\)nRT
∴ E_k ∝ T
వాయు అణువుల గతిజశక్తి పరమ ఉష్ణోగ్రతకు అనుపాతంలో ఉంటుంది. ఉష్ణోగ్రత పెరిగితే అణువుల గతిజశక్తి పెరుగుతుంది.

ప్రశ్న 32.
వాయు అణువుల RMS వేగం, సగటు వేగం, గరిష్ఠ సంభావ్యత వేగాల నిష్పత్తిని తెలపండి.
జవాబు:
U_mp : U_av : U_rms = 1 : 1.128 : 1.224

ప్రశ్న 33.
చలద్వాయు సమీకరణంలో RMS వేగాన్ని ఎందుకు తీసుకుంటారు ?
జవాబు:
వేగం అనేది సదిశరాశి. వాయు అణువులు నిరంతరం అన్ని దిశలలో క్రమ రాహిత్యంగా తిరుగుతూ ఉంటాయి. ఒక దిశలో వేగాన్ని ధనాత్మకంగా తీసికొంటే దానికి వ్యతిరేక దిశలో వేగం ఋణాత్మకం అవుతుంది. ఈ పరిస్థితులలో సరాసరి వేగం విలువ సున్న అయ్యే అవకాశం ఉంది. దానిని నివారించడానికి అన్ని వేగాలను వర్గం చేసి వాటి సరాసరిని కనుగొని ఆ సరాసరి విలువకు వర్గమూలాన్ని తీసుకున్నారు. అపుడు అది నిజమైన సరాసరి వేగం అవుతుంది. దీనినే RMS వేగం అంటారు.
RMS వేగం = u_rms = \(\sqrt{\frac{u_1^2+u_2^2+u_3^2+\ldots \ldots . u_n^2}{n}}\)

ప్రశ్న 34.
సంపీడన గుణకం అంటే ఏమిటి ?
జవాబు:
ఒకే ఉష్ణోగ్రతా పీడన పరిస్థితుల వద్ద నిజవాయువు మోలార్ ఘనపరిమాణాలకు ఆదర్శవాయు మోలార్ ఘనపరిమాణాలకు గల నిష్పత్తిని సంపీడన గుణకం అంటారు.

ఆదర్శ వాయువుకు Z = 1

ప్రశ్న 35.
బాయిల్ ఉష్ణోగ్రత అంటే ఏమిటి ?
జవాబు:
విస్తృత పీడనాల్లో ఏ ఉష్ణోగ్రత వద్దనైతే నిజవాయువు ఆదర్శ వాయు నియమాన్ని పాటిస్తుందో ఆ ఉష్ణోగ్రతను బాయిల్ ఉష్ణోగ్రత అంటారు. ఈ ఉష్ణోగ్రత వాయువు స్వభావం మీద ఆధారపడి ఉంటుంది.

ప్రశ్న 36.
సందిగ్ధ ఉష్ణోగ్రత అంటే ఏమిటి ? CO₂ కు దాని విలువ ఇవ్వండి.
జవాబు:
ఏ ఉష్ణోగ్రత కన్నా అధిక ఉష్ణోగ్రత వద్ద అధిక పీడనాన్ని ఉపయోగించినప్పటికి వాయువును ద్రవీకరింపచేయలేమో, ఆ ఉష్ణోగ్రతను సందిగ్ధ ఉష్ణోగ్రత అంటారు. వాయువును సందిగ్ధ ఉష్ణోగ్రత వద్దగాని, అంత కంటె తక్కువ ఉష్ణోగ్రత వద్ద గాని అధిక పీడనాన్ని ఉపయోగించి ద్రవీకరించవచ్చు. ఉదా : CO₂, కు సందిగ్ధ ఉష్ణోగ్రత = 30.98°C

ప్రశ్న 37.
సందిగ్ధ ఘనపరిమాణం అంటే ఏమిటి ?
జవాబు:
సందిగ్ధ ఉష్ణోగ్రత, సందిగ్ధ పీడనాల వద్ద ఒక మోల్ వాయువు ఆక్రమించే ఘనపరిమాణాన్ని సందిగ్ధ ఘనపరిమాణం (V_c) అంటారు.

ప్రశ్న 38.
సందిగ్ధ పీడనం అంటే ఏమిటి ?
జవాబు:
వాయువును సందిగ్ధ ఉష్ణోగ్రత వద్ద ఉంచి, ద్రవీకరింపచేయడానికి ఉపయోగించవలసిన పీడనాన్ని సందిగ్ధ పీడనం అంటారు.

ప్రశ్న 39.
సందిగ్ధ స్థిరాంకాలు అంటే ఏమిటి ?
జవాబు:
సందిగ్ధ ఉష్ణోగ్రత, సందిగ్ధ పీడనం మరియు సందిగ్ధ ఘనపరిమాణంలను సందిగ్ధ స్థిరాంకాలు అంటారు. (T_c, P_c, V_c)

ప్రశ్న 40.
ద్రవం బాష్పపీడనాన్ని నిర్వచించండి.
జవాబు:
ద్రవ ఉపరితలంపై దాని బాష్పం కలుగచేయు పీడనాన్ని ద్రవ బాష్పపీడనం అంటారు.
ద్రవ, బాష్పాల మధ్య సమతాస్థితి ఉన్నప్పుడు, ద్రవంపై బాష్పం కలుగచేయు పీడనాన్ని సంతృప్త బాష్పపీడనం అంటారు.

ప్రశ్న 41.
సాధారణ, ప్రమాణ బాష్పీభవన ఉష్ణోగ్రతలు అంటే ఏమిటి ? H₂O కు వాటి విలువలు ఇవ్వండి.
జవాబు:
పీడనం ‘1’ అట్మాస్ఫియర్ వద్ద ద్రవం మరిగే ఉష్ణోగ్రతను సాధారణ బాష్పీభవన స్థానం అంటారు. అదే 1 బార్ పీడనం వద్ద ద్రవం మరిగే ఉష్ణోగ్రతను ‘ప్రమాణ బాష్పీభవనస్థానం’ అంటారు.
నీటి సాధారణ బాష్పీభవన స్థానం 100°C. ప్రమాణ బాష్పీభవన స్థానం 99.6°C

ప్రశ్న 42.
కొండల మీద వంట చేయడానికి ప్రెజర్ కుక్కర్లను ఎందుకు వాడతారు ?
జవాబు:
ఎత్తు ప్రదేశాలలో వాతావరణ పీడనం తగ్గుతుంది. అందువల్ల ద్రవాల బాష్పీభవన స్థానాలు తగ్గుతాయి. కొండల మీద నీటి బాష్పీభవన స్థానం తక్కువగా ఉండుట వలన వంట చేయడానికి ప్రెజర్ కుక్కర్లను వాడతారు.

ప్రశ్న 43.
తలతన్యత అంటే ఏమిటి ?
జవాబు:
ద్రవాలు సాధ్యమైనంత తక్కువ ఉపరితల వైశాల్యం కలిగి ఉండేటట్లు ప్రయత్నిస్తాయి.
ద్రవం ఉపరితలంపై గీసిన రేఖకు లంబ దిశలో ఏకాంక పొడవుపై పనిచేసే బలాన్ని తలతన్యత అంటారు. ప్రమాణాలు Kg.S^-2 లేదా SI ప్రమాణాల్లో Nm^-1.

ప్రశ్న 44.
దళ ప్రవాహం అంటే ఏమిటి ?
జవాబు:
ఒక్కొక్క పొరలోని అణువులు వేరువేరు వేగాలతో ప్రయాణిస్తూ, ఒక క్రమపద్ధతిలో వేగాల్లో భేదాలున్న ఈ పొరల ప్రవాహాన్ని దళ ప్రవాహం అంటారు.

ప్రశ్న 45.
స్నిగ్ధతా గుణకం అంటే ఏమిటి ? దాని ప్రమాణాలు తెలపండి.
జవాబు:
ఏకాంక స్పర్శా వైశాల్యం, ఏకాంక వేగ ప్రవీణత గల ద్రవ ప్రవాహపు పొరపై పనిచేసే బలాన్ని స్నిగ్ధతా గుణకం అంటారు.
స్నిగ్ధతా గుణకం SI ప్రమాణాలు Ns m^-2 CGS ప్రమాణాలు poise (పాయిస్)
1 పాయిస్ = 1 g cm^-1 S^-1

లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 46.
బాయిల్ నియమాన్ని తెలిపి, వివరించండి.
జవాబు:
స్థిర ఉష్ణోగ్రత వద్ద నియమిత ద్రవ్యరాశి గల వాయువు యొక్క ఘనపరిమాణం దాని పీడనానికి విలోమానుపాతంలో ఉంటుంది.
V ∝ \(\frac{1}{\mathrm{P}}\) (స్థిర ఉష్ణోగ్రత)
V = \(\frac{K}{P}\)
PV = K (స్థిరం)
నియమిత ద్రవ్యరాశిగల ఒక వాయువు ఘనపరిమాణం పీడనం P₁ పీడనం వద్ద V₁ అనుకొనుము. అదే విధంగా P₂ పీడనం వద్ద ఘనపరిమాణం V₂ అయితే
P₁V₁ = P₂V₂
దీనిలో నాలుగు పదాలున్నాయి. ఏ మూడు పదాలు తెలిసినా నాల్గవ పదాన్ని లెక్క కట్టవచ్చు.

ప్రశ్న 47.
ఛార్లెస్ నియమాన్ని తెలిపి, వివరించండి.
జవాబు:
స్థిరపీడనం వద్ద నియమిత ద్రవ్యరాశి గల వాయువు యొక్క ఘనపరిమాణము దాని పరమ ఉష్ణోగ్రతకు అనులోమాను- పాలో ఉంటుంది.
V ∝ T (స్థిర పీడనం)
V = KT
\(\frac{V}{T}\) = K లేక \(\frac{V}{T}\) = K
నియమిత ద్రవ్యరాశిగల వాయువు యొక్క ఘనపరిమాణం T₁ ఉష్ణోగ్రత వద్ద V₁ అని, T₂ ఉష్ణోగ్రత వద్ద V₂ అయితే
\(\frac{V_1}{T_1}\) = \(\frac{V_2}{T_2}\). దీనిలో నాలుగు పదాలున్నాయి. ఏ మూడు పదాలు తెలిసినా నాల్గవ పదాన్ని లెక్కకట్టవచ్చు.

ప్రశ్న 48.
ఆదర్శ వాయు సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
ఆదర్శ వాయు సమీకరణం రాబట్టుట : బాయిల్, ఛార్లెస్ మరియు అవగాడ్రో సూత్రాలను కలిపి వ్రాస్తే ఘనపరిమాణము, పీడనం, పరమ ఉష్ణోగ్రత మరియు మోల్ల సంఖ్యలకు గల సంబంధాన్ని తెలియచేసే సమీకరణం వస్తుంది. దీనినే ఆదర్శ వాయు సమీకరణం అంటారు.
V ∝ \(\frac{1}{p}\) (T స్థిరం) బాయిల్ సూత్రం
V ∝ T(p స్థిరం) ఛార్లెస్ సూత్రం
V ∝ n (p, T లు స్థిరం) అవొగాడ్రో సూత్రం
పై మూడు సూత్రాలను కలిపి వ్రాస్తే
V ∝ \(\frac{1}{p}\) × T × n లేక V = R × \(\frac{1}{p}\) × T × n లేక pV = nRT
దీనినే ఆదర్శవాయు సమీకరణం అంటారు. దీనిలో p = పీడనం, V = ఘనపరిమాణము n = మోల్ల సంఖ్య, T = పరమ ఉష్ణోగ్రత, R = సార్వత్రిక వాయు స్థిరాంకం.
p₁ పీడనం, T₁ పరమ ఉష్ణోగ్రతల వద్ద ఒక వాయువు ఘనపరిమాణము V₁ అని అనుకొనుము. అదే విధంగా p₂ పీడనం, T₂ పరమ ఉష్ణోగ్రతల వద్ద అదే వాయువు ఘనపరిమాణము V₂ అని అనుకొనుము.
అపుడు \(\frac{\mathrm{p}_1 \mathrm{~V}_1}{\mathrm{~T}_1}\) = R మరియు \(\frac{\mathrm{p}_2 \mathrm{v}_2}{\mathrm{~T}_2}\) = R
∴ \(\frac{\mathrm{p}_1 \mathrm{~V}_1}{\mathrm{~T}_1}\) = \(\frac{\mathrm{p}_2 \mathrm{~V}_2}{\mathrm{~T}_2}\)
దీనిలో ఆరు పదాలు ఉన్నాయి. ఏ ఐదు పదాలు తెలిసినా ఆరవ పదాన్ని లెక్కగట్టవచ్చును.

ప్రశ్న 49.
గ్రాహం వాయు వ్యాపన నియమాన్ని తెలిపి, వివరించండి.
జవాబు:
స్థిర ఉష్ణోగ్రత, పీడన పరిస్థితుల వద్ద, ఒక వాయువు యొక్క వ్యాపన రేటు దాని సాంద్రత లేక బాష్ప సాంద్రత లేక అణుభారాల వర్గమూలానికి విలోమానుపాతంలో ఉంటుంది.

రెండు వాయువుల వ్యాపన రేట్లు వరుసగా r₁, r₂ లు అని, వాటి సాంద్రతలు d₁, d₂ లు అని అనుకుంటే
అపుడు, \(\frac{r_1}{r_2}\) = \(\sqrt{\frac{\mathrm{d}_2}{\mathrm{~d}_1}}\) …….. (1)
రెండు వాయువుల వ్యాపన రేట్లు వరుసగా 1,2 లు అని, వాటి బాష్ప సాంద్రతలు VD₁, VD₂ లు అని అనుకుంటే
అపుడు, \(\frac{r_1}{r_2}\) = \(\sqrt{\frac{\mathrm{VD}_2}{\mathrm{VD}_1}}\) …… (2)
రెండు వాయువుల వ్యాపన రేట్లు వరుసగా r₁, r₂ లు అని, వాటి అణు భారాలు M₁, M₂ లు అని అనుకుంటే అపుడు,
\(\frac{r_1}{r_2}\) = \(\sqrt{\frac{\mathrm{M}_2}{\mathrm{M}_1}}\) …. (3)
(1), (2), (3) ల నుండి
\(\frac{r_1}{r_2}\) = \(\sqrt{\frac{d_2}{d_1}}\) = \(\sqrt{\frac{\mathrm{VD}_2}{\mathrm{VD}_1}}\) = \(\sqrt{\frac{\mathrm{M}_2}{\mathrm{M}_1}}\)

ప్రశ్న 50.
డాల్టన్ పాక్షిక పీడనాల నియమాన్ని తెలిపి, వివరించండి.
జవాబు:
డాల్టన్ పాక్షిక పీడనాల నియమం : స్థిర ఉష్ణోగ్రత వద్ద రసాయనికంగా చర్య జరపని వాయు మిశ్రమం కలుగ చేసే మొత్తం పీడనం అందులోని ఘటక వాయువుల పాక్షిక పీడనాల మొత్తానికి సమానం.
ఒక పాత్రలో మూడు వాయువుల మిశ్రమాన్ని తీసుకోండి. ఈ మిశ్రమంలో అనుఘటక వాయువుల పాక్షిక పీడనాలు వరుసగా P₁, P₂ మరియు P₃ అయితే,
వాయు మిశ్రమం మొత్తం పీడనం p = p₁ + p₂ + p₃
వాయువుల మోల్ల సంఖ్యలు n₁, n₂, n₃
అయితే మోల్ భాగాలు x₁ = \(\frac{n_1}{n_1+n_2+n_3}\) ; x₂ = \(\frac{n_2}{n_1+n_2+n_3}\) ; x₃ = \(\frac{n_3}{n_1+n_2+n_3}\)
మొత్తం పీడనం P అయితే
పాక్షిక పీడనం p₁ = x₁· P
రెండవ వాయువు పాక్షిక పీడనం p₂ = x₂ . P
మూడవ వాయువు పాక్షిక పీడనం p₃ = x₃ . P

ప్రశ్న 51.
చలద్వాయు సమీకరణం నుండి
(a) బాయిల్ నియమం
(b) ఛార్లెస్ నియమం రాబట్టండి.
జవాబు:
(a) బాయిల్ నియమం : అణుచలన సిద్ధాంతంలోని అంశాల ప్రకారం, వాయు అణువుల సగటు గతిజ శక్తి దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది.
అంటే KE ∝ T
కాని KE = \(\frac{1}{2} \mathrm{mn} \mathrm{u}_{\mathrm{rms}}^2\)
∴ \(\frac{1}{2} \mathrm{mnu}_{\mathrm{rms}}^2\) ∝ T
\(\frac{1}{2} \mathrm{mnu}_{\mathrm{rms}}^2\) = KT ….. (1)
చలద్వాయు సమీకరణం ప్రకారం
PV = \(\frac{1}{3} \mathrm{mnu}^2{ }_{\mathrm{rms}}\) లేక PV = \(\frac{2}{3} \cdot \frac{1}{2} \mathrm{mnu}_{\mathrm{rms}}^2\)
(2) వ సమీకరణంలో (1) ని ప్రతిక్షేపిస్తే
PV = \(\frac{2}{3}\) . KT
లేక V = \(\frac{2 \mathrm{KT}}{3 \mathrm{P}}\)
“T” ను స్థిరం చేస్తే అప్పుడు
V = స్థిరరాశి × \(\frac{1}{\mathrm{P}}\)
లేక V ∝ \(\frac{1}{\mathrm{P}}\) (T స్థిరం)
స్థిర ఉష్ణోగ్రత వద్ద నియమిత ద్రవ్యరాశి గల వాయు ఘనపరిమాణం దాని పీడనానికి విలోమానుపాతంలో ఉంటుంది.
ఇదే బాయిల్ నియమం.

(b) ఛార్లెస్ నియమం : అణుచలన సిద్ధాంతంలోని అంశాల ప్రకారం వాయు అణువుల సగటు శక్తి దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది.

‘P’ ను స్థిరం చేస్తే అప్పుడు V = స్థిరం × Tలేక V ∝ T (P స్థిరం)
స్థిర పీడనం వద్ద నియమిత ద్రవ్యరాశి గల వాయువు ఘనపరిమాణం దాని పరమ ఉష్ణోగ్రతకు అనులోమాను- పాతంలో ఉంటుంది. ఇదే చార్లెస్ నియమం.

ప్రశ్న 52.
చలద్వాయు సమీకరణం నుండి (a) గ్రాహం నియమం (b) డాల్టన్ నియమం రాబట్టండి.
జవాబు:
V ఘనపరిమాణం గల ఒక పాత్రలో ఒక వాయువు ఒక్కొక్క అణువు భారం m₁. వాయువులోని n₁ అణువులు rms వేగం u_1rms కలిగి ఉందనుకొందాం. ఆ వాయువు పీడనం p₁ అనుకొంటే చలద్వాయు సమీకరణం ప్రకారం
P₁ V = \(\frac{1}{3}\) m₁n₁ \(\mathrm{u}_{1 \mathrm{rms}}^2\)
లేదా p₁ = \(\frac{1}{3} \frac{\mathrm{m}_1 \mathrm{n}_1 \mathrm{u}_{1 \mathrm{rms}}^2}{\mathrm{~V}}\)
పాత్రలోని వాయువును తొలగించి రెండో వాయువును తీసుకొంటే ఆ వాయువు ఘనపరిమాణం V, పీడనం p₂, ఒక్కో అణువు భారం m₂, అణువుల సంఖ్య n₂ అయితే

రెండు వాయువులను అదే పాత్రలో తీసుకొంటే వాయు మిశ్రమం కలిగించే పీడనాన్ని p_{మొత్తం} అనుకొంటే

గ్రాహం నియమం : ఒక వాయువుకు చల ద్వాయు సమీకరణం ప్రకారం p. V. = \(\frac{1}{3} \mathrm{mn} \mathrm{u}_{\mathrm{rms}}^2\)
mn = వాయువు ద్రవ్యరాశి, వాయువులో అవొగాడ్రో సంఖ్య అణువులు ఉంటే mn = M (మోలార్ ద్రవ్యరాశి)

కాబట్టి వాయువు వ్యాపనం రేటు దాని సాంద్రత వర్గమూలానికి విలోమానుపాతంలో ఉంటుంది. ఇదే గ్రాహం నియమం.

ప్రశ్న 53.
వాయు అణువుల గతిజశక్తికి సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
చలద్వాయు సమీకరణం ప్రకారం
P. V. = \(\frac{1}{3} \mathrm{mn} \mathrm{u}_{\mathrm{rms}}^2\)
n = N అయితే mn = M మోలార్ ద్రవ్యరాశి
p. V = \(\frac{1}{3} \mathrm{Mu}_{\mathrm{rms}}^2\) = \(\frac{2}{3}\left(\frac{1}{2} \mathrm{Mu}_{\mathrm{rms}}^2\right)\)
= \(\frac{2}{3} \mathrm{E}_{\mathrm{k}}\)….. (1)
E_k ఒక మోల్ వాయువు గతిజశక్తి ఒక మోల్ వాయువుకు p. V = RT …. (2)
పై సమీకరణాల ప్రకారం
\(\frac{2}{3}\)E_k = RT లేదా E_k = \(\frac{3}{2}\)RT
‘n’ మోల్ల వాయువుకు గతిజశక్తి E_k = \(\frac{3}{2}\)nRT
కాబట్టి నిర్దిష్ఠ ఉష్ణోగ్రత వద్ద ఒక మోల్ ఏ వాయువైనా ఒకే గతిజశక్తి కలిగి ఉంటుంది. ఒక వాయు అణువు గతిజశక్తి.
\(\frac{E_k}{N}\) = \(\frac{3}{2}\left(\frac{\mathrm{R}}{\mathrm{N}}\right) \mathrm{T}\) = \(\frac{3}{2} \mathrm{kT}\)
k ను బోల్ట్స్మన్ స్థిరాంకం అంటారు.
k = \(\frac{\mathrm{R}}{\mathrm{N}}\)
ఒక అణువు వాయువు యొక్క స్థిరాంకం బోల్ట్స్మన్ స్థిరాంకం
k = 1.38 × 10^-16 erg K^-1 molecule^-1 = 1.38 × 10^-23 JK^-1 molecule^-1

ప్రశ్న 54.
వాయు అణువుల
(a) rms వేగం
(b) సగటు వేగం
(c) గరిష్ఠ సంభావ్యత వేగాలను నిర్వచించి, వాటి మధ్యగల సంబంధాన్ని తెలపండి.
జవాబు:
a) rms వేగం : వాయువులోని అణువులు వేగాలు వర్గాల సగటు యొక్క వర్గ మూలాన్ని (root mean square velocity) RMS వేగం అంటారు.

b) సగటు వేగం : ఒక వాయువులో N అణువులు ఉండి, అణువుల వేగాలు u₁, u₂….. u_n గా ఉంటే వాయు అణువుల సగటు వేగం

c) గరిష్ఠ సంభావ్యతా వేగం : వాయువులో గరిష్ఠ సంఖ్య అణువులకుండే వేగాన్ని గరిష్ఠ సంభావ్యతా వేగం అంటారు.
u_mp = \(\sqrt{\frac{2 \mathrm{RT}}{\mathrm{M}}}\)
అణువేగాల నిష్పత్తి : వాయువులోని మూడు రకాల అణువేగాల నిష్పత్తి

సగటు వేగం = 0.9213 × u_rms
గరిష్ఠ సంభావ్యతా వేగం = 0.8166 × u_rms

ప్రశ్న 55.
వాండర్ వాల్స్ స్థిరాంకాల భౌతిక ప్రాధాన్యతను వివరించండి.
జవాబు:
(p + \(\frac{\mathrm{an}^2}{\mathrm{v}^2}\))(v – nb) = nRT ఈ సమీకరణాన్ని వాండర్ వాల్స్ సమీకరణం అంటారు. n మోల్ల సంఖ్య a, b లు వాండర్ వాల్ స్థిరాంకాలు. ‘a’ విలువలు వాయువు స్వభావం మీద ఆధారపడి ఉంటాయి. ‘a’ విలువ వాయు అణువుల మధ్య ఉండే అంతర అణు ఆకర్షణ బలాల పరిమాణాన్ని తెలుపుతుంది. దీని విలువ వాయు పీడనం, ఉష్ణోగ్రతలపై ఆధారపడి ఉండదు.
‘b’ అనునది వాయు అణువులు తమంతట తాము ఆక్రమించే ఘనపరిమాణానికి కొలత. అధిక పీడనాల వద్ద వాయు ఘనపరిమాణం స్వల్పం. వాయు అణువులు తమంతట తాము ఆక్రమించే ఘనపరిమాణాన్ని నిర్లక్ష్యం చేయడానికి వీలులేదు. b ని వర్జిత ఘనపరిమాణం అంటారు.

ప్రశ్న 56.
ద్రవాల తలతన్యత అంటే ఏమిటి ? ద్రవాల తలతన్యతపై ఉష్ణోగ్రత ప్రభావాన్ని వివరించండి.
జవాబు:
ద్రవాలలో ఉండే అంతర అణు ఆకర్షణ బలాలే స్నిగ్ధతకు కారణం. ఇది ద్రవాల అభిలాక్షణిక ధర్మం.

ద్రవం లోపల ఒక అణువును తీసుకుంటే దానిపై పనిచేసే అంతర అణు బలాలు అన్ని దిశలలో ఉండటం వల్ల దానిపై పనిచేసే నికరబలం ఏమీ ఉండదు. ఇది ద్రవంలోపల ఉన్న అన్ని అణువులకు వర్తిస్తుంది. అదే ద్రవ ఉపరితలంపై ఉన్న అణువును పరిశీలిస్తే దానిపై అంతర అణు బలాలు కేవలం లోపలివైపుకే పని చేస్తాయి. దీనివల్ల అణువు ద్రవంలోపలికి లాగబడుతుంది. అందువల్ల ద్రవం ఉపరితల వైశాల్యం సాధ్యమైనంతగా తగ్గడానికి ప్రయత్నిస్తుంది. దీనివల్ల ద్రవ ఉపరితలం మీద గల అణువులు అంతర అణుబలాల ద్వారా క్రింది వైపుకు లాగబడతాయి. ద్రవం లోపలి అణువుల కంటె ఎక్కువ శక్తితో ఉంటాయి. అందువల్ల ద్రవ ఉపరితలం తక్కువ సంఖ్యలో అణువులను కలిగి ఉండటానికి ప్రయత్నిస్తుంది. అందువల్ల ద్రవ ఉపరితలం కుచించుకు పోయినట్లుగా ప్రవర్తిస్తుంది. ద్రవాల ఈ ధర్మాన్నే (లేక) ప్రవృత్తినే తలతన్యత అంటారు.
ద్రవ ఉపరితలం అణువుపైన, లోపలి భాగం అణువుపైన పనిచేసే బలాలు.

ఉదా : 1) తలతన్యత కారణంగా ద్రవ బిందువులు గోళాకారంగా ఉంటాయి.
2) సందిగ్ధ ఉష్ణోగ్రత వద్ద ద్రవాల తలతన్యత సున్న.
3) తలతన్యత కారణంగానే కేశనాళికలోని ద్రవాలు పైకి ప్రసరిస్తాయి.
ద్రవ ఉపరితల వైశాల్యాన్ని ఒక యూనిట్ పెంచడానికి అవసరమయ్యే శక్తిని ఉపరితలశక్తి అంటారు. దీని ప్రమాణాలు Jm^-2. ద్రవ ఉపరితలంపై గీసిన రేఖకు లంబ దిశలో ఏకాంత పొడవుపై పనిచేసే బలాన్ని తలతన్యత అంటారు. తలతన్యత ప్రమాణాలు Kgs^-2 SI ప్రమాణాల్లో N m^-1

ఉష్ణోగ్రత పెరుగుదలతో పాటు ద్రవాల తలతన్యత తగ్గుతుంది. దీనికి కారణం ఉష్ణోగ్రత పెంచితే అణువుల శక్తి పెరిగి, అణువుల మధ్య ఆకర్షణా బలాలు తగ్గడమే.

ప్రశ్న 57.
ద్రవాల బాష్ప పీడనం అంటే ఏమిటి ? ద్రవాల బాష్ప పీడనం, వాటి బాష్పీభవన ఉష్ణోగ్రతల మధ్య సంబంధాన్ని తెలపండి.
జవాబు:
ద్రవ ఉపరితలంపై దాని బాష్పం కలగజేసే పీడనాన్ని ద్రవ బాష్పపీడనం అంటారు. ఏ ఉష్ణోగ్రత వద్ద ద్రవం బాష్పపీడనం బాహ్యపీడనానికి సమానమవుతుందో ఆ ఉష్ణోగ్రతను ఆ పీడనం వద్ద ద్రవం బాష్పీభవన ఉష్ణోగ్రత అంటారు. ద్రవం యొక్క బాష్పీకరణం ఉష్ణోగ్రత మీద ఆధారపడి ఉంటుంది. కనుక ద్రవం బాష్పపీడనాన్ని తెలిపేటప్పుడు ఉష్ణోగ్రతను తప్పకుండా పేర్కొనాలి.

ప్రశ్న 58.
స్నిగ్ధత, స్నిగ్ధతా గుణకాలను నిర్వచించండి. ద్రవాల స్నిగ్ధత ఉష్ణోగ్రతతో ఏవిధంగా మారుతుంది ?
జవాబు:
ఒక ద్రవం ప్రవహిస్తున్నపుడు ద్రవపు పొరలు ఒక దాని నుంచి ఇంకొకటి ముందుకు కదలడానికి ప్రయత్నిస్తాయి. ద్రవప్రవాహంలో పొరల మధ్య రాపిడి లేదా ఘర్షణ వల్ల ద్రవ ప్రవాహాన్ని నిరోధించే కొలతని స్నిగ్ధత అంటారు. ద్రవ అణువుల మధ్య ఉండే బలమైన అంతర అణుబలాలు ద్రవపు పొరలను కలిపి ఉంచి ఆ పొరలు ఒకదాని నుంచి ఇంకొకటి ముందుకు జారిపోకుండా అడ్డుపడతాయి. dz దూరంలో ఉన్న పొర వేగంలో మార్పు du అనుకొంటే ఆ పొర వేగ ప్రవీణత \(\frac{\mathrm{du}}{\mathrm{d} z}\) అవుతుంది. ద్రవపు పొరల ప్రవాహాన్ని నడపడానికి బలం కావాలి. ఈ బలం పొరల స్పర్శా వైశాల్యానికి, పొరవేగ ప్రవీణతకు అనులోమానుపాతంలో ఉంటుంది.
F ∝ A. \(\frac{d u}{d z}\)
F = ηA \(\frac{d u}{d z}\)

η అనుపాత స్థిరాంకం. దీనిని స్నిగ్ధతా గుణకం అంటారు. ఏకాంక స్పర్శా వైశాల్యం, ఏకాంక వేగ ప్రవీణత గల ద్రవ ప్రవాహపు పొరపై పనిచేసే బలాన్ని స్నిగ్ధతా గుణకం అంటారు. స్నిగ్ధతా గుణకానికి CGS ప్రమాణాలు పాయిస్.
ఉష్ణోగ్రతా ప్రభావం : ద్రవాల స్నిగ్ధత ఉష్ణోగ్రతలో పెరుగుదలతో పాటు తగ్గుతుంది. దీనికి కారణం అధిక ఉష్ణోగ్రతల వద్ద ద్రవ అణువుల గతిజ శక్తి పెరిగి, అంతర అణు బలాలను అధిగమించి అణువులు ఒక పొర నుండి మరొక పొరలోకి తేలికగా జారిపోతుంటాయి.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 59.
అంతర అణుబలాలను వివరించండి.
జవాబు:
ఒక పదార్థంలోని కణాలైన పరమాణువులు లేదా అణువుల మధ్య ఉండే ఆకర్షణ, వికర్షణ బలాలను అంతర
అణుబలాలు అంటారు.

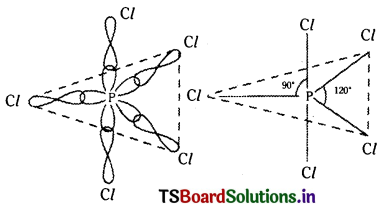
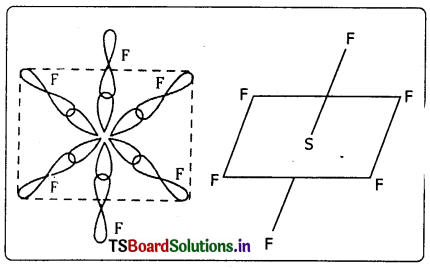
1. విక్షేపణ బలాలు లేక లండన్ బలాలు : పరమాణువులు, అధృవ అణువులు విద్యుదావేశ రహితాలు. అంతేకాక ఎలక్ట్రాన్ ఆవేశ మేఘం సౌష్టవంగా ఉండి అణువులకు ద్విధ్రువ భ్రామకం ఉండదు. అటువంటి అణువులు లేదా పరమాణువులలో కూడా తాత్కాలిక ద్విధ్రువం ఏర్పడవచ్చు. ఈ తాత్కాలిక ద్విధ్రువాల మధ్య ఆకర్షణ ఏర్పడుతుంది. ఈ విధమైన ఆకర్షణ బలాలను లండన్ బలాలు అంటారు. రెండు తాత్కాలిక ద్విధ్రువాల మధ్య ఉండే ఆకర్షణా బలాలను లండన్ బలాలు అంటారు. ఈ ఆకర్షణ బలాల అంతర చర్య శక్తి, అంతర చర్య జరిపే కణాల మధ్య దూరం యొక్క ఆరవ ఘాతాంకానికి విలోమానుపాతంలో ఉంటుంది. అంతర చర్య శక్తి ∝ \(\frac{1}{r^6}\)

2. ద్విధ్రువ-ద్విధ్రువ ఆకర్షణ బలాలు : శాశ్వత ద్విధ్రువాల మధ్య ఉండే బలాలను ద్విధ్రువ-ద్విధ్రువబలాలు అంటారు. ద్విధ్రువాల చివరలు పాక్షిక ఆవేశాలను కలిగి ఉంటాయి. ఈ ఆవేశాలను గ్రీకు అక్షరం (8) (డెల్టా)తో సూచిస్తారు. ఈ పాక్షిక ఆవేశాలు ఎలక్ట్రాన్ ఆవేశం (1.6× 10^-19 కులూంబులు) కంటే తక్కువగా ఉంటాయి. ధ్రువాణువుల సమీప అణువులతో అంతర చర్యలు జరుపుతాయి. ఈ ద్విధ్రువాల అంతర ఆకర్షణా బలాలు లండన్ విక్షేపణ బలాలకన్నా బలమైనవి. కాని అయాన్-అయాన్ అంతర ఆకర్షణల కంటే బలహీనమైనవి. ద్విధ్రువ-ద్విధ్రువ ఆకర్షణ బలాల శక్తి ధ్రువాణువుల మధ్య దూరానికి విలోమానుపాతంలో ఉంటుంది.

ధ్రువాణువుల మధ్య అంతర ఆకర్షణ బలాలు ∝ \(\frac{1}{r^3}\)
భ్రమణం చెందే ధృవాణువుల అంతర ఆకర్షణ బలాలు ∝ \(\frac{1}{r^6}\)

3. ద్విధ్రువ – ప్రేరిత ద్విధ్రువ బలాలు : ఈ బలాలు శాశ్వత ద్విధ్రువ భ్రామకం ఉన్న అణువుకు శాశ్వత ద్విధ్రువ భ్రామకం లేని అణువులకు మధ్య ఉత్పన్నమవుతాయి. శాశ్వత ద్విధ్రువ భ్రామకం గల ధ్రువాణువుల తటస్థ అణువుల ఎలక్ట్రాన్ మేఘాలను రూప భ్రంశం చెందిస్తాయి. ఆ తటస్థ అణువుల్లో ద్విధ్రువ లక్షణాన్ని ప్రేరేపిస్తాయి.

ఈ విధంగా ఏర్పడిన ద్విధ్రువ – ప్రేరిత ద్విధ్రువ బలాల అంతర చర్యశక్తి \(\frac{1}{r^6}\) కు అనులోమానుపాతంలో ఉంటుంది. ఇక్కడ r అనేది రెండు అణువుల మధ్య దూరం. ఈ ప్రేరిత ద్విధ్రువం, ద్విధ్రువ భ్రామకం విలువ, శాశ్వత ద్విధ్రువ అణువు ద్విధ్రువ భ్రామకం విలువ మీద, తటస్థ అణువు ధ్రువణ శీలత మీద ఆధారపడి ఉంటుంది.

ప్రశ్న 60.
బాయిల్, ఛార్లెస్, అవొగాడ్రో నియమాలను తెలిపి, ఆదర్శ వాయు సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
బాయిల్ నియమం : స్థిర ఉష్ణోగ్రత వద్ద నియమిత ద్రవ్యరాశి గల వాయు ఘనపరిమాణం పీడనానికి విలోమాను- పాతంలో ఉంటుంది.
V ∝ (n, Tలు స్థిరం)

ఛార్లెస్ నియమం : స్థిర పీడనం వద్ద నియమిత ద్రవ్యరాశిగల వాయు ఘనపరిమాణం పరమ ఉష్ణోగ్రతకు అనులోమాను- పాతంలో ఉంటుంది. V ∝ T (n, P లు స్థిరం)
అవొగాడ్రో నియమం : స్థిర ఉష్ణోగ్రత, పీడనాల వద్ద సమాన ఘనపరిమాణం గల వాయువులలో మోల్ల సంఖ్య సమానం. V ∝ (p, T లు స్థిరం)
పై మూడు నియమాలను కలిపి వ్రాస్తే ఘనపరిమాణం, పీడనం, పరమ ఉష్ణోగ్రత మరియు మోల్ల సంఖ్యకు మధ్యగల సంబంధాన్ని తెలియచేసే సమీకరణం వస్తుంది. దీనినే ఆదర్శవాయు సమీకరణం అంటారు.
V ∝ \(\frac{1}{P}\)(n, T లు స్థిరం) బాయిల్ నియమం
V ∝ T (p, n లు స్థిరం) ఛార్లెస్ నియమం
V ∝ n (p, Tలు స్థిరం) అవొగాడ్రో నియమం
పై మూడు సూత్రాలను కలిపి వ్రాస్తే
V ∝ \(\frac{1}{p}\). T. n లేక V = R. \(\frac{1}{p}\) . T . n
లేక pV = nRT ఇదే ఆదర్శవాయు సమీకరణం
p = పీడనం,
V = ఘనపరిమాణం,
T = పరమ ఉష్ణోగ్రత,
n = మోల్ల సంఖ్య,
R = వాయు స్థిరాంకం.

ప్రశ్న 61.
వాయువుల వ్యాపనంపై వ్యాసం రాయండి.
జవాబు:
స్థిర ఉష్ణోగ్రత, పీడనాల వద్ద వాయు వ్యాపన రేటు దాని సాంద్రత వర్గమూలానికి, లేదా బాష్పసాంద్రత వర్గ మూలానికి, లేదా అణుభారానికి విలోమానుపాతంలో ఉంటుంది. తేలికైన వాయువులు తొందరగా వ్యాపనం చెందుతాయి.

రెండు వాయువుల వ్యాపనరేట్లు r₁, r₂ మరియు సాంద్రతలు d₁, d₂ అయితే

Case 1 : వాయు వ్యాపన కాలాలు సమానమైతే

Case 2 : వాయువుల ఘనపరిమాణాలు సమానమైతే

వ్యాపనం అనువర్తనాలు :

1. వాయువుల వ్యాపన రేట్లు పోల్చి, ఒక వాయువు అణుభారం తెలిస్తే, రెండో వాయువు అణు భారాన్ని కనుక్కోవచ్చు.
2. U²³⁵, U²³⁸ ఐసోటోపులను, తేలికగా బాష్పంగా మారే U²³⁵F₆, U²³⁸F₆ గా మార్చి వ్యాపనం రేట్లలో తేడా వల్ల రెండు ఐసోటోపులను వేరు చేస్తారు.
3. బొగ్గు గనులలో వెలువడే ప్రమాదకరమైన మార్ష్ వాయువును గుర్తించే అన్సిల్ అలారం వాయువుల వ్యాపన ధర్మంపై ఆధారపడి పనిచేస్తుంది.

ప్రశ్న 62.
డాల్టన్ పాక్షిక పీడనాల సిద్ధాంతాన్ని వివరించండి.
జవాబు:
డాల్టన్ పాక్షిక పీడనాల నియమం : స్థిర ఉష్ణోగ్రత వద్ద రసాయనికంగా చర్య జరపని వాయు మిశ్రమం కలుగజేసే మొత్తం పీడనం అందులోని అనుఘటక వాయువుల పాక్షిక పీడనాల మొత్తానికి సమానం.
ఒక పాత్రలో మూడు వాయువుల మిశ్రమాన్ని తీసుకోండి. ఈ మిశ్రమంలో అనుఘటక వాయువుల పాక్షిక పీడనాలు వరుసగా p₁ p₂ మరియు p₃ అనుకొనుము. అపుడు డాల్టన్ పాక్షిక పీడనాల నియమం ప్రకారం P = p₁ + p₂ + p₃· ఇచ్చట P = వాయు మిశ్రమం మొత్తం పీడనం.

వాయువులను సాధారణంగా నీటిపైన సంగ్రహిస్తాం. ఆ సమయంలో వాయువుతో పాటు కొంచెం తేమ కూడా కలిసి ఉంటుంది. పొడి వాయువు పీడనాన్ని తెలుసుకోవడానికి, తడి వాయువు మొత్తం పీడనం నుండి నీటి బాష్పపీడనాన్ని తీసి వేయాలి. P_{పొడి వాయువు మొత్తం} = P_{మొత్తం} – నీటి ఆవిరి సంతృప్త బాష్పపీడనం.

V ఘనపరిమాణంగల పాత్రలో ఈ ఉష్ణోగ్రత వద్ద వాయువుల పాక్షిక పీడనాలు వరుసగా p₁, p₂, p₃ అయితే

n = మొత్తం మోత్ల సంఖ్య
∴ మొదటి వాయువు పాక్షిక పీడనం
p₁ = P_{మొత్తం} . x₁
p₂ = P_{మొత్తం} . x₂
p₃ = P_{మొత్తం} . x₃
x₁, x₂, x₃ లు వాయువుల మోల్ భాగాలు.
∴ పాక్షిక పీడనం = మొత్తం పీడనం × మోల్ భాగం
ఈ విధంగా మొత్తం పీడనం తెలిస్తే వ్యక్తిగత వాయువుల పాక్షిక పీడనాలను లెక్కకట్టవచ్చు.

ప్రశ్న 63.
వాయువుల అణుచలన సిద్ధాంతంలోని అంశాలను రాయండి. (March 2013)
జవాబు:
అణుచలన సిద్ధాంతంలోని ముఖ్యాంశాలు :

1. ప్రతి వాయువులోను అసంఖ్యాకమైన చిన్న చిన్న కణాలు ఉంటాయి. వీటిని అణువులు అంటారు.
2. వాయు అణువులు గట్టిగా, గోళాకారంగా ఉండి స్థితిస్థాపక ధర్మాన్ని కలిగి ఉంటాయి.
3. వాయు అణువులు అన్ని దిశలలో అధిక వేగాలతో ఋజు మార్గాలలో ప్రయాణిస్తూ ఉంటాయి. తత్ఫలితంగా అవి ఒక దానితో ఒకటి ఢీకొనడమే కాకుండా పాత్ర యొక్క గోడలతో కూడా ఢీ కొంటాయి. అందువలన అణువుల వేగాలు మరియు దిశా మార్గాలు నిరంతరం మారుతూ ఉంటాయి.
4. వాయు ఘనపరిమాణంతో పోలిస్తే వాయు అణువులు ఆక్రమించే ఘనపరిమాణం చాలా స్వల్పంగా ఉంటుంది.
5. వాయు అణువుల మధ్య ఆకర్షణ బలాలు గాని, వికర్షణ బలాలు గాని ఉండవు.
6. వాయు అణువులు ఒక దానితో ఒకటి ఢీ కొన్నప్పుడు గాని లేదా పాత్ర యొక్క గోడలతో ఢీకొన్నప్పుడు గాని గతిశక్తిలో మార్పు ఏమీ ఉండదు.
7. వాయు అణువులు పాత్ర గోడలతో ఢీ కొనడం వలన వాయువులకు పీడనం ఏర్పడుతుంది.
8. వాయు అణువు సగటు గతిశక్తి దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది. i.e. గతిశక్తి ∝ T.
9. వాయు అణువుల కదలికపై భూమ్యాకర్షణ బలాలు ఏవీ ఉండవు.

అణుచలన సిద్ధాంతం ఆధారంగా బాయిల్ సూత్రాన్ని వివరించుట : అణుచలన సిద్ధాంతం ప్రకారం, వాయు అణువులు పాత్ర గోడలతో ఢీ కొనడం వలన వాయువులకు పీడనం ఏర్పడుతుంది. స్థిర ఉష్ణోగ్రత వద్ద వాయు అణువులు పాత్ర యొక్క గోడలతో స్థిర సంఖ్యలో తాడనాలు చేస్తాయి. వాయు ఘనపరిమాణంను తగ్గిస్తే వాయు అణువులు ప్రయాణించవలసిన దూరం తగ్గిపోతుంది. తత్ఫలితంగా ప్రమాణ ఘనపరిమాణంపై వాయు అణువుల తాడనాలు పెరుగుతాయి. కాబట్టి వాయు పీడనం పెరుగుతుంది. అంటే స్థిర ఉష్ణోగ్రత వద్ద నియమిత ద్రవ్యరాశి గల వాయు ఘనపరిమాణం దాని పీడనానికి విలోమానుపాతంలో ఉంటుంది. ie V ∝ \(\frac{1}{p}\) (Tస్థిరం). ఇదే బాయిల్ నియమం. అణుచలన సిద్ధాంతం ఆధారంగా ఛార్లెస్ సూత్రాన్ని వివరించుట : అణుచలన సిద్ధాంతం ప్రకారం వాయు అణువుల సగటు గతిశక్తి దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది. i.e. KE ∝ T కాని KE = \(\frac{1}{2}\) mV².

∴ \(\frac{1}{2}\) mV² ∝ T లేక V² ∝ T లేక V ∝ T. దీనినిబట్టి ఉష్ణోగ్రత పెరిగితే వాయు అణువుల వేగం పెరుగుతుంది. తత్ఫలితంగా పాత్ర యొక్క గోడలపై వాయు అణువుల తాడనాలు పెరుగుతాయి. అప్పుడు వాయు పీడనం పెరుగుతుంది. కాని ఛార్లెస్ నియమానికి పీడనం స్థిరంగా ఉండాలి. ఉష్ణోగ్రత పెంచినా పీడనం స్థిరంగా ఉండాలంటే ఘనపరిమాణం పెరగాలి. మరొక విధంగా చెప్పాలంటే స్థిర పీడనం వద్ద నియమిత ద్రవ్యరాశి గల వాయు ఘనపరిమాణము దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది. i.e., V ∝ T (p స్థిరం). ఇదే ఛార్లెస్ నియమం.

ప్రశ్న 64.
చలద్వాయు సమీకరణం నుంచి వాయు నియమాలను రాబట్టండి.
జవాబు:
(a) బాయిల్ నియమం : అణుచలన సిద్ధాంతంలోని అంశాల ప్రకారం, వాయు అణువుల సగటు గతిజ శక్తి దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది.

“T” ను స్థిరం చేస్తే అప్పుడు
V = స్థిరరాశి × \(\frac{1}{P}\)
లేక V ∝ \(\frac{1}{P}\) (T స్థిరం)
స్థిర ఉష్ణోగ్రత వద్ద నియమిత ద్రవ్యరాశి గల వాయు ఘనపరిమాణం దాని పీడనానికి విలోమానుపాతంలో ఉంటుంది. ఇదే బాయిల్ నియమం.

(b) ఛార్లెస్ నియమం : అణుచలన సిద్ధాంతంలోని అంశాల ప్రకారం వాయు అణువుల సగటు శక్తి దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది.

‘P’ ను స్థిరం చేస్తే అప్పుడు V = స్థిరం × Tలేక V ∝ T (P స్థిరం)
స్థిర పీడనం వద్ద నియమిత ద్రవ్యరాశి గల వాయువు ఘనపరిమాణం దాని పరమ ఉష్ణోగ్రతకు అనులోమాను – పాతంలో ఉంటుంది. ఇదే ఛార్లెస్ నియమం.

c) డాల్టన్ పాక్షిక పీడనాల నియమం : V ఘనపరిమాణం గల ఒక పాత్రలో ఒక వాయువు ఒక్కొక్క అణువు భారం m₁. వాయువులోని n₁ అణువులు rms వేగం \(\mathrm{u}_{\mathrm{l}_{\mathrm{rms}}}\) కలిగి ఉందనుకొందాం. ఆ వాయువు పీడనం p₁ అనుకొంటే చలద్వాయు సమీకరణం ప్రకారం
P₁ V = \(\frac{1}{3} \mathrm{~m}_1 \mathrm{n}_1 \mathrm{u}_{1 \mathrm{rms}}^2\)
లేదా p₁ = \(\frac{1}{3} \frac{\mathrm{m}_1 \mathrm{n}_1 \mathrm{u}_{1 \mathrm{rms}}^2}{\mathrm{~V}}\)
పాత్రలోని వాయువును తొలగించి రెండో వాయువును తీసుకొంటే ఆ వాయువు ఘనపరిమాణం V, పీడనం p₂, ఒక్కో అణువు భారం m₂, అణువుల సంఖ్య n₂ అయితే

రెండు వాయువులను అదే పాత్రలో తీసుకొంటే వాయు మిశ్రమం కలిగించే పీడనాన్ని p_{మొత్తం} అనుకొంటే

p_{మొత్తం} = p₁ + p₂

d) గ్రాహం నియమం : ఒక వాయువుకు చల ద్వాయు సమీకరణం ప్రకారం p. V. = \(\frac{1}{3} \mathrm{mnu}_{\mathrm{rms}}^2\)
mn = వాయువు ద్రవ్యరాశి, వాయువులో అవొగాడ్రో సంఖ్య అణువులు ఉంటే mn = M (మోలార్ ద్రవ్యరాశి)

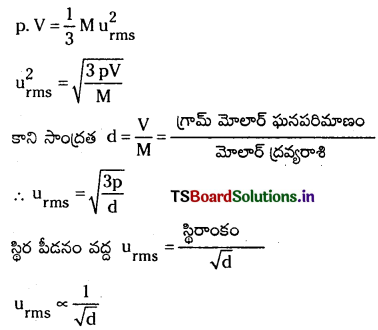
కాబట్టి వాయువు వ్యాపనం రేటు దాని సాంద్రత వర్గమూలానికి విలోమానుపాతంలో ఉంటుంది. ఇదే గ్రాహం నియమం.

ప్రశ్న 65.
మాక్స్వెల్ – బోల్డైమెన్ అణువేగాల పంపిణీ వక్రరేఖలను వివరించండి. ఈ రేఖల ఆధారంగా తెలిసిన అంశాలేమిటి? అణువేగాల పంపిణీపై ఉష్ణోగ్రత ప్రభావాన్ని చర్చించండి.
జవాబు:
అణుచలన సిద్ధాంతం ప్రకారం, వాయు అణువులు అన్ని దిశలలో క్రమ రాహిత్యంగా ప్రయాణిస్తూ ఉంటాయి. ఈ క్రమ రాహిత్య ప్రయాణ కాలంలో వాయు అణువులు ఒక దానితో ఒకటి ఢీకొనడమే కాకుండా పాత్ర యొక్క గోడలతో కూడా ఢీ కొంటాయి. తత్ఫలితంగా అణువులు వేగాలు నిరంతరం ఒక కనిష్ఠ విలువ నుండి (సున్నకు అతి దగ్గర విలువ) ఒక గరిష్ఠ విలువ వరకు మార్పు చెందుతూ ఉంటాయి. అసంఖ్యాక అణు తాడనాలతో సంబంధం లేకుండా ఒకానొక వేగ విలువ కలిగి ఉన్న అణువుల సంఖ్యకు మొత్తం అణువుల సంఖ్యకు గల నిష్పత్తి ఎల్లప్పుడూ స్థిరంగా ఉంటుంది. ఈ నిష్పత్తిని గణాంక పద్ధతుల ద్వారా నిర్ణయిస్తారు. మాక్స్వెల్ – బోల్టైమెన్ అణువేగాల పంపక రేఖలను క్రింది విధంగా సూచించినారు.

వక్రాల నుండి నిర్ణయాలు :

1. అతిస్వల్ప సంఖ్యలో అణువులు అత్యల్ప లేక అతి గరిష్ఠ వేగాలను కలిగి ఉంటాయి.
2. వక్రంలోని గరిష్ఠ బిందువు గరిష్ఠ సంభావ్యతా వేగాన్ని తెలియజేస్తుంది. గరిష్ఠ సంఖ్యలోని అణువులు కలిగి ఉండే వేగాన్ని గరిష్ఠ సంభావ్యతా వేగం అంటారు.
3. వాయు అణువుల సరాసరి వేగం, వాటి గరిష్ఠ సంభావ్యతా వేగం కన్నా ఎక్కువగా ఉంటుంది.
4. వాయు అణువుల RMS వేగం, వాటి గరిష్ఠ సంభావ్యతా వేగం మరియు సరాసరి వేగాల కన్నా ఎక్కువగా ఉంటుంది.
5. వాయు అణువుల వేగాలు పెరిగే కొలది, ఒకానొక ప్రత్యేక విలువ కలిగి ఉన్న అణువుల భాగం కూడా క్రమంగా పెరిగి గరిష్ఠ విలువను చేరుకుని ఆ తరువాత క్రమంగా తగ్గుతుంది.
6. ఉష్ణోగ్రత పెరిగే కొలది, వక్రం కుడివైపుకు జరగటమే కాకుండా వక్రం యొక్క ఎత్తు తగ్గి స్వల్పంగా సమతలంగా మారుతుంది. దీనినిబట్టి తెలిసేది ఏమనగా అధిక ఉష్ణోగ్రతల వద్ద అల్ప వేగాలు కలిగి ఉన్న అణువుల భాగం తగ్గి అధిక వేగాలు కలిగి ఉన్న అణువుల భాగం పెరుగుతుంది.

ప్రశ్న 66.
నిజ వాయువుల ప్రవర్తన, ఆదర్శ వాయు ప్రవర్తన నుంచి విచలనాన్ని వివరించండి.
జవాబు:
నిజవాయువుల ధర్మాలను తెలుసుకోవడానికి సంపీడన గుణకం చాలా అవసరం. దీనిని ‘Z’ తో సూచిస్తారు. దీని విలువను pV, nRT ల లబ్ధాల నిష్పత్తిగా సూచిస్తారు.
Z = \(\frac{\mathrm{pV}}{\mathrm{nRT}}\)
ఆదర్శ వాయువులకు pV = nRT కాబట్టి అన్ని ఉష్ణోగ్రత పీడనాలవద్ద ఆదర్శ వాయువులకు Z = 1 అవుతుంది. ఆదర్శ వాయువుల సంపీడన గుణకం Z, పీడనం p మధ్య గ్రాఫ్ పీడన అక్షానికి సమాంతరంగా సరళరేఖగా ఉంటుంది. అత్యల్ప పీడనాల వద్ద అన్ని వాయువులు 2 = 1 విలువ కలిగి ఉండి ఆదర్శ వాయువు వలె ప్రదర్శిస్తాయి.

అధిక పీడనాల వద్ద వాయువులు Z > 1 విలువను కలిగి ఉంటాయి. మధ్యస్థ పీడనాల వద్ద చాలా వాయువులు Z < 1 విలువను కలిగి ఉంటాయి.
కాబట్టి వాయువు ఆక్రమించే ఘనపరిమాణం ఎక్కువగా ఉండి, దానితో పోలిస్తే వాయు అణువులు ఆక్రమించే ఘ॥ప విస్మరించదగినదిగా ఉన్నపుడు వాయువులు ఆదర్శ ప్రవర్తనను కలిగి ఉంటాయి.

వాయువు ఆదర్శ వాయువు అయితే

ప్రశ్న 67.
వాండర్ వాల్స్ స్థితి సమీకరణాన్ని ఉత్పాదించండి. వాండర్ వాల్స్ సమీకరణం ప్రాముఖ్యతను వివరించండి.
జవాబు:
నిజవాయువులు అన్ని పరిస్థితులలోను బాయిల్ నియమం, ఛార్లెస్ నియమం, అవొగాడ్రో నియమాలను కచ్చితంగా పాటించవని ప్రయోగాల ద్వారా తెలిసింది.
దీనికి కారణం వాయువుల అణుచలన సిద్ధాంతంలోని రెండు లోప భూయిష్ఠమయిన ప్రతిపాదనలు.
a) వాయు అణువుల మధ్య ఎటువంటి ఆకర్షణ బలం ఉండదు.
b) వాయు అణువుల ఘనపరిమాణం, అవి ఆక్రమించే ఘనపరిమాణంతో పోలిస్తే విస్మరించదగినంత తక్కువగా ఉంటుంది.
ప్రతిపాదన (a) సరియైనదైతే, వాయువు ద్రవీకృతంకాదు. వాయువులను సంపీడ్యం చెందించి, చల్లబరిస్తే వాయువులు ద్రవీకరణం చెందుతాయి. అధిక పీడనాల వద్ద అణువులు చాలా దగ్గరగా వుండి అణువుల మధ్య అన్యోన్య చర్యలు మొదలవుతాయి. అందువల్ల వాయు అణువులు పాత్ర గోడలపై అనుకున్న దాని కంటే తక్కువ వేగంతో తాడనాలు కలుగచేస్తాయి. దీనికి కారణం వాయువులోని ఇతర అణువులు పాత్ర గోడలపై తాడనాలు చేసే అణువులను అంతర ఆకర్షణ బలాల వల్ల వెనక్కు లాగుతాయి. అందుచేత నిజవాయువులు కలుగచేసే పీడనం, ఆదర్శ వాయువులు కలుగచేసే పీడనం కంటే తక్కువగా ఉంటుంది.
p_{‘ఆదర్శ} = p_నిజ + \(\frac{\mathrm{an}^2}{\mathrm{~V}^2}\)
‘a’ వాండర్ వాల్ స్థిరాంకం.

ఘనపరిమాణానికి సవరణ : ప్రతిపాదన (b) సరియైనదైతే p – V గ్రాఫ్ నిజవాయువులకు ప్రయోగ పూర్వకంగా పొందినది, సిద్ధాంతపరంగా బాయిల్ నియమం ప్రకారం ఆదర్శవాయువుకు గణించినవి ఏకీభవించాలి. కాని అట్లా జరుగుట లేదు. వాయు అణువుల మధ్య ఉండే వికర్షణ బలాలు అణువులు సన్నిహితంగా ఉన్నపుడు ప్రాముఖ్యత కలిగి ఉంటాయి. అధిక పీడనాల వద్ద వాయు అణువుల మధ్య వికర్షణ బలాలను అల్ప వ్యాపక అంతర చర్య అంటారు. అది అణువులు చాలా దగ్గరగా ఉన్నపుడు మాత్రమే తగినంత ఉంటుంది. ఈ వికర్షణ బలాలు అణువులను చిన్న చిన్న చొచ్చుకుపోలేని గోళాలుగా ఉంచుతాయి. వాయు అణువులు ఆక్రమించే ఘనపరిమాణం కూడా ప్రాముఖ్యతను సంతరించుకుంటుంది. వాయు అణువులు V ఘనపరిమాణానికి బదులు (V – nb) అనే తక్కువ ఘనపరిమాణం గల ప్రదేశంలో చలించడానికి పరిమితమై ఉంటాయి. ఇక్కడ nb వాయు అణువుల మొత్తం ఘనపరిమాణాన్ని సూచిస్తుంది. ‘b’ స్థిరాంకం.

ఈ సవరణలతో ఆదర్శవాయు సమీకరణాన్ని కింది విధముగా వ్రాయవచ్చు.
(p + \(\frac{a n^2}{v^2}\))(V – nb) = nRT
ఈ సమీకరణాన్ని వాండర్ వాల్ సమీకరణం అంటారు. ‘n’ మోల్ల సంఖ్య. a, b లు వాండర్ వాల్ స్థిరాంకాలు. ‘a’ విలువ వాయు అణువుల మధ్య ఉండే అంతర అణు ఆకర్షణ బలాల పరిమాణాన్ని తెలుపుతుంది.
వాయు అణువుల మధ్య అంతర అణు ఆకర్షణ బలాలు దాదాపు శూన్యమయ్యే ఉష్ణోగ్రత పీడన పరిస్థితులలో నిజవాయువులు ఆదర్శ ప్రవర్తనను ప్రదర్శిస్తాయి.
వాండర్ వాల్ సమీకరణం ద్వారా నిజ వాయువుల ధన, ఋణ విచలనాలను వివరించవచ్చు.

ప్రశ్న 68.
వాయువుల ద్రవీకరణలో ఇమిడి ఉన్న సూత్రాన్ని వివరించండి.
జవాబు:
వాయువులను ద్రవీకరించాలంటే వాటి సందిగ్ధ ఉష్ణోగ్రత కంటే తక్కువ ఉష్ణోగ్రతకు చల్లబరచాలి. ఒక వాయువు ద్రవీకరణం చెందే గరిష్ఠ ఉష్ణోగ్రత దాని సందిగ్ధ ఉష్ణోగ్రత. శాశ్వత వాయువులను ద్రవీకరించాలంటే, వాటిని తగినంతగా సంపీడనం చెందించాలి. అంతేకాక చల్లబరచాలి. సంపీడనం చెందించినపుడు వాయు అణువులు సన్నిహితంగా వస్తాయి. చల్లబరిచినపుడు వాయు అణువుల కదలికలు తగ్గిపోయి అంతర అణు ఆకర్షణ బలాలు పెరిగి, అణువులు సన్నిహితంగా వచ్చి వాయువు ద్రవీకరించబడుతుంది.

30.98°C ఉష్ణోగ్రత వద్ద 73 అట్మా పీడనం వరకు CO₂ వాయువుగానే ఉంటుంది. 73 అట్మా పీడనం వద్ద ద్రవ CO₂ కనిపిస్తుంది. 30.98°C ఉష్ణోగ్రతను CO₂ సందిగ్ధ ఉష్ణోగ్రత T_C అంటారు.

ఏ ఉష్ణోగ్రత కన్నా అధిక ఉష్ణోగ్రత వద్ద అధిక పీడనాన్ని ఉపయోగించినప్పటికి వాయువును ద్రవీకరింప చేయలేమో ఆ ఉష్ణోగ్రతను సందిగ్ధ ఉష్ణోగ్రత అంటారు. (T_C) సందిగ్ధ ఉష్ణోగ్రత గది ఉష్ణోగ్రత కన్నా ఎక్కుగా ఉన్న వాయువులను సులభంగా ద్రవీకరించవచ్చు.

ప్రశ్న 69.
ద్రవాల క్రింది ధర్మాలను వివరించండి.
a) బాష్ప పీడనం
b) తలతన్యత
c) స్నిగ్ధత
జవాబు:
a) బాష్ప పీడనం : ద్రవం ఉపరితలంపై దాని బాష్పం కలుగచేసే పీడనాన్ని బాష్పపీడనం అంటారు. ఈ బాష్పం కలుగ చేసే పీడనం పెరిగి కొంత సేపటికి ఇచ్చిన ఉష్ణోగ్రత వద్ద బాష్పపీడనం స్థిరవిలువకు చేరి ద్రవానికి, బాష్పానికి మధ్య సమతాస్థితి ఏర్పడుతుంది. ఈ స్థితిలో స్థిరంగా ఉన్న బాష్పపీడనాన్ని సమతా బాష్పపీడనం లేదా సంతృప్త బాష్పపీడనం అంటారు.

ఒక ప్రత్యేకమైన ఉష్ణోగ్రత వద్ద బాష్పపీడనం, బాహ్యపీడనానికి సమానమవుతుంది. ఈ ఉష్ణోగ్రత వద్ద బాష్పీకరణం కేవలం ద్రవం ఉపరితలం నుంచే కాక, ద్రవం అంతర్భాగం నుండి జరిగి, బాష్పం పరిసరాల్లోకి వ్యాకోచం చెందుతుంది. ఈ విధంగా ద్రవం అంతా బాష్పీకరణం చెందడాన్ని బాష్పీభవనం అంటారు. ఏ ఉష్ణోగ్రత వద్ద ద్రవం బాష్పపీడనం బాహ్యపీడనానికి సమానం అవుతుందో ఆ ఉష్ణోగ్రతను ఆ పీడనం వద్ద ద్రవం బాష్పీభవన ఉష్ణోగ్రత అంటారు. ద్రవాల బాష్పీభవన స్థానం బాహ్యపీడనంలో మార్పువల్ల మారుతుంది.

b) తలతన్యత : ద్రవంలోని అణువును ఒకదాన్ని తీసుకొంటే దానిపై అన్ని వైపుల నుండి సమానంగా అంతర అణుబాలాలు పనిచేస్తాయి. కాబట్టి ఆ అణువుపై పనిచేసే నికర బలం ఏమీ ఉండదు. కాని ద్రవ ఉపరితలంపై ఉన్న అణువుపై పనిచేసే నికర బలం ద్రవ అణువును లోపలి వైపుకు లాగుతుంది. ద్రవాలు సాధ్యమైనంత తక్కువ ఉపరితల వైశాల్యం కలిగి ఉండేటట్లు ప్రయత్నిస్తాయి. దీనివల్ల ఉపరితలం మీద అణువులు ఎక్కువ శక్తితో ఉంటాయి. ద్రవం లోపలి భాగం నుంచి ఒక అణువును ద్రవ ఉపరితలానికి తీసుకువచ్చి ఉపరితలాన్ని పెంచాలనుకుంటే, ఆకర్షణ బలాలను అధిగమించవలసి వస్తుంది. దీనికి శక్తి కావాలి.

ద్రవం ఉపరితల వైశాల్యాన్ని ఒక యూనిట్ పెంచడానికి అవసరమయ్యే శక్తిని ఉపరితల శక్తి అంటారు. దీని ప్రమాణాలు Jm^-2. ద్రవం ఉపరితలంపై గీసిన రేఖకు లంబదిశలో ఏకాంక పొడవుపై పనిచేసే బలాన్ని తల- తన్యత అంటారు. తలతన్యత ప్రమాణాలు Kgs^-2 లేదా SI ప్రమాణాల్లో Nm^-1

ద్రవానికి ఉపరితల వైశాల్యం ఎంత తక్కువగా ఉంటే శక్తి అంత తక్కువగా ఉంటుంది. గోళాకార ఆకృతి ఈ ధర్మానికి అనుగుణంగా ఉంటుంది. అందువల్లే పాదరస బిందువులు గోళాకారంగా ఉంటాయి. అదే విధంగా వర్షపునీటి బిందువులు గోళాకార ఆకృతిని సంతరించుకొంటాయి. ఉష్ణోగ్రత పెరుగుదలతో బాటు ద్రవాల తలతన్యత తగ్గుతుంది.

c) స్నిగ్ధత : ఒక ద్రవం ప్రవహిస్తున్నపుడు ద్రవపు పొరలు ఒక దాని నుంచి ఇంకొకటి ముందుకు కదలడానికి ప్రయత్నిస్తాయి. ద్రవ ప్రవాహంలో పొరల మధ్య ఘర్షణ లేదా రాపిడివల్ల ద్రవప్రవాహాన్ని నిరోధించే కొలతనే స్నిగ్ధత అంటారు.
ఒక స్థిర ఘన ఉపరితలంపై ఒక ద్రవం ప్రవహిస్తున్నప్పుడు, ఉపరితలంపై ఉండే ద్రవపు పొరలోని అణువులు కదలిక లేక స్థిరంగా ఉంటాయి. తర్వాతి పొరలోని అణువులు కొద్దిగా కదులుతాయి. ఘన ఉపరితలం నుండి ఒక ద్రవపు పొర ఎంత దూరంగా ఉంటే, ఆ పొరలోని అణువులు అంత వేగంగా కదులుతాయి. ఈ విధంగా ఒక్కొక్క పొరలోని అణువులు వేరువేరు వేగాలతో ప్రయాణిస్తూ, ఒక క్రమ పద్ధతిలో వేగాల్లో భేదాలున్న ఈ పొరల ప్రవాహాన్ని దళ ప్రవాహం అంటారు. ప్రవహించే ద్రవంలో ఒక పొరను తీసుకొంటే దానిపైన ఉండే పొర మనం అనుకున్న పొర ప్రవాహాన్ని త్వరణం చెందిస్తే, దాని కింది పొర ప్రవాహ త్వరణాన్ని తగ్గిస్తుంది.

dz దూరంలో ఉన్న పొర వేగంలో మార్పు du అనుకుంటే ఆపొర వేగ ప్రవీణత \(\frac{d u}{d z}\) అవుతుంది. ద్రవపు పొరల ప్రవాహాన్ని నడపడానికి బలం కావాలి. ఈ బలం పొరల స్పర్శా వైశాల్యానికి పొర వేగ ప్రవీణతకు అనులోమానుపాతంలో ఉంటుంది.
F ∝ A. \(\frac{\mathrm{du}}{\mathrm{dz}}\)
⇒ F = η A \(\frac{d u}{d z}\)

η అనుపాత స్థిరాంకం. దీనిని స్నిగ్ధతా గుణకం అంటారు. ఏకాంక స్పర్శా వైశాల్యం, ఏకాంక వేగ ప్రవీణత గల ద్రవ ప్రవాహపు పొరపై పని చేసే బలాన్ని స్నిగ్ధతా గుణకం అంటారు.
SI ప్రమాణాలు NSm^-2 లేదా పాస్కల్ సెకండ్ PaS η కు CGS ప్రమాణాలు పాయిస్.
ద్రవాల స్నిగ్ధత, ఉష్ణోగ్రతలో పెరుగుదలతో బాటు తగ్గుతుంది. దీనికి కారణం అధిక ఉష్ణోగ్రతల వద్ద ద్రవ అణువుల గతిజ శక్తి పెరిగి, అంతర అణుబలాలను అధిగమించి అణువులు ఒక పొర నుండి మరొక పొరలోకి తేలికగా జారిపోతుంటాయి.

లెక్కలు

ప్రశ్న 4.1.
30°C వద్ద 500 dm³ ఘనపరిమాణం 1 bar పీడనం గల గాలిని 200 dm³ ఘనపరిమాణానికి సంపీడనం చెందించడానికి కావలసిన కనిష్ఠ పీడనం ఎంత ?
సాధన:
నియమిత ఉష్ణోగ్రత నియమిత ద్రవ్యరాశి గల వాయువుకు బాయిల్ నియమం ప్రకారం
p₁V₁ = p₂V₂
V₁ = 500 dm³ V₂ = 200 dm³
p₁ = 1 బార్ p₂ = ?
1 × 500 = p₂ × 200
P₂ = \(\frac{500}{200}\) = 2.5 బార్

ప్రశ్న 4.2.
35°C 1.2 బార్ పీడనం వద్ద 120 mL ఘనపరిమాణం గల పాత్రలో కొంత వాయువు ఉన్నది. ఈ వాయువును 180 mL ఘనపరిమాణంగల పాత్రలోనికి మార్చినప్పుడు దాని పీడనం ఎంత ఉంటుంది ?
సాధన:
బాయిల్ నియమం ప్రకారం స్థిర ఉష్ణోగ్రత వద్ద
p₁V₁ = p₂V₂
p₁ = 1.2 బార్ ; p₂ = ?
V₁ = 120 mL V₂ = 180 mL
1.2 × 120 = p₂ × 180
p₂ = \(\frac{1.2 \times 120}{180}\) = \(\frac{1.2 \times 2}{3}\) = \(\frac{2.4}{3}\) = 0.8 బార్

ప్రశ్న 4.3.
pV = nRT స్థితి సమీకరణాన్ని ఉపయోగించి, ఇచ్చిన ఉష్ణోగ్రత వద్ద ఒక వాయువు సాంద్రత దాని పీడనానికి అనులోమానుపాతంలో ఉంటుందని చూపండి.
సాధన:
pV = nRT
\(\frac{\mathrm{n}}{\mathrm{V}}\) = \(\frac{\mathrm{p}}{\mathrm{RT}}\)
కాని n = \(\frac{\mathrm{m}}{\mathrm{M}}\)
∴ \(\frac{\mathrm{m}}{\mathrm{MV}}\) = \(\frac{\mathrm{m}}{\mathrm{MV}}\)
కాని \(\frac{\mathrm{m}}{\mathrm{V}}\) = d సాంద్రత
∴ \(\frac{\mathrm{d}}{\mathrm{M}}\) = \(\frac{\mathrm{p}}{\mathrm{RT}}\)
d = \(\frac{\mathrm{pM}}{\mathrm{RT}}\)
స్థిర ఉష్ణోగ్రత వద్ద \(\frac{\mathrm{M}}{\mathrm{RT}}\) స్థిరాంకం
d = స్థిరాంకం × p
∴ d ∝ p

ప్రశ్న 4.4.
0°C వద్ద 2 బార్ పీడనం వద్ద ఒక వాయువు ఆక్సైడ్ సాంద్రత, 5 బార్ పీడనం వద్ద డై నైట్రోజన్ సాంద్రతకు సమానమవుతుంది. ఆక్సైడ్ మోలార్ ద్రవ్యరాశి ఎంత ?
సాధన:
N₂ సాంద్రత

ప్రశ్న 4.5.
27°C వద్ద 1 గ్రామ్ ఆదర్శ వాయువు A 2 బార్ పీడనం కలిగి ఉన్నది. అదే ఉష్ణోగ్రత వద్ద అదే పాత్రలోనికి 2g మరొక ఆదర్శవాయువు B ను పంపినపుడు పీడనం 3 బార్కు పెరిగింది. A, B వాయువుల మోలార్ ద్రవ్యరాశుల మధ్య సంబంధాన్ని కనుక్కోండి.
సాధన:
V = పాత్ర ఘనపరిమాణం
A ద్రవ్యరాశి = 1 గ్రా
సాంద్రత = \(\frac{1}{\mathrm{~V}}\) gm/Lit
B ద్రవ్యరాశి = 2 గ్రా.
సాంద్రత = \(\frac{2}{V}\)gm/Lit
మోలార్ ద్రవ్యరాశి M = \(\frac{\mathrm{dRT}}{\mathrm{P}}\)
వాయువులు ఒకే ఉష్ణోగ్రత వద్ద ఉన్నవి.
A యొక్క పాక్షిక పీడనం = 2 బార్
A యొక్క మోలార్ ద్రవ్యరాశి M
B యొక్క పాక్షిక పీడనం = 3 – 2 = 1 బార్
A యొక్క మోలార్ ద్రవ్యరాశి M_A = \(\frac{1}{\mathrm{~V}} \cdot \frac{\mathrm{RT}}{2}\) = \(\frac{\mathrm{RT}}{2 \mathrm{~V}}\)
B యొక్క మోలార్ ద్రవ్యరాశి M_B = \(\frac{2}{\mathrm{~V}} \cdot \frac{\mathrm{RT}}{1}\) = \(\frac{2 \mathrm{RT}}{\mathrm{V}}\)

ప్రశ్న 4.6.
డ్రైనేజ్లను శుభ్రపరిచే డ్రైనెక్స్ కొద్ది పాళ్లలో అల్యూమినియం కలిగి ఉండి కాస్టిక్ సోడాతో చర్య నొంది డైహైడ్రోజన్ ను ఇస్తుంది. 20°C 1 బార్ పీడనం వద్ద 0.15గ్రా అల్యూమినియం చర్యనొందిన, ఎంత ఘనపరిమాణం గల డైహైడ్రోజన్ విడుదలవుతుంది ?
సాధన:
రసాయన చర్య :

54 gల Al విడుదల చేసే హైడ్రోజన్ = 3 mol
0.15 ge Al విడుదలచేసే హైడ్రోజన్ = \(\frac{3 \times 0.15}{54}\) = 8.33 × 10^-3 mol.
8.33 × 10^-3 mol. మోల్ ల హైడ్రోజన్ ఘనపరిమాణం 20°C వద్ద 1 బార్ పీడనం వద్ద లెక్కించుట.
pV = nRT

ప్రశ్న 4.7.
27°C వద్ద 9 dm³ పాత్రలో 3.2 గ్రా మిథేన్, 4.4 గ్రా కార్బన్ డైఆక్సైడ్ కలిగి ఉన్న వాయు మిశ్రమం కలిగించే పీడనం ఎంత?
సాధన:
మిథేన్ మోల్ సంఖ్య = \(\frac{\mathrm{W}}{\mathrm{M}}\) = \(\frac{3.2}{16}\) = 0.2
CO₂ మోల్ల సంఖ్య = \(\frac{4.4}{44}\) = 0.1
మొత్తం మోల్ల సంఖ్య = 0.2 + 0.1 = 0.3
మిశ్రమం పీడనం p = \(\frac{n R T}{V}\) = \(\frac{0.3 \times 0.083 \times 300}{9}\)
p = 0.83 బార్
0.83 బార్ = 0.83 × 1.013 × 10⁵ = 8.31 × 10⁴ Pa

ప్రశ్న 4.8.
27°C వద్ద 1L పాత్రలోనికి 0.8 బార్ పీడనం కలిగిన 0.5 L డైహైడ్రోజన్, 0.7 బార్ కలిగిన 2.0 L డైఆక్సిజన్ పంపినపుడు ఆ వాయు మిశ్రమం కలిగించే పీడనం ఎంత ?
సాధన:
1లీ పాత్రలోనికి పంపిన తరువాత హైడ్రోజన్ పీడనం :
p₁V₁ = p₂V₂
0.8 × 0.5 = p₂ × 1
P₂ = 0.4 బార్
ఆక్సిజన్ పీడనం
p₁V₁ = p₂V₂
0.7 × 2 = p₂ × 1
మొత్తం పీడనం = పాక్షిక పీడనాల మొత్తం 0.4 + 1.4 = 1.8 బార్

ప్రశ్న 4.9.
27°C, 2 బార్ పీడనం వద్ద ఒక వాయువు సాంద్రత 5.46 g/dm³ ఉంటే, STP వద్ద దాని సాంద్రత ఎంత ?
సాధన:
M = \(\frac{\mathrm{dRT}}{\mathrm{p}}\) అని మనకు తెలియును
ఒకే వాయువుకు \(\frac{\mathrm{d}_1 \mathrm{~T}_1}{\mathrm{p}_1}\) = \(\frac{\mathrm{d}_2 \mathrm{~T}_2}{\mathrm{p}_2}\) అని వ్రాయవచ్చు
d₁ = 5.46 g / dm³ d₂ = ?
T₁ = 300 k T₂ = 273 K
P₁ = 2 బార్ P₂ = 1 బార్
\(\frac{\mathrm{d}_1 \mathrm{~T}_1}{\mathrm{p}_1}\) = \(\frac{\mathrm{d}_2 \mathrm{~T}_2}{\mathrm{p}_2}\)
d₂ = \(\frac{\mathrm{d}_1 \mathrm{~T}_1 \mathrm{p}_2}{\mathrm{p}_1 \mathrm{~T}_2}\)
d₂ = \(\frac{5.46 \times 300 \times 1}{2 \times 273}\)
= 2.998 = 3.0 g dm g^-3

ప్రశ్న 4.10.
546°C, 0.1 బార్ పీడనం వద్ద 34.05 mL ఫాస్ఫరస్ బాష్పం భారం 0.0625 g ఉంటే, ఫాస్ఫరస్ మోలార్ ద్రవ్యరాశి ఎంత ?
సాధన:
pV = nRT
ఫాస్ఫరస్ బాష్పం మోల్ల సంఖ్య n = \(\frac{\mathrm{pV}}{\mathrm{RT}}\)

ఫాస్ఫరస్ మోలార్ ద్రవ్యరాశి M g mol^-1
మోల్ల సంఖ్య = \(\frac{0.0625}{\mathrm{M}}\)
కాని m = \(\frac{0.0625}{\mathrm{M}}\) = 5 × 10^-4
∴ m = \(\frac{0.0625}{5 \times 10^{-4}}\) = 125 g mol^-1

ప్రశ్న 4.11.
27°C వద్ద ప్రయోగం చేసేటప్పుడు ఒక విద్యార్థి పాత్రలో చర్యా మిశ్రమాన్ని తీసుకోవడం మర్చిపోయి, పాత్రను వేడి చేస్తున్నాడు. కొంత సమయానికి తప్పు తెలుసుకొని పాత్ర ఉష్ణోగ్రతను పైరో మీటర్ ద్వారా చూస్తే, ఉష్ణోగ్రత 477 °C ఉన్నది. ఎంత భాగం గాలి బయటకు పోయిందో లెక్కకట్టండి.
సాధన:
పాత్ర ఘనపరిమాణం V ml.
T₁ = 27 + 273 = 300K
T₂ = 477 + 273 = 750 K
ఛార్లెస్ నియమం ప్రకారం
\(\frac{\mathrm{V}_1}{\mathrm{~T}_1}\) = \(\frac{V_2}{T_2}\)
V₂ = \(\frac{\mathrm{V}_1 \mathrm{~T}_2}{\mathrm{~T}_1}\) = \(\frac{\mathrm{V} \times 750}{300}\) = 2.5V
750K వద్ద బయటకు పోయిన గాలి = 2.5 V – V = 1.5 V
బయటకు పోయిన గాలి భాగం = \(\frac{1.5 \mathrm{~V}}{2.5 \mathrm{~V}}\) = \(\frac{3}{5}\) = 0.6

ప్రశ్న 4.12.
3.32 బార్ పీడనం వద్ద 4.0 మోల్ల వాయువు 5dm³ ఘనపరిమాణం ఆక్రమించిన, ఆ వాయువు ఉష్ణోగ్రతను లెక్కకట్టండి. (R = 0.083 బార్ dm³ K^-1 mol^-1).
సాధన:
pV = nRT
T = \(\frac{p V}{n R}\)
p = 3.32 బార్ V = 5 dm³
n = 4.0 R = 0.083
ఈ విలువలను ప్రతిక్షేపిస్తే

ప్రశ్న 4.13.
1.4g డైనైట్రోజన్ వాయువులో ఉన్న మొత్తం ఎలక్ట్రాన్ల సంఖ్యను లెక్క కట్టండి.
సాధన:
ప్రతి N₂ అణువులోను 14 ఎలక్ట్రానులుంటాయి.
నైట్రోజన్ అణువుల సంఖ్య = \(\frac{1.4}{28}\) × 6.023 × 10²³
ఎలక్ట్రానుల సంఖ్య = \(\frac{1.4}{28}\) × 6.023 × 10²³ × 14 = 4.215 × 10²³

ప్రశ్న 4.14.
ప్రతి సెకనుకు 10¹⁰ ధాన్యపు గింజలను పంచుకుంటూ పోతే అవొగాడ్రో సంఖ్య ధాన్యపు గింజలను పంచటానికి గింజలను పంచటానికి ఎంత కాలం పడుతుంది ?
సాధన:
10¹⁰ ధాన్యపు గింజలను పంచడానికి కాలం = 1 సె.
6.023 × 10²³ ధాన్యపు గింజలను పంచడానికి కాలం = ?
= \(\frac{6.0^{23} \times 10^{23}}{10^{10}}\) = 6.023 × 10¹³ సెకన్లు
= 1.909 × 10⁶ సంవత్సరాలు.

ప్రశ్న 4.15.
ఒక సన్నని రంధ్రం గుండా అమ్మోనియా వాయువు వ్యాపనం రేటు 0.5 lit min^-1. అదే పరిస్థితులలో క్లోరిన్ వాయువు వ్యాపనం రేటు ఎంత ?
సాధన:
రెండు వాయువుల వ్యాపన రేట్లు r₁, r₂, అణుభారాలు వరుసగా M₁, M₂ అయితే

ప్రశ్న 4.16.
CO₂, Cl₂ వాయువుల సాపేక్ష వ్యాపనం రేట్లు కనుక్కోండి.
సాధన:

ప్రశ్న 4.17.
150 mL కార్బన్ మోనాక్సైడ్ నిస్సరణం చెందడానికి 25 సె॥కాలం పడితే అదే కాలంలో ఎంత ఘనపరిమాణం గల మిథేన్ వాయువు నిస్సరణం చెందుతుంది ?
సాధన:


25 సె॥ వ్యాపనం చెందిన మిథేన్ 198.5 mL.

ప్రశ్న 4.18.
ఒక 100 మీటర్ల గొట్టంలోకి ‘A’ వైపు నుంచి హైడ్రోజన్ క్లోరైడ్, ‘B’ వైపు నుంచి అమ్మోనియా వాయువును ఒకే పరిస్థితులలో పంపితే, ‘A’ నుంచి ఎంత దూరంలో రెండు వాయువులు కలుసుకొంటాయి ?
సాధన:
హైడ్రోజన్ క్లోరైడ్ ప్రయాణించిన దూరం = x
అమ్మోనియా ప్రయాణించిన దూరం = 100 – x
ప్రయాణించే దూరం వ్యాపన రేటుకు అనులోమానుపాతంలో ఉంటుంది.

దీనిని సాధించగా x = 40.48 మీటరు. A వైపు నుండి 40.48 మీటర్ల దూరంలో రెండు వాయువులు కలుసుకుంటాయి.

ప్రశ్న 4.19.
27°C వద్ద 1 dm³ పాత్రలో ఉన్న 8గ్రా. డైఆక్సిజన్, 4గ్రా. డైహైడ్రోజన్ వాయువుల మిశ్రమం కలిగించే పీడనాన్ని లెక్కించండి. [R = 0.083 బార్ dm³ K^-1 mol^-1]
సాధన:
హైడ్రోజన్ మోత్ల సంఖ్య = \(\frac{4}{2}\) = 2.0 మోల్
ఆక్సిజన్ మోల్ సంఖ్య = \(\frac{8}{16}\) = 0.5 మోల్
మొత్తం మోల్ల సంఖ్య = 2.0 + 0.5 = 2.5 మోల్
pV = nRT

ప్రశ్న 4.20.
27°C వద్ద 5dm³ పాత్రలో ఉన్న 3.5గ్రా.డైనైట్రోజన్, 3.0గ్రా. డైహైడ్రోజన్, 8.0 గ్రా డైఆక్సిజన్ వాయువుల మిశ్రమం కలిగించే మొత్తం పీడనాన్ని కనుక్కోండి. (R = 0.083 బార్dm³K^-1mol^-1)
సాధన:
నైట్రోజన్ మోల్ ల సంఖ్య = \(\frac{3.5}{28}\) = 0.125
హైడ్రోజన్ మోల్ ల సంఖ్య = \(\frac{3.0}{2}\) = 1.5
ఆక్సిజన్ మోల్ల సంఖ్య = \(\frac{8.0}{32}\) = 0.25
మొత్తం మోత్ల సంఖ్య = 0.125 + 1.5 + 0.25 = 1.875
ఆదర్శవాయు సమీకరణం pV = nRT
p = \(\frac{\mathrm{nRT}}{\mathrm{V}}\) = \(\frac{1.875 \mathrm{~mol} \times 0.083 \times 300 \mathrm{k}}{5 \mathrm{dm}^3}\)
p = 9.33 బార్

ప్రశ్న 4.21.
స్థాన భ్రంశం చెందిన గాలి ద్రవ్యరాశి, బెలూన్ ద్రవ్యరాశుల మధ్య బేధాన్ని పేలోడ్ గా వ్యవహరిస్తారు. 27°C, 11.6 బార్ పీడనం వద్ద 10 మీ వ్యాసార్ధం, 100 kg ద్రవ్యరాశి గల, బెలూను హీలియం వాయువుతో నింపినప్పుడు ఒక బెలూన్ పేలోడ్ను లెక్కించండి. (గాలి సాంద్రత 1.2 kgm^-3, R = 0.083 బార్ dm³‘K^-1‘mol^-1).
సాధన:
బెలూన్ ఘనపరిమాణం = \(\frac{4}{3} \pi r^3\) = \(\frac{4}{3}\)π(10)³ = 4190.47 m³
స్థానభ్రంశం చెందే గాలి భారం = సాంద్రత × ఘనపరిమాణం

హీలియం భారం = 279364.6 × 4g = 1117.45 kg
బెలూన్ పే లోడ్ = గాలి భారం – He భారం – బెలూన్ భారం
= 5028.5 – 1117.45 100 = 3811.1 kg
= 279364.6 mol.

ప్రశ్న 4.22.
31.1°C, 1 బార్ పీడనం వద్ద 8.8 g CO₂ వాయువు ఆక్రమించే ఘనపరిమాణాన్ని లెక్కించండి. (R = 0.083 బార్ LK^-1mol^-1).
సాధన:
CO₂ మోల్ల సంఖ్య = \(\frac{8.8}{44}\) = 0.2
R = 0.083 బార్ Lk^-1mol^-1
T = 273 + 31.1 = 304.1 K
P = 1 బార్

ప్రశ్న 4.23.
95°C వద్ద 2.9 g ద్రవ్యరాశిగల ఒక వాయువు ఆక్రమించే ఘనపరిమాణం, అదే పీడనం వద్ద 17°C వద్ద 0. 184 g డైహైడ్రోజన్ ఆక్రమించే ఘనపరిమాణానికి సమానం. అయితే వాయువు మోలార్ ద్రవ్యరాశి ఎంత ?
సాధన:
వాయువు మోల్ ల సంఖ్య = \(\frac{2.9}{\mathrm{~m}}\)
p₁V₁ = nRT₁
p₁ V₁ = \(\frac{2.9}{\mathrm{~m}}\) . R . (95 + 273)
p₁ V₁ = \(\frac{2.9}{\mathrm{~m}}\) . R . 368
హైడ్రోజన్కు
హైడ్రోజన్ మోత్ల సంఖ్య = \(\frac{0.184}{2}\)
P₂ V₂ = \(\frac{0.184}{2}\).R.(17 + 273)
P₂ V₂ = \(\frac{0.184}{2}\).R.(290)
వాయువు పీడన, ఘనపరిమాణాలు సమానం.
p₁V₁ = p₂ V₂

ప్రశ్న 4.24.
1 బార్ పీడనం వద్ద డైహైడ్రోజన్, ఆక్సిజన్ వాయువుల మిశ్రమంలో డైహైడ్రోజన్ భారశాతం 20% అయినా, డైహైడ్రోజన్ పాక్షిక పీడనాన్ని లెక్కించండి.
సాధన:
మొత్తం భారం = 1గ్రా. అనుకొనుము.
హైడ్రోజన్ భారం = 0.2 గ్రా.
మోల్ల సంఖ్య = \(\frac{0.2}{2}\) = 0.1
ఆక్సిజన్ మోల్ల సంఖ్య = \(\frac{0.8}{32}\) = 0.025
హైడ్రోజన్ మోల్ భాగం = \(\frac{0.1}{0.125}\) = 0.8
హైడ్రోజన్ పాక్షిక పీడనం = మొత్తం పీడనం × H₂ మోల్భాగం
= 1 బార్ × 0.8 = 0.8 బార్

ప్రశ్న 4.25.
pV²T²/n విలువకు SI ప్రమాణం ఏమిటి ?
సాధన:
pV = nRT
p = \(\frac{\mathrm{nRT}}{\mathrm{V}}\)
\(\frac{p V^2 \mathrm{~T}^2}{\mathrm{n}}\) = \(\frac{\mathrm{nRT}}{\mathrm{V}}\) . V² . T² = RT³V
S.I. ప్రమాణాలు జౌల్. K^-1 mol^-1 . K³. m³ = జౌల్ . m³. K² mol^-1.

ప్రశ్న 4.26.
ఛార్లెస్ నియమం ప్రకారం – 273°C ను అత్యల్ప ఉష్ణోగ్రతగా ఎందుకు భావిస్తారో వివరించండి.
సాధన:
ఇవ్వబడిన పీడనం వద్ద వాయువుల ఘనపరిమాణ ఉష్ణోగ్రత రేఖలు సరళరేఖలుగా ఉండి, వాటిని పొడిగించినపుడు ఉష్ణోగ్రత అక్షాన్ని -273. 15°C వద్ద ఖండిస్తాయి. శూన్య ఘనపరిమాణం వద్ద అన్ని రేఖలు -273.15°C వద్ద కలుస్తాయి. -273.15°C ఉష్ణోగ్రత వద్ద వాయువుల ఘనపరిమాణం శూన్యమవుతుంది. అంటే వాయువుల ఉనికి లేకుండా పోతుంది. నిజానికి ఈ ఉష్ణోగ్రతకు రాకముందే అన్ని వాయువులు ద్రవాలుగా మారతాయి. వాయువులు శూన్య ఘనపరిమాణం కలిగి ఉండే కనిష్ఠ ఉష్ణోగ్రత – 273.15°C. ఈ ఉష్ణోగ్రతను పరమ శూన్య ఉష్ణోగ్రతగా భావిస్తారు. ఇదే కనిష్ఠ ఉష్ణోగ్రత.

ప్రశ్న 4.27.
కార్బన్ డై ఆక్సైడ్, మీథేన్ల సందిగ్ధ ఉష్ణోగ్రతలు వరుసగా 31.1°C, – 81.9°C అయినా, వీటిలో ఏ వాయువులో బలమైన అంతర అణు ఆకర్షణ బలాలుంటాయి ?
సాధన:
వాయువు సందిగ్ధ ఉష్ణోగ్రత ఎక్కువగా ఉంటే అంతర అణుబలాలు బలంగా ఉంటాయి. అటువంటి వాటిని సులభంగా ద్రవీకరణం చెందించవచ్చు.
CO₂ సందిగ్ధ ఉష్ణోగ్రత (31.1°C) మిథేన్ సందిగ్ధ ఉష్ణోగ్రత కన్నా ఎక్కువ. అందువల్ల CO₂ లో అంతర అణు ఆకర్షణ బలాలు బలంగా వుంటాయి.

ప్రశ్న 4.28.
గాలిని 25°C నుండి 0°C కు చల్లబరిచిన, అణువుల rms వేగంలో కలిగే తగ్గుదలను లెక్కించండి.
సాధన:

ప్రశ్న 4.29.
27°C వద్ద SO₂ వాయువు RMS వేగం, సగటు వేగం, గరిష్ఠ సంభావ్యతా వేగాలను కనుక్కోండి.
సాధన:
T = 27 + 273 = 300 K
R = 8.314 J mol^-1 K^-1
M = SO₂ ద్రవ్యరాశి = 64g/mol^-1
RMS వేగం u_rms = \(\sqrt{\frac{3 R T}{M}}\)
1 Joule = kg m² s^-2

= 3.42 × 10² ms^-1
సగటు వేగం
u_av = 0.9213 × u_rms
= 3.42 × 10² × 0.9213
= 3.15 × 10² ms^-1
గరిష్ఠ సంభావ్యతా వేగం = u_mp
u_mp = 0.8166 × u_rms
= 0.8166 × 3.42 × 10² = 2.79 × 10² ms^-1

ప్రశ్న 4.30.
27°C వద్ద O₂ RMS, సగటు, గరిష్ఠ సంభావ్యతా వేగాలను కనుక్కోండి.
సాధన:
T = 27 + 273 = 300K
R = 8.314 JK^-1 mol^-1
M = O₂ ద్రవ్యరాశి = 32 g/mol
1 Joule = Kg m²s^-2

u_rms = 4.614 × 10² ms^-1
సగటు వేగం = 0.9213 × 4.614 × 10² = 4.25 × 10² ms^-1
గరిష్ఠ సంభావ్యతా వేగం = 0.8166 × 4.614 × 10^{2/sup> = 3.77 × 102 m.s-1}

అదనపు లెక్కలు ప్రశ్నలు

ప్రశ్న 4.31.
27°C వద్ద CO₂ వాయువు RMS, సగటు గరిష్ట సంభావ్యతా వేగాలను కనుక్కోండి.
సాధన:
T = 27 + 273 = 300K
R = 8.314 J mol^-1 K^-1
M = CO₂ ద్రవ్యరాశి = 44g mol^-1
1J = kg m² s^-2

సగటు వేగం u_av = 0.9213 × RMS వేగం
= 0.9213 × 4.12 × 10² ms^-1 = 3.8 × 10² ms^-1
గరిష్ఠ సంభావ్యతా వేగం
u_mp = 0.8166 × 4.12 × 10² ms^-1 = 3.36 × 10² ms^-1

ప్రశ్న 4.32.
27°C వద్ద 5 మోల్ల నైట్రోజన్ వాయువు గతిజశక్తిని కనుక్కోండి. (March 2013)
సాధన:
గతిజశక్తి = \(\frac{3}{2}\)nRT
n = 5 moles, R = 8.314 J mol^-1K^-1
T = 27 + 273 = 300K
గతిజశక్తి = \(\frac{3}{2}\) × 5 mol × 8.314 J mol^-1K^-1 × 300 K = 18,706.5 J

ప్రశ్న 4.33.
-73°C వద్ద 4g మిథేన్ గతిజశక్తిని కనుక్కోండి.
సాధన:
n = మిథేన్ మోల్ల సంఖ్య = \(\frac{4 g}{16 g \mathrm{mn}^{-1}}\) = 0.25 mol
R = 8.314 J mol^-1 K^-1
T = -73°C + 273 = 200K
గతిజశక్తి E_k = \(\frac{3}{2}\) nRT
= \(\frac{3}{2}\) × 0.25 mol × 8.314 J mol^-1 K^-1 × 200K = 623.6 J

ప్రశ్న 4.34.
ఒకే ఉష్ణోగ్రత వద్ద 3g H₂, 4g O₂ వాయువుల గతిజశక్తి నిష్పత్తిని లెక్కకట్టండి.
సాధన:
హైడ్రోజన్ మోల్ల సంఖ్య = \(\frac{3}{2}\)
ఆక్సిజన్ మోల్ల సంఖ్య = \(\frac{4}{32}\) = \(\frac{1}{8}\)
రెండు వాయువులు ఒకే ఉష్ణోగ్రత వద్ద ఉన్నందున గతిజ శక్తుల నిష్పత్తి మోల్ సంఖ్యల నిష్పత్తికి సమానం.
H₂ మోల్ : O₂ మోల్ = \(\frac{3}{2}\) : \(\frac{1}{8}\) = 12 : 1

ప్రశ్న 4.35.
ఒక బెలూన్ గది ఉష్ణోగ్రత వద్ద హైడ్రోజన్ వాయువుతో నింపారు. పీడనం 0.2 బార్ కంటే ఎక్కువయితే బెలూన్ పగిలిపోతుంది. 1 బార్ పీడనం వద్ద వాయువు ఆక్రమించే ఘనపరిమాణం 2.27L అయితే ఎంత ఘనపరిమాణం వరకు బెలూను వ్యాకోచింప చేయవచ్చు ?
సాధన:
బాయిల్ నియమం ప్రకారం p₁V₁ = p₂V₂
p₁ = 1 బార్ అయితే V₁ = 2.27 L
p₂ = 0.2 బార్ అయితే V₂ = \(\frac{p_1 V_1}{p_2}\)
⇒

0.2 బార్ పీడనం వద్ద బెలూన్ పగిలిపోతుంది. కాబట్టి బెలూన్ ఘనపరిమాణం 11.35 కంటే తక్కువ ఉంచాలి.

ప్రశ్న 4.36.
23.4°C వద్ద పసిఫిక్ మహాసముద్రంలో ప్రయాణిస్తున్న ఓడలో 2L గాలితో నింపిన బెలూన్ ఉంది. ఆ ఓడ 26.1°C ఉష్ణోగ్రత వద్ద ఉన్న హిందూ మహాసముద్రం చేరుకున్నపుడు బెలూన్ ఘనపరిమాణం ఎంత ఉంటుంది ?
సాధన:
V₁ = 2L T₂ = 26.1 + 273 = 299.1 K
T₁ = 23.4 + 273 = 296.4 K
ఛార్లెస్ నియమం ప్రకారం
\(\frac{\mathrm{V}_1}{\mathrm{~T}_1}\) = \(\frac{\mathrm{V}_2}{\mathrm{~T}_2}\)
⇒ V₂ = \(\frac{\mathrm{V}_1 \mathrm{~T}_2}{\mathrm{~T}}\) = \(\frac{2 \mathrm{~L} \times 299 \mathrm{~K}}{296.4 \mathrm{~K}}\) = 2L × 1.009 = 2.018 L

ప్రశ్న 4.37.
25°C, 760 mm పాదరస పీడనం వద్ద ఒక వాయువు 600 మి.లీ. ఘనపరిమాణం ఆక్రమిస్తుంది. ఉష్ణోగ్రత 10°C వద్ద దాని ఘనపరిమాణం 640 మి.లీ. ఉంటే, ఆ వాయువు పీడనం ఎంత ?
సాధన:
p₁ = 760 mm V₁ = 600 mL
T₁ = 25 + 273 = 298
V₂ = 640 mL T₂ = 10 + 273 = 283 K
సంయుక్త వాయు నియమం ప్రకారం

ప్రశ్న 4.38.
360 cm³ మిథేన్ వాయువు 15ని॥ ఒక సచ్ఛిద్ర పాత్ర నుండి వ్యాపనం చెందింది. అదే పరిస్థితుల్లో 120 cm³ ఒక వాయువు 10 ని॥ వ్యాపనం చెందినట్లయితే ఆ వాయువు మోలార్ ద్రవ్యరాశి కనుక్కోండి.
సాధన:
మీథేన్ వాయువు వ్యాపన రేటు

మిథేన్ మోలార్ ద్రవ్యరాశి = 16 g mol^-1
రెండో వాయువు వ్యాపన రేటు :

వాయువు మోలార్ ద్రవ్యరాశి M₂ = ?
గ్రాహం వాయు వ్యాపన నియమం ప్రకారం

ఇరువైపులా వర్గం చేయగా
M₂ = \(\frac{24 \times 24 \times 16}{12 \times 12}\) = 64
వాయువు మోలార్ ద్రవ్యరాశి = 64 g mol^-1

ప్రశ్న 4.39.
కార్బన్ డైఆక్సైడ్, మరొక వాయువు ‘X’ ల వ్యాపన రేట్లు వరుసగా 0.290 ccs^-1, 0.271 ccs^-1 అయితే ‘X’ వాయువు బాష్పసాంద్రత కనుక్కోండి. CO₂ బాష్ప సాంద్రత 22.
సాధన:

ప్రశ్న 4.40.
70.6గ్రా. డైఆక్సిజన్, 167.5 గ్రా. నియాన్ వాయువులు గల వాయు మిశ్రమం కలుగచేసే పీడనం 25 బార్. అయితే డైఆక్సిజన్, నియాన్ వాయువుల పీడనాలను కనుక్కోండి.
సాధన:
డైఆక్సిజన్ (O₂) మోల్ల సంఖ్య = \(\frac{70.6 \mathrm{~g}}{32 \mathrm{~g} \mathrm{~mol}^{-1}}\) = నియాన్ (Ne) మోత్ల సంఖ్య = \(\frac{167.5 \mathrm{~g}}{20 \mathrm{~g} \mathrm{~mol}^{-1}}\) = 8.375 mol
డైఆక్సిజన్ మోల్ భాగం = \(\frac{2.21}{2.21+8.375}\) = \(\frac{2.21}{10.585}\) = 0.21
నియాన్ మోల్ భాగం = \(\frac{8.375}{10.585}\) = 0.79
పాక్షిక పీడనం = మోల్ భాగం × వాయు మిశ్రమం మొత్తం పీడనం
ఆక్సిజన్ పాక్షిక పీడనం = 0.21 × 25 = 5.25 బార్
నియాన్ పాక్షిక పీడనం = 0.79 × 25 = 19.75 బార్

ప్రశ్న 4.41.
ఐసోకోర్లు అంటే ఏమిటి ? అవి ఏ విధంగా వుంటాయి ?
సాధన:
స్థిర మోలార్ ఘనపరిమాణంగల వాయువు పీడన – ఉష్ణోగ్రత రేఖలను ‘ఐసోకోర్లు’ అంటారు.

ఈ రేఖా పటంలో V₁ < V₂ < V₃

ప్రశ్న 4.42.
సంయుక్త వాయు నియమాన్ని వ్రాయండి.
సాధన:
నియమిత ద్రవ్యరాశిగల ఒక వాయువు తొలి పీడనం ఘనపరిమాణం, పరమ ఉష్ణోగ్రతలు p₁, T₁, V₁ అయితే తుది పీడనం, ఘనపరిమాణం, పరమ ఉష్ణోగ్రతలు p₂, V₂, T₂ అయితే
⇒ \(\frac{\mathrm{p}_1 \mathrm{~V}_1}{\mathrm{~T}_1}\) = \(\frac{\mathrm{p}_2 \mathrm{~V}_2}{\mathrm{~T}_2}\)
ఈ సమీకరణంలోని ఆరు చక్రాంకాలలో ఏ ఐదు తెలిసినా ఆరోదాని విలువను గణించవచ్చు.
ఈ సమీకరణాన్ని సంయుక్త సమీకరణం అంటారు.

ప్రశ్న 4.43.
అణువేగాలపై ఉష్ణోగ్రతా ప్రభావం ఏమిటి ?
సాధన:
అణువేగాల పంపిణీ – ఉష్ణోగ్రతల వద్ద అణువుల సంఖ్యకు, అణువులవేగాలకు మధ్య గీసిన వక్రరేఖలు సూచించబడినాయి. ఈ వక్రరేఖల ద్వారా అత్యధికవేగం, అత్యల్పవేగం గల అణువుల సంఖ్య అత్యల్పమని తెలుస్తుంది. ఉష్ణోగ్రత పెరిగే కొద్దీ వక్రరేఖ వెడల్పు పెరుగుతుంది. అంటే అధిక ఉష్ణోగ్రతల వద్ద ఎక్కువ వేగాలు ఉన్న అణువుల సంఖ్య పెరుగుతుంది. అధిక ఉష్ణోగ్రత వద్ద వాయువుకు గల అన్నివేగాలూ పెరుగుతాయి. ఉష్ణోగ్రత పెంచితే గరిష్ఠ సంభావ్యతా వేగం, RMS వేగం, మరియు సరాసరి వేగాలు పెరుగుతాయి.

ప్రశ్న 4.44.
అమ్మోనియా, కార్బన్ డైఆక్సైడ్, వాయువుల సందిగ్ధ ఉష్ణోగ్రతలు వరుసగా 405.5K, 304.1K, 500K నుండి సందిగ్ధ ఉష్ణోగ్రతకు చల్లబరిచినపుడు వీటిలో ఏ వాయువు ముందుగా ద్రవీకరించబడుతుంది ?
సాధన:
అమ్మోనియా వాయువు ముందుగా ద్రవీకరించబడుతుంది. దీనికి కారణం దాని సందిగ్ధ ఉష్ణోగ్రత ముందుగా వస్తుంది.
CO₂ ద్రవీకరణకు అధిక చల్లదనం అవసరం.

ప్రశ్న 4.45.
బాయిల్ నియమాన్ని రేఖా పటం ద్వారా ఎలా చూపుతారు ?
సాధన:
బాయిల్ నియామాన్ని p – V సమోష్ణోగ్రతా రేఖల ద్వారా చూపవచ్చు. స్థిర ఉష్ణోగ్రత వద్ద p – V వక్రరేఖలు క్రింద చూపిన విధంగా వుంటాయి.

P, \(\frac{1}{V}\) గ్రాఫులు సరళరేఖలు. అధిక పీడనాల వద్ద వాయువులు బాయిల్ నియమాన్ని పాటించవు. కాబట్టి అధిక పీడనాల వద్ద P, \(\frac{1}{V}\) ల మధ్య గ్రాఫ్ సరళరేఖగా ఉండదు.

ప్రశ్న 4.46.
స్థిర ఉష్ణోగ్రత వద్ద వాయు పీడనానికి, సాంద్రతకుగల సంబంధాన్ని తెలపండి.
సాధన:
బాయిల్ నియమం ప్రకారం p = k. \(\frac{1}{v}\)
కాని వాయు సాంద్రత d = \(\frac{m}{v}\)
లేదా \(\frac{1}{v}\) = \(\frac{d}{m}\)
∴ p = k. \(\frac{d}{m}\) [\(\frac{k}{m}\) స్థిరాంకం]
∴ p ∝ d
స్థిర ఉష్ణోగ్రత వద్ద నియమిత ద్రవ్యరాశిగల వాయువు పీడనం దాని సాంద్రతకు అనులోమానుపాతంలో ఉంటుంది.

ప్రశ్న 4.47.
వేసవి కాలంలో టైర్లలోని గాలిపీడనం అనూహ్యంగా పెరిగి, టైరు పగిలి పోతుంది. ఎందువల్ల ?
సాధన:
గేలూసాక్ నియమం ప్రకారం స్థిర ఘనపరిమాణం వద్ద నియమిత ద్రవ్యరాశిగల వాయువు పీడనం పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది.
p ∝ T
⇒ \(\frac{\mathrm{p}}{\mathrm{T}}\) = స్థిరాంకం
వేసవి కాలంలో ఉష్ణోగ్రత పెరగడంవల్ల టైర్లలోని గాలి పీడనం పెరిగి టైరు పగిలి పోతుంది.

Students must practice these TS Intermediate Maths 1B Solutions Chapter 5 Three Dimensional Coordinates Ex 5(b) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Three Dimensional Coordinates 5(b)

I.
Question 1.
Find the ratio in which the XZ – plane divides the line joining A (-2, 3, 4) and B(l, 2, 3). (V.S.A.Q.)
Answer:
Ratio in which XZ – plane divides the AB
= – y₁ : y₂
= – 3 : 2

Question 2.
Find the coordinates of the vertex C of ∆ABC if its centroid is the origin and the vertices A, B are (1, 1, 1) and (-2, 4, 1) respectively. (V.S.A.Q.)
Answer:
Given A (1,1,1) and B (-2, 4, 1) as two vertices of a ∆ABC and suppose C (x, y, z) is the third vertex. Given O(0, 0, 0) is the centroid.
Then 0 = \(\frac{x+1-2}{3}\) ⇒ x – 1 = 0 ⇒ x = 1
o = \(\frac{y+1+4}{3}\) ⇒ y = -5
0 = \(\frac{z+1+1}{3}\) ⇒ z = -2
∴ Coordinates of third vertex C = (1, – 5, – 2)

Question 3.
If (3, 2, -1), (4, 1, 1) and (6, 2, 5) are the three vertices and (4, 2, 2) is the centroid of a tetrahedron, find the fourth vertex. (V.S.A.Q.) (May 2011, 2005)
Answer:
Let A (3, 2, -1), B (4, 1, 1), C (6, 2, 5) and D (x, y, z) be the coordinates of vertices of a tetrahedron.
Given G = (4, 2, 2) is the centroid. Then

∴ Coordinates of fourth vertex D = (3, 3, 3)

Question 4.
Find the distance between the mid point of the line segment \(\overline{\mathrm{AB}}\) and the point (3, -1, 2) where A (6,3, -4) and B (-2, -1,2). (V.S.A.Q.)
Answer:
Mid point of the line AB where A (6, 3, -4) and B (-2, -1, 2) is
P = \(\left(\frac{6-2}{2}, \frac{3-1}{2}, \frac{-4+2}{2}\right)\)
= (2, 1,-1)
Suppose Q (3, -1, 2) then
PQ = \(\sqrt{(3-2)^2+(-1-1)^2+(2+1)^2}\)
= \(\sqrt{1+4+9}\) = √14 units.

II.
Question 1.
Show that the points (5, 4, 2), (6, 2, -1) and (8, -2, -7) are collinear. (V.S.A.Q.)
Answer:
Let A (5,4, 2), B (6, 2, -1) and C (8, -2, -7) be the given points.

Since AB + BC = AC, the points A, B,.C are collinear.

Question 2.
Show that the points A (3, 2, -4), B( 5, 4, -6) and C (9, 8, -10) are collinear and find the ratio in which B divides \(\overline{\mathbf{A C}}\). (S.A.Q.)
Answer:
Given A (3, 2, -4), B (5, 4, -6), C (9, 8, -10) and

Since AB + BC = 2√3 + 4√3 = 6√3 = AC
We have the points A, B, C are collinear.
The ratio in which B divides AC is
AB : BC = 2√3 : 4√3 = 2 : 4 = 1 : 2

III.
Question 1.
If A (4, 8, 12), B (2, 4, 6), C (3, 5, 4) and D (5, 8, 5) are four points. Show that the lines \(\overleftrightarrow{\mathbf{A B}}\) and \(\overleftrightarrow{\mathbf{CD}}\) intersect. (E.Q.)
Answer:
Given A (4, 8, 12), B (2, 4, 6), C (3, 5, 4) and D (5, 8, 5) are the given points.
Coordinates of the points dividing AB in the ratio λ : 1 is
= \(\left(\frac{2 \lambda+4}{\lambda+1}, \frac{4 \lambda+8}{\lambda+1}, \frac{6 \lambda+12}{\lambda+1}\right)\) …………………….. (1)
Coordinates of the point dividing CD in the ratio μ : 1 is
= \(\left(\frac{5 \mu+3}{\mu+1}, \frac{8 \mu+5}{\mu+1}, \frac{5 \mu+4}{\mu+1}\right)\) …………………….. (2)
If the given lines intersect then these two points are same
∴ \(\frac{2 \lambda+4}{\lambda+1}=\frac{5 \mu+3}{\mu+1}\) …………………….. (3)
⇒ (2λ + 4) (μ + 1) = (5μ + 3) (λ + 1)
⇒ 2λμ + 4μ + 2λ + 4 = 5λμ + 3λ + 5μ + 3
⇒ 3λμ + λ + μ – 1 = 0
⇒ λ = – (3μ + 1) = – (μ – 1)
⇒ λ = – \(\left(\frac{\mu-1}{3 \mu+1}\right)\) ………………….. (4)
Also \(\frac{4 \lambda+8}{\lambda+1}=\frac{8 \mu+5}{\mu+1}\)
⇒ (4λ + 8) (μ + 1) = (8μ + 5) (λ + 1)
⇒ 4λμ + 8μ + 4λ + 8 = 8λμ + 5λ + 8μ + 5
⇒ 4λμ + λ – 3 = 0
⇒ (4μ + 1)λ = 3
⇒ (4μ + 1)\(\left(\frac{-(\mu-1)}{3 \mu+1}\right)\) = 3 (∵ from (4))
⇒ 4μ² – 4μ + μ – 1 = – 9μ – 3
⇒ 4μ² + 6μ + 2 = 0
⇒ 2μ² + 3μ + 1 = 0
⇒ (2μ + 1) (μ + 1) = 0
⇒ μ = – \(\frac{1}{2}\) (or) μ = – 1
μ = – 1 is not admissible
∴ μ = – \(\frac{1}{2}\)
Hence from (2)

Since the two points coincide, the given lines intersect.

Question 2.
Find the point of intersection of the lines \(\overleftrightarrow{\mathbf{A B}}\) and \(\overleftrightarrow{\mathbf{C D}}\) where
A = (7, -6, 1), B = (17, -18, -3)
C = (1, 4, -5) and D = (3, -4, 11) (E.Q.)
Answer:
Given A = (7, -6, 1), B = (17, -18, -3), C = (1, 4, -5) and D = (3, -4, 11)
Coordinates of the point dividing AB in the ratio λ : 1 are
= \(\left(\frac{17 \lambda+7}{\lambda+1}, \frac{-18 \lambda-6}{\lambda+1}, \frac{-3 \lambda+1}{\lambda+1}\right)\) …………………. (1)
Coordinates of the point dividing CD in the ratio μ : 1 are
= \(\left(\frac{3 \mu+1}{\mu+1}, \frac{-4 \mu+4}{\mu+1}, \frac{11 \mu-5}{\mu+1}\right)\) …………………. (2)
∴ \(\frac{17 \lambda+7}{\lambda+1}=\frac{3 \mu+1}{\mu+1}\)
⇒ (17λ + 4) (μ + 1) = (3μ + 1) (λ + 1)
⇒ 17λμ + 17λ + 7μ + 7 = 3λμ + 3μ + λ + 1
⇒ 14λμ + 16λ + 4μ + 6 = 0 …………………. (3)
Also \(\frac{-18 \lambda-6}{\lambda+1}=\frac{-4 \mu+4}{\mu+1}\)
⇒ – 18λμ – 6μ – 18λ – 6 = – 4λμ + 4λ – 4μ + 4
⇒ 14λμ + 22λ + 2μ + 10 = 0 ………………….. (4)
From (3) and (4)
– 6λ + 2μ – 4 = 0
⇒ 2μ = 6λ + 4 = 0
⇒ μ = 3λ + 2 ……………………… (5)
Substituting in (3) we get
⇒ 14λ (3λ + 2) + 16λ + 4(3λ + 2) + 6 = 0
⇒ 42λ² + 28λ + 16λ + 12λ + 8 + 6 = 0
⇒ 42λ² + 56λ + 14 = 0
⇒ 3λ² + 4λ + 1 = 0
⇒ (λ + 1) (3λ + 1) = 0
⇒ λ = – 1 or λ = – \(\frac{1}{3}\)
(λ = – 1 is not admissible)
∴ λ = – \(\frac{1}{3}\)

∴ These two points coincide
∴ The given lines \(\overleftrightarrow{\mathrm{AB}}\) and \(\overleftrightarrow{\mathrm{CD}}\) intersect
∴ Point of intersection = (2, 0, 3)

Question 3.
A (3, 2, 0), B(5, 3, 0, C (- 9, 6, – 3) are the vertices of a triangle. \(\overline{\mathbf{A D}}\), the bisector of ∠BAC meets \(\overline{\mathbf{B C}}\) at D. Find the coordinates of D. (E.Q.)
Answer:

Given A = (3, 2, 0), B = (5, 3, 2), C = (-9, 6, -3) are the vertices of ∆ABC

Question 4.
Show that the points O (0, 0, 0), A (2, -3, 3), B (-2, 3, -3) are collinear. Find the ratio in which each point divides the segment joining the other two. (S.A.Q.)
Answer:
Given points are O(0, 0, 0), A (2, -3, 3) B (-2, 3, -3)

Since OA + OB = AB, the points O, A, B are collinear. Ratio in which O divides AB =
OA : OB = √22 : √22 = 1 : 1
Ratio in which A divides OB
= OA : AB = -√22 : 2√22 = – 1 : 2
Ratio in which B divides OA = AB : BO
= – 2√22 : √22 = -2 : 1
∴ A and B divide externally.

Students must practice these TS Intermediate Maths 1B Solutions Chapter 5 Three Dimensional Coordinates Ex 5(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Three Dimensional Coordinates 5(a)

I.
Question 1.
Find the distance of P (3, -2, 4) from the origin. (V.S.A.Q.)
Answer:
OP = \(\sqrt{x^2+y^2+z^2}\)
= \(\sqrt{9+4+16}\) = √29 units

Question 2.
Find the distance of the points (3, 4, -2) and (1, 0, 7). (V.S.A.Q.)
Answer:
Let P = (3, 4, -2) and Q (1, 0, 7) then

II.
Question 1.
Find x if the distance between (5,-1,7) and (x, 5, 1) is 9 units. (V.S.A.Q.)
Answer:
Let P = (5, -1, 7) and Q (x, 5, 1)
and PQ = 9 ⇒ PQ² = 81
⇒ (x – 5)² + (5 + 1)² + (1 – 7)² = 81
⇒ x² – 10x + 25 + 36 + 36 = 81
⇒ x² – 10x + 25 = 9
⇒ (x – 5)² = 3²
⇒ x – 5 = ±3 ⇒ x = 2 or 8

Question 2.
Show that the points (2, 3, 5), (-1, 5, -1) and (4, -3, 2) form a right angled isosceles triangle. (V.S.A.Q.)
Answer:
Let A = (2, 3, 5), B = (-1, 5, -1) and C = (4, -3, 2) are the given points.
∴ AB² = (2 + 1)² + (3 – 5)² + (5 + 1)² = 9 + 4 + 36 = 49
BC² = (- 1 – 4)² + (5 + 3)² + (- 1 – 2)²
= 25 + 64 + 9 = 98
CA² = (4 – 2)² + (- 3 – 3)²+ (2 – 5)2²
= 4 + 36 + 9 = 49
∴ AB² = CA²
AB² + CA² = 49 + 49 = 98 = BC²
∆ABC is a right angled isosceles triangle.

Question 3.
Show that the points (1, 2, 3), (2, 3, 1) and (3, 1, 2) form an equilateral triangle. (V.S.A.Q.) (Board New Model Paper)
Answer:
Let A (1, 2, 3), B (2, 3, 1) and C (3, 1, 2) are the given points.
AB² = (1 – 2)² + (2 – 3)² + (3 – 1)² = 1 + 1 + 4 = 6
BC² = (2 – 3)² + (3 – 1)² + (1 – 2)² = 1 + 4 + 1 = 6
AC² = (1 – 3)² + (2 – 1)² + (3 – 2)² = 4 + 1 + 1 =6
∴ AB² = BC² = AC² ⇒ AB = BC = AC
∴ ABC is an equilateral triangle.

Question 4.
P is a variable point which moves such that 3PA = 2PB. If A (-2, 2, 3) and B (13, -3,13) prove that P satisfies the equation x² + y² + z² + 28x – 12y +10z – 247 = 0. (S.A.Q.)
Answer:
Given A (-2, 2, 3) and B (13, -3, 13) and suppose P = (x, y, z) then
3PA = 2PB ⇒ 9PA² = 4PB²
⇒ 9 [(x + 2)² + (y – 2)² + (z – 3)²]
= 4 [(x – 13)² + (y + 3)² + (z – 13)²]
⇒ 9 [x² + 4x + 4 + y² – 4y + 4 + z² – 6z + 9]
= 4 [x² – 26x +169 + y² + 6y + 9 + z² – 26z +169]
⇒ 9x² + 9y² + 9z² + 36x – 36y – 54z + 153
= 4x² + 4y² + 4z² – 104x + 24y – 104z + 1388
⇒ 5x² + 5y² + 5z² + 140x – 60y + 50z – 1235 = 0
⇒ x² + y² + z² + 28x – 12y + 10z – 247 = 0

Question 5.
Show that the points (1, 2, 3), (7, 0, 1) and (-2, 3, 4) are collinear. (V.S.A.Q.) (March 2007)
Answer:
Let A (1, 2, 3), B (7, 0, 1), C (-2, 3, 4) be the given points.

∴ BC = AB + AC
∴ A, B, C are collinear.

Question 6.
Show that ABCD is a square where A,B,C,D are the points (0, 4, 1), (2, 3, -1), (4, 5, 0) and (2, 6, 2) respectively. (S.A.Q.)
Answer:
Let A (0, 4, 1), B (2, 3, -1), C (4, 5, 0) and D (2, 6, 2) be the given points.
AB² = (0 – 2)² + (4 – 3)² + (1 + 1)² = 4 + 1 + 4 = 9
BC² = ( 2 – 4)² + (3 – 5)² + (- 1 – 0)² = 4 + 4 + 1 = 9
CD² = (4 – 2)² + (5 – 6)² + (0 – 2)² = 4 + 1 +4 = 9
AD² = (0 – 2)² + (4 – 6)² + (1 – 2)² = 4 + 4 + 1 = 9
∴ AB² = BC² = CD² = DA²
⇒ AB = BC = CD = DA
AC² = (0 – 4)² + (4 – 5)² + (1 – 0)² = 16 + 1 + 1 = 18
BD² = (2 – 2)² + (3 – 6)² + (- 1 – 2)² = 9 + 9= 18
∴ AC² = BD² ⇒ AC = BD
AB² + BC² = 9 + 9 = 18 = AC²
∴ ∠ABC = 90°
∴ ABCD is a square.

Here students can locate TS Inter 1st Year Accountancy Notes Chapter 9 Final Accounts of Sole Trading Concerns to prepare for their exam.

TS Inter 1st Year Accountancy Notes Chapter 9 Final Accounts of Sole Trading Concerns

→ To know the business results and financial position at the end of the period, the business prepares various statements which are called as final accounts.

→ Final accounts consist of two accounts and a balance sheet. The two accounts are

1. Trading account
2. Profit and Loss account

→ The expenses and incomes are three types :

1. Capital nature
2. Revenue nature
3. Deferred nature.

Revenue expenses and income appear in either trading account of profit and loss a/c. The capital nature appears in the balance sheet. The revenue part of the deferred part appears in Trading and Profit and Loss a/c, where he as the capital part of deferred nature expenditure and incomes appear in the Balance Sheet.

→ Trading account reveals either gross profit or gross loss. This is transferred to the profit and loss account.

→ Profit and loss account reveals either net profit or a net loss.

→ Balance Sheet is divided into two sides namely the assets side and the liabilities side. Assets are current assets, fixed assets, closing stock etc.

→ Liabilities are creditors, bank loans, bills payable, and net capital.

TS Inter 1st Year Accountancy Notes Chapter 9 సొంతవ్యాపార సంస్థల ముగింపు లెక్కలు

→ సంవత్సరాంతానికి వ్యాపార సంస్థ ఫలితాలు, ఆర్థిక పరిస్థితిని తెలుసుకోవడానికి తయారుచేసే నివేదికలను ముగింపు లెక్కలు అంటారు.

→ ముగింపు లెక్కలు రెండు ఖాతాలు మరియు ఆస్తి – అప్పుల పట్టీ సమూహము. ఆ రెండు ఖాతాలు

1. వర్తకపు ఖాతా
2. లాభనష్టాల ఖాతా

→ వ్యయాలను, ఆదాయాలను మూడు రకాలుగా విభజించవచ్చును.

1. మూలధన స్వభావము గలవి
2. రాబడి స్వభావము గలవి
3. విలంబిత స్వభావము గలవి

రాబడి వ్యయాలు, ఆదాయాలు, వర్తకపు లాభనష్టాల ఖాతాలలోను, మూలధన స్వభావము గలవి, ఆస్తి అప్పుల పట్టీలో చూపాలి. విలంబిత అంశాలు రాబడి స్వభావము గలవి, వర్తక లాభనష్టాల ఖాతాకు, మూలధన స్వభావము గల దానిని ఆస్తి – అప్పుల పట్టీలోను నమోదు చేయాలి.

→ వర్తకపు ఖాతా స్థూల లాభాన్ని లేదా స్థూల నష్టాన్ని సూచిస్తుంది. దీనిని లాభనష్టాల ఖాతాకు మళ్ళించాలి.

→ లాభనష్టాల ఖాతా నికర లాభము లేదా నికర నష్టమును తెలుపుతుంది.

→ ఆస్తి – అప్పుల పట్టీని రెండు భాగాలుగా విభజన చేసి అప్పులను ఎడమవైపు, ఆస్తులను కుడివైపు చూపాలి. ఆస్తులు, చరాస్తులు, స్థిరాస్తులు, ముగింపు సరుకు మొ||నవి. అప్పులు, ఋణదాతలు, బాంకు అప్పు, చెల్లింపు బిల్లులు మొ||నవి.

Here students can locate TS Inter 1st Year Accountancy Notes Chapter 8 Rectification of Errors to prepare for their exam.

TS Inter 1st Year Accountancy Notes Chapter 8 Rectification of Errors

→ దోషము అనగా తప్పు మరియు సవరణ అనగా జరిగిన తప్పును సరిచేయుట.

→ దోషాలను రెండు రకాలుగా విభజించవచ్చును.

• సిద్ధాంతపు దోషాలు
• రాతపూర్వక దోషాలు

→ రాతపూర్వక దోషాలు మరల దిగువ విధముగా వర్గీకరించవచ్చును.

• ఆకృత దోషాలు
• అకార్యాకరణ దోషాలు
• సరిపెట్టే దోషాలు

→ తప్పులను మరల రెండు రకాలుగా విభజించవచ్చును.

• అంకూ ద్వారా వెల్లడి అయ్యే తప్పులు
• అంకణా ద్వారా వెల్లడి కాని తప్పులు

→ అనామతు ఖాతా ఒక ఊహాజనిత ఖాతా మరియు తాత్కాలికమైనది. అంకజా సమానత్వము సాధించడానికి దీనిని తెరుస్తారు.

TS Inter 1st Year Accountancy Notes Chapter 8 తప్పుల సవరణ

→ An error is a mistake and rectification means correcting the mistake that has occured.

→ Errors are classified into two types.

1. Error of principle
2. Clerical errors.

→ Clerical errors are again classified into

• Error of omission
• Error of commission
• Compensating errors.

→ Errors are again classified as

1. Errors disclosed by trial balance
2. Errors not disclosed by trial balance.

→ Suspense account is an imaginary account opened temporarily for the purpose of tallying the trial balance.

Students must practice these Maths 1B Important Questions TS Inter 1st Year Maths 1B Differentiation Important Questions Long Answer Type to help strengthen their preparations for exams.

TS Inter 1st Year Maths 1B Differentiation Important Questions Long Answer Type

Question 1.
If y = \(\tan ^{-1}\left[\frac{\sqrt{1+x^2}+\sqrt{1-x^2}}{\sqrt{1+x^2}-\sqrt{1-x^2}}\right]\), then find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [Mar. ’18 (TS); Mar. ’16 (AP), ’12, ’10, ’09, ’04; May ’15 (AP & TS), ’12, ’97]
Solution:

Question 2.
If y = x^{tan x} + (sin x)^{cos x}, then find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [Mar. ’14, ’13 (Old), ’11, ’08, ’07; May ’13, ’06; Mar. ’18 (AP)]
Solution:
Given y = x^{tan x} + (sin x)^{cos x}
Differentiating on both sides with respect to ‘x’.
Let u = x^{tan x}
v = sin x^{cos x}
y = u + v
\(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{d}}{\mathrm{dx}}(\mathrm{u}+\mathrm{v})\)
\(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) ……(1)
Now, u = x^{tan x}
Taking logarithms on both sides,
log u = log x^{tan x}
log u = tan x log x
Differentiating on both sides with respect to ‘x’.

Now, v = (sin x)^{cos x}
Taking logarithms on both sides,
log v = log (sin x)^{cos x}
log v = cos x log(sin x)
Differentiating on both sides with respect to ‘x’.

Question 3.
If x = \(\frac{3 a t}{1+t^3}\), y = \(\frac{3 \mathrm{at}^2}{1+\mathrm{t}^3}\), then find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [B.P.]
Solution:
Given that x = \(\frac{3 a t}{1+t^3}\)
Differentiating on both sides with respect to ‘t’.

Question 4.
If \(\sqrt{1-x^2}+\sqrt{1-y^2}\) = a(x – y) then show that \(\frac{d y}{d x}=\sqrt{\frac{1-y^2}{1-x^2}}\). [Mar. ’17 (TS), ’08, ’05; May ’14, ’13 (Old), ’11, ’97]
Solution:
Given that \(\sqrt{1-x^2}+\sqrt{1-y^2}\) = a(x – y)
Put x = sin α ⇒ α = sin^-1x
y = sin β ⇒ β = sin^-1y
Now, \(\sqrt{1-\sin ^2 \alpha}+\sqrt{1-\sin ^2 \beta}\) = a(sin α – sin β)
\(\sqrt{\cos ^2 \alpha}+\sqrt{\cos ^2 \beta}\) = a(sin α – sin β)
cos α + cos β = a(sin α – sin β)

Question 5.
If y = \(\mathbf{x} \sqrt{\mathbf{a}^2+x^2}+a^2 \log \left(x+\sqrt{a^2+x^2}\right)\) then show that \(\frac{d y}{d x}=2 \sqrt{a^2+x^2}\). [Mar. ’19, ’15 (AP). ’09, ’02; May ’08]
Solution:
Given, that y = \(\mathbf{x} \sqrt{\mathbf{a}^2+x^2}+a^2 \log \left(x+\sqrt{a^2+x^2}\right)\)
Differentiating on both sides with respect to ‘x’.

Question 6.
If y = \(\tan ^{-1}\left(\frac{2 x}{1-x^2}\right)+\tan ^{-1}\left(\frac{3 x-x^3}{1-3 x^2}\right)\) – \(\tan ^{-1}\left(\frac{4 x-4 x^3}{1-6 x^2+x^4}\right)\) then show that \(\frac{\mathbf{d y}}{\mathbf{d x}}=\frac{1}{1+x^2}\). [May ’07]
Solution:
Given that

y = 2θ + 3θ – 4θ = θ
y = tan^-1x
Differentiating on both sides with respect to x.
\(\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{d}}{\mathrm{dx}} \tan ^{-1} \mathrm{x}\)
∴ \(\frac{d y}{d x}=\frac{1}{1+x^2}\)

Question 7.
If y = \(\frac{(1-2 x)^{2 / 3}(1+3 x)^{-3 / 4}}{(1-6 x)^{5 / 6}(1+7 x)^{-6 / 7}}\), then find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [May ’10]
Solution:

Question 8.
If y = (sin x)^{log x} + x^{sin x} then find \(\frac{\mathbf{d y}}{\mathbf{d x}}\). [Mar. ’17 (AP), ’15 (TS), ’13]
Solution:
Given that, let y = (sin x)^{log x} + x^{sin x}
Let, u = (sin x)^{log x} , v = x^{sin x} then y = u + v
Differentiating on both sides with respect to x.
\(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) …….(1)
Now, u = (sin x)^{log x}
Taking logarithms on both sides
log u = log (sin x)^{log x}
log u = log x . log (sin x)
Differentiating on both sides with respect to ‘x’.

Now, v = x^{sin x}
Taking logarithms on both sides
log v = log x^{sin x}
log v = sin x log x
Differentiating on both sides with respect to ‘x’.

Question 9.
If x^y + y^x = a^b then show that \(\frac{d y}{d x}=-\left[\frac{y x^{y-1}+y^x \log y}{x^y \log x+x y^{x-1}}\right]\). [Mar. ’03; Mar. ’16 (TS)]
Solution:
Given that, x^y + y^x = a^b
Let, x^y = u, y^x = v then, u + v = a^b
Differentiating on both sides with respect to x.
\(\frac{\mathrm{du}}{\mathrm{dx}}+\frac{\mathrm{dv}}{\mathrm{dx}}=0\) ……(1)
Now, u = x^y
Taking logarithms on both sides
log u = log x^y
log u = y log x
Differentiating on both sides with respect to ‘x’.

Now, v = y^x
Taking logarithms on both sides
log v = log y^x
log v = x log y
Differentiating on both sides with respect to ‘x’.

Question 10.
If f(x) = \(\sin ^{-1} \sqrt{\frac{x-\beta}{\alpha-\beta}}\) and g(x) = \(\tan ^{-1} \sqrt{\frac{x-\beta}{\alpha-x}}\) then show that f'(x) = g'(x), (β < x < α).
Solution:

Some More Maths 1B Differentiation Important Questions Long Answer Type

Question 11.
Find the derivative of 20^{log(tan x)}.
Solution:
Let y = 20^{log(tan x)}
Differentiating on both sides with respect to ‘x’.

Question 12.
If f(x) = e^2x log x (x > 0), then find f'(x).
Solution:
f(x) = e^2x (log x)
Let y = e^2x (log x)
Differentiating with respect to ‘x’ on both sides,

Question 13.
If y = \(\frac{\mathbf{a}-\mathbf{x}}{\mathbf{a}+\mathbf{x}}\), find \(\frac{\mathbf{d y}}{\mathbf{d x}}\).
Solution:
Given y = \(\frac{\mathbf{a}-\mathbf{x}}{\mathbf{a}+\mathbf{x}}\)
Differentiating with respect to x on both sides.

Question 14.
If y = sin^-1(cos x) then find \(\frac{d y}{d x}\).
Solution:
Let y = sin^-1(cos x)
Differentiating on both sides with respect to ‘x’.

Question 15.
If x⁴ + y⁴ – a²xy = 0, find \(\frac{\mathbf{d y}}{\mathbf{d x}}\).
Solution:
Given that x⁴ + y⁴ – a²xy = 0
Differentiating on both sides with respect to ‘x’.

Question 16.
Find the derivative of cos^-1(4x³ – 3x) with respect to ‘x’.
Solution:
Let y = cos^-1(4x³ – 3x)
Put x = cos θ
⇒ θ = cos^-1x
Now, y = cos^-1(4 cos³θ – 3 cos θ)
= cos^-1(cos 3θ)
= 3θ
y = 3 cos^-1x
Differentiating on both sides with respect to ‘x’.

Question 17.
Find the derivative of sec x from the first principle.
Solution:
Given, f(x) = sec x
Now, f(x + h) = sec (x + h)

Question 18.
Find the derivative of \(\sin ^{-1}\left(\frac{b+a \sin x}{a+b \sin x}\right)\).
Solution:
Let y = \(\sin ^{-1}\left(\frac{b+a \sin x}{a+b \sin x}\right)\)
Differentiating on both sides with respect to ‘x’.

Question 19.
Find the derivative of \(\tan ^{-1}\left(\frac{\cos x}{1+\cos x}\right)\)
Solution:
Let y = \(\tan ^{-1}\left(\frac{\cos x}{1+\cos x}\right)\)
Differentiating on both sides with respect to ‘x’.

Question 20.
Find the derivative of \(\tan ^{-1}\left(\frac{\sqrt{1+x^2}-1}{x}\right)\) with respect to tan^-1x. [May ’09]
Solution:

Question 21.
If f(x) = x e^x sin x, then find f'(x).
Solution:
f(x) = x . e^x . sin x
Let y = x . e^x . sin x
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{d}{d x}\) (x . e^x . sin x)
= x . e^x . \(\frac{d}{d x}\) (sin x) + x . sin x . \(\frac{d}{d x}\) (e^x) + sin x . e^x . \(\frac{d}{d x}\) (x)
= x . e^x . cos x + x . sin x . e^x + sin x . e^x (1)
= e^x (x cos x + x sin x + sin x)
∴ f'(x) = e^x (x cos x + x sin x + sin x)

Question 22.
If f(x) = sin(log x), (x > 0), then find f'(x). [Mar. ’18 (AP)]
Solution:
f(x) = sin(log x)
Let y = sin(log x)

Question 23.
If f(x) = (x³ + 6x² + 12x – 13)¹⁰⁰, then find f'(x).
Solution:
Given that, f(x) = (x³ + 6x² + 12x – 13)¹⁰⁰
Let y = (x³ + 6x² + 12x – 13)¹⁰⁰
Differentiating with respect to x on both sides.
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{d}{d x}\) (x³ + 6x² + 12x – 13)¹⁰⁰
= 100(x³ + 6x² + 12x – 13)^100-1 \(\frac{d}{d x}\)(x³ + 6x² + 12x – 13)
= 100(x³ + 6x² + 12x – 13)⁹⁹ (3x² + 6(2x) + 12(1) – 0)
= 100(x³ + 6x² + 12x – 13)⁹⁹ (3x² + 12x + 12)
= 100(x³ + 6x² + 12x – 13)⁹⁹ 3(x² + 4x + 4)
= 300(x + 2)² (x³ + 6x² + 12x – 13)⁹⁹
∴ f'(x) = 300(x + 2)² . (x³ + 6x² + 12x – 13)⁹⁹

Question 24.
Find the derivative of (ax + b)ⁿ (cx + d)^m.
Solution:
Given, f(x) = (ax + b)ⁿ (cx + d)^m
Let y = (ax + b)ⁿ (cx + d)^m
Differentiating with respect to ‘x’ on both sides.

Question 25.
Find the derivative of \(\frac{\mathbf{p} \mathbf{x}^2+\mathbf{q x}+\mathbf{r}}{\mathbf{a x}+\mathbf{b}}\).
Solution:
Given, f(x) = \(\frac{\mathbf{p} \mathbf{x}^2+\mathbf{q x}+\mathbf{r}}{\mathbf{a x}+\mathbf{b}}\)
Let y = \(\frac{\mathbf{p} \mathbf{x}^2+\mathbf{q x}+\mathbf{r}}{\mathbf{a x}+\mathbf{b}}\)
Differentiating with respect to ‘x’ on both sides.

Question 26.
Find the derivative of \(\log _7(\log x)\).
Solution:
Given that, f(x) = \(\log _7(\log x)\)
Let y = \(\log _7(\log x)\)
Differentiating with respect to ‘x’ on both sides.

Question 27.
Find the derivative of the function f(x) = (x² – 3)(4x³ + 1). [May ’15 (AP)]
Solution:

Question 28.
Find the derivative of tan^-1(log x). [Mar. ’19 (AP); May ’15 (TS)]
Solution:

Question 29.
If f(x) = 2x³ + 3x – 5, then prove that f'(0) + 3 . f'(-1) = 0. [Mar. ’16 (AP)]
Solution:
Given f(x) = 2x² + 3x – 5
Now f'(x) = 2(2x) + 3(1) – 0 = 4x + 3
f'(0) = 4(0) + 3 = 3
f(-1) = 4(-1) + 3 = -4 + 3 = -1
LHS = f'(0) + 3. f'(-1)
= 3 + 3(-1)
= 3 – 3
= 0
∴ f'(0) + 3 . f'(-1) = 0

Question 30.
If 2x² – 3xy + y² + x + 2y – 8 = 0, then find \(\frac{d \mathbf{y}}{\mathbf{d x}}\). [Mar. ’16 (TS)]
Solution:
Given 2x² – 3xy + y² + 2y – 8 = 0
differentiating on both sides with respect to ‘x’.

Question 31.
If ay⁴ = (x + b)⁵ then 5yy¹¹ = (y¹)². [Mar. ’17 (TS)]
Solution:

Question 32.
If y = x⁴ + tan x then find y¹¹. [Mar. ’18 (AP)]
Solution:
Given that y = x⁴ + tan x
y¹ = \(\frac{\mathrm{d}}{\mathrm{dx}}\)(x⁴ + tan x) = 4x³ + sec²x
y¹¹ = \(\frac{\mathrm{d}}{\mathrm{dx}}\)(4x³ + sec²x)
= 4(3x²) + 2 sec x \(\frac{\mathrm{d}}{\mathrm{dx}}\)(sec x)
= 12x² + 2 sec x (sec x tan x)
∴ y¹¹ = 12x² + 2 sec²x tan x

Question 33.
If y = \(\frac{2 x+3}{4 x+5}\), then find y”.
Solution:
y = \(\frac{2 x+3}{4 x+5}\)

Question 34.
If f(x) = log(tan e^x), then find f'(x). [Mar. ’19 (TS)]
Solution:

Question 35.
Evaluate \({Lim}_{x \rightarrow 0} \frac{\log _e(1+5 x)}{x}\). [Mar. ’19 (TS)]
Solution:

Question 36.
If x^{log y} = log x, then show that \(\frac{d y}{d x}=\frac{y}{x}\left(\frac{1-\log x \log y}{(\log x)^2}\right)\). [Mar. ’19 (TS)]
Solution:

Here students can locate TS Inter 1st Year Accountancy Notes Chapter 7 Trial Balance to prepare for their exam.

TS Inter 1st Year Accountancy Notes Chapter 7 Trial Balance

→ Trial balance may be defined as a statement of balances of accounts of a business and it is prepared mainly to check the arithmetical accuracy of accounts.

→ Trial balance is a statement but not an account. It contains a summary of the accounts and helps in the preparation of final accounts.

→ Trial balance can be prepared by two methods

• Total Balances method
• Net balances method.

→ Accounts pertaining to assets, expenses and losses appear on the debit side and accounts related capital, liabilities incomes and gains appear on the credit side.

TS Inter 1st Year Accountancy Notes Chapter 7 అంకణా

→ జంటపద్దు విధానములోని ఖాతాలు లేదా ఖాతా నిల్వల అంకగణిత ఖచ్చితాన్ని ఋజువు చేసే నిమిత్తము తయారు చేసే నివేదికయే అంకణా.

→ అంకళా నివేదికయే కాని ఖాతా కాదు. దీనిలో ఖాతాల సంక్షిప్త సమాచారము ఉండి ముగింపు లెక్కలు తయారు చేయడానికి దోహదము చేస్తుంది.

→ అంకణాను రెండు పద్ధతులలో తయారు చేయవచ్చు.

• మొత్తాల పద్ధతి
• నిల్వల పద్ధతి

→ ఆస్తులు, ఖర్చులు, నష్టాలకు సంబంధించిన ఖాతాలు డెబిట్ నిల్వను, మూలధనము, అప్పులు, ఆదాయాలు, లాభాలకు సంబంధించిన ఖాతాలు క్రెడిట్ నిల్వను చూపుతాయి.