Students must practice these TS Intermediate Maths 1B Solutions Chapter 6 Direction Cosines and Direction Ratios Ex 6(b) to find a better approach to solving the problems.
TS Inter 1st Year Maths 1B Direction Cosines and Direction Ratios 6(b)
Question 1.
Find the direction ratios of the line joining the points (3, 4, 0) and (4, 4, 4). (V.S.A.Q.)
Answer:
Let A = (3, 4, 0) and B = (4, 4, 4) be the given points.
Then d.r.’s of AB = ( 4 – 3, 4 – 4, 4 – 0) = (1, 0, 4)
Question 2.
The direction ratios of a line are (-6, 2, 3). Find its direction cosines. (V.S.A.Q.)
Answer:
d.r’s of the line are -6, 2, 3.
∴ \(\sqrt{a^2+b^2+c^2}\) = \(\sqrt{36+4+9}\) = √49 = 7
d.c.’s of the line are \(\frac{-6}{7}, \frac{2}{7}, \frac{3}{7}\).
![]()
Question 3.
Find the cosine of the angle between the lines whose direction cosines are
\(\left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right)\) and \(\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0\right)\).
Answer:
cos θ = l1 l2 + m1 m2 + n1n2
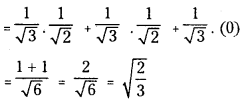
Question 4.
Find the angle between the lines whose d.r.’s are (1, 1, 2), (√3 , – √3, 0). (V.S.A.Q.)
Answer:
We have
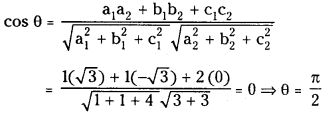
Question 5.
Show that the lines with direction cosines \(\left(\frac{12}{13}, \frac{-3}{13}, \frac{-4}{13}\right)\) and \(\left(\frac{4}{13}, \frac{12}{13}, \frac{3}{13}\right)\) are Perpendicular to each other. (V.S.A.Q.)
Answer:
We have the condition for two lines with d.c.’s (l1, m1, n1) and (l2, m2, n2) to be perpendicular is l1l2 + m1m2 + n1n2 = 0
∴ l1l2 + m1m2 + n1n2
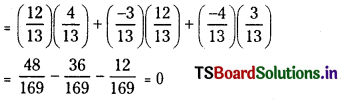
∴ The given lines are perpendicular.
Question 6.
O is the origin, P(2, 3, 4) and Q (1, k, 1) are points such that OP ⊥ OQ . Find k.
Answer:
d.r.’s of OP = 2, 3, 4
d.r.’s of OQ = 1, k, 1
OP and OQ are perpendicular.
⇒ a1a2 + b1b2 + c1c2 = 0
⇒ 2 + 3k + 4 = 0 ⇒ 3k + 6 = 0 ⇒ k = – 2
![]()
II.
Question 1.
If the direction ratios of a line are (3, 4, 0) find its direction cosines and also the angles made with the coordinate axes. (S.A.Q.)
Answer:
d.c.’s of the line are (3, 4, 0).
\(\sqrt{a^2+b^2+c^2}\) = \(\sqrt{9+16}\) = 5
∴ d.c.’s of the line are
If α, β, γ are angles made by the line with the
coordinate axes then cos α = \(\frac{3}{5}\), cos β = \(\frac{4}{5}\), cos γ = 0
∴ α = cos-1 (3/5), β = cos-1 (4/5), γ = \(\frac{\pi}{2}\)
∴ Angles made with coordinate axes are
cos-1 (3/5), cos-1 (4/5) and \(\frac{\pi}{2}\).
Question 2.
Show that the line through the points (1, -1, 2), (3, 4, -2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6). (S.A.Q.)
Answer:
Let A = (1, -1, 2), B = (3, 4, -2), C = (0, 3, 2) and D = (3, 5, 6) be the given points.
d.r.’s of AB = (3 – 1, 4 + 1, -2 – 2) = (2, 5,4)
d.r.’s of CD = (3 – 0, 5 – 3, 6 – 2) = (3, 2, 4)
∴ a1 a2 + b1 b2 + c1 c2 = 2(3) + 5(2) + (-4) (4) = 0
∴ AB and CD are perpendicular.
Question 3.
Find the angle between DC and AB where A = (3, 4, 5), B = (4, 6, 3), C = (-1, 2, 4) and D = (1, 0, 5). (S.A.Q.)
Answer:
d.r.’s of AB are (4 – 3, 6 – 4, 3 – 5) = (1, 2, -2)
d.r.’s of CD are (1 + 1, 0 – 2, 5 – 4) = (2, -2, 1)
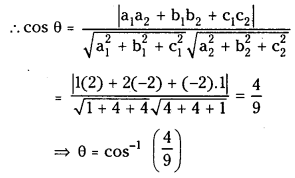
Question 4.
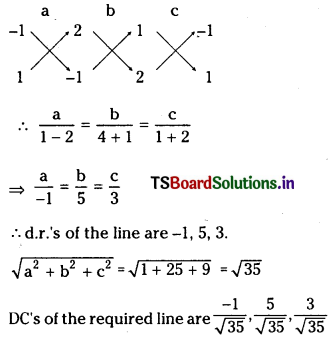
Find the direction cosines of a line which is perpendicular to the lines, whose direction ratios are (1, -1, 2) and (2, 1, -1). (S.A.Q.)
Answer:
Let the d.c.’s of the required line be a, b, c. This is perpendicular to the line whose d.r.’s are (1,-1, 2) and (2, 1, -1).
Then a – b + 2c = 0
and 2a + b – c = 0
![]()
Question 5.
Show that the points (2, 3, -4), (1, -2 ,3) and (3, 8, -11) are collinear. (S.A.Q.)
Answer:
Let A = (2, 3, -4), B = (1, -2, 3) and C = (3, 8, -11) be the three given points.

∵ AB + AC = 5√3 + 5√3 = 10√3 = BC
We have A, B, C are collinear.
Question 6.
Show that the points (4, 7, 8), (2, 3, 4), (-1, -2, 1), (1, 2, 5) are the vertices of a parallelogram. (S.A.Q.)
Answer:
Let A = (4, 7, 8), B = (2, 3, 4), C = (-1, -2, 1) and D = (1, 2, 5) be the four given points.
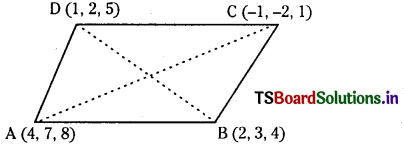
d.r.’s of \(\overline{\mathrm{AB}}\) = (2 – 4, 3 – 7, 4 – 8)
= (-2, -4, -4) ………………. (1)
d.r.’s of \(\overline{\mathrm{DC}}\) = (- 1 – 1, – 2 – 2, 1 – 5)
= (-2, -4, -4) ………………… (2)
d.r.’s of \(\overline{\mathrm{AB}}\) = DR’s of \(\overline{\mathrm{DC}}\) we have \(\overline{\mathrm{AB}}\) is parallel to \(\overline{\mathrm{DC}}\).
d.r.’s of \(\overline{\mathrm{AD}}\) = (1 – 4, 2 – 7, 5 – 8)
= (-3, -5, -3) ……………………. (3)
d.r.’s of \(\overline{\mathrm{BC}}\) = (-1 – 2, -2 – 3, 1 – 4)
= (-3, -5, -3) …………………….. (4)
∵ d.r.’s of \(\overline{\mathrm{AD}}\) = d.r.’s of \(\overline{\mathrm{BC}}\), we have \(\overline{\mathrm{AD}}\) is parallel to \(\overline{\mathrm{BC}}\).
From (1) and (3),
(-2) (-3) + (-4) (-5) + (-4) (-3) ≠ 0
From (2) and (4),
(-2) (-3) + (-4) (-5) + (-4) (-3) ≠ 0
We have \(\overline{\mathrm{AD}}\) is not perpendicular to \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{DC}}\) is not perpendicular to \(\overline{\mathrm{BC}}\).
Also d.r.’s of \(\overline{\mathrm{AC}}\) = (-1 – 4, -2 -7, 1 – 8)
= (-5, -9, -7) ………………….. (5)
d.r.’s of B\(\overline{\mathrm{BD}}\) = (1 – 2, 2 – 3, 5 – 4)
= (-1, -1, 1) ………………….. (6)
From (5) and (6)
(- 5) (- 1) + (- 9) (- 1) + (1) (-7) ≠ 0
Hence diagonals \(\overline{\mathrm{AC}}\) and \(\overline{\mathrm{BD}}\) are not perpendicular. Hence ABCD is a parallelogram.
III.
Question 1.
Show that the lines whose direction cosines are given by l + m + n = 0, 2mn + 3nl – 5lm= 0 are perpendicular to each other.(E.Q.) (March ’12)
Answer:
Given l + m + n = 0 ………………… (1)
and 2mn + 3nl – 5lm = 0 …………………….. (2)
From (1), l = – (m + n)
∴ From (2), 2mn – 3n(m + n) + 5m(m + n) = 0
⇒ 2mn – 3mn – 3n2 + 5m2 + 5mn = 0
⇒ 5m2 + 4mn – 3n2 = 0
⇒ 5\(\left(\frac{m}{n}\right)^2\) + 4\(\left(\frac{m}{n}\right)\) – 3 = 0
This is a quadratic equation in \(\left(\frac{m}{n}\right)\) and let \(\frac{m_1}{n_1}\) and \(\frac{m_2}{n_2}\) be the roots of the quadratic equation.
Then product of roots \(\frac{m_1}{n_1} \cdot \frac{m_2}{n_2}=\frac{-3}{5}\)
⇒ \(\frac{m_1 m_2}{3}=\frac{n_1 n_2}{-5}\) = k (suppose) …………… (3)
From (1), m = – (l + n)
– 2n (l + n) + 3nl + 5l (l + n) = 0
⇒ 5l2 + 6nl – 2n2 = 0

∴ l1l2 = 2k, m1m2 = 3k, n1n2 = – 5k
∴ l1l2 + m1m2 + n1n2 = 0
∴ The two lines are perpendicular.
![]()
Question 2.
Find the angle between the lines whose direction cosines satisfy the equations l + m + n = 0, l2 + m2 – n2 = 0. (E.Q.) (May 2014, ‘11,2007, Mar. ’13, ’07, June 2004)
Answer:
Given equations are
l + m + n = 0 ………………….. (1) and
l2 + m2 – n2 = 0 …………………… (2)
From (1), l = – (m + n)
From (2), [-(m + n)]2 + m2 – n2 = 0
⇒ m2 + n2 + 2mn + m2 – n2 = 0
⇒ 2m2 + 2mn = 0
⇒ 2m (m + n) = 0
⇒ m = 0 or m = -n
Case (i): If m = 0 then
l(0) + m (1) + n(0) = 0
and l + m + n = 0 ……………… (1)
Solving
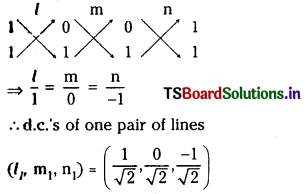
∴ d.c.’s of one pair of lines
(l1, m1, n1) = \(\left(\frac{1}{\sqrt{2}}, \frac{0}{\sqrt{2}}, \frac{-1}{\sqrt{2}}\right)\)
Case (ii): If m + n = 0 then
l(0) + m(1) + n(1) = 0
and l + m + n = 0
Solving
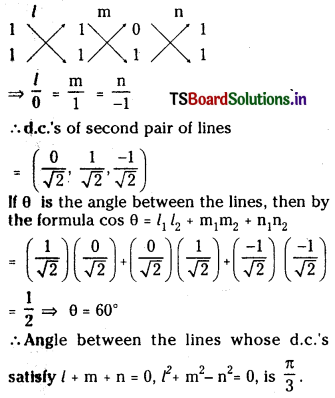
![]()
Question 3.
If a ray makes angles α, β, γ and δ with the four diagonals of a cube find a cube find cos2 α + cos2 β + cos2 γ + cos2 δ (E.Q.) (March 2005, May 2005)
Answer:
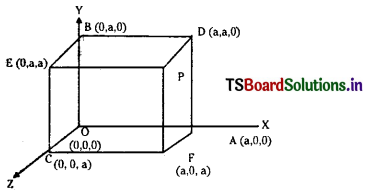
Let the side of the cube be of length ‘a’. Let one of the vertices of the cube through the origin ‘O’ and axes be along the three edges \(\overline{\mathrm{OA}}\), \(\overline{\mathrm{OB}}\) and \(\overline{\mathrm{OC}}\). The diagonals of the cube are OP, CD, AE and BF d.r.’s of the diagonals are (a, a, a), (a, a, -a), (-a, a, a) and (a, -a, a) respectively.
Let the d.c.’s of the given ray be l, m, n. If this make angles α, β, γ and δ with the four diagonals of the cube then

Question 4.
If (l1, two intersecting lines. Show that the d.c’s of two lines bisecting the angles between them are proportioned to l1 ± l2, m1 ± m2, n1 ± n2 (E.Q.)
Answer:
Let OA, OB be the given lines and A, B be the points at which distances from 0.
⇒ Coordinates of A = (l1, m1, n1) and B = (l2, m2, n2)
Mid point of AB, is:
P = \(\left(\frac{l_1+l_2}{2}, \frac{m_1+m_2}{2}, \frac{n_1+n_2}{2}\right)\)
∴ OP is the bisector of ∠AOB ⇒ d.r,’s of OP are l1 + l2, m1 + m2, n1 + n2
Now coordinates of B = (-l2, -m2, -n2) and mid point of AB’ is
Q = \(\left(\frac{l_1-l_2}{2}, \frac{m_1-m_2}{2}, \frac{n_1-n_2}{2}\right)\)
∴ OQ is a bisector of ∠AOB ⇒ d.r.’s of OQ are l1 – l2, m1 – m2, n1 – n2
Question 5.
A (-1, 2, -3), B (5, 0, -6), C (0, 4, -1) are three points. Show that the direction cosines of the bisector of ∠BAC are proportional to (25, 8, 5) and (-11, 20, 23). (E.Q.)
Answer:
Given A (-1, 2, -3), B (5, 0, -6) and C (0,4, -1) are three points.
d.r.’s of AB are = (5 + 1, 0 – 2, – 6 + 3) = (6, – 2, – 3)

Hence d.r.’s of other bisector are (-11, 20, 23) Hence direction cosines of the bisectors of ∠BAC are proportional to (25, 8, 5) and (-11, 20, 23).
![]()
Question 6.
If (6, 10, 10), (1, 0, -5), (6, – 10, 0) are vertices of a triangle. Find the direction ratios of its sides. Determine whether it is fight angled or isoceles. (S.A.)
Answer:
Let A (6,10,10), B (1, 0, -5) and C (6, -10, 0) are the vertices of ∆ABC
d.r.’s of AB = (-5, -10, -15) ⇒ (1,2, 3)
d.r.’s of BC = (5, -10, -5) ⇒ (1, -2, 1)
d.r.’s of AC = (0, 20, 10) ⇒ (0, 2, 1)
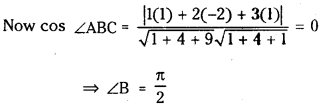
∴ The given triangle is a right angled triangle.
Question 7.
The vertices of a triangle are A (1, 4, 2), B (-2, 1, 2), C (2, 3, -4). Find ∠A, ∠B, ∠C. (S.A.Q.)
Answer:
Given A (1, 4, 2), B (-2, 1, 2) and C (2, 3, -4) are the vertices of ABC.
d.r.’s of AB are = 3, 3, 0 i.e., 1, 1, 0
d.r.’s of BC are = -4, -2, 6 i.e., 2, 1,- 3
d.r.’s of AC are – 1, 1, 6

Question 8.
Find the angle between the lines whose direction cosines are given by the equation 3l + m + 5n = 0 and 6mn – 2nl + 5lm = 0 (E.Q.) ( May’06, ’12))
Answer:
Given 3l + m + 5n = 0 ……………………. (1)
and 6mn – 2nl + 5lm = 0 ……………………. (2)
From (1), m = – (3l + 5n)
From (2)
– 6n (31 + 5n) – 2n/ – 5/ (31 + 5n) = 0
⇒ – 18nl – 30n2 – 2nl – 15l2 – 25ln = 0
⇒ – 15l2 – 45ln – 30n2 = 0
⇒ l2 + 3ln + 2n2 = 0
⇒ (l + 2n) (l + n) = 0
⇒ l + 2n = 0 or l + n = 0
⇒ l = – n or l = – 2n
If l = -n then m = 3n – 5n = – 2n
⇒ l : m : n = -n : -2n : n
= 1 : 2 : – 1
If l = -2n then m = 6n – 5n = n
⇒ l : m : n = -2n : n : n = 2 : -1 : -1
Hence d.r.’s of two lines are (1, 2, -1) and (2, -1,-1).
If θ is the angle between the two lines then

![]()
Question 9.
If a variable line in two adjacent positions has direction cosines (l, m, n) and (l + δl, m + δm, n + δn), show that the small angle δθ between two positions is given by (δθ)2 = (δl)2 + (δm)2 + (δn)2. (E.Q.)
Answer:
Given direction cosines of a variable line in two adjacent positions are (l, m, n) and (l + δl, m + δm, n + δn)
We have l2 + m2 + n2 = 1 …………………… (1)
and (l + δl)2 + (m + δm)2 + (n + δn)2 = 1 ………………… (2)
From (2) – (1) we have
(l + δl)2 + (m + δm)2 +(n + δn)2 – l2 – m2 – n2 = 0
⇒ 2 (l. δl + m . δm + n . δn) = – [(δl)2 + (δm)2 +(δn)2]
⇒ (δl)2 + (δm)2 + (δn)2 = – 2 (lδl + mδm + nδn) …………………… (3)
Now angle between two adjacent sides
cos δθ = l (l + δl) + m (m + δm) + n (n + δn)
= (l2 + m2 + n2) + l.δl + m.δm + n.δn
= 1 + l.δl + m.δm + n.δn
= 1 – \(\frac{1}{2}\) [(δl)2 + (δm)2 +(δn)2]
∴ (δl)2 + (δm)2 + (δn)2 = (1 – cos δθ)
Since δθ is very small, sin\(\left(\frac{\delta \theta}{2}\right)\) = \(\frac{\delta \theta}{2}\)
∴ (δl)2 + (δm)2 + (δn)2 = 4\(\frac{(\delta \theta)^2}{4}\) = (δθ)2
[∵ 1 – cosθ = 2 sin2\(\frac{\theta}{2}\)]
∴ (δθ)2 = (δl)2 + (δm)2 + (δn)2