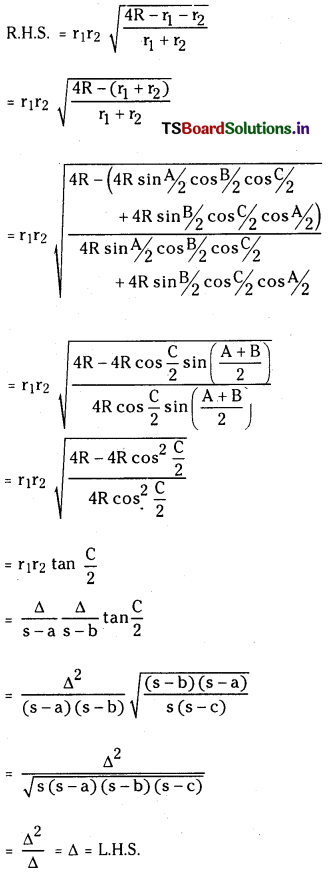
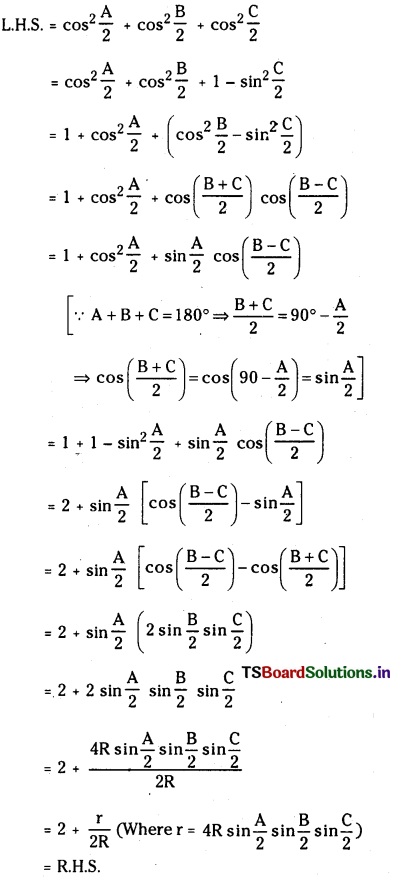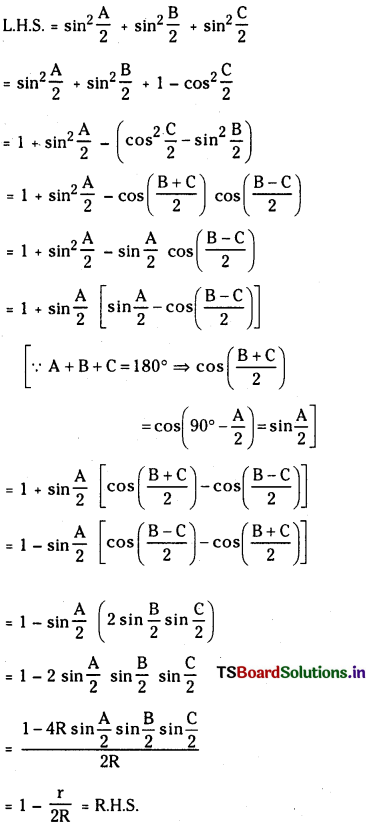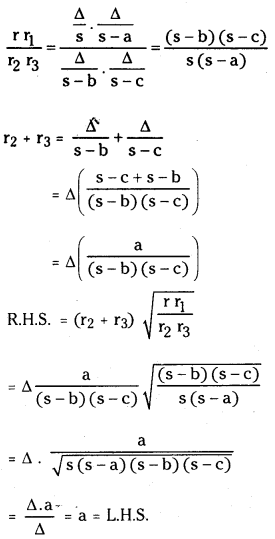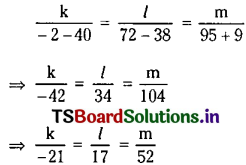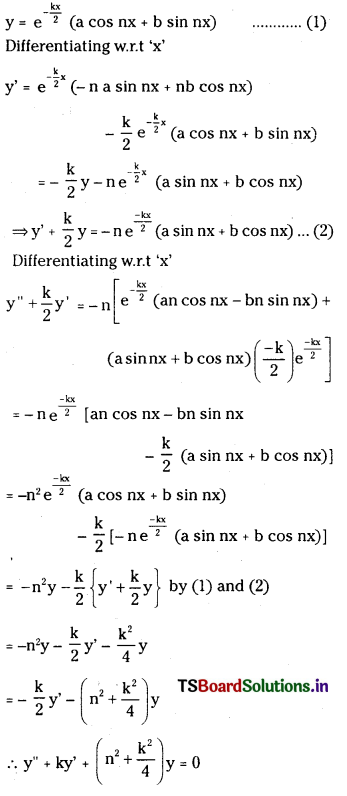Students must practice this TS Intermediate Maths 2B Solutions Chapter 1 Circle Ex 1(a) to find a better approach to solving the problems.
TS Inter 2nd Year Maths 2B Solutions Chapter 1 Circle Exercise 1(a)
I.
Question 1.
Find the equations of circles with centre C and radius r where
(i) C = (2, -3), r = 4
Solution:
Given C = (2, -3) = (h, k) and r = 4,
we have equation of circle as (x – h)2 + (y – k)2 = r2
(x – 2)2 + (y + 3)2 = 42
x2 + 4 – 4x + y2 + 9 + 6y = 16
x2 + y2 – 4x + 6y – 3 = 0
(ii) C = (-1, 2), r = 5
Solution:
Given C = (-1, 2) = (h, k) and r = 5, then
the equation of circle is (x – h)2 + (y – k)2 = r2
(x + 1)2 + (y – 2)2 = 52
x2 + y2 + 2x – 4y + 1 + 4 = 25
x2 + y2 + 2x – 4y – 20 = 0
(iii) C = (a, -b), r = a + b
Solution:
Given C = (a, -b) = (h, k) and r = a + b
we have the equation of circle as (x – h)2 + (y – k)2 = r2
(x – a)2 + (y + b)2 = (a + b)2
x2 + y2 – 2ax + 2by + a2 + b2 – (a + b)2 = 0
x2 + y2 – 2ax + 2by – 2ab = 0
(iv) C = (-a, -b), r = \(\sqrt{a^2-b^2}\) (|a| > |b|)
Solution:
Given C = (h, k) = (-a, -b) and r = \(\sqrt{a^2-b^2}\)
then the equation of circle is (x + a)2 + (y + b)2 = a2 – b2
x2 + y2 + 2ax + 2by + a2 + b2 – a2 + b2 = 0
x2 + y2 + 2ax + 2by + 2b2 = 0
(v) C = (cos α, sin α), r = 1
Solution:
Given C = (cos α, sin α) = (h, k) and r = 1
we have the equation of the circle as
(x – cos α)2 + (y – sin α)2 = 12
x2 + y2 – 2x cos α – 2y sin α + cos2α + sin2α – 1 = 0
x2 + y2 – 2x cos α – 2y sin α + 1 – sin2α + sin2α – 1 = 0
x2 + y2 – 2x cos α – 2y sin α = 0

(vi) C = (-7, -3), r = 4
Solution:
Given C = (-7, -3) = (h, k) and r = 4,
we have the equation of the circle as (x + y)2 + (y + 3)2 = 42
x2 + y2 + 14x + 6y + 49 + 9 – 16 = 0
x2 + y2 + 14x + 6y + 42 = 0
(vii) C = (\(\frac{-1}{2}\), -9), r = 5
Solution:
Given C = (\(\frac{-1}{2}\), -9) = (h, k) and r = 5,
the equation of the circle is (x – h)2 + (y – k)2 = r2
(x + \(\frac{1}{2}\))2 + (y + 9)2 = 0
x2 + y2 + x + 18y + \(\frac{1}{4}\) + 81 – 25 = 0
x2 + y2 + x + 18y + \(\frac{1}{4}\) + 56 = 0
4x2 + 4y2 + 4x + 72y + 225 = 0
(viii) C = \(\left(\frac{5}{2},-\frac{4}{3}\right)\), r = 6
Solution:
Given C = \(\left(\frac{5}{2},-\frac{4}{3}\right)\) = (h, k) and r = 6,
the equation of the circle is (x – h)2 + (y – k)2 = r2
\(\left(x-\frac{5}{2}\right)^2+\left(y+\frac{4}{3}\right)^2=6^2\)
x2 + y2 – 5x + \(\frac{8}{3} y+\frac{25}{4}+\frac{16}{9}\) – 36 = 0
36(x2 + y2) – 180x + 96y – 1007 = 0
∴ Equation of circle is 36(x2 + y2) – 180x + 96y – 1007 = 0
(ix) C = (1, 7), r = \(\frac{5}{2}\)
Solution:
The equation of the circle is (x – h)2 + (y – k)2 = r2
where C = (h, k) = (1, 7) and r = \(\frac{5}{2}\)
(x – 1)2 + (y – 7)2 = \(\frac{25}{4}\)
x2 + y2 – 2x – 14y + 50 = \(\frac{25}{4}\)
4(x2 + y2) – 8x – 56y + 200 – 25 = 0
4(x2 + y2) – 8x – 56y + 175 = 0
(x) C = (0, 0), r = 9
Solution:
Given C = (0, 0) = (h, k) and r = 9,
the equation of the circle is (x – h)2 + (y – k)2 = r2
x2 + y2 = 81
Question 2.
Find the equation of the circle passing through the origin and having the centre at (-4, -3).
Solution:
Let C = (-4, -3) and O(0, 0) be any point on the circumference of the circle.
Then OC = r will be the radius
∴ r = \(\sqrt{(0+4)^2+(0+3)^2}=\sqrt{16+9}\) = 5
The equation of a circle with centre (-4, -3) and radius ‘5’ is
(x + 4)2 + (y + 3)2 = 25
x2 + y2 + 8x + 6y + 16 + 9 – 25 = 0
x2 + y2 + 8x + 6y = 0
Question 3.
Find the equation of the circle passing through (2, -1) having the centre at (2, 3).
Solution:
Given C = (2, 3) and P = (2, -1)
∴ Radius of the circle PC = \(\sqrt{(2-2)^2+(3+1)^2}\) = 4
∴ The equation of the circle with centre (2, 3) and radius ‘4’ is
(x – 2)2 + (y – 3)2 = 42
x2 + y2 – 4x – 6y + 4 + 9 = 16
x2 + y2 – 4x – 6y – 3 = 0
Question 4.
Find the equation of the circle passing through (-2, 3) and having the centre at (0, 0).
Solution:
Given C = (0, 0) and P = (-2, 3)
We have radius PC = \(\sqrt{4+9}=\sqrt{13}\) = r
∴ Equation of circle with C(0, 0) and radius √13 is x2 + y2 = 13.
Question 5.
Find the equation of the circle passing through (3, 4) and having the centre at (-3, 4). (Mar. ’12)
Solution:
Given C = (-3, 4) and P = (3, 4)
The radius of the circle PC = \(\sqrt{(3+3)^2+(4-4)^2}\) = 6
∴ The equation of the circle with C = (-3, 4) and radius 6 is
(x + 3)2 + (y – 4)2 = 62
x2 + y2 + 6x – 8y + 9 + 16 – 36 = 0
x2 + y2 + 6x – 8y – 11 = 0
Question 6.
Find the value of ‘a’ if 2x2 + ay2 – 3x + 2y – 1 = 0 represents a circle and also find its radius. (Mar. ’13)
Solution:
If the given equation 2x2 + ay2 – 3x + 2y – 1 = 0 represents a circle then
coefficient of x2 = coefficient of y2
and the coefficient of the xy term is ‘0’.
2 = a
∴ a = 2
and the equation of circle is 2x2 + 2y2 – 3x + 2y – 1 = 0

Question 7.
Find the values of a and b if ax2 + bxy + 3y2 – 5x + 2y – 3 = 0 represents a circle. Also, find the radius and centre of the circle. (New Model Paper)
Solution:
Given ax2 + bxy + 3y2 – 5x + 2y – 3 = 0 represents a circle,
we have coefficient of x2 = coefficient of y2
and coefficient of xy term = 0
∴ a = 3 and b = 0
∴ Equation of circle is 3x2 + 3y2 – 5x + 2y – 3 = 0

Question 8.
If x2 + y2 + 2gx + 2fy – 12 = 0 represents a circle with centre (2, 3) find g, f, and its radius. (May ’11)
Solution:
Given x2 + y2 + 2gx + 2fy – 12 = 0 represents a circle with centre (2, 3) we have
(-g, -f) = (2, 3)
g = -2, f = -3
∴ Radius of the circle = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{4+9+12}\)
= 5

Question 9.
If x2 + y2 + 2gx + 2fy = 0 represents a circle with centre (-4, -3) then find g, f, and the radius of the circle.
Solution:
Centre = (-g, -f) = (-4, -3) (given)
g = 4 and f = 3
∴ Radius of the circle = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{16+9}\)
= 5
Question 10.
If x2 + y2 – 4x + 6y + c = 0 represents a circle with radius 6 then find the value of c. (Mar. ’09)
Solution:
Centre of the given circle = (2, -3)
and radius = 6 (given)
\(\sqrt{g^2+f^2-c}\) = 6
\(\sqrt{4+9-c}\) = 6
13 – c = 36
c = -23
Question 11.
Find the centre and radius of each of the circles whose equations are given below:
(i) x2 + y2 – 4x – 8y – 41 = 0
Solution:
x2 + y2 – 4x – 8y – 41 = 0
Comparing the given equation with x2 + y2 + 2gx + 2fy + c = 0, we have
2g = -4 and 2f = -8
∴ Centre = (-g, -f) = (2, 4)
Radius = \(\sqrt{g^2+f^2-c}=\sqrt{4+16+41}=\sqrt{61}\)
(ii) 3x2 + 3y2 – 5x – 6y + 4 = 0
Solution:
3x2 + 3y2 – 5x – 6y + 4 = 0
Writing the given equation in the standard form
\(x^2+y^2-\frac{5}{3} x-2 y+\frac{4}{3}=0\)
Compared with the standard equation, we get

(iii) 3x2 + 3y2 + 6x – 12y – 1 = 0
Solution:
3x2 + 3y2 + 6x – 12y – 1 = 0
Writing the given equation in the standard form, x2 + y2 + 2x – 4y – \(\frac{1}{3}\) = 0
∴ Centre = (-1, 2) and
radius = \(\sqrt{1+4+\frac{1}{3}}=\sqrt{\frac{16}{3}}=\frac{4}{\sqrt{3}}\)
(iv) x2 + y2 + 6x + 8y – 96 = 0
Solution:
x2 + y2 + 6x + 8y – 96 = 0
Centre = (-g, -f) = (-3, -4),
since 2g = 6, 2f = 8
and radius = \(\sqrt{9+16+96}=\sqrt{121}\) = 11
(v) 2x2 + 2y2 – 4x + 6y – 3 = 0
Solution:
2x2 + 2y2 – 4x + 6y – 3 = 0
Writing the given equation in the standard form,
x2 + y2 – 2x + 3y – \(\frac{3}{2}\) = 0
2g = -2, 2f = 3
g = -1, f = \(\frac{3}{2}\)
Centre = (-g, -f) = (1, \(-\frac{3}{2}\))
Radius = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{1+\frac{9}{4}+\frac{3}{2}}=\sqrt{\frac{19}{4}}=\frac{\sqrt{19}}{2}\)
(vi) 2x2 + 2y2 – 3x + 2y – 1 = 0
Solution:
2x2 + 2y2 – 3x + 2y – 1 = 0
Writing the given equation in the standard form \(x^2+y^2-\frac{3}{2} x+y-\frac{1}{2}=0\), we get

(vii) \(\sqrt{1+m^2}\) (x2 + y2) – 2cx – 2mcy = 0 (June ’10)
Solution:
Writing the given equation in the standard

(viii) x2 + y2 + 2ax – 2by + b2 = 0
Solution:
x2 + y2 + 2ax – 2by + b2 = 0
Compared with the general equation we get
2g = 2a and 2f = -2b
g = a and f = -b
∴ Centre = (-g, -f) = (-a, b)
radius = \(\sqrt{g^2+f^2-c}=\sqrt{a^2+b^2-b^2}\) = a

Question 12.
Find the equations of circles for which the points given below are the endpoints of a diameter.
(i) (1, 2), (4, 6)
Solution:
Equation of circle having A(x1, y1) and B(x2, y2) as extremities (endpoints) of the diameter is (x – x1) (x – x2) + (y – y1) (y – y2) = 0
∴ Taking A(x1, y1) = (1, 2) and B(x2, y2) = (4, 6)
We have the equation of a circle having A, B as extremities of the diameter is (x – 1) (x – 4) + (y – 2) (y – 6) = 0
x2 – 5x + 4 + y2 – 8y + 12 = 0
x2 + y2 – 5x – 8y + 16 = 0
(ii) (-4, 3), (3, -4)
Solution:
Take A(x1, y1) = (-4, 3) and B(x2, y2) = (3, -4)
We have equation of required circle as (x – x1) (x – x2) + (y – y1) (y – y2) = 0
(x + 4) (x – 3) + (y – 3) (y + 4) = 0
x2 + x – 12 + y2 + y – 12 = 0
x2 + y2 + x + y – 24 = 0
(iii) (1, 2), (8, 6)
Solution:
Take A = (1, 2) and B = (8, 6),
we have the equation of circle in the form (x – x1) (x – x2) + (y – y1) (y – y2) = 0
(x – 1) (x – 8) + (y – 2) (y – 6) = 0
x2 – 9x + 8 + y2 – 8y + 12 = 0
x2 + y2 – 9x – 8y + 20 = 0
(iv) (4, 2), (1, 5)
Solution:
Taking A = (4, 2) and B = (1, 5),
we have the equation of circle in the required form (x – x1) (x – x2) + (y – y1) (y – y2) = 0
(x – 4) (x – 1) + (y – 2) (y – 5) = 0
x2 – 5x + 4 + y2 – 7y + 10 = 0
x2 + y2 – 5x – 7y + 14 = 0
(v) (7, -3), (3, 5)
Solution:
Taking A = (7, -3) and B = (3, 5),
we have the equation of circle in the required form (x – x1) (x – x2) + (y – y1) (y – y2) = 0
(x – 7) (x – 3) + (y + 3) (y – 5) = 0
x2 – 10x + 21 + y2 – 2y – 15 = 0
x2 + y2 – 10x – 2y + 6 = 0
(vi) (1, 1), (2, -1)
Solution:
Taking A = (1, 1) and B = (2, -1),
we get the equation of circle in the required form (x – x1) (x – x2) + (y – y1) (y – y2) = 0
(x – 1) (x – 2) + (y – 1) (y + 1) = 0
x2 – 3x + 2 + y2 – 1 = 0
x2 + y2 – 3x + 1 = 0
(vii) (0, 0), (8, 5)
Solution:
Taking A = (0, 0) and B = (8, 5),
we get the equation of circle in the required form (x – x1) (x – x2) + (y – y1) (y – y2) = 0
(x – 0) (x – 8) + (y – 0) (y – 5) = 0
x2 – 8x + y2 – 5y = 0
x2 + y2 – 8x – 5y = 0
(viii) (3, 1), (2, 7)
Solution:
Taking A = (3, 1) and B = (2, 7),
the equation of circle in the required form is (x – x1) (x – x2) + (y – y1) (y – y2) = 0
(x – 3) (x – 2) + (y – 1) (y – 7) = 0
x2 – 5x + 6 + y2 – 8y + 7 = 0
x2 + y2 – 5x – 8y + 13 = 0

Question 13.
Obtain the parametric equation of each of the following circles.
(i) x2 + y2 = 4
Solution:
Given equation is in the form x2 + y2 = r2
centre C(h, k) = (0. 0), and the radius of the circle is r = 2
The parametric equations of the given circle are x = h + r cos θ, y = k + r sin θ
x = 2 cos θ, y = 2 sin θ, (0 ≤ θ ≤ 2π)
(ii) 4(x2 + y2) = 9
Solution:
The given equation can be written as x2 + y2 = \(\frac{9}{4}\)
Centre of the circle C(h, k) = (0, 0) and radius = \(\frac{3}{2}\)
∴ The parametric equations of the given circle are x = h + r cos θ, y = k + r sin θ
x = \(\frac{3}{2}\) cos θ, y = \(\frac{3}{2}\) sin θ, (0 ≤ θ ≤ 2π)
(iii) 2x2 + 2y2 = 7
Solution:
The given equation can be written as x2 + y2 = \(\frac{7}{2}\)
Centre of the circle C(h, k) = (0, 0) and radius = \(\sqrt{\frac{7}{2}}\)
∴ The parametric equations of the given circle are x = h + r cos θ, y = k + r sin θ
x = \(\sqrt{\frac{7}{2}}\) cos θ, y = \(\sqrt{\frac{7}{2}}\) sin θ, (0 ≤ θ ≤ 2π)
(iv) (x – 3)2 + (y – 4)2 = 82
Solution:
From the given equation,
centre C(h, k) = (3, 4) and radius r = 8
∴ Parametric equations are x = h + r cos θ, y = k + r sin θ
x = 3 + 8 cos θ, y = 4 + 8 sin θ, (0 ≤ θ ≤ 2π)
(v) x2 + y2 – 4x – 6y – 12 = 0 (Mar. ’11)
Solution:
Centre of the given circle C(h, k) = (2, 3)
and radius = \(\sqrt{4+9+12}\) = 5
∴ Parametric equations are x = h + r cos θ, y = k + r sin θ
x = 2 + 5 cos θ, y = 3 + 5 sin θ, (0 ≤ θ ≤ 2π)
(vi) x2 + y2 – 6x + 4y – 12 = 0 (Mar. ’10)
Solution:
Centre of the given circle C(h, k) = (3, -2)
and radius = \(\sqrt{4+9+12}\) = 5
∴ Parametric equations are x = h + r cos θ, y = k + r sin θ
x = 3 + 5 cos θ, y = -2 + 5 sin θ, (0 ≤ θ ≤ 2π)
II.
Question 1.
If the abscissae of points A, B are the roots of the equation x2 + 2ax – b2 = 0 and ordinates of A, B are the roots of y2 + 2py – q2 = 0 then find the equation of circle for which \(\overline{\mathrm{AB}}\) is a diameter.
Solution:
Let A(x1, y1) and B(x2, y2) be the extremities of diameter \(\overline{\mathrm{AB}}\) of a circle.
Abscissae of points A, B are x1, x2 which are the roots of x2 + 2ax – b2 = 0.
∴ x1 + x2 = -2a, and x1x2 = -b2
Similarly given that ordinates of A, B are y1, y2 which are the roots of y2 + 2py – q2 = 0, then
y1 + y2 = -2p and y1y2 = -q2
∴ The equation of a circle with A, B as the extremities of diameter is (x – x1) (x – x2) + (y – y1) (y – y2) = 0
x2 – x(x1 + x2) + x1x2 + y2 – y(y1 + y2) + y1y2 = 0
x2 – x(-2a) – b2 + y2 – y(-2p) – q2 = 0
x2 + 2ax – b2 + y2 + 2py – q2 = 0
x2 + y2 + 2ax + 2py – (b2 + q2) = 0
Question 2.
(i) Show that A(3, -1) lies on the circle x2 + y2 – 2x + 4y = 0. Also, find the other end of the diameter through A.
Solution:
Substituting x = 3, y = -1 in LHS of the equation of circle we have
32 + (-1)2 – 2(3) + 4(-1)
= 9 + 1 – 6 – 4
= 0
and A(3, -1) lies on the circle x2 + y2 – 2x + 4y = 0
Centre of the circle is, C = (1, -2)
Let the other end of the diameter be B(h, k).
Then C is the midpoint of AB.
∴ \(\frac{\mathrm{h}+3}{2}\) = 1 and \(\frac{\mathrm{k}-1}{2}\) = -2
h = -1 and k = -3
∴ The other end of the diameter through A is B = (-1, -3).
(ii) Show that A(-3, 0) lies on x2 + y2 + 8x + 12y + 15 = 0 and find the other end of the diameter through A.
Solution:
Substituting x = -3, y = 0 in LHS of the given equation of circle we have
(-3)2 + 02 + 8(-3) + 12(0) + 15
= 9 – 24 + 15
= 0
Hence the point A(-3, 0) lies on x2 + y2 + 8x + 12y + 15 = 0
Let B (h, k) be the end of the diameter \(\overline{\mathrm{AB}}\).
The centre ‘C’ of the given circle is C = (-4, -6)
Since c is the midpoint of the diameter \(\overline{\mathrm{AB}}\).
we have \(\frac{\mathrm{h}-3}{2}\) = -4 and \(\frac{\mathrm{k}+0}{2}\) = -6.
h = -5 and k = -12
∴ The other end of the diameter is (-5, -12).

Question 3.
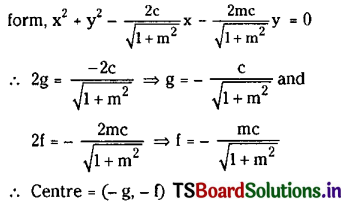
Find the equation of the circle which passes through (2, -3) and (-4, 5) and has the centre on 4x + 3y + 1 = 0.
Solution:
Let the equation of the required circle be
x2 + y2 + 2gx + 2fy + c = 0 ……….(1)
Since (1) passes through (2, -3) we have
22 + (-3)2 + 2g(2) + 2f(-3) + c = 0
4g – 6f + c = -13 ……….(2)
Similarly (1) passes through (-4, 5) we have
(-4)2 + 52 + 2g(-4) + 2f(5) + c = 0
16 + 25 – 8g + 10f + c = 0
8g – 10f – c = 41 ………..(3)
Also given that the centre of the circle (1)
i.e., (-5, -f) lies on the line 4x + 3y + 1 = 0, we have
-4g – 3f + 1 = 0
4g + 3f – 1 = 0 ……….(4)
From equations (2) and (3)
4g – 6f + c = -13 and 8g – 10f – c = 41
12g – 16f = 28
3g – 4f = 7 ………(5)
Solving equations (4) and (5) we get
g = 1, f = -1
∴ From equation (3)
8(1) – 10(-1) – c = 41
-c = 41 – 18 = 23
c = -23
Hence from (1), the equation of the required circle is x2 + y2 + 2(1)x + 2(-1)y – 23 = 0
x2 + y2 + 2x – 2y – 23 = 0
Question 4.
Find the equation of a circle that passes through (4, 1), (6, 5) and has the centre on 4x + 3y – 24 = 0. (Mar. ’12)
Solution:
Let the equation of the required circle be
x2 + y2 + 2gx + 2fy + c = 0 ………(1)
The centre of the circle is (-g, -f)
Since (1) passes through (4, 1) we have
42 + 12 + 2g(4) + 2f(1) + c = 0
8g + 2f + c = -17 ………(2)
Also since (1) passes through the point (6, 5) we have
62 + 52 + 2g(6) + 2f(5) + c = 0
12g + 10f + c = -61 ……….(3)
Given that the centre (-g, -f) lies on the line 4x + 3y – 24 = 0, we have
-4g – 3f – 24 – 0
4g + 3f = -24 ……….(4)
From (2) and (3)
8g + 2f + c = – 17 and 12g + 10f + c = -61
We have -4g – 8f – 44 = 0
g + 2f + 11 = 0 ……….(5)
Solving (4) and (5)
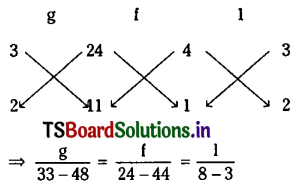
g = -3, f = -4
Substituting in (2) we get
8(-3) + 2(-4) – c = -17
-24 – 8 + c = -17
c = – 17 + 32 = 15
∴ From (1), the equation of the required circle is x2 + y2 + 2(-3)x + 2(-4)y + 15 = 0
x2 + y2 – 6x – 8y + 15 = 0
Question 5.
Find the equation of the circle which is concentric with x2 + y2 – 6x – 4y – 12 = 0 and passing through (-2, 14).
Solution:
The equation of the given circle is
x2 + y2 – 6x – 4y – 12 = 0 ………(1)
The equation of the circle which is concentric with the given circle (1) is
x2 + y2 – 6x – 4y + λ = 0 ……….(2)
where λ is a constant.
Circle (2) is passing through (-2, 14), and hence
4 + 196 + 12 – 56 + λ = 0
λ + 156 = 0
λ = -156
∴ The equation of a circle that is concentric with a circle (1) is x2 + y2 – 6x – 4y – 156 = 0.

Question 6.
Find the equation of the circle whose centre the lies on X-axis and passes through (-2, 3) and (4, 5). (Mar. ’10)
Solution:
Let the equation of a circle whose centre lies on the X-axis be
x2 + y2 + 2gx + c = 0 ………(1)
Since the circle passes through (-2, 3) we have
4 + 9 – 4g + c = 0
4g – c – 13 = 0 ……….(2)
Also, circle (1) passes through (4, 5) we have
16 + 25 + 8g + c = 0
8g + c + 41 = 0 ………(3)
Solving (2) and (3) we get

∴ From (1) we have the equation of the circle is
\(x^2+y^2+2\left(-\frac{7}{3}\right) x-\frac{67}{3}=0\)
3(x2 + y2) – 14x – 67 = 0
Question 7.
If ABCD is a square then show that the points A, B, C, and D are concyclic. (May ’09)
Solution:
Given that ABCD is a square
and Let AB = BC = CD = DA = a.
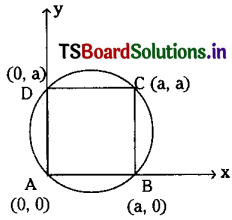
The two adjacent sides \(\overline{\mathrm{AB}}, \overline{\mathrm{AD}}\) are taken as coordinate axes.
∴ A = (0, 0), B = (a, 0), C = (a, a), D = (0, a).
Let the equation of the circle passing through A, B, D be
x2 + y2 + 2gx + 2fy + c = 0 ……….(1)
since (1) passes through (0, 0) we have c = 0
since (1) passes through B(a, 0), we have
a2 + 0 + 2g(a) + 2f(0) + c = 0
a2 + 2ga = 0 (∵ c = 0)
g = \(\frac{-a^2}{2 a}=\frac{-a}{2}\)
since (1) passes through C(0, a) we have
0 + a2 + 2g(0) + 2f(a) + c = 0
a2 + 2fa = 0 (∵ c = 0)
∴ The equation of the circle passing through points A, B, and D is
\(\mathrm{x}^2+\mathrm{y}^2-2\left(\frac{\mathrm{a}}{2}\right) \mathrm{x}-2\left(\frac{\mathrm{a}}{2}\right) \mathrm{y}=0\) …….(1)
Substituting the point C(a, a) in LHS of (2)
a2 + a2 – a2 – a2 = 0
equation (2) is satisfied.
Hence points A, B, C, D are concyclic.
III.
Question 1.
Find the equation of the circle passing through each of the following three points.
(i) (3, 4), (3, 2), (1, 4)
Solution:
Here (x1, y1) = (3, 4), (x2, y2) = (3, 2), (x3, y3) = (1, 4)
c1 = \(-\left(x_1^2+y_1^2\right)\)
= -(9 + 16)
= -25
c2 = \(-\left(x_2^2+y_2^2\right)\)
= -(9 + 4)
= -13
c3 = \(-\left(x_3^2+y_3^2\right)\)
= -(1 + 16)
= -17
The equation of a circle passing through the given three points is

-4(-51 + 13) – 25(12 – 2)
= 3(18) – 4(-38) – 250
= 54 + 142 – 250
= -44
∴ Equation of required circle is -4(x2 + y2) + 16x + 24y – 44 = 0
x2 + y2 – 4x – 6y + 11 = 0
(ii) (1, 2), (3, -1), (5, -6)
Solution:
Let (x1, y1) = (1, 2), (x2, y2) = (3, -4), (x3, y3) = (5, -6)
c1 = \(-\left(x_1^2+y_1^2\right)\)
= -(1 + 4)
= -5
c2 = \(-\left(x_2^2+y_2^2\right)\)
= -(9 + 16)
= -25
c3 = \(-\left(x_3^2+y_3^2\right)\)
= -(24 + 36)
= -61
The equation of a circle passing through the given three points is


= 1(244 – 150) – 2(-183 + 125) – 5(-18 + 20)
= 94 – 2(-58) – 10
= 94 + 116 – 10
= 200
∴ Equation of required circle is 8(x2 + y2) – 176x – 32y + 200 = 0
x2 + y2 – 22x – 4y + 25 = 0.
(iii) (2, 1), (5, 5), (-6, 7)
Solution:
(x1, y1) = (2, 1), (x2, y2) = (5, 5), (x3, y3) = (-6, 7)
c1 = \(-\left(x_1^2+y_1^2\right)\)
= -(4 + 1)
= -5
c2 = \(-\left(x_2^2+y_2^2\right)\)
= -(25 + 25)
= -50
c3 = \(-\left(x_3^2+y_3^2\right)\)
= -(36 + 49)
= -85
The equation of the circle passing through the above three non-collinear points is given by


= -150 + 725 – 325
= 725 – 475
= 250
∴ Equation of required circle is 50(x2 + y2) + 50x – 600y + 250 = 0
x2 + y2 + x – 12y + 5 = 0.
(iv) (5, 7), (8, 1), (1, 3) (June ’10)
Solution:
(x1, y1) = (5, 7), (x2, y2) = (8, 1), (x3, y3) = (1, 3)
c1 = \(-\left(x_1^2+y_1^2\right)\)
= -(25 + 49)
= -74
c2 = \(-\left(x_2^2+y_2^2\right)\)
= -(64 + 1)
= -65
c3 = \(-\left(x_3^2+y_3^2\right)\)
= -(1 + 9)
= -10
The equation of the required circle passing through the above points is


= 5(-10 + 195) – 7(-80 + 65) – 74(24 – 1)
= 5(185) – 7(-15) – 74(23)
= 925 + 105 – 1702
= -672
Equation of required circle is -36(x2 + y2) + 348x + 228y – 672 = 0
3(x2 + y2) – 29x – 19y + 56 = 0.

Question 2.
(i) Find the equation of the circle passing through (0, 0) and making intercepts 4, 3 on the X-axis and Y-axis respectively.
Solution:
Let the equation of the required circle be
x2 + y2 + 2gx + 2fy + c = 0 ……….(1)
Since the circle passes through the origin, c = 0
Given that the X-intercept = 4

∴ The equation of the required circle is x2 + y2 + 2(±2)x + 2(±\(\frac{3}{2}\))y = 0
x2 + y2 ± 4x ± 3y = 0.
(ii) Find the equation of the circle passing through (0, 0) and making 6 units on the X-axis and intercepting 4 units on the Y-axis.
Solution:
Let the equation of the required circle be
x2 + y2 + 2gx + 2fy + c = 0 ……….(1)
If this passes through (0, 0) then c = 0.
Given that the X-intercept = 6
\(2 \sqrt{g^2-c}\) = 6
4g2 = 36
g = ±3
and Y-intercept = 4
\(2 \sqrt{\mathrm{f}^2-\mathrm{c}}\) = 4
4f2 = 16
f2 = 4
f = ±2
∴ Equation of the required circle is x2 + y2 + 2(±3)x + 2(±2)y = 0
x2 + y2 ± 6x ± 4y = 0.
Question 3.
Show that the following four points in each of the following are concyclic and find the equation of the circle on which they lie.
(i) (1, 1) (-6, 0), (-2, 2), (-2, -8) (New Model Paper)
Solution:
To show that the given four points are concyclic, we have first to find the equation of the circle passing through the points
A(1, 1) = (x1, y1), B(-6, 0) = (x2, y2) and C(-2, +2) = (x3, y3) and verify whether the fourth point D(-2, -8) lies on the circle.
c1 = \(-\left(\mathrm{x}_1^2+\mathrm{y}_1^2\right)\)
= -(1 + 1)
= -2
c2 = \(-\left(\mathrm{x}_2^2+\mathrm{y}_2^2\right)\)
= -(36 + 0)
= -36
c3 = \(-\left(\mathrm{x}_3^2+\mathrm{y}_3^2\right)\)
= -(4 + 4)
= -8
The equation of the circle passing through points A, B, C is given by

= 1(0 + 72) – 1(48 – 72) – 2(-12 + 0)
= +72 + 24 + 24
= 120
∴ The equation of the circle passing through the points A, B, C is -10(x2 + y2) – 40x – 60y + 120 = 0
(x2 + y2) + 4x + 6y – 12 = 0
Substituting D(-2, -8) in LHS of above equation we get
4 + 64 – 8 – 48 – 12 = 0
Hence the given points A, B, C, D are concyclic.
(ii) (1, 2) (3, -4), (5, -6), (19, 8) (May ’11)
Solution:
Let A(1, 2) = (x1, y1), B = (3, -4) = (x2, y2), C = (5, -6) = (x3, y3) and D (19, 8).
To show that A, B, C, D are concyclic we have to find the equation of the circle passing through A, B, and C and verify whether D satisfies the resulting equation.
c1 = \(-\left(x_1^2+y_1^2\right)\)
= -(1 + 4)
= -5
c2 = \(-\left(x_2^2+y_2^2\right)\)
= -(9 + 16)
= -25
c3 = \(-\left(x_3^2+y_3^2\right)\)
= -(25 + 36)
= -61
The equation of the circle passing through points A, B, C is given by

= 1(244 – 150) – 2(-183 + 125) – 5(-18 + 20)
= 94 + 116 – 10
= 200
∴ The equation of the circle passing through A, B, C is 8(x2 + y2) – 176x – 32y + 200 = 0
x2 + y2 – 22x – 4y + 25 = 0.
Substituting (19, 8) in LHS of the above equation
(19)2 + 64 – 22(19) – 4(8) + 25 = 0
361 + 64 – 418 – 32 + 25 = 0
Hence points A, B, C, D are concyclic.
(iii) (1, -6) (5, 2), (7, 0), (-1, -4)
Solution:
Let A(1, -6) = (x1, y1), B = (5, 2) = (x2, y2), C = (5, -6) = (x3, y3) and D(-1, -4)
We first find the equation passing through points A, B, C.
c1 = \(-\left(x_1^2+y_1^2\right)\)
= -(1 + 36)
= -37
c2 = \(-\left(x_2^2+y_2^2\right)\)
= -(25 + 4)
= -29
c3 = \(-\left(x_3^2+y_3^2\right)\)
= -(49 + 0)
= -49
The equation of the circle passing through points A, B, C is

\(\left|\begin{array}{lll}
\mathbf{x}_1 & \mathbf{y}_1 & \mathrm{c}_1 \\
\mathbf{x}_2 & \mathbf{y}_2 & \mathrm{c}_2 \\
\mathrm{x}_3 & \mathbf{y}_3 & \mathrm{c}_3
\end{array}\right|=\left|\begin{array}{ccc}
1 & -6 & -37 \\
5 & 2 & -29 \\
7 & 0 & -49
\end{array}\right|\)
= 1(-98) + 6(-245 + 203) – 37(-14)
= -98 + 6(-42) + 518
= -98 – 252 + 518
= -350 + 518
= 168
∴ The equation of the circle passing through the points A, B, C is -24(x2 + y2) + 144x – 96y + 168 = 0
(x2 + y2) – 6x + 4y – 7 = 0 represents a circle.
Substituting D(-1, -4) in LHS of above equation
1 + 16 + 6 – 16 – 7 = 0, the equation is satisfied.
Hence points A, B, C, D are concyclic.
(iv) (9, 1), (7, 9), (-2, 12), (6, 10)
Solution:
Let A = (9, 1) = (x1, y1), B = (7, 9) = (x2, y2) C = (-2, 12) = (x3, y3) and D = (6, 10)
We first find the equation of a circle passing through points A, B, C.
To show that the four points A, B, C, D are concyclic
we verify whether point D lies on the circle or not.
c1 = \(-\left(x_1^2+y_1^2\right)\)
= -(81 + 1)
= -82
c2 = \(-\left(x_2^2+y_2^2\right)\)
= -(49 + 81)
= -130
c3 = \(-\left(x_3^2+y_3^2\right)\)
= -(4 + 144)
= -148
The equation of the circle passing through points A, B, C is


= 9(-1332 + 1560) – 1(-1036 – 260) – 82(84 + 18)
= 9(228) + 1296 – 82(102)
= 2052 + 1296 – 8364
= 3348 – 8364
= -5016
∴ The equation of the circle passing through A, B, C is 66(x2 + y2) – 396y – 5016 = 0
x2 + y2 – 6y – 76 = 0
Substituting D(6, 10) in LHS of the above equation. We get
36 + 100 – 60 – 76 = 0
∴ Points A, B, C, D are concyclic.

Question 4.
If (2, 0), (0, 1), (4, 5), and (0, c) are concyclic then find c.
Solution:
Let A = (2, 0) = (x1, y1), B = (0, 1) = (x2, y2) and C = (4, 5) = (x3, y3)
We have to find the equation of a circle passing through A, B, C.
c1 = \(-\left(x_1^2+y_1^2\right)\)
= -(4 + 0)
= -4
c2 = \(-\left(x_2^2+y_2^2\right)\)
= -(0 + 1)
= -1
c3 = \(-\left(x_3^2+y_3^2\right)\)
= -(16 + 25)
= -41
The equation of the circle passing through points A, B, C is given by

= 2(-41 + 5) – 4(-4)
= 2(-36) + 16
= -72 + 16
= -56
∴ The equation of the circle passing through the points A, B, C is -12(x2 + y2) – 52x + 68y – 56 = 0
12(x2 + y2) – 52x – 68y + 56 = 0
3(x2 + y2) – 13x – 17y + 14 = 0
Given that four points A(2, 0), B(0, 1), C(4, 5), and D(0, c) are concyclic, point D must lie on the above circle.
3(c2) – 13(0) – 17(c) + 14 = 0
3c2 – 17c + 14 = 0
3c2 – 14c – 3c + 14 – 0
3c(c – 1) – 14(c – 1) = 0
c = 1 or c = \(\frac{14}{3}\)
c = 1 is not admissive and hence c = \(\frac{14}{3}\).
Question 5.
Find the equation of the circumcircle of the triangle formed by the straight lines given in each of the following.
(i) 2x + y = 4, x + y = 6, x + 2y = 5
Solution:
Circumcircle is a circle that passes through the three vertices of the triangle.
Let L1 = 2x + y – 4 = 0
L2 = x + y – 6 = 0
L3 = x + 2y – 5 = 0
Suppose L1, L2; L2, L3; L3, L1 intersect at A, B and C respectively.
Consider a curve whose equation is
k(2x + y – 4) (x + y – 6) + l(x + y – 6) (x + 2y – 5) + m(x + 2y – 5) (2x + y – 4) = 0 ……….(1)
We can verify that the curve passes through A, B, C. So it represents a circle.
If equation (1) represents a circle then
coefficient of x2 = coefficient of y2
2k + l + 2m = k + 2l + 2m
k – l = 0 ………..(2)
coefficient of xy = 0
3k + 3l + 5m = 0 ………(3)
solving k – l + 0m = 0 and 3k + 3l + 5m = 0, we get
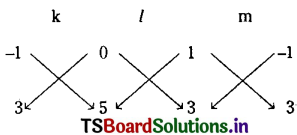
\(\frac{k}{-5}=\frac{l}{-5}=\frac{m}{6}\)
So the required equation is -5(2x + y – 4)(x + y – 6) – 5(x + y – 6) (x + 2y – 5) + 6(x + 2y – 5) (2x + y – 4) = 0
-5[2x2 + 2xy – 12x + xy + y2 – 6y – 4x – 4y + 24] – 5[x2 + 2xy – 5x + xy + 2y2 – 5y – 6x – 12y + 30] + 6[2x2 + xy – 4x + 4xy + 2y2 – 8y – 10x – 5y + 20] = 0
-3x2 – 3y2 + 51x + 57y – 150 = 0
x2 + y2 – 17x – 19y + 50 = 0
(ii) x + 3y – 1 = 0, x + y + 1 = 0, 2x + 3y + 4 = 0
Solution:
Circumcircle is a circle that passes through the three vertices of the triangle.
Let L1 = x + 3y – 1 = 0
L2 = x + y + 1 = 0
L3 = 2x + 3y + 4 = 0
Suppose L1, L2; L2, L3; L3, L1 intersect at A, B and C respectively.
Consider a curve whose equation is
k(x + 3y – 1) (x + y + 1) + l(x + y + 1)(2x + 3y + 4) + m(2x + 3y + 4) (x + 3y – 1) = 0 ……….(1)
We can verify that the curve passes through A, B, C. So it represents a circle.
If equation (1) represents a circle then
coefficient of x2 = coefficient of y2
k + 2l + 2m = 3k + 3l + 9m
2k + l + 7m = 0 ………(2)
coefficient of xy is zero.
4k + 5l + 9m = 0 ……….(3)
Solving (2) and (3), we get
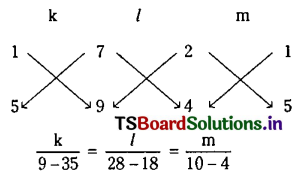
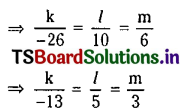
So the required equation is
-13(x + 3y – 1) (x + y + 1) + 5(x + y + 1) (2x + 3y + 4) + 3(2x + 3y + 4) (x + 3y – 1) = 0
-13[x2 + xy + x + 3xy + 3y2 + 3y – x – y – 1] + 5[2x2 + 3xy + 4x + 2xy + 3y2 + 4y + 2x + 3y + 4] + 3[2x2 + 3xy + 4x + 6xy + 9y2 + 12y – 2x – 3y – 4] = 0
3x2 + 3y2 + 36x + 36y + 21 = 0
x2 + y2 + 12x + 12y + 7 = 0
(iii) 5x – 3y + 4 = 0, 2x + 3y – 5 = 0, x + y = 0
Solution:
Circumcircle is a circle that passes through the three vertices of the triangle.
Let L1 = 5x – 3y + 4 = 0
L2 = 2x + 3y – 5 = 0
L3 = x + y = 0
Suppose L1, L2; L2, L3; L3, L1 intersect at A, B and C respectively.
Consider a curve whose equation is
k(5x – 3y + 4) (2x + 3y – 5) + l(2x + 3y – 5) (x + y) + m(x + y) (5x – 3y + 4) = 0 ………(1)
We can verify that the curve passes through A, B, C. So it represents a circle.
If equation (1) represents a circle then
coefficient of x2 = coefficient of y2
10k + 2l + 5m = -9k + 3l – 3m
19k – l + 8m = 0 ……….(2)
coefficient of xy is zero.
9k + 5l + 2m = 0 ……….(3)
Solving (2) and (3) we get
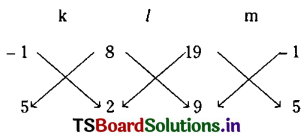
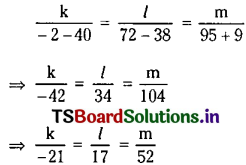
So the required equation is
-21(5x – 3y + 4) (2x + 3y – 5) + 17(2x + 3y – 5) (x + y) + 52(x + y) (5x – 3y + 4) = 0
-21[10x2 + 15xy – 25x – 6xy – 9y2 + 15y + 8x + 12y – 20] + 17[2x2 + 2xy + 3xy + 3y2 – 5x – 5y] + 52[5x2 – 3xy + 4x + 5xy – 3y2 + 4y] = 0
84(x2 + y2) + 480x – 444y + 420 = 0
7(x2 + y2) + 40x – 37y + 35 = 0
49(x2 + y2) + 280x – 259y + 245 = 0
(iv) x – y – 2 = 0, 2x – 3y + 4 = 0, 3x – y + 6 = 0
Solution:
Circumcircle is a circle that passes through the three vertices of the triangle.
Let L2 = x – y – 2 = 0
L2 = 2x – 3y + 4 = 0
L3 = 3x – y + 6 = 0
Suppose L1, L2; L2, L3; L3, L1 intersect at A, B and C
consider a curve whose equation is
k(x – y – 2) (2x – 3y + 4) + l(2x – 3y + 4) (3x – y + 6) + m(3x – y + 6)(x – y – 2) = 0 ………(1)
We can verify that the curve passes through A, B, C.
So we find k, l, and m such that equation (1) represents a circle, Hence
coefficient of x2 = coefficient of y2
2k + 6l + 3m = 3k + 3l + m
k – 3l – 2m = 0
coefficient of xy term = 0
-5k – 11l – 4m = 0
5k + 11l + 4m = 0 ……….(3)
Solving (2) and (3) we get
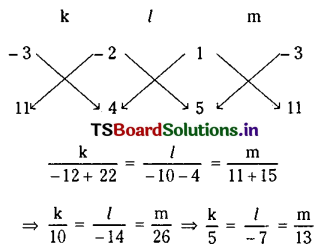
Hence from (1), the equation of a circle is
5(x – y – 2) (2x – 3y + 4) – 7(2x – 3y + 4) (3x – y + 6) + 13(3x – y + 6) (x – y – 2) = 0
5[2x2 – 3xy + 4x – 2xy + 3y2 – 4y – 4x + 6y – 8] – 7[6x2 – 12xy + 12x – 9xy + 3y2 – 18y + 12x – 4y + 24] + 13[3x2 – xy + 6x – 3xy + y2 – 6y – 6x + 2y – 12] = 0
7x2 + 7y2 – 168x + 112y – 364 = 0
x2 + y2 – 24x + 16y – 52 = 0
Question 6.
Show that the locus of the point of intersection of the lines x cos α + y sin α = a, x sin α – y cos α = b (α is a parameter) is a circle.
Solution:
The given lines are
x cos α + y sin α = a ………(1)
x sin α – y cos α = b ……….(2)
Let (x, y) be the point of intersection of (1) and (2).
The locus of the point (x, y) is obtained by eliminating a from equations (1) and (2).
Squaring and adding (1) and (2), we get
(x cos α + y sin α) (x sin α – y cos α) = a2 + b2
x2 cos2α + y2 sin2α + 2xy cos α sin α + x2 sin2α + y2 cos2α – 2xy cos α sin α = a2 + b2
x2 (cos2α + sin2α) + y2 (sin2α + cos2α) = a2 + b2
x2 + y2 = a2 + b2
∴ The locus of the point of intersection of the given lines is x2 + y2 = a2 + b2 is a circle.

Question 7.
Show that the locus of a point such that the ratio of the distance of it from two given points is constant k(≠ ±1) is a circle.
Solution:
Let P(x1, y1) be any point on the locus
and A = (-a, 0), B = (a, 0) be the two given points.
Given that PA : PB = k : 1

![]()
![]()