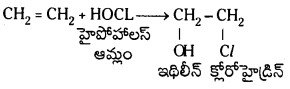
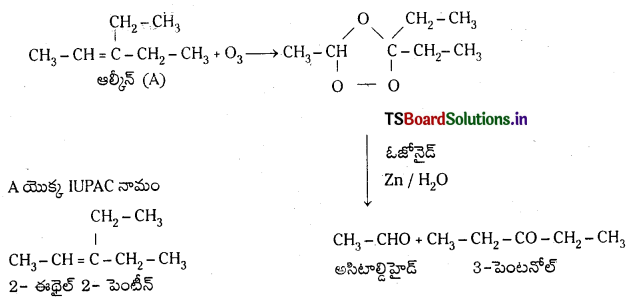
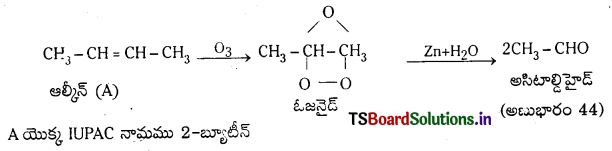
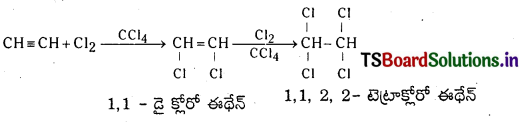
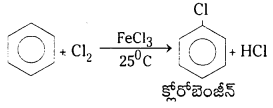
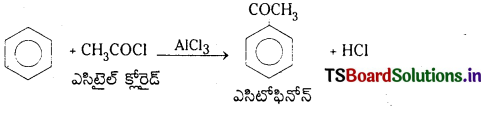
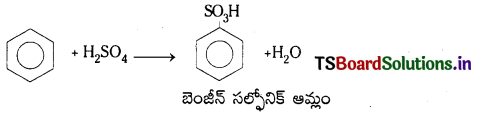
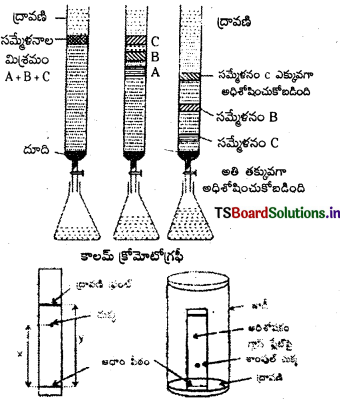
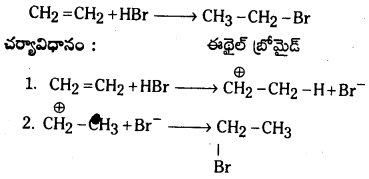
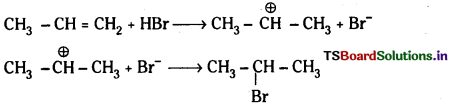
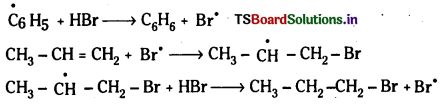
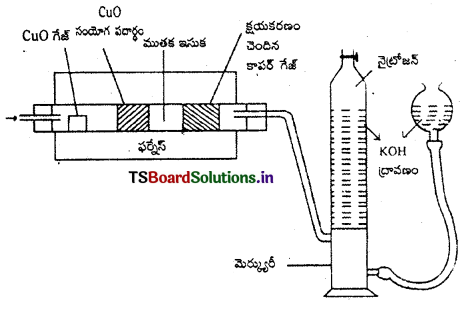
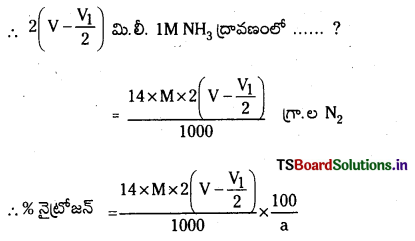
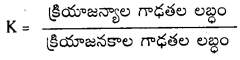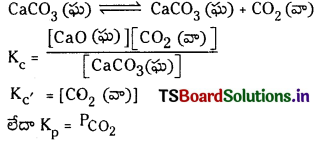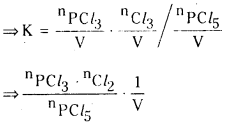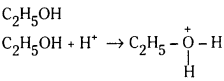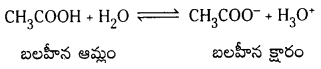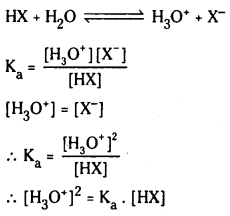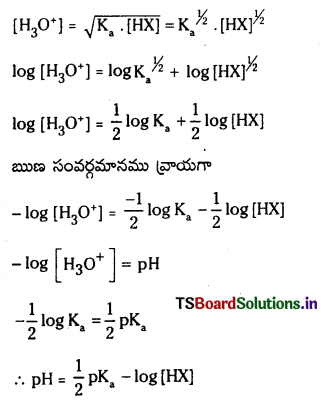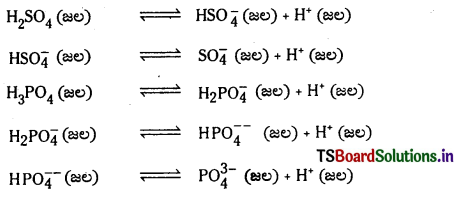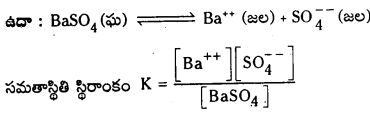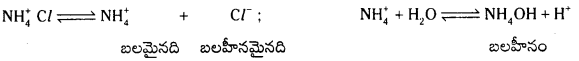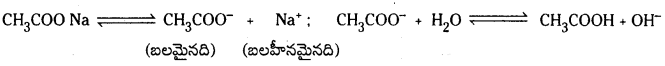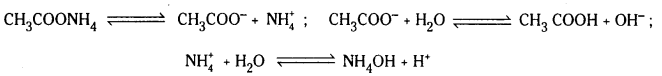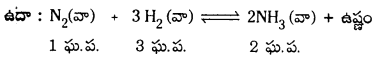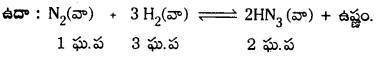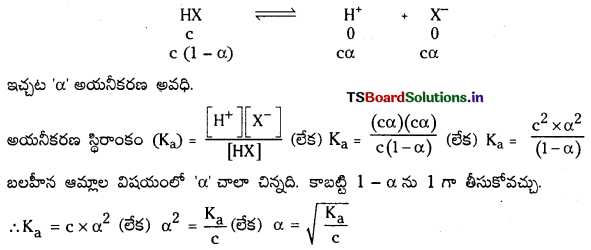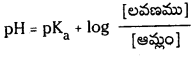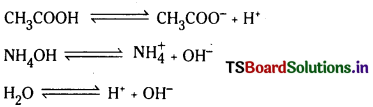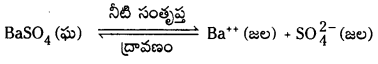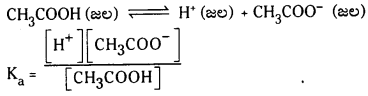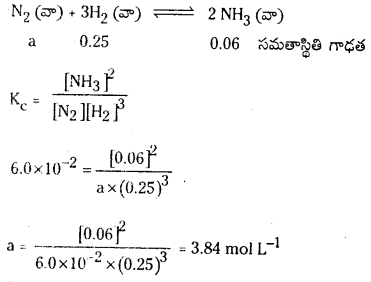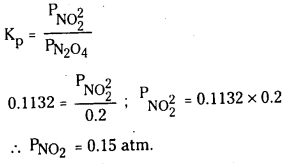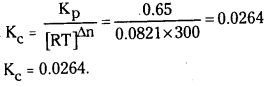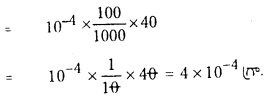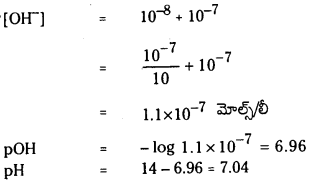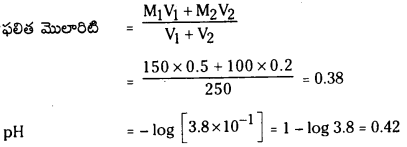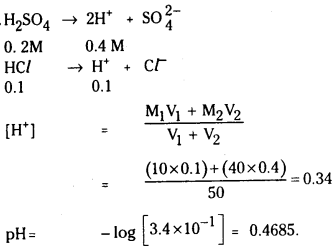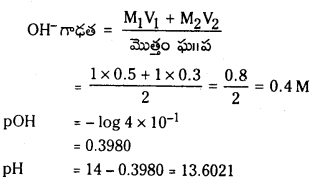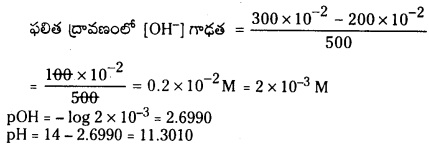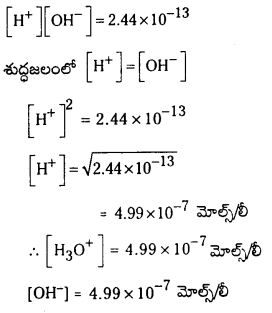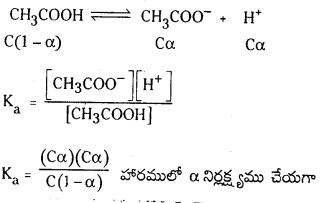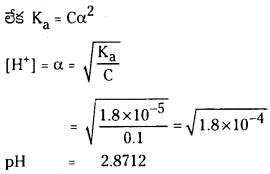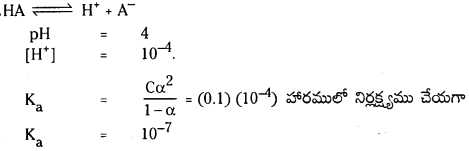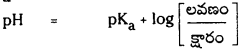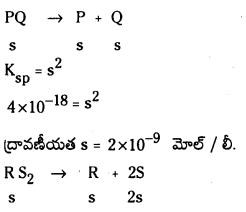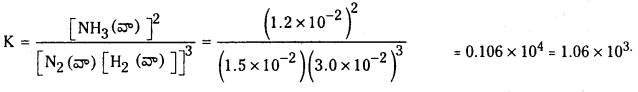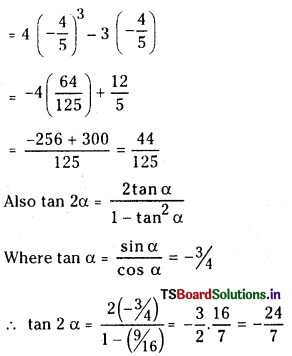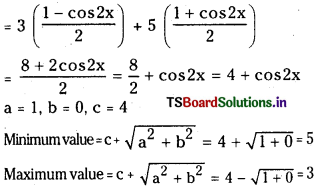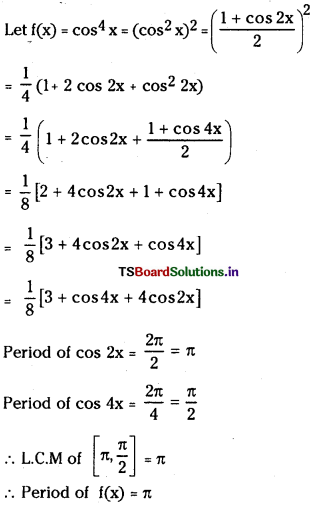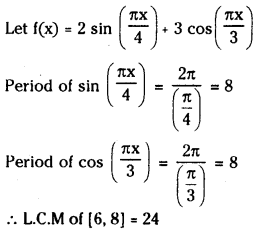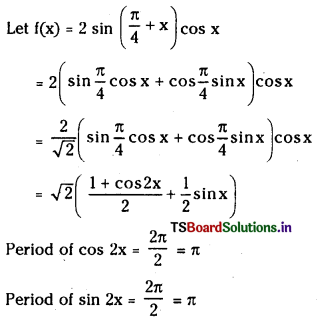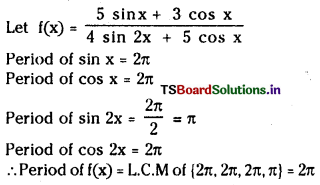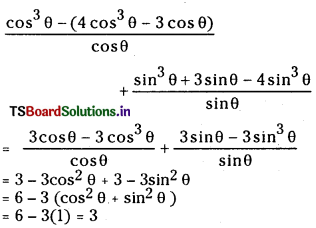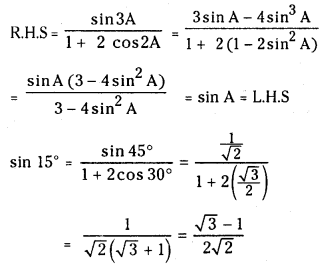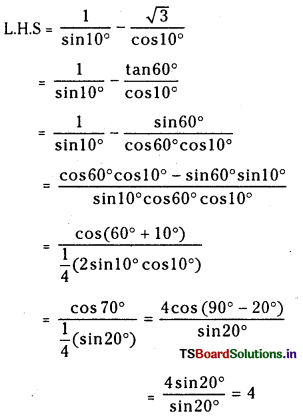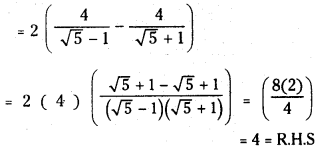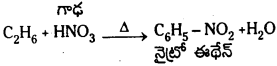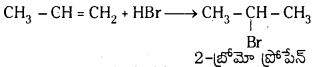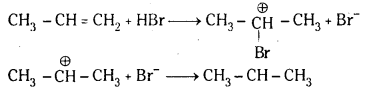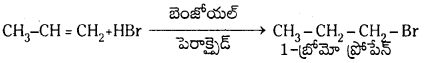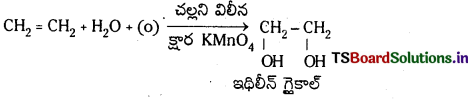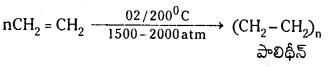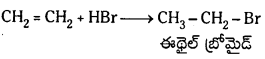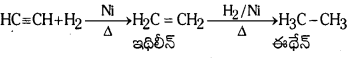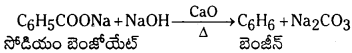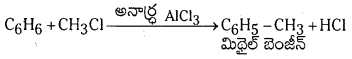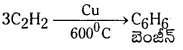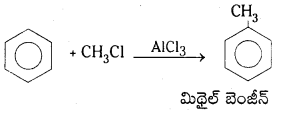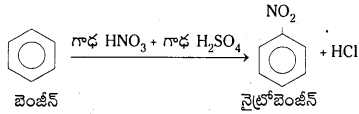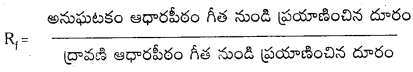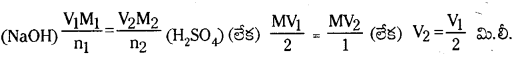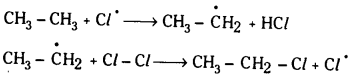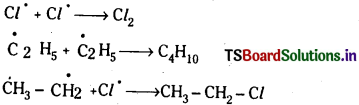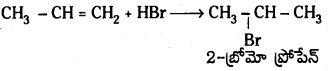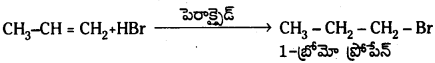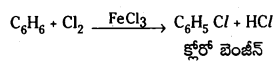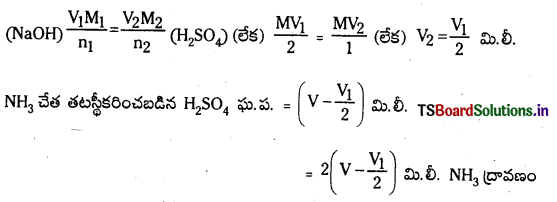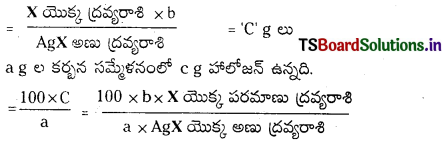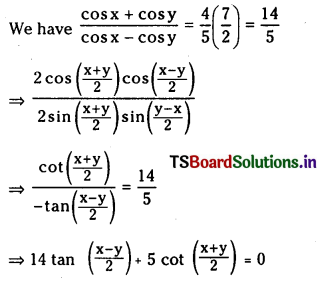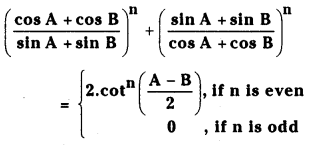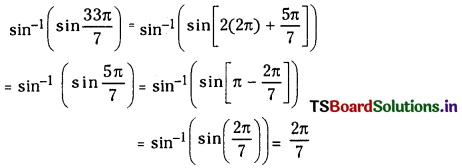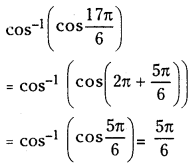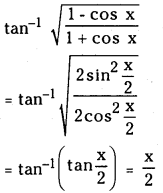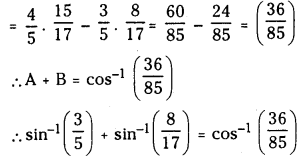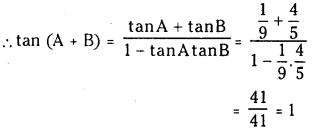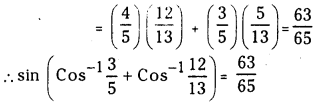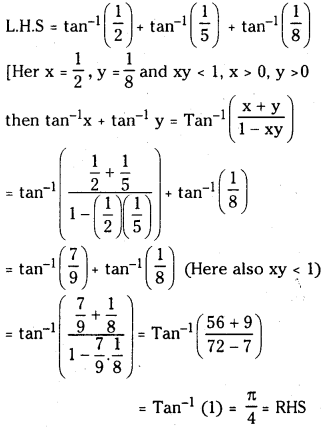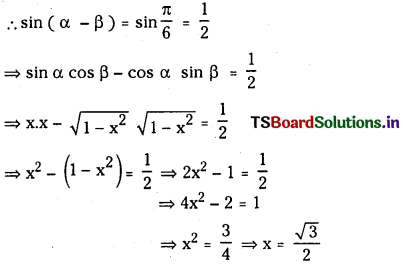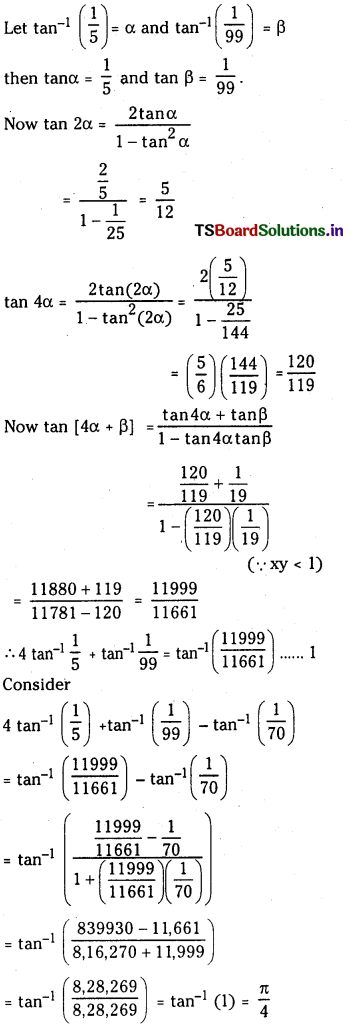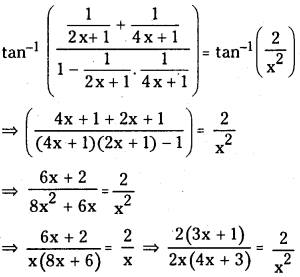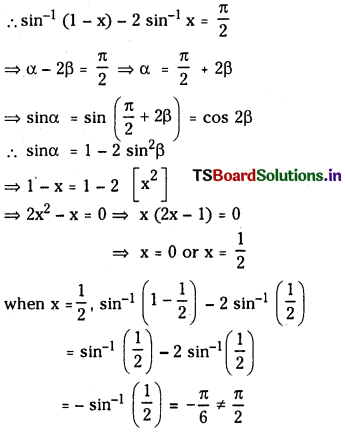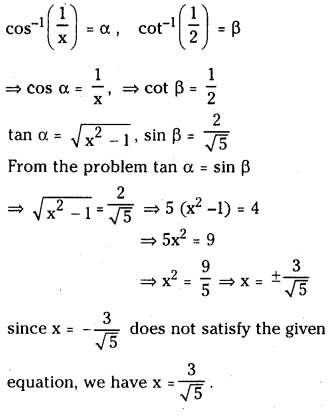Mahesh – Page 26 – TS Board Solutions

TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Ex 1.4

January 27, 2024January 25, 2024 by Mahesh

Students can practice TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Ex 1.4 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Exercise 1.4

Question 1.
Write the numbers using commas according to International system of numeration.
(i) 97645315
Answer:
97,645,315

(ii) 20048421
Answer:
20,048,421

(iii) 476356
Answer:
476,356

(iv) 9490026834
Answer:
9,490,026,834

Question 2.
Collect the mobile numbers of your friends and other family members. Write them using commas and read them in International system.
Answer:
1. 9,912,342,343
Nine billion nine hundred twelve mil-lion three hundred forty two thou-sand three hundred forty three.

2. 9,989,857,886
Nine billion nine hundred eighty nine million eight hundred fifty seven thousand eight hundred eighty six.

3. 9,849,258,633
Nine billion eight hundred forty nine million two hundred fifty eight thou-sand six hundred thirty three.

4. 9,032,050,053
Nine billion thirty two million fifty thousand fifty three.

5. 9,490,605,604
Nine billion four hundred ninety million six hundred five thousand six hundred four.

6. 9,440,824,201
Nine billion four hundred forty million eight hundred twenty four thousand two hundred one.

7. 9,949,584,445
Nine billion nine hundred forty nine million five hundred eighty four thousand four hundred forty five.

8. 9,848,212,356
Nine billion eight hundred forty eight million two hundred twelve thousand three hundred fifty six.

9. 9,440,172,042
Nine billion four hundred forty million one hundred seventy two thousand forty two.

10. 9,989,027,829
Nine billion nine hundred eighty nine million twenty seven thousand eight hundred twenty nine.

Question 3.
Write the numbers in words in both Indian and International system.
(i) 123115027
Answer:
Indian system: 12,31,15,027
Twelve crores thirty one lakh fifteen thousand twenty seven.

International system: 123,115,027 One hundred twenty three million one hundred fifteen thousand twenty seven.

(ii) 89643092
Answer:
Indian system: 8,96,43,092
Eight crores ninety six lakh forty three thousand ninety two.

International system: 89,643,092 Eighty nine million six hundred forty three thousand ninety two.

Question 4.
Read the number carefully and answer the following:
302,179,468
(i) The digit in millions place.
Answer:
The digit in millions place is 2.

(ii) The digit in hundreds place.
Answer:
The digit in hundreds place is 4.

(iii) The digit in ten millions place.
Answer:
The digit in ten millions place is 0.

(iv) How many millions are there in the number ?
Answer:
302 millions are there in the number.

TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Ex 1.3

January 27, 2024January 25, 2024 by Mahesh

Students can practice TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Ex 1.3 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Exercise 1.3

Question 1.
Write the numbers using commas according to place values.
(i) 11245670
Answer:
1,12,45,670

(ii) 22402151
Answer:
2,24,02,151

(iii) 30608712
Answer:
3,06,08,712

(iv) 190308020
Answer:
19,03,08,020

Question 2.
Write the numbers in words.
(i) 34,025
Answer:
34,025

(ii) 7,09,115
Answer:
7,09,115

(iii) 47,60,00,317
Answer:
47,60,00,317

(iv) 6,18,07,000
Answer:
6,18,07,000

Question 3.
Write the numbers in figures.
(i) Four lakh fifty seven thousand four hundred.
Answer:
4,57,400

(ii) Sixty lakh two thousand seven hundred seventy five.
Answer:
60,02,775

(iii) Two crore fifty lakh forty thousand three hundred and three.
Answer:
2,50,40,303

(iv) Sixty crore sixty lakh sixty thou-sand six hundred.
Answer:
60,60,60,600

Question 4.
Write the numbers in the expanded form.
(i) 6,40,156
Answer:
6,40,156 = (6 × 1,00,000) + (4 × 10,000) + (0 × 1,000) + (1 × 100) + (5 × 10) + (6 × 1)
= 60,00,000 + 40,000 + 100 + 50 + 6

(ii) 63,20,500
Answer:
63,20,500 = (6 × 10,00,000) +(3 × 1,00,000) + (2 × 10,000)+ (0 × 1,000) + (5 × 100) + (0 × 10) + (0 × 1)
= 60,00,000 + 3,00,000 + 20,000 + 500

(iii) 1,25,30,275
Answer:
1,25,30,275 = (1 × 1,00,00,000) + (2 × 10,00,000) + (5 × 1,00,000) + (3 × 10,000) + (0 × 1,000) + (2 × 100) + (7 × 10) + (5 × 1)
= 1,00,00,000 + 20,00,000 + 5,00,000 + 30,000 + 200 + 70 + 5

(iv) 75,80,19,202
Answer:
75,80,19,202 = (7 × 10,00,00,000) +(5 × 1,00,00,000) + (8 × 10,00,000) + (0 × 1,00,000) + (1 × 10,000) + (9 × 1,000) + (2 × 100) + (0 × 10) + (2 × 1)
= 70,00,00,000 + 5,00,00,000 + 80,00,000 + 10,000 + 9,000 + 200 + 2

Question 5.
Write the following numbers in short form (standard notation).
(i) 50,00,000 + 4,00,000 + 20,000 + 8,000 + 500 + 20 + 4
Answer:
54,28,524

(ii) 6,00,00,000 + 40,00,000 + 3,00,000 + 20,000 + 500 + 1
Answer:
6,43,20,501

(iii) 3,00,00,000 + 3,00,000 + 7,000 + 800 + 80 + 1
Answer:
3,03,07,881

(iv) 7,00,00,000 + 70,00,000 + 7,000 + 70
Answer:
7,70,07,070

Question 6.
Which is larger between each of these two? Use greater than symbol (>) and write.
(i) 4,67,612 or 18,71,964
Answer:
18,71,964 > 4,67,612
(∵ The number on the left side of the symbol has 7 digits while the number on the right side has only 6 digits)

(ii) 14,35,10,300 or 14,25,10,300
Answer:
14,35,10,300 > 14,25,10,300
(∵ The digits in ten lakhs place of left side number is greater than that of right side number (i.e.) 3 > 2)

Question 7.
Which is smaller between each of these two ? Use less than symbol (<) and write.
(i) 2,00,015 or 99,999
Answer:
99,999 < 2,00,015
(∵ The number on the left side of the symbol has 5 digits while the number on the right side has 6 digits).

(ii) 13,50,050 or 13,49,785
Answer:
13,49,785 < 13,50,050
(∵ The digit In ten thousands place of left side number is less than that of right side number (i.e.) 4 < 5).

Question 8.
Write any ten numbers with digits 5 in crores place, 2 in lakhs place, 1 in ten thousands place, 6 in tens place and 3 in ones place, (keep any digits in the remaining places)
Answer:
5 … 2 1 .. … 6 3 .
The required numbers are
(1) 5,92,18,563
(2) 5,82,17,463
(3) 5,72,16,363
(4) 5,62,15,263
(5) 5,52,14,163
(6) 5,42,13,063
(7) 5,32,11,963
(8) 5,22,10,863
(9) 5,12,09,763
(10) 5,02,08,663

TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Ex 1.5

January 25, 2024January 24, 2024 by Mahesh

Students can practice TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Ex 1.5 to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Exercise 1.5

Question 1.
The number of people who visited during common wealth games in New Delhi for the first four days was re-corded as 15,290, 14,181, 14,235 and 10,578. Find the total number of people visited in these four days ?
Answer:
Number of people visited common wealth games on the first day = 15,290
Number of people visited common wealth games on the second day = 14,181
Number of people visited common wealth games on the third day = 14,235
Number of people visited common wealth games on the fourth day = 10,578
Total number of people who visited in these four days = 15,290
= 15,290 + 14,181 + 14,235 + 10,578 = 54,284

Question 2.
In Lok Sabha election, the elected candidate got 5,87,500 votes and defeated candidate got 3,52,768. By how many votes did the winner win the election ?
Answer:
Number of votes the winner got = 5,87,500
Number of votes the defeated candidate got = 3,52,768
Number of votes that the winner got more than the defeated candidate
= 5,87,500 – 3,52,768 = 2,34,732
By 2,34,732 votes did the winner win the election.

Question 3.
Write the greatest and smallest 5- digit number formed by the digits 5, 3, 4, 0 and 7 and find their difference.
Answer:
The digits given are 5, 3, 4, 0, 7. The greatest 5-digit number formed with the given digits = 75430
The smallest number formed with the given digits = 30457
The difference between these numbers = 75430 – 30457 = 44973

Question 4.
A bicycle industry makes 3,125 bicycles each day. Find the total number of bicycles manufactured in the month of July ?
Answer:
Number of days in month of July = 31
Number of bicycles made in one day = 3,125
Number of bicycles made in 31 days = 31 × 3,125 = 96,875

Question 5.
A helicopter covers 600 km in 1 hour. How much distance will it cover in 4 hours ? Express your answer in metres.
Answer:
Distance covered by helicopter in 1 hour = 600 km
Distance covered in 4 hours = 4 × 600 km = 2400 km
We know that 1km = 1000 metres
∴ Distance covered by helicopter in 4 hours = 2400 km
= 2400 × 1000 metres
= 24,00,000 metres

Question 6.
The total weight of 5 biscuit packets of same size is 8 kg 400 grams. What is the weight of each packet ?
Answer:
The total weight of 5 biscuit packets (of same size) = 8 kg 400 grams
∴ The weight of each packet
= 8 kg 400 gms ÷ 5
= 1 kg 680 gms

Question 7.
Everyday Gayatri walks both the ways to attend the school. The distance between the school and her house is 1 km 875 m. Find the total distance she walked in 6 days ?
Answer:
Distance between the school and her house = 1 km 875 m
Distance Gayatri walks everyday from , her house to the school and vice-versa = 1 km 875 m + 1 km 875 m = 3 km 750 m
Total distance Gayatri walked in 6 days
= 3 km 750 m × 6 = 22 km 500 m

Question 8.
The cloth required to make a shirt of school uniform for each boy is 1 m 80 cm. How many shirts can tailor stitch using 40 m. of cloth ? How much cloth will be left ?
Answer:
The cloth to be stitched = 40 m = 40 × 100 cm
(∵ 1 metre = 100 cm)
= 4000 cm
The cloth required for one shirt
= 1 m 80 cm
= 180 cm (∵ 1 metre =100 cms)
Number of shirts can be stitched = \(\frac{4000}{180}\)
= 22\(\frac{2}{9}\)
The tailor can stitch 22 shirts.
The cloth will be left = \(\frac{2}{9}\) × 180
= 40 cm

Question 9.
The rate of petrol is ₹ 60 per litre. A petrol bunk sells 750 litres of petrol on a day. How much money do they get at the end of the day ?
Answer:
The rate of 1 litre of petrol = Rs. 60
The rate of 750 litres of petrol = ₹ 60 × 750 = ₹ 45000
The money they get at the end of the day = ₹ 45,000

TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(a)

January 25, 2024January 24, 2024 by Mahesh

Students must practice this TS Intermediate Maths 2B Solutions Chapter 3 Parabola Ex 3(a) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Exercise 3(a)

Question 1.
Find the vertex and focus of 4y² + 12x – 20y + 67 = 0.
Solution:
Given equation is 4y² + 12x – 20y + 67 = 0
⇒ 4y² – 20y = -12x – 67
⇒ 4(y² – 5y) = -12x – 67
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(a) I Q1

Question 2.
Find the vertex and focus of x² – 6x – 6y + 6 = 0.
Solution:
The given equation is x² – 6x – 6y + 6 = 0
⇒ x² – 6x = 6y – 6
⇒ x² – 6x + 9 = 6y – 6 + 9 = 6y + 3
⇒ (x – 3)² = \(6\left(y+\frac{1}{2}\right)=6\left(y-\left(-\frac{1}{2}\right)\right)\)
This is of the form (x – h)² = 4a(y – k)
where h = 3, 4a = 6 ⇒ a = \(\frac{3}{2}\) and k = \(\frac{-1}{2}\)
Vertex = (h, k) = (3, \(\frac{-1}{2}\))
Focus = (h, a + k) = (3, \(\frac{3}{2}-\frac{1}{2}\)) = (3, 1)

Question 3.
Find the equations of the axis and directrix of the parabola y² + 6y – 2x + 5 = 0.
Solution:
The given equation is y² + 6y – 2x + 5 = 0
⇒ y² + 6y = 2x – 5
⇒ y² + 6y + 9 = 2x – 5 + 9 = 2x + 4
⇒ (y + 3)² = 2(x + 2)
⇒ [y – (-3)]² = 2[x – (-2)]
This is of the form (y – k)² = 4a(x – h)
where k = -3, 4a = 2 ⇒ a = \(\frac{1}{2}\), h = -2
∴ Axis is y – k = 0 ⇒ y + 3 = 0
and Directrix is x – h + a = 0
⇒ x + 2 + \(\frac{1}{2}\) = 0
⇒ x + \(\frac{5}{2}\) = 0
⇒ 2x + 5 = 0

Question 4.
Find the equations of the axis and directrix of the parabola 4x² + 12x – 20y + 67 = 0.
Solution:
Given equation is 4x² + 12x – 20y + 67 = 0
⇒ 4(x² + 3x) = 20y – 67
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(a) I Q4

Question 5.
Find the equation of a parabola whose focus is S(1, -7) and whose vertex is A(1, -2). (New Model Paper, Mar. ’12)
Solution:
Given that vertex A(h, k) = (1, -2) and focus S = (1, -7).
Since the x coordinates of A and S are equal and equal to 1,
the axis of the parabola is x = 1 and it is a line parallel to the y-axis.
Also, the focus is below the vertex.
∴ The equation of the parabola is (x – h)² = -4a(y – k)
⇒ (x – 1)² = -4a(y + 2) ……..(1)
where a = AS = \(\sqrt{(1-1)^2+(-2+7)^2}\) = 5
∴ From (1) we have (x – 1)² = -20(y + 2)
Which is the equation of the required parabola.

Question 6.
Find the equation of the parabola whose focus is S(3, 5) and vertex is A(1, 3). (E.Q.)
Solution:
Given vertex A = (1, 3) and focus S = (3, 5)
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(a) I Q6
Let the directrix meets the axis of the parabola at Z(x, y), A is the midpoint of SZ.
Hence \(\frac{\mathrm{x}+3}{2}\) = 1 and \(\frac{\mathrm{y}+5}{2}\) = 3
⇒ x = -1 and y = 1
∴ Coordinates of Z = (-1, 1)
Slope of AZ = \(\frac{5-1}{3+1}\) = 1
∴ Slope of directrix = -1 (∵ directrix is perpendicular to \(\overline{\mathrm{AS}}\))
∴ Equation of directrix L = 0 is y – 1 = -1(x + 1)
⇒ x + y = 0
Let P(x₁, y₁) be any point on the parabola and PM is the perpendicular distance from P to the directrix L = 0 is
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(a) I Q6.1
⇒ \(\mathrm{x}_1^2+\mathrm{y}_1^2\) – 2x₁y₁ – 12x₁ – 20y₁ + 68 = 0
∴ Locus of (x₁, y₁) is the equation of parabola given by x² + y² – 2xy – 12x – 20y + 68 = 0.

Question 7.
Find the equation of the parabola whose latus rectum is the line segment joining points (-3, 2) and (-3, 1). (E.Q.)
Solution:
Given L = (-3, 2) and L’ = (-3, 1) be the two end points of the latus rectum of the parabola.
Since the x coordinates of L and L’ are ‘1’ we have an axis of the parabola parallel to the x-axis.
∴ The equation of the required parabola is (y – k)² = ±4a(x – h)
The length of the latus rectum LL’ = 4a
⇒ 4a = \(\sqrt{(-3+3)^2+(2-1)^2}\) = 1
⇒ a = \(\frac{1}{4}\)
Let S be the focus of the required parabola Then
S = mid point of LL’ = (h, k)
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(a) I Q7

Question 8.
Find the position (Interior or exterior or on) of the following points with respect to the parabola y² = 6x.
(i) (6, -6)
(ii) (0, 1)
(iii) (2, 3)
Solution:
Given the equation of a parabola is y² – 6x = 0
Comparing with y² = 4ax
we have 4a = 6
⇒ a = \(\frac{3}{2}\)
(i) Let P(x₁, y₁) = (6, -6) be the given point.
Then S₁₁ = \(\mathrm{y}_1{ }^2\) – 4ax₁
= (-6)² – 4(\(\frac{3}{2}\))(6)
= 36 – 36
= 0
∴ The point (6, -6) lies on the parabola y² = 6x.
(ii) Let P(x₁, y₁) = (0, 1) and \(\mathrm{y}_1{ }^2\) – 4ax₁
= 1 – 4(\(\frac{3}{2}\))(0)
= 1
∴ S₁₁ > 0 and the point (0, 1) lies outside the parabola y² = 6x.
(iii) Let P(x₁, y₁) = (2, 3) Then S₁₁ = \(\mathrm{y}_1{ }^2\) – 6x₁
= 9 – 6(2)
= -3 < 0
∴ Point (2, 3) lies inside the parabola y² = 6x.

Question 9.
Find the coordinates of the point on the parabola y = 8x whose focal distance is 10. (Mar. ’11)
Solution:
Given y² = 8x and Let P(x₁, y₁) be any point on the parabola y² = 8x
Comparing with y² = 4ax we get
4a = 8
⇒ a = 2
The focal distance of the parabola = x₁ + a = x₁ + 2
Given x₁ + 2 = 10
Since \(\mathrm{y}_1^2\), we have \(\mathrm{y}_1^2\) = 8(8) = 64
⇒ y₁ = ±8
Hence the required points on the parabola y² = 8x are given by (8, 8) and (8, -8).

Question 10.
If (\(\frac{1}{2}\), 2) is one extremity of a focal chord of the parabola y² = 8x. Find the coordinates of the other extremity. (June ’10)
Solution:
The given equation of a parabola is y² = 8x.
Comparing with y² = 4ax we get
4a = 8
⇒ a = 2
Let P(x₁, y₁) = (\(\frac{1}{2}\), 2) be one extremity of the focal chord.
Let Q(x₂, y₂) be the other extremity of the focal chord of the parabola y² = 8x.
∴ x₁x₂ = a² and y₁y₂ = -4a² (standard result)
⇒ \(\frac{1}{2}\)x₂ = 4
⇒ x₂ = 8
and 2y₂ = -4(4)
⇒ y₂ = -8
[∵ P(x₁, y₁) = (\(\frac{1}{2}\), 2)]
∴ The other extremity of the focal chord of the given parabola is (8, -8).

Question 11.
Prove that the point on the parabola y² = 4ax, (a > 0) nearest to the focus is its vertex.
Solution:
Given equation is y² = 4ax …….(1) and focus is S = (a, 0).
Let P(at², 2at) be any point on y² = 4ax.
Let f(t) = SP = \(\sqrt{\left(a t^2-a\right)+4 a^2 t^2}\)
= \(\sqrt{a^2\left[\left(t^2-1\right)^2+4 t^2\right]}\)
= a(t² + 1)
∴ f(t) = 2at and f”(t) = 2a > 0
∴ For f(t) to be minimum or maximum f'(t) = 0 ⇒ t = 0
∴ P = (0, 0).
Hence the f(t) has a minimum at t = 0 and the point on the parabola nearest to its focus is (0, 0).

Question 12.
A comet moves in a parabolic orbit with the sun as the focus. When the comet is 2 × 10⁷ Km. from the sun the line from the sun to it makes an angle \(\frac{\pi}{2}\) with the axis of the orbit. Find how near the comet comes to the sun.
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(a) I Q12
Let the equation of the parabolic orbit be y² = 4ax
Let S be the position of the sun (focus) on the axis of the parabola.
Let P be the position of a comet when it is at a distance of 2 × 10⁷ Km from the Sun ‘S’.
∴ SP = 2 × 10⁷
⇒ 2a = 2 × 10⁷ Km
⇒ a = 10⁷ Km
The distance of the comet from the Sun S is minimum when it is at the vertex.
∴ The nearest distance of the comet from the sun S is SA = a = 10⁷ Km.

II.

Question 1.
Find the locus of the point of trisection of the double ordinate of a parabola y² = 4ax, (a > 0).
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(a) II Q1
Let P(at², 2at), and P’ = (at², -2at) be the ends of double ordinate PP’ of the parabola y² = 4ax.
Let Q(x₁, y₁) be any point on the locus.
∴ Q(x₁, y₁) is the point of trisection of PP’.
⇒ Q(x₁, y₁) divides PP’ in the ratio 1 : 2.
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(a) II Q1.1
∴ 9\(\mathrm{y}_1^2\) = 4ax₁ and locus of (x₁, y₁) is 9y² = 4ax.

Question 2.
Find the equation of the parabola whose vertex and focus are on the positive x-axis at a distance ‘a’ and ‘a’ ‘ from the origin respectively.
Solution:
Let A(a, 0) be vertex and S(a’, 0) be the focus
We have
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(a) II Q2
∴ a = AS
∴ a = \(\sqrt{\left(a-a^{\prime}\right)^2}\) = a’ – a
The equation of the required parabola is (y – k)² = 4a(x – h)
⇒ (y – 0)² = 4(a’ – a) (x – a)
⇒ y² = 4(a’ – a) (2 – a)

Question 3.
If L and L’ are the ends of the latus rectum of the parabola x² = 6y, find the equation of OL and OL’ where ‘O’ is the origin. Also, find the angle between them.
Solution:
Given equation of parabola is x² = 6y ……..(1)
Comparing with y² = 4ax we have 4a = 6
⇒ a = \(\frac{3}{2}\)
Given L, L’, and the ends of the latus rectum of the parabola (1).
L = (2a, a) and L’ = (-2a, a)
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(a) II Q3

Question 4.
Find the equation of a parabola whose axis is parallel to the x-axis and which passes through the points (-2, 1), (1, 2), and (-1, 3).
Solution:
Let A = (-2, 1), B = (1, 2), C = (-1, 3) be the given points.
Let the equation of the parabola whose axis is parallel to the x-axis and passing through the points A, B, C be x = ly² + my + n …….(1)
If parabola (1) passes through A(-2, 1) then -2 = l + m + n …….(2)
If (1) passes through B(1, 2) then
1 = 4l + 2m + n ……..(3)
If (1) passes through C(-1, 3) then
-1 = 9l + 3m + n ……..(4)
From (2) and (3),
-3l – m = -3
⇒ 3l + m = 3 ……..(5)
From (3) and (4),
-5l – m = 2
⇒ 5l + m = -2 ………(6)
Solving (5) and (6), we get
-2l = 5
⇒ l = \(\frac{-5}{2}\)
and 5(\(\frac{-5}{2}\)) + m = -2
⇒ m = -2 + \(\frac{25}{2}\) = \(\frac{21}{2}\)
∴ From (2) we have l + m + n = 2
⇒ \(-\frac{5}{2}+\frac{21}{2}\) + n = -2
⇒ n + 8 = -2
⇒ n = -10
Hence the required equation of parabola from (1) is x = \(-\frac{5}{2} y^2+\frac{21}{2} y-10\)
⇒ 5y² + 2x – 21y + 20 = 0

Question 5.
Find the equation of the parabola whose axis is parallel to the y-axis and which passes through the points (4, 5), (-2, 11), and (-4, 21). (Mar. ’12)
Solution:
Let A(4, 5), B(-2, 11) and C(-4, 21) be the given points.
The equation of the parabola whose axis is parallel to the y-axis is
y = lx² + mx + n ………(1)
Since (1) passes through point A(4, 5) we have
5 = 16l + 4m + n ………(2)
Since (1) passes through point B(-2, 11) then
11 = 4l – 2m + n ……..(3)
Also since (1) passes through C(-4, 21) we have
21 = 16l – 4m + n ………(4)
From (2) and (3)
12l + 6m = -6
61 + 3m = -3
2l + m = -1 ……….(5)
From (3) and (4)
-12l + 2m = -10
⇒ -6l + m = -5
⇒ 6l – m = 5 ……….(6)
Solving (5) and (6) we get
8l = 4
⇒ l = \(\frac{1}{2}\)
∴ From (6)
3 – m = 5
⇒ -m = 2
⇒ m = -2
From (2) we have
16l + 4m + n = 5
⇒ 8 – 8 + n = 5
⇒ n = 5
∴ The equation of the required parabola passing through points A, B, C from (1) is
y = \(\frac{1}{2}\)x2 – 2x + 5
⇒ x2 – 4x – 2y + 10 = 0

III.

Question 1.
Find the equation of the parabola whose focus is (-2, 3) and whose directrix is the line 2x + 3y – 4 = 0. Also, find the length of the latus rectum and the equation of the axis of the parabola. (Mar. ’13)
Solution:
Let S = (-2, 3) be the focus and L = 2x + 3y – 4 = 0 be the directrix.
Let P(x₁, y₁) be any point on the parabola and PM be the perpendicular distance from P to the directrix.
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(a) III Q1
∴ The locus of P(x₁, y₁) is the equation of parabola given by 9x² – 12xy + 4y² + 68x – 54y + 153 = 0
The length of the latus rectum = 4a = 2(2a) = 2
The perpendicular distance from focus to the directrix = \(\frac{2|2(-2)+3(3)-4|}{\sqrt{4+9}}=\frac{2}{\sqrt{13}}\) units
Since the axis of the parabola is perpendicular to the directrix and passes through the focus (-2, 3).
The equation of the line passing through (-2, 3) and perpendicular to L = 0 is L(x – x₁) – a(y – y₁) = 0
⇒ 3(x + 2) – 2(y – 3) = 0
⇒ 3x – 2y + 12 = 0
∴ Axis of the parabola is 3x – 2y + 12 = 0.

Question 2.
Prove that the area of the triangle inscribed in the parabola y² = 4ax is \(\frac{1}{8a}\) |(y₁ – y₂) (y₂ – y₃) (y₃ – y₁)| sq. units. where y₁, y₂, y₃ are the ordinates of its vertices. (New Model Paper)
Solution:
Let A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) be the vertices of ∆ABC inscribed in a parabola y² = 4ax.
Then the area of the triangle ABC is ∆ = |\(\frac{1}{2}\)Σx₁(y₂ – y₃)| sq.units
In the parametric form x₁ = \(\mathrm{at}_1{ }^2\) and y₁ = 2at₁
∴ Take A = \(\left(a t_1{ }^2, 2 a t_1\right)\) = (x₁, y₁)
B = \(\left(a t_2{ }^2, 2 a t_2\right)\) = (x₂, y₂)
C = \(\left(a t_3{ }^2, 2 a t_3\right)\) = (x₃, y₃)
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(a) III Q2

∴ LHS = RHS and hence the area of the triangle inscribed in the parabola y² = 4ax is \(\frac{1}{8a}\) |(y₁ – y₂) (y₂ – y₃) (y₃ – y₁)| sq. units.

Question 3.
Find the coordinates of the vertex and focus, the equation of the directrix, and the axis of the following parabolas.
(i) y² + 4x + 4y – 3 = 0
Solution:
The given equation can be written as y² + 4y = -4x + 3
⇒ y² + 4y + 4 = -4x + 3 + 4 = -4x + 7
⇒ (y + 2)² = -4(x – \(\frac{7}{4}\))
⇒ \([y-(-2)]^2=-4\left[x-\left(\frac{7}{4}\right)\right]\)
Which is of the form (y – k)² = -4a(x – h)
Where (h, k) =(\(\frac{7}{4}\), 1) and a = 1,
Vertex = (h, k) = (\(\frac{7}{4}\), -2)
Focus = (h – a, k)
= (\(\frac{7}{4}\) – 1, -2)
= (\(\frac{3}{4}\), -2)
Axis of the parabola = y – k = 0
⇒ y + 2 = 0
Directrix of the parabola is x – h – a = 0
⇒ x – \(\frac{7}{4}\) – 1 = 0
⇒ x – \(\frac{11}{4}\) = 0
⇒ 4x – 11 = 0

(ii) x² – 2x + 4y – 3 = 0
Solution:
The given equation can be written as x² – 2y = -4y + 3
⇒ x² – 2x + 1 = -4y + 3 + 1 = -4y + 4
⇒ (x – 1)² = -4(y – 1)
This is of the form (x – h)² = -4a(y – k) whose a = 1, (h, k) = (1, 1)
Vertex = (h, k) = (1, 1)
Focus = (h, k – a) = (1, 1 – 1) = (1, 0)
Axis is x – h = 0 ⇒ x – 1 = 0
Directrix is y – k – a = 0
⇒ y – 1 – 1 = 0
⇒ y – 2 = 0
⇒ y = 2

TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు

January 27, 2024January 24, 2024 by Mahesh

Telangana TSBIE TS Inter 1st Year Chemistry Study Material 7th Lesson రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు Textbook Questions and Answers.

TS Inter 1st Year Chemistry Study Material 7th Lesson రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు

అత్యంత లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 1.
రసాయన సమతాస్థితి నియమం తెలపండి.
జవాబు:
నిర్దిష్ట ఉష్ణోగ్రత వద్ద, సమతుల్యం చేయబడిన రసాయన సమీకరణంలోని, క్రియాజన్యాల గాఢతలను సూచించే పదాలకు, వాటి సంబంధిత స్థాయికియోమెట్రిక్ గుణకాలను ఘాతాలుగా రాసి ఏర్పడిన గాఢత పదాల అంకగణిత లబ్ధాల విలువను సమీకరణంలోని క్రియాజనకాల గాఢతలను సూచించే పదాలకు వాటి స్థాయికియోమెట్రిక్ గుణకాలను ఘాతాలుగా రాసి, ఏర్పడిన గాఢత పదాల అంకగణిత లబ్ధం విలువతో భాగిస్తే, స్థిర విలువ లభిస్తుంది. దీనినే సమతాస్థితి నియమం లేదా రసాయన సమతాస్థితి నియమం అంటారు.
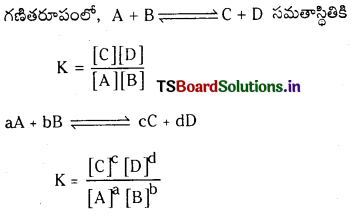
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 1
[A], [B], [C], [D] లు వరుసగా క్రియాజనకాల, క్రియాజన్యాల సమతాస్థితి గాఢతలు. K ను సమతా స్థిరాంకం అంటారు.
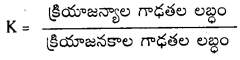
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 2

ప్రశ్న 2.
తెరచిన పాత్రలో నీరు, దాని బాష్పం మధ్య సమతాస్థితిని పొందగలమా ? వివరించండి.
జవాబు:
సమతాస్థితి ఏర్పడదు. బాష్పం తెరచి ఉన్న పాత్ర నుండి వాతావరణంలోనికి తప్పించుకొనిపోవుట వలన సమతాస్థితి ఏర్పడదు.

ప్రశ్న 3.
సమతాస్థితి స్థిరాంకం సమాసాలలో శుద్ధ ద్రవాల, శుద్ధ ఘనపదార్థాల గాఢతను ఎందుకు విస్మరిస్తాం ?
జవాబు:
విజాతీయ సమతాస్థితులలో శుద్ధద్రవాల, శుద్ధ ఘనపదార్థాల మోలార్ గాఢత స్థిరంగా ఉంటుంది. అందువల్ల సమతాస్థితి స్థిరాంకాల సమాసాలలో శుద్ధద్రవాల, శుద్ధ ఘనపదార్థాల గాఢతలను విస్మరించవచ్చు.
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 3

ప్రశ్న 4.
సమజాతి సమతాస్థితి అంటే ఏమి ? సమజాతి సమతాస్థితి చర్యలకు రెండు ఉదాహరణలు రాయండి.
జవాబు:
సమతాస్థితిలో ఉన్న అన్ని పదార్థాలు ఒకే ప్రావస్థలో ఉంటే ఆ సమతాస్థితిని సమజాతి సమతాస్థితి అంటారు.
ఉదా : N₂ (వా) + 3H₂ (వా) ⇌ 2NH₃ (వా)
CH₃COOH (ద్ర) + C₂H₂ OH (ద్ర) ⇌ CH₃COO C₂H₅ (ద్ర) ⇌ H₂O (ద్ర)

ప్రశ్న 5.
విజాతి సమతాస్థితి అంటే ఏమిటి ? విజాతి సమతాస్థితి చర్యలకు రెండు ఉదాహరణలు రాయండి.
జవాబు:
సమతాస్థితిలో ఉన్న పదార్థాలు భిన్న ప్రావస్థలలో ఉంటే, అటువంటి సమతాస్థితిని విజాతి సమతాస్థితి అంటారు.
ఉదా : CaCO₃ (ఘ) ⇌ CaO (ఘ) + CO₂ (వా)
H₂O (ద్ర) ⇌ H₂O (వా)

ప్రశ్న 6.
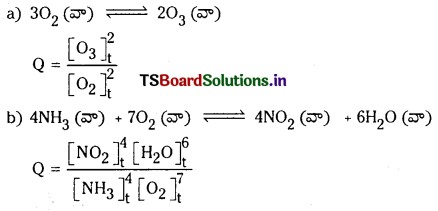
కింది చర్యలకు, చర్యా భాగఫలం Q విలువను రాయండి.
a) 3O₂ (వా) ⇌ 2O₃ (వా)
b) 4NH₃ (వా) + 7O₂ (వా) ⇌ 4NO₂ (వా) + 6H₂O (వా)
జవాబు:
చర్యా భాగఫలం :
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 4

ప్రశ్న 7.
సమతాస్థితి స్థిరాంకం నిర్వచించండి.
జవాబు:
సమతాస్థితిలో ఉన్న వ్యవస్థలో క్రియాజన్యాల గాఢతల లబ్ధానికి, క్రియాజనకాల గాఢతల లబ్ధానికి గల నిష్పత్తిని సమతాస్థితి స్థిరాంకం అంటారు. కింది సమీకరణంలో స్థాయికియోమెట్రిక్ గుణకాలు ఉన్నపుడు ఆ గుణకాలను సంబంధిత గాఢతా పదాలకు ఘాతాలుగా రాయవలెను.
aA + bB ⇌ cC + dD
K_c = \(\frac{[\mathrm{C}]^c[\mathrm{D}]^{\mathrm{d}}}{[\mathrm{A}]^{\mathrm{a}}[\mathrm{B}]^b}\) ; [A], [B], [C], [D] లు వరుసగా క్రియాజనకాల, క్రియాజన్యాల సమతాస్థితి గాఢతలు.

ప్రశ్న 8.
ఒక వాయుస్థితి చర్యకు, సమతాస్థితి స్థిరాంక సమాసం కింది విధంగా ఉంది.
K_c = \(\frac{\left[\mathrm{NH}_3\right]^4\left[\mathrm{O}_2\right]^5}{[\mathrm{NO}]^4\left[\mathrm{H}_2 \mathrm{O}^6\right]^6}\) దీనికి సంబంధించిన సమతుల్యం చేయబడిన రసాయన సమీకరణం రాయండి.
జవాబు:
4NO (వా) + 6H₂O (వా) ⇌ 4NH₃ + 5O₂ (వా)

ప్రశ్న 9.
K_p, K_c ల మధ్య సంబంధం రాయండి.
జవాబు:
K_p = K_c [RT]^Δn.
K_p = K. (∴ Δn = 0)
వాయు స్థితిలోని క్రియాజన్యాల మోల్ల సంఖ్య, వాయుస్థితిలోని క్రియాజనకాల మోత్ల సంఖ్యకు సమానమైనపుడు K_p విలువ, K_c విలువ సమానము.

ప్రశ్న 10.
ఏ పరిస్థితులలో ఒక చర్యకు K_p, K_cలు సంఖ్యాపరంగా సమానం ?
జవాబు:
వాయుస్థితిలోని క్రియాజన్యాల మోత్ల సంఖ్య, వాయుస్థితిలోని క్రియాజనకాల మోల్ల సంఖ్యకు సమానమైనపుడు
K_p విలువ, K_c విలువ సమానము. Δn = 0;
K_p = K_c [RT]^Δn
∴ K_p = K_c

ప్రశ్న 11.
K_p = K_c అయినటువంటి రెండు రసాయనిక సమతాస్థితి చర్యలను తెలపండి.
జవాబు:
H₂ (వా) + I₂ (వా) ⇌ 2HI (వా)
N₂ (వా) + O₂ (వా) ⇌ 2NO (వా)

ప్రశ్న 12.
K_p > K_c అయినటువంటి రెండు రసాయనిక సమతాస్థితి చర్యలను తెలపండి.
జవాబు:
2NOCl ⇌ 2NO (వా) + Cl₂ (వా)
CaCO₃ (ఘ) ⇌ CaO (ఘ) + CO₂ (వా)

ప్రశ్న 13.
K_p < K_c అయినటువంటి రెండు రసాయనిక సమతాస్థితి చర్యలను తెలపండి.
జవాబు:
N₂ (వా) + 3H₂ (వా) ⇌ 2NH₃ (వా)
2SO₂ (వా) + O₂ (వా) ⇌ 2SO₃ (వా)

ప్రశ్న 14.
K_cను K_p గా మార్చే సమీకరణాలను కింది చర్యలకు రాయండి.
a) CO (వా) + H₂O (వా) ⇌ CO₂ (వా) + H₂ (వా)
b) C₃H₈ (వా) + 5O₂ (వా) ⇌ 3CO₂ (వా) + 4H₂O (వా)
జవాబు:
a) CO (వా) + H₂O (వా)
Δn = 2 – 2 = 0

b) C₃H₈ (వా) + 5O₂ (వా) ⇌ 3CO₂ (వా) + 4H₂O (వా)
Δn = 7 – 6 = 1
K_p = K_c (RT)¹
K_p = K_c (RT)

ప్రశ్న 15.
రసాయనిక సమతాస్థితిని ప్రభావితం చేసే కారణాంశాలు ఏవి ?
జవాబు:

గాఢత
ఉష్ణోగ్రత
పీడనం.

ప్రశ్న 16.
వాయుస్థితి రసాయన సమతాస్థితిపై పీడనం ప్రభావం ఏమిటి ?
జవాబు:
వాయుస్థితి రసాయన స్థితిపై పీడన ప్రభావం, చర్యపై ఆధారపడి వుంటుంది.
a) మోల్ల సంఖ్యలో మార్పులేని చర్యలు.
N₂ (వా) + O₂ (వా) → 2NO (వా)
ఇటువంటి చర్యలపై పీడనం ప్రభావం ఉండదు.

b) N₂ (వా) + 3H₂ (వా) → 2NH₃ (వా)
ఈ రకం చర్యలలో పురోగామి చర్యలో మోల్ల సంఖ్య తగ్గుతుంది.
Δn = ఋణాత్మకం. ఇటువంటి చర్యలలో పీడనం పెంచితే ఘనపరిమాణం తగ్గే చర్య అనగా పురోగామి చర్య ప్రోత్సహించబడుతుంది.

c) PCl₅ (వా) ⇌ PCl₃ (వా) + Cl₂ (వా)
Δn = ధన్మాతకం.

ఇటువంటి చర్యలలో మోల్ల సంఖ్య పురోగామి చర్యలో పెరుగుతుంది. పీడనాన్ని పెంచినపుడు ఘనపరిమాణం తగ్గే చర్య అనగా తిరోగామి చర్య ప్రోత్సహించబడుతుంది.

ప్రశ్న 17.
సమతాస్థితి వద్ద ఉండే రసాయన చర్యలో క్రియాజనకాల గాఢతల మార్పు ప్రభావం ఏమిటి ?
జవాబు:
క్రియాజనకాల గాఢత పెరిగితే పురోగామి చర్య వేగం పెరుగుతుంది (సమతాస్థితి కుడివైపుకు జరుగుతుంది). క్రియాజన్యాలను కలిపితే క్రియాజన్యాల గాఢత పెరిగి, తిరోగామీ చర్య ప్రోత్సహించబడుతుంది.

ప్రశ్న 18.
సమతాస్థితిని ఉత్ప్రేరకం ప్రభావితం చేస్తుందా ?
జవాబు:
చేయలేదు. ఉత్ప్రేరకం, పురోగామి తిరోగామి చర్యలను సమానంగా ప్రోత్సహించి సమతాస్థితి త్వరితంగా ఏర్పడేటట్లు చేస్తుంది.

ప్రశ్న 19.
సమతాస్థితి స్థిరాంకం విలువ ఏ కారణాంశం మీద ఆధారపడి ఉంటుంది ?
జవాబు:
ఉష్ణోగ్రత. ఉష్ణోగ్రత మార్పువల్ల K_f, K_f లు ప్రభావితం అవుతాయి. అందువల్ల K = \(\frac{K_f}{K_b}\) విలువ ప్రభావితం అవుతుంది.

ప్రశ్న 20.
ఒక చర్య సమతాస్థితి స్థిరాంకాలు వరసగా 27°C, 127°C ల వద్ద 1.6 × 10^-3, 7.6 × 10^-2 ఈ చర్య ఉష్ణగ్రాహక చర్యా లేదా ఉష్ణమోచక చర్యా ?
జవాబు:
ఈ చర్యలో K_c విలువ పెరుగుతోంది. అందువల్ల ఈ చర్య ఉష్ణగ్రాహకచర్య. K_c = \(\frac{\mathrm{K}_{\mathrm{f}}}{\mathrm{K}_{\mathrm{b}}}\) ఉష్ణోగ్రత పెరిగితే K_f విలువ పెరిగి K_c విలువ కూడా పెరుగుతుంది. ఉష్ణోగ్రత పెరిగితే ఉష్ణగ్రాహక చర్యలు ప్రోత్సహించబడతాయి కాబట్టి పురోగామి చర్య ఉష్ణగ్రాహక చర్య.

ప్రశ్న 21.
సమతాస్థితి వద్ద ఉండే వ్యవస్థపై ఉష్ణోగ్రత ప్రభావం ఏమి ?
జవాబు:
ఉష్ణగ్రాహక చర్యలలో ఉష్ణరాశిని కూడా క్రియాజనకంగా పరిగణించవచ్చు. ఉష్ణోగ్రత పెరిగితే క్రియాజనకాలలో ఒకటైన ఉష్ణరాశి గాఢత పెరిగి, పురోగామి చర్య ప్రోత్సహించబడుతుంది. అనగా సమతాస్థితి కుడివైపుకు జరుగుతుంది.
N₂ (వా) + O₂ (వా) + ఉష్ణరాశి ⇌ 2NO (వా)
ఉష్ణోగ్రత పెరిగితే ఉష్ణగ్రాహకచర్య, ఉష్ణోగ్రతను తగ్గిస్తే ఉష్ణమోచక చర్య ప్రోత్సహించబడుతుంది.

ప్రశ్న 22.
ఒక ఉష్ణమోచక చర్య ఉష్ణోగ్రతను పెంచితే, ఆ చర్య సమతాస్థితి స్థిరాంకం ఏ మార్పుకు గురవుతుంది ?
జవాబు:
K_c = \(\frac{K_f}{K_b}\) ;
ఉష్ణోగ్రతను పెంచినపుడు ఉష్ణమోచక చర్య వేగం తగ్గుతుంది (K_f తగ్గుతుంది.) ఉష్ణగ్రాహక చర్య అయిన తిరోగామి చర్య వేగం పెరుగుతుంది (K_b పెరుగుతుంది.) అందువల్ల K విలువ తగ్గుతుంది.

ప్రశ్న 23.
వాయువు మాత్రమే పాల్గొనే చర్యకు AG° ద్వారా ఏ రకపు సమతాస్థిరాంకాన్ని లెక్కించవచ్చు ?
జవాబు:
ΔG° విలువ నుండి K_p విలువను లెక్కించవచ్చు.
AG° = – RT lnK
lnK = e^-ΔG°/RT
ఈ సమీకరణంలో ‘R’ ఉన్నది కనుక సమతాస్థిరాంకం K_p.

ప్రశ్న 24.
బ్రాన్ స్టెడ్ క్షారం అంటే ఏమిటి ? ఒక ఉదాహరణ తెలపండి.
జవాబు:
ప్రోటాన్ ను గ్రహించేది బ్రాన్టేడ్ క్షారం.
NH₃ + HCl ⇌ \(\mathrm{NH}_4^{+}\) + HCI^–
ఈ చర్యలో NH₃, HCl నుండి ప్రోటాన్ H⁺ ను స్వీకరిస్తుంది. అందువల్ల బ్రాన్టెడ్ క్షారం.

ప్రశ్న 25.
లూయీ ఆమ్లం అంటే ఏమిటి ? ఒక ఉదాహరణ తెలపండి.
జవాబు:
ఒంటరి ఎలక్ట్రాన్ జంటను స్వీకరించేది లూయీ ఆమ్లం. ఉదా : BF₃.

ప్రశ్న 26.
నీటి అయానిక అంటే ఏమిటి ?
జవాబు:
జలద్రావణంలో H⁺ అయానుల, OH^– అయానుల గాఢతల లబ్ధాన్ని నీటి అయానిక లబ్ధం అంటారు.
K_w = [H⁺] [OH^–]

ప్రశ్న 27.
K_w విలువ ఏమి ? దీని పరామితులు ఏమి ?
జవాబు:
K_w విలువ 25°C వద్ద 1.0 × 10^-14.
దాని యూనిట్లు మోల్² / లీ²

ప్రశ్న 28.
నీటి అయానిక లబ్ధం విలువపై ఉష్ణోగ్రత ప్రభావం తెలపండి.
జవాబు:
ఉష్ణోగ్రత పెరిగితే నీటి అయనీకరణం పెరిగి H⁺, OH^– ల గాఢతలు పెరుగుతాయి. అందువల్ల K_w విలువ పెరుగుతుంది.

ప్రశ్న 29.
H₂O + H₂O ⇌ H₃O⁺ + OH^–
25°C, 40°C ఉష్ణోగ్రతల వద్ద వరసగా నీటి అయానిక లబ్ధం విలువలు 1 × 10^–14, 3.0 × 10^-14 పై చర్య ఉష్ణమోచక చర్యా ? లేదా ఉష్ణగ్రాహక చర్యా ?
జవాబు:
ఉష్ణోగ్రత పెరిగితే నీటి అయానిక లబ్ధం విలువ పెరుగుతుంది. అందువల్ల నీటి అయనీకరణ చర్య ఉష్ణగ్రాహక చర్య అని తెలియుచున్నది. పై చర్య ఉష్ణగ్రాహక చర్య.

ప్రశ్న 30.
‘బ్రాన్ స్టెడ్ క్షారాలు అన్నీ లూయీ క్షారాలే’. వివరించండి.
జవాబు:
ప్రోటాను స్వీకరించేవి బ్రాన్స్టెడ్ క్షారాలు. ఒంటరి ఎలక్ట్రాన్ జంటను కలిగి ఉండి, దానిని దానం చేయగలిగే పదార్థాలన్నీ లూయీ క్షారాలు. ఈ పదార్థాలన్నీ ప్రోటాన్ ను స్వీకరించగలవు. అందువల్ల బ్రానెడ్ క్షారాలు లూయీ క్షారాలు ఒకటే.
H₃ N: + H⁺ → [H₃N → H]⁺

ప్రశ్న 31.
‘లూయీ ఆమ్లాలు అన్నీ బ్రానెడ్ ఆమ్లాలు కావు’. ఎందువల్ల ?
జవాబు:
ఒంటరి ఎలక్ట్రాన్ జంటను స్వీకరించే పదార్థాలు లూయీ ఆమ్లాలు.
ఉదా : BF₃ ఒంటరి ఎలక్ట్రాన్ జంట స్వీకరించగలదు. అందువల్ల లూయీ ఆమ్లం.
ప్రోటాన్ ను దానం చేయగలిగే పదార్థాలు బ్రాన్డెడ్ ఆమ్లాలు. ఉదా : HCl.
BF₃ లూయీ ఆమ్లం అయినప్పటికి దానియందు ప్రోటాన్ లేకపోవుట వలన బ్రాన్డెడ్ ఆమ్లం కాదు. అందువల్ల లూయీ ఆమ్లాలు బ్రాన్టెడ్ ఆమ్లాలు కానక్కరలేదు.

ప్రశ్న 32.
అయనీకరణం అవధి అంటే ఏమిటి ?
జవాబు:
అయనీకరణం చెందిన అణువుల సంఖ్యకు, మొత్తం అణువుల సంఖ్యకు గల నిష్పత్తిని అయనీకరణ అవధి అంటారు.

ప్రశ్న 33.
ఒక ఆమ్లం లేదా క్షారం బలాన్ని వ్యక్తం చేసే రాశి ఏది ?
జవాబు:
ఆమ్లము యొక్క విఘటన స్థిరాంకం K_a విలువ ఎక్కువగా ఉంటే అది బలమైన ఆమ్లము. అదేవిధంగా క్షారము యొక్క విఘటన స్థిరాంకం K_b విలువ ఎక్కువగా ఉంటే అది బలమైన క్షారం.

ప్రశ్న 34.
వాటి జలద్రావణాలలో, క్షార స్వభావం చూపే రెండు లవణాలను తెలపండి.
జవాబు:

సోడియం కార్బొనేట్ జలద్రావణం క్షారత్వాన్ని చూపుతుంది.
సోడియం ఎసిటేట్ జలద్రావణం క్షారత్వాన్ని చూపుతుంది.

ప్రశ్న 35.
వాటి జలద్రావణాలలో, ఆమ్ల స్వభావం చూపే రెండు లవణాలను తెలపండి.
జవాబు:

AlCl₃ జలద్రావణం ఆమ్ల స్వభావాన్ని చూపుతుంది.
CuSO₄ జలద్రావణం ఆమ్ల స్వభావాన్ని చూపుతుంది.

ప్రశ్న 36.
ఆమ్ల బఫర్ ద్రావణం pH ను లెక్కించడానికి ఏ సమీకరణాన్ని ఉపయోగిస్తారు ?
జవాబు:
ఆమ్ల బఫర్ ద్రావణం pH ను కనుక్కోవడానికి సమీకరణం :

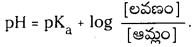
ప్రశ్న 37.
ఫాస్ఫారిక్ ఆమ్లం (H₃PO₄) కు మూడు అయనీకరణ స్థిరాంకాలు ఉన్నాయి. ఇవి K_a1, K_a2, K_a3. వీటిలో దేనికి కనిష్ఠ విలువ ఉంటుంది ? కారణాలు తెలపండి.
జవాబు:
K_a3 విలువ కనిష్ఠంగా ఉంటుంది. ఋణ అయాను (HP\(\mathrm{O}_4^{2-}\)) నుండి ప్రోటానును తొలగించుట కష్టం. దీనికి కారణం ఋణ అయానులో ప్రోటాను బలమైన స్థిర విద్యుదాకర్షణకు లోను కావడమే.

ప్రశ్న 38.
ఎత్తు ప్రదేశాలలో ఐస్ నెమ్మదిగా కరుగుతుంది. దీనికి కారణం వివరించండి.
జవాబు:
నీటికన్నా ఐస్కు ఘనపరిమాణం ఎక్కువ. పీడనం పెరిగితే ఐస్ నేరుగా మారే చర్య జరుగుతుంది. పీడనాన్ని తగ్గిస్తే ఈ చర్య నెమ్మదిగా జరుగుతుంది. ఎత్తు ప్రదేశాలలో పీడనం తక్కువగా ఉండడం వల్ల ఐస్ నెమ్మదిగా కరుగుతుంది.

లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 39.
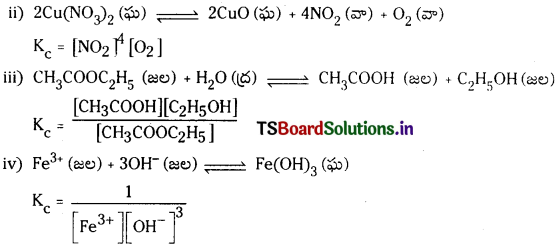
కింది చర్యలు ప్రతీదానికి సమతాస్థితి స్థిరాంకం K_c కు సమీకరణాలు రాయండి.
(i) 2NOCl (వా) ⇌ 2NO (వా) + Cl₂ (వా)
(ii) 2Cu (NO₃)₂ (ఘ) ⇌ 2CuO (ఘ) + 4NO₂ (వా) + O₂ (వా)
(iii) CH₃COOC₂H₅ (జల) + H₂O (ద్ర) ⇌ CH₃COOH (జల) + C₂H₅OH (జల)
(iv) Fe⁺³ (జల) + 3OH^– (జల) ⇌ Fe (OH)₃ (ఘ)
జవాబు:
i) 2NOCl (వా) ⇌ 2NO (వా) + Cl₂ (వా)
K_c = \(\frac{\left[\mathrm{NO}^2\left[\mathrm{Cl}_2\right]\right.}{[\mathrm{NOCl}]^2}\)
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 6

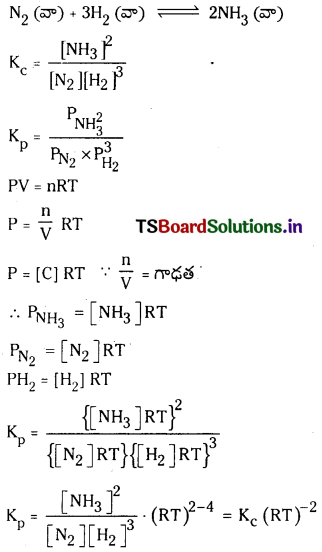
ప్రశ్న 40.
కింది సమతాస్థితి చర్యకు K_p, K_c ల మధ్య గల సంబంధాన్ని ఉత్పాదించండి. (March 2013)
N₂ (వా) + 3H₂ (వా) ⇌ 2H₃ (వా)
జవాబు:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 7

ప్రశ్న 41.
సమతాస్థితి స్థిరాంకాన్ని నిర్వచించండి. కింది చర్యకు, దాని ఉత్ర్కమణీయ చర్యకు సమతాస్థితి స్థిరాంకాన్ని రాయండి.
H₂ (వా) + I₂ (వా) ⇌ 2HI (వా)
ఈ రెండు స్థిరాంకాలు ఏ విధంగా సంబంధం కలిగి ఉన్నాయి ?
జవాబు:
సమతాస్థితిలో ఉన్న వ్యవస్థలో, క్రియాజన్యాల మోలార్ గాఢతల లబ్ధానికి, క్రియాజనకాల మోలార్ గాఢతల లబ్ధానికి గల నిష్పత్తిని సమతాస్థితి స్థిరాంకం అంటారు.
aA + bB ⇌ cC + dD
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 8

ప్రశ్న 42.
ఒక చర్య విస్తృతిని, సమతాస్థితి స్థిరాంకం ఏ విధంగా ఊహిస్తుంది ?
జవాబు:
ఒక చర్య సమతాస్థితి స్థిరాంకం సంఖ్యాత్మక విలువ, ఆ చర్య విస్తృతిని తెలుపుతుంది. K_c లేదా K_p ల పరిమాణం క్రియాజన్యాల గాఢతలకు అనులోమానుపాతంలోను, క్రియాజనకాల గాఢతలకు విలోమానుపాతంలోను ఉంటాయి. దీనిని అనుసరించి K విలువ అధికంగా ఉంటే క్రియాజన్యాలు అధికంగా ఏర్పడతాయి అని తెలుపుతుంది. అదేవిధంగా అల్పంగా ఉంటే క్రియాజన్యాలు అల్పంగా ఏర్పడతాయని తెలుస్తుంది.

K_c > 10³ అయితే క్రియాజనకాల కంటే క్రియాజన్యాలు అధికంగా వుంటాయి. అంటే K_c విలువ అత్యధికంగా ఉన్నట్లైతే చర్య సుమారుగా పూర్తిగా జరుగుతుందని ఊహించవచ్చు.

ఉదా : 500 K వద్ద H₂, O₂ తో జరిపే చర్యకు సమతాస్థితి స్థిరాంకం విలువ అత్యధికంగా ఉంది.
K_c = 2.4 × 10⁴⁷
K_c < 10^-3 అయితే క్రియాజనకాలు, క్రియాజన్యాల కంటే అధికంగా ఉంటాయి. K_c విలువ అతి తక్కువ అయితే ఆ చర్య అరుదుగా జరుగుతుంది.
ఉదా : 298 K వద్ద N₂ (వా) + O₂ (వా) ⇌ 2NO (వా) చర్యకు K_c = 4.8 × 10^-31
K_c విలువ 10^-3 కు మధ్యగా ఉండినట్లైతే చర్యలో గమనించదగిన గాఢతలలో క్రియాజన్యాలు, క్రియాజనకాలు కూడా ఉంటాయి.

ప్రశ్న 43.
సమతాస్థితి నియమాన్ని వివరించండి. సమతాస్థితి గాఢతలు కింది విధంగా ఉండే సమతాస్థితికి K_cను లెక్కించండి.
[SO₂] = 0.60 M, [O₂] = 0.82 M, [SO₃] = 1.90 M ?
2SO₂ (వా) + O₂ (వా) ⇌ 2SO₃ (వా)
జవాబు:
సమతాస్థితి నియమం : నిర్దిష్ట ఉష్ణోగ్రత వద్ద, సమతుల్యం చేయబడిన రసాయన సమీకరణంలోని, క్రియాజన్యాల గాఢతలను సూచించే పదాలకు, వాటి సంబంధిత స్థాయికియోమెట్రిక్ గుణకాలను ఘాతాలుగా రాసి ఏర్పడిన గాఢత పదాల అంకగణిత లబ్ధాల విలువను సమీకరణంలోని క్రియాజనకాల గాఢతలను సూచించే పదాలకు వాటి స్థాయికియోమెట్రిక్ గుణకాలను ఘాతాలుగా రాసి, ఏర్పడిన గాఢత పదాల అంకగణిత విలువతో భాగిస్తే, స్థిర విలువ లభిస్తుంది. దీనినే సమతాస్థితి నియమం లేదా రసాయన సమతాస్థితి నియమం అంటారు.
2SO₂ (వా) + O₂ (వా) ⇌ 2SO₃ (వా)
K_c = \(\frac{\left[\mathrm{SO}_3\right]^2}{\left[\mathrm{SO}_2\right]^2\left[\mathrm{O}_2\right]}\) = \(\frac{(1.9)^2}{(0.6)^2(0.82)}\) = 12.229 mol L^-1

ప్రశ్న 44.
సీలు చేయబడి ఉన్న సోడా నీటి సీసాను తెరచినప్పుడు ఎందుకు వాయువు బుసబుస పొంగుతూ బయటకు వస్తుంది?
జవాబు:
సీలు చేయబడిన సోడా నీటి సీసాలో పీడనం అధికం. CO₂ అధికంగా నీటియందు కరిగి ఉండి, సమతాస్థితిలో ఉంటుంది.
CO₂ (వా) + H₂O (ద్ర) ⇌ H₂CO₃ (వా)
పీడనం అధికంగా ఉన్నపుడు, సమతాస్థితి కుడివైపుకు జరిగి, CO₂ అధికంగా నీటిలో కరిగి ఉంటుంది. పీడనాన్ని తగ్గిస్తే, అంటే సీసా మూతను తెరిస్తే సమతాస్థితి ఎడమవైపుకు జరిగి, CO₂ ఏర్పడి బుసబుసమని పొంగుతూ బయటకు వస్తుంది.

ప్రశ్న 45.
కింది వాటి ప్రాముఖ్యం తెలపండి.
a) అతి ఎక్కువ K విలువ
b) అతి తక్కువ K విలువ
c) K విలువ 1.0 గా ఉన్నది.
జవాబు:
a) K విలువ అధికంగా వున్నపుడు క్రియాజనకాల కంటే క్రియాజన్యాలు అధికంగా వుంటాయి. అంటే K విలువ అత్యధికంగా వున్నట్లైతే చర్య సుమారుగా పూర్తిగా జరుగుతుంది.

b) K విలువ అల్పంగా ఉంటే క్రియాజనకాలు, క్రియాజన్యాల కంటే అధికంగా వుంటాయి. K విలువ అతి తక్కువ అయితే, ఆ చర్య అరుదుగా జరుగుతుంది.

c) K విలువ 1.0 అయితే క్రియాజనకాలు 50% వరకు క్రియాజన్యాలుగా మారినవని అర్థము. పురోగామి, తిరోగామి వేగ స్థిరాంకాలు సమానం అని అర్థము.

ప్రశ్న 46.
Q, K లను సరిపోల్చడం ఎందుకు ఉపయోగపడుతుంది ? కింది వాటిలో పరిస్థితులు ఏమి ?
(a) Q = K
(b) Q < K (c) Q>K
జవాబు:
క్రియాజన్యాల మోలార్ గాఢతల లబ్ధానికి, క్రియాజనకాల మోలార్ గాఢతల లబ్ధానికి గల నిష్పత్తిని చర్య యొక్క భాగఫల స్థిరాంకం Q అంటారు. Qను లెక్కించేటపుడు సమతాస్థితి గాఢతలను వాడనవసరం లేదు.
Q విలువను సమతాస్థితి స్థిరాంకం K తో పోలిస్తే, చర్య జరిగే దిశను ఊహించవచ్చు.

Q > K అయితే తిరోగామి చర్య ప్రోత్సహించబడుతుంది. (ఉత్రమ చర్య)
Q < K అయితే సమతాస్థితిని తిరిగి పొందే విధంగా చర్య పురోగామి దిశలో పయనిస్తుంది.
Q = K అయితే, చర్య సమతాస్థితిలో ఉంటుంది.

ప్రశ్న 47.
Cl₂ (వా) + F₂ (వా) ⇌ 2Cl F (వా), K_c = 19.9
పై చర్యలోని పదార్థాల గాఢతలు కింది విధంగా ఉంటే చర్య ఏ విధంగా జరుగుతుంది ?
[Cl₂] = 0.4 mol L^–; [F₂] = 0.2 mol L^-1, [Cl F] = 7.3 mol L^–?
జవాబు:
Q = \(\frac{[\mathrm{ClF}]^2}{\left[\mathrm{Cl}_2\right]\left[\mathrm{F}_2\right]}\) = \(\frac{(7.3)^2}{0.04 \times 0.2}\)
= 6.66 × 10³
K_c విలువ కన్నా Q విలువ చాలా ఎక్కువగా ఉన్నది. అందువల్ల మరల సమతాస్థితిని ఏర్పరచడానికి తిరోగామి దిశలో చర్య జరుగుతుంది.

ప్రశ్న 48.
కింది వాటిలో దేనిలో క్రియాజనకాలు, క్రియాజన్యాలు గుర్తించగలిగిన గాఢతలలో ఉంటాయి ?
a) Cl₂ (వా) ⇌ 2Cl(వా) K_c = 5 × 10^-39
b) Cl₂ (వా) + 2NO (వా) ⇌ 2NOCl (వా) K_c = 3.7 × 10⁸
c) Cl₂ (వా) + 2NO₂ (వా) ⇌ 2NO₂(వా) K_c = 1.8
జవాబు:
a) Cl₂ (వా) ⇌ 2Cl(వా) K_c = 5 × 10^-39
ఈ చర్యకు K_c విలువ చాలా స్వల్పం. అందువల్ల పురోగామి చర్య చాలా స్వల్పంగా జరుగుతుంది. అందువల్ల సమతా వ్యవస్థలో క్రియాజనకమైన క్లోరిన్ ప్రధానంగా ఉంటుంది.

b) Cl₂ (వా) + 2NO (వా) ⇌ 2NOCl (వా) K_c = 3.7 × 10⁸
K_c విలువ ఎక్కువగా ఉన్నందున, పురోగామి చర్య అధికంగా జరిగి, సమతాస్థితి వద్ద ఉత్పన్నాలు అధికంగా వుంటాయి. ఉత్పన్నాల గాఢత అధికంగా వుంటుంది.

c) Cl₂ (వా) + 2NO₂ (వా) ⇌ 2NO₂(వా) K_c = 1.8
ఈ చర్యలో పురోగామి చర్య 50% కన్నా కొద్దిగా ఎక్కువ జరుగుతుంది. అందువల్ల ఈ చర్యలో క్రియాజనకాలు, క్రియాజన్యాలు గుర్తింపదగిన గాఢతలో ఉంటాయి.

ప్రశ్న 49.
సమతాస్థితిలో ఉండే వ్యవస్థ పీడనం మార్పు ద్వారా ప్రభావితం అయ్యే పరిస్థితులను ఏ విధంగా తెలుసుకొంటాం?
జవాబు:
సమతాస్థితిలో ఉండే వ్యవస్థపై పీడన ప్రభావాన్ని లీచాట్లెయర్ సూత్రం ద్వారా తెలుసుకోవచ్చు.

i) ఒక చర్యలో వాయుస్థితిలో ఉండే క్రియాజనకాల మొత్తం మోల్ల సంఖ్య వాయుస్థితిలో ఉండే క్రియాజన్యాల మొత్తం మోల్ల సంఖ్యకు సమానంగా ఉంటే, సమతాస్థితిపై పీడన ప్రభావం ఉండదు.
ఉదా : N₂ (వా) + O₂ (వా) ⇌ 2NO (వా)
ఈ చర్యపై పీడన ప్రభావం ఉండదు.

ii) క్రియాజనకాల, క్రియాజన్యాల మోత్ల సంఖ్య సమానంగా లేనపుడు పీడనాన్ని పెంచినపుడు మోత్ల సంఖ్య తగ్గేదిశగా (ఘనపరిమాణం తగ్గే దిశలో చర్య ప్రోత్సహించబడుతుంది).

a) N₂ (వా) + 3H₂ (వా) ⇌ 2NH₃ (వా)
ఈ చర్యలో అమ్మోనియా ఏర్పడుటలో మోల్ల సంఖ్య తగ్గుతుంది. అందువల్ల పీడనాన్ని పెంచినపుడు ఘనపరిమాణం తగ్గే దిశలో జరుగుతున్న పురోగామి చర్య జరుగుతుంది. అమ్మోనియా అధికంగా ఏర్పడుతుంది. పీడనాన్ని తగ్గిస్తే ఉత్రమచర్య జరిగి అమ్మోనియా విడిపోతుంది.

b) PCl₅ (వా) ⇌ PCl₃ (వా) + Cl₂ (వా)
ఈ చర్య పురోగామి దిశలో మోల్ల సంఖ్య మరియు ఘనపరిమాణం పెరుగుతాయి. పీడనాన్ని పెంచినపుడు ఘనపరిమాణం తగ్గే చర్య అయిన ఉత్రమచర్య జరిగి PCl₅ (వా) విఘటనం తగ్గుతుంది. పీడనం తగ్గిస్తే పురోగామి చర్య జరుగుతుంది.

లీచాట్లీయర్ సూత్రం ప్రకారం సమతాస్థితి వ్యవస్థపై పీడనాన్ని పెంచినపుడు ఘనపరిమాణం తగ్గే చర్య ప్రోత్సహించబడుతుంది. అనగా మోల్ల సంఖ్య తగ్గే దిశలో జరిగే చర్య జరుగుతుంది.

ప్రశ్న 50.
సమతాస్థితి స్థిరాంకం విలువ పరిమాణంపై ఉష్ణోగ్రతలో మార్పు ప్రభావాన్ని తెలుసుకొనేందుకు చర్య ఏ ధర్మం ఉపయోగపడుతుంది ?
జవాబు:
చర్య ఉష్ణోగ్రతలో మార్పు తటస్థపడితే సమతాస్థితి స్థిరాకం Kl_c విలువ కూడా మారుతుంది. సాధారణంగా సమతాస్థితి స్థిరాంకం ఉష్ణోగ్రతపై ఆధారపడే విషయం చర్య ΔH విలువ సంజ్ఞను అనుసరించి ఉంటుంది.

ఉష్ణమోచక చర్యల (ఋణ ΔH విలువ గలవి) ఉష్ణోగ్రత పెరుగుదలతో సమతాస్థితి స్థిరాంకం విలువ తగ్గుతుంది.
ఉష్ణగ్రాహక చర్యలలో (ధన ΔH విలువ గలవి) ఉష్ణోగ్రత పెరుగుదలతో సమతాస్థితి స్థిరాంకం విలువ కూడా పెరుగుతుంది.

ఉష్ణోగ్రతలో నూర్పులు సమతాస్థితి స్థిరాంకాలను, చర్యల రేటులను కూడా ప్రభావితం చేస్తాయి.

N₂ (వా) + 3H₂ (వా) ⇌ 2NH₃ (వా)
ΔH = 92.38 K.J mol^-1 చర్య ఆధారంగా జరిగే అమ్మోనియా ఏర్పడే చర్య ఉష్ణమోచక చర్య. లీచాట్లెయర్ సూత్రం అనుసరించి చర్య ఉష్ణోగ్రతను పెంచినట్లైతే చర్య సమతాస్థితి ఎడమవైపుగా జరుగుతుంది. ఫలితంగా అమ్మోనియా సమతాస్థితి గాఢత తగ్గుతుంది. మరో విధంగా తెలపాలి అంటే అల్పస్థాయి ఉష్ణోగ్రతలు అమ్మోనియా దిగుబడిని పెంచుతాయి. కానీ అల్ప ఉష్ణోగ్రతలు చర్యవేగాన్ని తగ్గిస్తాయి.

ప్రశ్న 51.
ఘనపరిమాణాన్ని పెంచడం ద్వారా పీడనాన్ని తగ్గించే ప్రక్రియకు కింది సమతాస్థితులను గురిచేస్తే చర్యలోని క్రియాజనకాల, క్రియాజన్యాల మోల్ల సంఖ్య పెరుగుతుందా ?
i) PCl₅ (వా) ⇌ PCl₃ (వా) + Cl₂ (వా)
ii) CaO (ఘ) + CO₂ (వా) ⇌ CaCO₃ (ఘ)
జవాబు:
i) PCl₅ (వా) ⇌ PCl₃ (వా) + Cl₂ (వా)

లీచాట్లెయర్ సూత్రం ప్రకారం సమతాస్థితిలో ఉన్న వ్యవస్థ పీడనాన్ని తగ్గిస్తే ఘనపరిమాణం, పెరిగే దిశలో సమతాస్థితి జరుగుతుంది. PCl₅ పై విఘటనలలో PCl₃, Cl₂ ఏర్పడి మోల్లసంఖ్య మరియు ఘనపరిమాణం పెరుగుతుంది. కనుక ఈ చర్యలో పీడనాన్ని తగ్గిస్తే క్రియాజన్యాల మోత్ల సంఖ్య పెరుగుతుంది.

ii) CaO (ఘ) + CO₂ (వా) ⇌ CaCO₃ (ఘ)

ఈ చర్యలో పీడనాన్ని తగ్గించినపుడు CO₂ అణువుల సంఖ్య పెరుగుతుంది. CO₂ అణువుల సంఖ్య పెరగడం విఘటనం వల్ల జరుగుతుంది. అందువల్ల పీడనాన్ని తగ్గించినపుడు CaCO₃ విఘటనం చెందడం వల్ల CaCO₃ మోల్లల సంఖ్య తగ్గుతుంది.

ప్రశ్న 52.
పీడనం పెంపు ద్వారా కింది వాటిలో ఏ చర్యలు ప్రభావితం అవుతాయి ? ఈ ప్రభావం ద్వారా చర్య పురోగామి దిశలో జరుగుతుందా ? లేదా ? తిరోగామి దిశలో జరుగుతుందా ? తెలపండి.
i) COCl₂ (వా) ⇌ CO (వా) + Cl₂ (వా)
ii) CH₄ (వా) ⇌ CS₂ (వా) + 2H₂S (వా)
iii) CO₂ (వా) + C (ఘ) ⇌ 2 CO (వా)
iv) 4NH₃ (వా) + 5O₂ (వా) ⇌ 4 NO (వా) + 6H₂O (వా)
జవాబు:
i) COCl₂ (వా) ⇌ CO (వా) + Cl₂ (వా)
ఈ చర్యలో పీడనం పెంపువల్ల తిరోగామి చర్య జరుగుతుంది. క్రియాజన్యాల గాఢతలు తగ్గుతాయి.

ii) CH₄ (వా) ⇌ CS₂ (వా) + 2H₂S (వా)
ఈ చర్యలో మోల్ సంఖ్య సమానం. అందువల్ల పీడన ప్రభావం ఉండదు.

iii) CO₂ (వా) + C (ఘ) ⇌ 2 CO (వా)
ఈ చర్యలో పురోగామి దిశలో వాయుస్థితిలోని అణువుల సంఖ్య పెరుగుతున్నది. తిరోగామి దిశలో తగ్గుచున్నది. లీచాట్లెయర్ సూత్రం ప్రకారం పీడనాన్ని పెంచితే ఘనపరిమాణం తగ్గే చర్య ప్రోత్సహించబడుతుంది. అంటే ఇవ్వబడిన సమతాస్థితి చర్యలో తిరోగామి చర్య ప్రోత్సహింపబడుతుంది.

iv) 4NH₃ (వా) + 5O₂ (వా) ⇌ 4 NO (వా) + 6H₂O (వా)
ఈ చర్యలో వాయుస్థితిలోని క్రియాజనకాల మోత్ల సంఖ్య (9), క్రియాజన్యాల మోల్ సంఖ్య (10) కన్నా తక్కువ. లీచాట్లెయర్ సూత్రం ప్రకారం పీడనాన్ని పెంచితే సమతాస్థితి వ్యవస్థలో ఘనపరిమాణం తగ్గే చర్య ప్రోత్సహింపబడుతుంది. అనగా తిరోగామి చర్య ప్రోత్సహింపబడుతుంది.

ప్రశ్న 53.
కింది సమతాస్థితులను పీడనం పెరుగుదల ఏ విధంగా ప్రభావితం చేస్తుంది ? అదేవిధంగా ఉష్ణోగ్రతలలో పెరుగుదల ఏ విధంగా ప్రభావితం చేస్తుంది ?
i) 2NH₃ (వా) ⇌ N₂ (వా) + 3H₂ (వా) ΔH = 92 kJ
ii) N₂ (వా) + O₂ (వా) ⇌ 2 NO (వా) ΔH = -176 kJ
iii) 2O₃ (వా) ⇌ 3O₂ (వా) ΔH = -285 kJ
iv) CaO (ఘ) + CO₂ (వా) ⇌ CaCO₃ (ఘ) ΔH = – 176 kJ
జవాబు:
పీడన ప్రభావం : లీచాట్లెయర్ సూత్రం ప్రకారం పీడనాన్ని పెంచితే ఘనపరిమాణం కగ్గే చర్య ప్రోత్సహింపబడుతుంది. ఉష్ణోగ్రతా ప్రభావం : లీచాట్లెయర్ సూత్రం ప్రకారం ఉష్ణోగ్రతలో పెరుగుదల ఉష్ణగ్రాహక చర్యను ప్రోత్సహిస్తుంది.

i) 2NH₃ (వా) ⇌ N₂ (వా) + 3H₂ (వా) ΔH = 92 kJ
ఈ సమతాస్థితిలో అమ్మోనియా విఘటన చర్య అయిన పురోగామి చర్యలో ఘనపరిమాణం పెరుగుచున్నది. పీడనాన్ని పెంచితే ఘనపరిమాణం తగ్గే చర్య ప్రోత్సహించబడుతుంది. అంటే నైట్రోజన్, హైడ్రోజన్ కలసి NH₃.

ఏర్పడే చర్య జరుగుతుంది. ఈ చర్యలో పురోగామి చర్య ఉష్ణగ్రాహక చర్య. ఉష్ణోగ్రతలో పెరుగుదల ఉష్ణగ్రాహక చర్యను ప్రోత్సహిస్తుంది. అంటే అమ్మోనియా విఘటనం చెందుతుంది. అంటే పై చర్యలో పురోగామి చర్య ప్రోత్సహించబడుతుంది.

ii) N₂ (వా) + O₂ (వా) ⇌ 2 NO (వా) ΔH = 181 kJ
ఈ సమతావ్యవస్థలో మోల్ల సంఖ్యలో మార్పు లేదు. ఇటువంటి చర్యలపై పీడన ప్రభావం ఉండదు. పురోగామి చర్యలో ఉష్ణం గ్రహించబడుతున్నది. ఉష్ణోగ్రతలో పెరుగుదల ఉష్ణగ్రాహకచర్యను ప్రోత్సహిస్తుంది. అందువల్ల ఉష్ణోగ్రతను పెంచడం వల్ల NO ఏర్పడే చర్య జరుగుతుంది.

iii) 2O₃ (వా) ⇌ 3O₂ (వా) ΔΗ = -285 kJ

పీడన ప్రభావం : ఈ సమతాస్థితిలో ఓజోన్ విఘటన చర్య అయిన పురోగామి చర్యలో మోల్ల సంఖ్య పెరుగుట వలన ఘనపరిమాణం పెరుగుతుంది. తిరోగామి చర్యలో ఓజోన్ ఏర్పడి, ఘనపరిమాణం తగ్గుతుంది.
లీచాట్లెయర్ సూత్రం ప్రకారం అధిక పీడనాల వద్ద ఓజోన్ ఏర్పడే తిరోగామి చర్య ప్రోత్సహించబడుతుంది. సమతాస్థానం ఎడమవైపు జరుగుతుంది.

ఉష్ణోగ్రత ప్రభావం : ఓజోన్ విఘటన చర్య ఉష్ణమోచక చర్య. (ΔH = ఋణాత్మకం). పురోగామి చర్య ఉష్ణమోచక చర్య. తిరోగామి చర్య ఉష్ణగ్రాహక చర్య. లీచాట్లెయర్ సూత్రం ప్రకారం అధిక ఉష్ణోగ్రతల వద్ద ఉష్ణగ్రాహక చర్య అయిన తిరోగామి చర్య అయిన ఓజోన్ ఏర్పడే చర్య ప్రోత్సహించబడుతుంది.

iv) CaO (ఘ) + CO₂ (వా) ⇌ CaCO₃ (ఘ) ΔH = – 176 kJ
ఈ చర్యలో ఒకే ఒక వాయుస్థితిలోని క్రియాజనకం ఉన్నది. పీడనాన్ని పెంచినపుడు ఘనపరిమాణం తగ్గే చర్య అయిన పురోగామి చర్య ప్రోత్సహించబడుతుంది.
ఈ చర్యలో పురోగామి చర్య ఉష్ణమోచక చర్య. తిరోగామిచర్య ఉష్ణగ్రాహక చర్య. ఉష్ణోగ్రత పెరిగితే తిరోగామి దిశగా సమతాస్థానం జరుగుతుంది. తిరోగామి చర్య ప్రోత్సహించబడుతుంది.

ప్రశ్న 54.
HI విఘటనం చర్యపై అనువర్తితన పీడనం ఎటువంటి ప్రభావం చూపదు. అయితే PCl₅ విఘటనంపై ప్రభావం చూపుతుంది. వివరించండి.
జవాబు:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 9

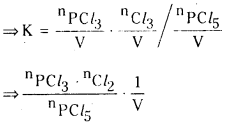
ఈ సమీకరణంలో ‘V’ పదం లేదు. అందువల్ల పీడనం ప్రభావం ఈ చర్యపై ఉండదు.
ఈ సమీకరణంలో ‘V’ పదం ఉంది. కనుక పీడనం వల్ల ఈ చర్య ప్రభావితం అవుతుంది.
స్థిర ఉష్ణోగ్రత వద్ద K_c విలువ స్థిరం. స్థిర ఉష్ణోగ్రత వద్ద పీడనాన్ని పెంచినపుడు \(\frac{1}{v}\) విలువ పెరుగుతుంది. కాని K_c విలువ స్థిరంగా ఉండుట కోసం \({ }^{{ }^n} \mathrm{Cl}_2\) ల విలువలు తగ్గాలి. అందువల్ల తిరోగామి చర్య ప్రోత్సహించబడుతుంది.

ప్రశ్న 55.
కింది పదాలను వివరించండి.
(i) విద్యుద్విశ్లేష్యకం
(ii) అవిద్యుద్విశ్లేష్యకం
(iii) బలహీన బలమైన విద్యుద్విశ్లేష్యకాలు
(iv) అయానిక సమతాస్థితి
జవాబు:
i) విద్యుద్విశ్లేష్యకం : కొన్ని పదార్థాలు తమ జలద్రావణాల గుండా విద్యుత్ను ప్రవహింపచేస్తాయి. వీటిని విద్యుత్ వాహకాలు అంటారు లేదా విద్యుద్విశ్లేష్యకాలు అంటారు. వీటి గుండా విద్యుత్ ప్రవహింపచేసినపుడు విద్యుత్ ప్రవాహంతోబాటు రసాయన మార్పును కూడ పొందుతాయి.

ii) కొన్ని పదార్థాలు తమ జలద్రావణాల ద్వారా విద్యుత్ను ప్రవహింపచేయవు. వీటిని అవిద్యుద్విశ్లేష్యకాలు అంటారు.

iii) బలమైన విద్యుత్ వాహకాలను నీటిలో కరిగించినపుడు అవి సుమారు సంపూర్ణంగా అయనీకరణం చెందుతాయి.

బలహీన విద్యుద్విశ్లేష్యాలు జలద్రావణాలలో పాక్షికంగా అయనీకరణం చెందుతాయి. ఉదా : సోడియం క్లోరైడ్ జలద్రావణంలో సోడియం అయాన్లు క్లోరైడ్ అయాన్లు మాత్రమే ఉంటాయి. ఎసిటిక్ ఆమ్ల జలద్రావణంలో ప్రధానంగా అయనీకరణం చెందని ఎసిటిక్ ఆమ్ల అణువులు, కొద్ది పరిమాణంలో ఎసిటేట్ అయాన్లు, హైడ్రోనియం అయాన్లు ఉంటాయి. దీనికి కారణం సోడియం క్లోరైడ్ బలమైన విద్యుత్ వాహకం కాబట్టి 100% అయనీకరణం చెందుతుంది. ఎసిటిక్ ఆమ్లం బలహీన విద్యుత్ వాహకం కాబట్టి 5% కంటే తక్కువ పరిమాణంలో మాత్రమే అయనీకరణం చెందుతుంది.

iv) బలహీన విద్యుత్ వాహకాల జలద్రావణాలలో, అయాన్లు అయనీకరణం చెందలేని అణువుల మధ్య సమతాస్థితి ఏర్పడి ఉంటుంది. అయాన్లు పాల్గొని ఏర్పడిన సమతాస్థితిని అయానిక సమతాస్థితి అంటారు.
CH₃COOH (జల) + H₂O (ద్ర) ⇌ CH₃COO^– (జల) + H₃O⁺ (జల)

ప్రశ్న 56.
కింది పదాలను వివరించండి :
(i) అయనీకరణం విస్తృతి, అది ఏ కారణాంశాలపై ఆధారపడుతుంది
(ii) విఘటనం
(iii) అయనీకరణం
జవాబు:
i) బలహీన విద్యుద్విశ్లేష్యాలు పాక్షికంగా అయనీకరణం చెందుతాయి. అయనీకరణం వల్ల ఏర్పడిన అయాన్లకు, అయనీకరణం చెందని అణువులకు మధ్య గతిక సమతాస్థితి ఏర్పడుతుంది.
సమతాస్థితి వద్ద అయనీకరణం చెందిన అణువుల సంఖ్యకు మొత్తం అణువుల సంఖ్యకు గల నిష్పత్తిని అయనీకరణ అవధి అంటారు. అయనీకరణ అవధిని శాతంగా మార్చితే అయనీకరణ విస్తృతి అంటారు.
అయనీకరణ విస్తృతి తి కింది అంశాలపై ఆధారపడుతుంది.

a) గాఢత : ద్రావణం గాఢత తక్కువగా వుంటే అయనీకరణ విస్తృతి ఎక్కువగా వుంటుంది.
b) ఉష్ణోగ్రత : ఉష్ణోగ్రత పెరిగితే అయనీకరణం పెరుగుతుంది.

ii) విఘటనం : కొన్ని పదార్థాలను వేడిచేస్తే అవి రెండు లేక అంతకంటే ఎక్కువ విభిన్న పదార్థాలుగా విడిపోతాయి. ఈ ప్రక్రియను విఘటనం అంటారు.
CaCO₃ → CaO + CO₂
iii) తటస్థ అణువు ద్రావణంలో విద్యుత్ ఆవేశపు అయాన్లుగా విచ్ఛిన్నం అయ్యే ప్రక్రియను అయనీకరణం అంటారు.

ప్రశ్న 57.
ఆర్హీనియస్ ఆమ్లాల, క్షారాల భావనలను వివరించండి.
జవాబు:
1) నీటిలో కరిగించినపుడు, వియోగం చెంది H⁺ (జల) అయాన్లను ఏర్పరచే పదార్థాలను ఆమ్లాలు అనీ, హైడ్రాక్సిల్ అయాన్లను ఏర్పరచే పదార్థాలను క్షారాలు అని ఆర్హీనియస్ ప్రతిపాదన.
HX (జల) ⇌ H⁺ (జల) + X (జల)
MOH (జల) ⇌ M (జల) + OH^– (జల)

2) HCl, HNO₃ వంటి ఆమ్లాలు జలద్రావణాలు దాదాపు సంపూర్ణంగా అయనీకరణం చెందుతాయి. అవి బలమైన ఆమ్లాలు. ఎసిటిక్ ఆమ్లం వంటి ఆమ్లాలు పాక్షికంగా అయనీకరణం చెందుతాయి. అవి బలహీన ఆమ్లాలు. అదేవిధంగా జలద్రావణంలో పూర్తిగా అయనీకరణం చెందే క్షారాలు బలమైన క్షారాలు. పాక్షిక అయనీకరణం చెందే క్షారాలు బలహీన క్షారాలు.

3) ఈ సిద్ధాంతం ప్రకారం ఆమ్ల, క్షార తటస్థీకరణ చర్య అనగా, H⁺, OH^– లు కలిసి నీరు ఏర్పడుటయే.
H⁺ (వా) + OH^– (వా) ⇌ H₂O (ద్ర)

ప్రశ్న 58.
కాంజుగేటు ఆమ్ల క్షార జంట అంటే ఏమిటి ? ఒక ఉదాహరణ ఇవ్వండి.
జవాబు:
ఆమ్ల-క్షారాల మధ్య తేడా ప్రోటాన్ మాత్రమే అయితే, ఆమ్ల క్షార జంటను సంయుగ్మ ఆమ్ల, క్షార జంట లేదా కాంజుగేటు ఆమ్లక్షార జంట అంటారు.
ఉదా :
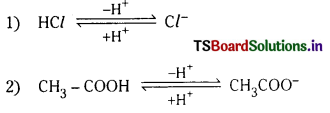
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 11

ప్రశ్న 59.
ఎసిటిక్ ఆమ్లం బలహీన ఆమ్లం. 1 M ఎసిటిక్ ఆమ్ల జలద్రావణంలో ఉండే అన్ని అయానిక అణు జాతుల గాఢతల అవరోహణ క్రమాన్ని తెలపండి.
జవాబు:
ఎసిటిక్ ఆమ్లం అయనీకరణం

ఎసిటిక్ ఆమ్లం బలహీన ఆమ్లం. అది అల్పంగా అయనీకరణం చెందుతుంది. అందువల్ల 1 M ఎసిటిక్ ఆమ్ల జలద్రావణంలో అన్ని అయానిక అణుజాతుల గాఢతల అవరోహణ క్రమం
[H₂O] > [CH₃COOH] > [CH₃COO ^–] = [H₃O⁺] > [OH^–]

ప్రశ్న 60.
తగిన సమీకరణాలతో కింది వాటిలో ప్రతీ జాతి బ్రానెడ్ ఆమ్లంగా ప్రవర్తిస్తుంది అని తెలపండి.
a) H₃O⁺
b) HCl
c) NH₃
d) HS\(\mathrm{O}_{\overline{4}}\)
జవాబు:
బ్రాన్ డ్ సిద్ధాంతం ప్రకారం హైడ్రోజన్ అయాన్ (H⁺) ను దానం చేయగలిగే పదార్థాలు ఆమ్లాలు.

a) H₃O⁺ + OH^– ⇌ 2H₂O
H₃O⁺, OH^–కు H⁺ ను దానం చేస్తుంది. అందువల్ల H₃O⁺ బ్రాన్డెడ్ ఆమ్లం.

b) HCl + H₂O ⇌ H₃O⁺ + Cl^–
HCl, H₂O కు H⁺ ను దానం చేస్తుంది. అందువల్ల HCl బ్రానెడ్ ఆమ్లం.

c) NH₃ + NH₃ ⇌ \(\mathrm{NH}_4^{+}\) + \(\mathrm{NH}_2^{-}\)
NH₃ మరియొక NH₃ కు H⁺ ను దానం చేస్తుంది. అందువల్ల NH₃ బ్రాన్టెస్టెడ్ ఆమ్లం.

d) HS\(\mathrm{O}_4^{-}\) + H₂O ⇌ H₃O⁺ + \(\mathrm{SO}_4^{-}\). అందువల్ల \(\mathrm{SO}_4^{-}\) బ్రాన్డెడ్ ఆమ్లం.
ఈ చర్యలో H\(\mathrm{SO}_4^{-}\), H₂O కు H⁺ ను దానం చేస్తున్నది. కావున ఆమ్లం.

ప్రశ్న 61.
తగిన సమీకరణాలతో కింది వాటిలో ప్రతీ జాతి బ్రాన్టెడ్ క్షారంగా ప్రవర్తిస్తుంది అని తెలపండి.
a) H₂O
b) OH^–
c) C₂H₅OH
d) HP\(\mathrm{O}_4^{-2}\)
జవాబు:
a) H₂O + H₂O ⇌ H₃O⁺ + OH^–.
నీటి అణువు మరియొక నీటి అణువు నుండి ప్రోటాన్ను స్వీకరిస్తుంది. అందువల్ల H⁺ స్వీకరిస్తున్న అణువు బ్రాన్ స్టెడ్ క్షారం.

b) HCl + OH^– → H₂O + Cl^–
OH^–, HCl నుండి ప్రోటాను స్వీకరిస్తుంది. అందువల్ల OH^– బ్రాన్టెడ్ క్షారం.

c)
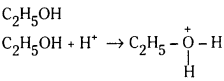
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 13
ఇథైల్ ఆల్కహాల్, ప్రోటాను స్వీకరిస్తున్నది. అందువల్ల బ్రాన్డ్ క్షారం.

d) HP\(\mathrm{O}_4^{2-}\)
HP\(\mathrm{O}_4^{2-}\) + HCl → H₂P\(\mathrm{O}_4^{-}\) + Cl^–
HP\(\mathrm{O}_4^{2-}\), HCl నుండి ప్రోటాను స్వీకరిస్తుంది. కనుక బ్రాన్ స్టెడ్ క్షారం.

ప్రశ్న 62.
H₂O, HC\(O_3^{-}\), HS\(O_4^{-}\), NH₃ లు బ్రానెడ్ ఆమ్లాలు, బ్రాస్టెస్టెడ్ క్షారాలుగా ప్రవర్తిస్తాయి. వాటికి సంబంధించిన కాంజుగేటు ఆమ్లం, క్షారం రాయండి.
జవాబు:
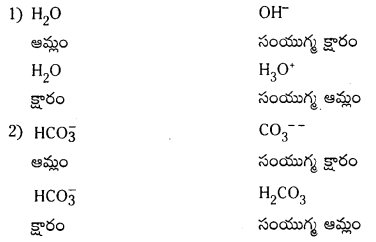
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 14

ప్రశ్న 63.
H₂P\(\mathrm{O}_4^{-}\) ఆమ్లంగాను, క్షారంగాను ప్రవర్తిస్తుంది అని తెలపడానికి సమీకరణం రాయండి.
జవాబు:
H₂P\(\mathrm{O}_4^{-}\) + H₂O ⇌ HP\(\mathrm{O}_4^{2-}\) + H₃O⁺
H₂P\(\mathrm{O}_4^{-}\) నీటికి ప్రోటాన్ను దానం చేస్తున్నది కనుక ఆమ్లం.
H₂\(\mathrm{O}_4^{-}\) + HCl ⇌ H₃PO₄ + Cl^–
H₂P\(\mathrm{O}_4^{-}\) ప్రోటాన్ ను HCl నుండి స్వీకరిస్తుంది. కావున క్షారం.

ప్రశ్న 64.
కింది వాటికి కాంజుగేటు ఆమ్లాన్ని, కాంజుగేటు క్షారాన్ని రాయండి.
a) OH^–
b) H₂O
c) HC\(\mathrm{O}_3^{-}\)
d) H₂O₂
జవాబు:
a) OH^– సంయుగ్మ క్షారం O^2-
OH^– సంయుగ్మ ఆమ్ల H₂O

b) H₂O సంయుగ్మ ఆమ్లం H₃O⁺
H₂O సంయుగ్మ క్షారం OH^–

c) HC\(\mathrm{O}_3^{-}\)
HC\(\mathrm{O}_3^{-}\) సంయుగ్మ ఆమ్ల H₂CO₃
HC\(\mathrm{O}_{\overline{3}}\) సంయుగ్మ క్షారం C\(\mathrm{CO}_3^{-}\)

d) H₂O₂
H₂O₂ సంయుగ్మ ఆమ్లం H₃[laex]\mathrm{O}_2^{+}[/latex]
H₂O₂ సంయుగ్మ క్షారం H\(\mathrm{O}_2^{-}\)

ప్రశ్న 65.
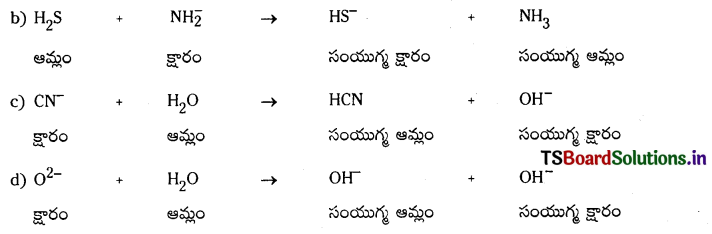
బ్రాన్టెస్టెడ్ ఆమ్లం, దాని కొంజుగేటు క్షారం, అదేవిధంగా బ్రానెడ్ క్షారం, దాని కాంజుగేటు ఆమ్లం, వీటిని కింది సమీకరణాలలో గుర్తించండి.
a) HSO₄ + Cl^– → HCl + HS\(O_4^{-}\)
b) H₂S + N\(\mathrm{H}_2^{-}\) → HS^– + NH₃
c) CN^– + H₂O → HCN + OH^–
d) O^-2 + H₂O → 2OH^–
జవాబు:
a)
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 16

ప్రశ్న 66.
AlCl₃, NH₃, Mg⁺², H₂O లను లూయీ ఆమ్లాలు, లూయీ క్షారాలుగా వర్గీకరించండి. జవాబును సమర్ధించండి.
జవాబు:
ఒంటరి ఎలక్ట్రాన్ జంట దాత క్షారం. ఒంటరి ఎలక్ట్రాన్ స్వీకర్త ఆమ్లం.
AlCl₃ ఎలక్ట్రాన్ జంటను స్వీకరించగలదు. కనుక లూయీ ఆమ్లం.
NH₃ ఒంటరి ఎలక్ట్రాన్ జంటను దానం చేయగలదు. కనుక లూయీ క్షారం. కేటయాన్లు ఎలక్ట్రాన్ జంటను స్వీకరించగలవు. కనుక Mg⁺⁺ లూయీ ఆమ్లం.
H₂O ఎలక్ట్రాన్ జంటను దానం చేయగలదు కనుక లూయీ క్షారం.

ప్రశ్న 67.
బలమైన ఆమ్లం, బలహీన ఆమ్లం, వీటి కాంజుగేటు క్షారాల బలాలను వివరించండి.
జవాబు:
HCl + H₂O ⇌ H₃O⁺ + Cl^–
ఈ చర్యలో HCl బలమైన ఆమ్లం. దీని సంయుగ్మ క్షారం బలహీనమైనది.
అందువల్ల Cl^–, H₃O⁺ నుండి H⁺ ను స్వీకరించే చర్య చాలా స్వల్పం.
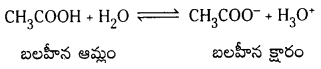
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 18
CH₃COOH బలహీన ఆమ్లం. దాని సంయుగ్మ క్షారం CH₃COO^– బలమైన క్షారం.

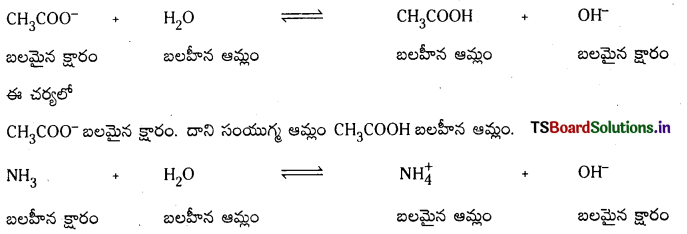
ప్రశ్న 68.
బలమైన క్షారం, బలహీన క్షారం, వీటి కాంజుగేటు ఆమ్లాల బలాలను వివరించండి.
జవాబు:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 19

ప్రశ్న 69.
“నీటి అయానిక లబ్ధం”, దీనిని వివరించండి. గది ఉష్ణోగ్రత వద్ద దీని విలువ ఎంత ?
జవాబు:
స్థిర ఉష్ణోగ్రత వద్ద శుద్ధ జలంలో లేదా జలద్రావణాలలో హైడ్రోజన్, హైడ్రాక్సైడ్ అయాన్ల గాఢతల లబ్ధాన్ని నీటి అక అంటారు. దీనిని K తో సూచిస్తారు. దీని విలువ 25°C వద్ద 1.0 × 10^-14 మోల్స్ ²/లీ²
శుద్ధ నీరు బలహీన విద్యుద్విశ్లేష్యం. దాని అయనీకరణ స్థితిని కింది విధంగా రాస్తారు.
H²O ⇌ H⁺ + OH^–
సమతా స్థితి స్థిరాంకం K_c = \(\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{H}_2 \mathrm{O}\right]}\)
K_c × [H₂O] = [H⁺] [OH^–]
[H₂O] విలువ స్థిరం. కాబట్టి K_c . [H₂O] విలువ కూడా స్థిరమే. దానిని K_w తో సూచిస్తారు.
K_w = [H⁺] [OH^–]
K_w ను నీటి అయానిక లబ్ధం అంటారు.
K_w విలువ ఉష్ణోగ్రత మీద ఆధారపడి ఉంటుంది. ఉష్ణోగ్రత పెరిగితే K_w విలువ పెరుగుతుంది. దీని కారణం నీటి అయనీకరణం పెరగడమే. నీరు తటస్థ ద్రావణి. కాబట్టి దానిలోని H⁺, OH^– అయాన్ల గాఢత సమానంగా ఉంటుంది.
K_w = [H⁺] [OH^–] = 1.0 × 10^-14 మోల్²/లీ²
∴ శుద్ధ నీటిలో [H⁺] = [OH^–] = 1.00 × 10^-7 మోల్/లీ
ఆమ్ల ద్రావణంలో [H⁺] > 1.0 × 10^-7 మోల్స్/లీ
క్షారద్రావణంలో [H⁺] < 1.0 × 10^-7 మోల్స్ / లీ లేదా క్షారద్రావణంలో [OH] > 1.00 × 10^-7 మోల్/లీ

ప్రశ్న 70.
pH ను నిర్వచించండి. బలహీన ఆమ్లం, బలహీన క్షారం వీటి మోలార్ గాఢతల నుంచి pH ను లెక్కించలేం. ఎందువల్ల ? బలహీన ఆమ్లం pH కు సమీకరణం ఉత్పాదించండి.
జవాబు:
pH = -log₁₀[H⁺]
H⁺ అయాన్ గాఢత యొక్క ఋణ సంవర్గమానాన్ని ఉదజని సూచిక pH అంటారు.
బలమైన ఆమ్లం, బలమైన క్షారం జల ద్రావణంలో పూర్తిగా అయనీకరణం చెందుతాయి. అందువల్ల H⁺, OH^– ల గాఢతలు వాటి మోలార్ గాఢతలకు సమానం.
బలహీన క్షారాలు, బలహీన ఆమ్లాలు పాక్షికంగా మాత్రమే అయనీకరణం చెందుతాయి. అందువల్ల H⁺, OH^– అయాన్ల గాఢతలు బలహీన ఆమ్లం, బలహీనక్షారం మోలార్ గాఢతలకు సమానం కావు. అందువల్ల బలహీన ఆమ్లం, బలహీన క్షారాల pH విలువలు వాటి మోలార్ గాఢతల నుండి లెక్కించలేము.

బలహీన ఆమ్లం pH :
HX బలహీన క్షారం. అయనీకరణం కింది విధంగా వ్రాయవచ్చు. బలహీన ఆమ్ల గాఢత ‘C’
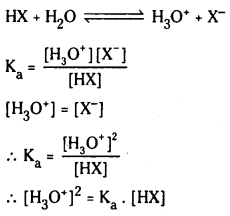
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 20

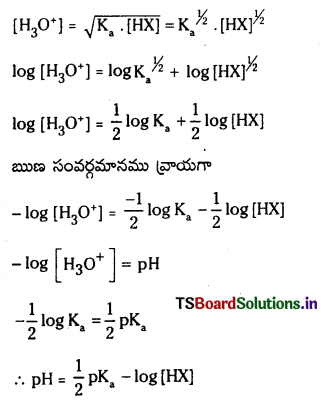
బలహీన ఆమ్లం అల్పంగా అయనీకరణం చెందుతుంది కాబట్టి బలహీన ఆమ్ల గాఢతనే సమతాస్థితి వద్ద HX గాఢతకు సమానంగా తీసుకోవచ్చు.
∴ pH = \(\frac{1}{2}\)pK_a – \(\frac{1}{2}\) log c

ప్రశ్న 71.
పాలిప్రోటిక్ ఆమ్లాలు H₂SO₄, H₃PO₄ ల అంచెలవారీ అయనీకరణాలను తెలిపే సమీకరణాలు రాయండి.
జవాబు:
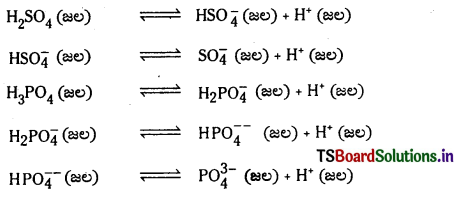
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 22

ప్రశ్న 72.
కింది వానిలో ఆమ్ల బలం ఏ విధంగా మారుతుంది ? వివరించండి. ఆవర్తన పట్టికలో
i) గ్రూపులోని మూలకాల హైడ్రైడ్లు
ii) పీరియడ్లోని మూలకాల హైడ్రేడ్లు
జవాబు:
ఒక గ్రూపులో పై నుంచి కిందకు మూలక పరమాణు పరిమాణం పెరుగుతుంది. అందువల్ల బంధ దూరం పెరిగి బంధ బలం తగ్గుతుంది. అందువల్ల అయనీకరణం సులభంగా జరుగుతుంది. అందువల్ల ఆమ్లబలం పెరుగుతుంది.
ఉదా : H-F < HCl < HBr < HI క్రమంలో ఆమ్ల బలం పెరుగుతుంది.
ఆవర్తన పట్టికలో ఎడమ నుంచి కుడికి బంధ ధ్రువణం పెరుగుతుంది. అందువల్ల H – A బంధం సులభంగా అయనీకరణం చెందుతుంది. అందువల్ల ఆమ్ల బలం పెరుగుతుంది.
CH₄ < NH₃ < H₂O < HF
ఋణ విద్యుదాత్మకత విలువలు పెరగడం వల్ల ఆమ్ల బలం పెరుగుతుంది.

ప్రశ్న 73.
ప్రోటోనిక్ భావన ఆధారంగా నీరు ఆమ్లంగాను, క్షారంగాను కూడా ప్రవర్తిస్తుంది అని తెలపండి.
జవాబు:

HCl (aq) + H₂O (aq) → H₃\(\mathrm{O}^{+}\)(జల) + Cl^– (జల) ఈ చర్యలో నీరు ప్రోటాన్ ను స్వీకరించి ఆమ్లంగా ప్రవర్తిస్తోంది.
CH₃COO^– + H₂O → CH₃COOH + OH^– ఈ చర్యలో నీరు H⁺ ను దానం చేసి క్షారంగా ప్రవర్తిస్తోంది. ఈ విధంగా నీరు ఆమ్లంగాను, క్షారంగాను కూడా ప్రవర్తించగలదు.

ప్రశ్న 74.
ఉభయ సామాన్య అయాన్ ఫలితం అంటే ఏమిటి ? వివరించండి.
జవాబు:
ఎసిటిక్ ఆమ్ల వియోజన సమతాస్థితి :
CH₃COOH (జల) ⇌ H⁺(జల) + CH₃COO^– (జల)
K_a = \(\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{CH}_3 \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_3 \mathrm{COOH}\right]}\)
ఎసిటిక్ ఆమ్లద్రావణానికి ఎసిటేట్ అయాన్లను కలిపితే హైడ్రోజన్ అయాన్ల గాఢత [H⁺] తగ్గుతుంది. అలాగే బాహ్యస్థానం నుంచి H⁺ అయాన్లను ద్రావణానికి చేర్చితే వియోజనం చెందని ఎసిటిక్ ఆమ్లం దిశ వైపుగా సమతాస్థితి పయనిస్తుంది. అంటే H⁺ అయాన్ల గాఢత తగ్గే దిశగా పయనిస్తుంది.

ఒక విద్యుద్విశ్లేష్యక జలద్రావణానికి దానిలోని, ఆనయాన్ లేక కేటయాన్ ఉభయ సామాన్యంగా ఉండే వేరొక విద్యుద్విశ్లేష్యకం కలిపినపుడు మొదటి విద్యుద్విశ్లేష్యకం ద్రావణీయత తగ్గిపోతుంది. దీనినే ఉభయసామాన్య అయాన్ ప్రభావం అంటారు. ఉమ్మడి అయాన్ సమక్షంలో బలహీన ఆమ్ల, బలహీన క్షార లేదా బలహీన విద్యుద్విశ్లేష్యం యొక్క అయనీకరణం అణచబడుతుంది.

ప్రాధాన్యత : రసాయన విశ్లేషణలో II గ్రూపులో S^— గాఢతను, III గ్రూపులో OH^– గాఢతను, HCl, NH₄Cl లు నియంత్రిస్తాయి. దీనికి కారణం ఉభయసామాన్య అయాను ప్రభావం. H⁺ అయాన్ సమక్షంలో H₂S అయనీకరణ అణచబడి S^— గాఢత తగ్గుతుంది. NH₄Cl సమక్షంలో NH₄OH అయనీకరణం అణచబడి OH^– గాఢత తగ్గుతుంది. సమీకరణాలను రాయండి.

ప్రశ్న 75.
“ద్రావణీయతా లబ్ధం” దీనిని నిర్వచించండి. కింది వాటికి ద్రావణీయతా
i) Ag₂Cr₂O₇
ii) Zr₃(PO₄)₄
జవాబు:
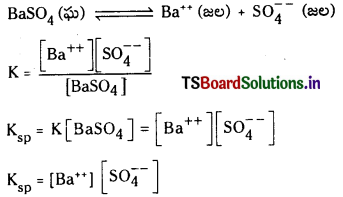
ద్రావణీయత లబ్ధం : గది ఉష్ణోగ్రత వద్ద ఒక లవణం సంతృప్త ద్రావణంలో కేటయాన్ల గాఢతకు, ఆనయాన్ల గాఢతకు తో సూచిస్తారు. దీని ప్రమాణాలు మధ్యగల లబ్ధాన్ని ఆ లవణం యొక్క ద్రావణీయత లబ్ధం అంటారు. దీనిని K_sp (మోల్స్/లీటర్)”.
n = అణువు అయనీకరణంలో ఏర్పరచే మొత్తం అయాన్ల సంఖ్య. అవి

i) పదార్థం స్వభావం
ii) ఉష్ణోగ్రత మీద ఆధారపడి ఉంటాయి.

ప్రాముఖ్యత : గుణాత్మక విశ్లేషణలో అవక్షేపణ ప్రక్రియలో అవక్షేపణ ప్రాధాన్యత విషయంలో ద్రావణీయత లబ్దం ఎంతగానో ఉపయోగపడుతుంది.
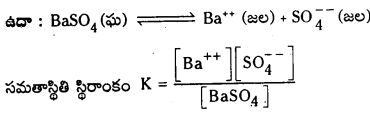
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 23
ఘనస్థితిలో గల శుద్ధ పదార్థానికి గాఢత స్థిరంగా ఉంటుంది.
K_sp = K . [BaSO₄] = [Ba⁺⁺] [latex]\mathrm{SO}_4^{–}[/latex]
K_sp ను ద్రావణీయత లబ్ధ స్థిరాంకం అంటారు. 298 K వద్ద K_sp విలువ 1.1 × 10^-10 మోల్² / లీ².
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 24

ప్రశ్న 76.
లవణాలను ఎలా వర్గీకరిస్తారు ? ఏ వర్గం లవణాలు జలవిశ్లేషణం చెందుతాయి ?
జవాబు:
లవణంలోని అయాన్లు నీటితో చర్య జరిపి H⁺ లేదా OH^– అయాన్లను విడుదల చేసే ప్రక్రియను లవణాల జలవిశ్లేషణ అంటారు. లవణాలు 4 రకాలు.
1) బలమైన ఆమ్లం – బలమైన క్షారం లవణాలు ఉదా : NaCl, KNO₃
2) బలమైన ఆమ్లం – బలహీన క్షారం లవణాలు ఉదా : NH₄ Cl, CuSO₄
3) బలహీన ఆమ్లం – బలమైన క్షారం లవణాలు ఉదా : Na₂CO₃, CH₃COONa
4) బలహీన ఆమ్లం – బలహీన క్షారం లవణాలు ఉదా : CH₃COONH₄, Ca₃ (PO₄)₂

1) బలమైన ఆమ్లం-బలమైన క్షారం లవణాలు : ఈ లవణాలు జలవిశ్లేషణం చెందవు. జలద్రావణంలో కేటయాన్లను, ఆనయాన్లను ఇస్తాయి.
ఉదా : NaCl జల విశ్లేషణ : NaCl అయనీకరణం చెంది Na⁺, Cl^– అయాన్లను ఇస్తుంది. ఈ అయాన్లు H₂Oతో చర్య జరిపి NaOH, HCl లను ఇస్తాయి. ఇవి బలమైన విద్యుద్విశ్లేష్యాలు. కాబట్టి పూర్తిగా అయనీకరణం చెంది H⁺, OH^– అయాన్లను ఇస్తాయి. ఇవి తిరిగి కలిసిపోయి అవిఘటిత H₂O ను ఇస్తాయి. అంటే జల విశ్లేషణ చెందవు. కాబట్టి (H⁺) అయాన్లు [OH^–] అయాన్ల గాఢతలో మార్పు ఉండదు. అందువల్ల ద్రావణం తటస్థంగా ఉంటుంది. దాని pH = 7 ఉంటుంది. [H⁺] = [OH^–] = 1.0 × 10^-7 మోల్స్ / లీటర్. లిట్మస్ కాగితాలతో ఎట్టి మార్పు చూపించదు.

2) బలమైన ఆమ్లం – బలహీన క్షారం లవణాల జలవిశ్లేషణ : ఈ లవణాలు జల విశ్లేషణం చెందే కేటయాన్లను ఇస్తాయి. అందువల్ల ఈ జలవిశ్లేషణను కేటయాన్ జలవిశ్లేషణ అంటారు.
ఉదా : NH₄Cl జలవిశ్లేషణ : NH₄ Cl అయనీకరణం చెంది N\(\mathrm{H}_4^{+}\), Cl^– అయాన్లను ఇస్తుంది. N\(\mathrm{H}_4^{+}\) బలమైనది. Cl^– బలహీనమైనది. అందువల్ల N\(\mathrm{H}_4^{+}\) నీటితో చర్య జరుపుతుంది.
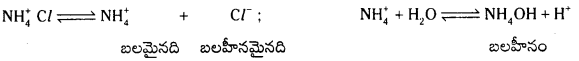
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 25
పై చర్యా ఫలితంగా ఏర్పడ్డ NH₄ OH బలహీనమైనది కాబట్టి అది అంతగా విఘటనం చెందలేదు. ద్రావణంలో H⁺ అయాన్ల గాఢత OH^– అయాన్ల కంటె ఎక్కువగా ఉంటుంది. ఫలితంగా ద్రావణానికి ఆమ్ల లక్షణం ఏర్పడుతుంది. pH < 7 ఉంటుంది. [H⁺] > 1.0 × 10^-7 ఉంటుంది. ద్రావణం నీలి లిట్మస్ కాగితాలను ఎర్రగా మారుస్తుంది.

3) బలహీన ఆమ్లం – బలమైన క్షారం లవణాల జలవిశ్లేషణ : ఈ లవణాలు జలవిశ్లేషణ చెందే ఆనయాన్లను ఇస్తాయి అందువల్ల ఈ జలవిశ్లేషణను ఆనయాన్ జలవిశ్లేషణ అంటారు.
ఉదా : CH₃COONa జలవిశ్లేషణ : CH₃COONa అయనీకరణ చెంది CH₃COO^–, Na⁺ అయాన్లను ఇస్తుంది. CH₃COO^– బలమైనది. Na⁺ బలహీనమైనది. అందువల్ల CH₃COO^– నీటితో చర్య జరుపుతుంది.
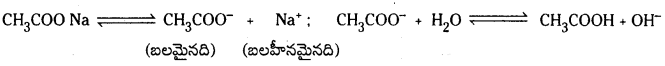
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 26
పై చర్యా ఫలితంగా ఏర్పడ్డ CH₃COOH బలహీనమైనది కాబట్టి అది అంతగా విఘటనం చెందలేదు. ద్రావణంలో OH^– అయాన్ల గాఢత H⁺ అయాన్ల కంటే ఎక్కువగా ఉంటుంది. ఫలితంగా ద్రావణానికి క్షారలక్షణం ఏర్పడుతుంది. pH > 7 ఉంటుంది. [OH^–] > 1.0 × 10^-7 ఉంటుంది. ద్రావణం ఎర్ర లిట్మస్ కాగితాలను నీలిరంగుగా మారుస్తుంది.

4) బలహీన ఆమ్లం – బలహీన క్షారం లవణాల జలవిశ్లేషణ : ఈ లవణాలు జలవిశ్లేషణం చెందే ఆనయాన్, కేటయాన్లను ఇస్తాయి.
ఉదా : CH₃COONH₄ జలవిశ్లేషణ : CH₃COONH₄ అయనీకరణం చెంది CH₃COO^–, N\(\mathrm{H}_4^{+}\), అయాన్లను ఇస్తాయి. ఈ రెండు అయాన్లు బలమైనవే. అందువల్ల అవి నీటితో చర్య జరుపుతాయి.
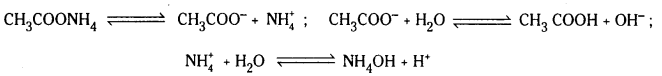
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 27
పై చర్యా ఫలితంగా ఏర్పడ్డ CH₃COOH, NH₄OH లు రెండూ బలహీనమైనవి. అందువల్ల అవి అంతగా విఘటనం చెందవు. ఇకపోతే ద్రావణంలో ఏర్పడ్డ H⁺, OH^– అయాన్లు సమానంగా కాని లేదా అసమానంగా గాని ఉండవచ్చు. అందువల్ల ద్రావణం తటస్థంగా లేదా ఆమ్లంగా లేదా క్షారంగా ఉండవచ్చు. ద్రావణ లక్షణం K_a, K_b లపై ఆధారపడి ఉంటుంది.
గమనిక : 2, 3, 4 రకాల లవణాలు మాత్రమే జలవిశ్లేషణ చెందుతాయి.

ప్రశ్న 77.
ఒక చర్యకు ΔG° విలువ కింది వాటిలో ఏ విధంగా ఉంటుంది ?
a) K > 1
b) K = 1
c) K < 1 జవాబు: a) K > 1 అయితే ΔG° విలువ ఋణాత్మకం. చర్య స్వచ్ఛందంగా పురోగామి దిశలో జరుగుతుంది. ఉత్పన్నాలు అధికంగా ఏర్పడతాయి.
b) K = 1 అయితే ΔG° = 0 వ్యవస్థ సమతాస్థితిలో ఉంటుంది.
c) K < 1 అయితే ΔG° విలువ ధనాత్మకం. ఈ స్థితిలో పురోగామి చర్య స్వల్పంగా మాత్రమే జరుగుతుంది. ఉత్పన్నాలు అల్ప పరిమాణంలో మాత్రమే ఏర్పడతాయి.

ప్రశ్న 78.
NH₄Cl జలద్రావణం ఆమ్ల గుణం చూపిస్తుంది. వివరించండి.
జవాబు:
NH₄Cl జలద్రావణం ఆమ్ల గుణం చూపిస్తుంది.
అమ్మోనియం క్లోరైడ్ జల ద్రావణంలో N\(\mathrm{H}_4^{+}\) అయానులు, Cl అయానులు ఉంటాయి. N\(\mathrm{H}_4^{+}\) అయానులు నీటితో చర్య పొందుతాయి. H₃O⁺ అయాన్లను విడుదల చేస్తాయి. అందువల్ల NH₄Cl జలద్రావణానికి ఆమ్ల లక్షణం ఉంటుంది. pH < 7.
N\(\mathrm{H}_4^{+}\) + H₂O ⇌ NH₃ + H₃O⁺
NH₄Cl + H₂O ⇌ NH₄OH + HCl
Cl^– అయానులు జలవిశ్లేషణ చెందవు. H₃O⁺ ఏర్పడుటవలన H₃O⁺ > 1.0 × 10^-7 ఉంటుంది. అందువల్ల NH₄Cl జలద్రావణం ఆమ్ల లక్షణం కలిగి ఉంటుంది.

ప్రశ్న 79.
CH₃COONa జలద్రావణం క్షార గుణం చూపిస్తుంది. వివరించండి.
జవాబు:
సోడియం ఎసిటేటు జలద్రావణంలో CH₃COO^– అయానులు జలవిశ్లేషణం చెందుతాయి. Na⁺ అయానులు జలవిశ్లేషణ చెందవు. OH^– ల గాఢత 1.0 × 10^-7 కన్నా అధికమైనందున CH₃COONa ద్రావణం క్షారత్వాన్ని చూపుతుంది.
CH₃COO^– + H₂O → CH₃COOH + OH^–
CH₃COONa + H₂O → CH₃COOH + NaOH

ప్రశ్న 80.
సోడియం ఎసిటేట్ ద్రావణంలో కరిగి ఉండి ఎసిటిక్ ఆమ్లం, సోడియం క్లోరైడు ద్రావణంలో కరిగి ఉండే దానికంటే బలహీనంగా ఉంటుంది. కారణం తెలపండి.
జవాబు:
ఎసిటిక్ ఆమ్ల బలం అయనీకరణం వల్ల విడుదలయ్యే H⁺ అయాన్ల సంఖ్యపై ఆధారపడి ఉంటుంది.
CH₃COOH ⇌ CH₃COO^– + H⁺
సోడియం ఎసిటేటు CH₃COONa, CH₃COOH లలో CH₃COO^– ఉభయ సామాన్య అయాను. సోడియం ఎసిటేటు విఘటనంలో CH3COO- అయానులు ఏర్పడతాయి.
CH₃COO Na → CH₃COO^– + Na⁺
ఉభయ సామాన్య అయాన్ అయిన CH₃COO^– అయాను సమక్షంలో ఎసిటిక్ ఆమ్లం విఘటనం అణచబడుతుంది. అందువల్ల బలహీనంగా వుంటుంది.
NaCl → Na⁺ + Cl^–
NaCl సమక్షంలో CH₃COOH కు ఉమ్మడి అయాను లేదు. అందు ఉభయసామాన్య ప్రభావం లేదు.

ప్రశ్న 81.
శుద్ధ నీటిలో కంటె, AgNO₃ లో AgCl తక్కువగా కరుగుతుంది. దీనిని వివరించండి.
జవాబు:
AgNO₃ ద్రావణంలో AgCl తక్కువగా కరుగుతుంది. ఎందులకనగా ఉభయ సామాన్య అయాన్ ప్రభావం వల్ల AgNO₃ ద్రావణీయత తగ్గిపోతుంది.
శుద్ధనీటిలో AgCl ఎక్కువగా కరుగుతుంది. కారణం ఏమనగా ఇచ్చట ఉభయ సామాన్య అయాన్ ప్రభావం ఉండదు.

ప్రశ్న 82.
CH₃COOH (జల) + Cl^– (జల) → చర్య ఎడమవైపు నుంచి కుడివైపుకు పురోగమిస్తుందా ? తెలపండి.
జవాబు:
CH₃COOH (జల) + Cl^–(జల) → CH₃COO^– + HCl. Cl^– బలహీన క్షారం. అందువల్ల అది CH₃COOH నుంచి H⁺ ను స్వీకరించలేదు. CH₃COOH బలహీన ఆమ్లం. అది ప్రోటానును బంధించి ఉంచుతుంది. అందువల్ల ఈ చర్య జరగదు.

ప్రశ్న 83.
H₂S జలద్రావణంలో H₂S, HS^-1, S^-2, H₃O⁺, OH^–, H₂O భిన్న గాఢతలలో ఉంటాయి. వీటిలో ఏ జాతి క్షారంగా పనిచేస్తుంది ? ఏది ఆమ్లంగా పనిచేస్తుంది ? ఏది ఆమ్లం, క్షారం రెండింటిగా పనిచేస్తుంది ?
జవాబు:
H₂O + H₂S ⇌ HS^– + H₃O⁺
H₂O + HS^– ⇌ S^— + H₃O⁺

a) S^2- క్షారంగా మాత్రమే పనిచేస్తుంది. అది ఆమ్లంగా పనిచేయదు. కారణం అది H⁺ లను కలిగి లేదు.
b) H₂S, H₃O⁺ లు ఆమ్లాలుగా పనిచేస్తాయి.
c) HS^–, OH^–, H₂O లు ఆమ్లాలుగాను, క్షారాలుగాను పనిచేస్తాయి. అవి H⁺ ను దానం చేయగలవు మరియు గ్రహించగలవు.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 84.
సమతాస్థితి ప్రక్రియలు అంటే ఏమిటి ? భౌతిక, రసాయన ప్రక్రియలలో ఈ సమతాస్థితిని సోదాహరణంగా వివరించండి..
జవాబు:
ఉత్రమణీయ చర్యలలో ఏ స్థితి వద్ద పురోగామి చర్యావేగం తిరోగామి చర్యావేగానికి సమానం అవుతుందో ఆ స్థితిని “సమతాస్థితి” అంటారు.

భౌతిక సమతాస్థితి ప్రక్రియలు : ఏ భౌతిక ప్రక్రియలలో పదార్థం యొక్క రెండు ప్రావస్థల (భౌతిక స్థితుల) మధ్య సమతాస్థితి ఏర్పడుతుందో వాటిని భౌతిక సమతాస్థితి ప్రక్రియలు అంటారు.

ఉదా : ఘన స్థితి ⇌ ద్రవస్థితి
ఘన స్థితి ⇌ బాష్పస్థితి

రసాయన సమతాస్థితి ప్రక్రియలు : ఏ రసాయన ప్రక్రియలలో క్రియాజనకాల మరియు క్రియాజన్యాల మధ్య సమతాస్థితి ఏర్పడుతుందో వాటిని రసాయన సమతాస్థితి ప్రక్రియలు అంటారు.
N₂ + 3H₂ ⇌ 2 NH₃
2SO₂ + O₂ ⇌ 2SO₃

ప్రశ్న 85.
గతిక సమతాస్థితి అంటే ఏమిటి ? సరైన ఉదాహరణలతో వివరించండి.
జవాబు:
సమతాస్థితి వద్ద పురోగామి చర్యావేగం మరియు తిరోగామి చర్యావేగాలు సమానంగా ఉంటాయి. ఆ స్థితి వద్ద క్రియాజనకాల గాఢతలో గాని, క్రియాజన్యాల గాఢతలో గాని ఎట్టి మార్పు కనిపించదు. ఆ పరిస్థితులలో చర్య జరగటం లేదేమోనని మనం భ్రమపడతాం. కాని చర్య జరుగుతూనే ఉంటుంది. అందువలన ఈ సమతాస్థితిని గతిక సమతాస్థితి అంటారు. అన్ని రసాయన సమతాస్థితి ప్రక్రియలు గతిక సమతాస్థితిని కలిగి ఉంటాయి.
ఉదా : N₂(వా) + 3H₂(వా) ⇌ 2NH₃ (వా)

మూత కలిగిన ఒక పాత్రలో N₂, H₂ వాయువులను 1: 3 నిష్పత్తిలో తీసికోండి. చర్య జరగడానికి ముందు పాత్రలో కేవలం N₂, H₂ లు మాత్రమే ఉంటాయి. వాటి గాఢత గరిష్ఠంగా ఉంటుంది. అపుడు పురోగామి చర్యావేగం కూడా గరిష్ఠంగా ఉంటుంది. కాలంతో పాటు N₂, H₂ ల గాఢతలు క్రమంగా తగ్గుతాయి. కాబట్టి పురోగామి చర్యావేగం క్రమంగా తగ్గుతుంది. క్రియాజన్యం (NH₃) గాఢత ఒక గరిష్ఠ విలువను చేరుకోగానే తిరోగామి చర్య ప్రారంభం అవుతుంది. అపుడు తిరోగామి చర్యావేగం గరిష్ఠంగా ఉంటుంది. కాలంతో పాటుగా క్రియాజన్యం (NH₃) గాఢత క్రమంగా తగ్గుతుంది. అపుడు తిరోగామి చర్యావేగం క్రమంగా తగ్గుతుంది. ఈ విధంగా పురోగామి, తిరోగామి చర్యల వేగాలు తగ్గుతూ, పెరుగుతూ ఒకానొక దశలో రెండు వేగాలు సమానం అవుతాయి. ఈ స్థితినే ఈ రసాయన చర్యయొక్క సమతాస్థితి అంటారు. సమతాస్థితిని చేరుకోగానే రెండు వేగాలు (పురోగామి, తిరోగామి) సమానంగా ఉండటం వల్ల క్రియాజనకాల గాఢతలో గాని, క్రియాజన్యాల గాఢతలో గాని మార్పు కనిపించదు. ఈ పరిస్థితులలో మనకు చర్య జరగటం లేదేమోనని భ్రమ కలుగుతుంది. కాని నిజానికి చర్య జరుగుతూనే ఉంటుంది. అందువలననే ఈ సమతాస్థితిని గతిక సమతాస్థితి అంటారు.

ప్రశ్న 86.
భౌతిక ప్రక్రియలలోని సమతాస్థితుల సాధారణ అభిలాక్షణిక ధర్మాలను తెలపండి.
జవాబు:
భౌతిక ప్రక్రియలలో సమతాస్థితి :

ద్రవబాష్పాల మధ్య సమతాస్థితి ఏర్పడుతుంది. ద్రవం ⇌ బాష్పం
ద్రవాలలో వాయువులు కరిగినప్పుడు సమతాస్థితి ఏర్పడుతుంది.

ఈ భౌతిక ప్రక్రియలలో కొన్ని అభిలాక్షణిక ధర్మాలు సమతాస్థితి వద్ద ఉండే అన్ని వ్యవస్థలకు ఉంటాయి.

నిర్దిష్ట ఉష్ణోగ్రత వద్ద సంవృత (మూసి ఉన్న) వ్యవస్థలలో మాత్రమే సమతాస్థితి ఏర్పడుతుంది.
పరస్పరం వ్యతిరేకించే రెండు చర్యలు (పురోగామి, తిరోగామి) ఒకే వేగంతో జరుగుతాయి. కాబట్టి గతిక సమతాస్థితి చోటుచేసుకొంటుంది. అయితే స్థిరపరిస్థితి కొనసాగుతుంది.
వ్యవస్థ కొలవడానికి వీలుండే అన్ని ధర్మాలు స్థిరంగా ఉంటాయి.
ఒక భౌతిక ప్రక్రియ సమతాస్థితిని చేరుకొన్న సందర్భంలో స్థిర ఉష్ణోగ్రత వద్ద దాని పరామితులలో ఒకదాని విలువ స్థిరంగా ఉండే అభిలాక్షణిక స్వభావాన్ని ఈ ప్రక్రియ కలిగి ఉంటుంది.
సమతాస్థితిని చేరుకొనక ముందుగా భౌతిక ప్రక్రియ ఎంత విస్తృతికి జరిగింది అనే విషయాన్ని ఈ పరామితుల పరిమాణాలు సూచిస్తాయి.

ప్రశ్న 87.
సమతాస్థితి స్థిరాంకం ముఖ్య లక్షణాలను తెలపండి. సమతాస్థితి స్థిరాంకం అనువర్తనాలు రెండింటిని తెలపండి.
జవాబు:
సమతాస్థితి స్థిరాంకాల అనువర్తనాలను గురించి తెలుసుకోవడానికి ముందుగా సమతాస్థితి స్థిరాంకాల ముఖ్య లక్షణాలివి.

సమతాస్థితి వద్ద క్రియాజనకాల గాఢతలు, క్రియాజన్యాల గాఢతలు స్థిర విలువలను చేరుకొన్న తరువాతే సమతాస్థితి స్థిరాంకం అనువర్తిస్తుంది.
సమతాస్థితి స్థిరాంకం విలువ క్రియాజనకాల, క్రియాజన్యాల ఆరంభ గాఢతల మీద ఆధారపడి ఉండదు.
సమతాస్థితి స్థిరాంకం విలువ చర్య ఉష్ణోగ్రత మీద ఆధారపడి ఉంటుంది. నిర్దిష్ట ఉష్ణోగ్రత వద్ద ప్రతీ చర్యకు దానిదైన ప్రత్యేకమైన సమతాస్థితి స్థిరాంకం విలువ ఉంటుంది. ఈ విలువ ఈ చర్య సమతుల్యం చేయబడిన రసాయన సమీకరణం మీద ఆధారపడి ఉంటుంది.
ఉత్రమణీయ చర్య (లేదా తిరోగామి దిశలో జరిగే చర్య) సమతాస్థితి స్థిరాంకం విలువ పురోగామి దిశలో జరిగే చర్య సమతా స్థితి స్థిరాంకం విలువకు ఉత్రమణీయ విలువగా ఉంటుంది.
మూల సమీకరణంతో సూచింపబడని ఒక చర్య సమతాస్థితి స్థిరాంకం K విలువ చర్య మూల సమీకరణం సూచించే సమతాస్థితి స్థిరాంకం (K) విలువతో సంబంధం కలిగి ఉంటుంది. ఈ సంబంధం నిర్ధారించడానికి మూల సమీకరణం ద్వారా సూచింపబడిన చర్యా సమీకరణాన్ని ఒక లఘు సంఖ్య (n) తో గుణించి లేదా భాగించి ఇచ్చిన చర్య సమీకరణాన్ని రాబడతారు.
K = Kⁿ

అనువర్తనాలు :

చర్య స్థిరాంక పరిమాణం ద్వారా చర్య విస్తృతిని ఊహించడం.
చర్య జరిగే దిశను (పురోగామి లేదా తిరోగామి) నిర్ధారించడం.
సమతాస్థితి గాఢతలను లెక్కించడం.

ప్రశ్న 88.
లీచాట్లెయర్ సూత్రం వివరించండి. సమతాస్థితిని ప్రభావితం చేసే అంశాలను వివరించండి.
జవాబు:
ప్రయోగ పరిస్థితులలో చోటుచేసుకొన్న మార్పులు సమతాస్థితిపై ఎటువంటి ప్రభావాన్ని కలుగజేస్తాయి అనే విషయాన్ని గుణాత్మకంగా తెలుసుకోవడానికి లీచాట్లెయర్ సూత్రం ఉపయోగపడుతుంది.
ఒక వ్యవస్థ సమతాస్థితిని నియంత్రించే కారణాంశాలలో దేనినైనా మార్పు చెందించినట్లైతే ఈ మార్పును తగ్గించే విధంగా లేదా పూర్తిగా ప్రతిఘటించే విధంగా లేదా తటస్థపరిచే విధంగా, వ్యవస్థ వ్యవహరిస్తుంది.
ఈ సూత్రం అన్ని భౌతిక, రసాయనిక సమతాస్థితులకు కూడా వర్తిస్తుంది.
సమతాస్థితిని ప్రభావితం చేసే అంశాలు :
గాఢతా ప్రభావం : H₂ (వాయువు) + I₂(వా) ⇌ 2HI(వా)
సమతాస్థితి వద్ద ఈ చర్యా మిశ్రమానికి H₂ ను కలిపినట్లైతే చర్యా సమతాస్థితి చెదిరిపోతుంది. కాబట్టి H₂ వినియోగపడే దిశలో చర్య పురోగమించి సమతాస్థితి పునరుద్ధరించబడుతుంది. అంటే HI ఏర్పడే విధంగా H₂, I₂ లు అధిక పరిమాణంలో చర్య జరిపి సమతాస్థితి పురోగామి దిశలో జరుగుతుంది. ఇదే విధంగా ఏర్పడిన హైడ్రోజన్ అయొడైడ్ను తొలగిస్తే కూడా పురోగామి దిశలో చర్య జరుగుతుంది.

సమతాస్థితిలో ఉండే ఒక రసాయన చర్యలోని క్రియాజనకాల లేదా క్రియాజన్యాల గాఢతను మార్చినట్లైతే ఈ గాఢత మార్పును కనిష్ఠపరిచే విధంగా సమతాస్థితి మిశ్రమం సంఘటనం మార్పు చెందుతుంది.

పీడన ప్రభావం : ఒక చర్యలో వాయు స్థితిలో ఉండే క్రియాజనకాలు మొత్తం మోల్ల సంఖ్య వాయుస్థితిలో ఉండే క్రియాజన్యాల మొత్తం మోల్ల సంఖ్యకు సమానంగా లేనప్పుడు ఆ సమతాస్థితిపై పీడన ప్రభావం ఉంటుంది. లీచాట్లెయర్ సూత్రం ప్రకారం సమతాస్థితి వ్యవస్థపై పీడనాన్ని పెంచినప్పుడు ఘనపరిమాణం తగ్గే దిశలో చర్య
జరుగుతుంది.

1) పీడన ప్రభావం :

a) పీడనంలో పెరుగుదల : సమతాస్థితి వద్ద ఉన్న వ్యవస్థపై పీడనాన్ని పెంచితే లీచాట్లెయర్ సూత్రం ప్రకారం ఈ ప్రభావం రద్దు అయ్యే వైపుకు అంటే ఘ.ప.,ల సంఖ్య తగ్గే వైపుకు సమతాస్థితి జరుగుతుంది.
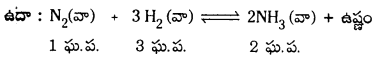
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 28
ఈ వ్యవస్థపై పీడనాన్ని పెంచితే పురోగామి చర్యవైపుకు సమతాస్థితి జరుగుతుంది.

b) పీడనంలో తగ్గుదల : సమతాస్థితి వద్ద ఉన్న వ్యవస్థపై పీడనాన్ని తగ్గిస్తే లీచాట్లెయర్ సూత్రం ప్రకారం ఈ ప్రభావం రద్దు అయ్యేవైపుకు అంటే ఘ.ప. ల సంఖ్య పెరిగే వైపుకు సమతాస్థితి జరుగుతుంది.
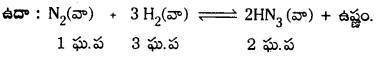
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 29
ఈ వ్యవస్థపై పీడనాన్ని తగ్గిస్తే తిరోగామిచర్య జరిగే వైపుకు సమతాస్థితి జరుగుతుంది.

2) ఉష్ణోగ్రతా ప్రభావం :

a) ఉష్ణోగ్రతలో పెరుగుదల : సమతాస్థితి వద్ద ఉన్న వ్యవస్థపై ఉష్ణోగ్రతను పెంచితే లీచాట్లెయర్ సూత్రం ప్రకారం, ఈ ప్రభావం రద్దు అయ్యే వైపుకు అంటే ఉష్ణగ్రాహక చర్య జరిగే వైపుకు సమతాస్థితి స్థానం జరుగుతుంది.
ఉదా : N₂(వా) + 3H₂(వా) ⇌ 2NH₃(వా) + ఉష్ణం.
దీనిలో పురోగామిచర్య = ఉష్ణమోచకం
తిరోగామి చర్య = ఉష్ణగ్రాహక చర్య
ఈ వ్యవస్థపై ఉష్ణోగ్రతను పెంచితే తిరోగామిచర్య జరిగే వైపుకు సమతాస్థితి జరుగుతుంది.

b) ఉష్ణోగ్రతలో తగ్గుదల : సమతాస్థితి వద్ద ఉన్న వ్యవస్థపై ఉష్ణోగ్రతను తగ్గిస్తే లీచాట్లెయర్ సూత్రం ప్రకారం, ఈ ప్రభావం రద్దు అయ్యే వైపుకు అంటే ఉష్ణమోచక చర్య జరిగే వైపుకు సమతాస్థితి స్థానం జరుగుతుంది.
ఉదా : N₂(వా) + 3 H₂ (వా) ⇌ 2NH₃ (వా) + ఉష్ణం
దీనిలో పురోగామి చర్య = ఉష్ణమోచక చర్య
తిరోగామి చర్య = ఉష్ణగ్రాహక చర్య
ఈ వ్యవస్థపై ఉష్ణోగ్రతను తగ్గిస్తే, పురోగామి చర్య జరిగే వైపుకు సమతాస్థితి జరుగుతుంది.

సమతాస్థితికి జడవాయువు చేర్చినపుడు కలిగే ప్రభావం : ఘనపరిమాణాన్ని స్థిరంగా ఉంచి ఆర్గాన్ వంటి జడవాయువును చర్యా మిశ్రమానికి చేర్చినట్లైతే అది చర్యలో పాల్గొనని కారణంగా సమతాస్థితి చెదిరిపోకుండా ఉంటుంది. స్థిరఘనపరిమాణం వద్ద చర్యలో పాల్గొనే పదార్థాల పాక్షిక పీడనాల విలువలో మార్పురాదు.

ఉత్ప్రేరక ప్రభావం : క్రియాజనకాలు క్రియాజన్యాలుగా మారేందుకు అల్ప ఉత్తేజిత శక్తిగల కొత్త మార్గాన్ని సమకూర్చడం ద్వారా ఉత్ప్రేరకం రసాయన చర్యావేగాన్ని పెంచుతుంది. ద్విగత చర్యలలో ఉత్ప్రేరకం పురోగామి, తిరోగామి చర్యల రెండింటి వేగాలను సమానంగా పెంచుతుంది. ఫలితంగా సమతాస్థితిపై ఎటువంటి ప్రభావం ఉండదు. సమతాస్థితి శీఘ్రంగా ఏర్పడడానికి ఉత్ప్రేరకం ఉపయోగిస్తుంది. అమ్మోనియా సంశ్లేషణలో ఇనుమును ఉత్ప్రేరకంగా వాడతారు.

ప్రశ్న 89.
అమ్మోనియా, సల్ఫర్ ట్రై ఆక్సైడ్ పారిశ్రామిక తయారీలలో, లీచాట్లెయర్ సూత్రం ఉపయోగాన్ని వివరించండి.
జవాబు:
లీచాట్లెయర్ సూత్రం : సమతాస్థితి వద్ద ఉన్న ఒక ఉత్రమణీయ రసాయన చర్యను, సమతాస్థితిని ప్రభావితం చేసే పీడనం లేదా ఉష్ణోగ్రత లేదా గాఢతల మార్పుకు గురిచేస్తే ఈ మార్పు ప్రభావాన్ని తగ్గించే వైపుకు లేదా రద్దు చేసే వైపుకు సమతాస్థితి మారుతుంది.
హేబర్ పద్ధతి ద్వారా అమ్మోనియా సంశ్లేషణ :
N₂(వా) + 3H₂(వా) ⇌ 2NH₃(వా) + ఉష్ణం – చర్యకు లీచాట్లియర్ సూత్రం అనువర్తన.

1) పీడన ప్రభావం : ఇవ్వబడిన చర్యలో, పురోగామి చర్య జరిగితే ఘ.ప. సంఖ్య తగ్గుతుంది. (4 ఘప → 2 ఘ. ప) తిరోగామి చర్య జరిగితే ఘ.ప. సంఖ్య పెరుగుతుంది. (2 ఘ. ప → 4 ఘ.ప)
అమ్మోనియా అధికంగా దిగుబడి కావాలంటే పురోగామి చర్య జరగాలి. అంటే ఘ.ప. సంఖ్య తగ్గే వైపుకు చర్య ప్రభావితం అవ్వాలి. దీనికి గానూ అధిక పీడనాలను ఉపయోగించాలి. ఇచ్చట ఉపయోగించవలసిన అధిక పీడనాల విలువ 200 అట్మాస్ఫియర్లు.

2) ఉష్ణోగ్రతా ప్రభావం : ఇవ్వబడిన చర్యలో
పురోగామి చర్య = ఉష్ణమోచకం
తిరోగామి చర్య = ఉష్ణగ్రాహకం
అమ్మోనియా అధికంగా దిగుబడి కావాలంటే పురోగామి చర్య జరగాలి. అంటే ఉష్ణమోచక చర్య జరిగే వైపుకు చర్య ప్రభావితం అవ్వాలి. దీనికి గానూ, అల్ప ఉష్ణోగ్రతలను ఉపయోగించాలి. ఇచ్చట ఉపయోగించవలసిన అల్ప ఉష్ణోగ్రత విలువ 725 – 775K.

3) గాఢతల ప్రభావం : క్రియాజనకాల గాఢతను పెంచినా లేదా క్రియాజన్యాల గాఢతను తగ్గించినా పురోగామి చర్య ప్రభావితం అయి అధికంగా అమ్మోనియా దిగుబడి అవుతుంది. అందువలన ఇవ్వబడిన సమతాస్థితి వ్యవస్థలో N₂, H₂ గాఢతను పెంచడం మరియు ఏర్పడిన NH₃ ని ఎప్పటికప్పుడు తీసివేయడం చేస్తూ ఉండాలి.

4) ఉత్ప్రేరక ప్రభావం : అధిక అమ్మోనియా దిగుబడి కావాలంటే ఇనుప పొడి మరియు మాలిబ్దినం పొడుల మిశ్రమాన్ని ఉత్ప్రేరకంగా వాడతారు. ఇచ్చట మాలిబ్ధినం పొడి ప్రవర్ధకంగా పనిచేస్తుంది.
అధిక అమ్మోనియా దిగుబడికి కావలసిన పరిస్థితులు :
పీడనం = 200 అట్మాస్ఫియర్లు
ఉష్ణోగ్రత = 725 – 775 K
ఉత్ప్రేరకం = ఇనుము పొడి
ప్రవర్ధకం = మాలిబ్దినం పొడి
క్రియాజనకాలైన N₂, H₂ ల గాఢతను పెంచుతూ ఉండాలి.
క్రియాజన్యమైన NH₃ ఎప్పటికప్పుడు తీసివేస్తూ ఉండాలి.

లీచాట్యర్ సూత్రం : సమతాస్థితి వద్ద ఉన్న ఒక ఉత్రమణీయ రసాయన చర్యను, సమతాస్థితిని ప్రభావితం చేసే పీడనం, లేదా ఉష్ణోగ్రత లేదా గాఢతల మార్పుకు గురి చేస్తే ఈ మార్పు ప్రభావాన్ని తగ్గించే వైపుకు లేదా రద్దు చేసే వైపుకు సమతాస్థితి మారుతుంది.

SO₃ సంశ్లేషణ పద్ధతి :
2SO₂(వా) + O₂(వా) ⇌ 2SO₃(వా) + ఉష్ణం – చర్యకు లీచాట్లెయర్ సూత్రం అనువర్తనం.

1) పీడన ప్రభావం : ఇవ్వబడిన పురోగామి చర్య జరిగితే ఘ.ప. ల సంఖ్య తగ్గుతుంది. (3 ఘ.ప. → 2 ఘ. ప ) తిరోగామి చర్య జరిగితే ఘ.ప. ల సంఖ్య పెరుగుతుంది. (2 ఘ. ఫ → 3 ఘ.ప) సల్ఫర్ ట్రై ఆక్సైడ్ అధికంగా దిగుబడి కావాలంటే పురోగామి చర్య జరగాలి. అంటే ఘ.ప. ల సంఖ్య తగ్గే వైపుకు చర్య ప్రభావితం అవ్వాలి. దీనికి గానూ అధిక పీడనాలు ఉపయోగించాలి. ఇచ్చట ఉపయోగించవలసిన అధిక పీడనాల విలువ 1.5 అట్మా 1.7 అట్మాస్ఫియర్లు.

2) ఉష్ణోగ్రతా ప్రభావం : ఇవ్వబడిన చర్యలో
పురోగామి చర్య = ఉష్ణమోచకం
తిరోగామి చర్య = ఉష్ణగ్రాహకం
సల్ఫర్ ట్రై ఆక్సైడ్ అధికంగా దిగుబడి కావాలంటే పురోగామి చర్య జరగాలి. అంటే ఉష్ణమోచక చర్య జరిగే వైపుకు చర్య ప్రభావితం అవ్వాలి. దీనికి గానూ అల్ప ఉష్ణోగ్రతలను ఉపయోగించాలి. ఇచ్చట ఉపయోగించవలసిన అల్ప ఉష్ణోగ్రతలు 673 K.

3) గాఢతల ప్రభావం : క్రియాజనకాల గాఢతను పెంచినా లేదా క్రియాజన్యాల గాఢతను తగ్గించినా పురోగామి చర్య ప్రభావితం అయి అధికంగా SO₃ దిగుబడి అవుతుంది. అందువలన ఇవ్వబడిన సమతాస్థితిలో SO₂, O₂ ల గాఢతలను పెంచడం మరియు ఏర్పడిన SO₃ ని ఎప్పటికప్పుడు తీసివేయడం చేస్తూ ఉండాలి.

4) ఉత్ప్రేరక ప్రభావం : అధిక SO₃ దిగుబడి కావాలంటే V₂O₅ ను ఉత్ప్రేరకంగా వాడతారు.
అధిక SO₃ దిగుబడికి అనుకూల పరిస్థితులు :

పీడనం : 1.5 – 1.7 అట్మాస్ఫియర్లు
ఉష్ణోగ్రత : 673 K
ఉత్ప్రేరకం : వనేడియం పెంటాక్సైడ్ (V₂O₅)
క్రియాజనకాలైన SO₂, O₂ ల గాఢతను పెంచుతూ ఉండాలి.
క్రియాజన్యమైన SO₃ ను ఎప్పటికప్పుడు తీసివేస్తూ ఉండాలి.

ప్రశ్న 90.
కింద పేర్కొన్న ఉష్ణగ్రాహక చర్య ఆధారంగా సహజ వాయువును, నీటి ఆవిరి ద్వారా పాక్షిక ఆక్సీకరణం చర్యకు గురిచేసి డైహైడ్రోజన్ వాయువును తయారుచేస్తారు.
CH (వా) + H₂O (వా) ⇌ CO (వా) + 3H₂ (వా)
a) పై చర్యకు K_p కు సమీకరణం రాయండి.
b) K_p విలువ సమతాస్థితి మిశ్రమం సంఘటనం ఏ విధంగా కింది వాటి ద్వారా ప్రభావితం అవుతాయి ?
i) పీడనం పెరుగుదల
ii) ఉష్ణోగ్రత పెరుగుదల
iii)ఉత్ప్రేరకం ఉపయోగం
జవాబు:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 30

1) ఈ సమీకరణంలో ‘P’ లవంలో ఉన్నది. పీడనాన్ని పెంచినపుడు K_p విలువను స్థిరంగా ఉంచే విధంగా హారం విలువ పెరగాలి. అందువల్ల తిరోగామిచర్య జరిగి ఉత్పన్నాల గాఢత తగ్గుతుంది.
లీచాటయర్ సూత్రం ప్రకారం పీడనాన్ని పెంచినపుడు ఘనపరిమాణం తగ్గే చర్య ప్రోత్సహించబడుతుంది. తిరోగామి చర్యలో ఘనపరిమాణం తగ్గుచున్నది కనుక తిరోగామి చర్య ప్రోత్సహించబడుతుంది.

2) ఈ చర్య ఉష్ణగ్రాహకచర్య కావున ఉష్ణోగ్రత పెరిగితే పురోగామి చర్య ప్రోత్సహించబడుతుంది. ఉత్పన్నాలు అధికంగా ఏర్పడతాయి.

3) ఉత్ప్రేరకం సమతాస్థానాన్ని ప్రభావితం చేయదు.

ప్రశ్న 91.
2H₂ (వా) + CO (వా) ⇌ CH₃ OH (వా) చర్య సమతాస్థితిపై కింది వాటి ప్రభావాన్ని తెలపండి.
a) H₂ సంకలనం
b) CH₃OH సంకలనం
c) CO తొలగింపు
d) CH₃OH తొలగింపు
జవాబు:
a) లీచాట్లెయర్ సూత్రం ప్రకారం, క్రియాజనకాల గాఢత పెంచితే పురోగామి చర్య ప్రోత్సహించబడుతుంది. H₂ సంకలనం (కలుపుట) వలన CH₃OH ఎక్కువగా ఏర్పడుతుంది.

b) లీచాట్లెయర్ సూత్రం ప్రకారం, క్రియాజన్యం కలిపినపుడు తిరోగామి చర్య జరుగుతుంది. H₂ మరియు CO ల గాఢత పెరుగుతుంది.

c) CO తొలగింపు : లీచాటయర్ సూత్రం ప్రకారం క్రియాజనకం తొలగిస్తే, తిరోగామి చర్య ప్రోత్సహించబడుతుంది. CH₃OH గాఢత తగ్గుతుంది.

d) CH₃OH తొలగింపు : లీచాట్లెయర్ సూత్రం ప్రకారం ఉత్పన్నాన్ని తొలగిస్తే పురోగామి చర్య ప్రోత్సహించబడుతుంది. అందువల్ల CH₃OH అధికంగా ఏర్పడుతుంది.

ప్రశ్న 92.
473K వద్ద ఫాస్ఫరస్ డెంటాక్లోరైడ్ PCl₅, విఘటనం చర్యకు సమతాస్థితి స్థిరాంకం విలువ K_c = 8.3 × 10^-3. ఈ విఘటన చర్యను కింది విధంగా వ్యక్తం చేస్తే.
PCl₅ (వా) ⇌ PCl₃ (వా) + Cl₂ (వా) ΔH = 124.0 kJmol^-1,
a) చర్యకు K_c ను వ్యక్తం చేసే సమాసం రాయండి.
b) అదే ఉష్ణోగ్రత వద్ద, ఉత్రమణీయ చర్యకు K_c విలువను తెలపండి.
c) K_c పై కింది వాని ప్రభావం తెలపండి.
i) PCl₅ అధిక సంకలనం
ii) పీడనం పెంచడం
iii) ఉష్ణోగ్రత పెంచడం
జవాబు:
a) K_c = \(\frac{\left[\mathrm{PCl}_3\right]\left[\mathrm{Cl}_2\right]}{\left[\mathrm{PCl}_5\right]}\)

b) ఉత్రమణీయ చర్యకు K_c’ = \(\frac{1}{\mathrm{~K}_{\mathrm{c}}}\)
K_c’ = \(\frac{1}{8.3 \times 10^{-3}}\) = 120.28

c) i) PCl₅ ను సమతాస్థితికి కలిపినపుడు పురోగామి చర్య దిశగా సమతాస్థానం కదులుతుంది. K విలువ మారదు.
ii) PCl₅ విఘటన చర్య ఉష్ణగ్రాహక చర్య. ఉష్ణోగ్రత పెరుగుదల ఉష్ణగ్రాహకచర్యను ప్రోత్సహించడం వల్ల PCl₅ విఘటనం పెరుగుతుంది. ఉష్ణోగ్రత పెరిగితే K_c విలువ పెరుగుతుంది.
iii) పీడనాన్ని పెంచుట వలన ఘనపరిమాణం తగ్గే చర్య అయిన తిరోగామి చర్య ప్రోత్సహించబడుతుంది. K_c విలువ మారదు.

ప్రశ్న 93.
బ్రాన్ స్టెడ్ ఆమ్లాలు, బ్రాన్స్టెడ్ క్షారాలు భావనలను సోదాహరణంగా వివరించండి.
జవాబు:
బ్రాన్డ్-లౌరి సిద్ధాంతం ప్రకారం హైడ్రోజన్ అయాన్ H⁺ ను దానం చేసే సామర్ధ్యం గల పదార్థాలు ఆమ్లాలు. హైడ్రోజన్ అయాన్ H⁺ ను స్వీకరించే సామర్థ్యం గల పదార్థాలు క్షారాలు. ప్రోటాన్ దాతలు ఆమ్లాలు. ప్రోటాన్ స్వీకర్తలు క్షారాలు.

బ్రాన్టెడ్ ఆమ్లాలు రెండు రకాలు. అవి

1) బలమైన ఆమ్లం
2) బలహీన ఆమ్లం..

బలమైన ఆమ్లం : ప్రోటాన్ ను సునాయాసంగా దానం చేయగలిగే ప్రవృత్తి గల పదార్థాన్ని బలమైన ఆమ్లం అంటారు. ఉదా : HClO₄, H₂SO₄, HCl, HNO₃ మొ||వి.
బలహీన ఆమ్లం : ప్రోటాను సునాయాసంగా దానం చేయలేని పదార్థాన్ని బలహీన ఆమ్లం అంటారు.
ఉదా : HF, CH₃COOH, H₂CO₃ మొ||వి.
బ్రాన్డ్ క్షారం : ఇతర పదార్థాల నుండి ప్రోటాను స్వీకరించే ప్రవృత్తి గల పదార్థాన్ని బ్రాన్స్టెడ్ క్షారం అంటారు.
ఉదా : H₂O, Cl^–, CH₃COO^– మొ|| వి.

బ్రాన్టెడ్ క్షారాలు రెండు రకాలు: అవి

1) బలమైన క్షారం,
2) బలహీన క్షారం.

బలమైన క్షారం : ప్రోటాను సునాయాసంగా స్వీకరించగలిగే పదార్థాన్ని బలమైన క్షారం అంటారు.
ఉదా : F^–, N\(\mathrm{O}_2^{-}\), CH₃COO^–, HC\(\mathrm{O}_3^{-}\), CN^– మొ|| వి.
బలహీన క్షారం : ప్రోటాను సునాయాసంగా స్వీకరించలేని పదార్థాన్ని బలహీన క్షారం అంటారు.
ఉదా : Cl\(\mathrm{O}_4^{-}\), HS\(\mathrm{O}_4^{-}\), Cl^–, N\(\mathrm{O}_3^{-}\) మొ||వి.

తటస్థీకరణం : ఆమ్ల, క్షారముల మధ్య జరిగే ప్రోటాన్ మార్పిడిని ‘తటస్థీకరణం’ అంటారు.
ఉదా : HCl + H₂O ⇌ H₃O⁺ + Cl^–
బ్రానెడ్ సిద్ధాంతం ప్రకారం ఆమ్ల, క్షారముల మధ్య జరిగే చర్యలు ద్విగత చర్యలుగా ఉంటాయి. కాంజుగేట్ ఆమ్ల-క్షార జంట : ఒక ప్రోటాన్ తేడాతో ఉండే ఆమ్లక్షార జంటను కాంజుగేట్ ఆమ్ల క్షార జంట అంటారు. ఉదా : (HCl, Cl^–), (H₂O, OH^–)
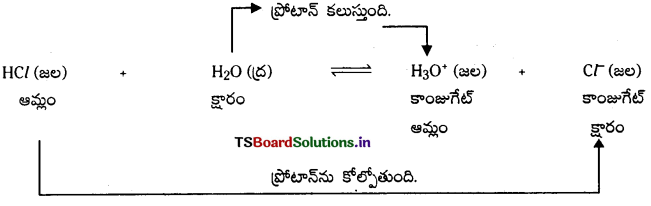
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 31
(HCl, Cl^–) అనే కాంజుగేట్ ఆమ్ల క్షార జంటలో HCl ఆమ్లం యొక్క కాంజుగేట్ క్షారం Cl^–. అలాగే Cl^– క్షారం యొక్క కాంజుగేట్ ఆమ్లం HCl.
(H₂O, OH^–) – అనే కాంజుగేట్ ఆమ్ల క్షార జంటలో H₂O ఆమ్లం యొక్క కాంజుగేట్ క్షారం OH^–. అలాగే OH^– క్షారం యొక్క కాంజుగేట్ ఆమ్లం H₂O.

కాంజుగేట్ ఆమ్ల-క్షార లక్షణాలు : ఒక కాంజుగేటు ఆమ్ల క్షార జంటలో ఆమ్లం బలమైనదైతే దాని కాంజుగేట్ క్షారం బలహీనమైనది అవుతుంది. అలాగే క్షారం బలమైనదైతే దాని కాంజుగేట్ ఆమ్లం బలహీనమైనది అవుతుంది.
ఉదా : (HCl, Cl^–) – కాంజుగేట్ ఆమ్ల క్షార జంటలో HCl బలమైన ఆమ్లం. కాబట్టి దాని కాంజుగేట్ క్షారం (Cl^–). బలహీనమైనది.
(CH₃COOH, CH₃COO^–) – కాంజుగేట్ ఆమ్ల క్షార జంటలో CH₃COOH బలహీన ఆమ్లం కాబట్టి, దాని కాంజుగేట్ క్షారం (CH₃COO^–) బలమైనది.

గమనిక : ఆమ్లం నుండి ప్రోటాన్ ను తీసివేస్తే కాంజుగేట్ క్షారం వస్తుంది. అలాగే క్షారానికి ప్రోటాన్ ను కలిపితే కాంజుగేట్ ఆమ్లం వస్తుంది.
స్థాయీ ప్రభావం : నీరు, అన్ని బలమైన ఆమ్లాలు ఆమ్లశక్తిని H₃O⁺ కు అలాగే అన్ని బలమైన క్షారాల క్షార శక్తిని OH^– సమానం చేస్తుంది. దీనినే స్థాయీ ప్రభావం అంటారు.

బ్రాన్డ్ సిద్ధాంతంలోని గొప్పతనాలు :

ఈ సిద్ధాంతం ఆమ్లాల మరియు క్షారాల స్వభావాలను జల మరియు జలేతర ద్రావణాలలో వివరిస్తుంది.
NH₃, CaO మొ||వి పదార్థాల క్షార స్వభావాన్ని, CO₂, SO₂ మొ||వి పదార్థాల ఆమ్ల స్వభావాన్ని చక్కగా
వివరిస్తుంది. బ్రాన్ స్టెడ్ సిద్ధాంతంలోని లోపాలు :
1. ప్రోటాను దానం చేయటం మరియు స్వీకరించటం ఇతర పదార్థాల సమక్షంలో మాత్రమే జరుగుతుంది.
2. AlCl₃, BCl₃ వంటి ఎలక్ట్రాన్ కొరత గల పదార్థాల ఆమ్ల స్వభావాన్ని వివరించలేదు.

ప్రశ్న 94.
తగిన ఉదాహరణలతో లూయీ ఆమ్ల క్షార సిద్ధాంతం వివరించండి. కింది జాతులను లూయీ ఆమ్లాలు, లూయీ క్షారాలుగా వర్గీకరించండి. ఇవి లూయీ ఆమ్లం/క్షారంగా ఏ విధంగా పనిచేస్తాయి ?
a) OH^–
b) F^–
c) H⁺
d) BCl₃
జవాబు:
ఎలక్ట్రాన్ జంటను స్వీకరించే జాతిని ఆమ్లం అని, ఎలక్ట్రాన్ జంటను దానంచేసే రసాయన జాతిని క్షారం అని లూయీ నిర్వచించెను.

ఎలక్ట్రాన్ జంట స్వీకర్త ఆమ్లం. ఎలక్ట్రాన్ జంట దాత క్షారం.
ఉదా :

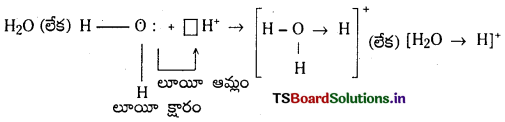
1) హైడ్రోనియం అయాన్ ఏర్పడటం :
జలాణువు H⁺ తో సంయోగం చెందడం వల్ల హైడ్రోనియం అయాన్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 32
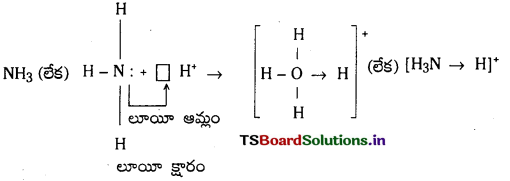
2) అమ్మోనియం అయాన్ ఏర్పడటం : అమ్మోనియా అణువు ప్రోటాన్తో సంయోగం చెందడం వల్ల అమ్మోనియం అయాన్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 33

లూయీ సిద్ధాంతం పరిమితులు :

ఆమ్లాల, క్షారాల బాలాలను వివరించలేదు.
HCl, H₂SO₄ వంటి ఆమ్లాలు NaOH, KOH వంటి క్షారాలతో చర్య జరుపుతాయి. కానీ సమన్వయ సమయోజనీయ బంధాలను ఏర్పరచవు.
సాధారణంగా ఆమ్ల క్షార చర్యలు అతి వేగంగా జరుగుతాయి. కాని లూయీ క్షారం, ఆమ్లాల మధ్య చర్యలు అతి నెమ్మదిగా జరుగుతాయి.

లూయీ ఆమ్లాలలోని రకాలు :

అన్ని కేటయాన్లు లూయీ ఆమ్లాలుగా పనిచేస్తాయి.
ఉదా : Ag⁺, CO³⁺, Cu⁺, Fe³⁺
ఖాళీ ఆర్బిటాల్ కలిగి ఉన్న కేంద్ర పరమాణువు గల ఎలక్ట్రాన్ కొరత గల సమ్మేళనాలు.
ఉదా : BF₃, BCl₃, AlCl₃, FeCl₃.
అష్టకాన్ని విస్తరించగల ఖాళీ ‘d’ ఆర్బిటాల్ గలవి.
ఉదా : SiF₄, SnCl₄, SF₄
బహుబంధాలు గల అణువులు
ఉదా : CO₂, SO₂, SO₃, NO₂

లూయీ క్షారాలలోని రకాలు :

అన్ని ఋణ అయాన్లు. ఉదా : Cl^–, OH^–, CN^–
కేంద్ర పరమాణువు వద్ద ఒంటరి ఎలక్ట్రాన్ జంట గల తటస్థ అణువులు : H₂O, NH₃, R – OH
బహుబంధాలు గల అణువులు : CO, NO, HC ≡ CH.

a) హైడ్రాక్సిల్ అయాన్, తాను ఒక ఎలక్ట్రాన్ జంటను దానం చేయగలగడం చేత లూయీ క్షారంగా పనిచేస్తుంది.
b) F^–, దానిపై ఉండే నాలుగు ఒంటరి ఎలక్ట్రాన్ జంటలలో ఒకదానిని దానంచేసి లూయీ క్షారంగా ప్రవర్తిస్తుంది.
c) హైడ్రాక్సిల్ అయాన్, ఫ్లోరైడ్ అయాన్ వంటి క్షారాల నుంచి, ఒక ఒంటరి ఎలక్ట్రాన్ జంటను స్వీకరించగలిగి ఉండటం కారణంగా, ప్రోటాన్ ఒక లూయీ ఆమ్లంగా పనిచేస్తుంది.
d) అమ్మోనియా లేదా ఏమీన్ అణువులనుంచి ఒక జంట ఒంటరి ఎలక్ట్రాన్లను BCl₃ స్వీకరించి లూయీ ఆమ్లంగా పనిచేస్తుంది.

ప్రశ్న 95.
బలహీన ఆమ్లాలు, బలహీన క్షారాలు, వీటికి సంబంధించినంతవరకు అయనీకరణ అవధి ఏమిటి ? HX, బలహీన ఆమ్లం విషయంలో సమతాస్థితి స్థిరాంకం విలువ K_a కు, అయనీకరణం అవధికి మధ్య గల సంబంధం ఏమిటి ?
జవాబు:
అయనీకరణ అవధి (α) : ఒక మోల్ ఆమ్లం లేక క్షారంలో ఎంత భాగం ఆమ్లం లేక క్షారం అయనీకరణం చెందుతుందో దానిని అయనీకరణ అవధి అంటారు. దీనిని α తో సూచిస్తారు. బలమైన ఆమ్లాలు లేక క్షారాలు పూర్తిగా అయనీకరణం చెందుతాయి. కాబట్టి వాటి α విలువ ‘ఒకటి’ ఉంటుంది.
‘c’ గాఢత గల బలహీన ఆమ్లం HX ను తీసికోండి. అది పాక్షికంగా అయనీకరణం చెందుతుంది. దాని అయనీకరణ సమతాస్థితిని క్రింది విధంగా సూచిస్తారు.
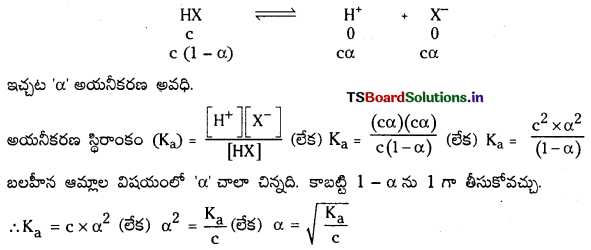
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 34

ప్రశ్న 96.
pH ను నిర్వచించండి. బఫర్ ద్రావణం అంటే ఏమిటి ? ఆమ్ల బఫర్ ద్రావణం pH విలువను లెక్కించడానికి ఉపయోగపడే హేండర్సన్ – హేజల్బాక్ సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
ఒక జలద్రావణంలోని హైడ్రోజన్ అయాన్ క్రియాశీలత విలువ యొక్క 10 ఆధారిత సంవర్ధమానం ఋణవిలువగా, ద్రావణం pH విలువను నిర్వచించవచ్చు. హైడ్రోజన్ అయాను (H) క్రియాశీలతను దాని గాఢత విలువ పరంగా (H⁺)గా వ్యక్తం చేస్తారు.
\(\mathrm{a}_{\mathrm{H}^{+}}\) = [H⁺]mol.L^-1

pH : హైడ్రోజన్ అయాన్ గాఢత యొక్క ఋణ సంవర్గమానాన్ని pH అంటారు.

pH = – log\(\mathrm{a}_{\mathrm{H}^{+}}\) = -log[H⁺]mol·L^-1

బఫర్ ద్రావణం : ద్రావణాలను విలీనం చేసినపుడు లేదా వాటికి అల్పపరిమాణంలో ఆమ్లాలను లేదా క్షారాలను కలిపినప్పుడు వాటి pH లో కలిగే మార్పును నిరోధించే శక్తి గల ద్రావణాలను బఫర్ ద్రావణాలు అంటారు.

ఆమ్ల బఫర్ : ఒక బలహీన ఆమ్లము, బలమైన క్షారంతో అది ఏర్పరచిన లవణముల మిశ్రమము ఆమ్ల బఫర్గా పనిచేస్తుంది. ఎసిటిక్ ఆమ్లం, సోడియం ఎసిటేట్ల మిశ్రమ ద్రావణం pH 4.75 పరిధిలో ఉండే బఫర్ ద్రావణంగా పనిచేస్తుంది.

క్షార బఫర్ : బలహీనమైన క్షారము, బలమైన ఆమ్లంతో అది ఏర్పరచిన లవణముల మిశ్రమము క్షార బఫర్గా పనిచేస్తుంది. అమ్మోనియం క్లోరైడు, అమ్మోనియా హైడ్రాక్సైడుల మిశ్రమ ద్రావణం pH 9.25 పరిధిలో ఉండే బఫర్ ద్రావణంగా పనిచేస్తుంది.

హేండర్సన్-హేజల్బాక్ సమీకరణం : నీటిలో అయనీకరణం చెందే బలహీన ఆమ్లము HA అయనీకరణం వల్ల A^– ఏర్పడుతుంది.
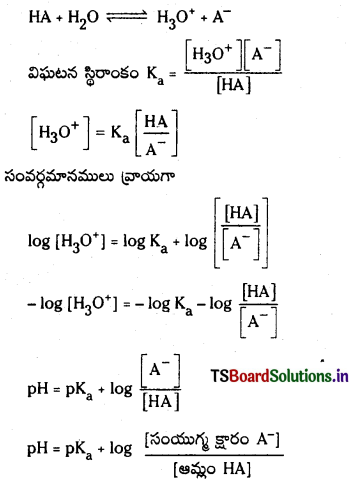
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 35
మిశ్రమంలో ఉండే ఆమ్లం యొక్క సంయుగ్మ క్షారం గాఢత, ఆమ్లం గాఢతల నిష్పత్తిని \(\frac{\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}\) రాశి తెలుపుతుంది. ఆమ్లం చాలా బలహీనమైనది కాబట్టి అల్ప విస్తృతిలో మాత్రమే అయనీకరణం చెందుతుంది. కాబట్టి బఫర్ను ఏర్పరచడానికి వాస్తవంగా ఉపయోగించిన ఆమ్లం గాఢతనుంచి సమతాస్థితి వద్ద (HA) గాఢత విలువ అల్పపరిమాణంలో మాత్రమే భేదిస్తుంది. ఈ ఆమ్ల సంబంధిత లవణం యొక్క అయనీకరణం చర్య ద్వారానే కాంజుగేటు క్షారం మొత్తం గాఢత A లభిస్తుంది. కాబట్టి లవణంగా గాఢతతో పోలిస్తే కాంజుగేటు క్షారం గాఢత ఏ మాత్రం భేదించదు. కాబట్టి పై సమీకరణాన్ని కింది రూపంలో రాయవచ్చు.
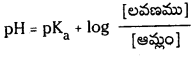
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 36

ప్రశ్న 97.
“లవణాల జలవిశ్లేషణం” పదాన్ని ఉదాహరణలతో వివరించండి. కింది లవణ ద్రావణాల pH విలువలను గురించి చర్చించండి.
i) బలహీన ఆమ్లం, బలమైన క్షారం ఏర్పరచిన లవణాలు
ii) బలమైన ఆమ్లం, బలహీన క్షారం ఏర్పరచిన లవణాలు
జవాబు:
లవణాల అయనీకరణంలో ఏర్పడిన కేటయాన్లు / ఏనయాన్లు ఆర్ద్రీకరణం చెందిన అయాన్లుగా జలద్రావణాలలో చోటు చేసుకొంటాయి. లేదా అవి నీటితో చర్య జరిపి, తిరిగి సంబంధిత ఆమ్లాలను/క్షారాలను లవణాల స్వభావాన్ని అనుసరించి ఏర్పరుస్తాయి. జలద్రావణంలో లవణాలు ఏర్పరచిన కేటయాన్లు/ఏనయాన్లు లేదా రెండు అయానులు నీటితో జరిపే అన్యోన్య చర్యను జలవిశ్లేషణం అంటారు.

బలమైన క్షారాలు ఏర్పరచే కేటయాన్లు (ఉదా : Na⁺, K⁺, Ca⁺⁺, Ba⁺⁺) బలమైన ఆమ్లాలు ఏర్పరచే ఏనయాన్లు (ఉదా : Cl^–, Br^–, N\(\mathrm{O}_3^{-}\), Cl\(\mathrm{O}_4^{-}\)) ఆర్ద్రీకరణం చెందుతాయి. కాని జలవిశ్లేషణం చెందవు. కాబట్టి బలమైన ఆమ్లాలు, బలమైన క్షారాలు చర్య జరిపి ఏర్పరచిన లవణాల జలద్రావణాలు తటస్థ స్వభావంతో ఉంటాయి. pH విలువ 7. బలహీన ఆమ్ల, క్షారాలు ఏర్పరచే లవణాలు జలవిశ్లేషణ చెందుతాయి.

i) బలహీన ఆమ్లాలు, బలమైన క్షారాలు ఏర్పరచిన లవణాలు ఉదా : CH₃COONa
ii) బలమైన ఆమ్లాలు, బలహీన క్షారాలు ఏర్పరచిన లవణాలు. ఉదా : NH₄ Cl
iii) బలహీన ఆమ్లాలు, బలహీన క్షారాలు ఏర్పరచిన లవణాలు. ఉదా : CH₃COONH₄

మొదటి రకం లవణాలలో ఏనయాన్ జలవిశ్లేషణ చెందుతుంది. OH^– అయాన్లు ఏర్పడతాయి. అందువల్ల జలద్రావణం క్షార స్వభావాన్ని కలిగి ఉంటుంది. pH > 7. ఉదా : సోడియం ఎసిటేట్.
సోడియం ఎసిటేటు జలద్రావణంలో పూర్తిగా అయనీకరణం చెందుతుంది.
CH₃COONa (జల) → CH₃COO^– (జల) + Na⁺ (జల)
CH₃COOH (జల) → H₂O (ద్ర) ⇌ CH₃COOH (జల) + OH^– (జల)
బలమైన ఆమ్లం, బలహీన క్షారం వల్ల ఏర్పడిన రెండోరకం లవణాలలో కేటయాన్ జలవిశ్లేషణ చెంది H₃O⁺ అయానును ఇస్తుంది. అందువల్ల ద్రావణం ఆమ్ల స్వభావాన్ని చూపుతుంది.

ఉదా : NH₄ Cl.
NH₄ Clపూర్తిగా జలద్రావణంలో అయనీకరణం చెందుతుంది.
NH₄Cl (జల) → N\(\mathrm{H}_4^{+}\) (జల) + Cl^– (జల)
N\(\mathrm{H}_4^{+}\) అయాన్లు నీటితో చర్య పొందుతాయి.
N\(\mathrm{H}_4^{+}\) (జల) + H₂O (ద్ర) → NH₄OH (జల) + H₃O⁺ (జల)
దీని ఫలితంగా H⁺ అయాన్ల గాఢత పెరుగుతుంది. కాబట్టి NH₄Cl జలద్రావణం pH 7 కంటే తక్కువగా వుంటుంది.

బలహీన ఆమ్లం, బలహీన క్షారం చర్య జరిపి ఏర్పరిచిన లవణానికి ఉదాహరణ CH₃COONH₄. ఇటువంటి లవణాలలో ఏనయాన్, కేటయాన్ కూడా చర్యల్లో పాల్గొంటాయి.
CH₃COO^– + N\(\mathrm{H}_4^{+}\) + H₂O ⇌ CH₃COOH + NH₄OH
CH₃COOH, NH₄OH లు రెండూ కూడా పాక్షికంగా అయనీకరణం చెందిన రూపాలలో ఉంటాయి.
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 37
అట్టి ద్రావణాల pH విలువలు వాటి ఆమ్ల క్షారాల pK విలువల మీద ఆధారపడి ఉంటుంది.
pH = 7 + 1/2 (pK_a – pk_b)
pK_a, pK_b ల భేదం విలువ ధనసంఖ్య కలిగి ఉంటే pH 7 కంటే ఎక్కువగా వుంటుంది. భేదం విలువ రుణసంఖ్య కలిగి ఉంటే pH 7 కంటే ఎక్కువగా ఉంటుంది.

గమనిక :

1) బలహీన ఆమ్లం, బలమైన క్షారం వల్ల ఏర్పడిన లవణాల జల ద్రావణాల pH ను లెక్కించుటకు సూత్రం
pH = \(\frac{1}{2} \mathrm{pK}_{\mathrm{w}}\) + \(\frac{1}{2} \mathrm{pK}_{\mathrm{a}}\) + \(\frac{1}{2}\)logC
pK_w విలువ 25°C వద్ద 14.
pk_a బలహీన ఆమ్లం యొక్క విలువ. pK_a = – log K_a
K_a అనునది ఆమ్ల విఘటన స్థిరాంకం.
C ఆమ్ల గాఢత.

2) బలమైన ఆమ్లం, బలహీన క్షారం వల్ల ఏర్పడిన లవణాల జలద్రావణాలు pH ను లెక్కించుటకు సూత్రం
pH = \(\frac{1}{2}\)pK_w – \(\frac{1}{2}\)pK_b – \(\frac{-1}{2}\)logC
K_b = క్షార విఘటన స్థిరాంకం. PK_b = – log K_b

ప్రశ్న98.
ద్రావణీయతా అంటే ఏమిటి ? అయానిక లవణాల ద్రావణీయతపై ఉభయ సామాన్య అయాన్ ప్రభావం వివరించండి.
జవాబు:
ఒక లవణ సంతృప్త ద్రావణంలో కేటయాన్, యానయాన్ గాఢతల లబ్ధాన్ని ద్రావణీయత లబ్ధం అంటారు. దీనిని తో సూచిస్తారు.
K_spకి ప్రమాణాలు (mole/lit)ⁿ
n = ఒక అణువు అయనీకరణంలో విడుదలయ్యే మొత్తం అయాన్ల సంఖ్య.
అద్రావణీయంగా ఉండే ఘనపదార్థం, దాని సంతృప్త ద్రావణంలో గల ఘనపదార్థం ఏర్పరచిన అయానుల మధ్య గల సమతాస్థితిని కింది సమీకరణం ద్వారా సూచించవచ్చు.
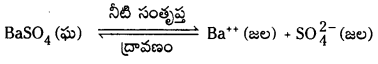
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 38

K = [Ba⁺⁺][S\(\mathrm{O}_4^{2-}\)]/[BaSO₄]
ఘనస్థితిలో గల శుద్ధ పదార్థానికి గాఢత స్థిరంగా వుంటుంది.
K_sp = K [BaSO₄] = [Ba⁺⁺] [S\(\mathrm{O}_4^{2-}\)]
K_sp ను ద్రావణీయతా లబ్ధ స్థిరాంకం అంటారు.
298 K వద్ద BaSO₄ ద్రావణీయత లబ్ధం 1.1 × 10^-10

ఉమ్మడి అయాను ప్రభావం : ఉభయ సామాన్య అయాను సమక్షంలో లవణం యొక్క ద్రావణీయత తగ్గుతుంది.
లీచాట్లీయర్ సూత్రాన్ని అనుసరించి ఒక అయాన్ గాఢతను పెంచినట్లైతే అది దాని ఆవేశానికి వ్యతిరేక ఆవేశం గల అయాన్తో సంయోగం చెంది K_sp = Q_sp అయ్యే విధంగా కొంత లవణాన్ని అవక్షేపణం చెందిస్తుంది. ఇదే విధంగా ఒక అయాను గాఢతను తగ్గిస్తే, K_sp = Q_sp అయ్యే విధంగా రెండు అయాన్ల గాఢతలు పెరిగే విధంగా లవణం అధిక పరిమాణంలో కరుగుతుంది. ఈ విషయం అధిక ద్రావణీయతను ప్రదర్శించే సోడియం క్లోరైడ్ వంటి లవణాలకు కూడా వర్తిస్తుంది. సోడియం క్లోరైడ్ సంతృప్త ద్రావణం తీసుకొని దానిలోని HCl వాయువును పంపినట్లైతే HCl విఘటనం ద్వారా ఏర్పడిన క్లోరైడ్ల గాఢత పెరగడం వల్ల సోడియం క్లోరైడ్ అవక్షేపణం చెందుతుంది. ఈ విధంగా లభ్యం అయిన సోడియం క్లోరైడ్ చాలా శుద్ధంగా ఉంటుంది.

ప్రశ్న 99.
కింది వాటి గురించి లఘు వ్యాఖ్యలు రాయండి.
i) ఉభయ సామాన్య అయాన్ ఫలితం
ii) అల్ప ద్రావణీయత లవణం BaSO₄ కు సంబంధించి K_sp కు, ద్రావణీయత (S) కు గల సంబంధం
జవాబు:
ఎసిటిక్ ఆమ్లం వియోజనం చర్య సమతాస్థితి
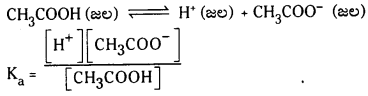
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 39

ఎసిటిక్ ఆమ్ల ద్రావణానికి, ఎసిటేట్ అయాన్లను కలిపితే హైడ్రోజన్ అయాన్ల గాఢత [H⁺] తగ్గుతుంది. అలాగే, బాహ్యస్థానం నుంచి H⁺ అయానులను ద్రావణానికి చేర్చితే, వియోజనం చెందని ఎసిటిక్ ఆమ్లం దిశవైపుగా సమతాస్థితి పయనిస్తుంది.

వియోజన సమతాస్థితిలో అప్పటికే ఏర్పడిన అయానిక రసాయన జాతి పరిమాణాన్ని పెంచే పదార్థాన్ని ద్రావణానికి కలిపితే సమతాస్థితిలో ప్రాప్తించే స్థానభ్రంశాన్ని ఉభయ సామాన్య అయాన్ ప్రభావం అంటారు.
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 40
ఈ రెండు అయానుల వ్యక్తిగత గాఢతలు, బేరియం సల్ఫేటు మోలార్ ద్రావణీయతకు సమానంగా ఉంటాయి. మోలార్ ద్రావణీయత ‘S’ అయితే
K_sp = [S] [S] = S²

సంఖ్యాత్మక సమస్యలు

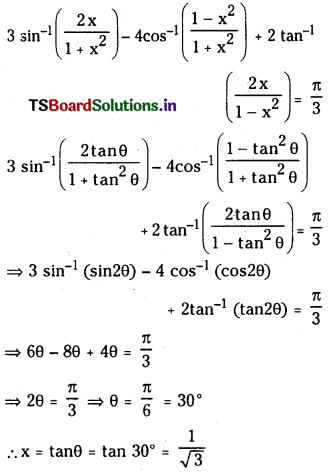
ప్రశ్న 1.
1 లీటరు ఘనపరిమాణం గల మూసిన పాత్రలో 1 మోల్ PCl₅ ను వేడిచేస్తే సమతాస్థితి వద్ద 0.4 మోల్లు క్లోరిన్ ఏర్పడింది. సమతాస్థితి స్థిరాంకాన్ని లెక్కించండి.
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 41

ప్రశ్న 2.
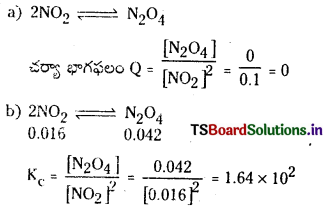
2NO₂ (వా) ⇌ N₂O₄ (వా) అనే సమీకరణం అనుసరించి నైట్రోజన్ డై ఆక్సైడు, డై నైట్రోజన్ టెట్రాక్సైడును ఏర్పరుస్తుంది. 0.1 mole NO 2 ను 1 లీటరు ఘనపరిమాణం గల ఫ్లాసుకు 25°C కలిపినప్పుడు గాఢత మార్పు చెంది సమతాస్థితి వద్ద [NO₂] = 0.016M, [N₂O₄] = 0.042 M గాను ఉన్నాయి.
a) ఏ చర్యా జరగక ముందు చర్య భాగఫలం Q విలువ ఎంత ?
b) చర్య సమతాస్థితి స్థిరాంకం విలువ ఎంత ?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 42

ప్రశ్న 3.
725 K వద్ద N₂ (వా) + 3H₂ (వా) ⇌ 2 NH₃ (వా) చర్య సమతాస్థితి స్థిరాంకం విలువ 6.0 × 10^–2. సమతాస్థితి వద్ద [H₂] = 0.25 mol L⁻¹, [NO₃] = 0.06 mol L^-1. N₂ సమతాస్థితి గాఢతను లెక్కించండి.
సాధన:
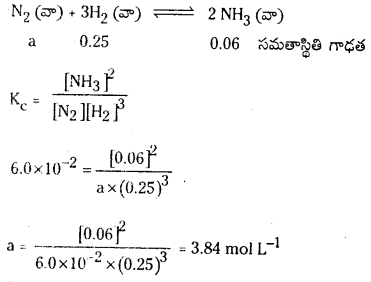
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 43
సమతాస్థితి వద్ద N₂ గాఢత = 3.84 mol.L⁻¹

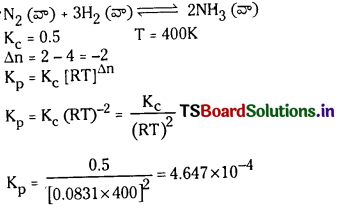
ప్రశ్న 4.
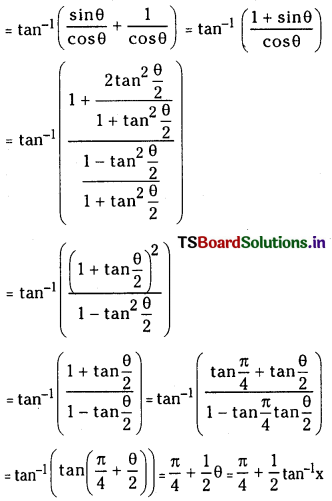
SO₂ (వా) + NO₂ (వా) ⇌ SO₃ (వా) + NO (వా) చర్యకు K విలువ నిర్దిష్ట ఉష్ణోగ్రత వద్ద 16. ఒక లీటరు పాత్రలో ఆరంభంలో నాలుగు వాయువులను ఒక్కొక్క మోల్ పరిమాణంలో తీసుకొన్నాం. NO, NÓ₂ ల సమతాస్థితి గాఢతలు ఏమిటి ?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 44

ప్రశ్న 5.
నిర్దిష్ట ప్రయోగ పరిస్థితులలో PCl₅ (వా), PCl₃ (వా), Cl₂(వా) గా విఘటనం చెందే చర్య సమతాస్థితి స్థిరాంకం విలువ 0.0211 mol L ^-1 .PCl₅ ఆరంభ గాఢత 1.00 M అయితే సమతాస్థితి వద్ద PCl₅, PCl₃, PCl₂ ల సమతాస్థితి గాఢతలను లెక్కించండి.
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 45

ప్రశ్న 6.
A + B ⇌ 3C చర్యకు సంబంధించి, 25°C వద్ద 3 లీటర్ల పాత్రలో A, B, C లు వరుసగా 1, 2, 4 మోల్లలో ఉన్నాయి. కింది పరిస్థితులలో చర్య జరిగే దిశను ఊహించండి.
a) చర్యకు K_c విలువ 10
b) చర్యకు K_c విలువ 10
c) చర్యకు K_c విలువ 10.66
సాధన:
A + B ⇌ 3C.
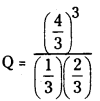
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 46
Q = 10.66
a) K_c = 10
Q > K_c కనుక తిరోగామి చర్య జరుగుతుంది.

b) K_c = 15
Q < K_c కనుక పురోగామి చర్య జరుగుతుంది.

c) K_c = 10.66
Q = K_c సమతాస్థితి ఏర్పడుతుంది.

ప్రశ్న 7.
5.0 × 10^-3 mol L^-1, 4.0 × 10^-3 mol L^-1, 2.0 × 10^-3 mol L^-1 గాఢతలలో వరుసగా H₂, N₂, NH₃ గల మిశ్రమాన్ని తయారుచేసి, 500K ఉష్ణోగ్రతకు వేడిచేస్తారు. 3H₂ (వా) + N₂ (వా) ⇌ 2NH₃ (వా) చర్యకు ఈ ఉష్ణోగ్రత వద్ద సమతాస్థితి స్థిరాంకం 60. ఈ గాఢత వద్ద అమ్మోనియా ఏర్పడుతుందా ? లేదా ? ఏర్పడిన అమ్మోనియా విఘటనం చెందుతుందా ?
సాధన:
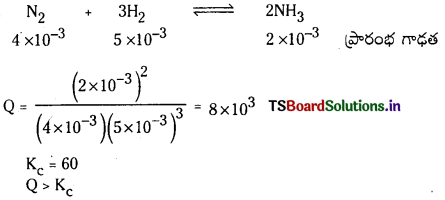
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 47
Q విలువ K_c కన్న ఎక్కువగా ఉంది కావున తిరోగామి చర్య జరుగుతుంది. అనగా అమ్మోనియా విఘటనం చెందుతుంది.

ప్రశ్న 8.
2 SO₂ (వా) + O₂ (వా) ⇌ 2SO₃ (వా) చర్యకు 500 K వద్ద K_p విలువ 2.5 × 10¹⁰. అదే ఉష్ణోగ్రత వద్ద కింది చర్యలకు K, విలువలను లెక్కించండి.
a) SO₂ (వా) + 1/2 O₂ (వా) ⇌ SO₃ (వా)
b) SO₃ (వా) ⇌ SO₂ (వా) + 1/2 O₂ (వా)
c) 3SO₂ (వా) + 3/2 O₂ (వా) ⇌ 3 SO₃ (వా)
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 48

ప్రశ్న 9.
25°C 3 N₂O₄ (వా) ⇌ 2NO₂ (వా) చర్యకు K విలువ 4.63 × 10^-3.
a) ఇదే ఉష్ణోగ్రత వద్ద K_p విలువ ఎంత ?
b) 25°C వద్ద ఉండే సమతాస్థితిలో N₂O₄ (వా) పాక్షిక పీడనం 0.2 atm, NO₂(వా) సమతాస్థితి పీడనం
లెక్కించండి.
సాధన:
a) K_p = K_c [RT]^Δn
N₂O₄ (వా) ⇌ 2NO₂ (వా)
Δn = 2 – 1 = 1
∴ K_p = 4.63 × 10⁻³ × 0.0821 × 298
= 0.1132 atm.

b)
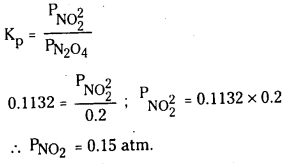
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 49

ప్రశ్న 10.
27°C వద్ద PCl5 (వా) ⇌ PCl₃ (వా) + Cl₂ (వా) ద్విగత చర్యకు K_p విలువ 0.65. K_cను లెక్కించండి.
సాధన:
K_p = K_c [RT]^Δn
ఇవ్వబడిన చర్యలో Δn = 2 – 1 = 1;
∴ K_p = K_c. RT = K_c
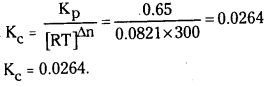
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 50

ప్రశ్న 11.
N₂ (వా) + 3H₂ (వా) ⇌ 2NH₃ (వా) కు 400K వద్ద K విలువ 0.5 అయిన K_p విలువ ఎంత ?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 51

ప్రశ్న 12.
A + B ⇌ C + D సమతాస్థితి చర్యలో ఆరంభంలో 1 మోల్ A ను, 1 మోల్ B ను 5 లీటర్ల ఫ్లాస్కులో తీసుకొన్నాం. సమతాస్థితి వద్ద 0.5 మోల్ C ఏర్పడింది. ఇదే చర్యను 2 మోల్ ల A, 1 మోల్ B తో 5 లీటర్ల ఫ్లాస్క్ అదే ఉష్ణోగ్రత వద్ద జరిపించినట్లైతే ప్రతిజాతి మోలార్ గాఢతలను లెక్కించండి.
సాధన:
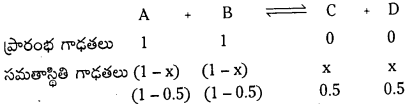
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 52

ప్రశ్న 13.
PCl₅(వా) ⇌ PCl₃ (వా) + Cl₂ (వా) 0.4 మోల్ లు PCl₃, 0.6 355 Cl₂ తీసుకొన్నాం. K విలువ 0.2 అయితే చర్య ఏ దిశలో జరుగుతుంది ? ఊహించండి.
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 54

ప్రశ్న 14.
A + B ⇌ C + D సమతాస్థితిలో, T ఉష్ణోగ్రత వద్ద A, B లను ఒక పాత్రలో తీసుకొన్నారు. A ఆరంభ గాఢత, B ఆరంభ గాఢతకు రెండు రెట్లు సమతాస్థితిని చేరుకొన్న తరువాత ‘C’ గాఢత B గాఢతకు మూడురెట్లు Kr విలువను లెక్కించండి.
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 55

ప్రశ్న 15.
2SO₂ (వా) + O₂ (వా) ⇌ 2SO₃ (వా) చర్యకు K విలువ 100 గ్రా. ఉండే ఉష్ణోగ్రత వద్ద SO₂, SO₃, O₂ వాయువులను 10 లీటర్ల ఫ్లాస్క్ లో తీసుకొన్నారు. సమతాస్థితి వద్ద
a) SO₃, SO₂ వాయువుల మోల్ల సంఖ్య ప్లాస్కులో సమానంగా ఉన్నాయి. O₂ మోల్లల సంఖ్య ఎంత ?
b) ప్లాస్క్ SO₃ మోల్ల సంఖ్య, SO₂ మోల్ల సంఖ్యకు రెట్టింపు అయితే, O₂ ఎన్ని మోల్లు ఉంది ?
సాధన:
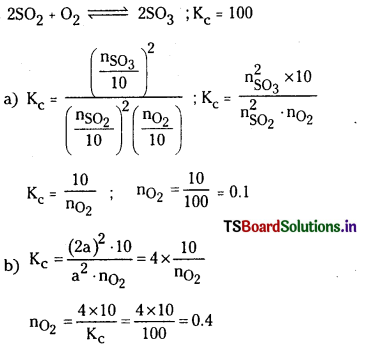
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 56

ప్రశ్న 16.
ఒక ఉష్ణోగ్రత వద్ద A + B ⇌ C సమతాస్థితి చర్యలో A, B ల సమతాస్థితి గాఢతలు 15 మోల్ L^-1 గా ఉన్నాయి. ఘనపరిమాణాన్ని రెండు రెట్లు గావించినపుడు A సమతాస్థితి గాఢత 10 మోల్^-1 గా ఉంది. కింది వాటిని లెక్కించండి.
a) K_c
b) మూల సమతాస్థితిలో C గాఢత
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 57

ప్రశ్న 17.
100K వద్ద ఒక పాత్రలో CO₂ వాయువు 0.5 atm పీడనం వద్ద ఉంది. గ్రాఫైటును కలిపినప్పుడు CO₂ లో కొంత భాగం CO గా మారింది. సమతాస్థితి వద్ద పీడనం 0.8 atm అయితే K విలువ లెక్కించండి.
సాధన:
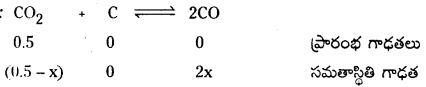
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 58
మొత్తం పీడనం = 0.8 atm
సమతాస్థితి మిశ్రమంలో CO మరియు CO₂ ఉంటాయి.
(0.5 + x) atm = 0.8 atm.
x = 0.3 atm
K_p = \(\frac{(0.6)^2}{0.2}\) = 1.8 atm.

ప్రశ్న 18.
460°C వద్ద H₂(వా) + I₂ (వా) ⇌ 2HI(వా) చర్యకు K_p విలువ 49. H₂, I₂ ల ఆరంభ గాఢతలు వరసగా 0.5 atm అయితే సమతాస్థితి వద్ద ప్రతీ వాయువు పాక్షిక పీడనాన్ని లెక్కించండి.
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 59

ప్రశ్న 19.
448°C వద్ద 10 లీటర్ల ఫ్లాస్క్ లో 0.5 మోల్ H₂, 0.5 మోల్ 12 చర్య జరిపాయి. H₂ (వా) + I₂ (వా) ⇌ 2HI(వా) చర్యకు సమతాస్థితి స్థిరాంకం K_c విలువ 50.
a) K_p విలువ ఎంత ?
b) సమతాస్థితి వద్ద I₂ మోల్ల సంఖ్య ఎంత ?
సాధన:
a) K_p = K_c [RT]^Δn.
H₂ (వా) + I₂ (వా) ⇌ 2HI (వా)
ΔN = 0
K_p = K_c = 50

b)
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 60

ప్రశ్న 20.
సమతాస్థితి వద్ద 0.1 మోల్ Cl₂ రాబట్టాలి అంటే 250°C వద్ద ఒక లీటరు పాత్రలో ఎంత PCl₅ తీసుకోవాలి?
PCl₅(వా) ⇌ PCl₃(వా) + Cl₂(వా)
సాధన:
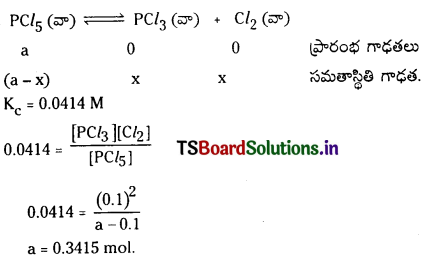
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 61
0.3415 మోల్ల PCl₅ ను 1 లీ. ప్లాస్కు కలిపితే 0.1 మోల్ క్లోరిన్ సమతాస్థితి వద్ద లభిస్తుంది.

ప్రశ్న 21.
400°C N₂(వా) + 3H₂(వా) ⇌ 2NH₃(వా) చర్యకు K_p Dev3 1.64 × 10^-4.
a) K_c ను లెక్కించండి.
b) K_c విలువ ఉపయోగించి ΔG° విలువ లెక్కించండి.
సాధన:
a) N₂(వా) + 3H₂(వా) ⇌ 2NH₃(వా) K_p = 1.64 × 10^-4 K_p = K_c [RT]^Δn
Δn = 2 – 4 = -2
K_p = K_c [RT]^-2
1.64 × 10^-4/(RT)^-2 = 1.64 × 10^-4 × (RT)²
K_c = 1.64 × 10^-4 × (0.0821 × 673)²
= 0.5129

b) ΔG° = -2.303 RT log K
= -2.303 × 0.0821 × 673 log 0.5129
= 3873 J

ప్రశ్న 22.
కింది ద్రావణాల pH విలువలను లెక్కించండి.
a) 10^-3 M HCl
b) 10⁻³ MH₂ HO₄
c) 10^-6 M HNO₃
d) 0.02 MH₂SO₄
సాధన:
a) pH = – log [H⁺]
= -log [1 × 10^-3]

b) H₂SO₄ → 2H⁺ + S\(\mathrm{O}_4^{2-}\)
1 మోల్ H₂SO₄ నుండి 2 మోల్ల H⁺ విడుదలవుతుంది.
[H⁺] = 2 × 10^-3 M
pH = -log 2 × 10^-3 = 3 – log 2
= 2.699

c) 10^-6 M HNO₃
pH = -log 10^-6 = 6

d) 0.02 M H₂SO₄
[H⁺] = 2 × 0.02 = 2 × 2 × 10^-2 = 4 × 10^-2
pH = – log 10-6 = 6
pH = -log 4 × 10^-2 = 2 – log 4
= 2 – 0.6021 = 1.4

ప్రశ్న 23.
కింది ద్రావణాల pH విలువలను లెక్కించండి.
a) 0.001 M NaOH
b) 0.01 M Ca(OH)₂
c) 0.0008M Ba(OH)₂
d) 0.004 M NaOH
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 62

ప్రశ్న 24.
ఒక ద్రావణం pH 3.6. దీని H₃O⁺ అయాన్ గాఢత లెక్కించండి.
సాధన:
pH = 3.6
– log [H⁺] = 3.6
log [H⁺] = -3.6 = \(\overline{4} .4\)
[H⁺] = anti log \(\overline{4} .4\) = 2.5 × 10^-4 మోల్/లీ

ప్రశ్న 25.
ఒక ద్రావణం pH విలువలు గల ద్రావణాలలో OH^– గాఢత ఎంత ?
సాధన:
pH = 8.6
РОН = 5.4
– log [OH^–] = 5.4
log [OH^–] = – 5.4 = \(\overline{6} .6\)
[OH^–] = anti log \(\overline{6} .6\)
[OH^–] = 3.98 × 10^-6 M.

ప్రశ్న 26.
కింది pH విలువలు గల ద్రావణాలలో [H⁺] గాఢత ఎంత ?
a) pH = 3
సాధన:
a) pH = 3
[H⁺] = 10^-3 M

b) pH = 4.75
– log [H⁺] = 4.75
– log [H⁺] = 4.75
log [H⁺] = -4.75 = \(\overline{5} .25\)
[H⁺] = anti log \(\overline{5} .25\)
= 1.778 × 10^-5 M.

c) pH = 4.4
– log [H⁺] = 4.4
log [H⁺] = – 4.4 = \(\overline{5} .6\)
log [H⁺] = 10^-5 × anti log 0.6
= 3.981 × 10^-6 M.

ప్రశ్న 27.
0.005 M₂ HSO₄ ద్రావణాన్ని 100 రెట్లు విలీనం చేసినప్పుడు విలీన ద్రావణం pH లెక్కించండి.
సాధన:
H₂SO₄ = 0.005 M
[H⁺] = 2 × 0.005 M = 0.01 M
pH = -log 0.01 = – log 10^-2 = 2
100 రెట్లు విలీనం చేస్తే pH విలువ 2 యూనిట్లు పెరుగుతుంది. pH = 4

ప్రశ్న 28.
HCl ద్రావణం pH = 3. ఈ ద్రావణం 1 mL ను 1 లీటరుకు విలీనం చేస్తే ఫలిత ద్రావణం pH విలువ ఎంత?
సాధన:
1 mL ను 1 లీకు (1000 ml) విలీనం చేస్తే 1000 రెట్లు విలీనం చేసినట్లు భావించాలి.
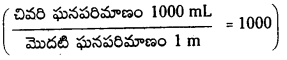
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 63
(10 రెట్లు విలీనం చేస్తే pH విలువ 1 యూనిట్ పెరుగుతుంది
100 రెట్లు విలీనం చేస్తే pH విలువ 2 యూనిట్లు పెరుగుతుంది
1000 రెట్లు విలీనం చేస్తే pH విలువ 3 యూనిట్లు పెరుగుతుంది.)
∴ ఫలిత ద్రావణం pH = 3 + 3 = 6

ప్రశ్న 29.
10^-8 M HCl pH విలువ ఎంత ?
సాధన:
HCl గాఢత = 10^-8 m.
ఈ సందర్భంలో నీటి అయనీకరణం వల్ల లభించిన H⁺ గాఢతను కూడా లెక్కించాలి.
మొత్తం H⁺ గాఢత = HCl అయనీకరణం వల్ల [H⁺] + నీటి అయనీకరణం వల్ల CH⁺]
[H⁺] = 10^-8 + 10^-7
= \(\frac{10^{-7}}{10}\) + 10^-7
= 10^-7(\(\frac{1}{10}\) + 1)
= 1.1 × 10^-7 = 7 – log 1.1
= 7 – 0.04 = 6.96

ప్రశ్న30.
కింది క్షార ద్రావణాల pH విలువలను లెక్కించండి. (March 2013)
a) [OH^–] = 0.05 M
b) [OH^–] = 2 × 10^-4 M
సాధన:
a) [OH^–] = 0.05 M
РОН = -log 5 × 10^-2
pH = 14 – 1.3 = 12.7

b) [OH^–] = 2 × 10^-4 M
РОН = -log 2 × 10^-4
= 4 – log 2 = 4 – 0.3010
= 3.7
pH = 14 – 3.7 = 10.3

ప్రశ్న31.
నీటిలో 2 గ్రా. NaOH ను కరిగించి ద్రావణాన్ని 1 లీటరుకు విలీనం చేస్తే, ద్రావణం pH విలువ ఎంత ?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 64

ప్రశ్న32.
కింది ద్రావణాల pH విలువలు లెక్కించండి.
a) 500 mL ద్రావణంలో 0.37 g of Ca(OH)₂ కరిగి ఉంది.
b) 200 mL ద్రావణంలో 0.3 g NaOH కరిగి ఉంది.
c) 0.1825% HCl జల ద్రావణం.
d) 1 లీటరు ద్రావణానికి 1 mL 13.6 M HCI ను విలీనం చేసి ఏర్పరచిన ద్రావణం
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 65

ప్రశ్న33.
10 pH గల 100 mL NaOH ద్రావణంలో ఎన్ని గ్రాములు NaOH కరిగి ఉంది ?
సాధన:
PH = 10
[H⁺] = 10^-PH = 10^-10 మోల్స్/లీ.
[H⁺] = 10^-PH = 10^-10 మోల్స్/లీ.
ద్రావిత భారం = మొలారిటి × ఘనపరిమాణం × గ్రా. అణుభారం
= 10^-4 × \(\frac{100}{1000}\) = 4 × 10^-4.
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 66

ప్రశ్న34.
ఒక ఉష్ణోగ్రత వద్ద నీటి K విలువ 9.55 × 10^-14 గా ఉంది. ఈ ఉష్ణోగ్రత వద్ద నీటి pH విలువ ఎంత ?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 67

ప్రశ్న35.
10^-8 M NaOH, pH విలువ లెక్కించండి.
సాధన:
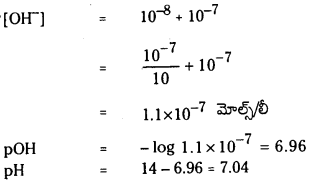
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 68

ప్రశ్న36.
150 mL 0.5 M HCl, 100 ml of 0.2 M HCl ద్రవణాలను కలిపి మిశ్రమం చేసారు. ఫలిత ద్రావణం ను లెక్కించండి pH ను లెక్కించండి.
సాధన:
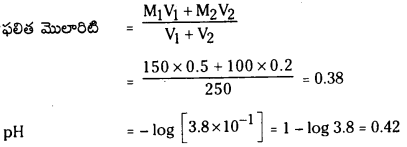
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 69

ప్రశ్న37.
100 mL 0.1 M HCl, 40 ml 0.2 M H₂SO₄ కలిపి మిశ్రమ ద్రావణం తయారు చేసారు. దీని pH విలువ లెక్కించండి.
లెక్కించండి.
సాధన:
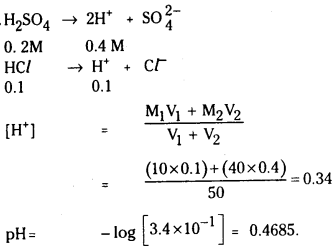
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 70

ప్రశ్న38.
100 mL pH = 4 ద్రావణం 100 mL pH = 6 ద్రావణం కలిపిన మిశ్రమ ద్రావణం ?
సాధన:
మొదటి ద్రావణం [H⁺] = 10^-4
రెండవ ద్రావణం = [H⁺] = 10^-6
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 71

ప్రశ్న39.
0.5 M NaOH ద్రావణాన్ని, 0.3 M KOH ద్రావణాన్ని సమ ఘనపరిమాణాలలో కలిపారు. ఫలిత ద్రావణం pOH, pH విలువలను లెక్కించండి.
సాధన:
NaOH మరియు KOH ద్రావణాల మిశ్రమ ద్రావణం
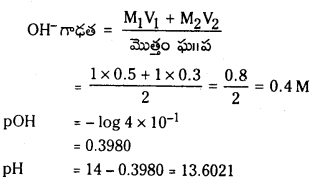
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 72

ప్రశ్న40.
60 mL 1 M HCI ద్రావణాన్ని, 40 mL 1M Na OH ద్రావణాన్ని కలిపారు. ఫలిత ద్రావణం pH విలువ ఎంత?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 73

ప్రశ్న41.
100 mL 0.1 M HCI ద్రావణం, 9.9 ml 1.0 M NaOH ద్రావణం గల మిశ్రమ ద్రావణం pH విలువ లెక్కించండి.
సాధన:
100 ml 0.1 M HC/ మిల్లీ తుల్యాంకాలు = 1000.1 = 10 meq
9.9 m l 1.0M NaOH
మిల్లీ తుల్యాంకాలు = 9.9 × 1 = 9.9 meq
HClను NaOH తటస్థపరిచినపుడు మిగిలిన ఆమ్ల మిల్లీ తుల్యాంకాలు = 10 – 9.9 = 0.1
ఆమ్ల నార్మాలిటి = \(\frac{0.1}{109.9}\) = 9 × 10^-4
pH = – log 9 × 10^-4
pH = 4 – log 9 = 3.0416

ప్రశ్న42.
200 mL pH = 2 గల HCI జల ద్రావణాన్ని 300 ml pH = 12 గల NaOH జల ద్రావణాన్ని కలిపినప్పుడు ఏర్పడిన మిశ్రమ ద్రావణం pH ఎంత ?
సాధన:
HCl pH = 2 ∴ [H⁺] = 10^-2 M
NaOH pH = 12 pOH = 2
∴ [OH^–] = 10^-2
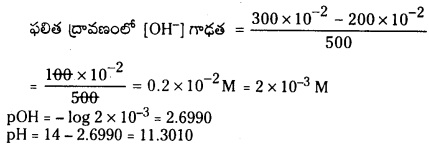
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 74

ప్రశ్న43.
0.2 M HCL ద్రావణం 50 mL, 0.1 M KOH ద్రావణం 30 mL కలిపి తయారుచేసిన మిశ్రమ ద్రావణం pH విలువ ఎంత ?
సాధన:
ఫలిత ద్రావణం ఆమ్ల లక్షణం కలదు.
[H⁺] = \(\frac{(50 \times 0.2)-(30 \times 0.1)}{80}\) = \(\frac{(50 \times 0.2)-(30 \times 0.1)}{80}\)
= 0.0875
pH = – log [8.75 × 10^-2]
= 1.0579

ప్రశ్న44.
40 mL 0.2 M HNO₃ ద్రావణం, 60 mL 0.3 M NaOH ద్రావణంతో చర్య జరిపి మిశ్రమ ద్రావణాన్ని ఏర్పరచింది. ఫలిత ద్రావణం pH విలువ ఎంత ?
సాధన:
NaOH మిల్లీ మోల్ సంఖ్య అధికంగా వుంది. ఫలిత ద్రావణం క్షారం.
ఫలిత మొలారిటి = \(\frac{60 \times 0.3-0.2 \times 40}{100}\)
= \(\frac{18-8}{100}\) = \(\frac{10}{100}\) = \(\frac{1}{10}\)
[OH^–] = 0.1 = 10^-1
РОН = 1
∴ pH = 14 – 1 = 13

ప్రశ్న45.
100mL 0.2 M HNO₃ ద్రావణానికి 50 mL ల 0.1 MH₂ SO₄ ద్రావణం కలపబడింది. మిశ్రమ ద్రావణాన్ని 300 ml లకు విలీనం చేశారు. ఫలిత ద్రావణం pH విలువ ఎంత ?
సాధన:
ఫలిత H⁺ గాఢత = \(\frac{100 \times 0.2+50 \times 0.2}{300}\)
\(\frac{20+10}{300}\) = \(\frac{30}{300}\) = \(\frac{1}{10}\) = 0.1
pH = -log 0.1 = -log 10^-1 = 1

ప్రశ్న46.
pKw విలువ 13.725g గల జలద్రావణం K_w విలువ ఎంత ?
సాధన:
pK_w = 13.725
– log K_w = 13.725
log K_w = -13.725 = \(\overline{14} .275\)
K_w = anti log \(\overline{14} .275\) = 1.
= 1.884 × 10⁻¹⁴

ప్రశ్న47.
80°C వద్ద నీటి అయానిక లబ్ధం విలువ 2.44 × 10^–13, 80°C వద్ద హైడ్రోనియం అయాన్, హైడ్రాక్సైడ్ అయాన్ల గాఢతలు శుద్ధ నీటిలో ఎంత ?
సాధన:
80°C వద్ద నీటి అయానిక లబ్ధం : 2.44 × 10^-13
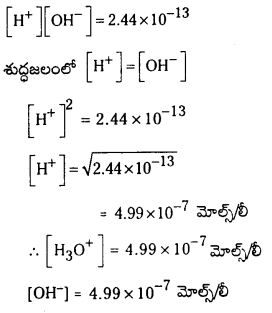
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 76

ప్రశ్న48.
40°C వద్ద నీటి అయనీకరణ స్థిరాంకం విలువ 2.9 × 10^-14. 40°C వద్ద శుద్ధ నీటికి [H₃O⁺], [OH], pH,
pOH లను లెక్కించండి.
సాధన:
నీటి అయనీకరణ స్థిరాంకం విలువ 40°C = 2.9 × 10^–14
K_w = [H⁺][OH^–] = 2.9 × 10^-14
[H⁺] = [OH^–] = \(\sqrt{2.9 \times 10^{-14}}\) = 1.703 × 10^-7
pH = − log [1.703 × 10^-7] = 6.7689
POH = – log [1.703 × 10^-7] = 6.7689

ప్రశ్న49.
కింది వాటి pH విలువలు లెక్కించండి.
a) 0.002 M ఎసిటిక్ ఆమ్ల ద్రావణం విఘటన శాతం 2.3%
b) 0.002 M NH₄ OH ద్రావణం విఘటన శాతం 2.3%
సాధన:
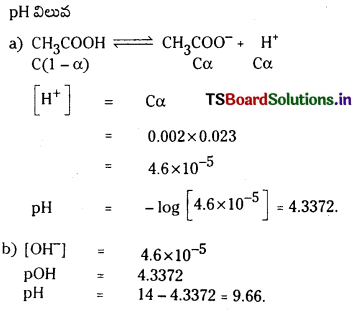
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 77

ప్రశ్న50.
కింద ఇచ్చిన సమతాస్థితి గాఢతల ఆధారంగా ఎసిటిక్ ఆమ్లం Ka ను లెక్కించండి.
[H₃O⁺] = [CH₃COO^–] = 1.34 × 10^-3 M
[CH₃COOH] = 9.866 × 10⁻² M.
సాధన:
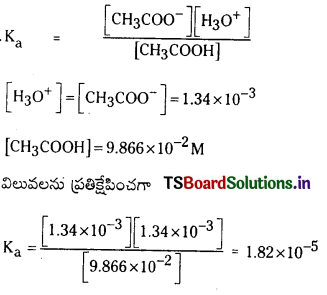
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 78

ప్రశ్న51.
Ka విలువ 1.8 × 10^-5 g గల 0.1 M ఎసిటిక్ ఆమ్లం pH విలువ లెక్కించండి.
సాధన:
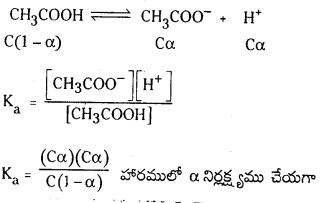
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 79

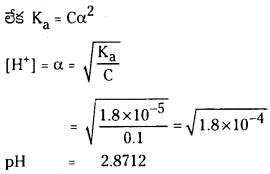
ప్రశ్న52.
0.1M గాఢత గల ఒక మోనోప్రోటిక్ ఆమ్లం pH విలువ 4.0 [H⁺], Ka లను లెక్కించండి.
సాధన:
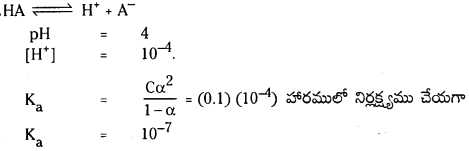
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 81

ప్రశ్న53.
0.02 M ఎసిటిక్ ఆమ్లం Ka విలువ 1.8 × 10^-5. అయిన కింది వాటిని లెక్కించండి.

a) [H₃O⁺]
b) pH
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 82

ప్రశ్న54.
298K వద్ద CH3COOH K విలువ 1.8 × 10^-5 అయిన 0.01 M ఎసిటిక్ ఆమ్ల ద్రావణం pH విలువ ఎంత?
సాధన:
α² = \(\frac{\mathrm{K}_{\mathrm{a}}}{\mathrm{C}}\)
= \(\frac{1.8 \times 10^{-5}}{0.01}\)
= 180 × 10^-5
α = 4.1 × 10^-2
∴ [H₃O⁺] = 0.01 × 4.1 × 10^-2 = 4.1 × 10^-4
pH = – log [H₃O⁺]
= -log (4.1 × 10^-4)
= 3.38.

ప్రశ్న55.
ఒక కర్బన పదార్థ ఆమ్లం 0.1 M ద్రావణం pH విలువ 4.0. ఆమ్లం విఘటన స్థిరాంకం విలువ లెక్కించండి.
సాధన:
ద్రావణం యొక్క pH = 4
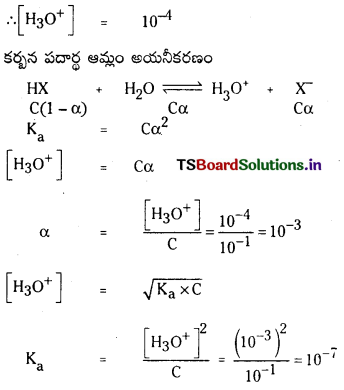
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 83

ప్రశ్న56.
298 K వద్ద HF, H COOH, HCN ల అయనీకరణ స్థిరాంకాల విలువలు వరుసగా 6.8 × 10^-4, 1.8 x 104, 4.8 x 100 వాటి కాంజుగేటు
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 84

ప్రశ్న57.
బలహీన క్షారమైన ట్రై మిథైల్ ఏమీన్ 0.25 M ద్రావణంలో హైడ్రాక్సిల్ అయాన్ గాఢత లెక్కించండి.
(CH₃)₃ N + H₂O ⇌ (CH₃)₃ N⁺H + OH,sup>- ; K_b = 7.4 × 10⁻⁵
సాధన:
బలహీన ఆమ్లం అయనీకరణ స్థిరాంకం K_b = 7.4 × 10^-5. క్షారం యొక్క అయనీకరణ అవధి a౫ అనుకొనుము.
సమతాస్థితి వద్ద
[ట్రై మిథైల్ ఏమిన్] = 0.25 (1 – α) = 0.25 M.
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 85

ప్రశ్న 58.
ఒక మోల్ క్షారిత ఆమ్ల 0.005 M ద్రావణం pH = 5. దీని అయనీకరణ అవధి ఎంత ?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 86

ప్రశ్న 59.
50 mL of 0.1 M NH₄ OH, 25 mL 2 M NH₄ Cl లను కలిపి బఫర్ ద్రావణం తయారుచేశారు. దీని pH ఎంత ? pK_a = 4.8.
సాధన:
బఫర్ ద్రావణం
pОН = pK_b + log \(\frac{M_1 V_1}{M_2 V_2}\)
M₁ లవణం మొలాలిటీ = 2 M₂ క్షారం మొలాలిటీ = 0.1
V₁ = లవణం ఘనపరిమాణం = 25 ml V₂ = క్షారం ఘనపరిమాణం = 50 ml
pОН = 4.8 + log \(\frac{2 \times 25}{0.1 \times 50}\)
= 4.8 + log 10 = 5.8
pH = 14 – 5.8 = 8.2

ప్రశ్న 60.
50 mL 0.2 M ఎసిటిక్ ఆమ్లం ద్రావణం, 25 mL సోడియం ఎసిటేట్ ద్రావణం కలిపి తయారుచేసిన బఫర్ ద్రావణం pH 4.8. దీని pK_a విలువ 4.8. CH₃COONa ద్రావణం గాఢత ఎంత ?
సాధన:

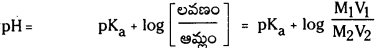
M₁ = లవణం మొలారిటీ ?
M₂ = క్షారం యొక్క మొలారిటీ = 0.2
V₁ = క్షారం ఘనపరిమాణం = 25ml V₂ = ఆమ్లం ఘనపరిమాణం = 50 ml
pH = 4.8
pKa = 4.8
లవణము గాఢత = ఆమ్లం గాఢత అయితే pH = pK_a.
∴ M₁ × 25 = 0.2 × 50
M₁ = \(\frac{0.2 \times 50}{25}\) = 0.4 M.

ప్రశ్న 61.
50 mL 0.1 M సోడియం ఎసిటేట్ను 25 mL 0.1 M సోడియం ఎసిటేట్ను 25 mL 0.2 M ఎసిటిక్ ఆమ్లాన్ని కలిపి బఫర్ ద్రావణం చేశారు. CH₃COOH, pK_a విలువ 4.8, బఫర్ ద్రావణం pH విలువ ఎంత ?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 88

ప్రశ్న 62.
20 mL 0.1 M NH₄ OH ద్రావణాన్ని 20 mL 1MNH₄ Cl ద్రావణానికి కలిపారు. బఫర్ ద్రావణం pH 8.2.
NH₄ OH, pK_a ఎంత ?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 89

ప్రశ్న 63.
1 లీటరు బఫర్ ద్రావణంలో 0.1 మోల్ ఎసిటిక్ ఆమ్లం, 1 మోల్ సోడియం ఎసిటేట్ ఉన్నాయి. CH₃COOH, pK_a విలువ 4.8. అయిన బఫర్ ద్రావణం pH ఎంత ?
సాధన:
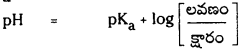
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 90
= 4.8 + log \(\frac{1}{0.1}\)
= 4.8 + log 10
= 4.8 + 1 = 5.8.

ప్రశ్న 64.
50 mL 1M CH₃COOH ద్రావణం, 50 mL 0.5 M NaOH ద్రావణం కలిపి తయారుచేసిన మిశ్రమ ద్రావణం pH విలువ ‘X’. ఎసిటిక్ ఆమ్లం pK_a 4.8 అయితే ‘X’ విలువ ఎంత ?
సాధన:
CH₃COOH + NaOH → CH₃COONa + H₂O
50 ml 0.5 M NaCH ఎసిటిక్ ఆమ్లాన్ని తటస్థీకరిస్తుంది.
V₁N₁ = V₂N₂
50 × 0.5 = V₂ × 1
∴ V₂ = \(\frac{50 \times 0.5}{1}\) = 50
కనుక ఎసిటిక్ ఆమ్లం 50% తటస్థీకరించబడింది. కనుక ఫలిత ద్రావణంలో సమాన పరిమాణం గల ఎసిటిక్ ఆమ్లము మరియు సోడియం ఎసిటేటు ఉంటాయి. ∴ pH = pK_a = 4.8

ప్రశ్న 65.
AgCl ద్రావణీయతా లబ్ధం విలువ 1.6 × 10^-10 mol² / L². దీని ద్రావణీయత ఎంత ?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 91

ప్రశ్న 66.
Zr (OH)₂ యొక్క ద్రావణీయతా లబ్ధం విలువ 4.5 × 10^-17 mol³ L^-1. దీని ద్రావణీయత ఎంత ?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 92

ప్రశ్న 67.
Ag₂ CrO₄ ద్రావణీయత 1.3 × 10^-4 మోల్ L^-1, దీని ద్రావణీయతా విలువ ఎంత ?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 93

ప్రశ్న 68.
A₂B = 2 × 10^-3 mol L^-1. దీని ద్రావణీయతా లబ్ధం విలువ ఎంత ?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 94

ప్రశ్న 69.
AB = 10^-10 mol2 L^-2. దీని ద్రావణీయతా లబ్ధం విలువ ఎంత ?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 95

ప్రశ్న 70.
PQ, RS₂లు అల్ప ద్రావణీయతా లవణాలు. వీటి ద్రావణీయతా లబ్ధం విలువలు సమానం. ప్రతీ దాని విలువ 4.0 × 10^–18, ఏ లవణం వీటిలో అధిక ద్రావణీయత కలిగి ఉంది ?
సాధన:
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 96
K_sp = [s] [2s]² = 4s³
4s³ = 4 × 10^-18
s³ = \(\frac{4 \times 10^{-18}}{4}\) = 1 × 10^-18
s = 1 × 10^-6 mole. L^-1
RS₂ కు అధిక ద్రావణీయత కలదు.

ప్రశ్న 71.
0.1M ఎసిటిక్ ఆమ్ల ద్రావణంలో ఆమ్లం 1.34% అయనీకరణం చెందింది. అయిన [H⁺], [CH₃COO^–], [CH₃COOH] లను లెక్కించండి. ఎసిటిక్ ఆమ్లం K_a విలువ లెక్కించండి.
సాధన:
CH₃⇌ COOH = CH₃COO^– + H⁺
అయనీకరణ అవధి = 1.34%
కనుక 0.1 M అయనీకరణం = \(\frac{1.34 \times 0.1}{100}\) = 1.34 × 10^-3 M
.·. [H⁺] = [CH₃COO⁻] = 1.34 × 10^-3 M
[CH₃COOH) = 1 – 1.34 × 10^-3 M
K_a = \(\frac{\left[\mathrm{CH}_3 \mathrm{COO}^{-}\right]\left[\mathrm{H}^{+}\right]}{\left[\mathrm{CH}_3 \mathrm{COOH}^3\right]}\) = \(\frac{1.34 \times 10^{-3} \times 1.34 \times 10^{-3}}{0.1}\) = 1.8 × 10^-5

అదనపు ప్రశ్నలు

ప్రశ్న 1.
ద్రవ్యరాశి క్రియానియమాన్ని వ్రాయండి. సమతాస్థితి స్థిరాంక సమీకరణాన్ని రాబట్టండి.
సాధన:
ద్రవ్యరాశి క్రియానియమం : ఏ క్షణమునందైనా నిర్దిష్ట ఉష్ణోగ్రత వద్ద రసాయన చర్యావేగం ఆ క్షణం వద్ద ఉండే క్రియాజనకాల క్రియాశీల ద్రవ్యరాశుల అంకగణిత లబ్ధానికి అనులోమానుపాతంలో ఉంటుంది.
A + B ⇌ C + D చర్యకు
పురోగామి చర్యావేగం α [A][B]
= K_f [A][B]
K_f ను పురోగామి వేగస్థిరాంకం అంటారు.
తిరోగామి చర్యావేగం α [C] [D]
= K_b [C] [D]
సమతాస్థితి వద్ద, పురోగామి చర్యావేగం = తిరోగామి చర్యావేగం
K_f [A] [B] = K_b [C] [D]
∴ K_c ను సమతాస్థిరాంకం అంటారు.

aA + bB ⇌ cC + dD చర్యకు
K_c = \(\frac{[C]^C[D]^d}{[A]^a[B]^b}\)

ప్రశ్న 2.
500 K వద్ద సమతాస్థితి ఉన్న N₂, H₂ ల ద్వారా NH₃ ను ఏర్పరిచే చర్యకు కింద సూచించిన గాఢతలు ఉన్నాయి. [N₂] = 1.5 × 10^-2 M. [H₂] = 3.0 × 10^-2 M, [NH₃] = 1.2 M × 10⁻² M. దీని సమతాస్థితి స్థిరాంకాన్ని లెక్కించండి.
జవాబు:
(N₂ (వా) + 2H₃ (వా) చర్యకు, సమతాస్థితి స్థిరాంకాన్ని కింద చూపిన విధంగా రాస్తాం.
TS Inter 1st Year Chemistry Study Material Chapter 7 రసాయనిక సమతాస్థితి, అమ్లాలు – క్షారాలు 97

ప్రశ్న 3.
2A ⇌ B + C చర్యకు K_c విలువ 2 × 10^-3. ఒక నిర్దేశిత కాలం వద్ద చర్యా మిశ్రమంలో [A] = [B] = [C] = 3 × 10^-4 M. ఏ దిశలో చర్య పురోగమిస్తుంది?
జవాబు:
చర్యకు భాగఫలం Q_c విలువను కింది సమీకరణం తెలుపుతుంది.
Q_c = [B] [C] / [A]²
కాని [A] = [B] = [C] = 3 × 10^-4 M కాబట్టి
Q_c = (3 × 10^-4)(3 × 10^-4)/(3 × 10^-4)² = 1
అంటే Q_c > K_c. కాబట్టి చర్య తిరోగామి దిశగా ప్రయాణిస్తుంది.

ప్రశ్న 4.
సుక్రోజ్ జలవిశ్లేషణాన్ని కింది సమీకరణం సూచిస్తుంది.
సుక్రోజ్ + H₂O ⇌ గ్లూకోజ్ + ఫ్రక్టోజు
చర్యకు సమతాస్థితి స్థిరాంకం K. విలువ 300 K వద్ద 2 × 10¹³, 300K వద్ద Δ\(\mathbf{G}^{\ominus}\) విలువ ఎంత ?
జవాబు:
Δ\(\mathbf{G}^{\ominus}\) = RTln K_c
Δ\(\mathbf{G}^{\ominus}\) = (-8.314 J mol^-1 K^-1) 300 K × ln (2 × 10¹³)
Δ\(\mathbf{G}^{\ominus}\) = −7.64 × 10⁴ J mol^-1

ప్రశ్న 5.
బ్రాన్టెస్టెడ్ ఆమ్లాలు : HF, H₂SO₄, HC\(\mathrm{O}_3^{-}\) లకు కాంజుగేటు క్షారాలను రాయండి.
జవాబు:
కాంజుగేటు క్షారాలు ఒక ప్రోటాను తక్కువగా కలిగి ఉండాలి. కాబట్టి ఈ ఆమ్లాల కాంజుగేటు క్షారాలు వరుసగా F^–,HS\(\mathrm{O}_4^{-}\), C\(\mathrm{O}_3^{2-}\) లు.

ప్రశ్న 6.
బ్రాన్టెస్టెడ్ క్షారాలు : N\(\mathrm{H}_2^{-}\), NH₃, HCOO^– లకు కాంజుగేటు ఆమ్లాలను రాయండి.
జవాబు:
కాంజుగేటు ఆమ్లంలో ఒక ప్రోటాను అధికంగా ఉండాలి. కాబట్టి కాంజుగేటు ఆమ్లాలు వరుసగా : NH₃, N\(\mathrm{H}_4^{+}\), HCOOH లు.

ప్రశ్న 7.
ఒక మృదుపానీయం నమూనా ద్రావణంలో హైడ్రోజన్ అయాన్ గాఢత 3.8 × 10^-3 = 3m. దీని pH విలువ ఎంత?
జవాబు:
pH = – log (3.8 × 10^-3)
= {-log (3.8) + log (10-3)}
= -[(0.58) + (-3.0)] = -[−2.42] = 2.42
కాబట్టి మృదుపానీయం pH విలువ 2.42. దీనిని అనుసరించి ఇది ఆమ్లగుణం కలిగి ఉంది అని తెలుస్తుంది.

ప్రశ్న 8.
1.0 × 10^-8 M గాఢత గల HCl ద్రావణం pH విలువ లెక్కించండి.
జవాబు:
2H₂O (ద్ర) ⇌ H₃O⁺ (జల) + OH (జల)
K_w = [OH^–] [H₃O⁺] = 10^-14
నీటిలో x = [OH] = [H₃O⁺] అనుకొందాం.
H₃O⁺ అయాన్ల గాఢత

(i) ద్రావణం స్థితిలో ఉండే HCl అయనీకరణం ప్రక్రియ మీద అంటే
HCl (జల) + H₂O (ద్ర) ⇌ H₃O⁺ (జల) + CF^– (జల)

(ii) H₂O అయనీకరణం ప్రక్రియ మీద ఆధారపడి ఉంటుంది. అతి విలీన ద్రావణాలలో H₃O⁺ కు సంబంధించిన రెండు ఉత్పత్తి స్థానాలను పరిగణనలోకి తీసుకోవాలి.
[H₃O⁺] = 10^-8 + x
K_w = (10^-8 + x) (x) = 10^-14
లేక x² + 10^-8 x – 10^-14 = 0
(OH^–) = x = 9.5 × 10^-8
pOH = 7.02, pH = 6.98.

ప్రశ్న 9.
ఎసిటిక్ ఆమ్లం pK_a అమ్మోనియా హైడ్రాక్సైడు pK_b విలువ వరుసగా 4.76, 4.75. అమ్మోనియం ఎసిటేట్ జలద్రావణం pH కనుక్కోండి.
జవాబు:
pH = 7 + \(\frac{1}{2}\) = [pK_a – pK_b]
= 7 + \(\frac{1}{2}\)[4.76 – 4.75] = 7 + \(\frac{1}{2}\)[0.01] = 7 + 0.005 = 7.005.

ప్రశ్న 10.
శుద్ధ నీటిలో A₂pX₃ ద్రావణీయతను లెక్కించండి. దీనిలో ఏర్పడిన ఏ అయాన్ నీటితో చర్య జరపదు అని ఊహించండి. A₂X₃ ద్రావణీయతా లబ్ధం విలువ K = 1.1 × 10^-23.
జవాబు:
A₂X₃ ⇌ 2A³⁺ + 3X^2–
K_sp = [A³⁺]² [X^2–]³
S = A₂X₃ ద్రావణీయత అయితే
[A³⁺] = 2S [X^2-] = 3S.
K_sp = (2S)² (3S)³ = 108S⁵ = 1.1 × 10^-23
S⁵ = 1 × 10^-25
S = 1.0 × 10^-5 మోల్ L^-1.

ప్రశ్న 11.
2NOCl (వా) ⇌ 2NO (వా) Cl₂ (వా) K్య విలువ 1069K వద్ద 3.75 × 10^-6 లో అయిన ఈ ఉష్ణోగ్రత వద్ద ఈ చర్యకు K_p విలువ లెక్కించండి.
జవాబు:
K_p = K_c (RT)^Δn
Δn = (2 + 1) – 2 = 1
K_p = 3.75 × 10^-6 (0.0831 × 1069) = 0.033

TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(b)

January 25, 2024January 24, 2024 by Mahesh

Students must practice this TS Intermediate Maths 2B Solutions Chapter 3 Parabola Ex 3(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Exercise 3(b)

Question 1.
Find the equations of the tangent and normal to the parabola y² = 6x at the positive end of the latus rectum.
Solution:
Given equation of parabola is y² = 6x ……..(1)
Comparing with y² = 4ax we get 4a = 6
⇒ a = \(\frac{3}{2}\)
Let L be the positive end of the latus rectum of the parabola y² = 6x
∴ L = (a, 2a) = (\(\frac{3}{2}\), 3)
The equation of tangent to the parabola (1) at (\(\frac{3}{2}\), 3) is yy₁ – 2a(x + x₁) = 0
y(3) = 3(x + \(\frac{3}{2}\))
⇒ 3y = 3x + \(\frac{9}{2}\)
⇒ 6y = 6x + 9
⇒ 2x – 2y + 3 = 0 ……(2)
The equation of normal to the parabola (1) at (\(\frac{3}{2}\), 3) is
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(b) I Q1

Question 2.
Find the equation of tangent and normal to the parabola x² – 4x – 8y + 12 = 0 at (4, \(\frac{3}{2}\)).
Solution:
Given equation of parabola is x² – 4x – 8y + 12 = 0 ……..(1)
Let P(x₁, y₁) = P(4, \(\frac{3}{2}\)) be the given point.
Differentiating (1) w.r.t x we get
2x – 4 – 8 \(\frac{d y}{d x}\) = 0
⇒ \(\frac{d y}{d x}=\frac{x-2}{4}\)
∴ The slope of the tangent at (4, \(\frac{3}{2}\)) is m = \(\frac{4-2}{4}=\frac{2}{4}=\frac{1}{2}\)
and slope of the normal at (4, \(\frac{3}{2}\)) is -2
The equation of a tangent to the parabola (1) at (4, \(\frac{3}{2}\)) is y – y₁ = m(x – x₁)
⇒ y – \(\frac{3}{2}\) = \(\frac{1}{2}\) (x – 4)
⇒ 2y – 3 = x – 4
⇒ x – 2y – 1 = 0 ………(2)
The equation of normal to the parabola (1) at (4, \(\frac{3}{2}\)) is y – y₁ = \(-\frac{1}{m}\)(x – x₁)
⇒ y – \(\frac{3}{2}\) = -2(x – 4)
⇒ 2y – 3 = -4(x – 4)
⇒ 4x + 2y – 19 = 0

Question 3.
Find the value of k if the line 2y = 5x + k is a tangent to the parabola y² = 6x.
Solution:
Given the equation of the line is 2y = 5x + k.
⇒ y = \(\frac{5}{2} x+\frac{k}{2}\) which is of the form y = mx + c where m = \(\frac{5}{2}\) and c = \(\frac{k}{2}\)
Comparing y² = 6x with y² = 4ax we get
4a = 6 ⇒ a = \(\frac{3}{2}\)
The condition for the line y = mx + c to be a tangent to the parabola y² = 4ax is y = mx + \(\frac{a}{m}\)
Where c = \(\frac{a}{m}\)
∴ \(\frac{k}{2}=\frac{3 / 2}{5 / 2}=\frac{3}{5}\)
⇒ k = \(\frac{6}{5}\)

Question 4.
Find the equation of normal to the parabola y² = 4x which is parallel to y – 2x + 5 = 0.
Solution:
Given equation of parabola is y² = 4x ………(1)
Comparing with y² = 4ax we get a = 1
Given y – 2x + 5 = 0, the slope, m = 2
∴ The slope of the line parallel to the above line is ‘2’.
The equation of normal to the parabola which is parallel to the line is having slope m = 2 is
y = mx – 2am – am³
= 2x – 4 – 8
= 2x – 12
⇒ 2x – y – 12 = 0
∴ The equation of the required normal is 2x – y – 12 = 0.

Question 5.
Show that the line 2x – y + 2 = 0 is a tangent to the parabola y² = 16x. Find also the point of contact.
Solution:
Given line is 2x – y + 2 = 0
and slope m = 2, and c = 2.
Comparing y² = 16x with y² = 4ax
we have a = 4
Condition for a line y = mx + c to be a tangent to the parabola y² = 4ax is c = \(\frac{a}{m}\)
∴ c = 2 and \(\frac{\mathrm{a}}{\mathrm{m}}=\frac{4}{2}\) = 2
∴ c = \(\frac{a}{m}\)
The point of contact = \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\) = (1, 4)

Question 6.
Find the equation of a tangent to the parabola y² = 16x inclined at an angle of 60° with its axis and also find the point of contact.
Solution:
Given parabola is y² = 16x ……..(1)
Comparing with y² = 4ax we get 4a = 16
⇒ a = 4
Given that inclination of the tangent line is 60°.
∴ Slope of the tangent is m = tan 60° = √3
∴ The equation of the tangent to the parabola (1) having slope √3 is y = mx + \(\frac{a}{m}\)
⇒ y = √3x + \(\frac{4}{\sqrt{3}}=\frac{3 x+4}{\sqrt{3}}\)
⇒ √3y = 3x + 5
⇒ 3x – √3y + 4 = 0
∴ Point of contact = \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)=\left(\frac{4}{3}, \frac{8}{\sqrt{3}}\right)\)

II.

Question 1.
Find the equations of tangents to the parabola y² = 16x which are parallel and perpendicular respectively to the line 2x – y + 5 = 0, also find the coordinates of their points of contact.
Solution:
Given equation of parabola y² = 16x …….(1)
and comparing with y² = 4ax we have 4a = 16
⇒ a = 4
Equation of any line parallel to the given line 2x – y + 5 = 0 is 2x – y + k = 0 …….(1)
⇒ y = 2x + k
∴ m = 2 and c = k
if (1) is a tangent to the parabola, then c = \(\frac{a}{m}\)
⇒ k = 2
∴ The equation of the required tangent is y = 2x + 2
⇒ 2x – y + 2 = 0
Point of contact = \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\) = (1, 4)
Equation of any line perpendicular at 2x – y + 5 = 0 is x + 2y + k = 0
⇒ 2y = -x – k ………(2)
⇒ y = \(-\frac{\mathrm{x}}{2}-\frac{\mathrm{k}}{2}\)
Here c = \(\frac{k}{2}\) and m = \(-\frac{1}{2}\)
If (2) is a tangent to the parabola then c = \(\frac{a}{m}\)
⇒ \(-\frac{k}{2}=\frac{4}{-1 / 2}=-8\)
⇒ k = 16
∴ The equation of the required tangent is x + 2y + 16 = 0 ……..(3)
Point of contact = \(\left(\frac{a}{m^2}, \frac{2 a}{m}\right)\)
= \(\left(\frac{4}{(1 / 4)}, \frac{8}{-1 / 2}\right)\)
= (16, -16)

Question 2.
If lx + my + n = 0 is a normal to the parabola y² = 4ax, then show that al³ + 2alm² + nm² = 0.
Solution:
Given equation of parabola is y² = 4ax ……..(1) and given lx + my + n = 0 is a normal to the parabola y² = 4ax ……(2)
Equation of normal at a point P(t) on the parabola y² = 4ax is y + xt = 2at + at³
⇒ xt + y = 2at + at³ …….(3)
Equations (2) and (3) represent the same line.
Eliminating ‘t’ from (2) and (3) we get,
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(b) II Q2

Question 3.
Show that the equation of the common tangents to the circle x² + y² = 2a² and the parabola y² = 8ax are y = ±(x + 2a). (Mar. ’10, ’09)
Solution:
Given equation of parabola is y² = 8ax …….(1) and circle is x² + y² = 2a² ……..(2)
The Centre of the circle is C = (0, 0) and the radius of the circle is r = √2a
Equation of the tangent to the parabola (1) having slope ‘m’ is y = mx + \(\frac{2a}{m}\)
⇒ my = m²x + 2a (∵ y² = 8ax is the parabola)
⇒ m²x – my + 2a = 0 ………(3)
Line (3) is also a tangent to circle (2).
∴ The perpendicular distance from C(0, 0) to line (3) is equal to radius √2a.
∴ \(\left|\frac{2 a}{\sqrt{m^4+m^2}}\right|=\sqrt{2 a}\)
⇒ \(\frac{4 a^2}{m^4+m^2}\) = 2a²
⇒ m⁴ + m² – 2 = 0
⇒ m⁴ + 2m² – m² – 2 = 0
⇒ (m² – 1) (m² + 2) = 0
⇒ m² = 1 or m² = -2
⇒ m² = 1 (∵ m² ≠ -2)
⇒ m = ±1
∴ The equations of the required tangents are y = \(\pm x+\frac{2 a}{\pm 1}\)
⇒ y = ±(x + 2a)

Question 4.
Prove that the tangents at the extremities of a focal chord of a parabola intersect at right angles on the directrix.
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(b) II Q4
Let y² = 4ax be the equation of a parabola and
Let P\(\left(a t_1^2, 2 a t_1\right)\), Q\(\left(a t_2^2, 2 a t_2\right)\) be two extremeties of the focal chord.
Since \(\overline{\mathrm{PQ}}\) is the focal chord we have t₁t₂ = -1 (standard result)
The equation of tangent to the parabola y² = 4ax at P(t₁) is x = \(\mathrm{yt}_1+\mathrm{at}{ }_1^2\) ………(1)
Slope of the tangent (m₁) = \(\frac{1}{t_1}\)
The equation of the tangent Q(t₂) to the parabola y² = 4ax is x = \(\mathrm{yt}_2+\mathrm{at}_2^2\) ……..(2)
Slope of the tangent (m₂) = \(\frac{1}{t_2}\)
Now m₁m₂ = \(\frac{1}{t_1 t_2}\) = -1 (∵ t₁t₂ = -1)
∴ The tangents drawn at P, Q are perpendicular to each other.
The point of intersection of tangents (1) and (2) = [at₁t₂, a(t₁ + t₂)]
= [-a, a(t₁ + t₂)]
Substituting this point of intersection on the directrix of the parabola y² = 4ax i.e., x + a = 0.
We have -a + a = 0 and hence the point of intersection of tangents lie on the directrix.
∴ The tangents drawn at the extremities of the focal chord of a parabola intersect at right angles on the directrix.

Question 5.
Find the condition for the line y = mx + c to be a tangent to the parabola x² = 4ay. (Mar. ’12)
Solution:
Given equation of parabola as x² = 4ay …….(1)
and given line is mx – y + c = 0 ……..(2)
Suppose (2) is a tangent to the parabola (1).
Let P(x₁, y₁) be the point of contact.
Then the equation of the tangent to the parabola (1) at (x₁, y₁) is xx₁ – 2a(y + y₁) = 0
⇒ xx₁ – 2ay – 2ay₁ = 0 ………(3)
Since equations (2) and (3) represent the same line, the corresponding coefficients are proportional.
∴ \(\frac{x_1}{m}=\frac{-2 a}{-1}=\frac{-2 a y_1}{c}\)
⇒ x₁ = 2am, y₁ = -c
Since P(x₁, y₁) is a point on x² = 4ay we have \(\mathbf{x}_1^2\) = 4ay₁
⇒ (2am)² = 4a(-c)
⇒ am² = -c
⇒ c = -am²
∴ The condition for the line y = mx + c to be a tangent to the parabola x² = 4ay is am² + c = 0.

Question 6.
Three normals are drawn from (k, 0) to the parabola y² = 8x one of the normal is the axis and the remaining two normals are perpendicular to each other, then find the value of k.
Solution:
Given equation of parabola is y² = 8x ………(1)
Comparing with y² = 4ax we have 4a = 8
⇒ a = 2
The equation of normal to the parabola (1) having slope ‘m’ is
y = mx – 2am – am²
⇒ y = mx – 4m – 2m³
Given that the normal passes through (k, 0).
Then 0 = mk – 4m – 2m³
⇒ m(2m² + 4 – k) = 0
⇒ m = 0 or 2m² – k + 4 = 0 ……(2)
Let m₁, m₂ be the roots of a quadratic equation (2) then
m₁ + m₂ = 0, m₁m₂ = \(\frac{4-k}{2}\)
Given that the two normals are perpendicular, we have m₁m₂ = -1
⇒ \(\frac{4-k}{2}\) = -1
⇒ k = 6

Question 7.
Show that the locus of the point of intersection of the perpendicular tangents to the parabola y² = 4ax is the directrix x + a = 0.
Solution:
Given y² = 4ay ………(1) and Let P(x₁, y₁) be the point of intersection of perpendicular tangents.
Any tangent to the parabola will be of the form y = mx + \(\frac{a}{m}\) of this passes through (x₁, y₁) then y₁ = mx₁ + \(\frac{a}{m}\)
⇒ m²x₁ – my₁ + a = 0 …….(2)
Let m₁, m₂ be the slopes of tangents drawn from P(x₁, y₁) to the parabola (1) which corresponds to the roots of a quadratic equation (2).
Then m₁ + m₂ = \(\frac{y_1}{x_1}\) and m₁m₂ = \(\frac{a}{x_1}\) …….(3)
Since the tangents are perpendicular we have m₁m₂ = -1 and hence from (3),
-1 = \(\frac{a}{x_1}\)
⇒ x₁ + a = 0
∴ The Locus of (x₁, y₁) is x + a = 0 which is the equation of the directrix of the parabola (1).

Question 8.
Two parabolas have the same vertex and equal length of latus rectum such that their axes are at the right angle. Prove that the common tangents touch each at the end of the latus rectum.
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(b) II Q8
Let the equations of parabolas having the same vertex and equal length of latus rectum be
y² = 4ax …….(1)
x² = 4ay …….(2)
Let the equation of the tangent to the parabola (1) having slope ‘m’ is
y = mx + \(\frac{a}{m}\) …….(3)
But this is also a tangent to x² = 4ay
∴ c = -am²
∴ \(\frac{a}{m}\) = -am²
⇒ m³ = -1
⇒ m = 1
∴ From (3), we have y = -x – a
⇒ x + y + a = 0 ………(4)
L'(a, -2a) is the end of latus rectum of parabola (1).
∴ From (4), x + y + a = a – 2a + a = 0
∴ The common tangents to the parabolas y² = 4ax, x² = 4ay will touch the parabola at the end of the latus rectum.

Question 9.
Show that the foot of the perpendicular from focus to the tangent of parabola y² = 4ax lies on the tangent at the vertex.
Solution:
Given parabola is y² = 4ax ……….(1)
Equation of any tangent to (1) is of the form y = mx + \(\frac{a}{m}\)
⇒ my = m²x + a
⇒ m²x – my + a = 0 ……..(2)
Equation of the line perpendicular to the line (2) and passing through S(a, 0) is -m(x – a) + m²(y – 0) = 0
⇒ x + my – a = 0 ……..(3)
From (2) and (3)
(m² + 1)x = 0
⇒ x = 0
From (3), my – a = 0
⇒ y = \(\frac{a}{m}\)
∴ The point of intersection of (2) and (3) is (0, \(\frac{a}{m}\))
∴ The point (0, \(\frac{a}{m}\)) lies on the y-axis which is a tangent at the vertex.

Question 10.
Show that the tangent at one extremity of a focal chord of a parabola is parallel to the normal at the other extremity.
Solution:
Let y² = 4ax be the given parabola.
Let P = \(\left(a t_1{ }^2, 2 a t_1\right)\) and Q = \(\left(a t_2{ }^2, 2 a t_2\right)\) be the two extremities of a focal chord. then t₁t₂ = -1
The equation of the tangent to the parabola at P(t₁) is x – yt₁ + \(\mathrm{at}_1{ }^2\) = 0 …….(1)
then m₁ = \(\frac{1}{t_1}\)
The equation of the normal at Q(t₂) is xt₂ + y – 2at₂ – \(\mathrm{at}_2^3\) = 0 ……..(2)
The slope of the normal (m₂) = -t₂
= \(-\left(\frac{-1}{t_1}\right)=\frac{1}{t_1}\) (∵ t₁t₂ = -1)
∴ m₁ = m₂ and the tangent at P(t₁) is parallel to the normal at Q(t₂) to the parabola y² = 4ax.
∴ The tangent at one extremity of a focal chord is parallel to the normal at other extremities.

III.

Question 1.
The normal at a point t₁ on y² = 4ax meets the parabola again at the point t₂. Then prove that t₁t₂ + \(t_1{ }^2\) + 2 = 0.
Solution:
Given equation of parabola is y² = 4ax ……..(1)
Let P = \(\left(a t_1^2, 2 a t_1\right)\) = P(t₁) be any point on (1).
The equation of normal at P(t₁) on the parabola (1) is y + xt₁ = 2at₁ + \(\mathrm{at}_1{ }^3\)
⇒ t₁x + y = 2at₁ + \(\mathrm{at}_1{ }^3\) ……..(2)
The normal drawn at P(t₁) meets the parabola at Q(t₂).
∴ PQ is the chord of the parabola.
The equation of chord \(\overline{\mathrm{PQ}}\) of the parabola y² = 4ax is y(t₁ + t₂) = 2x + 2at₁t₂
⇒ 2x = y(t₁ + t₂) + 2at₁t₂ = 0 ……….(3)
Since equations (2) and (3) represent the same line, the coefficients of line turns are proportional.
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(b) III Q1

Question 2.
From an external point, P tangents are drawn to the parabola y² = 4ax and these tangents make angles θ₁, θ₂ with its axis, such that cot θ₁ + cot θ₂ is a constant ‘d’. Then show that all such P lies on a horizontal line.
Solution:
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(b) III Q2
Given y² = 4ax ………(1) and Let P(x₁, y₁) be an external point.
Let the equation of a tangent to the parabola (1) having slope ‘m’ is y = mx + \(\frac{a}{m}\) …….(2)
if (2) passes through P(x₁, y₁) then y₁ = mx₁ + \(\frac{a}{m}\)
⇒ my₁ = m²x₁ + a
⇒ m²x₁ – my₁ + a = 0 …….(3)
Since this is a quadratic equation in ‘m’.
Let m₁ and m₂ be the roots. Then
m₁ + m₂ = \(\frac{y_1}{x_1}\) and m₁m₂ = \(\frac{\mathrm{a}}{\mathrm{x}_1}\)
Given that the tangents are making angles θ₁, θ₂ with its axis we have m₁ = tan θ₁ and m₂ = tan θ₂.
Also given that cot θ₁ + cot θ₂ = d
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(b) III Q2.1
∴ The Locus of P(x₁, y₁) is y = ad which is a line parallel to X-axis.
∴ P(x₁, y₁) lies on a horizontal line.

Question 3.
Show that the common tangents to the circle 2x² + 2y² = a² and the parabola y² = 4ax intersect at the focus of the parabola y² = -4ax.
Solution:
Given equation of circle is x² + y² = \(\frac{a^2}{2}\) ……..(1)
and the given equation of parabola is y² = 4 ax ……..(2)
Let y = mx + c be a common tangent to (1) and (2).
If y = mx + c is a tangent to (1) then by the condition of tangency
c² = \(\frac{a^2}{2}\) (1 + m2) ………(3)
Also if y = mx + c is a tangent to the parabola y² = 4ax then
c = \(\frac{a}{m}\) …….(4)
∴ From (3) and (4) we have \(\frac{a^2}{m^2}=\frac{a^2}{2}\left(1+m^2\right)\)
⇒ m⁴ + m² = 2
⇒ m⁴ + m² – 2 = 0
⇒ m⁴ + 2m² – m² – 2 = 0
⇒ (m² + 2) (m² – 1) = 0
⇒ m² + 2 = 0 or m² – 1 = 0
m² + 2 = 0 is not admissible.
∴ m² – 1 = 0
⇒ m = ±1
From y = mx + c we have
= mx + \(\frac{a}{m}\)
= \(\pm x+\frac{a}{\pm 1}\)
= ± x ± a
Also y = ± x ± a satisfy the focus (-a, 0) of the parabola y² = -4ax.
Hence the common tangents to the circle (1) and parabola (2) intersect at the focus of the parabola y² = -4ax.

Question 4.
The sum of the ordinates of two points on y² = 4ax is equal to the sum of the ordinates of two other points on the same curve. Show that the chord joining the first two points is parallel to the chord joining the other two points.
Solution:
Given equation of parabola is y² = 4ax …..(1)
Let A = \(\left(\mathrm{at}_1{ }^2, 2 \mathrm{at}_1\right)\), B = \(\left(\mathrm{at}_2{ }^2, 2 \mathrm{at}_2\right)\), C = \(\left(\mathrm{at}_3{ }^2, 2 \mathrm{at}_3\right)\) and D = \(\left(\mathrm{at}_4{ }^2, 2 \mathrm{at}_4\right)\) be the four points on the parabola (1).
Given that 2at₁ + 2at₂ = 2at₃ + 2at₄
⇒ t₁ + t₂ = t₃ + t₄ ………(2)
The equation of the chord \(\overline{\mathrm{AB}}\) of the parabola y² = 4ax is y(t₁ + t₂) = 2x + 2at₁t₂
⇒ 2x – (t₁ + t₂) y + 2at₁t₂ = 0 ………(3)
Let m₁ be the slope of line (3) then m₁ = \(\frac{2}{t_1+t_2}\)
The equation of the chord \(\overline{\mathrm{CD}}\) of the parabola (1) is y(t₃ + t₄) = 2x + 2at₃t₄ and slope of this chord m₂ = \(\frac{2}{t_3+t_4}\)
∴ From (2) we have t₁ + t₂ = t₃ + t₄
Hence m₁ = m₂
∴ Chord \(\overline{\mathrm{AB}}\) is parallel to the chord \(\overline{\mathrm{CD}}\).

Question 5.
If a normal chord at a point ‘t’ on the parabola y² = 4ax subtends a right angle at the vertex then prove that t = ±√2.
Solution:
Given equation of parabola is y² = 4ax ……(1)
The equation of normal at a point P(t) on (1) is xt + y = (2at + at³) …….(2)
Let the normal at P(t) meet (1) again at Q(t₁) then PQ is the chord of the parabola (1)
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(b) III Q5
Equation of chord \(\overline{\mathrm{PQ}}\) is y(t₁ + t) – 2x – 2at₁t = 0
⇒ -2x + (t₁ + t)y – 2at₁t = 0 ………(3)
Equations (2) and (3) represent the same straight line.
∴ Coefficients of like terms are proportional
TS Inter 2nd Year Maths 2B Solutions Chapter 3 Parabola Ex 3(b) III Q5.1

TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers InText Questions

January 25, 2024January 24, 2024 by Mahesh

Students can practice TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers InText Questions to get the best methods of solving problems.

TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Exercise InText Questions

Do This

Round off these numbers as directed:

Question 1.
48, 62, 81, 94, 27 to their nearest tens.
Answer:

48 is nearer to 50 than 40. So it is rounded off to 50.
62 is nearer to 60 than 70. So it is rounded off to 60.
81 is nearer to 80 than 90. So it is rouhded off to 80.
94 is nearer to 90 than 100. So it is rounded off to 90.
27 is nearer to 30 than 20. So it is rounded off to 30.

Question 2.
128, 275, 312, 695, 199 to their nearest hundreds.
Answer:
(i) 128 is nearer to 100 than 200.
So it is rounded off to 100.

(ii) 275 is nearer to 300 than 200.
So it is rounded off to 300.

(iii) 312 is nearer to 300 than 400.
So it is rounded off to 300.

(iv) 695 is nearer to 700 than 600.
So it is rounded off to 700.

(iv) 199 is nearer to 200 than 100.
So it is rounded off to 200.

Question 3.
7452, 8115, 3066, 7119, 9600 to their nearest thousands.
Answer:

7452 is nearer to 7000 than 8000. So it is rounded off to 7000.
8115 is nearer to 8000 than 9000. So it is rounded off to 8000.
3066 is nearer to 3000 than 4000. So it is rounded off to 3000.
7119 is nearer to 7000 than 8000. So it is rounded off to 7000.
9600 is nearer to 10000 than 9000. So it is rounded off to 10000.

Think, Discuss and Write

Discuss with your friends about rounding off numbers for ten thousands place.
Answer:
Rani and Uma both of them visited the Panchayat Office on their way back home and they observed the particulars on the wall.
Population of the village = 9,989.
The value 9,989 rounding off ten thousand.
Similarly, 10,007, 10,009, 10,015, ………… etc., are round off ten thousand.

Page No. 10(4)

Expand a number using place value.
Recall how you expand a two digit, three digit, four digit and five digit number.

Question 1.
Expand 64
Answer:
TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Intext Questions 1
= (6 × 10) + (4 × 1)
= 60 + 4

Question 2.
Expand 325
Answer:
TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Intext Questions 2
= (3 × 100) + (2 × 10) + (5 × 1)
= 300 + 20 + 5

Question 3.
Expand 5078
Answer:
TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Intext Questions 3
= (5 × 1000) + (0 × 100) + (7 × 10) + (8 × 1)
= 5000 + 0 + 70 + 8

Question 4.
Expand 29500
Answer:
TS 6th Class Maths Solutions Chapter 1 Knowing Our Numbers Intext Questions 4
= (2 × 10000) + (9 × 1000) + (5 × 100) + (0 × 10) + (0 × 1)
= 20000 + 9000 + 500 + 0 + 0
= 20000 + 9000 + 500

D0 This

Now expand the numbers as given in the example.

Number	Expansion	Expanded form
21504	(2 × 10000) + (1 × 1000) + (5 × 100) + (0 × 10) + (4 × 1)	20000 + 1000 + 500 + 4
38400	(3 × 10000) + (8 × 1000) + (4 × 100) + (0 × 10) + (0 × 1)	30000 + 8000 + 400
77888	(7 × 10000) + (7 × 1000) + (8 × 100) + (8 × 10) + (8 × 1)	70000 + 7000 + 800 + 80 + 8
20050	(2 × 10000) + (0 × 1000) + (0 × 100) + (5 × 10) + (0 × 1)	20000 + 50
41501	(4 × 10000) + (1 × 1000) + (5 × 100) + (0 × 10) + (1 × 1)	40000 + 1000 + 500 + 1

Page No: 14 (6)
Write the following numbers in expanded form and the way of reading.
(i) 4,57,000
Answer:
Expanded form :
= (4 × 1,00,000) + (5 × 10,000) + (7 × 1000) + (0 × 100) + (0 × 10) + (0 × 1)
= 4,00,000 + 50,000 + 7,000

Read as:
Four lakh fifty seven thousand.

(ii) 3,05,400
Answer:
Expanded form :
(3 × 1,00,000) + (0 × 10,000) + (5 × 1000) + (4 × 100) + (0 × 10) + (0×1)
= 3,00,000 + 5,000 + 400

Read as:
Three lakh five thousand four hundred.

(iii) 3,09,390
Answer:
Expanded form :
= (3 × 1,00,000) + (0 × 10,000) + (9 × 1000) + (3 × 100) + (9 × 10) + (0 × 1)
= 3,00,000 + 0 + 9000 + 300 + 90 + 0

Read as:
Three lakh nine thousand three hundred ninety

(iv) 2,00,035
Answer:
Expanded form :
= (2 × 1,00,000) + (0 × 10,000) + (0 × 1000) + (0 × 100) + (3 × 10) + (5×1)
= 2,00,000 + 30 + 5

Read as:
Two lakh thirty five.

(Try These)

Question 1.
Give any five examples using daily life situations where the number of things counted would be more than 6 digits.
Answer:

To calculate the population
To calculate the money which is more than 1 lakh
Count of white blood cells in the body
Count of cells in a leaf
Count of voters in Hyderabad city

Question 2.
Write the smallest and greatest of all two digit, three digit, four digit, five digit, six digit, seven digit, eight digit numbers.
Answer:

Digit	Smallest number	Greatest number
1. Two digit	10	99
2. Three digit	100	999
3. Four digit	1,000	9,999
4. Five digit	10,000	99,999
5. Six digit	1,00,000	9,99,999
6. Seven digit	10,00,000	99,99,999
7. Eight digit	1,00,00,000	9,99,99,999

Page No: 18

Question 1.
Read the numbers given below.
(i) 41430495
Answer:
4,14,30,495 = Four crore fourteen lakh thirty thousand four hundred ninety five.

(ii) 304512031
Answer:
30,45,12,031 = Thirty crore forty five lakh twelve thousand thirty one.

(iii) 241800240
Answer:
24,18,00,240 = Twenty four crore, eighteen lakh two hundred forty.

(iv) 69697100
Answer:
6,96,97,100 = Six crore ninety six lakh ninety seven thousand one hundred.

(v) 100091409
Answer:
10,00,91,409 = Ten crore, ninety one thousand four hundred nine.

Question 2.
Write the expansion of 12735045
Answer:
1,27,35,045 = (1×10000000) + (2 × 1000000) + (7 × 100000)+ (3 × 10000) + (5 × 1000) + (0 × 100) + (4 × 10) + (5 × 1)

Do This:

Question 1.
Expand the numbers using commas,
(i) 999999999
Answer:
99,99,99,999
= (9 × 10,00,00,000) + (9 × 1,00,00,000) + (9 × 10,00,000) + (9 × 1,00,000) + (9 × 10,000) + (9 × 1,000) + (9 × 100) + (9 × 10) + (9×l)
= 90,00,00,000 + 9,00,00,000 + 90,00,000 + 9,00,000 + 90,000 + 9,000 + 900 + 90 + 9

(ii) 34530678
Answer:
3,45,30,678
= (3 × 1,00,00,000) + (4 × 10,00,000) + (5 × 1,00,000) + (3 × 10,000) + (0 × 1,000) + (6 × 100) + (7 × 10) + (8 × 1)
= 3,00,00,000 + 40,00,000 + 5,00,000 + 30,000 + 600 + 70 + 8

(iii) 510010051
Answer:
51,00,10,051
= (5 × 10,00,00,000) + (1 × 1 ,00,00,000) + (0 × 10,00,000) + (0 × 1,00,000) + (1 × 10,000) + (0 × 1000) + (0 × 100) + (5 × 10) + (1 × 1)
= 50,00,00,000 + 1,00,00,000 + 10,000 + 50 + 1

Question 2.
Read these numbers and write in words.
(i) 5,06,45,075
Answer:
Five crore six lakhs forty five thousand seventy five.

(ii) 12,36,99,140
Answer:
Twelve crore thirty six lakhs ninety nine thousand one hundred forty.

(iii) 2,50,00,350
Answer:
Two crore fifty lakhs three hundred fifty.

Try These

Question 1.
Name four important towns in your district. Note the distance between them in km. Express these in centimeters and millimeters.
Answer:

Armar
Bheemgal
Balkonda
Bodhan.

The distance between Armur and Bheemgal is 62 km.
1 km = 100000 cm
∴ 62 km = 62 × 100000 = 6200000 cm
= 6200000 × 10 = 62000000 mm (∵ 1cm = 10 mm)
The distance between Bheemgal and Balkonda is 29 km.
29 km = 29 × 100000 = 2900000 cm
= 2900000 × 10 mm = 29000000 mm
The distance between Balknoda and Bodhan is 66 km. .
66km = 66 × 100000= 6600000 cm
= 6600000 × 10 mm = 66000000 mm
The distance between Bodhan and Armur is 53 km.
53km = 53 × 100000 = 5300000 cm
= 5300000 × 10 mm = 53000000 mm

Question 2.
Can you tell where we use milligrams?
Answer:
We use milligrams to measure

silver
gold
mercury
platinum, etc.

Question 3.
A box contains 1,00,000 tablets (medicine) each weighing 20 mg. What is the weight of all the tablets in the box in both grams and kilograms ?
Answer:
The weight of 1 tablet = 20 mg
The total weight of 1,00,000 tablets = 1,00,000 × 20 mg = 20,00,000 mg
= \(\frac{2000000}{1000}\) grams (∵1 gram = 1000 milli grams)
= 2000 grams
= \(\frac{2000}{1000}\) kgs (∵ 1 kg = 1000 grams)
= 2 kgs

Question 4.
A petrol tanker contains 20,000 litres of petrol. Express the quantity of petrol in kilolitres and millilitres.
Answer:
The quantity of petrol in a petrol tanker is 20,000 litres.
= \(\frac{20000}{1000}\) kiloliters (∵ 1000 litres = 1 kilolitre)
= 20 kilolitres
We know that 1 litre = 1000 millilitres
∴ 20000 litres = 20000 × 1000 millilitres
= 20000000 millilitres

Think, Discuss and Write

Question 1.
You live in Ahmedabad and you trav-elled 400 m by bus to reach the nearest station. Then you take a train to reach Gandhi Nagar which is 15 km. away. Then you take a cab to reach your aunt’s house which is 18 km. away.
(i) How much distance did you travel to reach your aunt’s house ?
(ii) If you travel for 7 days like this how much distance would you travel ?
Answer:
(i) Travelled by bus = 400 m
Travelled by train =15 km
Travelled by cab = 18 km
∴ I travelled to reach my aunt’s house = 400 m + 15 km + 18 km
= 33 km 400 m = 33.4 kms.

(ii) The distance travelled by me in 7 days = 7 × 33.4 kms
= 233.8 kms (or) 233 km 800 m

Question 2.
Every child in your school bring a water bottle containing 2 litres of water. If all the water is poured into a container which has 2 kilo litre capacity of water it was found that it needed 600 litre more to be filled. How many children poured water bottles in the container ?
Answer:
Capacity of water container = 2 kilolitres
= 2 × 1000 lts = 2000 litres
Each student bring the capacity of water bottle = 2 lts.
Required water to fill the tank is = 600 l
Already filled water in the container
= (2000 – 600) litres = 1400 litres
∴ Number of children poured water in the container = \(\frac{1400}{2}\) = 700
∴ 700 children poured water bottles in the container.

TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d)

January 23, 2024January 21, 2024 by Mahesh

Students must practice these TS Intermediate Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Trigonometric Ratios upto Transformations Solutions Exercise 6(d)

I.
Question 1.
Simplify
(i) \(\frac{\sin 2 \theta}{1+\cos 2 \theta}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 1

(ii) \(\frac{3 \cos \theta+\cos 3 \theta}{3 \sin \theta-\sin 3 \theta}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 2

Question 2.
Evaluate the following
(i) 6sin 20° – 8 sin³ 20°
Answer:
2(3 sin 20° – 4sin³ 20°) (Formula)
= 2.sin (3 × 20°) = 2 sin 60°
= \(\frac{2 \sqrt{3}}{-2}\) = √3

(ii) cos²72° – sin²54°
Answer:
cos²72° – sin²54°
= sin²18° – cos²36°
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 3

(iii) sin²42° – sin²12°
Answer:
sin²42° – sin²12° (Formula)
sin (42° + 12°) sin (42° – 12°)
= sin 54° sin 30°
= \(\left(\frac{\sqrt{5}+1}{4}\right) \frac{1}{2}=\frac{\sqrt{5}+1}{8}\)

Question 3.
(i) Express \(\frac{\sin 4 \theta}{\sin \theta}\) in terms of cos3 θ and cos θ.
Answer:
sin4θ = sin (3θ + θ) = sin 3θ cos θ +cos 3θ sin θ
= (3 sin θ – i sin 3θ) cos θ + (4 cos 3θ – 3 cos θ) sin θ
= 3 sin θ cos θ – 4 sin 3θ cos θ + 4 cos 3θ sin θ – 3 cos θ sin θ
= 4 cos 3θ sin θ – 4 sin 3θ cos θ
= sin θ(1 cos 3θ – 4 sin 2θ cos θ)
= sin θ [4 cos 3θ – 4 sin 2θ cos θ]
∴ \(\frac{\sin 4 \theta}{\sin \theta}=\frac{\sin \theta\left(4 \cos ^3 \theta-4 \sin ^2 \theta \cos \theta\right)}{\sin \theta}\)
= 4 cos 3θ – 4 sin 2θ cos θ
= 4 cos 3θ – 4 (1- cos 2θ) cos θ
= 8 cos 3θ – 4 cos θ

(ii) Express cos⁶ A + sin⁶ A in terms of sin 2A.
Answer:
cos⁶A + sin⁶A = (cos²A + sin²A)³
= (cos²A + sin²A)³ – 3 cos²A sin²A (cos²A + sin² A)
= 1 – 3 cos²A sin²A ……………(1)
= 1 – \(\frac{3}{4}\) (4 cos² A sin² A)
= 1 – \(\frac{3}{4}\)sin²2A

(iii) Express \(\frac{1-\cos \theta+\sin \theta}{1+\cos \theta+\sin \theta}\) in terms of tan \(\frac{\theta}{2}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 4

Question 4.
(i) If sin α = \(\frac{3}{5}\), where \(\frac{\pi}{2}\) < α < π, evaluate cos 3α and tan 2α. (March 2015-T.S)
Answer:
since \(\frac{\pi}{2}\) < α < π, a lies in second quadrant and given sin α = \(\frac{3}{5}\) we have cos α = –\(\frac{4}{5}\)
cos 3α = 4 cos³ α – 3 cos α
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 5

(ii) If cos A = \(\frac{7}{25}\) and \(\frac{3 \pi}{2}\) < A < 2π, then find the value of cot \(\frac{A}{2}\).
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 6

(iii) If 0 < θ < \(\frac{\pi}{8}\), show that \(\sqrt{2+\sqrt{2+\sqrt{2+2 \cos 4 \theta}}}\) = 2cos(θ/2)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 7

Question 5.
Find the extreme values of
(i) cos 2x + cos2x
Answer:
cos 2x + cos2x = 2 cos² x – 1 + cos² x
= 3 cos² x – 1
and 0 ≤ cos² x ≤ 1
⇒ 0 ≤ 3 cos² x ≤ 3
⇒ -1 ≤ 3 cos² x – 1 ≤ 2
Maximum value = 2
and minimum value = -1
(or) cos 2x + cos² x = cos 2x + \(\left(\frac{1+\cos 2 x}{2}\right)\)
We have -1 < cos 2x ≤ 1
⇒ -3 ≤ 3 cos 2x ≤ 3
⇒ -2 ≤ 3 cos 2x + 1 ≤ 4
⇒ -1 ≤ \(\frac{3 \cos 2 x+1}{2}\) ≤ 2
Maximum value = 2
Minimum value = -1
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 8

(ii) 3sin²x + 5 cos²x
Answer:
3sin²x + 5 cos²x
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 9

Question 7.
Find the periods for the following functions
(i) cos⁴x
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 10

(ii) 2sin\(\left(\frac{\pi \mathbf{x}}{\mathrm{4}}\right)\) + 3cos\(\left(\frac{\pi x}{3}\right)\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 11

(iii) sin²x + 2 cos²x
Answer:
Let f(x) = sin²x + 2cos²x
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 12

(iv) 2sin(\(\frac{\pi}{4}\) + x)cos x
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 13
Period of f(x) is LCM of [π, π] = π

(v) \(\frac{5 \sin x+3 \cos x}{4 \sin 2 x+5 \cos x}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 14

II.
Question 1.
(i) If 0 < A < \(\left(\frac{\pi}{4}\right)\), and cos A = \(\frac{4}{5}\), find the values of sin 2A and cos 2A.
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 15

(ii) For what values of A in the first quadrant, the expression \(\frac{\cot ^3 A-3 \cot A}{3 \cot ^2 A-1}\) is positive?
Answer:
\(\frac{\cot ^3 A-3 \cot A}{3 \cot ^2 A-1}\) > 0
⇒ cot³A – 3 cot A > 0
⇒ cot A (cot² A – 3) > 0
⇒ cot A > 0 or cot² A > 3
⇒ cot A > √3
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 16

(iii) Prove that \(\frac{\cos 3 A+\sin 3 A}{\cos A-\sin A}\) = 1 + 2 sin 2A
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 17

Question 2.
(i) Prove that cot(\(\frac{\pi}{4}\) – θ) = \(\frac{\cos 2 \theta}{1-\sin 2 \theta}\) and hence find the value of cot 15°.
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 18

(ii) If θ lies in third quadrant and sin θ = –\(\frac{4}{5}\), find the values of cosec\(\left(\frac{\theta}{2}\right)\) and tan\(\left(\frac{\theta}{2}\right)\).
Answer:
Given θ lies in third quadrant.
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 19

(iii) If 450° < θ < 540° and sin θ = \(\frac{12}{13}\), then calculate sin\(\left(\frac{\theta}{2}\right)\) and cos\(\left(\frac{\theta}{2}\right)\).
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 20

(iv) Prove that \(\frac{1}{\cos 290^{\circ}}+\frac{1}{\sqrt{3} \sin 250^{\circ}}=\frac{4}{\sqrt{3}}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 21

Question 3.
Prove that
(i) \(\frac{\sin 2 A}{(1-\cos 2 A)} \cdot \frac{(1-\cos A)}{\cos A}\) = tan\(\frac{\mathrm{A}}{2}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 22

(ii) \(\frac{\sin 2 x}{(\sec x+1)} \cdot \frac{\sec 2 x}{(\sec 2 x+1)}\) = tan\(\left(\frac{x}{2}\right)\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 23

(iii) \(\frac{\left(\cos ^3 \theta-\cos 3 \theta\right)}{\cos \theta}+\frac{\sin ^3 \theta+\sin 3 \theta}{\sin \theta}\) = 3.
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 24

Question 4.
(i) Show that cos A = \(\frac{\cos 3 A}{2 \cos 2 A-1}\). Hence find the value of cos 15°.
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 25

(ii) Show that sin A = \(\frac{\sin 3 A}{1+2 \cos 2 A}\). Hence find the value of sin 15°.
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 26

(iii) Prove that tan α = \(\frac{\sin 2 \alpha}{1+\cos 2 \alpha}\) and hence deduce the values of tan 15° and tan 22\(\frac{1}{2}\).
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 27

Question 5.
Prove that \(\frac{1}{\sin 10^{\circ}}-\frac{\sqrt{3}}{\cos 10^{\circ}}\) = 4
(i) \(\frac{1}{\sin 10^{\circ}}-\frac{\sqrt{3}}{\cos 10^{\circ}}\) = 4 (Mar’ 2003, Jun 2004)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 28

(ii) √3 cosec 20° – sec 20° = 4.
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 29

(iii) tan 9° – tan 27° – cot 27° + cot 9° = 4
Answer:
We have that tan A + cot A = \(\frac{\sin A}{\cos A}+\frac{\cos A}{\sin A}=\frac{1}{\sin A \cos A}\) = 2 cosec 2A
Put A = 9°, we have tan 9° + cot 9° = 2 cosec 18°
Put A = 27°, we have tan 27°+ cot 27° = 2 cosec 54°
∴ L.H.S
∴ tan 9° – tan 27° + cot 9° – cot 27° = 2 (cosec 17° – cosec 54°)
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 30

(iv) If \(\frac{\sin \alpha}{a}=\frac{\cos \alpha}{b}\), then prove that a sin 2α + b cos 2α = b.
Answer:
Given that \(\frac{\sin \alpha}{a}=\frac{\cos \alpha}{b}\)
⇒ b sin α + a cos α
L.H.S = a sin 2α + b cos 2α
= a (2 sin α cos α) + b ( 1 – 2 sin²α)
= 2 sin α (a cos α) + b – 2 b sin²α
= 2 sin α (b sin α) + b – 2b sin²α
= 2b sin²α + b – 2b sin²α = b

Question 6.
(i) In a ΔABC; if tan \(\frac{A}{2}=\frac{5}{6}\), and tan \(\frac{B}{2}=\frac{20}{37}\) then show that tan(C/2) = \(\frac{2}{5}\)
Answer:
In ΔABC, A + B + C = 180°
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 31

(ii) If cos θ = \(\frac{5}{13}\) and 270° < θ < 360°, evaluate sin \(\left(\frac{\theta}{2}\right)\) and cos \(\left(\frac{\theta}{2}\right)\).
Answer:
Given cos θ = \(\frac{5}{13}\), where 270° < θ < 360°,
⇒ 135° < \(\frac{\theta}{2}\) < 180°
⇒ \(\frac{\theta}{2}\) lies in second quadrant
since cos θ = \(\frac{5}{13}\)
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 32

(iii) If 180° < θ < 270° and sin θ = –\(\frac{4}{5}\) calculate sin\(\left(\frac{\theta}{2}\right)\) and cos\(\left(\frac{\theta}{2}\right)\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 33

Question 7.
(i) Prove that cos²\(\frac{\pi}{8}\) + cos²\(\frac{3 \pi}{8}\) + cos²\(\frac{5 \pi}{8}\) + cos²\(\frac{7 \pi}{8}\) = 2
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 34

(ii) Show that cos⁴\(\left(\frac{\pi}{8}\right)\) + cos⁴\(\left(\frac{3 \pi}{8}\right)\) + cos⁴\(\left(\frac{5 \pi}{8}\right)\) + cos⁴\(\left(\frac{7 \pi}{8}\right)=\frac{3}{2}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 35

III.
Question 1.
(i) If tan x + tan (x + \(\frac{\pi}{3}\)) + tan(x + \(\frac{2 \pi}{3}\)) = 3, show that tan 3x = 1
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 36

(ii) Prove that (March 2013)
sin\(\frac{\pi}{5}\) sin\(\frac{2 \pi}{5}\).sin\(\frac{3 \pi}{5}\).sin\(\frac{4 \pi}{5}=\frac{5}{16}\)
Answer:
L.H.S = sin\(\frac{\pi}{5}\) sin\(\frac{2 \pi}{5}\).sin\(\frac{3 \pi}{5}\).sin\(\frac{4 \pi}{5}\)
= sin 36° . sin 72° . sin 108° . sin 144°
= sin 36° . sin 72°. sin (90° + 18°) sin (180° – 36°)
= sin 36° . sin (90° – 18°) . sin (90° + 18°). sin (180° – 36°)
= sin 36° . cos 18° . cos 18° . sin 36°
= sin236° . cos218°
= \(\left(\frac{10-2 \sqrt{5}}{16}\right)\left(\frac{10+2 \sqrt{5}}{16}\right)\)
= \(\frac{100-20}{256}=\frac{80}{256}=\frac{5}{16}\)

(iii) Show that cos²\(\left(\frac{\pi}{10}\right)\) + cos²\(\left(\frac{2 \pi}{5}\right)\) + cos²\(\left(\frac{3 \pi}{5}\right)\) + cos²\(\left(\frac{9 \pi}{5}\right)\) = 2
Answer:
cos²18° + cos² 72°+ cos² 108° + cos² 162°
= cos²18° + cos² 72°+ cos2 (90 + 18) + cos²(108° – 18°)
= cos² 18° + sin² 18° + sin² 18° + cos² 18°
= 1 + 1 = 2

Question 2.
Prove that
(i) \(\frac{1-\sec 8 \alpha}{1-\sec 4 \alpha}=\frac{\tan 8 \alpha}{\tan 2 \alpha}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 37

(ii) (1 + cos \(\frac{\pi}{10}\))(1 + cos \(\frac{3 \pi}{10}\))(1 + cos \(\frac{7 \pi}{10}\))(1 + cos \(\frac{9 \pi}{10}\)) = \(\frac{1}{16}\). (March 2015-A.P)
Answer:
(1 + cos 18) (1 + cos 54) (1 + cos 126) (1 + cos 162)
= (1 + cos 18) (1 + sin 36) (1 – sin 36) (1 – cos 18)
= (1 + cos 18) (1 – cos 18) (1 + sin 36) (1 – sin 36)
= sin² 18° cos² 36°
= \(\left(\frac{\sqrt{5}-1}{4}\right)^2\left(\frac{\sqrt{5}+1}{4}\right)^2\)
= \(\frac{(5-1)^2}{256}=\frac{16}{256}=\frac{1}{16}\)

Question 3.
Prove that
(i) cos \(\frac{2 \pi}{7}\) cos\(\frac{4 \pi}{7}\) cos \(\frac{8 \pi}{7}=\frac{1}{8}\)
Answer:
Let \(\frac{2 \pi}{7}\) = α
and x = cos α cos2 α cos 4 α
and y = sin α sin2 α sin4 α (suppose)
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 38

(ii) cos \(\frac{\pi}{11}\) cos\(\frac{2 \pi}{11}\) cos\(\frac{3 \pi}{11}\)cos\(\frac{5 \pi}{11}\)cos\(\frac{4 \pi}{11}=\frac{1}{32}\)
Answer:
Let \(\frac{\pi}{11}\) = α
and x = cos α cos 2α cos 3α cos 4α cos 5α
and y = sin α sin 2α sin 3α sin 4α sin 5α
xy =
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 39

Question 4.
(i) If cos α = \(\frac{3}{5}\) and cos β = \(\frac{5}{13}\) and α, β are acute angles, then prove that
(a) sin²\(\left(\frac{\alpha-\beta}{2}\right)=\frac{1}{65}\) and
(b) cos²\(\left(\frac{\alpha+\beta}{2}\right)=\frac{16}{65}\)
Answer:
α, β are acute angles and cos α = \(\frac{3}{5}\) and cos β = \(\frac{5}{13}\)
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 40

(ii) If A is not an integral multiple of π, prove that cos A . cos 2A . cos 4A . cos 8A = \(\frac{\sin 16 A}{16 \sin A}\) and hence deduce that cos A. cos 2A . cos 4A .cos 8A = \(\frac{\sin 16 A}{16 \sin A}\) and hence deduce that
cos \(\frac{2 \pi}{15}\).cos\(\frac{4 \pi}{15}\).cos\(\frac{8 \pi}{15}=\frac{16 \pi}{15}=\frac{1}{16}\) (Mar 2012, May 2012)
Answer:
We have to prove that
16 sin A cos A cos 2A cos 4A cos 8A = sin 16A
L.H.S = 8(2 sinA cos A) cos2A cos 4A cos 8A = sin 16A
= 8 sin 2A cos 2A cos 4A cos 8A
= 4 (2 sin 2A cos 2A ) cos 4A cos 8A
= 4 sin 4A cos 4A cos 8A = 2 (2 sin 4A cos 4A) cos 8A
= 2 (sin 8A) (cos 8A)
= cos 16A
= R.H.S
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(d) 41

TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు

January 23, 2024January 21, 2024 by Mahesh

Telangana TSBIE TS Inter 1st Year Chemistry Study Material 13th Lesson కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు Textbook Questions and Answers.

TS Inter 1st Year Chemistry Study Material 13th Lesson కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు

అత్యంత లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 1.
బెంజీన్ న్ను మీథైల్ బెంజీన్ గా మార్చడానికి అవసరమైన కారకాలు రాయండి.
జవాబు:
AlCl₃ ఉత్ప్రేరకం సమక్షంలో బెంజీన్, మిథైల్ క్లోరైడ్ చర్య జరిపితే మిథైల్ బెంజీన్ ఏర్పడుతుంది.

ప్రశ్న 2.
నైట్రో బెంజీన్ను ఎలా తయారుచేస్తారు?
జవాబు:
బెంజీన్ ను 60°C కంటే తక్కువ ఉష్ణోగ్రత వద్ద గాఢ HNO₃ మరియు గాఢ H₂SO₄ ల మిశ్రమంతో వేడిచేస్తే నైట్రోబెంజీన్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 2

ప్రశ్న 3.
ఈథేన్ అనురూపకాలను రాయండి.
జవాబు:
ఈథేన్ – అనురూపాత్మక సాదృశ్యములు : ఈథేన్ అణువులో ఒక కార్బన్ పరమాణువు స్థానమును స్థిరీకరించి రెండవ కార్బన్ పరమాణువును C – C బంధ అక్షముపై చక్ర భ్రమణము చేయుట వలన అనేక ప్రాదేశిక అమరికలు గల రూపములు లభించును. ఈ రూపములను అనురూపాత్మక సాదృశ్యములందురు. ఈథేన్ ప్రధాన అనురూపాత్మక సాదృశ్యములు.

గ్రహణ ఆకృతి
అస్తవ్యస్త ఆకృతి

ప్రశ్న 4.
ఇథిలీన్ నుంచి ఈథైల్ క్లోరైడ్ను ఎలా తయారుచేస్తారు?
జవాబు:
ఇథిలీన్ ను HCl తో చర్య జరిపి ఈథైల్ క్లోరైడ్ను తయారు చేస్తారు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 4

ప్రశ్న 5.
కింది నిర్మాణాల IUPAC నామాలు రాయండి.
(a) CH₃-CH₂-CH₂-CH=CH₂
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 5
జవాబు:
(a) 1-పెంటీన్
(b) పెంటేన్-2-ఓన్, పెంటేన్-3-ఓన్
(c) 3-నైట్రో బెంజాల్డిహైడ్, 4-నైట్రో బెంజాల్డిహైడ్

ప్రశ్న 6.
కింది వాటి నిర్మాణాలను రాయండి.
(i) ట్రైక్లోరో ఇథనాయిక్ ఆమ్లం
(ii) నియోపెంటేన్
(iii) P-నైట్రో బెంజాల్డిహైడ్ (March 2013)
జవాబు:
(i) ట్రైక్లోరో ఇథనాయిక్ ఆమ్లం – CCl₃COOH
(ii) నియోపెంటేన్ TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 6
(iii) P-నైట్రో బెంజాల్డిహైడ్

ప్రశ్న 7.
లాసజీన్ చర్యను వివరించండి.
జవాబు:
లాసజీన్ చర్య : పొడిగా ఉన్న చిన్న Na లోహాన్ని గలన స్థితిలో మారే వరకు గలన నాళికలో వేడి చేయవలెను. ఈ గలన Naకు కర్బన సమ్మేళనం కలిపి ఎర్రగా మారేవరకు వేడి చేయవలెను. చైనా పాత్రలో ఈ ఎర్రగా కాలిన నాళికను వేసి నీటిని కలిపి మరిగించి చల్లబరచి వడపోయవలెను. ఈ వడపోత ద్రావణాన్ని లాసైన్ కషాయం అంటారు. ఈ పరీక్ష N, S, హాలోజన్లను గుర్తించుటకు ఉపయోగపడును.

నైట్రోజన్ను గుర్తించుట : కొద్దిగా లెసైన్ ద్రావణాన్ని పరీక్ష నాళికలో తీసుకొని దానికి కొన్ని చుక్కలు NaOH ద్రావణం కలిపి క్షారీకృతం చేసి దానికి అపుడే తయారు చేసిన ఫెర్రస్ సల్ఫేట్ ద్రావణాన్ని కలుపుతారు. దీనికి 2 లేక 3 చుక్కలు FeCl₃ ద్రావణం కలిపి చల్లబరిచి గాఢ HCl ద్రావణంతో ఆమ్లీకృతం చేస్తారు. ప్రశ్యన్ బ్లూ రంగు ఏర్పడుతుంది.

TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 8

ప్రశ్న 8.
క్రోమటోగ్రఫీ సిద్ధాంతాన్ని వివరించండి.
జవాబు:
క్రోమటోగ్రఫీని మిశ్రమ పదార్థాలను వేరు చేయడానికి, కర్బన పదార్థాలను శుద్ధి చేయడానికి, పదార్థాల పరిశుద్ధతను పరిశీలించడానికి ఉపయోగిస్తారు. ఈ పద్ధతిలో పదార్థాల మిశ్రమాన్ని ఒక స్థిర ప్రావస్థ మీద అధిశోషణం చేస్తారు. స్థిర ప్రావస్థగా ఘనపదార్థం కానీ ద్రవపదార్థం కానీ ఉండవచ్చు. స్వచ్ఛమైన ద్రావణి కానీ ద్రావణాల మిశ్రమం కానీ లేదా వాయువును కానీ స్థిరప్రావస్థ మీదకి మెల్లగా పంపిస్తారు. మిశ్రమంలోని పదార్థాలు క్రమంగా ఒకదాని నుంచి మరొకటి వేరు పడతాయి.

ప్రశ్న 9.
జలబాష్ప స్వేదనంలో కర్బన ద్రవం దాని బాష్పీభవన స్థానం కంటే తక్కువ ఉష్ణోగ్రత వద్ద ఎందుకు ఆవిరిగా మారుతుంది?
జవాబు:
జలబాష్ప స్వేదనంలో కర్బన ద్రవం బాష్పపీడనం P₁ నీటి ఆవిరి పీడనం P₂ల మొత్తం బాహ్య వాతావరణ పీడనం P కి సమానం అయినప్పుడు ద్రవం మరుగుతుంది. అంటే P = P₁ + P₂. కర్బన ద్రవ బాష్ప పీడనం P₁, P కంటే తక్కువ కాబట్టి అది దాని బాష్ప పీడన స్థానం కంటే తక్కువ ఉష్ణోగ్రత వద్ద బాష్పీకరణం చెందుతుంది.

ప్రశ్న 10.
కింది వాటిని వివరించండి.
(a) స్ఫటికీకరణం
(b) స్వేదనం
జవాబు:
(a) స్ఫటికీకరణం : మలిన పదార్థాన్ని అది కరిగే ద్రావణిలో దాని బాష్పీభవన స్థానం దగ్గర కరిగించి, మరిగించి సంతృప్త ద్రావణాన్ని తయారుచేసి ఆ గాఢ ద్రావణాన్ని చల్లార్చి పరిశుద్ధమైన సమ్మేళనాన్ని దాని స్ఫటిక రూపంలో పొందే ప్రక్రియను స్ఫటికీకరణం అంటారు.

ఈ పద్ధతిని ఘన సమ్మేళనాలను శుద్ధి చేయడానికి ఉపయోగిస్తారు. ఇవ్వబడిన మలిన ఘన సమ్మేళనాన్ని అది కరిగే ద్రావణిలో దాని బాష్పీభవన స్థానం దగ్గర కరిగించి దాదాపు సంతృప్త ద్రావణం వచ్చే వరకు మరిగించి వడపోయాలి. ద్రావణాన్ని నెమ్మదిగా చల్లారిస్తే పరిశుద్ధ సమ్మేళనం స్ఫటికాల రూపంలో బయటకు వస్తుంది. కరిగిన మలినాలు ద్రావణంలో మిగిలిపోతాయి.

(b) స్వేదనం : ఈ పద్ధతి

బాష్పశీల ద్రవాల నుంచి అబాష్పశీల మలినాలను వేరుచేయడానికి
బాష్పీభవన స్థానాలలో సరిపడ తేడా ఉన్న ద్రవాల మిశ్రమాన్ని వేరు చేయడానికి ఉపయోగిస్తారు.
విభిన్న బాష్పీభవన స్థానాలు ఉన్న ద్రవాలు వేరువేరు ఉష్ణోగ్రతల వద్ద పూర్తిగా బాష్పాలుగా మారతాయి. ఈ బాష్పాలను చల్లబరిస్తే ఏర్పడే ద్రవాలను వేరుగా సంగ్రహించవచ్చు.

ఉదా : క్లోరోఫారం (ద్ర.స్థానం 334 K) మరియు ఎనిలీన్ (ద్ర. స్థానం 457 K) మిశ్రమాన్ని స్వేదన పద్ధతిలో వేరుచేస్తారు.

లఘు సమాధాన ప్రశ్నలు

ప్రశ్న 11.
కింది చర్యలను పూరించి A, B, C ఉత్పన్నాల నామాలు రాయండి.

జవాబు:
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 10
A – ఎసిటిలీన్
B – బెంజీన్
C – మిథైల్ బెంజీన్

ప్రశ్న 12.
కింది చర్యలో ఏర్పడిన A, B, C ఉత్పన్నాల పేర్లను రాసి, చర్యా సమీకరణాన్ని రాయండి.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 11
జవాబు:

ప్రశ్న 13.
ఎసిటిలీన్ a) బ్రోమిన్ b) హైడ్రోజన్తో ఎట్లా చర్య జరుపుతుంది? పై చర్యలకు సమీకరణాలు రాసి ఉత్పన్నాల పేర్లను తెలపండి.
జవాబు:
a) ఎసిటిలీన్ CCl₄ సమక్షంలో బ్రోమిన్తో చర్య జరిపి 1, 1, 2, 2 – టెట్రా బ్రోమో ఈథేన న్ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 13

b) ఎసిటిలీన్ Ni లేదా Pt ఉత్ప్రేరకం సమక్షంలో హైడ్రోజన్తో చర్య జరిపి ఈథేన్ ను ఏర్పరుచును.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 14

ప్రశ్న 14.
ప్రతిక్షేపణ చర్య అంటే ఏమిటి? ఏవైనా రెండు బెంజీన్ ప్రతిక్షేపక చర్యలను తెలపండి.
జవాబు:
కర్బన సమ్మేళనంలోని ఏదేని పరమాణువు లేక పరమాణువుల సమూహాన్ని వేరొక పరమాణువు లేదా పరమాణువుల సమూహంతో ప్రతిక్షేపించుటను ప్రతిక్షేపణ చర్య అంటారు. బెంజీన్ ఎలక్ట్రోఫిలిక్ ప్రతిక్షేపణ చర్యలు జరుపుకుంటుంది. బెంజీన్ యొక్క ఎలక్ట్రోఫిలిక్ ప్రతిక్షేపణ చర్యలు :

1. హాలోజనీకరణం : బెంజీన్ను FeCl₃ సమక్షంలో క్లోరిన్హో చర్య జరపగా క్లోరో బెంజీన్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 15

2. నైట్రోకరణం : బెంజీన్ను నైట్రేషన్ మిశ్రమంతో (గాఢ HNO₃ + గాఢ H₂SO₄) 60°C కన్నా తక్కువ ఉష్ణోగ్రత వద్ద చర్య జరుపగా నైట్రో బెంజీన్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 16

ప్రశ్న 15.
డీహైడ్రోహాలోజినేషన్ చర్య అంటే ఏమిటి? ఆల్కైల్ హాలైడ్ నుంచి ఆల్కీన్ ఏర్పడే చర్యను రాయండి.
జవాబు:
డీహైడ్రోహాలోజనీకరణం : ఒక సమ్మేళనంలోని ప్రక్క ప్రక్కన గల కార్బన్ పరమాణువుల నుండి హైడ్రోజన్ మరియు హాలోజన్ పరమాణువులను హైడ్రోజన్ హాలైడ్ అణువుగా తొలగించు చర్యను డీహైడ్రోహాలోజనీకరణం అంటారు.

ఆల్కైల్ హాలైడ్ను ఆల్కహాలిక్ KOH తో వేడిచేయగా డీహైడ్రో హాలోజనీకరణం చెంది ఆల్కీన్ (ఇథిలీన్) ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 17

ప్రశ్న 16.
ఓజోన్తో ఎటువంటి సమ్మేళనాలు చర్యనొందుతాయి? ఏదైనా ఒక ఉదాహరణతో వివరించండి.
జవాబు:
అసంతృప్త హైడ్రోకార్బన్లు ఓజోన్లో చర్య జరుపుతాయి.

ఇథిలీన్, ఎసిటిలీన్, బెంజీన్ మొదలగునవి. ఓజోన్ తో చర్య జరిపి అస్థిరమైన ఓజనైడ్లను ఏర్పరుస్తాయి. ఇవి జల విశ్లేషణ చెంది కార్బొనైల్ సమ్మేళనాలను ఏర్పరుస్తాయి. ఈ చర్యను ఓజోనీకరణం అంటారు.
ఉదా : ఇథిలీన్, ఓజోన్తో చర్య జరిపి అస్థిర ఇథిలీన్ ఓజ నైడ్ను ఏర్పరుస్తుంది. ఇది జలవిశ్లేషణ చెంది ఫార్మాల్డిహైడ్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 18

ప్రశ్న 17.
స్థాన సాదృశ్యానికీ, ప్రమేయ సాదృశ్యానికీ క్రమంగా రెండు ఉదాహరణలు ఇవ్వండి. (March 2013)
జవాబు:
1) కర్బన శృంఖలంపై ఉన్న ప్రతిక్షేపకం లేదా ప్రమేయ సమూహ స్థానాల్లో భేదం వలన ఏర్పడే సాదృశ్యాన్ని స్థాన సాదృశ్యం అంటారు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 19

2) అణు సంకేతం ఒకటే ఉండి ప్రమేయ సమూహాలు వేరుగా ఉండటం వలన ఏర్పడిన సాదృశ్యాన్ని ప్రమేయ సమూహ సాదృశ్యం అంటారు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 20

ప్రశ్న 18.
మీథేన్ హాలోజనీకరణం చర్యాగతిని రాయండి.
జవాబు:
మీథేన్ హాలోజనీకరణం : సూర్యరశ్మి లేదా U.V కాంతి సమక్షంలో మీథేన్ హాలోజన్లతో చర్య జరుపుతుంది. ఈ చర్యలో మీథేన్లోని H పరమాణువులు హాలోజన్ పరమాణువులతో ప్రతిక్షేపక చర్య జరిపి మోనో, డై, ట్రై మరియు టెట్రాహలో మీథేన్లు వరసగా ఏర్పడతాయి.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 21

ప్రశ్న 19.
ఈథైల్ ఆల్కహాల్ నుంచి ఇథిలీన్ న్ను ఎట్లా తయారుచేస్తారు?
జవాబు:
ఈథైల్ ఆల్కహాల్ నుండి ఇథిలీన్ ను తయారు చేయుట :
ఈథైల్ ఆల్కహాల్ నిర్జలీకరణ : ఈథైల్ ఆల్కహాల్ను గాఢ H₂SO₄ తో కలిపి 170°C వద్ద వేడిచేస్తే ఇథిలీన్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 22

ప్రశ్న 20.
కింది వాటితో ఎసిటిలీన్ చర్యలను వివరించండి.
(a) Na/NH₃
(b) క్రోమిక్ ఆమ్లం సమీకరణాలను, ఉత్పన్నాల పేర్లను రాయండి
జవాబు:
a) ఎసిటిలీన్ సోడియం లోహంతో చర్య జరిపి మోనోసోడియమ్ ఈథనైడ్ మరియు డై సోడియం ఈథనైడు ఏర్పరుస్తుంది.
ఈ చర్య ఎసిటిలీన్ యొక్క ఆమ్ల ధర్మాన్ని వివరిస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 23

b) ఎసిటిలీన్ను క్రోమిక్ ఆమ్లం ఎసిటిక్ ఆమ్లంగా ఆక్సీకరణం చేస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 24

ప్రశ్న 21.
కర్బన ద్రవాలను శుద్ధి చేసే ప్రక్రియలు – స్ఫటికీకరణం, ఉత్పతనాలను వివరించండి.
జవాబు:
స్ఫటికీకరణం : మలిన పదార్థాన్ని అది కరిగే ద్రావణిలో దాని బాష్పీభవన స్థానం దగ్గర కరిగించి మరిగించి సంతృప్త ద్రావణాన్ని తయారుచేసి ఆ గాఢ ద్రావణాన్ని చల్లార్చి పరిశుద్ధమైన సమ్మేళనాన్ని దాని స్ఫటిక రూపంలో పొందే ప్రక్రియను స్ఫటికీకరణం అంటారు.

ఉత్పతనం : కొన్ని ఘనపదార్థాలను వేడిచేస్తే అవి ద్రవస్థితికి రాకుండా నేరుగా బాష్పస్థితికి చేరుకుంటాయి. మరల ఆ బాష్పాలను చల్లారిస్తే ద్రవస్థితిని పొందకుండా నేరుగా ఘనస్థితిని పొందుతాయి. దీనినే ఉత్పతనం అంటారు.

ఉదా : అపరిశుద్ధ సమ్మేళనాన్ని ఒక వాచ్ గ్లాసుతో మూసి ఉన్న బీకరులో తీసుకొని ఒక ఎలక్ట్రిక్ ప్లేటు మీద పెట్టి వేడిచేస్తారు. సమ్మేళనం ఉత్పతనం చెంది వాచ్స్ అడుగుభాగాన ఘనరూపంలో చేరుకుంటుంది. మలినాలు బీరలోనే ఉండిపోతాయి.

ప్రశ్న 22.
సమ్మేళనాన్ని శుద్ధిచేసే ద్రావణ నిష్కర్షణాన్ని తెలపండి.
జవాబు:
ద్రావణ నిష్కర్షణ : ఒక కర్బన పదార్థం ‘X’ నీటిలో కరగని కర్బన ద్రావణిలో, నీటిలో కంటే అధికంగా కరుగుతుంది.
కాని నీటిలో కరిగి ఉన్న ఆ పదార్థపు జల ద్రావణాన్ని కర్బన ద్రావణిలో కలిపి కుదిపితే ‘X’ కర్బన ద్రావణిలోకి అధికంగా వెళ్ళిపోతుంది. కర్బన ద్రావణాన్ని వేరు చేసి స్వేదనం చేస్తే కర్బన ద్రావణి బాష్పరూపంలో కర్బన సమ్మేళనం నుంచి వేరవుతుంది. సమ్మేళనం స్వేదన కుప్పెలో ఉంటుంది.

ప్రశ్న 23.
కర్బన సమ్మేళనంలోని ఫాస్ఫరస్, సల్ఫర్ల భారశాతాన్ని కనుక్కొనే విధానాలను తెలపండి.
జవాబు:
కర్బన సమ్మేళనంలోని ఫాస్ఫరస్ భారశాతం కనుక్కొనుట : ఫాస్ఫరస్ భారశాతాన్ని కనుక్కోవడానికి తెలిసిన ద్రవ్యరాశి గల కర్బన పదార్థాన్ని సధూమ నైట్రికామ్లంలో వేడి చేయాలి. ఫాస్ఫరస్ ఫాస్ఫారిక్ ఆమ్లంగా ఆక్సీకరణం చెందుతుంది. ఈ ఆమ్లానికి అమ్మోనియా, అమ్మోనియం మోలిబేట్ ద్రావణాలు కలిపి అమ్మోనియం ఫాస్ఫో మోలిబేట్ [(NH₄)₃ PO₄.12M0O₃]గా అవక్షేపించాలి.

కర్బన సమ్మేళనం ద్రవ్యరాశి = mg
అమ్మోనియం ఫాస్ఫోమోలిబేడ్ = m₁g
(NH₄)₃3PO₄ . 12 MoO₃ అణు ద్రవ్యరాశి = 1877g
ఫాస్ఫరస్ భారశాతం = \(\frac{31 \times \mathrm{m}_1 \times 100}{1877 \times \mathrm{m}}\)

కర్బన సమ్మేళనంలోని సల్ఫర్ భారశాతం కనుక్కొనుట : కర్బన సమ్మేళనంలోని సల్ఫర్ భారశాతం కనుక్కోవడానికి తెలిసిన భారం గల కర్బన సమ్మేళనాన్ని సోడియం పెరాక్సైడ్ లేదా సధూమ నైట్రికామ్లంతో కేరియస్ నాళికలో వేడిచేస్తారు. సమ్మేళనంలోని సల్ఫర్ H₂SO₄ గా ఆక్సీకరణం చెందుతుంది. ఈ ఆమ్లానికి అధికంగా జల బేరియం క్లోరైడ్ ద్రావణం కలిపి బేరియం సల్ఫేట్గా అవక్షేపింప చేస్తారు. ఈ అవక్షేపాన్ని వడపోత ద్వారా వేరుచేసి, కడిగి, పొడి చేసి భారాన్ని కనుక్కొంటారు.

తీసుకున్న కర్బన పదార్ధ భారం = mg
ఏర్పడిన బేరియం సల్ఫేట్ భారం = m₁g
m₁, gల బేరియం సల్ఫేట్లోని సల్ఫర్ = \(\frac{32 \times m_1}{233} \mathrm{~g}\)
(1 మోల్ BaSO₄ = 233 gm BaSO₄ = 32 gm సల్ఫర్)
సల్ఫర్ భారశాతం = \(\frac{32 \times \mathrm{m}_1 \times 100}{233 \times \mathrm{m}}\)

ప్రశ్న 24.
ప్రోపీన్ HBr సంకలన చర్యను అయానిక చర్యాగతితో వివరించండి.
జవాబు:
ప్రోపీన్తో HBr సంకలనం చెంది మార్కొనికాఫ్ నియమము ప్రకారం 2-బ్రోమో ప్రోపెన్ను ఇస్తుంది. కాని బెంజాయిల్ పెరాక్సైడ్ సమక్షంలో ప్రోపీను HBrను కలిపితే 1-బ్రోమో ప్రోపేను ఏర్పడుతుంది. ఇక్కడ యాంటి మార్కొనికాఫ్ నియమము ప్రకారము సంకలనం జరుగుతుంది.

యాంటి మార్కొనికాఫ్ నియమము : ఒక అసమకారకం ద్విబంధంతో పెరాక్సైడ్ల సమక్షంలో సంకలనం చెందేటపుడు అసమకారకం రుణావేశ భాగం ద్విబంధంలో ఎక్కువ హైడ్రోజన్లున్న కార్బన్పై సంకలనం చెందుతుంది. దీనినే ఖరాష్ ప్రభావం అని కూడా అంటారు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 27
చర్యావిధానం (స్వేచ్ఛా ప్రాతిపదిక సంకలన చర్య) :
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 28

ప్రశ్న 25.
సోడియం ప్రోపనోయేట్ను సోడా లైమ్ వేడిచేస్తే ఏ ఉత్పన్నం ఏర్పడుతుంది?
జవాబు:
సోడియం ప్రోపనోయేట్ను సోడాలైమ్తో వేడిచేస్తే ఈథేన్ ఏర్పడుతుంది. సోడాలైమ్ అనగా NaOH +
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 29

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 26.
హైడ్రోకార్బన్ల వర్గీకరణను వివరించండి.
జవాబు:
హైడ్రోకార్బన్ల వర్గీకరణ
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 30

ప్రశ్న 27.
కింది సమ్మేళనాల IUPAC నామాలు రాయండి.
(a) CH₂ = CH – CH = CH₂
(b) CH₂ = CH – C ≡ C-CH₃
(c) CH₃CH = C[CH₃]₂
(d) CH₂-CH₂ CH = CH₂
(e)
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 32
జవాబు:
(a) 1, 3 – బ్యూటా డై ఈన్
(b) పెంట్ 1 – ఈన్ – 3 – ఐన్
(c) 2-మిథైల్-2-బ్యూటీన్
(d) 4-ఫినైల్ 1-బ్యూటీన్
(e) 4-ఈథైల్ డెకా 1, 5, 8 ట్రైఈన్

ప్రశ్న 28.
ఈథేన్ ను తయారుచేసే రెండు పద్ధతులను, ఏవైనా ఈథేన్ మూడు చర్యలను రాయండి. (March 2013)
జవాబు:
ఈథేన్ ను తయారు చేయు పద్ధతులు :
1. ఆల్కైల్ హాలైడ్ల నుంచి : ఈథైల్ హాలైడ్లను Zn, సజల HCl సమక్షంలో క్షయకరణం చెందించి ఈథేన్ తయారుచేస్తారు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 33

2. ఉర్ట్ చర్య : మిథైల్ బ్రోమైడ్ను పొడి ఈథర్లో తీసుకుని సోడియంతో వేడిచేస్తే ఈథేన్ ఏర్పడుతుంది. ఈ చర్యనే ఉ చర్య అంటారు.

ఈథేన్ యొక్క ధర్మాలు : ఈథేన్ సాధారణంగా ప్రతిక్షేపణ చర్యలను జరుపుకుంటుంది. ఈ చర్యలలో ఒక పరమాణువు లేదా సమూహం ఇంకొక పరమాణువు లేదా సమూహంలో ప్రతిక్షేపించబడతాయి.

ఉదా :
1. హాలోజనీకరణం : ఈథేన్ ను UV కిరణాల సమక్షంలో Cl₂ తో చర్య జరిపిస్తే, ఈథేన్ ని H పరమాణువులు Cl పరమాణువులతో ప్రతిక్షేపణం చెందుతాయి.

2. నైట్రేషన్ : ఈథేన్ 400°C వద్ద HNO₃ తో చర్య జరిపి నైట్రో ఈథేనన్ను ఏర్పరచును. ఈ చర్యనే నైట్రేషన్ అంటారు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 36

3. దహనచర్య : గాలి లేదా డై ఆక్సిజన్ సమక్షంలో ఈథేన్ వేడిచేస్తే CO₂, H₂O లను ఏర్పరుస్తుంది. ఈ చర్యలో అధిక శక్తి విడుదలవుతుంది. ఈ చర్యను దహన చర్య అంటారు.
C₂H₆ + \(\frac{7}{2}\)O₂ → 2 CO₂ + 3 H₂O + శక్తి

ప్రశ్న 29.
కింద ఇచ్చిన ఫార్ములాలు ఏర్పరచగలిగిన సాదృశ్యాలను రాసి వాటి నిర్మాణాలు, IUPAC పేర్లు రాయండి :
(a) C₄H₈ (ఒక ద్విబంధం)
(b) C₅H₈ (ఒక త్రిబంధం)
(c) C₅H₁₂ (బహుబంధాలు లేవు)
జవాబు:
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 37

ప్రశ్న 30.
కింది హైడ్రోకార్బన్లు దహనచర్యలో జరిపే చర్యలను సమీకరణ రూపంలో రాయండి.
(a) బ్యూటేన్
(b) పెంటీన్
(c) హెక్సెన్
జవాబు:
(a) బ్యూటేన్ దహనచర్య
C₄H₁₀ + \(\frac{13}{2}\)O₂ → 4 CO₂ + 5H₂O + శక్తి

(b) పెంటీన్ దహనచర్య
C₅H₁₀ + \(\frac{15}{2}\)O₂ → 5 CO₂ + 5H₂O + శక్తి

ప్రశ్న 31.
ప్రోపీన్ HBr సంకలనం చెంది 2–బ్రోమో ప్రోపేన్ను ఇస్తుంది. అదే బెంజాయిల్ పెరాక్సైడ్ సమక్షంలో 1–బ్రోమోప్రోపేన్ ఏర్పడుతుంది. చర్యాగతిని రాసి తేడాను వివరించండి.
జవాబు:
ప్రోపీన్ తో HBr సంకలనం చెంది మార్కొనికాఫ్ నియమము ప్రకారం 2-బ్రోమో ప్రోపేన న్ను ఇస్తుంది. కాని బెంజాయిల్ పెరాక్సైడ్ సమక్షంలో ప్రోపీన్కు HBrను కలిపితే 1-బ్రోమో ప్రోపేన్ ఏర్పడుతుంది. ఇక్కడ యాంటి మార్కొనికాఫ్ నియమము ప్రకారము సంకలనం జరుగుతుంది.

యాంటి మార్కొనికాఫ్ నియమము : ఒక అసమకారకం ద్విబంధంతో పెరాక్సైడ్ సమక్షంలో సంకలనం చెందేటపుడు అసమకారకం రుణావేశ భాగం ద్విబంధంలో ఎక్కువ హైడ్రోజన్లున్న కార్బన్పై సంకలనం చెందుతుంది. దీనినే ఖారాష్ ప్రభావం అని కూడా అంటారు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 40
చర్యావిధానం (స్వేచ్ఛా ప్రాతిపదిక సంకలన చర్య) :
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 41

ప్రశ్న 32.
ఇథిలీన్ తయారుచేయడానికి రెండు విధానాలు తెలపండి. ఇథిలీన్ కింది వాటితో ఏర్పరిచే ఉత్పన్నాల చర్యలను తెలపండి.
(a) ఓజోన్
(b) హైపోహాలస్ ఆమ్లం
(c) చల్లని విలీన క్షార KMnO₄
(d) అధిక పీడనం వద్ద O₂ తో వేడిచేయుట
జవాబు:
ఇథిలీన్ ను తయారుచేయు పద్ధతులు :

1. డీహైడ్రోహాలోజనీకరణం : ఇథైల్ హాలైడ్లను ఆల్కహాలిక్ KOH తో వేడిచేయగా ఇథిలీన్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 42
2. ఇథైల్ ఆల్కహాల్ను గాఢ H₂SO₄ సమక్షంలో 170°C వద్ద వేడిచేస్తే ఇథిలీన్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 43

ఇథిలీన్ చర్యలు :

(a) ఓజోన్తో చర్య : ఇథిలీన్ ఓజోన్ తో చర్య జరిపి అస్థిరమైన ఇథిలీన్ ఓజోనైడ్ను ఏర్పరుస్తుంది. ఇది Zn/H₂O సమక్షంలో వియోగం చెంది ఫార్మాల్డిహైడు ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 44

(b) హైపోహాలస్ ఆమ్లంతో చర్య : ఇథిలీన్ HOCl తో చర్య జరిపి ఇథిలీన్ – క్లోరోహైడ్రినన్ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 45

(c) చల్లని, విలీన, క్షార KMnO₄ తో చర్య : ఇథిలీన్ KMnO₄ తో చర్య జరిపి ఇథిలీన్ గ్లైకాల్నిస్తుంది. చల్లని విలీన
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 46

(d) అధిక పీడనం వద్ద O₂తో చర్య : అధిక పీడనం వద్ద మరియు 200°C వద్ద ఇథిలీన్ O₂ తో చర్య జరిపిస్తే పాలిమరీకరణం జరుపుకొని పాలిథీన్ ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 47

ప్రశ్న 33.
కింది వాటితో ఇథిలీన్ చర్యలు రాయండి. సమీకరణాలు రాసి ఉత్పన్నాల పేర్లు రాయండి.
(a) హైడ్రోజన్ హాలైడ్
(b) హైడ్రోజన్
(c) బ్రోమీన్
(d) నీరు
(e) సిల్వర్ సమక్షంలో 200°C వద్ద ఆక్సిజన్తో చర్య
జవాబు:
ఇథిలీన్ – చర్యలు
(a) హైడ్రోజన్ హాలైడ్తో
చర్య: ఇథిలీన్ హైడ్రోజన్ హాలైడ్లో చర్యజరిపి ఇథైల్హాలైడ్లనిస్తుంది.
CH₂ = CH₂ + HX → CH₃ – CH₂X
ఉదా :
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 48

(b) హైడ్రోజన్తో చర్య : ఇథిలీన్ నికెల్ సమక్షంలో H₂ తో చర్యజరిపి ఈథేన్ ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 49

(c) బ్రోమీన్ చర్య : ఇథిలీన్ CCl₄ సమక్షంలో బ్రోమిన్తో చర్యజరిపి 1, 2 – డైబ్రోమో ఈథేన్ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 50

(d) నీటితో చర్య ఇథిలీన్ ఆమ్లీకృత నీటితో చర్య జరిపి ఈథైల్ ఆల్కహాల్ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 51

(e) సిల్వర్ సమక్షంలో 200°C O₂ తో చర్య : ఇథిలీన్ 200-400°C వద్ద సిల్వర్ సమక్షంలో ఆక్సిజన్తో చర్య జరిపి ఇథిలీన్ ఆక్సైడ్ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 52

ప్రశ్న 34.
‘A’ అను ఆల్కీన్ ఓజోనాలిసిస్ చర్యలో పాల్గొని ఇథనాల్, పెంటేన్-3-ఓన్ల మిశ్రమాన్ని ఏర్పరుస్తుంది. చర్యను రాసి, ఉత్పన్నాల, ఆల్కీన్ -Aల నిర్మాణాలు రాసి వాటి IUPAC పేరును తెల్పండి.
జవాబు:
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 53

ప్రశ్న 35.
‘A’ అనే ఆల్కీన్లో మూడు C – C ఎనిమిది C – H బంధాలు, ఒక C=C ద్విబంధం ఉన్నాయి. ఓజోనాలిసిస్ చర్యలో ‘A’ ఆల్కీన్ రెండు అణువుల ఆల్డిహైడ్ (అణుభారం 44)ను ఏర్పరుస్తుంది. ‘A’ యొక్క IUPAC పేరును రాయండి.
జవాబు:
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 54

ప్రశ్న 36.
ఎసిటిలీన్ తయారుచేయడానికి రెండు పద్ధతులను తెలపండి. ఎసిటిలీన్ నీటితో, ఓజోన్ తో జరుపు చర్యలు రాయండి.
జవాబు:
ఎసిటిలీన్ తయారుచేయు పద్ధతులు :

1. కాల్షియంకార్బైడ్ నుండి : కాల్షియం కార్బైడు జలవిశ్లేషణ చేయుట ద్వారా పారిశ్రామికంగా ఎసిటిలీన్ ను తయారు చేయవచ్చు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 55

2. అయొడీఫారం నుండి : అయొడీఫారంను సిల్వర్ పొడితో వేడిచేయగా ఎసిటిలీన్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 56

రసాయన ధర్మాలు :

1. నీటితో చర్య : ఎసిటిలీన్ HgSO₄ మరియు H₂SO₄ సమక్షంలో 60°C వద్ద నీటితో చర్య జరిపి అస్థిర వినైల్ ఆల్కహాల్ను ఏర్పరుస్తుంది. ఇది పునర్వ్యవస్థీకరణం చెంది అసిటాల్డిహైడ్ ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 57
2..ఓజోన్ చర్య : ఎసిటిలీన్ ఓజోన్ తో సంకలనం చెంది అస్థిర ఎసిటిలీన్ ఓజోనైడ్ను ఏర్పరుస్తుంది. ఇది. Zn/H₂O సమక్షంలో వియోగం చెంది గైఆక్సాల్ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 58

ప్రశ్న 37.
ఎసిటిలీన్ కిందివానితో ఏ విధంగా చర్య జరుపుతుంది? ఉత్పన్నాల పేర్లను రాసి చర్యలు రాయండి.
(a) ఎసిటిక్ ఆమ్లం
(b) నీరు
(c) హైడ్రోజన్
(d) హాలోజన్లు
(e) హైడ్రోజన్ హాలైడ్
(f) అమ్మోనికల్ సిల్వర్ నైట్రేట్, Cu₂Cl₂
జవాబు:
(a) ఎసిటిక్ ఆమ్లంతో చర్య : ఎసిటిలీన్, Hg⁺² అయాన్ల సమక్షంలో ఎసిటిక్ ఆమ్లంతో చర్య జరిపి మొదట వినైల్ ఎసిటేట్ ను తరువాత ఇథిలిడీన్ డైఎసిటేట్ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 59

(b) నీటితో చర్య : ఎసిటిలీన్ HgSO₄ మరియు H₂SO₄ సమక్షంలో 60°C వద్ద నీటితో చర్య జరిపి అస్థిర వినైల్ ఆల్కహాల్ను ఏర్పరుస్తుంది. ఇది పునర్వ్యవస్థీకరణం చెంది అసిటాల్డిహైడు ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 60

(c) హైడ్రోజన్ చర్య : ఎసిటిలీన్ Ni ఉత్ప్రేరకం సమక్షంలో H₂ తో వేడిచేయగా సంకలనం చెంది మొదట ఇథిలీన్ ను తరువాత ఈథేన్ ను ఏర్పరుస్తుంది. ఈ చర్యను సెబాటియర్ – సెండరెన్స్ చర్య అంటారు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 61

(d) హాలోజన్తో చర్య : ఎసిటిలీన్ క్లోరిన్తో సంకలన చర్య జరిపి మొదట 1, 2 – డై క్లోరో ఈథేన్ ను తరువాత 1, 1, 2, 2 – టెట్రాక్లోరో ఈథేనన్ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 62

(e) హైడ్రోజన్ హాలైడ్లో చర్య : ఎసిటిలీన్ HCl తో చర్య జరిపి మొదట వినైల్ క్లోరైడ్ను ఆ తరువాత ఇథిలిడీన్ క్లోరైడ్ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 63

(f) అమ్మోనికల్ AgNO₃ మరియు Cu₂ Cl₂ తో చర్యలు :
ఎసిటిలీన్ వాయువును అమ్మోనికల్ AgNO₃ ద్రావణం గుండా పంపినపుడు, సిల్వర్ ఎసిటిలైడ్ అవక్షేపం ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 64
ఎసిటిలీన్ వాయువును అమ్మోనికల్ Cu₂Cl₂ ద్రావణం గుండా పంపినపుడు, క్యూప్రస్ ఎసిటిలైడ్ అవక్షేపం ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 65

ప్రశ్న 38.
బెంజీన్ను తయారుచేసే ఏవైనా రెండు పద్ధతులను రాసి వాటి సమీకరణాలు రాయండి. బెంజీన్ ఆల్కీన్ లక్షణాలను చూపించదు – ఎందుకని? బెంజీన్ నుంచి మీథైల్ బెంజీన్ ను ఎలా తయారుచేస్తారు?
జవాబు:
బెంజీన్ ను తయారు చేయు పద్ధతులు
(a) డీ కార్బాక్సిలీకరణం : సోడియం బెంజోయేట్ను సోడాలైమ్ (NaOH + CaO) తో వేడిచేయగా బెంజీన్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 66

(b) ఫినోల్ క్షయకరణం : ఫినోల్ను జింక్ పొడితో వేడిచేయగా అది క్షయకరణం చెంది బెంజీన్ ఏర్పడుతుంది.

బెంజీన్ అణుఫార్ములా ఆల్కీన్ల వలె అసంతృప్తతను తెలియచేసినప్పటికి, ఇది అత్యంత స్థిరంగా ఉంటూ సంకలన చర్యల కంటే ప్రతిక్షేపణ చర్యలను ఎక్కువగా జరుపుతుంది. కారణం

బెంజీన్లోని π – ఎలక్ట్రాన్లు అస్థానీకృతం చెందుతాయి.
బెంజీన్ కున్న అధిక రెజోనెన్స్ శక్తి వలన దానికి అధిక స్థిరత్వం వస్తుంది. కావున ఇది ఆల్కీన్ల వలె ప్రవర్తించదు.

(c) బెంజీన్ నుంచి మిథైల్ బెంజీన్ ను తయారు చేయుట : బెంజీన్ అనార్ద్ర Al Cl₃ సమక్షంలో మిథైల్ క్లోరైడ్తో చర్య జరిపి మిథైల్ బెంజీన్ లేక టోలిన్ ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 68

ప్రశ్న 39.
ఎసిటిలీన్ నుంచి బెంజీన్ ఎట్లా ఏర్పడుతుంది? సమీకరణం రాయండి. బెంజీన్ యొక్క హాలోజినేషన్, ఆల్కైలేషన్, ఎసైలేషన్, నైట్రేషన్, సల్ఫోనేషన్ చర్యలను వివరించండి.
జవాబు:
ఎసిటిలీన్ నుండి బెంజీన్ ను తయారు చేయుట : ఎసిటిలీన్ వాయువును ఎర్రగా కాలుచున్న కాపర్ గొట్టాల గుండా పంపినపుడు అది పాలిమరీకరణ చెంది బెంజీన్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 69

బెంజీన్ యొక్క ఎలక్ట్రోఫిలిక్ ప్రతిక్షేపణ చర్యలు :

1. హాలోజినేషన్ (హాలోజనీకరణం) : బెంజీన్ న్ను FeCl₃ సమక్షంలో క్లోరిన్తో చర్య జరపగా క్లోరో బెంజీన్ ఏర్పడుతుంది..
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 70

2. ఆల్కైలేషన్ (ఆల్కైనీకరణం) : బెంజీన్ AlCl₃ సమక్షంలో ఆల్కైల్ హాలైడ్లతో చర్య జరిపి ఆల్కైల్ బెంజీన్ ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 71

3. ఎసైలేషన్ : బెంజీన్, AlCl₃ సమక్షంలో ఎసైల్ క్లోరైడ్తో చర్య జరిపి ఎసైల్ బెంజీన్ ను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 72

4. నైట్రేషన్ (నైట్రోకరణం) : బెంజీన్ ను నైట్రేషన్ మిశ్రమంతో (గాఢ HNO₃ + గాఢ H₂SO₄) 60°C కన్నా తక్కువ ఉ ష్ణోగ్రత వద్ద చర్య జరుపగా నైట్రో బెంజీన్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 73
5. సల్ఫోనేషన్ (సల్ఫోనీకరణం): బెంజీన్ సల్ఫ్యూరిక్ ఆమ్లంతో చర్య జరిపి బెంజీన్ సల్ఫోనిక్ ఆమ్లంను ఏర్పరుస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 74

ప్రశ్న 40.
నిర్మాణ సాదృశ్యాలు, త్రిమితీయ సాదృశ్యాల మధ్య తేడాలు వివరించండి.
జవాబు:
నిర్మాణాత్మక సాదృశ్యము:

అణువులోని పరమాణువుల లేదా సమూహాల అమరికలో తేడా వలన నిర్మాణాత్మక సాదృశ్యము ఏర్పడుతుంది. ఈ సాదృశ్యములకు ఒకే అణు ఫార్ములా ఉండి వేరు వేరు నిర్మాణాత్మక ఫార్ములాలు ఉంటాయి.
శృంఖల సాదృశ్యం, స్థానసాదృశ్యం, వలయశృంఖల సాదృశ్యం, ప్రమేయ సమూహ సాదృశ్యం, మెటామెరిజం, టాటామెరిజం మొదలగునవి నిర్మాణాత్మక సాదృశ్య రకానికి చెందినవి.
ఇవి ద్విమితీయంగా ఉంటాయి.

త్రిమితీయ సాదృశ్యము :

ఒకే అణుఫార్ములా మరియు నిర్మాణాత్మక ఫార్ములా కలిగి ఉండి, త్రిమితీయంగా పరమాణువులు లేదా గ్రూపుల ప్రాదేశిక అమరికలో భేదం వలన వచ్చు సాదృశ్యమును త్రిమితీయ సాదృశ్యము అంటారు.
క్షేత్ర సాదృశ్యము, దృక్ సాదృశ్యము, అనురూపక సాదృశ్యము మొదలగునవి త్రిమితీయ సాదృశ్య రకానికి చెందినవి.
ఇవి త్రిమితీయంగా ఉంటాయి.

ప్రశ్న 41.
సరళ శృంఖలాలు అనురూపత, విన్యాసంలందు తేడా ఏమిటి?
జవాబు:
అనురూపత లేదా అనురూపక సాదృశ్యాలు :

ఇవి త్రిమితీయ సాదృశ్యాలు. ఒక రూపం నుండి మరొక రూపంలోనికి C – C బంధాల భ్రమణం వలన మార్పు చెందుతాయి. ఇవి ఒకదానితో ఒకటి గతిక సమతాస్థితిలో ఉంటాయి.
సాధారణ పరిస్థితులలో వీటిని వేరు చేయలేము.
ఉదా : ఈథేన్ యొక్క E and S నిర్మాణాలు

విన్యాసం లేదా విన్యాస సాదృశ్యాలు :

1. ఇవి కూడా త్రిమితీయ సాదృశ్యాలు. ఇవి స్థిరమైనవి. ఇవి ఒక రూపం నుండి వేరొక రూపంలోకి మార్పు చెందవు.
2. ఒక రూపం నుండి వేరొక రూపంలోనికి మార్పు చెందుటకు బంధాలు విడిపోయి కలవవలెను. ఇవి రెండు రకాలు.

1. క్షేత్ర సాదృశ్యాలు : ఈ సాదృశ్యాలలో ద్విబంధంతో బంధించబడి ఉన్న కార్బన్ పరమాణువుల చుట్టూ ఉన్న పరమాణువుల లేక గ్రూపుల అమరికలో తేడా ఉంటుంది.
ఉదా : సిస్ 2-బ్యూటీన్ మరియు ట్రాన్స్ 2-బ్యూటీన్
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 76

2. దృశా సాదృశ్యాలు (ఆప్టికల్ ఐసోమర్లు) : ఈ సాదృశ్యాలలో అణువులోని కార్బన్ పరమాణువును అతకబడిన నాలుగు విభిన్న పరమాణువుల లేక రాడికల్స్ ప్రాదేశిక అమరికలో తేడా ఉంటుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 77

ప్రశ్న 42.
క్షేత్ర సాదృశ్యం అంటే ఏమిటి? 2-బ్యూటీన్ క్షేత్ర సాదృశ్యాలను రాయండి.
జవాబు:
ద్విబంధంతో బంధింపబడి ఉన్న కార్బన్ పరమాణువుల చుట్టూ ఆవరించి ఉన్న పరమాణువుల లేక గ్రూపుల అమరికలో తేడా వలన ఏర్పడే సాదృశ్యాన్ని క్షేత్ర సాదృశ్యం అంటారు.
ఉదా : 2-బ్యూటీన్కు క్రింది క్షేత్ర సాదృశ్యాలు ఉన్నాయి.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 78
ఒకే రకమైన సమూహాలు ద్విబంధానికి ఒకే వైపున బంధాలేర్పరచి ఉంటే ఆ సాదృశ్యమును సిస్ సాదృశ్యమని, ఒకే రకమైన సమూహాలు ద్విబంధానికి వ్యతిరేకదిశలో బంధాలు ఏర్పరచి ఉంటే ట్రాన్స్ సాదృశ్యమని అంటారు.

ప్రశ్న 43.
E-Z విన్యాసాలను గుర్తించే పద్ధతిని తెలిపి, CHCl = CFBr అణువుకు క్షేత్ర సాదృశ్యాలను రాయండి.
జవాబు:
ఈ పద్ధతి పరమాణు సంఖ్యల విలువలపై ఆధారపడి ఉంటుంది. ద్విబంధ కార్బన్ల మీద గ్రూపులు అధిక పరమాణు సంఖ్యలు గల పరమాణువుకు ద్విబంధ కార్బన్లు ఒకే వైపు బంధాలు ఏర్పరచి ఉంటే దానిని ‘Z’ విన్యాసం అనీ, అదే అధిక పరమాణు సంఖ్యల పరమాణువులు ద్విబంధానికి వ్యతిరేక ప్రక్కల బంధించబడి ఉంటే దానిని ‘E’ విన్యాసం అని అంటారు.

ఉదా : CHCl = CFBr
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 79

ప్రశ్న 44.
ఒక ఆల్కీన్లో ద్విబంధం వద్ద ఉన్న కార్బన్లపై Cl, Br, -CH₂,-CH₂-OH, CH (CH₃)₂ సమూహాలుంటే దాని E, Z విన్యాసాలు రాయండి.
జవాబు:
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 80

ప్రశ్న 45.
కింది వాటిని వివరించండి.
(a) స్వేదనం
(b) అంశిక స్వేదనం
(c) తక్కువ పీడనంలో స్వేదనం
(d) జలబాష్ప స్వేదనం
జవాబు:
(a) స్వేదనం : ఈ పద్ధతి

1) బాష్పశీల ద్రవాల నుంచి అబాష్పశీల మలినాలను వేరుచేయడానికి

2) బాష్పీభవన స్థానాలలో సరిపడ తేడా ఉన్న ద్రవాల మిశ్రమాన్ని వేరు చేయడానికి ఉపయోగిస్తారు.
విభిన్న బాష్పీభవన స్థానాలు ఉన్న ద్రవాలు వేరువేరు ఉష్ణోగ్రతల వద్ద పూర్తిగా బాష్పాలుగా మారతాయి. ఈ బాష్పాలను చల్లబరిస్తే ఏర్పడే ద్రవాలను వేరుగా సంగ్రహించవచ్చు.

ఉదా : క్లోరోఫారం (ద్ర. స్థానం 334K) మరియు ఎనిలీన్ (ద్ర. స్థానం 457K) మిశ్రమాన్ని స్వేదన పద్ధతిలో వేరుచేస్తారు.

(b) పాక్షిక అంశిక స్వేదనం : మిశ్రమంలోని రెండు ద్రవాల బాష్పీభవన స్థానాలలో తేడా తక్కువగా ఉన్నప్పుడు వీటి బాష్పాలు ఒకే ఉష్ణోగ్రత వద్ద ఏర్పడి ఒకేసారి ద్రవీకరణం చెందుతాయి. ఈ ద్రవాలను వేరు చేయడానికి పాక్షిక అంశిక స్వేదనాన్ని ఉపయోగిస్తారు.

ఈ పద్ధతిలో ద్రవాల మిశ్రమ బాష్పాలను ద్రవీకరణానికి ముందు అంశీకరణ నాళిక ద్వారా పంపించాలి. అంశిక నాళికను స్వేదన కుప్పె మూతికి బిగించాలి. ఇక్కడ ముఖ్య సూత్రం మిశ్రమ బాష్పాలు పొడవాటి అంశిక నాళికలో ప్రయోగించినపుడు ఎక్కువ బాష్పీభవన స్థానం ఉన్న ద్రవపు బాష్పం ముందుగా చల్లబడి ద్రవీకరణం చెంది స్వేదన కుప్పెలో చేరగా, తక్కువ బాష్పీభవన స్థానం ఉన్న ద్రవపు బాష్పం కండెన్సర్ ద్వారా ప్రయాణించి చల్లబడి ద్రవీకరణం చెంది సంగ్రహణ పాత్రను చేరుతుంది.

(c) తక్కువ పీడనంలో స్వేదనం : ఈ విధానం అధిక బాష్పీభవన స్థానాలున్న ద్రవాల్ని లేదా బాష్పీభవన స్థానాల కంటే తక్కువ ఉష్ణోగ్రతల వద్దనే వియోగం చెందే ద్రవాల్ని శుద్ధి చేయడానికి ఉపయోగపడుతుంది. బాష్పపీడనం తగ్గిస్తే ద్రవం తక్కువ ఉష్ణోగ్రత వద్దే ఎటువంటి వియోగమూ చెందకుండా బాష్పీభవనం చెందుతుంది. వచ్చిన బాష్పాల్ని చల్లబరచి పరిశుద్ధ ద్రవాన్ని పొందవచ్చు. మలినాలు స్వేదనం కుప్పెలో మిగులుతాయి.
ఉదా : గ్లిసరాలు సబ్బు పరిశ్రమలో ఉపయోగించిన గాఢ క్షార ద్రావణం నుంచి ఈ పద్ధతిలో వేరు చేయవచ్చు.

(d) జలబాష్ప స్వేదనం : ఈ పద్ధతిలో నీటిలో కరగని, జలబాష్పంతో బాష్పశీలత పొందే ద్రవాల్ని శుద్ధి చేస్తారు. ఈ విధానంలో వేడి మలిన ద్రవంలోకి నీటి ఆవిరిని పంపిస్తారు. ఈ నీటి ఆవిరి ద్రవబాష్పం రెండూ కండెన్సర్ ద్వారా ప్రయాణించి ద్రవ మిశ్రమమై సంగ్రహణ పాత్రలో చేరతాయి. అవి ఒకదానితో ఒకటి కలిసిపోవు. కాబట్టి వేర్పాటు గరాటుతో ‘నీటి నుంచి పదార్థాన్ని వేరుచేయవచ్చు.
ఉదా : ఈ పద్ధతిలో ఎనిలీన్ ను ఎనిలీన్-నీరు మిశ్రమం నుంచి వేరు చేయవచ్చు.

ప్రశ్న 46.
క్రోమటోగ్రఫీని విశదీకరించండి.
జవాబు:
ఒక మిశ్రమంలోని అనుఘటకాలను స్థిరప్రావస్థ, చలనశీల ప్రావస్థ అనే రెండు ప్రావస్థల మధ్య వేరు పరిచే విధానాన్ని క్రోమటోగ్రఫీ అంటారు.

క్రోమటోగ్రఫీలో క్రింది మూడు దశలు ఇమిడి ఉంటాయి.

స్థిర ప్రావస్థ మిశ్రమంలోని అనుఘటకాలను శోషించుకుని స్థిరంగా పట్టి ఉంచుతుంది. చలన శీల ప్రావస్థ ఆ అధిశోషించుకోబడిన అనుఘటకాలను వేరు పరచి స్థిర ప్రావస్థపై విభిన్న దూరాలకు తీసుకుపోతుంది.
పై విధంగా వేరు పరచబడిన అనుఘటకాలను చలనశీల ప్రావస్థను ఆపకుండా పంపి తిరిగి పొందడం. దీనిని నిక్షాళన అంటారు.
గుణాత్మక, పరిమాణాత్మక విశ్లేషణల ద్వారా నిక్షాళనం చేసి సాధించిన సమ్మేళనాలను తెలుసుకోవడం. అధిశోషణి, చలనశీల ప్రావస్థల భౌతిక స్థితులపై ఆధారపడి క్రోమటోగ్రఫీ పద్ధతులు అనేక రకాలుగా వర్గీకరింపబడ్డాయి.

TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 81
సాధారణ క్రోమటోగ్రఫీలో రెండు పద్ధతులు ఉన్నాయి. అవి

అధిశోషణ క్రోమటోగ్రఫీ
వితరణ క్రోమటోగ్రఫీ అధిశోషణ క్రోమటోగ్రఫీ మరల రెండు రకాలు. అవి
1. కాలమ్ క్రోమటోగ్రఫీ
2. పలుచనిపొర క్రోమటోగ్రఫీ.

ప్రశ్న 47.
కింది వాటిని వివరించండి :
(a) కాలమ్ క్రొమటోగ్రఫి
(b) పలచని పొర క్రొమటోగ్రఫి
(c) వితరణ క్రొమటోగ్రఫీ
జవాబు:
(a) కాలమ్ క్రొమటోగ్రఫి : దీనిలో స్టాప్ కాక్ అమరిక గల ఒక గాజు గొట్టంలో నింపి ఉన్న అధిశోషకం (స్థిరప్రావస్థ)పై భాగాన అనుఘటకాల మిశ్రమాన్ని ఉంచాలి. సరియైన నిక్షాలకాన్ని కాలమ్ పై నుండి కిందికి నెమ్మదిగా ప్రవహింపచేయాలి. అప్పుడు మిశ్రమంలోని అనుఘటకాలు విభిన్న అవధులలో అధిశోషణం చెంది వేరు అవుతాయి.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 82

(b) పలచని పొర క్రొమటోగ్రఫి : ఈ పద్ధతిలో అధిశోషకంగా వాడే సిలికాజెల్ను లేక అల్యూమినాను ఒక గాజు ప్లేటుపై పలుచని పొరగా పూత పూస్తారు. దీనిని TLC ప్లేట్ అంటారు. అనుఘటకాలను కలిగి ఉన్న మిశ్రమ ద్రావణాన్ని TLC ప్లేట్ కింది నుండి 2 లేక 3 సెం.మీ. దూరంలో ఒక చిన్న చుక్కగా ఉంచుతారు. ఈ ప్లేటును నిక్షాలకం కలిగి ఉన్న మూసిన పాత్రలో ‘ఉంచుతారు. నిక్షాలకం పైకి ప్రవహిస్తూ తనతో పాటు . మిశ్రమంలోని అనుఘటకాలను తీసికొని పోతుంది. కాని అనుఘటకాల అధిశోషణ అవధులపై ఆధారపడి అవి వివిధ దూరాలు ప్రయాణించి వేరువేరు చోట్ల అధిశోషితం అవుతాయి.

ఒక అనుఘటకం సాపేక్ష అధిశోషణం దాని మందన గుణకం R_f తో తెలుపుతారు.
అనుఘటకం ఆధారపీఠం గీత నుండి ప్రయాణించిన దూరం
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 83
ఈ పద్ధతి ద్వారా రంగులున్న అనుఘటకాలను తేలికగా గుర్తిస్తారు. రంగులేని వాటిని వాటి ప్రతిదీప్తి ధర్మం ఆధారంగా చేసుకొని UV కిరణాలను ఉపయోగించి గుర్తిస్తారు.

(c) వితరణ క్రోమటోగ్రఫీ : దీనిలో క్రొమటోగ్రఫీ పేపర్ను తీసికొని నీటిని దానిలో ఉంచుతారు. ఈ నీరు స్థిర ప్రావస్థగా పనిచేస్తుంది. ఈ పేపర్ ఆధారపీఠ గీతపై అనుఘటకాల మిశ్రమ ద్రావణాన్ని చుక్కగా పెట్టి దానిని సరియైన ద్రావణిలో వ్రేలాడదీస్తారు. ద్రావణి చలనశీల ప్రావస్థగా పనిచేస్తుంది. ద్రావణి, పేపర్ పైకి ప్రయాణించి మిశ్రమ బొట్టు మీదుగా పోతుంది. అప్పుడు పేపరు విభిన్న అనుఘటకాలను ప్రత్యేకంగా తనపై నిలుపుకొంటుంది. అనుఘటకాలు వాటి అభిలాక్షణిక ధర్మాలపై ఆధారపడి స్థిర ప్రావస్థ చలన శీల ప్రావస్థల మధ్య వేర్వేరుగా వితరణ చెందుతాయి. విడగొట్టబడిన రంగుల అనుఘటకాల . చుక్కలను పేపరుపై గుర్తించవచ్చు. రంగులేని అనుఘటకాలను ఇతర కారకాలను చల్లడం వంటి ప్రయత్నాల ద్వారా గుర్తించవచ్చు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 84

ప్రశ్న 48.
కర్బన సమ్మేళనంలో ఉన్న నైట్రోజన్ భార శాతాన్ని కింది విధానాలలో కనుక్కొనే పద్ధతిని రాయండి.
(a) డ్యూమాస్ పద్ధతి
(b) జెల్దాల్ పద్ధతి
జవాబు:
1. డ్యూమాస్ పద్ధతి : ఈ పద్ధతిలో తెలిసిన భారం ఉన్న కర్బన పదార్థానికి ముతక CuO కలిపి బాగా వేడి చేస్తారు. కార్బన్, హైడ్రోజన్లు CO₂, H₂O (ఆవిర్లు) గా ఆక్సీకరణం చెందుతాయి. నైట్రోజన్ N₂ వాయువుగా మారుతుంది. కొంత నైట్రోజన్ ఆక్సైడ్లుగా మారినా, ఆ ఆక్సైడ్లను వేడిగా ఉన్న కాపర్ జాలకం, N₂ వాయువుగా క్షయకరణం చెందిస్తుంది. ఉత్పన్న వాయువులను KOH ద్రావణం గుండా పంపుతారు. CO₂ వాయువు KOH ద్రావణంలో శోషణం చెందుతుంది. KOH ద్రావణంపై చేరుకున్న N₂ వాయువు ఘనపరిమాణాన్ని కొలుస్తారు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 85
గణన : గది ఉష్ణోగ్రత TK వద్ద గ్రా. ల సమ్మేళనం V మి.లీ. N₂ వాయువును ఇచ్చినదని అనుకొనుము.
ప్రయోగ పరిస్థితులు
P₁ = (P – p) మి. మీ
ఇచ్చట p = నీటి ఆవిరి పీడనం
T₁ = TK
V₁ = V మి.లీ.

STP పరిస్థితులు
P₂ = 760 మి. మీ
T₂ = 273 K
V₂ = ?

T₁ = TK
V₁ = V మి.లీ.
\(\frac{P_1 V_1}{T_1}\) = \(\frac{\mathrm{P}_2 \mathrm{~V}_2}{\mathrm{~T}_2}\)
∴ V₂ = \(\frac{P_1 V_1 T_2}{P_2 T_1}\) = \(\frac{(\mathrm{P}-\mathrm{p}) \times \mathrm{V} \times 273}{760 \times \mathrm{T}}\) = x మి.లీ.

22400 మి.లీ. N₂ వాయువు STP వద్ద 28 గ్రా. బరువు కలిగి ఉంటుంది
∴ x మి.లీ. N₂ …….. ?
= \(\frac{x \times 28}{22400}\) గ్రా. ల. N₂

2. జెల్దాల్ పద్ధతి : ఈ పద్ధతిలో తెలిసిన భారం గల కర్బన సమ్మేళనాన్ని CuSO₄ సమక్షంలో గాఢ H₂SO₄ తో వేడి చేస్తారు. అప్పుడు కర్బన సమ్మేళనంలోని నైట్రోజన్ అంతా పరిమాణాత్మకంగా అమ్మోనియం సల్ఫేటుగా మారుతుంది. ప్రయోగ పాత్రలోని అనుఘటకాలను వేరే పాత్రలోనికి మార్చి అధిక
NaOH ద్రావణంతో వేడి చేస్తారు. అమ్మోనియా వాయువు విడుదల అవుతుంది. ఈ అమ్మోనియా వాయువును తెలిసిన ఘ.ప. మరియు గాఢత గల అధిక గాఢ H₂SO₄ లోకి పంపి శోషణం చెందిస్తారు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 86
మిగిలిన ఆమ్లాన్ని ప్రమాణ క్షారంతో అంశమాపనం చేస్తారు. దీని నుండి అమ్మోనియాను తటస్థీకరించడానికి పట్టిన ఆమ్ల ప్రమాణాన్ని గణిస్తారు. దీని నుంచి ఎంత అమ్మోనియా ఏర్పడిందో గణించి దాని నుండి N₂ భారశాతాన్ని లెక్కిస్తారు.

చర్యలు : కర్బన సమ్మేళనం + H₂SO₄ → (NH₄)₂SO₄
(NH₄)₂SO₄ + 2NaOH → Na₂SO₄ + 2H₂O + 2NH₃
2NH₃ + H₂SO₄ + (NH₄)₂SO₄

గణన : కర్బన సమ్మేళనం భారం = a గ్రా. మొదటిగా తీసుకున్న H₂SO₄ ఘ.ప. = V మి.లీ.
H₂SO₄ మొలారిటి = M, పూర్తి తటస్థీకరణానికి పట్టిన ఘ.ప. = V₁ మి.లీ.
NaOH మొలారిటి = M
2NaOH + H₂SO₄ → Na₂SO₄ + 2H₂O
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 87
NH₃ చేత తటస్థీకరించబడిన H₂SO₄ ఘ.ప. = (v – \(\frac{\mathrm{V}_1}{2}\)] మి.లీ.
= 2(V – \(\frac{V_1}{2}\))మి.లీ. NH₃ ద్రావణం
1000 మి.లీ. 1M NH₃ ద్రావణంలో 17 గ్రా. NH₃ (లేదా) 14 గ్రా. N₂ ఉన్నది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 88

ప్రశ్న 49.
ప్రేరేపక ప్రభావాన్ని ఒక ఉదాహరణ ఇచ్చి వివరించండి.
జవాబు:
CH₃ – CH₂ – CH₂ – Cl అణువును తీసుకుంటే అందులో కార్బన్ – క్లోరిన్ పరమాణువుల మధ్య σ సమయోజనీయ బంధం ఉన్నది. అధిక ఋణ విద్యుదాత్మక Cl పరమాణువు ఎలక్ట్రాను తనవైపు ఎక్కువగా ఆకర్షిస్తుంది. దీనివల్ల ‘C’ పరమాణువు కంటె Cl పరమాణువు మీద ఋణ విద్యుదావేశ సాంద్రత ఎక్కువగా ఉంటుంది. ‘దీనిని (లేక)-C → Cl గా చూపిస్తారు. అయితే క్లోరిన్ బంధం ఏర్పరచిన కార్బన్ పరమాణువు తిరిగి వేరే కార్బన్తో ఏర్పరచి ఉండటం వల్ల ఈ ప్రభావం ఇతర కార్బన్ పరమాణువులకు కూడా ప్రసారం అవుతుంది.

క్లోరిన్ ఎలక్ట్రాన్ ఆకర్షణ ఫలితంగా C₁ కార్బన్కు కొంత ఎలక్ట్రాన్ న్యూనత ఏర్పడుతుంది. దీనిని సరిచేసికోవడానికి C, తిరిగి C,C, సమయోజనీయ బంధంలోని ఎలక్ట్రాన్ జంటను తనవైపు ఆకర్షిస్తుంది. ఇప్పుడు C₂ కార్బన్కు ఎలక్ట్రాన్ న్యూనత ఏర్పడుతుంది. అయితే ఈ ప్రభావం C₁ – Cl మధ్యకంటే C₁ – C₂ మధ్య తక్కువ. ఈ ప్రభావం చాలా వేగంగా పడిపోతూ C₃ తరువాత అతి తక్కువగా ఉండడం వల్ల గుర్తించదగ్గది కాదు. ఆ బంధాల ఎలక్ట్రాన్ పంపకంపై కనిపించే ఈ ప్రభావాన్ని ప్రేరేపక ప్రభావం అంటారు. ప్రేరేపక ప్రభావం, కార్బన్పై ఉన్న ప్రతిక్షేపకాల ఎలక్ట్రాన్ సాంద్రతను దానం చేసే లేదా ఆకర్షించే స్వభావంపై ఆధారపడి ఉంటుంది. ఈ స్వభావం ఆధారంగా ప్రతిక్షేపకాలను రెండు రకాలుగా వర్గీకరించారు. అవి

ఎలక్ట్రాన్ ఆకర్షక గ్రూపులు
ఎలక్ట్రాన్ దాన గ్రూపులు. ఎలక్ట్రాన్ దాన గ్రూపులు ధన ప్రేరక ప్రభావాన్ని, ఎలక్ట్రాన్ ఆకర్షక గ్రూపులు ఋణ ప్రేరక ప్రభావాన్ని చూపిస్తాయి.

ప్రేరక ప్రభావం రసాయన చర్యాశీలతల మీద మరియు భౌతిక ధర్మాల మీద ప్రభావాన్ని చూపిస్తుంది.

ప్రశ్న 50.
మీసోమరిక్ ప్రభావాన్ని వివరించండి.
జవాబు:
ఒక శృంఖలంలో సంయుగ్మ విధానంలో ఒక పరమాణువు లేదా గ్రూపు ఎలక్ట్రాన్ జంటలను స్థానభ్రంశం చేసే విధానాన్ని మీసోమరిక్ ప్రభావం అంటారు.

మీసోమరిక్ ప్రభావం ప్రధాన లక్షణాలు :

ఇది స్థిరమైన ప్రభావం. అణువు భూస్థితిలో ఉన్నప్పుడు జరుగుతుంది.
ఒంటరి జతలు, π ఎలక్ట్రాన్లతో సంయుగ్మ విధానంలో ఎలక్ట్రాన్ స్థానభ్రంశం జరుగుతుంది.
ఇది భౌతిక ధర్మాన్ని, చర్యావేగాన్ని ప్రభావితం చేస్తుంది.

ఏ గ్రూపులైతే మిగిలిన అణుభాగంలో ఎలక్ట్రాన్ సాంద్రతను పెంచుతాయో వాటికి +M ప్రభావం ఉన్నదని అంటారు. ఆ గ్రూపులలో ఒంటరి ఎలక్ట్రాన్ జంట ఉంటుంది.

TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 91

ప్రశ్న 51.
రెజోనెన్స్ ప్రభావాన్ని ఒక ఉదాహరణతో వివరించండి.
జవాబు:
ఒక అణువు ధర్మాలన్నింటిని కేవలం ఒక నిర్మాణంతో వివరించలేము. అటువంటి సందర్భంలో అణువుకు అనేక నిర్మాణాలు ఇవ్వవలసి వస్తుంది. ప్రతి ఒక్క నిర్మాణం అణువు యొక్క కొన్ని ధర్మాలను వివరిస్తుంది. అన్ని నిర్మాణాలు కలిసి అణువు యొక్క అన్ని ధర్మాలను వివరిస్తాయి. దీనినే రెజోనెన్స్ అంటారు. ఆ విధంగా అణువుకు ఊహించిన అన్ని నిర్మాణాలను రెజోనెన్స్ నిర్మాణాలు లేక కెనోనికల్ అంటారు.

రెజోనెన్స్ నిర్మాణాలకు ఉండవలసిన ముఖ్య లక్షణాలు :

అవి దాని నుంచి ఇంకొకటిగా మార్చేందుకు వీలుగా ఉంటాయి.
దీనిలో ఎలక్ట్రాన్ స్థానభ్రంశాలు తప్ప కేంద్రకాల స్థానాలలో ఎలాంటి మార్పులూ ఉండవు.
అణువులోని పరమాణువులన్నీ ఒకే తలంలో ఉంటాయి.
అన్ని నిర్మాణాలలోనూ, జత కూడిన లేక జతకూడని ఎలక్ట్రాన్ల సంఖ్య ఒకే విధంగా ఉండాలి.
కెనోనికల్ నిర్మాణాలన్నింటికి సాధ్యమైనంత వరకూ దాదాపు సమానశక్తి ఉండాలి.
రెజోనెన్స్ నిర్మాణం ఎంత ఎక్కువ స్థిరమైనదైతే అది అసలు నిర్మాణంలో అంత ఎక్కువగా పాల్గొంటుంది.
ఎలక్ట్రాన్లు ఎంత ఎక్కువ అస్థానీకృతం చెందితే స్థిరత్వం అంత ఎక్కువగా ఉంటుంది.
సమయోజనీయ బంధాలు ఎంత ఎక్కువగా ఉంటే ఆ నిర్మాణం అంతస్థిరమైనది.

రెజోనెన్స్ తం : పక్క పక్క పరమాణువుల మధ్య రెండు గా బంధాల లేదా ఒక 7 బంధం ఒక ఒంటరి జంటల మధ్య జరిగే అంతర చర్యల వల్ల ఉత్పన్నమయిన ధ్రువణాన్ని రెజోనెన్స్ ఫలితం అంటారు. ఈ ఫలితం శృంఖలం ద్వారా ప్రసారం అవుతుంది.

ఎలక్ట్రాన్ల బదలాయింపు ప్రతిక్షేపక పరమాణువు లేదా గ్రూపు నుండి అణువుపైకి సంయుగ్మ వ్యవస్థ ద్వారా జరిగితే దానిని (+R) తో సూచిస్తారు. అదే ఎలక్ట్రాన్ బదలాయింపు ప్రతిక్షేపక పరమాణువు లేక గ్రూపు వైపుకు అయితే దానిని (−R) తో సూచిస్తారు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 92
రెజోనెన్స్ శక్తి : అసలైన నిర్మాణం (రెజోనెన్స్ సంకర రూపం) శక్తికి, అత్యంత స్థిరమైన రెజోనెన్స్ నిర్మాణం శక్తికి మధ్య గల భేదాన్ని రెజోనెన్స్ శక్తి అంటారు.

ప్రశ్న 52.
కర్బన రసాయన చర్యలు ఎన్ని రకాలో వివరించండి.
జవాబు:
కర్బన రసాయన చర్యలు నాలుగు రకాలు. అవి
(1) సంకలన చర్యలు
(2) ప్రతిక్షేపణ చర్యలు
(3) విలోపన చర్యలు
(4) అణు పునరమరికలు.

1. సంకలన చర్యలు :*ఈ చర్యలలో క్రియాధారం, కారకం రెండూ కలసి ఉత్పన్నాన్ని ఇస్తాయి.
ఉదా :
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 93

2. ప్రతిక్షేపణ చర్యలు : ఈ చర్యలలో ఒక పరమాణువు లేదా గ్రూపు క్రియాధారంలోని వేరే పరమాణువు లేదా గ్రూపును స్థానభ్రంశం చేసి క్రియాధారంతో బంధం ఏర్పరుస్తుంది.
ఉదా :

3. విలోపన చర్యలు : ఇచ్చట రెండు లేక అంతకంటె ఎక్కువ పరమాణువులు లేదా గ్రూపులు క్రియాధారం నుండి విలోపనం చెందుతాయి. దీనివల్ల ద్విబంధం (లేక) త్రిబంధం ఉత్పన్నంలో ఏర్పడతాయి.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 95

4. అణువుల పునరమరికలు : దీనిలో తక్కువ స్థిరత్వం గల ఒక కర్బన పదార్థం స్థిరత్వం గల వేరొక కర్బన పదార్థంగా పునరమరిక చెందుతాయి. దీనిలో ఒకస్థానం నుండి వేరొక స్థానానికి ఒక పరమాణువు లేదా సమూహం బదిలీ అయి వెళ్ళిపోతుంది.
ఉదా :
1)
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 96

ఉదా :
2)
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 97

ప్రశ్న 53.
ఈథేన్ అనురూపకాలను రాసి వాటిలో దేనికి స్థిరత్వం ఎక్కువో తెలపండి.
జవాబు:
ఈథేన్ – అనురూపాత్మక సాదృశ్యములు : ఈథేన్ అణువులో ఒక కార్బన్ పరమాణువు స్థానమును స్థిరీకరించి రెండవ కార్బన్ పరమాణువును C – C బంధ అక్షముపై చక్ర భ్రమణము చేయుట వలన అనేక ప్రాదేశిక అమరికలు గల రూపములు లభించును. ఈ రూపములను అనురూపాత్మక సాదృశ్యములందురు. ఈథేన్ ప్రధాన అనురూపాత్మక సాదృశ్యములు.

1) గ్రహణ ఆకృతి
2) అస్తవ్యస్త ఆకృతి

అస్తవ్యస్త ఆకృతి (staggered form), గ్రహణ ఆకృతి (eclipsed form) కన్నా స్థిరమైనది. కారణం
గ్రహణ ఆకృతిలో రెండు కర్బన పరమాణువులపై గల హైడ్రోజన్ పరమాణువులు అతి సున్నితంగా ఉండుట వలన వీటి మధ్య వికర్షణ బలములు అధికము. కావున ఈ రూపమునకు స్థిరత్వము తక్కువ.
అస్తవ్యస్త ఆకృతిలో రెండు కర్బన పరమాణువులపై గల హైడ్రోజన్ పరమాణువులు వీలయినంత దూరంగా ఉండుటవలన, ఈ రూపములో వికర్షణ బలములు అతి స్వల్పము. కనుక శక్తి తక్కువ కావున దీనికి స్థిరత్వము అధికము.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 98

ప్రశ్న 54.
బెంజీన్ యొక్క ఏరోమాటిక్ ఎలక్ట్రోఫిల్లిక్ ప్రతిక్షేపణ చర్యలను వివరించండి.
జవాబు:
బెంజీన్ యొక్క ఏరోమాటిక్ ఎలక్ట్రోఫిల్లిక్ ప్రతిక్షేపణ చర్యా విధానము : బెంజీన్ యొక్క ఏరోమాటిక్ ఎలక్ట్రోఫిలిక్ ప్రతిక్షేపణ చర్య రెండు దశలలో జరుగుతుంది.
1. మొదటి దశలో ఎలక్ట్రోఫైల్ ఒక బెంజీన్ అణువులోని కార్బన్పై చర్య జరిపి కార్బోకాటయానన్ను ఏర్పరుస్తుంది. ఇది రెజోనెన్స్ ద్వారా స్థిరత్వం పొందుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 99
రెండవదశలో ఎరీనియం అయాన్ ఒక ప్రోటాన్ను కోల్పోతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 100

ప్రశ్న 55.
ఇథిలీన్ సంకలన చర్యలను (ఎలక్ట్రోఫిల్లిక్) చర్యాగతిని వివరించండి.
జవాబు:
ఇథిలీన్ ఎలక్ట్రోఫిల్లిక్ సంకలన చర్యా విధానము: ఇథిలీన్ C – C మధ్య ఉన్న ద్విబంధంలోని π – ఎలక్ట్రోఫైల్కు అందుబాటులో ఉంటాయి. ద్విబంధంపై ఎలక్ట్రోఫైల్ సంకలన చర్యలో రెండు క్రొత్త 6- ఏర్పడతాయి.
మొదటిదశ : ఇథిలీన్పై ఎలక్ట్రోఫైల్ చర్యలో కార్బోనియం అయాన్ ఏర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 101
పై దశలో ఏర్పడిన కార్బోనియం అయాన్పై న్యూక్లియోఫైల్ (Nu) చర్యలలో అంతిమ ఉత్పన్నమేర్పడుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 102
ఉదా : ఇథిలీన్, HBr తో సంకలనం చెంది ఇథైల్ బ్రోమైడ్నస్తుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 103

ప్రశ్న 56.
చర్యా సంవిధానం (Mechanism of the reaction) ద్వారా ఆల్కేన్ స్వేచ్ఛా ప్రాతిపదిక హాలోజినేషన్ చర్యను వివరించండి.
జవాబు:
ఆల్కేన్ స్వేచ్ఛా \(\mathbf{A}^{\ominus}\) ప్రాతిపదిక హాలోజినేషన్ లేదా హాలోజనీకరణం : స్వేచ్ఛాప్రాతిపదికా విధానంలో క్లోరినీకరణ మూడు దశల్లో జరుగుతుంది.

1. శృంఖల చర్య ప్రారంభ చర్య : ఇక్కడ క్లోరిన్ అణువు శక్తిని గ్రహించి క్లోరిన్ స్వేచ్ఛా ప్రాతిపదికలుగా విడిపోతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 104

2. శృంఖల చర్య వ్యాప్తి : పైన ఏర్పడిన క్లోరిన్ స్వేచ్ఛా ప్రాతిపదికలు ఈథేన్ అణువుతో చర్య జరుపుతాయి.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 105
ఈ చర్యలు అనేక మార్లు పునరావృతమై చర్యను శృంఖల చర్యగా మారుస్తాయి. ఈ చర్యలను చర్యావ్యాప్తి చర్యలు అంటారు.

3. శృంఖల చర్యల ముగింపు : స్వేచ్ఛా ప్రాతిపదికలు నేరుగా కలిసిపోయి శృంఖల చర్యలు అంతమవుతాయి.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 106

ప్రశ్న 57.
మార్కొనికాఫ్ నియమం, ఖరాష్ ప్రభావాల్ని వివరించండి.
జవాబు:
ప్రోపీన్తో HBr సంకలనం చెంది మార్కొనికాఫ్ నియమము ప్రకారం 2–బ్రోమో ప్రోపేన న్ను ఇస్తుంది. కాని బెంజాయిల్ పెరాక్సైడ్ సమక్షంలో ప్రోపీన్ క్కు HBrను కలిపితే 1-బ్రోమో ప్రోపేన్ ఏర్పడుతుంది. ఇక్కడ యాంటి మార్కొనికాఫ్ నియమము ప్రకారము సంకలనం జరుగుతుంది.

మార్కొనికాఫ్ నియమము : ఒక అసమకారకం ద్విబంధంలో సంకలనం చెందేటపుడు అసమకారకం రుణావేశ భాగం ద్విబంధంలో తక్కువ హైడ్రోజన్లున్న కార్బన్పై సంకలనం చెందుతుంది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 107
చర్యావిధానము (ఎలక్ట్రోఫిల్లిక్ సంకలన చర్య) :
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 108
యాంటి మార్కొనికాఫ్ నియమము : ఒక అసమకారకం ద్విబంధంతో పెరాక్సైడ్ సమక్షంలో సంకలనం చెందేటపుడు అసమకారకం రుణావేశ భాగం ద్విబంధంలో ఎక్కువ హైడ్రోజన్లున్న కార్బన్పై సంకలనం చెందుతుంది. దీనినే ఖరాష్ ప్రభావం అని కూడా అంటారు. బెంజోయల్
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 109
చర్యావిధానం (స్వేచ్ఛా ప్రాతిపదిక సంకలన చర్య) :
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 110

ప్రశ్న 58.
కింది సమ్మేళనాలను బెంజీన్ నుంచి ఎలా మార్చవచ్చు?
(a) క్లోరోబెంజీన్
(b) టోలీస్
(c) p–నైట్రోటోలీన్
జవాబు:
(a) క్లోరోబెంజీన్ : బెంజీన్ క్లోరిన్తో FeCl₃ సమక్షంలో చర్య జరిపి క్లోరోబెంజీన్ ను ఏర్పరచవచ్చు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 111

(b) టోలీస్ : బెంజీన్ ను CH₃Cl తో Al Cl₃ సమక్షంలో చర్య జరిపి టోలీన్ ను ఏర్పంచవచ్చు. (ఫీడల్ క్రాఫ్ట్ చర్య)
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 112

ప్రశ్న 59.
బేసి సంఖ్యలో కార్బన్లున్న ఆల్కేన్లను ఉర్ల చర్య ద్వారా ఎందుకు తయారుచేయలేరు? ఏదైనా ఉదాహరణతో వివరించండి.
జవాబు:
ఉర్వ్ చర్య : ఆల్కైల్ హాలైడ్ సోడియం లోహంతో పొడి ఈథర్ సమక్షంలో చర్య జరిపి ఆల్కేన్లను ఏర్పరచే చర్యను ఉర్ట్ చర్య అంటారు. R – X + 2Na + R – X→ R – R + 2NaX

ఉర్ట్ చర్యను బేసి సంఖ్యలో కార్బన్లు ఉన్న ఆల్కేన్లను తయారుచేయుటకు ఎక్కువగా ఉపయోగించరు. బేసి సంఖ్యలో కార్బన్లు ఉన్న ఆల్కేనులను తయారుచేయుటకు రెండు విభిన్నమైన ఆల్కైన్హాలైడ్లను తీసుకోవలెను. ఈ విధంగా తీసుకొనుట వలన ఏర్పడే ఉత్పన్నం మిశ్రమ రూపంలో ఉంటుంది. అంతేకాకుండా ఉత్పన్నం తక్కువ మొత్తంలో ఏర్పడుతుంది.

ప్రశ్న 60.
కర్బన సమ్మేళనాలలో నైట్రోజన్, సల్ఫర్, హాలోజన్లను గుణాత్మకంగా విశ్లేషించే సమీకరణాలను రాయండి.
జవాబు:
నైట్రోజన్ న్ను గుర్తించుట : కొద్దిగా లెసైన్ ద్రావణాన్ని పరీక్ష నాళికలో తీసికొని దానికి కొద్ది చుక్కలు NaOH ద్రావణం కలిపి క్షారీకృతం చేసి దానికి అపుడే తయారు చేసిన ఫెర్రస్ సల్ఫేట్ ద్రావణాన్ని కలుపుతారు. దీనికి 2 లేక 3 చుక్కలు FeCl, ద్రావణం కలిపి చల్లబరిచి గాఢ HCl ద్రావణంతో ఆమ్లీకృతం చేస్తారు. ప్రశ్యన బ్లూ లేదా ఆకుపచ్చని రంగు లేదా అవక్షేపం వస్తే నైట్రోజన్ ఉన్నట్లుగా గుర్తించాలి.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 113
సల్ఫర్ను గుర్తించుట : కొద్దిగా లెసైన్ ద్రావణాన్ని పరీక్ష నాళికలో తీసికుని దానికి తాజాగా తయారు చేసిన సోడియం నైట్రోపృసైడ్ ద్రావణం కలపాలి. ముదురు ఊదా రంగు వస్తుంది. సల్ఫర్ ఉన్నట్లుగా గుర్తించాలి.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 114

హాలోజన్లను గుర్తించుట : కొద్దిగా లెసైన్ ద్రావణాన్ని పరీక్ష నాళికలో తీసికొని నత్రికామ్లంతో ఆమ్లీకృతం చేసి AgNO, “ద్రావణాన్ని కలపాలి.
Ag⁺ + X^– → AgX

తెల్లని అవక్షేపం ఏర్పడి అది NH₄ OH ద్రావణంలో కరిగితే ఆ హాలైడ్ Cl^– లేత పసుపుపచ్చ అవక్షేపం ఏర్పడి అది NH₄ OH లో పాక్షికంగా కరిగితే ఆ హాలైడ్ Br పసుపు పచ్చ అవక్షేపం ఏర్పడి అది NH₄ OH లో కరగకపోతే ఆ హాలైడ్ I^–.

ప్రశ్న 61.
కర్బన సమ్మేళనంలో కార్బన్, హైడ్రోజన్ల భారశాతాన్ని కనుక్కోవడానికి అనువైన సమీకరణాలను రాయండి.
జవాబు:
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 115
తెలిసిన భారం గల కర్బన పదార్థానికి CuO ను కలిపి ఆ మిశ్రమాన్ని దహన నాళికలో తీసికొని అధికమైన గాలి సమక్షంలో పూర్తిగా దహనం చెందిస్తారు. అపుడు కర్బన పదార్థంలోని కార్బన్ CO₂ గానూ, హైడ్రోజన్ H₂O గానూ మారతాయి. ఆ విధంగా లభించిన CO₂, H₂O లను ముందుగా తూచిన నిర్జల CaCl₂, కాస్టిక్ పొటాష్లతో ఉన్న విడివిడి U – గొట్టాలలోకి పంపుతారు. CaCl₂ గొట్టంలో పెరిగిన బరువు వెలువడిన నీటి ఆవిరి బరువుగానూ, కాస్టిక్ పొటాష్ గొట్టంలో పెరిగిన బరువు వెలువడిన CO₂ భారంగానూ గుర్తించాలి.
గణన :’ ‘a’ గ్రా.ల కర్బన సమ్మేళనాన్ని దహనం చెందిస్తే ‘b’ గ్రా. ల నీటి ఆవిరి, ‘c’ గ్రా.ల CO₂ వచ్చాయి అనుకోండి.

కార్బన్ భారశాతం :
44 గ్రా. CO₂ లో 12 గ్రా. ‘C’ ఉన్నది.
∴ c గ్రా.ల C₂O …………?
= \(\frac{12 \times C}{44}\) గ్రా. కార్బన్
‘a’ గ్రా.ల కర్బన సమ్మేళనంలో \(\frac{12 \times c}{44}\)-గ్రా. కార్బన్ ఉన్నది.
∴ 100 గ్రా.ల కర్బన సమ్మేళనంలో ………… ?
∴ కార్బన్ భారశాతం = \(\frac{100 \times 12 \times \mathrm{c}}{44 \times \mathrm{a}}\) గ్రా.ల కార్బన్

హైడ్రోజన్ భారశాతం :
18 గ్రా. H₂O లో 12 గ్రా. ‘H’ ఉన్నది.
∴ b గ్రా.ల H₂O ……..
= \(\frac{2 \times b}{18}\) గ్రా. ‘H’
‘a’ గ్రా.ల కర్బన సమ్మేళనంలో \(\frac{2 \times b}{18}\) గ్రా. ‘H’ ఉన్నది.
∴ 100 గ్రా.ల కర్బన సమ్మేళనంలో…… 2
∴ ‘H’ భారశాతం = \(\frac{100 \times 2 \times b}{18 \times a}\) గ్రా.ల ‘H’

ప్రశ్న 62.
నైట్రోజన్ భారశాతాన్ని డ్యూమాస్, జెల్దాల్ పద్ధతిలో కనుక్కొనే విధానాన్ని వివరించండి.
జవాబు:
1. డ్యూమాస్ పద్ధతి : ఈ పద్ధతిలో తెలిసిన భారం ఉన్న కర్బన పదార్థానికి ముతక CuO కలిపి బాగా వేడి చేస్తారు. కార్బన్ హైడ్రోజన్లు CO₂, H₂O (ఆవిర్లు) గా ఆక్సీకరణం చెందుతాయి. నైట్రోజన్ N₂ వాయువుగా మారుతుంది. కొంత నైట్రోజన్ ఆక్సైడ్లుగా మారినా, ఆ ఆక్సైడ్లను వేడిగా ఉన్న కాపర్ జాలకం, N₂ వాయువుగా క్షయకరణం చెందిస్తుంది. ఉత్పన్న వాయువులను KOH ద్రావణం గుండా పంపుతారు. CO₂ వాయువు KOH ద్రావణంలో శోషణం చెందుతుంది. KOH ద్రావణంపై చేరుకున్న N₂ వాయువు ఘనపరిమాణాన్ని కొలుస్తారు.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 116
గణన : గది ఉష్ణోగ్రత TK వద్ద a గ్రా.ల సమ్మేళనం V మి.లీ. N₂ వాయువును ఇచ్చినదని అనుకొనుము.

ప్రయోగ పరిస్థితులు
P₁ = (P-p) మి . మీ
ఇచ్చట p = నీటి ఆవిరి పీడనం
T₁ = TK
V₁ = V మి.లీ.

STP పరిస్థితులు
P₂ = 760 మి.మీ.
T₂ = 273 K
V₂ = ?

T₁ = TK
V₁ = V మి.లీ.
\(\frac{P_1 V_1}{T_1}\) = \(\frac{\mathrm{P}_2 \mathrm{~V}_2}{\mathrm{~T}_2}\)
∴ V₂ = \(\frac{P_1 V_1 T_2}{P_2 T_1}\) = \(\frac{(P-p) \times V \times 273}{760 \times T}\) = xమి.లీ.
22,400 మి.లీ. N₂ వాయువు STP వద్ద 28 గ్రా. బరువు కలిగి ఉంటుంది.
∴ x మి.లీ. N₂ ……… ?
= \(\frac{x \times 28}{22400}\) గ్రా.లు.
‘a’ గ్రా.ల పదార్థం ………. \(\frac{28 \times x}{22400}\) గ్రా. N₂ కలిగి ఉన్నది.
∴ 100 గ్రా.ల పదార్థం …… ?
= \(\frac{100}{\mathrm{a}} \times \frac{28 \times \mathrm{x}}{22400}\) గ్రా.ల. N₂

2. జెల్దాల్ పద్ధతి : ఈ పద్ధతిలో తెలిసిన భారం గల కర్బన సమ్మేళనాన్ని CuSO₄ సమక్షంలో గాఢ H₂SO₄ తో వేడి చేస్తారు. అప్పుడు కర్బన సమ్మేళనంలోని నైట్రోజన్ అంతా పరిమాణాత్మకంగా అమ్మోనియం సల్ఫేటుగా మారుతుంది. ప్రయోగ పాత్రలోని అనుఘటకాలను వేరే పాత్రలోనికి మార్చి అధిక NaOH ద్రావణంతో వేడి చేస్తారు. అమ్మోనియా . వాయువు విడుదల అవుతుంది. ఈ అమ్మోనియా వాయువును తెలిసిన ఘ.ప. మరియు గాఢత గల అధిక గాఢ H₂SO₄ లోకి పంపి శోషణం చెందిస్తారు. మిగిలిన ఆమ్లాన్ని ప్రమాణ క్షారంతో అంశమాపనం చేస్తారు.
దీని నుండి అమ్మోనియాను తటస్థీకరించడానికి పట్టిన ఆమ్ల ప్రమాణాన్ని గణిస్తారు. దీని నుంచి ఎంత అమ్మోనియా ఏర్పడిందో గణించి దాని నుండి N₂ భారశాతాన్ని లెక్కిస్తారు.

చర్యలు : కర్బన సమ్మేళనం + H₂SO₄ → (NH₄)₂SO₄
(NH₄)₂SO₄ + 2NaOH → Na₂SO₄ + 2H₂O + 2NH₃
2NH₃ + H₂SO₄ → (NH₄)₂SO₄

గణన : కర్బన సమ్మేళనం భారం = a గ్రా. మొదటిగా తీసుకున్న H₂SO₄ ఘ.ప. = V మి.లీ.
H₂SO₄ మొలారిటి = M, పూర్తి తటస్థీకరణానికి పట్టిన ఘ.ప. = V₁ మి.లీ.
NaOH మొలారిటి = M
2NaOH + H₂SO₄ → Na₂SO₄ + 2H₂O
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 117
1000 మి.లీ. 1M NH₃ ద్రావణంలో 17 గ్రా. NH₃ (లేదా) 14 గ్రా. N₂ ఉన్నది.
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 118

ప్రశ్న 63.
కర్బన సమ్మేళనంలోని సల్ఫర్, ఫాస్ఫరస్, ఆక్సిజన్ల పరిమాణాత్మక విశ్లేషణను వివరించండి.
జవాబు:
కర్బన సమ్మేళనంలోని ఫాస్ఫరస్ భారశాతం కనుక్కొనుట : ఫాస్ఫరస్ భారశాతాన్ని కనుక్కోవడానికి తెలిసిన ద్రవ్యరాశి గల కర్బన పదార్థాన్ని సధూమ నైట్రికామ్లంలో వేడి చేయాలి. ఫాస్ఫరస్ ఫాస్ఫారిక్ ఆమ్లంగా ఆక్సీకరణం చెందుతుంది. ఈ ఆమ్లానికి అమ్మోనియా, అమ్మోనియం మోలిబేట్ ద్రావణాలు కలిపి అమ్మోనియం ఫాస్ఫో మోలిబేట్

[(NH₄)₃ PO₄.12M0O₃]గా అవక్షేపించాలి.
కర్బన సమ్మేళనం ద్రవ్యరాశి = mg
అమ్మోనియం ఫాస్ఫోమోలిబ్బేడ్ = m₁g
(NH₄)₃ PO₄ . 12 MoO₃ అణు ద్రవ్యరాశి = 1877g
ఫాస్ఫరస్ భారశాతం = \(\frac{31 \times \mathrm{m}_1 \times 100}{1877 \times \mathrm{m}}\)

కర్బన సమ్మేళనంలోని సల్ఫర్ భారశాతం కనుక్కొనుట కర్బన సమ్మేళనంలోని సల్ఫర్ భారశాతం కనుక్కోవడానికి తెలిసిన భారం గల కర్బన సమ్మేళనాన్ని సోడియం పెరాక్సైడ్ లేదా సధూమ నైట్రికామ్లంతో కేరియస్ నాళికలో వేడిచేస్తారు. సమ్మేళనంలోని సల్ఫర్ H₂SO₄ గా ఆక్సీకరణం చెందుతుంది. ఈ ఆమ్లాన్ని అధికంగా జల బేరియం క్లోరైడ్ ద్రావణం కలిపి బేరియం సల్ఫేట్గా అవక్షేపింప చేస్తారు. ఈ అవక్షేపాన్ని వడపోత ద్వారా వేరుచేసి, కడిగి, పొడి చేసి ‘భారాన్ని కనుక్కొంటారు.

తీసుకున్న కర్బన పదార్థ భారం = mg
ఏర్పడిన బేరియం సల్ఫేట్ భారం = m₁g
m₁, g ల బేరియం సల్ఫేట్లోని సల్ఫర్ = \(\frac{32 \times \mathrm{m}_1}{233}\)g
(1 మోల్ BaSO₄ = 233gm BaSO₄ = 32 gm సల్ఫర్)
సల్ఫర్ భారశాతం = \(\frac{32 \times m_1 \times 100}{233 \times m}\)

ఆక్సిజన్ పరిమాణాత్మక విశ్లేషణ : తెలిసిన ద్రవ్యరాశి గల కర్బన సమ్మేళనాన్ని నైట్రోజన్ వాయువు సమక్షంలో వేడిచేస్తారు. వెలువడిన ఉత్పన్న ఆక్సైడ్ వాయువుల మిశ్రమాన్ని ఎర్రటి వేడి బొగ్గు పైకి పంపి మొత్తం ఆక్సైడ్లలో ఉన్న ఆక్సిజన్ను CO గా మారుస్తారు. ఆ తరువాత మిశ్రమ వాయువులను వేడిగా ఉన్న I₂O₅ మీదుగా పంపుతారు. అపుడు CO తిరిగి CO₂ గా మారుతుంది. అయొడిన్ వెలువడుతుంది.
కర్బన సమ్మేళన భారం = a g
CO₂ భారం = b g
44 g CO₂ లో 32 g O₂ ఉన్నది.
∴ b g CO₂ …. ?
a g పదార్ధంలో \(\frac{\mathrm{b} \times 32}{44}\) g O₂ ఉంటే
100 g పదార్థంలో O₂ భారం శాతం = \(\frac{100 \times \mathrm{b} \times 32}{44 \times \mathrm{a}}\)g O₂.

ప్రశ్న 64.
కేరియస్ పద్ధతిలో జరిపే కర్బన సమ్మేళనంలోని హాలోజన్ ను పరిమాణాత్మక విశ్లేషణ వివరించండి.
జవాబు:
కేరియస్ పద్ధతిలో హాలోజన్ల పరిమాణాత్మక విశ్లేషణ : ఈ పద్ధతిలో తెలిసిన భారం గల కర్బన సమ్మేళనాన్ని సధూమ HNO₃ తో AgNO₃ సమక్షంలో ఒక ప్రత్యేకమైన బలమైన గాజు నాళికలో వేడి చేస్తారు. అప్పుడు సమ్మేళనంలోని C, H లు CO₂, H₂O లుగా ఆక్సీకరణం చెందుతాయి. హాలోజన్లు సిల్వర్ హాలైడ్లుగా మారతాయి. సిల్వర్ హాలైడ్లను వడపోత ద్వారా వేరుచేసి, కడిగి, పొడిగా చేసి భారం కనుక్కొంటారు.
గణన : కర్బన సమ్మేళన భారం = a g
సిల్వర్ హాలైడ్ భారం = b g
1 మోల్ AgX లో 1 మోల్ X ఉన్నది.
∴ b g e AgX లో హాలోజన్ ….. ?
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 119

ప్రశ్న 65.
కార్సినోజెనిసిటీ అంటే ఏమిటి? రెండు ఉదాహరణలతో వివరించండి.
జవాబు:
బెంజీన్, ఇంకా అనేక బహుకేంద్రక వలయాల హైడ్రోకార్బన్లు విషపదార్థాలే కాక క్యాన్సర్ కారకాలు. వాటిలో ఎక్కువ పదార్థాలు పొగాకు, పెట్రోలియం, బొగ్గు వంటి కర్బన పదార్థాలు పూర్తిగా దహనం చెందకుంటే ఏర్పడతాయి. ఇవి మానవ శరీరాల్లో అనేక రసాయన చర్యలకు లోనై DNA ను నాశనం చేసి క్యాన్సర్ను కలుగజేస్తాయి. దీనినే కార్సినోజెనిసిటీ అంటారు.
ఉదా :
TS Inter 1st Year Chemistry Study Material Chapter 13 కర్బన రసాయన శాస్త్రం – సామాన్య సూత్రాలు, విధానాలు 120

TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e)

January 23, 2024January 21, 2024 by Mahesh

Students must practice these TS Intermediate Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Trigonometric Ratios upto Transformations Solutions Exercise 6(e)

I.
Question 1.
prove that sin 50° – sin 70° + sin 10° = 0
Answer:
sin 50° – sin 70° + sin 10°
= 2 cos \(\left(\frac{50^{\circ}+70^{\circ}}{2}\right)\) sin \(\left(\frac{50^{\circ}-70^{\circ}}{2}\right)\) + sin 10°
= 2 cos 60° sin (- 10°) + sin 10°
= 2\(\left(\frac{1}{2}\right)\) (- sin 10°) + sin 10°
= – sin 10° + sin 10° = 0

Question 2.
Prove that \(\frac{\sin 70^{\circ}-\cos 40^{\circ}}{\cos 50^{\circ}-\sin 20^{\circ}}\) = \(\frac{1}{\sqrt{3}}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 1

Question 3.
Prove that cos55° + cos 65° + cos 175° = 0
Answer:
cos 55° + cos 65° + cos 175°
= 2 cos \(\left(\frac{55+65}{2}\right)\) cos \(\left(\frac{55-65}{2}\right)\)
= 2 cos 60° cos (- 5°) – cos 5°
= 2 \(\left(\frac{1}{2}\right)\) cos 5° cos 5° = cos 5° – cos 5° = 0

Question 4.
Prove that
4 (cos 66° + sin 84°) = √3 + √15
Answer:
4 (cos 66° + sin 84°)
= 4 [cos 66° + sin (90 – 6°)]
= 4 [cos 66° + cos 6°]
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 2

Question 5.
Prove that cos 20° cos 40° – sin 5° sin 25° = \(\frac{\sqrt{3}+1}{4}\)
Answer:
cos 20° cos 40° – sin 5° sin 25°
= \(\frac{1}{2}\) [2 c0s 20° c0s 40° – 2 sin 5° sin 25°]
= \(\frac{1}{2}\) [(cos 60 + cos 20) – (cos 20 – cos 30°)]
= \(\frac{1}{2}\) [cos 60° + cos 30°] = \(\frac{1}{2}\left[\frac{1}{2}+\frac{\sqrt{3}}{2}\right]\) = \(\frac{\sqrt{3}+1}{4}\)

Question 6.
Prove that cos 48° cos 12° = \(\frac{3+\sqrt{5}}{8}\)
Answer:
cos 48° cos 12°
= \(\frac{1}{2}\) [2 cos 48° cos 12°]
= \(\frac{1}{2}\) [cos 60° + cos 36°]
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 3

Short Answer Questions

II.
Question 1.
Prove that
cos θ + cos \(\left(\frac{2 \pi}{3}+\theta\right)\) + cos \(\left(\frac{4 \pi}{3}+\theta\right)\) = 0
Answer:
cos θ + cos (120 + θ) + cos (240 + θ)
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 4

Question 2.
Prove that sin² \(\left(\alpha-\frac{\pi}{4}\right)\) + sin² – sin² \(\left(\alpha+\frac{\pi}{12}\right)\) \(\left(\alpha-\frac{\pi}{12}\right)\) = \(\frac{1}{2}\)
Answer:
sin² (α – 45°) + sin² (α + 15°) – sin² (α – 15°)
= sin² (α – 45°) + sin (α + 15 + α – 15) sin (α + 15 – α + 15)
= sin² (α – 45°) + sin 2α sin 30°
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 5

Question 3.
If sin x + sin y = \(\frac{1}{4}\) and cos x + cos y = \(\frac{1}{3}\) then show that
(i) tan \(\left(\frac{x+y}{2}\right)\) = \(\frac{3}{4}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 6

(ii) cot (x + y) = \(\frac{7}{24}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 7

Question 4.
If neither [A – \(\frac{\pi}{12}\)] nor [A – \(\frac{5 \pi}{12}\)] is an integral multiple of π.
Prove that cot [\(\frac{\pi}{12}\) – A] + tan [\(\frac{\pi}{12}\) + A] = \(\frac{4 \cos 2 A}{1-2 \sin 2 A}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 8

Question 5.
Prove that 4 cos 12° cos 48° cos 72° = cos 36°
Answer:
4 cos 12° cos 48° cos 72°
= 2 cos 12° [2 cos 48° cos 72°]
= 2 cos 12° [cos (48° + 72°) + cos (48° – 72°)]
= 2 cos 12° [cos 120° + cos 24°]
= 2 cos 12° [- \(\frac{1}{2}\) + cos 24°]
= – cos 12° + 2 cos 12° cos 24°
= – cos 12° + cos (12° + 24°) + cos (12° – 24°)
= – cos 12° + cos 36° + cos 12°
= – cos 36°

Question 6.
Prove that
sin 10° + sin 20° + sin 40° + sin 50° = sin 70° + sin 80°
Answer:
sin 10° + sin 500 + sin 20° + sin 40°
= 2 sin \(\frac{\left(10^{\circ}+50^{\circ}\right)}{2}\) cos \(\frac{\left(10^{\circ}-50^{\circ}\right)}{2}\) + 2 sin \(\left(\frac{20^{\circ}+40^{\circ}}{2}\right)\) cos \(\left(\frac{20^{\circ}-40^{\circ}}{2}\right)\)
= 2 sin 30° cos 20° + 2 sin 30° cos 10°
= 2 \(\left(\frac{1}{2}\right)\) cos 20° + 2 \(\left(\frac{1}{2}\right)\) cos 10°
= cos 20° + cos 10°
= cos (90° – 70°) + cos (90° – 80°)
= sin 70° + sin 80°

III.
Question 1.
If cos x + cos y = \(\frac{4}{5}\) and cos x – cos y = \(\frac{2}{7}\).
find the value of 14 tan \(\left(\frac{x-y}{2}\right)\) + 5 cot \(\left(\frac{x+y}{2}\right)\)
Answer:
Given cos x + cos y = and cos x – cos y = \(\frac{2}{7}\)
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 9

Question 2.
If none of the denominators is zero, prove that
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 10
Answer:

If n is odd, since (- 1)ⁿ = 1
we have LHS = O
If n is even and (- 1)ⁿ = 1
L.H.S = 2 cot²\(\left(\frac{\mathrm{A}-\mathrm{B}}{2}\right)\)

Question 3.
If sin A = sin B and cos A = cos B, then prove that A = 2nπ + B for some integer n.
Answer:
sin A = sin B and cos A = cos B
⇒ sin A – sin B = 0 and cos A – cos B = 0
⇒ 2 cos \(\left(\frac{A+B}{2}\right)\) sin \(\left(\frac{A-B}{2}\right)\) = 0 ……………. (1)
and cos A – cos B = 0
⇒ 2 sin \(\left(\frac{A+B}{2}\right)\) sin \(\left(\frac{B-A}{2}\right)\) = 0 ……………… (2)
From (1) and (2),
sin \(\left(\frac{A-B}{2}\right)\) = o ⇒ \(\left(\frac{A-B}{2}\right)\) = nπ
⇒ A = 2nπ + B for some n ∈ Z

Question 4.
If cos nα ≠ 0 and cos \(\frac{\alpha}{2}\) ≠ 0 then show that
\(\frac{\sin (n+1) \alpha-\sin (n-1) \alpha}{\cos (n+1) \alpha+2 \cos n \alpha+\cos (n-1) \alpha}\) = tan \(\frac{\alpha}{2}\)
Answer:
L.H.S
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 12

Question 5.
If sec (θ + α) + sec (θ – α) = 2 sec θ and cos α ≠ 1, then show that cos θ = ± √2 cos \(\frac{\alpha}{2}\).
Answer:
Given(θ + α) + sec (θ – α) = 2 sec θ
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 13
⇒ cos α cos²θ = cos²θ – sin²α
⇒ cos² θ (1 – cos α) = sin²α
⇒ cos² θ (1 – cos α) = 1 – cos²α
⇒ cos² θ = 1 – cos α = [∵ cos α ≠ 1]
⇒ cos² θ = 2 cos² \(\frac{\alpha}{2}\)
⇒ cos θ = ±√2 cos \(\left(\frac{\alpha}{2}\right)\)

Question 6.
If none of x, y, z is an odd multiple of \(\frac{\pi}{2}\) and if sin (y + z – x), sin (z + x – y), sin (x + y – z) are In AP then prove that tan x, tan y, tan z are also in AP.
Answer:
sin (y + z – x), sin(z + x – y), sin(x + y – z) are in A.P
⇒ sin(z + x – y) – sin (y + z – x) = sin (x + y – z) – sin (z + x – y)
⇒ z cos z sin(x – y) 2 cos x sin(y – z)
⇒ cos z [sin x cos y – cos x sin y] = cos x [ sin y cos z – cos y sin z]
Dividing by cos x cos y cos z. We get,
\(\frac{\sin x}{\cos x}-\frac{\sin y}{\cos y}=\frac{\sin y}{\cos y}-\frac{\sin z}{\cos z}\)
⇒ tan x – tan y = tan y – tan z
⇒ tan x + tan z = 2 tan y
⇒ tan x, tan y, tan z are in A.P

Question 7.
If x, y, z are non zero real numbers and if x cos θ = y cos\(\left(\theta+\frac{2 \pi}{3}\right)\) = z c0s\(\left(\theta+\frac{4 \pi}{3}\right)\) for some θ ∈ R, then show that xy + yz + zx = 0
Answer:
x ≠ 0, y ≠ 0, z ≠ 0
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 14

Question 8.
If neither A nor A + B Is an odd multiple of \(\frac{\pi}{2}\) and if m sin B = n sin (2A + B), then prove that (m +n) tanA =(m – n) tan(A + B).
Answer:
Given, m sin B = n sin (2A + B)
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 15

Question 9.
If tan(A + B) = λ tan(A – B) show that (λ + 1) sin 2B = (λ – 1) sin 2A
Answer:
Given tan (A + B) = λ tan (A – B)
TS Inter 1st Year Maths 1A Solutions Chapter 6 Trigonometric Ratios upto Transformations Ex 6(e) 16

TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a)

January 23, 2024January 21, 2024 by Mahesh

Students must practice these TS Intermediate Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Solutions Exercise 8(a)

I.
1.
Evaluate the following:
(i) Sin^-1 \(\left(-\frac{\sqrt{3}}{2}\right)\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 1

(ii) Cos^-1\(\left(\frac{1}{\sqrt{2}}\right)\)
Answer:
cos^-1\(\frac{1}{\sqrt{2}}\) = cos^-1 (cos\(\frac{\pi}{4}\)) = \(\frac{\pi}{4}\)
(∵ cos^-1 (cos θ) = θ if θ ∈ [0, π])

(iii) Sec^-1 (- √2)
Answer:
= π – sec^-1 √2 [∵ x ∈ ( – ∞, – 1] ∪ [1, ∞)]
= π – sec^-1 (sec \(\frac{\pi}{4}\)) = π – \(\frac{\pi}{4}\) = \(\frac{3 \pi}{4}\)
[∵ sec^-1 (sec θ) = θ dor θ ∈ \(\left(0, \frac{\pi}{2}\right)\) ∪ \(\left(\frac{\pi}{2}, \pi\right)\)]

(iv) Cot^-1 (- √3)
Answer:
Cot^-1 (- √3) = π – cot^-1 (√3)
= π – cot^-1 (cot\(\frac{\pi}{6}\))
= π – \(\frac{\pi}{6}\) = \(\frac{5 \pi}{6}\)
(∵ cot^-1 (- x) = π – cot^-1x for any x ∈ R)

(v) sin (\(\frac{\pi}{3}\) – sin^-1\(\left(-\frac{1}{2}\right)\))
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 2

(vi) Sin^-1 \(\left(\sin \left(\frac{5 \pi}{6}\right)\right)\)
Answer:
sin^-1 \(\left(\sin \left(\pi-\frac{\pi}{6}\right)\right)\)
= sin^-1 (sin\(\frac{\pi}{6}\)) = \(\frac{\pi}{6}\)

(vii) Cos^-1\(\left(\cos \frac{5 \pi}{4}\right)\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 3

Question 2.
Find the value of
(i) Sin \(\left(\cos ^{-1}\left(\frac{3}{5}\right)\right)\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 4

(ii) Tan (cosec^-1 \(\left(\frac{65}{63}\right)\))
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 5

(iii) Sin (2 sin^-1 \(\frac{4}{5}\))
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 6

(iv) Sin^-1\(\left(\sin \frac{33 \pi}{7}\right)\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 7

(v) Cos^-1 (cos \(\frac{17 \pi}{6}\))
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 8

Question 3.
Simplify each of the following.
(i) Tan^-1\(\left(\frac{\sin x}{1+\cos x}\right)\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 9

(ii) tan^-1 (sec x + tan x)
Answer:
tan^-1 (sec x + tan x)
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 10

(iii) Tan^-1 \(\sqrt{\frac{1-\cos x}{1+\cos x}}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 11

(iv) Sin^-1 (2cos²θ – 1) + Cos^-1 (1 – 2 sin² θ)
Answer:
sin^-1 (2cos²θ – 1) + cos^-1 (1 – 2 sin² θ)
= sin^-1 (cos2θ) + cos^-1 (cos 2θ)
= sin^-1 (sin(\(\frac{\pi}{2}\) – 2θ) + cos^-1 (cos 2θ))
= \(\frac{\pi}{2}\) – 2θ + 2θ= \(\frac{\pi}{2}\)

(v) tan^-1 (x + \(\sqrt{1+x^2}\)) = ; x ∈ R
Answer:
Let x = tan θ then tan^-1 (x + \(\sqrt{1+x^2}\)) = tan^-1 (tan θ + sec θ)
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 12

II.
Question 1.
Prove that
(i) Sin^-1\(\frac{3}{5}\) + sin^-1\(\frac{8}{17}\) = Cos^-1\(\left(\frac{36}{85}\right)\) (May 2022)
Answer:
Use the property that If
x, y ∈ [0, 1] and x² + y² < 1
(Here x = \(\frac{3}{5}\) and y = \(\frac{8}{17}\)) then
sin^-1 x + sin^-1 y
= cos^-1 (\(\sqrt{1-x^2} \sqrt{1-y^2}\) – xy)
As an alternative preferably use
sin^-1\(\left(\frac{3}{5}\right)\) = A and sin^-1\(\left(\frac{8}{17}\right)\) = B
∴ sinA = \(\frac{3}{5}\) and sinB = \(\frac{8}{17}\)
∴ cosA = \(\frac{4}{5}\) andcosB = \(\frac{15}{17}\)
Now A + B ∈ (0, π) and cos (A + B)
= cos A cos B – sin A sin B
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 13

(ii) Sin^-1\(\left(\frac{3}{5}\right)\) + Cos^-1\(\left(\frac{12}{13}\right)\) = Cos^-1\(\left(\frac{33}{65}\right)\)
Answer:
Let sin^-1\(\left(\frac{3}{5}\right)\) = A and cos^-1\(\left(\frac{12}{13}\right)\) then A + B ∈ (0, π)
∴ sinA = \(\frac{3}{5}\) and cos B = \(\frac{12}{13}\)
∴ cosA = \(\frac{4}{5}\) and SinB = \(\frac{5}{13}\)
Consider cos (A + B) = cos A cos B – sin A sin B
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 14

(iii) tan (cot^-19 + Cosec^-1\(\frac{\sqrt{41}}{4}\)) = 1
Answer:
Let cot^-19 = A and cosec^-1\(\frac{\sqrt{41}}{4}\) = B
then cot A = 9 and cosec B = \(\frac{\sqrt{41}}{4}\)
∴ tan A = \(\frac{1}{9}\) and cot²B = cosec²B – 1 = \(\frac{41}{16}\) – 1 = \(\frac{25}{16}\)
⇒ cot B = \(\frac{41}{16}\) – 1 ⇒ tan B = \(\frac{25}{16}\)
⇒ cot B = \(\frac{5}{4}\) ⇒ tan B = \(\frac{4}{5}\)
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 15

(iv) Cos^-1\(\left(\frac{4}{5}\right)\) + sin^-1\(\left(\frac{3}{\sqrt{34}}\right)\) = tan^-1\(\left(\frac{27}{11}\right)\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 16

Question 2.
Find the value of
(i) sin (Cos^-1\(\frac{3}{5}\) + Cos^-1\(\frac{12}{13}\))
Answer:
Let Cos^-1\(\frac{3}{5}\) = A and Cos^-1\(\frac{12}{13}\) = B
then cos A = \(\frac{3}{5}\) and cos B = \(\frac{12}{13}\)
∴ sin A = \(\frac{4}{5}\) and sinB = \(\frac{5}{13}\)
∴ sin(A + B) = sin A cos B + cos A sin B
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 17

(ii) tan (sin^-1\(\left(\frac{3}{5}\right)\) + cos^-1\(\left(\frac{5}{\sqrt{34}}\right)\))
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 18

(iii) cos (Sin^-1 \(\frac{3}{5}\) + Sin^-1 \(\frac{5}{13}\))
Answer:
Let Sin^-1\(\left(\frac{3}{5}\right)\) = A and Sin^-1\(\left(\frac{5}{13}\right)\) = B
then sin A = \(\frac{3}{5}\) and sin B = \(\frac{5}{13}\)
∴ cosA = \(\frac{4}{5}\) and cos B = \(\frac{12}{13}\)
∴ cos (A + B) = cos A cos B – sin A sin B
= \(\left(\frac{4}{5}\right)\left(\frac{12}{13}\right)\) – \(\left(\frac{3}{5}\right)\left(\frac{5}{13}\right)\) = \(\frac{33}{65}\)

Question 3.
Prove that
(i) cos (2 Tan^-1\(\frac{1}{7}\)) = sin (2 Tan^-1\(\frac{3}{4}\))
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 19

(ii) cos {2[Tan^-1\(\left(\frac{1}{4}\right)\) + Tan^-1\(\left(\frac{2}{9}\right)\)]} = \(\frac{3}{5}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 20

Question 4.
Prove that
(i) Tan^-1\(\frac{1}{7}\) + Tan^-1\(\frac{1}{13}\) – Tan^-1\(\frac{2}{9}\) = 0
Answer:
L.H.S = (tan^-1\(\frac{1}{7}\) + tan^-1\(\frac{1}{13}\)) – tan^-1\(\frac{2}{9}\)
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 21

(ii) Tan^-1\(\frac{1}{2}\) + Tan^-1\(\frac{1}{5}\) – Tan^-1\(\frac{1}{8}\) = \(\frac{\pi}{4}\) (March 2015-A.P.) (March 2011, May 2006)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 22

(iii) Tan^-1\(\frac{3}{4}\) + Tan^-1\(\frac{3}{5}\) – Tan^-1\(\frac{8}{19}\) = \(\frac{\pi}{4}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 23

(iv) Tan^-1\(\frac{1}{7}\) + Tan^-1\(\frac{1}{8}\) = Cot^-1\(\frac{201}{43}\) + Cot^-1 18
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 24

Question 5.
Show that
(i) sec² (Tan^-12) + cosec² (Cot^-12) = 10
Answer:
Let α = tan^-12 tan α = 2
sec² α = 1 + tan²α = 1 + 4 = 5
Let β = cot^-1 2 ⇒ cot β = 2
∴ cosec² β = 1 + cot² β = 1 + 4 = 5
∴ sec² (tan^-1 2) + cosec² (cot^-12)
= sec²α + cosec²β = 5 + 5 = 10

(ii) Find the value of tan(Cos^-1\(\frac{4}{5}\) + Tan^-1\(\frac{2}{3}\)). (March 2012)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 25

(iii) If sin^-1x – Cos^-1 = \(\frac{\pi}{6}\), then find x.
Answer:
Let α = sin^-1x ⇒ sin α = x
and β = cos^-1x ⇒ cos β = x
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 26

III.
Question 1.
Prove that (May 2014, Mar. 14)
(i) 2 sin^-1\(\frac{3}{5}\) – cos^-1\(\frac{5}{13}\) = cos^-1\(\left(\frac{323}{325}\right)\)
Answer:
Let α = sin^-1\(\left(\frac{3}{5}\right)\) and β = cos^-1\(\left(\frac{5}{13}\right)\)
⇒ sin α = \(\frac{3}{5}\) and cos β = \(\frac{5}{13}\)
∴ LHS = 2α – β
Consider cos(2α – β)
= cos 2α cos β + sin 2α sin β
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 27

(ii) Sin^-1\(\left(\frac{4}{5}\right)\) + 2 Tan^-1 \(\left(\frac{1}{3}\right)\) = \(\frac{\pi}{2}\) (March 2015-T.S)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 28

(iii) 4 tan^-1\(\left(\frac{1}{5}\right)\) + Tan^-1\(\left(\frac{1}{99}\right)\) – Tan^-1\(\left(\frac{1}{70}\right)\) = \(\frac{\pi}{4}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 29

Question 2.
(i) If α = Tan^-1\(\left(\frac{\sqrt{1+x^2}-\sqrt{1-x^2}}{\sqrt{1+x^2}+\sqrt{1-x^2}}\right)\), then prove that x² = sin 2 α.
Answer:
Let x² = θ
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 30

(ii) Prove that tan\(\left\{2 {Tan}^{-1}\left(\frac{\sqrt{1+x^2}-1}{x}\right)\right\}\) = x.
Answer:
Let x = tan θ
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 31

(iii) Prove that
sin\(\left[{Cot}^{-1} \frac{2 x}{1-x^2}+{Cos}^{-1}\left(\frac{1-x^2}{1+x^2}\right)\right]\) = 1.
Answer:
Let x = tan θ then
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 32

(iv) prove that tan \(\left\{\frac{\pi}{4}+\frac{1}{2} \cos ^{-1}\left(\frac{a}{b}\right)\right\}\) + tan \(\left\{\frac{\pi}{4}-\frac{1}{2} \cos ^{-1}\left(\frac{a}{b}\right)\right\}\) = \(\frac{2 b}{a}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 33

Question 3.
(i) If Cos^-1 p + Cos^-1 q + Cos^-1 r = π, then prove that p² + q² + r² + 2pqr = 1. (June 2004, 2006, 2005)
Answer:
Let cos^-1p = A, cos^-1 q = B, cos^-1r = c
⇒ cos A = p, cos B = q, and cos C = π
then given A + B + C = π
To show that p² + q² + r² = 1 – 2 pqr
i.e., cos²A + cos² B + cos²C = 1 – 2 cos A cos B cos C
∴ cos² A + cos² B + cos² C = cos² A + cos² B + 1 – sin² C
= 1 + cos² A + cos (B +C) cos (B – C)
= 1 + cos² A – cos A cos (B – C)
= 1 + cos A [ cos A – cos (B – C)]
= 1 + cos A [ – cos (B + c) – cos (B – C)]
= 1 – cos A [ cos (B + C) + cos (B – C)]
= 1 – 2 cos A cosB cos C = 1 – 2 pqr

(ii) If sin^-1\(\left(\frac{2 p}{1+p^2}\right)\) – cos^-1\(\left(\frac{1-q^2}{1+q^2}\right)\) = Tan^-1\(\left(\frac{2 x}{1-x^2}\right)\), then prove that x = \(\).
Answer:
Let p = tan A, q = tan B and x = tan C
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 34
⇒ sin^-1 (sin 2A) – cos^-1 (cos 2B) = tan^-1 (tan 2C)
⇒ 2A – 2B = 2C
∴ tan C = \(\frac{\tan A \tan B}{1+\tan A \tan B}\) = \(\frac{p-q}{1+p q}\)
⇒ x = \(\frac{p-q}{1+p q}\)

(iii) If a, b, c are distinct non – zero real numbers having the same sign prove that
cot^-1\(\left(\frac{a b+1}{a-b}\right)\) + cot^-1\(\left(\frac{b c+1}{b-c}\right)\) + cot^-1\(\left(\frac{c a+1}{c-a}\right)\) = π or 2π.
Answer:
Let have (a – b) + (b – c) + (c – a) = 0 and (a – b), (b – c), (c – a) need not have the same sign. Then either two of these numbers may be positive and one negative or two may be negative and one will be positive. Suppose (a – b) (b – c) are both positive and (c – a) is negative.
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 35

(iv) If sin^-1x + sin^-1y + sin^-1z = π, then prove that
x \(\sqrt{1-x^2}\) + y\(\sqrt{1-y^2}\) + y\(\sqrt{1-z^2}\) = 2xyz (March 2006, May 2005)
Answer:
Let sin^-1 x = A, sin^-1 y = B and sin^-1 z = c
Then sin A = x, sin B = y and sin c = z
Also A + B + C = π
LHS
= x\(\sqrt{1-x^2}\) + y\(\sqrt{1-y^2}\) + z\(\sqrt{1-z^2}\)
= sin A cos A + sin B cos B + smC cos C
= \(\frac{1}{2}\) [sin 2A + sin 2B + sin 2C]
= \(\frac{1}{2}\) [2.sin(A + B) cos (A – B) + 2 sin C cos C]
= \(\frac{1}{2}\) [2 sin C cos (A – B) + 2 sin C cos C]
= sin C [cos (A – B) + cos C]
= sin C [cos (A – B) – cos (A + B)]
= 2 sin C sin A sin B = 2 sin A sin B sin C
= 2xyz = RHS

(v) (a) If Tan^-1 x + Tan^-1 y + Tan^-1 z = π, then prove that x + y + z = xyz. (March 2003)
Answer:
Let tan^-1 x = A, tan^-1 y = B and tan^-1 z = c then A + B + C = π and tan A = x, tan B = y, tan C = z.
∴ A + B = (π – C)
⇒ tan (A + B) = tan(π – C) = – tan C
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = – tan C
⇒ tan A + tan B = – tan C + tan A tan B tan C
⇒ tan A + tan B + tan C = tan A tan B tan C
⇒ x + y + z = XYZ.

(b) If Tan^-1x + Tan^-1y + Tan^-1z = \(\) then prove that xy + yz + zx = 1. (March 2001, June 2004)
Answer:
Let tan^-1 x = A, tan^-1 y = B, tan^-1 z = C
then A + B + C = \(\frac{\pi}{2}\)
∴ A + B + C = \(\frac{\pi}{2}\) – C
⇒ tan (A + B) = tan (\(\frac{\pi}{2}\) – C) = cot C = \(\frac{1}{\tan C}\)
∴ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = \(\frac{1}{\tan C}\)
⇒ tan A + tan B + tan B tan C + tan C tan A = 1
⇒ xy + yz + zx = 1

Question 4.
Solve the following equation for x:
(i) Tan^-1\(\left(\frac{x-1}{x-2}\right)\) + Tan^-1\(\left(\frac{x+1}{x+2}\right)\) = \(\frac{\pi}{4}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 36

(ii) Tan^-1\(\left(\frac{1}{2 x+1}\right)\) + Tan^-1\(\left(\frac{1}{4 x+1}\right)\) = Tan^-1\(\left(\frac{2}{x^2}\right)\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 37
⇒ x²(3x + 1) = 2x(4x + 3)
⇒ x = 0 or 6x² – 14x – 12 = 0
⇒ x = 0 or 3x² – 7x – 6 = 0
⇒ x = 0 or (3x² – 9x + 2x – 6) = 0
⇒ x = 0 or 3x(x – 3) + 2(x – 3) = 0
⇒ x = 0 or (x – 3) (3x – 2) = 0
⇒ x = 0 (or) x = 3 or x = – \(\frac{2}{3}\)

(iii) 3 sin^-1\(\left(\frac{2 x}{1+x^2}\right)\) – 4 cos \(\left(\frac{1-x^2}{1+x^2}\right)\) + 2 Tan^-1\(\left(\frac{2 x}{1-x^2}\right)\) = \(\frac{\pi}{3}\)
Answer:
Let x = tanθ then
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 38

(iv) sin^-1 (1 – x) – 2 sin^-1 x = \(\frac{\pi}{2}\)
Answer:
Let sin^-1 (1 – x) = α and sin^-1 x = β then sin α = 1 – x and sin β = x
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 39
Hence x = 0 is the only solution for the given equation.

Question 5.
Solve the following equations.
(i) Cot^-1 \(\left(\frac{1+x}{1-x}\right)\) = \(\frac{1}{2}\) Cot^-1\(\left(\frac{1}{x}\right)\), x > 0 and x ≠ 1.
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 40

(ii) Tan[Cos^-1\(\left(\frac{1}{\mathbf{x}}\right)\)] = Sin[Cot^-1\(\left(\frac{1}{2}\right)\)]; x ≠ 0.
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 41

(iii) Cos^-1 x + Sin^-1\(\left(\frac{x}{2}\right)\) = \(\frac{\pi}{6}\)
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 42
⇒ x⁴ – 5x² + 4 = x⁴ – 2x² + 1
⇒ 3x² – 3 = 0 ⇒ 3x² = 3 ⇒ x = ± 1
When x = – 1 then cos^-1 (- 1) + sin^-1\(\left(-\frac{1}{2}\right)\)
= π – \(\frac{\pi}{6}\) = \(\frac{5 \pi}{6}\) ≠ \(\frac{\pi}{6}\)
∴ x = – 1 is not admissible. Hence x = 1

(iv) Cos^-1 (√3x) + Cos^-1x = \(\frac{\pi}{2}\)
Answer:
Let cos^-1 (√3x) = α ⇒ cos α = √3x
and cos^-1x = β ⇒ cos β = x
cos (α + β) = \(\frac{\pi}{2}\)
⇒ √3x . x = \(\sqrt{1-3 x^2} \sqrt{1-x^2}\) = 0
⇒ √3x² = \(\sqrt{1-3 x^2} \sqrt{1-x^2}\)
⇒ 3x⁴ = (1 – 3x²) (1 – x²)
= 3x⁴ – 4x² + 1
⇒ 4x² = 1 ⇒ x = ±\(\frac{1}{2}\) ⇒ x = – \(\frac{1}{2}\) is not admissible.
∴ x = \(\frac{1}{2}\)

(v) sin[Sin^-1\(\left(\frac{1}{5}\right)\) + Cos^-1x] = 1
Answer:
TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) 43