TS Inter 1st Year Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a)

Students must practice these TS Intermediate Maths 1A Solutions Chapter 8 Inverse Trigonometric Functions Ex 8(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1A Inverse Trigonometric Functions Solutions Exercise 8(a)

I.
1.
Evaluate the following:
(i) Sin^-1 \(\left(-\frac{\sqrt{3}}{2}\right)\)
Answer:

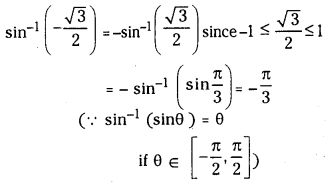
(ii) Cos^-1\(\left(\frac{1}{\sqrt{2}}\right)\)
Answer:
cos^-1\(\frac{1}{\sqrt{2}}\) = cos^-1 (cos\(\frac{\pi}{4}\)) = \(\frac{\pi}{4}\)
(∵ cos^-1 (cos θ) = θ if θ ∈ [0, π])

(iii) Sec^-1 (- √2)
Answer:
= π – sec^-1 √2 [∵ x ∈ ( – ∞, – 1] ∪ [1, ∞)]
= π – sec^-1 (sec \(\frac{\pi}{4}\)) = π – \(\frac{\pi}{4}\) = \(\frac{3 \pi}{4}\)
[∵ sec^-1 (sec θ) = θ dor θ ∈ \(\left(0, \frac{\pi}{2}\right)\) ∪ \(\left(\frac{\pi}{2}, \pi\right)\)]

(iv) Cot^-1 (- √3)
Answer:
Cot^-1 (- √3) = π – cot^-1 (√3)
= π – cot^-1 (cot\(\frac{\pi}{6}\))
= π – \(\frac{\pi}{6}\) = \(\frac{5 \pi}{6}\)
(∵ cot^-1 (- x) = π – cot^-1x for any x ∈ R)

(v) sin (\(\frac{\pi}{3}\) – sin^-1\(\left(-\frac{1}{2}\right)\))
Answer:

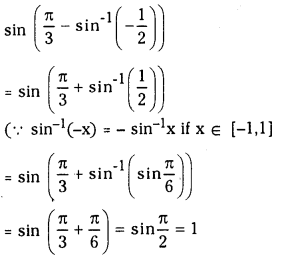
(vi) Sin^-1 \(\left(\sin \left(\frac{5 \pi}{6}\right)\right)\)
Answer:
sin^-1 \(\left(\sin \left(\pi-\frac{\pi}{6}\right)\right)\)
= sin^-1 (sin\(\frac{\pi}{6}\)) = \(\frac{\pi}{6}\)

(vii) Cos^-1\(\left(\cos \frac{5 \pi}{4}\right)\)
Answer:

Question 2.
Find the value of
(i) Sin \(\left(\cos ^{-1}\left(\frac{3}{5}\right)\right)\)
Answer:

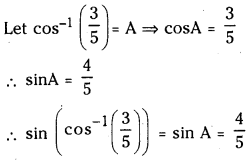
(ii) Tan (cosec^-1 \(\left(\frac{65}{63}\right)\))
Answer:

(iii) Sin (2 sin^-1 \(\frac{4}{5}\))
Answer:

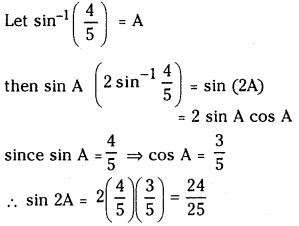
(iv) Sin^-1\(\left(\sin \frac{33 \pi}{7}\right)\)
Answer:

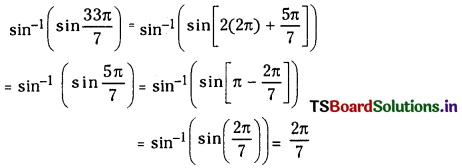
(v) Cos^-1 (cos \(\frac{17 \pi}{6}\))
Answer:

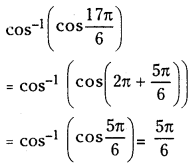
Question 3.
Simplify each of the following.
(i) Tan^-1\(\left(\frac{\sin x}{1+\cos x}\right)\)
Answer:

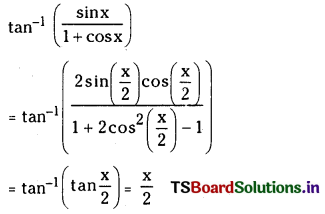
(ii) tan^-1 (sec x + tan x)
Answer:
tan^-1 (sec x + tan x)

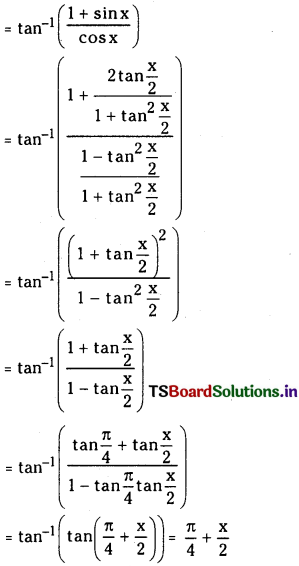
(iii) Tan^-1 \(\sqrt{\frac{1-\cos x}{1+\cos x}}\)
Answer:

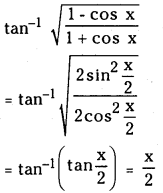
(iv) Sin^-1 (2cos²θ – 1) + Cos^-1 (1 – 2 sin² θ)
Answer:
sin^-1 (2cos²θ – 1) + cos^-1 (1 – 2 sin² θ)
= sin^-1 (cos2θ) + cos^-1 (cos 2θ)
= sin^-1 (sin(\(\frac{\pi}{2}\) – 2θ) + cos^-1 (cos 2θ))
= \(\frac{\pi}{2}\) – 2θ + 2θ= \(\frac{\pi}{2}\)

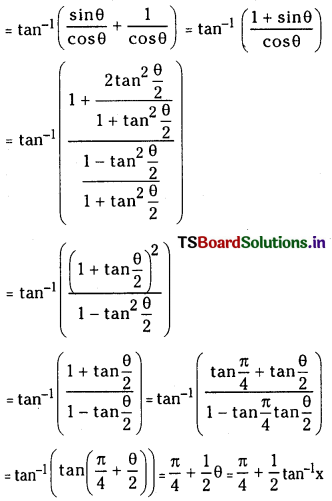
(v) tan^-1 (x + \(\sqrt{1+x^2}\)) = ; x ∈ R
Answer:
Let x = tan θ then tan^-1 (x + \(\sqrt{1+x^2}\)) = tan^-1 (tan θ + sec θ)

II.
Question 1.
Prove that
(i) Sin^-1\(\frac{3}{5}\) + sin^-1\(\frac{8}{17}\) = Cos^-1\(\left(\frac{36}{85}\right)\) (May 2022)
Answer:
Use the property that If
x, y ∈ [0, 1] and x² + y² < 1
(Here x = \(\frac{3}{5}\) and y = \(\frac{8}{17}\)) then
sin^-1 x + sin^-1 y
= cos^-1 (\(\sqrt{1-x^2} \sqrt{1-y^2}\) – xy)
As an alternative preferably use
sin^-1\(\left(\frac{3}{5}\right)\) = A and sin^-1\(\left(\frac{8}{17}\right)\) = B
∴ sinA = \(\frac{3}{5}\) and sinB = \(\frac{8}{17}\)
∴ cosA = \(\frac{4}{5}\) andcosB = \(\frac{15}{17}\)
Now A + B ∈ (0, π) and cos (A + B)
= cos A cos B – sin A sin B

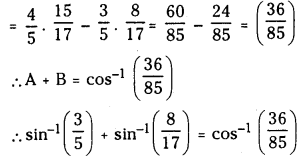
(ii) Sin^-1\(\left(\frac{3}{5}\right)\) + Cos^-1\(\left(\frac{12}{13}\right)\) = Cos^-1\(\left(\frac{33}{65}\right)\)
Answer:
Let sin^-1\(\left(\frac{3}{5}\right)\) = A and cos^-1\(\left(\frac{12}{13}\right)\) then A + B ∈ (0, π)
∴ sinA = \(\frac{3}{5}\) and cos B = \(\frac{12}{13}\)
∴ cosA = \(\frac{4}{5}\) and SinB = \(\frac{5}{13}\)
Consider cos (A + B) = cos A cos B – sin A sin B

(iii) tan (cot^-19 + Cosec^-1\(\frac{\sqrt{41}}{4}\)) = 1
Answer:
Let cot^-19 = A and cosec^-1\(\frac{\sqrt{41}}{4}\) = B
then cot A = 9 and cosec B = \(\frac{\sqrt{41}}{4}\)
∴ tan A = \(\frac{1}{9}\) and cot²B = cosec²B – 1 = \(\frac{41}{16}\) – 1 = \(\frac{25}{16}\)
⇒ cot B = \(\frac{41}{16}\) – 1 ⇒ tan B = \(\frac{25}{16}\)
⇒ cot B = \(\frac{5}{4}\) ⇒ tan B = \(\frac{4}{5}\)

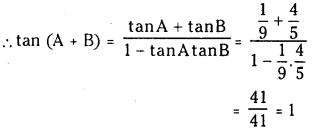
(iv) Cos^-1\(\left(\frac{4}{5}\right)\) + sin^-1\(\left(\frac{3}{\sqrt{34}}\right)\) = tan^-1\(\left(\frac{27}{11}\right)\)
Answer:

Question 2.
Find the value of
(i) sin (Cos^-1\(\frac{3}{5}\) + Cos^-1\(\frac{12}{13}\))
Answer:
Let Cos^-1\(\frac{3}{5}\) = A and Cos^-1\(\frac{12}{13}\) = B
then cos A = \(\frac{3}{5}\) and cos B = \(\frac{12}{13}\)
∴ sin A = \(\frac{4}{5}\) and sinB = \(\frac{5}{13}\)
∴ sin(A + B) = sin A cos B + cos A sin B

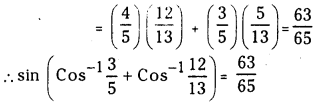
(ii) tan (sin^-1\(\left(\frac{3}{5}\right)\) + cos^-1\(\left(\frac{5}{\sqrt{34}}\right)\))
Answer:

(iii) cos (Sin^-1 \(\frac{3}{5}\) + Sin^-1 \(\frac{5}{13}\))
Answer:
Let Sin^-1\(\left(\frac{3}{5}\right)\) = A and Sin^-1\(\left(\frac{5}{13}\right)\) = B
then sin A = \(\frac{3}{5}\) and sin B = \(\frac{5}{13}\)
∴ cosA = \(\frac{4}{5}\) and cos B = \(\frac{12}{13}\)
∴ cos (A + B) = cos A cos B – sin A sin B
= \(\left(\frac{4}{5}\right)\left(\frac{12}{13}\right)\) – \(\left(\frac{3}{5}\right)\left(\frac{5}{13}\right)\) = \(\frac{33}{65}\)

Question 3.
Prove that
(i) cos (2 Tan^-1\(\frac{1}{7}\)) = sin (2 Tan^-1\(\frac{3}{4}\))
Answer:

(ii) cos {2[Tan^-1\(\left(\frac{1}{4}\right)\) + Tan^-1\(\left(\frac{2}{9}\right)\)]} = \(\frac{3}{5}\)
Answer:

Question 4.
Prove that
(i) Tan^-1\(\frac{1}{7}\) + Tan^-1\(\frac{1}{13}\) – Tan^-1\(\frac{2}{9}\) = 0
Answer:
L.H.S = (tan^-1\(\frac{1}{7}\) + tan^-1\(\frac{1}{13}\)) – tan^-1\(\frac{2}{9}\)

(ii) Tan^-1\(\frac{1}{2}\) + Tan^-1\(\frac{1}{5}\) – Tan^-1\(\frac{1}{8}\) = \(\frac{\pi}{4}\) (March 2015-A.P.) (March 2011, May 2006)
Answer:

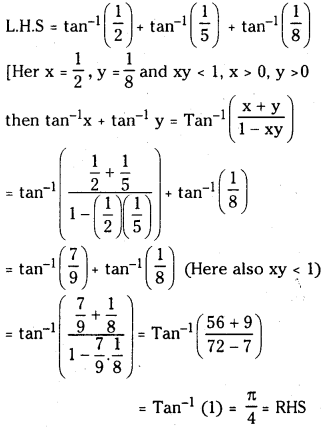
(iii) Tan^-1\(\frac{3}{4}\) + Tan^-1\(\frac{3}{5}\) – Tan^-1\(\frac{8}{19}\) = \(\frac{\pi}{4}\)
Answer:

(iv) Tan^-1\(\frac{1}{7}\) + Tan^-1\(\frac{1}{8}\) = Cot^-1\(\frac{201}{43}\) + Cot^-1 18
Answer:

Question 5.
Show that
(i) sec² (Tan^-12) + cosec² (Cot^-12) = 10
Answer:
Let α = tan^-12 tan α = 2
sec² α = 1 + tan²α = 1 + 4 = 5
Let β = cot^-1 2 ⇒ cot β = 2
∴ cosec² β = 1 + cot² β = 1 + 4 = 5
∴ sec² (tan^-1 2) + cosec² (cot^-12)
= sec²α + cosec²β = 5 + 5 = 10

(ii) Find the value of tan(Cos^-1\(\frac{4}{5}\) + Tan^-1\(\frac{2}{3}\)). (March 2012)
Answer:

(iii) If sin^-1x – Cos^-1 = \(\frac{\pi}{6}\), then find x.
Answer:
Let α = sin^-1x ⇒ sin α = x
and β = cos^-1x ⇒ cos β = x

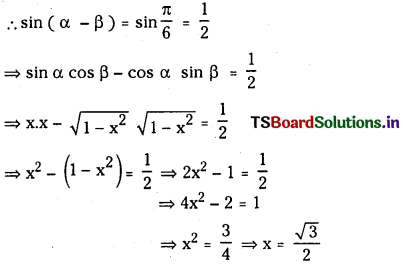
III.
Question 1.
Prove that (May 2014, Mar. 14)
(i) 2 sin^-1\(\frac{3}{5}\) – cos^-1\(\frac{5}{13}\) = cos^-1\(\left(\frac{323}{325}\right)\)
Answer:
Let α = sin^-1\(\left(\frac{3}{5}\right)\) and β = cos^-1\(\left(\frac{5}{13}\right)\)
⇒ sin α = \(\frac{3}{5}\) and cos β = \(\frac{5}{13}\)
∴ LHS = 2α – β
Consider cos(2α – β)
= cos 2α cos β + sin 2α sin β

(ii) Sin^-1\(\left(\frac{4}{5}\right)\) + 2 Tan^-1 \(\left(\frac{1}{3}\right)\) = \(\frac{\pi}{2}\) (March 2015-T.S)
Answer:

(iii) 4 tan^-1\(\left(\frac{1}{5}\right)\) + Tan^-1\(\left(\frac{1}{99}\right)\) – Tan^-1\(\left(\frac{1}{70}\right)\) = \(\frac{\pi}{4}\)
Answer:

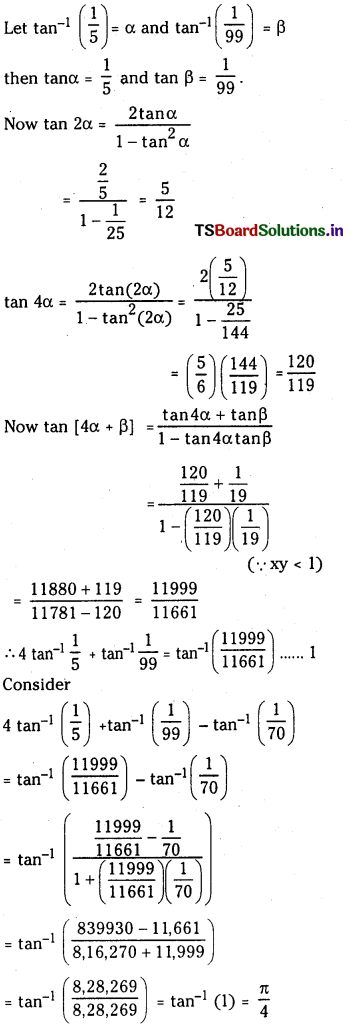
Question 2.
(i) If α = Tan^-1\(\left(\frac{\sqrt{1+x^2}-\sqrt{1-x^2}}{\sqrt{1+x^2}+\sqrt{1-x^2}}\right)\), then prove that x² = sin 2 α.
Answer:
Let x² = θ

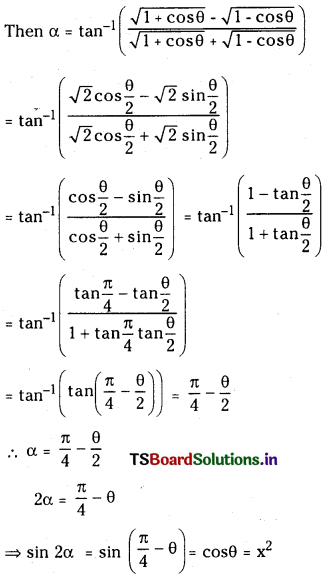
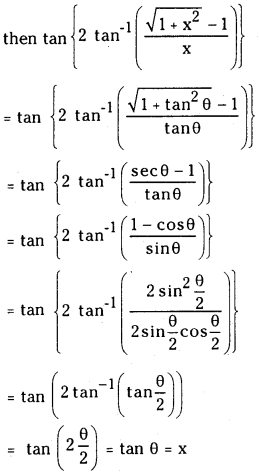
(ii) Prove that tan\(\left\{2 {Tan}^{-1}\left(\frac{\sqrt{1+x^2}-1}{x}\right)\right\}\) = x.
Answer:
Let x = tan θ

(iii) Prove that
sin\(\left[{Cot}^{-1} \frac{2 x}{1-x^2}+{Cos}^{-1}\left(\frac{1-x^2}{1+x^2}\right)\right]\) = 1.
Answer:
Let x = tan θ then

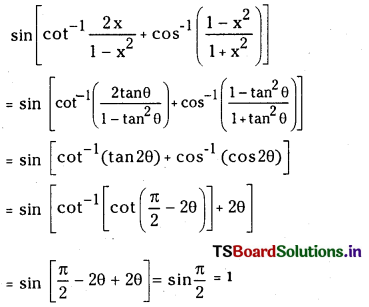
(iv) prove that tan \(\left\{\frac{\pi}{4}+\frac{1}{2} \cos ^{-1}\left(\frac{a}{b}\right)\right\}\) + tan \(\left\{\frac{\pi}{4}-\frac{1}{2} \cos ^{-1}\left(\frac{a}{b}\right)\right\}\) = \(\frac{2 b}{a}\)
Answer:

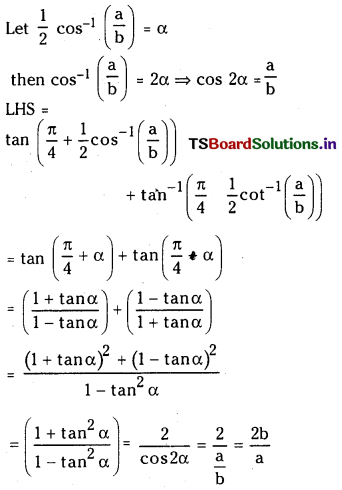
Question 3.
(i) If Cos^-1 p + Cos^-1 q + Cos^-1 r = π, then prove that p² + q² + r² + 2pqr = 1. (June 2004, 2006, 2005)
Answer:
Let cos^-1p = A, cos^-1 q = B, cos^-1r = c
⇒ cos A = p, cos B = q, and cos C = π
then given A + B + C = π
To show that p² + q² + r² = 1 – 2 pqr
i.e., cos²A + cos² B + cos²C = 1 – 2 cos A cos B cos C
∴ cos² A + cos² B + cos² C = cos² A + cos² B + 1 – sin² C
= 1 + cos² A + cos (B +C) cos (B – C)
= 1 + cos² A – cos A cos (B – C)
= 1 + cos A [ cos A – cos (B – C)]
= 1 + cos A [ – cos (B + c) – cos (B – C)]
= 1 – cos A [ cos (B + C) + cos (B – C)]
= 1 – 2 cos A cosB cos C = 1 – 2 pqr

(ii) If sin^-1\(\left(\frac{2 p}{1+p^2}\right)\) – cos^-1\(\left(\frac{1-q^2}{1+q^2}\right)\) = Tan^-1\(\left(\frac{2 x}{1-x^2}\right)\), then prove that x = \(\).
Answer:
Let p = tan A, q = tan B and x = tan C

⇒ sin^-1 (sin 2A) – cos^-1 (cos 2B) = tan^-1 (tan 2C)
⇒ 2A – 2B = 2C
∴ tan C = \(\frac{\tan A \tan B}{1+\tan A \tan B}\) = \(\frac{p-q}{1+p q}\)
⇒ x = \(\frac{p-q}{1+p q}\)

(iii) If a, b, c are distinct non – zero real numbers having the same sign prove that
cot^-1\(\left(\frac{a b+1}{a-b}\right)\) + cot^-1\(\left(\frac{b c+1}{b-c}\right)\) + cot^-1\(\left(\frac{c a+1}{c-a}\right)\) = π or 2π.
Answer:
Let have (a – b) + (b – c) + (c – a) = 0 and (a – b), (b – c), (c – a) need not have the same sign. Then either two of these numbers may be positive and one negative or two may be negative and one will be positive. Suppose (a – b) (b – c) are both positive and (c – a) is negative.

(iv) If sin^-1x + sin^-1y + sin^-1z = π, then prove that
x \(\sqrt{1-x^2}\) + y\(\sqrt{1-y^2}\) + y\(\sqrt{1-z^2}\) = 2xyz (March 2006, May 2005)
Answer:
Let sin^-1 x = A, sin^-1 y = B and sin^-1 z = c
Then sin A = x, sin B = y and sin c = z
Also A + B + C = π
LHS
= x\(\sqrt{1-x^2}\) + y\(\sqrt{1-y^2}\) + z\(\sqrt{1-z^2}\)
= sin A cos A + sin B cos B + smC cos C
= \(\frac{1}{2}\) [sin 2A + sin 2B + sin 2C]
= \(\frac{1}{2}\) [2.sin(A + B) cos (A – B) + 2 sin C cos C]
= \(\frac{1}{2}\) [2 sin C cos (A – B) + 2 sin C cos C]
= sin C [cos (A – B) + cos C]
= sin C [cos (A – B) – cos (A + B)]
= 2 sin C sin A sin B = 2 sin A sin B sin C
= 2xyz = RHS

(v) (a) If Tan^-1 x + Tan^-1 y + Tan^-1 z = π, then prove that x + y + z = xyz. (March 2003)
Answer:
Let tan^-1 x = A, tan^-1 y = B and tan^-1 z = c then A + B + C = π and tan A = x, tan B = y, tan C = z.
∴ A + B = (π – C)
⇒ tan (A + B) = tan(π – C) = – tan C
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = – tan C
⇒ tan A + tan B = – tan C + tan A tan B tan C
⇒ tan A + tan B + tan C = tan A tan B tan C
⇒ x + y + z = XYZ.

(b) If Tan^-1x + Tan^-1y + Tan^-1z = \(\) then prove that xy + yz + zx = 1. (March 2001, June 2004)
Answer:
Let tan^-1 x = A, tan^-1 y = B, tan^-1 z = C
then A + B + C = \(\frac{\pi}{2}\)
∴ A + B + C = \(\frac{\pi}{2}\) – C
⇒ tan (A + B) = tan (\(\frac{\pi}{2}\) – C) = cot C = \(\frac{1}{\tan C}\)
∴ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = \(\frac{1}{\tan C}\)
⇒ tan A + tan B + tan B tan C + tan C tan A = 1
⇒ xy + yz + zx = 1

Question 4.
Solve the following equation for x:
(i) Tan^-1\(\left(\frac{x-1}{x-2}\right)\) + Tan^-1\(\left(\frac{x+1}{x+2}\right)\) = \(\frac{\pi}{4}\)
Answer:

(ii) Tan^-1\(\left(\frac{1}{2 x+1}\right)\) + Tan^-1\(\left(\frac{1}{4 x+1}\right)\) = Tan^-1\(\left(\frac{2}{x^2}\right)\)
Answer:

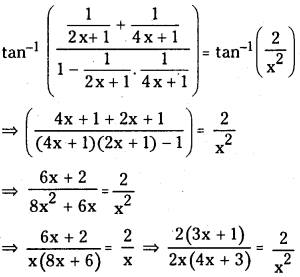
⇒ x²(3x + 1) = 2x(4x + 3)
⇒ x = 0 or 6x² – 14x – 12 = 0
⇒ x = 0 or 3x² – 7x – 6 = 0
⇒ x = 0 or (3x² – 9x + 2x – 6) = 0
⇒ x = 0 or 3x(x – 3) + 2(x – 3) = 0
⇒ x = 0 or (x – 3) (3x – 2) = 0
⇒ x = 0 (or) x = 3 or x = – \(\frac{2}{3}\)

(iii) 3 sin^-1\(\left(\frac{2 x}{1+x^2}\right)\) – 4 cos \(\left(\frac{1-x^2}{1+x^2}\right)\) + 2 Tan^-1\(\left(\frac{2 x}{1-x^2}\right)\) = \(\frac{\pi}{3}\)
Answer:
Let x = tanθ then

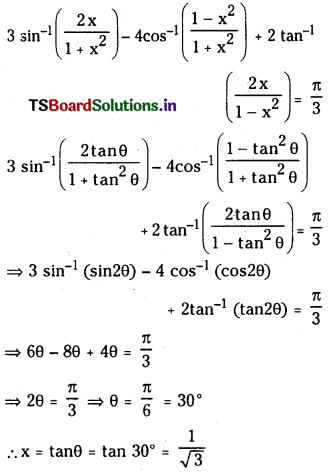
(iv) sin^-1 (1 – x) – 2 sin^-1 x = \(\frac{\pi}{2}\)
Answer:
Let sin^-1 (1 – x) = α and sin^-1 x = β then sin α = 1 – x and sin β = x

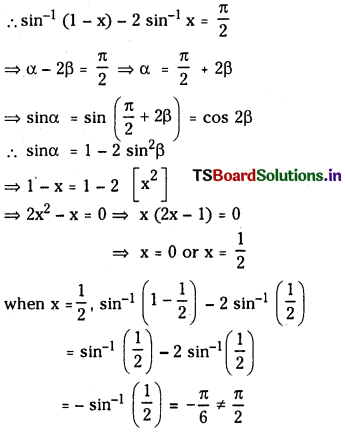
Hence x = 0 is the only solution for the given equation.

Question 5.
Solve the following equations.
(i) Cot^-1 \(\left(\frac{1+x}{1-x}\right)\) = \(\frac{1}{2}\) Cot^-1\(\left(\frac{1}{x}\right)\), x > 0 and x ≠ 1.
Answer:

(ii) Tan[Cos^-1\(\left(\frac{1}{\mathbf{x}}\right)\)] = Sin[Cot^-1\(\left(\frac{1}{2}\right)\)]; x ≠ 0.
Answer:

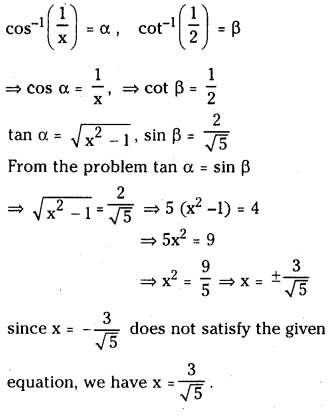
(iii) Cos^-1 x + Sin^-1\(\left(\frac{x}{2}\right)\) = \(\frac{\pi}{6}\)
Answer:

⇒ x⁴ – 5x² + 4 = x⁴ – 2x² + 1
⇒ 3x² – 3 = 0 ⇒ 3x² = 3 ⇒ x = ± 1
When x = – 1 then cos^-1 (- 1) + sin^-1\(\left(-\frac{1}{2}\right)\)
= π – \(\frac{\pi}{6}\) = \(\frac{5 \pi}{6}\) ≠ \(\frac{\pi}{6}\)
∴ x = – 1 is not admissible. Hence x = 1

(iv) Cos^-1 (√3x) + Cos^-1x = \(\frac{\pi}{2}\)
Answer:
Let cos^-1 (√3x) = α ⇒ cos α = √3x
and cos^-1x = β ⇒ cos β = x
cos (α + β) = \(\frac{\pi}{2}\)
⇒ √3x . x = \(\sqrt{1-3 x^2} \sqrt{1-x^2}\) = 0
⇒ √3x² = \(\sqrt{1-3 x^2} \sqrt{1-x^2}\)
⇒ 3x⁴ = (1 – 3x²) (1 – x²)
= 3x⁴ – 4x² + 1
⇒ 4x² = 1 ⇒ x = ±\(\frac{1}{2}\) ⇒ x = – \(\frac{1}{2}\) is not admissible.
∴ x = \(\frac{1}{2}\)

(v) sin[Sin^-1\(\left(\frac{1}{5}\right)\) + Cos^-1x] = 1
Answer: